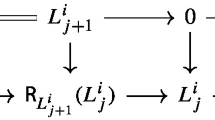A refined derived Torelli theorem for Enriques surfaces

Abstract

We prove that two general Enriques surfaces defined over an algebraically closed field of characteristic different from 2 are isomorphic if their Kuznetsov components are equivalent. We apply the same techniques to give a new simple proof of a conjecture by Ingalls and Kuznetsov relating the derived categories of the blow-up of general Artin–Mumford quartic double solids and of the associated Enriques surfaces.

1 Introduction

An Enriques surface is a smooth projective surface X with 2-torsion dualizing sheaf $\omega _X$ and such that $H^1(X,\mathcal O_X)=0$. In this paper, we assume that all varieties are defined over an algebraically closed field $\mathbb K$ of characteristic different from 2. Under this additional assumption, the above definition is equivalent to asking that X is the quotient of a K3 surface by a fixed-point-free involution.

Because of their construction, Enriques surfaces inherit certain properties from their K3 cousins. Of interest to us here is an important Hodge theoretic feature that they share: their period maps are injective. In other words, in characteristic zero, Hodge-theoretic Torelli theorems hold for both Enriques and K3 surfaces. More precisely, the formulation of the Torelli theorem for Enriques surfaces involves the weight-2 Hodge structure on the second integral cohomology group of the K3 surfaces which are their double covers.

On the other hand, the bounded derived category of coherent sheaves $\mathrm {D}^{\mathrm {b}}(X)$ has very different behaviour depending on whether X is a K3 surface or an Enriques surface. Indeed, in the first case, there might be numerous (albeit finitely many) non-isomorphic K3 surfaces with derived category equivalent to $\mathrm {D}^{\mathrm {b}}(X)$ (see [36, 39] in characteristic zero and [34] in positive characteristic). Moreover, $\mathrm {D}^{\mathrm {b}}(X)$ is indecomposable, i.e. it does not contain proper non-trivial admissible subcategories.

When X is an Enriques surface, however, $\mathrm {D}^{\mathrm {b}}(X)$ uniquely determines X up to isomorphism (see [8] in characteristic zero and [21] for the fields $\mathbb K$ of odd positive characteristic). In analogy to the Hodge theoretic result, we refer to this fact as the Derived Torelli Theorem for Enriques surfaces: two Enriques surfaces $X_1$ and $X_2$, defined over a field $\mathbb K$ as above, are isomorphic if and only if $\mathrm {D}^{\mathrm {b}}(X_1)\cong \mathrm {D}^{\mathrm {b}}(X_2)$. Moreover, we will recall in Sect. 3.1 that for an Enriques surface X there is a collection $\mathcal {L}:=\{ L_1,\dots ,L_{10}\}$ of 10 exceptional bundles. If X is generic, then it was shown in [40] that there is a collection $\mathcal {L}$ satisfying the additional property that there exists an isomorphism of graded vector spaces

In other words, the set $\mathcal L$ is a completely orthogonal exceptional collection. We then define the Kuznetsov component of X to be the admissible subcategory $\mathcal {K}\!u(X,\mathcal {L}):=\langle \mathcal L\rangle ^{\perp }$, giving the (non-trivial) semiorthogonal decomposition

$$\begin{aligned}\mathrm {D}^{\mathrm {b}}(X)=\langle \mathcal {K}\!u(X,\mathcal {L}), \mathcal {L}\rangle .\end{aligned}$$

This decomposition and the properties of $\mathcal {K}\!u(X,\mathcal {L})$ have been extensively studied in [24, 29]. The aim of this paper is to investigate further how much of the geometry of X is encoded by $\mathcal {K}\!u(X,\mathcal {L})$. The following result should be thought of as a refined version of the Derived Torelli Theorem for Enriques surfaces mentioned above.

Theorem A

Let $X_1$ and $X_2$ be Enriques surfaces. Assume that, for $i=1,2$, there exist semiorthogonal decompositions

$$\begin{aligned} \mathrm {D}^{\mathrm {b}}(X_i)=\langle \mathcal {K}\!u(X_i,\mathcal {L}_i),\mathcal {L}_i\rangle \end{aligned}$$

and an exact equivalence $\mathsf {F}:\mathcal {K}\!u(X_1,\mathcal {L}_1)\xrightarrow {\sim }\mathcal {K}\!u(X_2,\mathcal {L}_2)$ of Fourier–Mukai type, where $\mathcal L_i$ is a collection of 10 bundles satisfying ($\star$). Then $X_1\cong X_2$.

The terminology used above will be clarified in Sect. 2 while the proof of this result will be carried out in Sect. 5.2. More precisely, the result is an easy consequence of the more general Theorem 5.1.

The essence of the proof is in showing that the equivalence $\mathsf {F}$ can be extended to an equivalence $\mathrm {D}^{\mathrm {b}}(X_1)\cong \mathrm {D}^{\mathrm {b}}(X_2)$ by means of Propositions 2.4 and 2.5 and by adding step by step the 10 exceptional objects. Then the Derived Torelli Theorem implies our result. The way we obtain the latter global equivalence is by studying and classifying the so-called 3-spherical objects in $\mathcal {K}\!u(X_i,\mathcal {L}_i)$. This is done in Sect. 4. Note that the reason why we have to assume that the characteristic of $\mathbb K$ is not 2 is because the Derived Torelli Theorem for Enriques surfaces is only known to hold under this additional assumption, but the rest of our argument applies even in characteristic 2 for classical Enriques surfaces (see [16]).

It is clear that Theorem A has a trivial converse that, for the sake of completeness, we include in Theorem 5.2.

We develop the techniques we use to prove Theorem A in sufficient generality to give a short proof of a very interesting conjecture by Ingalls and Kuznetsov (see Conjecture 3.8). This will be explained in detail in Sect. 3.2, so we content ourselves here with a short summary.

Recall that a general Artin–Mumford quartic double solid is a double cover of the three dimensional projective space, ramified over a quartic symmetroid surface with 10 nodes, which is the degeneracy locus of a web of quadrics in $\mathbb {P}^3$. The 10 singular points correspond to quadrics of corank 2 in the family.

Consider the blow-up $Y'$ of a general Artin–Mumford double solid at its 10 singular points. It is a classical observation that $Y'$ has an associated Enriques surface X obtained as a quotient of the (desingularization) of the quartic symmetroid. It turns out that $\mathrm {D}^{\mathrm {b}}(X)$ has a semiorthogonal decomposition $\mathrm {D}^{\mathrm {b}}(X)=\langle \mathcal {K}\!u(X,\mathcal {L}),\mathcal {L}\rangle$ where $\mathcal {L}=\{L_1,\dots ,L_{10}\}$ satisfies ($\star$).

The main result of [24] shows that there is a semiorthogonal decomposition $\mathrm {D}^{\mathrm {b}}(Y')=\langle \mathcal A_{Y'},\mathcal B_{Y'}\rangle$, where $\mathcal B_{Y'}$ consists of 12 exceptional objects. The component $\mathcal A_{Y'}$ has a completely orthogonal exceptional collection $\mathcal {G}=\{G_1,\dots ,G_{10}\}$, and defining $\mathcal {K}\!u(Y',\mathcal G):=\langle \mathcal G\rangle ^\perp$ gives the semiorthogonal decomposition

$$\begin{aligned} \mathcal A_{Y'}=\langle \mathcal {K}\!u(Y',\mathcal {G}),\mathcal {G}\rangle . \end{aligned}$$

Most importantly, there is an exact equivalence $\mathcal {K}\!u(Y',\mathcal {G})\cong \mathcal {K}\!u(X,\mathcal L)$ of Fourier–Mukai type (see Theorem 3.7).

The following is our second main result.

Theorem B

Let $Y'$ be the blow-up of a general Artin–Mumford double solid at its 10 singular points. Let X be its associated Enriques surface. Then there is an exact equivalence

$$\begin{aligned}\mathrm {D}^{\mathrm {b}}(X)\cong \mathcal A_{Y'}\end{aligned}$$

which is of Fourier–Mukai type.

This statement, which is precisely the content of Conjecture 3.8 of Ingalls and Kuznetsov [24], was previously proved by Hosono and Takagi [22] using an intricate argument depending on Homological Projective Duality. Our more precise Theorem 5.4 in Sect. 5.2 implies Theorem B and, given its elementary proof, it provides a simpler proof of this conjecture.

This paper originates from the circle of ideas that stems out of [5]. Indeed, if $Y_1$ and $Y_2$ are cubic threefolds (i.e. smooth degree 3 hypersurfaces in the complex projective space $\mathbb {P}^4$) and $H_i$ is the class of a hyperplane section in Pic$(Y_i)$, then we have semiorthogonal decompositions

$$\begin{aligned} \mathrm {D}^{\mathrm {b}}(Y_i)=\langle \mathcal {K}\!u(Y_i),\mathcal O_{Y_i},\mathcal O_{Y_i}(H_i)\rangle . \end{aligned}$$

The main result in [5] shows that $Y_1\cong Y_2$ if and only if there is an exact equivalence $\mathcal {K}\!u(Y_1)\cong \mathcal {K}\!u(Y_2)$. To make the analogy with the paper [5] tighter, we should also mention cubic threefolds and Artin–Mumfold double solids are both Fano threefolds of index 2 and their derived categories admit very similar semiorthogonal decompositions (see Corollary 3.5 in [24]), even though Artin–Mumfold double solids are singular.

If we increase the dimension of the hypersurfaces by one and we consider two cubic fourfolds $W_1$ and $W_2$, then we get semiorthogonal decompositions similar to the one above but with additional exceptional objects $\mathcal O_{W_i}(2H_i)$. In this case, the admissible subcategories $\mathcal {K}\!u(W_i)$ behave like the derived category of a K3 surface. Thus, in view of the discussion above, we cannot expect that $W_1\cong W_2$ if and only if there is an exact equivalence $\mathcal {K}\!u(W_1)\cong \mathcal {K}\!u(W_2)$. And in fact, Huybrechts and Rennemo proved in [23] that such a statement needs an adjustment: the equivalence $\mathcal {K}\!u(W_1)\cong \mathcal {K}\!u(W_2)$ has to satisfy some additional and natural compatibility. Contrary to the approach we use in the present paper, the proofs of categorical Torelli for cubic threefolds in [5], and for cubic fourfolds in [4, Appendix] and [33], all make use of Bridgeland stability conditions.

In conclusion, it is worth pointing out that arbitrary semiorthogonal decompositions are in general non-canonical. However, Theorem A is further evidence of the fact that, when these decompositions originate from geometry, they usually encode important pieces of information.

2 Semiorthogonal decompositions and an extension result

In this section, we briefly recall some basic facts about semiorthogonal decompositions. We also prove an extension result for Fourier–Mukai functors of independent interest and which will be important in this paper.

2.1 Generalities

In complete generality, let $\mathcal {T}$ be a triangulated category. A semiorthogonal decomposition

$$\begin{aligned} \mathcal {T}= \langle \mathcal {D}_1, \dots , \mathcal {D}_m \rangle \end{aligned}$$

is a sequence of full triangulated subcategories $\mathcal {D}_1, \dots , \mathcal {D}_m$ of $\mathcal {T}$ such that:

• (a) $\mathop {\mathrm {Hom}}\nolimits (F, G) = 0$, for all $F \in \mathcal {D}_i$, $G \in \mathcal {D}_j$ and $i>j$;

• (b) For any $F \in \mathcal {T}$, there is a sequence of morphisms

  $$\begin{aligned} 0 = F_m \rightarrow F_{m-1} \rightarrow \cdots \rightarrow F_1 \rightarrow F_0 = F, \end{aligned}$$

  such that $\pi _i(F):=\mathrm {Cone}(F_i \rightarrow F_{i-1}) \in \mathcal {D}_i$ for $1 \le i \le m$.

The subcategories $\mathcal {D}_i$ are called the components of the decomposition.

The condition (a) implies that the factors $\pi _i(F)$ in (b) are uniquely determined and functorial. Hence, for all $i=1,\ldots ,m$, one can define the i-th projection functor $\pi _i:\mathcal {T}\rightarrow \mathcal {D}_i$ for all $F\in \mathcal {T}$.

Denote by $\alpha _i:\mathcal {D}_i\hookrightarrow \mathcal {T}$ the inclusion. We say that $\mathcal {D}_i$ is admissible if $\alpha _i$ has left adjoint $\alpha _{i}^*$ and right adjoint $\alpha _{i}^!$.

Let $\mathcal {T}_1=\langle \mathcal {D}_1^1,\mathcal {D}_2^1\rangle$ and $\mathcal {T}_2=\langle \mathcal {D}_1^2,\mathcal {D}_2^2\rangle$ be two triangulated categories with semiorthogonal decompositions by admissible subcategories $\alpha _{ij}:\mathcal {D}_i^j\hookrightarrow \mathcal {T}_j$. Following [31, Section 2.2], we can define the gluing functor¹

$$\begin{aligned} \Psi _j:=\alpha _{1j}^!\circ \alpha _{2j}:\mathcal {D}^j_2\rightarrow \mathcal {D}_1^j. \end{aligned}$$

Moreover, if $B\in \mathcal {D}_2^1$, then we denote by $\eta _B:\alpha _{11}\Psi _1(B)\rightarrow \alpha _{21}(B)$ the counit of adjunction.

The following result will be useful later.

Lemma 2.1

For $i=1,2$, let $\mathcal {T}_i=\langle \mathcal {D}_1^i,\mathcal {D}_2^i\rangle$ be a triangulated category with a semiorthogonal decomposition by admissible subcategories. Let $\mathsf {F}:\mathcal {T}_1\rightarrow \mathcal {T}_2$ be an exact functor with left and right adjoints and such that

• (a) $\mathsf {F}(\mathcal {D}^1_j)\subseteq \mathcal {D}^2_j$ and the induced functors $\mathsf {F}_j:=\mathsf {F}|_{\mathcal {D}_j^1}:\mathcal {D}_j^1\rightarrow \mathcal {D}_j^2$ are equivalences for $j=1,2$.

• (b) The morphism $\mathsf {F}(\eta _B)$ induces an isomorphism

  

  for all $A\in \mathcal {D}_1^1$ and all $B\in \mathcal {D}_2^1$.

Then $\mathsf {F}$ is an equivalence.

To help the reader to keep track of the numerous indices in our notation for categories and functors, we include here a diagram which summarizes them:

Proof

The objects of $\alpha _{11}(\mathcal {D}_1^1)$ and $\alpha _{21}(\mathcal {D}_2^1)$ form a spanning class $\Omega$ for $\mathcal {T}_1$ in the sense of [7]. Hence, by [7, Theorem 2.3], to prove that $\mathsf {F}$ is fully faithful it is enough to show that, for any $A, B \in \Omega$, the natural morphism

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (A,B)\rightarrow \mathop {\mathrm {Hom}}\nolimits (\mathsf {F}(A),\mathsf {F}(B)) \end{aligned}$$

induced by $\mathsf {F}$ is bijective.

Since $\mathsf {F}_j$ is an equivalence by (a) and the categories $\mathcal {D}_1^1$, $\mathcal {D}_2^1$ are semiorthogonal in $\mathcal {T}_1$ while $\mathcal {D}_1^2$, $\mathcal {D}_2^2$ are semiorthogonal in $\mathcal {T}_2$, it follows from the definition of a semiorthogonal decomposition that we need only verify that the morphism

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\alpha _{11}(A),\alpha _{21}(B))\rightarrow \mathop {\mathrm {Hom}}\nolimits (\alpha _{12}\mathsf {F}_1(A),\alpha _{22}\mathsf {F}_2(B)) \end{aligned}$$

induced by $\mathsf {F}$ is bijective, for all $A\in \mathcal {D}_1^1$ and $B\in \mathcal {D}_2^1$. To this extent, consider the commutative diagram

where the top and bottom rows are obtained by applying $\mathsf {F}$.

Note that the vertical arrows are isomorphisms by adjunction and (b). Since $\mathsf {F}_1$ is an equivalence by (a), the top row is an isomorphism. Thus the bottom one is an isomorphism as well.

The essential surjectivity can be deduced now, as the image of a fully faithful functor is triangulated, and the category $\mathcal {T}_2$ is generated by $\mathcal {D}^2_1$ and $\mathcal {D}^2_2$. $\square$

In the general situation where we have a semiorthogonal decomposition

$$\begin{aligned} \mathcal {T}=\langle \mathcal {D}_1,\mathcal {D}_2\rangle , \end{aligned}$$

then $\pi _1$ and $\pi _2$ coincide with the left adjoint $\alpha _1^*$ and and the right adjoint $\alpha _2^!$ of the embeddings $\alpha _i:\mathcal {D}_i\hookrightarrow \mathcal {T}$. The left mutation functor through $\mathcal {D}_i$ is denoted $\mathsf L_{\mathcal {D}_i}$ and is defined by the canonical functorial distinguished triangle

$$\begin{aligned} \alpha _i\alpha _i^!\xrightarrow {\eta _i}\mathsf {id}\rightarrow \mathsf L_{\mathcal {D}_i}, \end{aligned}$$

(2.1)

where $\eta _i$ denotes the counit of the adjunction.

From now on, let us assume that all categories are linear over a field $\mathbb K$. An object $E\in \mathcal {T}$ is exceptional if $\mathop {\mathrm {Hom}}\nolimits (E,E[p])=0$, for all integers $p\ne 0$, and $\mathop {\mathrm {Hom}}\nolimits (E,E)\cong \mathbb K$. A set of objects $\{E_1,\ldots ,E_m\}$ in $\mathcal {T}$ is an exceptional collection if $E_i$ is an exceptional object, for all i, and $\mathop {\mathrm {Hom}}\nolimits (E_i,E_j[p])=0$, for all p and all $i>j$. An exceptional collection $\{E_1,\ldots ,E_m\}$ is orthogonal if $\mathop {\mathrm {Hom}}\nolimits (E_i,E_j[p])=0$, for all $i,j=1,\ldots ,m$ with $i\ne j$ and for all integers p.

If $\mathcal T$ admits a semiorthogonal decomposition $\mathcal T=\langle \mathcal D_1,\mathcal D_2\rangle$ with $\mathcal D_2=\langle E_1,\dots ,E_m\rangle$, where $\{E_1,\dots ,E_m\}$ is an orthogonal exceptional collection, then the left mutation through $\mathcal D_2$ takes a particularly convenient form:

$$\begin{aligned} \mathsf {L}_{\mathcal D_2}(F)={{\,\mathrm{Cone}\,}}\left( \mathop {\mathrm {ev}}\nolimits :\bigoplus _{1\le i\le m,p}\mathop {\mathrm {Hom}}\nolimits (E_i,F[p])\otimes E_i[-p]\rightarrow F\right) . \end{aligned}$$

(2.2)

2.2 Extending Fourier–Mukai functors

Now let X and Y be smooth projective varieties over $\mathbb K$ with admissible embeddings

$$\begin{aligned}\alpha :\mathcal A\hookrightarrow \mathrm {D}^{\mathrm {b}}(X)\quad \text {and}\quad \beta :\mathcal B\hookrightarrow \mathrm {D}^{\mathrm {b}}(Y).\end{aligned}$$

Thus $\mathcal A$ (resp. $\mathcal B$) is endowed with a Serre functor $\mathsf {S}_{\mathcal A}$ (resp. $\mathsf {S}_\mathcal B$) by [24, Lemma 2.8]. Recall that an exact functor $\mathsf {F}:\mathcal A\rightarrow \mathcal B$ is of Fourier–Mukai type if there exists $\mathcal {E}\in \mathrm {D}^{\mathrm {b}}(X\times Y)$ such that the composition $\beta \circ \mathsf {F}$ is isomorphic to the restriction

$$\begin{aligned} \Phi _\mathcal E|_{\mathcal A}:\mathcal A\rightarrow \mathrm {D}^{\mathrm {b}}(Y). \end{aligned}$$

Here the exact functor $\Phi _{\mathcal E}$ is given by

$$\begin{aligned} \Phi _\mathcal {E}(-):=p_{2*}(\mathcal {E}\otimes p_1^*(-)), \end{aligned}$$

where $p_i$ is the ith natural projection. By construction, a morphism $\mathcal {E}_1\rightarrow \mathcal {E}_2$ in $\mathrm {D}^{\mathrm {b}}(X\times Y)$ induces a morphism

$$\begin{aligned} \Phi _{\mathcal {E}_1}(F)\longrightarrow \Phi _{\mathcal {E}_2}(F), \end{aligned}$$

for all $F\in \mathrm {D}^{\mathrm {b}}(X)$. Moreover, a distinguished triangle

$$\begin{aligned} \mathcal {E}_1\rightarrow \mathcal {E}_2\rightarrow \mathcal {E}_3 \end{aligned}$$

in $\mathrm {D}^{\mathrm {b}}(X\times Y)$ induces a distinguished triangle

$$\begin{aligned} \Phi _{\mathcal {E}_1}(F)\rightarrow \Phi _{\mathcal {E}_2}(F)\rightarrow \Phi _{\mathcal {E}_3}(F), \end{aligned}$$

for all $F\in \mathrm {D}^{\mathrm {b}}(X)$.

Remark 2.2

In the above setup, for a given Fourier–Mukai functor $\Phi _\mathcal {E}:\mathrm {D}^{\mathrm {b}}(X)\rightarrow \mathrm {D}^{\mathrm {b}}(Y)$ suppose that the induced exact functor $\mathsf {F}:=\Phi _\mathcal {E}|_{\mathcal A}:\mathcal A\rightarrow \mathrm {D}^{\mathrm {b}}(Y)$ factors through $\mathcal B$. By [27, Theorem 7.1], the projection functor onto the admissible subcategory $\mathcal A$ is of Fourier–Mukai type. Thus, if we precompose $\Phi _\mathcal {E}$ with the projection onto $\mathcal A$, we get a Fourier–Mukai functor $\Phi _{\mathcal {E}'}:\mathrm {D}^{\mathrm {b}}(X)\rightarrow \mathrm {D}^{\mathrm {b}}(Y)$ such that $\Phi _{\mathcal {E}'}|_{\mathcal A}=\mathsf {F}$ and $\Phi _{\mathcal {E}'}(\!^\perp \!\mathcal A)=0$.

Remark 2.3

It should be noted that, when $\mathsf {F}$ is an equivalence, [30, Conjecture 3.7] would imply that $\mathsf {F}$ is of Fourier–Mukai type. Unfortunately, this conjecture is not known to hold true in the generality needed in this paper. This expectation should be compared with the fact that any full functor $\mathsf {F}:\mathrm {D}^{\mathrm {b}}(X)\rightarrow \mathrm {D}^{\mathrm {b}}(Y)$ is of Fourier–Mukai type (see [11, 37]). As for this, it should be noted that in the seminal paper [37] such a result was proved under the assumption that $\mathsf {F}$ is fully faithful but in [9, 11] the assumptions were weakened. In particular, assuming full is enough.

We can now explain how to extend a Fourier–Mukai functor to an exceptional object.

Proposition 2.4

Let $\alpha :\mathcal {A}\hookrightarrow \mathrm {D}^{\mathrm {b}}(X)$ be an admissible embedding and let $E\in \!^\perp \!\mathcal {A}$ with counit of adjunction $\eta :\alpha \alpha ^!(E)\rightarrow E$ . Let $\Phi _{\mathcal {E}}:\mathrm {D}^{\mathrm {b}}(X)\rightarrow \mathrm {D}^{\mathrm {b}}(Y)$ be a Fourier–Mukai functor with the property that $\Phi _\mathcal {E}(^\perp \!\mathcal {A})\cong 0$. For any object F in $\mathrm {D}^{\mathrm {b}}(Y)$ and any morphism $\varphi :\Phi _\mathcal {E}(\alpha \alpha ^!(E))\rightarrow F$, there is an object $\mathcal {E}_\varphi \in \mathrm {D}^{\mathrm {b}}(X\times Y)$ and a morphism $\psi _F:\mathcal {E}_\varphi \rightarrow \mathcal {E}$ such that

• (1) the induced morphism $\Phi _{\mathcal {E}_\varphi }|_{\mathcal {A}}\xrightarrow {\psi _F}\Phi _\mathcal {E}|_{\mathcal {A}}$ is an isomorphism;

• (2) $\Phi _{\mathcal {E}_\varphi }|_{^\perp \!\langle \mathcal {A},E\rangle }=0$; and

• (3) there is an isomorphism $\Phi _{\mathcal {E}_\varphi }(E)\cong F$ such that the diagram

  

  (2.3)

  is commutative.

Proof

Consider the triangle (2.1) applied to the object E:

$$\begin{aligned} \alpha \alpha ^!(E)\xrightarrow {\eta } E\rightarrow \mathsf L_{\mathcal A}(E). \end{aligned}$$

(2.4)

Set $E':=\mathsf S_{X}\left( (\mathsf L_{\mathcal A}(E))^\vee \right)$. If we take the derived dual of (2.4) and we apply $\mathsf {S}_{X}$ we get the triangle

$$\begin{aligned} \mathsf S_{X}(E^\vee )\rightarrow \mathsf S_{X}\left( (\alpha \alpha ^!(E))^\vee \right) {\mathop {\longrightarrow }\limits ^{\gamma }} E'[1]. \end{aligned}$$

(2.5)

Next, we observe that, for any $K\in \mathrm {D}^{\mathrm {b}}(X\times Y)$, $M\in \mathrm {D}^{\mathrm {b}}(X)$ and $N\in \mathrm {D}^{\mathrm {b}}(Y)$, we get isomorphisms

$$\begin{aligned} \begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\Phi _K(M),N)&=\mathop {\mathrm {Hom}}\nolimits (p_{2*}(K\otimes p_1^*M),N)\\ {}&\cong \mathop {\mathrm {Hom}}\nolimits (K\otimes p_1^*M,p_2^!N)\\ {}&\cong \mathop {\mathrm {Hom}}\nolimits (K,\mathsf S_{X}(M^\vee )\boxtimes N) \end{aligned} \end{aligned}$$

(2.6)

which are functorial in K, M,  and N. Thus, we get a natural morphism

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\Phi _\mathcal {E}(\alpha \alpha ^! (E)),F)\cong \mathop {\mathrm {Hom}}\nolimits \left( \mathcal {E},\mathsf S_{X}\left( (\alpha \alpha ^!(E))^\vee \right) \boxtimes F\right) {\mathop {\longrightarrow }\limits ^{\gamma \boxtimes \mathop {\mathrm {id}}\nolimits _F}}\mathop {\mathrm {Hom}}\nolimits (\mathcal {E},E'\boxtimes F[1]), \end{aligned}$$

(2.7)

where the latter map is induced by the postcomposition by $\gamma \boxtimes \mathop {\mathrm {id}}\nolimits _F$ for $\gamma$ as in (2.5).

Such a morphism of vector spaces takes $\varphi$ as in the assumptions of the proposition to a morphism $\varphi ':\mathcal {E}\rightarrow E'\boxtimes F[1]$. We set $\psi _F:\mathcal {E}_\varphi \rightarrow \mathcal E$ to be the cocone of $\varphi '$ as in the distinguished triangle

$$\begin{aligned} \mathcal {E}_\varphi \xrightarrow {\psi _F}\mathcal {E}\xrightarrow {\varphi '}E'\boxtimes F[1]. \end{aligned}$$

(2.8)

Clearly, $\psi _F$ induces a natural transformation $\Phi _{\mathcal {E}_\varphi }\rightarrow \Phi _\mathcal {E}$ which we denote with the same symbol.

Note that ${}^\perp \langle \mathcal {A},E\rangle \subseteq {}^\perp \mathcal {A}$. Then, an easy computation using (2.6) shows that $\mathsf {L}_\mathcal {A}(E)\in \mathcal {A}^\perp$ and hence $\Phi _{E'\boxtimes F}(\mathcal {A})=0$ and, similarly, that $\mathsf {L}_\mathcal {A}(E)\in \langle \mathcal {A},E\rangle =({}^\perp \langle \mathcal {A},E\rangle )^\perp$ and hence $\Phi _{E'\boxtimes F}({}^\perp \langle \mathcal {A},E\rangle )=0$. Therefore

$$\begin{aligned} \Phi _{E'\boxtimes F}(\mathcal A)\cong \Phi _{E'\boxtimes F}(\!^\perp \!\langle \mathcal A,E\rangle )\cong 0\quad \Phi _{E'\boxtimes F}(E)\cong F. \end{aligned}$$

(2.9)

Since, by assumption, $\Phi _\mathcal {E}(^\perp \!\mathcal A)\cong 0$, the first two isomorphisms imply (1) and (2) in the statement.

To complete the proof of (3) and deduce the commutative diagram (2.3), we apply the Fourier–Mukai functors whose kernels are the objects in (2.8) to the triangle in (2.4). We obtain the commutative diagram

(2.10)

with rows and columns which are distinguished triangles. The zero in the bottom row of the diagrams comes from the fact that $\Phi _{E'\boxtimes F}(\alpha \alpha ^!(E))\cong 0$ by (2.9). The zero on the third column depends on the fact that $E\in {}^\perp \mathcal {A}$ and, by assumption, $\Phi _\mathcal {E}({}^\perp \mathcal {A})\cong 0$. In conclusion, the morphisms $\epsilon$ and $\psi _F(\alpha \alpha ^!(E))$ are both isomorphisms.

Now we can recast its top row and left column in the following commutative diagram

(2.11)

where we write $\varphi '$ as a shorthand for the natural transformation $\varphi '(\mathsf L_{\mathcal A} (E)[-1])$ coming from (2.11). Observe that the middle vertical map is an isomorphism by (2.11), since $\alpha \alpha ^!(E)\in \mathcal A$. Therefore, there is an isomorphism

$$\begin{aligned} \Phi _{\mathcal {E}_\varphi }(E)\rightarrow \Phi _{E'\boxtimes F[1]}(\mathsf L_{\mathcal A}(E)[-1])\cong F \end{aligned}$$

(2.12)

making all squares in (2.11) commutative. The right square is precisely (2.3) as the bottom morphism identifies with $\varphi$ under the maps (2.7) and the isomorphism $\Phi _{E'\boxtimes F[1]}(\mathsf L_{\mathcal A}(E)[-1])\cong \Phi _{E'\boxtimes F[1]}(E[-1])\cong F$. $\square$

Now we consider the case when $\Phi _{\mathcal E}|_{\mathcal A}$ is an equivalence onto its image.

Proposition 2.5

Let $\alpha :\mathcal {A}\hookrightarrow \mathrm {D}^{\mathrm {b}}(X)$ be an admissible embedding and let $E\in \!^\perp \!\mathcal {A}$ with counit of adjunction $\eta :\alpha \alpha ^!(E)\rightarrow E$ . Let $\Phi _{\mathcal {E}}:\mathrm {D}^{\mathrm {b}}(X)\rightarrow \mathrm {D}^{\mathrm {b}}(Y)$ be a Fourier–Mukai functor with the property that $\Phi _\mathcal {E}(^\perp \!\mathcal {A})\cong 0$. Suppose further that

• (a) $\Phi _{\mathcal E}|_\mathcal A$ is an equivalence onto an admissible subcategory $\mathcal B$ with embedding $\beta :\mathcal B\hookrightarrow \mathrm {D}^{\mathrm {b}}(Y)$, and

• (b) there is an exceptional object $F\in \!^\perp \!\mathcal B$ and an isomorphism $\rho :\Phi _\mathcal {E}(\alpha \alpha ^!(E))\xrightarrow {\sim }\beta \beta ^!(F)$.

Then the Fourier–Mukai functor $\Phi _{\mathcal {E}_\varphi }$ restricts to an equivalence between $\langle \mathcal {A},E\rangle$ and $\langle \mathcal B,F\rangle$, where $\mathcal E_{\varphi }$ is the object given by Proposition 2.4 for $\varphi :=\eta '\circ \rho$ and $\eta ':\beta \beta ^!(F)\rightarrow F$ is the counit of adjunction.

Proof

We apply Lemma 2.1. The assumption (a) of the lemma obviously holds. It is enough to check that for any object A in $\mathcal A$,

(2.13)

is an isomorphism. For this we consider the commutative diagram (2.3) in Proposition 2.4 (3), which takes the form

where the vertical arrows are isomorphisms for the same arguments as in the proof of Proposition 2.4 (see, in particular, the middle column in (2.10) for the isomorphism on the left and (2.12) for the one on the right).

Now the cone C of the morphism at the top is isomorphic to the cone of $\varphi$, which in turn is isomorphic to $\mathsf L_{\mathcal B}(F)\in \mathcal B^\perp$. It follows that $C\in \mathcal B^\perp$, so C is right orthogonal to $\Phi _{\mathcal {E}_\varphi }(A)\in \mathcal B$ for any $A\in \mathcal A$. Therefore, if we apply $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\Phi _{\mathcal {E}_\varphi }(A),-)$ to the distinguished triangle

we get the isomorphism (2.13). $\square$

2.3 A side remark: a dg category approach

Even though our approach in this paper is purely triangulated, this section ends with a short discussion concerning an alternative viewpoint via dg categories (the non-expert reader can have a look at [10] for a quick introduction to this subject). More precisely, this section should be considered as an indication of how an expert in dg categories might read the results in Sect. 2.2. On the other hand, the reader who is not interested in this higher categorical viewpoint can move to Sect. 3.

Let us first rediscuss semiorthogonal decompositions in terms of dg categories. Assume that $\mathcal {T}=\langle \mathcal {D}_1,\mathcal {D}_2 \rangle$ is a small $\mathbb K$-linear algebraic triangulated category, i.e. there is a small $\mathbb K$-linear pre-triangulated dg category $\mathcal {B}$ and an exact equivalence $\mathcal {T}\cong H^0(\mathcal {B})$, where $H^0(\mathcal {B})$ denotes the homotopy category of $\mathcal {B}$. Suppose that $\alpha _i:\mathcal {D}_i\hookrightarrow \mathcal {T}$ is the embedding of an admissible subcategory, for $i=1,2$. Then there exist two pre-triangulated dg subcategories $\mathsf {G}_i:\mathcal {B}_i\hookrightarrow \mathcal {B}$ such that $H^0(\mathcal {B}_i)\cong \mathcal {D}_i$ and $H^0(\mathsf {G}_i)\cong \alpha _i$. As it is explained for example in [31, Section 4], there exist a dg bimodule $\varphi$ (i.e. a $\mathcal {B}_1^\circ \otimes \mathcal {B}_2$-dg module), a pre-triangulated dg category $\mathcal {B}_1\times _\varphi \mathcal {B}_2$, whose definition depends on $\mathcal {B}_1$, $\mathcal {B}_2$ and $\varphi$, and an isomorphism $\mathcal {B}\cong \mathcal {B}_1\times _\varphi \mathcal {B}_2$ in $\mathrm {Ho}(\mathbf {dgCat})$. Here $\mathrm {Ho}(\mathbf {dgCat})$ denotes the homotopy category of the category $\mathbf {dgCat}$ of (small) dg categories which are linear over the field $\mathbb K$. We will refer to $\mathcal {B}_1\times _\varphi \mathcal {B}_2$ as the gluing of $\mathcal {B}_1$ and $\mathcal {B}_2$ along $\varphi$. By [31, Corollary 4.5], the dg bimodule $\varphi$ yields, at the triangulated level, the gluing functor in Sect. 2.1.

Assume that $\mathcal {C}_1$ and $\mathcal {C}_2$ are two pre-triangulated dg categories which are obtained by this gluing procedure. In explicit form, $\mathcal {C}_i=\mathcal {C}^i_1\times _{\varphi _i}\mathcal {C}^i_2$.

Example 2.6

For our applications and in accordance with the discussion and notations in the previous section, we should think of the case $\langle \mathcal {A},E\rangle \cong H^0(\mathcal {C}_1)$ and $\langle \mathcal {B},F\rangle \cong H^0(\mathcal {C}_2)$. The dg subcategories $\mathcal {C}_j^i$ are taken so that $\mathcal {A}\cong H^0(\mathcal {C}^1_1)$ $\mathcal {B}\cong H^0(\mathcal {C}^2_1)$, $\langle E\rangle \cong H^0(\mathcal {C}^1_2)$ and $\langle F\rangle \cong H^0(\mathcal {C}^2_2)$.

Let $\mathsf {J}_1:\mathcal {C}^1_1\rightarrow \mathcal {C}^2_1$ and $\mathsf {J}_2:\mathcal {C}^1_2\rightarrow \mathcal {C}^2_2$ be two isomorphisms in $\mathrm {Ho}(\mathbf {dgCat})$. We would like to conclude that $\mathsf {J}_1$ and $\mathsf {J}_2$ glue to an isomorphism $\mathsf {J}:\mathcal {C}_1\rightarrow \mathcal {C}_2$ in $\mathrm {Ho}(\mathbf {dgCat})$, under some reasonable assumptions. To this extent, consider the $(\mathcal {C}_1^1)^\circ \otimes \mathcal {C}_2^1$-module $\varphi '_1$ obtained from $\varphi _2$ by composing with $\mathsf {J}_1$ and $\mathsf {J}_2$.

The following is a well-known result, which should be thought of as the dg analogue of Propositions 2.4 and 2.5.

Proposition 2.7

Under the assumptions above, suppose that there is a quasi-isomorphism between $\varphi _1$ and $\varphi '_1$. Then there is an isomorphism $\mathsf {J}:\mathcal {C}_1\rightarrow \mathcal {C}_2$ in $\mathrm {Ho}(\mathbf {dgCat})$ whose restriction to $\mathcal {C}^1_j$ is $\mathsf {J}_j$, for $j=1,2$.

Proof

The argument is an easy adaptation of the proof of Propositions 4.11 and 4.14 in [31]. $\square$

Roughly, the existence of a quasi-isomorphism between $\varphi _1$ and $\varphi '_1$ means that $\varphi _1$ and $\varphi _2$ are compatible under the action of $\mathsf {J}_1$ and $\mathsf {J}_2$. In general, it is clear that this assumption is not easy to verify. On the other hand, if we look at the triangulated counterpart of this hypothesis in the simplified situation in Example 2.6, it corresponds to the assumptions on $\Phi _\mathcal E$ in Proposition 2.5. Hence, the reader should interpret the results in the previous section as a way to give a conceptually simple triangulated version of Proposition 2.7. In this case, the conditions under which one glue exact equivalences will be easy to check, see Sect. 5.1 for an application of this technique.

It should be noted that the dg approach to semiorthogonal decompositions discussed in this section was put in an even more general categorical setting in [38] (see, in particular, [38, Section 9.3]).

3 The geometric setting

In this section, we discuss the structure of the derived categories of Enriques surfaces and of Artin–Mumford quartic double solids. The emphasis is on the analogies which are at the core of this paper.

3.1 The case of Enriques surfaces

We work over an algebraically closed field $\mathbb K$ of characteristic different from 2. We refer to [17] for a quick but exhaustive introduction to the geometry of Enriques surfaces. For the moment, we recall several useful facts.

First note that the Serre functor $\mathsf S_X(-):=(-)\otimes \omega _X[2]$ satisfies the property $\mathsf S_X^2=[4]$, but $\mathsf {S}_X\ne [2]$ because the dualizing sheaf $\omega _X:=\mathcal O_X(K_X)$ is non-trivial but 2-torsion. Note that $\mathrm {NS}(X)_{\mathrm {tor}}\cong \mathbb {Z}/2\mathbb {Z}$ and it is generated by the class of $K_X$. We set $\mathop {\mathrm {Num}}\nolimits (X):=\mathrm {NS}(X)/\mathrm {NS}(X)_{\mathrm {tor}}$. If F is a line bundle on X and f is its class in $\mathop {\mathrm {Num}}\nolimits (X)$, then Riemann–Roch takes the simple form

$$\begin{aligned} \chi (F)=\frac{1}{2}f^2+1 \end{aligned}$$

(3.1)

for an Enriques surface.

Secondly, recall that an Enriques surface X is called unnodal if it contains no smooth rational curves. It is called nodal otherwise. Denote by $\mathbf {M}$ the 10-dimensional moduli space of Enriques surfaces. Nodal Enriques surfaces form an irreducible divisor in $\mathbf {M}$ (see, for example, [17, Section 5]).

Now let us make precise a result that was mentioned in the introduction. Indeed, as an application of the stronger statements [8, Proposition 6.1] and [21, Theorem 1.1], we get the following result.

Theorem 3.1

(Bridgeland–Maciocia, Honigs–Lieblich–Tirabassi) Let X and Y be smooth projective surfaces defined over an algebraically closed field $\mathbb K$ of characteristic different from 2. If X is an Enriques surface and there is an exact equivalence $\mathrm {D}^{\mathrm {b}}(X)\cong \mathrm {D}^{\mathrm {b}}(Y)$, then $X\cong Y$.

To the best of our knowledge, a similar statement is not known when $\mathbb K$ has characteristic 2, due to the additional complexity of the double cover structure. We should also observe that generalizations of Theorem 3.1 are available in the twisted setting (see [1] when the characteristic is 0 and [21] in positive characteristic).

As we mentioned in the introduction, the category $\mathrm {D}^{\mathrm {b}}(X)$ admits a very nice semiorthogonal decomposition. To describe it, we must begin with the relationship between Fano polarizations and canonical isotropic 10-sequences.

Definition 3.2

Let X be an Enriques surface.

• (a) A Fano polarization on X is a nef divisor $\Delta$ such that

  • (i) $\Delta ^2=10$;

  • (ii) $\Delta .F\ge 3$ for every nef divisor F with $F^2=0$.

• (b) An isotropic 10-sequence in $\mathop {\mathrm {Num}}\nolimits (X)$ is a set of 10 vectors $\mathcal {F}=\{f_1,\dots , f_{10}\}\subset \mathop {\mathrm {Num}}\nolimits (X)$ such that $f_i.f_j=1-\delta _{ij}$, where $\delta _{ij}$ is Kronecker delta.

If $\Delta$ is a Fano polarization, then by [18, Theorem 2.6] it determines an isotropic 10-sequence $\{f_1,\dots , f_{10}\}$ which is unique up to permutation and such that the numerical class $\delta$ of $\Delta$ satisfies

$$\begin{aligned} \delta =\frac{1}{3}(f_1+\dots +f_{10}). \end{aligned}$$

(3.2)

Even though this is not going to be used later, let us note that the statement above can be made more precise. Indeed, as explained in Sections 2.2 and 2.3 of [18], the isotropic 10-sequence $\{f_1,\dots ,f_{10}\}$ yielding (3.2) is canonical, i.e. it contains all the nef representatives of its orbit under the action of the Weyl group generated by the reflections in the classes of the $(-2)$-curves. Moreover, by [18, Theorem 2.7], the converse is also true: given a canonical isotropic 10-sequence $\{f_1,\dots ,f_{10}\}$, there is a Fano polarization $\Delta$ on X whose numerical class $\delta$ satisfies (3.2).

Remark 3.3

(i) By [19, Proposition 1], every Enriques surface possesses a Fano polarization $\Delta$. On the other hand, by [18, Proposition 2.7], a Fano polarization $\Delta$ is ample if and only if the corresponding isotropic 10-sequence $\{f_1,\dots , f_{10}\}$ is made of nef classes.

(ii) If X is unnodal, an easy application of [14, Theorem 3.2] shows that X has an ample Fano polarization $\Delta$. A generic nodal Enriques surface has the same property by [15, Theorem 3.2.2] and [18, Corollary 4.4]. Thus Enriques surfaces with an ample Fano polarization form an open subset in $\mathbf {M}$ whose complement has codimension at least 2.

Example 3.4

Let X be an unnodal Enriques surface defined over $\mathbb {C}$ with an ample Fano polarization $\Delta$. Let $\{f_1,\dots ,f_{10}\}$ be the isotropic 10-sequence associated to $\Delta$, and let $F_i^{\pm }\in \mathop {\mathrm {NS}}\nolimits (X)$ be the two preimages of $f_i$ under the quotient map $\mathop {\mathrm {NS}}\nolimits (X)\twoheadrightarrow \mathop {\mathrm {Num}}\nolimits (X)$. Then for $i=1,\dots ,10$, $F_i^+=F_i^-+K_X$ and the linear series

$$\begin{aligned}|2F_i^+|=|2F_i^-|\end{aligned}$$

has precisely two double fibers, supported on $F_i^+$ and $F_i^-$. As observed in [40, Example 2.6], $\{\mathcal O_X(F_i^+)\}_{1\le i\le 10}$ is an orthogonal exceptional collection. Each of the objects $\mathcal O_X(F_i^+)$ can be individually changed to $\mathcal O_X(F_i^-)$ just by tensoring by the canonical bundle and the new collection is still an orthogonal exceptional collection by Serre duality. Thus we have at least $2^{10}=1024$ possible choices of orthogonal exceptional collections of line bundles in $\mathrm {D}^{\mathrm {b}}(X)$. Of course, in every case the numerical class of the sum of all ten divisors remains unchanged, equal to $3\delta$. By [3, Theorem 3.11], there are exactly $2^{13}\cdot 3\cdot 17\cdot 31$ numerical classes of Fano polarizations up to the action of the Weyl group. So each of these give rise to 1024 different orthogonal exceptional collections as above.

We now want to discuss how to use isotropic 10-sequences to construct interesting collections of exceptional objects and generalize the picture in Example 3.4. The following is probably well-known to experts but we state and prove it here for the sake of completeness.

Proposition 3.5

Let X be an Enriques surface over $\mathbb K$ with a Fano polarization $\Delta$. Then $\mathrm {D}^{\mathrm {b}}(X)$ contains an admissible subcategory $\mathcal {L}=\langle \mathcal {L}_1,\dots ,\mathcal {L}_c\rangle$, where $\mathcal {L}_1,\dots ,\mathcal {L}_c$ are completely orthogonal admissible subcategories and

$$\begin{aligned} \mathcal {L}_i=\langle L^i_1,\dots ,L^i_{n_i}\rangle \end{aligned}$$

where

• (1) $L_j^i$ is a line bundle such that $L^i_j=L^i_1\otimes \mathcal O_X(R^i_1+\dots +R^i_{j-1})$ where $R^i_1,\dots ,R^i_{j-1}$ is a chain of $(-2)$-curves of $A_{j-1}$ type;

• (2) $\{L^i_1,\dots ,L^i_{n_i}\}$ is an exceptional collection; and

• (3) $n_1+\dots +n_c=10$.

Moreover, if $\Delta$ is ample, then $c=10$, $n_1=\dots =n_{10}=1$ and $\mathcal {L}$ is generated by an orthogonal exceptional collection $\{L_1,\dots ,L_{10}\}$ consisting of line bundles.

Proof

By Remark 3.3 (i), $\Delta$ determines a unique (up to reordering) isotropic 10-sequence $\mathcal {F}\subset \mathop {\mathrm {Num}}\nolimits (X)$. By [16, Lemma 3.3.1] (see also [18, Section 2] for an extensive discussion), such an isotropic 10-sequence can be written as a disjoint union

$$\begin{aligned} \mathcal {F}=\mathcal {F}_1\sqcup \dots \sqcup \mathcal {F}_c, \end{aligned}$$

(3.3)

where, for $i=1,\dots ,c$,

$$\begin{aligned} \mathcal {F}_i=\{f^i_1,\dots ,f^i_{n_i}\} \end{aligned}$$

and letting $F_j^{i,\pm }$ be the two lifts of $f_j^i$, we have

• (a) $F^{i,\pm }_j=F^{i,\pm }_1+ R^i_1+\dots +R^i_{j-1}$, where $R^i_1,\dots ,R^i_{j-1}$ is a chain of $(-2)$-curves of $A_{j-1}$ type;

• (b) $f_1^i$ is nef for all $i=1,\dots ,c$, and the classes $f^i_j$, for $j=1,\dots ,n_i$, are all the elements of $\mathcal {F}$ which are conjugate to $f^i_1$ under the Weyl group action and ordered in such a way that $f^i_{j+1}-f^i_j=R^i_j$; and

• (c) $n_1+\dots +n_c=10$.

Let $L_j^i=\mathcal O_X(F_j^{\pm })$. Since $H^s(X,\mathcal O_X)= 0$ for $s=1,2$, all line bundles are exceptional objects. Moreover, by construction, $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L^i_j,L^i_k)\cong 0$, for all $i=1,\dots ,c$ and all $j>k\in \{1,\dots ,n_i\}$ and so $\{L^i_1,\dots ,L^i_{n_i}\}$ is an exceptional collection for $i=1,\dots ,c$ (see [20, Theorem B]). By (a) and (c), conditions (1), (2), and (3) in the statement are satisfied by the $L^i_j$’s. Thus it remains to show that, if we set $\mathcal {L}_i=\langle L^i_1,\dots ,L^i_{n_i}\rangle$, then the block $\mathcal {L}_i$ is completely orthogonal to $\mathcal {L}_j$ when $i\ne j\in \{1,\dots ,c\}$.

To this extent, it is enough to show that $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L^j_l,L^k_m)\cong 0$, for all $j\ne k\in \{1,\dots ,c\}$, $l=1,\dots ,n_j$ and $m=1,\dots ,n_k$. But

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (L^j_l,L^k_m)\cong H^0(X,L^k_m\otimes (L^j_l)^\vee )=0 \end{aligned}$$

because $f^k_m-f^j_l$ is not effective by (b). Indeed, if $f^k_m-f^j_l$ is effective, then such a class is a $(-2)$-curve. Thus $f^k_m$ and $f^j_l$ would be in the same orbit under the action of the Weyl group, contradicting the fact that $j\ne k$.

Likewise, $\mathop {\mathrm {Hom}}\nolimits (L^k_m,L^j_l\otimes \mathcal O_X(K_X))= 0$ because $f^j_l-f^k_m$ is not effective. Therefore, it follows from Serre duality that

$$\begin{aligned} \mathop {\mathrm {Ext}}\nolimits ^2(L^j_l,L^k_m)^\vee \cong \mathop {\mathrm {Hom}}\nolimits (L^k_m,L^j_l\otimes \mathcal O_X(K_X))\cong 0. \end{aligned}$$

By Riemann–Roch (3.1), we have $\chi (L^j_l,L^k_m)=\chi (L^k_m\otimes (L^j_l)^\vee )=\frac{1}{2}(f^k_m-f^j_l)^2+1=0$, so we get orthogonality as claimed.

If $\Delta$ is ample then, by Remark 3.3 (i) all the vectors in $\mathcal {F}$ are nef. By [16, Lemma 3.3.1], we get $c=10$ in (3.3) and $n_i=1$ for $i=1,\dots ,10$. It follows from the argument above that $\mathcal {L}=\{L_1,\dots ,L_{10}\}$ is an orthogonal exceptional collection.² This concludes the proof. $\square$

Remark 3.6

(i) Assume that X has an ample Fano polarization so that the admissible subcategory $\mathcal {L}$ in Proposition 3.5 is generated by a collection of 10 orthogonal exceptional objects $L_1,\dots ,L_{10}$. It is clear that the choice of the $L_i$’s is not unique. For example, we can replace any $L_i$ by $L_i\otimes \mathcal O_X(K_X)$. Thus, as in Example 3.4, we have at least $2^{10}=1024$ choices of 10 orthogonal exceptional objects in $\mathrm {D}^{\mathrm {b}}(X)$.

(ii) In [25], the author provides examples of Enriques surfaces for which no Fano polarization $\Delta$ has a c (as in Proposition 3.5) equal to 10. By Remark 3.3 (i), it follows that X does not have an ample Fano polarization and Proposition 3.5 does not provide an orthogonal exceptional collection of line bundles of length 10.

In conclusion, let $\mathcal L$ be the admissible subcategory in Proposition 3.5, and define

$$\begin{aligned} \mathcal {K}\!u(X,\mathcal {L}):=\mathcal L^\perp =\langle \mathcal {L}_1,\dots ,\mathcal {L}_c\rangle ^\perp . \end{aligned}$$

Then $\mathrm {D}^{\mathrm {b}}(X)$ admits a semiorthogonal decomposition:

$$\begin{aligned} \mathrm {D}^{\mathrm {b}}(X)=\langle \mathcal {K}\!u(X,\mathcal {L}),\mathcal {L}\rangle . \end{aligned}$$

(3.4)

Moreover, if X has an ample Fano polarization (e.g. if X is an unnodal or a generic nodal Enriques surface), then again by Proposition 3.5 the admissible subcategory $\mathcal L=\{L_1,\dots ,L_{10}\}$ satisfies ($\star$) in the Introduction.

For an extensive discussion about some remarkable properties of $\mathcal {K}\!u(X,\mathcal {L})$ for nodal Enriques surfaces, one can have a look at [24].

3.2 Artin–Mumford quartic double solids

Let us now recall the construction of Artin–Mumford quartic double solids from [24]. Consider two vector spaces V and W of dimension 4 and the divisor

$$\begin{aligned} Q_s\subseteq \mathbb {P}(V)\times \mathbb {P}(W) \end{aligned}$$

of bidegree (2, 1) on $\mathbb {P}(V)\times \mathbb {P}(W)$ corresponding to a global section $s\in H^0\left( \mathcal O_{\mathbb {P}(V)\times \mathbb {P}(W)}(2,1)\right)$. Clearly, $Q_s$ can be thought of as a family of quadrics in $\mathbb {P}(V)$ parameterized by $\mathbb {P}(W)$. The degeneration locus of this family of quadrics is a (singular) quartic surface $D_s\subseteq \mathbb {P}(W)$ called a quartic symmetroid. Consider further the (singular) double covering $Y_s\rightarrow \mathbb {P}(W)$ ramified over $D_s$. For generic s, $D_s$ has 10 singular points, corresponding to the quadrics of corank 2, and we will refer to $Y_s$ as a general Artin–Mumford quartic double solid. It was explained in [15] that for generic s, the $Y_s$ are precisely the Artin–Mumford conic bundles constructed in [2] as examples of unirational, but not rational, conic bundles. From now on, we will assume that s is general so that the Artin–Mumford quartic double solid is general as well and, for simplicity, we will remove the section s from the notation.

Now Y is singular at precisely 10 points above the 10 singular points of D. Let $Y'$ be the blow-up of Y at these 10 singular points. By [24, Lemma 3.6], the variety $Y'$ is the double covering of the blow-up of $\mathbb {P}(W)$ at the 10 singular points of D ramified over the proper preimage (and not just the proper transform) $D'$ of D. So we have the following diagram:

(3.5)

It follows that $D'$ is the blow-up of D at its 10 singular points. As s is assumed to be generic, $D'$ is a smooth K3 surface with a fixed-point free involution $\tau$. Indeed, the surface $D'$ can be seen as the zero locus of the section s viewed as a global section of $W^\vee \otimes \mathcal O_{\mathbb {P}(V)\times \mathbb {P}(V)}(1,1)$ and $\tau$ is just the restriction of the transposition of factors in $\mathbb {P}(V)\times \mathbb {P}(V)$. The quotient $X:=D'/\langle \tau \rangle$ is then an Enriques surface which will be called the Enriques surface associated to Y. These Enriques surfaces are nodal (see [24, Remark 4.1] and the reference therein).

We now set some more notation. Let $e_i$ (resp. $Q_i$) be the class of the i-th exceptional divisor of $\text {Bl}_{\text {10 pts}}(\mathbb {P}(W))\rightarrow \mathbb {P}(W)$ (resp. $Y'\rightarrow Y$). Each $Q_i$ is isomorphic to $\mathbb {P}^1\times \mathbb {P}^1$ because it is the exceptional divisor of the blow-up along an ordinary double point. Let $G_i=\mathcal O_{Q_i}(-1,0)$. By [24, Corollary 3.8 and Lemma 3.12], we have a semiorthogonal decomposition

$$\begin{aligned} \mathrm {D}^{\mathrm {b}}(Y')=\langle \mathcal {K}\!u(Y'),\{G_i\}_{i=1}^{10},\mathcal O_{Y'}(-h),\{\mathcal O_{Y'}(-e_i)\}_{i=1}^{10},\mathcal O_{Y'}\rangle , \end{aligned}$$

(3.6)

where h is the pull-back of the hyperplane class in $\mathbb {P}(W)$. The subcategory $\mathcal {K}\!u(Y')$ is defined to be the right orthogonal to all the other objects while both $\{G_i\}_{i=1}^{10}$ and $\{\mathcal O_{Y'}(-e_i)\}_{i=1}^{10}$ are orthogonal exceptional collections. Set

$$\begin{aligned} \mathcal A_{Y'}:=\langle \mathcal {K}\!u(Y'),\{G_i\}_{i=1}^{10}\rangle \end{aligned}$$

(3.7)

and denote by $\mathsf {S}_{\mathcal A_{Y'}}$ its Serre functor.

Note that the action on $\mathrm {D}^{\mathrm {b}}(Y')$ of the Galois involution on $Y'$ given by the double cover $Y'\rightarrow \text {Bl}_{\text {10 pts}}(\mathbb {P}(W))$ in (3.5) preserves the exceptional collection $\{\mathcal O_{Y'}(-h),\{\mathcal O_{Y'}(-e_i)\}_{i=1}^{10},\mathcal O_{Y'}\}$ in (3.6) because they are pull-backs from $\text {Bl}_{\text {10 pts}}(\mathbb {P}(W))$. Thus the Galois involution preserves the residual category $\mathcal A_{Y'}$. We will explain later how $\mathsf {S}_{\mathcal A_{Y'}}$ is related to such an involution.

In [24], the authors exhibit an embedding of X inside the Grassmannian $\mathrm {Gr}(2,V)$, providing it with a Reye polarization (see [18, Section 2.4] for the definition), which is, in particular, an ample Fano polarization. By Proposition 3.5, the Enriques surface X associated to Y has an explicit semiorthogonal decomposition

$$\begin{aligned} \mathrm {D}^{\mathrm {b}}(X)=\langle \mathcal {K}\!u(X,\mathcal L),\mathcal L\rangle , \end{aligned}$$

where $\mathcal L=\{L_1,\dots ,L_{10}\}$ is an orthogonal exceptional collection of line bundles. The following statement collects the main results in [24] concerning $\mathcal A_{Y'}$ and $\mathcal {K}\!u(Y')$.

Theorem 3.7

[24, Corollary 3.8, Theorem 4.3] In the above setting:

• (1) There is an isomorphism of exact functors $\mathsf {S}_{\mathcal A_{Y'}}\cong \mathsf {I}[2]$ where $\mathsf {I}$ is the non-trivial involution of $\mathcal A_{Y'}$ (i.e. $\mathsf {I}\circ \mathsf {I}\cong \mathop {\mathrm {id}}\nolimits _{\mathcal A_{Y'}}$) induced by the Galois involution of $Y'$.

• (2) There is an equivalence $\mathcal {K}\!u(Y')\cong \mathcal {K}\!u(X,\mathcal L)$ of Fourier–Mukai type.

This result strongly suggests that $\mathcal A_{Y'}$ should be very much related to the derived category of X. In other words, it is very suggestive to guess that the correspondence between general Artin–Mumford quartic double solids and associated Enriques surfaces might have a nice categorical counterpart. This was made precise by the following [24, Conjecture 4.2]:

Conjecture 3.8

(Ingalls–Kuznetsov) If $Y'$ is the blow-up of a general Artin–Mumford quartic double solid Y at its 10 singular points, then there is an equivalence $\mathcal A_{Y'}\cong \mathrm {D}^{\mathrm {b}}(X)$, where X is the Enriques surface associated to Y.

This conjecture was proved by Hosono and Takagi in [22]. As we explained in the introduction, one of the aims of this paper is to give a shorter, simpler proof (see Theorem B and Theorem 5.4 in Sect. 5.2 for a more precise statement).

4 Spherical objects in Enriques categories

The proof of Theorem A is based on the classification of spherical objects in $\mathcal {K}\!u(X,\mathcal {L})$, for X an Enriques surface. We will explain this in a slightly more general setting which is suited to deal with the case of Artin–Mumford quartic double solids as well.

Recall that if $\mathcal A$ is a $\mathbb K$-linear triangulated category with Serre functor $\mathsf {S}_\mathcal A$ and d is a positive integer, we have the following.

Definition 4.1

An object $E\in \mathcal A$ is d-spherical if

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (E,E[p])\cong {\left\{ \begin{array}{ll} \mathbb K&{} \text{ if } p=0, d, \\ 0 &{} \text{ otherwise }\end{array}\right. } \end{aligned}$$

and $\mathsf {S}_\mathcal A(E)\cong E[d]$.

In particular, the graded $\mathop {\mathrm {Ext}}\nolimits$-algebra of a d-spherical object is isomorphic to the cohomology of a sphere of dimension d.

We are interested in studying this kind of objects in categories which resemble the derived category of an Enriques surface X.

Definition 4.2

A $\mathbb K$-linear triangulated category $\mathcal A$ is an m-Enriques category, for $m\ge 0$ a rational number in $\frac{1}{2}\mathbb {Z}$, if it possesses a Serre functor $\mathsf {S}_{\mathcal A}$ with the property that $\mathsf {S}^2_{\mathcal A}\cong [2m]$.

Remark 4.3

(i) The expert reader has certainly noticed that m-Enriques categories are in particular fractional Calabi–Yau categories of dimension m (see [28]).

(ii) If $\mathcal A$ is an m-Enriques category with $m\in \mathbb {Z}$, then we can write $\mathsf {S}=\mathsf {I}[m]$, where $\mathsf {I}$ is an autoequivalence of $\mathcal A$ such that $\mathsf {I}^2\cong \mathop {\mathrm {id}}\nolimits$. Indeed, we can just take $\mathsf {I}:=\mathsf {S}[-m]$.

(iii) In the special case when $\mathcal A$ is an m-Enriques category, $m\ge 1$ is an integer and $\mathsf {S}\cong [m]$, then, by Serre duality, $\mathcal A$ cannot contain exceptional objects.

Example 4.4

There are several examples of m-Enriques categories available in the literature. We discuss some of them here. The first two are particularly relevant given the scope of this paper.

(i) If X is an Enriques surface, then we already observed that the dualizing sheaf $\omega _X=\mathcal {O}_X(K_X)$ is 2-torsion. Thus the Serre functor $\mathsf {S}_X(-)=(-)\otimes \omega _X[2]$ satisfies $\mathsf {S}_X^2\cong [4]$ and $\mathrm {D}^{\mathrm {b}}(X)$ is a 2-Enriques category.

(ii) By the discussion in Sect. 3.2, if $Y'$ is the blow-up of a general Artin–Mumford quartic double solid at its 10 singular points, then the category $\mathcal {A}_{Y'}$ defined in (3.7) is a 2-Enriques category by Theorem 3.7(1).

(iii) Let X be a Gushel–Mukai variety of dimension n. It is a smooth intersection of the cone in $\mathbb {P}^{10}$ over the Grassmannian $\mathrm {Gr}(2,5)\hookrightarrow \mathbb {P}^9$ with $\mathbb {P}^{n+4}\subseteq \mathbb {P}^{10}$ and a quadric hypersurface $Q\subseteq \mathbb {P}^{n+4}$. As explained in [32], $\mathrm {D}^{\mathrm {b}}(X)$ always contains an admissible subcategory $\mathcal {A}_X$ which, by [32, Proposition 2.6], is a 2-Enriques category. If n is even, then $\mathsf {S}_{\mathcal {A}_X}=[2]$ and thus we are in the situation described in Remark 4.3 (iii). If n is odd, then $\mathsf {S}_{\mathcal {A}_X}$ is not a shift.

(iii) Other examples of m-Enriques categories with $m\ne 2$ can be found in [28].

We now work in the following setting:

Setup 4.5

$\mathcal A$ is an m-Enriques category with a semiorthogonal decomposition

$$\begin{aligned}\mathcal A=\langle \mathcal {K},L_1,\dots ,L_N\rangle ,\end{aligned}$$

where $\mathcal K$ is admissible, $N\ge 1$ is an integer, and $\mathcal {L}:=\{L_1,\dots ,L_N\}$ is an orthogonal exceptional collection.

Note that since $\mathcal {A}$ contains at least one exceptional object, by Remark 4.3 (iii), the Serre functor of $\mathcal {A}$ cannot be isomorphic to a shift.

Example 4.6

By Sects. 3.1 and 3.2 and Example 4.4 (i) and (ii), $\mathcal A=\mathrm {D}^{\mathrm {b}}(X)$, where X is either an Enriques surface, and $\mathcal A=\mathcal A_{Y'}$, where $Y'$ is the blow-up of an Artin–Momford quartic double solid, are both as in Setup 4.5. Indeed, in both cases, the 2-Enriques categories in Example 4.4 (i) and (ii) contain 10 orthogonal exceptional objects.

Suppose that we are in Setup 4.5, and let us simplify notation by setting $\mathsf {S}:=\mathsf {S}_{\mathcal A}$ and letting $\kappa :\mathcal {K}\rightarrow \mathcal {A}$ be the natural inclusion with left adjoint $\kappa ^*$. By Serre duality, we have $\mathop {\mathrm {Hom}}\nolimits (L_i,\mathsf {S}(L_i))\cong \mathbb K$, so we can define $S_i\rightarrow L_i$ to be the cocone of the unique non-zero (up to scaling) morphism $L_i\rightarrow \mathsf {S}(L_i)$. These objects fit in the distinguished triangle

$$\begin{aligned} S_i\rightarrow L_i\rightarrow \mathsf {S}(L_i). \end{aligned}$$

(4.1)

All the objects in (4.1) are clearly contained in $\mathcal {A}$. We claim that more is true

Lemma 4.7

For $i=1,\dots ,N$, we have $S_i\in \mathcal K$.

Proof

We must show that $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_j,S_i)=0$ for $j=1,\dots ,N$. If $j\ne i$, then $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_j,L_i)\cong \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_j,\mathsf {S}(L_i))=0$, by assumption (b) in Setup 4.5 and Serre duality. Thus $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_j,S_i)\cong 0$ for $j\ne i$. On the other hand, the morphism $L_i\rightarrow \mathsf {S}(L_i)$ in (4.1) yields an isomorphism $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_i,L_i)\cong \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_i,\mathsf {S}(L_i))$. Thus $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_i,S_i)\cong 0$ as well. $\square$

It then follows that in-fact we have

$$\begin{aligned} S_i=\kappa ^*(\mathsf {S}(L_i))[-1], \end{aligned}$$

(4.2)

for $i=1,\dots ,N$.

The following result summarizes the important properties of the $S_i$.

Lemma 4.8

In Setup 4.5, the object $S_i$ is $(2m-1)$-spherical in $\mathcal {K}$, for all $i=1,\dots ,N$. Moreover, $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (S_i,S_j)\cong 0$ and thus $S_i\not \cong S_j[k]$ for all $i\ne j\in \{1,\dots ,N\}$ and for any $k\in \mathbb {Z}$.

Proof

We begin by proving the first condition for being $(2m-1)$-spherical as well as the second statement of the lemma.

Since $\mathsf {S}$ is an autoequivalence, we get isomorphisms of graded vector spaces

$$\begin{aligned} \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\mathsf {S}(L_i),\mathsf {S}(L_j))\cong \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_i,L_j)\cong \mathbb K^{\delta _{ij}}, \end{aligned}$$

for $i,j=1,\dots ,N$. We also get the isomorphisms of graded vector spaces

$$\begin{aligned} \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\mathsf {S}(L_i),L_j)&\cong \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\mathsf {S}^2(L_i),\mathsf {S}(L_j))\\ \nonumber&\cong \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_i[2m],\mathsf {S}(L_j))\\\nonumber&\cong \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L_j,L_i[2m])^\vee \\\nonumber&\cong \mathbb K^{\delta _{ij}}[-2m], \end{aligned}$$

(4.3)

where the first, second, and third isomorphisms follow from $\mathsf {S}$ being an autoequivalence, the fact that $\mathsf {S}^2\cong [2m]$, and Serre duality, respectively. These two remarks show that if we apply $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\mathsf {S}(L_i),-)$ to (4.1), we get an isomorphism of graded vector spaces

$$\begin{aligned} \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\mathsf {S}(L_i),S_j)\cong \mathbb K^{\delta _{ij}}[-1]\oplus \mathbb K^{\delta _{ij}}[-2m]. \end{aligned}$$

(4.4)

Hence, if we apply $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (-,S_j)$ to (4.1) and we use that $S_j\in \mathcal {K}\subseteq L_i^\perp$ by Lemma 4.7, we get an isomorphism of graded vector spaces

$$\begin{aligned} \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (S_i,S_j)\cong \mathbb K^{\delta _{ij}}\oplus \mathbb K^{\delta _{ij}}[1-2m], \end{aligned}$$

as required.

It remains to show that $\mathsf {S}_\mathcal K(S_i)\cong S_i[2m-1]$, for $i=1,\dots ,N$. This easily follows from the following chain of isomorphisms

$$\begin{aligned} \mathsf {S}_{\mathcal {K}}^{-1}(S_i)&\cong \mathsf {L}_{\langle L_1,\dots ,L_{N}\rangle }(\mathsf {S}^{-1}(S_i))\\&\cong \mathsf {L}_{L_i}(\mathsf {S}^{-1}(S_i)) \\&\cong \mathsf {L}_{L_i}(\mathrm {Cone}(\mathsf {S}^{-1}(L_i)[-1]\rightarrow L_i[-1])) \\&\cong \mathsf {L}_{L_i}(\mathsf {S}^{-1}(L_i))\\&\cong S_i[-2m+1]. \end{aligned}$$

Observe that the first isomorphism follows from [28, Lemma 2.6], while for the second one we used (2.2), the fact that $\mathsf {S}$ is an equivalence, and (4.4). The third one and the last one use (4.1) (to which we apply $\mathsf {S}^{-1}$) and (4.3). The fourth isomorphism follows from $\mathsf {L}_{L_i}(L_i)\cong 0$. $\square$

Remark 4.9

(i) If we combine Serre duality and Lemma 4.7, then we get that

$$\begin{aligned}\mathop {\mathrm {Hom}}\nolimits (S_i,\mathsf {S}(L_i)[p-1])\cong \mathop {\mathrm {Hom}}\nolimits (L_i,S_i[1-p])^\vee \cong 0,\end{aligned}$$

for all p. So by applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (S_i,-)$ to (4.1), we see that there is a unique (up to scalars) morphism $f_i:S_i\rightarrow L_i$. For the same reason, the composition with $f_i$ provides an isomorphism $\mathop {\mathrm {Hom}}\nolimits (E,S_i) \cong \mathop {\mathrm {Hom}}\nolimits (E,L_i)$, for all $E\in \mathcal {K}$.

(ii) Let us reconsider the embedding $\kappa :\mathcal {K}\rightarrow \mathcal {A}$ realizing $\mathcal {K}$ as an admissible subcategory. An easy exercise with Serre duality shows that its right adjoint $\kappa ^!$ is described by the formula

$$\begin{aligned} \kappa ^!=\mathsf {S}_\mathcal {K}\circ \kappa ^*\circ \mathsf {S}_\mathcal {A}^{-1}, \end{aligned}$$

where $\mathsf {S}_\mathcal {K}$ and $\mathsf {S}_\mathcal {A}$ are the Serre functors of $\mathcal {K}$ and $\mathcal {A}$, respectively. Thus, as an application of (4.2) and Lemma 4.8, we get the isomorphisms

$$\begin{aligned} \kappa ^!(L_i)\cong \mathsf {S}_\mathcal {K}\circ \kappa ^*\circ \mathsf {S}_\mathcal {A}^{-1}(L_i)\cong \mathsf {S}_\mathcal {K}\circ \kappa ^*\circ \mathsf {S}_\mathcal {A}(L_i)[-2m]\cong \mathsf {S}_\mathcal {K}(S_i)[-2m+1]\cong S_i, \end{aligned}$$

for $i=1,\dots ,N$. For the second isomorphism we used that $\mathsf {S}_\mathcal {A}^2\cong [2m]$.

The lemma shows how to construct $(2m-1)$-spherical objects in $\mathcal {K}$. We want to prove now that the list is complete.

Proposition 4.10

Let $\mathcal A$ be an m-Enriques category with a semiorthogonal decomposition

$$\begin{aligned}\mathcal A=\langle \mathcal {K},L_1,\dots ,L_N\rangle ,\end{aligned}$$

where $\mathcal K$ is admissible, $N\ge 1$ is an integer, and $\mathcal {L}:=\{L_1,\dots ,L_N\}$ is an orthogonal exceptional collection. Let F be a $(2m-1)$-spherical object in $\mathcal {K}$. If $m\ge \frac{3}{2}$, then $F\cong S_i[k]$ for some $i=1,\dots , N$ and some integer k.

Proof

By [28, Lemma 2.6] and since $\mathsf {S}^2(F)\cong F[2m]$ (as in Definition 4.2), the isomorphism $\mathsf {S}_{\mathcal {K}}(F)\cong F[2m-1]$ is equivalent to the existence of an isomorphism $F\cong \mathsf {L}_{\langle L_1,\dots ,L_{N}\rangle }(\mathsf {S}(F))[-1]$. Define the object $P:=\bigoplus _{1\le i\le N} L_i$. It is polyexceptional in the sense that it is a direct sum of objects forming an orthogonal exceptional collection and so its endomorphism algebra is such that

$$\begin{aligned}\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (P,P)\cong \mathbb K^N,\end{aligned}$$

. It follows from (2.2) that F sits in a distinguished triangle

$$\begin{aligned} F\rightarrow P\otimes _{\mathbb K^N} \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (P,\mathsf {S}(F))\rightarrow \mathsf {S}(F). \end{aligned}$$

(4.5)

If we apply $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (F,-)$ to (4.5), then, by Serre duality and taking into account that F is $(2m-1)$-spherical, we get a distinguished triangle of graded $\mathbb K$-vector spaces

$$\begin{aligned} \mathbb K\oplus \mathbb K[-2m+1]\rightarrow \mathop {\mathbf {R}\mathrm {Hom}}\nolimits (F,P)\otimes _{\mathbb K^N}\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (F,P)^\vee \rightarrow \mathbb K\oplus \mathbb K[2m-1]. \end{aligned}$$

(4.6)

Hence, since $2m\ge 3$, the graded vector space $V:=\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (F,P)\otimes _{\mathbb K^N}\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (F,P)^\vee$ is 4-dimensional. Moreover, since $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (P,P)$ consists only of componentwise morphisms, V decomposes as

$$\begin{aligned} V\cong \bigoplus _{i=1}^N V_i\otimes V_i^\vee , \end{aligned}$$

where $V_i:=\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (F,L_i)$. For dimension reasons, we can only have two possibilities: either there are four non-trivial 1-dimensional $V_i$ or there is only one non-trivial 2-dimensional $V_i$. But in the former case, as $V_i\otimes V_i^\vee$ is concentrated in degree 0 for each i, we get a contradiction since V has 2-dimensional degree 0 piece by (4.6). Thus there must be only one non-trivial $V_i$ which then must satisfy

$$\begin{aligned} V_i\cong \mathbb K[k-2m+1]\oplus \mathbb K[k], \end{aligned}$$

for some $k\in \mathbb {Z}$. Thus, up to reordering the objects in $\mathcal {L}$ and shifting, we can assume $i=1$ and $k=0$. To simplify the notation, for the rest of the proof, we set $L:=L_1$. Hence

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (F,L[p])\cong {\left\{ \begin{array}{ll} \mathbb K&{} \text {if p=0,2m-1,}\\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(4.7)

Then (4.5) gets the following simplified form, after a rotation:

$$\begin{aligned} L[-1]\oplus L[2m-2]\rightarrow \mathsf {S}(F)[-1]\rightarrow F. \end{aligned}$$

(4.8)

We will show that $F\cong S_1$, as required.

To that end, let C be the cone of the unique (up to scalars) morphism $L[2m-2]\rightarrow \mathsf {S}(F)[-1]$ so that we get the following distinguished triangle

$$\begin{aligned} L[2m-2]\rightarrow \mathsf {S}(F)[-1]\rightarrow C. \end{aligned}$$

(4.9)

Note that it can put in the following commutative diagram of distinguished triangles

in view of the octahedron axiom. Thus C, F and L sit in a distinguished triangle

$$\begin{aligned} C{\mathop {\longrightarrow }\limits ^{k_1}} F\longrightarrow L. \end{aligned}$$

(4.10)

By applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (L,-)$ to (4.10) (resp. $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (-,L)$ to (4.9)) and using the fact that $F\in \mathcal {K}$ and Serre duality, we see that

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (L,C[j])\cong {\left\{ \begin{array}{ll} \mathbb K&{} \text {if }j=1 \\ 0 &{} \text {otherwise} \end{array}\right. }\quad \text {and}\quad \mathop {\mathrm {Hom}}\nolimits (C,L[j])\cong {\left\{ \begin{array}{ll} \mathbb K&{} \text {if }j=2m-1 \\ 0 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(4.11)

This and (4.7) show that the morphism $F\rightarrow L$ in (4.10) is not trivial. Otherwise $C\cong F\oplus L[-1]$, contradicting the second part of (4.11).

We claim that to show $F\cong S_1$, it suffices to show that $C\cong \mathsf {S}(L)[-1]$. Indeed, observe first that $F\not \cong \mathsf {S}(L)[-1]\oplus L$ because $\mathop {\mathrm {Hom}}\nolimits (F,F)\cong \mathbb K$ as F is a $(2m-1)$-spherical object. Thus, in view of (4.10), $C\cong \mathsf {S}(L)[-1]$ would imply that F is isomorphic to the cone of the (unique up to scalars) non-trivial map $L[-1]\rightarrow \mathsf {S}(L)[-1]$, which is $S_1$ by (4.1).

To show $C\cong \mathsf {S}(L)[-1]$, we first prove that it is exceptional and then produce non-trivial morphisms $f:\mathsf {S}(L)[-1] \rightarrow C$ and $g:C\rightarrow \mathsf {S}(L)[-1]$ whose composition $g\circ f$ is non-zero. As $\mathsf {S}(L)[-1]$ is exceptional, up to scaling f or g, we may assume that $g\circ f=\mathop {\mathrm {id}}\nolimits$. But then $\mathsf {S}(L)[-1]$ must be a direct summand of C, contradicting the fact that C is exceptional. Hence $C\cong \mathsf {S}(L)[-1]$.

By Serre duality and (4.11) we conclude that

$$\begin{aligned}&\mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],C)^\vee \cong \mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}^2(L)[-1])\cong \mathop {\mathrm {Hom}}\nolimits (C,L[2m-1])\cong \mathbb K,\\&\mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}(L)[-1])^\vee \cong \mathop {\mathrm {Hom}}\nolimits (L,C[1])\cong \mathbb K.\end{aligned}$$

Thus we let $f\in \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],C)$ and $g\in \mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}(L)[-1])$ be the unique (up to scalars) non-zero morphisms.

Before we prove that $g\circ f\ne 0$, we prove that C is exceptional, recording a useful result along the way. We claim indeed that

$$\begin{aligned}\mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}(F)[j])=0,\;\text {for all}\; j\in \mathbb {Z},\quad \text {and}\quad \mathop {\mathrm {Hom}}\nolimits (C,C[j])\cong {\left\{ \begin{array}{ll} \mathbb K&{} \text {if }j=0 \\ 0 &{} \text {otherwise.} \end{array}\right. }\end{aligned}$$

To that end, applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (F,-)$ to (4.10), we get $\mathop {\mathrm {Hom}}\nolimits (F,C[j])=0$ for every $j\le 2m-2$. By Serre duality, we get $\mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}(F)[j])=0$ for every $j\ge 2-2m\ge -1$ (note that $m\ge \frac{3}{2}$). At this point, we apply $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (-,\mathsf {S}(F))$ to (4.9) and get $\mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}(F)[j])=0$ for every $j\le -2$. Therefore, we conclude that $\mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}(F) [j])=0$, for every $j\in \mathbb {Z}$. Finally, if we apply $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (C,-)$ to (4.9), we get C is exceptional.

It remains to show that $g\circ f$ is non-zero. Let $k_2\in \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(F)[-1],\mathsf {S}(L)[-1])\cong \mathbb K$ be the unique (up to scalars) non-trivial morphism, and similarly, let $k_3$ be the unique (up to scalars) non-trivial morphism in $\mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],F)\cong \mathbb K$. We claim that $k_3\circ k_2\ne 0$. Indeed, applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\mathsf {S}(-),F)$ to (4.8), we get an exact sequence

$$\begin{aligned}&\mathop {\mathrm {Hom}}\nolimits (\mathsf {S}^2(F)[-1],F)\rightarrow \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],F)\oplus \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[2m-2],F)\\&\quad \rightarrow \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(F)[-1],F)\rightarrow \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}^2(F)[-2],F). \end{aligned}$$

Now for $i=0,1$, $\mathop {\mathrm {Hom}}\nolimits (\mathsf {S}^2(F)[-(i+1)],F)\cong \mathop {\mathrm {Hom}}\nolimits (F[2m-(i+1)],F)\cong 0$ because F is $(2m-1)$-spherical and $\mathsf {S}^2\cong [2m]$. Moreover, as $m\ge \frac{3}{2}$, it follows from (4.7) that

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[2m-2],F)\cong \mathop {\mathrm {Hom}}\nolimits (F,\mathsf {S}^2(L)[2m-2])^\vee \cong \mathop {\mathrm {Hom}}\nolimits (F,L[4m-2])^\vee \cong 0. \end{aligned}$$

Thus precomposition with $k_2$ induces an isomorphism

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],F)\xrightarrow {\sim }\mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(F)[-1],F). \end{aligned}$$

(4.12)

In particular, $k_3\ne 0$ has non-trivial image, i.e. $k_3\circ k_2\ne 0$.

Applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (-,C)$ to (4.9) and using (4.11), we see that there is a unique (up to scalars) non-trivial morphism $k_4\in \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(F)[-1],C)\cong \mathbb K$. The same argument as in the previous paragraph, by applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (-,\mathsf {S}(L)[-1])$ to (4.9), yields that precomposition with $k_4$ induces an isomorphism

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (C,\mathsf {S}(L)[-1])\xrightarrow {\sim }\mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(F)[-1],\mathsf {S}(L)[-1]). \end{aligned}$$

(4.13)

Now we claim that the composition of non-trivial morphisms

$$\begin{aligned} \mathsf {S}(F)[-1]{\mathop {\longrightarrow }\limits ^{k_4}} C{\mathop {\longrightarrow }\limits ^{g}} \mathsf {S}(L)[-1]{\mathop {\longrightarrow }\limits ^{k_3}} F \end{aligned}$$

is a non-trivial morphism. Indeed, by (4.13) $g\circ k_4$ is non-zero, so there exists $0\ne \mu \in \mathbb K$ such that $0\ne g\circ k_4=\mu k_2$. But then

$$\begin{aligned} k_3\circ g\circ k_4=\mu k_3\circ k_2\ne 0. \end{aligned}$$

In particular, it follows that the composition $k_3\circ g$ is non-zero.

Applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (C,-)$ to (4.10), we see that $\mathop {\mathrm {Hom}}\nolimits (C,F)\cong \mathbb K$ from a simple computation using (4.11) and the fact that $\mathop {\mathrm {Hom}}\nolimits (C,C)\cong \mathbb K$. Thus there exists $0\ne \lambda \in \mathbb K$ such that

$$\begin{aligned} k_3\circ g=\lambda k_1. \end{aligned}$$

Finally, applying $\mathop {\mathbf {R}\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],-)$ to (4.10), we get the isomorphism

$$\begin{aligned} \mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],C)\xrightarrow {\sim }\mathop {\mathrm {Hom}}\nolimits (\mathsf {S}(L)[-1],F), \end{aligned}$$

(4.14)

defined by the postcomposition by the non-trivial map $k_1$. In particular, since $f\ne 0$, we have $k_1\circ f\ne 0$. But then

$$\begin{aligned} 0\ne \lambda (k_1\circ f)=(\lambda k_1)\circ f=k_3\circ g\circ f, \end{aligned}$$

so $g\circ f\ne 0$, as required. $\square$

Remark 4.11

It would be interesting to study whether Proposition 4.10 can be generalized to situations where one has semiorthogonal decompositions as in Proposition 3.5 when the surface does not have an ample Fano polarization. Unfortunately, the proof provided above does not apply in this setting.

5 Proof of the main results

The proof of the main results in this paper is explained in Sect. 5.2 and it follows from a more general result which will be proved in the next section.

5.1 A general extension result

Let $Z_1$ and $Z_2$ be smooth projective varieties over $\mathbb K$ admitting admissible subcategories $\mathcal A_{Z_i}$ which fall under Setup 4.5. That is, the $\mathcal A_{Z_i}$ are m-Enriques and admit semiorthogonal decompositions

$$\begin{aligned}\mathcal A_{Z_i}=\langle \mathcal {K}\!u(Z_i),L^i_1,\dots ,L^i_{N_i}\rangle ,\end{aligned}$$

where $\mathcal {K}\!u(Z_i)$ is admissible in $\mathcal A_{Z_i}$, $N_i\ge 1$ is an integer, and $\mathcal {L}_i:=\{L^i_1,\dots ,L^i_{N_i}\}$ is an orthogonal exceptional collection. We can then prove the following general result.

Theorem 5.1

Under the assumptions above, let $\mathsf {F}:\mathcal {K}\!u(Z_1)\rightarrow \mathcal {K}\!u(Z_2)$ be an equivalence which is of Fourier–Mukai type. Then $N_1=N_2=N$ and there exists a Fourier–Mukai functor $\Phi _{\tilde{\mathcal {E}}}:\mathrm {D}^{\mathrm {b}}(Z_1)\rightarrow \mathrm {D}^{\mathrm {b}}(Z_2)$ such that

• (1) $\Phi _{\tilde{\mathcal {E}}}|_{\mathcal {K}\!u(Z_1)}\cong \mathsf {F}$;

• (2) $\Phi _{\tilde{\mathcal {E}}}|_{\mathcal {A}_{Z_1}}:\mathcal {A}_{Z_1}\rightarrow \mathcal {A}_{Z_2}$ is an equivalence; and

• (3) Up to reordering and shift, $\Phi _{\tilde{\mathcal {E}}}(L_i^1)\cong L_i^2$, for all $i=1,\dots ,N$.

Proof

We first observe that $N_1=N_2=N$. Indeed, by Lemma 4.8 and Proposition 4.10 applied to $\mathcal A_{Z_i}$, $\mathcal {K}\!u(Z_i)$ has to contain, up to shift, exactly $N_i$ pairwise non-isomorphic $(2m-1)$-spherical objects. Since such a number is invariant under equivalence and $\mathcal {K}\!u(Z_1)\cong \mathcal {K}\!u(Z_2)$, we must have $N_1=N_2$.

Now let $\mathcal {E}\in \mathrm {D}^{\mathrm {b}}(Z_1\times Z_2)$ be such that $\mathsf {F}=\Phi _{\mathcal E}|_{\mathcal {K}\!u(Z_1)}$. We would like to apply Proposition 2.5 with

$$\begin{aligned}\mathcal A=\mathcal A_{Z_1}\quad X=Z_1,\quad Y=Z_2,\quad \mathcal B=\mathcal A_{Z_2}.\end{aligned}$$

By Remark 2.2, we may choose $\mathcal {E}$ such that $\Phi _\mathcal E|_{\!^\perp \!\mathcal {K}\!u(Z_1)}=0$ without changing $\Phi _\mathcal E|_{\mathcal {K}\!u(Z_1)}$. Thus we can suppose without loss of generality that $\Phi _\mathcal E$ is as in Proposition 2.5 and that assumption (a) of the proposition is verified. Consider, for any $j=1,2$ and any $i=1,\ldots ,N$, the $(2m-1)$-spherical object $S_i^j\in \mathcal {K}\!u(Z_j)$ defined by the distinguished triangle

$$\begin{aligned} S_i^j\rightarrow L_i^j\rightarrow \mathsf {S}_{\mathcal A_{Z_j}}(L_i^j). \end{aligned}$$

By Proposition 4.10, we can assume $\mathsf {F}(S^1_i)\cong S^2_i$, up to reordering and shift, for all $i=1,\dots ,N$.

Denote by

$$\begin{aligned}\zeta _i:\mathcal {K}\!u(Z_i)\hookrightarrow \mathrm {D}^{\mathrm {b}}(Z_i)\quad \text {and}\quad \kappa _i:\mathcal {K}\!u(Z_i)\hookrightarrow \mathcal A_{Z_i}\end{aligned}$$

the relevant embeddings for $i=1,2$. Note that by Remark 4.9 (ii), the object $\kappa _j\kappa _j^!(L^j_i)\cong S_i^j$. An analogous computation shows that $\zeta _j\zeta _j^!(L^j_i)\cong S_i^j$, so we get an isomorphism

$$\begin{aligned}\mathsf {F}(\zeta _1\zeta _1^!(L^1_i))\cong \mathsf {F}(S_i^1)\cong S_i^2\cong \zeta _2\zeta _2^!(L^2_i).\end{aligned}$$

Thus assumption (b) of Proposition 2.5 is also satisfied if we set

$$\begin{aligned} X=Z_1\quad Y=Z_2\quad \mathcal {A}=\mathcal {K}\!u(Z_1)\quad \mathcal B=\mathcal {K}\!u(Z_2)\quad E=L_1^1\quad F=L_1^2. \end{aligned}$$

Therefore, by Proposition 2.5, we get a Fourier–Mukai type functor $\Phi _{{\tilde{EE}}_1}$ such that

$$\begin{aligned}&\Phi _{{\tilde{EE}}_1}|_{\langle \mathcal {K}\!u(Z_1),L_1^1\rangle }:\langle \mathcal {K}\!u(Z_1),L_1^1\rangle \xrightarrow {\sim }\langle \mathcal {K}\!u(Z_2),L_1^2\rangle ,\quad \Phi _{{\tilde{EE}}_1}|_{\mathcal {K}\!u(Z_1)}\cong \mathsf {F},\quad \Phi _{{\tilde{EE}}_1}(L_1^1)\cong L_1^2,\;\text {and}\\&\quad \Phi _{{\tilde{EE}}_1}(\!^\perp \!\langle \mathcal {K}\!u(Z_1),L_1^1\rangle )\cong 0. \end{aligned}$$

The argument proceeds inductively. To simplify the notation slightly, let us set $L_i:=L_i^1$ and $M_i:=L_i^2$. For $k\ge 2$, we assume that we have a Fourier–Mukai kernel ${\tilde{EE}}_{k-1}$ such that

$$\begin{aligned} \Phi _{{\tilde{EE}}_{k-1}}|_{\langle \mathcal {K}\!u(Z_1),L_1,\dots ,L_{k-1}\rangle }:\langle \mathcal {K}\!u(Z_1),L_1,\dots ,L_{k-1}\rangle \rightarrow \langle \mathcal {K}\!u(Z_2),M_1,\dots ,M_{k-1}\rangle \end{aligned}$$

is an equivalence satisfying

$$\begin{aligned} \Phi _{{\tilde{\mathcal E}}_{k-1}}|_{\mathcal {K}\!u(Z_1)} \cong \Phi _{{\tilde{EE}}_{k-2}}|_{\mathcal {K}\!u(Z_1)}\quad \text {and}\quad \Phi _{{\tilde{\mathcal E}}_{k-1}}(L_{i})\cong M_{i},\end{aligned}$$

for $i=1,\dots ,k-1$, where we set ${\tilde{\mathcal E}}_0:=\mathcal E$. To proceed to stage k, we apply again Proposition 2.5 with

$$\begin{aligned} \mathcal {A}=\langle \mathcal {K}\!u(Z_1),L_1,\dots ,L_{k-1}\rangle ,\quad \mathcal {B}=\langle \mathcal {K}\!u(Z_2),M_1,\dots ,M_{k-1}\rangle ,\quad E=L_k,\quad F=M_k. \end{aligned}$$

Here it is important to note that, since the exceptional objects $L_1,\ldots ,L_k$ (resp. $M_1,\ldots ,M_k$) are orthogonal, by Remark 4.9 (ii) the object $\alpha \alpha ^!(L_k)\cong S_k^1$ (resp. $\beta \beta ^!(M_k)\cong S_k^2$) is actually contained in $\mathcal {K}\!u(Z_1)$ (resp. $\mathcal {K}\!u(Z_2)$) and not just in $\mathcal {A}$ (resp. $\mathcal B$). Here $\alpha :\mathcal {A}\hookrightarrow \mathrm {D}^{\mathrm {b}}(Z_1)$ and $\beta :\mathcal B\hookrightarrow \mathrm {D}^{\mathrm {b}}(Z_2)$ are the admissible embeddings. Hence $\Phi _{{\tilde{\mathcal E}}_{k-1}}$ satisfies the assumptions of Proposition 2.5 by induction, and we can produce $\Phi _{{\tilde{\mathcal E}}_{k}}$. Continuing in this way, by Proposition 2.5, we get an equivalence $\Phi _{{\tilde{\mathcal E}}_{N}}:\mathrm {D}^{\mathrm {b}}(\mathcal {A}_{Z_1})\xrightarrow {\sim }\mathrm {D}^{\mathrm {b}}(\mathcal {A}_{Z_2})$ and we just set ${\tilde{\mathcal E}}:={\tilde{\mathcal E}}_N$. $\square$

5.2 Proof of Theorems A and B

As for Theorem A, we can actually prove the following more general version of it.

Theorem 5.2

Let $X_1$ and $X_2$ be Enriques surfaces. Then the following are equivalent:

• (i) There is a semiorthogonal decomposition $\mathrm {D}^{\mathrm {b}}(X_i)=\langle \mathcal {K}\!u(X_i,\mathcal {L}_i),\mathcal {L}_i\rangle ,$ satisfying ($\star$), for $i=1,2$ and an exact equivalence

  $$\begin{aligned}\mathsf {F}: \mathcal {K}\!u(X_1,\mathcal {L}_1)\xrightarrow {\sim }\mathcal {K}\!u(X_2,\mathcal {L}_2)\end{aligned}$$

  of Fourier–Mukai type;

• (ii) $X_1\cong X_2$ and either $\mathrm {D}^{\mathrm {b}}(X_1)$ or $\mathrm {D}^{\mathrm {b}}(X_2)$ has a semiorthogonal decomposition satisfying condition ($\star$).

Proof

The proof of the fact that (i) implies (ii) amounts to showing that, under the assumptions in (i), $X_1\cong X_2$. For this, we just apply Theorem 5.1 with

$$\begin{aligned}Z_i=X_i,\quad \mathcal A_{Z_i}=\mathrm {D}^{\mathrm {b}}(X_i),\quad N=10,\;\text {and}\quad \mathcal {K}\!u(Z_i)=\mathcal {K}\!u(X_i,\mathcal L_i),\mathcal L_i\rangle ,\end{aligned}$$

where $\mathcal L_i=\{L_1^i,\dots ,L_{10}^i\}$ is as in ($\star$), for $i=1,2$ (see Example 4.6). Indeed, the exact equivalence $\mathsf {F}:\mathcal {K}\!u(X_1,\mathcal L_1)\rightarrow \mathcal {K}\!u(X_2,\mathcal L_2)$ of Fourier-Mukai type extends to an equivalence $\mathrm {D}^{\mathrm {b}}(X_1)\cong \mathrm {D}^{\mathrm {b}}(X_2)$. By Theorem 3.1, we deduce that $X_1\cong X_2$.

On the other hand, assume that there exists an isomorphism $f:X_1\rightarrow X_2$ and a semiorthogonal decomposition for $\mathrm {D}^{\mathrm {b}}(X_2)$ satisfying ($\star$). Since $f^*:\mathrm {D}^{\mathrm {b}}(X_2)\rightarrow \mathrm {D}^{\mathrm {b}}(X_1)$ is an equivalence, we can take on $\mathrm {D}^{\mathrm {b}}(X_1)$ the semiorthogonal decomposition satisfying ($\star$) which is the image of the given one on $\mathrm {D}^{\mathrm {b}}(X_2)$ under $f^*$. Clearly, such a semiorthogonal decomposition on $\mathrm {D}^{\mathrm {b}}(X_1)$ satisfies ($\star$). Finally, $\mathsf {F}:=(f^*)^{-1}|_{\mathcal {K}\!u(X_1,\mathcal {L}_1)}:\mathcal {K}\!u(X_1,\mathcal {L}_1)\xrightarrow {\sim }\mathcal {K}\!u(X_2,\mathcal {L}_2)$ is an exact equivalence of Fourier–Mukai type by construction. The argument when $\mathrm {D}^{\mathrm {b}}(X_1)$ satisfies such a property is identical using the (quasi-)inverse of $f^*$ instead of $f^*$. $\square$

Remark 5.3

One way to generalize Theorem 5.2 to non-generic Enriques surfaces could be to consider semiorthogonal decompositions as in Proposition 3.5 when the surface does not have an ample Fano polarization. Let us briefly sketch the idea which was suggested to us by A. Perry. Indeed, one might try to deform $X_1$, $X_2$ and the equivalence $\mathsf {F}:\mathcal {K}\!u(X_1,\mathcal {L}_1)\rightarrow \mathcal {K}\!u(X_2,\mathcal {L}_2)$ to the generic case. In the generic case, we can then apply Theorem 5.2 and conclude that the deformed Enriques surfaces are isomorphic. The separatedness of the moduli space of (polarized) Enriques surfaces should then allow us to conclude that $X_1\cong X_2$.

Unfortunately, while in the generic case first order deformations of $X_i$ coincide with first order deformations of the subcategory $\mathcal {K}\!u(X_i,\mathcal {L})$, this seems not to be the case for nodal non-generic Enriques surfaces. Thus one needs to add some natural assumptions on $\mathsf {F}$. Namely, we need the equivalence to preserve commutative first order deformations of $X_1$ and $X_2$. This will be investigated in future work.

The proof of Theorem B is along the same lines. Indeed, let $Y'$ be the blow-up at the 10 singular points of a general Artin–Mumford quartic double solid Y with associated Enriques surface X. Consider the semiorthogonal decompositions of the 2-Enriques categories (see Sect. 3.2 and Example 4.6)

$$\begin{aligned} \mathcal A_{Y'}:=\langle \mathcal {K}\!u(Y'),\{G_i\}_{i=1}^{10}\rangle \quad \mathrm {D}^{\mathrm {b}}(X)=\langle \mathcal {K}\!u(X,\mathcal L),L_1\dots ,L_{10}\rangle \end{aligned}$$

discussed in Sect. 3.2. Moreover, we know that there is an exact equivalence $\mathcal {K}\!u(X,\mathcal L)\cong \mathcal {K}\!u(Y')$ of Fourier–Mukai type (see Theorem 3.7 (2)). We then apply Theorem 5.1.

In particular, we get the following more precise version of Theorem B.

Theorem 5.4

Under our assumptions, there is an exact equivalence $\mathrm {D}^{\mathrm {b}}(X)\cong \mathcal A_{Y'}$ induced by a Fourier–Mukai functor $\Phi _\mathcal E:\mathrm {D}^{\mathrm {b}}(X)\rightarrow \mathrm {D}^{\mathrm {b}}(Y')$ such that

• (1) $\Phi _\mathcal E|_{\mathcal {K}\!u(X,\mathcal {L})}:\mathcal {K}\!u(X,\mathcal {L})\rightarrow \mathcal {K}\!u(Y'))$ is the exact equivalence in Theorem 3.7 (2), and

• (2) Up to reordering and shifts, $\Phi _\mathcal E(L_i)=G_i$, for $i=1,\dots ,10$.

In a sense, this result proves a stronger version of Conjecture 3.8 since the equivalence we construct is automatically compatible with the semiorthogonal decompositions of $\mathrm {D}^{\mathrm {b}}(X)$ and $\mathcal {A}_{Y'}$.