Abstract
We prove Ihara’s lemma for the mod l cohomology of Shimura curves, localized at a maximal ideal of the Hecke algebra, under a large image hypothesis on the associated Galois representation. This was proved by Diamond and Taylor, for Shimura curves over \(\mathbb {Q}\), under various assumptions on l. Our method is totally different and can avoid these assumptions, at the cost of imposing the large image hypothesis. It uses the Taylor–Wiles method, as improved by Diamond and Kisin, and the geometry of integral models of Shimura curves at an auxiliary prime.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\Gamma = \Gamma _0(N)\) be the usual congruence subgroup of \(SL_2(\mathbb {Z})\), for some \(N \ge 1\), and let p be a prime not dividing N. Write \(\Gamma ' = \Gamma \cap \Gamma _0(p)\). If \(X_{\Gamma }\) and \(X_{\Gamma '}\) are the compactified modular curves of levels \(\Gamma \) and \(\Gamma '\), then there are two degeneracy maps
induced by the inclusions \(\Gamma ' \hookrightarrow \Gamma \) and \(\begin{pmatrix} p &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}\Gamma ' \begin{pmatrix} p &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}^{-1} \hookrightarrow \Gamma \). If l is another prime, then we have a map
As a consequence of a result of Ihara—[22] Lemma 3.2, and see also the proof of [30] Theorem 4.1—the kernel of \(\pi ^*\) may be determined. In particular:
Theorem
(Ihara’s Lemma) If \(\mathfrak {m}\) is a non-Eisenstein maximal ideal of the Hecke algebra acting on these cohomology groups (that is, \(\mathfrak {m}\) corresponds to an irreducible Galois representation), then the map \(\pi ^*\) is injective after localizing at \(\mathfrak {m}\).Footnote 1
This was used by Ribet in [30] to prove a level-raising result for modular forms: if \(f \in S_2(\Gamma )\) is a cuspidal eigenform such that \(\overline{\rho }_f\) is irreducible and the Fourier coefficient \(a_p\) satisfies
then there is a cuspidal eigenform \(g \in S_2(\Gamma ')^{p-\text {new}}\) such that \(\overline{\rho }_f \cong \overline{\rho }_g\).
Now suppose that F is a totally real number field and that D is a quaternion division algebra over F ramified at all but one infinite place. For \(K \subset (D \otimes \mathbb {A}_{F,f})^\times \) a compact open subgroup, \(\mathfrak {p}\) a finite place of F at which K and D are unramified, and l a prime, there is an obvious (conjectural) generalisation of Theorem 1 with \(X_\Gamma \) replaced by the Shimura curve \(X_K\). We refer to this as “Ihara’s Lemma at \(\mathfrak {p}\) for \(X_K\), localized at \(\mathfrak {m}\)”; it depends on K and on a maximal ideal \(\mathfrak {m}\) of the Hecke algebra acting on \(H^1(X_K, \mathbb {F}_l)\), to which is associated a Galois representation \(\overline{\rho }_\mathfrak {m}: G_F \rightarrow GL_2(\overline{\mathbb {F}}_l)\). The purpose of this paper is to prove:
Theorem 1.1
Suppose that \(l > 2\) and that the image of \(\overline{\rho }_{\mathfrak {m}}\) contains a subgroup of \(GL_2(\overline{\mathbb {F}}_l)\) conjugate to \(SL_2(\mathbb {F}_l)\) (and satisfies an additional Taylor–Wiles hypothesis if \(l = 5\) and \(\sqrt{5} \in F\)).
Then Ihara’s Lemma at \(\mathfrak {p}\) for \(X_K\), localized at \(\mathfrak {m}\), is true.
Ihara’s method of proof does not generalise, since it relies on the “congruence subgroup property of \(SL_2(\mathbb {Z}[\frac{1}{p}])\)”, the analogue of which is a longstanding conjecture of Serre in the quaternionic case. In [13], Diamond and Taylor overcame this difficulty for Shimura curves over \(\mathbb {Q}\) using the good reduction of Shimura curves at l and comparison of mod l de Rham and étale cohomology. This necessitates various conditions on l:
-
\(\mathfrak {p}\) does not divide l;
-
D and K must be unramified at l;
-
if the result is formulated with coefficients \({\text {Sym}}^{k-2}\mathbb {F}_l\), then the weight k satisfiesFootnote 2
$$\begin{aligned} k \le l - 1. \end{aligned}$$
It seems likely that the approach of [13] can be adapted to the totally real case with similar conditions on l, as in Cheng’s draft [8] (which the author tells us is not complete), but this has not yet been carried out in full detail.
Our method of proof is entirely different, and requires no such conditions on l. On the other hand, we have to impose a more stringent condition on \(\overline{\rho }_{\mathfrak {m}}\)—rather than merely being irreducible, its image must contain the subgroup \(SL_2(\mathbb {F}_l)\).
Our starting point is that Ihara’s Lemma is known (and easy) for the “Shimura sets” associated to definite quaternion algebras. Following a strategy introduced by Ribet in [31] we introduce an auxiliary prime \(\mathfrak {q}\), at which both K and D are unramified. Then there is a totally definite quaternion algebra \(\overline{D}\) ramified at the same finite places as D, together with \(\mathfrak {q}\), and a compact open subgroup \(K^{\mathfrak {q}} \subset (\overline{D} \otimes \mathbb {A}_{F,f})^\times \) agreeing with K at all places besides \(\mathfrak {q}\) and maximal at \(\mathfrak {q}\). Our goal will then be to reduce the statement of Ihara’s Lemma for \(X_K\) at \(\mathfrak {m}\) to the corresponding (known) statement for the Shimura set \(Y_{K^{\mathfrak {q}}}\) corresponding to \(K^{\mathfrak {q}}\).
The link between \(X_K\) and \(Y_{K^{\mathfrak {q}}}\) is given by the geometry of integral models of the Shimura curve \(X_{K_0(\mathfrak {q})}\), with \(\Gamma _0(\mathfrak {q})\)-level structure. Specifically, the special fibre of \(X_{K_0(\mathfrak {q})}\) at \(\mathfrak {q}\) consists of two components, both of which are isomorphic to the special fibre of \(X_K\), and has singularities at a finite set of points which are in bijection with \(Y_{K^\mathfrak {q}}\). This results in a filtration of \(H^1(X_{K_0(\mathfrak {q})}, \mathbb {F}_l)\) whose graded pieces are two copies of \(H^0(Y_{K^\mathfrak {q}}, \mathbb {F}_l)\) and one copy of \(H^1(X_K, \mathbb {F}_l)^{\oplus 2}\). This idea has been extensively studied by Mazur, Ribet [31], Jarvis [23] and others.
Unfortunately, the existence of this filtration does not directly imply any relation between the Hecke module structures of \(H^1(X_K, \mathbb {F}_l)\) and \(H^0(Y_{K^\mathfrak {q}}, \mathbb {F}_l)\). For example, the filtration could be split (in the sense that
as Hecke modules) which would not impose any relations between \(H^1(X_{K},\mathbb {F}_l)\) and \(H^0(Y_{K^\mathfrak {q}}, \mathbb {F}_l)\). So in order to deduce anything about \(H^1(X_{K},\mathbb {F}_l)\) and \(H^0(Y_{K^\mathfrak {q}}, \mathbb {F}_l)\), we need to have additional information about the Hecke module structure of \(H^1(X_{K_0(\mathfrak {q})},\mathbb {F}_l)\) and its interaction with the filtration.
The novelty of this paper, then, is to obtain this extra information. It takes the form of a certain “flatness” statement, which we formulate and prove by using the Taylor–Wiles–Kisin patching method. To our knowledge, this is the first time that patching has been combined with the geometry of integral models in this way.
Briefly, the Taylor–Wiles–Kisin method considers a ring \(R_\infty \), which is a power series ring over the completed tensor product of various local Galois deformation rings, and relates the Hecke modules \(H^1(X_{K},\mathbb {F}_l)\), \(H^0(Y_{K^\mathfrak {q}}, \mathbb {F}_l)\) and \(H^1(X_{K_0(\mathfrak {q})},\mathbb {F}_l)\) to certain maximal Cohen–Macaulay “patched” modules over \(R_\infty \). Our method proves that the “patched” module corresponding to \(H^1(X_{K_0(\mathfrak {q})},\mathbb {F}_l)\) is flatFootnote 3 over some specific local deformation ring at the prime \(\mathfrak {q}\). Using this and some commutative algebra we are able to deduce Ihara’s Lemma for \(X_K\) from the corresponding result for \(Y_{K^{\mathfrak {q}}}\).
Our strategy for proving this flatness is inspired by Taylor’s “Ihara avoidance” argument, used in the proof of the Sato–Tate conjecture [40]. We impose the condition that our auxiliary prime \(\mathfrak {q}\) satisfies \({\text {Nm}}(\mathfrak {q})\equiv 1\pmod {l}\), and consider a certain tamely ramified principal series deformation ring, \(R^{\mathrm {ps}}_{\mathfrak {q}} = R^{\mathrm {ps}}_{\overline{\rho }_{\mathfrak {m}}\vert _{G_{F_{\mathfrak {q}}}}, \mathcal {O}}\), which is a quotient of the universal local deformation ring \(R_{\mathfrak {q}} = R^{\square }_{\overline{\rho }_{\mathfrak {m}}|_{G_{F_{\mathfrak {q}}}},\mathcal {O}}\). The standard mapFootnote 4 from \(R_{\mathfrak {q}}\) to the mod l Hecke algebra acting on \(H^1(X_{K_0(\mathfrak {q})},\mathbb {F}_l)\) then factors through the quotient \(R^{\mathrm {ps}}_{\mathfrak {q}}\), even though the map from \(R_{\mathfrak {q}}\) to the integral Hecke algebra acting on \(H^1(X_{K_0(\mathfrak {q})},\mathbb {Z}_l)\) does not.
In our situation, the assumption on the image of \(\overline{\rho }_\mathfrak {m}\) allows us to choose the auxiliary prime \(\mathfrak {q}\) so that
In this case, the ring \(R^{\mathrm {ps}}_{\mathfrak {q}}\) is a regular local ringFootnote 5 (a calculation carried out in [34]). This is what enables us to gain a foothold—it is a standard principle going back to Diamond [11] that regular local deformation rings give rise to important structural results about Hecke modules. We apply a version of the miracle flatness criterion to prove that a particular patched module is flat over \(R^{\mathrm {ps}}_{\mathfrak {q}}\), which is the key fact needed to make our argument work.
The advantage of this argument, as opposed to that of [13], is that we do not need to make any assumptions about the structure of the local deformation rings at primes dividing l, or indeed at any primes besides \(\mathfrak {q}\), beyond knowing that they have the correct dimension (a fact which certainly holds in the generality we need). This is the reason we do not need to impose any of the restrictions on the prime l appearing in earlier results.
1.1 Applications
We briefly survey some of the applications of Ihara’s Lemma (for modular or Shimura curves, or Shimura sets) that are in the literature.
1.1.1 Representation theoretic reformulation
Suppose that \(K^{\mathfrak {p}} \subset (D \otimes \mathbb {A}_{F,f}^{\mathfrak {p}})^\times \) is a compact open subgroup, and let
where the limit runs over compact open subgroups \(K_{\mathfrak {p}} \subset GL_2(F_{\mathfrak {p}})\). Then V is a smooth admissible representation of \(GL_2(F_{\mathfrak {p}})\). Suppose that \(\mathfrak {m}\) is a maximal ideal of the Hecke algebra acting on V. Then we have:
Proposition 1.2
Suppose that, for \(K = K_{\mathfrak {p}}K^{\mathfrak {p}}\) with \(SL_2(\mathcal {O}_{F,\mathfrak {p}}) \subset K_{\mathfrak {p}} \subset GL_2(\mathcal {O}_{F,\mathfrak {p}})\) a compact open subgroup, Ihara’s Lemma is true for \(X_K\) at \(\mathfrak {m}\). Then the representation \(V_\mathfrak {m}\) of \(GL_2(F_\mathfrak {p})\) has no one-dimensional subrepresentations. \(\square \)
Remark 1.3
If \(l \ne p\) then there is a notion of genericity for smooth representations of \(GL_n(F_{\mathfrak {p}})\) (see, for instance, [16]); when \(n = 2\), the non-generic smooth irreducible representations are precisely the one-dimensional ones. It is this “no non-generic subrepresentations” property that conjecturally generalises to higher rank (see [9]).
1.1.2 Freeness results
If \(\mathbb {T}\) is the algebra of Hecke operators acting on \(\mathcal {H}= H_1(X_K, \mathcal {O})_\mathfrak {m}\), including those at primes at which K ramifies, then we can ask whether \(\mathcal {H}\) is free as a \(\mathbb {T}\)-module. For modular curves results along these lines were proved by Mazur, Ribet and others (see, for instance, [14] Theorem 9.2 and [6] Theorem 4.8). In the case of Shimura curves, there are results starting with [32]. Note that it is not always the case that \(\mathcal {H}\) is free; in many cases this can be explained by the geometry of local deformation rings, as in work of the first author [27].
In [11] section 3.2, it is explained how the Taylor–Wiles method and a ‘numerical criterion’ may be used to prove freeness results at minimal and non-minimal level for modular curves (some limited freeness results for Shimura curves are also given in [11] section 3.3). At non-minimal level, this relies crucially on Ihara’s Lemma, and so using our result we can extend these freeness results. For instance, we have the following, in which \(\Sigma \) denotes the set of places where we are allowing non-minimal level.
Theorem 1.4
Let F be a totally real number field, D be a quaternion algebra over F ramified at exactly one infinite place, \(\Sigma \) a finite set of finite places of F, and \(l > 2\) be a prime.
Let \(K = \prod _v K_v \subset (D \otimes \mathbb {A}_{F,f})^\times \) be a compact open subgroup and let \(k \ge 2\) be an integer. Let \(\mathcal {H}= H_1(X_{K}, {\text {Sym}}^{k-2}(\mathcal {O}_F^2 \otimes \mathbb {Z}_l))\), and let \(\mathbb {T}_K\) be the Hecke algebra acting on \(\mathcal {H}\) generated by the \(T_v\) and \(S_v\) for \(v \not \mid l\) at which \(K_v\) is maximal compact and D is split, and the \(U_v\) for each \(v\in \Sigma \).
Let \(\mathfrak {m}\) be a maximal ideal of \(\mathbb {T}_{K}\) containing l. Suppose that the Galois representation \(\overline{\rho }\) attached to \(\mathfrak {m}\) has non-exceptional image, and that the following conditions hold.
-
(1)
For all finite places \(v \mid l\) of F, \(F_v/\mathbb {Q}_l\) is unramified and D is split at v.
-
(2)
For all finite places \(v \in \Sigma \) not dividing l, D is split and \(\overline{\rho }\) is unramified at v.
-
(3)
For all finite places \(v \not \mid l\) of F, \(\overline{\rho }|_{G_{F_v}}\) has minimal Artin conductor \(n_v\) among all its twists by characters of \(G_{F_v}\).
-
(4)
For all finite places \(v \not \mid l\) of F at which D splits, either:
-
\(v \not \in \Sigma \) and \(K_v = U_1(v^{n_v})\); or
-
\(v \in \Sigma \) and \(K_v = U_1(v^2)\).
(See (2.4) below for the definition of \(U_1(v^n)\)).
-
-
(5)
For all finite places v of F at which D ramifies, \(K_v\) is the group of units in a maximal order of \(D \otimes F_v\), and if \(\overline{\rho }\) is unramified at v then either:
-
\({\text {Nm}}(v)\not \equiv \pm 1 \pmod {l}\);
-
\({\text {Nm}}(v) \equiv 1 \pmod l\) and \(\overline{\rho }({\text {Frob}}_v)\) is not scalar; or
-
\({\text {Nm}}(v) \equiv -1 \pmod l\), and \({\text {tr}}(\overline{\rho }({\text {Frob}}_v)) \ne 0\).
-
-
(6)
If \(v \not \mid l\) is a place of F at which D splits and \({\text {Nm}}(v) \equiv -1 \pmod l\), then either \(\overline{\rho }|_{G_{F_v}}\) is reducible or \(\overline{\rho }(I_{F_v})\) has order divisible by l.
-
(7)
One of the following holds.
-
(the Fontaine–Laffaille case) \(2 \le k \le l-1\) and \(K_v\) is a maximal compact subgroup for each \(v \mid l\); or
-
(the ordinary case) \(k = 2\) and, for each \(v \mid l\), either: \(v \not \in \Sigma \) and \(K_v\) is maximal compact; or \(v \in \Sigma \), \(F_v \cong \mathbb {Q}_l\), \(K_v = U_0(v)\), and \(\overline{\rho }|_{I_{F_v}} \cong \begin{pmatrix} \epsilon &{}\quad \star \\ 0 &{}\quad 1 \end{pmatrix}\).
-
Then \(\mathcal {H}_{\mathfrak {m}}\) is free of rank 2 over \(\mathbb {T}_{K, \mathfrak {m}}\).
Proof
(sketch) For \(v \in \Sigma \), let \(K_v^{\min } \subset (D \otimes F_v)^\times \) be a maximal compact subgroup; otherwise, let \(K_v^{\min } = K_v\). Let \(K^{\min } = \prod _{v}K_v^{\min }\). The numbered conditions were chosen to ensure that all the relevant local deformation rings corresponding to forms of level \(K^{\min }\) are formally smooth. Thus the Taylor–Wiles method gives a result analogous to [11] Theorem 3.1 at level \(K^{\min }\). The result at level K now follows exactly as in the proof of [11] Theorem 3.4, using Ihara’s Lemma at each prime in \(\Sigma \). See also [39] Theorem 3.2 for a similar result in the definite case. \(\square \)
Remark 1.5
-
(1)
In the ‘Fontaine–Laffaille case’, at least if \((k-1)[F:\mathbb {Q}] \le l-2\), the version of Ihara’s lemma required would presumably follow from the method of [13], as in [8], and so the condition on the image of \(\overline{\rho }\) could be relaxed to a Taylor–Wiles hypothesis. In the ‘ordinary case’ we require Ihara’s lemma at places of \(\Sigma \) dividing l, which is apparently not accessible by the method of [13].
-
(2)
Without a condition such as (5) where D ramifies, the module may genuinely not be free, see [27].
-
(3)
Conditions (3) and (6) could probably be omitted, and the set \(\Sigma \) of non-minimal places could probably be allowed to contain places where \(\overline{\rho }\) ramifies.
-
(4)
The requirement that the weights are parallel is for convenience. The restriction to the Fontaine–Laffaille range is not required for our version of Ihara’s lemma, but is required to prove minimal freeness results using the method of [11]. Nevertheless, in other situations where the multiplicity at minimal level can be determined (even if this multiplicity is not one), it seems plausible that Ihara’s Lemma could be used to deduce information about the multiplicity at non-minimal levels.
1.1.3 Local-global compatibility
In the work of Emerton [17] on local-global compatibility in the p-adic Langlands progam, Ihara’s lemma is essential to obtain results with integral coefficients. Generalisations of Emerton’s result to compact forms of U(2) over totally real fields in which l splits have been proved in [10]—the compactness assumption ensuring that Ihara’s Lemma is known. We expect that our results (and those of [13]) could be used to prove analogues of Emerton’s Theorem 1.2.6 for the completed cohomology of Shimura curves, at least in settings where multiplicity one still holds.
1.1.4 Iwasawa theory
In [1], Bertolini and Darmon proved one divisibility in the anticyclotomic Iwasawa Main Conjecture for (certain) elliptic curves over imaginary quadratic fields. The result of [13] on Ihara’s Lemma for Shimura curves was an important technical tool in the proof. Contingent on Ihara’s Lemma for Shimura curves over totally real fields, Longo [26] generalises Bertolini and Darmon’s work to the setting of Hilbert modular forms of parallel weight two; our results therefore make his results unconditional in many cases. Further generalisations are made by Chida and Hsieh [7] and Wang [41], and our work may be able to weaken some of their hypotheses.
1.1.5 Level raising
The works [30] and [13] apply Ihara’s Lemma to the problem of level-raising for modular forms—that is, of determining at which non-minimal levels there is a newform with a given residual Galois representation. Nowadays, there is an argument of Gee [18] using the Taylor–Wiles–Kisin method and a lifting technique of Khare–Wintenberger. Combined with the results of [19] and of [4], this gives (under a Taylor–Wiles hypothesis) level raising theorems for Hilbert modular forms in arbitrary weight. We thank Toby Gee for explaining this point to us. Since we also require the Taylor–Wiles hypothesis, it is unlikely that our theorem gives substantial new level raising results.
1.2 Outline of the paper
In Sect. 2 we recall the definitions of Shimura curves and Hecke operators. We also define the Shimura sets we will need, and recall the necessary results on integral models.
Most of Sect. 3 is taken up with the calculation of local deformation rings at the auxiliary prime \(\mathfrak {q}\). We also precisely define lattices in certain inertial types (representations of \(GL_2(\mathcal {O}_{F, \mathfrak {q}})\)).
Section 4 carries out the Taylor–Wiles–Kisin patching method. We use the formalism of patching functors, introduced in [15]. This is mostly standard, and we include it because we don’t know a reference for the fact that the filtrations of homology coming from integral models may be patched.
Section 5 contains calculations in commutative algebra over the local deformation rings at \(\mathfrak {q}\) that are at the technical heart of the proof.
Section 6 contains the precise statement and proof of our theorem.
A sensible order to read this article in would be to skim Sect. 2, to fix notation, and then turn to Sect. 6, referring back to the other sections as needed.
1.3 Notation
If k is a local or global field, then \(G_k\) will denote its absolute Galois group. If l is a prime distinct from the characteristic of k, then we write \(\epsilon : G_k \rightarrow \mathbb {Z}_l\) for the l-adic cyclotomic character and \(\overline{\epsilon }\) for its reduction modulo l.
If l is a prime and M is a \(\mathbb {Z}_l\)-module, then we write \(M^\vee \) for its Pontrjagin dual. If M is a finite free \(\mathbb {Z}_l\)-module (resp. an \(\mathbb {F}_l\)-vector space, resp. a \(\mathbb {Q}_l\)-vector space), then we write \(M^* = {\text {Hom}}_{\mathbb {Z}_l}(M, \mathbb {Z}_l)\) (resp. \({\text {Hom}}_{\mathbb {F}_l}(M, \mathbb {F}_l)\), resp. \({\text {Hom}}_{\mathbb {Q}_l}(M, \mathbb {Q}_l)\)).
2 Shimura curves
2.1 Let F be a totally real number field of degree d and let \(\mathcal {O}_F\) be the ring of integers of F. We write \(\mathbb {A}_{F,f}\) for the finite adeles of F. If v is a place of F then we write \(k_v\) for its residue field, \(\varpi _v\) for a fixed choice of uniformizer in \(F_v\), and \(\mathbb {A}^{v}_{F,f}\) for the finite adeles of F with the factor \(F_v\) dropped. If l is a rational prime then we write \(\Sigma _l\) for the set of places of F above l; we write \(\Sigma _\infty \) for the set of infinite places of F.
2.2 Let D be a quaternion division algebra over F split at either no infinite places (the definite case) or exactly one infinite place, \(\tau \) (the indefinite case), and let \(\mathcal {O}_D\) be a maximal order in D. We write \(\Delta \) for the set of finite places of F at which D ramifies. We assume that if \(F = \mathbb {Q}\) and we are in the indefinite case then \(\Delta \) is nonempty.
We write G for the algebraic group over \(\mathcal {O}_F\) associated to \(\mathcal {O}_D^\times \), and Z for its centre.
For every place v at which D splits we fix an isomorphism \(\kappa _v : \mathcal {O}_D \otimes _{\mathcal {O}_F} \mathcal {O}_{F,v} \xrightarrow {\sim }M_2(\mathcal {O}_{F,v})\). We also denote by \(\kappa _v\) the various isomorphisms, such as \((D \otimes _F F_v)^\times \xrightarrow {\sim }GL_2(F_v)\), obtained from it.
2.3 We fix a rational prime l and a finite place \(\mathfrak {p}\) of F such that \(\mathfrak {p}\not \in \Delta \); we do allow the possibility that \(\mathfrak {p}\mid l\).
2.4 Let K be a compact open subgroup of \(G(\mathbb {A}_{F,f})\). If v is a finite place of F then when it is possible to do so we will write \(K = K^vK_v\) for \(K^v \subset G(\mathbb {A}_{F,f}^v)\) and \(K_v \subset G(F_v)\). A compact open subgroup K of \(G(\mathbb {A}_{F,f})\) is unramified at v if \(v \not \in \Delta \) and \(K = K^vG(\mathcal {O}_{F,v})\) for some \(K^v\), and that it is ramified otherwise. We let
If \(v \not \in \Delta \) is a finite place of F, and \(n \ge 1\), then we define \(U_0(v^n)\) to be the subgroup
of \(G(\mathcal {O}_{F,v})\), and
If K is unramified at v then we write
2.5 Suppose that we are in the indefinite case. Letting \(\mathcal {H}= \mathbb {C}\setminus \mathbb {R}\) be acted on by \(GL_2(\mathbb {R})\) in the usual way, via \(\kappa _\tau \) we get an action of \(G(F_\tau ) \cong GL_2(\mathbb {R})\) on \(\mathcal {H}\). We say that K is sufficiently small if the action of \(G(F) \cap gKg^{-1} / Z(F) \cap gKg^{-1}\) on \(\mathcal {H}\) is free for every \(g \in G(\mathbb {A}_{F,f})\). We will assume throughout that all our compact open subgroups are sufficiently small. We let
a compact Riemann surface. By the theory of Shimura varieties, there is a smooth projective curve \(X_K\) over F such that, when F is considered as a subfield of \(\mathbb {C}\) via \(\tau \), the \(\mathbb {C}\)-points of \(X_K\) are given by the above formula. For \(\mathcal {F}\) a sheaf of abelian groups on \(X_K(\mathbb {C})\) we write \(H^i(X_K, \mathcal {F}) = H^i(X_K(\mathbb {C}), \mathcal {F}).\)
2.6 Write \([\gamma ,x]\) for the point in \(X_K(\mathbb {C})\) corresponding to \(\gamma \in G(\mathbb {A}_{F,f})\) and \(x \in \mathcal {H}\). If \(K' \subset K \subset G(\mathbb {A}_{F,f})\) are compact open subgroups then there is a map \(X_{K'} \rightarrow X_K\) given on complex points by \([\gamma , x] \mapsto [\gamma , x]\). For \(g \in G(\mathbb {A}_{F,f})\) there is a map \(\rho _g : X_K \rightarrow X_{g^{-1}Kg}\) given on \(\mathbb {C}\)-points by
The maps \(\rho _g\) define a right action of \(G(\mathbb {A}_{F,f})\) on the inverse system \((X_K)_K\); if \(g^{-1}Kg \subset K'\) then we will also write \(\rho _g\) for the composite map
2.7 Let M be an abelian group. Suppose that \(K_1, K_2 \subset G(\mathbb {A}_{F,f})\) are sufficiently small and that \(g \in G(\mathbb {A}_{F,f})\). Then, as in [3] section 4, there are double coset operators
for \(i = 0, 1, 2\). If \(v \not \in \Sigma (K)\cup \Sigma _\infty \) then we define the Hecke operators \(T_v\) and \(S_v\) to be the double coset operators
and
If A is a ring and S is a finite set of places containing \(\Delta \cup \Sigma _\infty \) then we write
a polynomial ring in infinitely many variables which acts on \(H^i(X_{K}, M)\) for any K for which \(\Sigma (K) \subset S\) and any A-module M.
If \(v\not \in \Delta \), then we define the Hecke operator \(U_{v}\) to be the double coset operator
acting on any \(H^i(K, M)\) for M an abelian group (note that \(U_v = T_v\) if K is unramified at v).
2.8 Now suppose that we are in the definite case. A compact open subgroup \(K \subset G(\mathbb {A}_{F,f})\) is sufficiently small if, for every \(g \in G(\mathbb {A}_{F,f})\), we have
Again, we will always assume that our compact open subgroups are sufficiently small. We define
which is a finite set. Exactly as in the indefinite case, we define an action of \(G(\mathbb {A}_{F,f})\) on the inverse system \((Y_K)_K\), and actions of double coset operators \([K_1gK_2]\) and Hecke operators \(T_v\), \(S_v\) and \(U_v\) on the groups \(H^0(Y_K, M)\), for any abelian group M. In particular, we obtain an action of \(\mathbb {T}_A^S\) on \(H^0(Y_K, M)\) for any finite set of places S containing \(\Sigma (K)\), ring A, and A-module M.
2.9 Suppose that we are in the definite or indefinite case, and that A is a finite \(\mathbb {Z}_l\)-algebra, so that the residue field of any maximal ideal of A is a finite extension of \(\mathbb {F}_l\).
Definition 2.1
A maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}_{A}^S\) is G-automorphic of level K if it is in the support of \(H^i(X_K, A)\) (in the indefinite case) or \(H^i(Y_K, A)\) (in the definite case) for some i. It is G-automorphic if it is G-automorphic of level K for some K.
If \(\mathfrak {m}\) is a G-automorphic maximal ideal of \(\mathbb {T}_{A}^S\) then there is an associated semisimple representation
characterised by \({\text {char}}_{\overline{\rho }_{\mathfrak {m}}({\text {Frob}}_v)}(X) = X^2 - T_vX + {\text {Nm}}(v)S_v\) for all \(v \not \in S \cup \Sigma _l\).
Definition 2.2
An G-automorphic maximal ideal of \(\mathbb {T}_{A}^S\) is non-Eisenstein if \(\overline{\rho }_{\mathfrak {m}}\) is absolutely irreducible, and Eisenstein otherwise. A \(\mathbb {T}_{A}^S\)-module is Eisenstein if every maximal ideal in its support is Eisenstein.
It is non-exceptional if \(\overline{\rho }_{\mathfrak {m}}(G_F)\) contains a subgroup of \(GL_2(\overline{\mathbb {F}}_l)\) conjugate to \(SL_2(\mathbb {F}_l)\); equivalently if it is non-Eisenstein and the image of \(\overline{\rho }_{\mathfrak {m}}\) contains an element of order l. Otherwise, it is exceptional.
Proposition 2.3
Suppose that we are in the indefinite case. The \(\mathbb {T}^S_A\)-modules \(H^0(X_K, A)\) and \(H^2(X_K, A)\) are Eisenstein.
Proof
Let \(\nu : G \rightarrow \mathbb {G}_{m,F}\) be the reduced norm. There is (see [5] section 1.2) a bijection
where \(F^{\times ,+}\) is the set of totally positive elements of \(F^{\times }\). Write \(C_K\) for the group on the right. If \(g \in G(\mathbb {A}_{F,f})\) then \(C_K = C_{g^{-1}Kg}\) and the diagram

commutes. This implies that \(\mathbb {T}^S_{A}\) acts on \(H^0(X_K(\mathbb {C}), A) \cong A[C_K]\) via the homomorphism \(\mathbb {T}^S_{A} \rightarrow A[C_K]\) given by
where we write [g] for the basis element of \(A[C_K]\) corresponding to g. If \(\mathfrak {n}\) is a maximal ideal of \(A[C_K]\) with residue field \(\mathbb {F}\), corresponding to a character \(\chi : C_K \rightarrow \mathbb {F}^\times \), then \(T_v\) and \(S_v\) act on \(A[C_K]/\mathfrak {n}\) as \(({\text {Nm}}(v) + 1)\chi (\varpi _v)\) and \(\chi (\varpi _v^2)\) respectively. If \(\psi :G_F \rightarrow \mathbb {F}^\times \) is the character of \(G_F\) associated to \(\chi \) by class field theory, and \(\overline{\rho }= \psi \oplus \epsilon \psi \), then \(T_v\) and \({\text {Nm}}(v)S_v\) act on \(A[C_K]/\mathfrak {n}\) by the scalars \({\text {tr}}(\overline{\rho }({\text {Frob}}_v))\) and \(\det (\overline{\rho }({\text {Frob}}_v))\), so that the action of \(\mathbb {T}^S_A\) on \(A[C_K]/\mathfrak {n}\) factors through an Eisenstein maximal ideal as required. It follows that the action of \(\mathbb {T}^S_A \) on \(H^0(X_K,A)\) is Eisenstein.
The statement for \(H^2\) follows from Poincaré duality
and the formulae \(S_v^* = S_v^{-1}\) and \(T_v^{*} = S_v^{-1}T_v\) for the adjoints of \(T_v\) and \(S_v\). \(\square \)
2.10 Let A be a finite \(\mathbb {Z}_l\)-algebra. There is an exact functor \(M \mapsto \mathcal {L}_M\) from the category of A[K]-modules on which \(K \cap Z(F)\) acts trivially, to the category of local systems of A-modules on \(X_K(\mathbb {C})\) or \(Y_K\). If S is a finite set of places of F containing \(\Sigma (K) \cup \Sigma _l\cup \Delta \cup \Sigma _\infty \), and such that the action of K on M factors through \(\prod _{v \in S} K_v\), then we obtain an action of the Hecke algebra \(\mathbb {T}^S_A\) on each cohomology group \(H^i(X_K, \mathcal {L}_M)\) or \(H^0(Y_K, \mathcal {L}_M)\).
Proposition 2.4
Suppose that we are in the indefinite case. For any A, M and S as above, the \(\mathbb {T}^S_{A}\)-module \(H^i(X_K, \mathcal {L}_M)\) is Eisenstein for \(i = 0, 2\).
Proof
This is proved just as in Proposition 2.3. \(\square \)
2.11 Suppose that K is unramified at \(\mathfrak {p}\). Let \(\omega = \begin{pmatrix} \varpi _\mathfrak {p} &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}\). Then since \(\omega K_0(\mathfrak {p}) \omega ^{-1} \subset K\), we have two degeneracy maps \(\pi _1, \pi _2\) defined (in the notation of 2.6) by
(with similar formulae in the definite case). If A is an abelian group then we obtain maps
with, again, similar formulae in the definite case. We write
If M, \(\mathcal {L}_M\), and S are as in 2.10 and if \(\mathfrak {p}\not \in \Sigma (K)\cup \Sigma _\infty \) is such that the action of K on M factors through \(K^{\mathfrak {p}}\), then we can similarly define
(and analogous maps in the definite case).
2.12 Define the finite abelian (class) group \(\Gamma _K\) by
It acts freely on \(X_K\) and \(Y_{K}\) by our assumption that K is sufficiently small.
Suppose that A is a finite \(\mathbb {Z}_l\)-algebra and that \(\psi \) is a character \(\mathbb {A}_{F,f}^\times /F^\times \rightarrow A^\times \) that vanishes on \(K \cap Z(\mathbb {A}_{F,f})\) (regarded as a subgroup of \(Z(\mathbb {A}_{F,f}) = \mathbb {A}_{F,f}^\times \)), so that we may consider \(\psi \) as a character of \(\Gamma _K\). For M any \(A[\Gamma _K]\)-module, we write \(M[\psi ]\) for the largest submodule of M on which \(\Gamma _K\) acts as \(\psi \) and \(M_\psi \) for the largest quotient module of M on which \(\Gamma _K\) acts as \(\psi \).
Lemma 2.5
Let A be as above, and let \(\mathfrak {m}\) be a non-Eisenstein maximal ideal of \(\mathbb {T}^S_A\). Then \(H^0(Y_{K},A^\vee )_\mathfrak {m}\) and \(H^1(X_K,A^\vee )_\mathfrak {m}\) are injective \(A[\Gamma _K]\)-modules.
Proof
In the indefinite case, we use the Hochschild–Serre sequence and fact that \(\mathfrak {m}\) is non-Eisenstein. Let V be an \(A[\Gamma _K]\)-module and let \(\mathcal {L}_V^\vee \) be the local system on \(X_K/\Gamma _K\) associated to \(V^\vee \). The action of the Hecke operators away from ramified primes descends to an action on \(H^i(X_K/\Gamma _K, \mathcal {L}_V^\vee )\). Then
is Eisenstein by Proposition 2.4, and the same is true for \(H^2(X_K/\Gamma _K, \mathcal {L}_V^\vee )\) by Poincaré duality. As \(H^0(X_K, \mathcal {L}_V^\vee )_\mathfrak {m}\) vanishes by Proposition 2.4,
and the latter is an exact functor of V as \(\mathfrak {m}\) is non-Eisenstein. In the definite case the proof is similar but easier (and the assumption on \(\mathfrak {m}\) is not actually necessary). \(\square \)
2.13 For the rest of this section we suppose that we are in the indefinite case, and fix a finite place \(\mathfrak {q}\not \in \Delta \cup \Sigma _l\) of F, let \(\mathcal {O}_{(\mathfrak {q})}\) be the localization of \(\mathcal {O}_F\) at \(\mathfrak {q}\), let k be the residue field of \(\mathfrak {q}\), and let \(\overline{k}\) be an algebraic closure of k. By a model of \(X_K\) we will mean a proper flat \(\mathcal {O}_{(\mathfrak {q})}\)-scheme \(\mathfrak {X}_K\) equipped with an isomorphism \(\mathfrak {X}_K \otimes _{\mathcal {O}_{(\mathfrak {q})}} F \xrightarrow {\sim }X_K\).
We will consider K that are (sufficiently small and) of the form \(K^{\mathfrak {q}}GL_2(\mathcal {O}_{F,\mathfrak {q}})\) or \(K^{\mathfrak {q}}U_0(\mathfrak {q})\). For such K, there are models \(\mathfrak {X}_K\) of \(X_K\) constructed by Morita [29] (in the first case) and by Jarvis [23], following Carayol [5] (in the second). They have the following properties:
Theorem 2.6
Suppose that K is unramified at \(\mathfrak {q}\).
-
(1)
The curve \(\mathfrak {X}_K\) is smooth over \(\mathcal {O}_{(\mathfrak {q})}\).
-
(2)
The curve \(\mathfrak {X}_{K_0(\mathfrak {q})}\) is regular and \(\mathfrak {X}_{K_0(\mathfrak {q})} \otimes _{\mathcal {O}_{(\mathfrak {q})}} \overline{k}\) is the union of two curves, each isomorphic to \(\mathfrak {X}_{K} \otimes _{\mathcal {O}_{(\mathfrak {q})}}\overline{k}\), that intersect transversely at a finite set of points.
Remark 2.7
We will use implicitly the functoriality of these models. For instance, if \(K \subset K'\) are as above then the morphism \(X_{K} \rightarrow X_{K'}\) extends uniquely to a finite flat morphism between the models. If \(K_{\mathfrak {q}}\) is fixed, then the action of \(G(\mathbb {A}_{F,f}^{\mathfrak {q}})\) on the inverse system \((X_{K^{\mathfrak {q}}K_{\mathfrak {q}}})_{K^\mathfrak {q}}\) extends uniquely to the inverse system of models. This action is compatible with varying \(K_{\mathfrak {q}}\), and with the maps \(\mathfrak {X}_K \otimes _{\mathcal {O}_{(\mathfrak {q})}} \overline{k} \rightarrow \mathfrak {X}_{K_0(\mathfrak {q})} \otimes _{\mathcal {O}_{(\mathfrak {q})}} \overline{k}\) implicit in part 2 of the theorem.
2.14 Suppose that K is unramified at \(\mathfrak {q}\).
Definition 2.8
The set of points where the two components of \(\mathfrak {X}_{K_0(\mathfrak {q})} \otimes \overline{k}\) intersect maps injectively to \(\mathfrak {X}_{K}\otimes \overline{k}\) under the natural map \(\mathfrak {X}_{K_0(\mathfrak {q})} \rightarrow \mathfrak {X}_{K}\). The image is a finite set of points called the supersingular points and is denoted \(\mathfrak {X}_K^{\text {ss}}\).
There is an adelic description of this set that we now explain. Let \(\overline{D}\) be a quaternion algebra over F ramified at \(\Delta \cup \{\mathfrak {q}, \tau \}\) and let \(\overline{G}\) be the algebraic group over F associated to \(\overline{D}^\times \). We fix a continuous isomorphism
Let \(\mathcal {O}_{\overline{D},\mathfrak {q}}\) be the unique maximal order of \(D \otimes _F F_\mathfrak {q}\). Then we write
Remark 2.9
It follows from the Jacquet–Langlands correspondence that, if K is unramified at \(\mathfrak {q}\) and \(\mathfrak {m}\) is in the support of \(H^0(Y_{K^\mathfrak {q}}, A)\), then \(\mathfrak {m}\) is in the support of \(H^1(X_{K_0(\mathfrak {q})}, A)\).
Theorem 2.10
([5] (11.2)) There is a \(G(\mathbb {A}_{F,f}^\mathfrak {q})\)-equivariant isomorphism of inverse systems
2.15 Suppose that K is unramified at \(\mathfrak {q}\) and that \(\mathbb {F}\) is a finite extension of \(\mathbb {F}_l\). The geometry of \(\mathfrak {X}_{K_0(\mathfrak {q})}\) and the theory of vanishing cycles allow us to relate \(H^1(X_{K_0(\mathfrak {q})}, \mathbb {F})\), \(H^1(X_{K}, \mathbb {F})\) and \(H^0(Y_{K^{\mathfrak {q}}}, \mathbb {F})\). In the case at hand, this is worked out in [23], sections 14-18. We recall the result in our notation:
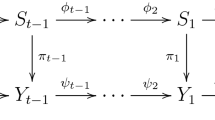
Theorem 2.11
Suppose that K is unramified at \(\mathfrak {q}\). Let S be a finite set of places containing \(\Sigma (K) \cup \{\mathfrak {q}\} \cup \Sigma _\infty \cup \Delta \) and let \(\mathfrak {m}\) be a non-Eisenstein maximal ideal of \(\mathbb {T}^S_K\). Then there is a filtration
together with isomorphisms
and
The filtration, and isomorphisms, are compatible with the transition morphisms for varying \(K^{\mathfrak {q}}\) and with the action of the Hecke operators \(T_v\) and \(S_v\) for \(v \not \in \Sigma (K) \cup \{\mathfrak {q}\}\cup \Delta \) and \(U_v\) for \(v\not \in \{\mathfrak {q}\}\cup \Delta \).
Proof
As mentioned, this is proved in [23]: we give references to that paper. The key diagram is that at the end of section 14, which relates Hecke-modules X(H), Y(H), \({\tilde{X}}(H)\), \({\tilde{Y}}(H)\), M(H), and R(H). In particular, there is a filtration of M(H) with graded pieces \({\tilde{X}}(H)\), R(H), and \({\tilde{Y}}(H)\). Choosing the group H in that paper appropriately, taking the sheaf there called \(\mathcal {F}\) to be the constant sheaf \(\mathbb {F}\), and after localizing at \(\mathfrak {m}\), we have that \(M(H)_\mathfrak {m}\) is our \(H^1(X_{K_0(\mathfrak {q})}, \mathbb {F})_\mathfrak {m}\), while \(R(H)_\mathfrak {m}\) is our \(H^1(X_K,\mathbb {F})_\mathfrak {m}^{\oplus 2}\) (see [23] Corollary 16.3). A choice of ordering of the irreducible components of each connected component of the special fibre of \(\mathfrak {X}_{K_0(\mathfrak {q})}\) gives, by Theorem 2.10, an isomorphism between \(Y(H)_\mathfrak {m}\) and \(H^0(Y_{K^{\mathfrak {q}}}, \mathbb {F})_\mathfrak {m}\). By Proposition 2.3, or [23] Lemma 18.1, we have \(Y(H)_\mathfrak {m}\cong {\tilde{Y}}(H)_\mathfrak {m}\). By [23] Proposition 17.4 and Lemma 18.2, we have (Hecke-equivariant) isomorphisms \({\tilde{X}}(H)_\mathfrak {m}\cong X(H)_\mathfrak {m}\cong Y(H)_\mathfrak {m}\). The result follows. \(\square \)
It follows from Lemma 2.5 that we can take \(\psi \)-parts in the filtration of Theorem 2.11 to obtain a filtration of \(H^1(X_{K_0(\mathfrak {q})}, \mathbb {F})_\mathfrak {m}[\psi ]\) with graded pieces \(H^0(Y_{K^{\mathfrak {q}}}, \mathbb {F})_\mathfrak {m}[\psi ]\), \(H^1(X_K,\mathbb {F})_\mathfrak {m}^{\oplus 2}[\psi ]\), \(H^0(Y_{K^{\mathfrak {q}}}, \mathbb {F})_\mathfrak {m}[\psi ]\) for any non-Eisenstein maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}^S_\mathbb {F}\).
3 Types and local deformation rings
For this section, let L be a local field of characteristic 0, with residue field k of order q. Let \(\Gamma \) be the absolute Galois group of L, I its inertia subgroup, and P its wild inertia subgroup. Let \(\sigma \in I\) be a lift of a topological generator of I/P, and let \(\phi \in \Gamma \) be a lift of arithmetic Frobenius. Then we have the well-known relation \(\phi \sigma \phi ^{-1} = \sigma ^q\) in \(\Gamma /P\).
For this section and Sect. 4 we assume that \(l > 2\). By a coefficient system we will mean a triple \((E, \mathcal {O}, \mathbb {F})\) where: \(E/\mathbb {Q}_l\) is a finite extension, with ring of integers \(\mathcal {O}\), uniformizer \(\varpi \), and residue field \(\mathbb {F}= \mathcal {O}/\varpi \). For now, we will take an arbitrary coefficient system; later we will impose further conditions on \(E/\mathbb {Q}_l\).
Let \(\mathcal {C}_\mathcal {O}\) (resp. \(\mathcal {C}_\mathcal {O}^\wedge \)) be the category of Artinian (resp. complete Noetherian) local \(\mathcal {O}\)-algebras with residue field \(\mathbb {F}\). We say that a functor \(\mathcal {F}:\mathcal {C}_\mathcal {O}\rightarrow \mathbf{Set}\) is pro-represented by some \(R\in \mathcal {C}^\wedge _\mathcal {O}\) if \(\mathcal {F}\) is naturally isomorphic to \({\text {Hom}}_{\mathcal {O}}(R,-)\).
Now fix a continuous representation \(\overline{\rho }:\Gamma \rightarrow GL_2(\mathbb {F})\). The primary goal of this section is to introduce various deformation rings of \(\overline{\rho }\). Many treatments of this material assume that the coefficient ring \(\mathcal {O}\) is sufficiently ramified. For our purposes, it will be necessary to precisely control the ramification of \(\mathcal {O}\), and so a little more care will be needed in certain parts.
Consider the (framed) deformation functor \(\mathcal {C}_\mathcal {O}\rightarrow \mathbf{Set}\) defined on objects A by
It is well-known that this functor is pro-representable by some \(R^\square _{\overline{\rho },\mathcal {O}}\in \mathcal {C}^\wedge _\mathcal {O}\). Furthermore, \(\overline{\rho }\) admits a universal lift \(\rho ^\square :\Gamma \rightarrow GL_2(R^\square _{\overline{\rho },\mathcal {O}})\).
For any continuous homomorphism, \(x:R^\square _{\overline{\rho },\mathcal {O}}\rightarrow \overline{E}\), we obtain a Galois representation \(\rho _x:\Gamma \rightarrow GL_2(\overline{E})\) lifting \(\overline{\rho }\), from the composition \(\Gamma \xrightarrow {\rho ^\square } GL_2(R^\square _{\overline{\rho },\mathcal {O}})\xrightarrow {x} GL_2(\overline{E})\).
For any character \(\psi : \Gamma \rightarrow \mathcal {O}^\times \) with \(\det \overline{\rho }\cong \psi \epsilon ^{-1} \pmod {\varpi }\) define \(R^{\square ,\psi }_{\overline{\rho },\mathcal {O}}\) to be the quotient of \(R^\square _{\overline{\rho },\mathcal {O}}\) on which \(\det \rho ^{\square }= \psi \epsilon ^{-1}\). Equivalently, \(R^{\square ,\psi }_{\overline{\rho },\mathcal {O}}\) is the ring pro-representing the functor of lifts of \(\overline{\rho }\) with determinant \(\psi \epsilon ^{-1}\).
As \(l > 2\), we have an isomorphism
where \(R_{\det (\overline{\rho }), \mathcal {O}}\) is the universal deformation ring of the character \(\det (\overline{\rho })\).
3.1 Deformation rings when \(l\not \mid q\)
For this subsection, we assume that \(l\not \mid q\). In this case, the \(\mathcal {O}\)-algebras \(R^{\square ,\psi }_{\overline{\rho },\mathcal {O}}\) and \(R^{\square }_{\overline{\rho },\mathcal {O}}\) are flat of relative dimensions 3 and 4, respectively. The second statement follows from [36] Theorem 2.5. The first statement follows from the second, the isomorphism (1), and the flatness of the deformation ring of a character (see for example [35] Lemma 2.5). Shortly, we will analyse these rings in more detail in a particular case.
3.2 Deformation rings when l|q
Now assume that l|q, so that l is the residue characteristic of L. If \(L'/L\) is any finite extension, then by [24] there is a quotient \(R^{\square , L'\text {-st}}_{\overline{\rho }, \mathcal {O}}\) of \(R^\square _{\overline{\rho }, \mathcal {O}}\) such that a continuous \(\mathcal {O}\)-algebra homomorphism \(x : R^{\square }_{\overline{\rho }, \mathcal {O}} \rightarrow \overline{E}\) factors through \(R^{\square , L'\text {-st}}_{\overline{\rho }, \mathcal {O}}\) if and only if \(\rho _x|_{G_{L'}}\) is semistable with parallel Hodge–Tate weights \(\{0,1\}\). For \(\psi \) a finite order character of \(\Gamma \) that factors through \({\text {Gal}}(L'/L)\), there is a quotient \(R^{\square , \psi , L'\text {-st}}_{\overline{\rho }, \mathcal {O}}\) of \(R^{\square , L'\text {-st}}_{\overline{\rho }, \mathcal {O}}\) on which we additionally impose the condition \(\det (\rho ) = \psi \epsilon ^{-1}\). We have that \({\text {Spec}}R^{\square , \psi , L'\text {-st}}_{\overline{\rho }, \mathcal {O}}\) is equidimensional of dimension \(3 + [L:\mathbb {Q}_l]\).
3.3 Deformation rings at the auxiliary prime \(\mathfrak {q}\)
In this subsection, we study the specific local deformation ring \(R_{\mathfrak {q}} = R^{\square }_{\overline{\rho }_\mathfrak {m}|_{F_\mathfrak {q}},\mathcal {O}}\) that will occur at the auxiliary prime \(\mathfrak {q}\) in our argument, and define and compute certain quotients of it.
From now on assume that \(q\equiv 1 \pmod {l}\) (so that in particular \(l\not \mid q\)), and let \(\overline{\rho }: \Gamma \rightarrow GL_2(\mathbb {F})\) be the unramified representation with \(\overline{\rho }(\phi )=\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}\). Note that both \(\overline{\epsilon }\) and \(\det (\overline{\rho })\) are the trivial character.
We will now impose a hypothesis on our coefficient system:
Hypothesis 3.1
The coefficient system \((E, \mathcal {O}, \mathbb {F})\) is such that \(\mathcal {O}= W(\mathbb {F})[\zeta + \zeta ^{-1}]\) for a primitive lth root of unity \(\zeta \in \mathcal {O}\).
Under this hypothesis, we write \(W=W(\mathbb {F})\) be the ring of Witt vectors and let \(E_0 = W[1/l]\), so that \(E_0\) is an unramified extension of \(\mathbb {Q}_l\) with residue field \(\mathbb {F}\). We fix \(\zeta \in \overline{E}_0\) a primitive lth root of unity. We also let
and note that this is a uniformizer of \(\mathcal {O}\).
We define the following quotients of \(R^\square _{\overline{\rho }, \mathcal {O}}\) in terms of the subfunctors that they represent:
-
\(R^{\mathrm {nr}}_{\overline{\rho }, \mathcal {O}}\) parametrises lifts \(\rho \) of \(\overline{\rho }\) that are unramified.
-
\(R^{N}_{\overline{\rho }, \mathcal {O}}\) parametrises lifts \(\rho \) of \(\overline{\rho }\) such that
$$\begin{aligned} {\text {char}}_{\rho (\sigma )}(T) = (T-1)^2 \end{aligned}$$and
$$\begin{aligned} ({\text {tr}}\rho (\phi ))^2q = (q+1)^2 \det \rho (\phi ). \end{aligned}$$ -
\(R^{\mathrm {unip}}_{\overline{\rho }, \mathcal {O}}\) parametrises lifts \(\rho \) of \(\overline{\rho }\) such that
$$\begin{aligned} {\text {char}}_{\rho (\sigma )}(T) = (T-1)^2 \end{aligned}$$and
$$\begin{aligned} \left( ({\text {tr}}\rho (\phi ))^2q - (q+1)^2 \det \rho (\phi )\right) \cdot (\rho (\sigma ) - 1) = 0. \end{aligned}$$ -
\(R^{\mathrm {ps}}_{\overline{\rho }, \mathcal {O}}\) parametrises lifts \(\rho \) of \(\overline{\rho }\) such that
$$\begin{aligned} {\text {char}}_{\rho (\sigma )}(T)&= T^2 - (\zeta + \zeta ^{-1})T + 1 \\&= (T- \zeta )(T - \zeta ^{-1}). \end{aligned}$$
Remark 3.2
The relation “\(q{\text {tr}}(\phi )^2 = (q + 1)^2 \det (\phi )\)” should be thought of as saying that the eigenvalues of \(\rho (\phi )\) are in the ratio q : 1, which is the case for all characteristic zero lifts of \(\overline{\rho }\) for which the image of inertia is non-trivial and unipotent.
Remark 3.3
It is important for us that \(R^\mathrm {ps}_{\overline{\rho }, \mathcal {O}}\) be defined over \(\mathcal {O}\) and not just \(\mathcal {O}[\zeta ]\).
Fix an unramified character \(\psi : \Gamma \rightarrow \mathcal {O}^\times \) lifting the trivial character \(\det (\overline{\rho })\overline{\epsilon }\). Note that, on each of these quotients, we have that \(\det (\rho ^\square )\) is unramified, and so agrees with \(\psi \epsilon ^{-1}\) on I. For \(? \in \{N, \mathrm {nr}, \mathrm {unip}, \mathrm {ps}\}\), we make the following definitions:
-
\(R^{?, \psi }_{\overline{\rho }, \mathcal {O}}\) is the quotient of \(R^?_{\overline{\rho }, \mathcal {O}}\) on which \(\det (\rho ^\square ) = \psi \epsilon ^{-1}\);
-
\(\overline{R}^?_{\overline{\rho }} = R^?_{\overline{\rho },\mathcal {O}}\otimes _\mathcal {O}\mathbb {F}\);
-
\(\overline{R}^{?, \psi }_{\overline{\rho }} = R^{?, \psi }_{\overline{\rho }, \mathcal {O}}\otimes _\mathcal {O}\mathbb {F}\).
We will need somewhat explicit descriptions of these rings, which were obtained in Proposition 5.8 of [34] and its proof. Let
and
We will choose more convenient coordinates. We may replace B by \(X = \frac{B}{1+R}\), Q by \(T = {\text {tr}}(\rho ^\square (\phi )) - 2\), and S by \(\delta = \det (\rho ^{\square }(\phi )) - 1\). By this we mean that the natural map
is surjective, which follows from the formulae \(B = (1+R)X\), \(Q = T - P\), and \(S = (1+R)^{-1}(T + P(T-P) - \delta )\). Then we may replace T by either
or
by which we mean that the natural maps
are surjections. This follows from the equation \(T = \sqrt{4 + Y_1 + 4\delta } - 2\) in the first case—where the square root is defined by a convergent Taylor series, as \(l > 2\)—and a similar expression in the second. We have maps
Remark 3.4
Write \(\gamma = \epsilon (\phi )^{-1}\psi (\phi ) - 1 \in \mathcal {O}\). Then the maps \(\alpha _i\) descend to maps, also denoted \(\alpha _i\),
In the proofs of all of the following propositions we work without fixing determinants. For each \(? \in \{N, \mathrm {nr}, \mathrm {unip}, \mathrm {ps}\}\) we already have that \(\det (\rho ^\square )\) is unramified on the quotient \(R^?_{\mathcal {O}, \overline{\rho }}\). This means that to get the fixed determinant versions in the statements, we simply quotient by \(\delta - \gamma \).
Proposition 3.5
The ring \(R^{\mathrm {ps}, \psi }_{\overline{\rho }, \mathcal {O}}\) is isomorphic (via \(\alpha _1\)) to
In particular, it is regular.
Proof
This follows from the proof of [34] Proposition 5.8 part 2. The quantity denoted y in the proof of that proposition is here equal to 1. The variables \(X_1, \ldots X_5\) in that proof are our variables \(X, Y_1, P, R, 2P - T\), but by the above remarks we can replace \(2P- T\) with \(\delta \) and obtain that \(\alpha _1\) defines an isomorphism
The result with fixed determinant follows. \(\square \)
Proposition 3.6
The ring \(R^{\mathrm {unip}, \psi }_{\overline{\rho }, \mathcal {O}}\) is isomorphic (via \(\alpha _2\)) to
and its quotients \(R^{\mathrm {nr}, \psi }_{\overline{\rho }, \mathcal {O}}\) and \(R^{N, \psi }_{\overline{\rho }, \mathcal {O}}\) are, respectively,
In particular, these last two deformation rings are formally smooth.
Proof
This is not quite in [34] Proposition 5.8, as the quotient \(R^{\mathrm {unip}}_{\overline{\rho }, \mathcal {O}}\) is not considered there, but the method of proof extends easily—we will be brief. The proof shows that, if we write \(U = P-Q\) and \(\alpha (T) = \frac{(q-1)(2+T)}{q+1}\), then \(R^{\mathrm {unip}}_{\overline{\rho }, \mathcal {O}}\) is cut out of \(\mathcal {O}[[A,X,C,D,U,T,R,S]]\) by the following equations:
Here \(\star \) denotes each of A, X, C, D, so that the third line is really four equations. Note that the third line can be rewritten as \(\star Y_2 = 0\). The first, fourth and sixth lines show that A, C and D may be written in terms of X, T, S and U. Making these substitutions we see that this set of equations is equivalent to the single equation \(X(4(1+R)S + (U^2 - \alpha (T)^2)) = 0\). But if we now replace T, S and U by \(Y_2\), \(\delta \) and P as discussed above, we obtain that \(R^{\mathrm {unip}}_{\mathcal {O}, \overline{\rho }}\) is the quotient of \(\mathcal {O}[[X,Y_2, P, R, \delta ]]\) by \(XY_2 = 0\) as required.
The expressions for the quotients \(R^{\mathrm {nr}}_{\overline{\rho }, \mathcal {O}}\) and \(R^N_{\overline{\rho }, \mathcal {O}}\) follow immediately, and finally we eliminate \(\delta \) by imposing the fixed determinant condition. \(\square \)
Proposition 3.7
The images of \(Y_1\) and \(Y_2\) are equal in \(\overline{R}^{\square , \psi }_{\overline{\rho }}\). Denoting this common image by Y, the diagram

commutes.
Proof
That the images of \(Y_1\) and \(Y_2\) are equal is immediate from \(q \equiv 1 \pmod l\). The diagram commutes since \(\alpha _1\) and \(\alpha _2\) are equal as maps \(\mathbb {F}[[X,Y,P,R]] \rightarrow \overline{R}^{\square }_{\overline{\rho }}\). \(\square \)
Remark 3.8
In [34] it is assumed that \(\zeta \in \mathcal {O}\), which is not the case for us—however, this assumption is not used (only the assumption that \(\zeta + \zeta ^{-1} \in \mathcal {O}\), which is required to even define \(R^{\mathrm {ps}}_{\mathcal {O}, \overline{\rho }}\)).
Remark 3.9
The proofs above show that each of our deformation rings \(R^{?}_{\overline{\rho }, \mathcal {O}}\) turns out to be reduced and l-torsion free, and therefore is one of the fixed-type deformation rings defined by a Zariski closure operation in [34].
3.4 Types
Next we define various representations of \(GL_2(\mathcal {O}_L)\) over W (or extensions of W). Let \(\mathcal {G}= GL_2(k)\) and \(\mathcal {B}\) be its subgroup of upper triangular matrices. We will always regard representations of \(\mathcal {G}\) as representations of \(GL_2(\mathcal {O}_L)\) by inflation. If A is a ring, then we will write \(\mathbb {1}_A\) for A with the trivial action of any group under consideration.
Since \(q + 1 = [\mathcal {G}: \mathcal {B}]\) is invertible in W, the natural map
splits, and so we define \({\text {St}}_W\) by the formula
If A is a W-algebra, then define \({\text {St}}_A = {\text {St}}_W \otimes _W A\); then we have \({\text {Ind}}_{\mathcal {B}}^{\mathcal {G}} \mathbb {1}_A = \mathbb {1}_A \oplus {\text {St}}_A\).
Now let \(E_1 = E[\zeta ]\) and \(\chi :k^\times \rightarrow E_1\) be a non-trivial character. Let \(\chi \otimes \chi ^{-1}: \mathcal {B}\rightarrow E_1^\times \) be the character
Let
If \(E = E_0[\zeta + \zeta ^{-1}]\) as before then \(\sigma ^{\mathrm {ps}}_{E_1}\) is isomorphic to its conjugate under the nontrivial element of \({\text {Gal}}(E_1/E)\), which switches \(\chi \) and \(\chi ^{-1}\). It therefore has a model \(\sigma _E^{\mathrm {ps}}\) over E, by the calculation of the Schur index of a character of a finite general linear group in [21] Theorem 2a—see also Lemma 3.1.1 of [15]. By [15] Lemma 4.1.1, there is a unique \(\mathcal {O}\)-lattice \(\sigma ^{\mathrm {ps}}_\mathcal {O}\) in \(\sigma _E^{\mathrm {ps}}\) such that there is a nonsplit short exact sequence
For A an \(\mathcal {O}\)-algebra, we let \(\sigma _A^{\mathrm {ps}} = \sigma _{\mathcal {O}}^{\mathrm {ps}} \otimes _{\mathcal {O}}A\).
3.5 The local Langlands correspondence
Suppose first that we are in the setting of Sect. 3.3. For \(\rho :G_L \rightarrow GL_2(\overline{E}_0)\) a continuous representation, let \(\pi (\rho )\) be the smooth admissible representation of \(GL_2(L)\) associated to \(\rho \) by the local Langlands correspondence, and let \(x : R^{\square }_{\overline{\rho }, \mathcal {O}} \rightarrow \overline{E}\) be the associated homomorphism. Then we have:
Proposition 3.10
-
(1)
If \(\pi (\rho )|_{GL_2(\mathcal {O}_L)}\) contains \(\mathbb {1}_{\overline{E}}\), then x factors through \(R^{\mathrm {nr}}_{\overline{\rho }, \mathcal {O}}\).
-
(2)
If \(\pi (\rho )|_{GL_2(\mathcal {O}_L)}\) contains \({\text {St}}_{\overline{E}}\), then x factors through \(R^{\mathrm {unip}}_{\overline{\rho }, \mathcal {O}}\).
-
(3)
If \(\pi (\rho )\) is discrete series and \(\pi (\rho )|_{GL_2(\mathcal {O}_L)}\) contains \({\text {St}}_{\overline{E}}\), then x factors through \(R^{N}_{\overline{\rho }, \mathcal {O}}\).
-
(4)
If \(\pi (\rho )|_{GL_2(\mathcal {O}_L)}\) contains \(\sigma _{\overline{E}}^{\mathrm {ps}}\), then x factors through \(R^{\mathrm {ps}}_{\overline{\rho }, \mathcal {O}}\).
Now suppose that we are in the setting of Sect. 3.2. Suppose that \(D_L\) is a quaternion algebra over L and K is a compact open subgroup of \(D_L\). If \(\pi \) is an irreducible admissible representation of \(D_L\) over \(\overline{E}\), then by the local Langlands and Jacquet–Langlands correspondences there is an associated Weil–Deligne representation \((r_\pi , N_\pi )\). We may and do choose a finite extension \(L_K/L\) such that, for all \(\pi \) having a K-fixed vector, the restriction \(r_\pi |_{G_{L_K}}\) is unramified. It follows that, if \(\pi \) has a K-fixed vector and \(\rho : G_L \rightarrow GL_2(E)\) is a de Rham representation of parallel Hodge–Tate weights \(\{0,1\}\) such that \(WD(\rho )^{ss} \cong (r_\pi , N_\pi )\), then \(\rho |_{G_{L_K}}\) is semistable and so corresponds to a point of \(R^{\square , L_K\text {-st}}_{\overline{\rho }, \mathcal {O}}\). We write
for
We will say that a lift \(\rho : \Gamma \rightarrow GL_2(A)\) of \(\overline{\rho }\) is K-semistable if the associated map \(R^{\square }_{\overline{\rho }, \mathcal {O}} \rightarrow A\) factors through \(R^{\square , K\text {-st}}_{\overline{\rho }, \mathcal {O}}\).
4 Patching
The goal of this section is to summarize the Taylor–Wiles–Kisin patching construction, and to prove the results about it that will be needed for the proof of Theorem 6.5. We choose a coefficient system \((E,\mathcal {O},\mathbb {F})\), which we will eventually require to satisfy Hypothesis 3.1.
4.1 Ultrapatching
In this section we summarize the commutative algebra behind the patching method. For convenience we will use the “ultrapatching” construction introduced by Scholze in [33]; we follow closely the exposition of [27] section 4.
From now on, fix a nonprincipal ultrafilter \(\mathfrak {F}\) on the natural numbers \(\mathbb {N}\) (it is well known that such an \(\mathfrak {F}\) must exist, provided we assume the axiom of choice). For convenience, we will say that a property \(\mathcal {P}(n)\) holds for \(\mathfrak {F}\)-many i if there is some \(I\in \mathfrak {F}\) such that \(\mathcal {P}(i)\) holds for all \(i\in I\).
For any sequence of sets \(\mathscr {A}=\{A_n\}_{n\ge 1}\), we define their ultraproduct to be the quotient
where we define the equivalence relation \(\sim \) by \((a_n)_n\sim (a_n')_n\) if \(a_i = a_i'\) for \(\mathfrak {F}\)-many i.
If the \(A_n\)’s are sets with an algebraic structure (eg. groups, rings, R-modules, R-algebras, etc.) then \(\mathcal {U}\!\left( \mathscr {A}\right) \) naturally inherits the same structure.
If each \(A_n\) is a finite set, and the cardinalities of the \(A_n\)’s are bounded (this is the only situation we will consider in this paper), then \(\mathcal {U}\!\left( \mathscr {A}\right) \) is also a finite set and there are bijections \(\mathcal {U}\!\left( \mathscr {A}\right) \xrightarrow {\sim } A_i\) for \(\mathfrak {F}\)-many i. Moreover if the \(A_n\)’s are sets with an algebraic structure, such that there are only finitely many distinct isomorphism classes appearing in \(\{A_n\}_{n\ge 1}\) (which happens automatically if the structure is defined by finitely many operations, eg. groups, rings or R-modules or R-algebras over a finite ring R) then these bijections may be taken to be isomorphisms. This is merely because our conditions imply that there is some A such that \(A\cong A_i\) for \(\mathfrak {F}\)-many i and hence \(\mathcal {U}\!\left( \mathscr {A}\right) \) is isomorphic to the “constant” ultraproduct \(\mathcal {U}\!\left( \{A\}_{n\ge 1}\right) \) which is easily seen to be isomorphic to A if A is a finite set.
Lastly, in the case when each \(A_n\) is a module over a finite local ring R, there is a simple algebraic description of \(\mathcal {U}\!\left( \mathscr {A}\right) \). Specifically, the ring \(\displaystyle \mathcal {R}= \prod _{n=1}^\infty R\) contains a unique maximal ideal \(\mathfrak {Z}_\mathfrak {F}\in {\text {Spec}}\mathcal {R}\) for which \(\mathcal {R}_{\mathfrak {Z}_\mathfrak {F}}\cong R\) and \(\displaystyle \left( \prod _{n=1}^\infty A_n \right) _{\mathfrak {Z}_\mathfrak {F}}\cong \mathcal {U}\!\left( \mathscr {A}\right) \) as R-modules. This shows that \(\mathcal {U}\!\left( -\right) \) is a particularly well-behaved functor in our situation. In particular, it is exact.
For the rest of this section, fix a power series ring \(S_\infty = \mathcal {O}[[z_1,\ldots ,z_d]]\) and consider the ideal \(\mathfrak {n}= (z_1,\ldots ,z_d)\). Fix a sequence of ideals \(\mathcal {I}_n\subseteq S_\infty \) such that for any open ideal \(\mathfrak {a}\subseteq S_\infty \) we have \(\mathcal {I}_n\subseteq \mathfrak {a}\) for all but finitely many n. Also define \(\overline{S}_\infty = S_\infty /(\varpi ) = \mathbb {F}[[z_1,\ldots ,z_d]]\) and \(\overline{\mathcal {I}}_n = (\mathcal {I}_n+(\varpi ))/(\varpi )\subseteq \overline{S}_\infty \).
For any finitely generated \(S_\infty \)-module M, we will say that the \(S_\infty \)-rank of M, denoted by \({\text {rank}}_{S_\infty }M\), is the cardinality of a minimal generating set for M as an \(S_\infty \)-module.
We can now make our main definitions:
Definition 4.1
Let \(\mathscr {M}= \{M_n\}_{n\ge 1}\) be a sequence of finitely generated \({S_\infty }\)-modules with \(\mathcal {I}_n\subseteq {\text {Ann}}_{S_\infty }M_n\) for all but finitely many n.
-
We say that \(\mathscr {M}\) is a weak patching system if the \({S_\infty }\)-ranks of the \(M_n\)’s are uniformly bounded. If we further have \(\varpi M_n = 0\) for all but finitely many n, we say that \(\mathscr {M}\) is a residual weak patching system
-
We say that \(\mathscr {M}\) is a patching system if it is a weak patching system, and we have \({\text {Ann}}_{S_\infty }(M_n)=\mathcal {I}_n\) for all but finitely many n.
-
We say that \(\mathscr {M}\) is a residual patching system if it is a residual weak patching system, and we have \({\text {Ann}}_{\overline{S}_\infty }(M_n)=\overline{\mathcal {I}}_n\) for all but finitely many n.
-
We say that \(\mathscr {M}\) is MCM (resp. MCM residual) if \(\mathscr {M}\) is a patching system (resp. residual patching system) and \(M_n\) is free over \(S_\infty /\mathcal {I}_n\) (resp. \(\overline{S}_\infty /\overline{\mathcal {I}}_n\)) for all but finitely many n.
Furthermore, assume that \(\mathscr {R}= \{R_n\}_{n\ge 1}\) is a sequence of finite local \({S_\infty }\)-algebras.
-
We say that \(\mathscr {R}= \{R_n\}_{n\ge 1}\) is a (weak, residual) patching algebra, if it is a (weak, residual) patching system.
-
If \(M_n\) is an \(R_n\)-module (viewed as an \({S_\infty }\)-module via the \({S_\infty }\)-algebra structure on \(R_n\)) for all n we say that \(\mathscr {M}= \{M_n\}_{n\ge 1}\) is a (weak, residual) patching \(\mathscr {R}\)-module if it is a (weak, residual) patching system.
Let \(\mathfrak {wP}\) be the category of weak patching systems, with the obvious notion of morphism. Note that this is naturally an abelian category.
Now for any weak-patching system \(\mathscr {M}\), we define its patched module to be the \(S_\infty \)-module
where the inverse limit is taken over all open ideals of \(S_\infty \). We may treat \(\mathscr {P}\) is as functor from \(\mathfrak {wP}\) to the category of \(S_\infty \)-modules.
If \(\mathscr {R}\) is a weak patching algebra and \(\mathscr {M}\) is a weak patching \(\mathscr {R}\)-module, then \(\mathscr {P}(\mathscr {R})\) inherits a natural \(S_\infty \)-algebra structure, and \(\mathscr {P}(\mathscr {M})\) inherits a natural \(\mathscr {P}(\mathscr {R})\)-module structure.
In the above definition, the ultraproduct essentially plays the role of the pigeonhole principal in the classical Taylor–Wiles–Kisin construction, with the simplification that it is not necessary to explicitly define a “patching datum” before making the construction. Indeed, if one were to define patching data for the \(M_n/\mathfrak {a}\)’s (essentially, imposing extra structure on each of the modules \(M_n/\mathfrak {a}\)) then the machinery of ultraproducts would ensure that the patching data for \(\mathcal {U}\!\left( \mathscr {M}/\mathfrak {a}\right) \) would agree with that of \(M_n/\mathfrak {a}\) for infinitely many n. It is thus easy to see that our definition agrees with the classical construction (cf. [33]).
Thus the standard patching Lemmas (cf. [25], Proposition 3.3.1) can be rephrased as follows:
Proposition 4.2
Let \(\mathscr {R}\) be a weak patching algebra, and let \(\mathscr {M}\) be an MCM patching \(\mathscr {R}\)-module. Then:
-
(1)
\(\mathscr {P}(\mathscr {R})\) is a finite type \(S_\infty \)-algebra, and \(\mathscr {P}(\mathscr {M})\) is a finitely generated free \(S_\infty \)-module.
-
(2)
The structure map \(S_\infty \rightarrow \mathscr {P}(\mathscr {R})\) (defining the \(S_\infty \)-algebra structure) is injective, and thus \(\dim \mathscr {P}(\mathscr {R}) = \dim S_\infty \).
-
(3)
The module \(\mathscr {P}(\mathscr {M})\) is maximal Cohen–Macaulay over \(\mathscr {P}(\mathscr {R})\), and \((\varpi ,z_1,\ldots ,z_d)\) is a regular sequence for \(\mathscr {P}(\mathscr {M})\).
Proposition 4.3
Let \(\mathscr {R}\) be a weak patching algebra, and let \(\overline{\mathscr {M}}\) be an MCM residual patching \(\mathscr {R}\)-module. Then:
-
(1)
\(\mathscr {P}(\mathscr {R})/(\varpi )\) is a finite type \(\overline{S}_\infty \)-algebra, and \(\mathscr {P}(\overline{\mathscr {M}})\) is a finitely generated free \(\overline{S}_\infty \)-module.
-
(2)
The structure map \(\overline{S}_\infty \rightarrow \mathscr {P}(\mathscr {R})/(\varpi )\) is injective, and thus \(\dim \mathscr {P}(\mathscr {R})/(\varpi ) = \dim \overline{S}_\infty \).
-
(3)
The module \(\mathscr {P}(\overline{\mathscr {M}})\) is maximal Cohen–Macaulay over \(\mathscr {P}(\mathscr {R})/(\varpi )\), and \((z_1,\ldots ,z_d)\) is a regular sequence for \(\mathscr {P}(\overline{\mathscr {M}})\).
Proposition 4.4
Let \(\mathfrak {n}= (z_1,\ldots ,z_d)\subseteq S_\infty \), as above. Let \(R_0\) be a finite type \(\mathcal {O}\)-algebra, and let \(M_0\) be a finitely generated \(R_0\)-module. If, for each \(n\ge 1\), there are isomorphisms \(R_n/\mathfrak {n}\cong R_0\) of \(\mathcal {O}\)-algebras and \(M_n/\mathfrak {n}\cong M_0\) of \(R_n/\mathfrak {n}\cong R_0\)-modules, then we have \(\mathscr {P}(\mathscr {R})/\mathfrak {n}\cong R_0\) as \(\mathcal {O}\)-algebras and \(\mathscr {P}(\mathscr {M})/\mathfrak {n}\cong M_0\) as \(\mathscr {P}(\mathscr {R})/\mathfrak {n}\cong R_0\)-modules.
From the set up of Proposition 4.2 there is very little we can directly conclude about the ring \(\mathscr {P}(\mathscr {R})\). However in practice one generally takes the rings \(R_n\) to be quotients of a fixed ring \(R_\infty \) of the same dimension as \(S_\infty \) (and thus as \(\mathscr {P}(\mathscr {R})\)). Thus we define a cover of a weak patching algebra \(\mathscr {R}= \{R_n\}_{n\ge 1}\) to be a pair \((R_\infty ,\{\varphi _n\}_{n\ge 1})\), where \(R_\infty \) is a complete, topologically finitely generated \(\mathcal {O}\)-algebra of Krull dimension \(\dim S_\infty \) and \(\varphi _n:R_\infty \rightarrow R_n\) is a surjective \(\mathcal {O}\)-algebra homomorphism for each n. It is straightforward to show the following (cf. [27])
Proposition 4.5
If \((R_\infty ,\{\varphi _n\})\) is a cover of a weak patching algebra \(\mathscr {R}\), then the \(\varphi _n\)’s induce a natural continuous surjection \(\varphi _\infty :R_\infty \twoheadrightarrow \mathscr {P}(\mathscr {R})\).
Combining this with Propositions 4.2 and 4.3 we get the following (using the fact [37, Lemma 0AAD] that if \(f:A\twoheadrightarrow B\) is a surjection of noetherian local rings, then a B-module M is Cohen–Macaulay as an A-module if and only if it is Cohen–Macaulay as a B-module):
Corollary 4.6
Let \(\mathscr {R}\) be a weak patching algebra and let \((R_\infty ,\{\varphi _n\})\) be a cover of \(\mathscr {R}\). If \(\mathscr {M}\) is an MCM patching \(\mathscr {R}\)-module, then \(\mathscr {P}(\mathscr {M})\) is a maximal Cohen–Macaulay \(R_\infty \)-module. If \(\overline{\mathscr {M}}\) is an MCM residual patching \(\mathscr {R}\)-module, then \(\mathscr {P}(\overline{\mathscr {M}})\) is a maximal Cohen–Macaulay \(R_\infty /(\varpi )\)-module.
In our arguments, it will be necessary to patch the filtration from Theorem 2.11. This would certainly be possible if \(\mathscr {P}\) were an exact functor. However, this is not true in general,Footnote 6 but we can prove a weaker statement which suffices for our purposes:
Lemma 4.7
The functor \(\mathscr {P}(-)\) is right-exact. Moreover, if
is an exact sequence of weak patching systems then
is exact, provided that either:
-
\(\mathscr {C}\) is MCM, or
-
\(\mathscr {A}\), \(\mathscr {B}\) and \(\mathscr {C}\) are all residual weak patching systems, and \(\mathscr {C}\) is MCM residual.
Proof
Let \(\mathbf {Ab}\) be the category of abelian groups. For any countable directed set I, let \(\mathbf {finAb}^I\) be the category of inverse systems of finite abelian groups indexed by I.
Now note that any \((A_i,f_{ji}:A_j\rightarrow A_i)\in \mathbf {finAb}^I\) clearly satisfies the Mittag-Leffler condition: For any \(i\in I\) there is a \(j\ge i\) for which \({\text {im}}(f_{ki}) = {\text {im}}(f_{ji})\) for all \(k\ge j\) (since \(A_i\) is finite, and \(\{{\text {im}}(f_{ji})\}_{j\ge i}\) is a decreasing sequence of subgroups). Thus by [37, Lemma 0598] it follows that \(\varprojlim :\mathbf {finAb}^I\rightarrow \mathbf {Ab}\) is exact.
Now assume that \(\mathscr {A}\), \(\mathscr {B}\) and \(\mathscr {C}\) are weak patching systems, and that we have an exact sequence
Then for any \(\mathfrak {a}\subseteq {S_\infty }\), \(\mathscr {A}/\mathfrak {a}\rightarrow \mathscr {B}/\mathfrak {a}\rightarrow \mathscr {C}/\mathfrak {a}\rightarrow 0\) is exact, so by the exactness of \(\mathcal {U}\!\left( -\right) \) we get the exact sequence
Thus we have an exact sequence of inverse systems
But now as \(\mathcal {U}\!\left( \mathscr {A}/\mathfrak {a}\right) \), \(\mathcal {U}\!\left( \mathscr {B}/\mathfrak {a}\right) \) and \(\mathcal {U}\!\left( \mathscr {C}/\mathfrak {a}\right) \) are all finite, and there are only countably many open ideals of \(S_\infty \), the above argument shows that taking inverse limits preserves exactness, and so indeed
is exact.
Now assume that one of the further conditions of the lemma holds. Write \(\mathscr {A}= \{A_n\}_{n\ge 1}\), \(\mathscr {B}= \{B_n\}_{n\ge 1}\) and \(\mathscr {C}= \{C_n\}_{n\ge 1}\). Then letting \(I_n = {\text {Ann}}_{S_\infty }C_n\) (so that either \(I_n = \mathcal {I}_n\) or \(\overline{\mathcal {I}}_n\) for all \(n\gg 0\)), we get that for all \(n\gg 0\),
is an exact sequence of \(S_\infty /I_n\)-modules, and \(C_n\) is a free \(S_\infty /I_n\)-module (this is true regardless of which case we are in). It follows that
for all \(\mathfrak {a}\subseteq S_\infty \), and so
is exact for all \(n\gg 0\). The same argument as above now shows that
is exact. \(\square \)
This now implies that \(\mathscr {P}\) preserves filtrations in the cases that will be relevant to us:
Corollary 4.8
Let \(\mathscr {V}\) be a residual weak patching system with a filtration
by residual weak patching systems \(\mathscr {V}^k\). For \(k=1,\ldots ,r\) let \(\mathscr {M}^k = \mathscr {V}^k/\mathscr {V}^{k-1}\). Assume that the \(\mathscr {M}^k\)’s are all MCM residual. Then \(\mathscr {P}(\mathscr {V})\) has a filtration
with \(\mathscr {P}(\mathscr {V}^k)/\mathscr {P}(\mathscr {V}^{k-1})\cong \mathscr {P}(\mathscr {M}^k)\) for all \(k=1,\ldots ,r\).
One can also make an analogous statement about filtrations of weak patching systems, instead of residual weak patching systems, but we will not need that result.
Proof
For any \(k\ge 1\) we have an exact sequence
As \(\mathscr {M}^k\) is MCM residual, Lemma 4.7 implies that the map \(\mathscr {P}(\mathscr {V}^{k-1}) \rightarrow \mathscr {P}(\mathscr {V}^{k})\) is an inclusion, and that \(\mathscr {P}(\mathscr {V}^k)/\mathscr {P}(\mathscr {V}^{k-1})\cong \mathscr {P}(\mathscr {M}^k)\). The result follows. \(\square \)
4.2 Global deformation rings
We fix the following data:
-
a quaternion division algebra D over F split at exactly one infinite place, as in Sect. 2;
-
a coefficient system \((E, \mathcal {O}, \mathbb {F})\) satisfying Hypothesis 3.1;
-
a non-Eisenstein maximal ideal \(\mathfrak {m}\subseteq \mathbb {T}^S_\mathcal {O}\) (for some set S, which we will not fix yet) which is G-automorphic;
-
a finite order character \(\psi :G_F\rightarrow \mathcal {O}^\times \) for which \(\psi \equiv \det \overline{\rho }\epsilon \pmod \varpi \). We also write \(\psi \) for the character \(\psi \circ {\text {Art}}\), where \({\text {Art}}: \mathbb {A}_{F,f}^\times /F^\times \rightarrow G_F^{{\text {ab}}}\) is the global Artin map.
Enlarging \(\mathbb {F}\) if necessary, we assume that the residue field of \(\mathfrak {m}\) is \(\mathbb {F}\). By definition, \(\mathfrak {m}\) is G-automorphic of some level \(K_{\mathfrak {m}} \subset G(\mathbb {A}_{F,f})\), which we fix temporarily. Now we fix, for the rest of this section:
-
a finite place \(\mathfrak {q}\not \in \Sigma _l \cup \Sigma (K_{\mathfrak {m}})\) of F at which \(\overline{\rho }\) is unramified;
-
a finite set \(\Sigma \) of finite places of F that contains \(\Sigma _l \cup \{\mathfrak {q}\} \cup \Sigma (K_{\mathfrak {m}})\) (which means that we can, and will, regard \(\mathfrak {m}\) as a maximal ideal of \(\mathbb {T}^\Sigma _\mathcal {O}\) rather than \(\mathbb {T}^S_\mathcal {O}\));
-
for each \(v \in \Sigma _l\), a compact open subgroup \(K^0_v \subset K_{\mathfrak {m}} \cap G(F_v)\).
We will use S to denote a finite set of places of F. In the following, S and K will sometimes vary but we will always impose the following hypotheses on the pair (S, K):
Hypotheses 4.9
-
\(\mathfrak {m}\) is G-automorphic of level K;
-
S contains \(\Sigma \cup \Sigma (K) \cup \Sigma _\infty \);
-
\(F^\times (K\cap Z(\mathbb {A}_{F,f})) \subset \ker (\psi )\) (this implies that \(\psi \) is unramified outside of S);
-
for all \(v \in \Sigma _l\), \(K \cap G(F_v) \supset K^0_v\);
-
K has the form \(K^\mathfrak {q}K_\mathfrak {q}\) for some \(K^\mathfrak {q}\subset G(\mathbb {A}_{F,f}^\mathfrak {q})\) and \(K_\mathfrak {q}\subset G(F_{\mathfrak {q}})\).
Let \(\overline{\rho }= \overline{\rho }_{\mathfrak {m}}:G_F\rightarrow GL_2(\mathbb {F})\), and note that \(\overline{\rho }\) is absolutely irreducible and unramified outside of S. For any place v of F, let \(\overline{\rho }_{v} = \overline{\rho }|_{G_{F_v}}\). By taking a quadratic extension of \(\mathbb {F}\) if necessary, we will assume that for each \(g\in G_F\), all of the eigenvalues of \(\overline{\rho }(g)\) lie in \(\mathbb {F}^\times \).
As in [25, section 3.2], define \(R^{\square }_{F,S}(\overline{\rho })\in \mathcal {C}_{\mathcal {O}}^\wedge \) to be the \(\mathcal {O}\)-algebra pro-representing the functor \(\mathcal {D}^{\square }_{F,S}(\overline{\rho }):\mathcal {C}_\mathcal {O}\rightarrow \mathbf{Set}\) which sends A to the set of equivalence classes of tuples
where:
-
\(\rho : G_{F,S} \rightarrow GL_2(A)\) is a continuous lift of \(\overline{\rho }\);
-
for each \(v\in \Sigma \), \(\beta _v \in 1 + M_2(\mathfrak {m}_A)\) (we think of this as basis for \(A^2\) lifting the standard basis of \(\mathbb {F}^2\));
-
for each \(v \mid l\) the restriction \(\rho \mid _{G_{F_v}}\) is \(K^0_{v}\)-semistable, in the notation of Sect. 3.5;
-
two such collections \((\rho , (\beta _v)_{v \in \Sigma })\) and \((\rho ', (\beta '_v)_{v \in \Sigma })\) are equivalent if there is \(\gamma \in 1 + M_2(\mathfrak {m}_A)\) such that \(\rho ' = \gamma \rho \gamma ^{-1}\) and \(\beta '_v = \gamma \beta _v\) for all \(v\in \Sigma \).
Now let \(\mathcal {D}^{\square ,\psi }_{F,S}(\overline{\rho }):\mathcal {C}_\mathcal {O}\rightarrow \mathbf{Set}\) be the subfunctor of \(\mathcal {D}^{\square }_{F,S}(\overline{\rho })\) consisting of the tuples \(\left( \rho , (\beta _v)_{v\in \Sigma } \right) \) with \(\det \rho = \psi \epsilon ^{-1}\), and let \(R^{\square ,\psi }_{F,S}(\overline{\rho })\in \mathcal {C}_{\mathcal {O}}^\wedge \) be the \(\mathcal {O}\)-algebra pro-representing \(\mathcal {D}^{\square ,\psi }_{F,S}(\overline{\rho })\).
Also define the unframed deformation ring \(R_{F,S}(\overline{\rho })\) to be the \(\mathcal {O}\)-algebra pro-representing the functor \(\mathcal {C}_\mathcal {O}\rightarrow \mathbf{Set}\) which sends A to the set of equivalence classes of lifts \(\rho : G_{F,S} \rightarrow GL_2(A)\) such that \(\rho |_{G_{F_v}}\) is \(K^0_{v}\)-semistable for all \(v \mid l\), two such lifts being equivalent if they are conjugate by an element of \(1 + M_2(\mathfrak {m}_A)\). Finally, define \(R^{\psi }_{F,S}(\overline{\rho })\) to be the quotient of \(R_{F,S}(\overline{\rho })\) on which \(\det \rho (g) = \psi (g)\) for all \(g\in G_{F,S}\). The unframed deformation rings \(R_{F,S}(\overline{\rho })\) and \(R_{F,S}^\psi (\overline{\rho })\) exist because \(\overline{\rho }\) is absolutely irreducible. We will let \(\rho ^{{\text {univ}}}_{S}:G_{F,S}\rightarrow GL_2(R_{F,S}(\overline{\rho }))\) be a representative for the universal equivalence class of lifts of \(\overline{\rho }\), which induces a homomorphism \(\rho ^{{\text {univ}}}_{S,\psi }:G_{F,S}\rightarrow GL_2(R_{F,S}^\psi (\overline{\rho }))\).
There is a ‘forgetful’ map \(R^{\psi }_{F,S}(\overline{\rho }) \rightarrow R^{\square ,\psi }_{F,S}(\overline{\rho })\), which by [25, (3.4.11)] is formally smooth of dimension \(j = 4|\Sigma |-1\), and so we may identify \(R^{\square ,\psi }_{F,S} = R^\psi _{F,S}[[w_1,\ldots ,w_j]]\).
Lastly, for any \(v\in \Sigma \), let \(R_v = R^{\square ,\psi |_{G_{F_v}}}_{\overline{\rho }|_{G_{F_v}},\mathcal {O}}\) if \(v\not \mid l\) and \(R_v = R^{\square , \psi , K^0_v\text {-st}}_{\overline{\rho },\mathcal {O}}\) if v|l. If \((\rho , (\beta _v)_{v\in \Sigma })\) is as in equation (3) then, for each \(v \in \Sigma \), \(\beta _v^{-1}\rho \beta _v\) is a lift of \(\overline{\rho }\) that only depends on the equivalence class of \((\rho , (\beta _v)_{v \in \Sigma })\). Restricting each \(\beta _v^{-1}\rho \beta _v\) to \(G_{F_v}\) induces a map
We write \(R_{\mathrm {loc}}\) for \(\displaystyle {\widehat{\otimes }}_{v\in \Sigma }R_v\).
The Taylor–Wiles–Kisin patching construction relies on carefully picking sets of auxiliary primes to add to the level, using the following lemma (see [25] Proposition 3.2.5).
Lemma 4.10
Assume that \(\overline{\rho }\) satisfies the following conditions:
-
(1)
\(\overline{\rho }|_{G_{F(\zeta _l)}}\) is absolutely irreducible.
-
(2)
If \(l = 5\) and the image of the projective representation \({\text {proj}}\overline{\rho }_{\mathfrak {m}}:G_F\rightarrow GL_2(\overline{\mathbb {F}}_5)\twoheadrightarrow PGL_2(\overline{\mathbb {F}}_5)\) is isomorphic to \(PGL_2(\mathbb {F}_5)\), then \(\ker {\text {proj}}\overline{\rho }_{\mathfrak {m}}\not \subseteq G_{F(\zeta _5)}\). (This condition holds automatically whenever \(\sqrt{5}\not \in F\).)
Suppose that \(S = \Sigma \cup \Sigma _\infty \). Then there exist integers \(r,g\ge 0\) such that for each \(n\ge 1\), there is a finite set \(Q_n\) of primes of F for which:
-
\(\# Q_n = r\).
-
\(Q_n\cap S = \emptyset \).
-
For any \(v\in Q_n\), \({\text {Nm}}(v)\equiv 1\pmod {l^n}\).
-
For any \(v\in Q_n\), \(\overline{\rho }({\text {Frob}}_v)\) has two distinct eigenvalues in \(\mathbb {F}^\times \).
-
There is a surjection \(R_{\mathrm {loc}}[[x_1,\ldots ,x_g]]\twoheadrightarrow R^{\square ,\psi }_{F,S\cup Q_n}(\overline{\rho })\) extending the map \(R_{\mathrm {loc}}\rightarrow R^{\square ,\psi }_{F,S\cup Q_n}(\overline{\rho })\).
Moreover, we have \(\dim R_{\mathrm {loc}} = r+j-g+1\).
From now on, fix integers r, g and a sequence \(\mathcal {Q}= \{Q_n\}_{n\ge 1}\) of sets of primes satisfying the conclusions of Lemma 4.10. Define \(R_n=R^{\psi }_{F,S\cup Q_n}(\overline{\rho })\), \(R_n^\square =R^{\square ,\psi }_{F,S\cup Q_n}(\overline{\rho })\) for \(n\ge 1\) and
so that we have surjections \(R_\infty \twoheadrightarrow R_n^\square \) for all n. Also let \(R_0=R^{\psi }_{F,S}(\overline{\rho })\) and \(R_0^{\square }=R^{\square ,\psi }_{F,S}(\overline{\rho })\). Note that \(R_n^\square \cong R_n[[w_1,\ldots ,w_j]]\) for all \(n\ge 0\) and \(\dim R_\infty = r+j+1\).
4.3 Patched modules over Shimura curves and sets
As before, we use S to denote a finite set of places of F containing \(\Sigma \cup \Sigma _\infty \), and K to denote a compact open subgroup of \(G(\mathbb {A}_{F,f})\), such that S and K satisfy Hypotheses 4.9. In particular, there is a maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}^S_{\mathcal {O}}\) that is G-automorphic of level K. Let \(\mathbb {T}(K,S)\) denote the image of \(\mathbb {T}^S_{\mathcal {O},\mathfrak {m}}\) in \({\text {End}}_{\mathcal {O}}(H^1(X_{K},\mathcal {O})_{\mathfrak {m}}[\psi ])\). Then \(\mathbb {T}(K,S)\) is a finite rank free \(\mathcal {O}\)-algebra which is local with maximal ideal \(\mathfrak {m}\). Note that \(\mathbb {T}(K,S)\) depends on the choices of \(\mathfrak {m}\) and \(\psi \) but we suppress these from the notation.
As in section 6 of [15] we have the following:
Lemma 4.11
For any compact open K and set S as above, there exists a natural surjection \(R^\psi _{F,S}(\overline{\rho })\twoheadrightarrow \mathbb {T}(K,S)\) with the property that \(\rho ^{{\text {univ}}}_{S,\psi }({\text {tr}}({\text {Frob}}_v))\mapsto T_v\) and \(\rho ^{{\text {univ}}}_{S,\psi }(\det ({\text {Frob}}_v))\mapsto {\text {Nm}}(v)S_v\) for any \(v\not \in S\). These maps are compatible with the restriction maps \(\mathbb {T}(K',S')\rightarrow \mathbb {T}(K,S)\) for \(K'\subseteq K\) and \(S \subset S'\).
If \(S \subset S'\) are sets as above, then by Lemma 4.11 and the definitions we have a commutative diagram

where the left hand vertical map and the horizontal maps are surjections. It follows that the right hand vertical map, injective by definition, is an isomorphism. We therefore drop S from the notation and write
for any K and S satisfying Hypotheses 4.9.
These Hecke algebras also act on the spaces \(H^0(Y_{K^{\mathfrak {q}}},\mathcal {O})_\mathfrak {m}[\psi ]\), by the following lemma.
Lemma 4.12
For any compact open K and set S as above such that K is unramified at \(\mathfrak {q}\), the map \(\mathbb {T}_{\mathcal {O}, \mathfrak {m}}^S \rightarrow {\text {End}}(H^0(Y_{K^\mathfrak {q}},\mathcal {O})_\mathfrak {m}[\psi ])\) factors through the quotient \(\mathbb {T}_{K_0(\mathfrak {q})}\).
Proof
As \(H^0(Y_{K^\mathfrak {q}},\mathcal {O})_\mathfrak {m}[\psi ]\) is torsion-free, we may check this after inverting l. It is then a consequence of the Jacquet–Langlands correspondence and the semisimplicity of \(H^0(Y_{K^\mathfrak {q}},\mathcal {O})_\mathfrak {m}[\psi ]\) as a module over \(\mathbb {T}^S_{\mathcal {O},\mathfrak {m}}\). \(\square \)
We now fix S to be the union of \(\Sigma \cup \Sigma _\infty \), and let \(\mathcal {Q}= \{Q_n\}_{n\ge 1}\) be the sequence of sets of places provided by Lemma 4.10. For any \(n\ge 1\), let \(\Delta _n\) be the maximal l-power quotient of \(\displaystyle \prod _{v\in Q_n}k_v^\times \). Consider the ring \(\Lambda _n=\mathcal {O}[\Delta _n]\), and note that:
where \(l^{e(n,i)}\) is the l-part of \({\text {Nm}}(v)-1 = \# k_v^\times \), so that \(e(n,i)\ge n\) by assumption. Let \(\mathfrak {a}_n = (y_1,\ldots ,y_r)\subseteq \Lambda _n\) be the augmentation ideal. Also define
Now let \(\displaystyle H_n = \ker \left( \prod _{v\in Q_n}k_v^\times \twoheadrightarrow \Delta _n\right) \). For any finite place v of F, there is a group homomorphism \(U_0(v)\rightarrow k_v^\times \) given by \(\begin{pmatrix}a&{}b\\ c&{}d\end{pmatrix}\mapsto ad^{-1}\pmod {v}\). Now let \(\displaystyle U_H(Q_n)\subseteq \prod _{v\in Q_n}U_0(v)\) be the preimage of \(\displaystyle H_n\subseteq \prod _{v\in Q_n}k_v^\times \) under the map
Finally, for any K (satisfying 4.9 for the set S), let \(K_n\) be the preimage of \(U_H(Q_n)\) under
We also let \(K_0 = K\), and remark that for \(n \ge 1\), \(K_n\) and \(S \cup Q_n\) satisfy 4.9; in particular, \(K_n = K_n^\mathfrak {q}K_\mathfrak {q}\). For any \(n\ge 0\), let \(\mathbb {T}_{n,K} = \mathbb {T}_{K_n}\).
Now for any \(n\ge 1\) consider the \(\mathcal {O}\)-algebra
Now for each \(v\in Q_n\) fix a choice \(\alpha _v\in \mathbb {F}^\times \) of eigenvalue for \(\overline{\rho }({\text {Frob}}_v)\) (recall that by assumption, for each \(v\in Q_n\) \(\overline{\rho }({\text {Frob}}_v)\) has two distinct eigenvalues in \(\mathbb {F}^\times \), and so there are \(2^{|Q_n|}\) ways to pick the system \((\alpha _v)_{v\in Q_n}\)). Now define the ideal
Now for each \(n\ge 1\), define \(\widetilde{\mathbb {T}}_{n,K} = \left( \mathbb {T}_{n,K}\left[ U_v\right] _{v\in Q_n}\right) _{\widetilde{\mathfrak {m}}_n}\). Also define \(\widetilde{\mathbb {T}}_{0,K} = \mathbb {T}_{0,K}\) and \(\widetilde{\mathfrak {m}}_0 = \mathfrak {m}\).
As in [39, section 2] we have:
Lemma 4.13
The ring \(\widetilde{\mathbb {T}}_{n,K}\) is a finite \(\mathbb {T}_{n,K}\)-algebra and \(\widetilde{\mathfrak {m}}_n\) is a maximal ideal of it lying over \(\mathfrak {m}\). The composite map
is surjective. Moreover, there exist \(\mathcal {O}\)-algebra maps \(\Lambda _n\rightarrow R_n\) and \(\Lambda _n\rightarrow \widetilde{\mathbb {T}}_{n,K}\) making the above map a surjection of \(\Lambda _n\)-algebras.
By definition, \(\mathbb {T}_{n,K}\left[ U_v\right] _{v\in Q_n}\) acts on \(H^1(X_{K_n},\mathcal {O})_{\mathfrak {m}}[\psi ]\) and \( H^1(X_{K_n},\mathbb {F})_{\mathfrak {m}}[\psi ]\) (the latter through its quotient \(\mathbb {T}_{n,K}\left[ U_v\right] _{v\in Q_n}\otimes _{\mathcal {O}}\mathbb {F}\)). Also, by Theorem 2.11, if K is unramified at \(\mathfrak {q}\) then \(\mathbb {T}_{n,K_0(\mathfrak {q})}\left[ U_v\right] _{v\in Q_n}\otimes _{\mathcal {O}}\mathbb {F}\) acts on \(H^0(Y_{K^\mathfrak {q}_n},\mathbb {F})_{\mathfrak {m}}[\psi ]\).
So now for any \(n\ge 0\) we can define
and
The reason for dualizing is that the patching argument works more naturally with homology rather than cohomology.
Note that \(M_{n,K}\) and \(\overline{M}_{n,K}\) are naturally \(\mathbb {T}_{n,K}\)-modules and, if K is unramified at \(\mathfrak {q}\), then \(N_{n, K^{\mathfrak {q}}}\) and \(\overline{N}_{n,K^\mathfrak {q}}\) are naturally \(\mathbb {T}_{n,K_0(\mathfrak {q})}\)-modules by Lemma 4.12. In particular we may regard them all as \(R_n\)-modules.
We now have the following result, a standard ingredient in the patching argument (see for instance [2, 25], and [15]):
Proposition 4.14
For any \(n\ge 1\) and any K, the map \(\Lambda _n\rightarrow R_n\) from Lemma 4.13 makes \(M_{n,K}\) and \(N_{n,K^{\mathfrak {q}}}\) into finite rank free \(\Lambda _n\)-modules. In particular, the maps \(\Lambda _n \rightarrow R_n\) and \(\Lambda _n \rightarrow \widetilde{\mathbb {T}}_{n,K}\) are injective. Moreover, the natural maps define an isomorphism \(R_n/\mathfrak {a}_n\cong R_0\) and isomorphisms \(M_{n,K}/\mathfrak {a}_n\cong M_{0,K}\) and \(N_{n,K^{\mathfrak {q}}}/\mathfrak {a}_n\cong N_{0,K^{\mathfrak {q}}}\) of \(R_0\)-modules.
Similarly \(\overline{M}_{n,K}\) and \(\overline{N}_{n,K^{\mathfrak {q}}}\) are finite rank free \(\overline{\Lambda }_n\)-modules and we have \(\overline{M}_{n,K}/\mathfrak {a}_n\cong \overline{M}_{0,K}\) and \(\overline{N}_{n,K^{\mathfrak {q}}}/\mathfrak {a}_n\cong \overline{N}_{0,K^{\mathfrak {q}}}\).
In particular, \({\text {rank}}_{\Lambda _n}R_n = {\text {rank}}_\mathcal {O}R_0\),
and
for all \(n\ge 1\), and so these ranks are independent of n.
We can now define framed versions of all of these objects. First let
Now define
and define \(\overline{M}_{n,K}^\square \), \(N_{n, K^{\mathfrak {q}}}^\square \), and \(\overline{N}_{n,K^{\mathfrak {q}}}^\square \) similarly. Also note that \(R_n^\square \cong R_n\otimes _{\Lambda _n}\Lambda _n^\square \cong R_n[[w_1,\ldots ,w_r]]\).
Now let \(S_\infty =\mathcal {O}[[y_1,\ldots ,y_r,w_1,\ldots ,w_j]]\) and consider the ideals
Note that:
Lemma 4.15
For any open ideal \(\mathfrak {a}\subseteq S_\infty \), we have \(\mathcal {I}_n\subseteq \mathfrak {a}\) for all but finitely many n.
Proof
As \({S_\infty }/\mathfrak {a}\) is finite, and the group \(1+\mathfrak {m}_{S_\infty }\) is pro-l, the group \((1+m_{S_\infty })/\mathfrak {a}= {\text {im}}(1+m_{S_\infty }\hookrightarrow {S_\infty }\twoheadrightarrow {S_\infty }/\mathfrak {a})\) is a finite l-group. Since \(1+y_i\in 1+m_{S_\infty }\) for all i, there is an integer \(k\ge 0\) such that \((1+y_i)^{\ell ^k}\equiv 1 \pmod {\mathfrak {a}}\) for all \(i=1,\ldots ,r\). Then for any \(n\ge k\), \(e(n,i)\ge n\ge k\) for all i, and so indeed \(\mathcal {I}_n\subseteq \mathfrak {a}\) by definition. \(\square \)
Thus we may apply the results of Sect. 4.1 with this ring \(S_\infty \) and these ideals \(\mathcal {I}_n\). Note that
Let \(\mathfrak {n}=(y_1,\ldots ,y_r,w_1,\ldots ,w_j)\subseteq S_\infty \), and identify \(\Lambda _n^\square \) with \(S_\infty /\mathcal {I}_n\) via the above isomorphism.
Tensoring everything in Proposition 4.14 with \(\Lambda _n^\square \), we get that \(M_{n,K}^\square \) is free of rank \({\text {rank}}_\mathcal {O}M_{0,K}\) over \(\Lambda _n^\square \) for all n with \(M_{n,K}^\square /\mathfrak {n}\cong M_{n,K}/\mathfrak {a}_n\cong M_{0,K}\). Similar statements hold for \(\overline{M}_{n,K}^\square \), \(N_{n,K^{\mathfrak {q}}}^\square \), and \(\overline{N}_{n,K^{\mathfrak {q}}}^\square \).
Summarizing the results of this section in the language of Sect. 4.1, we have:
Proposition 4.16
The sequence \(\mathscr {R}^\square =\{R_n^\square \}_{n\ge 1}\) is a patching algebra and \(R_\infty \) is a cover of \(\mathscr {R}^{\square }\). The sequences
are MCM patching \(\mathscr {R}^\square \)-modules, and the sequences
are MCM residual patching \(\mathscr {R}^\square \)-modules.
For all \(n\ge 1\) we have \(R_n^\square /\mathfrak {n}\cong R_0\) and \(M_{n,K}^\square /\mathfrak {n}\cong M_{0,K}\), \(\overline{M}_{n,K}^\square /\mathfrak {n}\cong \overline{M}_{0,K}\), \(N_{n,K^{\mathfrak {q}}}^\square /\mathfrak {n}\cong N_{0,K^{\mathfrak {q}}}\) and \(\overline{N}_{n,K^{\mathfrak {q}}}^\square /\mathfrak {n}\cong \overline{N}_{0,K^{\mathfrak {q}}}\) as \(R_0\)-modules.
So now define the patched modules:
All of these modules are technically framed objects but, following standard convention, we are suppressing the \(\square \) in our notation.
By Corollary 4.6 it follows that \(M_{\infty ,K}\) and \(N_{\infty ,K^{\mathfrak {q}}}\) are maximal Cohen–Macaulay \(R_\infty \)-modules, and \(\overline{M}_{\infty ,K}\) and \(\overline{N}_{\infty ,K^{\mathfrak {q}}}\) are maximal Cohen–Macaulay \(\overline{R}_\infty =R_\infty /(\varpi )\)-modules.
Moreover, Proposition 4.4 gives that \(M_{\infty ,K}/\mathfrak {n}\cong M_{0,K}\), \(\overline{M}_{\infty ,K}/\mathfrak {n}\cong \overline{M}_{0,K}\), \(N_{n,K^{\mathfrak {q}}}^\square /\mathfrak {n}\cong N_{0,K^{\mathfrak {q}}}\), and \(\overline{N}_{\infty ,K^{\mathfrak {q}}}/\mathfrak {n}\cong \overline{N}_{0,K^{\mathfrak {q}}}\), as \(R_0\)-modules.
Now consider the filtration from Theorem 2.11. By dualizing this, completing at \(\mathfrak {m}\), and applying \(-\otimes _{\Lambda _n}\Lambda _n^\square \) we get a filtration
of \(R_n^\square \)-modules, with isomorphisms
and
for all \(n\ge 1\), where we are writing \(K = K^{\mathfrak {q}}G(\mathcal {O}_{F,\mathfrak {q}})\) and \(K_0(\mathfrak {q}) = K^{\mathfrak {q}}U_0(\mathfrak {q})\) as in Sect. 2.
Thus Corollary 4.8 and the above work give the following:
Theorem 4.17
There is a filtration
of \(\overline{R}_\infty \)-modules, with isomorphisms
and
4.4 Patching functors
Theorem 4.17 provides a link between the modules \(\overline{M}_{\infty ,K}\) and \(\overline{N}_{\infty ,K^{\mathfrak {q}}}\). However, in order to use this to deduce properties of \(\overline{M}_{\infty ,K}\) from those of \(\overline{N}_{\infty ,K^{\mathfrak {q}}}\) we will need additional information about the structure of \(\overline{M}_{\infty ,K_0(\mathfrak {q})}\), namely a flatness statement for a particular submodule of \(M_{\infty ,K^{\mathfrak {q}}}({\text {St}}_\mathbb {F})\subset \overline{M}_{\infty ,K_0(\mathfrak {q})}\).
To prove this, we will first need to introduce the notion of a patching functor, \(\sigma \mapsto M_{\infty ,K}(\sigma )\). We will largely follow the presentation in [15].
We consider pairs (S, K) satisfying 4.9, and we take K to be of the form \(K^\mathfrak {q}K_\mathfrak {q}\) for a fixed \(K^{\mathfrak {q}}\subseteq G(\mathbb {A}^{\mathfrak {q}}_{F,f})\). For any \(n\ge 0\) let \(K^{\mathfrak {q}}_n\subseteq G(\mathbb {A}^{\mathfrak {q}}_{F,f})\) be as in Sect. 4.3.
We note that
for any \(n\ge 0\).
Define
where the direct limit is taken over all compact open subgroups \(K_{\mathfrak {q}}\subseteq G(\mathcal {O}_{F,\mathfrak {q}})\). Note that this carries a continuous action of \(G(\mathcal {O}_{F,\mathfrak {q}})\cong GL_2(\mathcal {O}_{F,\mathfrak {q}})\).
As the action of \(\mathbb {T}^S_{\mathfrak {m}}\) on \(H^1(X_{K^{\mathfrak {q}}K_{\mathfrak {q}}},\mathcal {O})_{\mathfrak {m}}[\psi ]\) factors through \(\mathbb {T}_{K^{\mathfrak {q}}K_{\mathfrak {q}}}\), the action of \(\mathbb {T}^S_{\mathfrak {m}}\) on \(\Pi _{K^{\mathfrak {q}}}\) factors through
Note that by Lemma 4.11 we have natural surjections \(R^\psi _{F,S}(\overline{\rho })\twoheadrightarrow \mathbb {T}_{K^{\mathfrak {q}}K_{\mathfrak {q}}}\) for all \(K_{\mathfrak {q}}\), and so we have a surjection \(R^\psi _{F,S}(\overline{\rho })\twoheadrightarrow \mathbb {T}_{K^{\mathfrak {q}}_n}\).
Now following [15], let \(\mathcal {C}\) be the category of finitely generated \(\mathcal {O}\)-modules with a continuous action of \(G(\mathcal {O}_{F,\mathfrak {q}})\). Let \(\overline{\psi }= (\det \overline{\rho }|_{I_{\mathfrak {q}}} \overline{\epsilon })\!\circ \!{\text {Art}}:\mathcal {O}_{F,\mathfrak {q}}^\times \rightarrow \mathbb {F}^\times \) be the character corresponding to \(\det \overline{\rho }|_{I_{\mathfrak {q}}}:I_{\mathfrak {q}}\rightarrow \mathbb {F}^\times \) via local class field theory. Write \(Z = Z(G(\mathcal {O}_{F,\mathfrak {q}}))\cong \mathcal {O}_{F,\mathfrak {q}}^\times \) and let \(\mathcal {C}_Z\) be the subcategory of \(\mathcal {C}\) consisting of those \(\sigma \in \mathcal {C}\) possessing a central character which lifts \(\overline{\psi }\) and agrees with \(\psi \) on \(I_{\mathfrak {q}}\) (in other words, is unramified). Also let \(\mathcal {C}_Z^{{\text {fin}}}\) be the subcategory of finite length objects of \(\mathcal {C}_Z\).
Remark 4.18
In [15], the condition that the central character of \(\sigma \) agrees with \(\psi \) is not imposed; this necessitates a ‘twisting’ argument. We only need to patch \(\sigma \) with unramified central character, so we avoid this technicality.
Now for any \(\sigma \in \mathcal {C}_Z\) and any \(n\ge 0\), define
For any \(\sigma \), this is a \(\mathbb {T}_{K^{\mathfrak {q}}_n}\)-module, and hence an \(R_n\)-module. Thus we may define the \(R_n^\square \)-module:
Now as in section 6 of [15], if \(\sigma \in \mathcal {C}_Z^{{\text {fin}}}\), \(\mathscr {M}_{K^{\mathfrak {q}}}^{\square }(\sigma )=\{M_{n,K^{\mathfrak {q}}}^{\square }(\sigma )\}_{n\ge 1}\) is a weak patching \(\mathscr {R}^\square \)-module and thus we may define \(M_{\infty ,K^{\mathfrak {q}}}(\sigma )=\mathscr {P}(\mathscr {M}_{K^{\mathfrak {q}}}^{\square }(\sigma ))\). We can extend this definition to all of \(\mathcal {C}_Z\) by setting
This definition agrees with the “patching functor” constructed in section 6.4 of [15], up to a technicality: the construction in [15] factors out the Galois representation in the indefinite case, whereas we have not done so. In the notation of [15] the module \(M_{\infty ,K^{\mathfrak {q}}}(\sigma )\) we have constructed is \(S(\sigma )^\vee _{\mathfrak {m}}\cong M_\infty (\sigma )\otimes _{\mathbb {T}(\sigma )_{\mathfrak {m}}}\rho (\sigma )_{\mathfrak {m}}\). However, this is simply isomorphic to \(M_\infty (\sigma )^{\oplus 2}\) as a \(\mathbb {T}(\sigma )_{\mathfrak {m}}\)-module (again in the notation of [15]) and so this does not present an issue. We therefore have:
Theorem 4.19
([15]) \(M_{\infty ,K^{\mathfrak {q}}}(\sigma )\) satisfies the following properties:
-
(1)
The functor \(\sigma \mapsto M_{\infty ,K^{\mathfrak {q}}}(\sigma )\), from \(\mathcal {C}_Z\) to the category of finitely generated \(R_\infty \)-modules, is exact.
-
(2)
For any \(\sigma \in \mathcal {C}_Z\), \(M_{\infty ,K^{\mathfrak {q}}}(\sigma )/\mathfrak {n}\cong M_{0,K^{\mathfrak {q}}}(\sigma )\).
-
(3)
If \(\sigma \in \mathcal {C}_Z\) is a finite free \(\mathcal {O}\)-module, then \(M_{\infty ,K^{\mathfrak {q}}}(\sigma )\) is maximal Cohen–Macaulay over \(R_\infty \).
-
(4)
If \(\overline{\sigma }\in \mathcal {C}_Z\) is a finite dimensional \(\mathbb {F}\)-vector space, then \(M_{\infty ,K^{\mathfrak {q}}}(\overline{\sigma })\) is maximal Cohen–Macaulay over \(\overline{R}_\infty \).
From now on assume that \(\mathfrak {q}\) satisfies the assumptions of Sect. 3.3. That is, \({\text {Nm}}(\mathfrak {q})\equiv 1\pmod {l}\), \(\overline{\rho }\) is unramified at \(\mathfrak {q}\) and \(\overline{\rho }({\text {Frob}}_{\mathfrak {q}}) = \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}\). Thus the computations of Sect. 3.3 will apply to \(R_{\mathfrak {q}}\). Under the map \(R_{\mathfrak {q}}\hookrightarrow R_{\mathrm {loc}}\hookrightarrow R_\infty \), we may view any \(R_\infty \)-module as being a \(R_\mathfrak {q}\)-module.
In addition to the results listed in Theorem 4.19, [15] also describes the supports of \(M_{\infty ,K^{\mathfrak {q}}}(\sigma )\) as \(R_{\mathfrak {q}}\)-modules, for certain \(\sigma \)’s corresponding to inertial types of \(F_{\mathfrak {q}}\). In order to avoid having to give a formal treatment of inertial types, we will simply state their results for the specific modules \(\sigma =\mathbb {1}_A,{\text {St}}_A\) and \(\sigma ^{\mathrm {ps}}_A\), for \(A=\mathcal {O},\mathbb {F}\), defined in section 3.5 (noting that we have assumed that \(\mathcal {O}= W(\mathbb {F})[\zeta +\zeta ^{-1}]\)):
Proposition 4.20
([15]) Viewing each \(M_{\infty ,K^{\mathfrak {q}}}(\sigma )\) as an \(R_{\mathfrak {q}}\)-module,
-
(1)
\(M_{\infty ,K^{\mathfrak {q}}}(\mathbb {1}_\mathcal {O})\) (resp. \(M_{\infty ,K^{\mathfrak {q}}}(\mathbb {1}_\mathbb {F})\)) is supported on \(R_\mathfrak {q}^{\mathrm {nr}}\) (resp. \(\overline{R}_\mathfrak {q}^{\mathrm {nr}}\)),
-
(2)
\(M_{\infty ,K^{\mathfrak {q}}}({\text {St}}_\mathcal {O})\) (resp. \(M_{\infty ,K^{\mathfrak {q}}}({\text {St}}_\mathbb {F})\)) is supported on \(R_\mathfrak {q}^{\mathrm {unip}}\) (resp. \(\overline{R}_\mathfrak {q}^{\mathrm {unip}}\)),
-
(3)
\(M_{\infty ,K^{\mathfrak {q}}}(\sigma ^{\mathrm {ps}}_{\mathcal {O}})\) (resp. \(M_{\infty ,K^{\mathfrak {q}}}(\sigma ^{\mathrm {ps}}_{\mathbb {F}})\)) is supported on \(R_\mathfrak {q}^{\mathrm {ps}}\) (resp. \(\overline{R}_\mathfrak {q}^{\mathrm {ps}}\)).
Proof
Follows from Proposition 3.10 and the fact that \(M_{\infty ,K^{\mathfrak {q}}}(-)\) is a patching functor in the sense of [15]. \(\square \)
We also record the support of the modules \(N_{\infty ,K^{\mathfrak {q}}}\) and \(\overline{N}_{\infty ,K^{\mathfrak {q}}}\) from Sect. 4.3 here.
Proposition 4.21
As \(R_{\mathfrak {q}}\)-modules, \(N_{\infty ,K^{\mathfrak {q}}}\) is supported on \(R^N_{\mathfrak {q}}\) and \(\overline{N}_{\infty ,K^{\mathfrak {q}}}\) is supported on \(\overline{R}^N_{\mathfrak {q}}\).
Proof
As \(\overline{N}_{\infty , K^{\mathfrak {q}}} = N_{\infty , K^{\mathfrak {q}}} \otimes _\mathcal {O}\mathbb {F}\) and \(\overline{R}^N_{\mathfrak {q}} = R^N_\mathfrak {q}\otimes _\mathcal {O}\mathbb {F}\), it suffices to prove the statement for \(N_{\infty , K^{\mathfrak {q}}}\).
By the definition of \(N_{\infty ,K^{\mathfrak {q}}}\) it suffices to prove that, for any \(n\ge 1\), the map
factors through \(R_{\mathfrak {q}}\twoheadrightarrow R^N_{\mathfrak {q}}\). We will prove this using Proposition 3.10.
Let \(\mathbb {T}^N_{n,K}\) be the image of \(\mathbb {T}^{S\cup Q_n}_\mathcal {O}\) in \({\text {End}}(N_{n, K^\mathfrak {q}})\). Note that the map \(R_n \rightarrow {\text {End}}_\mathcal {O}(N_{n, K^\mathfrak {q}})\) factors through \(\mathbb {T}^N_{n,K}\). Define \(\mathbb {T}^{N, \square }_{n,K} = \mathbb {T}^N_{n,K} \otimes _{R_n} R_n^\square \cong \mathbb {T}^N_{n,K}[[w_1, \ldots , w_j]]\); thus \(\gamma _n\) defines a map \(R^\mathfrak {q}\rightarrow \mathbb {T}^{N, \square }_{n,K}\). Since \(\mathbb {T}^N_{n,K}\) is reduced and l-torsion free, it suffices to show that, for every \(\mathcal {O}\)-algebra homomorphism
the composition \(x \circ \gamma _n\) factors through \(R_{\mathfrak {q}}^N\).
To x we have an associated homomorphism
such that, for every \(v \not \in S \cup Q_n\), \({\text {tr}}(\rho _x({\text {Frob}}_v)) = x(T_v)\). In particular, the isomorphism class of \(\rho _x\) is the Galois representation associated to \(x|_{\mathbb {T}_{n,K}}\).
The composition \(x \circ \gamma _n\) is the homomorphism \(R_{\mathfrak {q}} \rightarrow \overline{E}\) corresponding to \(\rho _x |_{G_{F_\mathfrak {q}}}\). By local-global compatibility and properties of the Jacquet–Langlands correspondence, \(\rho |_{G_{F_{\mathfrak {q}}}}\) is an inertially unipotent representation corresponding to a discrete series representation under the local Langlands correspondence. It follows that \(\rho |_{I_{F_{\mathfrak {q}}}}\) is a non-trivial unipotent representation, and therefore that \(x\circ \gamma _n:R_{\mathfrak {q}}\rightarrow \overline{E}\) factors through \(R_{\mathfrak {q}}\twoheadrightarrow R_{\mathfrak {q}}^N\) by Proposition 3.10. The result follows. \(\square \)
We finish this section by relating the patching functors of this section to the patched modules \(\overline{M}_{\infty ,K}\) considered in Sect. 4.3.
Proposition 4.22
For any compact open subgroup \(K_{\mathfrak {q}}\subseteq G(\mathcal {O}_{F,\mathfrak {q}})\) we have
In particular, letting \(K=K^{\mathfrak {q}}G(\mathcal {O}_{F,\mathfrak {q}})\) and \(K_0(\mathfrak {q}) = K^{\mathfrak {q}}U_0(\mathfrak {q})\), \(\overline{M}_{\infty ,K}\cong M_{\infty ,K^{\mathfrak {q}}}(\mathbb {1}_{\mathbb {F}})\) and
Proof
By the fact that \(\mathfrak {m}\) is non-Eisenstein, we have
It follows that \(M_{n,K^{\mathfrak {q}}}^{\square }\left( {\text {Ind}}_{K_{\mathfrak {q}}}^{G(\mathcal {O}_{F,\mathfrak {q}})}\mathbb {1}_{\mathbb {F}}\right) \cong \overline{M}_{n,K^{\mathfrak {q}}K_{\mathfrak {q}}}^\square \) and so
The last two statements follow from \({\text {Ind}}_{G(\mathcal {O}_{F,\mathfrak {q}})}^{G(\mathcal {O}_{F,\mathfrak {q}})}\mathbb {1}_{\mathbb {F}}= \mathbb {1}_\mathbb {F}\) and \({\text {Ind}}_{U_0(\mathfrak {q})}^{G(\mathcal {O}_{F,\mathfrak {q}})}\mathbb {1}_{\mathbb {F}}= \mathbb {1}_\mathbb {F}\oplus {\text {St}}_\mathbb {F}\). The statement that \(M_{\infty ,K^{\mathfrak {q}}}(\mathbb {1}_{\mathbb {F}}\oplus {\text {St}}_{\mathbb {F}})\cong M_{\infty ,K^{\mathfrak {q}}}(\mathbb {1}_{\mathbb {F}})\oplus M_{\infty ,K^{\mathfrak {q}}}({\text {St}}_{\mathbb {F}})\) is just a consequence of the exactness of \(M_{\infty ,K^{\mathfrak {q}}}(-)\). \(\square \)
Corollary 4.23
The \(R_\infty \)-module
has a filtration
with \(V_1\cong V_3/V_2\cong \overline{N}_{\infty ,K^{\mathfrak {q}}}\) and \(V_2/V_1\cong M_{\infty ,K^{\mathfrak {q}}}(\mathbb {1}_{\mathbb {F}})^{\oplus 2}\).
Proof
By Proposition 4.22 this is just a rephrasing of Theorem 4.17. \(\square \)
5 Commutative algebra lemmas
The following is a mild generalisation of the “miracle flatness criterion”, for which see [28] Theorem 23.1 or [37, Lemma 00R4]. A similar generalisation, in the setting of noncommutative completed group rings, also appears in [20].
Lemma 5.1
Let \(A \rightarrow R\) be a local homomorphism of noetherian local rings, and let M be a finite R-module. Let \(\mathfrak {m}\) be the maximal ideal of A. Suppose that:
-
(1)
A is regular;
-
(2)
M is maximal Cohen–Macaulay; and
-
(3)
\(\dim R = \dim A + \dim R/\mathfrak {m}R\).
Then M is a flat A-module.
Proof
The proof is essentially the same as that of [37, Lemma 00A4]. If M is zero, the result is clear; so suppose that M is nonzero. The proof is then by induction on \(d = \dim A\). The base case \(d = 0\) is trivial, as then A is a field.
In general, suppose the lemma is true when \(\dim A < d\). Choose \(x \in \mathfrak {m}\setminus \mathfrak {m}^2\). Then x is the first element in a regular system of parameters \((x, x_2, \ldots , x_d)\) for A. The third condition implies that \((x, x_2, \ldots , x_d)\) extends to a system of parameters \((x, x_2, \ldots , x_d, x_{d+1}, \ldots , x_e)\) for R which is therefore also a system of parameters for M (by the hypothesis that M is maximal Cohen–Macaulay). Since M is Cohen–Macaulay, this is a regular sequence on M. In particular, x is a non-zerodivisor on M.
Now, A/xA is regular of dimension \(\dim A - 1\), \(\dim (R/xR) = \dim R - 1\) (since x is part of a system of parameters for R), and M/xM is a maximal Cohen–Macaulay R/xR-module. So, by induction, M/xM is a flat A/xA-module. Moreover, \({\text {Tor}}_1^A(M, A/(x)) = 0\) as x is a non-zerodivisor on M. Therefore, by the local criterion for flatness in the form of [37, Lemma 00ML], M is a flat A-module. \(\square \)
Lemma 5.2
Let \(A = \mathbb {F}[[X,Y]]/(X^2Y)\) and let R be an A-algebra. Let \(0 \rightarrow L \rightarrow M \rightarrow N\rightarrow 0\) be a short exact sequence of R-modules such that
-
(1)
M is a flat A-module;
-
(2)
\((X) \subset {\text {ann}}_{A}(L)\);
-
(3)
\((XY) \subset {\text {ann}}_{A}(N)\).
Then \(N = M\otimes _{A} A/(XY)\) and so N is a flat A/(XY)-module. Moreover we have an isomorphism \(N/XN\cong L\) of R-modules.
Proof
By the snake lemma, as multiplication by X is zero on L, there is an exact sequence of R modules
But we have an exact sequence \(0 \rightarrow (XY) \rightarrow A \rightarrow (X) \rightarrow 0\) (the second map being multiplication by X). As M is flat this is still exact when tensored over A with M, and for any ideal I we can identify \(I \otimes _{A} M\) with \(IM \subset M\). Thus \(M[X] = XYM\). But as N is killed by XY, this implies that the map \(M[X] \rightarrow N[X]\) is zero. From the displayed exact sequence, we see that \(L = M[X] = XYM\), and so \(N = M/L = M/XYM\). This is flat over A/(XY).
Now as \(L=XYM\) and M/XM is killed by X, the map \(L\rightarrow M/XM\) in the above exact sequence is zero, which implies that the map \(N[X]\rightarrow L\) is an isomorphism of R-modules.
But now we have an exact sequence \(0\rightarrow A/(X) \xrightarrow {\cdot Y} A/(XY)\xrightarrow {\cdot X} XA/(XY)\rightarrow 0\). As N is flat over A/(XY), the sequence of R-modules \(0 \rightarrow N/XN\xrightarrow {Y} N \xrightarrow {X} XN \rightarrow 0\) is exact, and so we get the desired isomorphism \(N/XN\cong N[X]\cong L\) of R-modules.
\(\square \)
Lemma 5.3
Let \(B = \mathbb {F}[[X,Y]]/(XY)\) and let R be a complete local noetherian B-algebra with residue field \(\mathbb {F}\). Suppose that L, M, N and P are R-modules such that:
-
(1)
M is flat over B;
-
(2)
\((Y) \subset {\text {ann}}_{B}(N)\) and N is flat over B/(Y);
-
(3)
there is an isomorphism of R-modules \(L \xrightarrow {\sim }M/XM\);
-
(4)
there is an isomorphism of R-modules \(\alpha : P \xrightarrow {\sim }L \oplus M\);
-
(5)
there is a filtration \(0 \subset P_1 \subset P_2 \subset P\) by R-modules and isomorphisms of R-modules \(P_1 \xrightarrow {\sim }N\), \(P_2/P_1 \xrightarrow {\sim }L \oplus L\), and \(P/P_2 \xrightarrow {\sim }N\).
Then there is a short exact sequence of R-modules
Proof
Since L is flat over B/X by points (1) and (3), it has no Y-torsion, and so \(\alpha \) induces an isomorphism \(P[Y] \xrightarrow {\sim }M[Y]\). From the short exact sequence
of point (5), we have \(P_2[Y] = P_1[Y] \cong N\).
From the other short exact sequence
of point (5), we get an exact sequence
By the flatness of M, we can identify M[Y] with \(X\cdot M\), and so the image of M[Y] in N is XN. Since N is flat over B/(Y), \(N \cong XN\). Thus we have a short exact sequence
Finally, since M is flat over B there is an isomorphism \(M/YM \xrightarrow {\sim }XM\). We get the desired short exact sequence:
\(\square \)
6 Ihara’s lemma
Let D be a quaternion division algebra over F ramified at exactly one infinite place, so that we are in the indefinite case of Sect. 2. Suppose that \(\mathfrak {p}\) is a finite place of F at which D is unramified.
6.1 Statements
Let \(K\subseteq G(\mathbb {A}_{F,f})\) be unramified at \(\mathfrak {p}\) and sufficiently small, and let S be any finite set of finite places of F containing \(\Sigma (K)\cup \Sigma _l\cup \{\mathfrak {p}\} \cup \Sigma _\infty \). There are two natural degeneracy maps \(\pi _1,\pi _2:X_{K_0(\mathfrak {p})}\rightarrow X_K\), defined in section 2.11.
Conjecture 6.1
Suppose that \(\Lambda \) is the local system on \(X_K\) attached to a finite-dimensional continuous \(\mathbb {F}_l\)-representation of \(K^{\mathfrak {p}}\). Then for any non-Eisenstein maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}^S_{\mathbb {Z}_l}\) the map
is injective.
For \(\Lambda \) the constant sheaf \(\mathbb {F}_l\), this becomes:
Conjecture 6.2
For any non-Eisenstein maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}^S_{\mathbb {Z}_l}\), the map
is injective.
We also have an equivalent dualized version:
Conjecture 6.3
For any non-Eisenstein maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}^S_{\mathbb {Z}_l}\), the map
is surjective.
Lemma 6.4
Conjecture 6.2 (or, equivalently, Conjecture 6.3) for all K implies Conjecture 6.1 for all K.
Proof
Suppose that Conjecture 6.2 holds for all K. Suppose that \(\Lambda \) and \(\mathfrak {m}\) are as in the statement of Conjecture 6.1, and that \(\Lambda \) is associated to a representation V of \(K^{\mathfrak {p}}\). Let \(H^\mathfrak {p}\subset K^\mathfrak {p}\) be an open subgroup that acts trivially on V, and \(H = H^\mathfrak {p}K_\mathfrak {p}\). Let \(f : X_H \rightarrow X_K\) be the projection. The Hochschild–Serre spectral sequence provides a (Hecke-equivariant) exact sequence
After localizing at \(\mathfrak {m}\), the first term vanishes by Lemma 2.3. Noting that \(f^*\Lambda \) is constant, we get an inclusion
that commutes with the maps \(\pi ^*\). Since Conjecture 6.2 holds for the subgroup H by assumption, we deduce Conjecture 6.1 for the subgroup K. \(\square \)
Our main result is the following:
Theorem 6.5
If \(l > 2\), then Conjectures 6.1, 6.2 and 6.3 are true for any non-Eisenstein maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}^S_{\mathbb {Z}_l}\) satisfying the conditions:
-
(1)
\(l|\#\overline{\rho }_{\mathfrak {m}}(G_F)\). That is, \(\mathfrak {m}\) is not exceptional.
-
(2)
If \(l = 5\) and the image of the projective representation \({\text {proj}}\overline{\rho }_{\mathfrak {m}}:G_F\rightarrow GL_2(\overline{\mathbb {F}}_5)\twoheadrightarrow PGL_2(\overline{\mathbb {F}}_5)\) is isomorphic to \(PGL_2(\mathbb {F}_5)\), then \(\ker {\text {proj}}\overline{\rho }_{\mathfrak {m}}\not \subseteq G_{F(\zeta _5)}\). (This condition is automatically satisfied whenever \(\sqrt{5}\not \in F\).)
Remark 6.6
Condition (1) implies the Taylor–Wiles condition that \(\overline{\rho }_{\mathfrak {m}}|_{G_{F(\zeta _l)}}\) is absolutely irreducible. Condition (2) is simply the other Taylor–Wiles condition (see [25, 3.2.3]).
The reason for including the stronger assumption that \(\mathfrak {m}\) is not exceptional, instead of just the usual Taylor–Wiles conditions, is that this assumption will be necessary for picking the auxiliary prime \(\mathfrak {q}\). See Lemma 6.9 below.
Remark 6.7
We have assumed that K is sufficiently small, for convenience. This assumption could be removed by the standard device of introducing auxiliary level structure at a place \(\mathfrak {q}_0\) at which there are no congruences, as in [27] section 4.2 or [15] section 6.2.
6.2 Definite quaternion algebras
Let \(\overline{D}\) be a totally definite quaternion algebra over F, unramified at \(\mathfrak {p}\). Let \(\overline{G}\) be the associated algebraic group. If \(H \subset \overline{G}(\mathbb {A}_{F,f})\) is a compact open subgroup unramified at \(\mathfrak {p}\) then we have degeneracy maps \(\pi _1,\pi _2:Y_{H_0(\mathfrak {p})}\rightarrow Y_{H}\). Let S be a finite set of places of F containing \(\Sigma _l \cup \Sigma _\infty \cup \{\mathfrak {p}\}\) and all places at which H or \(\overline{D}\) ramify. The following version of Ihara’s Lemma is known:
Theorem 6.8
If \(H\subseteq \overline{G}(\mathbb {A}_{F,f})\) is unramified at \(\mathfrak {p}\), then for any non-Eisenstein maximal ideal \(\mathfrak {m}\) of \(\mathbb {T}_{\mathbb {Z}_l}^S\), the map
is injective.
Proof
Versions of this have been proved by Ribet (over \(\mathbb {Q}\), [31] Theorem 3.15) and Taylor (over F, [38] Lemma 4). There it is proved that with \(\mathbb {Z}_l\) coefficients, without localizing at \(\mathfrak {m}\), \(\pi ^*\) has saturated image, from which the theorem may be easily deduced—but the method for doing this actually directly gives the result in the form we need. For \(\mathbb {Q}\) this is carried out in [13] Lemma 2 and the general case is no harder. We include the proof for completeness.
Suppose that (f, g) is in the kernel of \(\pi ^*\). Regard f and g as H-invariant functions on \(\overline{G}(F) \backslash \overline{G}(\mathbb {A}_{F,f})\). Then \(f(x) = -g(x\omega )\) for all x in this quotient, where \(\omega = \begin{pmatrix} \varpi _\mathfrak {p} &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}\) (making use of the isomorphism \(\overline{G}(F_\mathfrak {p}) \cong GL_2(F_\mathfrak {p})\)). Then f is invariant under H and \(\omega ^{-1}H\omega \). These subgroups generate a subgroup containing \(H^\mathfrak {p}SL_2(F_\mathfrak {p})\), under which f is invariant. Let \(\overline{G}'\) be the subgroup of \(\overline{G}\) of elements with reduced norm 1. Then by the strong approximation theorem in \(\overline{G}'\), the function f factors through the reduced norm map:
But the functions factoring through this map form a module over \(\mathbb {T}_H^S\) that is supported on Eisenstein maximal ideals (the argument is similar to that of Proposition 2.3). The theorem follows. \(\square \)
6.3 The auxiliary prime
Recall our assumption that \(l|\#\overline{\rho }_\mathfrak {m}(G_F)\). After conjugating \(\overline{\rho }_\mathfrak {m}\) if necessary, we may thus assume that \(\overline{\rho }_\mathfrak {m}(G_F)\) contains the matrix \(\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}\). We now get the following:
Lemma 6.9
There are infinitely many primes \(\mathfrak {q}\) for which:
-
(1)
\(\mathfrak {q}\not \in \Delta \cup \Sigma (K)\cup \Sigma _l\cup \{\mathfrak {p}\}\)
-
(2)
\(\overline{\rho }_\mathfrak {m}\) is unramified at \(\mathfrak {q}\)
-
(3)
\({\text {Nm}}(\mathfrak {q})\equiv 1\pmod {l}\)
-
(4)
\(\overline{\rho }_\mathfrak {m}({\text {Frob}}_\mathfrak {q}) = \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}\)
Proof
All but finitely many primes satisfy (1) and (2), so it suffices to find infinitely many primes satisfying (3) and (4).
Pick a number field L/F for which \(F(\zeta _l)\subseteq L\) and \(\overline{\rho }_\mathfrak {m}:G_F\rightarrow GL_2(\overline{\mathbb {F}}_l)\) factors through \({\text {Gal}}(L/F)\). Let \(\overline{\epsilon }:{\text {Gal}}(L/F)\twoheadrightarrow {\text {Gal}}(F(\zeta _\ell )/F)\hookrightarrow (\mathbb {Z}/l\mathbb {Z})^\times \) be the cyclotomic character. By the Chebotarev density theorem, it suffices to find some \(\sigma \in {\text {Gal}}(L/F)\) for which \(\overline{\rho }_\mathfrak {m}(\sigma ) = \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}\) and \(\overline{\epsilon }(\sigma ) = 1 \in (\mathbb {Z}/l\mathbb {Z})^\times \).
Now by our assumption on the image of \(\overline{\rho }_\mathfrak {m}\), there is some \(\sigma _0\in {\text {Gal}}(L/F)\) for which \(\overline{\rho }_\mathfrak {m}(\sigma _0) = \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}\). Let \(\sigma = \sigma _0^{1-l}\in {\text {Gal}}(L/F)\). Then we indeed have
and
\(\square \)
For the rest of the proof we fix such a prime \(\mathfrak {q}\). Note that it satisfies the requirements of sections 2.13 and 3.3. We let \(\overline{D}\) be a definite quaternion algebra ramified at \(\Delta \cup \{\mathfrak {q}, \tau \}\).
6.4 The proof
Choose \(\mathbb {F}\) large enough that \(\overline{\rho }_\mathfrak {m}\) is defined over \(\mathbb {F}\), and let \((E, \mathcal {O}, \mathbb {F})\) be the coefficient system satisfying Hypothesis 3.1. Let \(\psi : G_F \rightarrow \mathcal {O}^\times \) be a finite order character lifting \(\det (\overline{\rho }_\mathfrak {m}) \overline{\epsilon }\), and also write \(\psi \) for the character \(\psi \circ {\text {Art}}_F\) of \(\mathbb {A}_{F,f}^\times /F^\times \). We make sure that \(F^\times (K \cap Z(\mathbb {A}_{F,f})) \subset \ker (\psi )\) and that the prime \(\mathfrak {q}\) is chosen so that \(\psi \) is unramified at \(\mathfrak {q}\).
Let S be as in Sect. 6.1. Enlarging S if necessary (which is allowed, by Lemma 4.11), we assume that \(\mathfrak {q}\in S\). We write \(\Sigma \) for the set of finite places in S. The results of Sect. 2 imply that there is a filtration of \(H^1(X_{K_0(\mathfrak {q})}, \mathbb {F})_\mathfrak {m}[\psi ]\) (by \(\mathbb {T}^S\)-submodules) whose graded pieces are
In Sect. 4 we explain how these cohomology groups and this filtration (more precisely, their duals) may be ‘patched’ using the Taylor–Wiles method. For each place \(v \in \Sigma \) let \(R_v\) be
-
if \(v \not \mid l\), the universal fixed determinant framed deformation ring \(R^{\square , \psi }_{\overline{\rho }_\mathfrak {m}|_{G_{F_v}}, \mathcal {O}}\) of \(\overline{\rho }_\mathfrak {m}|_{G_{F_v}}\);
-
if \(v \mid l\), the potentially semistable (over a fixed extension depending only on \(K \cap G(F_v)\), and of parallel Hodge–Tate weights \(\{0,1\}\)) deformation ring \(R^{\square , \psi , K\cap G(F_v)\text {-st}}_{\overline{\rho }_\mathfrak {m}|_{G_{F_v}},\mathcal {O}}\) defined in Sect. 3.5.
For some integers \(g,d \ge 0\) (determined in Sect. 4, with \(d=r+j\) in the notation of that section) we let
and
and recall that d and g were chosen so that \(R_\infty \) and \(S_\infty \) have the same dimension.
Then in Sect. 4.4 we constructed an injective homomorphism \(S_\infty \rightarrow R_\infty \), maximal Cohen–Macaulay \(R_\infty \)-modules \(M_{\infty ,K}\) and \(N_{\infty , K^\mathfrak {q}}\), and an exact functor \(M_{\infty , K^\mathfrak {q}}\) from the category of finitely-generated \(\mathcal {O}\)-modules with a continuous action of \(GL_2(\mathcal {O}_{F,\mathfrak {q}})\) (satisfying a condition on the central character) to the category of finitely-generated \(R_\infty \)-modules. Moreover, \(M_{\infty , K^\mathfrak {q}}\) has the property that if \(\sigma \) is a finite free \(\mathcal {O}\)-module (resp. a finite dimensional \(\mathbb {F}\)-vector space) then \(M_{\infty , K^\mathfrak {q}}(\sigma )\) is maximal Cohen–Macaulay over \(R_\infty \) (resp. \(\overline{R}_\infty = R_\infty \otimes _{\mathcal {O}}\mathbb {F}\)). These are equipped with isomorphisms
and
In Table 1, for various patched modules, we write down a corresponding quotient \(R^{?}_{\mathfrak {q}}\) of \(R_\mathfrak {q}\) on which they are supported. Here ? is an element of \(\{\mathrm {nr}, N, \mathrm {unip}, \mathrm {ps}\}\), and we write
and
as shorthand for the rings defined in Sect. 3.3. The claims of Table 1 follow from the properties of the Jacquet–Langlands correspondence and local-global compatibility, and are the content of Propositions 4.20 and 4.21. Furthermore, for \(? \in \{\mathrm {nr}, N, \mathrm {unip}, \mathrm {ps}\}\) we define the quotient
of \(R_\infty \).
The filtration provided by Theorem 2.11 may be patched as in Sect. 4. Thus (see Corollary 4.23) there is a filtration of
by \(R_\infty \)-modules

together with isomorphisms
and
To go further, we need the structure of the local deformation rings at \(\mathfrak {q}\). The deformation rings \(R^{\mathrm {nr}}_{\mathfrak {q}}\), \(R^N_\mathfrak {q}\) and \(R^{\mathrm {ps}}_\mathfrak {q}\) are regular by Propositions 3.5 and 3.6. Therefore, by Lemma 5.1, we have:
Proposition 6.10
-
(1)
\(M_{\infty , K^{\mathfrak {q}}}(\mathbb {1}_\mathcal {O})\) is flat over \(R_\mathfrak {q}^{\mathrm {nr}}\).
-
(2)
\(N_{\infty , K^{\mathfrak {q}}}\) is flat over \(R^N_\mathfrak {q}\).
-
(3)
\(M_{\infty , K^{\mathfrak {q}}}(\sigma ^{\mathrm {ps}}_\mathcal {O})\) is flat over \(R^{\mathrm {ps}}_\mathfrak {q}\).
By Proposition 3.7, there are isomorphisms
and
compatible with the natural surjection \(\overline{R}^{\mathrm {ps}}_\mathfrak {q}\twoheadrightarrow \overline{R}^{\mathrm {unip}}_\mathfrak {q}\) and so that
and
By section 3.5, equation (2), we have an exact sequence
Proposition 6.11
The module \(M_{\infty ,K}({\text {St}}_\mathbb {F})\) is flat over \(R_\mathfrak {q}^{\mathrm {unip}}\) and there is an isomorphism
Proof
By Proposition 6.10 and the above exact sequence, the hypotheses of Lemma 5.2 apply with \(R = R^{\mathrm {unip}}_\infty \otimes _\mathcal {O}\mathbb {F}\) (made into an \(\mathbb {F}[[X,Y]]/(X^2Y)\)-algebra in the evident way), \(L = M_{\infty , K^{\mathfrak {q}}}(\mathbb {1}_\mathbb {F})\), \(M = M_{\infty , K^{\mathfrak {q}}}(\sigma ^{\mathrm {ps}}_\mathbb {F})\), and \(N = M_{\infty , K^{\mathfrak {q}}}({\text {St}}_\mathbb {F})\). The proposition follows. \(\square \)
Now we know that \(M_{\infty , K^{\mathfrak {q}}}({\text {St}}_\mathbb {F})\) is flat, the filtration (\(\star \)) can be used to “transfer information” between \(N_\infty \) and \(M_\infty \). More precisely, we have:
Proposition 6.12
There is a short exact sequence of \(R_\infty \)-modules
Proof
By Proposition 6.11 and the filtration (\(\star \)), the hypotheses of Lemma 5.3 apply with \(R= R^{\mathrm {ps}}_\infty \otimes _{\mathcal {O}} \mathbb {F}\) (made into an \(\mathbb {F}[[X,Y]]/(XY)\)-algebra in the evident way), \(L = M_{\infty ,K^{\mathfrak {q}}}(\mathbb {1}_\mathbb {F})\), \(M = M_{\infty ,K^{\mathfrak {q}}}({\text {St}}_{\mathbb {F}})\), \(P = \overline{M}_{\infty , K_0(\mathfrak {q})}\), \(N = \overline{N}_{\infty , K^{\mathfrak {q}}}\), and \(P_1\) and \(P_2\) given by (\(\star \)). The proposition follows. \(\square \)
Proof of Theorem 6.5
Now we are ready to prove our main result. We may carry out the constructions and arguments above equally well with \(K^\mathfrak {q}\) replaced by \(K_0(\mathfrak {p})^\mathfrak {q}\) in a way compatible with the degeneracy maps \(\pi _*\). We therefore obtain a commuting diagram

By Theorem 6.8 the outer maps are surjective after applying \(\otimes _{S_\infty } \mathbb {F}\), and so by Nakayama’s Lemma they are surjective. It follows that the middle map is surjective, and by Nakayama’s Lemma again that the map
is surjective. Tensoring with \(\overline{R}^{\mathrm {nr}}_{\mathfrak {q}}\) and applying Proposition 6.11 this gives that \(\overline{M}_{\infty ,K_0(\mathfrak {p})}\rightarrow \left( \overline{M}_{\infty ,K}\right) ^{\oplus 2}\) is surjective. Applying \(\otimes _{S_\infty } \mathbb {F}\), we see that
is surjective. By Nakayama’s Lemma, we obtain that
is surjective. This proves Conjecture 6.3 and hence Theorem 6.5 for this \(\mathfrak {m}\). \(\square \)
Notes
In fact, if we instead take \(\Gamma = \Gamma _1(N)\) then \(\pi ^*\) is already injective. For us, however, localizing at a maximal ideal of the Hecke algebra will be crucial.
See the end of [12] for \(k = l-1\).
This is a slight simplification.
Suppressing minor issues due to framing and fixed determinants.
Provided that one carefully controls the ramification in the coefficient ring \(\mathcal {O}\).
For an easy counterexample, assume that \(S_\infty /\mathcal {I}_n\) is \(\varpi \)-torsion free for all n (a condition which will be satisfied for our choice of \(\mathcal {I}_n\) below) and let \(\mathscr {M}=\{S_\infty /\mathcal {I}_n\}_{n\ge 1}\). Define \(\varphi =\{\varphi _n\}_{n\ge 1}:\mathscr {M}\rightarrow \mathscr {M}\) by \(\varphi _n(x) = \varpi ^nx\). Then \(\varphi :\mathscr {M}\rightarrow \mathscr {M}\) is injective, \(\mathscr {P}(\mathscr {M}) = S_\infty \), and \(\mathscr {P}(\varphi ):S_\infty \rightarrow S_\infty \) is the zero map.
References
Bertolini, M., Darmon, H.: Iwasawa’s main conjecture for elliptic curves over anticyclotomic \({\mathbb{Z}}_p\)-extensions. Ann. Math. (2) 162(1), 1–64 (2005)
Breuil, C., Diamond, F.: Formes modulaires de Hilbert modulo \(p\) et valeurs d’extensions entre caractères galoisiens. Ann. Sci. Éc. Norm. Supér. (4) 47(5), 905–974 (2014)
Buzzard, K., Diamond, F., Jarvis, F.: On Serre’s conjecture for mod \(\ell \) Galois representations over totally real fields. Duke Math. J. 155(1), 105–161 (2010)
Barnet-Lamb, T., Gee, T., Geraghty, D., Taylor, R.: Potential automorphy and change of weight. Ann. Math. (2) 179(2), 501–609 (2014)
Carayol, H.: Sur la mauvaise réduction des courbes de Shimura. Composit. Math. 59(2), 151–230 (1986)
Calegari, F., Geraghty, D.: Modularity lifting beyond the Taylor–Wiles method. Invent. Math. 211(1), 297–433 (2018)
Chida, M., Hsieh, M.-L.: On the anticyclotomic Iwasawa main conjecture for modular forms. Compos. Math. 151(5), 863–897 (2015)
Cheng, C.: Ihara’s lemma for Shimura curves over totally real fields and multiplicity two, unpublished, available at https://www.math.uni-bielefeld.de/~ccheng/Research/Multi2.pdf
Clozel, L., Harris, M., Taylor, R.: Automorphy for some \(l\)-adic lifts of automorphic mod \(l\) Galois representations, Publ. Math. Inst. Hautes Études Sci. (2008), no. 108, 1–181, With Appendix A, summarizing unpublished work of Russ Mann, and Appendix B by Marie-France Vignéras
Chojecki, P., Sorensen, C.: Strong local-global compatibility in the \(p\)-adic Langlands program for \(U(2)\). Rend. Semin. Mat. Univ. Padova 137, 135–153 (2017)
Diamond, F.: The Taylor–Wiles construction and multiplicity one. Invent. Math. 128(2), 379–391 (1997)
Diamond, F., Taylor, R.: Lifting modular mod \(l\) representations. Duke Math. J. 74(2), 253–269 (1994)
Diamond, F., Taylor, R.: Nonoptimal levels of mod \(l\) modular representations. Invent. Math. 115(3), 435–462 (1994)
Edixhoven, B.: The weight in Serre’s conjectures on modular forms. Invent. Math. 109(3), 563–594 (1992)
Emerton, M., Gee, T., Savitt, D.: Lattices in the cohomology of Shimura curves. Invent. Math. 200(1), 1–96 (2015)
Emerton, M., Helm, D.: The local Langlands correspondence for \({\rm GL}_n\) in families. Ann. Sci. Éc. Norm. Supér. (4) 47(4), 655–722 (2014)
Emerton, M.: Local-global compatibility in the \(p\)-adic Langlands programme for \(GL_2/{\mathbb{Q}}\), 2011, draft available at http://www.math.uchicago.edu/~emerton/preprints.html
Gee, T.: Automorphic lifts of prescribed types. Math. Ann. 350(1), 107–144 (2011)
Gee, T., Liu, T., Savitt, D.: The weight part of Serre’s conjecture for \({\rm GL} (2)\). Forum Math. Pi 3, e2, 52 (2015)
Gee, T., Newton, J.: Patching and the completed homology of locally symmetric spaces, (2016)
Gow, R.: On the Schur indices of characters of finite classical groups. J. Lond. Math. Soc. (2) 24(1), 135–147 (1981)
Ihara, Y.: On modular curves over finite fields, Discrete subgroups of Lie groups and applications to moduli (Internat. Colloq., Bombay, Oxford Univ. Press, Bombay 1975, 161–202 (1973)
Jarvis, F.: Mazur’s principle for totally real fields of odd degree. Compos. Math. 116(1), 39–79 (1999)
Kisin, M.: Potentially semi-stable deformation rings. J. Am. Math. Soc. 21(2), 513–546 (2008)
Kisin, M.: Moduli of finite flat group schemes, and modularity. Ann. Math. (2) 170(3), 1085–1180 (2009)
Longo, M.: Anticyclotomic Iwasawa’s main conjecture for Hilbert modular forms. Comment. Math. Helv. 87(2), 303–353 (2012)
Manning, J.: Patching and multiplicity \(2^k\) for Shimura curves, (2019), available at https://arxiv.org/abs/1902.06878
Matsumura, H.: Commutative ring theory, second ed., Cambridge Studies in Advanced Mathematics, vol. 8, Cambridge University Press, Cambridge, 1989, Translated from the Japanese by M. Reid
Morita, Y.: Reduction modulo \({\mathfrak{P}}\) of Shimura curves. Hokkaido Math. J. 10(2), 209–238 (1981)
Ribet, K.A.: Congruence relations between modular forms, Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Warsaw, 1983), PWN, Warsaw, pp. 503–514 (1984)
Ribet, K.A.: On modular representations of \({\rm Gal}(\overline{ Q}/{ Q})\) arising from modular forms. Invent. Math. 100(2), 431–476 (1990)
Ribet, K.A.: Multiplicities of Galois representations in Jacobians of Shimura curves, Festschrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part II (Ramat Aviv, : Israel Math. Conf. Proc., vol. 3. Weizmann, Jerusalem 1990, 221–236 (1989)
Scholze, P.: On the \(p\)-adic cohomology of the Lubin-Tate tower. Ann. Sci. Éc. Norm. Supér. (4) 51(4), 811–863 (2018)
Shotton, J.: Local deformation rings for \({\rm GL}_2\) and a Breuil-Mézard conjecture when \(\ell \ne p\). Algebra Number Theory 10(7), 1437–1475 (2016)
Shotton, J.: Local deformation rings for \(2\)-adic representations of \({G}_{{\mathbb{Q}}_l}\), \(l \ne 2\), (2017) Appendix to Yongquan Hu, Vytautas Paškūnas, On crystabelline deformation rings of \({\rm Gal} (\overline{\mathbb{Q}}_p/\mathbb{Q}_p)\)
Shotton, J.: The Breuil-Mézard conjecture when \(l\ne p\). Duke Math. J. 167(4), 603–678 (2018)
The Stacks Project Authors, Stacks Project, http://stacks.math.columbia.edu, 2017
Taylor, R.: On Galois representations associated to Hilbert modular forms. Invent. Math. 98(2), 265–280 (1989)
Taylor, R.: On the meromorphic continuation of degree two \(L\)-functions, Doc. Math. (2006), no. Extra Vol., 729–779
Taylor, R.: Automorphy for some \(l\)-adic lifts of automorphic mod \(l\) Galois representations. II, Publ. Math. Inst. Hautes Études Sci. (2008), no. 108, 183–239
Wang, H.: Anticyclotomic Iwasawa theory for Hilbert modular forms, ProQuest LLC, Ann Arbor, MI, 2015, Thesis (Ph.D.)–The Pennsylvania State University
Acknowledgements
Firstly, we thank Matthew Emerton for suggesting that we collaborate on this project and for many enlightening conversations. We also thank Chuangxun Cheng, Fred Diamond, Toby Gee, Yongquan Hu, David Loeffler, Matteo Longo, and Matteo Tamiozzo for useful comments or discussions. Part of this work was written up while the second author was at the Max Planck Institute for Mathematics, and he thanks them for their support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Wei Zhang.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Manning, J., Shotton, J. Ihara’s Lemma for Shimura curves over totally real fields via patching. Math. Ann. 379, 187–234 (2021). https://doi.org/10.1007/s00208-020-02048-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-020-02048-8