1 Introduction

A fundamental aspect of water-wave theory is the decay with depth of the wave-induced motion, the classical tenet (see [14]) being that the effects are negligible below a depth of one half the wavelength of the surface wave, called the wave base in oceanography. The precept that the wave-induced water motion essentially ceases at the wave base has important practical implications for offshore and coastal marine science. For example, in deep water, submarines commonly escape the uncomfortable and sometimes dangerous motions due to large waves by diving to the quiescent water below the wave base of the longest surface waves that are typical for the respective sea or ocean area. On the other hand, in coastal regions that are shallower than the wave base, bottom sediments and the seafloor are stirred by the passage of the surface waves.

Despite the common reliance on the concept of wave base in studies of the sediment movement on shallow marine shelves, its inaccuracy is often quite notable (see the discussion in [36]). While in part the inaccuracy is caused by observational error, it is mainly due to flaws in the underlying theory. First, there is the reliance on linear theory. The other serious shortcoming is the oversimplification made by ignoring the possible presence of underlying currents. These two pitfalls are actually interconnected. To see this, let us briefly describe the main data gathering procedure for surface waves on the continental shelf. Approximately 7.5% of the Earth’s ocean floor consists of continental shelves that are practically flat, with average depth about 50 m and average width of around 65 km; in some places they are almost nonexistent (e.g. along the coast of California), while in others, as along the northern coast of Siberia, their width exceeds 1000 km; see [17]. The waves that propagate at the surface of the sea over a continental shelf occupy a broad range of space-time scales and are wind driven. They are formed by the frictional drag of wind across the water surface, during a transfer process of energy from wind to water, with the energy being subsequently transported faster than the water through which it travels, with an insignificant energy loss (unless wave breaking occurs). In the absence of currents and assuming the validity of linear theory, explicit expressions for two-dimensional surface wave trains and for their underlying velocity field are available, and the equipartition of energy holds (see [14]). In view of this equality between the excess potential energy (with respect to the potential energy of the water at rest) and the kinetic energy, the total energy is the double of the excess potential energy. In this setting the excess potential energy pattern can thus be inferred by means of satellite images from the wave height. The explicit formulas that are available now show (see [14]) that below the wave base the amplitude of the wave-induced motion is merely 4% of the surface values, and thus essentially negligible. The drawback of this classical approach is that no explicit formulas are available for genuine wave solutions of the nonlinear governing equations, for which the equipartition of energy fails (with field data showing that in certain circumstances there is a transfer of kinetic energy into currents). Therefore the potential and kinetic energy contributions have to be estimated separately. The difficulty lies in handling the decay with depth of the kinetic energy, in the nonlinear setting of the governing equations.

In this paper we will prove some rigorous results on the vertical attenuation of the wave-induced motion beneath a wave which is periodic in space and propagates at the surface of a water flow of constant vorticity over a flat bed. Periodicity in time, however, is not required, so that the obtained decay rates are valid not only for travelling waves but also for more general wave patterns (in particular, they apply to nonlinear combinations of travelling waves of different wavelengths with a common fundamental frequency, which ensures that the interference is spatially periodic). After presenting some preliminary considerations in Sect. 2, we prove in Sect. 3 some results about the mean flow beneath the waves, which can be interpreted as the underlying current. In Sect. 4 we show that the decay of the wave-induced motion is exponential, so that at great depths the flow pattern approaches the pure current state. These results are valid for the nonlinear governing equations for water waves, without any restriction on the wave amplitude, and show the need for a fundamental re-examination of the classical theory which ignores the possible presence of underlying currents and neglects nonlinear effects altogether.

2 Preliminaries

The waves propagating at the surface of the sea are typically generated by wind [29]. They transport huge amounts of energy over large distances and their primary restoring force, which causes the displacements of the free surface to be accelerated back toward the mean level, is gravity. Note that the energy of ocean waves is concentrated in the long-wave range [19]. While the ocean surface rarely has the form of a uniform periodic travelling wave (since the wind generates waves of many periods and heights and waves from neighbouring wind fields may interact), the vast majority of long surface ocean waves are approximately two-dimensional (propagating in the predominant wind direction) and periodic [39]. This coherence manifests itself most notably in space and to a lesser degree temporally. Indeed, the large-scale patterns of wind movement are spatially relatively stable in each open ocean location, being basically determined by the response of the Earth’s atmosphere to the Sun’s uneven heating and by the effect of the Earth’s rotation [33]. For localised, potentially messy, disturbances of varying wave-periods and heights it can be shown—in the linear setting—that the water waves travel with a (slowly-varying) group velocity, and this leads eventually to the appearance of coherent wave trains of uniform spatial periodicity emerging in the far-field. On the other hand, the impact of gustiness often leads to large temporal wind variances [25]. On most areas of the continental shelf, the ocean flow is strongly conditioned by the presence of currents, the most significant being tidal currents (the horizontal movement of water accompanying the rise and fall of water during the flood and ebb tidal changes) and local wind-generated currents. The unsteadiness of tidal currents is relevant for times scales of several hours, while for times of the order of one hour the tidal currents are practically uniform with depth (see the discussion in [35]). Note that velocities of tidal currents are about 0.1 m/s, while the speed \(c(\lambda )\) of small-amplitude travelling waves of wavelength \(\lambda \), propagating at the surface of a water flow with no underlying currents, over a flat bed water of mean depth h, is given by the dispersion relation

$$\begin{aligned} c(\lambda )=\sqrt{gh \,\frac{\tanh (2\pi h/\lambda )}{2\pi h/\lambda }} \end{aligned}$$
(2.1)

(see the discussion in [6]); here g is the constant acceleration of gravity (about 9.8 m/s\(^2\)). The formula (2.1) is relevant since a uniform current is equivalent to still water viewed from a reference frame moving with the current velocity. For the continental shelf the representative choices \(h \approx 50\) m, \(\lambda \approx 80\) m in (2.1) yield speeds of about 11 m/s, so that in a one-hour window these waves travel distances that exceed several hundred times the wavelength. Therefore the spatial periodicity is of relevance, even if temporal periodicty fails as changes of the flow pattern will occur in due time. The effect of tidal currents being easily accounted for on areas of the continental shelf, the challenge remains to investigate wind-driven flows.

When wind blows over water, it accelerates the surface in the direction of the wind and subsequently a development of the velocity profile of the wind-drift current occurs in the near-surface layer. A systematic collection of wind drift data provides guidance for the velocities of wind-generated currents as functions of the depth [16], with the horizontal fluid velocity profile of the pure current state over the flat bed \(y=-d\), in the absence of the wave-induced vertical velocities, given by

$$\begin{aligned} u_0(y)=\left\{ \begin{array}{l} s\,\Big (1+ \displaystyle \frac{y}{d_0}\Big )\quad \hbox {for}\quad -d_0 \le y \le 0,\\ 0 \quad \hbox {for}\quad -d \le y \le -d_0, \end{array}\right. \end{aligned}$$
(2.2)

where \(d_0>0\) is the reference depth of 50 m and where the magnitude s of the surface wind-drift (at \(y=0\)) corresponds to about 2–7% of the wind velocity measured at 10 m above sea level; note that while quantified information is available the details are not yet known with sufficient precision for a more accurate estimation (see [41]), the scale ranging from 2% for moderate wind speeds (below 20 m/s) and short to moderate fetch (of the order of 10 km), and increasing towards the upper limit with the gust factor (see [37]). The presence of an adverse tidal current can lead to the appearance of critical levels, where the speed vanishes and flow-reversal occurs. Critical levels are of great importance in wave–current interactions since they can trigger instabilities in marginally stable flows, and these are places where a significant energy exchange between the waves and the underlying current can occur (see the discussion in [2]).

Due to the absence of critical layers in irrotational flows, a non-zero vorticity (associated with a shear flow) is essential for the occurence of such flow patterns; for example, the vorticity of the wind-drift current (2.2) is \(s/d_0\). In this paper we consider two-dimensional inviscid waves which are spatially periodic and propagate in a flow with constant vorticity. Inviscid theory is the usual framework for the study of water waves that are not near breaking since the most significant effects of viscosity in the open sea are to produce wave-amplitude reduction, and diffusion of the deeper motions, over timescales and lengthscales that are far larger than those (wave periods and wavelengths) of the dynamical processes at the surface [13]. The choice of constant vorticity is not merely a mathematical simplification: for long waves propagating at the surface of water over a nearly flat bed (with wavelengths that exceed the mean water depth), it is the existence of a non-zero mean vorticity that is important rather than its specific distribution (see the discussion in [13]).

We conclude our preliminary considerations by pointing out two examples of real-world flows where field data matches the premises of our theoretical study. In both examples the tides are weak and the currents are largely driven by winds blowing parallel to the coast, in the east-west direction:

  1. (i)

    (arctic region) The continental shelf off of the coast of Siberia is the widest continental shelf in the world, extending more than 1000 km offshore, along a continental coastline that exceeds 3000 km. Known as the East Siberian Sea, this shallow marginal sea in the Arctic Ocean is ice-covered for most of the year, except in the summer, when 2-3 m high waves with wavelengths of the order of 60-90 m propagate at the surface of a largely remarkably flat bed of mean depth 45 m, interacting with the eastward wind-driven underlying current (see [18, 20, 28]) in a dynamical process that presents strong nonlinear features (see the discussion in [44]). The winds are typically of moderate strength (with speeds that rarely exceed 15 m/s) and the speed of the surface wind-drift current is about 0.5 m/s, while the speeds of the tidal currents in this region are of the order of 0.05 m/s (see [34]).

  2. (ii)

    (tropical region) The continental shelf of the Gulf of Mexico off the Yucatán Peninsula (Campeche Bank) extends more than 100 km offshore, over a coastal region whose length exceeds 500 km. Large parts of this northern, submerged extension of the Yucatán platform lie at a depth of about 50 m. The wind-generated surface current flows westward with a speed of about 0.33 m/s, the average wind speed being about 6 m/s (see the data in [27, 45]). The typical wavelengths and wave heights of the wind waves are about 70 m and 2m, respectively, but wave heights of up to 9 m are reached for gale-force winds with speeds up to 33 m/s (see [42]). The tidal currents are weak, with speeds less than 0.1 m/s and with the corresponding sea level oscillations that do not exceed 0.1 m in amplitude (see [21]).

3 The mean flow beneath the surface waves

The governing equations for two-dimensional water waves are the equation of mass conservation

$$\begin{aligned} u_x + v_y=0,\qquad -d \le y \le \eta (x,t), \end{aligned}$$
(3.1)

coupled with the Euler equation

$$\begin{aligned} \left\{ \begin{array}{l} u_t + uu_x +vu_y= - \displaystyle \frac{1}{\rho }\,p_x,\\ v_t +uv_x +vv_y =-\displaystyle \frac{1}{\rho }\,p_y\,-g, \end{array}\right. \qquad -d \le y \le \eta (x,t), \end{aligned}$$
(3.2)

The corresponding boundary conditions are the dynamic boundary condition

$$\begin{aligned} p=p_{atm}\quad \hbox {on}\quad y=\eta (x,t), \end{aligned}$$
(3.3)

which decouples the motion of the water from that of the air above the free surface \(y=\eta (x,t)\), and the kinetic boundary conditions

$$\begin{aligned}&v=\eta _t + u\eta _x\quad \hbox {on}\quad y=\eta (x,t), \end{aligned}$$
(3.4)
$$\begin{aligned}&v=0\quad \hbox {on}\quad y=-d, \end{aligned}$$
(3.5)

which ensure that particles on the interfaces are confined to them at all times, for the free surface \(y=\eta (x,t)\) and for the flat bed \(y=-d\), respectively. Here \(\rho \) is the water’s constant density (about 1000 kg/m\(^3\)), g is the constant acceleration of gravity and \(p_{atm}\) is the constant atmospheric pressure at sea level (about 10\(^5\) kg/ms\(^2\)); see the discussion in [6]. The free surface is a spatially periodic disturbance of the mean level \(y=0\), so that

$$\begin{aligned} \int _0^\lambda \eta (x,t)\,dx=0 \quad \hbox {at all times}\quad t, \end{aligned}$$
(3.6)

where \(\lambda \) is the wavelength. The vorticity

$$\begin{aligned} \gamma =u_y-v_x,\qquad -d \le y \le \eta (x,t), \end{aligned}$$
(3.7)

of the water flow beneath the surface wave is a measure of the local spin of a fluid element (see the discussion in [6]). Irrotational flows are characterised by a complete absence of vorticity, \(\gamma \equiv 0\) throughout the flow, and non-zero vorticity is the hallmark of the interaction of waves with underlying sheared currents. As pointed out in Sect. 2, a uniform current does not affect the surface wave’s physical properties, even though the perception of the wave field changes in the sense that the apparent speed of the waves will depend on the motion of the observer’s reference frame. In practice, real currents are rarely uniform, the strongest nonuniformity being usually in the vertical spatial direction, caused commonly by wind drift [35], for which, as argued in Sect. 2, the assumption of a constant vorticity \(\gamma \ne 0\) is adequate. Recent advances occured in the existence theory for solutions to the governing equations (3.1)-(3.9), in the setting of spatially periodic free-surface flows. In this context, a classical solution consists of a continuously differentiable free surface profile \(\eta (x,t)\), pressure p(x, y, t) and velocity field \((u(x,y,t),\,v(x,y,t))\) throughout the fluid domain

$$\begin{aligned} {{\mathcal {D}}}(t)=\{ (x,y): \ -d \le y \le \eta (x,t)\}. \end{aligned}$$

Note that the structure of the governing equations ensures automatically a spatial gain of regularity. Indeed, (3.1) permits us to introduce a stream function \(\psi (x,y,t)\) by means of the differential relations

$$\begin{aligned} \psi _y=u,\qquad \psi _x=-v,\qquad (x,y) \in {{\mathcal {D}}}(t), \end{aligned}$$
(3.8)

which define \(\psi \) uniquely up to an additive constant that is merely time-dependent. Thus the vorticity equation (3.7) becomes

$$\begin{aligned} \Delta \psi =\gamma ,\qquad -d \le y \le \eta (x,t), \end{aligned}$$
(3.9)

and the harmonicity of the function \((x,y) \rightarrow \psi (x,y,t)- \tfrac{1}{2}\,\gamma (y+d)^2\) yields by elliptic regularity that \(\psi \) is real-analytic in \({{\mathcal {D}}}(t)\). In view of (3.8) and (3.2), this implies that the velocity field (u, v) and the pressure p are real-analytic in the spatial variables (x, y) throughout the fluid domain. The well-posedness of the governing equations, concerning the evolution in time of the surface profile and of the velocity field from quite general initial states, is a difficult and important issue where considerable progress was recently achieved; some of the key papers are [1, 3, 12, 22]. Another relevant direction of investigation concerns travelling waves: flows for which the (x, t)-dependence of \(\eta \), u, v, and p is in the form of functions of \((x-ct)\), for some constant wave speed c. For travelling waves one can use the moving coordinate frame \(x-ct\), whereby the time t completely disappears and this steady-state framework was used to gain quite detailed insight into the flow dynamics of waves of large amplitude (see [3, 5, 7, 10, 11, 23, 30, 38]). These studies highlight two types of phenomena brought about by the effect of non-zero vorticity: the possibility of flow-reversal (near regions with critical layers) and the possible appearance of travelling waves with overturning profiles (see the discussion in [11]). While rigorous analytic studies are devoted to travelling waves in flows of constant vorticity which exhibit critical layers (a typical feature of the dynamics being the “Kelvin cat’s eye” pattern), the second aspect is at the moment confined to the realm of numerical simulations. The technical challenges related to well-posedness issues and the new qualitative phenomena encountered in steady-state flows show clearly substantial differences between the irrotational flows and flows with non-zero vorticity.

Let us now identify some general features of flows with constant vorticity beneath spatially periodic smooth two-dimensional surface waves. Throughout this paper we assume a continuously differentiable dependence of the free surface and of the fluid velocity on the space-time variables (x, t). As noted above, the constant vorticity setting ensures at any instant t a real-analytic dependence of the velocity field on the spatial variable x. Assuming the natural physical condition that initially the normal derivative of the pressure is negative on the smooth free surface, the short-time existence of a smooth subsequent free surface is ensured by the considerations in [12, 31]. While the solution generated by such an initial state might develop into a breaking wave (see the discussion in [8]), in which case our considerations refer to any time up to the breaking time, it is known (see [24]) that small localized data ensure the long-time existence of solutions even outside the class of travelling waves. Let us also point out that smooth surface wave profiles of constant-vorticity flows are quite common: in particular, a travelling wave profile that is Hölder continuously differentiable must be real analytic (see [9]).

In studies of water flows the pressure plays a fundamental role, capturing the reaction of the fluid to the constraint of incompressibility and keeping the evolution of the velocity within the space of divergence-free vectors. For irrotational flows the pressure turns out to be superharmonic, and this property confers considerable mathematical advantages in the analysis of these flows, for example by being the key ingredient to unlocking specific properties of the velocity field at the surface and beneath it (see the discussion in [6]). Unfortunately, it turns out that non-zero vorticity alters considerably this advantageous feature, the pressure being generally only bi-subharmonic i.e. \(\Delta ^2 p \ge 0\) throughout the fluid.

Theorem 3.1

The pressure in a flow with constant non-zero vorticity exhibits at every instant \(t_0\) both regions where it is strictly superharmonic, as well as regions where it is strictly subharmonic, unless we have a pure current state with \(v(x,y,t_0)=0\) and \([u(x,y,t_0)-\gamma y]\) constant throughout the fluid.

Proof

Taking the x-derivative of the first equation in (3.2) and adding to this the y-derivative of the second equation in (3.2) yields

$$\begin{aligned} -\frac{1}{\rho }\,\Delta p=2(u_x^2+u_y^2 -\gamma u_y),\qquad -d< y < \eta (x,t), \end{aligned}$$
(3.10)

in view of (3.1) and (3.7). The function \(\alpha (x,y,t)=u_x^2+u_y^2 -\gamma u_y\) is subharmonic throughout the fluid at every instant of time since

$$\begin{aligned} \Delta \alpha =4(u_{xx}^2 +u_{xy}^2) \ge 0,\qquad -d< y < \eta (x,t), \end{aligned}$$

follows at once using the fact that u is harmonic, due to (3.1) and (3.7). Consequently, at every time t, the maximum of \(\alpha (x,y,t)\) throughout the closure of the fluid domain \({{\mathcal {D}}}(t)\) is attained on its boundary. Since (3.5) and (3.7) yield

$$\begin{aligned} u_y(x,-d,t)=\gamma ,\qquad x \in {{\mathbb {R}}}, \end{aligned}$$
(3.11)

we see that this maximum is non-negative. We now show that, unless we are in a pure current state, the maximum of \(\alpha \) has to be strictly positive. For this, observe that (3.1) and (3.7) ensure the analyticity of the complex function

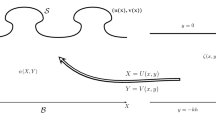
$$\begin{aligned} \beta (x+iy,t)=u_y(x,y,t) - \frac{\gamma }{2} + iu_x(x,y,t) \end{aligned}$$

in the strip-like domain \(\{x+iy \in {{\mathbb {C}}}:\ -d< y < \eta (x,t)\}\) of the complex plane. For every fixed t, this function is continuous on the closure of this domain and, due to (3.11), the Schwarz reflection principle applied to the complex function \(i\big (\beta - \tfrac{\gamma }{2}\big )\), that is real-valued on \(y=-d\), enables us to extend it to an analytic function in the strip-like symmetric domain

$$\begin{aligned} {{\mathcal {S}}}(t)=\{x+iy \in {{\mathbb {C}}}:\ -2d -\eta (x,t)< y < \eta (x,t)\}, \end{aligned}$$

with continuity up to the boundary (see Fig. 1), by setting

$$\begin{aligned} \beta (x+iy,t)&=\frac{3}{2}\,\gamma - u_y(x,-2d-y,t) + iu_x(x,-2d-|y,t), \\&\quad -2d -\eta (x,t) \le y <-d. \end{aligned}$$
Fig. 1
figure 1

Depiction of the strip-like region \({{\mathcal {S}}}(t)\), obtained by reflecting the fluid domain in the flat bed \(y=-d\) at the instant t

Full size image

From (3.11) we see that \(\alpha (x,-d,t_0)=0\) for all \(x \in {{\mathbb {R}}}\) holds at some instant \(t_0\) only if \(u_x(x,-d,t_0)=0\) for all \(x \in {{\mathbb {R}}}\), that is, if \(\beta =\gamma /2\) all along the horizontal line \(y=-d\), which, being in the interior of \({{\mathcal {S}}}(t_0)\), forces \(\beta \equiv \gamma /2\) throughout \({{\mathcal {S}}}(t_0)\), by the identity theorem. Using (3.1) and (3.7), together with (3.5), we infer that in this case \(v(x,y,t_0) = 0\) and \(u(x,y,t_0)=\gamma y + u_0\) must hold throughout the flow, for some constant \(u_0\).

Let us now discuss the case when \(\alpha (x_1,-d,t_0) >0\) for some \(x_1 \in {{\mathbb {R}}}\). Note that (3.11) then yields \(u_x(x_1,-d,t_0) \ne 0\), and from (3.10) and (3.11) we infer the existence of a near-bed region near \((x_1,-d)\) in which p is strictly superharmonic at the instant \(t_0\). It remains to prove that at the instant \(t_0\) there are flow regions in which p is strictly subharmonic. To this end, note that \(u(\cdot ,-d,t_0)\) is non-constant and consider the set \(Z(t_0)=\{(x_0,-d):~u_x(x_0,-d,t_0)=0\}\). The periodicity of u in the x-variable ensures that this set is nonvoid. In particular, this implies that \(\beta \) is non-constant in \({\mathcal {S}}(t_0)\), since (3.11) yields

$$\begin{aligned} |\beta (x_1-id,t_0)|^2=\alpha (x_1,-d,t_0) + \frac{\gamma ^2}{4}>\frac{\gamma ^2}{4} \end{aligned}$$

and \(\beta =\frac{\gamma }{2}\) on the set \(Z(t_0)\). Therefore, for any \(z_0=x_0-id\in Z(t_0)\) we can write

$$\begin{aligned} \beta (z,t_0) =\frac{\gamma }{2}+(z-z_0)^n\beta _0(z),\quad z\in {\mathcal {S}}(t_0), \end{aligned}$$
(3.12)

where \(n\in {\mathbb {N}}\), and \(\beta _0\) is analytic in \({\mathcal {S}}(t_0)\), with \(\beta _0(z_0)\ne 0\). For \(z=x+iy\in {\mathcal {D}}(t_0)\) we have

$$\begin{aligned} \alpha (x,y,t_0)=|\beta (z,t_0)|^2-\frac{\gamma ^2}{4} =\gamma \,\text {Re}\{(z-z_0)^n\beta _0(z)\}+|z-z_0|^{2n}|\beta _0(z)|^2. \end{aligned}$$

For \(z=z_0+re^{i\theta }\) with \(r>0\) and \(0<\theta <\pi \), let us assume that

$$\begin{aligned} \gamma \,\text {Re}\{e^{in\theta }\beta _0(z_0)\}<0. \end{aligned}$$
(3.13)

Then from the above we obtain that for \(r\rightarrow 0\),

$$\begin{aligned} \alpha (x,y,t_0)=\gamma \,r^n\text {Re}\{e^{in\theta }\beta _0(z_0)\}+o(r^n), \end{aligned}$$

i.e. \(\alpha (x,y,t_0)<0\) if \(\theta \) satisfies (3.13) and \(r>0\) is sufficiently small. To validate (3.13), we proceed as follows. Clearly, if there exists \(z_0\in Z(t_0)\) such that (3.12) holds with \(n>1\), then there exists \(\theta \in (0,\pi )\) satisfying (3.13). On the other hand, if (3.12) holds with \(n=1\) for all \(z_0\in Z(t_0)\), then

$$\begin{aligned} \beta _0(z_0)=\beta '(z_0,t_0)=\beta _x(z_0,t_0)=iu_{xx}(x_0,-d,t_0)\ne 0, \quad z_0=x_0-id\in Z(t_0), \end{aligned}$$

due to (3.11), and the condition (3.13) becomes

$$\begin{aligned} \gamma u_{xx}(x_0,-d,t_0)>0. \end{aligned}$$

The above inequality can be achieved by choosing \(z_0\) according to the sign of \(\gamma \) such that the point \((x_0,-d)\) is a maximum or a minimum of the restriction of u to the bed \(y=-d\), at time \(t_0\). The proof is complete. \(\square \)

In the context of Theorem 3.1, it is quite natural to enquire how the pure current state can occur and whether it may persist.

Theorem 3.2

Unless the free surface is flat, a pure current state at time \(t_0\), with \(u(x,y,t_0)=\gamma y +u_0\) and \(v(x,y,t_0)=0\) throughout the fluid, is instantly destroyed by developing into a genuine wave–current interaction.

Proof

Due to (3.10), a pure current state implies that p is harmonic throughout \({{\mathcal {D}}}(t_0)\). Since (3.5) and the second equation in (3.2) yield

$$\begin{aligned} p_y=-\rho g \quad \hbox {on}\quad y =-d, \end{aligned}$$
(3.14)

defining

$$\begin{aligned} p(x,y,t_0)=p(x,-2d-y,t_0) - 2\rho g(y+d)\quad \hbox {for}\quad - 2d-\eta (x,t_0) \le y <-d, \end{aligned}$$
(3.15)

we extend \((x,y) \mapsto p(x,y,t_0)\) by symmetry to a smooth harmonic function in the strip-like domain \({{\mathcal {S}}}(t_0)\) introduced in the proof of Theorem 3.1, with a continuous extension to the closure. In particular, from (3.3) we get

$$\begin{aligned} p=p_{atm} + 2\rho g[\eta (x,t_0)+d]\quad \hbox {on}\quad y=- 2d-\eta (x,t_0), \end{aligned}$$
(3.16)

so that, in view of the periodicity in the x-variable, standard results on the Dirichlet problem for the Laplace operator show that the specification of the wave profile \(\eta (x,t_0)\) at the instant \(t_0\) determines p uniquely throughout \({{\mathcal {S}}}(t_0)\). This unique solution exhibits the symmetry imposed in (3.16), since, as a harmonic function with homogeneous Dirichlet boundary conditions, the function

$$\begin{aligned} (x,y) \mapsto p(x,y,t_0)-p(x,-2d-y,t_0) + 2\rho g(y+d) \end{aligned}$$

must vanish throughout \({{\mathcal {S}}}(t_0)\); in particular, (3.14) must hold since \(y=-d\) is the symmetry axis of the region \({{\mathcal {S}}}(t_0)\). Having established that a pure current state at the instant \(t_0\) ensures that the free surface \(\eta (x,t_0)\) determines the harmonic pressure \(p(\cdot ,\cdot ,t_0)\) throughout the fluid, let us now show that it also dictates univoquely the subsequent time-evolution of the flow. For this, we can invoke the well-posedness result in [12] since the harmonicity of \(p(\cdot ,\cdot ,t_0)\) in \({{\mathcal {D}}}(t_0)\) together with (3.3) and (3.14) ensure, combining the strong maximum principle with Hopf’s maximum principle, that the minimum of p in \({{\mathcal {D}}}(t_0)\) is attained all along the free surface (where, by (3.3), p is constant). Consequently, at the instant \(t_0\), in view of another application of Hopf’s maximum principle, the outward normal derivative of p at every point on the surface must be strictly negative, so that spatial periodicity ensures that the outward normal derivative of p is bounded away from zero, uniformly along the surface. This condition (called the Rayleigh-Taylor stability condition) guarantees the well-posedness of gravity water waves (see [12]). These considerations show that a pure current state can be interpreted physically as the initial state that is set up at the time \(t=t_0\) by the action of the wind, a state with a spatially periodic free surface \(\eta (x,t_0)\). Other than being continuously differentiable, the only further constraint is that \(\eta (\cdot ,t_0)\) is a perturbation of the flat mean level state, so that (3.6) holds at \(t=t_0\). Some invariants of the motion permit us now to make predictions about the subsequent evolution of the flow. Firstly, mass conservation leads at once to (3.6) for times \(t>t_0\). On the other hand, since in a two-dimensional flow the vorticity of each individual water particle is constant as the particle moves about (see [6]), we see that the vorticity \(\gamma \), defined by (3.7), being constant will also hold for \(t>t_0\). The fact that the governing equations admit a Hamiltonian structure (see [43]), whose functional is the total energy per unit width in a periodic cell, given at time t by

$$\begin{aligned} \rho \int _0^\lambda \int _{-d}^{\eta (x,t)} \Big \{ \frac{u^2+v^2}{2} + g y\Big \} dydx, \end{aligned}$$

means that up to the (possible) breaking time the energy is preserved. Thus the profile of the free surface at the instant when the flow is in a pure current state determines the value of the total energy of the flow. To see that, unless the free surface is flat (with no waves), a pure current state is instantly destroyed, it suffices to point out that a velocity field of the form \(u(x,y,t)=\gamma (y+d) + u_0(t)\) with \(v \equiv 0\) for some time-interval \((t_0,t_0+\varepsilon )\) with \(\varepsilon >0\) forces \(u_0'(t)=0\) for all \(t \in (t_0,t_0+\varepsilon )\), due to the first equation in (3.2) and the periodicity in the x-variable. Using now (3.2), (3.3) and (3.6), we infer that \(p(x,y,t)=p_{atm}-\rho g y\) and \(\eta (x,t)=0\) for all \(x \in {{\mathbb {R}}}\) and all \(t \in (t_0,t_0+\varepsilon )\).

\(\square \)

The failure of the applicability of potential theory for the water pressure in wind-driven wave–current interactions, due to the result stated in Theorem 3.1, directs the hope for gaining insight in the direction of other flow characteristics in the bulk of the fluid, namely the components of the velocity field. The fact that they are both harmonic functions, in view of (3.8) and (3.9), suggests the relevance of averaging processes and leads naturally to the study of mean-flow properties.

At every instant t we determine uniquely the stream function \(\psi (x,y,t)\) by requiring that

$$\begin{aligned} \psi (x,-d,t)=0,\qquad x \in {{\mathbb {R}}},\quad t \ge 0. \end{aligned}$$
(3.17)

Since

$$\begin{aligned} \psi (x,y,t)=\int _{-d}^y u(x,s,t)\,ds,\qquad (x,y) \in {\mathcal {D}}(t), \end{aligned}$$
(3.18)

we see that \(\psi \) has period \(\lambda \) in the x-variable. Therefore, if

$$\begin{aligned} \eta _0(t)=\min \limits _{x \in [0,\lambda ]} \{\eta (x,t)\}>-d \end{aligned}$$
(3.19)

is the depth of the wave trough at time t, from (3.8) we get

$$\begin{aligned} \frac{1}{\lambda } \int _0^\lambda v(x,y,t)\,dx=0,\qquad -d \le y \le \eta _0(t). \end{aligned}$$
(3.20)

On the other hand,

$$\begin{aligned} \partial _y \Big (\frac{1}{\lambda } \int _0^\lambda u(x,y,t)\,dx\Big )= \frac{1}{\lambda } \int _0^\lambda \psi _{yy}(x,y,t)\,dx=\gamma ,\qquad -d< y < \eta _0(t), \end{aligned}$$

since (3.8) and (3.7) yield

$$\begin{aligned} \Delta \psi =\gamma ,\qquad -d< y < \eta (x,t). \end{aligned}$$
(3.21)

On the other hand, (3.5) together with the first equation in (3.2), evaluated on \(y=-d\), yields

$$\begin{aligned} \partial _t \Big (\frac{1}{\lambda } \int _0^\lambda u(x,-d,t)\,dx\Big )=0, \end{aligned}$$

due to the periodicity of u and p in the x-variable, so that

$$\begin{aligned} \frac{1}{\lambda } \int _0^\lambda u(x,y,t)\,dx=\gamma (y+d) + u_0,\qquad -d \le y \le \eta _0(t). \end{aligned}$$
(3.22)

for some time-independent constant \(u_0\). The physical interpretation of (3.20) and (3.22) is that the mean flow beneath the surface wave is a time-independent current with vorticity \(\gamma \); see Fig. 2.

Fig. 2
figure 2

Depiction of the sheared profile of the wind-drift current beneath the surface waves, in terms of the mean flow, by means of black-and-white arrows. The non-zero vorticity accommodates a decay of the horizontal mean flow with depth, with the wind effects generally noticeable along the flat bed of a continental shelf

Full size image

Other than the mean flow properties described by (3.20) and by (3.22), the behaviour of mean square fluctuations of the flow speed is of great interest in energy considerations, since the density of the kinetic energy is \(\rho (u^2+v^2)/2\).

Theorem 3.3

If \(u_0\) is the time-independent mean flow along the flat bed of a wave–current interaction with constant vorticity \(\gamma \), then the mean square flow speed is a decreasing function of depth if and only if \(u_0\gamma \ge 0\).

Proof

Let us fix a time t. Defining the depth of the wave trough by (3.19), the mean square of the fluid speed at a fixed depth \(y \in [-d,\eta _0(t)]\) is given by

$$\begin{aligned} {\mathfrak {M}}(y,t)=\frac{1}{\lambda } \int _0^\lambda [u^2(x,y,t)+v^2(x,y,t)]\,dx. \end{aligned}$$
(3.23)

Using (3.1), (3.5) and (3.22), we compute

$$\begin{aligned} \frac{\partial }{\partial y}\,{\mathfrak {M}} \Big |_{y=-d}=\frac{2}{\lambda } \Big \{\int _0^\lambda [uu_{y} + vv_{y}]\,dx\Big \}\Big |_{y=-d}= \frac{2\gamma u_0}{\lambda }, \end{aligned}$$

a relation that proves the necessity of the condition \(u_0\gamma \ge 0\). To prove the sufficiency, note that (3.8) and (3.21) ensure that both u and v are harmonic throughout the fluid domain \({{\mathcal {D}}}(t)\), so differentiating (3.23) twice with respect to y yields

$$\begin{aligned} \frac{\partial ^2}{\partial y^2}\,{\mathfrak {M}}= & {} \frac{2}{\lambda } \int _0^\lambda [u_y^2 +uu_{yy} + v_y^2 +vv_{yy}]\,dx \\= & {} \frac{2}{\lambda } \int _0^\lambda [u_y^2 -uu_{xx} + v_y^2 -vv_{xx}]\,dx =\frac{2}{\lambda } \int _0^\lambda [u_y^2 +u_x^2 + v_y^2 +v_x^2]\,dx \ge 0, \end{aligned}$$

using on the second line the fact that u as well as v are \(\lambda \)-periodic in the x-variable. Therefore \(\frac{\partial }{\partial y}\,{\mathfrak {M}}(y,t)\) is a non-decreasing function of \(y \in [-d,\eta _0(t)]\), which permits us to conclude the argument. \(\square \)

Remark 3.4

  1. (i)

    In the mean square flow speed, the relative sizes of the mean squares of the velocity components generally vary quadratically with depth. Indeed, (3.1) and (3.7) yield

    $$\begin{aligned}&\frac{\partial }{\partial y}\, \Big \{ \int _0^\lambda [u^2(x,y,t)-v^2(x,y,t)]\,dx\Big \} = 2 \int _0^\lambda [uu_y-vv_y]\,dx \\&\qquad = 2 \int _0^\lambda [u(v_x+\gamma )+vu_x]\,dx=2\gamma \int _0^\lambda u\,dx=2\gamma \lambda [\gamma (y+d) +u_0], \end{aligned}$$

    using the periodicity of u and v in the x-variable in combination with (3.22). If the flow is irrotational (\(\gamma =0\)), then we recover a result of Longuet-Higgins [32]: since the mean squares of the velocity components differ by a constant and their sum is a decreasing function of y, each separately must be a decreasing function of y.

  2. (ii)

    The typical circumstance encountered in flows on the continental shelf is that the wind-drift current reaches down to the flat bed, so that the situations [\(\gamma >0\) with \(u_0>0\)] and [\(\gamma <0\) with \(u_0<0\)] are frequent (see Fig. 2 as a visual aid). Theorem 3.3 shows that in such occurrences the presence of a sheared underlying current does not alter qualitatively the behaviour of the (mean square) flow speed, as compared with the irrotational setting, for which the underlying current has to be uniform, corresponding to the choice \(\gamma =0\) in (3.22).

4 Main result

Observations suggest that far below the surface the flow field is very nearly in a pure current state. Our aim is to provide quantitative estimates that support this claim, for wind-generated wave–current interactions, modelled as rotational wave flows with constant non-zero vorticity.

Theorem 4.1

In any space-periodic wave–current interaction of constant vorticity the flow field tends exponentially fast to the underlying mean flow: if

$$\begin{aligned} {\mathfrak {s}}(x,y,t)=\sqrt{[u-\gamma (y+d)-u_0]^2+v^2} ,\qquad (x,y) \in {{\mathcal {D}}}(t), \end{aligned}$$

then the maximum \({\mathfrak {S}}(t)\) of the map \((x,y) \rightarrow {\mathfrak {s}}(x,y,t)\) in the closure of the fluid domain \({{\mathcal {D}}}(t)\) is attained on the free surface \(y=\eta (x,t)\) and

$$\begin{aligned} {\mathfrak {s}}(x,y,t) \le \frac{e^{\tfrac{\pi }{4}}}{2\sinh (\tfrac{\pi }{4})}\,e^{ky}[1+e^{-2k(d+y)}] \,{\mathfrak {S}}(t) \,\mathfrak {m}(t),\quad -d \le y \le \min _{x \in [0,\lambda ]}\{\eta (x,t)\}- \frac{\lambda }{4}, \end{aligned}$$
(4.1)

where \(k=\tfrac{2\pi }{\lambda }\) is the wave number and \({\mathfrak {m}}(t)=\tfrac{1}{\lambda }\,\int _0^\lambda e^{-k\eta (x,t)}\sqrt{1+\eta ^2_x(x,t)}\,dx\).

Remark 4.2

For typical surface wind-waves, even for those classified as large-amplitude waves, the trough is always within one tenth of the wavelength beneath the mean level of the surface (see [6]): the inequality \(\min \nolimits _{x \in [0,\lambda ]}\{\eta (x,t)\} > - \frac{\lambda }{10}\) holds. With \(e^{-k\eta (x,t)} \le e^{\pi /4}\), we get from (4.1) that

$$\begin{aligned} {\mathfrak {s}}(x,y,t) \le \frac{e^{\tfrac{\pi }{2}}}{2\sinh (\tfrac{\pi }{4})}\,e^{ky}[1+e^{-2k(d+y)}] \,{\mathfrak {S}}(t) \, \frac{\int _0^\lambda \sqrt{1+\eta ^2_x(x,t)}\,dx}{\lambda }, \end{aligned}$$

for \(-d \le y \le \min _{x \in [0,\lambda ]}\{\eta (x,t)\}- \frac{\lambda }{4}\). Since the function \(y \mapsto e^{ky}[1+e^{-2k(d+y)}]\) is nondecreasing on \([-d,- \frac{\lambda }{2}]\), with its value at \(y=- \frac{\lambda }{2}\) less than \(2e^{-\pi }\), the fact that \(\tfrac{e^{-\frac{\pi }{2}}}{\sinh (\tfrac{\pi }{4})} \approx 0.2\) permits us to infer that the deviation of the flow from the pure current state, at a depth of half a wavelength (\(y=- \frac{\lambda }{2}\)), is reduced fivefold from its (maximal) free-surface value.

Proof

At any fixed instant t, let us introduce the harmonic function

$$\begin{aligned} \Psi (x,y,t)=\psi (x,y,t) - \frac{\gamma }{2}\,(y+d)^2 - u_0 (y+d),\qquad -d \le y \le \eta (x,t). \end{aligned}$$

Then the function

$$\begin{aligned} f(x+iy,t)=-\,\Psi _x + i\, \Psi _y=v+i[u-\gamma (y+d)-u_0], \end{aligned}$$

is analytic in the domain \(\{x+iy \in {{\mathbb {C}}}:\ -d< y < \eta (x,t)\}\), continuous on its closure and such that

$$\begin{aligned} \frac{1}{\lambda } \int _0^\lambda f(x+iy,t)\,dx=0,\qquad -d< y < \eta _0(t), \end{aligned}$$
(4.2)

due to (3.20) and (3.22); here \(\eta _0(t)=\min \nolimits _{x \in [0,\lambda ]} \{\eta (x,t)\}\). Since the real part of f vanishes on the lower boundary \(y=-d\), by the Schwartz reflection principle, it has an analytic continuation (denoted also by f) to the domain

$$\begin{aligned} {{\mathcal {B}}}(t)=\{x+iy \in {{\mathbb {C}}}:~0<x<\lambda ,~-2d-\eta (x,t)<y<-d\}, \end{aligned}$$

given by

$$\begin{aligned} f(x+iy,t)=-\overline{f(x-i(2d+y),t)}, \qquad -2d-\eta (x,t)<y<-d. \end{aligned}$$

Let

$$\begin{aligned} F(z,t)=-ike^{-ikz}f(z,t), \qquad z\in {\mathcal {B}}(t). \end{aligned}$$
(4.3)

By the residue theorem we have

$$\begin{aligned} f(z_0,t)=\frac{1}{2\pi i}\int _{\partial {\mathcal {B}}(t)} \frac{F(z,t)}{e^{-ikz}-e^{-ikz_0}}\,dz,\qquad z_0\in {\mathcal {B}}(t). \end{aligned}$$
(4.4)

The boundary \(\partial {\mathcal {B}}(t)\) of \({\mathcal {B}}(t)\) consists of two vertical lines

$$\begin{aligned} L^r(t)= & {} \{\lambda +iy:~-2d-\eta (\lambda ,t)\le y\le \eta (\lambda ,t)\},\\ L^l(t)= & {} \{ iy:~-2d-\eta (0,t)\le y\le \eta (0,t)\}, \end{aligned}$$

and two “horizontal” curves

$$\begin{aligned} C^-(t)= \{y{=}-2d{-}\eta (x,t):~ 0\le x \le \lambda \},\qquad C^+(t)=\{y=\eta (x,t):~ 0\le x \le \lambda \}. \end{aligned}$$

Since \(F(\cdot ,t)\) is \(\lambda \)-periodic in the horizontal direction, we have

$$\begin{aligned} \int _{L^r(t)}\frac{F(z,t)}{e^{-ikz}-e^{-ikz_0}}\,dz-\int _{L^l(t)} \frac{F(z,t)}{e^{-ikz}-e^{-ikz_0}}\,dz=0, \end{aligned}$$

so that (4.4) yields

$$\begin{aligned} f(z_0,t)=\frac{1}{2\pi i}\int _{C^-(t)} \frac{F(z,t)}{e^{-ikz}-e^{-ikz_0}}\,dz- \frac{1}{2\pi i}\int _{C^+(t)} \frac{F(z,t)}{e^{-ikz}-e^{-ikz_0}}\,dz. \end{aligned}$$

The above relation can be rewritten as

$$\begin{aligned} f(z_0,t)= & {} \frac{1}{2\pi i}\int _{C^-(t)} \frac{F(z,t)}{e^{-ikz}-e^{-ikz_0}}\,dz -\frac{1}{2\pi i}\int _{C^+(t)} e^{ikz}F(z,t)\,dz\\&-\frac{e^{-ikz_0}}{2\pi i}\int _{C^+(t)} \frac{e^{ikz}F(z,t)}{e^{-ikz}-e^{-ikz_0}}\,dz, \end{aligned}$$

so that, due to (4.3), we get

$$\begin{aligned} f(z_0,t)= & {} \frac{k}{2\pi }\int _0^\lambda \frac{[1-i\eta _x(x,t)]\, \overline{f(x+i\eta (x,t),t)}\,e^{-ik[x-2id-i\eta (x,t)]}}{e^{-ik[x-2id-i\eta (x,t)]}-e^{-ikz_0}} \, dx \\&+ \frac{k}{2\pi }\int _0^\lambda [1+i\eta _x(x,t)]\, f(x+i\eta (x,t),t) \, dx \\&+ \frac{k}{2\pi }\,e^{-ikz_0}\int _0^\lambda \frac{[1+i\eta _x(x,t)]\,f(x+i\eta (x,t),t)}{e^{-ik[x+i\eta (x,t)]}-e^{-ikz_0}} \, dx, \end{aligned}$$

that is,

$$\begin{aligned} f(z_0,t)= & {} \frac{1}{\lambda }\int _0^\lambda \frac{\overline{[1+i\eta _x(x,t)]\,f(x+i\eta (x,t),t)}\, e^{-ik[x-2id-i\eta (x,t)]}}{e^{-ik[x-2id-i\eta (x,t)]}-e^{-ikz_0}} \, dx \nonumber \\&+ \frac{1}{\lambda }\int _0^\lambda [1+i\eta _x(x,t)]\, f(x+i\eta (x,t),t) \, dx \nonumber \\&+ \frac{1}{\lambda }\,e^{-ikz_0}\int _0^\lambda \frac{[1+i\eta _x(x,t)]\,f(x+i\eta (x,t),t)}{e^{-ik[x+i\eta (x,t)]}-e^{-ikz_0}} \, dx . \end{aligned}$$
(4.5)

Note that

$$\begin{aligned} \int _0^\lambda [1+i\eta _x(x,t)]\, f(x+i\eta (x,t),t) \, dx=0. \end{aligned}$$
(4.6)

Indeed, the left side of (4.6) equals

$$\begin{aligned} \int _0^\lambda \Big \{ v-u\eta _x + \gamma (\eta +d)\eta _x +u_0\eta _x + i[u+v\eta _x -\gamma (\eta +d)-u_0 ]\Big \}\Big |_{y=\eta (x,t)}\,dx . \end{aligned}$$

Observe that the periodicity of f in the x-variable and (3.6) yield

$$\begin{aligned} \int _0^\lambda \gamma (\eta +d)\,dx=\lambda \gamma d,\quad \int _0^\lambda \eta _x\,dx=0 \quad \hbox {and}\quad \int _0^\lambda \gamma (\eta +d)\eta _x\,dx=0, \end{aligned}$$

respectively, while from (3.4) and (3.6) we infer that

$$\begin{aligned} \int _0^\lambda (v-u\eta _x)\Big |_{y=\eta (x,t)}\,dx=\int _0^\lambda \eta _t\,dx=0. \end{aligned}$$

The relation (4.6) now follows since, by applying Green’s second identity to the pair of functions \((1,\psi )\) in the domain

$$\begin{aligned} {{\mathcal {D}}}_0(t)=\{(x,y): 0<x<\lambda ,\ -d<y<\eta (x,t)\}, \end{aligned}$$

we get

$$\begin{aligned} \iint _{{{\mathcal {D}}}_0(t)} \Delta \psi \,dxdy=\int _0^\lambda (u+v \eta _x)\Big |_{y=\eta (x,t)}\,dx - \int _0^\lambda u\Big |_{y=-d}\,dx, \end{aligned}$$

using (3.8) and the periodicity of \(\psi \) in the x-variable. The above relation in combination with (3.6), (3.21), (3.22) yields

$$\begin{aligned} \int _0^\lambda (u+v \eta _x)\Big |_{y=\eta (x,t)}\,dx =\gamma \lambda d +\lambda u_0, \end{aligned}$$

and the validity of (4.6) is thus established.

The relations (4.5) and (4.6) lead us to the representation formula

$$\begin{aligned} f(x_0+iy_0,t)= & {} \frac{1}{\lambda } \int _0^\lambda \frac{\overline{[1+i\eta _x] \,f(x+i\eta (x,t),t)}\,e^{-ik\{(x-x_0)-i[2d+\eta (x,t)+y_0]\}}}{e^{-ik\{(x-x_0)-i[2d+\eta (x,t)+y_0]\}}-1}\,dx\\&+ \frac{1}{\lambda } \int _0^\lambda \frac{[1+i\eta _x] \,f(x+i\eta (x,t),t)\,e^{ik\{(x-x_0)+i[\eta (x,t)-y_0]\}}}{1-e^{ik\{(x-x_0) +i[\eta (x,t)-y_0]\}}} \,dx \end{aligned}$$

for all \(x_0,\,y_0 \in {{\mathbb {R}}}\) with \(-d \le y_0 < \eta (x_0,t)\). Since for \(-d \le y_0 \le \eta (x,t)-\tfrac{\lambda }{4}\) we have

$$\begin{aligned} k[2d+y_0+\eta (x,t)] \ge k[\eta (x,t)-y_0] \ge \tfrac{\pi }{2}, \end{aligned}$$

and therefore

$$\begin{aligned}&\Big |\frac{e^{ik\{(x-x_0)+i[\eta (x,t)-y_0]\}}}{1-e^{ik\{(x-x_0) +i[\eta (x,t)-y_0]\}}}\Big | \le \frac{e^{k[y_0-\eta (x,t)]}}{1-e^{k[y_0-\eta (x,t)]}} \le \frac{e^{k[y_0-\eta (x,t)]}}{1-e^{-\pi /2}},\\&\Big |\frac{e^{-ik\{(x-x_0)-i[2d+\eta (x,t)+y_0]\}}}{1-e^{-ik\{(x-x_0)-i[2d+\eta (x,t)+y_0]\}}}\Big | \le \frac{e^{-k[2d+y_0+\eta (x,t)]}}{1-e^{-k[2d+y_0+\eta (x,t)]}} \le \frac{e^{-k[2d+y_0+\eta (x,t)]}}{1-e^{-\pi /2}}, \end{aligned}$$

we get

$$\begin{aligned} |f(x_0+iy_0,t)| \le \,\frac{e^{ky_0}+e^{-k[2d+y_0]}}{1-e^{-\pi /2}}\,\mathfrak {m}(t)\,\max _{x \in [0,\lambda ]} \{|f(x+i\eta (x,t),t)|\}, \end{aligned}$$
(4.7)

for \(-d \le y_0 \le \eta _0(t)-\frac{\lambda }{4}\). This is precisely (4.1). Indeed, by the maximum modulus principle applied to the analytic function f in the extended region \(\{x+iy \in {\mathbb {C}}:\ -2d-\eta (x,t)<y<\eta (x,t)\}\), of which \({{\mathcal {B}}}(t)\) is a periodicity cell, \({\mathfrak {S}}(t)\) is attained on the boundary of the region and the symmetry inherent to the reflection principle permits us to choose a location on the upper boundary \(C^+(t)\). \(\square \)

Remark 4.3

Instead of (4.1), we could consider the region \({\mathcal {B}}(t)\) intersected with the horizontal strip \(-2d-\eta _0(t) \le y \le \eta _0(t)\), and use the residue theorem, as in the previous proof, to derive a bound that resembles (4.1) with \(\eta (x,t)\) replaced by \(\eta _0(t)\) on the right side. This approach, for the case of irrotational flows with no underlying currents (that is, for \(\gamma =0\) and \(u_0=0\)), would provide an alternative proof of the result in [32], giving in this setting a quantitative estimate for the exponential decay of the motion to zero, with depth. However, in practical terms, the bound (4.1) involves solely the surface values of the velocity and the slope of the free surface, and these data are readily available in a specific area of the continental shelf by remote sensing, using satellite altimeters or airborne synthetic aperture radar (SAR). In contrast to this, the alternative approach would require a prohibitely large number of immersed wave buoys, needed to perform in situ measurements of the velocity field at some level beneath the wave trough.