Abstract
Time-periodic solutions to partial differential equations of parabolic type corresponding to an operator that is elliptic in the sense of Agmon–Douglis–Nirenberg are investigated. In the whole- and half-space case we construct an explicit formula for the solution and establish coercive \(L^{p}\) estimates. The estimates generalize a famous result of Agmon, Douglis and Nirenberg for elliptic problems to the time-periodic case.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We investigate time-periodic solutions to parabolic boundary value problems
where \(A\) is an elliptic operator of order 2m and \(B_1,\ldots ,B_m\) satisfy an appropriate complementing boundary condition. The domain \(\Omega \) is either the whole-space, the half-space or a bounded domain, and \(\mathbb {R}\) denotes the time-axis. The solutions \(u(t,x)\) correspond to time-periodic data \(f(t,x)\) and \(g_j(t,x)\) of the same (fixed) period \(T>0\). Using the simple projections
we decompose (1.1) into an elliptic problem
and a purely oscillatory problem
The problem (1.2) is elliptic in the sense of Agmon–Douglis–Nirenberg, for which a comprehensive \(L^{p}\) theory was established in [3]. In this article, we develop a complementary theory for the purely oscillatory problem (1.3). Employing ideas going back to Peetre [22] and Arkeryd [7], we are able to establish an explicit formula for the solution to (1.3) when the domain is either the whole- or the half-space. We shall then introduce a technique based on tools from abstract harmonic analysis to show coercive \(L^{p}\) estimates. As a consequence, we obtain a time-periodic version of the celebrated theorem of Agmon, Douglis and Nirenberg [3].
The decomposition (1.2)–(1.3) is essential as the two problems have substantially different properties. In particular, we shall show in the whole- and half-space case that the principle part of the linear operator in the purely oscillatory problem (1.3) is a homeomorphism in a canonical setting of time-periodic Lebesgue–Sobolev spaces. This is especially remarkable since the elliptic problem (1.2) does not satisfy this property. Another remarkable characteristic of (1.3) is that the \(L^{p}\) theory we shall develop for this problem leads directly to a similar \(L^{p}\) theory, sometimes referred to as maximal regularity, for the parabolic initial-value problem associated to (1.1).
We consider general differential operators
with complex coefficients \(a_\alpha :\Omega \rightarrow \mathbb {C}\) and \(b_{j,\alpha }:\partial \Omega \rightarrow \mathbb {C}\). Here, \(\alpha \in \mathbb {N}^{n}\) is a multi-index and \(D^\alpha :=(-i)^{|\alpha |}\partial _{x_1}^{\alpha _1}\ldots \partial _{x_n}^{\alpha _n}\). The order of \(A\) and \(B_j\) is 2m and \(m_j\) (\(j=1,\ldots ,m\)), respectively, with no restrictions other than \(m\in \mathbb {N}\) and \(m_j\in \mathbb {N}_0\). We denote the principle part of the operators by
We shall assume that \(A^H\) is elliptic in the following classical sense:
Definition 1.1
(Properly Elliptic) The operator \(A^H\) is said to be properly elliptic if for all \(x\in \Omega \) and all \(\xi \in \mathbb {R}^n\setminus \{0\}\) it holds \(A^H(x,\xi )\ne 0\), and for all \(x\in \Omega \) and all linearly independent vectors \({\zeta },\xi \in \mathbb {R}^n\) the polynomial \(P(\tau ):= A^H(x,{\zeta }+\tau \xi )\) has m roots in \(\mathbb {C}\) with positive imaginary part, and m roots in \(\mathbb {C}\) with negative imaginary part.
Ellipticity, however, does not suffice to establish maximal \(L^{p}\) regularity for the time-periodic problem. We thus recall Agmon’s condition, also known as parameter ellipticity.
Definition 1.2
(Agmon’s Condition) Let \(\theta \in [-\pi ,\pi ]\). A properly elliptic operator \(A^H\) is said to satisfy Agmon’s condition on the ray \({{\mathrm{e}}}^{i\theta }\) if for all \(x\in \Omega \) and all \(\xi \in \mathbb {R}^n\setminus \{0\}\) it holds \(A^H(x,\xi )\notin \{r{{\mathrm{e}}}^{i\theta }\ |\ r\ge 0\}\).
If \(A^H\) satisfies Agmon’s condition on the ray \({{\mathrm{e}}}^{i\theta }\), then, since the roots of a polynomial depend continuously on its coefficients, the polynomial \(Q(\tau ):=-r{{\mathrm{e}}}^{i\theta }+A^H(x,{\zeta }+\tau \xi )\) has m roots \(\tau _h^+(r{{\mathrm{e}}}^{i\theta },x,{\zeta },\xi )\in \mathbb {C}\) with positive imaginary part, and m roots \(\tau _h^-(r{{\mathrm{e}}}^{i\theta },x,{\zeta },\xi )\in \mathbb {C}\) with negative imaginary part (\(h=1,\ldots ,m\)). Consequently, the following assumption on the operator \((A^H,B^H_1,\ldots ,B^H_m)\) is meaningful.
Definition 1.3
(Agmon’s Complementing Condition) Let \(\theta \in [-\pi ,\pi ]\). If \(A^H\) is a properly elliptic operator, then \((A^H,B^H_1,\ldots ,B^H_m)\) is said to satisfy Agmon’s complementing condition on the ray \({{\mathrm{e}}}^{i\theta }\) if:
-
(i)
\(A^H\) satisfies Agmon’s condition on the ray \({{\mathrm{e}}}^{i\theta }\).
-
(i)
For all \(x\in \partial \Omega \), all pairs \({\zeta },\xi \in \mathbb {R}^n\) with \({\zeta }\) tangent to \(\partial \Omega \) and \(\xi \) normal to \(\partial \Omega \) at x, and all \(r\ge 0\), let \(\tau _h^+(r{{\mathrm{e}}}^{i\theta },x,{\zeta },\xi )\in \mathbb {C}\) (\(h=1,\ldots ,m\)) denote the m roots of the polynomial \({Q(\tau ):=-r{{\mathrm{e}}}^{i\theta }+A^H(x,{\zeta }+\tau \xi )}\) with positive imaginary part. The polynomials \(P_j(\tau ):=B^H_j(x,{\zeta }+\tau \xi )\) (\(j=1,\ldots ,m\)) are linearly independent modulo the polynomial \(\Pi _{h=1}^m \big (\tau -\tau _h^+(r{{\mathrm{e}}}^{i\theta },x,{\zeta },\xi )\big )\).
The property specified in Definition 1.3 was first introduced by Agmon in [2], and later by Agranovich and Vishik in [5] as parameter ellipticity. We note that it is equivalent to the Lopatinskiĭ-Shapiro condition, see Remark 1.7 below. The condition was introduced in order to identify the additional requirements on the differential operators needed to extend the result of Agmon, Douglis and Nirenberg [3] from the elliptic case to the corresponding parabolic initial-value problem. The theorem of Agmon, Douglis and Nirenberg [3] requires \((A^H,B^H_1,\ldots ,B^H_m)\) to satisfy Agmon’s complementing condition only at the origin (not on a full ray), in which case \((A^H,B^H_1,\ldots ,B^H_m)\) is said to be elliptic in the sense of Agmon–Douglis–Nirenberg. Analysis of the associated initial-value problem relies heavily on properties of the resolvent equation
It was shown by Agmon [2] that a necessary and sufficient condition for the resolvent of \((A^H,B^H_1,\ldots ,B^H_m)\) to lie in the negative complex half-plane, which leads to the generation of an analytic semi-group, is that Agmon’s complementing condition is satisfied for all rays with \({|\theta |}\ge \frac{\pi }{2}\). The step from analyticity of the semi-group to maximal \(L^{p}\) regularity for the parabolic initial-value problem is more complicated though. In the celebrated work of Dore and Venni [12], a framework was developed with which maximal regularity could be established comprehensively from the assumption that Agmon’s condition is satisfied for all rays with \({|\theta |}\ge \frac{\pi }{2}\). To apply [12], one has to show that \((A^H,B^H_1,\ldots ,B^H_m)\) admits bounded imaginary powers. Later, it was shown that maximal regularity is in fact equivalent to \({\mathcal R}\)-boundedness of an appropriate resolvent family; see [11]. Remarkably, our result for the time-periodic problem (1.3) leads to a new and relatively short proof of maximal regularity for the parabolic initial-value problem without the use of either bounded imaginary powers or the notion of \({\mathcal R}\)-boundedness; see Remark 1.6 below. Under the assumption that \((A^H,B^H_1,\ldots ,B^H_m)\) generates an analytic semi-group, maximal regularity for the parabolic initial-value problem follows almost immediately as a corollary from our main theorem. We emphasize that our main theorem of maximal regularity for the time-periodic problem does not require the principle part of \((A,B_1,\ldots ,B_m)\) to generate an analytic semi-group. As a novelty of the present paper, and in contrast to the initial-value problem, we establish that maximal \(L^{p}\) regularity for the time-periodic problem requires Agmon’s complementing condition to be satisfied only on the two rays with \(\theta =\pm \,\frac{\pi }{2}\), that is, only on the imaginary axis.
The references above to the theory of maximal \(L^{p}\) regularity for parabolic initial-value problems would not be complete without mention of the extensive work of Solonnikov on initial-value problems for parabolic systems; see [23] and the references therein. The investigation of systems requires a more involved definition of parabolicity and complementary condition than Definition 1.1–1.3, but the arguments towards an \(L^{p}\) theory follow similar ideas as in the scalar case. As pointed out by Wang [28], the approach of Solonnikov can be reduced to an argument based on Fourier multipliers. This rationale was also proposed by Arkeryd [7] in his study of elliptic boundary value problems and will also be used in our approach in the time-periodic case.
Our main theorem for the purely oscillatory problem (1.3) concerns the half-space case and the question of existence of a unique solution satisfying a coercive \(L^{p}\) estimate in the Sobolev space \(W^{1,2m,p}_{\mathrm {per}}(\mathbb {R}\times \mathbb {R}^n_+)\) of time-periodic functions on the time-space domain \(\mathbb {R}\times \mathbb {R}^n_+\). We refer to Sect. 2 for definitions of the function spaces.
Theorem 1.4
Let \(p\in (1,\infty )\), \(T>0\), \(n\ge 2\). Assume that \(A^H\) and \((B^H_1,\ldots ,B^H_m)\) have constant coefficients. If \(A^H\) is properly elliptic and \((A^H,B^H_1,\ldots ,B^H_m)\) satisfies Agmon’s complementing condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\), then for all functions \(f\in {\mathcal P}_\bot L_{\mathrm {per}}^{p}(\mathbb {R}\times \mathbb {R}^n_+)\) and \(g_j\in {\mathcal P}_\bot W^{\kappa _j,2m\kappa _j,p}_{\mathrm {per}}(\mathbb {R}\times \partial \mathbb {R}^n_+)\) with \(\kappa _j:=1-\frac{m_j}{2m}-\frac{1}{2mp}\)\((j=1,\ldots ,m)\) there exists a unique solution \(u\in {\mathcal P}_\bot W^{1,2m,p}_{\mathrm {per}}(\mathbb {R}\times \mathbb {R}^n_+)\) to
Moreover,
with \( = (p,T,n)\).
Our proof of Theorem 1.4 contains two results that are interesting in their own right. Firstly, we establish a similar assertion in the whole-space case. Secondly, we provide an explicit formula for the solution; see (3.8) below. Moreover, our proof is carried out fully in a setting of time-periodic functions and follows an argument adopted from the elliptic case. This is remarkable in view of the fact that analysis of time-periodic problems in existing literature typically is based on theory for the corresponding initial-value problem; see for example [18]. A novelty of our approach is the introduction of suitable tools from abstract harmonic analysis that allow us to give a constructive proof and avoid completely the classical indirect characterizations of time-periodic solutions as fixed points of a Poincaré map, that is, as special solutions to the corresponding initial-value problem. The circumvention of the initial-value problem also enables us to avoid having to assume Agmon’s condition for all \({|\theta |}\ge \frac{\pi }{2}\) and instead carry out our investigation under the weaker condition that Agmon’s condition is satisfied only for \(\theta =\pm \frac{\pi }{2}\).
We shall briefly describe the main ideas behind the proof of Theorem 1.4. We first consider the problem in the whole space \(\mathbb {R}\times \mathbb {R}^n\) and replace the time axis \(\mathbb {R}\) with the torus \({\mathbb T}:=\mathbb {R}/T\mathbb {Z}\) in order to reformulate the \(T\)-time-periodic problem as a partial differential equation on the locally compact abelian group \(G:={\mathbb T}\times \mathbb {R}^n\). Utilizing the Fourier transform \(\mathscr {F}_G\) associated to \(G\), we obtain an explicit representation formula for the time-periodic solution. Since \(\mathscr {F}_G=\mathscr {F}_{\mathbb T}\circ \mathscr {F}_{\mathbb {R}^n}\), this formula simply corresponds to a Fourier series expansion in time of the solution and subsequent Fourier transform in space of all its Fourier coefficients. While it is relatively easy to obtain \(L^{p}\) estimates (in space) for each Fourier coefficient separately, it is highly non-trivial to deduce from these individual estimates an \(L^{p}\) estimate in space and time via the corresponding Fourier series. Instead, we turn to the representation formula given in terms of \(\mathscr {F}_G\) and show that the corresponding Fourier multiplier defined on the dual group \(\widehat{G}\) is an \(L^{p}(G)\) multiplier. For this purpose, we use the so-called Transference Principle for Fourier multipliers in a group setting, and obtain the necessary estimate in the whole-space case. In the half-space case, Peetre [22] and Arkeryd [7] utilized the Paley–Wiener Theorem in order to construct a representation formula for solutions to elliptic problems; see also [26, Section 5.3]. We adapt their ideas to our setting and establish \(L^{p}\) estimates from the ones already obtained in the whole-space case.
Theorem 1.4 can be reformulated as the assertion that the operator
is a homeomorphism. By a standard localization and perturbation argument, a purely periodic version of the celebrated theorem of Agmon, Douglis and Nirenberg [3] in the general case of operators with variable coefficients and \(\Omega \) being a sufficiently smooth domain follows. In fact, combining the classical result [3] for the elliptic case with Theorem 1.4, we obtain the following time-periodic version of the Agmon–Douglis–Nirenberg Theorem:
Theorem 1.5
(Time-Periodic ADN Theorem) Let \(p\in (1,\infty )\), \(T>0\), \(n\ge 2\) and \(\Omega \) be a domain with a boundary that is uniformly \(C^{2m}\)-smooth. Assume \(a_\alpha \) is bounded and uniformly continuous on \(\overline{\Omega }\) for \({|\alpha |}=2m\), and \(a_\alpha \in L^{\infty }(\Omega )\) for \({|\alpha |}<2m\). Further assume \(b_{j,\beta }\in C^{2m-m_j}(\partial \Omega )\) with bounded and uniformly continuous derivatives up to the order \(2m-m_j\). If \(A^H\) is properly elliptic and \((A^H,B^H_1,\ldots ,B^H_m)\) satisfies Agmon’s complementing condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\), then the estimate
holds for all \(u\in W^{1,2m,p}_{\mathrm {per}}(\mathbb {R}\times \Omega )\), where \(\kappa _j:=1-\frac{m_j}{2m}-\frac{1}{2mp}\)\((j=1,\ldots ,m)\).
Since time-independent functions are trivially also time-periodic, we have \(W^{2m,p}(\Omega )\subset W^{1,2m,p}_{\mathrm {per}}(\mathbb {R}\times \Omega )\). If estimate (1.9) is restricted to functions in \(W^{2m,p}(\Omega )\), Theorem 1.5 reduces to the classical theorem of Agmon–Douglis–Nirenberg [3], which has played a fundamental role in the analysis of elliptic boundary value problems for more then half a century now. This classical theorem for scalar equations was extended to systems in [4]. We shall only treat scalar equations in the following, but will address systems in future works.
We briefly return to the decomposition (1.2)–(1.3). It is well-known in the bounded domain case that ellipticity of (1.2) in the sense of Agmon–Douglis–Nirenberg is equivalent to the corresponding linear operator being Fredholm in the setting of classical Sobolev spaces. From Theorem 1.4 and the similar assertion in the whole-space case, which as mentioned above shall also be provided, one can show that also the operator of the purely oscillatory problem (1.3) is Fredholm in the setting of time-periodic Sobolev spaces. Indeed, since we show that the operator is a homeomorphism in the whole- and half-space cases, a localization argument (see for example [29, Proof of Theorem 13.1] or [30, Proof of Theorem 9.32]) yields existence of a left and right regularizer in the bounded domain case, which in turn implies the Fredholm property. Since both the elliptic and purely oscillatory problem possess the Fredholm property, so does the full time-periodic problem on bounded domains. Due to the work of Geymonat [15], a comprehensive Fredholm theory is available for the elliptic problem (1.2). Since our proof of Theorem 1.5 successfully demonstrates that time-periodic problems can be approached in much the same way as elliptic problems, it seems likely that a similar comprehensive Fredholm theory can be developed for the purely oscillatory problem (1.3). Although we shall leave this investigation to future works, we note that the Fredholm properties of the operator in (1.3) will in general be different from the Fredholm properties of the elliptic problem (1.2). In fact, the simple example of the Laplace equation with a Neumann boundary condition in a bounded domain shows that the defect numbers of the two problems can be different. This observation further underlines the importance of the decomposition (1.2)–(1.3).
Time-periodic problems of parabolic type have been investigated in numerous articles over the years, and it would be too far-reaching to list them all here. We mention only the article of Liebermann [18], the recent article by Geissert, Hieber and Nguyen [14], as well as the monographs [16, 27], and refer the reader to the references therein. Finally, we mention the article [17] by the present authors in which some of the ideas utilized in the following were introduced in a much simpler setting.
Remark 1.6
The half-space case treated in Theorem 1.4 is also pivotal in the \(L^{p}\) theory for parabolic initial-value problems. Denote by \(A^H_B\) the realization of the operator \(A^H(D)\) in \(L^{p}(\mathbb {R}^n_+)\) with domain
Maximal regularity for parabolic initial-value problems of Agmon–Douglis–Nirenberg type is based on an investigation of the initial-value problem
Maximal regularity for (1.10) means that for each function \(f\in L^{p}(0,T;L^{p}(\mathbb {R}^n_+))\) there is a unique solution \(u\in L^{p}(0,T;D(A^H_B))\cap W^{1,p}(0,T;L^{p}(\mathbb {R}^n_+))\) which satisfies the estimate
We shall briefly sketch how to obtain maximal regularity for (1.10) from Theorem 1.4. For this purpose, it is required that \(-A^H_B\) generates an analytic semi-group \(\{{{\mathrm{e}}}^{-tA^H_B}\}_{t>0}\), which follows from resolvent estimates going back to Agmon [2, Theorem 2.1] derived under the assumption that \((A^H,B^H_1,\ldots ,B^H_m)\) satisfies Agmon’s complementing condition for all rays with \({|\theta |}\ge \frac{\pi }{2}\); see also [25, Theorem 5.5]. We would like to point out that these resolvent estimates can also be established with the arguments in our proof of Theorem 1.4. One can periodically extend any \(f\in L^{p}(0,T;L^{p}(\mathbb {R}^n_+))\) to a \(T\)-periodic function \(f\in L_{\mathrm {per}}^{p}(\mathbb {R}\times \mathbb {R}^n_+)\). With \(u\) denoting the solution from Theorem 1.4 corresponding to \({\mathcal P}_\bot f\), the function
is the unique solution to (1.10). The desired \(L^{p}\) estimates of \(u\) follow from Theorem 1.4, while estimates of the two latter terms on the right-hand side in (1.12) follow by standard theory for analytic semi-groups; see for example [20, Theorem 4.3.1]. For more details, see also [21, Theorem 5.1]. The connection between maximal regularity for parabolic initial-value problems and corresponding time-periodic problems was observed for the first time in the work of Arendt and Bu [6, Theorem 5.1].
Remark 1.7
If \(A^H\) is a properly elliptic operator that satisfies Agmon’s condition on the ray \({{\mathrm{e}}}^{i\theta }\), \(\theta \in [-\pi ,\pi ]\), then \((A^H,B^H_1,\ldots ,B^H_m)\) is said to satisfy the Lopatinskiĭ-Shapiro condition on the ray \({{\mathrm{e}}}^{i\theta }\), if for all \(x\in \partial \Omega \), all pairs \(\xi ,\zeta \in \mathbb {R}^n\) with \(\zeta \) tangent to \(\partial \Omega \) and \(\xi \) normal to \(\partial \Omega \) at x, all \(r\ge 0\) and all \(g=(g_0,\ldots ,g_{m-1})\in \mathbb {C}^m\) the system of ordinary differential equations
admits a unique solution \(u\in W^{2m,2}(\mathbb {R}_+)\). Often, the Lopatinskiĭ-Shapiro condition is preferred over Agmon’s complementing condition specified in Definition 1.3, but the two definitions are fully equivalent, which follows from Lemma 3.10. Although the purely algebraic nature of the complementing condition may seem favorable, in practice it is sometimes easier to verify the Lopatinskiĭ-Shapiro condition.
2 Preliminaries and notation
2.1 Notation
Unless otherwise indicated, x denotes an element in \(\mathbb {R}^n\) and \(x':=(x_1,\ldots ,x_{n-1})\in \mathbb {R}^{n-1}\). The same notation is employed for \(\xi \in \mathbb {R}^n\) and \(\xi ':=(\xi _1,\ldots ,\xi _{n-1})\in \mathbb {R}^{n-1}\).
We denote by \(\mathbb {C}_+:=\{z\in \mathbb {C}\ |\ {{\mathrm{Im}}}(z)>0\}\) and \(\mathbb {C}_-:=\{z\in \mathbb {C}\ |\ {{\mathrm{Im}}}(z)<0\}\) the upper and lower complex plane, respectively.
The notation \(\partial _j:=\partial _{x_j}\) is employed for partial derivatives with respect to spatial variables. Throughout, \(\partial _t\) shall denote the partial derivative with respect to the time variable.
We introduce the parabolic length
We call a generic function gparabolically\(\alpha \)-homogeneous if \(\lambda ^\alpha g(\eta ,\xi ) = g(\lambda ^{2m}\eta ,\lambda \xi )\) for all \(\lambda >0\).
2.2 Paley–Wiener theorem
Definition 2.1
The Hardy space \(\mathscr {H}_+^2(\mathbb {R})\) consists of all functions \(f\in L^{2}(\mathbb {R})\) admitting a holomorphic extension to the lower complex plane \({\tilde{f}}:\mathbb {C}_-\rightarrow \mathbb {C}\) with
The Hardy space \(\mathscr {H}_-^2(\mathbb {R})\) consists of all functions \(f\in L^{2}(\mathbb {R})\) admitting a similar holomorphic extension to the upper complex plane.
Proposition 2.2
(Paley–Wiener Theorem) Let \(f\in L^{2}(\mathbb {R})\). Then \({{\mathrm{supp}}}f\subset \overline{\mathbb {R}_+}\) if and only if \(\widehat{f}\in \mathscr {H}_+^2\). Moreover, \({{\mathrm{supp}}}f\subset \overline{\mathbb {R}_-}\) if and only if \(\widehat{f}\in \mathscr {H}_-^2\).
Proof
See for example [31, Theorems VI.4.1 and VI.4.2]. \(\square \)
2.3 Time-periodic function spaces
Let \(\Omega \subset \mathbb {R}^n\) be a domain and
the space of smooth time-period functions with compact support in the spatial variable. Clearly,
are norms on \(C^{\infty }_{0,\mathrm {per}}(\mathbb {R}\times \Omega )\). We define Lebesgue and anisotropic Sobolev spaces of time-periodic functions as completions
One may identify
On a similar note, one readily verifies that
provided \(\Omega \) satisfies the segment condition.
We introduce anisotropic fractional order Sobolev spaces (Sobolev-Slobodeckiĭ spaces) by real interpolation:
For a \(C^{2m}\)-smooth manifold \(\Gamma \subset \mathbb {R}^n\), anisotropic Sobolev spaces \(W^{s,2ms,p}_{\mathrm {per}}(\mathbb {R}\times \Gamma )\) are defined in a similar manner. We can identify (see also Sect. 2.4 below) the trace space of \(W^{1,2m,p}_{\mathrm {per}}(\mathbb {R}\times \Omega )\) as \(W^{1-1/2mp,2m-1/p,p}_{\mathrm {per}}(\mathbb {R}\times \partial \Omega )\) in the sense that the trace operator maps the former continuously onto the latter.
2.4 Function spaces and the torus group setting
We shall further introduce a setting of function spaces in which the time axis \(\mathbb {R}\) in the underlying domains is replaced with the torus \({\mathbb T}:=\mathbb {R}/T\mathbb {Z}\). In such a setting, all functions are inherently \(T\)-time-periodic. We shall therefore never have to verify periodicity of functions a posteriori, and it will always be clear in which sense the functions are periodic.
The setting of \({\mathbb T}\)-defined functions is formalized in terms of the canonical quotient mapping \(\pi :\mathbb {R}\times \mathbb {R}^n \rightarrow {\mathbb T}\times \mathbb {R}^n,\ \pi (t,x):=([t],x)\). A differentiable structure on \({\mathbb T}\times \mathbb {R}^n\) is inherited via the quotient mapping form \(\mathbb {R}\times \mathbb {R}^n\). More specifically, for any domain \(\Omega \subset \mathbb {R}^n\) we let
and define for \(u\in C^{\infty }({\mathbb T}\times \Omega )\) derivatives by \(\partial ^\alpha u:= \big (\partial ^\alpha [u\circ \pi ]\big )\circ \pi _{|[0,T)\times \Omega }^{-1}\). We let
denote the space of compactly supported smooth functions. Introducing the normalized Haar measure on \({\mathbb T}\), we define norms \(||\cdot ||_p\) and \(||\cdot ||_{1,2m,p}\) on \(C^{\infty }_0({\mathbb T}\times \Omega )\) as in (2.1)–(2.2). The quotient mapping trivially respects derivatives and is isometric with respect to \(||\cdot ||_p\) and \(||\cdot ||_{1,2m,p}\). Letting
we thus obtain Lebesgue and Sobolev spaces that are isometrically isomorphic to the spaces \(L_{\mathrm {per}}^{p}(\mathbb {R}\times \Omega )\) and \(W^{1,2m,p}_{\mathrm {per}}\big (\mathbb {R}\times \Omega \big )\), respectively. Defining weak derivatives with respect to test functions \(C^{\infty }_0({\mathbb T}\times \Omega )\), one readily verifies that
provided \(\Omega \) satisfies the segment property.
For \(s\in (0,1)\), we define fractional ordered Sobolev spaces by real interpolation
and thereby obtain spaces isometrically isomorphic to \(W^{s,2ms,p}_{\mathrm {per}}(\mathbb {R}\times \Omega )\). In the half-space case, we clearly have
Hence, for \(l\in \mathbb {N}, l\le 2m\) the trace operator
extends to a bounded operator
that is onto; see for example [26, Theorem 1.8.3]. The existence of a bounded right inverse to \({{\mathrm{Tr}}}_l\) can be shown by applying [26, Theorem 2.9.1].
We further introduce the operators
which are clearly complementary projections. Since \({\mathcal P}f\) is independent of the time variable \(t\in \mathbb {R}\), we may at times treat \({\mathcal P}f\) as a function of the space variable \(x\in \Omega \) only. Both \({\mathcal P}\) and \({\mathcal P}_\bot \) extend to bounded operators on the Lebesgue space \(L^{p}({\mathbb T}\times \Omega )\) and Sobolev space \(W^{1,2m,p}\big ({\mathbb T}\times \Omega \big )\). We employ the notation \(L^{p}_\bot ({\mathbb T}\times \Omega ):={\mathcal P}_\bot L^{p}({\mathbb T}\times \Omega )\) and \(W^{1,2m,p}_{\bot }\big ({\mathbb T}\times \Omega \big ):={\mathcal P}_\bot W^{1,2m,p}\big ({\mathbb T}\times \Omega \big )\) for the subspaces of \({\mathcal P}_\bot \)-invariant functions. This notation is canonically extended to other spaces such as interpolation spaces of Lebesgue and Sobolev spaces. We sometimes refer to functions with \(f={\mathcal P}_\bot f\) as purely oscillatory.
Finally, we let
and put
2.5 Schwartz–Bruhat spaces and distributions
When the spatial domain is the whole-space \(\mathbb {R}^n\), we employ the notation \({G:={\mathbb T}\times \mathbb {R}^n}\). Equipped with the quotient topology via \(\pi \), \(G\) becomes a locally compact abelian group. Clearly, the \(L^{p}(G)\) space corresponding to the Haar measure on \(G\), appropriately normalized, coincides with the \(L^{p}({\mathbb T}\times \mathbb {R}^n)\) space introduced in the previous section.
We identify \(G\)’s dual group by \(\widehat{G}=\frac{2\pi }{T}\mathbb {Z}\times \mathbb {R}^n\) by associating \((k,\xi )\in \frac{2\pi }{T}\mathbb {Z}\times \mathbb {R}^n\) with the character \(\chi :G\rightarrow \mathbb {C},\ \chi (x,t):={{\mathrm{e}}}^{ix\cdot \xi +ik t}\). By default, \(\widehat{G}\) is equipped with the compact-open topology, which in this case coincides with the product of the discrete topology on \(\frac{2\pi }{T}\mathbb {Z}\) and the Euclidean topology on \(\mathbb {R}^n\). The Haar measure on \(\widehat{G}\) is simply the product of the Lebesgue measure on \(\mathbb {R}^n\) and the counting measure on \(\frac{2\pi }{T}\mathbb {Z}\).
The Schwartz–Bruhat space \(\mathscr {S}(G) \) of generalized Schwartz functions (originally introduced in [9]) can be described in terms of the semi-norms
as
The vector space \(\mathscr {S}(G)\) is endowed with the semi-norm topology.
The topological dual space \(\mathscr {S^\prime }(G)\) of \(\mathscr {S}(G)\) is referred to as the space of tempered distributions on \(G\). Observe that both \(\mathscr {S}(G)\) and \(\mathscr {S^\prime }(G)\) remain closed under multiplication by smooth functions that have at most polynomial growth with respect to the spatial variables. For a tempered distribution \(u\in \mathscr {S^\prime }(G)\), distributional derivatives \(\partial _t^\alpha \partial _x^\beta u\in \mathscr {S^\prime }(G)\) are defined by duality in the usual manner. Also the support \({{\mathrm{supp}}}u\) is defined in the classical way. Moreover, we may restrict the distribution \(u\) to a subdomain \({\mathbb T}\times \Omega \) by considering it as a functional defined only on the test functions from \(\mathscr {S}(G)\) supported in \({\mathbb T}\times \Omega \).
A differentiable structure on \(\widehat{G}\) is obtained by introduction of the space
The Schwartz–Bruhat space on the dual group \(\widehat{G}\) is defined in terms of the semi-norms
as
We also endow \(\mathscr {S}(\widehat{G})\) with the corresponding semi-norm topology and denote by \(\mathscr {S^\prime }(\widehat{G})\) the topological dual space.
2.6 Fourier transform
As a locally compact abelian group, \(G\) has a Fourier transform \(\mathscr {F}_{G}\) associated to it. The ability to utilize a Fourier transform that acts simultaneously in time \(t\in {\mathbb T}\) and space \(x\in \mathbb {R}^n\) shall play a key role in the following.
The Fourier transform \(\mathscr {F}_G\) on \(G\) is given by
If no confusion can arise, we simply write \(\mathscr {F}\) instead of \(\mathscr {F}_G\). The inverse Fourier transform is formally defined by
It is standard to verify that \(\mathscr {F}:\mathscr {S}(G)\rightarrow \mathscr {S}(\widehat{G})\) is a homeomorphism with \(\mathscr {F}^{-1}\) as the actual inverse, provided the Lebesgue measure \({\mathrm d}\xi \) is normalized appropriately. By duality, \(\mathscr {F}\) extends to a bijective mapping \(\mathscr {F}:\mathscr {S^\prime }(G)\rightarrow \mathscr {S^\prime }(\widehat{G})\). The Fourier transform provides us with a calculus between the differential operators on \(G\) and the polynomials on \(\widehat{G}\). As one easily verifies, for \(u\in \mathscr {S^\prime }(G)\) and \((\alpha ,\beta )\in \mathbb {N}_0\times \mathbb {N}_0^n\) we have \(\mathscr {F}\big (\partial _t^\alpha \partial _x^\beta u\big )=i^{{|\alpha |}+{|\beta |}}\,k^\alpha \,\xi ^\beta \,\mathscr {F}(u)\) as an identity in \(\mathscr {S^\prime }(\widehat{G})\).
The projections introduced in (2.5) can be extended trivially to projections on the Schwartz–Bruhat space \({\mathcal P},{\mathcal P}_\bot :\mathscr {S}(G)\rightarrow \mathscr {S}(G)\). Introducing the delta distribution \(\delta _\mathbb {Z}\) on \(\frac{2\pi }{T}\mathbb {Z}\), that is, \(\delta _\mathbb {Z}(k):=1\) if \(k=0\) and \(\delta _\mathbb {Z}(k):=0\) for \(k\ne 0\), we observe that \({\mathcal P}u= \mathscr {F}^{-1}_G\big [\delta _\mathbb {Z}\mathscr {F}_G[u]\big ]\) and \({\mathcal P}_\bot u= \mathscr {F}^{-1}_G\big [(1-\delta _\mathbb {Z}) \mathscr {F}_G[u]\big ]\). Using these representations for \({\mathcal P}\) and \({\mathcal P}_\bot \), we naturally extend the projections to operators \({\mathcal P},{\mathcal P}_\bot :\mathscr {S^\prime }(G)\rightarrow \mathscr {S^\prime }(G)\). In accordance with the notation introduced above, we put \(\mathscr {S^\prime _\bot }(G):={\mathcal P}_\bot \mathscr {S^\prime }(G)\).
In general, we shall utilize smooth functions \(\mathsf {m}\in C^{\infty }(\widehat{G})\) with at most polynomial growth as Fourier multipliers by introducing the corresponding operator
We call \(\mathsf {m}\) an \(L^{p}(G)\)-multiplier if \(\mathsf {op}\,[\mathsf {m}]\) extends to a bounded operator on \(L^{p}(G)\) for any \(p\in (1,\infty )\). The following lemmas provide us with criteria to determine if \(\mathsf {m}\) is an \(L^{p}(G)\)-multiplier.
Lemma 2.3
Let \(p\in (1,\infty )\) and  . If
. If  for some parabolically 0-homogeneous \(\mathfrak {m}:\mathbb {R}\times \mathbb {R}^n\rightarrow \mathbb {C}\), then
for some parabolically 0-homogeneous \(\mathfrak {m}:\mathbb {R}\times \mathbb {R}^n\rightarrow \mathbb {C}\), then  extends to a bounded operator
extends to a bounded operator  .
.
Proof
The Transference Principle (established originally by de Leeuw [10] and later extended to a general setting of locally compact abelian groups by Edwards and Gaudry [13, Theorem B.2.1]), makes it possible to “transfer” the investigation of Fourier multipliers from one group setting into another. In our case, [13, Theorem B.2.1] yields that \(\mathsf {m}\) is an \(L^{p}(G)\)-multiplier, provided \(\mathfrak {m}\) is an \(L^{p}(\mathbb {R}\times \mathbb {R}^n)\)-multiplier. To show the latter, we can employ one of the classical multiplier theorems available in the Euclidean setting. Since \(\mathfrak {m}\) is parabolically 0-homogeneous, it is easy to verify that \(\mathfrak {m}\) meets for instance the conditions of the Marcinkiewicz’s multiplier theorem ([24, Chapter IV, §6]). Thus, \(\mathfrak {m}\) is an \(L^{p}(\mathbb {R}\times \mathbb {R}^n)\)-multiplier and by [13, Theorem B.2.1] \(\mathsf {m}\) therefore an \(L^{p}(G)\)-multiplier. \(\square \)
Lemma 2.4
Let \(p\in (1,\infty )\),  and \(\alpha \le 0\). If
and \(\alpha \le 0\). If  for some parabolically \(\alpha \)-homogeneous function \(\mathfrak {m}:\mathbb {R}\times \mathbb {R}^n\setminus \{(0,0)\}\rightarrow \mathbb {C}\), then
for some parabolically \(\alpha \)-homogeneous function \(\mathfrak {m}:\mathbb {R}\times \mathbb {R}^n\setminus \{(0,0)\}\rightarrow \mathbb {C}\), then  extends to a bounded operator
extends to a bounded operator  .
.
Proof
Let \(\chi \in C^{\infty }(\mathbb {R})\) be a “cut-off” function with \(\chi (\eta )=0\) for \({|\eta |}<\frac{\pi }{T}\) and \(\chi (\eta )=1\) for \({|\eta |}\ge \frac{2\pi }{T}\). Put \(\mathfrak {M}(\eta ,\xi ):=\chi (\eta )\mathfrak {m}(\eta ,\xi )\). Utilizing that \(\mathfrak {m}\) is \(\alpha \)-homogeneous and \(\alpha \le 0\), one readily verifies that \(\mathfrak {M}\) satisfies the conditions of Marcinkiewicz’s multiplier theorem ([24, Chapter IV, §6]). Consequently, \(\mathfrak {M}\) is an \(L^{p}(\mathbb {R}\times \mathbb {R}^n)\)-multiplier. For \(u\in L^{p}_\bot (G)\), we have \(u={\mathcal P}_\bot u\) and thus
Since \(\mathsf {m}(1-\delta _\mathbb {Z})=\mathfrak {M}_{|\widehat{G}}\), we obtain from [13, Theorem B.2.1] that \(\mathsf {m}(1-\delta _\mathbb {Z})\) is an \(L^{p}(G)\)-multiplier. Consequently, \(||\mathsf {op}\,[\mathsf {m}](u)||_p\le ||u||_p\) for all \(u\in L^{p}_\bot (G)\). \(\square \)
Corollary 2.5
Let \(p\in (1,\infty )\) and \(\beta \in [0,1]\). If \(M\in C^{\infty }(\frac{2\pi }{T}\mathbb {Z}\setminus \{0\}\times \mathbb {R}^{n})\) is parabolically 0-homogeneous, then op [M] extends to a bounded operator op\([M]:W^{\beta ,2m\beta ,p}_{\bot }(G)\rightarrow W^{\beta ,2m\beta ,p}_{\bot }(G)\).
2.7 Time-periodic Bessel Potential spaces
Time-periodic Bessel Potential spaces can be defined via the Fourier transform \(\mathscr {F}_G\). We shall only introduce Bessel Potential spaces of purely oscillatory distributions:
Utilizing Lemma 2.4, one readily verifies that \(H^{s,p}_{\bot }\) is a Banach space with respect to the norm
Time-periodic Bessel Potential spaces on the half-space are defined via restriction of distributions in the time-periodic Bessel Potential spaces defined above:
Identifying \(H^{s,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) as a factor space of \(H^{s,p}_{\bot }\) in the canonical way, we see that \(H^{s,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) is a Banach space in the norm \(||\cdot ||_{s,p,{\mathbb T}\times \mathbb {R}^n_+}\).
Proposition 2.6
Let \(p\in (1,\infty )\). Then \(H^{2m,p}_{\bot }(G)=W^{1,2m,p}_{\bot }(G)\) and \(H^{2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)=W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) with equivalent norms.
Proof
It follows from Lemma 2.4 that \(\mathsf {op}\,\big [|\eta ,\xi |^{-m}\big ]\) extends to a bounded operator on \(L^{p}_\bot (G)\), which implies that \(||f||_{m,p}\) is equivalent to the norm \(||f||_p+||f||_{m,p}\). From this, we infer that \(H^{2m,p}_{\bot }=W^{1,2m,p}_{\bot }(G)\). A standard method (see for example [1, Theorem 4.26]) can be used to construct an extension operator \({{\mathrm{Ext}}}:W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\rightarrow W^{1,2m,p}_{\bot }(G)\). The existence of an extension operator combined with the fact that \(H^{2m,p}_{\bot }=W^{1,2m,p}_{\bot }(G)\) implies \(H^{2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)=W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\). \(\square \)
Proposition 2.7
Let \(s\in \mathbb {R}\). Then



for all \(u\in \mathscr {S^\prime }(G)\).
Proof
The complex function \(z\mapsto (-iz+|k,\xi '|)^{-1}\) is holomorphic in the upper complex plane. Due to Lemma 2.3, we can employ Proposition 2.2 to conclude
for all \(\psi \in \mathscr {S}_\bot (G)\). By duality, the same is true for all \(\psi \in \mathscr {S^\prime _\bot }(G)\). We employ Lemma 2.3 to estimate
It follows from (2.9) that
We thus conclude
and thereby (2.6). Furthermore,
where the last inequality follows by an application of Lemma 2.4. We have thus shown (2.7). One may verify (2.8) in a similar manner. \(\square \)
Lemma 2.8
Let \(\beta \in (0,1)\) and \(\alpha \in \big (2m(\beta -1),2m\beta \big )\). Then  extends to a bounded operator
extends to a bounded operator  .
.
Proof
By interpolation, we directly obtain that \(\mathsf {op}\,\big [|k,\xi |^\alpha \big ]\) extends to a bounded operator
for any \(\theta \in (0,1)\). Choose \(\theta :=\frac{2m\beta -\alpha }{2m-\alpha }\). Using a dyadic decomposition of the Fourier space with respect to the parabolic length, \(H^{s,p}_{\bot }\) can be identified as the complex interpolation space \([H^{s_0,p}_{\bot },H^{s_1,p}_{\bot }]_{\omega }\) with \(s=(1-\omega )s_0+\omega s_1\) by verifying that it is a retract of \(L^p(l^{s,2})\) as in [8, Theorem 6.4.3]. In fact, relying on the Transference Principle, we have a Mikhlin’s multiplier theorem at our disposal, which is the key ingredient in [8, Theorem 6.4.3]. Hence, by reiteration and Proposition 2.6
Similarly, \(\big (L^{p}_\bot ({\mathbb T}\times \mathbb {R}^n),H^{2m-\alpha ,p}_{\bot }\big )_{\theta ,p}= W^{\beta -\frac{\alpha }{2m},2m\beta -\alpha }_{\bot }({\mathbb T}\times \mathbb {R}^n)\). \(\square \)
Finally, we characterize the trace spaces of the time-periodic Bessel Potential spaces.
Lemma 2.9
Let \(p\in (1,\infty )\). The trace operator \({{\mathrm{Tr}}}_m\) defined in (2.3) extends to a bounded operator
that is onto and has a bounded right inverse. If \(u\in H^{m,p}_{\bot }(G)\) with \({{\mathrm{supp}}}(u)\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\), then \({{\mathrm{Tr}}}_m\big (u_{|{\mathbb T}\times \mathbb {R}^n_+}\big )=0\). If \(u\in H^{m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) with \({{\mathrm{Tr}}}_m\big (u_{|{\mathbb T}\times \mathbb {R}^n_+}\big )=0\), then \(u\) is the restriction of a function \(U\in H^{m,p}_{\bot }(G)\) with \({{\mathrm{supp}}}U\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\).
Proof
For either \(I=\mathbb {R}\) or \(I=\mathbb {R}_+\), put
We first verify that \(H^{m,p}_{\bot }=V(\mathbb {R})\) with equivalent norms. It is straightforward to obtain the embedding \(H^{m,p}_{\bot }\hookrightarrow V(\mathbb {R})\). To show the reverse embedding, consider \(u\in V(\mathbb {R})\). Then \(||\mathsf {op}\,[|k,{\xi '}|^m]u||_p\le ||u||_{V(\mathbb {R})}\) and \(||\mathsf {op}\,[\xi _n^m]u||_p\le ||u||_{V(\mathbb {R})}\). By Lemma 2.3,
is an \(L^{p}(G)\) multiplier. It follows that \(||\mathsf {op}\,[|k,\xi |^m]u||_p\le ||u||_{V(\mathbb {R})}\) and thus the embedding \(V(\mathbb {R})\hookrightarrow H^{m,p}_{\bot }\). We conclude \(H^{m,p}_{\bot }=V(\mathbb {R})\). It is standard to show existence of an extension operator \(V(\mathbb {R}_+)\rightarrow V(\mathbb {R})\); see for example [26, Lemma 2.9.1]. By restriction to \({\mathbb T}\times \mathbb {R}^n_+\), it thus follows that \(H^{m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)=V(\mathbb {R}_+)\). The classical trace method now implies that trace operator extends to a bounded operator
that is onto; see for example [26, Theorem 1.8.3]. The existence of a bounded right inverse can be shown as in [26, Theorem 2.9.1]. Again by reiteration we identify
Thus, we conclude (2.10).
Consider now \(u\in H^{m,p}_{\bot }(G)\) with \({{\mathrm{supp}}}(u)\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\). As above we can identify \(u\) as an element of \(V(\mathbb {R})\), which necessarily satisfies \(u(0)=0\). It follows that \({{\mathrm{Tr}}}_m\big (u_{|{\mathbb T}\times \mathbb {R}^n_+}\big )=0\). If on the other hand \(u\in H^{m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) with \({{\mathrm{Tr}}}_m\big (u_{|{\mathbb T}\times \mathbb {R}^n_+}\big )=0\), then it is standard to show that \(u\) can be approximated by a sequence of functions from \(C^{\infty }_0({\mathbb T}\times \mathbb {R}^n_+)\); see for example [26, Theorem 2.9.1]. Clearly, this sequence also converge in \(H^{m,p}_{\bot }(G)\). The limit function \(U\in H^{m,p}_{\bot }(G)\) satisfies \({{\mathrm{supp}}}U\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\) and \(U_{|{\mathbb T}\times \mathbb {R}^n_+}=u\). \(\square \)
3 Constant coefficients in the whole- and half-space
In this section, we establish the assertion of Theorem 1.4. We first treat the whole-space case, and then show the theorem as stated in the half-space case. Since we consider only the differential operators with constant coefficients in this section, we employ the simplified notation \(A(D)\) instead of \(A(x,D)\). Replacing the differential operator D with \(\xi \in \mathbb {R}^n\), we refer to \(A(\xi )\) as the symbol of \(A(D)\).
3.1 The whole space
We consider first the case of the spatial domain being the whole-space \(\mathbb {R}^n\). The time-space domain then coincides with the locally abelian group \(G\), and we can thus employ the Fourier transform \(\mathscr {F}_G\) and base the proof on an investigation of the corresponding Fourier multipliers.
Lemma 3.1
Assume that \(A^H\) is properly elliptic and satisfies Agmon’s condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Let \(p\in (1,\infty )\), \(s\in \mathbb {R}\) and

Then the linear operators

extend uniquely to bounded operators

In the setting (3.2), A\(^{-1}\) is the actual inverse of A.
Proof
Let
Clearly, \(\mathfrak {m}\) is parabolically 0-homogeneous. By Lemma 2.4, it follows that \(\mathsf {m}:=\mathfrak {m}_{|\widehat{G}}\) is an \(L^{p}(G)\)-multiplier. Since \(\mathsf {M}={|k,\xi |^{2m}\mathsf {m}(k,\xi )}\), we conclude that
Since \(A^H\) satisfies Agmon’s condition for \(\theta =\pm \frac{\pi }{2}\), it follows that \(A^H(\xi )\notin i\mathbb {R}\) for all \(\xi \in \mathbb {R}^n\setminus \{0\}\). Consequently, \(\mathfrak {m}^{-1}:\mathbb {R}\times \mathbb {R}^n\setminus \{(0,0)\}\rightarrow \mathbb {C}\) is well-defined and clearly parabolically 0-homogeneous. We deduce as above that
Consequently, \(\mathsf {A}\) and \(\mathsf {A}^{-1}\) extend uniquely to bounded operators \(\mathsf {A}:H^{s,p}_\bot \rightarrow H^{s-2m,p}_\bot \) and \(\mathsf {A}^{-1}:H^{s-2m,p}_\bot \rightarrow H^{s,p}_\bot \), respectively. Clearly, \(\mathsf {A}^{-1}\) is the actual inverse of \(\mathsf {A}\). \(\square \)
Theorem 3.2
Assume \(A^H\) is properly elliptic and satisfies Agmon’s condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Let \(s\in \mathbb {R}\) and \(p\in (1,\infty )\). There is a constant \( >0\) such that
for all \(u\in H^{s,p}_\bot (G)\).
Proof
Since \(\mathsf {A}u= \partial _tu+ A^Hu\), we employ Lemma 3.1 to estimate
Since the differential operator \(A-A^H\) contains derivatives of at most of order \(2m-1\), we conclude (3.3) by a similar multiplier argument as in the proof of Lemma 3.1. \(\square \)
3.2 The half space with Dirichlet boundary condition
In the next step, we consider the case of the spatial domain being the half-space \(\mathbb {R}^n_+\) and boundary operators corresponding to Dirichlet boundary conditions. As in the whole-space case, we shall work with the symbol of \(\partial _t+A^H\). In the following lemma, we collect its key properties.
Lemma 3.3
Assume \(A^H\) is properly elliptic and satisfies Agmon’s condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Let
-
(1)
For every \((\eta ,\xi ')\in {\mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}}\) the complex polynomial \(z\mapsto \mathfrak {M}(\eta ,\xi ',z)\) has exactly m roots \(\rho _j^+(\eta ,\xi ')\in \mathbb {C}_-\) in the upper complex plane, and m roots \(\rho _j^-(\eta ,\xi ')\in \mathbb {C}_+\) in the lower complex plane \((j\in \{1,\ldots ,m\})\).
-
(2)
The functions
$$\begin{aligned}&\mathfrak {M}_\pm :\mathbb {R}\times \mathbb {R}^n\setminus \{(\eta ,\xi )\ |\ (\eta ,{\xi '})=(0,0)\} \rightarrow \mathbb {C},\nonumber \\&\mathfrak {M}_\pm (\eta ,\xi ):=\prod _{j=1}^{m}\big (\xi _n-\rho _j^\pm (\eta ,\xi ')\big ) \end{aligned}$$(3.4)are parabolically m-homogeneous.
-
(3)
The coefficients of the polynomials \(z\mapsto \mathfrak {M}_\pm (\eta ,\xi ',z)\), more specifically the functions \(c^\pm _\alpha : \mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\rightarrow \mathbb {C}\)\((\alpha =0,\ldots ,m)\) with the property that
$$\begin{aligned} \mathfrak {M}_\pm (\eta ,\xi ',z) = \sum _{\alpha =0}^m c^\pm _\alpha (\eta ,{\xi '})z^{m-\alpha }, \end{aligned}$$(3.5)are analytic. Moreover, \(c^\pm _\alpha \) is parabolically \(\alpha \)-homogeneous.
Proof
-
(1)
Since \(A^H\) is properly elliptic, the polynomial \(z\mapsto \mathfrak {M}(0,\xi ',z)\) has exactly m roots in the upper and lower complex plane, respectively. Recall that \(A^H(x,\xi )\notin i\mathbb {R}\) for all \(\xi \in \mathbb {R}^n\setminus \{0\}\). Since the roots of a polynomial depend continuously on the polynomial’s coefficients, we deduce part (1) of the lemma.
-
(2)
Since \(\mathfrak {M}\) is parabolically 2m-homogeneous, the roots \(\rho _j^\pm \) are parabolically 1-homogeneous. It follows that \(\mathfrak {M}_\pm \) is parabolically m-homogeneous.
-
(3)
The analyticity of the coefficients \(c^\pm _\alpha \) follows by a classical argument; see for example [25, Chapter 4.4]. The coefficient \(c^\pm _\alpha \) being parabolically \(\alpha \)-homogeneous is a direct consequence of \(\mathfrak {M}_\pm \) being m-homogeneous. \(\square \)
Lemma 3.4
Assume \(A^H\) is properly elliptic and satisfies Agmon’s condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Put  , where \(\mathfrak {M}_\pm \) is defined by (3.4). Let \(p\in (1,\infty )\) and \(s\in \mathbb {R}\). Then the linear operators
, where \(\mathfrak {M}_\pm \) is defined by (3.4). Let \(p\in (1,\infty )\) and \(s\in \mathbb {R}\). Then the linear operators

extend uniquely to bounded and mutually inverse operators  and
and  , respectively.
, respectively.
Proof
The assertion of the lemma follows as in the proof of Lemma 3.1, provided we can show that the restriction to \(\widehat{G}\) of the multiplier
and its inverse are \(L^{p}_\bot (G)\)-multipliers. Although \(\mathfrak {m}\) is parabolically 0-homogeneous, we cannot apply Lemma 2.4 directly since \(\mathfrak {m}\) is not defined on all of \(\mathbb {R}\times \mathbb {R}^n\setminus \{(0,0)\}\). Instead, we recall (3.5) and observe that
Owing to the \(\alpha \)-homogeneity of \(c^\pm _\alpha \), Lemma 2.4 yields that both \({\mathfrak {m}_1^\alpha }_{|\widehat{G}}\) and \({\mathfrak {m}_2^\alpha }_{|\widehat{G}}\) are \(L^{p}(G)\)-multipliers. Consequently, also \(\mathfrak {m}\) is an \(L^{p}(G)\)-multiplier, and we thus conclude as in the proof of Lemma 3.1 that \(\mathsf {A}_{\pm }\) extends uniquely to a bounded operator \(\mathsf {A}_{\pm }:H^{s,p}_\bot (G)\rightarrow H^{s-m,p}_\bot (G)\).
To show the corresponding property for \(\mathsf {A}_{\pm }^{-1}\), we introduce a cut-off function \(\chi \in C^{\infty }(\mathbb {R})\) with \(\chi (\eta )=0\) for \({|\eta |}<\frac{\pi }{T}\) and \(\chi (\eta )=1\) for \({|\eta |}\ge \frac{2\pi }{T}\). We claim that
is an \(L^{p}(\mathbb {R}\times \mathbb {R}^n)\)-multiplier. Indeed, utilizing that \(\mathfrak {M}_\pm \) is m-homogeneous, we see that \(\mathfrak {M}_\pm \) can be bounded below by
where the infimum above is strictly positive due to the roots in definition (3.4) satisfying \(\lim _{(\eta ,{\xi '})\rightarrow (0,0)}\rho _j^\pm (\eta ,{\xi '})=0\). Using only (3.7) and the \(\alpha \)-homogeneity of the coefficients \(c^\pm _\alpha \) as in (3.6), it is now straightforward to verify that \(\mathfrak {\widetilde{m}}\) satisfies the condition of the Marcinkiewicz’s multiplier theorem ([24, Chapter IV, §6]). Thus, \(\mathfrak {\widetilde{m}}\) is an \(L^{p}(\mathbb {R}\times \mathbb {R}^n)\)-multiplier and by [13, Theorem B.2.1] \({\mathfrak {\widetilde{m}}}_{|{\widehat{G}}}\) therefore an \(L^{p}(G)\)-multiplier. Since the restriction of the corresponding operator \(\mathsf {op}\,\big [{\mathfrak {\widetilde{m}}}_{|{\widehat{G}}}\big ]:L^{p}_\bot (G)\rightarrow L^{p}_\bot (G)\) to the subspace of purely periodic functions coincides with \(\mathsf {op}\,\big [{\mathfrak {m}^{-1}}_{|{\widehat{G}}}\big ]:L^{p}_\bot (G)\rightarrow L^{p}_\bot (G)\), we deduce as in the proof of Lemma 3.1 that \(\mathsf {A}_{\pm }^{-1}\) extends uniquely to a bounded operator \(\mathsf {A}_{\pm }^{-1}:H^{s-m,p}_\bot (G)\rightarrow H^{s,p}_\bot (G)\). \(\square \)
The lemma above provides us with at decomposition of the differentiable operators in (3.2), that is, for \(\mathsf {A}:H^{s,p}_\bot (G)\rightarrow H^{s-2m,p}_\bot (G)\) and \(\mathsf {A}^{-1}:H^{s-2m,p}_\bot (G)\rightarrow H^{s,p}_\bot (G)\) the decompositions \(\mathsf {A}=\mathsf {A}_+\mathsf {A}_-=\mathsf {A}_-\mathsf {A}_+\) and \(\mathsf {A}^{-1}=\mathsf {A}_+^{-1}\mathsf {A}_-^{-1}=\mathsf {A}_-^{-1}\mathsf {A}_+^{-1}\) are valid provided \(\mathsf {A}\) is normalized accordingly. Employing the Paley–Wiener Theorem, we shall now show that the operators \(\mathsf {A}_\pm \) and \(\mathsf {A}^{-1}_\pm \) “respect” the support of a function in the upper (lower) half-space.
Lemma 3.5
Assume \(A^H\) is properly elliptic and satisfies Agmon’s condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Let \(p\in (1,\infty )\), \(s\in \mathbb {R}\) and consider \(u\in H^{s,p}_\bot (G)\).
-
(i)
If \({{\mathrm{supp}}}u\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\), then
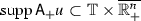 and
and 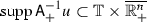 .
. -
(ii)
If \({{\mathrm{supp}}}u\subset {\mathbb T}\times \overline{\mathbb {R}^n_-}\), then
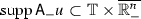 and
and 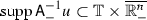 .
.
Proof
We shall prove only part (i), for part (ii) follows analogously. We employ the notation \({H}:={\mathbb T}\times \mathbb {R}^{n-1}\) and the canonical decomposition \(\mathscr {F}_G=\mathscr {F}_{H}\mathscr {F}_\mathbb {R}\) of the Fourier transform. In view of Lemma 3.4, it suffices to consider only \(u\in \mathscr {S}(G)\) with \({{\mathrm{supp}}}u\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\).
For fixed \({k}\in \frac{2\pi }{T}\mathbb {Z}\setminus \{0\}\) and \(\xi '\in \mathbb {R}^{n-1}\), we let \(\mathsf {D}({k},\xi '):=\mathscr {F}_{\mathbb {R}}^{-1}\mathsf {M}_+({k},\xi ',\cdot )\mathscr {F}_{\mathbb {R}}\). Since \(\mathsf {M}_+\) is a polynomial with respect to the variable \(\xi _n\), \(\mathsf {D}({k},\xi ')\) is a differential operator in \(x_n\) and hence \({{\mathrm{supp}}}(\mathsf {D}({k},\xi ')f)\subset \overline{\mathbb {R}_+}\) for every \(f\in \mathscr {S}'(\mathbb {R})\) with \({{\mathrm{supp}}}f\subset \overline{\mathbb {R}_+}\). Clearly, \({{\mathrm{supp}}}([\mathscr {F}_{H}u]({k},\xi ',\cdot ))\subset \overline{\mathbb {R}_+}\). Since \(\mathscr {F}_{H}[\mathsf {A}_+u]({k},\xi ',\cdot )=[\mathsf {D}({k},\xi ')\mathscr {F}_{H}u]({k},\xi ',\cdot )\), we conclude \({{\mathrm{supp}}}\mathsf {A}_+u\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\).
To show the same property for \(\mathsf {A}_+^{-1}u\), we employ the version of the Paley–Wiener Theorem presented in Proposition 2.2. Since \(u\in \mathscr {S}(G)\subset L^{2}(G)\), we immediately obtain that for fixed \({k}\in \frac{2\pi }{T}\mathbb {Z}\) and \(\xi '\in \mathbb {R}^{n-1}\), the Fourier transform \([\mathscr {F}_Gu]({k},\xi ',\cdot )\) is in the Hardy space \(\mathscr {H}_+^2(\mathbb {R})\). Let
denote the extension of \(\mathsf {M}_+^{-1}({k},\xi ',\cdot )\) to the lower complex plane. Since all the roots \(\rho _j^+\) lie in the upper complex plane, this extension is holomorphic and bounded. It follows that \([\mathsf {M}_+^{-1}\mathscr {F}_Gu]({k},\xi ',\cdot )\in \mathscr {H}_+^2(\mathbb {R})\). Hence, taking the inverse Fourier transform, Proposition 2.2 yields \({{\mathrm{supp}}}\mathsf {A}_+^{-1}u\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\). \(\square \)
The above properties of \(\mathsf {A}_\pm \) and \(\mathsf {A}^{-1}_\pm \) lead to a surprisingly simple representation formula, see (3.8) below, for the solution \(u\) to the problem \(\partial _tu+A^Hu=f\) in the half-space \({\mathbb T}\times \mathbb {R}^n_+\) with Dirichlet boundary conditions. The problem itself can be formulated elegantly as (3.9).
Lemma 3.6
Assume \(A^H\) is properly elliptic and satisfies Agmon’s condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Let \(p\in (1,\infty )\) and \(f\in H^{-m,p}_\bot (G)\). Let \(Y_+\) denote the characteristic function on \({\mathbb T}\times \mathbb {R}^n_+\). Then

is the unique solution in \(H^{m,p}_{\bot }(G)\) to

Moreover, there is a constant \(c=c(n,p)>0\) such that
Proof
By Lemma 3.4, \(\mathsf {A}_-^{-1}f\in L^{p}_\bot (G)\). Clearly then \(Y_+\mathsf {A}_-^{-1}f\in L^{p}_\bot (G)\) and trivially \({{\mathrm{supp}}}(Y_+\mathsf {A}_-^{-1}f)\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\). Lemma 3.5 now implies \({{\mathrm{supp}}}(\mathsf {A}_+^{-1}Y_+\mathsf {A}_-^{-1}f)\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\), which concludes the first part of (3.9). Since \({{\mathrm{supp}}}\big ((Y_+-{{\mathrm{\textsf {id}}}})\mathsf {A}_-^{-1}f\big )\subset {\mathbb T}\times \overline{\mathbb {R}^n_-}\), Lemma 3.5 implies \({{\mathrm{supp}}}\big (\mathsf {A}_-(Y_+-{{\mathrm{\textsf {id}}}})\mathsf {A}_-^{-1}f\big )\subset {\mathbb T}\times \overline{\mathbb {R}^n_-}\). However, \(\mathsf {A}u-f=\mathsf {A}_-(Y_+-{{\mathrm{\textsf {id}}}})\mathsf {A}_-^{-1}f\), whence the second part of (3.9) follows.
To show uniqueness, let \(v\in H^{m,p}_{\bot }\) be a solution to (3.9) with \(f=0\). Since \(\mathsf {A}_+v=\mathsf {A}_-^{-1}\mathsf {A}v\), Lemma 3.5 yields \({{\mathrm{supp}}}(\mathsf {A}_+v)\subset {\mathbb T}\times \overline{\mathbb {R}^n_-}\). On the other hand, \({{\mathrm{supp}}}v\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\) by assumption, whence \({{\mathrm{supp}}}\mathsf {A}_+v\subset {\mathbb T}\times \overline{\mathbb {R}^n_+}\) by Lemma 3.5. Recalling that \(\mathsf {A}_+v\in L^{p}_\bot (G)\) by Lemma 3.4, we thus deduce \(\mathsf {A}_+v=0\) and consequently \(v=0\). This concludes the assertion of uniqueness.
It remains to show (3.10). For \(F\in H^{-m,p}_{\bot }(G)\) with \({{\mathrm{supp}}}(F-f)\subset {\mathbb T}\times \overline{\mathbb {R}^n_-}\), we can utilize Lemmas 3.4 and 3.5 as above to conclude that \(Y_+\mathsf {A}_-^{-1}F = Y_+\mathsf {A}_-^{-1}f\), which in turn implies \(u=\mathsf {A}_+^{-1}Y_+\mathsf {A}_-^{-1}F\). Recalling Lemma 3.1, we estimate
\(\square \)
Finally, we can establish the main theorem in the case of the spatial domain being the half-space \(\mathbb {R}^n_+\) and boundary operators corresponding to Dirichlet boundary conditions.
Theorem 3.7
Assume \(A^H\) is properly elliptic and satisfies Agmon’s condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Let \(p\in (1,\infty )\). For \(f\in L^{p}_\bot ({\mathbb T}\times \mathbb {R}^n_+)\) and \(g\in T_\bot ^{\iota ,p}({\mathbb T}\times \mathbb {R}^n_+)\) there is a unique \(u\in W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) subject to
Moreover, there is a constant \(c=c(n,p)>0\) such that
Proof
We first assume \(g=0\). Extending \(f\) by zero to the whole space \({\mathbb T}\times \mathbb {R}^n\), we have \(f\in L^{p}_\bot (G)\subset H^{-m,p}_\bot (G)\). Let \(u\in H^{m,p}_{\bot }(G)\) be the solution to (3.9) from Lemma 3.6. Lemma 2.9 yields \({{\mathrm{Tr}}}_{m}u=0\). Thus, \(u\) is a solution to (3.11). We shall establish higher order regularity of \(u\) iteratively. For this purpose, we employ Proposition 2.7 to estimate
Since the symbol of \(\mathsf {A}\) reads \(\mathsf {M}({k},\xi ',\xi _n)=a\xi _n^{2m}+i{k}+\sum _{k=0}^{2m-1}\sum _{|\alpha |= 2m-k} a_{\alpha ,k}(\xi ')^\alpha \xi _n^k\) with \(a\ne 0\), we deduce with the help of Lemma 2.4 that
Consequently,
Clearly, \(\mathsf {op}\,\big [|k,{\xi '}|\big ]\) commutes with \(\mathsf {A}_+^{-1}Y_+\mathsf {A}_-^{-1}\), whence
By Lemma 3.6, we finally obtain
Iterating this procedure, we obtain after m steps the desired regularity \(u\in H^{2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) together with the estimate \(||u||_{2m,p,{\mathbb T}\times \mathbb {R}^n_+}\le ||f||_p\). Recalling from Proposition 2.6 that \(H^{2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)=W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\), we conclude (3.12) in the case \(g=0\).
If \(g\ne 0\), we recall the properties (2.4) of the trace operator and choose a function \(v\in W^{1,2m,p}({\mathbb T}\times \mathbb {R}^n_+)\) with \({{\mathrm{Tr}}}_mv=g\) and \(||v||_{2m,p}\le ||g||_{T_\bot ^{\iota ,p}({\mathbb T}\times \mathbb {R}^n_+)}\). With \(w:=u-v\), problem (3.11) is then reduced to
and the assertion readily follows from the homogeneous part already proven.
To show uniqueness, assume \(u\in W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) is a solution the (3.11) with homogeneous data \(f=g=0\). By Lemma 2.9 there is an extension \(U\in W^{1,2m,p}_{\bot }(G)\) of \(u\) with \({{\mathrm{supp}}}U\in {\mathbb T}\times \overline{\mathbb {R}^n_+}\). By Lemma 3.6, \(U=0\). \(\square \)
3.3 The half space with general boundary conditions
Let \(\Omega :=\mathbb {R}^n_+\) and \((A,B_1,\ldots ,B_m)\) be differential operators of the form (1.4) with constant coefficients.
Lemma 3.8
Assume \(A^H\) is properly elliptic and \((A^H,B^H_1,\ldots ,B^H_m)\) satisfies Agmon’s complementing condition on the two rays \({{\mathrm{e}}}^{i\theta }\) with \(\theta =\pm \frac{\pi }{2}\). Let \((k,\xi ')\in \frac{2\pi }{T}\mathbb {Z}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\). Consider as polynomials in z the mappings  and \(z\mapsto B^H_j(\xi ',z)\), where
and \(z\mapsto B^H_j(\xi ',z)\), where  is defined as in Lemma 3.4. For \(j=1,\ldots ,m\) let \(F_{(j-1)l}(k,\xi ')\), \(l=0,\ldots ,m-1\), denote the coefficients of the polynomial
is defined as in Lemma 3.4. For \(j=1,\ldots ,m\) let \(F_{(j-1)l}(k,\xi ')\), \(l=0,\ldots ,m-1\), denote the coefficients of the polynomial  . The corresponding matrix \(F(k,\xi ')\in \mathbb {C}^{m\times m}\) is called characteristic matrix. The characteristic matrix function \(F:\frac{2\pi }{T}\mathbb {Z}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\rightarrow \mathbb {C}^{m\times m}\) has an extension \(F:\mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\rightarrow \mathbb {C}^{m\times m}\) that satisfies \((j,l=0,\ldots ,m-1)\)
. The corresponding matrix \(F(k,\xi ')\in \mathbb {C}^{m\times m}\) is called characteristic matrix. The characteristic matrix function \(F:\frac{2\pi }{T}\mathbb {Z}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\rightarrow \mathbb {C}^{m\times m}\) has an extension \(F:\mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\rightarrow \mathbb {C}^{m\times m}\) that satisfies \((j,l=0,\ldots ,m-1)\)
Moreover, \(F(\eta ,{\xi '})\) is invertible and the inverse matrix function \(F^{-1}(\eta ,{\xi '})\) satisfies
Proof
For \(j=1,\ldots ,m\) the coefficients \(F_{(j-1)l}(\eta ,\xi ')\), \(l=0,\ldots ,m-1\), of the polynomial \(z\mapsto \big [B^H_j(\xi ',z)\mod \mathfrak {M}_+(\eta ,\xi ',z)\big ]\) is clearly an extension of the j’th row of the characteristic matrix \(F\) to \((\eta ,{\xi '})\in \mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\). By definition we have
for some polynomial \(z\mapsto Q_j(\eta ,\xi ',z)\). Recalling (3.4) and that the roots \(\rho _j^+\) are parabolically 1-homogeneous, we deduce for \(\lambda >0\) that
for some polynomial \(z\mapsto \widetilde{Q_j}(\eta ,\xi ',z)\). Comparing coefficients in the two expressions for the polynomial \(z\mapsto B^H_j(\xi ',z)\) above yields (3.13). By (3.4) we have \(\mathfrak {M}_+(k,\xi ',z) = \sum _{\alpha =0}^m c_\alpha (\eta ,{\xi '})z^{m-\alpha }\) with coefficients \(c_\alpha (\eta ,{\xi '})\in C^{\infty }\big (\mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\big )\) and \(c_0(\eta ,{\xi '})=1\). Polynomial division of \(z\mapsto B^H_j({\xi '},z)\) with \(z\mapsto \mathfrak {M}_+(k,\xi ',z)\) thus yields a polynomial with coefficients in \(C^{\infty }\big (\mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\big )\), which establishes (3.14). Choosing \(\lambda :=|\eta ,{\xi '}|^{-1}\) in (3.13) we obtain \({|F_{jl}(\eta ,{\xi '}) |}\le {|\eta ,{\xi '}|}^{m_{j+1}-l} \sup _{|s,\gamma |=1}{|F_{jl}(s,\gamma ) |}\) and thus (3.15). As a direct consequence of Definition 1.3, the rows of \(F(k,\xi ')\) are linearly independent and \(F(k,{\xi '})\) therefore invertible for \((k,{\xi '})\in \frac{2\pi }{T}\mathbb {Z}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\). The scaling property (3.13) implies that \(F(\eta ,{\xi '})\) is also invertible for \((\eta ,{\xi '})\in \mathbb {R}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\). The corresponding scaling property (3.16) for the inverse \(F^{-1}(\eta ,{\xi '})\) follows by multiplying (3.13) with \(\lambda ^lF^{-1}_{l\alpha }(\eta ,{\xi '})F_{\beta j}(\lambda ^{2m}\eta ,\lambda {\xi '})\) and summing over j and l. Since \(F^{-1}(\eta ,{\xi '})=\big (\det F(\eta ,{\xi '})\big )^{-1}{{\mathrm{cof}}}F(\eta ,{\xi '})^\top \), (3.17) follows from (3.14). Finally, (3.18) follows from (3.16) in the same way (3.15) was derived from (3.13). \(\square \)
Lemma 3.9
Let \(p\in (1,\infty )\). Under the same assumptions as in Lemma 3.8, the operators  and
and  extend to bounded operators
extend to bounded operators


where we recall the definitions of the trace spaces \(T_\bot ^{\iota ,p}({{\mathbb T}\times \mathbb {R}^{n-1}})\) and \(T_\bot ^{\kappa ,p}({{\mathbb T}\times \mathbb {R}^{n-1}})\) in Sect. 2.4.
Proof
For \(g\in \mathscr {S}_\bot ({{\mathbb T}\times \mathbb {R}^{n-1}})^m\) we recall Lemma 2.8 and estimate
By (3.16), \(|k,\xi '|^{m_l-(j-1)}F^{-1}_{(j-1)(l-1)}(k,{\xi '})\) is parabolically 0-homogeneous. Corollary 2.5 thus implies (3.21). Assertion (3.20) is shown in a similar manner. \(\square \)
Lemma 3.10
Let the assumptions be as in Lemma 3.8. Let \((k,\xi ')\in \frac{2\pi }{T}\mathbb {Z}\times \mathbb {R}^{n-1}\setminus \{(0,0)\}\) and \(\gamma \) be a rectifiable Jordan curve in \(\mathbb {C}\) that encircles all the roots \(\rho _j^+(k,\xi ')\)\((j=0,\ldots ,m-1)\) of  . Let \(c_l^+(k,\xi ')\in \mathbb {C}\), \(l=0,\ldots ,m\), denote coefficients such that
. Let \(c_l^+(k,\xi ')\in \mathbb {C}\), \(l=0,\ldots ,m\), denote coefficients such that  . Put
. Put

Then for any \(g=(g_0,\ldots ,g_{m-1})\in \mathbb {C}^m\) the unique solution \(u\in W^{2m,2}(\mathbb {R}_+)\) to

is given by \(u(k,\xi ',x_n) = L(k,\xi ',x_n)\cdot g\). Moreover,
Proof
With \(u\) as above, Cauchy’s integral theorem yields
On the same token
Since
which follows by choosing \(\gamma \) to be a circle of sufficiently large radius R and letting \(R\rightarrow \infty \) (see for example [19, Chapter 2, Proposition 4.1]), (3.23) follows. \(\square \)
Lemma 3.11
Let the assumptions be as in Lemma 3.8. If \(u\in W^{1,2m,2}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) satisfies  , then
, then  .
.
Proof
Employ the partial Fourier transform \(\mathscr {F}_{{{\mathbb T}\times \mathbb {R}^{n-1}}}\) to the equation \(\mathsf {A}u=0\), which in view of Plancherel’s theorem implies \(\mathsf {A}(k,\xi ',D_n)\mathscr {F}_{{{\mathbb T}\times \mathbb {R}^{n-1}}}(u)=0\) for almost every \((k,\xi ')\). By Lemma 3.10, \(B^H_j(\xi ',D_n)\mathscr {F}_{{{\mathbb T}\times \mathbb {R}^{n-1}}}(u)={F_{(j-1)l}(k,\xi ')\big ({{\mathrm{Tr}}}_m u(0)\big )_l}\). Employing \(\mathscr {F}^{-1}_{{{\mathbb T}\times \mathbb {R}^{n-1}}}\), we obtain \(B^Hu= \mathsf {op}\,[F]{{\mathrm{Tr}}}_mu\). \(\square \)
Theorem 3.12
Assume \(A^H\) is properly elliptic and \((A^H,B^H_1,\ldots ,B^H_m)\) satisfies Agmon’s complementing condition on the two rays \(\theta =\pm \frac{\pi }{2}\). Let \(p\in (1,\infty )\). For \(f\in L^{p}_\bot ({\mathbb T}\times \mathbb {R}^n_+)\) and \(g\in T_\bot ^{\kappa ,p}({\mathbb T}\times \partial \mathbb {R}^n_+)\) there is a unique \(u\in W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) subject to
Moreover,
where \(c=c(n,p)>0\).
Proof
As in the proof of Theorem 3.7, it suffices to show existence of a solution to (3.24) satisfying (3.25) for \(f=0\) and \(g\in \mathscr {S}_\bot ({{\mathbb T}\times \mathbb {R}^{n-1}})^m\). Since \(F^{-1}\) is smooth away from the origin (3.17) and has at most polynomial growth (3.15), it follows that \(\mathsf {op}\,[F^{-1}] g\in \mathscr {S}_\bot ({{\mathbb T}\times \mathbb {R}^{n-1}})\). Consequently, Theorem 3.7 yields existence of a solution \(u\in W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\cap W^{1,2m,2}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) to
From Lemma 3.11 it follows that \(u\) is in fact a solution to (3.24). Additionally, Theorem 3.7 and Lemma 3.9 imply
It remains to show uniqueness. Assume for this purpose that \(u\in W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) is a solution to (3.24) with homogeneous right-hand side \(f=g=0\). Let \(\{g_n\}_{n=1}^\infty \subset \mathscr {S}_\bot ({{\mathbb T}\times \mathbb {R}^{n-1}})^m\) be a sequence with \(\lim _{n\rightarrow \infty }g_n={{\mathrm{Tr}}}_mu\) in \(T_\bot ^{\iota ,p}({{\mathbb T}\times \mathbb {R}^{n-1}})\). By virtue of Theorem 3.7 there is a \(u_n\in W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\cap W^{1,2m,2}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) with \(\big [\partial _t+A^H\big ]u_n=0\) and \({{\mathrm{Tr}}}_mu_n=g_n\). Theorem 3.7 and Lemma 3.9 imply that \(\lim _{n\rightarrow \infty }u_n=u\) in \(W^{1,2m,p}_{\bot }({\mathbb T}\times \mathbb {R}^n_+)\) and thus \(B^Hu_n\rightarrow B^Hu=0\) in \(T_\bot ^{\kappa ,p}({{\mathbb T}\times \mathbb {R}^{n-1}})\). By Lemma 3.11, \(B^Hu_n=\mathsf {op}\,[F]g_n\). Lemma 3.9 thus yields \({{\mathrm{Tr}}}_mu= \lim _{n\rightarrow \infty }g_n=0\). We conclude \(u=0\) by Theorem 3.7. \(\square \)
4 Proof of the main theorems
Proof of Theorem 1.4
As already noted in Sect. 2.4, the canonical bijection between \(C^{\infty }_0({\mathbb T}\times \mathbb {R}^n_+)\) and \(C^{\infty }_{0,\mathrm {per}}(\mathbb {R}\times \mathbb {R}^n_+)\) implies that \(W^{1,2m,p}\big ({\mathbb T}\times \mathbb {R}^n_+\big )\) and \(W^{1,2m,p}_{\mathrm {per}}(\mathbb {R}\times \mathbb {R}^n_+)\) are isometrically isomorphic. It follows that \(W^{1,2m,p}_{\bot }\big ({\mathbb T}\times \mathbb {R}^n_+\big )\) and \({\mathcal P}_\bot W^{1,2m,p}_{\mathrm {per}}(\mathbb {R}\times \mathbb {R}^n_+)\) as well as \(T_\bot ^{\kappa ,p}({\mathbb T}\times \partial \mathbb {R}^n_+)\) and \(\Pi _{j=1}^m {\mathcal P}_\bot W^{\kappa _j,2m\kappa _j,p}_{\mathrm {per}}(\mathbb {R}\times \partial \mathbb {R}^n_+)\) are isometrically isomorphic. Consequently, Theorem 1.4 follows from Theorem 3.12. \(\square \)
Proof of Theorem 1.5
Theorem 1.5 follows from Theorem 1.4 by a standard localization and perturbation argument. One can even apply the argument used in the elliptic case [3]; see also [25, Chapter 4.8]. \(\square \)
References
Adams, R.A.: Sobolev Spaces. Academic Press, New York (1975)
Agmon, S.: On the eigenfunctions and on the eigenvalues of general elliptic boundary value problems. Commun. Pure Appl. Math. 15, 119–147 (1962)
Agmon, S., Douglis, A., Nirenberg, L.: Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions. I. Commun. Pure Appl. Math. 12, 623–727 (1959)
Agmon, S., Douglis, A., Nirenberg, L.: Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions. II. Commun. Pure Appl. Math. 17, 35–92 (1964)
Agranovich, M., Vishik, M.: Elliptic problems with a parameter and parabolic problems of general type. Russ. Math. Surv. 19(3), 53–157 (1964)
Arendt, W., Bu, S.: The operator-valued Marcinkiewicz multiplier theorem and maximal regularity. Math. Z. 240(2), 311–343 (2002)
Arkeryd, L.: On the \(L^P\) estimates for elliptic boundary problems. Math. Scand. 19, 59–76 (1967)
Bergh, J., Löfström, J.: Interpolation Spaces. An Introduction. Springer, Berlin (1976)
Bruhat, F.: Distributions sur un groupe localement compact et applications à l’étude des représentations des groupes \(p\)-adiques. Bull. Soc. Math. Fr. 89, 43–75 (1961)
de Leeuw, K.: On \(L_p\) multipliers. Ann. Math. 2(81), 364–379 (1965)
Denk, R., Hieber, M., Prüss, J.: \({\cal{R}}\)-boundedness, Fourier multipliers and problems of elliptic and parabolic type. Mem. Am. Math. Soc. 788, 114 (2003)
Dore, G., Venni, A.: On the closedness of the sum of two closed operators. Math. Z. 196, 189–201 (1987)
Edwards, R., Gaudry, G.: Littlewood–Paley and Multiplier Theory. Springer, Berlin (1977)
Geissert, M., Hieber, M., Nguyen, T.H.: A general approach to time periodic incompressible viscous fluid flow problems. Arch. Ration. Mech. Anal. 220(3), 1095–1118 (2016)
Geymonat, G.: Sui problemi ai limiti per i sistemi di equazioni lineari ellittici. Atti Accad. Naz. Lincei VIII. Ser. Rend. Cl. Sci. Fis. Mat. Nat. 37, 35–39 (1964)
Hess, P.: Periodic-Parabolic Boundary Value Problems and Positivity. Longman Scientific and Technical, Harlow; Wiley, New York (1991)
Kyed, M., Sauer, J.: A method for obtaining time-periodic \(L^{p}\) estimates. J. Differ. Equ. 262(1), 633–652 (2017)
Lieberman, G.M.: Time-periodic solutions of linear parabolic differential equations. Commun. Partial Differ. Equ. 24(3–4), 631–663 (1999)
Lions, J., Magenes, E.: Non-homogeneous Boundary Value Problems and Applications. Translated from the French by P. Kenneth, vol. I, 1st edn. Springer, Berlin (1972)
Lunardi, A.: Analytic Semigroups and Optimal Regularity in Parabolic Problems. Reprint of the 1995 hardback edition. Birkhäuser, Basel (2013)
Maekawa, Y., Sauer, J.: Maximal regularity of the time-periodic Stokes operator on unbounded and bounded domains. J. Math. Soc. Jpn. 69(4), 1403–1429 (2017)
Peetre, J.: On estimating the solutions of hypoelliptic differential equations near the plane boundary. Math. Scand. 9, 337–351 (1961)
Solonnikov, V.A.: On boundary value problems for linear parabolic systems of differential equations of general form. Trudy Mat. Inst. Steklov. 83, 3–163 (1965)
Stein, E.M.: Singular Integrals and Differentiability Properties of Functions. Princeton University Press, Princeton (1970)
Tanabe, H.: Functional Analytic Methods for Partial Differential Equations. Marcel Dekker, New York (1997)
Triebel, H.: Interpolation Theory. Function Spaces. Differential Operators. Deutscher Verlag des Wissenschaften, Berlin (1978)
Vejvoda, O.: Partial Differential Equations: Time-Periodic Solutions. The Hague, Boston; Martinus Nijhoff Publishers, Prague; SNTL, Publishers of Technical Literature (1982)
Wang, R.-H.: A Fourier method on the Lp theory of parabolic and elliptic boundary value problems. Sci. Sin. 14, 1373–1376 (1965)
Wloka, J.: Partial Differential Equations. Cambridge University Press, Cambridge (1987)
Wloka, J.T., Rowley, B., Lawruk, B.: Boundary Value Problems for Elliptic Systems. Cambridge University Press, Cambridge (1995)
Yosida, K.: Functional Analysis, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 123, 6th edn. Springer, Berlin (1980)
Acknowledgements
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Y. Giga.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kyed, M., Sauer, J. On time-periodic solutions to parabolic boundary value problems. Math. Ann. 374, 37–65 (2019). https://doi.org/10.1007/s00208-018-1721-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-018-1721-9



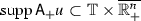 and
and 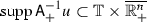 .
.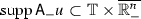 and
and 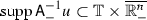 .
.