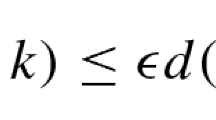Abstract
Given a convex representation \(\rho :\Gamma \rightarrow {{\mathrm{PGL}}}(d,\mathbb {R})\) of a convex cocompact group \(\Gamma \) of \({{\mathrm{Isom}}}_+\mathbb {H}^k,\) we find upper bounds for the quantity \(\alpha h_\rho ,\) where \(h_\rho \) is the entropy of \(\rho \) and \(\alpha \) is the Hölder exponent of the equivariant map \({{\partial }_{\infty }}\Gamma \rightarrow \mathbb {P}(\mathbb {R}^d).\) We also give rigidity statements when the upper bound is attained. This provides an analog of Thurston’s metric for convex cocompact groups of \({{\mathrm{Isom}}}_+\mathbb {H}^k.\) We then prove that if \(\rho :\pi _1\Sigma \rightarrow {{\mathrm{PSL}}}(d,\mathbb {R})\) is in the Hitchin component then \(\alpha h_\rho \le 2/(d-1)\) (where \(\alpha \) is the Hölder exponent of Labourie’s equivariant flag curve) with equality if and only if \(\rho \) is Fuchsian.
Similar content being viewed by others
Notes
These are also called divisible convex sets with strictly convex boundary or strictly convex projective structures on closed manifolds.
In [20] this is called the exponential growth rate of the cocycle.
References
Abramov, L.M.: On the entropy of a flow. Dokl. Akad. Nauk. SSSR 128, 873–875 (1959)
Benoist, Y.: Propriétés asymptotiques des groupes linéaires. Geom. Funct. Anal. 7(1), 1–47 (1997)
Benoist, Y.: Convexes divisibles I. In: Algebraic Groups and Arithmetic, pp. 339–374. Tata Inst. Fund. Res. (2004)
Benoist, Y.: Convexes divisibles III. Ann. Sci. École Norm. Sup. 38, 793–832 (2005)
Bourdon, M.: Structure conforme au bord et flot géodésique d’un CAT \((-1)\)-espace. Enseign. Math. 2(41), 63–102 (1995)
Bourdon, M.: Sur le birraport au bord des CAT\((-1)\)-espaces. Publ. Math. I.H.E.S. 83, 95–104 (1996)
Bowen, R., Ruelle, D.: The ergodic theory of axiom A flows. Invent. Math. 29, 181–202 (1975)
Bridgeman, M., Canary, R., Labourie, F., Sambarino, A.: The pressure metric for Anosov representations. http://arxiv.org/abs/1301.7459 (2013)
Courtois, G.: Critical exponents and rigidity in negative curvature. In: Séminaires & Congrés, Géométries à courbure négative ou nulle, groupes discrets et rigidité, vol. 18, pp. 293–319. Société mathématique de France (2009)
Crampon, M.: Entropies of compact strictly convex projective manifolds. J. Modern Dyn. 3, 511–547 (2009)
Guichard, O.: In preparation
Guichard, O., Wienhard, A.: Anosov representations: domains of discontinuity and applications. Invent. Math. 190, 357–438 (2012)
Hamenstädt, U.: Time preserving conjugacies of geodesic flows. Ergodic Theor. Dyn. Syst. 12, 67–74 (1992)
Hitchin, N.J.: Lie groups and Teichmüller space. Topology 31(3), 449–473 (1992)
Knapp, A.: Lie groups beyond an introduction, Birkhauser (2002)
Labourie, F.: Anosov flows, surface groups and curves in projective space. Invent. Math. 165, 51–114 (2006)
Ledrappier, F.: Structure au bord des variétés à courbure négative. Séminaire de théorie spectrale et géométrie de Grenoble 71, 97–122 (1994–1995)
Otal, J.-P.: Le spectre marqué des longueurs des surfaces à courbure négative. Ann. Math. 131, 151–162 (1990)
Pollicott, M.: Symbolic dynamics for Smale flows. Am. J. Math. 109(1), 183–200 (1987)
Sambarino, A.: Quantitative properties of convex representations. Comment. Math. Helv. 89(2), 443–488 (2014)
Sigmund, K.: On the space of invariant measures for hyperbolic flows. Am. J. Math. 94, 31–37 (1972)
Sullivan, D.: The densitiy at infinity of a discrete group of hyperbolic motions. Publ. Math. de l’I.H.E.S. 50, 171–202 (1979)
Tits, J.: Représentations linéaires irréductibles d’un groupe réductif sur un corps quelconqe. J. Reine Angew. Math. 247, 196–220 (1971)
Yue, C.: The ergodic theory of discrete isometry groups on manifolds of variable negative curvature. Trans. A.M.S. 348(12), 4965–5005 (1996)
Acknowledgments
The author is extremely thankful to Martin Bridgeman, Dick Canary, Francois Labourie, Alejandro Passeggi and Rafael Potrie for useful discussions. He would like to particularly thank Yves Benoist, Matias Carrasco and Jean-François Quint for discussions that considerably improved the statements of this work, and Qiongling Li for pointing out an error on the first version of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
The author was partially supported by the European Research Council under the European Community’s seventh Framework Program (FP7/2007-2013)/ERC grant agreement No. FP7-246918.
Rights and permissions
About this article
Cite this article
Sambarino, A. On entropy, regularity and rigidity for convex representations of hyperbolic manifolds. Math. Ann. 364, 453–483 (2016). https://doi.org/10.1007/s00208-015-1215-y
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-015-1215-y