S-Duality for surfaces with $A_n$-type singularities

Abstract

We show that the generating series of Euler characteristics of Hilbert schemes of points on any algebraic surface with at worst $A_n$-type singularities is described by the theta series determined by integer valued positive definite quadratic forms and the Dedekind eta function. In particular it is a Fourier development of a meromorphic modular form with possibly half integer weight. The key ingredient is to apply the flop transformation formula of Donaldson–Thomas type invariants counting two dimensional torsion sheaves on threefolds proved in the author’s previous paper.

Appendix: Combinatorics on Quot schemes of points on \(A_{n-1}\)

In this appendix, we describe $\chi (\mathop {\mathrm{Quot}}\nolimits ^{m}(\mathcal {O}_{A_{n-1}}(jD)))$ in terms of certain combinatorial data on Young diagrams. In what follows, we regard a Young diagram as a subset in $\mathbb {Z}_{\ge 0}^{2}$ in the usual way, say:

$$\begin{aligned} Y= \begin{array}{l} \square \!\square \! \\ \square \!\square \!\square \end{array} \ \Leftrightarrow \ \{(0, 0), (1, 0), (2, 0), (1, 0), (1, 1) \}. \end{aligned}$$

Recall that there is a one to one correspondence between the set of ideals $I \subset \mathbb {C}[x, y]$ generated by monomials and that of Young diagrams, by assigning $I$ with the Young diagram $Y_I$:

$$\begin{aligned} Y_I := \{(a, b) \in \mathbb {Z}_{\ge 0}^2 : x^a y^b \notin I\}. \end{aligned}$$

(26)

For a Young diagram $Y$, we introduce the following notation:

$$\begin{aligned}&Y^{\rightarrow } := \{Y+(1, 0)\} \cup \{\{0\} \times \mathbb {Z}_{\ge 0}\} \\&Y^{\nearrow } := \{Y+(1, 1)\} \cup \{\mathbb {Z}_{\ge 0} \times \{0\}\} \cup \{\{0\} \times \mathbb {Z}_{\ge 0}\}. \end{aligned}$$

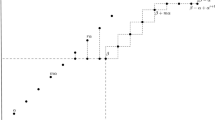
Note that $Y^{\rightarrow }$ and $Y^{\nearrow }$ are Young diagrams with infinite number of blocks. See the following picture:

$$\begin{aligned} Y= \begin{array}{l} \square \!\square \! \\ \square \!\square \!\square \end{array} \ \Rightarrow \ Y^{\rightarrow }= \begin{array}{l} \vdots \\ \square \! \\ \square \! \\ \square \! \\ \square \!\square \!\square \! \\ \square \!\square \!\square \!\square \! \end{array} \ Y^{\nearrow }= \begin{array}{l} \vdots \\ \square \! \\ \square \! \\ \square \!\square \!\square \! \\ \square \!\square \!\square \!\square \! \\ \square \!\square \!\square \!\square \!\square \!\square \!\cdots \end{array} \end{aligned}$$

Lemma 4.1

For $0\le j\le n-1$, the number $\chi (\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_{n-1}}(-jD)))$ coincides with the number of $n$-tuples of Young diagrams $(Y_0, Y_1, \ldots , Y_{n-1})$ satisfying

$$\begin{aligned} Y_{n-1} \subset \cdots \subset Y_j \subset Y_{j-1}^{\rightarrow } \subset \cdots \subset Y_0^{\rightarrow } \subset Y_{n-1}^{\nearrow }, \quad \sum _{i=0}^{n-1} |Y_i |=m. \end{aligned}$$

(27)

Proof

Giving a point in $\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_{n-1}}(-jD))$ is equivalent to giving an ideal $I \subset \mathcal {O}_{A_{n-1}}$ such that $I \subset \mathcal {O}_{A_{n-1}}(-jD)$ and $\mathcal {O}_{A_{n-1}}(-jD)/I$ is a $m$-dimensional $\mathbb {C}$-vector space. As a $\mathbb {C}$-vector space, we have the decomposition

$$\begin{aligned} I=\bigoplus _{k=0}^{n-1} I_k \cdot z^k \end{aligned}$$

(28)

for sub vector spaces $I_k \subset \mathbb {C}[x, y]$. Since $I$ is an ideal in $\mathcal {O}_{A_{n-1}}$, each $I_k$ is an ideal in $\mathbb {C}[x, y]$. Moreover since $I$ must be closed under the multiplication by $z$, we have

$$\begin{aligned} xy I_{n-1} \subset I_0 \subset I_1 \subset \cdots \subset I_{n-1}. \end{aligned}$$

(29)

Since $\mathcal {O}_{A_{n-1}}(-jD)=(x, z^j)$, the condition $I \subset \mathcal {O}_{A_{n-1}}(-jD)$ is equivalent to $I_k \subset (x)$ for $0\le k \le j-1$. Hence for $0\le k\le j-1$, we have $I_k=I_k' \cdot (x)$ for some ideal $I_k' \subset \mathbb {C}[x, y]$. We obtain the sequence of ideals in $\mathbb {C}[x, y]$:

$$\begin{aligned} I_0', \ldots , I_j', I_{j+1}, \ldots I_{n-1}. \end{aligned}$$

(30)

The condition that $\mathcal {O}_{A_{n-1}}(-jD)/I$ is $m$-dimensional is equivalent to

$$\begin{aligned} \sum _{k=0}^{j-1} \dim \mathbb {C}[x, y]/I_k' + \sum _{k=j}^{n-1}\dim \mathbb {C}[x, y]/I_k =m. \end{aligned}$$

(31)

Conversely suppose that we have a sequence of ideals (30) in $\mathbb {C}[x, y]$ satisfying (31) and (29) for $I_k=I_k' \cdot (x)$ with $0\le k\le j-1$. Then we obtain an ideal $I \subset \mathcal {O}_{A_{n-1}}$ by setting (28), which gives a point in $\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_{n-1}}(-jD))$. Note that $T=(\mathbb {C}^{*})^{\times 2}$ acts on $A_{n-1}$ via $(t_1, t_2) \cdot (x, y, z)=(t_1^n x, t_2 ^n y, t_1 t_2 z)$, and the ideal (28) is $T$-fixed if and only if the corresponding ideals in (30) are generated by monomials. Therefore the $T$-fixed locus of $\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_{n-1}}(-jD))$ is identified with the set of $n$-tuples of Young diagrams $(Y_0, \ldots , Y_n)$ satisfying (27), by assigning a sequence (30) with

$$\begin{aligned} (Y_0, \ldots , Y_n)= (Y_{I_0'}, \ldots , Y_{I_{j-1}'}, Y_{I_j}, \ldots , Y_{I_{n-1}}) \end{aligned}$$

as in (26). By the $T$-localization, we obtain the desired result. $\square$

Remark 4.2

The number $\chi (\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_{n-1}}(-jD)))$ in Lemma 4.1 and the coefficients in the LHS of (7) are related by

$$\begin{aligned} \chi (\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_{n-1}}(-jD)))= \chi (\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_{n-1}}((n-j)D))) \end{aligned}$$

(32)

as $\mathcal {O}_{A_{n-1}}(nD) \cong \mathcal {O}_{A_{n-1}}$.

We compare the formula (7) with the numbers of $n$-tuples of Young diagrams in Lemma 4.1 in examples:

Example 4.3

• (i) If $n=2$ and $j=0$, then the formula (7) implies

  $$\begin{aligned} \sum _{m\ge 0} \chi (\mathop {\mathrm{Hilb}}\nolimits ^m(A_1))q^m = 1+ q+3q^2 + 5q^3 + 9q^4 + 14q^5 + \cdots . \end{aligned}$$

  For instance, $\chi (\mathop {\mathrm{Hilb}}\nolimits ^5(A_1))$ corresponds to the following 14 pairs of Young diagrams $(Y_0, Y_1)$:

  $$\begin{aligned}&\left( \begin{array}{l} \square \! \\ \square \! \\ \square \! \\ \square \! \\ \square \! \end{array}, \emptyset \right) , \ \left( \begin{array}{l} \square \! \\ \square \! \\ \square \! \\ \square \!\square \! \end{array}, \emptyset \right) , \ \left( \begin{array}{l} \square \! \\ \square \! \\ \square \!\square \!\square \! \end{array}, \emptyset \right) , \ \left( \begin{array}{l} \square \! \\ \square \!\square \!\square \!\square \! \end{array}, \emptyset \right) , \\&\left( \begin{array}{l} \square \!\square \!\square \!\square \!\square \! \end{array}, \emptyset \right) , \ \left( \begin{array}{l} \square \! \\ \square \! \\ \square \! \\ \square \! \end{array}, \begin{array}{l} \\ \\ \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \! \\ \square \! \\ \square \!\square \! \end{array}, \begin{array}{l} \\ \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \!\square \! \\ \square \!\square \! \end{array}, \begin{array}{l} \\ \square \! \end{array} \right) , \\&\left( \begin{array}{l} \square \! \\ \square \!\square \!\square \! \end{array}, \begin{array}{l} \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \!\square \!\square \!\square \! \end{array}, \begin{array}{l} \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \! \\ \square \! \\ \square \! \end{array}, \begin{array}{l} \\ \square \! \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \! \\ \square \!\square \! \end{array}, \begin{array}{l} \square \! \\ \square \! \end{array} \right) , \\&\left( \begin{array}{l} \square \! \\ \square \!\square \! \end{array}, \begin{array}{l} \\ \square \!\square \! \end{array} \right) , \ \left( \begin{array}{l} \square \!\square \!\square \! \end{array}, \begin{array}{l} \square \!\square \! \end{array} \right) . \end{aligned}$$

• (ii) If $n=2$ and $j=1$, then (7) and (32) yield

  $$\begin{aligned} \sum _{m\ge 0} \chi (\mathop {\mathrm{Quot}}\nolimits ^m(\mathcal {O}_{A_1}(-D)))q^m = 1+ 2q+3q^2 + 6q^3 + 10q^4 + 16q^5 + \cdots . \end{aligned}$$

  Similarly to (i), $\chi (\mathop {\mathrm{Quot}}\nolimits ^5(\mathcal {O}_{A_1}(-D)))$ corresponds to the following 16 pairs of Young diagrams $(Y_0, Y_1)$:

  $$\begin{aligned}&\left( \begin{array}{l} \square \!\square \!\square \!\square \!\square \! \end{array}, \emptyset \right) , \ \left( \begin{array}{l} \square \!\square \!\square \!\square \! \end{array}, \begin{array}{l} \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \! \\ \square \!\square \!\square \! \end{array}, \begin{array}{l} \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \!\square \!\square \! \end{array}, \begin{array}{l} \square \!\square \! \end{array} \right) , \\&\left( \begin{array}{l} \square \! \\ \square \!\square \! \end{array}, \begin{array}{l} \\ \square \!\square \! \end{array} \right) , \ \left( \begin{array}{l} \square \! \\ \square \! \\ \square \! \end{array}, \begin{array}{l} \\ \square \! \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \square \! \\ \square \!\square \! \end{array}, \begin{array}{l} \square \! \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \\ \square \!\square \!\square \! \end{array}, \begin{array}{l} \square \! \\ \square \! \end{array} \right) , \\&\left( \begin{array}{l} \\ \\ \square \!\square \! \end{array}, \begin{array}{l} \square \! \\ \square \! \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \\ \square \!\square \! \end{array}, \begin{array}{l} \square \! \\ \square \!\square \! \end{array} \right) , \ \left( \begin{array}{l} \square \!\square \! \end{array}, \begin{array}{l} \square \!\square \!\square \! \end{array} \right) , \ \left( \begin{array}{l} \\ \square \! \\ \square \! \end{array}, \begin{array}{l} \square \\ \square \! \\ \square \! \end{array} \right) , \\&\left( \begin{array}{l} \square \! \\ \square \! \end{array}, \begin{array}{l} \square \! \\ \square \!\square \! \end{array} \right) , \ \left( \begin{array}{l} \\ \\ \\ \square \! \end{array}, \begin{array}{l} \square \! \\ \square \! \\ \square \! \\ \square \! \end{array} \right) , \ \left( \begin{array}{l} \\ \\ \square \! \end{array}, \begin{array}{l} \square \! \\ \square \! \\ \square \!\square \! \end{array} \right) , \ \left( \emptyset , \begin{array}{l} \square \! \\ \square \! \\ \square \! \\ \square \! \\ \square \! \end{array} \right) . \end{aligned}$$