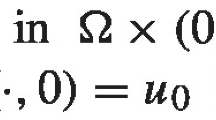Abstract
We prove the existence of a unique solution of the following Neumann problem \(u_t = (\phi_m(u))_{xx}\), u > 0, in (a, b) × (0, T), u(x, 0) = u 0(x) ≥ 0 in (a, b), \((\phi_m(u))_x(a,t) = g(t)\) and \((\phi_m(u))_x(b,t)=-f(t) \forall 0 < t < T\), where \(\phi_m(u) = u^m/m\) if m < 0, \(\phi_m(u) = \log u\) if m = 0, and \(T = \sup\{t' > 0: \int_{-a}^bu_0dx > \int_0^{t'}(f+g)\,dt\}\) m≤ 0, \(0 \le f, g \in L_{loc}^{\infty}([0,\infty))\), \(0\le u_0\in L^{\infty}(a,b)\) and the case −1 < m ≤ 0, \(f, g \in L_{loc}^{\infty}([0,\infty))\), \(0 \le u_0 \in L^p(a,b)\) for some constant p > 1 − m. We also obtain a similar result in higher dimensions. As a corollary we will give a new proof of a result of A. Rodriguez and J.L. Vazquez on the existence of infinitely many finite mass solutions of the above equation in \(\mathbb{R} \times (0,T)\) for any −1 < m ≤ 0. We also obtain the exact decay rate of the solution at infinity.
Similar content being viewed by others

References
Anderson J.R. (1991). Local existence and uniqueness of solutions of degenerate parabolic equation. Comm. P.D.E. 16: 105–143
Aronson D.G. (1986). The porous medium equation, CIME Lectures, in Some problems in Nonlinear Diffusion, Lecture Notes in Mathematics 1224. Springer, New York
Aronson D.G., Bénilan P. (1979). Régularité des solutions de l’équation des milieux poreux dans R N. C. R. Acad. Sc. Paris, Série A, t. 288: 103–105
Dahlberg B.E.J., Kenig C. (1986). Non-negative solutions of generalized porous medium equations. Revista Matemática Iberoamericana 2: 267–305
Dahlberg B.E.J., Kenig C. (1988). Non-negative solutions to fast diffusions. Revista Matemática Iberoamericana 4: 11–29
Davis S.H., Dibenedetto E., Diller D.J. (1996). Some a priori estimates for a singular evolution equation arising in thin-film dynamics. SIAM J. Math. Anal. 27(3): 638–660
Dibenedetto, E., Diller, D.J.: About a singular parabolic equation arising in thin film dynamics and in the Ricci flow for complete \(\mathbb{R}^2\). In: Marcellini, P., Giorgio, G. Talenti, Vesentini, E. (eds.) Partial differential equations and applications, Lecture Notes in Pure and Applied Mathematics, vol. 177, pp. 103–119, Dekker, New York (1996)
Daskalopoulos P., Del Pino M.A. (1995). On a singular diffusion equation. Comm. Anal. Geometry 3(3): 523–542
Daskalopoulos P., Del Pino M.A. (1997). On nonlinear parabolic equations of very fast diffusion. Arch Rational Mech. Anal. 137: 363–380
Esteban J.R., Rodriguez A., Vazquez J.L. (1988). A nonlinear heat equation with singular diffusivity. Commun. P.D.E. 13(8): 985–1039
Evans L.C., Spruck J. (1991). Motion of level sets by mean curvature I. J. Differ. Geometry 33(3): 635–681
Evans L.C., Spruck J. (1992). Motion of level sets by mean curvature II. Trans. Amer. Math. Soc. 330(1): 321–332
Folland G.B. (1976). Introduction to partial differential equations, Mathematical notes series 17. Princeton University Press, Princeton
Giga Y., Goto S. (1992). Motion of hypersurfaces and geometric equations. J. Math. Soc. Jpn. 44: 99–111
Giga Y., Yamaguchi K. (1993). On a lower bound for the extinction time of surfaces moved by mean curvature. Cal. Var. 1: 413–428
Hsu S.Y. (2003). Asymptotic behaviour of solution of the equation u t = Δlog u near the extinction time. Adv. Differ. Eqn. 8(2): 161–187
Hsu S.Y. (2001). Global existence and uniqueness of solutions of the Ricci flow equation. Differ. Integral Eqn. 14(3): 305–320
Hsu S.Y. (2001). Large time behaviour of solutions of the Ricci flow equation on R 2. Pac. J. Math. 197(1): 25–41
Hsu S.Y. (2003). Uniqueness of solutions of a singular diffusion equation. Differ. Integral Eqn. 16(2): 181–200
Hsu S.Y. (2002). Dynamics near extinction time of a singular diffusion equation. Math. Annalen 323(2): 281–318
Hui, K.M.: Singular limit of solutions of the equation \(u_t=\Delta (\frac{u^m}{m})\) as m → 0. Pac. J. Math. 187(2), 297–316 (1999)
Hui K.M. (1999). Existence of solutions of the equation u t = Δlog u. Nonlinear Anal. TMA 37: 875–914
Hui K.M. (2001). Asymptotic behaviour of solutions of u t = Δlog u in a bounded domain. Differ. Integral Eqn. 14(2): 175–188
Hui, K.M.: Singular limit of solutions of the very fast diffusion equation (preprint)
Kato T. (1973). Schrödinger operators with singular potentials. Israel J. Math. 13: 135–148
Kurtz T.G. (1973). Convergence of sequences of semigroups of nonlinear operators with an application to gas kinetics. Trans. Amer. Math. Soc. 186: 259–272
Ladyzenskaya, O.A., Solonnikov, V.A., Uraltceva, N.N.: Linear and quasilinear equations of parabolic type Transl. Math. Mono. vol 23, Amer. Math. Soc. Providence, R.I. (1968)
Lions P.L., Toscani G. (1997). Diffusive limit for finite velocity Boltzmann kinetic models. Revista Matematica Iberoamericana 13(3): 473–513
Peletier, L.A.: The porous medium equation in applications of nonlinear analysis in the physical sciences. In: Amann, H., Bazley, N., Kirchgassner, K. (eds) Pitman, Boston (1981)
Rosen G. (1979). Nonlinear heat conduction in solid H 2. Phys. Rev. B 19: 2398–2399
Rodriguez A., Vazquez J.L. (1990). A well posed problem in singular Fickian diffusion. Arch Rational Mech. Anal. 110: 141–163
Soner H.M., Souganidis P.E. (1993). Singularities and uniqueness of cylindrically symmetric surfaces moving by mean curvature. Comm. P.D.E. 18: 859–894
Vazquez, J.L.: Nonexistence of solutions for nonlinear heat equations of fast-diffusion type. J. Math. Pures Appl. 503–526 (1992)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hui, K.M. Existence of solutions of the very fast diffusion equation in bounded and unbounded domain. Math. Ann. 339, 395–443 (2007). https://doi.org/10.1007/s00208-007-0119-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-007-0119-x