A Maximisation Technique for Solitary Waves: The Case of the Nonlocally Dispersive Whitham Equation

Abstract

Recently, two different proofs for large and intermediate-size solitary waves of the nonlocally dispersive Whitham equation have been presented, using either global bifurcation theory or the limit of waves of large period. We give here a different approach by maximising directly the dispersive part of the energy functional, while keeping the remaining nonlinear terms fixed with an Orlicz-space constraint. This method is, to the best of our knowledge new in the setting of water waves. The constructed solutions are bell-shaped in the sense that they are even, one-sided monotone, and attain their maximum at the origin. The method initially considers weaker solutions than in earlier works, and is not limited to small waves: a family of solutions is obtained, along which the dispersive energy is continuous and increasing. In general, our construction admits more than one solution for each energy level, and waves with the same energy level may have different heights. Although a transformation in the construction hinders us from concluding the family with an extreme wave, we give a quantitative proof that the set reaches ‘large’ or ‘intermediate-sized’ waves.

1 Introduction

We propose in this paper a new and somewhat different variational method towards solitary waves in dispersive equations. Solitary waves in nonlinear dispersive settings go back to the discoveries of John Scott Russell, Boussinesq, Lord Rayleigh and Korteweg-de Vries in the 1800s, but a rigorous theory emerged first with works such as Lavrentieff’s [21], Friedrich–Hyers’ [15] and Ter-Krikorov’s [33] in the mid twentieth century. Early on, limiting procedures for long but small waves, and perturbative expansions around flowing parallel streams were used. The small-amplitude theory was later extended by Beale using the Nash–Moser implicit function theorem [4], with which he established smooth parameter-dependence for all waves of small amplitude. Amick and Toland similarly extended the existence results from small to large amplitudes, yielding for the water-wave equations a full family of waves with increasing maximal slope all the way up to the wave of greatest height [1, 2]. Although variational formulations of the water wave problem existed much earlier, Turner seems to have been the first to develop a variational existence theory, simultaneously for periodic and solitary waves [36], based on joint work with Bona and Bose [7]. The latter two authors also gave a large-amplitude functional-analytic theory for solitary waves in nonlinear equations together with Benjamin [5]. At this time, Lions introduced the method of concentration-compactness [23], and Weinstein made use of it in his constructions of shallow-water solitary waves using constrained minimisation [37]. Trivial solutions of water-wave equations are generally global minimisers, so critical points are found as constrained minimisers or saddle points; a common construction has been $L^2$ or otherwise quadratically constrained minimisation in Sobolev spaces, see for example Buffoni [9], Groves–Wahlén [18] and Buffoni–Groves–Sun–Wahlén [10] on waves with surface tension, among other works.

For nonlinear equations with negative-order dispersion, such as the Whitham equation,

$$\begin{aligned} \eta _t + K*\eta _x+ \partial _x( \eta ^2) =0, \end{aligned}$$

(1.1)

with a convolution kernel K given by the Fourier symbol

$$\begin{aligned} m(\xi )=\left( \frac{\tanh (\xi )}{\xi }\right) ^{\frac{1}{2}}, \end{aligned}$$

(1.2)

solitary waves were first obtained in [11] by Ehrnström–Groves–Wahlén. That proof uses a combination of $L^2$-constrained variation, minimisation sequences built on perodic minimisers, and Lions’ concentration-compactness technique. The symbol (1.2) describes the linear dispersion of gravity surface waves in water of finite depth, and as made precise by Emerald [14], the equation can be shown to be in this sense slightly superior to KdV and other models of the same order in the small-amplitude long-wave regime. Different and modified perturbative proofs for small-amplitude solitary waves in (1.1) have since been suggested, for example by Stefanov–Wright [32], who used an implicit-function type theorem, and Hildrum [19], who also included more irregular nonlinearities. But it was first with Truong–Wahlén–Wheeler [35] and Ehrnström–Nik–Walker [12] that large solitary waves for the Whitham equation were found. The regularity theory for highest waves, including solitary such, had been established by Ehrnström–Wahlén in [13], and so had symmetry and decay by Bruell–Ehrnström–Pei in [8], but there were no proofs of large-amplitude existence in the solitary case.

The proof presented in the paper at hand should be viewed as an alternative construction, for the Whitham equation, and for dispersive model equations in general. It is inspired by a method by Stefanov–Kevrekidis on solitary waves in Hertzian and monomer chains from [30, 31], which we have adapted to the weakly dispersive case. Among the things that make the dispersive theory different, is that the linear operator and equation are of opposite character from [30, 31], and that the theory for ‘large’ solutions is unique to the dispersive case.

Returning to our problem, we shall be interested in travelling wave solutions $\eta (t,x)=\varphi (x- \mu t)$, so that $\lim _{|z|\rightarrow \infty } \varphi (z) =0$. This yields the nonlinear nonlocal equation

$$\begin{aligned} -\mu \varphi + K*\varphi +\varphi ^2 =0, \end{aligned}$$

(1.3)

where $\mu > 0$, and $\varphi$ will be called a steady Whitham solution if it satisfies (1.3) almost everywhere. If $\varphi$ is furthermore in $L^p({\mathbb R})$, for some $p \in [1,\infty )$, we shall call it a solitary wave. The idea behind our approach is the following: if the energy functional for a nonlinear equation is of the structural form

$$\begin{aligned} \int \varphi ^2 + \int \varphi L \varphi + \int N(\varphi ), \end{aligned}$$

with $L$ a linear dispersive operator and $N(\varphi )$ a primitive of the nonlinearity in the original equation, then critical points in a subspace of $L^2$ may be found through more than one form of constraint. Most commonly, the term $\int \varphi ^2$ is fixed while minimising the remaining part of the functional; this yields an energetic type of stability, as described by Mielke in the work [24]. But the nonlinear term $\int N(\varphi )$, too, could be taken as a constraint, see for example Arnesen [3] and Zeng [38]. We for our part shall keep the combination $\int \varphi ^2 + \int N(\varphi )$ fixed, while maximising the dispersive part $\int \varphi L \varphi$. This is made possible by working in an Orlicz space, which essentially equates the nonlinear function $\Psi (\varphi ) = \varphi ^2 + N(\varphi )$ with the function $|\varphi |^p$ in $L^p$-theory. For this to work, however, the above $\Psi$ will be cut off and extended at a point corresponding to the appearance of highest waves, which also coincides with the point where $\Psi$ seizes to be convex.

We suggest this method as a possible alternative to other existence methods for solitary dispersive waves. Its distinct features are: it is based on $L^p$-theory instead of Sobolev theory; it immediately provides bell-shapedness of constrained maximisers (they are even, positive and one-sided monotone); and it is not restricted to solutions of small sizes. In our particular case, we have not been able to prove that we reach the highest wave via this method, but this seems to be a difficulty related to uniqueness rather than a constraint of the maximisation method; and we establish that we reach at least medium-sized waves.

The paper starts in Section 2 with a walk-through of properties of the convolution kernel $K$, the functional, and Orlicz spaces. Some of these results are new, other are by alternative proofs. We introduce the symmetric rearrangement of a function, the Riesz convolution–rearrangement inequality, and the necessary prerequisites to prove that a maximiser of our functional solves the correct Euler–Lagrange equation.

Section 3 introduces the functional

$$\begin{aligned} {\mathcal {J}}(f) = \langle f, K*f\rangle ^\frac{1}{2}, \end{aligned}$$

with the constraint that $\int ( \alpha f^2-\frac{1}{3} f^3) \, \textrm{d}x= 1$ for $0\leqq f \leqq \alpha$ (and something else when $f > \alpha$). There is an intricate relationship between $\alpha$ and the wave speed $\mu$ (see Theorem 5.3), but eventually large values of $\alpha$ will correspond to small solutions in the original problem. Very small values of $\alpha$, on the other hand, will later be shown not to be solutions at all to the Whitham equation. This is brought about by the specific Orlicz function $\Psi$ introduced in (3.4), which extends the constraint of our functional outside the regime of that equation. Initially, for each fixed $\alpha >0$ we will be looking for solutions in $L^2 \cap L^3$.

By setting up a sequence of problems for $supp \ f\subset [-2^l, 2^l]$, we show that the maximum $J_l$ is approximately $\alpha ^{-1/2}$, with some sharper estimates given in Lemma 3.3. For each $l$ large enough, and $\alpha> \alpha _0 > 0$, we find a bell-shaped maximiser $f_l$ that satisfies the Euler–Lagrange equation

$$\begin{aligned} K* f_l(x)=\frac{J_l^2}{\left\langle f_l,\Psi '(f_l) \right\rangle } \Psi '(f_l(x)), \quad -2^l<x<2^l, \end{aligned}$$

and fulfils $f_l(0) < \alpha$ with a non-degenerate condition. This is Lemma 3.5. The hardest part of the paper is Proposition 3.6, a detailed rearrangement proof to show that maximisers are bounded from above by a value close to $\alpha$, a result that later gives us some control on the size of solutions. The proof is technical, though rudimentary in technique, and is based on moving parts of the mass of a possible maximiser with too large supremum to obtain a contradiction. The proof contains a Slobodeckij-type difference characterisation (3.28) of the quadratic form $\langle f, K*f\rangle$, itself equivalent to a squared $H^{-1/4}(\mathbb R)$-norm, that makes it possible to relate ‘flatness’ of $f$ to the functional ${\mathcal {J}}(f)$. Section 3 additionally covers the limit $l \rightarrow \infty$, which is achieved through weak convergence arguments and properties of the compactly supported maximisers. As in many other investigations considering long waves converging towards solitary solutions, the limit as $l \rightarrow \infty$ need not be unique.

Section 4 is about the dependence of maximisers upon the parameter $\alpha$. We prove that $\alpha \rightarrow \infty$ corresponds to the small-amplitude limit of the maximisers, while $\alpha \rightarrow 0$ gives maximisers that, as earlier mentioned, are outside the valid regime of the Euler–Lagrange—that is, the Whitham—equation. An estimate for the largest obtained waves is given. At the threshold value $\alpha = \alpha _0$, there is a solution satisfying $f(0) \geqq \alpha _0$, and another satisfying $g(0) \leqq \alpha _0$, but because of lack of uniqueness we cannot exclude that these are different, to reach the desired conclusion that in fact $f(0) = g(0) = \alpha _0$. That would correspond to a highest wave. A solution with $f(0)> \alpha _0$ would, on the other hand, correspond to a maximiser outside the valid regime.

Finally, we go back to the original equation through the somewhat implicit transformation $\varphi = \frac{J_{\alpha }^2 f_{\alpha }}{2-\frac{1}{3}\int f_{\alpha }^3 \, \textrm{d}x}.$ We find an injective curve of bell-shaped solutions parameterised by $\alpha \in [\alpha _0,\infty )$, with the function $\alpha \mapsto \alpha J_\alpha ^2 \in (1, {\textstyle \frac{3}{2}})$ strictly decreasing and continuous with unit limit as $\alpha \rightarrow \infty$. We give some $L^p$-estimates of these waves, and show that the small waves converge to the expected bifurcation point for solitary waves. The main result can be summarised as follows, with further details given in Theorem 5.3:

MainTheorem(abridged)

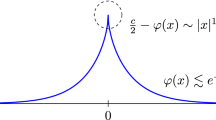
For any maximiser $f_\alpha$ satisfying $f_\alpha (0)\leqq \alpha$, there is a is a positive, even and one-sided strictly monotone solution $\varphi$ of the steady Whitham equation (1.3) with wave speed $\mu \in (1,2)$, satisfying $0 < \varphi \leqq \frac{\mu }{2}.$ The solutions are parameterized by $\alpha \in [\alpha _0,\infty )$, and the function

$$\begin{aligned}{}[\alpha _0,\infty ) \ni \alpha \mapsto \alpha J_\alpha ^2 \in \left( 1, {\textstyle \frac{3}{2}}\right) \end{aligned}$$

is strictly decreasing and continuous with the limit $1$ as $\alpha \rightarrow \infty$. For $\alpha >\alpha _0$ the waves satisfy $0<\varphi <\frac{\mu }{2}$ and are smooth, while for $\alpha = \alpha _0$ one has $\varphi (0)\leqq \frac{\mu }{2}$. The solutions scale as $\varphi \simeq \frac{f_\alpha }{\alpha },$ and vanish in $L^p({\mathbb R})$, for any $p \in [1, \infty ]$, as $\alpha \rightarrow \infty$.

2 Preliminaries

Throughout this paper, $\lesssim$, $\gtrsim$ and $\eqsim$ shall indicate (in)equalities that hold up to uniform positive factors. When the factors involved depend on some additional parameter or function, this will be indicated with subscripts such as $\gtrsim _\mu$. We shall call an element in $L^p(\mathbb R)$ bell-shaped if it lies in the closure of the set of even, continuous and positive functions which are decreasing on the positive half-axis. Then this element has a representative in its $L^p(\mathbb R)$ equivalence class that is continuous almost everywhere; and that is even, non-negative, and decreasing on the positive half-axis.

We furthermore define the Fourier transform ${\mathcal {F}}$ by

$$\begin{aligned} {\mathcal {F}}(f)(\xi ) =\int _{\mathbb R} f(x) e^{- i x\xi } \, \textrm{d}x, \qquad f \in S(\mathbb R), \end{aligned}$$

extended by duality from the Schwartz space $S(\mathbb R)$ of rapidly decaying smooth functions to $S^\prime (\mathbb R)$, the space of tempered distributions on $\mathbb R$. We shall write $\hat{f}$ interchangeably with ${\mathcal {F}}(f)$. The inverse of $\mathcal F$ with this normalisation is then given by $f(x)=\frac{1}{2\pi } \int _{\mathbb R} \hat{f}(\xi ) e^{ i x\xi } \, \textrm{d}\xi$.

2.1 The family of kernels $\{K_\alpha \}_\alpha$

The kernel $K$ in (1.1) arises from the linear dispersion relation in the free-boundary Euler equations [20], where its symbol $m(\xi )$ describes the dependence of wave speed of a travelling wave-train upon its frequency $\xi$. Since $m$ is real and even, the operator $L = K *$ has a well-defined square root given by ${\mathcal {F}} (\sqrt{L}f) = \sqrt{m(\cdot )} \mathcal {F} f$. More generally, every symbol

$$\begin{aligned} \widehat{K_\alpha }(\xi )=\left( \frac{\tanh (\xi )}{\xi }\right) ^{\alpha }, \qquad \alpha \in (0,1) \end{aligned}$$

(2.1)

gives rise to a corresponding operator $L_\alpha = K_\alpha *$, for which one has the following result:

Lemma 2.1

The kernel $K_\alpha$ in (2.1) satisfies the following properties:

• (i) $K_\alpha$ is smooth outside the origin, and rapidly decaying: for each fixed $\alpha \in (0,1)$ and $N \geqq 1$ one has

  $$\begin{aligned} K_\alpha (x)\lesssim x^{-N}, \qquad x>0. \end{aligned}$$

• (ii) $K_\alpha$ is bell-shaped, and strictly convex on $(0, \infty )$.

• (iii) $K_\alpha$ has unit operator norm: $\Vert K_\alpha \Vert _{L^1}=\int _{\mathbb R} K_\alpha (x) \, \textrm{d}x=\widehat{K_\alpha }(0)=1$.

• (iv) $K_\alpha$ belongs to $L^p(\mathbb R)$ exactly for $p<1/(1-\alpha )$. In particular, $K_{\frac{1}{4}}$ is in $L^{p}(\mathbb R)$ for any $1\leqq p<\frac{4}{3}$.

Remark 2.2

There are several approaches towards the properties of $K_\alpha$. We choose here to give an elementary and direct proof. A more subtle method yielding somewhat more information about the kernels can be found in [13]. The kernel $K_{\frac{1}{4}}$ is the square root of $K$, and as such appears in the symmetric form of the functional ${\mathcal {J}}$.

Proof

• (i) To prove the decay and smoothness of $K_\alpha$, we write

  $$\begin{aligned} \begin{aligned} K_\alpha (x)&= \frac{1}{2\pi } \int _{\mathbb R} \left( \frac{\tanh (\xi )}{\xi }\right) ^{\alpha } \varrho (\xi ) e^{ i x\xi } \, \textrm{d}\xi \\&\quad + \frac{1}{2\pi } \int _{\mathbb R} \left( \frac{\tanh (\xi )}{\xi }\right) ^{\alpha } (1-\varrho (\xi )) e^{ i x\xi } \, \textrm{d}\xi , \\&= K_\alpha ^1(x)+K_\alpha ^2(x), \end{aligned} \end{aligned}$$

  (2.2)

  where $\varrho \in C_0^\infty (\mathbb R)$ is even, supported in $(-\frac{1}{2},\frac{1}{2})$, and satisfies $\varrho (\xi )=1$ for $|\xi |<\frac{1}{4}$. Since the function $\xi \rightarrow \frac{\tanh (\xi )}{\xi }$ is smooth (in fact, real analytic) and strictly positive, we have that $\widehat{K_\alpha ^1}$ is a $C^\infty _0$-function, whence $K_\alpha ^1$ is a Schwartz function.

$K_\alpha ^2$ can be dealt with using integration by parts. Taking the form of the multiplier $m$ into account, one readily sees that

$$\begin{aligned} K_\alpha ^2(x)=x^{-l} \int _{\mathbb R} m_{l, \alpha }(\xi ) e^{ i x\xi } \, \textrm{d}\xi , \qquad x >0, \end{aligned}$$

(2.3)

where $m_{l, \alpha }$ is $C^\infty$ function with $|m_{l, \alpha }(\xi )|\lesssim _{l,\alpha } |\xi |^{-l-\alpha }$, $l$ being an arbitrary positive integer. This proves the super-polynomial decay rate for $K_\alpha$. Also, differentiating under the integral sign in (2.3) yields that $K_\alpha ^2$ is of class $C^{l-1}$ outside the origin. Since $l$ is arbitrary, we conclude that $K_\alpha$ is in fact smooth on the same domain.

• (ii) Note that the integral obtained by differentiating under the integral sign as in

  $$\begin{aligned} {{\,\textrm{D}\,}}_x K(x) = - \frac{2}{\pi } \int _0^\infty (\xi \tanh (\xi ))^{1/2} \sin (x\xi )\, \textrm{d}\xi , \end{aligned}$$

  is not well-defined. Thus, even a formal argument is hard to invoke for the one-sided monotonicity of $K$. To circumvent this difficulty, we consider instead of ${{\,\textrm{D}\,}}_x K_\alpha (x)$ the product $-x {{\,\textrm{D}\,}}_x K_\alpha (x)$. This is an element of $S^\prime$, and we show that its Fourier transform is positive definite. Hence, $x {{\,\textrm{D}\,}}_x K_\alpha (x) < 0$ for all $x \ne 0$ and all $\alpha \in (0,1]$. We carry out the calculation first for the Whitham kernel (the case $\alpha = \frac{1}{2}$). Relying on Bochner’s Theorem [6], we want to prove that

  $$\begin{aligned} {{\,\textrm{D}\,}}_\xi (\xi m(\xi )) = -{{\,\mathrm{{{\mathcal {F}}}}\,}}(x {{\,\textrm{D}\,}}_x K(x)) \end{aligned}$$

  is absolutely continuous; then $x {{\,\textrm{D}\,}}_x K(x) = - {{\,\mathrm{{{\mathcal {F}}}}\,}}^{-1} ( {{\,\textrm{D}\,}}_\xi (\xi m(\xi )))$ will be negative. Notice that ${{\,\textrm{D}\,}}_\xi (\xi m(\xi ))$ is even in $\xi$, so that it is enough to consider non-negative $\xi$ in the calculations to come. Now,

  $$\begin{aligned} {{\,\textrm{D}\,}}_\xi (\xi m(\xi ))&= \frac{1}{2} \frac{\xi }{\sqrt{\xi \tanh (\xi )}} \left( \frac{\tanh (\xi )}{\xi } + \frac{1}{\cosh ^2(\xi )}\right) \nonumber \\&= \frac{1}{2}m(\xi ) \left( 1 + \frac{\xi }{\tanh (\xi ) \cosh ^2(\xi )}\right) \nonumber \\&=\frac{1}{2}m(\xi )\left( 1 + \frac{2\xi }{\sinh (2\xi )}\right) , \end{aligned}$$

  (2.4)

  which is positive definite in view of that $[\xi \mapsto 1]$, $[\xi \mapsto \xi /\sinh (\xi )]$ and $m$ all are (for the latter facts, see [6]). For a general $\alpha \in (0,1)$, a calculation like (2.4) shows that

  $$\begin{aligned} {{\,\textrm{D}\,}}_{\xi } \left( \xi m(\xi ) \right) ^{2\alpha } = \left( m(\xi ) \right) ^{2\alpha } \left( 1- \alpha + \alpha \frac{2\xi }{\sinh (2\xi )}\right) , \end{aligned}$$

  which is positive definite for $0 \leqq \alpha \leqq 1$, in view of that $\xi /\sinh (\xi )$ and $1-\alpha$ are, and that $m$ is infinitely divisible, meaning that any positive power of it is positive definite. To prove the convexity of $K_\alpha$, one can use theory for Stieltjes and completely monotone functions [13]. In the case $\alpha \leqq \frac{1}{2}$, it is however possible with a more straightforward approach. As above, one calculates that

  $$\begin{aligned} \begin{aligned}&{{\,\mathrm{{{\mathcal {F}}}}\,}}\left( x^2 {{\,\textrm{D}\,}}_x^2 {{\,\mathrm{{{\mathcal {F}}}}\,}}^{-1}\left( m(\xi )^{2\alpha }\right) \right) \\&\quad = m(\xi )^{2\alpha } \bigg ( (1-\alpha )(2-\alpha ) + \frac{2\alpha (2-\alpha ) \xi }{\sinh (\xi ) \cosh (\xi )} + \frac{\alpha ^2 \xi ^2}{\sinh ^2(\xi )\cosh ^2(\xi )}\\&\qquad - \frac{\alpha \xi ^2}{\sinh ^2(\xi )} - \frac{\alpha \xi ^2}{\cosh ^2(\xi )} \bigg )\\&\quad = m(\xi )^{2\alpha } \bigg ( (1-\alpha )(2-\alpha )\\&\qquad + \frac{\alpha \xi }{\sinh (\xi )} \left( \frac{\alpha \xi }{\sinh (\xi )} \frac{1}{\cosh ^2(\xi )} + \frac{\nu }{\cosh (\xi )} - \frac{\xi }{\sinh (\xi )}\right) _1 \\&\qquad + \frac{\alpha }{\cosh (\xi )} \left( \frac{(4-2\alpha - \nu )\xi }{\sinh (\xi )} - \frac{\xi ^2}{\cosh (\xi )}\right) _2 \bigg ), \end{aligned} \end{aligned}$$

  (2.5)

where $\nu$ is an arbitrary real number. The Fourier transforms of all factors appearing in the outmost parenthesis are explicitly known [25, 34], and one can find a value $\nu$ such that the entire expression is positive definite.¹ Since $m(\xi )$ is infinitely divisible, the convexity of the kernel away from the origin is therefore guaranteed (in the case $\alpha \leqq 1/2$, one can see directly from the explicit Fourier transforms that the convexity is strict).

• (iii) The proof of this is directly given in the statement.

• (iv) We deduct the homogeneous part of $\hat{K}_\alpha$. Write

  $$\begin{aligned} \hat{K}_\alpha (\xi ) = \left( \frac{\tanh \xi }{\xi }\right) ^\alpha = \frac{1}{|\xi |^\alpha } + \frac{(\tanh |\xi |)^\alpha -1}{|\xi |^{\alpha }}, \end{aligned}$$

  which is valid since $\hat{K}_\alpha$ is even. Then

  $$\begin{aligned} K_\alpha (x) \eqsim \frac{1}{|x|^{1-\alpha }} + {{\,\mathrm{{{\mathcal {F}}}}\,}}\left( \frac{(\tanh |\xi |)^\alpha -1}{|\xi |^{\alpha }}\right) (x). \end{aligned}$$

  (2.6)

  The first part is clearly in $L^p_\text {loc}(\mathbb R)$ for $1 \leqq p < 1/(1-\alpha )$, and for no greater $p$. The second part is the Fourier transform of an $L^1$-function with exponential decay, and hence smooth by a version of Schwartz’s (Paley–Wiener) theorem [29]. Since, by (i), $K_\alpha$ has rapid decay, $K_\alpha \in L^{p}(\mathbb R)$ exactly when $p < 1/(1-\alpha )$.$\square$

As above, we shall use the convention that $K = K_{\frac{1}{2}}$. Recall that $L_\alpha$ is the operator with symbol $\hat{K}_\alpha$, defined for $\alpha \in (0,1)$.

Lemma 2.3

The operator $L_\alpha$ is an isomorphism $L^2(\mathbb R) \rightarrow H^\alpha (\mathbb R)$, with its inverse given by the symbol $\hat{K}_{-\alpha }$. For fixed $\alpha$ and $1 \leqq q\leqq p<\infty$ satisfying $\frac{1}{q}-\frac{1}{p}\leqq \alpha$, we have

$$\begin{aligned} \Vert K_\alpha *f\Vert _{L^p}\lesssim \Vert f\Vert _{L^q}, \end{aligned}$$

and for fixed $q>1/\alpha$,

$$\begin{aligned} \Vert K_\alpha *f\Vert _{L^\infty }\lesssim \Vert f\Vert _{L^q}. \end{aligned}$$

Proof

To see that $L_\alpha :L^2(\mathbb R) \rightarrow H^\alpha (\mathbb R)$ is an isomorphism, note that $\left( \frac{\xi }{\sqrt{1+\xi ^2}\tanh (\xi )}\right) ^{\alpha }$ is an isomorphism on $L^2$, since it is a positive and bounded function which is also bounded away from the origin.

The $L^q$–$L^p$-estimate is almost a direct consequence of Young’s inequality, which states that

$$\begin{aligned} \Vert f * g \Vert _{L^p} \leqq \Vert f \Vert _{L^q} \Vert g \Vert _{L^r}, \quad \text { when }\quad \frac{1}{r} + \frac{1}{q} = 1 + \frac{1}{p}, \end{aligned}$$

and $1 \leqq q,p,r \leqq \infty$. In view of that $K_\alpha \in L^r$ whenever $1/r \in (1-\alpha ,1]$, the statement follows for $\frac{1}{q}-\frac{1}{p}< \alpha$. The same argument for $p = \infty$ gives the continuity $L^q \rightarrow L^\infty$ of $L_\alpha$ whenever $q > 1/\alpha$. For the case $\frac{1}{q}-\frac{1}{p} = \alpha$, one must use the generalisation of Young’s inequality to the weak $L^{r, \infty }$-space, namely

$$\begin{aligned} \Vert K_a * f \Vert _{L^p} \leqq \Vert K_a \Vert _{L^{r, \infty }} \Vert f \Vert _{L^q}, \end{aligned}$$

which is valid for the same relation between $p$, $q$ and $r$ (although not for $p=\infty$ or $q=1$, see for example [16, Theorem 1.4.24]). Since $|x|^{\alpha -1} \in {L^{1/(\alpha -1), \infty }}$, it follows from the formula $K_\alpha (x) \eqsim |x|^{\alpha - 1} + \tilde{f}(x)$, $\tilde{f} \in C^\infty (\mathbb R)$, deduced in the proof of Lemma 2.1 (iv), and the decay of $K_\alpha$, that also $K_\alpha \in {L^{r,\infty }}$. This proves the continuity $L^q \rightarrow L^p$ of $L_\alpha$ for $\frac{1}{q}-\frac{1}{p} = \alpha$. $\square$

Lemma 2.4

$L_\alpha$ preserves bell-shapedness, and the maximum of $L_\alpha f$ for any non-constant bell-shaped function $f$ is attained only at the origin.

Proof

Recall that $L_\alpha$ acts by convolution with $K_\alpha$, which according to Lemma 2.1 is itself bell-shaped. The convolution of two even and positive functions is clearly even and positive, so it remains to show that $K_\alpha *f$ is decreasing on the positive half-axis if $f \in L^p(\mathbb R)$ is bell-shaped, where $p$ is some number in $[1,\infty ]$. Consider the difference

$$\begin{aligned}&K_\alpha *f(x + h) - K_\alpha *f(x)\\&\quad = \int _0^{\infty } \textstyle \left( K_\alpha (z+x+\frac{h}{2}) - K_\alpha (z-x-\frac{h}{2}) \right) \left( f(z - \frac{h}{2}) - f(z + \frac{h}{2}) \right) \, \textrm{d}z, \end{aligned}$$

where we have used the evenness of $K_\alpha$ and $f$ to rewrite the integral. For $x > 0$ and $0 < h \ll 1$ the factors in the integrand have differing signs, whence the first assertion follows.

To see that the maximum of $L_\alpha f$ is attained only at one point, fix $x_0 > 0$ and consider $g_{x_0}(y):=f(x_0+y)$. By in [22, Theorem 3.4], one has

$$\begin{aligned} K*f(x_0)= & {} \int K(y) f(x_0-y) \, \textrm{d}y=\int K(y) f(x_0+y) \, \textrm{d}y\\= & {} \int K(y) g_{x_0}(y) \, \textrm{d}y\leqq \int K^*(y) (g_{x_0})^*(y) \, \textrm{d}y= \int K(y) f(y) \, \textrm{d}y= K*f(0). \end{aligned}$$

where we have used that the decreasing rearrangement of a translate of a bell-shaped function coincides with the function itself:

$$\begin{aligned} (g_x)^*=(g_0)^*=f^*=f. \end{aligned}$$

Thus the function $x \mapsto K*f(x)$ achieves its maximum at $x=0$. Moreover, since K is strictly symmetric decreasing, equality is possible (again, according to [22, Theorem 3.4]) only when $g_{x_0}=g_{x_0}^*$. But that would imply $f(x_0+y)=f(y)$ for all y, meaning that $f$ is everywhere constant. $\square$

2.2 Orlicz spaces

The following subsection is a short introduction to Orlicz spaces. The reader will find here all the basic results used in this paper.

2.2.1 Distribution functions and convolution rearrangement inequalities

For a measurable function $f:\mathbb R\rightarrow \mathbb R$, let

$$\begin{aligned} d_f(\alpha ):=|\{x\in \mathbb R: |f(x)|>\alpha \}| \end{aligned}$$

be its distribution function. For every increasing $\varphi \in C^1(\mathbb R)$ with $\varphi (0) = 0$, one has (cf. [16, Eq. (1.1.7)]) the layer cake representation formula

$$\begin{aligned} \int _{\mathbb R} \varphi (|f(x)|) \, \textrm{d}x= \int _0^\infty \varphi '(\alpha ) d_f(\alpha )\,\textrm{d}\alpha . \end{aligned}$$

(2.7)

The non-increasing rearrangement, $f^*$, of the function f is the inverse function of $d_f$, provided that $\alpha \rightarrow d_f(\alpha )$ is strictly decreasing. In general, we define $f^*:\mathbb R_+\rightarrow \mathbb R_+$ by

$$\begin{aligned} f^*(t)=\inf \{s>0: d_f(s)\leqq t\}, \qquad t >0. \end{aligned}$$

Then $f^*$ is a non-increasing function, and one furthermore has that $d_{f^*}(\alpha )=d_f(\alpha )$. Let $f^\#(t)=f^*(2|t|)$, $t \in \mathbb R$. Then $f^\#$ provides us with a convenient way of characterizing bell-shapedness, namely, an $L^p$ function f is bell-shaped if and only if $f^\# =f$. For a general measurable function $f$, this property can instead be taken as a definition of bell-shapedness, the equality being required almost everywhere.

The function $f^\#$ is equidistributed with f, in the sense that $d_{f^\#}(\alpha )=d_f(\alpha )$ for all $\alpha >0$. Moreover,

$$\begin{aligned} {{\,\textrm{supp}\,}}\ f\subset [-L,L] \Longrightarrow {{\,\textrm{supp}\,}}\ f^\#\subset [-L,L]. \end{aligned}$$

(2.8)

Indeed, for $t>L$, we have

$$\begin{aligned} 0 \leqq f^*(2 t)&=\inf \{s>0: |\{x: |f(x)|>s\}|\leqq 2 t\}\\&\leqq \inf \{s>0: |\{x: |f(x)|>s\}|\leqq 2 L\} =0, \end{aligned}$$

since $|\{x: |f(x)|>s\}|\leqq |{{\,\textrm{supp}\,}}f|\leqq 2 L$ for any $s>0$. Thus, for $|t|>L$, we have $f^\#(t)=f^*(2t)=0$, hence ${{\,\textrm{supp}\,}}\ f^\#\subset [-L,L]$.

A result that will be essential to our investigation is the Riesz convolution–rearrangement inequality. This has later been generalized in several ways, see, for example, [26, 28]).

Lemma 2.5

(Riesz) Let $f$, $g$ and $h$ be measurable real functions with $\int _{\mathbb R^2} |f(y) g(x-y) h(x)| \, \textrm{d}x\, \textrm{d}y< \infty$. Then

$$\begin{aligned} \int _{\mathbb R^2}f(y) g(x-y) h(x) \, \textrm{d}x\, \textrm{d}y\leqq \int _{\mathbb R^2} f^\#(y) g^\#(x-y) h^\#(x) \, \textrm{d}x\, \textrm{d}y. \end{aligned}$$

(2.9)

2.2.2 Young’s functions

We mainly follow the exposition in the book of Rao and Ren [27], to which we refer the reader for further details.

We shall say that a function $\Psi : \mathbb R\rightarrow \mathbb R_+$ is a Young function, if it is even, convex, and satisfies $\Psi (0) = 0$, $\lim _{x\rightarrow \infty } \Psi (x)=\infty$. In the literature, a continuous Young function that satisfies

$$\begin{aligned} \Psi (x) = 0 \Longleftrightarrow x = 0, \qquad \lim _{x\rightarrow 0} \frac{\Psi (x)}{x}=0, \quad \text { and }\quad \lim _{x\rightarrow \infty } \frac{\Psi (x)}{x}=\infty , \end{aligned}$$

(2.10)

is sometimes called a nice Young function (or an N-function). We shall, however, only work with functions satisfying (2.10), and will therefore make these requirements also for Young functions.

2.2.3 Orlicz spaces

Orlicz spaces are function spaces built on a Young function $\Psi$. More specifically, for a Borel measure²$\mu$ on ${\mathbb R}$, consider

$$\begin{aligned} {\mathcal {L}}^\Psi = \{f:{\mathbb R}\rightarrow {\mathbb R}: \int _{{\mathbb R}} \Psi (\alpha f(x)) \,\textrm{d}\mu (x)<\infty \ \ for some \ \ \alpha >0\}. \end{aligned}$$

(2.11)

Identifying $\alpha$ with $1/\lambda$, one may define a norm via the so-called Minkowski gauge functional,

$$\begin{aligned} N_\Psi (f)=\inf \{\lambda >0: \int _{{\mathbb R}} \Psi \left( \frac{f(x)}{\lambda }\right) \,\textrm{d}\mu (x)\leqq 1\}. \end{aligned}$$

(2.12)

With this definition the pair $({\mathcal {L}}^\Psi , N_\Psi )$ becomes a Banach space, called the Orlicz space for $\Psi$. Note that the Orlicz norm is a lattice norm. Here, a Banach space X is called a lattice if it has a partial ordering (in this case induced by the almost everywhere pointwise $\max$ and $\min$ of any two functions and the $\leqq$ ordering), and the inequality $|f| \leqq |g|$ implies that $\Vert f\Vert _X\leqq \Vert g\Vert _X$.

The norm $N_\Psi$ is usually referred to as the gauge norm. A Young function $\Psi$ is said to satisfy a global $\Delta _2$-condition ($\Psi \in \Delta _2$, for short) if one has

$$\begin{aligned} \Psi (2x)\lesssim \Psi (x). \end{aligned}$$

(2.13)

for all $x\geqq 0$. In the case when $\Psi$ is strictly increasing, continuous and satisfies a $\Delta _2$-condition, one may alternatively take

$$\begin{aligned} \int _{{\mathbb R}} \Psi \left( \frac{f(x)}{N_\Psi (f)}\right) \, \textrm{d}x= 1 \end{aligned}$$

(2.14)

as a definition of the gauge norm $N_\Psi$. The next result is adapted from [27, p. 280] and shows that under additional regularity assumptions on the Young function $\Psi$, the gauge norm has directional derivatives.

Lemma 2.6

[27] Let $\Psi$ be a differentiable and strictly convex Young function with a strictly positive derivative on the positive half-axis. Then $N_{\Psi }(\cdot )$ is Gateaux differentiable, with derivative

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\varepsilon } N_{\Psi }(f_0+\varepsilon h)|_{\varepsilon =0} =\frac{\left\langle h,\Psi '(f_0) \right\rangle }{\left\langle f_0,\Psi '(f_0) \right\rangle }, \end{aligned}$$

whenever $N_{\Psi }(f_0)=1$.

The next lemma relates the gauge norm to the distribution function. We shall make use of this in our construction of bell-shaped solutions.

Lemma 2.7

Let $\Psi$ be a $C^1$-Young function, strictly convex Young function with a strictly positive derivative on the positive half-axis, which in addition satisfies the $\Delta _2$ condition. Let $f\in {\mathcal {L}}^\Psi$. Then

$$\begin{aligned} N_{\Psi }(f)=N_{\Psi }(f^*)=N_{\Psi }(f^\#). \end{aligned}$$

In particular, $f^*$ and $f^\#$ both belong to ${\mathcal {L}}^\Psi$.

Proof

By rescaling, we can assume that $N_{\Psi }(f)=1$, so that $\int _{\mathbb R} \Psi (|f(x)|) \, \textrm{d}x=1$. We need to show that $N_{\Psi }(f^*)=N_{\Psi }(f^\#)=1$. According to (2.7) and the fact that $d_{f^*}(\alpha )=d_{f^\#}(\alpha )=d_{f}(\alpha )$, we have that

$$\begin{aligned} 1=\int _{\mathbb R} \Psi (|f(x)|) \, \textrm{d}x&= \int _0^\infty \Psi '(\alpha ) d_f(\alpha ) \,\textrm{d}\alpha \\&= \int _0^\infty \Psi '(\alpha ) d_{f^\#}(\alpha ) \,\textrm{d}\alpha = \int _{\mathbb R} \Psi (f^\#(t)) \,\textrm{d}t. \end{aligned}$$

It follows that $N_{\Psi }(f^\#)=1$. The argument for $N_{\Psi }(f^*)=1$ is analogous. $\square$

3 The Variational Problem

In order to construct a solution to (1.3), one naturally considers a constrained optimization problem connected to it. Formally, if $f$ is a maximiser of

$$\begin{aligned} {\mathcal {J}}(f) = \left\| K_{\frac{1}{4}}*f\right\| _{L^2} \end{aligned}$$

(3.1)

under the constraint that

$$\begin{aligned} {\mathcal {I}}(f) = \int \left( f^2(x) - {\textstyle \frac{1}{3}} f^3(x) \right) \, \textrm{d}x=1, \end{aligned}$$

(3.2)

one obtains a solitary solution of the steady Whitham equation (1.3) by a rescaling argument (the wave speed arises from a Lagrange multiplier principle). The above problem, however, is not well-posed, since there is no finite supremum of (3.1) over functions fulfilling (3.2). One way to see this is by taking a dilated and scaled characteristic function $\chi _N(x)=\chi (x/N)$, where $\chi (x)=3$ for $|x|<1$, and vanishes elsewhere, so that ${\mathcal {I}}(\chi _N) = 0$. Adding a Schwartz function $\phi _N(x):=\phi (\cdot -N)$, where $\phi$ is supported in (0, 1), and fulfilling ${\mathcal {I}}(\phi _N) = {\mathcal {I}}(\phi )=1$, the sum fulfills the constraint ${\mathcal {I}}(\chi _N + \phi _N) = 1$. The quadratic energy ${\mathcal {J}}(\chi _N + \phi _N)$ on the other hand scales like $\sqrt{N}$, as the dilation in $\chi _N$ contributes $N$ to the functional, but the translation in $\phi _N$ results only in a phase-shift. Therefore,

$$\begin{aligned} {\mathcal {J}}(\chi _N + \phi _N)^2 = \left\| K_{\frac{1}{4}}*\chi _N\right\| ^2+\left\langle K_{\frac{1}{4}}*\chi _N,K_{\frac{1}{4}}*\phi _N \right\rangle +\left\| K_{\frac{1}{4}}*\phi _N\right\| ^2 \end{aligned}$$

for large $N$ is dominated by

$$\begin{aligned} \Vert K_{\frac{1}{4}}*\chi (\cdot /N)\Vert ^2 \eqsim \int _{{\mathbb R}} \left| \frac{\tanh (\xi )}{\xi }\right| ^{\frac{1}{2}} \frac{\sin ^2(N\xi )}{\xi ^2}\textrm{d}\xi \eqsim N, \end{aligned}$$

where we have used Plancherel’s theorem and $\widehat{\chi _N}=N \widehat{\chi }(N\xi )=6\frac{\sin (N\xi )}{\xi }$.

One way to remedy this is to consider functions that additionally satisfies

$$\begin{aligned} \sup f \leqq 1. \end{aligned}$$

(3.3)

As we shall show, the resulting problem is solvable and yields a fairly rich family of solutions of the Whitham equation. Technically, though, (3.2) poses challenges as it does not describe a function space. One way of dealing with this problem is to work in a ball in a regular Sobolev space $H^s(\mathbb R)$, for which both (3.2) and (3.3) may be fulfilled. Variants of this approach have been used in [11, 17] and other investigations, and yields small-amplitude solutions of the original problem.

3.1 The Orlicz space of constraints

Our approach does not per se rely on smallness. As is often done, we deal with the loss of compactness on $\mathbb R$ by considering a sequence of problems on increasing intervals. To handle (3.2) and (3.3), we enlarge the set of functions allowed for by considering the Orlicz function

$$\begin{aligned} \Psi (f)= {\left\{ \begin{array}{ll} \alpha f^2-\frac{1}{3} f^3, \qquad &{} 0\leqq f < \alpha , \\ \frac{2}{3} \alpha ^3 + \alpha ^2 (f-\alpha )+ (f-\alpha )^3, \qquad \quad &{} f \geqq \alpha , \end{array}\right. } \end{aligned}$$

(3.4)

for fixed and positive values of $\alpha > 0$. By varying $\alpha >0$, we obtain a non-trivial family of waves, and we show that the relevant waves exist in an interval of the form $\alpha \in [\alpha _0, \infty )$, with $\alpha _0$ to be appropriately defined later. Generally speaking, small waves of the Whitham equation (1.3) correspond to maximisers with large $\alpha$ and vice versa.

Lemma 3.1

The function $\Psi$ defined by (3.4) is a strictly convex, strictly increasing, $C^2$-Young function for which (2.14) defines a norm. For any fixed value of $\alpha > 0$, the corresponding Orlicz space $\mathcal {L}^{\Psi }$ satisfies

$$\begin{aligned} \mathcal {L}^{\Psi } \cong L^2(\mathbb R) \cap L^3(\mathbb R), \end{aligned}$$

in the sense that

$$\begin{aligned} N_{\Psi }(f) \eqsim \max ( \Vert f\Vert _{L^2}, \Vert f\Vert _{L^3} ). \end{aligned}$$

(3.5)

The estimates $\Vert f\Vert _{L^2(\mathbb R)} \lesssim \frac{1}{\sqrt{\alpha }} N_\Psi (f)$ and $\Vert f\Vert _{L^3(\mathbb R)} \lesssim N_\Psi (f)$ are furthermore uniform in $\alpha >0$.

Proof

The function $\Psi$ is of class $C^2$ by construction, with $\Psi ^\prime (f) > 0$ for $f > 0$ and $\Psi ^{\prime \prime }(f) > 0$ for all $f \ne \pm \alpha$. Hence, $\Psi$ is strictly increasing and convex in the sense of a Young function. To see that it is indeed Young, note that (2.10) trivially holds. Similarly, the $\Delta _2$-condition (2.13) can be easily checked. Then (2.11) defines an Orlicz space with norm given, equivalently, by (2.12) and (2.14).

To prove that this Orlicz space is, for given $\alpha > 0$, isomorphic to $L^2(\mathbb R) \cap L^3(\mathbb R)$ in the above sense, pick first $f$ with $N_{\Psi }(f)=1$. Then $1 = \int _\mathbb R\Psi (f) \, \textrm{d}x$. For $0 \leqq f \leqq \alpha$ we have that $\frac{2 \alpha }{3} f^2 \leqq \alpha f^2 - \frac{1}{3}f^3 \leqq \alpha f^2,$ and for $f > \alpha$ that $\frac{2 \alpha ^3}{3} + (f-\alpha )^3 \leqq \frac{2 \alpha ^3}{3} + \alpha ^2(f-\alpha ) + (f-\alpha )^3 \leqq 3 f^3.$ A simple consideration of $f \gtrless 2\alpha$ shows that the left-hand side is uniformly bounded from below by $\frac{1}{12} f^3$. Combining these estimates we obtain

$$\begin{aligned} \int (\alpha f^2 + f^3) \, \textrm{d}x\lesssim N_{\Psi }(f) \lesssim \int (\alpha f^2 + f^3) \, \textrm{d}x, \end{aligned}$$

uniformly in $\alpha > 0$ for $N_{\Psi }(f) = 1$. Since for such $f$ one has $(N_{\Psi }(f))^p = 1$ for all $p$, a rescaling argument yields (3.5). $\square$

Relative to $\Psi$, we now consider the problem of maximising ${\mathcal {J}}(f)$ under the constraint that

$$\begin{aligned} N_{\Psi }(f)=1, \end{aligned}$$

(3.6)

for a given positive value of $\alpha$. Note that by scaling, the maximisers of  (3.1), if any, under the constraint (3.6) are the same if one enlarges the constraint to include the whole closed ball $\{N_\Psi (f)\leqq 1\}$ in $\mathcal {L}^\Psi$. To handle compactness, we consider first local versions of this maximisation problem.

3.2 A family of local problems

For the purpose of obtaining a convergent subsequence, we consider functions f supported on an interval $[-2^l, 2^l]$, $l \in \mathbb N$. More precisely, in this section we find functions $f = f_l$ that realize the maximum of ${\mathcal {J}}(f)$ under the constraint that $N_{\Psi }(f)=1$, and that additionally satisfy

$$\begin{aligned} supp \ f\subset [-2^l, 2^l]. \end{aligned}$$

(3.7)

The value of the parameter $\alpha > 0$ will for now be held constant. Define

$$\begin{aligned} J = \sup _{N_{\Psi }(f)=1} \Vert K_{\frac{1}{4}}*f\Vert _{L^2}, \end{aligned}$$

so that $J = \max {\mathcal {J}}$ under the constraint $N_{\Psi }(f)=1$ when a maximiser exists, and similarly

$$\begin{aligned} J_l = \sup \limits _{\begin{array}{c} N_{\Psi }(f)=1 \\ {{\,\textrm{supp}\,}}f\subset [-2^l, 2^l] \end{array}} \Vert K_{\frac{1}{4}}*f\Vert _{L^2}, \qquad l \in \mathbb N. \end{aligned}$$

(3.8)

Both $J$ and $J_l$ depend on $\alpha$.

Lemma 3.2

For any fixed value of $\alpha$, one has

$$\begin{aligned} \lim _{l\rightarrow \infty } J_l = J \lesssim \frac{1}{\sqrt{\alpha }}, \end{aligned}$$

(3.9)

where the latter bound is uniform in $\alpha$.

Proof

We already know that $J_{l}\leqq J$. From Hausdorff–Young’s inequality and Lemma 3.1,

$$\begin{aligned} \Vert K_{\frac{1}{4}}*f\Vert _{L^2}\leqq \Vert K_{\frac{1}{4}}\Vert _{L^1} \Vert f\Vert _{L^2}\lesssim \alpha ^{-1/2} N_{\Psi }(f) = \alpha ^{-1/2}, \end{aligned}$$

whenever f satisfies the constraint. Thus, $J \lesssim \alpha ^{-1/2}$, uniformly in $\alpha$.

Also, it is clear from the definition that $\{J_{l}\}_l$ is an increasing sequence. We will now show that (3.9) holds. Indeed, let $\varepsilon >0$. Then there exists $f^\varepsilon$ with $N_\Psi (f^\varepsilon )=1$ such that

$$\begin{aligned} \Vert K_{\frac{1}{4}}*f^\varepsilon \Vert _{L^2}>J-\varepsilon . \end{aligned}$$

For this function $f^\varepsilon \in {\mathcal {L}}^{\Psi }\hookrightarrow L^2$ there is also an l so that $\Vert f^\varepsilon \chi _{|x|>2^l}\Vert _{L^2}<\varepsilon$. Note that since ${\mathcal {L}}^\Psi$ is a lattice, then $N_\Psi (f^\varepsilon \chi _{|x|<2^l})\leqq 1$. Thus,

$$\begin{aligned} J_l&\geqq \Vert K_{\frac{1}{4}}*(f^\varepsilon \chi _{|x|<2^l})\Vert _{L^2} \geqq \Vert K_{\frac{1}{4}}*f^\varepsilon \Vert _{L^2}- \Vert K_{\frac{1}{4}}*(f^\varepsilon \chi _{|x|>2^l}) \Vert _{L^2}\\&\geqq J - 2\varepsilon , \end{aligned}$$

where in the last inequality, we have estimated

$$\begin{aligned} \Vert K_{\frac{1}{4}}* (f^\varepsilon \chi _{|x|>2^l} ) \Vert _{L^2}\leqq \Vert K_{\frac{1}{4}}\Vert _{L^1} \Vert f^\varepsilon \chi _{|x|>2^l}\Vert _{L^2}\leqq \varepsilon . \end{aligned}$$

Thus (3.9) holds. $\square$

Our next lemma establishes a lower bound on J, consistent with the estimate $J \lesssim \alpha ^{-1/2}$ from Lemma 3.2. Most of the time, we shall just need a simple corollary of the below result, namely that $J \geqq \alpha ^{-1/2}.$

Lemma 3.3

There exists an absolute and positive constant $c_0$ such that

$$\begin{aligned} J_l \geqq \frac{1}{\sqrt{\alpha }} \left( 1+\frac{c_0}{1 +\alpha ^2}\right) \end{aligned}$$

(3.10)

for all $\alpha >0$ and all $l \gtrsim |\log (\alpha )|$. In particular, $J - \frac{1}{\sqrt{\alpha }}$ is positive for any fixed $\alpha$.

Proof

The exists a positive constant $c >0$ such that $(\frac{\tanh (\xi )}{\xi })^{1/2} \geqq 1 - c \xi ^2$, for all $\xi \in \mathbb R$. Hence,

$$\begin{aligned} \int \left( \frac{\tanh (\xi )}{\xi }\right) ^{1/2} |\hat{f}(\xi )|^2 \, \textrm{d}\xi&\geqq \int |\hat{f}(\xi )|^2 \, \textrm{d}\xi - c \int | \xi \hat{f}(\xi )|^2 \, \textrm{d}\xi , \end{aligned}$$

with $c$ independent of $f$. Letting ${{\,\textrm{supp}\,}}(f) \subset [-2^l,2^l]$ we obtain the lower estimate

$$\begin{aligned} J_l^2&\geqq \Vert f\Vert _{L^2}^2 - c \Vert f'\Vert _{L^2}^2 = {\textstyle \frac{1}{\alpha }} \left( 1 + {\textstyle \frac{1}{3}} \Vert f\Vert _{L^3}^3 \right) - c \Vert f'\Vert _{L^2}^2, \end{aligned}$$

(3.11)

for any function $f \leqq \alpha$ satisfying the constraint $N_\Psi (f) = 1$. To eliminate the $\alpha$-dependence in $\int \Psi (f) \, \textrm{d}x= 1$, introduce a smooth test function $q$ with ${{\,\textrm{supp}\,}}(q) \subset [-1,1]$, $0 \leqq q \leqq 1$, and consider

$$\begin{aligned} f(x) = \alpha q(\alpha ^3 x). \end{aligned}$$

Then $N_\Psi (f) = 1$ if and only if $\int q^2(x) - \frac{1}{3} q^3(x) \, \textrm{d}x= 1$, and it is evident that we can find $q$ satisfying this additional assumption. Replacing $f$ in (3.11) by $f = \alpha q(\alpha ^3 \cdot )$, we find that

$$\begin{aligned} J_l^2 \geqq {\textstyle \frac{1}{\alpha }} \left( 1 + {\textstyle \frac{1}{3}} \Vert q\Vert _{L^3}^3 \right) - c \alpha ^5 \Vert q'\Vert _{L^2}^2, \end{aligned}$$

(3.12)

provided that $\alpha ^3 2^l \geqq 1$, to satisfy the constraint that ${{\,\textrm{supp}\,}}(f) \subset [-2^l,2^l]$. Thus, there exists a positive constant $c_0$ such that $J_l^2 \geqq {\textstyle \frac{1}{\alpha }} \left( 1 + c_0 \right)$ whenever $2^{-l/3} \leqq \alpha \leqq \alpha _0$, where $\alpha _0$ is independent of $l$.

For the general case of $\alpha \in (0,\infty )$, introduce the additional scaling

$$\begin{aligned} \tilde{q}(x) = \mu q(\mu ^2 \eta x), \end{aligned}$$

where $\mu \ll 1$ is small parameter, and $\eta$ is to satisfy the constraint $N_\Psi (f) = 1$. Indeed, if we let $\eta = \Vert q\Vert _{L^2}^2 - \frac{\mu }{3}\Vert q\Vert _{L^3}^3$, then

$$\begin{aligned} \int \tilde{q}^2(x) - \frac{1}{3} \tilde{q}^3(x)\, \textrm{d}x&= \int \left( \mu q(\mu ^2 \eta x)\right) ^2 - \frac{1}{3}\left( \mu q(\mu ^2 \eta x)\right) ^3\, \textrm{d}x\\&= \frac{1}{\eta } \int ( q^2(x) - \frac{\mu }{3} q^3(x) )\, \textrm{d}x= 1. \end{aligned}$$

The function $f(x) = \alpha \tilde{q}( \alpha ^3 x)$ has support in $[-2^l,2^l]$ if

$$\begin{aligned} \alpha ^3 \mu ^2 \eta 2^l \geqq \alpha ^3 \mu ^2 (1- {\textstyle \frac{\mu }{3}}) \Vert q\Vert _{L^2}^2 2^l \geqq 1. \end{aligned}$$

On the other hand, (3.11) now becomes

$$\begin{aligned} J_l^2&\geqq {\textstyle \frac{1}{\alpha }} \left( 1 + {\textstyle \frac{\mu }{3 \eta }} \Vert q\Vert _{L^3}^3 \right) - c {\textstyle \frac{\mu ^4 \alpha ^5}{\eta }} \Vert q'\Vert _{L^2}^2, \end{aligned}$$

with $\eta \eqsim 1$. Here, the $\mu$-scaling in $\tilde{q}$ brings about a factor $\mu ^6$ from $(\tilde{q}')^2 = \mu ^6 q^2(\mu ^2 \cdot )$, and a factor $\mu ^{-2}$ from the change of variables from $\tilde{q}$ to $q$ in the $L^2$-integral, yielding the final $\mu ^4 \alpha ^5$ (the $\alpha ^5$ is the same as in (3.12), and $\eta \eqsim 1$). Choosing $\mu = \frac{\varepsilon }{1+ \alpha ^{2}}$ for a small enough $\varepsilon \ll 1$, then yields

$$\begin{aligned} J_l^2 \geqq \frac{1}{\alpha }+ \frac{\varepsilon }{\alpha (1+\alpha ^2)\eta } \left[ \frac{\Vert q\Vert _{L^3}^3}{3} - \frac{c \varepsilon ^3 \alpha ^6}{(1+\alpha ^2)^3} \Vert q'\Vert _{L^2}^2 \right] \geqq \frac{1}{\alpha } \left( 1 + \frac{c_0}{1 + \alpha ^2}\right) , \end{aligned}$$

whenever $l \gtrsim |\log (\alpha )|$. This lower bound on $J_l$ is uniform in $\alpha$ because of how $f \leqq \alpha$ was constructed. Finally, as $J \geqq J_l$ by definition, the same bound is valid for $J$, independently of $l$. $\square$

Lemma 3.4

For each $l\geqq 0$ there exists a bell-shaped maximiser $f_l$ of the local maximisation problem fulfilling (3.8).

Proof

We start first with an argument that shows that any function f is at best no better than its rearrangement $f^\#$, as far as the local constrained maximisation problem is concerned. Indeed, let $f\in {\mathcal {L}}^\Psi$ satisfy $N_\Psi (f)=1$ with ${{\,\textrm{supp}\,}}(f) \subset [-2^l, 2^l]$. By Lemma 2.7, we then have that $N_\Psi (f^\#) =N_\Psi (f) =1$. Moreover, due to the bell-shapedness of $K_{\frac{1}{4}}$, and in view of Riesz’s convolution–rearrangement inequality (2.9), we have that for all Schwartz functions g,

$$\begin{aligned} \iint _{\mathbb R^2} K_{\frac{1}{4}}(x-y) f(y) g(x) \, \textrm{d}x\, \textrm{d}y\leqq \iint _{\mathbb R^2} K_{\frac{1}{4}}(x-y) f^\#(y) g^\#(x) \, \textrm{d}x\, \textrm{d}y. \end{aligned}$$

(3.13)

Taking the supremum in (3.13) over all functions $g$ such that $\Vert g\Vert _{L^2}=1$, we obtain

$$\begin{aligned} \Vert K_{\frac{1}{4}}*f\Vert _{L^2}\leqq \Vert K_{\frac{1}{4}}*f^\#\Vert _{L^2}, \end{aligned}$$

in view of that for such $g$ one also has $\Vert g^\#\Vert _{L^2}=1$. The supremum in (3.8) may thus be considered with respect to only bell-shaped functions. The eventual maximiser will then be bell-shaped as well.

We now prove that there is a maximiser of (3.8) in the subspace of bell-shaped functions. To that aim, let $\{f_n\}_n$ be a maximising sequence, that is, a sequence of bell-shaped functions with $N_\Psi (f_n)=1$, ${{\,\textrm{supp}\,}}(f_n) \subset [-2^l, 2^l]$, and $\Vert K_{\frac{1}{4}}*f_n\Vert _{L^2}\rightarrow J_l$ as $n \rightarrow \infty$. By weak compactness, and up to passing to a subsequence, we may assume that

$$\begin{aligned} f_n \rightharpoonup f_0 \qquad \text { weakly in }\qquad {\mathcal {L}}^\Psi . \end{aligned}$$

Note that $f_0$ is bell-shaped (which can be seen by testing against characteristic functions) and, by the lower semicontinuity of the norm,

$$\begin{aligned} N_\Psi ( f_0) \leqq \liminf _{n \rightarrow \infty } N_\Psi (f_n)=1. \end{aligned}$$

(3.14)

Let $g_n=K_{\frac{1}{4}}*f_n$. Then $g_n \in H^{1/4}(\mathbb R)$ by Lemma 2.3 and, in fact, $\Vert g_n\Vert _{H^{1/4}} \eqsim \Vert f_n\Vert _{L^2}\lesssim \alpha ^{-1/2}N_\Psi (f_n)=\alpha ^{-1/2}$. By weak compactness, it again follows that there is a function $g_0 \in H^{1/4}(\mathbb R)$ such that $g_n \rightharpoonup g_0$. By uniqueness of weak limits, $g_0=K_{\frac{1}{4}}*f_0$. In addition, from the integral representation of $g_n$ and the decay of $K_{\frac{1}{4}}$ proved in Lemma 2.1, for all $|x|>2^{l+1}$ one has

$$\begin{aligned} 0 <g_n(x)&=\int _{-2^l}^{2^l} K_{\frac{1}{4}}(x-y) f_n(y) \, \textrm{d}y\lesssim _N |x|^{-N} \int _{-2^l}^{2^l} f_n(y) \, \textrm{d}y\lesssim _N 2^{\frac{l}{2}} |x|^{-N}, \end{aligned}$$

where $N \geqq 1$ is arbitrary. It follows that $\{g_n\}_n$ is a compact sequence in $L^2(\mathbb R)$ and hence has a convergent subsequence $\{g_{n_m}\}_m$, that, by uniqueness of limits, converges to $g_0$. In effect,

$$\begin{aligned} \Vert K_{\frac{1}{4}}*f_0\Vert _{L^2}=\Vert g_0\Vert _{L^2}=\lim _{m \rightarrow \infty } \Vert g_{n_m}\Vert _{L^2}=J_l. \end{aligned}$$

By (3.14) we have $N_\Psi (f_0)\leqq 1$; a strict inequality would contradict the definition of $J_l$ and we conclude that $N_\Psi (f_0)=1$, and $f_0$ is the bell-shaped maximiser sought for. $\square$

Now that we have established the existence of maximisers of the local problem (3.8), let us proceed to derive the corresponding Euler–Lagrange equation.

Lemma 3.5

Every maximiser $f_l$ realizing (3.8) satisfies the Euler–Lagrange equation

$$\begin{aligned} K* f_l(x)=\frac{J_l^2}{\left\langle f_l,\Psi '(f_l) \right\rangle } \Psi '(f_l(x)), \quad -2^l<x<2^l. \end{aligned}$$

(3.15)

In addition, $f_l$ is non-degenerate in $L^2$ and $L^3$; there is a constant $c_0>0$ such that

$$\begin{aligned} \Vert f_l\Vert _{L^3}^3\geqq 3\frac{c_0}{1+\alpha ^2}. \end{aligned}$$

(3.16)

Also, the estimate

$$\begin{aligned} 0<f_l(x)\lesssim \alpha , \quad -2^l<x<2^l, \end{aligned}$$

(3.17)

holds uniformly for $\alpha >0$, and there exists $\alpha _0$ such that

$$\begin{aligned} f_{l}(0)< \alpha , \end{aligned}$$

for all $\alpha >\alpha _0$. These estimates hold uniformly for $l\gtrsim |\log (\alpha )|$.

Proof

It is straightforward to show that for any non-negative function f, we have $f\Psi '(f)\simeq \Psi (f)$ (see also Lemma 3.7 below) and hence

$$\begin{aligned} \left\langle f_l,\Psi '(f_l) \right\rangle \eqsim \int \Psi (f_l(x)) \, \textrm{d}x=1, \end{aligned}$$

uniformly in $\alpha >0$ and $l\gtrsim |\log (\alpha )|$, whence the denominator in (3.15) is bounded away from zero. By Lemma 2.6, the Gateaux derivative of the function $N_{\Psi }(\cdot )$ when $N_{\Psi }(f_l)=1$ may be determined as

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}\varepsilon } N_{\Psi }(f_l+\varepsilon h)|_{\varepsilon =0}=\frac{\left\langle h,\Psi '(f_l) \right\rangle }{\left\langle f_l,\Psi '(f_l) \right\rangle }. \end{aligned}$$

Since $f_l$ is a constrained maximiser, we have

$$\begin{aligned} \Vert K_{\frac{1}{4}}*(f_l+\varepsilon h)\Vert _{L^2}^2\leqq J_l^2 N_{\Psi }(f_l+\varepsilon h)^2, \end{aligned}$$

for every $L^2$-function h with ${{\,\textrm{supp}\,}}\ h\subset [-2^l,2^l]$. Expanding in $\varepsilon$, we obtain

$$\begin{aligned} 2\varepsilon \left\langle K*f_l-\frac{J_l^2}{\left\langle f_l,\Psi '(f_l) \right\rangle } \Psi '(f_l), h \right\rangle +o(\varepsilon )\leqq 0. \end{aligned}$$

In view of that $h$ is free to vary only on the interval $[-2^l,2^l]$, we have established (3.15). Next we prove the non-degeneracy in $L^2$ and $L^3$. As $\Vert K_\frac{1}{4}\Vert _{L^1}=1$, we have that

$$\begin{aligned} \Vert f_l\Vert _{L^2}^2\geqq \Vert K_\frac{1}{4}*f_l\Vert _{L^2}^2=J_l^2\geqq \frac{1}{\alpha }\left( 1+\frac{c_0}{1+\alpha ^2}\right) , \end{aligned}$$

where the last inequality follows from Lemma 3.3. For the $L^3$-bound, note that

$$\begin{aligned} f^3\geqq 3(\alpha f^2-\Psi (f)), \end{aligned}$$

with equality only when $f\leqq \alpha$. As $\int \Psi (f_l)\, \textrm{d}x=1$, it follows that

$$\begin{aligned} \Vert f_l\Vert _{L^3}^3\geqq 3\left( \alpha \Vert f_l\Vert _{L^2}^2-1\right) \geqq 3\frac{c_0}{1+\alpha ^2}. \end{aligned}$$

Now we prove (3.17). Note first that since $f_l$ is bell-shaped, and $K$ is everywhere strictly positive, the left-hand side of (3.15) cannot vanish unless $f_l$ is identically zero, which is clearly not the case for a maximiser. Hence, the right-hand side is also non-vanishing, and therefore $f_l(x) > 0$ for $x$ in the open interval $(-2^l, 2^l)$; outside this interval, the Euler–Lagrange equation (3.15) does not hold. Recall that $\left\langle f_l,\Psi '(f_l) \right\rangle \lesssim 1$ (cf. Lemma 3.7) and $J_l > \alpha ^{-1/2}$ for $l \gtrsim |\log (\alpha )|$ according to Lemma 3.3. So wherever $f_l > \alpha$, we have from (3.4) and (3.15) that

$$\begin{aligned} \alpha ^2+3 \left( f_l-\alpha \right) ^2 \leqq \frac{\langle f_l, \Psi '(f_l) \rangle }{J_l^2} |K*f_l| \lesssim \alpha \Vert f_l\Vert _{\infty }, \end{aligned}$$

(3.18)

uniformly in $\alpha >0$, where we have used that $|K*f_l | \leqq \Vert K\Vert _{L^1} \Vert f_l\Vert _{\infty }$. This inequality gives the uniform upper bound on $\Vert f_l\Vert _\infty$ in (3.17).

Lastly we prove that $f_l(0)<\alpha$ for all $\alpha$ sufficiently large. Assuming that $f_\alpha (0)>\alpha$, we have according to (3.18) evaluated at $x=0$, Lemma 2.3 and Lemma 3.1 that

$$\begin{aligned} \alpha ^2\lesssim \alpha \Vert K*f_l\Vert _{L^\infty }\lesssim \alpha \Vert f_l\Vert _{L^3}\lesssim \alpha , \end{aligned}$$

uniformly in $\alpha$ and $l \gtrsim |\log (\alpha )|$. Clearly, this is a contradiction for all large enough $\alpha$, whence $f_l(0)<\alpha$ for all such $\alpha$ and $l$. $\square$

In the previous lemma we established that $\Vert f_l\Vert _{L^\infty }\lesssim \alpha$ uniformly in $\alpha >0$ and $l\gtrsim |\log (\alpha )|$. The following proposition provides more precise information about this upper bound, pushing maximisers below the value $B$. While the idea of the proposition is simple, the proof requires quite a rigorous balancing of terms and estimates. This is, to us, one of the first quantitative size estimates for a ’small amplitude’ theory (which establish that they are not small at all in fact), and it takes up a sizeable part of the paper. We shall use it in the following, but it is strictly not needed for the construction of very small waves. The reader who is dominantly interested in the construction method may move forward to Lemma 3.7.

Proposition 3.6

For any $\alpha >0$ and $\varepsilon >0$, there is an $l_0$, such that for all $l>l_0$, the maximisers $f_l$ satisfy

$$\begin{aligned} \int _{f_l\geqq B}|f_l-B|\, \textrm{d}x<\varepsilon , \end{aligned}$$

(3.19)

where $B=\frac{4}{\sqrt{3}}\cos \left( \frac{5\pi }{18}\right) \alpha \approx 1.48 \alpha$ is the unique solution in ${\mathbb R}_+$ to $2\Psi (y)=y\Psi '(y)$.

Proof

Let $\varepsilon >0$. For a contradiction, we assume that for any $l_0$, there exists maximisers $f_l$, $l>l_0$, such that

$$\begin{aligned} \int _{f_l\geqq B}|f_l-B|\, \textrm{d}x\geqq \varepsilon . \end{aligned}$$

(3.20)

The idea of the proof is that $y^2/\Psi (y)$ has its maximum at B so that B is the optimal height for maximising the $L^2$-norm for fixed $N_\Psi$-norm, as shown below. Hence we can construct a function $\tilde{f_l}$ with ${{\,\textrm{supp}\,}}(\tilde{f_l}) \subset [-2^l,2^l]$, $\tilde{f_l}(0)=B$ and $N_\Psi (\tilde{f_l})=1$ that is "flatter" than $f_l$ and such that $\Vert \tilde{f_l}\Vert _{L^2}>\Vert f_l\Vert _{L^2}$. Generally, the difference between $\Vert K_\frac{1}{4}*f\Vert _{L^2}$ and $\Vert f\Vert _{L^2}$ is smaller the "flatter" and less oscillating f is (see (3.28)). The restriction to $[-2^l,2^l]$ causes some technical difficulties due to the jump-discontinuity at the endpoints, but for large enough l we can show that $\Vert K_\frac{1}{4}*\tilde{f_l}\Vert _{L^2}>\Vert K_\frac{1}{4}*f_l\Vert _{L^2}$, contradicting the assumption that $f_l$ is a maximiser.

Let now $l>0$ be such that

$$\begin{aligned} \int _{-2^l}^{2^l}\Psi (B)\, \textrm{d}x>1. \end{aligned}$$

(3.21)

For $y>0$, we define

$$\begin{aligned} g(x,y) = {\left\{ \begin{array}{ll} y, \quad &{} |x|\leqq \frac{1}{2\Psi (y)} \\ 0, \quad &{} |x|> \frac{1}{2\Psi (y)}. \end{array}\right. } \end{aligned}$$

Then $N_\Psi (g(\cdot ,y))=1$ for all $y>0$. Let

$$\begin{aligned} h(y)=\Vert g(\cdot ,y)\Vert _{L^2}^2=\frac{y^2}{\Psi (y)}. \end{aligned}$$

We then have that

$$\begin{aligned} h'(y)=\frac{2y}{\Psi (y)}-y^2\frac{\Psi '(y)}{\Psi (y)^2}=\frac{y}{\Psi (y)^2}(2\Psi (y)-y\Psi '(y)). \end{aligned}$$

(3.22)

Using the definition of $\Psi$, some straightforward calculations show that $2\Psi (y)-y\Psi '(y)=0$ (a cubic equation) has a single real-valued solution, namely B,³ whence $h'(B)=0$. Moreover,

$$\begin{aligned} (B-y)h'(y)>0&\quad \text { for } \quad 0 < y \ne B. \end{aligned}$$

(3.23)

Let $(-a,a)$ be the interval where $f_l>B$. For $\delta >0$, we define

$$\begin{aligned} \tilde{f}(x)= {\left\{ \begin{array}{ll} B, \quad &{} |x| \leqq a+\delta , \\ f_l(|x|-\delta ), \quad &{} |x|>a+\delta . \end{array}\right. } \end{aligned}$$

In view of the assumption (3.20) and $N_\Psi (f_l)=1$, one has $N_\Psi (\tilde{f}) <1$ for $\delta = 0$. As the gauge norm is continuous and grows unboundedly as $\delta \rightarrow \infty$, there exists a smallest $\delta >0$ such that $N_\Psi (\tilde{f})=1$. Fix that $\delta >0$. It is obvious that

$$\begin{aligned} \int \limits _{|x|> a+\delta } \tilde{f}^2 \, \textrm{d}x=\int \limits _{|x|> a} f_l^2 \, \textrm{d}x, \quad \text { and }\quad \int \limits _{|x|> a+\delta } \Psi (\tilde{f})\, \textrm{d}x=\int \limits _{|x| > a} \Psi (f_l)\, \textrm{d}x, \end{aligned}$$

and by choice of $\delta$, also

$$\begin{aligned} \int \limits _{|x| \leqq a+\delta } \Psi (\tilde{f})\, \textrm{d}x=\int \limits _{|x| \leqq a} \Psi (f_l)\, \textrm{d}x. \end{aligned}$$

(3.24)

Now, in the whole interval $(-a-\delta , a + \delta )$, one has

$$\begin{aligned} h(\tilde{f}) = h(B) = \max h \geqq h(f_l), \end{aligned}$$

in view of (3.23); and in $(-a,a)$, where has $f_l(x)>B=\tilde{f}(x)$, one has

$$\begin{aligned} h(\tilde{f}) = h(B) = \max h > h(f_l). \end{aligned}$$

This means that $y^2$ is relatively smaller than $\Psi (y)$ in the range where $f_l$ resides. More precisely,

$$\begin{aligned} \Vert \tilde{f}\Vert _{L^2}^2-\Vert f_l\Vert _{L^2}^2&= \int \limits _{|x| \leqq a+ \delta } \tilde{f}^2\, \textrm{d}x-\int \limits _{|x| \leqq a} f_l^2\, \textrm{d}x\\&= \int \limits _{|x| \leqq a+ \delta } \Psi (\tilde{f}) h(\tilde{f}) \, \textrm{d}x-\int \limits _{|x| \leqq a} \Psi (f_l) h(f_l) \, \textrm{d}x\\&= h(B) \Bigg ( \int \limits _{|x| \leqq a+ \delta } \Psi (\tilde{f}) \, \textrm{d}x- \int \limits _{|x| \leqq a} \Psi (f_l) \frac{h(f_l)}{h(\tilde{f})} \, \textrm{d}x\Bigg ) > 0, \end{aligned}$$

in view of (3.24) and the above inequalities for $h$. We shall quantify this inequality. Using (3.24) and the definition of $\tilde{f}$, one finds the following explicit relationship between $f_l$ and $\tilde{f}$:

$$\begin{aligned} \int \limits _{|x| \leqq a+\delta } \tilde{f}^2\, \textrm{d}x=2(a+\delta )B^2= \frac{B^2}{\Psi (B)}\int \limits _{|x| \leqq a + \delta } \Psi (\tilde{f})\, \textrm{d}x= \frac{B^2}{\Psi (B)}\int \limits _{|x| \leqq a} \Psi (f_l)\, \textrm{d}x. \end{aligned}$$

Hence, by the Taylor expansion

$$\begin{aligned} \Psi (f_l) = \Psi (B) + \Psi '(B) (f_l-B) + {\textstyle \frac{1}{2}} \Psi ''(c(x)) (f_l-B)^2, \end{aligned}$$

for some $c(x)\in (B, f_l(x))$, one finds

$$\begin{aligned} \begin{aligned} \Vert \tilde{f}\Vert _{L^2}^2-\Vert f_l\Vert _{L^2}^2=&\frac{1}{\Psi (B)}\int _{-a}^a B^2 \Psi (f_l)-\Psi (B)(B+(f_l-B))^2\, \textrm{d}x\\ =&\frac{1}{\Psi (B)}\int _{-a}^a \left( B^2 \Psi '(B)-2\Psi (B)B\right) (f_l-B)\, \textrm{d}x\\&+\frac{1}{\Psi (B)}\int _{-a}^a\left( \frac{B^2}{2} \Psi ''(c(x))-\Psi (B)\right) (f_l-B)^2\, \textrm{d}x. \end{aligned} \end{aligned}$$

(3.25)

From (3.22), we have $B^2 \Psi '(B)-2\Psi (B)B=0$ as $h'(B)=0$. And since $\Psi ''$ is strictly increasing on $[\alpha ,\infty )$, we get

$$\begin{aligned} \frac{B^2}{2}\Psi ''(c(x))-\Psi (B)>\frac{B^2}{2}\Psi ''(B)-\Psi (B) \geqq \alpha ^3, \end{aligned}$$

by an explicit calculation. It follows from (3.20) and Jensen’s inequality that

$$\begin{aligned} \Vert \tilde{f}\Vert _{L^2}^2-\Vert f_l\Vert _{L^2}^2 =\frac{1}{\Psi (B)}\int _{-a}^a\left( \frac{B^2}{2}\Psi ''(c(x))-\Psi (B)\right) (f_l-B)^2\, \textrm{d}x\gtrsim \varepsilon ^2, \end{aligned}$$

(3.26)

uniformly for all l sufficiently large (note also that there is a uniform upper bound on a, imposed by $N_\Psi (f_l)=1$). Using the same kind of Taylor expansion, we can also get the following row of equalities, that will be used later. Here, the first equality is a rewrite of (3.24), and the last of (3.25).

$$\begin{aligned} 2\delta =&\frac{1}{\Psi (B)}\int _{-a}^a \Psi (f_l)-\Psi (B)\, \textrm{d}x=\int _{-a}^a \frac{\Psi '(B)}{\Psi (B)}(f_l-B)+\frac{\Psi ''(c(x))}{2\Psi (B)}(f_l-B)^2\, \textrm{d}x\nonumber \\ =&\frac{2}{B}\int _{-a}^a (f_l-B)\, \textrm{d}x+\frac{1}{B^2}(\Vert \tilde{f}\Vert _{L^2}^2-\Vert f_l\Vert _{L^2}^2)+\frac{1}{B^2}\int _{-a}^a (f_l-B)^2\, \textrm{d}x. \end{aligned}$$

(3.27)

Next we want to show that $\Vert K_{\frac{1}{4}}*\tilde{f}\Vert _{L^2}>\Vert K_{\frac{1}{4}}*f_l\Vert _{L^2}$ if l is sufficiently large. As $\Vert K\Vert _{L^1}=1$, we have for any $f\in L^2$ that

$$\begin{aligned} \iint _{{\mathbb R}^2} |f(x+h)-f(x)|^2K(h)\, \textrm{d}x\, \textrm{d}h =&\iint _{{\mathbb R}^2} |\widehat{f}(\xi )|^2 \big |\textrm{e}^{ih\xi }-1\big |^2 K(h)\, \textrm{d}\xi \, \textrm{d}h \nonumber \\ =&\int _{{\mathbb R}} |\widehat{f}(\xi )|^2 \int _{{\mathbb R}} 2(1-\cos (h\xi ))K(h) \, \textrm{d}h\, \textrm{d}\xi \nonumber \\ =&2\int _{{\mathbb R}} (1-\widehat{K}(\xi ))|\widehat{f}(\xi )|^2\, \textrm{d}\xi \nonumber \\ =&2\left( \Vert f\Vert _{L^2}^2-\Vert K_\frac{1}{4}*f\Vert _{L^2}^2\right) . \end{aligned}$$

(3.28)

Hence,

$$\begin{aligned} \begin{aligned}&\Vert K_{\frac{1}{4}}*\tilde{f}\Vert _{L^2}^2 -\Vert K_{\frac{1}{4}}*f_l\Vert _{L^2}^2 = \Vert \tilde{f}\Vert _{L^2}^2-\Vert f_l\Vert _{L^2}^2 \\&\qquad -\frac{1}{2} \iint _{{\mathbb R}^2} \left( |\tilde{f}(x+h)-\tilde{f}(x)|^2-|f_l(x+h)-f_l(x)|^2\right) K(h)\, \textrm{d}x\, \textrm{d}h. \end{aligned} \end{aligned}$$

(3.29)

Since $\Vert \tilde{f}\Vert _{L^2} - \Vert f_l\Vert _{L^2} \gtrsim \varepsilon ^2$, we only need to show that the double integral in the second line in (3.29) is smaller than that expression. By evenness of $\tilde{f}$, $f_l$ and $K$, this integral is equal to

$$\begin{aligned} \int _0^\infty \left( \int _{\mathbb R}\left( |\tilde{f}(x+h)-\tilde{f}(x)|^2-|f_l(x+h)-f_l(x)|^2\right) \, \textrm{d}x\right) K(h)\, \textrm{d}h, \end{aligned}$$

(3.30)

where we shall concentrate on the inner integral. Hence, let $h \geqq 0$. For $|x| \geqq a + \delta$, the function $\tilde{f}$ is just a $\delta$-translation of $f_l$, so

$$\begin{aligned}&\int _{\mathbb R}| \tilde{f}(x+h) - \tilde{f}(x)|^2 \, \textrm{d}x\\&\quad = \left( \int _{-\infty }^{-a-\delta -h} + \int _{-a-\delta -h}^{a+\delta } + \int _{a+\delta }^\infty \right) | \tilde{f}(x + h) - \tilde{f}(x)|^2 \, \textrm{d}x\\&\quad = \left( \int _{-\infty }^{-a-h} + \int _a^\infty \right) | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x+ \int _{-a-\delta -h}^{a+\delta } | \tilde{f}(x + h) - \tilde{f}(x)|^2 \, \textrm{d}x\end{aligned}$$

Hence, the inner integral in (3.30) reduces to

$$\begin{aligned} \begin{aligned} E_l(h)&:= \int _{\mathbb R}\left( | \tilde{f}(x+h) - \tilde{f}(x) |^2 - | f_l(x+h) - f_l(x) |^2 \right) \, \textrm{d}x\\&\;= \int _{-a-\delta -h}^{a+\delta } \left| \tilde{f}(x + h) - \tilde{f}(x)|^2 \, \textrm{d}x- \int _{-a-h}^a | f_l(x + h) - f_l(x)\right| ^2 \, \textrm{d}x. \end{aligned} \end{aligned}$$

(3.31)

We study $0 \leqq h \leqq 2a$ and $h \geqq 2a$ separately. In the following, we will make ample use of the definition of $\tilde{f}$, as well as translations and (even) changes of variables in the integrals to reduce and compare the terms. Recall that $\tilde{f} = B$ on $[-a-\delta , a + \delta ]$. $\square$

3.3 The case $0 \leqq h \leqq 2a$.

In the simplest case, when $h \in [0, 2a]$, one has

$$\begin{aligned}&\int _{-a-\delta -h}^{a+\delta } | \tilde{f}(x+h)-\tilde{f}(x)|^2 \, \textrm{d}x\\&\quad = \left( \int _{-a-\delta -h}^{-a-\delta } + \int _{-a-\delta }^{a+\delta -h} + \int _{a+\delta -h}^{a+\delta } \right) | \tilde{f}(x+h)-\tilde{f}(x)|^2 \, \textrm{d}x\\&\quad = \int _{-a-h}^{-a} |B-f_l(x)|^2 \, \textrm{d}x+ \int _{a-h}^a |f_l(x+h)-B|^2 \, \textrm{d}x\\&\quad = 2\int _{-a-h}^{-a} |B-f_l(x)|^2 \, \textrm{d}x, \end{aligned}$$

by the changes of variables $x + h \mapsto x \mapsto -x$. So the correction term $E_l(h)$ from (3.31) in the case when $h \in [0,2a]$ is given by

$$\begin{aligned}&2\int _{-a-h}^{-a} |B-f_l(x)|^2 \, \textrm{d}x- \int _{-a-h}^a | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x\\&\quad = 2\int _{-a-h}^{-a} |B-f_l(x)|^2 \, \textrm{d}x- \left( \int _{-a-h}^{-a} + \int _{-a}^{a-h} - \int _{a-h}^{a}\right) | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x\\&\quad = 2\int _{-a-h}^{-a} \left( |B-f_l(x)|^2 - | f_l(x + h) - f_l(x)|^2 \right) \, \textrm{d}x- \int _{-a}^{a-h} | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x. \end{aligned}$$

Both latter terms are negative, as $f_l(\cdot +h) \geqq B$ on $[-a-h,-a]$ when $h \leqq 2a$, and $f_l(\cdot ) \leqq B$ on the same interval when $h \geqq 0$. To quantify the negative contribution, we relate it to the norm difference (3.26) via the expression $\int _{-a}^a |B- f_l|^2 \, \textrm{d}x$. Since

$$\begin{aligned} |B-f_l(x)|^2 - | f_l(x + h) - f_l(x)|^2 = B^2 - 2Bf_l(x) - f_l^2(x+h) + 2f_l(x) f_l(x+h), \end{aligned}$$

one gets after the change of variables $x + h \mapsto x \mapsto -x$, and subsequent addition and subtraction of $|B-f_l(x)|^2$, that

$$\begin{aligned}&2\int _{-a-h}^{-a} \left( |B-f_l(x)|^2 - | f_l(x + h) - f_l(x)|^2 \right) \, \textrm{d}x\\&\quad = -2\int _{a-h}^{a} \left( |B-f_l(x)|^2 + 2(f_l(x)-B)(B-f_l(x+h)) \right) \, \textrm{d}x\\&\quad \leqq -2\int _{a-h}^{a} |B-f_l(x)|^2 \, \textrm{d}x. \end{aligned}$$

Therefore, going back to (3.30), when $h \in [0,2a]$, the correction to the $L^2$-terms in (3.29) can be bounded, by using positivity of the inner integrand, as

$$\begin{aligned} \begin{aligned} \int _0^{2a} E_l(h) K(h)\, \textrm{d}h&\leqq -2\int _0^{2a} \int _{a-h}^{a} | B - f_l(x) |^2 \, \textrm{d}x\, K(h) \, \textrm{d}h\\&\leqq -2\int _a^{2a} \int _{0}^{a} | B - f_l(x) |^2 \, \textrm{d}x\, K(h) \, \textrm{d}h\\&\simeq -a\left( \Vert \tilde{f}\Vert _{L^2}^2 -\Vert f_l\Vert _{L^2}^2\right) , \end{aligned} \end{aligned}$$

(3.32)

by (3.26). Moreover, by (3.20) and (3.17), there is a lower bound on a that depends only on $\varepsilon$ and $\alpha$; in particular it is uniform in l.

3.4 The case $h \geqq 2a$.

We divide the integral $\int _{-a-\delta -h}^{a+\delta } | \tilde{f}(x + h) - \tilde{f}(x)|^2 \, \textrm{d}x$ in (3.31) according to

$$\begin{aligned} \int _{-a-\delta -h}^{a + \delta } = \int _{-a-\delta -h}^{a-\delta - h} + \int _{a-\delta -h}^{a+\delta - h} + \int _{a+\delta -h}^{-a-\delta } + \int _{-a-\delta }^{-a+\delta } + \int _{-a + \delta }^{a + \delta }. \end{aligned}$$

(I)

Note that $a + \delta - h = -a - \delta$ exactly when $h = 2(\alpha + \delta )$, so the behaviour of the middle integrals in the right-hand side will depend on whether $2a \leqq h \leqq 2(a + \delta )$ or $h \geqq 2(a + \delta )$. We deal with the integrals in order. When $x \in (-a-\delta -h,a-\delta - h)$, $\tilde{f}(x+h)$ is constantly equal to $B$, and $\tilde{f}(x)$ is a $\delta$-translation of $f_l(x)$, so one has

$$\begin{aligned} \int _{-a-\delta -h}^{a-\delta - h} | \tilde{f}(x + h) - \tilde{f}(x)|^2 \, \textrm{d}x= \int _{-a - h}^{a - h} |B- f_l(x)|^2 \, \textrm{d}x. \end{aligned}$$

(I1)

Using the changes of variables $x + h \mapsto x \mapsto -x$, the second integral in (I) may be rewritten as a copy of the fourth:

$$\begin{aligned} \int _{a-\delta -h}^{a+\delta - h} | \tilde{f}(x + h) - \tilde{f}(x)|^2 \, \textrm{d}x&= \int _{-a-\delta }^{-a+\delta } | \tilde{f}(x) - \tilde{f}(x+h)|^2 \, \textrm{d}x. \end{aligned}$$

(I2)

The third integral only has a contribution when $h \geqq 2(a + \delta )$. For $2a \leqq h \leqq 2(a+\delta )$, its integrand is identically zero, because both $\tilde{f}(x)$ and $\tilde{f}(x+h)$ equal $B$ for $x \in [-a-\delta , a + \delta -h]$ for such $h$. When instead $h \geqq 2(a + \delta )$, both $x + h \geqq a + \delta$ and $x \leqq -a - \delta$ on the interval of integration, so we can express the contribution as

$$\begin{aligned} \begin{aligned}&\chi _{(2(a+\delta ),\infty )}(h) \int _{a+\delta -h}^{-a-\delta }|f_l(x+h - \delta )-f_l(x+\delta )|^2 \, \textrm{d}x\\&\quad = \chi _{(2(a+\delta ),\infty )}(h) \int _{a-h}^{-a-2\delta }|f_l(x+h)-f_l(x+2\delta )|^2 \, \textrm{d}x, \end{aligned} \end{aligned}$$

(I3)

where $\chi$ is an indicator function. The fourth integral has already been show to be a copy of the second, see (I2). When $h \geqq 2a$ the contribution from these integrals depends further on the value of $h$. It simplifies to write (I2) as

$$\begin{aligned} \int _{-a-\delta +h}^{-a+\delta +h} | \tilde{f}(x-h) - \tilde{f}(x)|^2 \, \textrm{d}x. \end{aligned}$$

(I2')

Here, for $2a \leqq h \leqq 2(a+\delta )$, the subinterval of integration $[-a-\delta +h,a+\delta ]$ is non-void. The integrand however contributes nothing, as $\tilde{f}(x-h)$ and $\tilde{f}(x)$ both equal $B$ over this interval. On the remaining interval of integration, $[a+\delta ,-a+\delta + h]$, one has $x \geqq a + \delta$ but $x-h \in [-a-\delta ,-a+\delta ]$, so there exactly one of the two terms $\tilde{f}(x)$ and $\tilde{f}(x-h)$ equals $B$. The latter situation will happen also when $h \geqq 2(a + \delta )$. Therefore,

$$\begin{aligned} \begin{aligned} (I2) = \int _{-a-\delta +h}^{-a +\delta + h} |\tilde{f}(x) - B|^2 \, \textrm{d}x&= \int _{\max \{a+\delta , -a-\delta +h\}}^{-a +\delta + h} |f_l (x-\delta ) - B|^2 \, \textrm{d}x\\&= \int _{a - h}^{\min \{-a, a+2\delta -h\}} |f_l (x) - B|^2 \, \textrm{d}x, \end{aligned} \end{aligned}$$

(I4)

by the change of variables $x - \delta \mapsto x \mapsto -x$.

Finally, the fifth can be shown to be a copy of the first:

$$\begin{aligned} \begin{aligned}&\int _{-a + \delta }^{a + \delta } | \tilde{f}(x + h) - \tilde{f}(x)|^2 \, \textrm{d}x\\&\quad = \int _{-a + \delta }^{a + \delta } | f_l(x + h - \delta ) - B|^2 \, \textrm{d}x\\&\quad = \int _{-a-h}^{a -h} | f_l(x) - B|^2 \, \textrm{d}x= (I1), \end{aligned} \end{aligned}$$

(I5)

by the change of variables $x + h - \delta \mapsto x \mapsto - x$. Let $r(h) = \min \lbrace a+2\delta -h,-a\rbrace$. Then Equations (I1)–(I5) summarise as

$$\begin{aligned} \begin{aligned}&\int _{-a-\delta -h}^{a+\delta }|\tilde{f}(x+h)-\tilde{f}(x)|^2\, \textrm{d}x\\&\quad = 2\int _{-a-h}^{r(h)}|f_l(x)-B|^2\, \textrm{d}x\\&\qquad +\chi _{(2(a+\delta ),\infty )}(h)\int _{a-h}^{-a-2\delta }|f_l(x+h)-f_l(x+2\delta )|^2\, \textrm{d}x. \end{aligned} \end{aligned}$$

(3.33)

This shall be compared with the term $\int _{-a-h}^a | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x$ from (3.31) in $E_l(h)$. We divide the latter term into parts, according to

$$\begin{aligned} \begin{aligned} - \int _{-a-h}^a | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x&= - \left( \int _{-a-h}^{a-h} + \int _{a-h}^{-a} + \int _{-a}^a \right) | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x\\&= - \left( 2 \int _{-a-h}^{a-h} + \int _{a-h}^{-a} \right) | f_l(x + h) - f_l(x)|^2 \, \textrm{d}x, \end{aligned} \end{aligned}$$

(3.34)

by the changes of variables. The $2\int _{-a-h}^{a-h}$-integral will be used for the $2\int _{-a-h}^{r(h)}$-integral in (3.33), and the $\int _{a-h}^{-a}$-integral for the $\chi$-part. We start with the former, writing

$$\begin{aligned}&2\int _{-a-h}^{r(h)}|f_l(x)-B|^2\, \textrm{d}x-2\int _{-a-h}^{a-h} |f_l(x+h)-f_l(x)|^2\, \textrm{d}x\nonumber \\&= 2\int _{a-h}^{r(h)}|f_l(x)-B|^2\, \textrm{d}x+ 2\int _{-a-h}^{a-h}|f_l(x)-B|^2\, \textrm{d}x\nonumber \\&\quad -2\int _{-a-h}^{a-h} |f_l(x+h)-f_l(x)|^2\, \textrm{d}x\nonumber \\&= 2\int _{a-h}^{r(h)}|B-f_l(x)|^2\, \textrm{d}x\nonumber \\&\quad -4\int _{-a-h}^{a-h} (B-f_l(x))(f_l(x+h)-B)\, \textrm{d}x-2\int _{-a}^{a}|f_l(x)-B|^2\, \textrm{d}x,\nonumber \\ \end{aligned}$$

(3.35)

which is achieved by adding and subtracting $2 \int _{-a-h}^{a-h} |f_l(x+h) - B|^2 \, \textrm{d}x$, where the negative term is expressed as $-2 \int _{-a}^{a} |f_l(x) - B|^2 \, \textrm{d}x$. Note that the terms ${B-f_l(x)}$ and $f_l(x+h)-B$ in the $\int _{-a-h}^{a-h}$-integral are both positive, so the total contribution from that term is negative. Quantifying with the help of the mean value theorem, we have that (3.35) equals

$$\begin{aligned} \begin{aligned}&2\int _{a-h}^{r(h)}|B-f_l(x)|^2\, \textrm{d}x-4\int _{-a-h}^{a-h} (B-f_l(x))(f_l(x+h)-B)\, \textrm{d}x\\&\quad -2\int _{-a}^{a}|f_l(x)-B|^2\, \textrm{d}x\\&\quad = 2(r(h)-a+h)(B-f_l(c_1))^2_{c_1 \in (a-h,-a)}\\&\qquad -4(B-f_l(c_2))_{c_2 \in (-a-h,a-h)}\int _{-a}^{a} |f_l(x)-B|\, \textrm{d}x- 2\int _{-a}^{a}|f_l(x)-B|^2\, \textrm{d}x, \end{aligned} \end{aligned}$$

(3.36)

where furthermore $f_l(c_2) \leqq f_l(c_1) \leqq B$ and $0 \leqq r(h) - a + h \leqq 2\delta$ for $h \geqq 2a$ by definition of $r(h)$. We may therefore use (3.27) to bound (3.36), finding that it is less than

$$\begin{aligned} \begin{aligned}&4|B-f_l(c_1)|\left( \delta (B-f_l(c_1)) -\int _{-a}^a|f_l(x)-B|\, \textrm{d}x\right) -2\int _{-a}^{a}|f_l(x)-B|^2\, \textrm{d}x\\&\quad = 2\left( 1-\frac{f_l(c_1)}{B}\right) \left( \Vert \tilde{f}\Vert _{L^2}^2 -\Vert f_l\Vert _{L^2}^2\right) \\&\qquad - \frac{2 f_l(c_1)}{B}\int _{-a}^a | f_l(x) - B|^2 \, \textrm{d}x-4\delta (B-f_l(c_1))f_l(c_1)\\&\quad \leqq 2 \left( \Vert \tilde{f}\Vert _{L^2}^2 -\Vert f_l\Vert _{L^2}^2\right) . \end{aligned} \end{aligned}$$

(3.37)

Turning to the $\chi$-part of (3.33), it is only present when $h>2(a+\delta )$, in which case we are to balance it against the remaining $\int _{a-h}^{-a}$-integral in (3.34). Note that changes of variables can be used to re-express terms, for example, $\int _{a-h}^{-a-2\delta } f_l^2(x+h) \, \textrm{d}x= \int _{a-h}^{-a-2\delta } f_l^2(x+2\delta ) \, \textrm{d}x$ by the change $x+h \mapsto -x - 2\delta$. Using similar identities and the mean-value theorem, one finds

$$\begin{aligned}&\int _{a-h}^{-a-2\delta } |f_l(x+h)-f_l(x+2\delta )|^2\, \textrm{d}x-\int _{a-h}^{-a} |f_l(x+h)-f_l(x)|^2\, \textrm{d}x\nonumber \\&\quad = -2\int _{a-h}^{-a-2\delta }f_l(x+h)(f_l(x+2\delta )-f_l(x))\, \textrm{d}x\nonumber \\&\qquad +2\int _{-a-2\delta }^{-a}f_l(x+h)(f_l(x)-f_l(x+h))\, \textrm{d}x\nonumber \\&\quad = -2f_l(c_3)\int _{a-h}^{-a-2\delta } ( f_l(x+2\delta )-f_l(x) ) \, \textrm{d}x\nonumber \\&\qquad +2f_l(c_4)\int _{-a-2\delta }^{-a} ( f_l(x)-f_l(x+h) ) \, \textrm{d}x\nonumber \\&\quad = -2(f_l(c_3)-f_l(c_4))\left( \int _{-a-2\delta }^{-a} f_l(x)\, \textrm{d}x-\int _{-a-2\delta +h}^{-a+h}f_l(x)\, \textrm{d}x\right) <0, \end{aligned}$$

(3.38)

where $c_3\in (a,-a-2\delta +h)$, $c_4\in (-a-2\delta +h,-a+h)$. As $f_l$ is bell-shaped, it follows that the expression above is negative. As K is positive and $\int _0^\infty K(h) \, \textrm{d}h =\frac{1}{2}$, summing up $\int _0^{\infty } E_l(h) K(h)\, \textrm{d}h$ from the negative quantified contribution from (3.32), the positive quantified from (3.37), and the negative from (3.38), we find that there is a constant $0<C<1$, depending only on $\varepsilon$ and $\alpha$ such that

$$\begin{aligned}&\frac{1}{2} \iint _{\mathbb R^2} \left( |\tilde{f}(x+h)-\tilde{f}(x)|^2-|f_l(x+h)-f_l(x)|^2\right) K(h)\, \textrm{d}x\, 4\textrm{d}h \\&\quad <C \left( \Vert \tilde{f}\Vert _{L^2}^2-\Vert f_l\Vert _{L^2}^2\right) , \end{aligned}$$

for all l sufficiently large. From (3.29), we then get that

$$\begin{aligned} \Vert K_{\frac{1}{4}}*\tilde{f}\Vert _{L^2}^2 -\Vert K_{\frac{1}{4}}*f_l\Vert _{L^2}^2>(1-C) \left( \Vert \tilde{f}\Vert _{L^2}^2-\Vert f_l\Vert _{L^2}^2\right) >0. \end{aligned}$$

(3.39)

3.5 The modified $\tilde{f}$

Because $\tilde{f}$ is only guaranteed to have support within $[-2^l-\delta ,2^l+\delta ]$, it is not necessarily an admissible maximiser, and we therefore modify it to yield the desired contradiction (in case it would have support within $[-2^l,2^l]$ this part is not needed, but can still be carried out). By (3.21) and the properties of $\tilde{f}$, there exists $\gamma >0$ such that $a+\delta +\gamma <2^l$ and

$$\begin{aligned} \int _0^{\gamma }\Psi \left( B\right) \, \textrm{d}x=\gamma \Psi (B)=\int _{-2^l}^{-2^l+\delta +\gamma }\Psi (f_l)\, \textrm{d}x. \end{aligned}$$

Now set $\tilde{\delta }=\delta +\gamma$, and define $\tilde{f_l}$ by

$$\begin{aligned} \tilde{f_l}(x)= {\left\{ \begin{array}{ll} B, \quad &{} x\in [-a-\tilde{\delta },a+\tilde{\delta }], \\ f_l(x-\tilde{\delta }), \quad &{} x\in (a+\tilde{\delta },2^l), \\ f_l(x+\tilde{\delta }), \quad &{} x\in (-2^l,-a-\tilde{\delta }), \\ 0, \quad &{} |x|\geqq 2^l. \\ \end{array}\right. } \end{aligned}$$

Then ${{\,\textrm{supp}\,}}(\tilde{f_l}) \subset [-2^l,2^l]$ and $N_\Psi (\tilde{f}_l)=1$. We claim that

$$\begin{aligned} \lim _{l\rightarrow \infty } \left( \Vert \tilde{f}-\tilde{f_l}\Vert _{L^2}+\Vert K_{\frac{1}{4}}*\tilde{f}-K_{\frac{1}{4}}*\tilde{f_l}\Vert _{L^2}\right) =0, \end{aligned}$$

(3.40)

in which case it follows from (3.39) and (3.26) that

$$\begin{aligned} \Vert K_{\frac{1}{4}}*\tilde{f_l}\Vert _{L^2}^2 -\Vert K_{\frac{1}{4}}*f_l\Vert _{L^2}^2>0 \end{aligned}$$

for all l sufficiently large, contradicting the assumption that $f_l$ is a maximiser. To prove (3.40), note that

$$\begin{aligned} \begin{aligned}&\int |\tilde{f}(x)-\tilde{f}_l(x)|^2\, \textrm{d}x\\&\quad = 2\left( \int _{-2^l-\delta }^{-2^l}\tilde{f}^2\, \textrm{d}x+\int _{-2^l}^{-a-\tilde{\delta }}|\tilde{f}(x)-\tilde{f}_l(x)|^2\, \textrm{d}x+\int _{-a-\tilde{\delta }}^{-a-\delta }|B-\tilde{f}(x)|^2\, \textrm{d}x\right) \\&\quad \leqq 2\delta f_l(-2^l+\delta )^2+2B^2 \gamma +2\int _{-2^l+\delta }^{-a-\gamma }|f_l(x+\gamma )-f_l(x)|^2\, \textrm{d}x. \end{aligned} \end{aligned}$$

(3.41)

Let f be a non-negative, bell-shaped function satisfying $N_\Psi (f)=1$. As f is bell-shaped, we have that if $f(x)=k$, then $f(y)\geqq k$ and $\Psi (f(y))\geqq \Psi (k)$ for all $|y|\leqq |x|$. The condition $N_\Psi (f)=1$ thus implies that

$$\begin{aligned} f(x)\leqq \Psi ^{-1} \left( \frac{1}{2|x|}\right) , \end{aligned}$$

(3.42)

for all $x \ne 0$, and that for all $k>0$, $|\lbrace x: f(x)\geqq k\rbrace |\leqq \frac{1}{\Psi (k)}$. In particular, there is an upper bound on $\tilde{\delta }$ that is independent of l, say $\tilde{\delta }<C$, and

$$\begin{aligned} f_l(-2^l+\tilde{\delta })\leqq \Psi ^{-1} \left( \frac{1}{2|-2^l+C|}\right) \rightarrow 0 \end{aligned}$$

as $l\rightarrow \infty$. This also implies that $\gamma \rightarrow 0$. Hence the two first terms in (3.41) vanish and, to prove our claim, it is sufficient to show that the convergence

$$\begin{aligned} \lim _{h\rightarrow 0^+}\int _{|x|<2^l-h}|f_l(x+h)-f_l(x)|^2\, \textrm{d}x=0 \end{aligned}$$

is uniform in l. Let $h>0$ and $x\in (-2^l,2^l-h)$. As $J_l$ is bounded below and $\langle f_l, \Psi '(f_l)\rangle$ is bounded above, uniformly in l, we get from the Euler–Lagrange equation (3.15) that

$$\begin{aligned} \left| \Psi '(f_l(x+h))-\Psi '(f_l(x))\right| =&\frac{\langle f_l, \Psi '(f_l)\rangle }{J_l^2}\left| K*f_l(x+h)-K*f_l(x)\right| \\ \lesssim&\Vert f_l\Vert _{L^\infty }\int \left| K(y-h)-K(y)\right| \, \textrm{d}y\\ \lesssim&\Vert f_l\Vert _{L^\infty } h^\frac{1}{2}, \end{aligned}$$

uniformly in l. Here, we have used the regularity and decay properties of K, cf. Lemma 2.1 and (2.6), in particular that $\int \left| |y-h|^{-1/2} - |y|^{-1/2} \right| \, \textrm{d}y\eqsim |h|^{1/2}$ by the change of variables $y = h\tau$. As $\Vert f_l\Vert _{L^\infty }\lesssim \alpha$ uniformly in l, $\Psi '(x)>0$ for all $x>0$ and $\Psi ''(x)>0$ for all $x\ne \alpha$, this implies that $f_l(x+h)-f_l(x)\rightarrow 0$ as $h\rightarrow 0$ uniformly in l and x. In particular, for any fixed R,

$$\begin{aligned} \int _{|x|\leqq R} |f_l(x+h)-f_l(x)|^2\, \textrm{d}x\rightarrow 0, \end{aligned}$$

uniformly in l. To deal with $|x|>R$, we improve on the estimate of the difference. By (3.42) we can pick $R\gg 1$ such that $f_l(R)<\frac{\alpha }{2}$ for all l. Let $|x|>R\gg 1$ and $0<h\ll 1$. Then

$$\begin{aligned} \left| \Psi '(f_l(x+h))-\Psi '(f_l(x))\right|&=|f_l(x+h)-f_l(x)|(2\alpha -f_l(x+h)-f_l(x))\\&\geqq \alpha |f_l(x+h)-f_l(x)|, \end{aligned}$$

and, by Lemma 2.1 and the bell-shapedness of $f_l$,

$$\begin{aligned} |K*&f_l(x+h)-K*f_l(x)|= \left| \int \left( K(x+h-y)-K(x-y)\right) f_l(y)\, \textrm{d}y\right| \\&\simeq \int _{|y|<\frac{|x|}{2}}h|K'(x-y)|f(y)\, \textrm{d}y+\int _{|y|\geqq \frac{|x|}{2}}\left| K(x+h-y)-K(x-y)\right| f(y)\, \textrm{d}y\\&\leqq h|x|\left| K'\left( \frac{|x|}{2}\right) \right| \Vert f_l\Vert _{L^\infty }+f_l\left( \frac{x}{2}\right) \int \left| K(x+h-y)-K(x-y)\right| \, \textrm{d}y\\&\lesssim _N h \alpha |x|^{-N}+h^\frac{1}{2}f_l\left( \frac{x}{2}\right) , \end{aligned}$$

uniformly in l for any $N>0$. Picking any $N>1$, it follows from the Euler–Lagrange equation (3.15) and the above estimates that

$$\begin{aligned} \int _{R<|x|<2^l-h}|f_l(x+h)-f_l(x)|^2\, \textrm{d}x\lesssim&\int _{|x|>R} |K*f_l(x+h)-K*f_l(x)|^2 \, \textrm{d}x\\ \lesssim&h^2 \alpha ^2+h \Vert f_l\Vert _{L^2}^2 \\ \lesssim&h^2\alpha ^2+\frac{h}{\alpha }, \end{aligned}$$

uniformly in l. This proves the claim.

Lemma 3.7

The quantity $\langle f, \Psi '(f) \rangle$ is bounded from below by $N_\Psi (f)$ for any $f \in \mathcal {L}^{\Psi }$. For the maximisers $f_l$, one has $1 < \langle f_l, \Psi '(f_l) \rangle$ and

$$\begin{aligned}&\langle f_l, \Psi '(f_l) \rangle = 2 - \frac{1}{3} \int _{f_l < \alpha } f_l^3\, \textrm{d}x+ \int _{f_l \geqq \alpha } \alpha ^2 \left( {\textstyle \frac{2\alpha }{3}} - f_l\right) \\ {}&\quad + \left( (f_l-\alpha )^3 + 3\alpha (f_l-\alpha )^2 \right) \, \textrm{d}x\lesssim 1 \end{aligned}$$

uniformly in $l \in \mathbb N$ and $\alpha \in (0,\infty )$. Moreover, for any $\alpha >0$, there exists $l_0$ such that

$$\begin{aligned} \langle f_l, \Psi '(f_l) \rangle <2, \end{aligned}$$

for all $l>l_0$.

Proof

For $0<f <\alpha$ one has

$$\begin{aligned} f \Psi '(f)&= 2 \alpha f^2 - f^3 = 2\left( \alpha f^2 - {\textstyle \frac{1}{3}} f^3 \right) - {\textstyle \frac{1}{3}} f^3 = 2 \Psi (f) - {\textstyle \frac{1}{3}} f^3>\Psi (f), \end{aligned}$$

and, for $f \geqq \alpha$,

$$\begin{aligned} f \Psi '(f)&= \alpha ^2 f + 3(f-\alpha )^2 f\\&= 2 \left( {\textstyle \frac{2}{3}} \alpha ^3 + \alpha ^2 (f-\alpha ) + (f-\alpha )^3 \right) \\&\quad + \alpha ^2 \left( {\textstyle \frac{2\alpha }{3}} - f \right) + \left( (f-\alpha )^3 + 3\alpha (f-\alpha )^2 \right) \\&= 2 \Psi (f) + \alpha ^2 \left( {\textstyle \frac{2 \alpha }{3}} - f \right) + \left( (f-\alpha )^3 + 3\alpha (f-\alpha )^2 \right) \\&>\Psi (f). \end{aligned}$$

In view of that $\int \Psi (f_l)\, \textrm{d}x= N_\Psi (f_l)$, the first part of the lemma and the lower bound on $\langle f_l, \Psi '(f_l)\rangle$ now follows from integrating the above expressions over $\mathbb R$.

For the upper bound, we have that

$$\begin{aligned} \langle f_l, \Psi '(f_l)\rangle \leqq 2 +\int _{f_l\geqq \alpha } (f_l-\alpha )^3+3\alpha (f_l-\alpha )^2\, \textrm{d}x\lesssim 2 +\int f_l^3\, \textrm{d}x\lesssim 1, \end{aligned}$$

uniformly in $\alpha >0$ and l, where the last inequality follows from Lemma 3.1. As shown above, we have

$$\begin{aligned} \langle f_l, \Psi '(f_l) \rangle =&\, 2-\frac{1}{3}\int _{f_l<\,\alpha }f_l^3\, \textrm{d}x\\&+\int _{f_l\geqq \, \alpha }\alpha ^2\left( \frac{2\alpha }{3}-f_l\right) +\left( (f_l-\alpha )^3+3\alpha (f_l-\alpha )^2\right) \, \textrm{d}x. \end{aligned}$$

Letting B be as in Proposition 3.6, we have that the integrand in the second integral is strictly negative for $\alpha \leqq f_l<B$. Hence, if $f_l(0)\leqq B$, then $\langle f_l, \Psi '(f_l) \rangle <2$. Assume therefore that $f_l(0)>B$. For any $\varepsilon >0$, we have by Proposition 3.6 that

$$\begin{aligned} \int _{f_l\geqq B}\alpha ^2\left( \frac{2\alpha }{3}-f_l\right) +\left( (f_l-\alpha )^3+3\alpha (f_l-\alpha )^2\right) \, \textrm{d}x<\varepsilon , \end{aligned}$$

for all l sufficiently large. Hence

$$\begin{aligned} \langle f_l, \Psi '(f_l) \rangle<&2-\frac{1}{3}\int _{f_l<\alpha }f_l^3\, \textrm{d}x\nonumber \\&+\int _{\alpha \leqq f_l<B}\alpha ^2\left( \frac{2\alpha }{3}-f_l\right) +\left( (f_l-\alpha )^3+3\alpha (f_l-\alpha )^2\right) \, \textrm{d}x+\varepsilon . \end{aligned}$$

(3.43)

In particular, $\langle f_l, \Psi '(f_l) \rangle <2+\varepsilon$ and using this estimate and the regularity of K, we have by Lemma 3.5 that

$$\begin{aligned} |\Psi '(f_l(x))-\Psi '(f_l(y))|&= \frac{\langle f_l, \Psi '(f_l) \rangle }{J_l^2}|K*f_l(x)-K*f_l(y)| \\&< 3\alpha |K*f_l(x)-K*f_l(y)| \\&\lesssim \alpha \Vert f_l\Vert _\infty |x-y|^{1/2} \\&\lesssim \alpha ^2 |x-y|^{1/2}, \end{aligned}$$

uniformly in $\alpha$ and l, where we used that K is smooth away from the origin and rapidly decaying, and $K(x)\simeq |x|^{-1/2}$ for $|x| \ll 1$. As $\Psi '\in C^1$, this implies that if $f_l=\alpha$ at some point, then for any $0<c<\alpha$, the measure $|\lbrace x: c\leqq f_l(x)\leqq \alpha \rbrace |$ is uniformly bounded below by a positive constant depending only on c and $\alpha$. Taking $c:=\frac{\alpha }{2}$, this implies that for any $l\geqq |\ln (\alpha )|$, such that $f_l(0)\geqq \alpha$, we have

$$\begin{aligned} \frac{1}{3}\int _{f_l<\alpha }f_l^3\, \textrm{d}x\geqq \frac{1}{3}\int _{\frac{\alpha }{2}<f_l<\alpha }f_l^3\geqq \frac{\alpha ^3}{24} |\lbrace x : \frac{\alpha }{2}\leqq f_l(x)\leqq \alpha \rbrace |\geqq \delta _\alpha . \end{aligned}$$

As $\varepsilon >0$ above was arbitrary, we can choose $\varepsilon <\delta _\alpha$ in (3.43) to conclude that $\langle f_l, \Psi '(f_l) \rangle <2$ for all l sufficiently large. $\square$

Corollary 3.8

For all $\alpha >0$ and all l sufficiently large, the family $\{f_{l}\}_l$ satisfies the estimate

$$\begin{aligned} \Vert f_l\Vert _{L^1}+|xf_l(x)|\lesssim 1+\alpha ^{-2}, \end{aligned}$$

uniformly in $x \in {\mathbb R}$, $\alpha >0$ and $l>l_0$, where $l_0$ is as in Lemma 3.7.

Proof

By Lemma 3.5, $\Vert f_l\Vert _{L^\infty }\lesssim \alpha$ uniformly in l and the condition $N_\Psi (f_l)=1$ implies that

$$\begin{aligned} 1 \geqq \int _{f_l \geqq a} \left( {\textstyle \frac{2}{3}} \alpha ^3 + \alpha ^2 (f-\alpha ) + (f-\alpha )^3 \right) \, \textrm{d}x\geqq {\textstyle \frac{2}{3}} \alpha ^3 \int _{f_l \geqq a} \, \textrm{d}x, \end{aligned}$$

so that $|\lbrace x: f_l(x)\geqq \alpha \rbrace |\leqq \frac{3}{2 \alpha ^3}$ uniformly in l. Hence

$$\begin{aligned} \int _{f_l\geqq \alpha } f_l \, \textrm{d}x\lesssim \alpha ^{-2}, \end{aligned}$$

uniformly in l. For $x\in (-2^l,2^l)$ such that $f_l(x)<\alpha$, we have by Lemma 3.5 that

$$\begin{aligned} 2\alpha f_l-f_l^2=\frac{\langle f_l, \Psi '(f_l)\rangle }{J_l^2} K*f_l. \end{aligned}$$

We can rewrite this as

$$\begin{aligned} \left[ 2 -\frac{\langle f_l, \Psi '(f_l)\rangle }{\alpha J_l^2} K*\right] f_l=\frac{f_l^2}{\alpha }. \end{aligned}$$

(3.44)

We now show that we can invert the operator in (3.44). Introducing

$$\begin{aligned} T_l:=\frac{\langle f_l, \Psi '(f_l)\rangle }{2\alpha J_l^2} K*\end{aligned}$$

we can clearly solve (3.44) by a von Neumann expansion by showing that the series $\sum _{m=0}^\infty T_l^m$ converges in $B(L^1(\mathbb R))$. To this end, we estimate

$$\begin{aligned} \Vert T_l\Vert _{L^1\rightarrow L^1}=\frac{|\langle f_l, \Psi '(f_l)\rangle |}{2\alpha J_l^2} \Vert K\Vert _{L^1}\leqq \frac{1}{\alpha J_l^2 }\leqq \frac{1+\alpha ^2}{1+\alpha ^2+c_0}<1 \end{aligned}$$

where we have used $\Vert K\Vert _{L^1}=1$, $\langle \Psi '(f_{l}), f_{l} \rangle \leqq 2$, and the bound $J_l^2\geqq \frac{1}{\alpha }\left( 1+\frac{c_0}{1+\alpha ^2}\right)$ from Lemma 3.3. This shows convergence of the expansion, and also that

$$\begin{aligned} \left\| \left[ 2 -\frac{\langle f_l, \Psi '(f_l)\rangle }{\alpha J_l^2} K*\right] ^{-1}\right\| _{L^1\rightarrow L^1}\leqq \frac{1}{2} \frac{1}{1-\Vert T_l\Vert _{L^1\rightarrow L^1}}\lesssim 1+\alpha ^2, \end{aligned}$$

From the Euler–Lagrange equation we get

$$\begin{aligned} \int _{f_l<\alpha } f_l\, \textrm{d}x\leqq \left\| \left[ 2 -\frac{\langle f_l, \Psi '(f_l)\rangle }{\alpha J_l^2} K*\right] ^{-1}\right\| _{L^1\rightarrow L^1} \frac{\Vert f_l\Vert _{L^2}^2}{\alpha }\lesssim 1+\alpha ^{-2}, \end{aligned}$$

uniformly in $\alpha >0$ and $l>l_0$, where we used that $\Vert f_l\Vert _{L^2}\lesssim \alpha ^{-1/2}$ (cf. Lemma 3.1). Adding the integrals over $f_l\geqq \alpha$ and $f_l<\alpha$ together gives the uniform $L^1$ bound. As $f_l$ is bell-shaped, we have for $x\in (0,2^l)$,

$$\begin{aligned} x f_l(x)\leqq \int _0^x f_l(y)\, \textrm{d}y\leqq \Vert f_l\Vert _{L^1}\lesssim 1+\alpha ^{-2}. \end{aligned}$$

As $f_l$ is supported on $[-2^l,2^l]$, this estimate also trivially holds for $|x| > 2^l$; and for $|x| = 2^l$ by continuity in the integrals. This concludes the proof. $\square$

3.6 The limit as $l \rightarrow \infty$

We now proceed to find the limit as $l\rightarrow \infty$.

Lemma 3.9

For any $\alpha >0$, any sequence $\lbrace f_l\rbrace _l$ of local maximisers from Lemma 3.5 (recall that we have no proof of uniqueness) has a subsequence $\{f_{l_k}\}_{k}$ that converges point-wise and in $L^p(\mathbb R)$, $p > 1$, and the limit $f_\alpha$ is a non-trivial bell-shaped solution of the global constrained maximisation problem

$$\begin{aligned} \sup \limits _{ N_{\Psi }(f)=1} \Vert K_{\frac{1}{4}}*f\Vert _{L^2}. \end{aligned}$$

(3.45)

The function $f_\alpha$ furthermore satisfies the Euler–Lagrange equation

$$\begin{aligned} \frac{\left\langle f_\alpha ,\Psi '(f_\alpha ) \right\rangle }{J_\alpha ^2}K*f_\alpha =\Psi '(f_\alpha ). \end{aligned}$$

(3.46)

Proof

By the upper bound on $\Vert f_l\Vert _{L^\infty }$ in Lemma 3.5 and the estimates in Corollary 3.8, we have that for any fixed choice of $\alpha >0$, there exists an $l_0$ such that that

$$\begin{aligned} f_l(x)\lesssim \frac{1}{1+|x|} \qquad \text { for all }\quad x, \end{aligned}$$

(3.47)

uniformly in $l>l_0$.

Next, since $\{f_l\}_l$ belongs to the unit sphere of ${\mathcal {L}}^\Psi$, and $\Vert f_l\Vert _{L^2(\mathbb R)} \lesssim \alpha ^{-1/2} N_\Psi (f_l)$ holds uniformly by Lemma 3.1. Also, by (3.17), we have the uniform in l bound $\Vert f_l\Vert _{L^\infty }\leqq C\alpha$. Thus, $\sup _l \Vert f_l\Vert _{L^\sigma }\leqq C$ for any $\sigma \in (2, +\infty ]$. By weak compactness and uniqueness of weak limits, there is $f_\alpha \in L^2\cap L^\infty$, and a weakly convergent in $L^\sigma (\mathbb R), \sigma \in (2, \infty )$ subsequence such that

$$\begin{aligned} f_{l_k} \rightharpoonup f_\alpha . \end{aligned}$$

By testing against characteristic functions, one sees that $f_\alpha$ is bell-shaped as well. We want to obtain convergence in the Euler–Lagrange equation (3.15). Since $\left\langle f_{l},\Psi '(f_{l}) \right\rangle \eqsim 1$ by Lemma 3.7, and $J_l$ is bounded from above and below by Lemmas 3.2 and 3.3 for any fixed $\alpha$, we may without loss of generality assume that $\lim _k \left\langle f_{l_k},\Psi '(f_{l_k}) \right\rangle \ne 0$ and

$$\begin{aligned} J_\alpha = \lim _{k} J_{l_k} \geqq \frac{1}{\sqrt{\alpha }} \end{aligned}$$

both exist. The above convergence for $f_{l_k}$ furthermore yields that

$$\begin{aligned} K*f_{l_k}(x)&=\int K(x-y) f_{l_k}(y) \, \textrm{d}y\\&=\left\langle K(x-\cdot ),f_{l_k} \right\rangle \rightarrow \left\langle K(x-\cdot ),f_\alpha \right\rangle =K*f_\alpha (x) \end{aligned}$$

for every fixed $x\in \mathbb R$, since $K \in L^q$ for $q < 2$. Thus, we have established the point-wise convergence

$$\begin{aligned} \lim _{k \rightarrow \infty }K*f_{l_k}(x) = K*f_\alpha (x), \qquad x \in \mathbb R. \end{aligned}$$

Let $g_l =\Psi '(f_l)$. Given $x\in \mathbb R$, for all k sufficiently large such that $|x|<2^{l_k}$, we have that

$$\begin{aligned} \begin{aligned} g_{l_k}(x)&=\frac{\left\langle f_{l_k},\Psi '(f_{l_k}) \right\rangle }{J_{l_k}^2}K*f_{l_k}(x)\\&\rightarrow \frac{\lim \left\langle f_{l_k},\Psi '(f_{l_k}) \right\rangle }{J_\alpha ^2}K*f_\alpha (x) =: g_\alpha (x), \end{aligned} \end{aligned}$$

(3.48)

converges point-wise as well. We can now readily deduce the point-wise convergence of $f_{l_k}$, since $\Psi '$ is strictly positive away from the origin. Indeed, for $|x| \leqq 2^l$ the value of $f_l(x)$ is given by $f_l(x) = (\Psi ')^{-1} \circ g_l(x)$. More explicitly,

$$\begin{aligned} f_l(x)= \left( \alpha -\sqrt{\alpha ^2-g_l(x)} \right) \chi _{g_l(x)\leqq \alpha ^2}+ \Big (\alpha +\sqrt{\frac{g_l(x)-\alpha ^2}{3}}\Big )\chi _{g_l(x)>\alpha ^2}, \end{aligned}$$

(3.49)

whence the latter expression has a point-wise limit along the subsequence $l_k$. By uniqueness, the point-wise and weak limits of $f_{l_k}$ coincide, so that

$$\begin{aligned} \lim _{k \rightarrow \infty } f_{l_k}(x)=f_\alpha (x), \end{aligned}$$

and (3.49) thus holds with $f_\alpha$ and $g_\alpha$ exchanged for $f_l$ and $g_l$, respectively. Equivalently, $g_\alpha =\Psi '(f_\alpha )$, so that (3.48) implies that

$$\begin{aligned} \Psi '(f_\alpha )=g_\alpha =\frac{\lim \left\langle f_{l_k},\Psi '(f_{l_k}) \right\rangle }{J_\alpha ^2}K*f_\alpha . \end{aligned}$$

(3.50)

This equality is valid on the entire real line, since for each $x \in \mathbb R$, (3.49) will eventually hold as $l_k \rightarrow \infty$.

It is now time to discuss the existence and value of $\lim _{k\rightarrow \infty } \left\langle f_{l_k},\Psi '(f_{l_k}) \right\rangle$. By Lemma 3.7, we have

$$\begin{aligned} \langle f_{l_k}, \Psi '(f_{l_k}) \rangle =&\,2 - \frac{1}{3} \int _{f_{l_k} <\, \alpha } f_{l_k}^3 \, \textrm{d}x\\&+ \int _{f_{l_k} \geqq \, \alpha } \alpha ^2 \left( \frac{2\alpha }{3} - f_{l_k}\right) +(f_{l_k}-\alpha )^3 + 3\alpha (f_{l_k}-\alpha )^2 \, \textrm{d}x, \end{aligned}$$

with $f_{l_k}(x) \rightarrow f_\alpha (x)$ for all $x$. By (3.47), the sequence $\lbrace f_l\rbrace$ is dominated by a function that is in $L^p$ for all $p>1$. As $f_{l_k}$ converges point-wise, Lebesgue’s dominated convergence theorem then implies that

$$\begin{aligned} \lim _{k\rightarrow \infty } \int f_{l_k}^p\, \textrm{d}x=\int f_\alpha ^p\, \textrm{d}x, \end{aligned}$$

for all $p>1$. In particular, we get that

$$\begin{aligned} \lim _{k \rightarrow \infty } \langle f_{l_k}, \Psi '(f_{l_k}) \rangle =&2 - \frac{1}{3} \int _{f_\alpha <\alpha } f_\alpha ^3\, \textrm{d}x, \\&+ \int _{f_\alpha \geqq \alpha } \alpha ^2\left( \frac{2\alpha }{3}-f_\alpha \right) +(f_\alpha -\alpha )^3+3\alpha (f_\alpha -\alpha )^2\, \textrm{d}x, \end{aligned}$$

and

$$\begin{aligned} 1=\lim _{k\rightarrow \infty } \int \Psi (f_{l_k})\, \textrm{d}x=\int \Psi (f_\alpha )\, \textrm{d}x. \end{aligned}$$

(3.51)

It follows that (cf. Lemma 3.7) $\lim _{k \rightarrow \infty } \langle f_{l_k}, \Psi '(f_{l_k}) \rangle = \langle f_{\alpha }, \Psi '(f_{\alpha }) \rangle$, and by (3.50) we then have that

$$\begin{aligned} \Psi '(f_\alpha )=\frac{\langle f_{\alpha }, \Psi '(f_{\alpha }) \rangle }{J_\alpha ^2}K*f_\alpha . \end{aligned}$$

Multiplying both sides by $f_\alpha$ and integrating, we get

$$\begin{aligned} \langle f_{\alpha }, \Psi '(f_{\alpha }) \rangle =\frac{\langle f_{\alpha }, \Psi '(f_{\alpha }) \rangle }{J_\alpha ^2} \langle K*f_\alpha ,f_\alpha \rangle . \end{aligned}$$

It follows that $J_\alpha ^2= \left\langle K*f_\alpha ,f_\alpha \right\rangle =\Vert K_{\frac{1}{4}}*f_\alpha \Vert ^2$. By (3.51), $N_\Psi (f_\alpha )=1$, and it follows that $f_\alpha$ is a maximiser. $\square$

Corollary 3.10

For any $\alpha >0$, every bell-shaped maximiser $f_\alpha$ of the global constrained maximisation problem satisfies

$$\begin{aligned}{} & {} f_\alpha (0)\leqq \frac{4}{\sqrt{3}}\cos \left( \frac{5\pi }{18}\right) \alpha \approx 1.48 \alpha , \nonumber \\{} & {} 1\leqq \langle f_\alpha , \Psi '(f_\alpha )\rangle \leqq 2, \end{aligned}$$

(3.52)

$$\begin{aligned}{} & {} \Vert f_\alpha \Vert _{L^1} + |x f_\alpha (x)| \lesssim 1+\alpha ^{-2}, \end{aligned}$$

(3.53)

$$\begin{aligned}{} & {} \Vert f_\alpha \Vert _{L^3}^3 \gtrsim \frac{1}{1+\alpha ^2}, \end{aligned}$$

(3.54)

and for each fixed $\delta >0$,

$$\begin{aligned} \Vert f_\alpha \Vert _{L^\infty } \lesssim \alpha ^{-\frac{1}{2}+\delta }. \end{aligned}$$

(3.55)

All these estimates are uniform in $\alpha >0$. Moreover, there is a number $\alpha _0\geqq 0$ such that for all $\alpha >\alpha _0$, there are maximisers $f_\alpha$ satisfying $f_\alpha (0)<\alpha$.

Proof

The smoothing effect of $K*$ implies that $K*f_\alpha$ is continuous, cf. Lemma 2.3, and hence so is the left-hand side of the Euler–Lagrange (3.46). As $\Psi '$ in the right-hand side is strictly increasing, and continuous, on the range of $f_\alpha$, one can solve for $f_\alpha$, obtaining $f_\alpha =(\Psi ')^{-1}\left[ \frac{\left\langle f_\alpha ,\Psi '(f_\alpha ) \right\rangle }{J_\alpha ^2}K*f_\alpha \right]$, whence the function $f_\alpha$ is in fact continuous. If $f_\alpha (0)>\frac{4}{\sqrt{3}}\cos \left( \frac{5\pi }{18}\right) \alpha =B$, then

$$\begin{aligned} \int _{f_\alpha \geqq B} |f_\alpha -B|\, \textrm{d}x>0. \end{aligned}$$

The upper bound (3.52) then follows from Proposition 3.6 by taking $l\rightarrow \infty$. The bounds $1 \leqq \langle f_\alpha , \Psi '(f_\alpha )\rangle \leqq 2$, (3.53) and (3.54) then follow directly from Lemma 3.7, Corollary 3.8 and Lemma 3.5, respectively.

It only remains to show that the solutions $f_\alpha$ vanish in $L^\infty$ as $\alpha \rightarrow \infty$. For all $\alpha$ sufficiently large we have that $f_\alpha (0)<\alpha$, so by the Euler–Lagrange equation (3.46) applied to $x=0$, and the bounds $J_\alpha \geqq \alpha ^{-1/2}$ and $\langle f_\alpha , \Psi '(f_\alpha ) \rangle \eqsim 1$, we obtain from Lemma 2.3 that

$$\begin{aligned} 2\alpha f_\alpha (0) - f_\alpha ^2(0)= \frac{\langle f_\alpha , \Psi '(f_\alpha )\rangle }{J_\alpha ^2} K*f_\alpha (0)\lesssim _q \alpha \Vert f_\alpha \Vert _{L^q}, \end{aligned}$$

for all $q>2$. Interpolating between the $L^2$ and the $L^3$ bounds of Lemma 3.1 we get that $\Vert f_\alpha \Vert _{L^q}\lesssim \alpha ^{1-\frac{3}{q}}$, $q\in (2,3)$. Since this is available for all $q \in (2,3)$, we obtain the inequality

$$\begin{aligned} f_\alpha ^2(0)-2\alpha f_\alpha (0)+C_\delta \alpha ^{\frac{1}{2}+\delta }\geqq 0, \end{aligned}$$

with $0 < \delta \ll 1$ arbitrary small and $C_\delta$ a positive constant depending on it. In view of that $f_\alpha (0) \leqq \alpha$, the solution to the above inequality is

$$\begin{aligned} f_\alpha (0) \leqq \alpha -\sqrt{\alpha ^2- D_\delta \alpha ^{\frac{1}{2}+\delta }}\lesssim _\delta \alpha ^{\delta -\frac{1}{2}}. \end{aligned}$$

$\square$

4 Dependence on the Parameter $\alpha$

In this section we investigate the dependence on the parameter $\alpha$ for the maximisers $f_\alpha$. In particular we are interested in the maximisers that satisfy $f_\alpha \leqq \alpha$, as other maximisers are not solutions of the Whitham equation. We therefore introduce the threshold parameter

$$\begin{aligned} \alpha _0:=\inf \{\xi >0 :\text {for any } \alpha \in (\xi , \infty ) \text { there exists a maximiser } f_{\alpha }(0)<\alpha \}. \end{aligned}$$

(4.1)

From Corollary 3.10 it follows that $\alpha _0$ exists and is a finite number. Below we will prove that $\alpha _0>0$, meaning that there are maximisers found in this paper that either attain or exceed the height $f_\alpha (0) = \alpha$. We will also prove that $\alpha _0<\frac{5}{2}$, which means that we have solutions also for intermediate (and perhaps small) values of $\alpha$. Note that $\alpha$ is in fact in opposite relation to the wave-height of the final solution constructed in Section 5; the solutions vanish as $\alpha \rightarrow \infty$.

Lemma 4.1

$\alpha \mapsto \alpha J_\alpha ^2$ is continuous and strictly decreasing on $(0,\infty )$, with

$$\begin{aligned} \lim _{\alpha \rightarrow \infty } \alpha J_\alpha ^2&=1, \\ \lim _{\alpha \searrow 0} \alpha J_\alpha ^2&=\frac{3\tilde{B}^2}{2+3(\tilde{B}-1)+3(\tilde{B}-1)^3}>\frac{3}{2}, \end{aligned}$$

where $\tilde{B}=\frac{4}{\sqrt{3}}\cos \left( \frac{5\pi }{18}\right) \approx 1.48$.

Proof

Let $\alpha \in (0,\infty )$ and write $f_\alpha = \alpha q_\alpha ( \alpha ^3 \cdot )$. Then $N_\Psi (f_\alpha )=1$ implies that

$$\begin{aligned} \int _{q_\alpha <1} q_\alpha ^2 - \frac{1}{3} q_\alpha ^3\, \textrm{d}x+\int _{q_\alpha \geqq 1}\frac{2}{3}+(q_\alpha -1)+(q_\alpha -1)^3\, \textrm{d}x= 1, \end{aligned}$$

with $0<q_\alpha \leqq \alpha ^{-1} \max (f_\alpha )$. From this we see that, in fact, for any $\tilde{\alpha }\in (0,\infty )$, we have $N_\Psi (\tilde{\alpha }q_\alpha (\tilde{\alpha }^3\cdot ))=1$. Let $\alpha _1<\alpha$. As $\widehat{K}(\xi )$ is strictly decreasing in $|\xi |$, we have that $\widehat{K}(\alpha _1^3\xi )>\widehat{K}(\alpha ^3\xi )$ for all $\xi \ne 0$, hence

$$\begin{aligned} \alpha _1 J_{\alpha _1}^2&= \alpha _1 \int \widehat{K}(\xi )|\widehat{f_{\alpha _1}}(\xi )|^2\, \textrm{d}\xi \\&\geqq \int \widehat{K}(\alpha _1^3 \xi )|\widehat{q_\alpha }(\xi )|^2\, \textrm{d}x>\int \widehat{K}(\alpha ^3 \xi )|\widehat{q_\alpha }(\xi )|^2\, \textrm{d}\xi =\alpha J_\alpha ^2. \end{aligned}$$

As $\alpha \in (0,\infty )$ was arbitrary, this proves that $\alpha \mapsto \alpha J_\alpha ^2$ is strictly decreasing. Similarly, we have that

$$\begin{aligned} \alpha J_\alpha ^2\geqq \int \widehat{K}(\alpha ^3 \xi )|\widehat{q_{\alpha _1}}(\xi )|^2\, \textrm{d}\xi , \end{aligned}$$

and hence

$$\begin{aligned} 0<\alpha _1 J_{\alpha _1}^2-\alpha J_\alpha ^2\leqq&\int \left( \widehat{K}(\alpha _1^3 \xi )-\widehat{K}(\alpha ^3 \xi )\right) |\widehat{q_{\alpha _1}}(\xi )|^2\, \textrm{d}\xi \\ \leqq&|\alpha ^3-\alpha _1^3| \int \max _{\alpha _1 \leqq \tau \leqq \alpha } |\xi \widehat{K}'(\tau ^3 \xi )| |\widehat{q_{\alpha _1}}(\xi )|^2\, \textrm{d}\xi . \end{aligned}$$

The final integral is bounded as $\alpha \rightarrow \alpha _1$ (or contrariwise): $K'(0) = 0$, and $\xi \mapsto |\xi \widehat{K}'( \tau \xi )|$ is smooth and decaying, uniformly for $\tau$ in any compact subset of ${\mathbb R}$; furthermore $\Vert q_\alpha \Vert _{L^2}^2 \lesssim 1$ uniformly for all $\alpha$ (in fact $\Vert q_\alpha \Vert _{L^2}^2 \eqsim 1$, see Remark 4.2). This proves continuity.

To see what happens as $\alpha \rightarrow \infty$, we assume $f_\alpha \leqq \alpha$, which holds for all $\alpha \geqq \alpha _0$, and hence $0\leqq q_\alpha \leqq 1$; and rewrite the Euler–Lagrange equation (3.46) with $f_\alpha =\alpha q_\alpha (\alpha ^3 \cdot )$ in terms of $q_\alpha$:

$$\begin{aligned} 2 q_\alpha (x) - q_\alpha ^2(x) = \frac{2 - \frac{1}{3} \int q_\alpha ^3 \, \textrm{d}x}{\alpha J_\alpha ^2} \frac{1}{\alpha ^3} \int K\left( \frac{x-y}{\alpha ^3}\right) q_\alpha (y)\, \textrm{d}y. \end{aligned}$$

Since $0 \leqq q_\alpha \leqq 1$ and $\alpha J_\alpha ^2 \geqq 1$, we see that for any $p \in (1,2)$,

$$\begin{aligned} \Vert q_\alpha \Vert _{\infty } \leqq 2 \Vert \alpha ^{-3}K[ \alpha ^{-3}(x-y)]\Vert _{L^p} \Vert q_\alpha \Vert _{L^{p^*}} \leqq C \Vert K\Vert _{L^p} \alpha ^{-\frac{3(p-1)}{p}}, \end{aligned}$$

(4.2)

where we have used that $\int |q_\alpha (x)|^{p^*} \, \textrm{d}x\leqq \int q_\alpha ^2(x) \, \textrm{d}x\leqq \frac{3}{2}$ when $\frac{1}{p} + \frac{1}{p^{*}} = 1$ and $p < 2$ (recall that $K \not \in L^2$). By (4.2),

$$\begin{aligned} \Vert q_\alpha \Vert _{L^3}^3 \leqq \Vert q_\alpha \Vert _{L^\infty } \Vert q_\alpha \Vert _{L^2}^2 \leqq C_p \alpha ^{-\frac{3(p-1)}{p}} \Vert q_\alpha \Vert _{L^2}^2 \rightarrow 0, \end{aligned}$$

and by the constraint $N_\Psi (f_\alpha ) = 1$ this in turn means that

$$\begin{aligned} \lim _{\alpha \rightarrow \infty } \alpha \Vert f_\alpha \Vert _{L^2} = \lim _{\alpha \rightarrow \infty } \Vert q_\alpha \Vert _{L^2}^2 = 1. \end{aligned}$$

In general, as $\widehat{K} \leqq 1$, we have

$$\begin{aligned} \alpha J_\alpha ^2 = \alpha \int \widehat{K}(\xi ) |\widehat{f_\alpha }(\xi )|^2 \, \textrm{d}\xi = \int \widehat{K}(\alpha ^3 \xi )|\widehat{q_\alpha }(\xi )|^2 \, \textrm{d}\xi \leqq \Vert q_\alpha \Vert _{L^2}^2, \end{aligned}$$

(4.3)

and it follows that $\limsup _{\alpha \rightarrow \infty } \alpha J_\alpha ^2\leqq 1$. On the other hand, from Lemma 3.3 we know that $\alpha J_\alpha ^2\geqq 1$ for all $\alpha$, and we conclude that

$$\begin{aligned} \lim _{\alpha \rightarrow \infty } \alpha J_\alpha ^2= 1. \end{aligned}$$

Now we turn to the limit $\alpha \searrow 0$ for $\alpha J_\alpha ^2$. Note that $N_\Psi (f_\alpha )=1$ means

$$\begin{aligned} 1 = \int _{q_\alpha \leqq 1} \left( q_\alpha ^2 - \frac{1}{3} q_\alpha ^3 \right) \, \textrm{d}x+ \int _{q_\alpha \geqq 1} \left( {\textstyle \frac{2}{3}} + (q_\alpha -1) + (q_\alpha -1)^3 \right) \, \textrm{d}x. \end{aligned}$$

(4.4)

According to (3.22), the quotient $f^2/\Psi (f)$ of the weights in the $L^2$ and the Orlicz norms is maximised for $f =B$. For the scaling $q_\alpha$ fulfilling (4.4), it follows that

$$\begin{aligned} \Vert q_\alpha \Vert _{L^2}^2 = \frac{\int q_\alpha ^2}{\int \tilde{\Psi }(q_\alpha )} = \frac{\int \frac{q_\alpha ^2}{\tilde{\Psi }(q_\alpha )} \tilde{\Psi }(q_\alpha )}{\int \tilde{\Psi }(q_\alpha )} \leqq \frac{\int \frac{\tilde{B}^2}{\tilde{\Psi }(\tilde{B})} \tilde{\Psi }(q_\alpha )}{\int \tilde{\Psi }(q_\alpha )} = \frac{\tilde{B}^2}{\frac{2}{3}+(\tilde{B}-1)+(\tilde{B}-1)^3}, \end{aligned}$$

(4.5)

where we note that $q_\alpha > 0$, and $\Psi _1$ is the scaled constraint function $\Psi$ used in (4.4). As $\alpha J_\alpha ^2$ is a maximum, this means that

$$\begin{aligned} \int \widehat{K}(\alpha ^3 \xi )|\widehat{q}(\xi )|^2 \, \textrm{d}\xi \leqq \alpha J_\alpha ^2 \leqq \frac{\tilde{B}^2}{\frac{2}{3}+(\tilde{B}-1)+(\tilde{B}-1)^3}, \end{aligned}$$

(4.6)

for any other choice of the function $q$ fulfilling the constraint. But equality in (4.5) is obtained for

$$\begin{aligned} q_0=\tilde{B}\chi _{[-\frac{1}{2}(\frac{2}{3}+(\tilde{B}-1)+(\tilde{B}-1)^3)^{-1} ,\frac{1}{2}(\frac{2}{3}+(\tilde{B}-1)+(\tilde{B}-1)^3)^{-1}]}, \end{aligned}$$

a function that also fulfils the constraint (4.4). Now fix $q = q_0$ and let $\alpha \searrow 0$ in (4.6). As $\widehat{K}$ is smooth with $\widehat{K}(0)=1$, this forces $\alpha J_\alpha ^2$ to the desired value. $\square$

Remark 4.2

One can prove $\Vert q_\alpha \Vert _{L^2} \eqsim 1$, for all $\alpha \in {\mathbb R}$. By the constraint (4.4), at least one of the integrals to the right in that equation is of size $1/2$ or bigger. If this is true for the first integral, then

$$\begin{aligned} \int _{q_\alpha \leqq 1} q_\alpha ^2 \, \textrm{d}x\geqq \int _{q_\alpha \leqq 1} \left( q_\alpha ^2 - \frac{1}{3} q_\alpha ^3 \right) \, \textrm{d}x\geqq \frac{2}{3} \int _{q_\alpha \leqq 1} q_\alpha ^2 \, \textrm{d}x\end{aligned}$$

because $0 \leqq q_\alpha \leqq 1$ holds on that region of integration; and because $q_\alpha \leqq \frac{3}{2}$ in general by Lemma 3.6 and (3.52), and $\int _{q_\alpha \geqq 1} \, \textrm{d}x\leqq \frac{3}{2}$ by (4.4), we have $\int _{q_\alpha \geqq 1} q_\alpha ^2 \, \textrm{d}x\leqq \left( \frac{3}{2} \right) ^2 \int _{q_\alpha \geqq 1} \, \textrm{d}x\leqq \left( \frac{3}{2}\right) ^3,$ whence $\int _{{\mathbb R}} q_\alpha ^2 \, \textrm{d}x\eqsim 1$. If instead the second integral in (4.4) is the bigger one, then

$$\begin{aligned} \frac{1}{2}&\leqq \int _{q_\alpha \geqq 1} \left( {\textstyle \frac{2}{3}} + (q_\alpha -1) + (q_\alpha -1)^3 \right) \, \textrm{d}x\\&\leqq \int _{q_\alpha \geqq 1} \left( {\textstyle \frac{2}{3}} + ({\textstyle \frac{3}{2}}-1) + ({\textstyle \frac{3}{2}} -1)^3 \right) \, \textrm{d}x= \frac{31}{24} |\{x :q_\alpha (x) \geqq 1\}|, \end{aligned}$$

so $\frac{12}{31} \leqq |\{x :q_\alpha (x) \geqq 1\}| \leqq \frac{3}{2}$, and therefore $\int _{q_\alpha \geqq 1} q_\alpha ^2 \, \textrm{d}x\eqsim 1,$ by the upper bound on $q_\alpha$. As earlier, $\int _{q_\alpha \leqq 1} q_\alpha ^2 \, \textrm{d}x\eqsim \int _{q_\alpha \leqq 1} \left( q_\alpha ^2 - \frac{1}{3} q_\alpha ^3 \right) \, \textrm{d}x\leqq 1$, so in total $\Vert q_\alpha \Vert _{L^2} \eqsim 1$ in both cases.

As an immediate corollary, we get that $\alpha _0>0$.

Corollary 4.3

The threshold parameter $\alpha _0$ is strictly positive and $1<\alpha _0J_{\alpha _0}^2<\frac{3}{2}$.

Proof

Assume that for every $\alpha >0$, there exists a maximiser $f_\alpha (0)<\alpha$ and let $f_\alpha = \alpha q_\alpha ( \alpha ^3 \cdot )$. Then $q_\alpha (0)<1$. In general, the condition $\int q^2-\frac{1}{3}q^3 \, \textrm{d}x=1$, $q\leqq 1$, implies that $\Vert q\Vert _{L^2}^2\leqq \frac{3}{2}$ with equality if and only if $q=\chi _{[-\frac{3}{4},\frac{3}{4}]}$. Hence $\Vert q_\alpha \Vert _{L^2}^2<\frac{3}{2}$ and by (4.3) we get

$$\begin{aligned} \alpha J_\alpha ^2<\frac{3}{2}, \end{aligned}$$

for all $\alpha >0$. This contradicts Lemma 4.1, and it follows that $\alpha _0>0$. $\square$

We can also provide a rough upper bound on $\alpha _0$. The estimates in the below proof may be improved, but the purpose of the proposition is to establish maximisers with $f_\alpha (0)<\alpha$ also for intermediate values of $\alpha$.

Proposition 4.4

The threshold parameter satisfies $\alpha _0<\left( \frac{3}{2}\right) ^{4/3}\left( \frac{2}{\pi }+1\right) ^{2/3} \approx 2.385$.

Proof

From Lemma 3.2 we have $J_\alpha ^2> \alpha ^{-1}$ and by Young’s inequality $\Vert K*f_\alpha \Vert _{L^\infty }\leqq \Vert K\Vert _{L^{3/2}} \Vert f_\alpha \Vert _{L^3}$. Hence, if $f_\alpha \leqq \alpha$, we get from the Euler–Lagrange equation that

$$\begin{aligned} 2\alpha f_\alpha -f_\alpha ^2 =\frac{\langle f_\alpha , \Psi '(f_\alpha )\rangle }{J_\alpha ^2}K*f_\alpha < \alpha \langle f_\alpha , \Psi '(f_\alpha )\rangle \Vert K\Vert _{L^{3/2}} \Vert f_\alpha \Vert _{L^3}. \end{aligned}$$

If $f_\alpha \leqq \alpha$, then the condition $N_\Psi (f_\alpha )$ implies that $\Vert f_\alpha \Vert _{L^3}^3<\frac{3}{2}$ and $\langle f_\alpha , \Psi '(f_\alpha )\rangle =2-\frac{1}{3}\Vert f_\alpha \Vert _{L^3}^3$, so $\langle f_\alpha , \Psi '(f_\alpha )\rangle \Vert f_\alpha \Vert _{L^3}<\left( \frac{3}{2}\right) ^{4/3}$. So if $f_\alpha (0)=\alpha$, we get

$$\begin{aligned} \alpha ^2< \left( \frac{3}{2}\right) ^{4/3}\Vert K\Vert _{L^{3/2}}\alpha . \end{aligned}$$

(4.7)

As K is positive, strictly monotone on $(0,\infty )$ and $\Vert K\Vert _{L^1}=1$, there is an $a>0$ such that $K(a)=1$ and

$$\begin{aligned} \Vert K\Vert _{L^{3/2}}^{3/2}&=2\int _0^\infty K(x)^{3/2} \, \textrm{d}x\\&< 2\left( \int _0^{a} K(x)^{3/2}\, \textrm{d}x+ \int _a^\infty K(x)\, \textrm{d}x\right) \\&<2\int _0^{a} \left( K(x)^{3/2}-K(x) \right) \, \textrm{d}x+1. \end{aligned}$$

Writing $\widehat{K}(\xi )=\frac{1}{\sqrt{|\xi |}}+\frac{\sqrt{\tanh (|\xi |)}-1}{\sqrt{|\xi |}}$, we have that the first term has inverse Fourier transform $1/\sqrt{2\pi |x|}$, while the second term is integrable and exponentially decaying and hence has a real-analytic transform. Moreover, the inverse transform of the second term is clearly negative around the origin. Hence $K(x)<\frac{1}{\sqrt{2\pi |x|}}$ for $|x|\leqq a$ and $a<\frac{1}{2\pi }$, and we get that

$$\begin{aligned} \int _0^{a} K(x)^{3/2}-K(x)\, \textrm{d}x&<\int _0^{a} (2\pi x)^{-3/4}-(2\pi x)^{-1/2}\, \textrm{d}x\\&=\frac{4}{(2\pi )^{3/4}} a^{1/4}-\sqrt{\frac{2}{\pi }}a^{1/2}<\frac{1}{\pi }. \end{aligned}$$

It follows that $\Vert K\Vert _{L^{3/2}}<\left( \frac{2}{\pi }+1\right) ^{2/3}$, and from (4.7) we get that

$$\begin{aligned} \alpha <\left( \frac{3}{2}\right) ^{4/3}\left( \frac{2}{\pi }+1\right) ^{2/3} \approx 2.385. \end{aligned}$$

It follows that $\alpha _0$ must satisfy this upper bound. $\square$

Lemma 4.5

For $\alpha >0$, let $\lbrace \alpha _j\rbrace _j \subset (0,\infty )$ be a sequence that converges to $\alpha$ and let $f_{\alpha _j}$ be a maximiser corresponding to $\alpha _j$. Then a subsequence $\lbrace f_{\alpha _{j_k}}\rbrace _k$ converges point-wise and in $L^p$, simultaneously for all $p\in (1,\infty ]$, to a maximiser of the corresponding maximisation problem for $\alpha$.

Proof

For ease of notation, let $f_{\alpha _j}=f_j$. By Lemma 3.1, we have

$$\begin{aligned} \Vert f_j\Vert _{L^2}\lesssim \frac{1}{\sqrt{\alpha _j}}\leqq \frac{1}{\inf _j \sqrt{\alpha _j}}<\infty , \end{aligned}$$

uniformly in j. Hence there is a subsequence $\lbrace f_{j_k}\rbrace _k$ and a $f_{\alpha }\in L^2$ such that

$$\begin{aligned} f_{j_k}\rightharpoonup f_{\alpha }. \end{aligned}$$

This implies that

$$\begin{aligned} K*f_{j_k}(x)=\langle K(x-\cdot ),f_{j_k}\rangle \rightarrow \langle K(x-\cdot ),f_{\alpha }\rangle =K*f_{\alpha }(x) \end{aligned}$$

converges point-wise. Let $\Psi _j$ be the $\Psi$-function corresponding to $\alpha _j$, and let $g_j=\Psi _j'(f_j)$. By Corollary 3.10, $1<\langle f_{j_k},\Psi _{j_k}'(f_{j_k})\rangle <2$ for all k, so we can without loss of generality assume that $\lim _{k\rightarrow \infty } \langle f_{j_k},\Psi _{j_k}'(f_{j_k})\rangle >1$ exists. As $J_\alpha$ is continuous in $\alpha$, we get that

$$\begin{aligned} g_{j_k}(x)=\frac{\langle f_{j_k},\Psi _{j_k}'(f_{j_k})\rangle }{J_{\alpha _{j_k}}^2} K*f_{j_k}(x)\rightarrow \frac{\lim _k \langle f_{j_k},\Psi _{j_k}'(f_{j_k})\rangle }{J_{\alpha }^2} K*f_{\alpha }(x)=:g_{\alpha }(x) \end{aligned}$$

also converges point-wise. We have that

$$\begin{aligned} f_j(x)= \left( \alpha _j-\sqrt{\alpha _j^2-g_j(x)} \right) \chi _{g_j(x)\leqq \alpha _j^2}+ \left( \alpha _j+\sqrt{\frac{g_j(x)-\alpha _j^2}{3}}\right) \chi _{g_j(x)>\alpha _j^2}. \end{aligned}$$

The right-hand side has a point-wise limit along the subsequence $j_k$, hence $f_{j_k}\rightarrow f_{\alpha }$ also converges point-wise. Moreover,

$$\begin{aligned} g_{\alpha }=\Psi _{\alpha }'(f_{\alpha }). \end{aligned}$$

By Corollary 3.10, we have the following estimate, uniform in j:

$$\begin{aligned} |x|f_j(x)\lesssim 1+\alpha _j^{-2}\leqq 1+(\inf _j \alpha _j)^{-2}. \end{aligned}$$

Hence we get that

$$\begin{aligned} f_j(x)\lesssim \frac{1}{1+|x|}, \end{aligned}$$

(4.8)

uniformly in j. The right-hand side is in $L^p$ for all $p>1$, so the point-wise convergence and Lebesgue’s dominated convergence theorem gives that

$$\begin{aligned} \lim _{k\rightarrow \infty }\int f_j^p\, \textrm{d}x=\int f_\alpha ^p\, \textrm{d}x<\infty , \end{aligned}$$

for all $p>1$. This implies that $N_{\Psi _\alpha }(f_\alpha )=1$ and

$$\begin{aligned} \lim _{k\rightarrow \infty } \langle f_{j_k},\Psi _{j_k}'(f_{j_k})\rangle = \langle f_\alpha , \Psi _\alpha '(f_\alpha )\rangle . \end{aligned}$$

It follows that

$$\begin{aligned} \Psi _\alpha '(f_\alpha )=\frac{\langle f_\alpha , \Psi _\alpha '(f_\alpha )\rangle }{J_\alpha ^2}K*f_\alpha . \end{aligned}$$

Multiplying by $f_\alpha$ on both sides and integrating over ${\mathbb R}$, we get that $\Vert K_{\frac{1}{4}}*f_\alpha \Vert _{L^2}=J_\alpha$, and as $N_{\Psi _\alpha }(f_\alpha )=1$, this implies that $f_\alpha$ is a maximiser. $\square$

Corollary 4.6

At the threshold parameter $\alpha _0$, there exists a maximiser $f_{\alpha _0}$ satisfying $f_{\alpha _0}(0)\leqq \alpha _0$ and a maximiser $g_{\alpha _0}$ satisfying $g_{\alpha _0}(0)\geqq \alpha _0$.

Remark 4.7

Any $g_{\alpha _0}$ with $g_{\alpha _0}(0)>\alpha _0$ would be a maximiser, but not a solution to the Whitham equation.

Proof

Let $\lbrace \alpha _j\rbrace _j$ be a monotonically decreasing sequence with $\alpha _j\searrow \alpha _0$. By the definition of $\alpha _0$, we have that for all j there are maximisers $f_j$ for $\alpha _j$ satisfying $f_j(0)<\alpha _j$. It follows from Lemma 4.5 that a subsequence of $\lbrace f_j\rbrace _j$ converges point-wise to a maximiser $f_{\alpha _0}$, which by the point-wise convergence must satisfy

$$\begin{aligned} f_{\alpha _0}(0)\leqq \alpha _0. \end{aligned}$$

Similarly, letting $\lbrace \alpha _j\rbrace _j\subset (0,\alpha _0)$ be a monotonically increasing sequence with $\alpha _j\nearrow \alpha _0$, we have, for each j, maximisers $g_j$ satisfying $g_j(0)\geqq \alpha _j$, and we conclude that there is a maximiser $g_{\alpha _0}$ such that

$$\begin{aligned} g_{\alpha _0}(0)\geqq \alpha _0. \end{aligned}$$

This proves the result. $\square$

Remark 4.8

Note that if we have equality $f_{\alpha _0}(0)=\alpha _0$, then this will correspond to a solitary wave of maximal height for the Whitham equation (see Section 5). We would expect that $f_{\alpha _0}=g_{\alpha _0}$ in the above result, in which case $f_{\alpha _0}(0)=\alpha _0$. However, presently we have no uniqueness results or other results that precludes the possibility that the maximisers are distinct and $g_{\alpha _0}(0)>\alpha _0 > f_{\alpha _0}(0)$.

5 Solitary Waves of the Full-Dispersion Equation

The next proposition shows that the range of bell-shaped solutions are confined to the ‘natural’ region $(0,\frac{\mu }{2}]$ where the end-points correspond to the zero solution and the Whitham highest wave, respectively. All solitary waves have super-critical wave speed bounded from above by twice the critical wave speed, a result in line with both [11] and [13].

Proposition 5.1

Let $\mu >0$ and $\varphi \in L^p({\mathbb R})$ for some $p\in (2, +\infty ]$ be a non-constant, bell-shaped solution of (1.3). Then, it satisfies $0 < \varphi (x) \leqq \frac{\mu }{2}$, with $\sup \varphi \geqq \mu - 1$ and

$$\begin{aligned} \varphi (x)=\frac{\mu - \sqrt{\mu ^2-4 K*\varphi (x)}}{2} \end{aligned}$$

(5.1)

almost everywhere. If $\varphi \in L^1(\mathbb R)$, then the wave speed $\mu$ belongs to the open interval  (1, 2).

Remark 5.2

In spirit of the main method of this paper, Proposition 5.1 and its proof have been written for an $L^p$-setting. Note, however, that this is not to indicate that solutions are non-smooth. As explained in the proof Corollary 3.10, one can bootstrap from an $L^p$-solution in equation (5.1), to obtain a continuous solution, due to the smoothing effect of $K*$.

Proof

To prove $0 < \varphi (x) \leqq \frac{\mu }{2}$, denote

$$\begin{aligned} z(x)=K*\varphi (x). \end{aligned}$$

Then z is bell-shaped, too, and in fact it is strictly decreasing in $(0, \infty )$ in accordance with the proof of Lemma 2.4. The assumption that $\varphi \in L^p({\mathbb R})$ for some $p\in (2, +\infty ]$ guarantees that $z$ is everywhere pointwise defined. From the quadratic equation $z=\mu \varphi - \varphi ^2$ we conclude that

$$\begin{aligned} 2\varphi (x)= {\left\{ \begin{array}{ll} \mu +\sqrt{\mu ^2-4 z(x)}, \quad &{} x\in A_+, \\ \mu -\sqrt{\mu ^2-4 z(x)}, \quad &{} x\in A_-, \end{array}\right. } \end{aligned}$$

for some disjoint sets $A_\pm$ with $A_+\cup A_-=[0,\infty )$. Assume for a contradiction that $A_+$ has positive measure. Then there are sets $A^1_+$, $A^2_+$ in $A_+$ of positive measure with $A^1_+$ to the left of $A^2_+$. Let $0<x_1<x_2$ be two arbitrary elements in $A^1$ and $A^2$, respectively. Since $\varphi$ is bell-shaped, we have $\varphi (x_1)\geqq \varphi (x_2)$. But solving the inequality

$$\begin{aligned} \mu +\sqrt{\mu ^2-4 z(x_1)} \geqq \mu +\sqrt{\mu ^2-4 z(x_2)} \end{aligned}$$

yields $z(x_2)\geqq z(x_1)$, so that $z|_{A^2_+}\geqq z|_{A^1_+}$. This contradicts the strict monotonicity of $z$, whence $A_+$ must have zero measure, and $\varphi =\varphi _-$ almost everywhere. Thus (5.1) holds, $\varphi (x)\leqq \frac{\mu }{2}$, and $\varphi$ is non-negative by assumption since it is bell-shaped, which gives that it is non-zero in view of that $z = K *\varphi$ is strictly monotone.

To prove the remaining bounds, note that, for an integrable solution $\varphi$ of (1.3),

$$\begin{aligned} \int \varphi (x) \, \textrm{d}x= \int K*\varphi (x) \, \textrm{d}x=\mu \int \varphi (x) \, \textrm{d}x- \int \varphi (x)^2 \, \textrm{d}x. \end{aligned}$$

It follows that $(\mu -1) \int \varphi (x) \, \textrm{d}x= \int \varphi (x)^2 \, \textrm{d}x$, whence $\mu >1$. By taking the supremum in (1.3) one furthermore obtains

$$\begin{aligned} \mu \Vert \varphi \Vert _\infty \leqq \Vert K *\varphi \Vert _\infty + \Vert \varphi ^2 \Vert _\infty \leqq \Vert \varphi \Vert _\infty + \Vert \varphi \Vert _\infty ^2. \end{aligned}$$

This proves that $\mu \leqq 1 + \Vert \varphi \Vert _\infty$ for non-zero solutions. When $\varphi \leqq \frac{\mu }{2}$ we also obtain $\mu \leqq 2$ from the same inequality, with equality if and only if $\Vert K *\varphi \Vert _\infty = \Vert \varphi \Vert _\infty$. For bell-shaped solutions, the latter means

$$\begin{aligned} \int K(y) \varphi (y) \, \textrm{d}y= \varphi (0), \end{aligned}$$

which can happen only if $\varphi$ equals $\varphi (0)$ almost everywhere. Consequently, $\mu < 2$ for non-constant solutions (this bound is general, and does not require integrability). $\square$

Theorem 5.3

For any maximiser $f_\alpha$ satisfying $f_\alpha (0)\leqq \alpha$, the function

$$\begin{aligned} \varphi = \frac{J_{\alpha }^2 f_{\alpha }}{2-\frac{1}{3}\int f_{\alpha }^3 \, \textrm{d}x}, \qquad \end{aligned}$$

is a positive, even and one-sided strictly monotone solution of the steady Whitham equation (1.3) with wave speed

$$\begin{aligned} \mu = \frac{2\alpha J_{\alpha }^2}{2-\frac{1}{3}\int f_{\alpha }^3(x) \, \textrm{d}x} \in (1,2), \end{aligned}$$

satisfying $0 < \varphi \leqq \frac{\mu }{2}$. In particular, there is an injective curve of solutions parameterized by $\alpha \in [\alpha _0,\infty )$, and the function

$$\begin{aligned}{}[\alpha _0,\infty ) \ni \alpha \mapsto \alpha J_\alpha ^2 \in (1, {\textstyle \frac{3}{2}}) \end{aligned}$$

is strictly decreasing and continuous with the limit $1$ achieved as $\alpha \rightarrow \infty$. For $\alpha >\alpha _0$ the waves satisfy $0<\varphi <\frac{\mu }{2}$ and these waves are all smooth, while for $\alpha = \alpha _0$ the wave satisfies $\varphi (0)\leqq \frac{\mu }{2}$, with potential equality. The solutions scale as

$$\begin{aligned} \varphi \simeq \frac{f_\alpha }{\alpha }, \end{aligned}$$

(5.2)

with the estimate being uniform in $\alpha$. In particular, the waves are small for large values of the parameter $\alpha$ in the sense that $\Vert \varphi \Vert _{L^p}\lesssim \alpha ^{-1}$ for $\alpha \gg 1$ and all $p\in [1,\infty ]$. As $\alpha \rightarrow \infty$, one further has $\mu \rightarrow 1$, the bifurcation point for solitary waves.

Proof

Let $\alpha \geqq \alpha _0$. By the definition of $\alpha _0$, maximisers satisfy $f_\alpha (0)<\alpha$ for $\alpha >\alpha _0$ and by Corollary 4.6, there exists a maximiser $f_{\alpha _0}$ that satisfies $f_{\alpha _0}(0)\leqq \alpha _0$. Then, by the Euler–Lagrange equation for the maximisers,

$$\begin{aligned} K*f_{\alpha }= \frac{J_{\alpha }^2}{2-\frac{1}{3}\int f_{\alpha }^3 \, \textrm{d}x} [2\alpha f_{\alpha } - f_{\alpha }^2], \end{aligned}$$

so by letting $\beta =\frac{2-\frac{1}{3}\int f_{\alpha }^3(x) \, \textrm{d}x}{J_{\alpha }^2}$, $\mu = \frac{2\alpha }{\beta }$ and $\varphi =\frac{f_{\alpha }}{\beta }$ one immediately sees that $\varphi$ satisfies the Whitham equation with wave speed $\mu$. Since $f_\alpha$ belongs to $L^1$ (cf. Corollary 3.10), is bell-shaped and one-sided strictly monotone, so is its scaling $\varphi$, and we see that $\varphi$ satisfies $0<\varphi \leqq \frac{\mu }{2}$, with equality being achieved if and only if $f_\alpha (0)=\alpha$, which can potentially only happen for $\alpha =\alpha _0$. Proposition 5.1 then guarantees that $\mu \in (1,2)$. The smoothness of waves satisfying $\varphi < \frac{\mu }{2}$ follows from [13, Theorem 5.1]. The monotonicity, continuity and end-point limits of $\alpha \rightarrow \alpha J_\alpha ^2$ have been established in Lemma 4.1 and Corollary 4.3.

To find a full set of solutions, we start by showing that the map $f_\alpha \rightarrow \varphi$ is injective. Let $\alpha _1, \alpha _2 \in [\alpha _0, \infty )$ (they can be equal) and say that $f_{\alpha _1}$ and $f_{\alpha _2}$, would correspond to the same solution $\varphi$. Then, by the definition of $\varphi$,

$$\begin{aligned} \frac{J_{\alpha _1}^2 f_{\alpha _1}}{2-\frac{1}{3}\int f_{\alpha _1}^3 \, \textrm{d}x} = \frac{J_{\alpha _2}^2 f_{\alpha _2}}{2-\frac{1}{3}\int f_{\alpha _2}^3 \, \textrm{d}x}. \end{aligned}$$

(5.3)

That is, $f_{\alpha _2}$ is a scaling of $f_{\alpha _1}$; $f_{\alpha _2} = \lambda f_{\alpha _1}$ for some $\lambda \in {\mathbb R}_+$, and

$$\begin{aligned} J_{\alpha _2}^2 = (\mathcal {J}(f_{\alpha _2}))^2 = (\mathcal {J}(\lambda f_{\alpha _1}))^2 = \lambda ^2 (\mathcal {J}(f_{\alpha _1}))^2 = \lambda ^2 J_{\alpha _1}^2. \end{aligned}$$

Insertion of this into (5.3) yields a linear equation in $\lambda ^3$, which has as its only solution $\lambda = 1$, since our maximisers are all positive. Thus the map $f_\alpha \mapsto \varphi$ is injective. Next, note that for any $\alpha >0$ and any positive function $f\in L^2\cap L^3$ that satisfies $f\leqq 2\alpha$ (which all maximisers do - cf. (3.52)),

$$\begin{aligned} \int \Psi _{\alpha }(f)\, \textrm{d}x\end{aligned}$$

is strictly increasing in $\alpha$. This follows from the pointwise derivative of $\Psi _\alpha (f)$, which is $f^2$ for $0 \leqq f < \alpha$, and for $f > \alpha$ is easily seen to be positive exactly for $f \in (\alpha , 2\alpha )$. Hence the (possibly multi-valued) map $\alpha \mapsto f_\alpha$ is also injective. Thus, if for each $\alpha \in [\alpha _0,\infty )$ we pick one solution $f_\alpha$, we find a full injective curve $[\alpha _0,\infty ) \ni \alpha \mapsto \varphi$.

To get the estimates for $\varphi$, note that by the definition of $\varphi$ and $\mu$, we have

$$\begin{aligned} \varphi =\frac{1}{2\alpha } \mu f_\alpha , \end{aligned}$$

and (5.2) then follows directly from the fact that $\mu \in (1,2)$. By Corollary 3.10, $\Vert f_\alpha \Vert _{L^1}\lesssim 1$ for $\alpha \gg 1$ and $\Vert f_\alpha \Vert _{L^\infty }\lesssim \alpha ^{-1/2+\delta }$ for each fixed $\delta >0$. Interpolation then gives the $L^p$-estimates for $\varphi$. As mentioned in Remark ?? this estimate can be improved for $p\geqq 2$, for example by interpolation and the additional estimate $\Vert f_\alpha \Vert _{L^2}^2\lesssim \alpha ^{-1}$. Finally, the limit $\mu \rightarrow 1$ as $\alpha \rightarrow \infty$ follows directly from the definition of $\mu$ and Lemma 4.1. $\square$

Remark 5.4

We have the uniform bound $\Vert f_\alpha \Vert _{L^2}>J_\alpha >\alpha ^{-1/2}$, and it follows that $\Vert \varphi \Vert _{L^2}>\frac{1}{2}\alpha ^{-3/2}$. As we have solutions for all $\alpha \in [\alpha _0,\infty )$ and $\alpha _0<2.4$ (cf. Proposition 4.4), it follows that the curve of solutions in Theorem 5.3 also includes solitary waves of intermediate size.