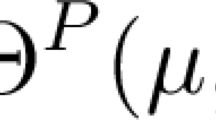Abstract
We consider the Abelian Yang–Mills–Higgs functional, in the non-self dual scaling, on a complex line bundle over a closed Riemannian manifold of dimension \(n\ge 3\). This functional is the natural generalisation of the Ginzburg–Landau model for superconductivity to the non-Euclidean setting. We prove a \(\Gamma \)-convergence result, in the strongly repulsive limit, on the functional rescaled by the logarithm of the coupling parameter. As a corollary, we prove that the energy of minimisers concentrates on an area-minimising surface of dimension \(n-2\), while the curvature of minimisers converges to a solution of the London equation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \((M, \, g)\) be a smooth, compact, connected, oriented, Riemannian manifold without boundary, of dimension \(n\ge 3\). Let \(E\rightarrow M\) be a Hermitian complex line bundle on M, equipped with a (smooth) reference connection \({{\,\textrm{D}\,}}_0\), compatible with the metric. For any 1-form \(A\in W^{1,2}(M, \, \textrm{T}^*M)\), we denote by \({{\,\textrm{D}\,}}_A:= {{\,\textrm{D}\,}}_0 - iA\) the associated connection and by \({-iF_A}\) the curvature 2-form of \({{\,\textrm{D}\,}}_A\). We will assume throughout the paper that A is real-valued (i.e., it is represented by real-valued functions in any local trivialisation of \(E \rightarrow M\)), implying that also \(F_A\) is real-valued and that \({{\,\textrm{D}\,}}_A\) is compatible with the metric. (Conversely, any metric connection on \(E \rightarrow M\) is of the form \({{\,\textrm{D}\,}}_A\), for some real-valued 1-form A; see, e.g., Appendix 4.1.) From now on, we will refer to \(F_A\) as the curvature of \({{\,\textrm{D}\,}}_A\).
Let \(\varepsilon > 0\) be a small parameter. For any section \(u\in W^{1,2}(M, \, E)\) of E and any (real-valued) 1-form \(A\in W^{1,2}(M, \, \textrm{T}^* M)\), we consider the Ginzburg–Landau or Abelian Yang–Mills–Higgs functional
In this paper, we prove a convergence result for minimisers in the limit as \(\varepsilon \rightarrow 0\): given a sequence of minimisers \(\{(u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\}\), the energy density of \(\{(u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\}\) concentrates on an \((n-2)\)-dimensional surface \(S_*\), which is area-minimising in a distinguished homology class, determined by the topology of the bundle \(E\rightarrow M\) (i.e., the Poincaré-dual to the first Chern class \(c_1(E)\in H^2(M; \, \mathbb Z)\)). On the other hand, the curvature of \(A_\varepsilon ^{\min }\) converges to a solution of the London equation, with a singular source term carried by \(S_*\). This convergence result for minimisers is stated in Corollary B and it is deduced from our main result, Theorem A, below, which provides a full \(\Gamma \)-convergence theorem for the functionals \(G_\varepsilon \). Moreover, and in agreement with known results in the Euclidean setting (c.f., e.g., [2, 42]), Theorem A shows that energy concentration on topological singular sets is not unique to minimisers but is a general feature for sequences \(\{(u_\varepsilon ,\,A_\varepsilon )\}\) satisfying a (natural) logarithmic asymptotic bound on the energy.
Functionals of the form (1) were originally proposed by V. Ginzburg and L. Landau in 1950 [33] as a model of superconductors subject to a magnetic field (where u is an order parameter such that \(\left| u \right| ^2\) is proportional to the density of electronic Cooper pairs, while A is the vector potential for the magnetic field). The theory accounts for most commonly observed effects (such as the quantisation of magnetic flux, the Meissner effect, and the emergence of Abrikosov vortex lattices, see e.g. [66]); moreover, it can be justified as a suitable limit of Bardeen, Cooper and Schrieffer’s microscopic theory [8]. Ginzburg–Landau functionals, or variants thereof, arise in other areas of physics—for instance, superfluidity (see e.g. [29]) and particle physics, for (1) is the Abelian version of Yang–Mills–Higgs action functional in gauge theory (see e.g. [39]).
Being invariant under gauge transformations is, indeed, one of the most prominent features of the functional (1). In a Euclidean domain \(\Omega \subseteq \mathbb R^n\), the functional (1) reduces to
where \(u \in W^{1,2}(\Omega ,\,\mathbb C)\) is a complex-valued map and \(A \in W^{1,2}(\Omega , \, \textrm{T}^* \Omega )\) is a real-valued one-form on \(\Omega \). Assuming for simplicity that \(\Omega \) is simply connected (in which case, by classical results in [17], any function \(\varphi \in W^{2,2}(\Omega ,\mathbb {S}^1)\) can be lifted to \(\theta \in W^{2,2}(\Omega ,\mathbb R)\)), the invariance of (2) under gauge-transformations can be expressed as there follows: for any \((u, \, A) \in W^{1,2}(\Omega ,\,\mathbb C) \times W^{1,2}(\Omega ,\,\textrm{T}^* \Omega )\) and any \(\theta \in W^{2,2}(\Omega , \, \mathbb R)\), it holds that
The property (3) suggests that Ginzburg–Landau functionals are naturally set in the context of complex line bundles over a manifold. Indeed, the gauge group \(\mathbb {S}^1\simeq \textrm{U}(1)\) acts on a pair \((u, \, A)\) precisely in the same way as transition functions of a bundle act (locally) on sections and connection forms. In this general setting, gauge-invariance takes the following general form: for any \((u, \, A)\in W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\) and \(\Phi \in W^{2,2}(M, \, \mathbb {S}^1)\), consider the transformation
where \(\Phi u\) is defined by the fibre-wise action of the structure group \(\textrm{U}(1)\simeq \mathbb {S}^1\) on E. Then it holds that
(Notice that, if M is simply connected, then \(\Phi \) can be lifted to \(\theta \in W^{2,2}(M,\mathbb R)\), by adapting results in [17].)
Gauge-invariance will play a crucial rôle in this paper. Physically, each observable quantity must be gauge-invariant and the energy is only one of them. For instance, each term in the energy density of \(G_\varepsilon \) is gauge-invariant, as well as \(F_A\) (whose physical counterpart in superconductivity is, in fact, the magnetic field).
Minimisers of gauge-invariant functionals on manifolds, such as (1), include several examples of physically relevant objects (such as Bogomolnyi monopoles, vortices, instantons, Hermite-Einstein connections on Kälher manifolds). Moreover, such objects play an important rôle in topology and complex geometry. For example, Yang-Mills minimisers are used in the classification of stable holomorphic vector bundles on complex manifolds (this is the content of Donaldson, Uhlenbeck and Yau’s theorem [28, 67]; for generalisations to Yang–Mills–Higgs minimisers, see e.g. [19, 20, 31]). Functionals such as (1) may also be coupled to Einstein equations; this approach is relevant to cosmology, as it provides a model for gravity-driven spontaneous symmetry breaking [64].
We are interested in the asymptotic regime as \(\varepsilon \rightarrow 0\), which is known as the London limit within the context of superconductivity, or the strongly repulsive limit, within the context of particle physics. This limit is characterised by the emergence of topological singularities—the energy of minimisers concentrates, to leading order, on \((n-2)\)-dimensional sets, whose global structure depends on the topology of the bundle \(E\rightarrow M\). We are interested in providing a variational characterisation, in the sense of \(\Gamma \)-convergence, of those singularities as being area-minimising in a homology class. We expect that this variational characterisation will provide indications on the dynamics of singularities arising in the limit of the corresponding time-dependent models. For instance, for a generalisation of (1) on a Lorentzian manifold, we expect that the energy concentrate on time-like relativistic strings or M-branes (see e.g. [9, 10, 41] for the analysis of related problems in Minkowski space-time). Moreover, we expect the heat flow of (1) to be related to motion by mean curvature (see [15] for the asymptotics of a non-gauge-invariant problem, with no dependence on A, in the Euclidean setting).
The asymptotic analysis of (1) in the limit as \(\varepsilon \rightarrow 0\) heavily relies on analogous results for the simplified Ginzburg–Landau functional, i.e.
The functional (6) was first considered by Bethuel, Brezis and Hélein [11], in case \(\Omega \) is a two-dimensional Euclidean domain. \(\Gamma \)-convergence results for (6), in case \(\Omega \subseteq \mathbb R^n\) with \(n\ge 2\), were proved in [2, 42]. These results show that energy concentration on area-minimising surfaces (of codimension two) is already a feature of the simplified functionals (6)—cf. Modica and Mortola’s \(\Gamma \)-convergence result in the real-valued case, [46]. In fact, both the functionals (2), (6) and the corresponding heat flows have been extensively studied in Euclidean domains (see e.g. [40, 51, 56, 57, 59]), as well as on Riemannian manifolds [25, 27, 65].
In case E is the tangent bundle on a closed Riemann surface and the connection \({{\,\textrm{D}\,}}_A\) is fixed, the asymptotics for minimisers and gradient-flow solutions are available in [24, 37]. Minimisers of (1) in the limit as \(\varepsilon \rightarrow 0\) were studied in case the base manifold M is two-dimensional [50, 55]. Other results address a self-dual variant of the functional (1), in which the curvature term \(\left| F_A \right| ^2\) is replaced by \(\varepsilon ^2 \left| F_A \right| ^2\)—see e.g. [36] for the two-dimensional case and [53, 54] for the higher-dimensional case. In a way, self-duality is a sort of additional symmetry in the Yang–Mills–Higgs functionals, with applications in the theory of minimal surfaces, as explored e.g. in the recent papers [26, 53, 54]. However, the non self-dual scaling (1) appears to be more closely related to the original physical motivation of the Ginzburg–Landau functional. To better explain this point, let us introduce the gauge-invariant Jacobian \(J(u, \, A)\) of a pair \((u, \, A)\), defined pointwise (when the right-hand-side of (7) below makes sense) as the 2-form
for any smooth test field X, Y on M. Here \(\left\langle \cdot , \, \cdot \right\rangle \) is the real-valued scalar product induced by the Hermitian form on E. Plainly, \(J(u,\, A)\) is well-defined for any \((u, \, A)\in W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\) such that \(G_\varepsilon (u, \, A) < +\infty \). In superconductivity, there is a physical observable associated with gauge-invariant Jacobians: the supercurrent vorticity (cf., e.g., [66, Chapter 5] and [39, Chapter 1]).
As it is easy to check, for minimisers \((u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) of the non-self dual functional (1), the curvatures \(F_\varepsilon := F_{A_\varepsilon ^{\min }}\) satisfy the (gauge-invariant) London equation
a distinctive feature of superconductivity (see, e.g., [66, Chapters 1 and 5]). In Corollary B below, we show that the curvatures \(F_\varepsilon = F_{A^{\min }_\varepsilon }\) converge, up to extraction of a subsequence, to a solution \(F_*\) of the (limiting) London equation
The right-hand side \(J_*\) of (9) is the limit of the Jacobians, i.e. \(J_\varepsilon \rightarrow \pi J_*\) (cf. Theorem A). \(J_*\) is a singular measure, with values in 2-forms, carried by an area-minimising set of dimension \(n-2\).
By contrast, minimisers of the self-dual functionals do not converge to solutions of (9); in the limit as \(\varepsilon \rightarrow 0\), there holds \(F_* = 2\pi J_*\) instead. Moreover, while minimisers of the self-dual functionals have uniformly bounded energy as \(\varepsilon \rightarrow 0\), minimisers \((u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) of (1) on a non-trivial bundle must satisfy \(G_\varepsilon (u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\rightarrow +\infty \) as \(\varepsilon \rightarrow 0\)—in fact, \(G_\varepsilon (u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) is of the order of \(\left| \log \varepsilon \right| \), as we will see below (cf. Remark 2). Such a large amount of energy allows for wild oscillations in the phases of the maps \(u_\varepsilon \), preventing compactness even in weak topologies in Sobolev spaces and making the proof of Theorem A quite challenging, as in fact is for its Euclidean counterpart in [2, 42].
One might expect that critical points of (1) converge, in a suitable sense, to minimal surfaces, as is the case for (15) (see [12]) and for the self-dual Yang–Mills–Higgs energies (see [54]). Here, we prove this result for sequences of minimisers of (1) (see Corollary B below); we investigate non-minimising critical points in [23].
Main results. We consider sequences \(\{(u_\varepsilon , A_\varepsilon )\}\subset W^{1,2}(M,E) \times W^{1,2}(M,\textrm{T}^*M)\) that satisfy a logarithmic energy bound
Our main result, Theorem A below, is a \(\Gamma \)-convergence result for the rescaled functionals \(\frac{G_\varepsilon }{\left| \log \varepsilon \right| }\). The topology of the \(\Gamma \)-convergence is defined in terms of the Jacobian of \((u_\varepsilon , \, A_\varepsilon )\).
We denote by \(\star \) the Hodge dual operator, regarded as a map from k-forms to \((n-k)\)-currents and from k-currents to \((n-k)\)-forms (upon composition with the natural isomorphism between vectors and covectors, induced by the metric—see (1.1) below and Appendix 4.1 for more details). We consider a distinguished, non-empty class \(\mathcal {C}\) of integer-multiplicity, rectifiable \((n-2)\)-currents with no boundary. The class \(\mathcal {C}\) is uniquely defined in terms of the topology of the bundle \(E\rightarrow M\); more precisely, \(\mathcal {C}\in H_{n-2}(M; \, \mathbb Z)\) is Poincaré-dual to the first Chern class \(c_1(E)\in H^2(M; \, \mathbb Z)\) of the bundle (see (1.6) below for more details).
Theorem A
The following statements hold.
-
(i)
Let \(\{(u_\varepsilon , \, A_\varepsilon )\}_\varepsilon \) be a sequence in \(W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\) that satisfies (10). Then, there exist a (non-relabelled) subsequence and a bounded measure \(J_*\), with values in 2-forms, such that \(J(u_\varepsilon , \, A_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any p with \(1 \le p < n/(n-1)\) and
$$\begin{aligned} \pi \left| J_* \right| \!(M) \le \liminf _{\varepsilon \rightarrow 0}\frac{G_\varepsilon (u_\varepsilon , \, A_\varepsilon )}{\left| \log \varepsilon \right| } \end{aligned}$$(11)Moreover, \(\star J_*\) is an integer-multiplicity, rectifiable \((n-2)\)-cycle in the class \(\mathcal {C}\).
-
(ii)
Let \(S_*\) be an integer-multiplicity, rectifiable \((n-2)\)-cycle in the class \(\mathcal {C}\) and let \(J_*:= \star S_*\) be the dual 2-form. Then, there exists a sequence \(\{(u_\varepsilon , \, A_\varepsilon )\}_\varepsilon \) such that \(J(u_\varepsilon , \, A_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any p with \(1 \le p < n/(n-1)\) and
$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\frac{G_\varepsilon (u_\varepsilon , \, A_\varepsilon )}{\left| \log \varepsilon \right| } \le \pi \left| J_* \right| \!(M) \end{aligned}$$(12)
Remark 1
Not every pair \((u, \, A)\in W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\) has finite energy. Conversely, not every Sobolev pair \((u, \, A)\in W^{1,1}(M, \, E)\times W^{1,1}(M, \, \textrm{T}^*M)\) with \(G_\varepsilon (u, \, A)<+\infty \) is such that \((u, \, A)\in W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\) (for instance, it may or may not be true that \(\left| {{\,\textrm{D}\,}}_0u \right| = \left| {{\,\textrm{D}\,}}_A u + iAu \right| \in L^2(M)\)). For simplicity, we have chosen to state our results in terms of \(W^{1,2}\)-pairs, but our results extend to all Sobolev pairs of finite energy, with no significant change in the proofs.
Remark 2
Since the class \(\mathcal {C}\) is always not empty, a straightforward consequence of Theorem A is that the energy of sequences of minimisers of \(G_\varepsilon \) is automatically of order \(\left| \log \varepsilon \right| \) as \(\varepsilon \rightarrow 0\).
As a corollary, we obtain a variational characterisation for the limit of a sequence of minimisers. Given \((u, \, A)\in W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\), we denote the (rescaled) energy density of \((u, \, A)\) as
Corollary B
Let \((u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) be a minimiser of \(G_\varepsilon \) in \(W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\). Then, there exist bounded measures \(J_*\), \(F_*\), with values in 2-forms, and a (non-relabelled) subsequence such that
for any \(p < n/(n-1)\), and \(\mu _\varepsilon (u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\rightharpoonup \pi \left| J_* \right| \) weakly\(^*\) as measures. Moreover, the current \(\star J_*\) belongs to \(\mathcal {C}\) and has minimal mass among all the currents in \(\mathcal {C}\), while \(F_*\) satisfies the London equation
In other words, the energy of the minimisers \((u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) concentrate, to leading order, on the support of a \((n-2)\)-dimensional current, which is dual to the limit Jacobian \(J_*\) and minimises of the area in its homology class. Moreover, the limit curvature \(F_*\) is uniquely determined from \(J_*\), via the London equation. Due to gauge-invariance (5), we cannot expect compactness for the minimisers themselves, \(u_\varepsilon ^{\min }\), \(A_\varepsilon ^{\min }\). However, it seems plausible that compactness (in suitable norms) should be restored if we make a suitable choice of the gauge. We plan to address this point in a forthcoming paper [23].
As an intermediate step towards the proof of Theorem A, we prove a \(\Gamma \)-convergence result for a simpler functional that only depends on the variable u. For any \(u\in W^{1,2}(M, \, E)\), we consider
The functional \(E_\varepsilon \) is analogous to the non-gauge-invariant version of the Ginzburg–Landau functional, (6). We define \(J(u):= J(u, \, 0)\), i.e. J(u) is the Jacobian of u with respect to the reference connection \({{\,\textrm{D}\,}}_0\).
Theorem C
The following statements hold:
-
(i)
Let \(\{u_\varepsilon \}_\varepsilon \subset W^{1,2}(M, \, E)\) be a sequence such that
$$\begin{aligned} \sup _{\varepsilon >0} \frac{E_\varepsilon (u_\varepsilon )}{\left| \log \varepsilon \right| } < +\infty \end{aligned}$$(16)Then, there exists a (non-relabelled) subsequence and a bounded measure \(J_*\), with values in 2-forms, such that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any p with \(1 \le p < n/(n-1)\) and
$$\begin{aligned} \pi \left| J_* \right| \!(M) \le \liminf _{\varepsilon \rightarrow 0}\frac{E_\varepsilon (u_\varepsilon )}{\left| \log \varepsilon \right| } \end{aligned}$$(17)Moreover, \(\star J_*\) is an integer-multiplicity, rectifiable \((n-2)\)-cycle in the class \(\mathcal {C}\).
-
(ii)
Let \(S_*\) be an integer-multiplicity, rectifiable \((n-2)\)-cycle in the class \(\mathcal {C}\) and let \(J_*:= \star S_*\) be the dual 2-form. Then, there exists a sequence \(\{u_\varepsilon \}_\varepsilon \) in \(W^{1,2}(M, \, E)\) such that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any p with \(1 \le p < n/(n-1)\) and
$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}\frac{E_\varepsilon (u_\varepsilon )}{\left| \log \varepsilon \right| } \le \pi \left| J_* \right| \!(M) \end{aligned}$$
The proof of Theorem C depends heavily on analogous \(\Gamma \)-convergence results obtained in the Euclidean setting [2, 42]. The most delicate point is, probably, showing that the limit Jacobian \(J_*\) satisfies \(\star J_*\in \mathcal {C}\), for this is a global topological property that cannot be deduced from localisation arguments. The proof of this fact is contained in Sect. 2.1.3.
Once Theorem C is proved, the upper bound (ii) in the statement of Theorem A follows immediately. On the other hand, the proof of the lower bound in Theorem A relies crucially on the London equation, as well as Theorem C. More precisely, given a sequence \(\{(u_\varepsilon , \, A_\varepsilon )\}\) that satisfies the logarithmic energy bound (10), we construct a sequence of bounded sections \(\{v_\varepsilon \}\) and a sequence of 1-forms \(\{B_\varepsilon \}\) in such a way that \(G_\varepsilon ({v_\varepsilon }, \, B_\varepsilon ) \le G_\varepsilon (u_\varepsilon , \, A_\varepsilon )\), the difference \(J(u_\varepsilon , \, A_\varepsilon ) - J({v_\varepsilon }, \, B_\varepsilon )\) is small in \(W^{-1,p}(M)\) and, most importantly, the curvatures \(F_{B_\varepsilon }\) satisfy the London Eq. (8). Specifically, the sections \(v_\varepsilon \) are obtained from the corresponding \(u_\varepsilon \) by a truncation argument while the 1-forms \(B_\varepsilon \) are obtained by minimising the auxiliary energy functionals
in a suitable class, while keeping \(v_\varepsilon \) fixed (see Sect. 3 for full details). As mentioned few lines above, the fact that the new curvatures \(F_{B_\varepsilon }\) satisfy the London Eq. (8) is of the utmost importance to our argument. Indeed, by exploiting the ellipticity and the gauge-invariance of the London equation, and up to a suitable choice of gauge, we can then show that the difference \(G_\varepsilon (v_\varepsilon , \, B_\varepsilon ) - E_\varepsilon (v_\varepsilon )\) is of order smaller than \(\left| \log \varepsilon \right| \). Once this is done, the conclusion follows by Theorem C.
The rest of that paper is organised as follows: in Sect. 1, we set some notation and recall a few useful properties of the Jacobian, \(J(u, \, A)\). Section 2 is devoted to the proof of Theorem C, while Sect. 3 contains the proof of Theorem A and Corollary B. The paper is completed by a series of appendices, which contain a review of some background material on Sobolev spaces for sections of a vector bundle and currents, as well as the proof of a few technical results.
2 Preliminaries
We will frequently encounter Sobolev spaces of sections of a bundle. For the convenience of the reader, we provide the definitions and state some basic properties in Appendix 4. The notation we use is fairly self-explanatory. However, we stress that the symbols such as \(W^{1,p}(M, \, E)\) denote Sobolev spaces of \(W^{1,p}\)-sections of the bundle \(E\rightarrow M\). In case E is a trivial bundle, \(E=M\times \mathbb C\) or \(E=M\times \mathbb R\), we write \(W^{1,p}(M, \, \mathbb C)\), \(W^{1,p}(M, \, \mathbb R)\) instead of \(W^{1,p}(M, \, M\times \mathbb C)\), \(W^{1,p}(M, \, M\times \mathbb R)\).
The notation we use for differential forms is rather standard, too. For instance, we denote as \(\#:\Lambda ^k\textrm{T}^* M\rightarrow \Lambda _k\textrm{T}M\), \(\flat :\Lambda _k\textrm{T}M \rightarrow \Lambda ^k\textrm{T}^* M\) the isometric isomorphisms between vectors and forms induced by the metric on M, and by \(*:\Lambda ^k\textrm{T}^*M\rightarrow \Lambda ^{n-k}\textrm{T}^* M\) the Hodge dual operator induced by the metric and the orientation of M. We define an operator
as follows: for any k-form \(\omega \) and any k-vector v,
The operator \(\star \) can be extended to an operator between currents and form-valued distributions; see Appendix 4.1 for details. We denote by \({{\,\textrm{d}\,}}\), \({{\,\textrm{d}\,}}^*\) the exterior differential and codifferential of forms, respectively. The codifferential of a k-form \(\omega \) is defined by \({{\,\textrm{d}\,}}^*\omega := (-1)^{n(k-1)+1} *{{\,\textrm{d}\,}}* \, \omega \).
We recall a few basic notions about currents in Appendix 4.1. Given a current S, we will write \(\partial S\) for its boundary (defined as in (B.1) below), \(\mathbb {M}(S)\) for its mass (see (B.4) below) and \(\mathbb {F}(S)\) for its (integer-multiplicity) flat norm (see (B.7) below).
It is convenient to revisit the definition of Jacobian, (7). Given a pair \((u, \, A)\in W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\) such that \({{\,\textrm{D}\,}}_Au \in L^2(M, \, \textrm{T}^* M\otimes E)\), we define the gauge-invariant pre-Jacobian as the 1-form
Under the assumptions above, \(j(u, \, A)\) is integrable, so it makes sense to consider its differential in the sense of distributions. We define the (distributional) gauge-invariant Jacobian as
Such a quantity is used in the mathematical literature on the Ginzburg–Landau model at least since [58] (in the Euclidean case; the natural extension to Hermitian line bundles probably appeared firstly in [53]). In case the pair \((u, \, A)\) is smooth, an explicit computation shows that the Jacobian as defined by (1.3) agrees with (7). The same remains true if \((u, \, A)\) satisfies \(G_\varepsilon (u, \, A) <+\infty \), by a truncation and density argument. However, (1.3) allows us to define the Jacobian for a broader class of pairs \((u, \, A)\)—for instance, when \(u\in W^{1,1}(M, \, E)\cap L^\infty (M, \, E)\) and \(A\in L^1(M, \, \textrm{T}^*M)\). We stress that both \(j(u,\,A)\) and \(J(u,\,A)\) are, by definition, local operators; in particular, they commute with restrictions.
Remark 1.1
Let \(u:M\rightarrow E\), \(A:M\rightarrow \textrm{T}^*M\), \(B:M\rightarrow \textrm{T}^* M\) be such that \(J(u, \, A)\), \(J(u, \, B)\) are well-defined—for instance, \(u\in (W^{1,1}\cap L^\infty )(M, \, E)\), \(A\in L^1(M, \, \textrm{T}^*M)\), \(B\in L^1(M, \, \textrm{T}^*M)\). As an immediate consequence of (1.2)–(1.3), we have
In particular, if \(\left| u \right| =1\) a.e., then \(J(u, \, A) = J(u, \, B)\).
The distributional Jacobian is continuous with respect to suitable notions of weak convergence. For the convenience of the reader, we recall a result in this direction. We denote by j(u), J(u) the pre-Jacobian and Jacobian with respect to the reference connection \({{\,\textrm{D}\,}}_0\), i.e.
where \(F_0\) is the curvature of the reference connection \({{\,\textrm{D}\,}}_0\). j(u) and J(u) are well-defined for any \(u\in (W^{1,p}\cap L^q)(M, \, E)\), with \(p\in [1, \, +\infty ]\) and \(q:= p^\prime \in [1, \, +\infty ]\) such that \(1/p + 1/q = 1\).
Proposition 1.2
Let \(p\in [1, \, +\infty ]\) and \(q:= p^\prime \in [1, \, +\infty ]\) be such that \(1/p + 1/q = 1\). If the sequence \(\{u_\varepsilon \}\subset (W^{1,p}\cap L^q)(M, \, E)\) is such that \(u_\varepsilon \rightarrow u\) weakly in \(W^{1,p}(M)\) and strongly in \(L^q(M)\), then \(J(u_\varepsilon )\rightharpoonup ^* J(u)\) weakly\(^*\) in the sense of distributions.
Proof
Thanks to (1.5), it suffices to show that \(j(u_\varepsilon )\rightharpoonup ^* j(u)\) weakly\(^*\) in the sense of distributions. This follows from the Hölder inequality.\(\quad \square \)
In fact, the Jacobian \(J(u, \, A)\) satisfies suitable continuity properties as a function of both u and A (see e.g. [53, Proposition 3.1]).
Finally, we introduce a distinguished (homology) class of \((n-2)\) currents, \(\mathcal {C}\in H_{n-2}(M; \, \mathbb Z)\), as follows. Let \(w:M\rightarrow E\) be a smooth section of E. We assume that w is transverse to the zero-section of E; that means, for any point \(p\in M\) such that \(w(p) = 0\), the differential \({{\,\textrm{d}\,}}_p w\) induces a surjective linear map
where \(E_p\) is the fibre of E at p. Such a section w exists; in fact, by Thom’s transversality theorem (see e.g. [21, Theorem 14.6]), any smooth section can be approximated (e.g., uniformly) by transverse sections. Transversality implies that the inverse image \(Z:= w^{-1}(0)\) is a smooth manifold without boundary, of dimension \(n - 2\). As both M and E are oriented manifolds (the orientation on E is the one induced by the complex structure on each fibre), the manifold Z can be given an orientation, in a natural way [18, Proposition 12.7]. As a consequence, there is a well-defined \((n-2)\)-current \(\llbracket Z\rrbracket \), carried by Z, with unit multiplicity. We have \(\partial \llbracket Z\rrbracket = 0\), because Z is manifold without boundary. We define
The class \(\mathcal {C}\) does not depend on the choice of w (see [18, Proposition 12.8]). Moreover, by the boundary rectifiability theorem (see e.g. [62, Theorem 6.3]), all the elements of \(\mathcal {C}\) are integer-multiplicity, rectifiable \((n-2)\)-currents with no boundary. In the topological jargon, \(\mathcal {C}\in H_{n-2}(M; \, \mathbb Z)\) is Poincaré-dual to the first Chern class \(c_1(E)\in H^2(M; \, \mathbb Z)\). Equivalently, \(\mathcal {C}\) is Poincaré-dual to the Euler class of E, regarded as a real bundle over M with the orientation induced by the complex structure. The following statement motivates our interest in the class \(\mathcal {C}\):
Proposition 1.3
Let \(u\in W^{1,1}(M, \, E)\) be such that \(\left| u \right| =1\) a.e. If J(u) is a bounded measure, then \(\frac{1}{\pi }\star J(u)\) is an integer-multiplicity rectifiable \((n-2)\)-current and
Proposition 1.3 establishes a topological relationship between the singular set of a unit-norm section \(M\rightarrow E\) and the zero set of a generic smooth section. A similar principle applies to several different contexts; see, for instance, [1, Theorem 3.8] and [2, Proposition 5.3] for results in the Euclidean setting, [4, Proposition 2.8] for sections of real line bundles, [6] for sections of a principal \(\mathbb Z\)- or \(\mathbb Z/p\mathbb Z\)-bundle, [53, Corollary 3.3] for sections of complex line bundles. For the reader’s convenience, we reproduce below the key steps of the proof in our context, emphasising the topological aspects.
Sketch of the proof of Proposition 1.3
Let w be a smooth section of \(E\rightarrow M\) that is transverse to the zero section of E, as above. Let \(u_0:= w/\left| w \right| \). The section \(u_0\) is well-defined and smooth away from \(Z:= w^{-1}(0)\). Moreover, \(u_0\in W^{1,p}(M, \, E)\) for any \(p\in [1, \, 2)\). Indeed, since w is transverse to the zero section of E, the differential \({{\,\textrm{d}\,}}w\) restricted to the normal bundle \(\textrm{N}Z\) of Z is a fibre-wise isomorphism \(\textrm{N}Z\rightarrow E\). As M is compact, it follows that there exists a constant C such that, for any \(x\in M\),
Therefore,
The integral at the right-hand side is finite for any \(p\in [1, \, 2)\), because Z has codimension 2 (see e.g. [2, Lemma 8.3]). Moreover, for a suitable orientation of Z (as in [18, Proposition 12.7]), if holds that
As the Jacobian is a local operator, it suffices to check that (1.9) is satisfied in an arbitrary coordinate neighbourhood \(U\subseteq M\). Due to Remark 1.1, \(J(u_{0|U})\) is equal to the Jacobian of \(u_{0|U}\) with respect to the flat connection, \(\bar{J}:= \frac{1}{2} {{\,\textrm{d}\,}}\langle {{\,\textrm{d}\,}}u_0, iu_0\rangle \). For the latter, we have \(\star \bar{J} = \pi \llbracket Z\rrbracket \) in U (this computation is similar to, e.g., [43, Example 3.4]) and hence (1.9) follows.
Let \(u\in W^{1,1}(M)\) be such that \(\left| u \right| =1\) a.e. in M. We define a map \(\Phi :M\rightarrow \mathbb C\) as
so that \(u = \Phi u_0\). As \(\left| u \right| = \left| u_0 \right| = 1\) a.e., we have \(\left| \Phi \right| =1\) a.e. in M. Moreover, \(\Phi \in W^{1,1}(M)\) and, by explicit computation,
where \(\bar{J}(\Phi ):= \frac{1}{2} {{\,\textrm{d}\,}}\left\langle {{\,\textrm{d}\,}}\Phi , \, i\Phi \right\rangle \). Let \(E\subseteq M\) be the set of points where \(\Phi \) is not approximately differentiable. Then, E is negligible (with respect to the volume measure) and \(M\setminus E\) can be written as a finite union of closed sets, \(M\setminus E = \bigcup _{j=1}^{+\infty } F_j\), such that \(\Phi \) is Lipschitz-continuous on each \(F_j\) (see e.g. [30, 3.1.18], [35, Theorems 11 and 12]). As a consequence, for \(\mathcal {H}^1\)-a.e. \(y\in \mathbb {S}^1\), the set \(N_y:= \Phi ^{-1}(y)\setminus E\) is countably \(\mathcal {H}^{n-1}\)-rectifiable and, by the coarea formula, \(\mathcal {H}^{n-1}(N_y) <+\infty \) (the details of the argument are as in [1, Section 7.5]). For a.e. \(y\in \mathbb {S}^1\), we have
Indeed, for each coordinate neighbourhood \(U\subseteq M\), we have \(\star \bar{J}(\Phi ) = \pi \, (-1)^{n-1} \, \partial \llbracket N_y\rrbracket \) in U due to [1, Theorem 3.8]. As the Jacobian is a local operator, (1.11) follows by partition of unity. In particular, \(\frac{1}{\pi }\star \bar{J}(\Phi )\) is the boundary of an integer-multiplicity, rectifiable \((n-1)\)-current. Suppose now that J(u) is a bounded measure. Then, \(\bar{J}(\Phi )\) is a bounded measure, too. By combining (1.10) and (1.11), we obtain that \(\frac{1}{\pi }\star \bar{J}(\Phi )\) belongs to the class \(\mathcal {C}\) defined by (1.6). By Federer and Fleming’s boundary rectifiability theorem [30, 4.2.16(2)], if J(u) has finite mass, then \(\frac{1}{\pi }\star J(u)\) is an integer-multiplicity rectifiable \((n-2)\)-current. This completes the proof.\(\quad \square \)
3 \(\Gamma \)-Convergence for the Functional \(E_\varepsilon \)
The aim of this section is to prove Theorem C.
3.1 Compactness for the Jacobians
3.1.1 A Truncation Argument
In some of the arguments below, it will be useful to assume that sequence \(u_\varepsilon \) is uniformly bounded in \(L^\infty (M, \, E)\). Fortunately, it is possible to reduce to this case by means of a classical truncation argument. We formulate this argument in terms of pairs \((u_\varepsilon , \, A_\varepsilon )\), for later use. Let \(\{(u_\varepsilon , \, A_\varepsilon )\} \subset W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\) be a sequence that satisfies
For each \(\varepsilon >0\), we define \(v_\varepsilon \in W^{1,2}(M, \, E)\) as
By construction, \(\left| v_\varepsilon \right| \le 1\) in M for all \(\varepsilon > 0\).
Lemma 2.1
The sequence \(\{ v_\varepsilon \}\) defined by (2.2) satisfies
for any \(\varepsilon > 0\). Moreover, under the assumption (2.1) if holds that
as \(\varepsilon \rightarrow 0\).
In the proof of Lemma 2.1 and in the sequel, we will make repeated use of the following observation:
Lemma 2.2
For any \(u\in W^{1,2}(M, \, E)\) and any \(A\in W^{1, 2}(M, \, \textrm{T}^*M)\), if holds that
a.e. in the set \(\{u\ne 0\}\).
Proof
In \(\{u\ne 0\}\), the pair \((u, \, iu)\) is an orthogonal frame for (the real bundle associated with) E. Therefore, keeping in mind that the connection \({{\,\textrm{D}\,}}_A\) is compatible with the metric (i.e., (A.21)), we obtain
in \(\{u\ne 0\}\).\(\quad \square \)
Proof of Lemma 2.1
Towards the proof of (2.3), we observe that Lemma 2.2 implies
in the set \(\{\left| u_\varepsilon \right| > 1\}\). As a consequence,
in \(\{\left| u_\varepsilon \right| > 1\}\). On the other hand, in \(\{\left| u_\varepsilon \right| > 1\}\) we obviously have \(0 = (1 - \left| v_\varepsilon \right| ^2)^2 \le (1-\left| u_\varepsilon \right| ^2)^2\), hence the inequality (2.3) follows. From (2.5), we obtain \(j(v_\varepsilon , \, A_\varepsilon ) = j(u_\varepsilon , \, A_\varepsilon ) \left| u_\varepsilon \right| ^{-2}\) in \(\{\left| u_\varepsilon \right| > 1\}\), and hence,
By the energy estimate (2.1), we deduce that \(\left\| j(u_\varepsilon , \, A_\varepsilon ) - j(v_\varepsilon , \, A_\varepsilon ) \right\| _{L^1(M)} \lesssim \varepsilon \left| \log \varepsilon \right| \). Since \(J(u_\varepsilon , \, A_\varepsilon ) - J(v_\varepsilon , \, A_\varepsilon ) = \frac{1}{2}{{\,\textrm{d}\,}}(j(u_\varepsilon , \, A_\varepsilon ) - j(v_\varepsilon , \, A_\varepsilon ))\), it follows that
Let us consider the 2-form \(\sigma (u_\varepsilon , \, A_\varepsilon )\) defined by \(\sigma (u_\varepsilon , \, A_\varepsilon )[X, \, Y]:= \left\langle i{{\,\textrm{D}\,}}_{A_\varepsilon , X} u_\varepsilon , \, {{\,\textrm{D}\,}}_{A_\varepsilon , Y}u_\varepsilon \right\rangle \) for any smooth vector fields X, Y. By a direct computation, we have
From (2.9) and the energy estimate (2.1), we deduce that
Lemma C.1 implies
where \(\alpha = 1 + n/p - n\). Therefore, (2.4) follows.\(\quad \square \)
3.1.2 The Jacobians are Compact in \(W^{-1,p}(M)\)
Throughout the rest of this section, we consider a sequence \(\{u_\varepsilon \}\subset W^{1,2}(M, \, E)\) that satisfies the energy bound
We work with the reference connection \({{\,\textrm{D}\,}}_0\) on E and denote by \(j(u_\varepsilon ):= j(u_\varepsilon , \, 0)\), \(J(u_\varepsilon ):= J(u_\varepsilon , \, 0)\) the pre-Jacobian and Jacobian of \(u_\varepsilon \) with respect to \({{\,\textrm{D}\,}}_0\) (see (1.5)). Our first goal is to prove that \(\{ J(u_\varepsilon )\}\) is compact in \(W^{-1,p}(M)\), for any \(p < n/(n-1)\).
Lemma 2.3
Let \(u_\varepsilon \in W^{1,2}(M, \, E)\) be a sequence that satisfies (2.11). Then, there exists a (non-relabelled) subsequence and a bounded measure \(J_*\), with values in 2-forms, such that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any p such that \(1 \le p < n/(n-1)\).
In the next subsection, we will prove that the Hodge dual of the limiting measure \(J_*\), i.e., \(\star J_*\), is an integer-multiplicity rectifiable current, belonging to a distinguished homology class of \(E \rightarrow M\); see Proposition 2.7 for details.
In the Euclidean setting, compactness results analogous to Lemma 2.3 are well-known [2, 42]. We will deduce Lemma 2.3 from its Euclidean counterparts by a localisation argument. Let \(U\subset M\) be a smooth, contractible domain in M, all contained in a coordinate chart of M. By working in local coordinates, we identify U with a subset of \(\mathbb R^n\), equipped with a smooth Riemannian metric g. Moreover, as U is contractible, the bundle \(E\rightarrow M\) trivialises over U. Therefore, we can (and do) identify sections of E with maps \(U\rightarrow \mathbb C\). The reference connection \({{\,\textrm{D}\,}}_0\), restricted to U, may be written as
where \({{\,\textrm{d}\,}}\) is the Euclidean connection on \(\mathbb R^n\) (that is, \({{\,\textrm{d}\,}}u = {{\,\textrm{d}\,}}\Re (u) + i{{\,\textrm{d}\,}}\Im (u)\) for any \(u:U\rightarrow \mathbb C\)) and \(\gamma _0:U\rightarrow (\mathbb R^n)^*\) is a smooth real-valued 1-form. It will be useful to compare the restriction of \(E_\varepsilon \) to U, that is,
with its Euclidean counterpart
The integral in (2.14) is taken with respect to the Lebesgue measure \({{\,\textrm{d}\,}}x\), not the volume form \({{\,\textrm{vol}\,}}_g\) induced by the metric g. The functional (2.14) is precisely the Ginzburg–Landau functional, in the simplified form that was introduced by Bethuel, Brezis and Hélein [11]. Given \(u\in W^{1,2}(U, \, \mathbb C)\), we denote the pre-Jacobian and the Jacobian of u with respect to the flat connection \({{\,\textrm{d}\,}}\) as
The quantities j(u), \(\bar{\jmath }(u)\) and J(u), \(\bar{J}(u)\), respectively, are related to each other by
where \(\gamma _0\) is given by (2.12).
Remark 2.4
Notice that, if \(u \in W^{1,2}(M,E)\) is a global section of E, then J(u) is local and commutes with restrictions. In particular, \(J(u_{|U}) = J(u)_{|U}\) for any open set \(U \subset M\) such that E is trivial over U.
We recall a well-known compactness result for the Euclidean Ginzburg–Landau functional (2.14). For any \(\alpha \in (0, \, 1)\), we let \(C^{0,\alpha }_0(U)\) be the space of \(\alpha \)-Hölder continuous functions \(\varphi :U\rightarrow \mathbb R\) such that \(\varphi =0\) on \(\partial U\). We let \((C^{0,\alpha }_0(U))^\prime \) denote the topological dual of \(C^{0,\alpha }_0(U)\).
Theorem 2.5
([2, 42]) Let \((u_\varepsilon )_{\varepsilon >0}\) be a sequence in \(W^{1,2}(U, \, \mathbb C)\) such that
Then, there exists a bounded measure \(\pi J_*\), with values in 2-forms, and a (non-relabelled) countable subsequence such that the following properties hold:
-
(i)
\(\bar{J}(u_\varepsilon )\rightarrow \pi J_*\) in \((C^{0,\alpha }_0(U))^\prime \) for any \(\alpha \in (0, \, 1)\).
-
(ii)
\(\star J_*\) is an integer-multiplicity, rectifiable \((n-2)\)-current with finite mass, which satisfies \(\partial (\star J_*) = 0\) in U.
-
(iii)
If holds that
$$\begin{aligned} \pi \left| J_* \right| \!(U) \le \liminf _{\varepsilon \rightarrow 0} \frac{\bar{E}_\varepsilon (u_\varepsilon ; \, U)}{\left| \log \varepsilon \right| }. \end{aligned}$$
Remark 2.6
By Sobolev embedding, the linear map \(\mathcal {R} :(C^{0,\alpha }_0(U))^\prime \rightarrow W^{-1,p}(U)\), sending each element L of \((C^{0,\alpha }_0(U))^\prime \) to its restriction \(L\vert _{W^{1,p'}_0(U)} \in W^{-1,p}(U)\), is continuous (and surjective) for every
Therefore, Theorem 2.5 implies that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(U)\) for any p with \(1 \le p < n/(n-1)\).
We deduce Lemma 2.3 from Theorem 2.5.
Proof of Lemma 2.3
Let \(\{u_\varepsilon \}\subset W^{1,2}(M, \, E)\) be a sequence that satisfies (2.11). We assume throughout the proof that \(p \ge 1\).\(\quad \square \)
Step 1
(Local convergence) Let \(U\subset M\) be a contractible, smooth, open subset of M, which we identify with a subset of \(\mathbb R^n\). Since the manifold M is compact and smooth, there exists a constant C (depending on M only) such that \({{\,\textrm{d}\,}}x \le C {{\,\textrm{vol}\,}}_g\). Writing \({{\,\textrm{d}\,}}u = {{\,\textrm{D}\,}}_0 u +i\gamma _0 u\), we deduce
If a sequence \(\{u_\varepsilon \}\) satisfies the energy estimate (2.11), then \(\{u_\varepsilon \}\) is uniformly bounded in \(L^2(M)\). Then, (2.18) implies
By Theorem 2.5, we may extract a subsequence and find a bounded measure \(J_U\) on U, with values in 2-forms, such that
Recall from (2.17) that \(J({u_\varepsilon }_{|U}) - \bar{J}({u_\varepsilon }_{|U}) = \frac{1}{2}{{\,\textrm{d}\,}}(\gamma _0(1 - \left| u_\varepsilon \right| ^2))\). The energy estimate (2.11) implies \(\gamma _0(1 - \left| u_\varepsilon \right| ^2) \rightarrow 0\) in \(L^2(U)\) as \(\varepsilon \rightarrow 0\) and hence, \(J({u_\varepsilon }_{|U}) - \bar{J}({u_\varepsilon }_{|U})\rightarrow 0\) in \(W^{-1,2}(U)\) as \(\varepsilon \rightarrow 0\). Thus, we have proven that
Step 2
(Covering argument) Let \(\{U_\alpha \}_{\alpha }\) be any open cover of M in contractible open sets. Over each set \(U_\alpha \), E is trivial, as \(U_\alpha \) is contractible for any index \(\alpha \). Moreover, since M is compact, we can extract from \(\{U_\alpha \}\) a finite open cover \(\{U_k\}_{k=1}^N\) of M which is still trivializing for E. Let \(\{ \rho _k \}_{k=1}^N\) be any partition of unity subordinate to the open cover \(\{U_k\}\). Obviously, \(J(u_\varepsilon ) = \sum _{k=1}^N \rho _k J(u_\varepsilon )\) and, on the other hand, \(\rho _k J(u_\varepsilon ) = \rho _k J(u_\varepsilon )_{|U_k}\) for each \(k=1,\dots ,N\). According to Remark 2.4, \(J(u_\varepsilon )\) is local and commutes with restrictions, i.e., \(J(u_\varepsilon )_{|U_k} = J({u_\varepsilon }_{|U_k})\) for each \(k = 1, \dots , N\). By Step 1, on each open set \(U_k\) we have \(J(u_\varepsilon )_{|U_k} \rightarrow \pi J_{U_k}\) in \(W^{-1,p}(U_k)\) for any \(p < \frac{n}{n-1}\), where \(J_{U_k}\) is a bounded measure on \(U_k\) with values in 2-forms. Thus, as \(\varepsilon \rightarrow 0\),
where \(J_*\) is a bounded measure on M with values into 2-forms which is well-defined because, as it can be easily checked, it is independent of the chosen partition of unity and of the chosen trivialization. \(\quad \square \)
3.1.3 Identifying the Homology Class of \(\star J_*\)
Our next goal is to show that the limit of the Jacobians, \(\star J_*\), is an integer-multiplicity rectifiable current that belongs to the homology class \(\mathcal {C}\) (the Poincaré dual of the first Chern class of E; see (1.6)).
Proposition 2.7
Let \(\{u_\varepsilon \}\subset W^{1,2}(M, \, E)\) be a sequence that satisfies (2.11). We extract a (non-relabelled) subsequence in such a way that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any \(p < n/(n-1)\). Then, \(\star J_*\) is an integer-multiplicity rectifiable current and \(\star J_*\in \mathcal {C}\).
The proof of Proposition 2.7 relies on the following result:
Lemma 2.8
Let \(1< p < n/(n-1)\). Let \(\{u_\varepsilon \}\subset W^{1,2}(M, \, E)\) be a sequence that satisfies (2.11), and let \(J_*\) be a bounded measure, with values in 2-forms, such that that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\). Then, there exists \(w_*\in W^{1,p}(M, \ E)\) such that \(\left| w_* \right| = 1\) a.e. and \(J(w_*) = \pi J_*\).
Proposition 2.7 follows immediately from Proposition 1.3 and Lemma 2.8. It only remains to prove Lemma 2.8. We will need an auxiliary result, again borrowed from [53]. We denote by \({{\,\textrm{Harm}\,}}^1(M)\) the space of harmonic 1-forms on M and by \({{\,\textrm{vol}\,}}_{\mathbb {S}^1}\) the volume form of \(\mathbb {S}^1\).
Remark 2.9
If \(\Phi \in W^{1,1}(M,\,\mathbb {S}^1)\), then \(\Phi ^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1})\) has a pointwise a.e. meaning, and we have the pointwise a.e. equality
Lemma 2.10
For any \(\varphi \in W^{1,2}(M, \, \mathbb R)\) and \(\xi \in {{\,\textrm{Harm}\,}}^1(M)\), there exist a map \(\Phi : M\rightarrow \mathbb {S}^1\), as regular as \(\varphi \), and a form \(\bar{\xi }\in {{\,\textrm{Harm}\,}}^1(M)\) such that
where \(C_M > 0\) is a constant that depends only on M.
Remark 2.11
By Hodge theory, the space \({{\,\textrm{Harm}\,}}^1(M)\) has finite dimension. Therefore, the difference \(\xi -\bar{\xi }\) is bounded not only in \(L^2(M)\), but also in any other norm.
Proof
The proof follows very closely the argument of [53, Lemma 3.4]. Since, however, that lemma is designed to deal with a slightly different situation and cannot be used directly in our case, we provide full details for reader’s convenience.
We notice that, for all smooth maps \(f,g: M \rightarrow \mathbb {S}^1\), the map \(\phi := fg: M \rightarrow \mathbb {S}^1\) is still smooth, and we can pull back \({{\,\textrm{vol}\,}}_{\mathbb {S}^1}\) by \(\phi \). Next, since \(\mathbb {S}^1\) is an Abelian Lie group with an invariant volume form, there holds \(\phi ^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1}) = f^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1}) + g^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1})\). For any smooth function \(\psi : M \rightarrow \mathbb R\) and \(f: M \rightarrow \mathbb {S}^1\) harmonic, if we set \(g:= e^{i \psi }\), we have \(\phi = f e^{i\psi }\) and, by the previous formula and the translational invariance of \({{\,\textrm{vol}\,}}_{\mathbb {S}^1}\), we end up with \(\phi ^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1}) = f^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1}) + {{\,\textrm{d}\,}}\psi \). Moreover, \(f^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1})\) is a harmonic one-form on M (because \(f: M \rightarrow \mathbb {S}^1\) is harmonic, see [3, Example 4.2.6]). Following [53] and [3, Example 3.3.8], we observe that f can be chosen so that \(\Vert \xi - f^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1}) \Vert _{L^\infty (M)} \le C(M)\), where \(C(M) > 0\) is a constant depending only on M. Therefore, if \(\varphi \) is smooth, the conclusion follows setting \(\psi = -\varphi \), \(\Phi = e^{-i\varphi } f\) and \(\bar{\xi } = f^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1})\). If \(\varphi \) is only of class \(W^{1,2}(M,\mathbb R)\), the conclusion is however still true thanks to a standard density argument. Finally, by definition, it easily seen that \(\Phi \) is as regular as \(\varphi \).\(\quad \square \)
Proof of Lemma 2.8
We can assume without loss of generality that \(\{u_\varepsilon \}\) is bounded in \(L^\infty (M)\), independently of \(\varepsilon \)—for otherwise, we replace each map \(u_\varepsilon \) by the truncated map \(v_\varepsilon \) defined in (2.2) and apply Lemma 2.1 (with \(A_\varepsilon = 0\)). Then, it follows that \(j(u_\varepsilon )\in L^2(M, \, \textrm{T}^* M)\) and that
due to the energy estimate (2.11). We are going to construct a sequence of maps of the form
for suitable functions \(\rho _\varepsilon :M\rightarrow \mathbb R\) and maps \(\Phi _\varepsilon :M\rightarrow \mathbb {S}^1\), such that \(J(w_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\), \(\left| w_\varepsilon \right| \rightarrow 1\) a.e. and \(w_\varepsilon \) is bounded in \(W^{1,p}(M)\). Then, we will obtain a map \(w_*\) with the desired properties by passing to the (weak) limit in the \(w_\varepsilon \)’s. We split the proof into several steps.
Step 1
We consider the Hodge decomposition of \(j(u_\varepsilon )\)—that is, we write (in a unique way)
for some (co-exact) form \(\varphi _\varepsilon \in W^{1,2}(M, \, \mathbb R)\), some (exact) form \(\psi _\varepsilon \in W^{1,2}(M, \, \Lambda ^2\textrm{T}^*M)\), and some \(\xi _\varepsilon \in {{\,\textrm{Harm}\,}}^1(M)\). This decomposition (recalled in Proposition A.14) is orthogonal in \(L^2(M)\). Then, \(\psi _\varepsilon \) is closed and \(L^2\)-orthogonal to all harmonic 2-forms. By taking the differential in (2.23), we obtain
where \(F_0\) is the curvature of the reference connection \({{\,\textrm{D}\,}}_0\). By Lemma 2.3, we know that \(J(u_\varepsilon )\) in bounded in \(W^{-1,p}(M)\), independently of \(\varepsilon \). By applying Lemma C.4, we deduce
for some constant \(C_p\) that depends on p (and on \(F_0\)), but not on \(\varepsilon \).
Step 2
In this step, we construct suitable maps \(\Phi _\varepsilon :M\rightarrow \mathbb {S}^1\), in such a way that \(j(\Phi _\varepsilon u_\varepsilon )\) is bounded in \(L^p(M)\). We do so by applying Lemma 2.10. By Lemma 2.10, for each \(\varepsilon > 0\) there exist a map \(\Phi _\varepsilon :M\rightarrow \mathbb {S}^1\) and a form \(\bar{\xi }_\varepsilon \in {{\,\textrm{Harm}\,}}^1(M)\) such that
where \(C_M\) is a constant depending only on M. We consider the section \(\Phi _\varepsilon u_\varepsilon \). We have
As the decomposition in (2.23) is orthogonal in \(L^2\), we obtain
and hence, recalling the energy estimate (2.11),
We claim that
for some constant \(C_p\) depending on p, M and \({{\,\textrm{D}\,}}_0\), but not on \(\varepsilon \). Indeed, due to (2.23) and (2.26), we have
Let \(q > 2\) be such that \(1/p = 1/q + 1/2\). As \(\left\| u_\varepsilon \right\| _{L^\infty (M)} \le C\), by generalised Hölder’s inequality and interpolation we obtain
up to a multiplicative constant which depends only on M and p. Hence, recalling (2.11) and (2.28),
up to a constant depending only on M and p. Now (2.30) follows by (2.25), (2.27), (2.31), (2.32) and Remark 2.11. As a byproduct of (2.32), we obtain
Step 3
The estimate (2.30) is not enough to guarantee that \(\Phi _\varepsilon u_\varepsilon \) is bounded in \(W^{1,p}(M)\): we also need to control the differential of \(\left| u_\varepsilon \right| \). Although we cannot make sure that \(\left\| {{\,\textrm{d}\,}}\left| u_\varepsilon \right| \right\| _{L^p(M)}\) is bounded, in general (see Remark 2.13 below), we can construct suitable functions \(\rho _\varepsilon :M\rightarrow \mathbb R\) so that \(w_\varepsilon := \rho _\varepsilon \, \Phi _\varepsilon u_\varepsilon \) satisfies the desired estimates.
For any \(\varepsilon >0\), we take a smooth nonnegative function \(f_\varepsilon :\mathbb R\rightarrow \mathbb R\) such that
We define
We have \(j(w_\varepsilon ) = \rho _\varepsilon ^2 \, j(\Phi _\varepsilon u_\varepsilon )\). Moreover, \(\rho _\varepsilon \rightarrow 1\) uniformly as \(\varepsilon \rightarrow 0\), because of (2.34), (2.35). Therefore, from (2.30) we deduce
as \(\varepsilon \rightarrow 0\). In particular, (2.33), (2.38) and the fact that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) imply
as \(\varepsilon \rightarrow 0\). We estimate the \(L^2\)-norm of \({{\,\textrm{D}\,}}_0w_\varepsilon \). By explicit computation, we have
The second term at the right-hand side is bounded by (2.29). To estimate the other term, we recall (2.35) and observe that \(\left\| {{\,\textrm{d}\,}}(\left| u_\varepsilon \right| ) \right\| _{L^2(M)}\le \left\| {{\,\textrm{D}\,}}_0u_\varepsilon \right\| _{L^2(M)}\), by Lemma 2.2. Then,
Finally, using (2.35) and the fact that \(\left| u_\varepsilon \right| \rightarrow 1\) in \(L^2(M)\) (due to our assumption (2.11)), we deduce
as \(\varepsilon \rightarrow 0\).
Step 4
Eventually, we will show that the sequence \(w_\varepsilon \) is bounded in \(W^{1,p}(M)\). As an intermediate step, we prove that
Indeed, let
By construction, \(\left| w_\varepsilon \right| = \left| u_\varepsilon \right| f_\varepsilon (\left| u_\varepsilon \right| )\) in M and \(\left| w_\varepsilon \right| = 1\) in \(M{\setminus } S_\varepsilon \), so
Lemma 2.2, the Hölder inequality and the energy estimate (2.11) imply
On the other hand, \((\left| u_\varepsilon \right| ^2 - 1)^2\ge \varepsilon \) on \(S_\varepsilon \), so the energy estimate (2.11) implies
Combining (2.43) with (2.44), we obtain (2.42).
Step 5
We claim that
Once (2.45) is proved, the lemma follows. Indeed, if (2.45) holds, then we extract a subsequence such that \(w_\varepsilon \rightharpoonup w_*\) weakly in \(W^{1,p}(M)\). The limit \(w_*\in W^{1,p}(M, \, E)\) satisfies \(J(w_*) = \pi J_*\), due to (2.39) and Proposition 1.2. Moreover, the estimate (2.41) implies that \(\left| w_* \right| = 1\), as required.
We proceed to the proof of (2.45). Let
On the one hand, Lemma 2.2 gives
On the other hand, the energy estimate (2.11) implies that \({{\,\textrm{vol}\,}}_g(T_\varepsilon )\lesssim \varepsilon ^2\left| \log \varepsilon \right| \). By applying the Hölder inequality, we obtain
Now, (2.46) and (2.47) imply (2.45).\(\quad \square \)
As a byproduct of the arguments above, we have proven
Corollary 2.12
Let \(u_\varepsilon \in W^{1,2}(M, \, E)\) be such that
Then, there exists functions \(\rho _\varepsilon :M\rightarrow \mathbb R\), maps \(\Phi _\varepsilon :M\rightarrow \mathbb {S}^1\) and a (non-relabelled) subsequence such that \(w_\varepsilon : = \rho _\varepsilon \, \Phi _\varepsilon u_\varepsilon \) converges weakly in \(W^{1,p}(M)\), for any \(p \in [1, \, n/(n-1))\), to a limit map \(w_*\in W^{1,p}(M, \, E)\) with \(\left| w_* \right| = 1\) a.e. Moreover, \(J(u_\varepsilon ) - J(w_\varepsilon ) \rightarrow 0\) in \(W^{-1,p}(M)\) for any \(p \in [1, \, n/(n-1))\).
Thus, any sequence \(\{u_\varepsilon \}\) bounded in \(L^\infty (M)\) and with \(E_\varepsilon \)-energy of order \(\left| \log \varepsilon \right| \) can be split into a compact and a non-compact part (with respect to the weak \(W^{1,p}\)-topology). Moreover, Corollary 2.12 asserts that the compact part stores the information necessary to determine the topological energy-concentration set, while the non-compact part of the sequence is, in this sense, “topologically irrelevant”.
On a qualitative level, the lack of compactness is due to wild oscillations in the phases made possible by the large amount of energy at disposal. At first glance, this inconvenient seems to be “cured” by the gauge transformations \(\Phi _\varepsilon \). However, we must emphasise that the “penalisations” \(\rho _\varepsilon \), even if small in uniform norm as \(\varepsilon \rightarrow 0\), play a subtle rôle. Indeed, Remark 2.13 below points out that gauge transformations alone are in general not sufficient to perform the splitting and obtain compactness.
Remark 2.13
Let \(u_\varepsilon \in W^{1,2}(M, \, E)\) be a sequence that satisfies (2.48). In general, it may not be possible to find maps \(\Phi _\varepsilon :M\rightarrow \mathbb {S}^1\) such that \(\Phi _\varepsilon u_\varepsilon \) is bounded in \(W^{1,p}(M)\). (A counterexample, when \(M = (0, \, 1)\subseteq \mathbb R\) and E is the trivial bundle \(E = M\times \mathbb C\), is given by the sequence \(u_\varepsilon (x):= 1 + \varepsilon \sin (\left| \log \varepsilon \right| ^{1/2} x/\varepsilon )\)). However, if \(u_\varepsilon \) are solutions of the Ginzburg–Landau equations (i.e., critical points of \(E_\varepsilon \)) in Euclidean domains, then it is possible to obtain compactness for a sequence of the form \(\Phi _\varepsilon u_\varepsilon \)—see [13, Section 4] and [7, Lemma 2.2], [14, Proposition 2.13].
3.2 Lower Bounds
Again, we consider a sequence \(u_\varepsilon \in W^{1,2}(M, \, E)\) that satisfies the energy bound (2.11). By Lemma 2.3, we know that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any \(p < n/(n-1)\). The aim of this section is to prove the following:
Proposition 2.14
If the sequence \(\{u_\varepsilon \}\subset W^{1,2}(M, \, E)\) satisfies (2.11), then for any open set \(V\subset M\) it holds that
We stress that, in the statement of Proposition 2.14, the open set V may be chosen arbitrarily; it does not need to be contained in a coordinate chart. For instance, we may take \(V = M\). Therefore, once Proposition 2.14 is proved, Statement (i) of Theorem C follows at once.
Proof of Theorem C, Statement (i)
The statement follows from Lemma 2.3, Proposition 2.7 and Proposition 2.14.\(\quad \square \)
In the rest of this section, we deduce Proposition 2.14 from its Euclidean counterpart [2, 42] by means of a localisation argument.
Lemma 2.15
Let \(\delta > 0\) be smaller than the injectivity radius of M. Let \(U\subset M\) be a smooth, contractible domain, entirely contained in a geodesic ball of radius \(\delta \). Then,
Proof
We identify U with a subset of \(\mathbb R^n\), by local coordinates, and write \({{\,\textrm{D}\,}}_0 = {{\,\textrm{d}\,}}- i \gamma _0\), where \({{\,\textrm{d}\,}}\) is the flat connection on U and \(\gamma _0\) is a smooth 1-form that depends on \({{\,\textrm{D}\,}}_0\) only. We consider again the functional \(\bar{E}_\varepsilon \) given by (2.14). Thanks to (A.1) (which we can apply as U is supposed to be contained in a geodesic ball), we can write
The last line follows by Young’s inequality (which gives, for each choice of \(\sigma > 0\), the pointwise bound \(\left\langle {{\,\textrm{D}\,}}_0 u_\varepsilon , \, i\gamma _0 u_\varepsilon \right\rangle \le \frac{\sigma }{2} \left| {{\,\textrm{D}\,}}_0 u \right| ^2 + \frac{1}{2\sigma } \left| \gamma _0 u_\varepsilon \right| ^2\), and then the previous inequality follows by choosing \(\sigma = \delta ^2\)). Consequently, we obtain
Since this holds for every \(\varepsilon > 0\), we can pass both sides to the \(\liminf \) as \(\varepsilon \rightarrow 0\) keeping the inequality. On doing so, the last term on the right above vanishes, because the energy estimate (2.11) implies that \(u_\varepsilon \) is bounded in \(L^2(M)\). Therefore, we get the desired estimate recalling (iii) of Theorem 2.5.\(\quad \square \)
We deduce Proposition 2.14 from Lemma 2.15 by applying a Vitali-Besicovitch-type covering theorem, which we recall here.
Theorem 2.16
(Federer, [30]) Let M be a compact Riemannian manifold. Let \(\mathcal {F}\) be a collection of closed geodesic balls in M, such that
Let \(\mu \) be a non-negative Borel measure on M and \(V\subset M\) an open set. Then, there exists a countable subfamily \(\mathcal {F}^\prime \subset \mathcal {F}\) of pairwise-disjoint balls such that
The proof of Theorem 2.16 can be found in [30, Theorem 2.8.14, Corollary 2.8.15]. The statements in [30] apply not only to compact Riemannian manifolds, but also to a more general class of metric spaces, i.e. ‘directionally limited’ metric spaces. (Moreover, they apply to outer measures as well as measures.) However, the statement given here is sufficient for our purposes.
The next lemma is an immediate consequence of Theorem 2.16.
Lemma 2.17
For any \(\delta > 0\) and any open set \(V\subset M\), there exists a countable family \(\{U_j\}_{j\in \mathbb N}\) of pairwise-disjoint, open geodesic balls, of radius less than \(\delta \), such that \(U_j\subset V\) for any j and
Proof
We apply Theorem 2.16 to the bounded measure \(\mu := \left| J_* \right| \) and the collection of (closed) balls
Since \(\left| J_* \right| \) is a finite measure, we have \(\left| J_* \right| (\partial B_r(x_0)) = 0\) for a.e. \(r\in (0, \, \delta )\). Then, the assumptions of Theorem 2.16 are satisfied, and the lemma follows.\(\quad \square \)
Proof of Proposition 2.14
Let \(V\subset M\) be an open set. Let \(\delta >0\) be a small parameter—in particular, smaller than the injectivity radius of M. By Lemma 2.17, there exists a countable family \(\{U_j\}_{j\in \mathbb N}\) of pairwise-disjoint, open geodesic balls, of radius smaller than \(\delta \), such that \(U_j\subset V\) for any j and
From (2.50), Lemma 2.15 and Fatou’s lemma, we deduce
Letting \(\delta \rightarrow 0\), the proposition follows.\(\quad \square \)
3.3 Upper Bounds
The goal of this section is to prove Statement (ii) of Theorem C. First, we introduce some notation. Let \(u:M\rightarrow E\) be a section of the bundle \(E\rightarrow M\), and let \({{\,\textrm{D}\,}}_0\) be our reference (smooth) connection on E. Let \(X\subset M\) be a closed set. Following [1, 2], we say that u has a nice singularity at X (with respect to \({{\,\textrm{D}\,}}_0\)) if \(\left| u \right| = 1\) in \(M{\setminus } X\), u is locally Lipschitz on \(M\setminus X\) and there exists a constant \(C>0\) such that
If u has a nice singularity at X with respect to \({{\,\textrm{D}\,}}_0\), then u has a nice singularity at X with respect to any smooth connection \({{\,\textrm{D}\,}}\), because \({{\,\textrm{D}\,}}\) can be written as \({{\,\textrm{D}\,}}= {{\,\textrm{D}\,}}_0 -iA\) for some smooth 1-form A. Therefore, there is no ambiguity in saying that u has a nice singularity at X without specifying the reference connection \({{\,\textrm{D}\,}}_0\). If X is a finite union of submanifolds of dimension q or less and u has a nice singularity at X, then \(u\in (L^\infty \cap W^{1, p})(M, \, E)\) for any \(p < n - q\). This is a consequence of the following lemma:
Lemma 2.18
If \(X\subset M\) is contained in a finite union of Lipschitz submanifolds of dimension q, then
for any \(p\in [1, \, n-q)\).
Proof
When \(M = \mathbb R^n\), the proof may be found e.g. in [2, Lemma 8.3]. When M is a compact, smooth manifold, we reduce to the Euclidean case by working in coordinate charts.\(\quad \square \)
Remark 2.19
If u has a nice singularity on a closed Lipschitz set X of dimension \(n-2\) at most, then \(u\in (L^\infty \cap W^{1,1})(M, \, E)\) (because of Lemma 2.18) and J(u) is well-defined. Moreover, J(u) is supported on X. Indeed, for any smooth vector field v we have \(\left\langle {{\,\textrm{D}\,}}_{0,v} u, \, u\right\rangle = {{\,\textrm{d}\,}}(\left| u \right| ^2/2) = 0\) at almost every point of \(M\setminus X\) (as \(\left| u \right| =1\) in \(M\setminus X\), by definition). In particular, for any smooth vector fields v, w, \({{\,\textrm{D}\,}}_{0,v} u\) and \({{\,\textrm{D}\,}}_{0,w} u\) are both orthogonal to u (and, hence, parallel to one another) at almost every point of \(M\setminus X\). This implies \(J(u)[v, \, w] = \left\langle i {{\,\textrm{D}\,}}_{0,v} u, \, {{\,\textrm{D}\,}}_{0,w} u\right\rangle = 0\) a.e. in \(M\setminus X\), for any smooth vector fields v, w.
We consider smooth triangulations on M, as defined e.g. in [48, Definition 8.3]. In particular, such triangulations consist of a finite number of simplices. Given a triangulation \(\mathcal {T}\) of M and an integer \(q\in \{0, \, 1, \, \ldots , \, n\}\), we call \(\mathcal {T}_q\) the set of all q-dimensional simplices of \(\mathcal {T}\). We denote by \({{\,\textrm{Sk}\,}}_q\mathcal {T}\) the q-dimensional skeleton of \(\mathcal {T}\), that is,
Recall that \(\mathcal {R}_q(M)\) is the set of integer-multiplicity rectifiable q-chains in M. We say that a chain \(S\in \mathcal {R}_q(M)\) is polyhedral if there exist a triangulation \(\mathcal {T}\) of M and a function \(\theta :\mathcal {T}_q\rightarrow \mathbb Z\) such that
When (2.51) holds, we say that the current S is carried by the triangulation \(\mathcal {T}\). To construct a recovery sequence for \(E_\varepsilon \), we borrow a result by Parise, Pigati and Stern [53, Proposition 4.2]. For the convenience of the reader, we reproduce the statement here, using the notation we introduced above.
Proposition 2.20
([53]) For any cycle \(S\in \mathcal {R}_{n-2}(M)\), there exists a sequence of polyhedral \((n-2)\)-cycles \(S_j\), homologous to S, such that \(\mathbb {F}(S_j-S)\rightarrow 0\) and \(\mathbb {M}(S_j)\rightarrow \mathbb {M}(S)\) as \(j\rightarrow +\infty \). Moreover, if S is a polyhedral \((n-2)\)-cycle in the class \(\mathcal {C}\) and \(\mathcal {T}\) is a triangulation that carries S, then there exists a section \(u:M\rightarrow E\) that has a nice singularity at \({{\,\textrm{Sk}\,}}_{n-2}\mathcal {T}\) and satisfies \(\star J(u) = \pi S\).
Remark 2.21
In the statement of [53, Proposition 4.2], the authors do not say explicitly that the approximating chains \(S_j\) and S are homologous, but this fact is contained in the proof.
Let \(\mathcal {T}\) be a triangulation of M and let \(\gamma >0\) be a small parameter. For any simplex \(K\in \mathcal {T}_{n-2}\), we define
(cf. Equation (5.1) of [1]). In the next couple of results, we study the properties of \(V_K\) when \(\gamma \) is small enough.
Lemma 2.22
There exist positive constants \(\gamma _*\) and \(C_*\), depending only on M and \(\mathcal {T}\), such that for any \(\gamma \in (0, \, \gamma _*]\) and \(K\in \mathcal {T}_{n-2}\) the following properties hold:
-
(i)
\(V_K\) is the closure of a Lipschitz domain;
-
(ii)
\(V_K\) is contractible;
-
(iii)
any \(x\in V_K\) satisfies
$$\begin{aligned} {{\,\textrm{dist}\,}}(x, \, K) \le C_*\gamma {{\,\textrm{dist}\,}}(x, \, \partial K); \end{aligned}$$ -
(iv)
conversely, if \(x\in M\) satisfies
$$\begin{aligned} {{\,\textrm{dist}\,}}(x, \, K) \le \frac{\gamma }{\gamma + 1} {{\,\textrm{dist}\,}}(x, \, \partial K), \end{aligned}$$(2.53)then \(x\in V_K\).
Proof
Before proceeding with the proof of (i)–(iv), we need some preparation. Let \(K\in \mathcal {T}_{n-2}\). We claim that there exists a (by no means unique) open submanifold N of M, of dimension \(n-2\), such that K is contained in the interior of N. This fact is standard and we include a proof only for the reader’s convenience.
By definition of triangulation [48, Definition 8.3] (see also Definition 1.2 and Theorem 1.5), there exist a Euclidean simplex \(H\subseteq \mathbb R^\ell \) of dimension \(n-2\) and a function \(h:H\rightarrow K\subseteq M\) that is smooth (i.e., it can be extended smoothly to a neighbourhood of H), bijective, and whose differential has rank \(n-2\) at any point of H. Let \(\Pi \) be the affine \((n-2)\)-plane that contains H, let U be an open neighbourhood of H in \(\mathbb R^\ell \), and let \(f:U\rightarrow M\) be a smooth extension of f. If U is small enough, then the differential of \(f_{|\Pi \cap U}\) has rank \(n-2\) at any point of \(\Pi \cap U\) (by continuity of the Jacobian minors) and f is injective. Indeed, suppose there is no neighbourhood U of H such that \(f_{|\Pi \cap U}\) is injective. Then, there exist sequences \(\{x_n\}_{n\in \mathbb N}\), \(\{y_n\}_{n\in \mathbb N}\) in \(\Pi \) such that \(x_n\ne y_n\), \(f(x_n) = f(y_n)\) and \({{\,\textrm{dist}\,}}(x_n, \, H) \rightarrow 0\), \({{\,\textrm{dist}\,}}(y_n, \, H)\rightarrow 0\) as \(n\rightarrow +\infty \). In particular, both \(\{x_n\}\) and \(\{y_n\}\) are bounded, so we can extract (non-relabelled) subsequences such that \(x_n\rightarrow x\in H\), \(y_n \rightarrow y\in H\) and \(f(x) = f(y)\). As \(f_{|H} = h\) is injective, we must have \(x = y\). On the other hand, the differential of \(f_{|\Pi }\) has constant rank \(n - 2\) in a neighbourhood of x and hence, by the constant rank theorem, f is locally injective near x. This is a contradiction. Therefore, by taking a smaller U is necessary, we can assume without loss of generality that \(f_{|\Pi \cap U}\) is injective—and in fact, a smooth embedding. Then, the image \(N:= f(\Pi \cap U)\) is an open \((n-2)\)-sumanifold of M which contains K. We can also assume that the injectivity radius of N is strictly positive—for otherwise, we replace N with \(N^\prime := f(\Pi \cap U^\prime )\), where \(U^\prime \supseteq H\) is an open set whose closure is contained in U.
For any \(x\in V_K\), we have \({{\,\textrm{dist}\,}}(x, \, K) \le \gamma \,\text {diam}\, M\), as an immediate consequence of (2.52). Therefore, there exists a small constant \(\gamma _* > 0\) such that, if \(\gamma \in (0, \, \gamma _*]\), then \(V_K\) is contained in a tubular neighbourhood of N. In particular, if \(\gamma \le \gamma _*\) then any point of \(V_K\) has a unique closest projection on N—that is, for any \(x\in V_K\) there exists a unique \(\pi _N(x)\in N\) such that \({{\,\textrm{dist}\,}}(x, \, \pi _N(x))={{\,\textrm{dist}\,}}(x, \, N)\). (The constant \(\gamma _*\) can be chosen uniformly with respect to \(K\in \mathcal {T}_{n-2}\), because \(\mathcal {T}\) contains only finitely many simplices.) We claim that, if \(\gamma _*\) is small enough and \(\gamma \in (0, \, \gamma _*]\), then
Indeed, suppose that \(\pi _N(x)\notin K\) for some \(x\in V_K\). Let \(y\in K\) be such that \({{\,\textrm{dist}\,}}(x, \, y) = {{\,\textrm{dist}\,}}(x, \, K) \le \gamma {{\,\textrm{dist}\,}}(y, \, \partial K)\), as in the definition (2.52). The distance between y and \(\pi _N(x)\) can be estimated by applying the triangle inequality, as
(the last inequality follows because \(x\in V_K\)). By reducing the value of \(\gamma _*\) if necessary, we can assume that the distance between y and \(\pi _N(x)\) is smaller than the injectivity radius of N, which we assumed to be positive. As a consequence, there exists a minimising geodesic \(\beta :[0, \, 1]\rightarrow N\) from y to \(\pi _N(x)\), with values in N. Since \(\beta (0) = y\in K\) and we have assumed that \(\beta (1) =\pi _N(y)\notin K\), by continuity there must be \(t\in [0, \, 1]\) such that \(\beta (t)\in \partial K\). Then,
On the other hand, having chosen y as in (2.52), we have
For \(\gamma < 1/2\), we deduce that \(x\in K\) and hence, \(\pi _N(x) = x\in K\), against our assumption. This proves (2.54).
Now, the set \(V_K\) can be equivalently characterised as
Indeed, the inclusions in both directions are rather straightforward consequences of (2.52), (2.54) and the definition of \(\pi _N\). In turn, (2.58) implies that \(V_K\) is the image, under a Lipschitz map with Lipschitz inverse, of
A Lipschitz map (with Lipschitz inverse) that carries \(W_H\) to \(V_K\) is defined by changing variables in a suitable (tubular) neighbourhood of N and identifying K with H by means of the smooth embedding \(f_{|\Pi \cap U}\). The set \(W_H\) is the closure of a contractible, Lipschitz domain, hence \(V_K\) is.
To prove (iii), we observe that the map \(\pi _N\) is smooth in a neighbourhood of K, because N is a smooth submanifold. Therefore, for \(\gamma \) small enough, the restriction of \(\pi _N\) to \(V_K\) is Lipschitz. Since \(\pi _N\) is the identity on \(\partial K\), for any \(x\in V_K\) we deduce
where \(C_K\) is the Lipschitz constant of \(\pi _N\) restricted to \(V_K\). The statement (iii) follows, with \(C_*:= \max _{K\in \mathcal {T}_{n-2}} C_K\). Finally, let \(\gamma ^\prime := \frac{\gamma }{\gamma + 1}\) and let \(x\in M\) satisfy (2.53). Let \(y\in K\) be such that \({{\,\textrm{dist}\,}}(x, \, y) = {{\,\textrm{dist}\,}}(x, \, K)\). (Such a y exists, because \({{\,\textrm{dist}\,}}(x, \, \cdot )\) is continuous and K is compact.) Then,
This implies \({{\,\textrm{dist}\,}}(x, \, K) \le \gamma {{\,\textrm{dist}\,}}(y, \, \partial K)\) and hence, \(x\in V_K\), thus completing the proof.\(\quad \square \)
Lemma 2.23
If \(\gamma > 0\) is small enough, then, for any \(K\in \mathcal {T}_{n-2}\) and \(K^\prime \in \mathcal {T}_{n-2}\), the intersection \(V_K\cap V_{K^\prime }\) is either empty or a common boundary face of K, \(K^\prime \) of dimension \(n-3\) at most.
Proof
First, we claim that there exists a constant \(C>0\) (depending on the triangulation \(\mathcal {T}\)) such that, for any \(K\in \mathcal {T}_{n-2}\) and \(K^\prime \in \mathcal {T}_{n-2}\), it holds that
Indeed, let \(z_0\in K^\prime \) be given. It suffices to find a constant C that satisfies (2.59) for any z close enough to \(z_0\); we will then able to find C that satisfies (2.59) for any \(z\in K^\prime \), as claimed, because \(K^\prime \) is compact. Moreover, as there are only finitely many simplices in \(\mathcal {T}\), the constant C in (2.59) may be chosen uniformly with respect to K, \(K^\prime \). If \(z_0\in K^\prime {\setminus } K\), then the quotient \({{\,\textrm{dist}\,}}(\cdot , \, \partial K)/{{\,\textrm{dist}\,}}(\cdot , \, K)\) is bounded in a neighbourhood of \(z_0\), and (2.59) follows. Suppose now that \(z_0\in K\cap K^\prime \). By definition (see [48, Definition 8.3], \(\mathcal {T}\) is the homeomorphic image of a simplicial complex in \(\mathbb R^\ell \) (for some \(\ell \ge n\)), via a piecewise smooth map with injective differential. (As the differential of the parametrisation is injective, it follows that K, \(K^\prime \) meet at a non-zero angle at \(z_0\).) Upon composition with the parametrisation, which is a Lipschitz map with Lipschitz inverse, we may assume without loss of generality that K, \(K^\prime \) are affine simplices in an affine plane \(\Pi \) of dimension \(n-1\). Then, for z sufficiently close to \(z_0\), we have
where \(\alpha \) is the (acute) angle between the simplices K and \(K^\prime \) in the plane \(\Pi \). Then, (2.59) is satisfied in a neighbourhood of \(z_0\), because \(\alpha \) is non-zero. This completes the proof of (2.59).
Now, we claim that, for any \(\gamma \) small enough, there exists a constant \(C^\prime \) such that, for any simplices \(K\in \mathcal {T}_{n-2}\), \(K^\prime \in \mathcal {T}_{n-2}\) and any point \(x\in V_K\), it holds that
Indeed, given any \(x\in V_K\), there exists \(z\in K^\prime \) such that \({{\,\textrm{dist}\,}}(x, \, z) = {{\,\textrm{dist}\,}}(x, \, K^\prime )\), because \(K^\prime \) is compact. Then, the triangle inequality and (2.59) imply
By Statement (iii) in Lemma 2.22, we deduce
where \(C_* > 0\) is a constant that does not depend on K, \(\gamma \). Choosing \(\gamma \) small enough that \(C_*C\gamma \le 1/2\), and setting \(C^\prime := 2 + 2C\), we obtain (2.60).
Finally, let \(K\in \mathcal {T}_{n-2}\), \(K^\prime \in \mathcal {T}_{n-2}\) be such that \(V_{K}\cap V_{K^\prime }\ne \emptyset \). Let \(x\in V_{K}\cap V_{K^\prime }\), and let
As \(x\in V_{K}\), by Statement (iii) in Lemma 2.22, we have
for some constant \(C_*\) that does not depend on \(\gamma \). Similarly, \(d^\prime \le {C_*}C^\prime \gamma \, d\) and hence, \(d + d^\prime \le {C_*} C^\prime \gamma (d + d^\prime )\). If we take \(\gamma < {(C_* C^\prime )^{-1}}\), then \(d + d^\prime = 0\), that is, \(x\in K\cap K^\prime \) (and, in fact, \(x \in \partial K \cap \partial K^\prime \)). Conversely, the definition (2.52) immediately implies that \(K\cap K^\prime \subset V_K\cap V_{K^\prime }\). This proves the lemma.\(\quad \square \)
We can now prove Statement (ii) of Theorem C.
Proof of Theorem C, Statement (ii)
Let \(S_*\) be an integer-multiplicity rectifiable \((n-2)\)-cycle in the homology class \(\mathcal {C}\), and let \(J_*:= \star S_*\) be the dual 2-form. Let \(\delta > 0\). We claim that, for any \(\varepsilon > 0\), there exists \(u_\varepsilon \in W^{1,2}(M, \, E)\) such that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,1}(M)\) as \(\varepsilon \rightarrow 0\) and
Once (2.61) is proved, Lemma 2.3 implies that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) not only for \(p=1\), but also for any \(p < n/(n-1)\). Then, Statement (ii) in Theorem C follows from a diagonal argument.
Thanks to Proposition 2.20, and up to a diagonal argument, we may assume without loss of generality that \(S_*\) is a polyhedral \((n-2)\)-cycle in the homology class \(\mathcal {C}\). Let \(\mathcal {T}\) be a triangulation that carries \(S_*\). Up to a subdivision, we may assume without loss of generality that each simplex \(K\in \mathcal {T}\) has diameter \(\textrm{diam} \, K \le \delta \). For each \((n-2)\)-simplex \(K\in \mathcal {T}_{n-2}\), we define \(V_K\) as in (2.52). (We choose the parameter \(\gamma \) small enough, so that sets \(V_K\) have pairwise disjoint interiors, as in Lemma 2.23.) Let
By Proposition 2.20, there exists a section \(u:M\rightarrow E\) that has a nice singularity at \({{\,\textrm{Sk}\,}}_{n-2}\mathcal {T}\) and satisfies \(J(u) = \pi J_*\).
Construction of the recovery sequence out of V. We claim that u is of class \(W^{1,2}\) in \(M\setminus V\). Indeed, let \(x\in M\setminus V\). By Statement (iv) in Lemma 2.22, such a point x satisfies

and hence, \({{\,\textrm{dist}\,}}(x, \, {{\,\textrm{Sk}\,}}_{n-2}\mathcal {T})\ge {\frac{\gamma }{\gamma + 1}}{{\,\textrm{dist}\,}}(x, \, {{\,\textrm{Sk}\,}}_{n-3}\mathcal {T})\). As u has a nice singularity at \({{\,\textrm{Sk}\,}}_{n-2}\mathcal {T}\), we obtain
because of Lemma 2.18. Moreover, as the Jacobian is a local operator (Remark 2.4), Remark 2.19 implies
In view of (2.62), (2.63), it makes sense to take \(u_\varepsilon := u\) on \(M\setminus V\).
Construction of the recovery sequence on each \(V_K\). Let \(K\in \mathcal {T}_{n-2}\). As \(\textrm{diam}\,\mathcal {T} \le \delta \), we have \(\textrm{diam}\, V_K \le C\delta \), for some constant C that depends only on \(\gamma \). When \(\delta \) small enough, the diameter of \(V_K\) is smaller than the injectivity radius of \(V_K\). By working in geodesic normal coordinates, we may identify \(V_K\) with a subset of \(\mathbb R^n\). We also identify sections \(V_K\rightarrow E\) with complex-valued maps defined on a subset of \(\mathbb R^n\). The restriction \(u_{|\partial V_K}\) has a nice singularity at \(\partial K\) and hence, \(u\in W^{1,p}(\partial V_K, \, E)\) for any \(p<2\), because of Lemma 2.18. By Sobolev embeddings, it follows that \(u\in W^{1/2,2}(\partial V_K, \, E)\). Therefore, we are in position to apply \(\Gamma \)-convergence results for the Ginzburg–Landau functional in Euclidean settings. Thanks to [2, Theorem 5.5 p. 32 and Remark i p. 33], there exists a sequence of complex-valued maps \(u_\varepsilon ^K\), of class \(W^{1,2}\) in the interior of \(V_K\), such that \(u_\varepsilon ^K = u\) on \(\partial V_K\) (in the sense of traces),

Here, as in (2.15), \(\bar{J}(u_\varepsilon ^K):= \frac{1}{2}{{\,\textrm{d}\,}}\left\langle {{\,\textrm{d}\,}}u_\varepsilon ^K, \, iu_\varepsilon ^K\right\rangle \) and \({{\,\textrm{d}\,}}x\) denotes the Lebesgue measure on \(V_K\). The reference connection \({{\,\textrm{D}\,}}_0\) can be written as \({{\,\textrm{D}\,}}_0 = {{\,\textrm{d}\,}}- i\gamma _0\) on \(V_K\), for some smooth 1-form \(\gamma _0\). Therefore, \(J(u_\varepsilon ^K) - \bar{J}(u_\varepsilon ^K) = \frac{1}{2}{{\,\textrm{d}\,}}(\gamma _0(1 - |u_\varepsilon ^K|^2))\). The energy estimate (2.65) implies that \(J(u_\varepsilon ^K) - \bar{J}(u_\varepsilon ^K) \rightarrow 0\) in \(W^{-1,2}(M)\) and hence,
We recall that the volume form \({{\,\textrm{vol}\,}}_g\), in geodesic coordinates on a ball of radius r, satisfies \({{\,\textrm{vol}\,}}_g \le (1 + Cr^2){{\,\textrm{d}\,}}x\), where C is a constant that depends only on the curvature of M, not on r. Then, keeping in mind that the difference \({{\,\textrm{D}\,}}_0 - {{\,\textrm{d}\,}}\) is bounded independently of \(\varepsilon \), from (2.65) we deduce

for \(\delta \) small enough.
Conclusion. Recall that we have defined \(u_\varepsilon := u\) in \(M\setminus V\). Now, we take \(u_\varepsilon := u_\varepsilon ^K\) on each \(V_K\). Since the \(V_K\)’s have pairwise disjoint interiors, the section \(u_\varepsilon \) is well-defined and is of class \(W^{1,2}\). As the Jacobian is a local operator, from (2.63) and (2.66) we deduce that \(J(u_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,1}(M)\). The inequality (2.61) follows from (2.62) and (2.67). This completes the proof.\(\quad \square \)
4 \(\Gamma \)-Convergence for the Functional \(G_\varepsilon \)
In this section, we prove Theorem A relying on Theorem C and Corollary B relying, in turn, on Theorem A. Since the recovery sequence in the proof of (ii) of Theorem C essentially works as well for the functional \(G_\varepsilon \), almost all the work in this section is addressed to the proof of Statement (i) of Theorem A. The key idea is that the given sequence \(\{(u_\varepsilon , A_\varepsilon )\}\) in Statement (i) of Theorem A can always be replaced, in the proof, with a better sequence to the purpose, which we call an optimised sequence (Definition 3.1). The relevant properties of optimised sequences are listed in Lemma 3.5. They allow, in the end, both to find a lower bound for the limit inferior of the rescaled energies (see Corollary 3.9 and Remark 3.10) and to show the flat convergence of gauge-invariant Jacobians (see Lemma 3.5, Remark 3.6, and Corollary 3.9) with much less effort than needed to deal directly with the “original” sequence \(\{(u_\varepsilon , A_\varepsilon )\}\) in Statement (i) of Theorem A.
We begin this section dealing with an auxiliary problem, involved in the construction of optimised sequences. As a preliminary step, recall from Remark A.11 that an exact 2-form \(\psi \in W^{1,2}(M, \Lambda ^2 \textrm{T}^*M)\) with \({{\,\textrm{d}\,}}^* \psi \in W^{1,2}(M, \textrm{T}^*M)\) actually belongs to \(W^{2,2}(M, \, \Lambda ^2\textrm{T}^*M)\). In fact, there holds more: by Remark A.17 there is a constant \(C > 0\), depending only on M, such that the estimate
holds for all exact 2-forms \(\psi \in W^{2,2}(M,\,\Lambda ^2\textrm{T}^*M)\).
Now we can introduce the mentioned auxiliary problem. Let \({{\,\textrm{D}\,}}_0\) be a smooth reference connection, let \(A \in W^{1,2}(M, \textrm{T}^*M)\), and set
Lemma 3.1
For all \(A \in W^{1,2}(M,\,\textrm{T}^*M)\), the corresponding set [A], defined in (3.2), is not empty and it is sequentially weakly closed in \(W^{1,2}(M, \textrm{T}^*M)\).
Proof
Since \(A \in [A]\) for every \(A \in W^{1,2}(M,\,\textrm{T}^*M)\), [A] is always not empty. Fix \(A \in W^{1,2}(M,\,\textrm{T}^*M)\), assume \(\{B_j\} \subset [A]\) is a weakly convergent sequence in \(W^{1,2}(M,\,\textrm{T}^*M)\), and let B denote the weak limit of \(\{B_j\}\). Clearly, \(B \in W^{1,2}(M,\,\textrm{T}^*M)\). We have to show that B writes as \(A + {{\,\textrm{d}\,}}^* \psi \) for an exact 2-form \(\psi \in W^{2,2}(M,\,\Lambda ^2 \textrm{T}^* M)\). Since \(\{B_j\}\) is weakly convergent in \(W^{1,2}(M,\,\textrm{T}^*M)\), \(\{B_j\}\) is bounded in \(W^{1,2}(M,\,\textrm{T}^*M)\). Consequently, \(\{{{\,\textrm{d}\,}}^* \psi _j\}\) is a bounded sequence in \(W^{1,2}(M,\,\textrm{T}^*M)\) and, since each \(\psi _j\) is exact, by (3.1) the sequence \(\{\psi _j\}\) is bounded in \(W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M)\). Thus, \(\{\psi _j\}\) contains a (not relabeled) subsequence which converges weakly in \(W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M)\) to some \(\psi \in W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M)\). By the compactness of M, the embedding \(W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M) \hookrightarrow W^{1,2}(M,\,\Lambda ^2 \textrm{T}^*M)\) is continuous—as it is, in fact, compact. By Hodge decomposition (A.14), this implies that the co-exact and harmonic parts of \(\psi \) are zero, hence \(\psi \) is still exact. From the above, we have \(B_j \rightharpoonup A + {{\,\textrm{d}\,}}^* \psi \) weakly in \(W^{1,2}(M, \textrm{T}^*M)\) as \(j \rightarrow \infty \). By the uniqueness of the weak limit, it follows that \(B = A + {{\,\textrm{d}\,}}^* \psi \). Since \(\psi \) is exact, we have eventually \(B \in [A]\), proving that [A] is sequentially weakly closed.\(\quad \square \)
Fix a smooth reference connection \({{\,\textrm{D}\,}}_0\), a 1-form \(A \in W^{1,2}(M,\,\textrm{T}^*M)\), and a section \(u \in W^{1,2}(M,\,E)\). Let \(\mathcal {F}(\,\cdot \,; u, A, {{\,\textrm{D}\,}}_0): [A] \rightarrow \mathbb R\) be the functional defined as follows:
Proposition 3.2
For every choice of a reference smooth connection \({{\,\textrm{D}\,}}_0\), of \(A \in W^{1,2}(M, \textrm{T}^*M)\) and of \(u \in W^{1,2}(M,E)\), the functional \(\mathcal {F}( \,\cdot ; u, A, {{\,\textrm{D}\,}}_0): [A] \rightarrow \mathbb R\) defined in (3.3) (where [A] is the set defined by (3.2)) has a minimiser over [A]. Furthermore, if \({{\,\textrm{D}\,}}_A u \in L^2(M,\,\textrm{T}^*M \otimes E)\), then any minimiser B of \(\mathcal {F}(\,\cdot ; u, A, {{\,\textrm{D}\,}}_0)\) over [A] satisfies the London equation, i.e.,
in the sense of \(\mathcal {D}^\prime (M)\). In addition, it holds that
for every \(\varepsilon > 0\).
Proof
To shorten the notation, let us omit the dependence on u, A, and \({{\,\textrm{D}\,}}_0\) and simply write \(\mathcal {F}\) in place of \(\mathcal {F}( \,\cdot \,; u, A, {{\,\textrm{D}\,}}_0)\). From Lemma 3.1, [A] is not empty and sequentially weakly closed. Obviously, \(\mathcal {F}\) is bounded below, and thus, to prove existence of minimisers of \(\mathcal {F}\) over [A], we only have to prove that \(\mathcal {F}\) is sequentially coercive and sequentially lower semicontinuous over [A]. Once this is done, the conclusion follows immediately by the direct method in the calculus of variations.
Step 1
(\(\mathcal {F}\) is sequentially coercive)
As [A] is sequentially weakly closed in the reflexive space \(W^{1,2}(M,\textrm{T}^*M)\), it suffices to prove that \(\mathcal {F}(B) \ge C_1 \left\| B \right\| _{W^{1,2}(M)}^2 - C_2\) for \(B \in [A]\), where \(C_1\) and \(C_2\) are positive constants independent of B. Thus, let \(B \in [A]\). Then, \(B = A + {{\,\textrm{d}\,}}^* \psi \) for some exact 2-form \(\psi \in W^{2,2}(M, \Lambda ^2 \textrm{T}^*M)\). Notice that \(F_B = F_A + {{\,\textrm{d}\,}}{{\,\textrm{d}\,}}^* \psi \) and that \({{\,\textrm{d}\,}}{{\,\textrm{d}\,}}^* \psi = -\Delta \psi \) because \(\psi \) is an exact form belonging to \(W^{2,2}(M,\Lambda ^2 \textrm{T}^*M)\). Also, recall that \(\left\| \Delta \psi \right\| _{L^2(M)}\) is a norm equivalent to \(\left\| \psi \right\| _{W^{2,2}(M)}\) on exact forms of class \(W^{2,2}\). Thus, using Young’s inequality,
where \(C_1, C_2 > 0\) are constants independent of B (that is, independent of \(\psi \)). Thus, \(\mathcal {F}\) is sequentially coercive over [A], for every choice of \({{\,\textrm{D}\,}}_0\), A, and u.
Step 2
(\(\mathcal {F}\) is sequentially weakly lower semicontinous) Let \(\{B_j\}\) be a sequence in [A]. Then, for each \(j \in \mathbb N\) there is an exact 2-form \(\psi _j \in W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M)\) such that \(B_j = A + {{\,\textrm{d}\,}}^* \psi _j\). Assume \(\{B_j\}\) converges weakly to \(B \in W^{1,2}(M, \textrm{T}^*M)\). Then, \(B \in [A]\), \(\{\psi _j\}\) converges weakly in \(W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M)\) to some \(\psi \in W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M)\), and \(B = A + {{\,\textrm{d}\,}}^*\psi \). Since M is compact, the embedding \(W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M) \hookrightarrow W^{1,2}(M,\,\Lambda ^2 \textrm{T}^*M)\) is compact, and therefore \({{\,\textrm{d}\,}}^*\psi _j \rightarrow {{\,\textrm{d}\,}}^* \psi \) strongly in \(L^2(M,\,\textrm{T}^*M)\) as \(j \rightarrow \infty \) and almost everywhere on a (not relabelled) subsequence. Thus, we have \({{\,\textrm{D}\,}}_{B_j} u \rightarrow {{\,\textrm{D}\,}}_B u\) pointwise a.e. on M and from Fatou’s lemma it follows that
On the other hand, \(\Delta \psi _j \rightarrow \Delta \psi \) weakly in \(L^2(M,\,\Lambda ^2 \textrm{T}^*M)\), and hence we have (recall that \({{\,\textrm{d}\,}}{{\,\textrm{d}\,}}^* \omega = -\Delta \omega \) if \(\omega \) is an exact form of class \(W^{2,2}\))
by the sequential weak lower semicontinuity of the \(L^2\)-norm.
Since \(F_{B_j} = F_A + {{\,\textrm{d}\,}}{{\,\textrm{d}\,}}^* \psi _j\), from the above we get
and then, by the direct method in the calculus of variations, there exist a minimiser B of \(\mathcal {F}\) over [A]. Then, it is obvious that (3.4) holds.
Step 3
(If \(\mathcal {F} \not \equiv +\infty \), every minimiser satisfies the London equation and (3.4)). Assume, in addition to the previous hypotheses, that \({{\,\textrm{D}\,}}_A u \in L^2(M,\, \textrm{T}^*M \otimes E)\). Then, \(\mathcal {F}(A) < +\infty \), hence minimisers of \(\mathcal {F}\) over [A] have finite energy (in fact, slightly more mildly, we could have required directly finite energy for minimisers in the statement). Let B be a minimiser of \(\mathcal {F}\) over [A]. To see that \(F_B\) satisfies the London equation, take any \(\eta \in C^\infty (M,\,\Lambda ^2\textrm{T}^*M)\) and set \(B_t:= B + t {{\,\textrm{d}\,}}^* \eta \) for \(t \in \mathbb R\). By Hodge decomposition, only the exact part of \(\eta \) contributes to \(B_t\), whence \(\mathcal {F}(B) \le \mathcal {F}(B_t)\) for every \(t \in \mathbb R\) and every choice of \(\eta \in C^\infty (M,\,\Lambda ^2\textrm{T}^*M)\). Thus, we must have \(\left. \frac{{{\,\textrm{d}\,}}}{{{\,\textrm{d}\,}}t}\right| _{t=0} \mathcal {F}(B_t) = 0\), and so
As (3.6) holds for any \(\eta \in C^\infty (M,\,\Lambda ^2 \textrm{T}^*M)\), it follows that
in the sense of distributions, whence (as \(F_{B}\) is closed)
in the sense of distributions.
Remark 3.3
For \(u \equiv 0\) the functional \(\mathcal {F}\) reduces to the Yang-Mills functional \(\mathcal{Y}\mathcal{M}(B):= \int _M \left| F_B \right| ^2 {{\,\textrm{vol}\,}}_g\), considered over the class [A]; i.e., \(\mathcal {F}(B\,; 0, A,{{\,\textrm{D}\,}}_0) = \mathcal{Y}\mathcal{M}(B)\) for \(B \in [A]\). An argument very similar to that in the proof of Proposition 3.2 yields existence of \(U(1)\)-Yang-Mills connections over \(E \rightarrow M\) in [A], for every \(A \in W^{1,2}(M,\,\textrm{T}^*M)\). Indeed, the existence of a minimiser B of \(\mathcal{Y}\mathcal{M}\) over [A] was already proved in Step 1 and Step 2. The fact that for any such minimiser \(F_B\) satisfies the Yang-Mills equations \({{\,\textrm{d}\,}}^* F_B = 0\) in the sense of distributions follows easily similarly to as in Step 3. Indeed, if \(t \in \mathbb R\) and \(\psi \in C^\infty (M,\,\Lambda ^2\textrm{T}^*M)\) is any exact 2-form, then \(B_t:= B + t {{\,\textrm{d}\,}}^*\psi \in [A]\) and \(F_{B_t} = F_B + t {{\,\textrm{d}\,}}({{\,\textrm{d}\,}}^* \psi )\). Hence,
for every \(\psi \in C^\infty (M,\,\Lambda ^2 \textrm{T}^*M)\). On the other hand, for any \(\omega \in C^\infty (M,\,\textrm{T}^*M)\), we have \(\omega = {{\,\textrm{d}\,}}\varphi + {{\,\textrm{d}\,}}^*\psi + \xi \) for some \(\varphi \in C^\infty (M)\), \(\psi \in C^\infty (M,\,\Lambda ^2 \textrm{T}^*M)\) exact, and \(\xi \in {{\,\textrm{Harm}\,}}^1(M)\), hence
for every \(\omega \in C^\infty (M,\,\textrm{T}^*M)\). Thus, \({{\,\textrm{d}\,}}^* F_B = 0\) in the sense of \(\mathcal {D}'(M)\).
Since we want to prove a \(\Gamma \)-convergence result, and since \(\left| \log \varepsilon \right| \) is the energy scaling of minimisers of \(G_\varepsilon \) according to Remark 2, it is natural to be concerned with sequences \(\{(u_\varepsilon , A_\varepsilon )\} \subset W^{1,2}(M,E) \times W^{1,2}(M,\textrm{T}^*M)\) satisfying
We are now going to explore the consequences of this additional assumption.
Lemma 3.4
Let \(\{(u_\varepsilon , A_\varepsilon )\}\) be a sequence in \(W^{1,2}(M,\,E)\times W^{1,2}(M,\,\textrm{T}^*M)\). For each \(\varepsilon > 0\), let \(B_\varepsilon \) be a minimiser of \(\mathcal {F}(\,\cdot ; u_\varepsilon , A_\varepsilon , {{\,\textrm{D}\,}}_0)\) over \([A_\varepsilon ]\), where \([A_\varepsilon ]\) is defined as in (3.2). Assume that \(\{(u_\varepsilon , A_\varepsilon )\}\) satisfies (3.7). Then,
for all \(\varepsilon > 0\).
Proof
For each \(\varepsilon > 0\) there is an exact form \(\psi _\varepsilon \in W^{2,2}(M,\,\Lambda ^2 \textrm{T}^*M)\) such that \(B_\varepsilon = A_\varepsilon + {{\,\textrm{d}\,}}^* \psi _\varepsilon \), and
By (3.7) and the minimality of \(B_\varepsilon \), we have
up to a constant depending only on M, and therefore
By (3.1),
whence
Then,
for all \(\varepsilon > 0\), and the right hand side tends to zero sending \(\varepsilon \rightarrow 0\). Consequently, recalling (1.4), it follows from (3.10) that, for all \(\varepsilon > 0\),
which is the conclusion.\(\quad \square \)
Definition 3.1
For any given sequence \(\{(u_\varepsilon , A_\varepsilon )\} \subset W^{1,2}(M,\,E) \times W^{1,2}(M,\,\textrm{T}^* M)\), we define a new sequence \(\{(v_\varepsilon , B_\varepsilon )\} \subset (L^\infty \cap W^{1,2})(M,\,E) \times W^{1,2}(M,\,\textrm{T}^*M)\) as follows. First, we replace each \(u_\varepsilon \) with \(v_\varepsilon \), the essentially bounded section associated with \(u_\varepsilon \) by (2.2). Secondly, we replace each \(A_\varepsilon \) with a corresponding minimiser \(B_\varepsilon \) of \(\mathcal {F}(\,\cdot \,; v_\varepsilon , A_\varepsilon , {{\,\textrm{D}\,}}_0)\) over \([A_\varepsilon ]\), where \([A_\varepsilon ]\) is defined as in (3.2). We call \(\{(v_\varepsilon , B_\varepsilon )\}\) an optimised sequence associated with \(\{(u_\varepsilon , A_\varepsilon )\}\).
Lemma 3.5
(Reduction lemma) For any sequence \(\{(u_\varepsilon , A_\varepsilon )\} \subset W^{1,2}(M,E) \times W^{1,2}(M, \textrm{T}^* M)\), let \(\{(v_\varepsilon , B_\varepsilon )\} \subset (L^\infty \cap W^{1,2})(M,E) \times W^{1,2}(M, \textrm{T}^* M)\) be an associated optimised sequence (defined in Definition 3.1). Then, \(\{(v_\varepsilon , B_\varepsilon )\}\) satisfies the London equation (8), i.e.,
and, moreover,
for any \(\varepsilon > 0\). Consequently,
Moreover, under the assumption (3.7) it holds that
as \(\varepsilon \rightarrow 0\).
Proof
The fact that \((v_\varepsilon , B_\varepsilon )\) satisfies, for any \(\varepsilon > 0\), the London equation (8) follows by definition of optimised sequence (Definition 3.1) and Proposition 3.2. Inequality (3.11) follows by construction. Indeed, by (3.4) and (2.3) we have
for all \(\varepsilon > 0\). Then, obviously, the inequality remains true dividing both sides by \(\left| \log \varepsilon \right| \) and passing both sides to the limit inferior, i.e., inequality (3.12) holds.
In view of Lemma 2.1 and, more specifically, of (2.4), to prove (3.13) it is enough to prove that
as \(\varepsilon \rightarrow 0\). The case \(p = 1\) is proved in Lemma 3.4. We will rely on that case and interpolation to extend the same conclusion to all \(1\le p < \frac{n}{n-1}\). To this purpose, we notice that (2.9), (3.7) and Hölder’s inequality imply
On the other hand, from (2.9), (3.7), and (3.9) it follows that
Thus, by Lemma 3.4, (3.14), (3.15), and Lemma C.1, we get, that
as \(\varepsilon \rightarrow 0\), for any \(1 \le p < \frac{n}{n-1}\).\(\quad \square \)
Remark 3.6
In view of (3.12) and (3.13), it is always possible to pass to an optimised sequence in the proof of Statement (i) of Theorem A (i.e., to replace, in the proof, the given sequence \(\{(u_\varepsilon , A_\varepsilon )\}\) with any associated optimised sequence). As we will see later, a decisive advantage of doing so is that the curvature of the connections of an optimised sequence satisfy the London equation (8).
It is convenient to introduce the following notation: if \(\Phi \in W^{2,2}(M,\,\mathbb {S}^1)\) is a gauge transformation and \(A \in W^{1,2}(M, \textrm{T}^*M)\), we set (cf. Remark 2.9)
The next technical lemma produces a family of gauge transformations playing a crucial rôle thorough out the rest of this section.
Lemma 3.7
Let \(\{(u_\varepsilon ,A_\varepsilon )\} \subset (L^\infty \cap W^{1,2})(M,E)\times W^{1,2}(M,\textrm{T}^*M)\) be an optimised sequence satisfying (3.7). Then, for each \(\varepsilon > 0\) there exists gauge transformations \(\Phi _\varepsilon \in W^{2,2}(M,\, \mathbb {S}^1)\) so that it holds that
for all \(\varepsilon > 0\), whence
for all \(\varepsilon > 0\).
Proof
By Lemma 2.10, for all \(\varepsilon > 0\) we find a gauge transformation such that we can write \(\Phi _\varepsilon \cdot A_\varepsilon = {{\,\textrm{d}\,}}^*\psi _\varepsilon + \zeta _\varepsilon \), where \(\zeta _\varepsilon \in {{\,\textrm{Harm}\,}}^1(M)\). Indeed, denote \(A_\varepsilon = {{\,\textrm{d}\,}}\varphi _\varepsilon + {{\,\textrm{d}\,}}^* \psi _\varepsilon + \xi _\varepsilon \) the Hodge decomposition of \(A_\varepsilon \), where \(\varphi \in W^{2,2}(M)\) is co-exact, \(\psi \in W^{2,2}(M,\Lambda ^2 \textrm{T}^*M)\) is exact, and \(\xi \in {{\,\textrm{Harm}\,}}^1(M)\). Then, Lemma 2.10 provides us, for each \(\varepsilon > 0\), with a gauge transformation \(\Phi _\varepsilon \in W^{2,2}(M,\,\mathbb {S}^1)\) and a harmonic 1-form \(\bar{\xi }_\varepsilon \) so that \(\Phi _\varepsilon ^*({{\,\textrm{vol}\,}}_{\mathbb {S}^1}) = - {{\,\textrm{d}\,}}\varphi _\varepsilon - \bar{\xi }_\varepsilon \). In addition, by Remark 2.11, \(\Vert \zeta _\varepsilon \Vert _{L^\infty (M)} \le C_M\), where \(\zeta _\varepsilon := \xi _\varepsilon - \bar{\xi }_\varepsilon \) and \(C_M\) is a constant depending only on M (whence of course \(\sup _{\varepsilon > 0} \left\| \zeta _\varepsilon \right\| _{L^\infty (M)} \le C_M\)). Let \(\varepsilon > 0\) be arbitrary, and recall that we denote \(F_0\) the curvature 2-form of the reference connection \({{\,\textrm{D}\,}}_0\). As \(\psi _\varepsilon \) is exact and of class \(W^{2,2}\), it holds that
by (A.26). In particular, \(F_{A_\varepsilon } - F_0\) is an exact 2-form (hence, orthogonal to every harmonic 2-form) and therefore we deduce from Lemma A.16 that, for all \(\varepsilon > 0\),
where the last inequality follows from (3.7). Hence, recalling (A.4),
for all \(\varepsilon > 0\); i.e., (3.17) is proved. From (3.17), (3.7), and the gauge-invariance of \(G_\varepsilon \),
for all \(\varepsilon > 0\).\(\quad \square \)
Remark 3.8
In general, we cannot assert that the original sequence \(\{A_\varepsilon \}\) satisfies (3.17), as we have no control on the exact part of the Hodge decomposition of the maps \(A_\varepsilon \) (i.e., on \({{{\,\textrm{d}\,}}\varphi _\varepsilon }\)).
We immediately make use of Lemma 3.7 to prove
Corollary 3.9
Let \(\{(u_\varepsilon , A_\varepsilon )\} \subset (L^\infty \cap W^{1,2})(M, E) \times W^{1,2}(M,\textrm{T}^*M)\) be an optimised sequence satisfying (3.7). Then, up to extraction of a (not relabelled) subsequence, \(J(u_\varepsilon , A_\varepsilon ) \rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\) as \(\varepsilon \rightarrow 0\), where \(J_*\) is a bounded measure with values in 2-forms. In addition, \(\star J_*\) is an integer-multiplicity rectifiable \((n-2)\)-cycle belonging to \(\mathcal {C}\).
Proof
Let \(\{\Phi _\varepsilon \}\) be the family of gauge transformations in Lemma 3.7. In view of (3.18), we can apply Theorem C to the sequence \(\{\Phi _\varepsilon u_\varepsilon \}\). By Statement (i) of Theorem C, we obtain a (not relabelled) subsequence \(\{\Phi _\varepsilon u_\varepsilon \}\) and a bounded measure \(J_*\) with values in 2-forms such that \(J(\Phi _\varepsilon u_\varepsilon ) \rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\) as \(\varepsilon \rightarrow 0\). Since we already know from Statement (i) of Theorem C that \(\star J_*\) is a current with the desired properties, it only remains to prove that \(J(u_\varepsilon , A_\varepsilon ) \rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\) as \(\varepsilon \rightarrow 0\).
To prove this, we observe that, by the gauge-invariance of the Jacobians, we have \(J(u_\varepsilon , A_\varepsilon ) = J(\Phi _\varepsilon u_\varepsilon , \Phi _\varepsilon \cdot A_\varepsilon )\) for all \(\varepsilon > 0\). Thus,
for all \(\varepsilon > 0\). By definition of \(J_*\), we need only to show that
To this purpose, we recall that from (1.4) we have
for all \(\varepsilon > 0\). By (3.17) and the energy estimate (3.18) (or, equivalently, (3.7), since \(\left| \Phi _\varepsilon u_\varepsilon \right| = \left| u_\varepsilon \right| \) a.e.), for each \(\varepsilon > 0\) it holds that
whence
for all \(\varepsilon > 0\). Then (3.20) follows by using Lemma C.1 exactly as in the last part of Lemma 2.1. The conclusion is now immediate by triangle inequality.\(\quad \square \)
Remark 3.10
In view of (3.13), Corollary 3.9 proves a half of Statement (i) of Theorem A.
The following proposition is the last piece of information we need to combine the above results with Theorem C to deduce the lower bound (11), concluding the proof of Theorem A. Here we will use in a crucial way the fact that the curvatures \(F_{A_\varepsilon }\) satisfy the London equation (8), as alluded in Remark 3.6.
Proposition 3.11
Let \(\{(u_\varepsilon , A_\varepsilon )\} \subset (L^\infty \cap W^{1,2})(M,\,E) \times W^{1,2}(M,\,\textrm{T}^*M)\) be an optimised sequence satisfying (3.7). Then, up to extraction of a (not relabelled) subsequence:
-
(i)
\(\{F_{A_\varepsilon }\}\) is a Cauchy sequence in \(W^{1,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\).
-
(ii)
If \(\{\Phi _\varepsilon \}\) is the family of gauge transformations in Lemma 3.7, the sequence \(\{ \Phi _\varepsilon \cdot A_\varepsilon \}\) is a bounded sequence in \(W^{2,p}(M,\,\textrm{T}^*M)\) for any \(1 \le p < \frac{n}{n-1}\).
-
(iii)
Up to a further (not relabelled) subsequence, \(\{\Phi _\varepsilon \cdot A_\varepsilon \}\) converges strongly in \(W^{2,p}(M,\,\textrm{T}^*M)\), for any \(1 \le p < \frac{n}{n-1}\), to some \(A_*\), where \(A_*\) writes
$$\begin{aligned} A_* = {{\,\textrm{d}\,}}^* \psi _* + \zeta _* \end{aligned}$$(3.21)for \(\psi _* \in W^{3,p}(M,\,\Lambda ^2 \textrm{T}^*M)\) an exact 2-form and \(\zeta _*\) a harmonic 1-form.
Proof
Let us set \(F_\varepsilon := F_{A_\varepsilon }\) for convenience. Since each of the curvatures \(F_\varepsilon \) satisfies the London equation (8), we have
for all indexes n, \(m \in \mathbb N\). By Lemma C.3, we deduce the crucial estimate
where the right hand side tends to zero as \(n, m \rightarrow \infty \) as a trivial consequence of Corollary 3.9, and this holds for any \(1 \le p < \frac{n}{n-1}\). Thus, \(\{F_{A_\varepsilon }\}\) is a Cauchy sequence in \(W^{1,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\). This proves (i).
To prove (ii), arguing as in Lemma 3.7, by the choice of \(\{\Phi _\varepsilon \}\), for each gauge-transformed connection \(\Phi _\varepsilon \cdot A_\varepsilon \) we have the decomposition \(\Phi _\varepsilon \cdot A_\varepsilon = {{\,\textrm{d}\,}}^* \psi _\varepsilon + \zeta _\varepsilon \) for an appropriate exact 2-form \(\psi _\varepsilon \) satisfying (3.19) and a suitable harmonic 2-form \(\zeta _\varepsilon \). Furthermore, there holds \(\sup _{\varepsilon > 0} \left\| \zeta _\varepsilon \right\| _{L^\infty (M)} < +\infty \) (cf. Remark 2.11). By (3.19), Part (i) and elliptic regularity (i.e., Lemma A.16) it follows that \(\{ \psi _\varepsilon \}\) is a bounded sequence in \(W^{3,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\). Hence, recalling again that \(\Phi _\varepsilon \cdot A_\varepsilon = {{\,\textrm{d}\,}}^*\psi _\varepsilon + \zeta _\varepsilon \), it follows that the sequence \(\{\Phi _\varepsilon \cdot A_\varepsilon \}\) is bounded in \(W^{2,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\).
(iii) Writing again \(\Phi _\varepsilon \cdot A_\varepsilon = {{\,\textrm{d}\,}}^* \psi _\varepsilon + \zeta _\varepsilon \) exactly as in (ii), from (3.19) we have
for any n, \(m \in \mathbb N\). Therefore, by Part (i) it follows that \(\{\Delta \psi _{\varepsilon _n}\}\) is a Cauchy sequence in \(W^{1,p}(M,\,\Lambda ^2\textrm{T}^*M)\) and, since each \(\psi _{\varepsilon _n}\) is exact, by Lemma A.16 and Remark A.17 it follows that \(\{\psi _{\varepsilon _n}\}\) is Cauchy sequence in \(W^{3,p}(M,\,\Lambda ^2\textrm{T}^*M)\), for any \(1 \le p < \frac{n}{n-1}\). Hence, by the completeness of \(W^{3,p}(M,\,\Lambda ^2 \textrm{T}^*M)\), \(\{\psi _{\varepsilon _n}\}\) converges strongly in \(W^{3,p}(M,\,\Lambda ^2 \textrm{T}^*M)\), for any \(1 \le p < \frac{n}{n-1}\), to some \(\psi _*\). By the \(L^p\)-Hodge decomposition (Proposition A.14) and the strong \(W^{3,p}\)-convergence, \(\psi _*\) is still an exact 2-form.
Next, since the space \({{\,\textrm{Harm}\,}}^1(M)\) is finite-dimensional and \(\{\zeta _{\varepsilon _n}\}\) is bounded in the \(L^\infty (M)\)-norm, \(\{\zeta _{\varepsilon _n}\}\) is also bounded with respect to the \(W^{2,p}(M)\)-norm. In addition, we can also extract from \(\{\zeta _{\varepsilon _n}\}\) a (not relabelled) Cauchy sequence, which is a fortiori a Cauchy sequence in \(W^{2,p}(M,\,\textrm{T}^*M)\), for any \(1 \le p < \frac{n}{n-1}\), and hence it converges in \(W^{2,p}(M,\,\textrm{T}^*M)\) to some \(\zeta _*\). Again, by Hodge decomposition and strong convergence, \(\zeta _*\) is still a harmonic 1-form.
Thus, up to a not relabelled subsequence, and letting \(A_*:= {{\,\textrm{d}\,}}^* \psi _* + \zeta _*\), we have \(\Phi _\varepsilon \cdot A_\varepsilon \rightarrow A_*\) in \(W^{2,p}(M,\,\textrm{T}^*M)\) as \(\varepsilon \rightarrow 0\), for any \(1 \le p < \frac{n}{n-1}\).\(\quad \square \)
Remark 3.12
Lemma 3.7, Corollary 3.9, and Proposition 3.11 are still valid, with the same proof, for any sequence \(\{(u_\varepsilon ,\,A_\varepsilon )\} \subset (W^{1,2}\cap L^\infty )(M,\,E)\times W^{1,2}(M,\,\textrm{T}^*M)\) of critical points of \(G_\varepsilon \) that satisfies the logarithmic energy bound (3.7). Indeed, for any critical pair \(\{(u_\varepsilon ,\,A_\varepsilon )\}\) with \(u_\varepsilon \in L^\infty (M, \, E)\), \(u_\varepsilon \) satisfies \(\left\| u_\varepsilon \right\| _{L^\infty (M)} \le 1\) (by maximum principle, as in e.g. [16, Proposition II.2]) and \(F_{A_\varepsilon }\) satisfies the London equation (8). These two facts are all that we are really using about optimised sequences in the proof of the mentioned results, as well as in the proof of Theorem A below.
We now have at disposal everything we need to prove Theorem A.
Proof of Theorem A
(i) As emphasized in Remark 3.6, we can always pass to an optimised sequence associated with \(\{(u_\varepsilon , A_\varepsilon )\}\). Hence, we may assume, for notational convenience, that \(\{(u_\varepsilon , A_\varepsilon )\}\) is already optimised. Let \(\{\Phi _\varepsilon \} \subset W^{2,2}(M,\,\mathbb {S}^1)\) be, once again, the family of gauge transformations of Lemma 3.7. By (3.18), we can apply Statement (i) of Theorem C to the sequence \(\{\Phi _\varepsilon u_\varepsilon \}\). Let \(J_*\) be the bounded measure with values in 2-forms associated with \(\{\Phi _\varepsilon u_\varepsilon \}\) by Statement (i) of Theorem C. The claimed convergence of the gauge-invariant Jacobians \(J(u_\varepsilon , A_\varepsilon )\) to \(J_*\) follows from Corollary 3.9 (and, back to the original sequence, Remark 3.10). Therefore, we still have to prove only the lower bound (11).
To infer (11), we note that, by the gauge-invariance of \(G_\varepsilon (u_\varepsilon , A_\varepsilon )\), it suffices to prove that
Once we have proven (3.22), the conclusion follows immediately from Statement (i) of Theorem C.
Towards the proof of (3.22), we notice that, by interpolation, Proposition 3.11, (3.17), and the (continuous) Sobolev embedding \(W^{1,2}(M, \textrm{T}^* M) \hookrightarrow L^{2^*}(M, \textrm{T}^*M)\) [60, Theorem 1.3.3], for each \(\varepsilon > 0\) we have
whence \(\left\| \Phi _\varepsilon \cdot A_\varepsilon \right\| _{L^2(M)} = \textrm{o}\left( \left| \log \varepsilon \right| ^\frac{1}{2}\right) \) as \(\varepsilon \rightarrow 0\). On the other hand, (3.18) implies
for any \(\varepsilon > 0\). Therefore, since
and
we deduce
As remarked, the claimed conclusion now follows from (i) of Theorem C (and, back to the original, not necessarily optimised, sequence \(\{(u_\varepsilon ,A_\varepsilon )\}\), inequality (3.12)).
(ii) Given any \(S_* \in \mathcal {C}\), let \(J_*:= \star S_*\) be the corresponding measure with values in 2-forms \(J_*\) and denote \(\{u_\varepsilon \} \subset W^{1,2}(M,E)\) the recovery sequence given by (ii) of Theorem C. Then the sequence \(\{(u_\varepsilon , 0)\} \subset W^{1,2}(M,E) \times W^{1,2}(M, \textrm{T}^*M)\) satisfies \(J(u_\varepsilon , 0) \rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any \(1 \le p < \frac{n}{n-1}\) as \(\varepsilon \rightarrow 0\) (simply because \(J(u_\varepsilon ,0) = J(u_\varepsilon )\) by definition). In addition,
because the inequality holds for \(E_\varepsilon (u_\varepsilon )\) by (ii) of Theorem C and because for all \(\varepsilon > 0\) we have \(G_\varepsilon (u_\varepsilon ,0) = E_\varepsilon (u_\varepsilon ) + \frac{1}{2}\left\| F_0 \right\| ^2_{L^2(M)}\), where as usual \(F_0\) is the curvature of the reference connection \({{\,\textrm{D}\,}}_0\). The proof is finished.\(\quad \square \)
Remark 3.13
As alluded in Remark 3.12 above, not only the proof of the auxiliary results Lemma 3.7, Corollary 3.9, and Proposition 3.11, but also the proof of Theorem A itself does not really exploit the full power of optimised sequences. In fact, in all these results we really used only that the new sections satisfy \(\left\| u_\varepsilon \right\| _{L^\infty (M)} \le 1\) and that the new curvatures satisfy the London equation (8). With respect to the aims of the present paper, the relevance of the “optimisation procedure” settled in this section lies exactly in providing a method to obtain the above properties that can be applied without loss of generality (c.f. Lemma 3.5) in our \(\Gamma \)-convergence framework.
Remark 3.14
There is a local analogue of the \(\Gamma \)-lower inequality for \(G_\varepsilon \). More precisely, let \(\{(u_\varepsilon , \, A_\varepsilon )\}\subset W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^* M)\) be a sequence that satisfies (3.7) and let \(V\subset M\) an arbitrary open set. Up to extraction of a subsequence, assume that \(J(u_\varepsilon , \, A_\varepsilon )\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any p with \(1 \le p < n/(n-1)\). Then
The proof of (3.24) is completely analogous to the proof of (3.23) above and is based on the local \(\Gamma \)-lower inequality for \(E_\varepsilon \) (Proposition 2.14).
Corollary B is now an almost immediate consequence of Theorem A.
Proof of Corollary B
Let \((u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) be a minimiser of \(G_\varepsilon \) in \(W^{1,2}(M, \, E)\times W^{1,2}(M, \, \textrm{T}^*M)\), for any \(\varepsilon > 0\). As the class \(\mathcal {C}\) is non-empty, Theorem A and a comparison argument imply that
for some \(\varepsilon \)-independent constant C. By applying Theorem A again, we find a limit 2-form \(J_*\) such that, up to extraction of a subsequence, \(J(u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\rightarrow \pi J_*\) in \(W^{-1,p}(M)\) for any \(p < \frac{n}{n-1}\). Moreover, \(\star J_*\in \mathcal {C}\) and \(\star J_*\) is a chain of minimal mass in \(\mathcal {C}\). Indeed, by (ii) of Theorem A any cycle \(S_*\) in the class \(\mathcal {C}\) can be realised as limit of the Jacobians of a sequence \((v_\varepsilon , B_\varepsilon ) \in W^{1,2}(M,\,E) \times W^{1,2}(M,\,\textrm{T}^*M)\) satisfying (10) and (12) and this yields
in view again of Theorem A and of item (v) of Proposition B.1.
As \((u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) is a minimiser of \(G_\varepsilon \) it follows that \(\left| u_\varepsilon \right| \le 1\) (by a truncation argument, along the lines of Lemma 2.1) and that \(\{(u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\}\) is an optimised sequence. Then, Proposition 3.11 implies that the curvatures \(F_{A_\varepsilon ^{\min }}\) converge to a limit \(F_*\) in \(W^{1,p}(M)\) for any \(p<\frac{n}{n-1}\). Each \(F_{A_\varepsilon ^{\min }}\) satisfies the London equation
(by the arguments of Proposition 3.2). By passing to the limit as \(\varepsilon \rightarrow 0\) in (3.26), it follows that \(F_*\) satisfies the London equation
It only remains to prove that the rescaled energy densities \(\mu _\varepsilon := \mu _\varepsilon (u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) (defined in (13)) converge to the total variation \(\pi \left| J_* \right| \). Due to (3.25), we can extract a subsequence in such a way that \(\mu _\varepsilon \rightharpoonup \mu _*\), weakly as measures, as \(\varepsilon \rightarrow 0\). Equation (3.24) implies that
for any open set \(V\subseteq M\) such that \(\mu _*(\partial V) = 0\). As \(\mu _*\) is a bounded Borel measure, it follows that \(\pi \left| J_* \right| \le \mu _*\) as measures. However, Statement (ii) in Theorem A implies that
Therefore, \(\mu _* = \pi \left| J_* \right| \), as claimed.\(\quad \square \)
Remark 3.15
For any sequence \(\{(u_\varepsilon ,\,A_\varepsilon )\} \subset (W^{1,2}\cap L^\infty ) (M,\,E) \times W^{1,2}(M,\,\textrm{T}^*M)\) of critical points of \(G_\varepsilon \) that satisfy the logarithmic energy bound (3.7), there exist bounded measures \(J_*\), \(F_*\), with values in 2-forms, and a (non-relabelled) subsequence such that
for any \(p < n/(n-1)\). Moreover, \(F_*\) satisfies the London equation (3.27). The proof of this claim follows by the same arguments we used in the proof of Corollary B, word by word. Indeed, the assumption that \((u_\varepsilon ^{\min }, \, A_\varepsilon ^{\min })\) is a sequence of minimisers is only needed to show that the limit \(J_*\) is area-minimising in its homology class. As for the rest, the arguments of Corollary B only depend on the fact that \(F_{A_\varepsilon }\) satisfies the London equation (8) and that Proposition 3.11 can be applied. But, according to Remark 3.12, both these facts continue to hold for any sequence of critical points satisfying (3.7).
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Alberti, G., Baldo, S., Orlandi, G.: Functions with prescribed singularities. J. Eur. Math. Soc. (JEMS) 5(3), 275–311, 2003
Alberti, G., Baldo, S., Orlandi, G.: Variational convergence for functionals of Ginzburg–Landau type. Indiana Univ. Math. J. 54(5), 1411–1472, 2005
Baird, P., Wood, J.: Harmonic Morphisms Between Riemannian Manifolds. London Mathematical Society Monographs. New Series, vol. 29. The Clarendon Press, Oxford University Press, Oxford, 2003.
Baldo, S., Orlandi, G.: Cycles of least mass in a Riemannian manifold, described through the “phase transition’’ energy of the sections of a line bundle. Math. Z. 225(4), 639–655, 1997
Baldo, S., Orlandi, G.: A note on the Hodge theory for functionals with linear growth. Manuscr. Math. 97, 453–467, 1998
Baldo, S., Orlandi, G.: Codimension one minimal cycles with coefficients in \(\mathbb{Z} \) or \(\mathbb{Z} _p\), and variational functionals on fibered spaces. J. Geom. Anal. 9(4), 547–568, 1999
Baldo, S., Orlandi, G., Weitkamp, S.: Convergence of minimizers with local energy bounds for the Ginzburg–Landau functionals. Indiana Univ. Math. J. 58(5), 2369–2407, 2009
Bardeen, J., Cooper, L.N., Schrieffer, J.R.: Microscopic theory of superconductivity. Phys. Rev. 106, 162–164, 1957
Bellettini, G., Novaga, M., Orlandi, G.: Time-like minimal submanifolds as singular limits of nonlinear wave equations. Phys. D 239(6), 335–339, 2010
Bellettini, G., Novaga, M., Orlandi, G.: Lorentzian varifolds and applications to relativistic strings. Indiana Univ. Math. J. 61(6), 2251–2310, 2012
Bethuel, F., Brezis, H., Hélein, F.: Ginzburg–Landau Vortices. Progress in Nonlinear Differential Equations and their Applications, vol. 13. Birkhäuser Boston Inc., Boston 1994.
Bethuel, F., Brezis, H., Orlandi, G.: Asymptotics for the Ginzburg–Landau equation in arbitrary dimensions. J. Funct. Anal. 186(2), 432–520, 2001
Bethuel, F., Orlandi, G.: Uniform estimates for the parabolic Ginzburg–Landau equation. ESAIM: COCV 8, 219–238, 2002
Bethuel, F., Orlandi, G., Smets, D.: Motion of concentration sets in Ginzburg-Landau equations. Annales de la Faculté des sciences de Toulouse : Mathématiques, Ser. 6 13(1), 3–43, 2004
Bethuel, F., Orlandi, G., Smets, D.: Convergence of the parabolic Ginzburg–Landau equation to motion by mean curvature. Ann. Math. 163(1), 37–163, 2006
Bethuel, F., Rivière, T.: Vortices for a variational problem related to superconductivity. Ann. Inst. H. Poincaré Anal. Non Linéaire 12(3), 243–303, 1995
Bethuel, F., Zheng, X.M.: Density of smooth functions between two manifolds in Sobolev spaces. J. Funct. Anal. 80(1), 60–75, 1988
Bott, R., Tu, L.W.: Differential Forms in Algebraic Topology. Graduate Texts in Mathematics, vol. 82. Springer, New York, 1982
Bradlow, S.B.: Vortices in holomorphic line bundles over closed Kähler manifolds. Commun. Math. Phys. 135(1), 1–17, 1990
Bradlow, S.B.: Special metrics and stability for holomorphic bundles with global sections. J. Differ. Geom. 33(1), 169–213, 1991
Bröcker, T., Jänich, K.: Introduction to Differential Topology. Cambridge University Press, Cambridge: Translated from the German by C. Thomas, B. Thomas and M. J, 1982
Budney, R. L.: Regularity of \(\cal{A}\)-Harmonic Forms. PhD thesis, Syracuse University, 1996
Canevari, G., Dipasquale, F., Orlandi, G.: The Yang-Mills-Higgs functional on complex line bundles: asymptotics for critical points. arXiv:2034.11346, 2023
Canevari, G., Segatti, A.: Dynamics of Ginzburg–Landau vortices for vector fields on surfaces. arXiv:2108.01321, 2015
Chen, K.-S., Sternberg, P.: Dynamics of Ginzburg-Landau and Gross–Pitaevskii vortices on manifolds. Discrete Contin. Dyn. Syst. 34(5), 1905–1931, 2014
Cheng, D.R.: Stable solutions to the abelian Yang–Mills–Higgs equations on \({S}^2\) and \({T}^2\). J. Geom. Anal. 31(10), 9551–9572, 2021
Colinet, A.: Structural descriptions of limits of the parabolic Ginzburg–Landau equation on closed manifolds. arXiv:2107.13582, 2021
Donaldson, S.K.: Anti self-dual Yang–Mills connections over complex algebraic surfaces and stable vector bundles. Proc. Lond. Math. Soc. s3–50(1), 1–26, 1985
Du, Q., Gunzburger, M., Peterson, J.: Analysis and approximation of the Ginzburg–Landau model of superconductivity. SIAM Rev. 34(1), 54–81, 1992
Federer, H.: Geometric measure theory. Die Grundlehren der mathematischen Wissenschaften, Band, vol. 153. Springer, New York, 1969
García-Prada, O.: Invariant connections and vortices. Commun. Math. Phys. 156(3), 527–546, 1993
Giaquinta, M., Modica, G., Souček, J.: Cartesian Currents in the Calculus of Variations. I, Volume 37 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Springer, Berlin, 1998. Cartesian currents.
Ginzburg, V.L., Landau, L.D.: On the theory of superconductivity. In: ter Haar, D. (ed.), Collected Papers of L. D. Landau. Pergamon, New York, pp. 546–568, 1965
Güneysu, B.: Covariant Schrödinger Semigroups on Riemannian Manifolds. Operator Theory: Advances and Applications. Birkhäuser, Cham, 2017
Hajłasz, P.: Sobolev mappings, co-area formula and related topics. In: Proceedings on Analysis and Geometry (Russian) (Novosibirsk Akademgorodok, 1999). Izdat. Ross. Akad. Nauk Sib. Otd. Inst. Mat., Novosibirsk, pp. 227–254, 2000
Hong, M.-C., Jost, J., Struwe, M.: Asymptotic limits of a Ginzburg–Landau type functional. In: Jost, J. (ed.), Geometric Analysis and the Calculus of Variations for Stefan Hildebrandt. International Press, pp. 99–124, 1996
Ignat, R., Jerrard, R.L.: Renormalized energy between vortices in some Ginzburg–Landau models on 2-dimensional Riemannian manifolds. Arch. Ration. Mech. Anal. 239(3), 1577–1666, 2021
Iwaniec, T., Scott, C., Stroffolini, B.: Nonlinear Hodge theory on manifolds with boundary. Mat. Ann. Pura Appl. 177(1), 37–115, 1999
Jaffe, A., Taubes, C.: Vortices and Monopoles, Volume 2 of Progress in Physics. Birkhäuser, Boston, 1980. Structure of static gauge theories
Jerrard, R.L.: Lower bounds for generalized Ginzburg–Landau functionals. SIAM J. Math. Anal. 30(4), 721–746, 1999
Jerrard, R.L.: Defects in semilinear wave equations and timelike minimal surfaces in Minkowski space. Anal. PDE 4(2), 285–340, 2011
Jerrard, R.L., Soner, H.M.: The Jacobian and the Ginzburg–Landau energy. Cal. Var. Partial Differ. Equ. 14(2), 151–191, 2002
Jerrard, R.L., Soner, H.M.: Functions of bounded higher variation. Indiana Univ. Math. J. 51(3), 645–677, 2003
Jost, J.: Riemannian geometry and geometric analysis. Universitext, 7th edn. Springer, Cham, 2017
Lee, J.M.: Manifolds and Differential Geometry. Graduate Studies in Mathematics, vol 107. American Mathematical Society, Providence, Rhode Island, 2009
Modica, L., Mortola, S.: Un esempio di \(\Gamma ^{-}\)-convergenza. Boll. Un. Mat. Ital. B (5) 14(1), 285–299, 1977
Morrey, Jr., C.B.: Multiple Integrals in the Calculus of Variations. Die Grundlehren der mathematischen Wissenschaften, Band 130. Springer, New York, 1966
Munkres, J. R.: Elementary Differential Topology. Annals of Mathematics Studies, No. 54. Princeton University Press, Princeton, Revised edition, 1966. Lectures given at Massachusetts Institute of Technology, Fall, 1961
Nicolaescu, L.: Lectures on the Geometry of Manifolds, 3rd edn. World Scientific Publishing Co. Pte. Ltd., New Jersey, 2021
Orlandi, G.: Asymptotic behavior of the Ginzburg–Landau functional on complex line bundles over compact Riemann surfaces. Rev. Math. Phys. 08(03), 457–486, 1996
Pacard, F., Rivière, T.: Linear and Nonlinear Aspects of Vortices. Progress in Nonlinear Differential Equations and their Applications, Vol. 39. Birkhäuser Boston, Inc., Boston, 2000. The Ginzburg–Landau model
Palais, R.S.: Foundations of Global Non-Linear Analysis. W.A. Benjamin Inc, New York, 1968
Parise, D., Pigati, A., Stern, D.: Convergence of the self-dual \({{\rm U}}(1)\)-Yang–Mills–Higgs energies to the \((n-2)\)-area functional. arXiv:2103.14615, 2021.
Pigati, A., Stern, D.: Minimal submanifolds from the abelian Higgs model. Invent. Math. 223(3), 1027–1095, 2021
Qing, J.: Renormalized energy for Ginzburg–Landau vortices on closed surfaces. Math. Z. 225(1), 1–34, 1997
Rivière, T.: Ginzburg–Landau vortices: the static model. Astérisque 276, 73–103, 2002. Séminaire Bourbaki, Vol. 1999/2000
Sandier, É.: Lower bounds for the energy of unit vector fields and applications. J. Funct. Anal. 152(2), 379–403, 1998. See Erratum, ibidem 171, 1 (2000), 233
Sandier, E., Serfaty, S.: A product estimate for Ginzburg–Landau and application to the gradient-flow. C. R. Math. Acad. Sci. Paris 336(12), 997–1002, 2003
Sandier, É., Serfaty, S.: Vortices in the Magnetic Ginzburg–Landau Model. Progress in Nonlinear Differential Equations and their Applications, vol. 70. Birkhäuser Boston, Inc., Boston, 2007
Schwarz, G.: Hodge Decomposition—A Method for Solving Boundary Value Problems Lecture Notes in Mathematics, vol. 1607. Springer, Berlin, 1995
Scott, C.: \({L}^p\) theory of differential forms on manifolds. Trans. Am. Math. Soc. 347(6), 2075–2096, 1995
Simon, L.: Lectures in Geometric Measure Theory. Centre for Mathematical Analysis. Australian National University, Canberra, 1984
Spivak, M.: A Comprhensive Introduction to Differential Geometry, vol. 2, 2nd edn. Publish or Perish, Houston, 1999
Spruck, J., Yang, Y.S.: Regular stationary solutions of the cylindrically symmetric Einstein-matter-gauge equations. J. Math. Anal. Appl. 195(1), 160–190, 1995
Stern, D.: Existence and limiting behavior of min-max solutions of the Ginzburg–Landau equations on compact manifolds. J. Differ. Geom. 118(2), 335–371, 2021
Tinkham, M.: Introduction to Superconductivity. Dover Publications, Mineola, 2004
Uhlenbeck, K., Yau, S.T.: On the existence of Hermitian–Yang–Mills connections in stable vector bundles. Commun. Pure App. Mater. 39(S1), S257–S293, 1986
Warner, F.W.: Foundations of Differentiable Manifolds and Lie Groups. Graduate Texts in Mathematics. Springer, New York, 1983
Wehrheim, K.: Uhlenbeck Compactness EMS. Series of Lectures in Mathematic. European Mathematical Society, Helsinki, 2004
Acknowledgements
G.C. and G.O. were partially supported by GNAMPA-INdAM and by RIBA 2019, No. RBVR199YFL, Geometric Evolution of Multi Agent Systems.
Funding
Open access funding provided by Universitá degli Studi di Verona within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Communicated by A. Braides.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Bundles on a Closed Riemannian Manifold
1.1 A.1 Sobolev Spaces of Sections and Differential Forms
We recall below the main definitions and facts concerning several spaces of differential forms and, more broadly, of section of Hermitian vector bundles. We shall do so in a slightly greater generality than strictly needed in this work to make the presentation more transparent and the comparison with the relevant literature easier. The main reference for this appendix is [52], especially Chapters 4, 5, 9, and 19, where the abstract framework is developed in a much more general context (and using the language of category theory, that we avoid for reader’s convenience). A more recent useful reference is [34, Chapter 1]. Both in [52] and in [34] equivalence with other approaches to Sobolev spaces of sections is discussed. (See also [49, Chapter 10], [60, Chapter 1], [69, Appendix B].)
Let \(\mathbb K\) be either \(\mathbb R\) or \(\mathbb C\), and let \(\pi : E \rightarrow M\) be a \(\mathbb K\)-vector bundle of rank \(\ell \) over a \(C^\infty \)-smooth compact orientable Riemannian manifold \(M = (M^n, g)\) without boundary. We assume the differentiable structure of M is fixed once and for all.
Regular bundle atlases. Using the compactness of M, it is easily shown that it is always possible to find finite bundle atlases \(\mathcal {A} = \{ (U_i, \varphi _i, \chi _i)\}_{i = 1}^N\), where \(N \in \mathbb N\), the maps \(\varphi _i :U_i \rightarrow \mathbb R^n\) are local charts and \(\chi _i :\pi ^{-1}(U_i) =: E \vert _{U_i} \rightarrow U_i \times \mathbb K^\ell \) local trivialisations, so that:
-
(A1)
For all \(i \in \{1,2,\dots ,N\}\), \(U_i\) is contractible and, moreover, \(\varphi _i(U_i) =: \Omega _i \subset \mathbb R^n\) is a bounded contractible open set with smooth boundary.
-
(A2)
For all \(i \in \{1,2,\dots ,N\}\), \((U_i, \varphi _i)\) can be extended to a smooth chart \((V_i,\psi _i)\) contained in the differentiable structure of M, so that \(\overline{U_i} \subset V_i\) and \(\varphi _i = \psi _i \vert _{U_i}\). This ensures that, for all \(i, j \in \{1, 2, \dots , N\}\), whenever \(U_i \cap U_j \ne \varnothing \), each coordinate change \(\varphi _i \circ \varphi _j^{-1}: \varphi _j(U_i \cap U_j) \rightarrow \varphi _i(U_i \cap U_j)\) is smooth up to the boundary of \(\varphi _j(U_i \cap U_j)\) (hence, all its derivatives are bounded).
-
(A3)
For all \(i \in \{1,2,\dots ,N\}\), \(E \rightarrow M\) trivialises over \(U_i\), i.e, we have \(E \vert _{U_i} \overset{\chi _i}{\simeq }\ U_i \times \mathbb K^\ell \) (actually, this comes for free, as the \(U_i\) are contractible). In addition, each local trivialisation \(\chi _i: \pi ^{-1}(U_i) \rightarrow U_i \times \mathbb K^\ell \) extends to a smooth map over the corresponding coordinates patches \(V_i\) associated with \(U_i\) as in (A2) (up to slightly shrinking \(V_i\), if necessary). Consequently, for all \(i, j \in \{1,2,\dots ,N\}\) such that \(U_i \cap U_j \ne \varnothing \), we have that \(\chi _i \circ \chi _j^{-1}\) extends smoothly to a neighbourhood of \(\overline{U_i \cap U_j}\). Recall that
$$\begin{aligned} \widehat{\chi _i}:= (\varphi _i, \textrm{id}_{\mathbb K^\ell } ) \circ \chi _i: E \vert _{U_i} \rightarrow \Omega _i \times \mathbb K^\ell \qquad (i \in \{1,2,\dots ,N\}), \end{aligned}$$are the charts of E (as an \((n + \ell )\)-manifold if \(\mathbb K= \mathbb R\), and as an \((n+2\ell )\) real manifold if \(\mathbb K= \mathbb C\)) and notice that, under our assumptions, all the derivatives of all coordinate changes \(\widehat{\chi _i} \circ \widehat{\chi _j}^{-1}: \Omega _j \times \mathbb K^\ell \rightarrow \Omega _i \times \mathbb K^\ell \) are bounded. Consequently, denoting \(\textrm{pr}_2\) the projection onto the second factor of a product of the type \(\Omega \times \mathbb K^\ell \), with \(\Omega \subset \mathbb R^n\), the maps \(\textrm{pr}_2 \circ \widehat{\chi _i} \circ \widehat{\chi _j}^{-1}: \Omega _j \times \mathbb K^\ell \rightarrow \mathbb K^\ell \) are smooth and all their derivatives are bounded.
For convenience, we refer to atlases of M satisfying (A1) and (A2) as regular atlases and to bundle atlases satisfying (A1)–(A3) as regular bundle atlases. We call regular the charts of regular atlases and of regular bundle atlases.
Remark A.1
Since we always cover M by contractible open sets \(U_i\), every vector bundle over M, and not only the given bundle \(\pi : E \rightarrow M\), trivialises over them.
Remark A.2
(Normal coordinates) As it is well-know (see, e.g., [63, pp. 166-167]), around any point \(x_0 \in M\), one can choose normal coordinates so that in the geodesic ball \(B_\delta (x_0)\) centered at \(x_0\), there holds
whence \(\sqrt{\det g} = 1 + \frac{1}{2} \sum _{i,k,l=1}^n \partial ^2_{kl} g_{ii}(x_0) x^k x^l + \textrm{o}(\left| x \right| ^2)\), and consequently
Given any atlas of M, by compactness it can be refined so to have a regular atlas in which the local coordinates are normal coordinates.
Sobolev spaces of sections of vector bundles A measurable section of a \(\mathbb K\)-vector bundle \(E \rightarrow M\) of rank \(\ell \) is a Borel measurable function \(u:M \rightarrow E\) so that the equation \(\pi \circ u(x) = x\) holds for almost every \(x \in M\) with respect to the measure induced by \({{\,\textrm{vol}\,}}_g\). Let us denote \(\Gamma (M,\,E)\) the linear space of all such sections.
Fix a regular bundle atlas \(\mathcal {A}\) for \(E \rightarrow M\) and a partition of unity \(\{\rho _i\}_{i=1}^N\) subordinate to \(\mathcal {A}\). For \(m \ge 0\) an integer and \(p \in [1,\infty ]\), we say (according to [52, Chapter 4]) that a measurable section \(u \in \Gamma (M,\, E)\) belongs to \(W^{m,p}_{\mathcal {A}}(M,\,E)\) if and only if every local representation
of u belongs to the usual Sobolev space \(W^{m,p}(\Omega _i, \,\mathbb K^\ell )\). We endow \(W^{m,p}_{\mathcal {A}}(M,E)\) with the norm
where the inner sum runs over all multi-indexes \(\alpha \) of length at most m. Of course, we let \(L^p_{\mathcal {A}}(M,E):= W^{0,p}_{\mathcal {A}}(M,E)\).
Armed with the above definition and (A1)–(A3), it is not difficult to prove that (cf. e.g., [34, 52, 60, 69])
-
(S1)
\(W^{m,p}_{\mathcal {A}}(M,E)\) is Banach space (Hilbert if \(p = 2\)), separable if \(p \in [1,\infty )\), and reflexive if \(p \in (1,\infty )\).
-
(S2)
\(C^\infty (M,E)\) (i.e., the space of classical smooth sections of \(E \rightarrow M\)) is dense into \(W^{m,p}_{\mathcal {A}}(M,E)\) for the norm \(\left\| \cdot \right\| _{W^{m,p}_{\mathcal {A}}(M,E)}\) for every integer \(m \ge 0\) and every \(p \in [1, \infty )\).
-
(S3)
The classical embedding (including compact embeddings) theorems hold.
-
(S4)
Any two partitions of unity subordinate to \(\mathcal {A}\) induce equivalent norms, hence different choices for the partition of unity yield equivalent Banach spaces \(W^{m,p}_{\mathcal {A}}(M,E)\), for which properties (S1)–(S3) hold.
-
(S5)
For any regular bundle atlases \(\mathcal {A}_1\), \(\mathcal {A}_2\) of \(E \rightarrow M\), the sets \(W^{m,p}_{\mathcal {A}_1}(M,E)\) and \(W^{m,p}_{\mathcal {A}_2}(M,E)\) coincide. Moreover, the corresponding norms \(\left\| \cdot \right\| _{W^{m,p}_{\mathcal {A}_1}}\), \(\left\| \cdot \right\| _{W^{m,p}_{\mathcal {A}_2}}\), defined by (A.2), induce equivalent norms on \(\Gamma (M,E)\). Then, \(W^{m,p}_{\mathcal {A}_1}(M,E)\) and \(W^{m,p}_{\mathcal {A}_2}(M,E)\) are actually equivalent Banach spaces, for which properties (S1)–(S4) hold.
Remark A.3
In view of (S1)–(S5), we can identify a linear subspace \(W^{m,p}(M,E)\) of \(\Gamma (M,E)\), the members of which have finite \(\left\| \cdot \right\| _{W^{m,p}_\mathcal {A}}\)-norm, independently of the chosen regular bundle atlas \(\mathcal {A}\) (and of subordinate partitions of unity). All the norms \(\left\| \cdot \right\| _{W^{m,p}_\mathcal {A}}\) are equivalent on \(W^{m,p}(M,E)\), and hence induce the same topology on \(W^{m,p}(M,E)\), that is therefore independent of the regular bundle atlas \(\mathcal {A}\) chosen for \(E \rightarrow M\) (and of subordinate partitions of unity). In particular, properties (S1)–(S3) hold for \(W^{m,p}(M,E)\), and in view of (S4)-(S5) we can choose for computations any regular bundle atlas and subordinate partitions of unity.
Definition A.1
Let M be a smooth, compact, connected oriented, Riemannian manifold without boundary, of dimension \(n \in \mathbb N\), and let \(E \rightarrow M\) be a \(\mathbb K\)-vector bundle over M of rank \(\ell \). For \(m \ge 0\) an integer and \(p \in [1,\infty ]\), we denote by \(W^{m,p}(M,E)\) the linear space of sections of \(E \rightarrow M\) having finite \(\left\| \cdot \right\| _{W^{m,p}_\mathcal {A}(M,E)}\)-norm for some, and hence all (see Remark A.3), choices of a regular bundle atlas \(\mathcal {A}\). We provide the space \(W^{m,p}(M,E)\) with the topology induced by any of the (equivalent) norms \(\left\| \cdot \right\| _{W^{m,p}_{\mathcal {A}(M,E)}}\). This topology does not depend on the chosen regular bundle atlas \(\mathcal {A}\) (see again Remark A.3).
We denote by \(W^{-m,q}(M,\,E^\prime )\) the topological dual of \(W^{m,p}(M,\,E)\), i.e.,
Here, \(q:= p'\) is the Hölder-conjugate exponent of p.
Remark A.4
To simplify the notation, we will henceforth drop the subscript \(\mathcal {A}\) when we denote the norm of a section \(u \in W^{m,p}(M,E)\). More precisely, we will write \(\left\| u \right\| _{W^{m,p}(M,E)}\) to mean actually that we have fixed a regular bundle atlas \(\mathcal {A}\) (and a subordinate partition of unity) and we are evaluating \(\left\| u \right\| _{W^{m,p}_\mathcal {A}(M,E)}\) according to (A.2).
Remark A.5
If \(E \rightarrow M\) is a trivial \(\mathbb K\)-bundle of rank \(\ell \), i.e., if \(E = M \times \mathbb K^\ell \), we can identify \(W^{m,p}(M,E)\) and \(W^{m,p}(M,\mathbb K^\ell )\). Indeed, if \(u: M \rightarrow M \times \mathbb K^\ell \) is a measurable section, then \(\tilde{u}:= \mathrm{pr_2} \circ \widehat{\chi } \circ u: M \rightarrow \mathbb K^\ell \) is a measurable function. Vice versa, if \(\tilde{u}: M \rightarrow \mathbb K^\ell \) is a measurable function, the map \(x \mapsto (x, \tilde{u}(x))\) gives rise to a section \(u \in \Gamma (M,E)\). Moreover, the local representations of u and \(\tilde{u}\) coincide a.e. with respect to the Lebesgue measure. Hence, \(u \in W^{m,p}(M,M\times \mathbb K^\ell )\) if and only if \(\tilde{u} \in W^{m,p}(M,\mathbb K^\ell )\), and the norms are the same. Therefore, we can identify these two spaces, and we shall do so when convenient even without explicit mention.
Sobolev spaces of differential forms Let \(0 \le k \le n\) be an integer and \(E = \Lambda ^k \textrm{T}^* M\), the bundle of k-covectors over M. For \(m \ge 0\) an integer and \(p \in [1,\infty ]\), let the space \(W^{m,p}(M,\Lambda ^k \textrm{T}^*M)\) be defined according to Definition A.1. Then, the spaces \(W^{m,p}(M, \Lambda ^k \textrm{T}^* M)\) agree with the Sobolev spaces of differential k-forms over M considered in [22, 38, 47, 61]. For the purpose of exposition, it is convenient to refer this definition of Sobolev spaces of differential k-forms over M to as the classical definition.
Remark A.6
Recall that the bundles \(\Lambda ^k \textrm{T}^*M \rightarrow M\) are constructed canonically starting from any atlas of M. In particular, any regular atlas \(\{ (U_i, \varphi _i) \}_{i=1}^N\) for M induces a regular bundle atlas \(\mathcal {A}_k\) for \(\Lambda ^k \textrm{T}^* M \rightarrow M\) for every \(k \in \{0,1,\dots ,n\}\). Thus, for convenience, in this paragraph we use the symbol \(\mathcal {A}\) to denote the given atlas for M, i.e., \(\mathcal {A} = \{(U_i,\varphi _i)\}_{i=1}^N\), although in the previous paragraph it has been used to denote bundle atlases.
We set
for any two measurable maps \(\omega \), \(\eta :M \rightarrow \Lambda ^k \textrm{T}^* M\) such that the right hand side is well-defined. We say that \(\omega \in L^1(M, \Lambda ^k \textrm{T}^*M)\) has weak exterior differential \({{\,\textrm{d}\,}}\omega \) if there exists \(\Omega \in L^1(M, \Lambda ^{k+1} \textrm{T}^*M)\) such that there holds
for all smooth test forms \(\eta \in C^\infty (M, \Lambda ^{k+1} \textrm{T}^*M)\). In such case, we set \({{\,\textrm{d}\,}}\omega := \Omega \). Symmetrically, we say that \(\omega \in L^1(M, \Lambda ^k \textrm{T}^*M)\) has weak exterior codifferential \({{\,\textrm{d}\,}}^* \omega \) if there exists \(\Psi \in L^1(M, \Lambda ^{k-1} \textrm{T}^*M)\) such that the equation
holds for every \(\eta \in C^\infty (M, \Lambda ^{k-1} \textrm{T}^*M)\), and we set \({{\,\textrm{d}\,}}^*\omega := \Psi \). Clearly, when they exists, \({{\,\textrm{d}\,}}\omega \) and \({{\,\textrm{d}\,}}^* \omega \) are unique, and they coincide with the classical exterior differential and codifferential of \(\omega \) if \(\omega \) is smooth.
Thus, for \(m \ge 1\), the operators
are well-defined, linear and continuous. For \(p \in (1,\infty )\), they are the unique extensions by linearity and density of the classical exterior differential and codifferential. Thus, by density, we have the following “integration by parts” formula: if \(p, q \in (1,\infty )\) satisfy \(1/p+1/q = 1\), then
for all \(\omega \in W^{1,p}(M, \Lambda ^{k-1} \textrm{T}^* M)\) and all \(\eta \in W^{1,q}(M, \Lambda ^k \textrm{T}^* M)\). On the other hand, if \(\omega \in W^{1,\infty }(M,\Lambda ^k \textrm{T}^*M)\), then \(\omega \) is differentiable almost everywhere on M and, since M is compact, by Hölder inequality \(\omega \) belongs to \(W^{1,p}(M,\Lambda ^k \textrm{T}^*M)\) for every \(p \in [1,\infty ]\). Furthermore, for every form \(\omega \) of class at least \(W^{2,p}\),
The explicit expressions of \({{\,\textrm{d}\,}}\), \({{\,\textrm{d}\,}}^*\) in coordinates will not be needed in this work. Formally, they are the same as in the classical case (see, e.g., [47, Chapter 7]). They can be expressed in terms of the metric g of M on the Levi-Civita connection on \(\textrm{T}M\) (which classically induce canonical Riemannian metrics and linear connections over all tensor bundles of M), see e.g. [60, Chapter 1].
Remark A.7
When defined, \({{\,\textrm{d}\,}}\), \({{\,\textrm{d}\,}}^*\) satisfy the same properties as in the classical case. For instance, they are local and commute with restrictions.
Remark A.8
The definition of \({{\,\textrm{d}\,}}\), \({{\,\textrm{d}\,}}^*\) extends without difficulties, by duality, to form-valued distributions, see (B.8), (B.9) below. In particular, \({{\,\textrm{d}\,}}\), \({{\,\textrm{d}\,}}^*\) extend to continuous linear operators also between Sobolev spaces of negative order.
It has been firstly shown in [61] that, for M compact and without boundary, the classical definition of \(W^{1,p}(M,\,\Lambda ^k \textrm{T}^*M)\) is equivalent to the following geometrical one [61, Proposition 4.11]:
The continuous embedding of \(W^{1,p}(M,\,\Lambda ^k \textrm{T}^*M)\) into \(\mathcal {W}^{1,p}(M, \,\Lambda ^k \textrm{T}^*M)\) is obvious, as the pointwise inequality (Eq. (2.6) in [61])
holds a.e. within any open region \(U \subset M\) compactly contained in a regular coordinate chart. Here, we are using the notation of [61], according to which \(\left| \nabla \omega \right| ^p:= \left( \sum \left| \frac{\partial \omega _I}{\partial x^k} \right| ^2\right) ^{\frac{p}{2}}\), \(\omega = \sum \omega _I {{\,\textrm{d}\,}}x^I\), \(I = \{ 1 \le i_1< i_2 < \dots i_k \le n \}\), and \(\varphi \equiv (x^1, \dots , x^n)\) are the local (regular) coordinates on U.
The proof that \(W^{1,p}(M, \Lambda ^k \textrm{T}^*M) = \mathcal {W}^{1,p}(M, \Lambda ^k \textrm{T}^*M)\) then amounts to prove the reverse continuous embedding. The latter stems on the following \(L^p\)-version of Gaffney’s inequality [61, Proposition 4.10].
Proposition A.9
(Gaffney’s inequality) Let M be a compact orientable smooth Riemannian manifold without boundary. Then a regular bundle atlas \(\mathcal {A}\) of M can be found so that the following happens: there exists a positive constant \(C_p\), depending on p, n, and \(\mathcal {A}\), so that
for all \(\omega \in W^{1,p}(M,\,\Lambda ^k \textrm{T}^*M)\) and all integers \(0 \le k \le n\).
Gaffney’s-type inequalities hold, for compact manifolds without boundary, also for higher order derivatives. This is the content of Proposition A.10 below. Before stating the result, we recall that measurable differential forms on any n-dimensional manifold M form the graded algebra
where at right-hand-side we have a direct sum of moduli over the algebra of measurable functions over M, see, e.g., [45, Section 8.2] (although the book [45] deals with smooth objects, it is clear from the construction of the exterior algebra in [45, Section 8.1] that the decomposition above does not depend on the smoothness of the forms, that can also be merely measurable). This allows for giving a meaning to the sum of forms of different degrees. In particular, if M is a compact, oriented, smooth Riemannian manifold and \(\omega _1\), \(\omega _2\), ...\(\omega _\ell \) are differential forms on M, with degrees \(k_1\), \(k_2\), ..., \(k_\ell \) all distinct, then we define
We can now state the aforementioned generalisation of Gaffney’s inequality.
Proposition A.10
Let M be a compact oriented smooth Riemannian manifold without boundary, endowed with the regular atlas \(\mathcal {A}\) in Proposition A.9. Then, for every \(p \in (1,\infty )\) and every integer \(m \ge 0\) there is a constant \(C_{m,p}\), depending only on p, n, m and \(\mathcal {A}\), so that
for all \(\omega \in W^{m,p}(M,\Lambda ^k \textrm{T}^*M)\) and all integers \(0 \le k \le n\).
Sketch of the proof
Take \(\omega \in C^\infty (M,\Lambda ^k \textrm{T}^*M)\). For each open set \(U_i\) of the covering provided by \(\mathcal {A}\), inequality (A.5) is proven for the local representation of \(\omega \) in [22, Theorem 4.2.1] (see also [22, Proposition 4.2.2]). Then the local inequalities can be glued together (using crucially the fact that \(\mathcal {A}\) is regular) to give (A.5) as in [61, Proposition 4.10]. This concludes the proof if \(\omega \) is smooth. For general \(\omega \in W^{m,p}(M,\Lambda ^k \textrm{T}^*M)\), the result follows by density.\(\quad \square \)
Remark A.11
In particular, the classical Sobolev spaces \(W^{2,p}(M, \Lambda ^k \textrm{T}^*M)\) coincide, when M is as in Proposition A.10, with the space of measurable differential k-forms \(\omega \) such that
A k-form \(\omega \in L^p(M, \Lambda ^k \textrm{T}^* M)\) such that \({{\,\textrm{d}\,}}\omega \), \({{\,\textrm{d}\,}}^* \omega \) exist in the weak sense and
is called harmonic (or a harmonic field). Harmonic k-forms are automatically smooth [61, Proposition 5.2], hence Equations (A.6) actually hold in the classical sense. For each integer \(k \ge 0\), we let
Letting
be the Laplace-Beltrami operator, we have the equivalent characterization (e.g., [32, Proposition 5.2.4.3])
Remark A.12
Viewed as an operator from \(W^{2,p}(M, \Lambda ^k \textrm{T}^* M)\) into \(L^p(M, \Lambda ^k \textrm{T}^*M)\), \(\Delta \) is a bounded (linear) operator for every \(p \in [1,\infty ]\) and any integer \(k \ge 0\), with kernel \({{\,\textrm{Harm}\,}}^k(M)\).
For every integer \(k \ge 0\), \({{\,\textrm{Harm}\,}}^k(M)\) is a finite dimensional linear space (e.g., [38, Remark 4.9]). Hence, any two norms are equivalent on \({{\,\textrm{Harm}\,}}^k(M)\). We denote (cf. [61, (5.4)])
As established in [61, Lemma 5.6], for every \(\omega \in L^1(M, \Lambda ^k \textrm{T}^*M)\) there is a unique \(H(\omega ) \in {{\,\textrm{Harm}\,}}^k(M)\) such that
We call \(H(\omega )\) the harmonic part of \(\omega \). The assignment \(\omega \mapsto H(\omega )\) defines a surjective linear operator (a projection, in fact) \(H :L^1(M, \Lambda ^k \textrm{T}^*M) \rightarrow {{\,\textrm{Harm}\,}}^k(M,\Lambda ^k \textrm{T}^*M)\), called harmonic projection, which is bounded regardless of the norm on \({{\,\textrm{Harm}\,}}^k(M)\) [61, Proposition 5.9].
From the classical \(L^2\)-theory of differential forms as developed for instance in [68, Chapter 6], there is a linear operator, called Green’s operator,
providing the unique solution in \(({{\,\textrm{Harm}\,}}^k(M))^\perp \) to the equation
With Gaffney’s inequality (A.4) at hands, C. Scott [61] extended, for every \(p \in (1,\infty )\), G to a bounded linear operator, still called Green’s operator (and denoted with the same letter),
which still satisfies (A.10) ([61, Proposition 6.1]).
Remark A.13
For future reference, we notice that
for every \(\omega \in W^{2,p}(M, \Lambda ^k \textrm{T}^*M)\), \(p \in (1,\infty )\), and \(0 \le k \le n\) integer. For smooth forms, this is well-known (e.g., [68, Proposition 6.10]). For forms of class \(W^{2,p}\), see [22, Proposition 6.24] or argue directly by density of \(C^\infty (M,\Lambda ^k \textrm{T}^* M)\) in \(L^p(M,\Lambda ^k \textrm{T}^* M)\) and the continuity of \(G:L^p(M,\Lambda ^k \textrm{T}^* M) \rightarrow W^{2,p}(M,\Lambda ^k \textrm{T}^* M) \cap ({{\,\textrm{Harm}\,}}^k)^\perp \) and \(\Delta : W^{2,p}(M,\Lambda ^k \textrm{T}^* M) \rightarrow L^p(M,\Lambda ^k \textrm{T}^* M)\). Equation (A.12) and the continuity of G imply
for any \(\omega \in W^{2,p}(M, \Lambda ^k \textrm{T}^*M)\) and some constant C that depends only on M, k and p.
Finally, the following fundamental result is proved in [61].
Proposition A.14
(\(L^p\)-Hodge decomposition, [61, Proposition 6.5]) Let M be a smooth compact oriented Riemannian manifold without boundary and \(1< p < \infty \). For any integer \(0 \le k \le n\), we have
Moreover, \({{\,\textrm{d}\,}}(W^{1,p}(M, \,\Lambda ^{k-1}\textrm{T}^*M)) = {{\,\textrm{d}\,}}{{\,\textrm{d}\,}}^* G(L^p)\) and \({{\,\textrm{d}\,}}^*(W^{1,p}(M,\,\Lambda ^{k+1}\textrm{T}^*M)) = {{\,\textrm{d}\,}}^* {{\,\textrm{d}\,}}G(L^p)\).
Consequently, any \(\omega \in L^p(M, \Lambda ^k \textrm{T}^* M)\) can be uniquely written as
where \(\varphi \in W^{1,p}(M, \Lambda ^{k-1}\textrm{T}^*M)\) is co-exact, \(\psi \in W^{1,p}(M, \Lambda ^{k+1}\textrm{T}^*M)\) is exact and \(\xi \in {{\,\textrm{Harm}\,}}^k(M)\) is a harmonic k-form. In addition, there exists a constant \(C > 0\), depending only on p, k and M, such that there holds
for every \(\omega \in L^p(M,\,\Lambda ^k\textrm{T}^*M)\), where \(\varphi \), \(\psi \) and \(\xi \) are as in (A.15).
Remark A.15
The choice of using the \(L^\infty \)-norm for the harmonic part of \(\omega \) in estimate (A.16) is somewhat arbitrary. However, since \({{\,\textrm{Harm}\,}}^k(M)\) has finite dimension, the \(L^\infty \)-norm can be replaced by any other norm (up to enlarging C, if necessary).
For later reference, we point out the following elliptic regularity lemma, immediate consequence of Propositions A.14, A.10, and the Open Mapping Theorem.
Lemma A.16
Let \(j \ge 0\) be an integer and \(p\in (1, \infty )\). For every \(f\in W^{j,p}(M, \, \Lambda ^k\textrm{T}^*M)\) such that \((f,\xi ) = 0\) for any \(\xi \in {{\,\textrm{Harm}\,}}^k(M)\), there exists a unique \(v\in W^{j+2,p}(M, \, \Lambda ^k\textrm{T}^*M)\) such that
Moreover, v satisfies
for some constant \(C_{p,j}\) depending only on M, j, k, p.
Proof
Suppose first \(j = 0\) (hence, \(f \in L^p(M, \,\Lambda ^k \textrm{T}^*M)\)). Existence and uniqueness of a solution \(v \in W^{1,p}(M,\,\Lambda ^k \textrm{T}^*M)\) to (A.17) readily follow from Proposition A.14. Moreover, \(\Delta v \in L^p(M,\,\Lambda ^k \textrm{T}^*M)\) and by Proposition A.10 we obtain that \(v \in W^{2,p}(M, \,\Lambda ^k \textrm{T}^*M)\) and (A.18) follows immediately from (A.13) (or, alternatively, from the general argument below). Thus, for any \(j \ge 0\), by iterated application of Proposition A.10 we obtain that
is a continuous bijection, hence a Banach space isomorphism by the Open Mapping Theorem. Estimate (A.18) is an immediate consequence of this latter fact.\(\quad \square \)
Remark A.17
Clearly, if \(\psi \in W^{2,p}(M,\,\Lambda ^k \textrm{T}^*M)\) is (co)exact, \(\Delta \psi \) is (co)exact as well. Then the estimate (A.18), the fact that \(-\Delta \psi = {{\,\textrm{d}\,}}{{\,\textrm{d}\,}}^*\psi \), and Remark A.11 imply that there is a constant \(C > 0\), depending only on k, p and M, such that the estimate
holds for all exact k-forms \(\psi \in W^{2,p}(M,\,\Lambda ^k \textrm{T}^*M)\). (If \(\psi \) is co-exact, \({{\,\textrm{d}\,}}^* \psi \) must be replaced by \({{\,\textrm{d}\,}}\psi \) in the right hand side of (A.19).) This fact is used in Sect. 3.
To conclude this section, we notice that neither Gaffney’s inequality nor the \(L^p\)-Hodge decomposition hold for \(p = 1\), as shown in [5]. However, in the same paper it also proven that Green’s operator exists even in this case as a map from measure k-forms into \(W^{1,p}(M, \Lambda ^k \textrm{T}^*M)\) for every \(1< p < \frac{n}{n-1}\). Importantly, measure k-forms can be regarded as Radon vector measures on M with values in k-forms, as [5, Proposition 2.2] shows. In the language of the present paper, measure k-forms are simply k-currents with finite mass (cf. [5, Definition 2.1] and Appendix 4.1).
1.2 Hermitian Line Bundles, Connections, and Weak Covariant Derivatives of Sobolev Sections
A Hermitian metric on a complex line bundle \(E \rightarrow M\) is an assignment, for each \(x \in M\), of a positive definite Hermitian form \(h_x: E_x \times E_x \rightarrow \mathbb C\) that is smooth in the sense that, for all sections \(u_1\), \(u_2 \in C^\infty (M,\,E)\), the function \(x \mapsto h_x(u_1(x), u_2(x))\) is smooth. In this case we say that \(E \rightarrow M\) is a Hermitian line bundle. The typical fibre of \(E \rightarrow M\) is of course \(\mathbb C\). The structure group of a Hermitian line bundle \(E \rightarrow M\) automatically reduces to \(U(1)\) [45, pp. 280–281]. Naturally, the metric allows to identify \(E'\) and E. Associated with a Hermitian metric, there is a canonical scalar product, i.e., its real part, that we denote \(\left\langle \cdot , \, \cdot \right\rangle \). In other words, we set
A (smooth) connection \({{\,\textrm{D}\,}}\) on a vector bundle \(E \rightarrow M\) is a linear map
satisfying Leibniz’ rule:
For every fixed \(u \in C^\infty (M,E)\), we can view \({{\,\textrm{D}\,}}u\) a map taking a vector field, say X, on M as argument and giving back a section \({{\,\textrm{D}\,}}u(X)\) of \(E \rightarrow M\). We set \({{\,\textrm{D}\,}}_X u:= {{\,\textrm{D}\,}}u(X)\) and call \({{\,\textrm{D}\,}}_X u\) the covariant derivative of u with respect to X.
A metric connection on a Hermitian line bundle \(E \rightarrow M\) is a connection \({{\,\textrm{D}\,}}\) that is compatible with the metric, i.e., satisfying \({{\,\textrm{D}\,}}h \equiv 0\). This implies
Explicitly, (A.21) means that, for every pair of sections u, \(v \in C^\infty (M,\,E)\) and every smooth vector field \(X \in C^\infty (M,\,\textrm{T}M)\), there holds
We recall the following important facts:
-
For every \(u \in C^\infty (M,\,E)\) and every \(X \in C^\infty (M, \, \textrm{T}M)\), the value \(({{\,\textrm{D}\,}}_X u)(x)\) of \({{\,\textrm{D}\,}}_X u\) at each \(x \in M\) depends only on X(x) and the values of u along any smooth curve representing X(x) [45, p. 502]. In fact, \({{\,\textrm{D}\,}}_A\) is a local operator and behaves naturally with respect to restrictions [45, Section 12.1].
-
Let \(U \subset M\) be an open set so that \(E \rightarrow M\) is trivial over U, \(\chi _U: E\vert _U \rightarrow U \times \mathbb C\) a corresponding local trivialisation, and \(e_U\) a reference section for \(E \rightarrow M\) over U. Then every \(u \in C^\infty (M, \, E)\) writes as \(u = \widetilde{u} e_U\) for some smooth complex-valued function \(\widetilde{u}\) and we have, with respect to the local trivialisation \(\chi _U\),
$$\begin{aligned} {{\,\textrm{D}\,}}u = \left( {{\,\textrm{d}\,}}\widetilde{u} + A_U \widetilde{u} \right) \otimes e_U \qquad \text{ in } U, \end{aligned}$$where \(A_U \in C^\infty (U, \, \textrm{T}^* U)\) is a complex-valued 1-form, called the connection 1-form of \({{\,\textrm{D}\,}}\) over \(E \vert _U\) with respect to \(\chi _U\). If \(\widetilde{\chi }_U: E \vert _U \rightarrow U \times \mathbb C\) is another local trivialisation for \(E \rightarrow M\) over U, set \(g_U:= \widetilde{\chi }_U \circ \chi _U^{-1}\) (notice that \(g_U \in C^\infty (U \times \mathbb C, \, U \times \mathbb C)\)). Denoting \(\widetilde{A}_U\) the connection 1-form of \({{\,\textrm{D}\,}}\) with respect to \(\widetilde{\chi }_U\), then the transformation law
$$\begin{aligned} A_U = \widetilde{A}_U + g_U^{-1} {{\,\textrm{d}\,}}g_U \end{aligned}$$(A.22)holds. From (A.22) it is readily seen that \({{\,\textrm{d}\,}}A_U\) does not depend on the local trivialisation.
-
It is a general fact that connections on a vector bundle \(E \rightarrow M\) form an affine space modelled over \(C^\infty (M, \textrm{T}^*M \otimes \textrm{End}(E))\), where \(\textrm{End}(E)\) is the bundle of endomorphisms of E. This means that, upon choosing a reference connection \({{\,\textrm{D}\,}}_0\), any other connection on \(E \rightarrow M\) writes as
$$\begin{aligned} {{\,\textrm{D}\,}}_A := {{\,\textrm{D}\,}}_0 + A, \end{aligned}$$(A.23)for some \(A \in C^\infty (M, \textrm{T}^*M \otimes \textrm{End}(E))\). In the case of a Hermitian line bundle with a reference metric connection \({{\,\textrm{D}\,}}_0\), \({{\,\textrm{D}\,}}_A\) is still a (smooth) metric connection if and only if A belongs to the smaller space \(C^\infty (M, \textrm{T}^*M \otimes \textrm{Ad}(E))\). Here, \(\textrm{Ad}(E)\) denotes the bundle of endomorphisms of E which are skew Hermitian on each fiber. Thus, the typical fiber of \(\textrm{Ad}(E)\) is the Lie algebra of the structure group of E. In our case, \(\textrm{Ad}(E)\) is a trivial bundle with typical fiber \(U(1)\). As the latter can be identified with \(i \mathbb R\), A should take purely imaginary values in any local trivialisation. In addition, we have
$$\begin{aligned} C^\infty (M,\, \textrm{T}^*M \otimes \textrm{Ad}(E)) \simeq C^\infty (M, \, \textrm{T}^* M), \end{aligned}$$with canonical isomorphism. Thus, we can identify A with a 1-form with purely imaginary coefficients. However, it is customary to assume instead that A is real-valued, writing \(-iA\) in place of A. We then rewrite (A.23) as
$$\begin{aligned} {{\,\textrm{D}\,}}_A := {{\,\textrm{D}\,}}_0 - i A. \end{aligned}$$(A.24)Explicitly, (A.24) means that, for every \(u \in C^\infty (M,\,E)\) and every smooth vector field X on M, we have
$$\begin{aligned} {{\,\textrm{D}\,}}_{A,\,X} u = {{\,\textrm{D}\,}}_{0,\,X}u -i A(X) u. \end{aligned}$$
The curvature \({{\,\textrm{D}\,}}^2_A\) of a connection \({{\,\textrm{D}\,}}_A\) is given by the following formula: for all \(u \in C^\infty (M,\,E)\) and all \(X, Y \in C^\infty (M,\,\textrm{T}M)\),
One easily checks [45, Section 12.5] that there exists a closed \(\textrm{End}(E)\)-valued 2-form \(F_A\), called the curvature form of \({{\,\textrm{D}\,}}_A\), such that
As for A, if \({{\,\textrm{D}\,}}_A\) is a metric connection on a Hermitian line bundle, \(F_A\) is an \(\textrm{Ad}(E)\)-valued 2-form taking purely imaginary values in any local trivialisation. Thus, \(F_A\) is identified with a 2-form on M which is assumed to be real-valued, replacing \(F_A\) with \(-i F_A\) in the above formula. Then, denoting \(F_0\) the curvature form of the reference connection, there holds
So far, we have dealt with smooth sections and smooth connections. We now extend the previous discussion to Sobolev sections and connections. To this end, we have to define the concept of weak covariant derivative of a non-smooth section \(u: M \rightarrow E\). For the moment being, we still assume A is a smooth 1-form on M.
The first ingredient we need is the extension, for every integer \(0 \le k \le n\), of \({{\,\textrm{D}\,}}_A\) to an operator from \(C^\infty (M, \, \Lambda ^k \textrm{T}^*M \otimes E)\) into \(C^\infty (M, \, \Lambda ^{k+1} \textrm{T}^*M \otimes E)\). This is standardly done by introducing the exterior covariant derivative induced by \({{\,\textrm{D}\,}}_A\), which we denote \({{\,\textrm{d}\,}}^A\). For the definition of \({{\,\textrm{d}\,}}^A\), we address the reader to [45, Section 12.9]. The properties of \({{\,\textrm{d}\,}}^A\) are formally similar to those of \({{\,\textrm{D}\,}}_A\) and they are summarised in [45, Theorem 12.57]. Here we only stress that, obviously, \({{\,\textrm{d}\,}}^A\) coincides with \({{\,\textrm{D}\,}}_A\) on \(C^\infty (M, \, E)\), i.e., if \(k=0\).
Next, we extend \(*\) to an operator from \(\Gamma (M, \,\Lambda ^k \textrm{T}^*M \otimes E)\) to \(\Gamma (M,\,\Lambda ^{n-k} \textrm{T}^*M \otimes E)\), which we still denote \(*\). To this purpose, it is enough to define the action of \(*\) on simple elements of \(\Gamma (M,\,\Lambda ^k \textrm{T}^*M \otimes E)\) by letting
for \(u \in \Gamma (M,\,E)\) and \(\omega \in \Gamma (M,\,\Lambda ^k \textrm{T}^*M)\). The rule (A.27), extended linearly, gives a meaning to \(* \sigma \) for every \(\sigma \in \Gamma (M,\,\Lambda ^k \textrm{T}^*M \otimes E)\) and \(0 \le k \le n\) integer. Using the scalar product associated with the metric of E and the scalar product of k-forms induced by the metric, we define
for every \(u_1\), \(u_2 :M \rightarrow E\) measurable sections and measurable k-forms \(\omega _1\), \(\omega _2\), and a.e. \(x \in M\). From (A.28) we define a corresponding \(L^2\)-product
anytime the right hand side of (A.29) exists. Once again, extending (bi)linearly the rule (A.29), we can define the \(L^2\)-product of arbitrary \(\sigma _1\), \(\sigma _2 \in \Gamma (M,\,\Lambda ^k \textrm{T}^*M \otimes E)\) by letting
anytime the integral at right hand side exists.
With all this machinery at disposal, we can define the formal adjoint of \({{\,\textrm{d}\,}}^A\) as the operator
which is formally adjoint to \({{\,\textrm{d}\,}}^A\) with respect to the \(L^2\)-product (A.30). An explicit computation yields (cf., e.g., [44, Section 4.2])
where \({{\,\textrm{d}\,}}^0\) denotes the exterior covariant derivative induced by the reference connection \({{\,\textrm{D}\,}}_0\). For \(k = 1\), we set \({{\,\textrm{D}\,}}_A^*:= ({{\,\textrm{d}\,}}^A)^*\).
We can finally define the concept of weak covariant derivative of a section \(u \in L^1(M,\,E)\). We say that \(u \in L^1(M,\,E)\) has weak covariant derivative \({{\,\textrm{D}\,}}_A u\) if there exists a section \(\sigma _u \in L^1(M,\,\textrm{T}^*M \otimes E)\) such that
for every \(\tau \in C^\infty (M,\,\textrm{T}^*M \otimes E)\). In such case, \(\sigma _u\) is uniquely determined, and we set \({{\,\textrm{D}\,}}_A u:= \sigma _u\). In particular, if \(u \in W^{1,2}(M,\,E)\), then (A.31) defines a linear bounded operator
We are now in position to weaken the requirement \(A \in C^\infty (M, \, \textrm{T}^*M)\) in force so far. Indeed, if \(u \in W^{1,2}(M, \, E)\) and \({{\,\textrm{D}\,}}_0\) is a smooth reference connection, then \({{\,\textrm{D}\,}}_0 u\) is well-defined through (A.31) and belongs to \(L^2(M,\,\textrm{T}^*M \otimes E)\) (and in turn to \(L^1(M,\,\textrm{T}^*M \otimes E)\), by the compactness of M). For \(A \in W^{1,2}(M, \,\textrm{T}^*M)\), we have \(Au \in L^1(M, \textrm{T}^*M)\), hence we can define
Clearly, \({{\,\textrm{D}\,}}_A u\) belongs to \(L^1(M, \,\textrm{T}^*M \otimes E)\). Moreover, if \(u \in (L^\infty \cap W^{1,2})(M, \, E)\), then \({{\,\textrm{D}\,}}_A u \in L^2(M, \,\textrm{T}^*M \otimes E)\). Notice that, even in this context, \({{\,\textrm{D}\,}}_X\) is a local operator and behaves naturally with respect to restrictions.
For \(A \in W^{1,2}(M,\,\textrm{T}^*M)\), we define the curvature 2-form of \({{\,\textrm{D}\,}}_A\) by Equation (A.26), i.e., we define \(F_A:= F_0 + {{\,\textrm{d}\,}}A\). In such a way, \(F_A \in L^2(M,\,\Lambda ^2 \textrm{T}^*M)\) for any \(A \in W^{1,2}(M,\,\textrm{T}^*M)\).
Remark A.18
Although of no use in this work, we record the following fact which will be needed in the forthcoming work [23]. We can associate with \({{\,\textrm{D}\,}}_A\) its formal adjoint \({{\,\textrm{D}\,}}_A^*\), i.e., its adjoint with respect to the \(L^2\)-product \(((\cdot ,\cdot ))\), as follows. Given A a 1-form on M (measurable, but not necessarily of class \(W^{1,2}(M)\)), \(\sigma \in L^2(M,\,\textrm{T}^*M \otimes E)\), and any section \(u \in \Gamma (M,\,E)\) such that there exists \({{\,\textrm{D}\,}}_0 u\) as a weak derivative and such that \({{\,\textrm{D}\,}}_A u \in L^2(M,\,{\textrm{T}^*M \otimes } E)\), we let
(The above assumptions are satisfied, for instance, if \(A \in L^2(M,\,\textrm{T}^*M)\) and \(u \in (L^\infty \cap W^{1,2})(M,\,E)\).) For every fixed \(\sigma \in L^2(M,\,\textrm{T}^*M \otimes E)\), the right hand side of (A.32) defines a linear form \(u \mapsto ({{\,\textrm{D}\,}}_A^*\sigma )(u)\) on the linear space
By Schwarz inequality, such a linear form is continuous if \(W_A\) is endowed with the norm \(\left\| u \right\| _{W_A}:= \left\| u \right\| _{L^2(M)} + \left\| {{\,\textrm{D}\,}}_A u \right\| _{L^2(M)}\). Furthermore, if \(A \in L^2(M,\,\textrm{T}^*M)\), then \(W_A\) embeds continuously into \(W^{1,1}(M,\,E)\). Moreover, if A is a smooth 1-form, then \(W_A = W^{1,2}(M,\,E)\), and (A.32) defines a continuous linear operator \({{\,\textrm{D}\,}}_A^* :L^2(M, \,\textrm{T}^*M \otimes E) \rightarrow W^{-1,2}(M, \,E)\), cf., e.g., [69, Chapter 4].
Remark A.19
The pointwise scalar product \(\langle \langle \cdot , \cdot \rangle \rangle \) and the \(L^2\)-product \(((\cdot , \cdot ))\) will be simply denoted \(\left\langle \cdot , \, \cdot \right\rangle \) and \((\cdot ,\cdot )\) respectively anytime no ambiguity arises.
B Currents and Form-Valued Distributions
Currents. We recall some standard terminology for currents on smooth manifolds, and refer e.g. to [30, 62] for more details. We equip \(C^\infty (M, \, \Lambda ^k\textrm{T}^*M)\) with the topology induced by the family of \(C^h\)-seminorms, for all integers \(h\ge 1\). The space of k-currents \(\mathcal {D}^\prime (M, \, \Lambda _k\textrm{T}M)\) is defined as the topological dual of smooth k-forms, \(\mathcal {D}^\prime (M, \, \Lambda _k\textrm{T}M):= (C^\infty (M, \, \Lambda ^k\textrm{T}^*M))^\prime \). Currents come with a boundary operator, \(\partial :\mathcal {D}^\prime (M, \, \Lambda _k\textrm{T}M) \rightarrow \mathcal {D}^\prime (M, \, \Lambda _{k-1}\textrm{T}M)\), defined as
for any k-current S and any smooth \((k-1)\)-form \(\omega \). The boundary operator is sequentially continuous with respect to the weak\(^*\) convergence of distributions.
Given a point \(x\in M\) and a k-covector \(\omega \in \Lambda ^k \textrm{T}_x M^*\), we define the comass of \(\omega \) as
(here, \(\left| \cdot \right| \) is the norm on \(\Lambda _k\textrm{T}_x M\) induced by the Riemannian metric on M). The comass is a norm on \(\Lambda _k\textrm{T}^* M\), which does not coincide with the norm \(\left| \cdot \right| \) induced by the Riemannian metric. However, there exists a constant \(C_{n,k}\), depending on n and k only, such that
for any \(\omega \in \Lambda _{k}\textrm{T}_x^* M\) and any \(x\in M\). The equality \(\left\| \omega \right\| = \left| \omega \right| \) holds if and only if \(\omega \) is simple. For any k-current S, the mass of S is defined as
Let \(E\subset M\) be a k-rectifiable set, oriented by a measurable, simple k-vector field \(v_E:E\rightarrow \Lambda _k\textrm{T}M\) that is tangent to E and satisfies \(\left| v_E \right| = 1\) at \(\mathcal {H}^k\)-almost any point of E. Let \(\theta :E\rightarrow \mathbb Z\) be a measurable function, such that . We denote by \(\llbracket E, \, \theta \rrbracket \) the current carried by E with multiplicity \(\theta \), defined by
for any smooth k-form \(\tau \). In case \(\theta = 1\) identically, We write \(\llbracket E \rrbracket := \llbracket E, \, 1\rrbracket \). A current that can be written in the form (B.5) is called an integer-multiplicity rectifiable k-current. The mass of an integer-multiplicity rectifiable current is given by
We denote by \(\mathcal {R}_k(M)\) the set of integer-multiplicity rectifiable k-currents with finite mass.
Finally, we define the flat norm of a current \(S\in \mathcal {D}^\prime (M, \, \Lambda _k\textrm{T}M)\) as
(with the understanding that \(\inf \emptyset = +\infty \)).
Form-valued distributions. We equip the space of smooth k-vector fields, \(C^\infty (M, \, \Lambda _k\textrm{T}M)\), with the topology induced by the family of \(C^h\)-seminorms, for all integers \(h\ge 1\). The space of distributions with values in k-forms is defined as the topological dual of smooth k-vectors, \(\mathcal {D}^\prime (M, \, \Lambda ^k\textrm{T}^*M):= (C^\infty (M, \, \Lambda _k\textrm{T}M))^\prime \). The differential and the codifferential extends to operators on form-valued distributions, by duality:
for any \(\omega \in \mathcal {D}^\prime (M, \, \Lambda ^k\textrm{T}^* M)\), \(v\in C^\infty (M, \, \Lambda _{k+1}\textrm{T}M)\) and \(w\in C^\infty (M, \, \Lambda _{k-1}\textrm{T}M)\). The definitions (B.8), (B.9) are consistent with (A.3).
The Hodge dual of currents and forms. There are natural operators
defined as follows: for any \(\omega \in \mathcal {D}^\prime (M, \, \Lambda ^k\textrm{T}^*M)\) the current \(\star \omega \) is defined as
for any \(\tau \in C^\infty (M, \, \Lambda ^{n-k}\textrm{T}^*M)\). Similarly, given \(S\in \mathcal {D}^\prime (M, \, \Lambda _k\textrm{T}M)\), we define the form-valued distribution \(\star S = * S^\flat \in \mathcal {D}^\prime (M, \, \Lambda ^{n-k}\textrm{T}^*M)\) as
In case \(\omega \), S are smooth (or, more generally, they are represented by \(L^1\)-vector or covector fields), the definitions (B.10) and (B.11) are consistent with (1.1), i.e.
Indeed, for any smooth k-form \(\omega \) and any smooth \((n-k)\)-form \(\tau \), there holds
by the very definition of \(*\).
As an immediate consequence of (B.10), (B.11), the operator \(\star \) is sequentially continuous with respect to the weak\(^*\) convergence in the sense of distributions. We recall a few other properties of \(\star \). For any \(\omega \in \mathcal {D}^\prime (M, \, \Lambda ^k\textrm{T}^*M)\), we denote by \(\left| \omega \right| \!(M)\) the total variation of \(\omega \) induced by the Riemannian metric on M, that is
Proposition B.1
For any \(\omega \in \mathcal {D}^\prime (M, \, \Lambda ^k\textrm{T}^*M)\) and \(S\in \mathcal {D}^\prime (M, \, \Lambda _k\textrm{T}M)\), the following properties hold:
-
(i)
\(\star \star \omega = (-1)^{k(n-k)} \omega \) and \(\star \star S = (-1)^{k(n-k)} S\);
-
(ii)
\(\partial (\star \omega ) = (-1)^{k+1} \star {{\,\textrm{d}\,}}\omega \);
-
(iii)
\(\star (\partial S) = (-1)^{k} {{\,\textrm{d}\,}}(\star S)\);
-
(iv)
there exists a constant \(C_{n,k}\), depending only on n and k, such that
$$\begin{aligned} |\!\star S|(M) \le \mathbb {M}(S) \le C_{n,k} \, |\!\star S|(M) \end{aligned}$$ -
(v)
if S is an integer-multiplicity rectifiable current, then \(\mathbb {M}(S) = |\!\star S|(M)\).
The proof of Proposition B.1 is a rather direct application of the definitions above and we omit it for the sake of brevity.
C A Few Technical Results
1.1 C. 1 An Interpolation Lemma
Let \(k\in \{0, \, 1, \, \ldots , n\}\) and \(p\in [1, \, +\infty ]\). We define the space of \(W^{-1,p}\)-forms of dimension k as a topological dual,
where \(q\in [1, \, +\infty ]\) is the Hölder conjugate of p, such that \(1/p + 1/q = 1\).
Lemma C.1
Let \(k\in \mathbb Z\), \(p\in \mathbb R\) be such that \(0\le k \le n\), \(1< p < n/(n-1)\). For any bounded Radon measure \(\omega \) with values in k-forms, there holds
where \(\alpha := 1 + n/p - n \in (0, \, 1)\).
Lemma C.1 is a special case of the more general result below (which is of some independent interest).
Lemma C.2
Let \(d\in \mathbb N\) and \(1< p < \frac{n}{n-1}\). For any Radon vector measure \(\nu \) on M, with values in \(\mathbb R^d\), there holds
where \(\alpha := 1 + n/p - n \in (0, \, 1)\).
Proof
Let \(\mathcal {A} = \{(U_i,\varphi _i)\}_{i=1}^N\) be a finite regular atlas for M, where the (bounded) open sets \(U_i\) are contractible, and let \(\{\rho _i\}_{i=1}^N\) be a partition of unity subordinate to the covering \(\{U_i\}\). Write \(\nu = (\nu _1, \dots , \nu _k)\) and, for each \(k \in \{1,2,\dots ,d\}\) and \(i \in \{1,2,\dots ,n\}\), define \(\mu _{k,i}:= (\rho _i \nu _k ) \circ \varphi _i^{-1}\). Then, for every \(i \in \{1,2,\dots ,n\}\) and every \(k \in \{1,2,\dots ,d\}\), \(\mu _{k,i}\) is a Radon measure on \(\Omega _i:= \varphi _i(U_i) \subset \mathbb R^n\). Therefore, we can argue exactly as in [42, Lemma 3.3] to deduce that
On the other hand, since the bounded open sets \(\Omega _i\) have smooth boundary, we have \(C^{0,1}_0(\Omega _i) = W^{1,\infty }_0(\Omega _i)\) as Banach spaces, for every \(i \in \{1,2,\dots ,n\}\). Consequently, \((C^{0,1}_0(\Omega _i))^\prime = W^{-1,1}(\Omega _i)\) as Banach spaces for every \(i \in \{1,2,\dots ,n\}\). Since for \(1< p < \frac{n}{n-1}\) and \(\alpha = 1 + n/p - n\) any functional in \((C^{0,\alpha }_0(\Omega ))^\prime \) restricts to a functional in \(W^{-1,p}(\Omega )\) and the restriction map is continuous (by Sobolev embedding, cf. Remark 2.6), we infer
Thus, as each \(\mu _{k,i}\) is the push-forward of \(\rho _i\nu _k\) through \(\varphi _i\),
Now, we claim that for any \(i \in \{1,\dots ,N\}\), any \(k \in \{1,\dots ,d\}\), and any \(p \in \left[ 1, \frac{n}{n-1}\right) \) there holds
Assuming (\(\star \)) for a moment, we obtain
for every \(k = 1, 2, \dots , d\), and the claimed conclusion follows immediately.
Proof of \((\star )\). Let \(q:= p'\). The first inequality in (\(\star \)) follows immediately, because for any \(u \in W^{1,q}_0(U_i)\) the extension of u by zero in \(M {\setminus } U_i\) belongs to \(W^{1,q}(M)\) and preserves the norm.
As for the second inequality, let \(V_i:= {{\,\textrm{spt}\,}}\rho _i\) and recall that, by definition, \(V_i \subset \subset U_i\). Let us fix any cutoff function \(\zeta _i \in C^\infty _c(U_i, [0,1])\) such that \(\zeta _i \equiv 1\) in \(V_i\) and such that \(W_i:= {{\,\textrm{spt}\,}}\zeta _i\) satisfies \(V_i \subset \subset W_i \subset \subset U_i\). Then, for any \(u \in W^{1,q}(M)\) we have \(\zeta _i u \in W^{1,q}_0(U_i)\) and
hence, taking the supremum as u ranges over all functions in \(W^{1,q}(M)\) with \(\left\| u \right\| _{W^{1,q}(M)} = 1\) in the above inequalities, the conclusion follows (moreover, we see that the implicit constant at right-hand-side of (\(\star \)) is less than or equal to \(\left\| \zeta _i \right\| _{W^{1,\infty }(U_i)}\)).\(\quad \square \)
Proof of Lemma C.1
Similarly to as at the end of [5, p. 462], we observe that, by means of Whitney’s embedding theorem, we may embed \(M \hookrightarrow \mathbb R^{n+r}\), for some \(r \in \mathbb N\), and then we can look at \(\Lambda ^k \textrm{T}^*M\) as a subbundle of \(\Lambda ^k \textrm{T}^* \mathbb R^{n+r}\). Consequently, every measure \(\omega \) with values in k-forms can be regarded as a (Radon) vector measure \(\nu _\omega \) on M with values in the Euclidean inner product space \(\mathcal {V}:= \Lambda ^k (\mathbb R^{n+r})^\prime \cong \mathbb R^{\left( {\begin{array}{c}n+r\\ k\end{array}}\right) }\). Moreover, again by Whitney’s theorem, there holds
for any \(p \in \left[ 1, \frac{n}{n-1}\right) \), where the implicit constants depend only on M and p, and
where the implicit constants depend only on M. Thus, we can apply Lemma C.2 with \(d = \left( {\begin{array}{c}n+r\\ k\end{array}}\right) \) and reach the conclusion. \(\quad \square \)
1.2 C. 2 Elliptic Regularity
We establish here two results concerning existence, uniqueness and estimates for solutions to London (Lemma C.3) and Poisson (Lemma C.4) equations for differential k-forms and data in \(W^{-1,p}\). Although Lemmas C.3 and C.4 are certainly known to experts, we have not found explicit proofs in the literature. Since they are crucial to our arguments, we provide detailed proofs.
Lemma C.3
Let \(p\in (1, \, 2)\). For any k-form \(f\in W^{-1,p}(M, \, \Lambda ^k\textrm{T}^*M)\), the equation
has a unique solution \(v\in W^{1,p}(M, \, \Lambda ^k\textrm{T}^* M)\), which satisfies
for some constant \(C_p\) depending only on M, k, p.
The proof of Lemma C.3 depends on Gaffney’s inequality, see Proposition A.9.
Proof of Lemma C.3
We split the proof into several steps.
Step 1
Let \(q > 2\). We claim the following: for any \(f\in L^q(M, \, \Lambda ^k\textrm{T}^*M)\), the equation (C.1) has a unique solution \(v\in W^{2,q}(M, \, \Lambda ^k\textrm{T}^*M)\), which satisfies
for some constant \(C_q\) that depends only on M, k and q.
For any \(f\in L^2(M, \, \Lambda ^k\textrm{T}^*M)\), existence and uniqueness of a solution \(v\in W^{1,2}(M, \, \Lambda ^k\textrm{T}^* M)\) follow from Lax-Milgram lemma (with respect to the scalar product \(\left\langle \cdot , \, \cdot \right\rangle \) such that \(\left\langle v, \, v\right\rangle = \int _M \left( \left| {{\,\textrm{d}\,}}v \right| ^2 + \left| {{\,\textrm{d}\,}}^* v \right| ^2 + \left| v \right| ^2 \right) \,{{\,\textrm{vol}\,}}_g\)) combined with Gaffney’s inequality, Proposition A.9. By elliptic regularity (see, for instance, [49, Theorem 10.3.11]), if \(f\in L^q(M, \, \Lambda ^k\textrm{T}^* M)\) then \(u\in W^{2,q}(M, \, \Lambda ^k\textrm{T}^* M)\) and
for some constant \(C_q\) that depends only on M, k and q. Now, there exists a number \(s > q\) such that \(W^{2,q}(M, \, \Lambda ^k\textrm{T}^*M)\) embeds continuously in \(L^{s}(M, \, \Lambda ^k\textrm{T}^*M)\) (see, e.g., [60, Theorem 1.3.6]). By interpolation, there exists a number \(\alpha = \alpha (q, \, s)\in (0, \, 1)\) such that
By applying Young’s inequality, for any \(\delta >0\) we find a constant \(C_\delta \) (depending on \(\alpha \), M, k and q as well) such that
By comparing (C.4) and (C.5), and choosing \(\delta \) small enough, we deduce
However, by testing the equation (C.1) against v, we obtain
and (C.3) follows.
Step 2
Now, take \(p\in (1, \, 2)\). We claim that, for any \(f\in W^{-2,p}(M, \, \Lambda ^k\textrm{T}^* M)\), the equation (C.1) has exactly one solution \(v\in L^p(M, \, \Lambda ^k\textrm{T}^*M)\), which satisfies
for some constant \(C_p\) that depends only on M, k and p. To prove the claim, we will first show existence and uniqueness of a duality solution \(v \in L^p(M, \Lambda ^k \textrm{T}^*M)\) and then we will prove that every solution \(v \in L^p(M, \Lambda ^k \textrm{T}^*M)\) in the sense of \(\mathcal {D}'(M)\) is a duality solution.
We notice in first place that \(p \in (1,2)\) implies \(q:= p' > 2\). By Step 1, given \(h \in L^q(M, \Lambda ^k \textrm{T}^*M)\), there exists a uniquely determined \(w_h \in W^{2,q}(M, \Lambda ^k \textrm{T}^*M)\) such that \(w_h = (-\Delta + \textrm{Id})^{-1}h\) (that it is to say, solving \(-\Delta w_h + w_h = h\)), which moreover satisfies \(\left\| w_h \right\| _{W^{2,q}} \le C_p \left\| h \right\| _{L^q}\), where \(C_p > 0\) is constant depending only on p, k and M.
The map \(V:L^q(M, \Lambda ^k \textrm{T}^*M) \rightarrow \mathbb R\) defined by
is a bounded linear functional over \(L^q(M, \Lambda ^k \textrm{T}^*M)\). Indeed, by Step 1,
hence
where the constant \(C_p\) depends only on p, k and M. Consequently, Riesz’ theorem implies the existence of a unique \(v \in L^p(M,\,\Lambda ^k \textrm{T}^*M)\) such that
i.e., replacing h by the corresponding \(w = w_h \in W^{2,q}(M, \Lambda ^k \textrm{T}^* M)\),
Hence, v is the unique duality solution of (C.1) for the given \(f \in W^{-2,p}(M,\Lambda ^k \textrm{T}^*M)\). Since Riesz’ theorem also implies \(\left\| v \right\| _{L^p} = \left\| V \right\| _{(L^q)'}\), by (C.9) v satisfies the estimate (C.4).
Conversely, every distributional solution to (C.1) is a duality solution. Indeed, suppose \(v \in L^p(M, \Lambda ^k \textrm{T}^*M)\) is a distributional solution to (C.1) for \(f \in W^{-2,p}(M, \Lambda ^k \textrm{T}^*M)\). Then, for every \(w \in C^\infty (M, \Lambda ^k \textrm{T}^*M)\),
Letting again \(h = -\Delta w + w\), then \(h \in L^q(M,\,\Lambda ^k \textrm{T}^*M)\) and, from (C.8) and (C.10), we have \((v,h) = V(h)\). By the density of \(C^\infty (M,\,\Lambda ^k \textrm{T}^*M)\) into \(W^{2,q}(M,\, \Lambda ^k \textrm{T}^*M)\), the equality \((v,h) = V(h)\) actually holds for every \(h \in L^q(M, \Lambda ^k \textrm{T}^*M)\). Thus, v is duality solution. Therefore, for every \(f \in W^{-2,p}(M,\,\Lambda ^k \textrm{T}^*M)\), Equation (C.1) has a unique distributional solution in \(L^p(M,\,\Lambda ^k \textrm{T}^*M)\), which is the duality solution.
Step 3
Let \(f\in W^{-1,p}(M, \, \Lambda ^k\textrm{T}^* M)\) and let v be the unique solution of (C.1). By Step 2, we have
By differentiating the equation (C.1), we obtain \(-\Delta ({{\,\textrm{d}\,}}v) + {{\,\textrm{d}\,}}v = {{\,\textrm{d}\,}}f\). Therefore, Step 2 implies
Similarly, \(-\Delta ({{\,\textrm{d}\,}}^* v) + {{\,\textrm{d}\,}}^* v = {{\,\textrm{d}\,}}^* f\) and hence
Combining (C.11), (C.12), (C.13) with Gaffney’s inequality (Proposition A.9), the lemma follows. \(\quad \square \)
Here is a variant of Lemma C.3, which will also be useful.
Lemma C.4
Let \(p\in (1, \, 2)\). Let \(f\in W^{-1,p}(M, \, \Lambda ^k\textrm{T}^*M)\) be a k-form such that
Then, there exists a unique \(v\in W^{1,p}(M, \, \Lambda ^k\textrm{T}^*M)\) such that
Moreover, v satisfies
for some constant \(C_p\) depending only on M, k, p.
Proof
We proceed in three steps.\(\quad \square \)
Step 1
(Existence and uniqueness of a duality solution) Set \(q:= p'\). We claim that for any \(f \in W^{-2,p}(M, \Lambda ^k \textrm{T}^* M)\) such that \(\left\langle f, \, \star \xi \right\rangle _{W^{-2,p},W^{2,q}} = 0\) for every \(\xi \in {{\,\textrm{Harm}\,}}^k(M)\) there exists a unique distributional solution \(v \in L^p(M,\,\Lambda ^k \textrm{T}^*M)\) to (C.14), which satisfies the estimate
Define \(V:L^q(M, \Lambda ^k \textrm{T}^*M) \rightarrow \mathbb R\) setting
where \(G: L^q(M, \Lambda ^k \textrm{T}^*M) \rightarrow W^{2,q}(M, \Lambda ^k \textrm{T}^*M) \cap ({{\,\textrm{Harm}\,}}^k(M))^\perp \) is Green’s operator, which is linear and bounded (see Sect. 4). Then V is linear and bounded, because
whence
It then follows from Riesz’ Representation theorem that there exists a uniquely determined \(v \in L^p(M, \Lambda ^k \textrm{T}^* M)\) representing V, i.e., such that \(V(\alpha ) = (v,\alpha )\) for all \(\alpha \in L^q(M, \Lambda ^k \textrm{T}^*M)\). Thus,
and moreover \(\left\| v \right\| _{L^p} = \left\| V \right\| _{(L^q)'}\), whence \(\left\| v \right\| _{L^p} \lesssim \Vert f\Vert _{W^{-2,p}}\), i.e., (C.16). In addition, (C.17) implies \((v,\xi ) = 0\) for every \(\xi \in {{\,\textrm{Harm}\,}}^k(M)\).
We now show that v solves (C.14) in the sense of \(\mathcal {D}'(M)\). To this purpose, we first recall from Remark A.13 that \(\Delta G(\xi ) = G(\Delta \xi )\) for every form \(\xi \in W^{2,q}(M,\Lambda ^k \textrm{T}^* M)\). Then, we notice that, upon writing \(\xi = \Delta G(\xi ) + H(\xi )\), where \(H(\xi )\) is the harmonic part of \(\xi \), by assumption we have \(\left\langle f, \, \star H(\xi )\right\rangle _{W^{-2,p},W^{2,q}} = 0\). Hence, by (C.17) we deduce that
for all \(\xi \in W^{2,q}(M, \Lambda ^k \textrm{T}^*M)\). Thus, v solves (C.14) in the sense of distributions and satisfies estimate (C.16).
Step 2
(Every distributional solution is a duality solution) We argue exactly as in (C.10), with the operator \(-\Delta + \textrm{Id}\) replaced by \(\Delta G\).
Step 3
(Estimate) To conclude, let \(f \in W^{-1,p}(M, \Lambda ^k \textrm{T}^*M)\) and let \(v \in L^p(M, \Lambda ^k \textrm{T}^*M)\) be the corresponding unique solution to (C.14). By (C.16), we have
By differentiating Equation (C.14) exactly as we did for (C.1) in Step 3 of the proof of Lemma C.3, we obtain
Then, both \(v \in W^{1,p}(M,\,\Lambda ^k \textrm{T}^*M)\) and estimate (C.15) follow by (C.18), (C.19), and Gaffney’s inequality (Proposition A.9). \(\quad \square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Canevari, G., Dipasquale, F.L. & Orlandi, G. The Yang–Mills–Higgs Functional on Complex Line Bundles: \(\Gamma \)-Convergence and the London Equation. Arch Rational Mech Anal 247, 104 (2023). https://doi.org/10.1007/s00205-023-01933-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-023-01933-1