Abstract
A variational model for the interaction between homogenization and phase separation is considered. The focus is on the regime where the latter happens at a smaller scale than the former, and when the wells of the double well potential are allowed to move and to have discontinuities. The zeroth and first order \(\Gamma \)-limits are identified. The topology considered for the latter is that of two-scale, since it encodes more information on the asymptotic local microstructure. In particular, when the wells are non-constant, the first order \(\Gamma \)-limit describes the contribution of microscopic phase separation, even in situations where there is no macroscopic phase separation. As a corollary, the minimum of the mass constrained minimization problem is characterized, and it is shown to depend on whether or not the wells are discontinuous. In the process of proving these results, the theory of inhomogeneous Modica Mortola functionals is strengthened.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Modica–Mortola functional is the prototypical mathematical model for phase separation in a homogeneous material. After the initial works [24, 25] by Modica and Mortola that proved the conjecture by Gurtin (see [20]) in the scalar case, several variants of the functional were studied in the literature (see, for instance, [18, 21, 30]) to prove the sharp interface limit in full generality. We refer to [10] for a more comprehensive overview of the gradient theory of phase separation. From the mathematical point of view, the main feature of such models is that both the potential and the wells do not depend on the spatial point, modeling homogeneity of the medium.
Modern technologies, such as temperature-responsive polymers, take advantage of engineered inclusions or natural heterogeneities of the medium to obtain novel composite materials with specific physical properties. To model such situations by using a variational approach based on the gradient theory, the potential and the wells have to depend on the spatial point, even in a discontinuous way.
The study of phase separation in heterogeneous media with inhomogeneous conditions is a challenging mathematical problem that has recently drawn the attention of researchers. A mathematical model for phase separation of homogeneous materials in an inhomogeneous setting was considered in the scalar case by Bouchitté [4], by using techniques heavily relying on the scalar nature of the functions. A similar problem was also considered by Sternberg [30] in the two dimensional setting and with a double well required to satisfy strong regularity assumptions. The first author and Gravina [10] have recently extended the above mentioned results to the vector-valued case under some strict conditions on the behavior of the double well potential around the wells. A first result in understanding phase separation in heterogeneous media was obtained by Braides and Zeppieri [5], where the interaction between periodic microstructure and interfacial energies is studied in the scalar case in dimension one for inhomogeneous conditions. While on the one hand, the authors consider several regimes and higher order \(\Gamma \) expansion, on the other hand their approach relies heavily on the explicit choices of the potential and on the wells, and on the many advantages of working in the one dimensional scalar case. In particular, the several limiting functionals identified in their work are with respect to weak-\(L^2\) convergence, and the techniques used are not easily extended to the multidimensional vectorial case. In [8] (see also [9]) the authors analyzed the case when the scale of the periodic microstructure and interface are of the same order, in the case of fixed wells, but without any restriction on the dimensions. Finally, we should mention that in [3], the homogenization is in the singular perturbation term which leads to fundamentally different phenomenon.
In this paper, we consider a variational model for phase separation within a periodically heterogeneous composite material with inhomogeneous conditions, when wells may depend on the spatial variable and have discontinuities. Fixed \(\varepsilon ,\delta >0\), the energy can be written as
Here \(\Omega \subset {\mathbb {R}}^N\) is an open bounded Lipschitz set, and \(u\in W^{1,2}(\Omega ;{\mathbb {R}}^M)\). The double well potential W is Q-periodic in the spatial variable, where \(Q:= (-1/2,1/2)^N\), modeling a periodic structure of the material. In the functional \(G_{\varepsilon ,\delta }\), the parameter \(\varepsilon \) relates to the scale of the diffuse transition layer, while the scale of the periodic microstructure is \(\delta \). The main novelty of the paper is the general framework in which the asymptotic behaviour of the functional \(G_{\varepsilon ,\delta }\) is studied: first of all there is no restriction on the dimensions \(N,M\ge 1\); moreover, for each \(x\in \Omega \), the potential W vanishes on two wells \(a(x), b(x)\in {\mathbb {R}}^M\), where the Q-periodic functions \(x\mapsto a(x)\) and \(x\mapsto b(x)\) are allowed to have discontinuities. These assumptions extend significantly those in previous works. Indeed, in [8] (see also [9]) the vectorial wells were required to be fixed, and in [5] only the case \(N=M=1\) is considered and an explicit potential W and wells a, b are used.
The core of this work is to identify the first order \(\Gamma \)-limit with respect to the two-scale convergence in the regime where \(\varepsilon \) is negligible with respect to \(\delta \), namely when the heterogeneities of the material are of a larger scale than that of the diffuse interface between different phases. The choice of working with the two-scale convergence is to maintain in the limit fine information about the asymptotic local microstructure. The second order \(\Gamma \)-limit, as well as other regimes, will be the content of forthcoming investigations.
Finally, we note that this regime is of particular relevance to the biological phenomenon of lipid rafts. This is the theory that within the cell membrane there are many coexisting fluid phases consisting of various varieties of bonded lipids and disordered lipid phases. It was shown through the work of many collaborators (see [29] for a summary) that at physiological parameters, the phase separation occurs at the scale of nanometers which is inaccessible to microscopes. Furthermore, in [27] it is noted that there is no macroscopic phase separation and that thermal fluctuations play a role in the formation of these nanodomains. This provides an apt setting to use the tools of homogenization to derive an effective theory for the material consisting of these nanodomains.
1.1 Main Results
In this paper, we consider the regime \(\varepsilon \ll \delta \), namely when the phase separation process happens at a finer scale than that of the heterogeneities of the material. Our main result is the integral representation of the \(\Gamma \)-expansion of order one of \(G_{\varepsilon ,\delta }\), that rigorously justifies the equation
We explicitly identify the functionals \(G^0\) and \(G^1\). The main novelty of this manuscript is in the characterization of the scale \(\frac{\varepsilon }{\delta }\) and the functional \(G^1\). Despite being more classical, for completeness, we also include a description of the functional \(G^0\). This zeroth order \(\Gamma \)-limit captures the averaging effect of the mixing of the two phases
where \(W^{\textrm{hom}}\) is the homogenized functional (see Definition 4.1 for the precise definition), which gives the best way to obtain a local density u(x) without caring about the energy given by the singular perturbation. Moreover, as we show in Corollary 4.4, the minimum of \(G^0\) is zero.
The functional \(G^1\), on the other hand, exhibits an interaction between the periodic microstructure and phase separation. In order to maintain the information on the local microstructure, we use the notion of two-scale \(\Gamma \)-convergence (see [6]), so that \(G^1\) is defined on the space \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\). The first order limiting energy has the character of a bulk energy in the first variable, and of an interfacial energy in the second variable, namely it is of the form
where, for each \(x\in \Omega \), \(\widetilde{u}(x,\cdot )\) is the Q-periodic extension of the function \(y\mapsto u(x,y)\), and \(\widetilde{G}^1\) is the local energy of the microstructure defined, for a function \(v\in BV_{\textrm{loc}}({\mathbb {R}}^N;{\mathbb {R}}^M)\), as
Here \(\widetilde{Q}:= [-1/2,1/2)^N\), \(\textrm{d}_{\textrm{W}}\) is a degenerate geodesic distance related to the double well potential \(\sqrt{W(y,\cdot )}\) (see Definition 5.3), and \(J_v\) is the jump set of the function v. Due to the technical nature of all of the assumptions and the definitions required to properly introduce all of the functionals above, in this section we prefer to sacrifice rigor and to focus on commenting on the peculiarities and the difficulties of the proofs. The precise assumptions are introduced and discussed in Sect. 3, while the zeroth and the first order limiting functionals are introduced in Sect. 4 and 5, respectively.
First of all, we note that the asymptotic expansion (1.3) does not depend on the rate at which \(\varepsilon /\delta \) goes to zero. Another interesting observation we gain from the form of \(G^1\) is that, at first order, there is no energy penalty to pass from one local microstructure to another. To be precise, consider the situation in Fig. 1. Given a function \(u:\Omega \times Q\rightarrow {\mathbb {R}}^M\) we refer to \(u(x,\cdot ):Q\rightarrow {\mathbb {R}}^M\) as the local microstructure at the point \(x\in \Omega \). As expected, this function will takes values in the wells a, b. Assume that u is piecewise constant in the first variable, namely that it equals some \(u_1:Q\rightarrow {\mathbb {R}}^M\) in the blue region, and some other function \(u_2:Q\rightarrow {\mathbb {R}}^M\) in the green region. Then a recovery sequence for u will have to approximate a \(\delta Q\)-periodic structure in the blue region, to transition between the two microstructures in the purple region, and to approximate another \(\delta Q\)-periodic structure in the green region. It is possible to construct the recovery sequence in such a way that the energy in each cube does not depend on the parameters \(\varepsilon \) and \(\delta \). Therefore, since the number of such cubes is asymptotically negligible with respect to the total number of cubes, also the energetic contribution of the recovery sequence in this region will be asymptotically negligible. In particular, the energy of the recovery sequence will essentially be the sum of the energies needed to recover the two Q-periodic microstructures. This is the reason why in the functional \(\widetilde{G}^1\) the jump set on \(\widetilde{Q}\) is considered.
The choice of working with a potential vanishing on only two wells is based on convenience of notation; indeed, our proofs directly extend to the case of multiple wells satisfying assumptions similar to these we use here.
We also would like to stress the following difference with the case of a potential W that does not depend on the spatial position: in such a case, this intermediate scaling \(\varepsilon /\delta \) would lead to a trivial \(\Gamma \)-limit; the relevant scaling would be \(\varepsilon \) that is expected to capture a macroscopic phase separation. On the other hand, in our case, at first order we see a microscopic phase separation (namely in the second variable), but not a macroscopic phase separation, since this is averaged over the entire domain. At the next order of the \(\Gamma \)-expansion, we expect to see a macroscopic phase separation of a similar form as the one arising from homogenization of interfaces. However, this problem will be more challenging as \(\min G^1\) can be nonzero (see Corollary 5.11), and the structure of minimizers of the mass constrained minimization problem (which is what is most interesting for applications) might be hard to identify.
Finally, for more general singular terms, namely when \(|\nabla u|^2\) is replaced by a general function of the form \(h(x,\nabla u(x))\), we also expect the \(\Gamma \)-limit to capture microscopic, but not macroscopic, phase separation. The only difference would be in the formula for the computation of the limiting energy density of \(\widetilde{G}^1\): in our case, it is given by a one dimensional profile, while in the more general case, as it happens for the homogeneous case (see [17]), a more involved cell formula will be needed.
1.2 Outline of the Paper and Comments on the Proofs
The paper is divided in two parts: the first is devoted to the zeroth order \(\Gamma \)-limit, and the second to the first order expansion.
In the realm of solid-solid phase separation, the zeroth order \(\Gamma \)-limit is a well-studied problem. Francfort and Müller [19] have studied this problem in a similar framework, which was later extended by Shu [28] to many regimes including dimension reduction. The strategy for the proof of the zeroth order \(\Gamma \)-limit \(G^0\) we use here is, in most aspects, similar to previous work, though in the limsup inequality we employ an argument based on two-scale convergence and measurable selections. The study of the minimization problem carried out in Corollary 4.4 allows to identify the general structure of minimizers of \(G^0\), which are of the form
for some \(\mu \in L^2\left( \Omega ; L^\infty (Q;[0,1]) \right) \). In particular, the minimum of the zeroth order asymptotic energy is zero.
Next step is to identify a class of minimizers we are interested in, and hopefully to characterize such a class by the rate of convergence to zero of the energy of a recovery sequence. Our focus will be on the class of functions that describe a geometric microstructure. Namely, those for which, for almost every \(x\in \Omega \), the function \(y\mapsto \mu (x,y)\) is a function of bounded variation taking values in \(\{0,1\}\). By some heuristic computations addressed at the beginning of Sect. 5, we get that for a function u of this form, the energy of a optimal recovery sequence is of the order \(\varepsilon /\delta \). Therefore, to study the behaviour of the energy \(G_{\varepsilon ,\delta }\), we multiply it by \(\delta /\varepsilon \), and unfold it using the two-scale unfolding operator. We study the \(\Gamma \)-limit of the rescaled functional which, up to a negligible error, can be written as
Note that the nature of the limiting functional \(G^1\) is clear from (1.4). Compactness for sequences of uniformly bounded energy (see Lemma 5.12) follows from an application of the Chacon biting lemma (see [16, Lemma 2.63]) together with Vitali Convergence Theorem. The proofs of the first order \(\Gamma \)-limit (see Theorem 5.8) improve the results of [10] to get the inner functional \(\widetilde{G}^1\), namely that relate to the phase separation in Q. Since in this paper we work with more general assumptions, the results of [10] cannot be directly applied, and a uniform bound on the Euclidean length of a family of geodesic problems has to be proved. Section 5.4.1 is entirely devoted to the proof of such bound. In particular, the result of Sect. 5.4.1 can also be applied to the functional studied in [10] (phase separation without homogenization) but with the potential satisfying the weaker assumptions considered in here. With these theorems at our disposal, which gives the liminf inequality for the internal energy, the liminf inequality for the whole functional follows by using Fatou’s lemma (see Proposition 5.13). The proof of the limsup inequality (see Proposition 5.23) is based on an approximation argument. First, we consider the case where the limiting function \(u\in L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\) is piecewise constant in the first variable, namely, when
where \(\Omega _1,\dots ,\Omega _m\) is a polyhedral partition of \(\Omega \), and the functions of bounded variation \(u_i\)’s take values on the wells. It is possible to identify each of such \(u_i\)’s with a set of finite perimeter \(A_i\subset Q\), by setting \(A_i:=\{u_i=a\}\). In this case, the recovery sequences for each of the microstructures \(u_i\) provided by [10] are glued together in such a way that the transition between them has an asymptotically negligible energy (see Fig. 1). In order to obtain a recovery sequence for a general function \(u\in L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\), we use a density argument. This requires to being able to construct, for each \(\varepsilon >0\), a function v of the form (1.5) such that
In order to get the second inequality, as it is well known in the Calculus of Variations, the partition \(\Omega _1,\dots ,\Omega _m\) cannot be imposed a priori, but it has to be determined by the function u itself. In particular, for measurability reasons, we need to have at our disposal a countable family \({\mathcal {C}}=\{C_i\}_{i\in {\mathbb {N}}}\) of sets of finite perimeter in Q such that
for some \(j\in {\mathbb {N}}\), where we naturally see the functional \(\widetilde{G}^1\) as a geometric functional. The family \({\mathcal {C}}\) is constructed in Lemma 5.25.
The first order \(\Gamma \) expansion can also be considered with respect to the weak-\(L^2\) topology (see Corollary 5.9). Moreover, the proofs we present are stable for the addition of a mass constraint to the functional (see Corollary 5.10). Finally, the minimization problem for the functional \(G^1\) is investigated in Corollary 5.11.
2 Preliminaries
2.1 Two-Scale Convergence and Unfolding
Two-scale convergence is a powerful tool, first introduced by Nguetseng [26] and developed further in [1]. Later, it was separately established by Visintin [31, 32] and Cioransecu, Damlamian, and Griso [7] to be equivalent to a topology on the product space via the use of an ’unfolding’ operator. We present here some definitions and basic results obtained in the above references, which we will use in the sequel.
We begin with the classical definitions of weak and strong two-scale convergence.
Definition 2.1
We say that \(\{u_\delta \}_{\delta >0}\subset L^2(\Omega ;{\mathbb {R}}^M)\) weakly two-scale converge to v in \(L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\), and we write \(u_\delta \overset{2-s}{\rightharpoonup }v\), if
for every \(\varphi \in L^{2}(\Omega ;C_\textrm{per}(Q;{\mathbb {R}}^M))\). Here \(C_\textrm{per}(Q;{\mathbb {R}}^M)\) is the space of periodic continuous functions on \({\mathbb {R}}^N\) with period Q.
Two-scale convergence encodes more information than classical weak-\(L^2\) convergence. This property is highlighted in the following compactness result.
Proposition 2.2
Let \(\{u_\delta \}_{\delta >0} \subset L^2(\Omega ;{\mathbb {R}}^M)\) be bounded. Then, there exists \(v\in L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\) such that, up to the extraction of a (not relabeled) subsequence, \(u_\delta \overset{2-s}{\rightharpoonup }v\). Additionally,
weakly in \(L^2(\Omega ;{\mathbb {R}}^M)\).
Now we recall the unfolding operator, with a definition that is tailored to the use that we will make of this tool.
Definition 2.3
For \(\delta >0\), let
where \(I_\delta \) is the set of points \(z_i\in \delta {\mathbb {Z}}^N\) such that \(\overline{z_i+\delta Q}\subset \Omega \). The unfolding operator \(T_{\delta }:L^2(\Omega ;{\mathbb {R}}^M)\rightarrow L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\) is defined as
where, given an enumeration \(\{z_i\}_{i\in {\mathbb {N}}}\) of \({\mathbb {Z}}^N\),
is the integer part of \(x\in {\mathbb {R}}^N\), and \(a:\Omega \rightarrow {\mathbb {R}}^M\) is the function given in (W3) in Sect. 4.
Remark 2.4
This definition of the unfolding operator is nonstandard as we make the unfolding operator nonzero in the small boundary set \(\Lambda _\delta \times Q\). While this prevents our definition of the unfolding operator from being linear, it still preserves the main compactness property (see Theorem 2.5), and allows us to simplify some algebraic arguments.
Theorem 2.5
Given \(\{u_\delta \}_{\delta >0} \subset L^2(\Omega ;{\mathbb {R}}^M)\) and \(v\in L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\), the following conditions are equivalent:
-
(i)
\(u_\delta \overset{2-s}{\rightharpoonup }v\quad \text {weakly two scale in } L^2(\Omega ;L^2(Q;{\mathbb {R}}^M)),\)
-
(ii)
\(T_{\delta }u_\delta \rightharpoonup v\) weakly in \(L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\).
Finally, we use the unfolding operator to define a variant of two-scale convergence that will be useful in proving our results.
Definition 2.6
A sequence \(\{u_\delta \}_{\delta >0} \subset L^1(\Omega ;{\mathbb {R}}^M)\) is said to converge strongly two-scale in \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\) to \(u \in L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\) if \(T_\delta u_\delta \rightarrow u\) strongly in \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\).
2.2 Measurable Selection
Here, we recall the measurable selection theorem tailored to our usage that will be needed for the construction of the recovery sequences. For a further reference, see [16, Sect. 6.1].
Definition 2.7
A multifunction \({\mathcal {F}}: \Omega \rightarrow 2^Y{\setminus } \{\emptyset \}\), where Y is a topological space, is said to be Lebesgue measurable if for every closed set \(S \subset Y\) the set
belongs to the Lebesgue \(\sigma -\)algebra on \(\Omega \).
The next result ensures the existence of a measurable selection (see [16, Theorem 6.10]).
Theorem 2.8
Let Y be a complete separable metric space, and consider a Lebesgue measurable multifunction \({\mathcal {F}}: \Omega \rightarrow 2^Y{\setminus } \{\emptyset \}\) be with values on a closed subsets of Y. Then there exists a sequence of Lebesgue measurable selections for \(u_n: \Omega \rightarrow Y\), \(n \in {\mathbb {N}}\), such that \(\{u_n(x)\}_{n}\) is dense in \({\mathcal {F}}(x)\) for every \(x \in \Omega \).
2.3 Sets of Finite Perimeter
We recall the definition and some well known facts about sets of finite perimeter. For more details, we refer the reader to [2, 15, 23].
Definition 2.9
Let \(E\subset {\mathbb {R}}^M\) with \(|E|<\infty \), and let \(A\subset {\mathbb {R}}^M\) be an open set. We say that E has finite perimeter in A if
Remark 2.10
A set \(E\subset {\mathbb {R}}^M\) is a set of finite perimeter in A if and only if \(\chi _E\in BV(A)\), i.e., the distributional derivative \(D\chi _E\) is a finite vector valued Radon measure in A, with
for all \(\varphi \in C^1_c(A;{\mathbb {R}}^M)\), and \(|D\chi _E|(A)=P(E;A)\). In particular, the outer regularity property of Radon measures, allows us to define the perimeter of a set \(E\subset {\mathbb {R}}^M\) in a Borel set \(D\subset {\mathbb {R}}^M\) as
Definition 2.11
Let \(E\subset {\mathbb {R}}^M\) be a set of finite perimeter in the open set \(A\subset {\mathbb {R}}^M\). We define \(\partial ^* E\), the reduced boundary of E, as the set of points \(x\in {\mathbb {R}}^M\) for which the limit
exists and is such that \(|\nu _E(x)|=1\). The vector \(\nu _E(x)\) is called the measure theoretic exterior normal to E at x.
We now recall the De Giorgi’s structure theorem for sets of finite perimeter.
Theorem 2.12
Let \(E\subset {\mathbb {R}}^M\) be a set of finite perimeter in the open set \(A\subset {\mathbb {R}}^M\). Then
-
(i)
for all \(x\in \partial ^* E\) the set \(E_r:= \frac{E-x}{r}\) converges locally in \(L^1({\mathbb {R}}^M)\) as \(r\rightarrow 0\) to the halfspace orthogonal to \(\nu _E(x)\) and not containing \(\nu _E(x)\);
-
(ii)
 ;
; -
(iii)
the reduced boundary \(\partial ^* E\) is \({\mathcal {H}}^{N-1}\)-rectifiable, i.e., there exist Lipschitz functions \(f_i:{\mathbb {R}}^{M-1}\rightarrow {\mathbb {R}}^M\), \(i\in {\mathbb {N}}\), such that
$$\begin{aligned} \partial ^* E=\bigcup _{i=1}^\infty f_i(K_i), \end{aligned}$$where each \(K_i\subset {\mathbb {R}}^{M-1}\) is a compact set.
We now recall a strong approximation result by Gromard (see [13], and also [12]).
Theorem 2.13
Let \(A\subset {\mathbb {R}}^M\) be an open set, and let \(E\subset A\) be a set of finite perimeter in A. Then, for each \(\varepsilon >0\) there exist a set \(F\subset A\) of finite perimeter in A, and a compact set \(C\subset A\) such that
-
(i)
\(\partial F\cap A\) is contained in a finite union of \(C^1\) hypersurfaces;
-
(ii)
\(\Vert {\mathbb {1}}_{E} - {\mathbb {1}}_{F} \Vert _{BV(A)}<\varepsilon \);
-
(iii)
\({\mathcal {H}}^{N-1}(\partial F\cap A\setminus \partial ^* E)<\varepsilon \);
-
(iv)
\(F\subset E+B(0,\varepsilon )\), and \(D\setminus F\subset (A\setminus E)+B(0,\varepsilon )\);
-
(v)
\(C \subset A\cap \partial ^* E \cap \partial F\);
-
(vi)
\(\nu _E(x) = \nu _F(x)\) for all \(x\in C\);
-
(vii)
\(|D{\mathbb {1}}_E|(D\setminus C)<\varepsilon \).
3 Assumptions
Let \(\Omega \subset {\mathbb {R}}^N\) be a bounded open set, and \(N, M \ge 1\). Let \(Q:= (-1/2,1/2)^N\) be the unit cube in \({\mathbb {R}}^N\), and write \({\mathcal {L}}^N\)-a.e. point \(x\in \Omega \) as
where \(y\in Q\), and \(\lfloor x \rfloor \) is the integer part of \(x\in {\mathbb {R}}^N\), defined in (2.2). Consider measurable functions \(W:\Omega \times {\mathbb {R}}^M\rightarrow [0,+\infty )\) and \(a,b:\Omega \rightarrow {\mathbb {R}}^M\), and pairwise disjoint open sets \(E_1,\dots ,E_k\subset Q\) with piecewise affine boundary and with
such that the following assumptions are satisfied:
-
(W1)
For all \(p\in {\mathbb {R}}^M\), the function \(x\mapsto W(x,p)\) is Q-periodic;
-
(W2)
For \({\mathcal {L}}^N\)-a.e. \(x\in \Omega \), by using the writing in (3.1), it holds
$$\begin{aligned} W(x,p) = \sum _{i=1}^k \chi _{E_i}(y) W_i(y,p), \end{aligned}$$where, for each \(i \in \{1, \dots , k\}\), the function \(W_i:\overline{E_i}\times {\mathbb {R}}^M\rightarrow [0,\infty )\) is locally Lipschitz continuous;
-
(W3)
For \({\mathcal {L}}^N\)-a.e. \(x\in \Omega \), it holds
$$\begin{aligned} a(x) = \sum _{i=1}^k \chi _{E_i}(y) a_i(y),\quad \quad \quad b(x) = \sum _{i=1}^k \chi _{E_i}(y) b_i(y), \end{aligned}$$where, for each \(i\in \{1,\dots ,k\}\), the functions \(a_i, b_i:\overline{E_i}\rightarrow {\mathbb {R}}^M\) are Lipschitz continuous. Moreover, for \({\mathcal {L}}^N\)-a.e. \(x\in \Omega \), it holds
$$\begin{aligned} W(x,p)=0\quad \text { if and only if }\quad p\in \{a(x), b(x) \}; \end{aligned}$$ -
(W4)
For every \(i\in \{1,\dots ,m\}\), and for \({\mathcal {L}}^N\)-a.e. \(y_0\in \overline{E_i}\setminus \{a_i=b_i\}\), there exist \(\mu >0\), \(R >0\), \(c_1 > 0\), such that, for all \(y\in B(y_0,\mu )\),
$$\begin{aligned} \frac{1}{c_1} |p-a_i(y)|^2\le W_i(y,p) \le c_1 |p-a_i(y)|^2, \end{aligned}$$if \(|p-a_i(y)|\le R\), and
$$\begin{aligned} \frac{1}{c_1} |p-b_i(y)|^2\le W_i(y,p) \le c_1 |p-b_i(y)|^2, \end{aligned}$$if \(|p-b_i(y)| \le R\);
-
(W5)
There exists \(c_2>0\) such that, for \({\mathcal {L}}^N\)-a.e. \(x\in \Omega \),
$$\begin{aligned} W(x,p)\ge \frac{1}{c_2}|p|^2, \end{aligned}$$if \(|p|\ge c_2 \), and
$$\begin{aligned} W(x,p)\le c_2(1+|p|^2), \end{aligned}$$for every \(p\in {\mathbb {R}}^M\).
We would like to make several comments on the assumptions made.
Remark 3.1
(Axes of periodicity) The periodicity of the potential W and of the wells a and b are meant to model a situation of a periodic medium, while the dependence on x of all of the above functions allow to consider more general physical settings, like an inhomogeneous one. The choice of asking for periodicity with respect to the principal axes is not restrictive: our results hold also in the case of periodicity with respect to any basis of \({\mathbb {R}}^N\).
Remark 3.2
(Discontinuities of the wells) The possible discontinuities of the potential W and on the wells a and b make the model suitable for studying material inclusion. Our framework includes the assumptions used in the work by Braides and Zeppieri [5], where \(W:{\mathbb {R}}\times {\mathbb {R}}\rightarrow [0,\infty )\) is given by
with \(\widetilde{W}(t):= \min \{ (t-1)^2, (t+1)^2 \}\), and thus the wells are
Finally, note that there is no loss of generality in assuming that the partition \(E_1,\dots ,E_k\) is the same for all of the functions, and that we are also including the case where the previous functions are continuous along \(\partial E_i\cap \partial E_j\).
Remark 3.3
(Assumptions on the wells) We note that in the work [10] of the first author and Gravina, a stronger condition than (W2) was assumed, i.e, that the potential W is exactly quadratic near the well. This restriction is relaxed in here, by asking only for quadratic bounds. Moreover, here we also allow wells to merge; namely, we do not impose them to be well separated.
Remark 3.4
(On the sets \(E_i\)’s) Assuming that the sets \(E_i\)’s to have piecewise affine boundaries is just for reader’s convenience. Indeed, the only technical point where we use this assumption is in the construction of the recovery sequence for the first order \(\Gamma \)-limit (see Proposition 5.27). In particular, the piecewise affine regularity of the \(\partial E_i\)’s allows us to apply directly the limsup inequality proved in [10]. For a partition with piecewise \(C^1\) boundaries, a careful adaptation of the argument used to prove [10, Proposition 4.3], should give the result also in that case. Finally, if the boundaries are only Lipschitz continuous, then a Lusin type approximation with piecewise \(C^1\) sets will allow to conclude.
Remark 3.5
(Growth at infinity of the potential) Finally, the quadratic growth of W can be generalized to any q-growth for \(q>1\). If only the results for mass-constrained functional is of interest, then the growth can also be linear, as proved in [22]. In all of these cases, the results will hold with the space \(L^2\) substituted by the space \(L^q\).
Remark 3.6
(Lower bound on the potential) Using assumptions (W2), (W3), (W4), and (W5), it is possible to show that, for every \( r >0\), there exists \(C_r>0\) such that
Remark 3.7
(Extension to multiple wells) Finally, we note that the choice of having two wells a and b is only for notational convenience. A similar result holds if any number of wells satisfying the above assumptions is considered.
We are now in position to define the sequence of functionals that will be studied in this paper.
Definition 3.8
Let \(\{\varepsilon _n\}_{n}, \{\delta _n\}_{n}\) be infinitesimal sequences such that
For \(n\in {\mathbb {N}}\), define the functional \(G_n: L^2(\Omega ;{\mathbb {R}}^M)\rightarrow [0,+\infty ]\) as
Remark 3.9
The choice of writing the functionals by using sequences instead of using the notation \(G_{\varepsilon ,\delta }\) is purely based on convenience, because when proving a \(\Gamma \)-convergence result, we would have had to fix some \(\{\varepsilon _n\}_n, \{\delta _n\}_n\). In particular, note that, as long as they satisfy the required rate of convergence, the choice of sequences do not affect the results we present. Furthermore, the two scale results hold even when considering the subsequences indexed in n.
4 Zeroth-Order \(\Gamma \)-Expansion
This section is devoted to proving the zeroth order \(\Gamma \)-expansion of the functionals \(G_n\) (see Definition 3.8). We start by introducing the limiting functional.
Definition 4.1
Define the functional \(G^0: L^2(\Omega ;{\mathbb {R}}^M)\rightarrow [0,+\infty ]\) as
where, for \(p \in {\mathbb {R}}^M\),
Here, for each \(y\in Q\), the function \(p\mapsto W^{**}(y,p)\) is the convex envelope of the function \(p\mapsto W(y,p)\).
Remark 4.2
By using the upper and lower bounds on W (see (W5)), it is easy to see that, for \(p\in {\mathbb {R}}^M\), the minimization problem defining \(W^{\textrm{hom}}(p)\) has a minimizer \(\phi \). To be precise, this occurs because W does not take the value \(+\infty \) and grows at least quadratically at infinity, which means we can find an affine function in the p-variable below W(y, p). In this scenario, it is classical that the bipolar \(W^{**}(y,\cdot )\), can be identified with the convex envelope of \(W(y,\cdot )\) and it is known that functionals with convex integrands are weakly lower semicontinuous (see [16, Propositions 6.31, 6.43, and Theorem 6.54]).
The main result of this section is the characterization of the zeroth order effective energy through \(\Gamma -\)convergence. A similar theorem has been proven before by Francfort and Müller [19] for the case of solid to solid phase separation where they consider the same energy, with \(u, \nabla u\) replaced by \(\nabla u, \nabla ^2 u\). While they use delicate approximation techniques to prove their result, we give an alternate proof through two-scale and measurable selection techniques to embody the spirit of this paper. In particular, techniques used in the proof will be later used when we will consider the first order \(\Gamma \)-limit.
Theorem 4.3
(0th-order \(\Gamma \)-convergence) Let \(\{\varepsilon _n\}_{n}, \{\delta _n\}_{n}\subset (0,1)\) be infinitesimal sequences such that
Let \(\{u_n\}_{n}\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) with
Then, up to a subsequence (not relabeled), \(u_n\rightharpoonup u\) in \(L^2(\Omega ;{\mathbb {R}}^M)\) for some \(u\in L^2(\Omega ;{\mathbb {R}}^M)\) with \(G^0(u)<\infty \). Moreover, \(G_n {\mathop {\rightarrow }\limits ^{\Gamma }} G^0\) with respect to the weak-\(L^2\) convergence.
Proof of Theorem 4.3
Part 1: Compactness.
Consider a sequence \(\{u_n\}_{n}\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) with
The lower bound (W5) ensures pre-compactness in the weak-\(L^2(\Omega ;{\mathbb {R}}^M)\) topology. The fact that any cluster point has finite \(G^0\) energy will follow from next step.
Part 2: Liminf inequality. Let \(\{u_n\}_n \in W^{1,2}(\Omega ;{\mathbb {R}}^M)\) be such that \(u_n \rightharpoonup u\) in \(L^2(\Omega ;{\mathbb {R}}^M)\). Since \(\{u_n\}_n\) is bounded in \(L^2\), Proposition 2.2, we may find a function \(u \in L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\) such that
Assume that \(\underset{n \rightarrow \infty }{\liminf }\;G_n(u_n) < + \infty \), as otherwise the inequality is satisfied trivially. Firstly, we drop the gradient term, and rewrite the energy using the unfolding operator to obtain
Note in the last equality we have used the fact that \(W^{**}(y,a(y)) = 0\). By Theorem 2.5 and the definition of two-scale convergence, we know that \(T_{\delta _n}u_n \rightharpoonup u(x,y) = u(x) + v(x,y)\) for some \(v \in L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\) with \(\int _Q v(x,y) \hbox {d}y = 0\). Now the desired inequality comes directly from Remark 4.2, using the fact that the bipolar is convex and thus is weakly lower semicontinuous. We conclude that
Part 3: Limsup inequality. We divide the argument in several steps.
Step 1. Firstly, we note that it suffices to show the limsup inequality for \(u \in C^\infty _c(\Omega ; {\mathbb {R}}^M)\).
Indeed, for \(u \in L^2(\Omega ; {\mathbb {R}}^M)\) we can find by density a sequence \(\{u_j\}\subset C^\infty _c(\Omega ; {\mathbb {R}}^M)\) such that \(u_j \rightarrow u\) strongly in \(L^2\). Furthermore, using the fact that the \(\Gamma \)-limsup is lower semicontinuous [11, Proposition 6.8] with respect to weak-\(L^2\), and that \(G^0\) is upper-semicontinuous with respect to strong \(L^2\) convergence, we have
for all \(u\in L^2(\Omega ;{\mathbb {R}}^M)\).
Step 2. For \(u \in C^\infty _c(\Omega ; {\mathbb {R}}^M)\) and \(\varphi \in C^{\infty }_c(\Omega ;C^{\infty }_{\textrm{per}}(Q;{\mathbb {R}}^M))\) with
define
Then, we have that
where in the last step we used that
Applying the unfolding operator to this functional and noting that
we obtain
Thanks to the equiboundedness of \(u_n^\varphi (x)\), the boundary term vanishes in the limit. Furthermore, using the convergences \(T_{\delta _n}u \rightarrow u\) and \(T_{\delta _n}\varphi _n \rightarrow \varphi \) strongly in \(L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\), we conclude that
By taking an infimum over all admissible \(\varphi \), we can see that
where
Step 3. We claim that
where \(W^{**}\) is the convexification of W with respect to the second variable.
Consider the functional \(H:L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\rightarrow [0,\infty ]\) defined as
where \(g(x,y,v):= W(y,u(x)+v(x,y))\).
Then, by definition and density, it is possible to see that
Since it is not clear that H has minima, we relax the functional H. A standard relaxation theorem (see [16, Theorem 6.68]), together with the fact that the constraint is continuous, yields
where \(g^{**}\) is the convexification of g with respect to the last variable. A direct computation shows that
for all \(x\in \Omega \), \(y\in Q\), and \(p\in {\mathbb {R}}^M\). This, together with (4.2), and the fact that H is coercive in \(L^2\) (thanks to (W5)), proves (4.1).
Step 4. In order to finish the proof of the recovery sequence, we will show that \(\hat{G}^0(u) = G^0(u)\).
It is easy to see that \(\hat{G}^0(u) \ge G^0(u)\). Next, we will show the other inequality.
Note that by Remark 4.2, for every \(x \in \Omega \), we can find minimizers \(\varphi ^x\) such that:
We use Theorem 2.8 in order to extract a measurable selection. By coercivity of \(W^{**}\) and since \(\Vert u\Vert _\infty <+\infty \), there exists \(R_0>0\) such that any minimizer \(\varphi ^x\) must be contained in the closed ball \(B:= \overline{B(0,R_0)} \subset L^2(Q;{\mathbb {R}}^M)\). We consider \(Y:= B\) equipped with the weak topology, which is metrizable since \(L^2(Q;{\mathbb {R}}^M)\) is reflexive. In particular, it is separable and complete as well, and so satisfies the conditions in Theorem 2.8. Define the multifunction
As noted before, this is nonempty for every \(x \in \Omega \).
Furthermore, we claim that for every \(x \in \Omega \), \({\mathcal {F}}(x)\) is a closed subset of Y under the weak topology. Indeed, we just need to show it is sequentially closed, so take \(\{\varphi _n\}_n\subset {\mathcal {F}}(x)\) and suppose \(\varphi _n \rightharpoonup \varphi \). Note that the zero average condition passes to the limit, and by sequential weak lower semicontinuity of the integrand, we have
and we conclude that \(\varphi \in {\mathcal {F}}(x)\). The last condition needed to be checked in order to apply Theorem 2.8 is that the multifunction is Lebesgue measurable. Take S which is closed in Y under the weak topology. We will show that \({\mathcal {F}}^-(S)\), as given in Definition 2.7, is also closed. Again it suffices to check sequential closure, so we take \(\{x_n\}_n \subset {\mathcal {F}}^-(S)\) such that \(x_n \rightarrow x\) in \(\Omega \). By definition of \({\mathcal {F}}^-(S)\), we can find for each \(x_n\) a corresponding \(\varphi _n \in {\mathcal {F}}(x_n) \cap S\). The sequence \(\{\varphi _n\}_n\) is uniformly bounded in \(L^2(Q;{\mathbb {R}}^M)\) by definition of Y, and so we can find a weakly converging subsequence to some limit \(\varphi \). Furthermore, as S is closed with respect to weak convergence, we must have \(\varphi \in S\) and the zero average condition is preserved. We pass to that subsequence in both \(\{x_n\}_n\) and \(\{\varphi _n\}_n\), without relabeling. As \(x_n \rightarrow x\) in the sense of \({\mathbb {R}}^N\), by continuity of u we have \(u(x_n)\rightarrow u(x)\). Once again, we can apply the sequential weak lower semicontinuity of the integrand and the upper semicontinuity of \(W^{\textrm{hom}}\), to get
Thus, all inequalities are actually equalities and we have by definition, \(\varphi \in {\mathcal {F}}(x) \cap S\). This means that \(x \in {\mathcal {F}}^-(S)\), and the set is closed. Since the set is closed, it is a Borel set, which is contained in the Lebesgue \(\sigma -\)algebra. This proves that the multifunction is Lebesgue measurable, and so we have checked all the hypotheses of Theorem 2.8. This allows us to find a measurable function \(v: \Omega \rightarrow Y\) such that \(v(x) \in {\mathcal {F}}(x)\). Furthermore, since \(v(x) \in Y\), we have that \(\Vert v(x)\Vert _{L^2(Q;{\mathbb {R}}^M)} \le R_0\). In particular, as \(\Omega \) is a bounded set in \({\mathbb {R}}^N\), we have that
Therefore, we have that \(v \in L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\) and by definition of \({\mathcal {F}}(x)\), we have \(\int _Q{v(x,y)\hbox {d}y} = 0\). Thus, v is an admissible competitor for the infimum in \(\hat{G}^0(u)\). We deduce that
and this concludes the proof. \(\quad \square \)
It is also possible to get the explicit value of the minimum of the limiting functional \(G^0\), as well as a characterization of the set of its minimizers.
Corollary 4.4
(Minimizers of \(G^0\)) It holds that
Furthermore, \(u\in L^2(\Omega ;{\mathbb {R}}^M)\) is such that \(G^0(u)=0\) if and only if
where \(\mu \in L^2(\Omega ;L^\infty (Q;[0,1]))\). Namely, for a.e. \(x\in \Omega \), \(u(x)\in K\), where
and such selection of elements of K is measurable.
Proof
Step 1: Minima of Convex Envelope.
Note that \(W^{**}(y, p+ \phi (y))=0\) if and only if
for some \(f(y)\in [0,1]\). This is due to the fact that W is only zero at a, b which is the minimum (see (W3)).
Step 2: Sufficiency. First, suppose
for some \(\mu \in L^2(\Omega ;L^\infty (Q;[0,1]))\). Consider
Note that \(\phi ^x \in L^2(Q;{\mathbb {R}}^M)\) with \(\int _Q \phi ^x(y) \,\hbox {d}y = 0\). Thus, it is admissible competitor in the minimization problem defining \(W^{\textrm{hom}}\). Furthermore, using convexity, we can deduce that
where in the last inequality we used the fact that, for every \(y\in Q\),
Since \(W\ge 0\) and, in turn, \(W^{\textrm{hom}}\ge 0\), we conclude that \(W^{\textrm{hom}}(u(x)) = 0\) for \({\mathcal {L}}^N\)-a.e. \(x \in \Omega \). Thus, we obtain \(G^0(u) = 0\).
Step 3: Necessity. Let \(u\in L^2(\Omega ;{\mathbb {R}}^M)\) be such that \(G^0(u) = 0\). In the proof of the limsup inequality above, we showed that by a measurable selection, we can find \(\varphi \in L^2(\Omega ;L^2(Q;{\mathbb {R}}^M))\) such that \(\int _Q{\varphi (x,y)\hbox {d}y} = 0\) and
In particular, for \({\mathcal {L}}^N\)-a.e. \(y\in Q\) and \({\mathcal {L}}^N\)-a.e. \(x\in \Omega \), we must have that \(W^{**}(y, u(x)+ \varphi (x,y)) = 0\). Since a, b, and \(\varphi \) are measurable, we can find \(\mu \in L^2(\Omega ;L^\infty (Q;[0,1]))\) such that
Integrating (4.4) in Q and using the fact that \(\varphi \) has zero average, we get (4.3). \(\square \)
Finally, as it is well-known in the general context of this work, adding a mass constraint to the problem does not require to change significantly the proof of Theorem 4.3.
Definition 4.5
Let \(\overline{m}\in {\mathbb {R}}^M\). For \(n\in {\mathbb {N}}\), define \({\mathcal {G}}_n: L^2(\Omega ;{\mathbb {R}}^M)\rightarrow [0,+\infty ]\) as
and \({\mathcal {G}}^0: L^2(\Omega ;{\mathbb {R}}^M)\rightarrow [0,+\infty ]\) as
The analogous of Theorem 4.3 and of Corollary 4.4 hold also for the mass constrained functional. The small changes needed in the proof are classical, and therefore we will not report them here (see, e.g., [10, 18]).
Theorem 4.6
Fix \(\overline{m}\in {\mathbb {R}}^M\). Let \(\{u_n\}_n\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) be such that
Then, up to a subsequence (not relabeled), \(u_n\rightharpoonup u\) in weak-\(L^2(\Omega ;{\mathbb {R}}^M)\) for some \(u\in L^2(\Omega ;{\mathbb {R}}^M)\) with \({\mathcal {G}}^0(u;\overline{m})<\infty \). Moreover, \({\mathcal {G}}_n(\cdot ;\overline{m}) {\mathop {\rightarrow }\limits ^{\Gamma }} {\mathcal {G}}^0(\cdot ;\overline{m})\) with respect to the weak-\(L^2\) convergence. Finally,
and \(u\in L^2(\Omega ;{\mathbb {R}}^M)\) is such that \({\mathcal {G}}^0(u;\overline{m})=0\) if and only if
where \(\mu \in L^2(\Omega \times Q;[0,1)])\) with \(\int _\Omega u\,\textrm{d}x = \overline{m}\).
5 First-Order \(\Gamma \)-Expansion
In view of Corollary 4.4, we know that minimizers of \(G^0\) are of the form
for some \(\mu \in L^2\left( \Omega ; L^\infty (Q;[0,1]) \right) \). We would like to study the behaviour of the sequence of functionals \(G_n\) close to the subclass \({\mathcal {R}}\) of functions u as in (5.1) such that
where, for a.e. \(x\in \Omega \), the set \(A(x)\subset Q\) has finite perimeter. The class \({\mathcal {R}}\) corresponds to geometric microstructures, and we will see that this is the only class for which equipartition of surface energy holds. We proceed as follows: in next section we identify the proper scaling \(\omega (\varepsilon )\) of the energy by using heuristic arguments, while rigorous arguments will be employed in the following sections to prove the \(\Gamma \)-expansion result.
5.1 Heuristics for the Scaling Analysis
Let \(u_0\in L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\), and let \(\{u_n\}_n\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) be such that \(u_n\overset{2-s}{\rightharpoonup }u_0\). By using a change of variable, and neglecting the contribution of cells that intersect \(\partial \Omega \), we have that
We will focus on the behaviour of the energy in each cube. Fix \(x\in \Omega \), \(n\in {\mathbb {N}}\), and consider the function \(\widetilde{u}_n:Q\rightarrow {\mathbb {R}}^M\) defined as \(\widetilde{u}_n(x,y):= T_{\delta _n}u_n(x,y)\). It holds \(\widetilde{u}_n\rightharpoonup u_0(x,\cdot )\).
We first assume that \(u_0(x,y)\in \{a(y), b(y)\}\) almost everywhere, and identify the scaling \(\omega _n\) of (5.3) in each cube. Then we show that, if for a generic \(u_0\in L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\) and \(\{u_n\}_n\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) with \(u_n\overset{2-s}{\rightharpoonup }u_0\) the sequence \(\{G_n(u_n)\}_n\) behaves like the scaling \(\omega _n\), then the limiting function \(u_0\) must be such that \(u_0(x,y)\in \{a(y), b(y)\}\) almost everywhere.
Let \(\mu _n>0\), to be chosen later, and subdivide the cube Q into smaller cubes \(\mu _n Q\). In each of these little cubes we perform the construction detailed in Fig. 2. Namely, for \(\gamma _n, \eta _n>0\) with
the function \(\tilde{u}_n(y)\) is either a(y) or b(y) in most of the cube, with \(\eta _n\) being the thickness of the interface between a and b, and \(\gamma _n\) being the thickness of the cut-off region. Both are needed to ensure that \(u_n(y) \in W^{1,2}(Q;{\mathbb {R}}^M)\).
We now evaluate the order of the energy of such a configuration. We have
where the terms in the square parenthesis correspond to the energy of the purple region, the green region, and the blue region respectively.
In the case \(u_0(x,y)\in \{a(y), b(y)\}\) almost everywhere, we have that \(\mu _n\) must be of order 1. Moreover, it is possible to see that for each choice of vanishing sequences \(\{\eta _n\}_n,\{\gamma _n\}_n\), the first term is always of higher order than the last two. In particular, there is no rescaling that allows to see that energy contribution (the bulk energy). On the other hand, it is possible to make the last two terms of the same order if and only if \(\eta _n=\gamma _n=\frac{\varepsilon _n}{\delta _n}\). Therefore, we guess that \(\omega _n=\frac{\varepsilon _n}{\delta _n}\).
We now show that this scaling identifies functions \(u_0\in {\mathcal {R}}\). Dividing (5.5) by \(\frac{\varepsilon _n}{\delta _n}\) we get
which is finite as \(\varepsilon _n\rightarrow 0\) if and only if \(\mu _n\) is of order 1 and \(\gamma _n=\eta _n=\frac{\varepsilon _n}{\delta _n}\).
This is the heuristic reason to choose the scaling \(\omega _n=\frac{\varepsilon _n}{\delta _n}\): it is expected to give equipartition of the surface energies and to select minimizers of \(u_0\) of the form (5.2). We will rigorously prove in the next sections that indeed, this is the correct scaling.
5.2 The Limiting Functional
Motivated by the heuristics of the previous section, we introduce the new family of functionals.
Definition 5.1
For \(n\in {\mathbb {N}}\), the functional \(G^1_n: L^1(\Omega ;{\mathbb {R}}^M)\rightarrow [0,+\infty ]\) as
Remark 5.2
In the following, it is convenient to write the functional \(G^1_n\) by using the undfolding operator. For \(n\in {\mathbb {N}}\), define the functional \(\widetilde{G}_n: L^1(Q;{\mathbb {R}}^M)\rightarrow [0,\infty )\) as
and note that it is possible to write
where, recalling (2.1), we set
In particular, we can see \(G^1_n\) as a functional defined on \(L^1(\Omega ; L^1(Q;{\mathbb {R}}^M))\) as follows:
there
These representations will be useful throughout the rest of the paper.
We now introduce the interfacial energy density of the limiting functional. It is convenient to introduce the function \(\chi :{\mathbb {R}}^M\rightarrow \{1,\dots ,k\}\) defined as \(\chi (y):= i\) if \(y\in E_i\). Note that \(\chi \in SBV({\mathbb {R}}^M)\) and its jump set \(J_\chi \) corresponds to points \(y\in {\mathbb {R}}^M\) such that there exist only two indexes \(i\ne j\) with \(y\in \partial E_i\cap \partial E_j\). It can be identified as \(S_\chi {\setminus } J_\chi \), where \(S_\chi \) is the set of singular points of \(\chi \).
Definition 5.3
For \(p,q,z_0\in {\mathbb {R}}^M\), consider the class
Define \(\textrm{d}_{\textrm{W}}: \left[ \, J_\chi \cup \left( \overline{Q}{\setminus } S_\chi \right) \,\right] \times {\mathbb {R}}^M\times {\mathbb {R}}^M \rightarrow [0, \infty )\) as
if \(\chi ^-(y)=i\) and \(\chi ^+(y)=j\), where the infimum is taken over points \(z_0\in {\mathbb {R}}^M\), and over curves \(\gamma \in {\mathcal {A}}(p,q,z_0)\).
Remark 5.4
Note that in the case \(\chi ^-(y)=\chi ^+(y)\), we have that
where the infimum is taken over curves \(\gamma \in W^{1,1}([-1,1]; {\mathbb {R}}^M)\) such that \(\gamma (-1) = p\), and \(\gamma (1) = q\).
In the case \(\chi ^-(y)\ne \chi ^+(y)\) we cannot impose a priori the point \(v_0\in {\mathbb {R}}^M\) where the profile will pass through at time \(t=0\), and therefore we need to infimize also over that parameter.
Definition 5.5
Let
where \(Q_0:= Q\setminus \{x\in Q: a(x)=b(x)\}\), and define the class
where \(\widetilde{v}:{\mathbb {R}}^N\rightarrow {\mathbb {R}}^M\) denotes the Q-periodic extension of \(v\in L^1(Q;{\mathbb {R}}^M)\).
We are now in position to define the limiting functional.
Definition 5.6
Let \(G^1:L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\rightarrow [0,+\infty ]\) be defined as
where, for a function \(v\in L^1({\mathbb {R}}^N;{\mathbb {R}}^M)\), we set
and \(\widetilde{Q}:= [-\frac{1}{2},\frac{1}{2})^N\).
Remark 5.7
Note that the energy \(G^1\) is well defined. Indeed, for \(u\in {\mathcal {R}}\), by using the measurability of \(x\mapsto \widetilde{u}(x,\cdot )\), it is easy to see that the function \(x\mapsto \widetilde{G}^1(\widetilde{u}(x,\cdot ))\) is measurable. Moreover, the jump set \(J_v\) of a measurable function \(v:{\mathbb {R}}^M\rightarrow {\mathbb {R}}\) is \({\mathcal {H}}^{M-1}\)-rectifiable (see [14]). Finally, as noted in [10, Remark 1.8], there are functions \(v\in L^1({\mathbb {R}}^N;{\mathbb {R}}^M)\) for which \(\widetilde{G}^1(v)<\infty \), but \(v\not \in \textrm{BV}({\mathbb {R}}^N;{\mathbb {R}}^M)\).
The main result of this section is the following:
Theorem 5.8
Let \(\{\varepsilon _n\}_{n}, \{\delta _n\}_{n}\subset (0,1)\) be infinitesimal sequences such that
If \(\{u_n\}_{n}\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) is such that
then there exists \(u\in {\mathcal {R}}\) with \(G^1(u)<\infty \) such that, up to a subsequence (not relabeled), \(u_n\overset{2-s}{\rightarrow }u\) strongly in \(L^1(\Omega ; L^1(Q;{\mathbb {R}}^M))\). Moreover,
with respect to strong two-scale convergence in \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\).
The result of Theorem 5.8 is written in the language of two-scale convergence. Using it we can also write the \(\Gamma \)-convergence result with respect to the weak \(L^2\) convergence without reference to the microscopic variable y.
Corollary 5.9
Let \(\{\varepsilon _n\}_{n}, \{\delta _n\}_{n}\subset (0,1)\) be infinitesimal sequences such that
Then
with respect to the weak \(L^2(\Omega ;{\mathbb {R}}^M)\) convergence. Here
where
Moreover, if \(\{u_n\}_{n}\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) is such that
then there exists \(u\in {\mathcal {R}}\) with \(H^1(u)<\infty \) such that, up to a subsequence (not relabeled), \(u_n\rightharpoonup u\) weakly in \(L^2(\Omega ; {\mathbb {R}}^M)\).
Moreover, as for the case of the zeroth order \(\Gamma \)-limit, the mass constraint passes to the limit. Namely, the following holds:
Corollary 5.10
Let \(\{\varepsilon _n\}_{n}, \{\delta _n\}_{n}\subset (0,1)\) be infinitesimal sequences such that
Fix \(\overline{m}\in {\mathbb {R}}^M\), and define
Then it holds that \({\mathcal {G}}^1_n {\mathop {\rightarrow }\limits ^{\Gamma }} {\mathcal {G}}^1\) with respect to the strong two-scale convergence in \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\), where
A similar result holds, with the obvious modifications, for the functionals considered in Corollary 5.9.
Finally, we study the minimization problem for the limiting functional, with and without mass constraint. The proofs follow easily from the definition of the functionals, and by using a measurable selection result like that used in step 1 of the proof of Theorem 4.3.
Corollary 5.11
It holds that
if and only if the Q-periodic extension of the whole \({\mathbb {R}}^N\) of the functions a and b are continuous. Fix \(\overline{m}\in {\mathbb {R}}^M\). Then
if and only if the Q-periodic extension of the whole \({\mathbb {R}}^N\) of the functions a and b are continuous, and there exists \(u\in {\mathcal {R}}\) with \(\int _\Omega \int _Q u\, \textrm{d}y\,\textrm{d}x = \overline{m}\).
5.3 Compactness
This section is devoted to the proof of compactness, that we state separately.
Lemma 5.12
Let \(\{u_n\}_n\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) be such that
Then, up to a subsequence (not relabeled), \(u_n\rightarrow u\) strongly two scale in \(L^1(\Omega ; L^1(Q;{\mathbb {R}}^M))\) for some \(u\in {\mathcal {R}}\) with \(G^1(u)<\infty \).
Proof
For the sake of notation, we will write \(\hat{u}_n\) in place of \(T_{\delta _n}u_n\).
Step 1. Recalling Remark 5.2, we can write
where
Note that the right-hand side of the above inequality tends to zero as \(n\rightarrow \infty \). Thus, from (5.6) we get that
for some \(C<\infty \).
Step 2. We claim that if is possible to find a subsequence \(\{u_{n_j}\}_{j\in {\mathbb {N}}}\) such that, for \({\mathcal {L}}^N\)-a.e. \(x\in \Omega \), it holds that
For each \(n\in {\mathbb {N}}\) define the function \(f_n:\Omega \rightarrow [0,+\infty ]\) by
Then, by assumption, since \(W\ge 0\), we have \(\sup _n\Vert f_n\Vert _{L^1(\Omega )}<+\infty \). By the Chacon biting lemma (see [16, Lemma 2.63]), we have the following. There exists a subsequence \(\{f_{n_k}\}_{k\in {\mathbb {N}}}\), and a sequence \(\{r_{n_k}\}_{k\in {\mathbb {N}}}\subset (0,+\infty )\) with \(\lim _{k\rightarrow \infty } r_{n_k}=+\infty \) such that, setting
we have \(|F_j|\rightarrow 0\) as \(j\rightarrow \infty \). Set
Since it is possible to write
and \(\{F_j\}_{j\in {\mathbb {N}}}\) is a decreasing sequence of sets contained in \(\Omega \), we obtain that \(|F|=0\).
Step 3. Let \(x\in \Omega \setminus F\). Considering a sequence of compact sets \(\{K_i\}_i\) invading \(Q\setminus Q_0\) (where \(Q_0\) is defined in Definition 5.5), using (5.7), and [10, Proposition 4.1] (see also the proof of Theorem 1.9 in [10]) we can extract a subsequence \(\{u_{n_k}(x,\cdot )\}_{k\in {\mathbb {N}}}\) (possibly depending on \(x\in \Omega \setminus F\)), and find a function \(v_x\in L^1(Q;{\mathbb {R}}^M)\) such that
-
(i)
\(v_x(y)\in \{a(y), b(y)\}\) for a.e. \(y\in Q\);
-
(ii)
\(\hat{u}_{n_k}(x,\cdot )\rightarrow v_x\) strongly in \(L^1(Q;{\mathbb {R}}^M)\) as \(k\rightarrow \infty \);
-
(iii)
\(v_x\in BV_{loc}(Q\setminus Q_0;{\mathbb {R}}^M)\);
-
(iv)
\(\widetilde{G}^1(v_x)<\infty \).
We want to prove that the subsequence does not depend on the point \(x\in \Omega \setminus F\). Note that (5.6) implies that
and thus Theorem 4.3 gives the existence of a subsequence \(\{u_{n_j}\}_{j}\) and of a function \(\widetilde{u}\in L^2(\Omega ;{\mathbb {R}}^M)\) such that \(u_{n_j}\rightharpoonup \widetilde{u}\) in \(L^2(\Omega ;{\mathbb {R}}^M)\). In particular, since
by applying Proposition 2.2, we get that there exists a (not relabeled) subsequence such that \(u_{n_j}\rightharpoonup u\) weakly two-scale in \(L^2(\Omega ;L^2(\Omega ;{\mathbb {R}}^M))\), for some \(u\in L^2(\Omega ;L^2(\Omega ;{\mathbb {R}}^M))\). Therefore
for a.e. \(x\in \Omega \), and, by using (ii), it easy to see that \(\hat{u}_{n_j}(x,\cdot )\rightarrow u(x,\cdot )\) strongly in \(L^1(Q;{\mathbb {R}}^M)\) for all \(x\in \Omega \setminus F\).
Finally, we claim that \(u_{n_j}\rightarrow u\) strongly two scale in \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\). Define, for each \(j\in {\mathbb {N}}\), \(g_j:\Omega \rightarrow [0,\infty )\) as
Then from (5.8) we get
Using De la Valée Poussin criteria, we have that \(\{g_j\}_{j}\) is equiintegrabile. Furthermore, by (ii), we get that \(g_j \rightarrow 0\) pointwise almost everywhere. We can now apply Vitali Convergence Theorem to conclude that \(g_j\rightarrow 0\) in \(L^p(\Omega )\) strong for any \(p\in [1,2)\). This concludes the proof of the compactness result. \(\square \)
5.4 Liminf Inequality
The main result of this section is the following:
Proposition 5.13
Let \(u\in L^1(\Omega ; L^1(Q;{\mathbb {R}}^M))\) and let \(\{u_n\}_{n}\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) with \(u_n\rightarrow u\) strongly two scale in \(L^1(\Omega ; L^1(Q;{\mathbb {R}}^M))\). Then
The proof of Proposition 5.13 is based on the liminf inequality for a single periodicity cell Q. In the language of this paper, it writes as follows:
Proposition 5.14
Let \(v\in L^1(Q;{\mathbb {R}}^M)\) such that \(v(y)\in \{a(y), b(y) \}\) for a.e. \(y\in Q\). Let \(\{v_n\}_n\subset W^{1,2}(Q;{\mathbb {R}}^M)\) with \(v_n\rightarrow v\) in \(L^1(Q;{\mathbb {R}}^M)\). Then
Remark 5.15
While this result is essentially the same as [10, Proposition 4.2], we cannot directly apply it due to our weaker assumptions on W. Thus, we need to use a slightly different strategy and additional technical lemmata in order to achieve the result. Indeed, Proposition 5.14 shows that the sharp interface result of [10] holds under more general hypotheses.
We decided to show how to get Proposition 5.13 once Proposition 5.14 is established, and then to move to the technical results needed to obtain this later.
Proof of Proposition 5.13
Let \(u\in L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\), and take \(\{u_n\}_n\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) such that \(u_n\rightarrow u\) strongly two-scale in \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\). Without loss of generality, we can assume that
otherwise there is nothing to prove. By the compactness result (see Lemma 5.12), we get that \(u\in {\mathcal {R}}\). Therefore, recalling the arguments in the proof of Lemma 5.12 we get that
where the previous to last step follows by the Fatou’s lemma, while last step is justified by the fact that \(T_{\delta _n}u_n(x,\cdot )\rightarrow u(x,\cdot )\) for a.e. \(x\in \Omega \), together with Proposition 5.14. This concludes the proof of the liminf inequality. \(\quad \square \)
5.4.1 Bound on the Euclidean Length of Geodesics
First, we prove a technical lemma on bounds of Euclidean length of geodesics necessary for the liminf inequality in Q. While the overall proof strategy is similar to that in [10] and [30], our construction by estimating the energy within each level set (see Step 2 of Lemma 5.22) is novel.
In this section, in order to make the notation lighter, we will make the following abuse of notation. Fix a vector \(\nu \in {\mathbb {S}}^{N-1}\), a point \(x_0\in Q\), and a unit square C centered at the origin and with two faces orthogonal to \(\nu \). For \(t>0\), we denote by \(Q'_t:= (x_0 + t C)\cap \nu ^\perp \). For \(y'\in Q'_t\) and \(z\in {\mathbb {R}}\), we denote point \(y'+z\nu \) by \((y',z)\). Note that the fact that some of the above points could be outside \(\Omega \) is of no concern for us, since all of the functions that we consider are Q periodic, and thus can be naturally extended from \(\Omega \) to the whole \({\mathbb {R}}^N\).
We are now in position to introduce the minimization problem that will be investigated in this section.
Definition 5.16
For \(p,q \in {\mathbb {R}}^M\), let
For \(\varepsilon >0\), \(y'\in Q'_\varepsilon \), and \(p, q\in {\mathbb {R}}^M\), define
where
The main result of this section is the following:
Theorem 5.17
Fix \(x_0\in Q\), \(\nu \in {\mathbb {S}}^{N-1}\), and \(\widetilde{R}>0\). If \(x_0\in \cup _{i=1}^k \partial E_i\), assume that it belongs to only one of those sets. Then there exist \(\varepsilon _1>0\) and \(L>0\) such that, given any \(\varepsilon \in (0,\varepsilon _1)\), \(y'\in Q'_\varepsilon \), and \(p,q\in B(0,\widetilde{R})\), the minimization problem defining \(H_\varepsilon (y',p,q)\) admits a solution \(\gamma \in {\mathcal {A}}(p,q)\) such that
The strategy to prove Theorem 5.17 is the following: first we consider the case where the point \(x_0\in Q{\setminus } \cup _{i=1}^k \partial E_i\). This means that \(W=W_i\) for some \(i\in \{1,\dots ,k\}\), and, in particular, it is Lipschitz in the second variable. Consider a minimizing sequence \(\{\gamma _j\}_{j\in {\mathbb {N}}}\subset {\mathcal {A}}(p,q)\) for the minimization problem defining \(H_\varepsilon (y',p,q)\). The first step is to investigate the behaviour of the sequence of curves, for \(\varepsilon \) sufficiently small, close by and far away from the wells. In particular, in Lemma 5.22 we prove that the portion of the curves \(\gamma _j\) that is sufficiently close to \(a(y',0)\) (or to \(b(y',0)\)) has uniformly bounded Euclidean length. Then, by using a lower bound on \(F_\varepsilon \) far from the wells, we conclude that also the Euclidean length of the sequence \(\{\gamma _j\}_{j\in {\mathbb {N}}}\) is uniformly bounded in that region. The proof of Theorem 5.17 then follows by using a standard argument based on the Ascoli–Arzelà Theorem ensuring the existence of minimizing geodesics for the minimization problem defining \(H_\varepsilon (y',p,q)\). We refer to (see [10, Lemma 3.1] for details. Finally, the case \(x_0\in \cup _{i=1}^k \partial E_i\) may be deduced from the previous case.
We start by collecting some basic properties of \(F_\varepsilon \), which can verified easily from the definition. In particular, for a proof of (3), we refer to [10, Proposition 3.2].
Proposition 5.18
(Properties of \(F_\varepsilon \)) The following holds:
-
(1)
The function \((y',p)\mapsto F_\varepsilon \) is Lipschitz;
-
(2)
We have \(F_\varepsilon (y',p) = 0\) if and only if \(p \in \{a(y',t),b(y',t)\}\) for some \(t \in [-\varepsilon ,\varepsilon ]\);
-
(3)
If there is a function \(g: S \rightarrow {\mathbb {R}}^M\) such that
$$\begin{aligned} W(y',y_n,p) = |p-g(y',y_n)|^2, \end{aligned}$$then \(F_\varepsilon (y',p) = \textrm{dist}(p,{\textrm{Gr}}_\varepsilon ^g(y'))\), where
$$\begin{aligned} {\textrm{Gr}}_\varepsilon ^g(y'):= \{g(y',t) :\; y'\in Q', \;|t|\le \varepsilon \}. \end{aligned}$$
Next, we state a useful property, based on the parameterization invariant characteristic of the minimization problem defining \(H_\varepsilon \)..
Proposition 5.19
Let \(p,q \in {\mathbb {R}}^M\), \(y' \in Q'_\varepsilon \), and \(\gamma \in {\mathcal {A}}(p,q)\) such that
for some \(j\in {\mathbb {N}}\). Then
for all \([t_1,t_2] \subset [-1,1]\).
The main idea in the proof of the bound of the Euclidean length close by the wells is to consider level sets of \(F(y',\gamma (\cdot ))\) in the construction of a competitor for the minimization problem defining \(H_\varepsilon (y',p,q)\).
Definition 5.20
For \(\varepsilon >0\), \(y' \in Q'_\varepsilon \), \(p,q\in {\mathbb {R}}^M\), and \(\gamma \in {\mathcal {A}}(p,q)\), and \(k\in {\mathbb {N}}{\setminus }\{0\}\), we define
Remark 5.21
Note that by continuity of \(F_\varepsilon \), we have that
Now we are ready to prove the key technical lemma of this section.
Lemma 5.22
Let \(x_0\in Q\setminus \cup _{i=1}^k \partial E_i\) and \(\nu \in {\mathbb {S}}^{N-1}\). Then there exist \(r_0>0\), \(\varepsilon _0 > 0\), and \(L_1>0\), such that, for any \(0<\varepsilon < \varepsilon _0\), \(y' \in Q'_\varepsilon \), \(p,q \in B_{r_0}(y'):= B_{r_0}(a(y',0))\), the following property holds: letting \(\{\gamma _j\}_j \subset {\mathcal {A}}(p,q)\) be a minimizing sequence for the minimization problem defining \(H_\varepsilon (y',p,q)\),
where \(T_j:= \{t\in [-1,1] :\, \gamma _j(t)\in B_{r_0}(y') \}\). The same result holds with \(B_{r_0}(y'):= B_{r_0}(b(y',0))\).
Proof
Let \(R>0\) be as in (W4). We define
where \(\textrm{Lip}(a)\) denotes the maximum over the index i of the Lipschitz constant of \(a_i\) in \(E_i\). Moreover, by using the uniform lower bound on \(W(x,\cdot )\) close to the wells, it is possible to choose \(r_0>0\) so small such that
for all \(\varepsilon \in (0,\varepsilon _0)\) and all \(y'\in Q'_\varepsilon \). Up to further decreasing the value of \(r_0\), we can also suppose that \(r_0\le R/2\).
Case 1. Assume that \(H_\varepsilon (y',p,q)=0\). Note that this happens if and only if \(p,q\in Z_\varepsilon := \{ a(y',t): t\in [-1,1] \}\). In this case, the solution to the minimization problem defining \(H(y', p, q)\) is given by the curve lying in \(Z_\varepsilon \) joining the two points. By using the Lipschitz regularity of a, we get that its Euclidean length is less than \(2\textrm{Lip}(a)\varepsilon _0\).
Case 2. Assume that \(H_\varepsilon (y',p,q)>0\). Without loss of generality, we can assume that
for all \(j\in {\mathbb {N}}\).
Step 1: Bounds on \(F_\varepsilon \). We claim that if \(\varepsilon \in (0,\varepsilon _0)\) and \(r\in (0,r_0)\), for all \(y'\in Q'_\varepsilon \) and \(z \in B_r(y')\) it holds that
Indeed, by the triangle inequality and Lipschitz regularity of a, we get, for \(p \in B_{r_0}(y')\),
This inequality gives that \(B_{r_0}(y') \subset T_{R}({\textrm{Gr}}_\varepsilon ^a(y'))\), and the desired inequality follows by applying Property 2 in Proposition 5.18.
From (5.10), we easily have the bound \(F_\varepsilon (y',z)\le \sqrt{c_1}R\) for \(z \in B_{r_0}(y')\).
Step 2: Bounding the energy in a level set. Fix \(j, k\in {\mathbb {N}}{\setminus }\{0\}\). Without loss of generality, we will suppose that
Furthermore, to ease notation, we will set
We want to get a uniform bound on the Euclidean length of the curves \(\gamma _j\)’s in the set \(T_\varepsilon (y')\). Let
and
Using the definition of \(L_\varepsilon (y')\) and the choice of \(t_1,t_2\), we get the following simple lower bound on the energy:
We employ the geometric property of \(H_\varepsilon \) given in Proposition 5.19 and (5.10) to deduce that for any \(\gamma \in {\mathcal {A}}(p_1,p_2)\), we have the bound
In order to further bound from above the right-hand side of the above expression, we will construct a suitable competitor \(\tilde{\gamma }\in {\mathcal {A}}(p_1,p_2)\). First, note that there exist \(z_1, z_2 \in {\textrm{Gr}}_\varepsilon ^a(y')\) such that
We define \(\tilde{\gamma }\in {\mathcal {A}}(p_1, p_2)\) as the union of the following three curves (see Fig. 3):
-
(1)
The segment between \(p_1\) and \(z_1\);
-
(2)
The portion of \({\textrm{Gr}}_\varepsilon ^a(y')\) that connects the points \(z_1\) and \(z_2\);
-
(3)
The segment between \(z_2\), and \(p_2\).
Note that, since the energy is parameterization invariant, we do not have to specify the precise parametrization of \(\tilde{\gamma }\). We now estimate the energy of \(\tilde{\gamma }\). Again, by the parametrization invariant property of the functional, we can use \(\pm 1\) as initial and final time respectively for each of the three curves. Note only the two segments contributes to the energy of the curve, and by a direct evaluation, we get that
where the previous to last inequality follows from (5.10), while last step is justified by the fact that, since \(p_1, p_2 \in \gamma _j(\overline{T_\varepsilon (y')})\), it holds that
Thus, combining (5.11), (5.12), and (5.13), we get
which yields the upper bound, for all \(j\in {\mathbb {N}}\),
Step 3: Bounding the Euclidean length. We have that
where last step follows from (5.14) and the estimate obtained in case 1. Note that the right-hand side is independent of \(\varepsilon , y'\), and thus we achieve the desired result. \(\quad \square \)
Now we are ready to prove the main result of this section.
Proof of Theorem 5.17
Fix \(x_0\in Q\), \(\nu \in {\mathbb {S}}^{N-1}\), \(\widetilde{R}>0\). Take \(p,q\in B(0,\widetilde{R})\).
Case 1 Assume \(x_0\in Q{\setminus } \cup _{i=1}^k \partial E_i\).
Step 1: Choice of \(\varepsilon _1\). Let \(r_0, \varepsilon _0\) be given by Lemma 5.22. Define
Note that for every \(z \notin \overline{B_{r_1}(b(y',0))} \cup \overline{B_{r_1}(a(y',0))}\) and for every \(|t|\le \varepsilon <\varepsilon _1\) we have
Fix \(0<\varepsilon <\varepsilon _1\) and \(y'\in Q'_\varepsilon \).
Step 2: Estimate of the Euclidean length. Let \(\{\gamma _j\}_j\subset {\mathcal {A}}(p,q)\) be a sequence satisfying (5.9). We will bound the Euclidean length of each \(\gamma _j\) in each of the following regions separately:
and
We start with the last region. By (5.16) and (5.17), together with Remark 3.6, we get that there is \(C_\frac{r_0}{2}>0\) such that
Therefore
where
and the previous to last step follows by considering as a competitor the segment joining p and q.
We now bound the Euclidean length in the regions \({\mathcal {R}}^1_j\) and \({\mathcal {R}}^2_j\). By using Proposition 5.19, together with Lemma 5.22, we obtain that
where the constant \(L_1<\infty \) depends only on \(x_0\) and \(\nu \).
Step 3: Existence of a geodesic. Using (5.18) and (5.19), there exists \(L>0\) depending only on \(\widetilde{R}, x_0\), and \(\nu \), such that
for all \(j\in {\mathbb {N}}\). A standard argument based on the Ascoli–Arzelà Theorem (see [10, Lemma 3.1] for more details) yields the desired result.
Case 2. Assume that \(x_0\in \partial E_i{\setminus } \cup _{j\ne i}\partial E_j\), and that \(\chi ^-(y)=i\), \(\chi ^+(y)=j\). It is easy to see that there exist \(S>0\), depending only on \(\widetilde{R}, x_0\), and \(\nu \) such that, for every \(0<\varepsilon <\varepsilon _1\) and \(y'\in Q'_{\varepsilon }\) it is possible to find \(z_0\in B(0,S)\) and curves \(\gamma _i, \gamma _j\in W^{1,1}([-1,1];{\mathbb {R}}^M)\), with
such that (recall that the functional is invariant by reparametrization)
where
Thus, by applying case 1 to \(\gamma _i\) and \(\gamma _j\), and \(S>0\), we also conclude this case. \(\square \)
We are now in position to prove the liminf inequality in Q. Since the strategy follows a similar argument to that of [10, Proposition 4.2], we will sketch the main ingredients of the proof, focusing on the points where the two arguments differ.
Proof of Proposition 5.14
Let \(\{v_n\}_n\subset W^{1,2}(Q;{\mathbb {R}}^M)\) with \(v_n\rightarrow v\) in \(L^1(Q)\). Without loss of generality, we can assume that
Note that, thanks to assumption (W4), we can use the compactness argument in [10, Proposition 4.1, and Theorem 1.9] to get that \(v\in \widetilde{{\mathcal {R}}}\) with \(\widetilde{G}^1(v)<\infty \). Fix \(x_0\in J_v\cap K\), where \(K\subset Q_0\) is a compact set. The idea is to use a blow-up argument, as in the proof of [10, Proposition 4.2]. Note that, thanks to the continuity of the wells \(a_i\)’s and \(b_i\)’s, together with the fact that the blow up is a local argument, and thanks to assumption (W4), we can use of the estimate on the Euclidean length of solutions to the minimization problem defining \(\textrm{d}_{\textrm{W}}\) provided by Theorem 5.17. The only difference with the argument used in the proof of [10, Proposition 4.2] is in step 2, where the functional \(F_m\) (see equation (100) in [10]) is defined here as
where \(g_m(t):= r_m t\nu \), for some \(\nu \in {\mathbb {S}}^{N-1}\) and \(r_m \rightarrow 0\) as chosen in [10]. Using Theorem 5.17, we obtain that the Euclidean length of the solutions to the geodesic problem
where the infimum is taken over \(\gamma \in W^{1,1}([-1,1];{\mathbb {R}}^M)\) with \(\gamma (-1)=p\) and \(\gamma (1)=q\), are uniformly bounded with respect to \(r_m\) and \(x'\). We now have all the elements that allow us to conclude by following the same strategy. \(\quad \square \)
5.5 Limsup Inequality
This section is devoted to the construction of the recovery sequence.
Proposition 5.23
Let \(u\in L^1(\Omega ; L^1(Q;{\mathbb {R}}^M))\). Then there exists a sequence \(\{u_n\}_n\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) with \(u_n\rightarrow u\) strongly two scale in \(L^1(\Omega ; L^1(Q;{\mathbb {R}}^M))\) such that \(G_n(u_n)\rightarrow G^1(u)\) as \(n\rightarrow \infty \).
The construction of the recovery sequence will be done in three steps: first for the class of simple functions in \({\mathcal {B}}\) (see Definition 5.26), then, in the second step, using a density argument based on the approximation result Lemma 5.25 to conclude in the general case of a jump set defining a Caccioppoli partition of Q, while in the last step follows from the density result of Caccioppoli partitions obtained in [10, Lemma 5.3]. As usually happens, given a general \(u\in L^2(\Omega ; BV(Q;\{a,b\}))\), we cannot choose the sequence of piecewise constant functions that approximate it both in configuration and in energy. Instead, we need to construct it based on the function u itself to dictate such piecewise approximation. This requires to have at our disposal a countable family \({\mathcal {C}}\) of sets of finite perimeter in Q that are dense both in \(L^1\) and also in energy.
The goal of Lemma 5.25 is to construct such a countable family \({\mathcal {C}}\). Note that we have to pay extra care in the construction of the recovery sequence, since the zeros \(a, b:Q\rightarrow {\mathbb {R}}^M\) might be discontinuous on \(\cup _{i=1}^k \partial E_i\). Indeed, given \(A\subset Q\) of finite perimeter, in order to approximate A both in configuration and in energy we also need the approximating sequence \(\{A_n\}_n\subset {\mathcal {C}}\) to be such that
The countable family we choose to obtain the approximation is the following:
Definition 5.24
Let \({\mathcal {C}}\) be the family of open sets \(G\subset Q\) such that there exist \(\nu _1,\dots ,\nu _m\in {\mathbb {S}}^{N-1}\cap {\mathbb {Q}}^M\), and \(q_1,\dots ,q_m\in {\mathbb {Q}}^M\), for which
for some \(m\in {\mathbb {N}}\).
In the rest of the paper it will be convenient to adopt the following abuse of notation. Given a set \(A\subset Q\) with finite perimeter in Q, we will write \(\widetilde{G}^1(A)\) in place of \(\widetilde{G}^1(\widetilde{v_A})\), where \(\widetilde{v}:Q\rightarrow {\mathbb {R}}^M\) is defined as
Note that, using the fact that A has finite perimeter, we have that \(\widetilde{v_A}\in \widetilde{{\mathcal {R}}}\) (see Definition 5.5).
We are now in position to prove the first technical result.
Lemma 5.25
For every \(\lambda >0\) and every set of finite perimeter \(A\subset Q\), there exists \(E\in {\mathcal {C}}\) such that
Proof
Step 1. Without loss of generality, we can assume that
Indeed, we can find \(v\in {\mathbb {R}}^M\) such that the above condition is satisfied by the sets \(A+v\) and \(E_i +v\) in place of A and \(E_i\) respectively. We then consider the sets \(E_i+v\), \(A+v\), and use the energy \(\widetilde{G}_1^v\) defined as
where \(\widetilde{W}(y):= W(y-v)\).
Step 2. Fix \(\widetilde{\lambda }>0\), that will be chosen later. Let \(F\subset Q\) be the set of finite perimeter given by Theorem 2.13 relative to A and \(\widetilde{\lambda }\). In particular,
and, using (iii), (v), and (vii) of Theorem 2.13, we obtain
for some constant \(C_1>0\) depending only on the wells a and b.
Step 3. We now approximate the set F with a set \(G\in {\mathcal {C}}\). Note that if the wells a and b were continuous, then the proof would be easier, since every piecewise-\(C^1\) set in Q can be approximated in the Hausdorff metric with a polyhedral set and, every polyhedral set in Q can be approximated by a set in \({\mathcal {C}}\). Due to the fact that the boundary of the approximated has to coincide as much as possible with the boundary of F on \(\cup _{i=1}^k \partial E_i\), the construction requires a more delicate argument.
First, we isolate the singularities of \(\cup _{i=1}^k \partial E_i\) as follows. It is possible to find \(S_1,\dots ,S_m\in {\mathcal {C}}\) with \(\partial F\) orthogonal to \(\partial S_i\) for each \(i=1,\dots ,m\), such that
and
Now we isolate the part of \(\partial F\) on \(\cup _{i=1}^k \partial E_i\). Set
Recalling that \(S_i\in {\mathcal {C}}\) for each \(i=1,\dots ,m\), and thus that each \(S_i\) is open, we get that K is compact. By the outer regularity of the \({\mathcal {H}}^{N-1}\) measure on \(\cup _{i=1}^m \partial E_i\), it is then possible to find \(R_1,\dots ,R_n\in {\mathcal {C}}\) with \(\partial F\) orthogonal to \(\partial R_i\) for each \(i=1,\dots ,n\) such that
and
and
Since K is compact, there exist smooth open set \(B\subset \cup _{i=1}^n R_i \) with \(K\subset B\). Without loss of generality, we can assume that \(R_i\cap K\ne \emptyset \) for all \(i\in \{1,\dots ,n\}\). Up to rearranging the order of the sets, we can assume that
if and only if \(i\in \{1,\dots , n_1\}\), for some \(n_1\le n\), where \(\widetilde{\partial } B\) is the relative boundary of B in \(\cup _{i=1}^k \partial E_i\). In particular, this means that
Thanks to (5.23), we have that
for some \(C>0\).
To conclude, Let \(T_1,\dots ,T_p\) be the connected components of
For each \(i=1,\dots ,p\), it is possible to find \(\mu _i>0\) such that the sets \(T_i + B(0,\mu _i)\) are pairwise disjoint. Consider the sets \(F_1,\dots ,F_p\), defined as
Find \(E_i,\dots ,E_p\in {\mathcal {C}}\) such that \(E_i\subset T_i +B(0,\mu _i)\), and define
Up to choosing \(\mu _1,\dots ,\mu _p>0\) and \(\widetilde{\lambda }>0\) sufficiently small, thanks to (5.22), (5.24), and (5.26), we get
for some \(C>0\). Thus, by using step 1 and by selecting \(\widetilde{\lambda }>\) sufficiently small, we conclude. \(\quad \square \)
We now introduce the class of piecewice constant functions for which we will construct the recovery sequence directly.
Definition 5.26
Denote by \({\mathcal {B}}\) the space of functions \(u\in L^2(\Omega ; L^1(Q;{\mathbb {R}}^M))\) such that
where, for each \(i=1,\dots ,m\), \(\partial \Omega _i\cap \Omega \) is a polyhedral set, and
for a set \(A(x)\subset Q\) with finite perimeter in Q.
We recall the main result that ensures the existence of a recovery sequence for a microstructure in the cube Q. The construction is based on [10, Theorem 1.9], with the additional complication of having to approximate the possible discontinuity of the wells on \(\partial E_i\cap \partial E_j\) for \(i\ne j\).
Proposition 5.27
Let \(v\in L^1(Q;{\mathbb {R}}^M)\) be such that \(v(y)\in \{a(y), b(y) \}\) for a.e. \(y\in Q\), and such that \(A:= \{v=a\}\) has finite perimeter in Q. Then there exists a sequence of Q-periodic functions \(\{v_n\}_n\subset W^{1,2}(Q;{\mathbb {R}}^M)\) with \(v_n\rightarrow v\) in \(L^1(Q;{\mathbb {R}}^M)\) such that
and \(\sup _n \Vert v_n\Vert _{L^\infty }<\infty \).
Remark 5.28
Note that we can apply the mentioned result thanks to Theorem 5.17. Moreover, the proof presented in [10, Theorem 1.9] has to be adapted in order to take care of the fact that here we consider the perimeter in Q seen as the periodic flat torus: this can be done as in step 1 of the proof of Lemma 5.25. Finally, considering zeros a, b with possible discontinuities is not an issue, since it is simply possible to consider the functions \(a_z,\dots ,a_k\) and \(b_1,\dots ,b_k\) as separate zeros (multiple wells).
We are now ready to prove that main result of this section.
Proof of Proposition 5.23
Without loss of generality, we can assume that \(G^1(u)<\infty \), otherwise there is nothing to prove.
Step 1. First assume \(u\in {\mathcal {B}}\). Write it as
where, for each \(i=1,\dots ,m\), the set \(\partial \Omega _i\cap \Omega \) is polyhedral, and
for a set \(A_i\in {\mathcal {C}}\). For each \(n\in {\mathbb {N}}\), consider a grid \(\{Q_j^n\}_{j=1}^{k_n}\) of disjoint cubes of the form
for some \(z_j\in \delta _n{\mathbb {Z}}^N\), such that \(Q^n_j\cap \Omega \ne \emptyset \). For each \(n\in {\mathbb {N}}\) and \(i=1,\dots ,m\), let
and set
Since \(\partial \Omega \) is regular, we have that
Moreover, define
for each \(i\in \{1,\dots , k_n \}\). Let
and, for each \(n\in {\mathbb {N}}\), let \(\varphi _n:\Omega \rightarrow [0,1]\) be such that
and satisfying
for some \(C>0\). We remark that it is possible to construct such a family of cut-off functions satisfying this last estimate because
whenever \(i\ne j\). For each \(i\in \{1,\dots , m\}\), let \(\{v^i_n\}_n\subset W^{1,2}(Q;{\mathbb {R}}^M)\) be the recovery sequence for the microstructure \(u_i\) provided by Proposition 5.27. Note that each \(v^i_n\) is Q-periodic, and that
Define, for \(n\in {\mathbb {N}}\), the function \(u_n\in W^{1,2}(\Omega ;{\mathbb {R}}^M)\) as
Then it is easy to see that \(u_n\overset{2-s}{\rightarrow }u\) in \(L^1(\Omega ;L^1(Q;{\mathbb {R}}^M))\). We now prove the convergence in energy. Set
and observe that
and that, thanks to (5.28),
Using (5.29) and (5.31), as \(n\rightarrow \infty \) we get
where, in the last step, the convergence of the first integral follows from (5.30), while for the last integral from the fact that a is Lipschitz, and \(\frac{\varepsilon _n}{\delta _n}\rightarrow 0\). Thus, by using a change of variable and the fact that \(\{v^i_n\}_n\), from (5.32) and (5.27), we get
This proves that \(\{u_n\}_n\) is a recovery sequence.
Step 2. We now consider \(u\in L^1(\Omega ;BV(Q;\{a,b\}))\). We will construct a recovery sequence by using a diagonal argument. To be precise, fixed \(\lambda >0\) we will construct a function \(v^\lambda \in {\mathcal {B}}\) with
for some constant \(C>0\) independent of \(\lambda \). Thanks to step 1, we can find a sequence \(\{v^\lambda _n\}_n\subset W^{1,2}(\Omega ;{\mathbb {R}}^M)\) with \(v^\lambda _n\rightarrow v^\lambda \) as \(n\rightarrow \infty \) such that
The conclusion will follow by using the estimates above together with the arbitrariness of \(\lambda \) and a diagonal argument.
We are now left with constructing the function \(v^\lambda \in {\mathcal {B}}\). Since \(G^1(u)<\infty \), it is possible to find \(\mu >0\) such that
whenever \(E\subset \Omega \) is a measurable set with \(|E|\le \mu \). Without loss of generality, we can assume \(\mu < \lambda \). Let \({\mathcal {C}}=\{ F_i \}_{i\in {\mathbb {N}}}\) be the countable family given by Lemma 5.25. The idea is to set the function \(v^n\in {\mathcal {B}}\) as
for some \(n_0\in {\mathbb {N}}\), where
The sets \(\Omega _1,\dots \Omega _{i_n}\) will be defined in several steps. For \(i\in {\mathbb {N}}\), let
where \(A(x):= \{ y\in Q :\, u(x,y)=a(y) \}\), and we set \(\widetilde{\Omega }_{-1}:= \emptyset \). Note that the sets \(\widetilde{\Omega }_i\) are measurable, pairwise disjoint, and, thanks to Lemma 5.25, we also get that
Let \(n_0\in {\mathbb {N}}\) be such that
Let
We claim that it is possible to construct a partition \(\Omega _1,\dots ,\Omega _{n_0+1}\) of polyhedral sets with
for all \(i=1,\dots ,n_0\), and such that
Indeed, since the sets \(\widetilde{\Omega }_i\) are measurable, by the inner and the outer regularity of the Lebesgue measure, for each \(i=1,\dots ,n_0\), there exist a compact set \(K_i \) and an open set \(A_i\) with \(K_i\subset \widetilde{\Omega }_i \subset A_i\) and
By using smooth approximation of the characteristic function of \(K_i\), we can find a polyhedral set \(\Omega _i\subset A_i\) satisfying (5.36). Starting from constructing \(\Omega _1\) and for each \(i=2,\dots ,n_0\), substracting the union of the previous polyhedral sets from \(\Omega _i\), we can assume that they are pairwise disjoint. Finally, we define
This partition of \(\Omega \) satisfies all of the required properties.
We now show that the desired estimates hold. First of all, we note that
where the previous to last inequality follows from (5.34) and (5.37), \(C>0\) is a constant depending only the wells a, b and on \(|\Omega |\), and we recall that in the last inequality we used the fact that we are assuming, without loss of generality, that \(\mu \le \lambda \). In a similar way, we have that
where the last inequality follows from (5.35), (5.36), and (5.37), together with the fact that \(\mu \le \lambda \). This provides the required function \(v^\lambda \).
Step 3. We conclude for the case of a general case of \(u\in {\mathcal {R}}\) by using step 2 together with [10, Lemma 5.3]. This concludes the proof of the proposition.
Data Availability Statement
Data sharing not applicable to this article, as no datasets were generated or analysed during the current study.
References
Allaire, G.: Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518, 1992
Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems, Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 2000
Ansini, N., Braides, A., Chiadò Piat, V.: Gradient theory of phase transitions in composite media. Proc. R. Soc. Edinb. Sect. A 133, 265–296, 2003
Bouchitte, G.: Singular perturbations of variational problems arising from a two-phase transition model. Appl. Math. Optim. 21, 289–314, 1990
Braides, A., Zeppieri, C.I.: Multiscale analysis of a prototypical model for the interaction between microstructure and surface energy. Interfaces Free Bound. 11, 61–118, 2009
Cherdantsev, M., Cherednichenko, K.: Two-scale \(\Gamma \)-convergence of integral functionals and its application to homogenisation of nonlinear high-contrast periodic composites. Arch. Ration. Mech. Anal. 204, 445–478, 2012
Cioranescu, D., Damlamian, A., Griso, G.: The periodic unfolding method in homogenization. SIAM J. Math. Anal. 40, 1585–1620, 2008
Cristoferi, R., Fonseca, I., Hagerty, A., Popovici, C.: A homogenization result in the gradient theory of phase transitions. Interfaces Free Bound. 21, 367–408, 2019
Cristoferi, R., Fonseca, I., Hagerty, A., Popovici, C.: Erratum to: A homogenization result in the gradient theory of phase transitions. Interfaces Free Bound. 22, 245–250, 2020
Cristoferi, R., Gravina, G.: Sharp interface limit of a multi-phase transitions model under nonisothermal conditions. Calc. Var. Partial Differ. Equ., 60. Article number 142, 2021
Dal Maso, G.: An Introduction to \(\Gamma \)-Convergence. Springer, Berlin, 1993
De Gromard, T.Q.: Approximation forte des ensembles dans \(BV(\Omega )\) par des ensembles à frontière \(C^1\). C. R. Acad. Sci. Paris 301, 261–264, 1985
De Gromard, T.Q.: Strong approximation of sets in \(BV(\Omega )\). Proc. R. Soc. Edinb Sect. A 138, 1291–312, 2008
Del Nin, G.: Rectifiability of the jump set of locally integrable functions. Ann. Sci. Norm. Super. Pisa Cl. Sci. 22, 1233–1240, 2021
Evans, L.C., Gariepy, R.F., Measure theory and fine properties of functions, Textbooks in Mathematics, , revised ed. CRC Press, Boca Raton, FL, 2015
Fonseca, I., Leoni, G.: Modern Methods in the Calculus of Variations: \(L^p\) Spaces. Springer Monographs in Mathematics, Springer, New York, 2007
Fonseca, I., Popovici, C.: Coupled singular perturbations for phase transitions. Asymptot. Anal. 44, 299–325, 2005
Fonseca, I., Tartar, L.: The gradient theory of phase transitions for systems with two potential wells. Proc. R. Soc. Edinb. Sect. A 111, 89–102, 1989
Francfort, G.A., Müller, S.: Combined effects of homogenization and singular perturbations in elasticity. J. Reine Angew. Math. 454, 1–35, 1994
Gurtin, M.E.: Some results and conjectures in the gradient theory of phase transitions. In: Metastability and Incompletely Posed Problems (Minneapolis, Minn., 1985), vol. 3 of IMA Vol. Math. Appl., Springer, New York, pp. 135–146, 1987
Kohn, R.V., Sternberg, P.: Local minimisers and singular perturbations. Proc. R. Soc. Edinb Sect. A 111, 69–84, 1989
Leoni, G.: A remark on the compactness for the Cahn-Hilliard functional. ESAIM Control Optim. Calc. Var. 20, 517–523, 2014
Maggi, F.: Sets of Finite Perimeter and Geometric Variational Problems, vol. 135 of Cambridge Studies in Advanced Mathematics, Cambridge University Press, Cambridge (2012). An Introduction to Geometric Measure Theory
Modica, L.: The gradient theory of phase transitions and the minimal interface criterion. Arch. Ration. Mech. Anal. 98, 1987
Modica, L., Mortola, S.: Un esempio di \(\Gamma \)-convergenza. Boll. Un. Mat. Ital. B 5(14), 285–299, 1977
Nguetseng, G.: A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20, 608–623, 1989
Sengupta, P., Baird, B., Holowka, D.: Lipid rafts, fluid/fluid phase separation, and their relevance to plasma membrane structure and function. Semin. Cell Dev. Biol. 18, 583–590, 2007
Shu, Y.: Heterogeneous thin films of martensitic materials. Arch. Ration. Mech. Anal. 153, 39–90, 2000
Silvius, J.R.: Fluorescence energy transfer reveals microdomain formation at physiological temperatures in lipid mixtures modeling the outer leaflet of the plasma membrane. Biophys. J . 85, 1034–1045, 2003
Sternberg, P.: The effect of a singular perturbation on nonconvex variational problems. Arch. Ration. Mech. Anal. 101, 209–260, 1988
Visintin, A.: Towards a two-scale calculus, ESAIM: control. Optim. Calc. Var. 12, 371–397, 2006
Visintin, A.: Two-scale convergence of some integral functionals. Calc. Var. Partial. Differ. Equ. 29, 239–265, 2007
Acknowledgements
The research of I.F. and L.G. was partially supported under grants NSF-DMS1411646 and NSF-DMS1906238.
Funding
Open Access funding provided by Carnegie Mellon University
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to this article.
Additional information
Communicated by A. Braides
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cristoferi, R., Fonseca, I. & Ganedi, L. Homogenization and Phase Separation with Space Dependent Wells: The Subcritical Case. Arch Rational Mech Anal 247, 94 (2023). https://doi.org/10.1007/s00205-023-01920-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-023-01920-6


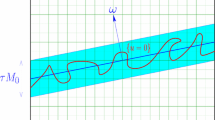


 ;
;
