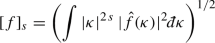Abstract
In this paper we consider the Cauchy problem for neo-Hookean incompressible elasticity in spatial dimension \(d \geqq 2\). The Cauchy problem can be formulated in terms of maps \(x(t,\cdot )\) with domain a reference space \({\mathbb {R}}^d_\xi \), and with values in space \({\mathbb {R}}^d_x\). Initial data consists of initial deformation \(\phi (\xi ) = x(0,\xi )\) and velocity \(\psi (\xi ) = \partial x(t,\xi )/\partial t |_{t=0}\). We consider the initial deformations of the form \(x(0, \xi ) = A \xi + \varphi (\xi )\), where A is a constant \(SL(d, {\mathbb {R}})\) matrix. We assume that \(\varphi \) and \(\psi \) are in Sobolev spaces \((\varphi , \psi ) \in H^{s+1}({\mathbb {R}}^d)\times H^{s}({\mathbb {R}}^d)\). If \(s>s_{crit}= d/2+1\), well-posedness is well-known. We are here interested primarily in the low regularity case, \(s \le s_{crit}\). For \(d = 2, 3\), we prove existence and uniqueness for \(s_0 < s\le s_{crit}\), and we can prove the well-posedness, but for a smaller range, \(s_1 < s \le s_{crit}\), where, if \(d = 2\), \(s_0 = 7/4\) and \(s_1 = 7/4 + (\sqrt{65}-7)/8\), and if \(d=3\), then \(s_0=2\) and \(s_1 = 1 + \sqrt{3/2}\). For the full range (in s) results, as indicated above, we need additional Hölder regularity assumptions on certain combinations of second order derivatives of \(\varphi \). A key observation in the proof is that the equations of evolution for the vorticities decompose into a first-order hyperbolic system, for which a Strichartz estimate holds, and a coupled transport system. This allows one to set up a bootstrap argument to prove local existence and uniqueness. Continuous dependence on initial data is proved using an argument inspired by Bona and Smith, and Kato and Lai, with a modification based on new estimates for Riesz potentials. The results of this paper should be compared to what is known for the ideal fluid equations, where, as shown by Bourgain and Li, the requirement \(s > s_{crit}\) is necessary.
Similar content being viewed by others
Change history
11 April 2023
A Correction to this paper has been published: https://doi.org/10.1007/s00205-023-01873-w
Notes
We use lower case latin indices a, b, c for Lagrangean coordinates, and \(i,j,k,\dots \) for Eulerian coordinates. In the summation the repeated indices run from 1 to d.
There is a huge literature on global existence for small initial data, but here we concentrate on low regularity.
References
Beale, J.T., Kato, T., Majda, A.: Remarks on the breakdown of smooth solutions for the \(3\)-D Euler equations. Comm. Math. Phys. 94(1), 61–66, 1984
Bergh, J., Löfström, J.: Interpolation Spaces. An Introduction. Grundlehren der Mathematischen Wissenschaften, No. 223. Springer, Berlin, 1976
Bona, J.L., Smith, R.: The initial-value problem for the Korteweg–de Vries equation. Philos. Trans. R. Soc. Lond. Ser. A 278(1287), 555–601, 1975
Bourgain, J., Li, D.: On an endpoint Kato–Ponce inequality. Differ. Integr. Equ. 27(11–12), 1037–1072, 2014
Bourgain, J., Li, D.: Strong ill-posedness of the incompressible Euler equation in borderline Sobolev spaces. Invent. Math. 201(1), 97–157, 2015
Bourgain, J., Li, D.: Strong illposedness of the incompressible Euler equation in integer \(C^m\) spaces. Geom. Funct. Anal. 25(1), 1–86, 2015
Brezis, H., Mironescu, P.: Gagliardo–Nirenberg inequalities and non-inequalities: the full story. Ann. Inst. H. Poincaré Anal. Non Linéaire 35(5), 1355–1376, 2018
Christ, F.M., Weinstein, M.I.: Dispersion of small amplitude solutions of the generalized Korteweg–de Vries equation. J. Funct. Anal. 100(1), 87–109, 1991
Ebin, D.G., Saxton, R.A.: The initial value problem for elastodynamics of incompressible bodies. Arch. Rational Mech. Anal. 94(1), 15–38, 1986
Fefferman, C.L., McCormick, D.S., Robinson, J.C., Rodrigo, J.L.: Higher order commutator estimates and local existence for the non-resistive MHD equations and related models. J. Funct. Anal. 267(4), 1035–1056, 2014
Gordon, W.B.: On the diffeomorphisms of Euclidean space. Am. Math. Mon. 79, 755–759, 1972
Grafakos, L.: Fractional differentiation: Leibniz meets Hölder. In Excursions in Harmonic Analysis, Vol. 5, Applied and Numerical Harmonic Analysis, pp. 17–33. Birkhäuser/Springer, Cham, 2017
Hanche-Olsen, H., Holden, H.: The Kolmogorov–Riesz compactness theorem. Expo. Math. 28(4), 385–394, 2010
Hörmander, L.: Lectures on Nonlinear Hyperbolic Differential Equations, volume 26 of Mathématiques & Applications (Berlin) [Mathematics & Applications]. Springer, Berlin, 1997
Hörmander, L.: The Analysis of Linear Partial Differential Operators. III. Classics in Mathematics. Springer, Berlin, 2007. Pseudo-differential operators, Reprint of the 1994 edition
Kapitanskiĭ, L.V.: Estimates for norms in Besov and Lizorkin–Triebel spaces for solutions of second-order linear hyperbolic equations. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI), 171(Kraev. Zadachi Mat. Fiz. i Smezh. Voprosy Teor. Funktsiĭ. 20):106–162, 185–186 (1989)
Kapitanskiĭ, L.V.: Some generalizations of the Strichartz–Brenner inequality. Algebra i Analiz 1(3), 127–159, 1989
Kato, T., Lai, C.Y.: Nonlinear evolution equations and the Euler flow. J. Funct. Anal. 56(1), 15–28, 1984
Kato, T., Ponce, G.: Commutator estimates and the Euler and Navier–Stokes equations. Comm. Pure Appl. Math. 41(7), 891–907, 1988
Kubo, R.: Large elastic deformation of rubber. J. Phys. Soc. Jpn. 3, 312–317, 1948
Lagrange, J.L.: Analytical Mechanics, volume 191 of Boston Studies in the Philosophy of Science. Kluwer, Dordrecht, 1997. Translated from the 1811 French original, with an introduction and edited by Auguste Boissonnade and Vickor N. Vagliente, With a preface by Craig G. Fraser
Leray, J.: Sur le mouvement d’un liquide visqueux emplissant l’espace. Acta Math. 63(1), 193–248, 1934
Majda, A.J., Bertozzi, A.L.: Vorticity and Incompressible Flow, volume 27 of Cambridge Texts in Applied Mathematics. Cambridge University Press, Cambridge, 2002
Marsden, J.E., Hughes, T.J.R.: Mathematical Foundations of Elasticity. Dover, New York, 1994. Corrected reprint of the 1983 original
Meyer, Y.: The role of oscillations in some nonlinear problems. In: European Congress of Mathematics, Vol. I (Barcelona, 2000), volume 201 of Progress in Mathematics, pp. 75–99. Birkhäuser, Basel, 2001
Meyer, Y., Coifman, R.: Wavelets, volume 48 of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge, 1997. Calderón–Zygmund and multilinear operators, Translated from the 1990 and 1991 French originals by David Salinger
Moser, J.: A rapidly convergent iteration method and non-linear partial differential equations. I. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (3) 20, 265–315, 1966
Peetre, J.: New Thoughts on Besov Spaces. Mathematics Department, Duke University, Durham, 1976. Duke University Mathematics Series, No. 1
Rivlin, R.S.: Large elastic deformations of isotropic materials. I. Fundamental concepts. Philos. Trans. R. Soc. Lond. Ser. A 240, 459–490, 1948
Runst, T.: Mapping properties of nonlinear operators in spaces of Triebel–Lizorkin and Besov type. Anal. Math. 12(4), 313–346, 1986
Runst, T., Sickel, W.: Sobolev Spaces of Fractional Order, Nemytskij Operators, and Nonlinear Partial Differential Equations, volume 3 of De Gruyter Series in Nonlinear Analysis and Applications. Walter de Gruyter & Co., Berlin, 1996
Schochet, S.: The incompressible limit in nonlinear elasticity. Comm. Math. Phys. 102(2), 207–215, 1985
Sideris, T.C., Thomases, B.: Global existence for three-dimensional incompressible isotropic elastodynamics. Comm. Pure Appl. Math. 60(12), 1707–1730, 2007
Soudský, F., Molchanova, A., Roskovec, T.: Interpolation between Hölder and Lebesgue spaces with applications. J. Math. Anal. Appl. 466(1), 160–168, 2018
Taylor, M.E.: Tools for PDE, volume 81 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, 2000. Pseudodifferential operators, paradifferential operators, and layer potentials
Triebel, H.: Theory of Function Spaces, volume 78 of Monographs in Mathematics. Birkhäuser Verlag, Basel, 1983
Truesdell, C., Noll, W.: The Non-linear Field Theories of Mechanics, 3rd ed. Springer, Berlin, 2004. Edited and with a preface by Stuart S. Antman
Acknowledgements
L.K. would like to thank the Max-Planck Institute for Gravitational Physics (Albert Einstein Institute) for hospitality during his visits, where a substantial part of the work was done.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. Dafermos.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised to correct Lars Andersson’s affiliation from “101400 Beijing, Germany” to “101400 Beijing, China.
Appendices
Function Spaces
For the convenience of the reader, we include some background on the function spaces used in this paper. All spaces we use belong to the scales of Besov spaces \(B^s_{p, q}({{\mathbb {R}}}^d)\) and Lizorkin–Triebel spaces \(F^s_{p, q}({{\mathbb {R}}}^d)\). Also, we use the homogenous versions of these spaces. For their definition and basic properties we rely on [36].
The \(L^p({{\mathbb {R}}}^d)\) norm of a function, f, is denoted \(\Vert f\Vert _p\) or, if it is convenient, in one of the following forms:
Similar forms are used for the norms in other function spaces. The integral \(\int \) is the Lebesgue integral over \({{\mathbb {R}}}^d\). \({{{\mathcal {S}}}} = {{{\mathcal {S}}}}({{\mathbb {R}}}^d)\) is the Schwartz space of rapidly decreasing test functions, and \({{{\mathcal {S}}}}^\prime = {{{\mathcal {S}}}}^\prime ({{\mathbb {R}}}^d)\) is its dual, the space of tempered distributions. The pairing between \({{{\mathcal {S}}}}^\prime \) and \({{{\mathcal {S}}}}\) is denoted \(\langle f, g\rangle \) and, for a regular distribution \(f\in L^1\subset {{{\mathcal {S}}}}^\prime \), \(\langle f, g\rangle = \int f(x)\,g(x)\,\textrm{d}x\).
-
The Fourier transform \({{{\mathcal {F}}}}\) is defined as
$$\begin{aligned} {{{\mathcal {F}}}}_{x\rightarrow \kappa } f = {{{\hat{f}}}}(\kappa ) = \int e^{-i x \kappa } f(x)\,\textrm{d}x, \end{aligned}$$with the inverse
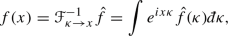
where
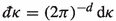 .
. -
Notation for the Riesz and Bessel potentials: \(D^s = \left( -\Delta \right) ^{s/2} = {{{\mathcal {F}}}}^{-1}_{\kappa \rightarrow \cdot } |\kappa |^s {{{\mathcal {F}}}}_{x\rightarrow \kappa }\) and \(J^s = \left( 1 - \Delta \right) ^{s/2} = {{{\mathcal {F}}}}^{-1}_{\kappa \rightarrow \cdot }\left( 1 + |\kappa |^2\right) ^{s/2} {{{\mathcal {F}}}}_{x\rightarrow \kappa }\), with \(s\in {{\mathbb {R}}}\).
-
In this paper, all function spaces are subspaces of \({{{\mathcal {S}}}}^\prime \). If \(A_1\) and \(A_2\) are such Banach spaces, their intersection, \(A_1 \cap A_2\), is viewed as a Banach space with the norm \(\Vert f\,\big |\,A_1 \cap A_2\Vert = \max \left( \Vert f\,\big |\,A_1\Vert ,\,\Vert f\,\big |\,A_2\Vert \right) \).
1.1 Littlewood–Paley decomposition
Pick a smooth function \(\psi _0: [0, +\infty )\rightarrow [0, 1]\) such that \(\psi _0(s) = 1\) if \(s \le 1\), \(\psi _0(s) = 0\) if \(s \ge 2\), and \(0< \psi _0(s) < 1\) if \(1< s < 2\). Set \(\varphi _0(s) = \psi _0(s) - \psi _0(2\,s)\). Then \(\hbox {supp}\,\varphi _0 = [ 2^{-1}, 2]\). For \(n\in {{\mathbb {Z}}}\), define \(\psi _n(t) = \psi _0(2^{-n}t)\) and \(\varphi _n(t) = \varphi _0(2^{-n}t)\). Then, for all integer n,
and
Also, for all \(N\in {{\mathbb {Z}}}\) and for all \(t\ge 0\), we have
Abusing the notation we write \(\varphi _n(\kappa )\) instead of \(\varphi _n(|\kappa |)\), where \(\kappa \in {{\mathbb {R}}}^d\), and similarly understood are \(\psi _n(\kappa )\). Also, we write \(\varphi _n(D)\), \(\psi _n(D)\), etc. for the corresponding pseudodifferential operators, i.e.,

Thanks to the first identity in (A.1), any tempered distribution \(f\in {{{\mathcal {S}}}}^\prime \) can be expanded as (the Littlewood–Paley decomposition)
where the series converges in \({{{\mathcal {S}}}}^\prime \). We will abbreviate sometimes \(f_n = \varphi _n (D) f\).
1.2 Homogeneous Besov and Lizorkin–Triebel spaces
Following Triebel [36], define \({{{\mathcal {Z}}}} = {{{\mathcal {Z}}}}({{\mathbb {R}}}^d)\) as the subspace of \({{\mathcal {S}}}\) consisting of those test functions \(\eta \) which satisfy the condition \(\int x^\alpha \,\eta (x)\,\textrm{d}x = 0\) for all multiindices \(\alpha = (\alpha _1,\dots , \alpha _d)\in {{\mathbb {Z}}}^d\) with all \(\alpha _j\ge 0\). Equivalently, \(\eta \in {{{\mathcal {Z}}}}\) iff (\(\eta \in {{{\mathcal {S}}}}\) and) \(\partial ^\alpha {{{\hat{\eta }}}}(0) = 0\) for all nonnegative multiindices \(\alpha \). With the topology inherited from \({{\mathcal {S}}}\), \({{\mathcal {Z}}}\) is a complete locally convex space. Polynomials when viewed as elements of \({{{\mathcal {S}}}}^\prime \), annihilate \({{\mathcal {Z}}}\): If P is a polynomial, \(P(x) = \sum c_\alpha x^\alpha \), and if \(\eta \in {{{\mathcal {Z}}}}\), then
Conversely, any tempered distribution f that annihilates \({{{\mathcal {Z}}}}\) is a polynomial. Indeed, if \(\langle f, \eta \rangle = 0\) for all \(\eta \in {{{\mathcal {Z}}}}\), then, in particular, \(\langle {{{\hat{f}}}}, {{{\hat{\eta }}}}\rangle = 0\) for every \(\eta \) with \(0\notin \hbox {supp}\,{{{\hat{\eta }}}}\). Hence, \(\hbox {supp}\,{{{\hat{f}}}} = \{0\}\). Therefore, f is a polynomial. Denote by \({{{\mathcal {Z}}}}^\prime \) the topological dual of \({{\mathcal {Z}}}\). If \(\ell \) is a linear continuous functional on \({{{\mathcal {Z}}}}\), then there exist constants \(C\ge 0\) and \(K\in {{\mathbb {Z}}}\), \(K\ge 0\), such that
By the Hahn-Banach theorem, there exists a linear extension of \(\ell \) from \({{{\mathcal {Z}}}}\) to \({{\mathcal {S}}}\) with the same inequality valid for all \(\eta \) in \({{\mathcal {S}}}\). As elements of \({{{\mathcal {S}}}}^\prime \), any two such extensions must differ by a polynomial. This leads to identification of \({{{\mathcal {Z}}}}^\prime \) with the quotient space of \({{{\mathcal {S}}}}^\prime \) by the subspace \(P\subset {{{\mathcal {S}}}}^\prime \) of all polynomials: \({{{\mathcal {Z}}}}^\prime \simeq {{{\mathcal {S}}}}^\prime /P\). The following Littlewood–Paley decomposition applies to distributions in \({{{\mathcal {Z}}}}^\prime \):
which really means that for every \(f\in {{{\mathcal {S}}}}^\prime \) there exist an integer \(K\ge 0\), a sequence of polynomials \(p_N(x)\) of degree not greater than K, and a polynomial \(p_\infty (x)\) such that
(see [28]).
-
The homogeneous Besov space \({\dot{B}}^s_{p, q} = {\dot{B}}^s_{p, q}({{\mathbb {R}}}^d)\) with the parameters \(s\in {{\mathbb {R}}}\), \(1\le p\le \infty \), and \(1\le q < \infty \), is the subspace of \({{{\mathcal {Z}}}}^\prime \) composed of those \(f\in {{{\mathcal {S}}}}^\prime \) for which the norm
$$\begin{aligned} \Vert f\;\big |\; {\dot{B}}^s_{p, q}\Vert = \left( \sum _{n=-\infty }^\infty 2^{s n q} \Vert \varphi _n (D) f\Vert _p^q\right) ^{1/q} \end{aligned}$$(A.5)is finite. If \(q = \infty \), then
$$\begin{aligned} \Vert f\;\big |\; {\dot{B}}^s_{p, \infty }\Vert = \sup _{n\in {{\mathbb {Z}}}} 2^{s n} \Vert \varphi _n(D) f\Vert _p \end{aligned}$$(A.6) -
For \(s\in {{\mathbb {R}}}\), \(1\le p < \infty \), and \(1\le q < \infty \), the homogeneous Lizorkin–Triebel space \({\dot{F}}^s_{p, q} = {\dot{F}}^s_{p, q}({{\mathbb {R}}}^d)\) is the subspace of \({{{\mathcal {Z}}}}^\prime \) composed of those \(f\in {{{\mathcal {S}}}}^\prime \) for which the norm
$$\begin{aligned} \Vert f\;\big |\; {\dot{F}}^s_{p, q}\Vert = \Vert \left( \sum _{n=0}^\infty 2^{s n q}\,|\varphi _n(D) f|^q \right) ^{1/q}\;\big |\;L^p\Vert \end{aligned}$$is finite. A modification as above is needed in the case \(q = \infty \). (The case \(p=\infty \) requires a special treatment, see [36].)
-
The homogeneous Sobolev space \({\dot{H}}^s_p = {\dot{H}}^s_p({{\mathbb {R}}}^d)\) is the space of all \(f\in {{{\mathcal {Z}}}}^\prime \) such that the norm
$$\begin{aligned} \Vert f\;\big |\; {\dot{H}}^s_{p}\Vert = \Vert \sum _{n=-\infty }^\infty D^s \varphi _n(D)f\;\big |\;L^p\Vert \end{aligned}$$(A.7)is finite (the range of parameters is \(-\infty< s < +\infty \), \(1\le p\le \infty \)). When \(p = 2\), we write \({\dot{H}}^s\) instead of \({\dot{H}}^s_2\).
-
Basic embeddings.
$$\begin{aligned} \begin{aligned}&{\dot{B}}^s_{p, q_1}\subset {\dot{B}}^s_{p, q_2},\quad {\dot{F}}^s_{p, q_1}\subset {\dot{F}}^s_{p, q_2},\;\text {if}\; 1\le q_1\le q_2\le \infty \\&{\dot{B}}^s_{p, \min (p,q)}\subset {\dot{F}}^s_{p, q}\subset {\dot{B}}^s_{p, \max (p,q)},\\&{\dot{B}}^{s_1}_{p_1, q_1} \subset {\dot{B}}^{s_2}_{p_2, q_2}\;\text {if}\;1\le p_1\le p_2\le \infty , \; 1\le q_1\le q_2\le \infty , \;s_2 - \frac{d}{p_2} = s_1 - \frac{d}{p_1} \\&{\dot{F}}^{s_1}_{p_1, q_1} \subset {\dot{F}}^{s_2}_{p_2, q_2}\;\text {if}\;1\le p_1< p_2 < \infty , \; 1\le q_1,\, q_2\le \infty , \;s_2 - \frac{d}{p_2} = s_1 - \frac{d}{p_1} \end{aligned} \end{aligned}$$(A.8) -
For all \(s, r\in {{\mathbb {R}}}\), the operator \(D^r = (-\Delta )^{r/2} = {{{\mathcal {F}}}}^{-1}_{\kappa \rightarrow \cdot }|\kappa |^r{{{\mathcal {F}}}}_{x\rightarrow \kappa }\) is an isomorphism between \({\dot{B}}^{s+r}_{p, q}\) and \({\dot{B}}^{s}_{p, q}\) if \(p, q\in [1,\infty ]\), and between \({\dot{F}}^{s+r}_{p, q}\) and \({\dot{F}}^{s}_{p, q}\), when \(1\le p < \infty \), \(1\le q\le \infty \), see Theorem 5.2.3.1 in [36].
-
The topological dual of \({\dot{B}}^s_{p,q}\) is \({\dot{B}}^{-s}_{p^\prime ,q^\prime }\) and the topological dual of \({\dot{F}}^s_{p,q}\) is \({\dot{F}}^{-s}_{p^\prime ,q^\prime }\), where \(s\in {{\mathbb {R}}}\), \(1\le q <\infty \), and \(1\le p <\infty \). (As usual, \(1/p+1/p^\prime = 1/q+1/q^\prime = 1\).)
-
Interpolation inequalities. If \(0< \theta < 1\), \(s = (1-\theta ) s_0 + \theta s_1\), and if
$$\begin{aligned} \frac{1}{p} = \frac{1-\theta }{p_0} + \frac{\theta }{p_1},\quad \frac{1}{q} = \frac{1-\theta }{q_0} + \frac{\theta }{q_1}, \end{aligned}$$where \(1\le p_0, p_1\le \infty \) and \(1\le q_0, q_1\le \infty \), then
$$\begin{aligned} \Vert f\;\big |\; {\dot{B}}^s_{p, q}\Vert \lesssim \Vert f\;\big |\; {\dot{B}}^{s_0}_{p_0, q_0}\Vert ^{1-\theta }\;\Vert f\;\big |\; {\dot{B}}^{s_1}_{p_1, q_1}\Vert ^{\theta }. \end{aligned}$$This is due to the fact that \({\dot{B}}^s_{p, q} = \left[ {\dot{B}}^{s_0}_{p_0, q_0}, {\dot{B}}^{s_1}_{p_1, q_1}\right] _\theta \), the complex interpolation. The analogous result is true for the Lizorkin–Triebel spaces:
$$\begin{aligned} \Vert f\;\big |\; {\dot{F}}^s_{p, q}\Vert \lesssim \Vert f\;\big |\; {\dot{F}}^{s_0}_{p_0, q_0}\Vert ^{1-\theta }\;\Vert f\;\big |\; {\dot{F}}^{s_1}_{p_1, q_1}\Vert ^{\theta }. \end{aligned}$$ -
Isomorphisms between spaces.
$$\begin{aligned} \begin{aligned}&{\dot{F}}^0_{p,2} \simeq L^p,\quad {\dot{F}}^s_{p,2}\simeq {\dot{H}}^s_p,\; 1< p < \infty , s\in {{\mathbb {R}}}\\&{\dot{F}}^s_{p,p} \simeq {\dot{B}}^s_{p,p} \end{aligned} \end{aligned}$$(A.9)It is known ([36]) that, for \(r\in (0, 1)\), the \({\dot{B}}^r_{\infty , \infty }\)-seminorm is equivalent to the homogeneous Hölder \({\dot{C}}^r\) seminorm:
$$\begin{aligned} \sup _{n\in {{\mathbb {Z}}}} 2^{rn}\;\Vert {{{\mathcal {F}}}}^{-1}\varphi _n {{{\mathcal {F}}}} f\Vert _\infty \quad \simeq \quad \{f\}_r = \sup _{x \ne y} \frac{|f(x) - f(y)|}{|x - y|^r}, \end{aligned}$$and, for \(1\le p < \infty \), the \({\dot{B}}^r_{p, p}\)-seminorm is equivalent to the Gagliardo seminorm
$$\begin{aligned} \left[ f\;\big |\;{\dot{B}}^r_{p, p}\right] _* = \left( \int \int \frac{|f(x) - f(y)|^p}{|x - y|^{r p + d}} \right) ^{1/p} \end{aligned}$$An equivalent seminorm in \({\dot{H}}^s\) is
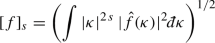
-
The nonhomogeneous Besov and Lizorkin–Triebel spaces are made of tempered distributions with the norms
$$\begin{aligned} \Vert f\;\big |\; B^s_{p, q}\Vert = \Vert \psi _0(D)\,f\Vert _p + \left( \sum _{n=0}^\infty 2^{s n q} \Vert \varphi _n (D) f\Vert _p^q\right) ^{1/q} \end{aligned}$$and
$$\begin{aligned} \Vert f\;\big |\; F^s_{p, q}\Vert = \Vert \psi _0(D)\,f\Vert _p + \Vert \left( \sum _{n=0}^\infty 2^{s n q}\,|\varphi _n(D) f|^q \right) ^{1/q}\;\big |\;L^p\Vert , \end{aligned}$$respectively. Equivalent norms are obtained when the part \(\Vert \psi _0(D)\,f\Vert _p\) is replaced with \(\Vert f\Vert _p\). For all \(s, r\in {{\mathbb {R}}}\), the operator \(J^r = (1-\Delta )^{r/2} = {{{\mathcal {F}}}}^{-1}_{\kappa \rightarrow \cdot }(1+|\kappa |^2)^{r/2}{{{\mathcal {F}}}}_{x\rightarrow \kappa }\) is an isomorphism between the nonhomogeneous spaces \({ B}^{s+r}_{p, q}\) and \({ B}^{s}_{p, q}\) if \(p, q\in [1,\infty ]\), and between \({ F}^{s+r}_{p, q}\) and \({ F}^{s}_{p, q}\), when \(1\le p < \infty \), \(1\le q\le \infty \). The nonhomogeneous spaces are monotone with respect to the parameter S:
$$\begin{aligned} B^{s_1}_{p, q} \subset B^{s_2}_{p, q}\quad \text {and}\quad F^{s_1}_{p, q} \subset F^{s_2}_{p, q} \end{aligned}$$when \(s_1\ge s_2\). The corresponding homogeneous spaces are not monotone with respect to s. However, the following result is easy to prove.
Lemma A.1
Let \(s > 0\), \(1\le m\le p\le \infty \), and \(1\le q\le \infty \). Then \(L^m\cap {\dot{B}}^s_{p, q} = L^m\cap { B}^s_{p, q}\). If \(s_1> s_2 > 0\), then \(L^m\cap {\dot{B}}^{s_1}_{p, q}\subset L^m\cap {\dot{B}}^{s_2}_{p, q}\). Moreover, if \(s_1 \ge s_2 > 0\), \(1\le m\le p_2\le p_1\le \infty \), and
then \(L^m\cap {\dot{B}}^{s_1}_{p_1, q} \subset L^m\cap {\dot{B}}^{s_2}_{p_2, q}\) (for any \(1\le q\le \infty \)).
Proof
Assume \(f\in L^m\cap {\dot{B}}^s_{p, q}\). Then, for any \(g\in L^{p^\prime }\),
where

By Young’s convolution inequality,
if
Since \(m \le p\), this equality defines \(\ell \) so that \(1\le \ell < \infty \). Clearly, \(h\in L^\ell \), since \(\psi _0\) is smooth and has compact support. Thus,
This proves that \(f\in L^m\cap { B}^s_{p, q}\) and \(L^m\cap {\dot{B}}^s_{p, q} \subset L^m\cap { B}^s_{p, q}\). If \(s > 0\), then \({ B}^s_{p, q}\subset {\dot{B}}^s_{p, q}\). Together, these observations prove the isomorphism of spaces: \(L^m\cap {\dot{B}}^s_{p, q} = L^m\cap { B}^s_{p, q}\). The remaining statements follow from the corresponding statements for non-homogeneous Besov spaces.
\(\square \)
1.3 Gagliardo–Nirenberg inequality and Runst’s lemma
Recall the classical Gagliardo–Nirenberg inequality:
where j and m are integers such that \(0< j < m\), \(1 \le p_1 < \infty \), \(1 \le \,p_2 \le \infty \), and
For more general forms/versions of this inequality see [7, 34].
Runst’s inequality is a type of a Gagliardo–Nirenberg inequality stated in terms of the Lizorkin–Triebel spaces. Its interesting feature is that there is no restriction on the parameters \(q_1\) and q within the range \((0, +\infty ]\) (though the constants depend on their choice).
Lemma A.2
Let \(\alpha \in (0, 1)\) and \(0< p < \infty \), and \(0 < q_1, q \le \infty \), \(r > 0\). Then, for any \(g\in L^\infty \cap F^s_{p, q_1}\),
Also, for any \(g\in L^\infty \cap {\dot{F}}^r_{p, q_1}\),
Proof
The proof in the nonhomogeneous case, (A.11), is given by Runst, see Lemma 1, Section 5.2 of [30], and also Lemma 1, Section 5.3.7 [31]). It relies on Oru’s lemma, [7, Lemma 3.7]. For the homogeneous spaces one needs a slight generalization of Oru’s lemma, namely,
Lemma A.3
If \(-\infty< s_1< s_2 < +\infty \), \(0< q < \infty \), \(0< \alpha < 1\), and \(s = \alpha s_1 + (1 - \alpha ) s_2\), then
for any sequence \(\{a_j\}_{j=-\infty }^\infty \).
We leave its proof to the reader and continue with the proof of (A.12).
Denote \(g_n = {{{\mathcal {F}}}}^{-1} \varphi _n {{{\mathcal {F}}}}g\). With \(s = \alpha r\), \(s_1 = r\), and \(s_2 = 0\), it follows from Lemma A.3 that
and, consequently,
Since \(\sup _n 2^{r n} |g_n| \le \left( \sum _{n\in {{\mathbb {Z}}}} 2^{r n q_1} |g_n|^{q_1} \right) ^{1/q_1}\) for any \(q_1 > 0\), and since \(\Vert \sup _n |g_n|\Vert _\infty \lesssim \Vert g\Vert _\infty \), we have
Take the \(L^{p/\alpha }\) norm of both sides to obtain (A.12). \(\square \)
Norms of Products and Compositions of Functions
1.1 Norms of products
There are several results (sometimes called the fractional Leibniz rule) on the Sobolev/Lizorkin–Triebel norms of products of functions.
Lemma B.1
If \(s > 0\) and \(1< p < \infty \), then
provided that
The same inequality is true with \(D^s\) replaced by the operator \(J^s = (1 - \Delta )^{s/2}\), with the same restrictions on the parameters:
As a corollary, if \(s > 0\) and \(1< p < \infty \), then
provided that
For the proofs of (B.1) and (B.2) see [12, Theorem 1] and [4, Theorem1.1]. Some more general inequalities are established in [31]. For earlier results see the Christ and Weinstein paper [8, Prop. 3.3] and [35, Prop. 2.1.1].
1.2 Norms of compositions
Lemma B.1 is used, in particular, to estimate the \(H^s\) norms of compositions f(u), where f is a sufficiently smooth functions and \(u\in H^s\cap L^\infty \). The simplest result deals with the case \(0 < s \le 1\).
Lemma B.2
Suppose that \(f: {{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) is a locally Lipschitz function such that \(f(0) = 0\). Then, if \(0 < s \le 1\) and \(1< p < \infty \),
for any function \(u\in F^s_{p, 2}({{\mathbb {R}}}^d)\) (recall that \(F^s_{p, 2}({{\mathbb {R}}}^d) = H^{s, p}({{\mathbb {R}}}^d)\)). Here
The proof of Lemma B.2 relies on the fact that \(|f(u(x)) - f(u(y))|\le C_f(\Vert u\Vert _\infty )\,|u(x) - u(y)|\), see [35, Prop. 2.4.1]. Next, consider larger s. In the main body of the paper we need only the case of the Sobolev scale \(H^s\).
Lemma B.3
Let \(s > 0\). Let \(f: {{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) be \(r =\lfloor s \rfloor \) times continuously differentiable function such that its r th derivative is locally Lipschitz, and \(f(0) = 0\). Then there is a continuous, nondecreasing function \(C_{f, s, d}: {{\mathbb {R}}}_+\rightarrow {{\mathbb {R}}}_+\) such that
for any function \(u\in H^s({{\mathbb {R}}}^d)\cap L^\infty ({{\mathbb {R}}}^d)\).
Proof
For infinitely differential functions f, there is an elegant and short proof of (B.4) in Hörmander’s book [14, Theorem 8.5.1]. However, having in mind finitely differentiable f, we present a different argument. It can be used for other purposes as well (we use it to prove regularity of the inverse map in Lemma 3.1).
For s an integer, to prove (B.4) we follow Moser’s argument on p. 273 of paper [27]. Let \(s = r\) be an integer greater than 1. Observe that \(|f(u)|\le C_f(|u|)\,|u|\), and hence \(\Vert f(u)\Vert \le C_f(\Vert u\Vert _\infty )\,\Vert u\Vert \). Now it suffices to consider the derivatives of the order r of f(u(x)). Schematically,
where \(\alpha _1 + 2\alpha _2 + \dots + r\alpha _r = r\) and \(C_{k \alpha }\) are non-negative constants. We have that
where \(1\le p_m\le \infty \) and \(\sum _m 1/p_m = 1\). The right choice of \(p_m\) is
because then
and
by the Gagliardo–Nirenberg inequality. Collecting all the terms, we obtain
Now consider the case of fractional s. Assume \(s = r + \gamma \), \(r \ge 1 \) is an integer and \(0< \gamma < 1\). Since we have the \(H^r\) norm of f(u) already bounded, it remains to show that the \(H^\gamma \) norm of each term of the form
is bounded (see (B.5)). First, consider the case g(u) is not a constant. Use the product estimate (B.2) to obtain that
where
Since \(\Vert g(u)\Vert _\infty \lesssim C_g(\Vert u\Vert _\infty )\,\Vert u\Vert _\infty \), the first term on the right will be treated later (with the case \(g(\cdot ) = const\)). Thus, look at the second term. The choice of q is dictated by the following computation. First, use Hölder’s inequality,
Then,
The norm \(\Vert u\;\big |\; F^m_{2 q \alpha _m p_m, 2}\Vert \) will be bounded using (A.11) as follows:
This means the indices should satisfy
and \(1\le p_m \le \infty \),
Consequently, we must have that
Then
Since \(\sum m \alpha _m = r\) and we want \(\sum 1/p_m = 1\), we must have \(q = s/r\).
To estimate the norm \(\Vert g(u)\,\big |\; F^\gamma _{2q^\prime , 2}\Vert \) We apply Lemma B.2 to get that
By Runst’s Lemma A.2,
Collecting the estimates, we get that
where we have used that, by construction,
Finally, consider the case \(g(u) \equiv const\). To estimate \(\Vert \prod _m (\partial ^m u)^{\alpha _m}\;\big |\;{H^\gamma }\Vert \) we use (B.3) to get that
where \(q_1, \dots , q_r\) will be chosen later (and will satisfy \(\sum _j 1/q_j = 1\)). The factors in the product are bounded first as
and then Runst’s lemma is applied to get that
Lemma A.2 imposes the following restrictions:
i.e.,
Thus,
for \(j\ne m\).
Next, consider \( \Vert (\partial ^m u)^{\alpha _m}\;\big |\; F^\gamma _{2 q_m, 2}\Vert \). Assuming \(\alpha _m > 0\), first use (B.3) with equal exponents to get that
and continue as follows:
Now each norm is bounded using (A.11). We have
where
and \(q_m\) must be chosen so that
Similarly,
where \(q_m\) is as above and
Bringing the estimates together, we obtain
as claimed.
\(\square \)
Estimates on Riesz Transforms
The Riesz transform operators \({{{\mathcal {R}}}}_j\), \(j = 1, \dots , d\), will be defined by the formula
It is well known (see [26, Theorem 10.2.1]) that \({{{\mathcal {R}}}}_j\) is bounded in \({\dot{B}}^s_{\infty , \infty }\), when \(s > 0\), but not in \({ B}^s_{\infty , \infty }\). The Riesz transform is a special case of a more general class of pseudo-differential operators which we shall now discuss.
Denote by \(S^0_{ph}\) the space of all smooth functions \(a: {{\mathbb {R}}}^d{\setminus }\{0\}\rightarrow {{\mathbb {R}}}\) which are positively homogeneous of degree 0 and satisfy
for any multiindex \(\alpha \). Each symbol \(a\in S^0_{ph}\) gives rise to a pseudodifferential operator \({{\mathfrak {a}}}:\,f\mapsto {{\mathfrak {a}}}[f]\), where

Any finite composition of the Riesz transforms has its symbol in \(S^0_{ph}\). An observation: if, as usual, q and \(q^\prime \) are conjugate exponents, and \( 1\le q^\prime \le 2\le q \le \infty \), then (change of variables)

In particular, the integrals  represent smooth functions with uniformly in n bounded \(L^1\) norms.
represent smooth functions with uniformly in n bounded \(L^1\) norms.
Lemma C.1
Let the symbol \(a\in S^0_{ph}\) be given.
-
1.
For any \(r \in {{\mathbb {R}}}\) and any \(p\in [2, +\infty ]\),
$$\begin{aligned} \Vert {{\mathfrak {a}}}[f]\;\big |\; {\dot{B}}^r_{p, p}\Vert \lesssim \Vert f\;\big |\; {\dot{B}}^r_{p, p}\Vert . \end{aligned}$$(C.2) -
2.
Assume the parameters r, p, and q satisfy the conditions \(1\le p, q \le \infty \) and \(r > \frac{d}{p}\). Then there exists a constant \(C_1\) such that
$$\begin{aligned} \Vert {{\mathfrak {a}}}[f]\Vert _\infty \le C_1\; [f]_{-1}^{\gamma _1}\;\Vert f\;\big |\;{\dot{B}}^r_{p, q}\Vert ^{1 - \gamma _1} \end{aligned}$$(C.3)for every \(f\in {\dot{H}}^{-1}\cap {\dot{B}}^r_{p, q}\), where
$$\begin{aligned} \gamma _1 = \gamma _1(d, r, p) = \frac{r - \frac{d}{p}}{r + 1 + d\,\frac{p-2}{2p}}. \end{aligned}$$(C.4) -
3.
Assume the parameters r, p, and q satisfy the conditions \(1\le p, q \le \infty \) and \(r > \frac{d}{p} - 1\). Then there exists a constant \(C_2 > 0\) such that
$$\begin{aligned} \Vert D^{-1}\,{{\mathfrak {a}}}[f]\Vert _\infty \le C_2\; [f]_{-1}^{\gamma _2}\;\Vert f\;\big |\;{\dot{B}}^r_{p, q}\Vert ^{1 - \gamma _2} \end{aligned}$$(C.5)for every \(f\in {\dot{H}}^{-1}\cap {\dot{B}}^r_{p, q}\), where
$$\begin{aligned} \gamma _2 = \gamma _2(d, r, p) = \frac{r + 1 - \frac{d}{p}}{r + 1 + d\,\frac{p-2}{2p}} \end{aligned}$$(C.6)
Proof
To prove the first claim we need to show that
where \(f_m = \varphi _m(D) f\). This follows from the estimate
which is easy to prove. Indeed,
and

Then (see (C.1))

Thus we have (C.7), and this implies (C.2).
To prove the remaining two claims, consider the expansion (A.2) for f, \(f = g_N + h_N\), where
the integer N will be chosen later. We have
and
Therefore,
Next,
and hence,
Pick a \(p\ge 1\) and observe that

Applying (C.1), we obtain
If \( r > \frac{d}{p}, \) then, for any \(q\ge 1\),
Thus,
Combine this with (C.8) to obtain
Now choose N so that the two terms have (almost) the same magnitudes:
( \(\lfloor \cdot \rfloor \) is the floor function). The resulting inequality is
with
The second part is proved similarly. First we have
After that, consider \(\Vert D^{-1}{{\mathfrak {a}}}[h_N]\Vert _\infty \). We have
Now,

and

This leads to
and we proceed as in the first part. Now the restriction on r will be \( r > \frac{d}{p} - 1 \) and then
This time we obtain
Again, choose N so that
i.e.,
Plugging this value into the inequality above we obtain
with
\(\square \)
Strichartz Estimates
In this section we derive the homogeneous \({{\mathbb {R}}}^d\) version of the Strichartz estimates in Theorem 2 [17]. We work with functions of \(x\in {{\mathbb {R}}}^d\) and the Fourier variables are \(\kappa \). Note, that the estimates are applied in Section 5 to functions of \(\xi \) with the dual Fourier variables k.
Consider the Cauchy problem
where \(D = \sqrt{- \Delta }\) in \({{\mathbb {R}}}^d\). Given \(w_0\in {\dot{H}}^\theta \) and \(f\in L^1_{loc}({{\mathbb {R}}}\rightarrow {\dot{H}}^\theta )\), there exists a unique solution w of equation (D.1) such that w(t) is a continuous functions of t with values in \({\dot{H}}^\theta \), and
with the positive constant \(C_\theta \) independent of the particular choice of \(w_0\) and f.
Theorem D.1
Let \(2\le q \le \infty \) and let p be such that if \(d = 2\), then \(2 \le p \le +\infty \), and if \(d \ge 3\), then \(2 \le p < \frac{2(d-1)}{d - 3}\). Assume the parameters r and \(\theta \) satisfy the conditions
There exists a constant \(C > 0\) (dependent on d, r, and p) such that, for any \(T > 0\), the following estimate is true for the solutions of (D.1):
Corollary D.2
Two special cases: If \(d = 2\), then take \(p = q = \infty \), \(0< r < 1\), and \(\theta = r + \frac{3}{4}\), and obtain
If \(d = 3\), take \(2\le p = q < \infty \), and \(\theta = r + \frac{p-2}{p}\), and obtain
Proof of Theorem D.1
For fixed \(w_0\) and f, the solution of the problem (D.1) is given by the formula
Each term on the right can be analyzed separately. Take a \(g\in {{{\mathcal {S}}}}\) and consider \(e^{i t\,D}g\). In fact, we need to look at the dyadic pieces \(\varphi _n(D)e^{i t\,D}g = e^{i t\,D}g_n\), where \(g_n = \varphi _n(D) g\). Since
we examine the terms \(\varphi _j(D)\,e^{i t\,D}g_n\). The first important observation in the Strichartz analysis is the following bound on the operator \(\varphi _j(D)\,e^{i t\,D}\) as an operator from \(L^{p^\prime }\) to \(L^p\), \(2\le p\le \infty \):
As a corollary,
for any \(p\in [2, +\infty ]\). This estimate, implies the estimates in the homogeneous Besov spaces with
\(r\in {{\mathbb {R}}}\) and \(1\le q \le \infty \). The second important observation is the space-time estimate for the homogeneous term \(e^{i t\,D} g\). The argument uses duality. Let h(t, x) be a sufficiently smooth function. Then
Now,
Choose \(\theta \) so that
i.e.,
and assume that
(then \(q^\prime \le 2 \le q\) and \({\dot{B}}^{-r}_{p^\prime , q^\prime } \subset {\dot{B}}^{-r}_{p^\prime , q}\)). Then
with
The last inequality is a consequence of the Hardy–Littlewood–Sobolev inequality (see [15, Theorem 4.5.3]). It requires the following restrictions on p:
i.e., if \(d = 2\), then \(2 \le p \le +\infty \), and if \(d \ge 3\), then \(2 \le p < \frac{2(d-1)}{d - 3}\). In any case,
Hence, by duality,
where the exponent \(\frac{4 p}{(d-1)(p-2)}\) is the conjugate of m. This proves estimate (D.4) for the homogeneous equation (D.1). The estimate on \(\int _0^t e^{i (t - \tau ) D} f(\tau )\,\textrm{d}\tau \) is obtained as in the second part of the proof of Theorem 2 in [17] (with necessary slight modifications).
\(\square \)
Norms in Euler and Lagrange Coordinates
In this section \(\xi \rightarrow x(\xi )\) is a \(C^1\) volume preserving diffeomorphism of the form \(x(\xi ) = A \xi + \varphi (\xi )\) satisfying the assumptions of Lemma 3.1. In particular, A is a constant \(SL(d, {{\mathbb {R}}})\) matrix and \(\varphi \in H^{s+1}({{\mathbb {R}}}^d_\xi )\) with \(s > d/2\). This transformation from the Lagrangean coordinates, \(\xi \), to the Eulerian coordinates, x, pushes back the functions f(x) to the functions \({{{\tilde{f}}}}( \xi ) = f(x(\xi ))\). This is a linear isometry from \(L^p({{\mathbb {R}}}^d, \textrm{d}x)\) to \(L^p({{\mathbb {R}}}^d, \textrm{d}\xi )\), \(1\le p \le \infty \). To analyze other norms, we use the superscripts L and E on functions to indicate the coordinate system used. Denote by \(v^i_a(x)\) the entries of the Jacobian matrix, \(\partial x/\partial \xi \), expressed in Eulerian coordinates, i.e., as functions of x. We have \(v^i_a(x) = A^i_a + u^i_a(x)\), where \(u^i_a \in H^s({{\mathbb {R}}}^d_x)\). Notation \(v_a\) or \(u_a\) is used to represent a generic \(v_a\) or \(u_a\), or when in a norm, the maximal over a norm, e.g., \(\Vert v_a\Vert _\infty = \max _a \Vert v_a\Vert _\infty \). For the norms in \(L^p\) we skip the superscripts E and L.
1.1 Homogenous Besov and Sobolev spaces
The following proposition contains inequalities between the homogeneous Besov norms \(\{g\}_{r,p}\) and between the homogeneous \(L^2\) Sobolev norms \([g]_\theta \) in the Euler and Lagrange coordinates. The range of r, p, and \(\theta \) is restricted to the demands of the main body of the paper. All the spaces are over \({{\mathbb {R}}}^d\), \(d \ge 2\).
Lemma E.1
-
(a)
Assume \(0< r < 1\), \(0 \le \theta \le 1\), and \(2\le p \le \infty \). Then, for all \(g\in {{{\mathcal {S}}}}({{\mathbb {R}}}^d)\),
$$\begin{aligned}&\{g^L\}_{r,p} \lesssim \Vert v_a\Vert _\infty ^r\;\{g^E\}_{r,p},\quad&\{g^E\}_{r,p} \lesssim \Vert v_a\Vert _\infty ^{(d-1)r}\;\{g^L\}_{r,p}, \end{aligned}$$(D.14)$$\begin{aligned}&[g^L]_\theta \lesssim \Vert v_a\Vert _\infty ^\theta \;[g^E]_\theta ,\quad&[g^E]_\theta \lesssim \Vert v_a\Vert _\infty ^{(d - 1)\theta }\;[g^L]_\theta \end{aligned}$$(E.1) -
(b)
Assume \(1<\theta < 2\), then
$$\begin{aligned}{}[g^L]_\theta \lesssim \Vert v_a\Vert _\infty ^{\theta -1}\;\left( \Vert v_a\Vert _\infty + \Vert u_a\Vert _\infty ^{2 - \theta }\;\Vert u_a\,\big |\;{\dot{F}}^1_{d, 2}({{\mathbb {R}}}^d)\Vert ^{\theta - 1}\right) \;[g^E]_\theta . \end{aligned}$$(E.2)
Proof
We first prove the inequalities for Sobolev norms in part a). Compare the norms \(\Vert g^L\;\big |\;{\dot{H}}^1({{\mathbb {R}}}^d_\xi )\Vert \) and \(\Vert g^E\;\big |\;{\dot{H}}^1({{\mathbb {R}}}^d_x)\Vert \). We have
If \(0< \theta < 1\), then \({\dot{H}}^\theta \) is an interpolation space between \(L^2\) and \({\dot{H}}^1\), \({\dot{H}}^\theta = (L^2, {\dot{H}}^1)_{\theta , 2}\) (see [2, Theorem 6.3.1]). This explains why \([g^L]_\theta \lesssim \Vert v_a\Vert _\infty ^\theta \,[g^E]_\theta \). Similarly, \([g^E]_\theta \lesssim \Vert v_a\Vert _\infty ^{(d - 1)\theta } \,[g^L]_\theta \), where \((d - 1)\) appears because of the \(L^\infty \) bound on \(\partial \xi ^a/\partial x^i\) in terms of \(\Vert v_a\Vert _\infty \).
The Besov norm inequalities in part a) can be obtained by interpolation between the inequalities for \({\dot{B}}^r_{2, 2} \simeq {\dot{H}}^r\), which we already have, and the inequalities for \({\dot{B}}^r_{\infty , \infty } \simeq {\dot{C}}^r\), the homogeneous Hölder spaces. For the Hölder seminorms we have
Thus, \(\{g^L\}_r \le \Vert v_a\Vert _\infty ^r\,\{g^E\}_r\). The norm \(\{g^E\}_r\) is bounded similarly.
Now turn to part b). Assume \(1< \theta < 2\) and proceed with
Apply the fractional product rule (B.1):
Note that the homogeneous Lizorkin–Triebel norms of \(v_a\) and \(u_a\) are the same. So, we have
The parameters \(q_1\) and \(q_2\) must satisfy \(2\le q_1, q_2 \le \infty \) and
We choose \(q_1\) and \(q_2\) as follows
Then \({\dot{H}}^{\theta -1}({{\mathbb {R}}}^d)\subset L^{q_1}({{\mathbb {R}}}^d)\), and so
As for the other factor, use (A.12):
Collecting the pieces, we arrive at (E.3).
\(\square \)
1.2 Vorticities
Let v be a vectorfield on \({{\mathbb {R}}}^d\) such that \(\hbox {div}\,v = 0\). Denote \(\omega ^{mn} = \partial _m v^n - \partial _n v^m\). In terms of Fourier transform,
From \(\omega ^{mn}\) one recovers v as follows:
In our notation,
In dimension \(d=2\), \(\omega = \partial _1 v^2 - \partial _2 v^1\) and
We also have pseudovelocities \(v_a\) with the components \(v^i_a = u^i_a + A^i_a\), and the corresponding pseudovorticities \(\omega _a = \partial _1 v^2_a - \partial _2 v^1_a = \partial _1 u^2_a - \partial _2 u^1_a\).
Lemma E.2
-
1.
In the case \(d = 2\), assume that \(u\in L^2\) and \(\omega = \textrm{curl}\, u\in {\dot{C}}^r\) for some \(r\in (0, 1)\). Then \(u\in L^\infty \) and \(\nabla u\in L^\infty \), and the following inequalities are true:
$$\begin{aligned} \Vert u\Vert _\infty \lesssim \Vert u\Vert ^{(r + 1)/(r + 2)}\;\{\omega \}_r^{1/(r + 2)} \end{aligned}$$(E.6)and
$$\begin{aligned} \Vert \nabla u\Vert _\infty \lesssim \Vert u\Vert ^{r/(r + 2)}\;\{\omega \}_r^{2/(r + 2)}. \end{aligned}$$(E.7) -
2.
In the case \(d = 2\), assume that \(u\in L^2\) and \(\omega = \textrm{curl}\, u\in {\dot{H}}^\theta \) for some \(\theta \in (0, 1)\). Then \(u\in L^\infty \) and the following inequality is true:
$$\begin{aligned} \Vert u\Vert _\infty \lesssim \Vert u\Vert ^{\theta /(\theta +1))}\;[\omega ]_\theta ^{1/(\theta +1)}. \end{aligned}$$(E.8)If \(\omega \in {\dot{H}}^\theta \) with \(\theta > 1\), then \(\nabla u\in L^\infty \) and
$$\begin{aligned} \Vert \nabla u\Vert _\infty \lesssim \Vert u\Vert ^{(\theta - 1)/(\theta + 1)}\;[\omega ]_\theta ^{2/(\theta +1)}. \end{aligned}$$(E.9) -
3.
In the case \(d \ge 3\), assume that \(u\in L^2\) and \(\omega \in {\dot{B}}^r_{p, p}\), where
$$\begin{aligned} r\in (0, 1),\;r > \frac{d}{p},\;\;1\le p \le \infty . \end{aligned}$$Then \(u\in L^\infty \), \(\nabla u\in L^\infty \), and
$$\begin{aligned} \Vert u\Vert _\infty \lesssim \Vert u\Vert ^{(r + 1 - d/p)/(r + 1 - d/p + d/2)}\;\Vert \omega \;\big |\;{\dot{B}}^r_{p, p}\Vert ^{(d/2)/(r + 1 - d/p + d/2)}\nonumber \\ \end{aligned}$$(E.10)and
$$\begin{aligned} \Vert \nabla u\Vert _\infty \lesssim \Vert u\Vert ^{(r - d/p)/(r + 1 - d/p + d/2)}\;\Vert \omega \;\big |\;{\dot{B}}^r_{p, p}\Vert ^{(1 + d/2)/(r + 1 - d/p + d/2)}.\nonumber \\ \end{aligned}$$(E.11) -
4.
In the case \(d \ge 3\) assume that \(u\in L^2\) and \(\omega = \textrm{curl}\, u \in {\dot{H}}^\theta \). If \(\theta > \frac{d}{2} - 1\), then \(u\in L^\infty \) and
$$\begin{aligned} \Vert u\Vert _\infty \lesssim \Vert u\Vert ^{(\theta + 1 - d/2)/(\theta + 1)}\;[\omega ]_\theta ^{d/2/(\theta + 1)}. \end{aligned}$$(E.12)If \(\theta > \frac{d}{2}\), then \(\nabla u\in L^\infty \) and
$$\begin{aligned} \Vert \nabla u\Vert _\infty \lesssim \Vert u\Vert ^{(\theta - d/2)/(\theta + 1)}\,[\omega ]_\theta ^{(d/2 + 1)/(\theta + 1)}. \end{aligned}$$(E.13)
The inequalities follow immediately from Lemma C.1 part 2 and the observation that \([\omega ]_{-1} \simeq \Vert u\Vert \) and \(\nabla u \simeq {{{\mathcal {R}}}} \omega \).
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Andersson, L., Kapitanski, L. Cauchy Problem for Incompressible Neo-Hookean Materials. Arch Rational Mech Anal 247, 21 (2023). https://doi.org/10.1007/s00205-023-01851-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00205-023-01851-2



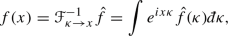
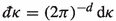 .
.