Skip to main content
SpringerLink
Log in

On the Regularity of Optimal Transports Between Degenerate Densities

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

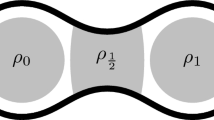
We study the most common image and informal description of the optimal transport problem for quadratic cost, also known as the second boundary value problem for the Monge–Ampère equation—what is the most efficient way to fill a hole with a given pile of sand?—by proving regularity results for optimal transports between degenerate densities. In particular, our work contains an analysis of the setting in which holes and sandpiles are represented by absolutely continuous measures concentrated on bounded convex domains whose densities behave like nonnegative powers of the distance functions to the boundaries of these domains.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Benamou, J.-D., Brenier, Y.: Weak existence for the semigeostrophic equation formulated as a coupled Monge–Ampère/transport problem. SIAM J. Appl. Math. 58, 1450–1461, 1998

    Article  MathSciNet  Google Scholar 

  2. Brenier, Y.: Polar factorization and monotone rearrangement of vector-valued functions. Commun. Pure Appl. Math. 44(4), 365–417, 1991

    Article  MathSciNet  Google Scholar 

  3. Caffarelli, L.A.: The regularity of mappings with a convex potential. J. Am. Math. Soc. 5(1), 99–104, 1992

    Article  MathSciNet  Google Scholar 

  4. Caffarelli, L.A.: Boundary regularity of maps with convex potentials. Commun. Pure Appl. Math. 45(9), 1141–1151, 1992

    Article  MathSciNet  Google Scholar 

  5. Caffarelli, L.A.: Boundary regularity of maps with convex potentials II. Ann. Math. (2) 144(3), 453–496, 1996

    Article  MathSciNet  Google Scholar 

  6. Calabi, E.: Improper affine hypersurfaces of convex type and a generalization of a theorem by K. Jörgens. Mich. Math. J. 5, 105–126, 1958

    Article  Google Scholar 

  7. Chen, S., Liu, J., Wang, X.-J.: Global regularity for the Monge–Ampère equation with natural boundary condition. Ann. Math. (2) 194(3), 745–793, 2021

    Article  MathSciNet  Google Scholar 

  8. Chen, S., Liu, J., Wang, X.-J.: Boundary Regularity for the Second Boundary-Value Problem of Monge–Ampère Equations in Dimension Two. arXiv:1806.09482

  9. Delanoë, P.: Classical solvability in dimension two of the second boundary-value problem associated with the Monge–Ampère operator. Ann. Inst. H. Poincaré Anal. Non Linéaire 8(5), 443–457, 1991

    Article  ADS  MathSciNet  Google Scholar 

  10. De Philippis, G., Figalli, A.: Partial regularity for optimal transport maps. Publ. Math. Inst. Hautes Études Sci. 121, 81–112, 2015

    Article  MathSciNet  Google Scholar 

  11. De Silva, D., Savin, O.: On certain degenerate one-phase free boundary problems. SIAM J. Math. Anal. 53(1), 649–680, 2021

    Article  MathSciNet  Google Scholar 

  12. Figalli, A.: Regularity properties of optimal maps between nonconvex domains in the plane. Commun. Partial Differ. Equ. 35(3), 465–479, 2010

    Article  MathSciNet  Google Scholar 

  13. Figalli, A.: “The Monge–Ampère equation and its applications”, Zürich Lectures in Advanced Mathematics. European Mathematical Society, Zürich, 2007. x+200 pp

  14. Figalli, A., Kim, Y.-H.: Partial regularity of Brenier solutions of the Monge–Ampère equation. Discrete Contin. Dyn. Syst. 28(2), 559–565, 2010

    Article  MathSciNet  Google Scholar 

  15. Figalli, A., Maggi, F., Pratelli, A.: A mass transportation approach to quantitative isoperimetric inequalities. Invent. Math. 182(1), 167–211, 2010

    Article  ADS  MathSciNet  Google Scholar 

  16. Giusti, E.: “Minimal Surfaces and Functions of Bounded Variation”, Monographs in Mathematics, vol. 80. Birkhäuser Verlag, Basel, 1984. xii+240 pp

  17. Goldman, M.: An \(\epsilon \)-regularity result for optimal transport maps between continuous densities. Atti. Accad. Naz. Lincei Rend. Lincei Mat. Appl. 31(4), 971–979, 2020

    Article  MathSciNet  Google Scholar 

  18. Goldman, M., Otto, F.: A variational proof of partial regularity for optimal transportation maps. Ann. Sci. Éc. Norm. Supér. (4) 53(5), 1209–1233, 2020

    Article  MathSciNet  Google Scholar 

  19. Gutiérrez, C.E.: “The Monge–Ampè’re Equation”, Progress in Nonlinear Differential Equations and Their Applications, vol. 44. Birkhäuser Boston, Boston, MA, 2001

  20. Jhaveri, Y.: On the (in)stability of the identity map in optimal transportation. Calc. Var. Partial Differ. Equ. 58(3), 96, 25, 2019

    Article  MathSciNet  Google Scholar 

  21. Jörgens, K.: Über die Lösungen der Differentialgleichung \(rt-s^2 = 1\). Math. Ann. 127, 130–134, 1954

    Article  MathSciNet  Google Scholar 

  22. Le, N.Q., Savin, O.: Schauder estimates for degenerate Monge–Ampère equations and smoothness of the eigenfunctions. Invent. Math. 207(1), 389–423, 2017

    Article  ADS  MathSciNet  Google Scholar 

  23. Lott, J., Villani, C.: Ricci curvature for metric-measure spaces via optimal transport. Ann. Math. (2) 169(3), 903–991, 2009

    Article  MathSciNet  Google Scholar 

  24. McCann, R.J.: Existence and uniqueness of monotone measure-preserving maps. Duke Math. J. 80, 309–323, 1995

    Article  MathSciNet  Google Scholar 

  25. McCann, R.J.: Displacement convexity of Boltzmann’s entropy characterizes the strong energy condition from general relativity. Camb. J. Math. 8(3), 609–681, 2020

    Article  MathSciNet  Google Scholar 

  26. Pogorelov, A.V.: On the improper affine hypersurfaces. Geom. Dedicata 1, 33–46, 1972

    Article  Google Scholar 

  27. Savin, O., Yu, H.: Regularity of optimal transport between planar convex domains. Duke Math. J. 169(7), 1305–1327, 2020

    Article  MathSciNet  Google Scholar 

  28. Urbas, J.: On the second boundary value problem for equations of Monge–Ampère type. J. Reine Angew. Math. 487, 115–124, 1997

    MathSciNet  MATH  Google Scholar 

  29. Villani, C.: “Topics in optimal transportation”, Graduate Studies in Mathematics, vol. 58. American Mathematical Society, Providence, RI, 2003. xvi+370 pp

  30. Villani, C.: “Optimal Transport. Old and New.” Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 338. Springer, Berlin, 2009. xxii+973 pp

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Columbia University, 2990 Broadway, New York, NY, 10027, USA

    Yash Jhaveri & Ovidiu Savin

Authors
  1. Yash Jhaveri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ovidiu Savin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yash Jhaveri.

Additional information

Communicated by A. Figalli.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Yash Jhaveri was supporting in part by NSF Grant DMS-1954363. Ovidiu Savin was supported in part by NSF Grants DMS-1800645 and DMS-2055617.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jhaveri, Y., Savin, O. On the Regularity of Optimal Transports Between Degenerate Densities. Arch Rational Mech Anal 245, 819–861 (2022). https://doi.org/10.1007/s00205-022-01796-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-022-01796-y

Search

Navigation