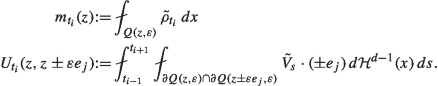Abstract
We consider the problem of dynamic optimal transport with a density constraint. We derive variational limits in terms of \(\Gamma \)-convergence for two singular phenomena. First, for densities constrained near a hyperplane we recover the optimal flow through an infinitesimal permeable membrane. Second, for rapidly oscillating periodic constraints we obtain the optimal flow through a homogenized porous medium.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last few years, optimal transport has become a vibrant research area with many different applications. In particular, density-constrained flow problems have garnered significant interest starting with the seminal work of Ford and Fulkerson [11].
In recent years, the theory of constraints has been adapted to optimal transport, first as a static version in [14] and then as dynamic constraints in [8] and [9].
The model we use is based on the dynamic formulation of the Kantorovich distance due to Benamou and Brenier [3],
Here the infimum is taken over all curves of probability measures \((\rho _t)_{t\in [0,1]} \subset {\mathcal P}({\mathbb R}^d)\) with fixed endpoints.
In this paper, we constrain the densities of all intermediate measures \(\rho _t\) by some measurable maximal density \(h:\Omega \rightarrow [0,\infty ]\). In this article \(\Omega \) is a manifold with boundary, typically \({\mathbb R}^d\) or the torus \({\mathbb T}^d {:}{=}{\mathbb R}^d/{\mathbb Z}^d\).
More precisely we consider first the space \({\mathcal M}_+(\Omega )\) of finite nonnegative Radon measures on \(\Omega \) equipped with the weak-\(*\) (also called narrow) topology in duality with \({\mathcal C}_b(\Omega )\).
By extension the space of weakly-\(*\) continuous curves of finite nonnegative Radon measures is
We study in this article the constrained transport functional \(E_h:{\mathcal {CM}}_+(\Omega ) \rightarrow [0,\infty ]\),
Note that the constraint is closed under weak-\(*\) convergence by the Portmanteau theorem.
For \(h=\infty \) we recover the classical Benamou-Brenier formula. If \(h\in L^1_{\mathrm {loc}}(\Omega )\) then every admissible \(\rho \) is absolutely continuous with density \(\frac{d\rho }{dx}\le h(x)\) almost everywhere. The case \(h=\mathbb {1}_U\) for some nonconvex \(U\subset \Omega \), e.g. an hourglass (see Fig. 1), models optimal transport of an incompressible but sprayable fluid. This specific problem was treated in [16, 17]. If U is convex, \(W_2\)-geodesics between two measures \(\rho _0,\rho _1\le \mathbb {1}_U\) satisfy the density constraints. If U is not convex, optimal curves under the constraint are not \(W_2\)-geodesics and interact with the constraint.
We find the variational limits of two singular phenomena.
1.1 Thin permeable membranes
The first is the derivation of an infinitesimal membrane from the constraint
for some \(\alpha \in ( 0, \infty )\).
Then, as \(\varepsilon \rightarrow 0\), we derive an effective variational model in the sense of \(\Gamma \)-convergence as introduced by De Giorgi. We refer to [5] and [10] for comprehensive overviews of the theory.
The limit functional acts on curves of nonnegative Radon measures on the topological disjoint union \({\mathbb R}^d_- \sqcup {\mathbb R}^d_+\) of the closed half-spaces
and is given by \(E_0:{\mathcal {CM}}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+) \rightarrow [0,\infty ]\),
where we use the identification \({\mathcal M}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+) = {\mathcal M}_+({\mathbb R}^d_-) \times {\mathcal M}_+( {\mathbb R}^d_+)\). The infimum is taken over all pairs of distributional solutions to the continuity equations
meaning that in both half-spaces, for all \(\phi ^\pm \in {\mathcal C}^\infty _c((0,1)\times {\mathbb R}^d_\pm )\) the following equation holds
Here \(V^\pm _t\in {\mathcal M}({\mathbb R}_\pm ^d;{\mathbb R}^d)\) is a vector-valued finite Radon measure which is absolutely continuous with respect to \(\rho ^\pm _t\) and \(f_t\in L^2({\mathbb R}^{d-1}) = L^2(\partial {\mathbb R}^d_\pm )\) is the flux through the membrane, with positive sign denoting flux from the lower into the upper half-space.
Theorem 1.1
Let \(\varepsilon >0\). Then, as \(\varepsilon \rightarrow 0\), the energies \(E_{h^\varepsilon }:{\mathcal {CM}}_+({\mathbb R}^d)\rightarrow [0,\infty ]\) \(\Gamma \)-converge to the limit functional \(E_0 :{\mathcal {CM}}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\rightarrow [0,\infty ]\) in the sense that
- (lower bound):
-
if \(\rho _t^\varepsilon |_{{\mathbb R}^{d}_-} {\mathop {\rightharpoonup }\limits ^{*}}\rho _t^-\) in \({\mathcal M}_+({\mathbb R}^{d}_-)\) for every \(t\in [0,1]\), and \(\rho _t^\varepsilon |_{({\mathbb R}^d_+)^\circ } {\mathop {\rightharpoonup }\limits ^{*}}\rho _t^+\) in \({\mathcal M}_+({\mathbb R}^{d}_+)\) for every \(t\in [0,1]\) then
$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0} E_{h^\varepsilon }((\rho _t^\varepsilon )_{t\in [0,1]})\ge E_0((\rho _t^-,\rho _t^+)_{t\in [0,1]}) \end{aligned}$$(7) - (upper bound):
-
for all curves \((\rho _t^-,\rho _t^+)_{t\in [0,1]}\) with \(E_0((\rho _t^-,\rho _t^+)_{t\in [0,1]})<\infty \) there exists a sequence \((\rho _t^\varepsilon )_{t\in [0,1]}\) in \({\mathcal {CM}}_+({\mathbb R}^d)\) with \(\rho _t^\varepsilon |_{{\mathbb R}^{d}_-} {\mathop {\rightharpoonup }\limits ^{*}}\rho _t^-\) in \({\mathcal M}_+({\mathbb R}^{d}_-)\) for every \(t\in [0,1]\), and \(\rho _t^\varepsilon |_{({\mathbb R}^d_+)^\circ } {\mathop {\rightharpoonup }\limits ^{*}}\rho _t^+\) in \({\mathcal M}_+({\mathbb R}^{d}_+)\) for every \(t\in [0,1]\) and
$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0}E_{h^\varepsilon }((\rho _t^\varepsilon )_{t\in [0,1]})\le E_0((\rho _t^-,\rho _t^+)_{t\in [0,1]}). \end{aligned}$$(8)
We prove this theorem in Sect. 6. Note that the part \(\rho _t^\varepsilon |_{({\mathbb R}^d_+)^\circ }\) includes the mass in the membrane, which is locally bounded by \(\alpha \varepsilon ^2\).
Since \(\Gamma \)-convergence implies the convergence of minimizers, the associated minimal energies between two measures \((\rho _0^-,\rho _0^+),(\rho _1^-,\rho _1^+)\in {\mathcal M}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\) of equal mass converge as well, as do the minimizing curves themselves.
1.2 Homogenization of periodic constraints
The second result concerns the effective limit as \(\varepsilon \rightarrow 0\) for
where \(h:{\mathbb R}^d \rightarrow [0,\infty )\) is \({\mathbb Z}^d\)-periodic. This problem is related to the periodic homogenization of elliptic functionals, see [6]. In fact it is a special case of \({\mathcal A}\)-quasiconvex homogenization treated in [7]. In particular it includes perforated domains, where \(h(x) = \mathbb {1}_U\) for some periodic open set \(U\subset {\mathbb R}^d\), modelling the optimal flow of an incompressible fluid through a porous medium (see Fig. 2), which has received a lot of attention in recent years, see e.g. [19, 24]. To the best knowledge of the authors this is a new development in the derivation of porous media equations from inhomogenous materials via optimal transport.
We will assume throughout the article that \(h : {\mathbb R}^d\rightarrow [0,\infty )\) satisfies
-
(A1)
h is \({\mathbb Z}^d\)-periodic.
-
(A2)
\(\{h>0\}\subset {\mathbb R}^d\) is open, connected, and Lipschitz bounded.
-
(A3)
h is measurable.
-
(A4)
\(h(x) \in \{0\}\cup [\alpha ,\frac{1}{\alpha }]\) for some \(\alpha \in (0,1]\), for almost every \(x\in {\mathbb R}^d\).
We note that h can be interpreted as either a function on the torus \({\mathbb T}^d\) or as a periodic function on \({\mathbb R}^d\). The connectedness of \(\{h>0\}\subset {\mathbb R}^d\) is stronger than connectedness of \(\{h>0\} \subset {\mathbb T}^d\).
Under these admissibility assumptions, we show \(\Gamma \)-convergence of \(E_{h_\varepsilon }\) to the homogenized transport cost \(E_{\hom }: {\mathcal {CM}}_+({\mathbb T}^d) \rightarrow [0,\infty ]\),
where only absolutely continuous curves \(\rho _t, V_t \ll {\mathcal L}^d\) are allowed. Otherwise \(E_{\hom }\) is defined to be \(\infty \).
The homogenized energy density \(f_{\hom }: [0,\infty ) \times {\mathbb R}^d \rightarrow [0,\infty ]\) is given by
and the infimum is taken among all \(\nu \in L^\infty ({\mathbb T}^d)\) such that \(0\le \nu (x) \le h(x)\) almost everywhere and \(\int _{{\mathbb T}^d} \nu (x)\,dx = m\), and all \(W\in L^2({\mathbb T}^d;{\mathbb R}^d)\) such that \({{\,\mathrm{div}\,}}W=0\text { in }\mathcal D'({\mathbb T}^d)\), and \(\int _{{\mathbb T}^d}W(x)\,dx = U\).
Theorem 1.2
Let \(h:{\mathbb T}^d\rightarrow [0,\infty )\) satisfy the assumptions (A1)– (A4). Then, as \(\varepsilon \rightarrow 0\), and \(\rho _t^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}\rho _t\) in \({\mathcal M}_+({\mathbb T}^d)\) for every \(t\in [0,1]\), \(E_{h_\varepsilon } : {\mathcal {CM}}_+({\mathbb T}^d) \rightarrow [0,\infty ]\) \(\Gamma \)-converges to \(E_{\hom }:{\mathcal {CM}}_+({\mathbb T}^d) \rightarrow [0,\infty ]\) in the sense that
- (lower bound):
-
if \(\rho _t^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}\rho _t\) in \({\mathcal M}_+({\mathbb T}^d)\) for every \(t\in [0,1]\), then
$$\begin{aligned} \liminf _{\varepsilon \rightarrow 0} E_{h_\varepsilon }((\rho _t^\varepsilon )_{t\in [0,1]})\ge E_{\hom }((\rho _t)_{t\in [0,1]}) \end{aligned}$$(12) - (upper bound):
-
for all curves \((\rho _t)_{t\in [0,1]}\) with \(E_{\hom }((\rho _t)_{t\in [0,1]})<\infty \) there exists a sequence \((\rho _t^\varepsilon )_{t\in [0,1]}\) in \({\mathcal {CM}}_+({\mathbb T}^d)\) with \(\rho _t^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}\rho _t\) in \({\mathcal M}_+({\mathbb T}^{d})\) for every \(t\in [0,1]\), and
$$\begin{aligned} \limsup _{\varepsilon \rightarrow 0} E_{h_\varepsilon }((\rho _t^\varepsilon )_{t\in [0,1]})\le E_{\hom }((\rho _t)_{t\in [0,1]}). \end{aligned}$$(13)
Remark 1.3
In the one-dimensional case \(E_{\hom }\) is given by
where \(F(m) {:}{=}\left( \inf \{\int _0^1\frac{1}{\nu (x)}\, dx: \nu \le h,\int _0^1\nu =m\} \right) ^{-1}\) is the mobility. Since \(f_{\hom }(m,U) = \frac{U^2}{F(m)}\) is convex (see Lemma 7.1), this means that the mobility \(m \mapsto F(m)\le m\) must be concave, which signifies a congestion effect.
In Sect. 2 we prove lower-semicontinuity and compactness of the functionals \(E_h\), \(E_0\) and \(E_{\hom }\), which is relevant for later sections. In Sect. 3 we find the dual problems of (3), (5) and (10) and characterize the minimizers by the respective Euler-Lagrange equations. In Sect. 4 we state the PDE solved by the steepest descent of the Helmholtz free energy functional \(\rho \mapsto RT\int _{\Omega }\rho (x)\log \rho (x)\, dx+\int _{\Omega }\rho (x)\psi (x)\, dx\) for each cost. Additionally, in Sect. 5 we give an example of an optimal curve under a nontrivial density constraint. Finally, in Sects. 6 and 7 we prove Theorem 1.1 and Theorem 1.2 respectively.
2 Compactness
Lemma 2.1
The functionals \(E_h\), \(E_0\), and \(E_{\hom }\) defined in (3), (5), and (10) are lower semicontinuous with respect to pointwise weak-\(*\) convergence on \({\mathcal {CM}}_+(\Omega )\), where \(\Omega \) is \({\mathbb R}^d\) or \({\mathbb T}^d\), \({\mathbb R}^d_-\sqcup {\mathbb R}^d_+\), or \({\mathbb T}^d\) respectively.
Given a fixed finite Radon measure \(\rho _0\in {\mathcal M}_+(\Omega )\), all families of curves starting in \(\rho _0\) with bounded energies have a subsequence converging pointwise weak-\(*\) in \({\mathcal {CM}}_+(\Omega )\).
Proof
Compactness in the constrained and homogenized case follows from the fact that in (3), (10), the functional is bounded from below by the Wasserstein action (1). For (10), this bound is shown in Lemma 7.1. The compactness then follows from the tightness of balls in Wasserstein space and the uniform continuity of sequences of curves with finite energy.
We show compactness in the membrane case in two steps. First, for \(0<r<R\) define a test function \(\eta _{r,R}\in \mathcal C_c^\infty ({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\) such that \(\eta _{r,R}(x) = \eta _{r,R}(|x|)\), \(\eta _{r,R} = 0\) outside of \(B(0,2R)\setminus B(0,r/2)\), \(\eta = 1\) in \(B(0,R) \setminus B(0,r)\), and \(|\nabla \eta _{r,R}| \le \frac{C}{r}\). Then
The last term is uniformly small in n as \(r\rightarrow \infty \), showing tightness of the \((\rho _t^{-,n},\rho _t^{+,n})_{t\in [0,1],n\in {\mathbb N}} \subset {\mathcal M}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\).
Now pick a countable family \((\eta _i)_{i\in {\mathbb N}} \subset \mathcal C_c^\infty ({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\) that is dense in \(\mathcal C_c^0({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\). Then whenever \(0\le t_0 \le t_1 \le 1\), \(n,i\in {\mathbb N}\), we have
It follows that \(\lim _{h \rightarrow 0} \sup _{n,t} \left| \langle \rho _{t+h}^n- \rho _t^n, \eta _i \rangle \right| = 0 \) for every i. By Helly’s Selection Theorem there exists a subsequence \((\rho _t^{n_k})_{t,\in [0,1], k\in {\mathbb N}}\) and a curve \((\rho _t^-,\rho _t^+)_{t\in [0,1]} \subset {\mathcal M}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\) such that \(\langle \rho _t^{n_k}, \eta _i \rangle \rightarrow \langle \rho _t, \eta _i \rangle \) for every \(i\in N\) and every \(t\in [0,1]\). By tightness, \(\rho _t^{n_k} {\mathop {\rightharpoonup }\limits ^{*}}\rho _t\) for every \(t\in [0,1]\), which proves the compactness.
In cases (3) and (10), to prove the lower bound, take a sequence of curves \((\rho _t^n,V_t^n)_{t\in [0,1],n\in {\mathbb N}}\) with finite energy. We see by Hölder’s inequality that
where \(E=E_{h}\) or \(E=E_{\hom }\), respectively. The right hand side is bounded, so that a subsequence \(V_t^n\) converges vaguely (not necessarily weak-\(*\) in the case of (5)) to some \(V\in {\mathcal M}([0,1]\times \Omega ;{\mathbb R}^d)\). We note that \(V_t\) is absolutely continuous with respect to dt, so that by the disintegration theorem \(V = \int _0^1 V_t\,dt\) for some \(V_t\in {\mathcal M}(\Omega ;{\mathbb R}^d)\) defined for almost every t, and \(\partial _t \rho _t + {{\,\mathrm{div}\,}}V_t = 0\) in \({\mathcal D}'((0,1)\times \Omega )\).
The same argument works in case (5), yielding finite measures \((V_t^-,V_t^+)_{t\in [0,1]} \subset {\mathcal M}({\mathbb R}^d_- \sqcup {\mathbb R}^d_+;{\mathbb R}^d)\). Additionally, \(f_t^n \rightharpoonup f_t\) in \(L^2([0,1] \times {\mathbb R}^{d-1})\). The limits then solve \(\partial _t \rho _t^\pm + {{\,\mathrm{div}\,}}V_t^\pm \pm f_t{\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm }=0\) in \({\mathcal D}'((0,1)\times ({\mathbb R}^d_- \sqcup {\mathbb R}^d_+))\), and by Fubini’s theorem and the weak lower semicontinuity of the norm
To show lower semicontinuity of the remaining term
with \(\Omega \in \{{\mathbb R}^d, {\mathbb R}^d_- \sqcup {\mathbb R}^d_+, {\mathbb T}^d\}\), we use Theorem 2.34 in [2], which states that for \(g:{\mathbb R}^M \rightarrow [0,\infty ]\) convex, lower semicontinuous, with recession function \(g^\infty :{\mathbb R}^M \rightarrow [0,\infty ]\), the functional defined on \({\mathcal M}(\Omega ;{\mathbb R}^M)\)
is vaguely sequentially lower semicontinuous. We apply this to the sequence \(P^n_t {:}{=}(\rho _t^n,V_t^n) \in {\mathcal M}(\Omega ;{\mathbb R}^{d+1})\), which in any case converges vaguely to \(P_t {:}{=}(\rho _t,V_t)\). The function g is either \(g(m,U) = \frac{|U|^2}{m}\) in cases (3) and (5) or \(g=f_{\hom }\) in case (10). We now have to do some extra work depending on the case:
In case (3), we have to show that \(\rho _t(A) \le \int _A h(x)\,dx\) for every open set \(A\subset \Omega \). This is the Portmanteau theorem, found in e.g. [2, Example 1.63].
In case (10), we know from Lemma 7.1 that \(f_{\hom }\) is convex and lower semicontinuous. We have to make sure that the singular part of \((\rho _t,V_t)\) vanishes. Indeed, this holds if \(h \in L^1({\mathbb T}^d)\), as in that case \(\frac{d\rho _t^n}{dx} \le \int _{{\mathbb T}^d} h(y)\,dy\) for every n, and this property is inherited by \(\rho _t\). Moreover, \(V_t \ll \rho _t\) if the energy is finite.
In case (5), we have nothing more to show. This completes the proof. \(\square \)
3 Duality and minimality
In this section, we characterize the dual problems to (3), (5), and (10) and find the Euler-Lagrange equations. To this end, we fix endpoints \(\rho _0,\rho _1\in {\mathcal M}_+(\Omega )\) with finite and equal mass.
3.1 Constrained optimal transport
Here we minimize the action functional
subject to \(0\le \rho _t(A) \le \int _A h(x)\,dx\) for every open \(A\subset \Omega \) and \(\partial _t \rho _t + {{\,\mathrm{div}\,}}V_t = 0\) in \({\mathcal D}'((0,1)\times \Omega )\), and \(\rho _0,\rho _1\) fixed. We introduce the Lagrange multiplier \(\phi _t\in {\mathcal C}^1([0,1]\times \Omega )\) and write by Sion’s minimax theorem
The last term is the constrained dual problem. Note that wherever \(h=\infty \), we formally recover the Kantorovich dual.
By the complementary slackness theorem, the minimizer \((\rho _t)_{t\in [0,1]}\) and maximizer \((\phi _t)_{t\in [0,1]}\) are characterized by the Euler-Lagrange equations
Here \(p_t:\Omega \rightarrow [0,\infty )\) is the Lagrange multiplier to the constraint on \(\rho _t\) acting as a pressure on the potential.
3.2 Optimal membrane transport
Here we minimize
subject to \(0\le \rho _t^\pm \) and \(\partial _t \rho _t^\pm + {{\,\mathrm{div}\,}}V_t^\pm \pm f_t{\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm }=0\) in \({\mathcal D}'((0,1)\times ({\mathbb R}^d_- \sqcup {\mathbb R}^d_+))\), and \(\rho _0^\pm ,\rho _1^\pm \) fixed. We introduce the Lagrange multipliers \(\phi _t^\pm \in {\mathcal C}^1([0,1]\times {\mathbb R}^d_\pm )\) and write by Sion’s minimax theorem, denoting \([\phi _t]({{\tilde{x}}}) = \phi _t^+({{\tilde{x}}}) - \phi _t^-({{\tilde{x}}}):{\mathbb R}^{d-1}\rightarrow {\mathbb R}\),
The last term is the constrained dual problem. Note that as \(\alpha \rightarrow \infty \), we formally recover the Kantorovich dual problem in \({\mathbb R}^d\), whereas as \(\alpha \rightarrow 0\), we formally recover two separate Kantorovich dual problems in \({\mathbb R}^d_\pm \).
By the complementary slackness theorem, the minimizers \((\rho _t^\pm )_{t\in [0,1]}\) and maximizers \((\phi _t^\pm )_{t\in [0,1]}\) are characterized by the Euler-Lagrange equations
3.3 Homogenized optimal transport
Here we minimize
subject to \(\partial _t \rho _t + {{\,\mathrm{div}\,}}V_t = 0\) in \({\mathcal D}'((0,1)\times {\mathbb T}^d)\), and \(\rho _0,\rho _1\) fixed. We introduce the Lagrange multiplier \(\phi _t\in {\mathcal C}^1([0,1]\times {\mathbb T}^d)\) and write by Sion’s minimax theorem
The last term is the dual problem. We check that for \(f_{\hom }(m,U) = \frac{|U|^2}{2m}\) on \([0,\infty ) \times {\mathbb R}^d\), we have
as expected.
By the complementary slackness theorem, the minimizer \((\rho _t)_{t\in [0,1]}\) and maximizer \((\phi _t)_{t\in [0,1]}\) are characterized by the Euler-Lagrange differential inclusions, which are stated in terms of the partial Legendre transform \(f_{\hom }^{*U}(m,P) {:}{=}\sup _U P\cdot U - f_{\hom }(m,U)\) as
This is a general formulation of congested mean field games. A similar model of congested mean field game is treated in e.g. [4].
To be more specific, in the idealized case \(f_{\hom }(m,U) = \frac{|U|^2}{2m^{1-\beta }}\), \(\beta \in [0,1)\), the mean field game equation is given by
4 Gradient flows
We now look at the formal constrained gradient flows of the functionals
with \(\psi \in \mathcal C^1(\Omega )\) the Gibbs free energy, and \(R,T>0\) the gas constant and the temperature respectively.
We will write down the PDE corresponding to steepest descent of F with costs given by (3), (5), and (10). Without loss generality we assume \(RT=1\).
4.1 Constrained gradient flow
Given \(\rho \in L^1\), we want to find \(V\in L^1_{\mathrm {loc}}(\Omega ;{\mathbb R}^d)\) minimizing
subject to \({{\,\mathrm{div}\,}}V \ge 0\) on \(\{\rho = h\}\). We introduce a Lagrange multiplier \( p \in L^1(\Omega )\), \(p \ge 0\), \(p(h-\rho ) = 0\), and write the above problem as
We see that the minimizer can be written \(V(x) = -\rho \nabla \phi (x)\), where \(\phi :\Omega \rightarrow {\mathbb R}\) solves the elliptic obstacle problem
Physically, the difference between \(\phi (x)\) and the chemical potential \( \log \rho (x) + \psi (x)\) acts as a hydrostatic pressure \(p(x)\ge 0\) with \(p(x)(h(x)-\rho (x)) = 0\).
Inserting V into the continuity equation yields a constrained version of the Fokker-Planck equation,
Note that in [13], the authors rigorously derive the unconstrained Fokker-Planck equation as the \(W_2\)-gradient flow of F. We note that this version of the constrained Fokker-Planck equation differs from the Stefan problem treated in e.g. [18], which is not mass-preserving.
4.2 Membrane gradient flow
Here, given \((\rho ^-,\rho ^+)\in L^1({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\), and a Gibbs free energy \((\psi ^-,\psi ^+)\in \mathcal C^1({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\), we find \(V^-,V^+,f\) minimizing
Inserting the minimizers into the continuity equation yields two Fokker-Planck equations coupled through the Teorell equation on the membrane [23],
4.3 Homogenized gradient flow
Given \(\rho \in L^1({\mathbb T}^d)\), we find \(V\in L^1_{\mathrm {loc}}({\mathbb T}^d;{\mathbb R}^d)\) minimizing
We see that \(V(x) \in \partial _P^- f_{\hom }^{*U}(\rho , - \nabla \log \rho (x) - \nabla \psi (x))\). Note that for \(f_{\hom }(m,U) = \frac{|U|^2}{2m^{1-\beta }}\), \(\beta \in (0,1)\), which is a reasonable choice according to Remark 1.3, and \(\psi = 0\), we recover the porous medium equation
We note that Theorem 1.2 does not imply convergence of gradient flows (35), (36) with \(h=h_\varepsilon \) to (40).
5 The stark constraint
In the following we give a simple one-dimensional example of an optimal curve under a nontrivial density constraint, which bounds the density by \(\lambda >0\) on \((0,\infty )\).
where \(\lambda ,m>0\). We call this the stark constraint. We construct an optimal curve \((\rho _t)_{t\in [0,1]}\) starting in \(\rho _0 =m \delta _0\) and ending in the uniform density \(\rho _1 = \lambda \mathbb {1}_{(0,\frac{m}{\lambda })}\,dx\).
We choose this example because the solution breaks conservation of momentum, while kinetic energy is conserved. The calculations in this case are straightforward but already quite lengthy. The complexity only increases in higher dimensions and with more variation in h.
We choose the following ansatz for the optimal curve:
We see that any \(\rho _t(A) \le \lambda {\mathcal L}(A)\) for any Borel \(A\subseteq (0,\infty )\), and the boundary conditions are satisifed if and only if \(x_0 = 0\) and \(x_1 = \frac{m}{\lambda }\). The momentum field \(V_t=\lambda \dot{x}_t{\mathcal L}|_{(0,x_t)}\) solves the continuity equation
with action given by
where \(G(y)=\frac{2}{3} \lambda ^{1/2}y^{3/2}\). The minimizer satisfies \(\frac{d}{dt}G(x_t)=c\), where c is the unique constant compatible with the boundary conditions \(x_0=0\) and \(x_1=\frac{m}{\lambda }\). We see that
and consequently
We claim that \(\rho _t\) is optimal among all curves independent of the ansatz. To see this we consider the dual problem. Let
where \(\phi _0(0)=0\) and \(\phi _0(x)=\infty \) for \(x>0\). Formally, we have
which is half the primal cost \(\int _0^1|\frac{d}{dt}G(x_t)|^2\, dt\). By duality \(\rho _t\) and \(\phi _t\) must be optimal. In fact, they formally solve (23) with pressure
However, at \(x=0\), \(\phi _t\) is not differentiable and at \(t=0\), it is not continuous. To make the optimality precise, we approximate \(\phi \) with \(\mathcal C^1\)-functions \(\phi _t^\varepsilon (x) = \frac{2}{3} \frac{m}{\lambda }t^{-\frac{1}{3}}\eta ^\varepsilon (x)\), with \(\eta ^\varepsilon \rightarrow x_+\) uniformly and \((\eta ^\varepsilon )' - \mathbb {1}_{[0,\infty )} \rightarrow 0\) in \(L^1({\mathbb R})\). Then for every \(\delta >0\), we have
This shows that \((\rho _t)_{t\in [\delta ,1-\delta ]}\) is optimal. Letting \(\delta \rightarrow 0\), optimality of \((\rho _t)_{t\in [0,1]}\) follows.
6 The membrane limit
We now prove Theorem 1.1. Recall that \(h^\varepsilon :{\mathbb R}^d\rightarrow [0,\infty ]\) is given by the stark constraint
with \(\alpha \in (0,\infty )\) fixed and \(\varepsilon \rightarrow 0\).
Because \(\Gamma \)-convergence is compatible with partial minimization, the minimum costs for all curves also \(\Gamma \)-converge.
Proof
(Proof of the lower bound) Consider a family of curves of bounded nonnegative measures \((\rho _t^\varepsilon )_{t\in [0,1],\varepsilon >0} \subset {\mathcal M}_+({\mathbb R}^d)\) with \(\rho _t^\varepsilon (dx) \le h^\varepsilon (x)\, dx\), where \(\rho _t^\varepsilon |_{{\mathbb R}^{d-1}\times (-\infty ,0]}{\mathop {\rightharpoonup }\limits ^{*}}\rho _t^-\) and \(\rho _t^\varepsilon |_{{\mathbb R}^{d-1}\times (0,\infty )}{\mathop {\rightharpoonup }\limits ^{*}}\rho _t^+\). Also find the respective minimizing momentum fields \((V_t^\varepsilon )_{t\in [0,1],\varepsilon >0} \subset {\mathcal M}({\mathbb R}^d, {\mathbb R}^d)\) such that \(\partial _t \rho _t^\varepsilon + {{\,\mathrm{div}\,}}V_t^\varepsilon = 0\) in \({\mathcal D}'((0,1)\times {\mathbb R}^d)\) and
We shall assume throughout the proof that (52) is bounded by some constant independent of \(\varepsilon \) by extracting a subsequence, as without the existence of a bounded energy subsequence there is nothing to prove.
We now employ the standard dimension reduction technique of blowing up the thin constrained region, as was done in e.g. [12]. We introduce the notation \(x = ({{\tilde{x}}}, x_d) \in {\mathbb R}^d\). To that end, let \(T_\varepsilon : {\mathbb R}^d \rightarrow {\mathbb R}^d\) be defined by
so that \(T_\varepsilon ({\mathbb R}^{d-1}\times (0,1)) = {\mathbb R}^{d-1}\times (0,\varepsilon )\).
We define \(\pi _t^\varepsilon = (T_\varepsilon )_\# \rho _t^\varepsilon \) and \(W_t^\varepsilon (x) = DT_\varepsilon (T_\varepsilon ^-1(x)) V_t^\varepsilon (T_\varepsilon ^{-1}(x))\), i.e.
By this choice, \(\partial _t \pi _t^\varepsilon + {{\,\mathrm{div}\,}}W_t^\varepsilon = 0\), and
Because \(\pi _t^\varepsilon \le \alpha \varepsilon ^2\) in \({\mathbb R}^{d-1} \times (0,1)\), it follows that \({{\tilde{W}}}_t^\varepsilon \rightarrow 0\) strongly in \(L^2([0,1] \times {\mathbb R}^{d-1}\times (0,1))\), and that a subsequence of \((W_t^\varepsilon )_d\) converges weakly in \(L^2([0,1] \times {\mathbb R}^{d-1} \times (0,1))\) to some \(f_t \in L^2([0,1] \times {\mathbb R}^{d-1} \times (0,1))\). In addition, \(\pi _t^\varepsilon \rightarrow 0\) in \(L^\infty ([0,1]\times {\mathbb R}^{d-1} \times (0,1))\). Thus, the continuity equation holds for the limit, i.e. \(0 = \partial _t 0 + {{\,\mathrm{div}\,}}(0,f_t) = \partial _d f_t\) in \({\mathcal D}'((0,1)\times {\mathbb R}^{d-1} \times (0,1))\), i.e. \(f_t({{\tilde{x}}}, x_d) = f_t({{\tilde{x}}})\). By Mazur’s Lemma, it follows that
Dividing both sides by \(\alpha \) yields the part of the lower bound in the membrane \({\mathbb R}^{d-1} \times (0,\varepsilon )\). For the outer part of the membrane we find by Jensen’s inequality
because the energy is finite. Also \(\int _0^1 \Vert W^\varepsilon _t\Vert _{L^2({\mathbb R}^{d-1}\times (0,1))}^2 \,dt \le C\), from which we infer that a subsequence of \(W^\varepsilon _t\) converges vaguely to some Radon measure \(W = (W_t)_{t\in [0,1]} \in {\mathcal M}([0,1]\times {\mathbb R}^d;{\mathbb R}^d)\) with \(\partial _t \pi _t + {{\,\mathrm{div}\,}}W_t = 0\), where
By Lemma 2.1 (\(h=\infty \)) we have
All in all we obtain
We define \(V_t^-:=W_t|_{{\mathbb R}^{d-1}\times (-\infty ,0]}\) and \(V_t^+:=W_t(\cdot -e_d)|_{{\mathbb R}^{d-1}\times (0,\infty )}\). Let \(\phi \in {\mathcal C}_c^\infty ((0,1)\times {\mathbb R}^d_-)\) and let \(\Phi \in {\mathcal C}^\infty _c((0,1)\times {\mathbb R}^{d-1}\times (-\infty ,1))\) be an extension of \(\phi \). Then
which shows the continuity eq. (6) in the lower half-space. The upper half-space works similarly. \(\square \)
To prove the upper bound, we find it is useful to represent the limit problem in Lagrangian coordinates. For curves in \(W_2({\mathbb R}^d)\) with finite kinetic action, this is done by the well-known superposition principle due to Smirnov [22] and applied to optimal transport in e.g. [1]. Here, the particle trajectories may jump between the half-spaces and are thus not continuous. A natural class of curves are the special curves of bounded variation defined below, see also Fig. 3.
Definition 6.1
Given \(d\in {\mathbb N}\setminus \{0\}\), we define the class \(SBV_2^\div \) of curves in \({\mathbb R}^d_- \sqcup {\mathbb R}^d_+\) containing all \(X : [0,1] \rightarrow {\mathbb R}^d_- \sqcup {\mathbb R}^d_+\) such that X is absolutely continuous up to a finite jump set \(J_X \subset (0,1)\), with velocity \(\int _{[0,1] \setminus J_X} |\dot{X}_t|^2\,dt < \infty \), and mirrored traces at the jumps \(X_{t^-} = SX_{t^+}\) for all \(t\in J_X\), where \(S:{\mathbb R}^d_- \sqcup {\mathbb R}^d_+ \rightarrow {\mathbb R}^d_- \sqcup {\mathbb R}^d_+\) is the mirror function mapping \(({{\tilde{x}}}, x_d)\in {\mathbb R}^d_\pm \) to \( ({{\tilde{x}}}, -x_d) \in {\mathbb R}^d_\mp \).
We also define the subclass \(SBV_2^0\) as all curves \(X\in SBV_2^\div \) with jump traces on the boundary \(\partial {\mathbb R}^d_\pm \).
We equip \(SBV_2^\div \) with the notion of weak convergence, where \(X^k \rightharpoonup X\) if \(X^k {\rightarrow } X\) in \(L^1([0,1];{\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\), \(\dot{X}^k \rightharpoonup \dot{X}\) weakly in \(L^2([0,1];{\mathbb R}^d)\), and the measures \(\left( \sum _{t\in J_{X^k}} \sigma (t) \delta _t\right) _{k\in {\mathbb N}} \subset {\mathcal M}([0,1])\) converge weakly-\(*\) in \({\mathcal M}([0,1])\) to some \(\nu \), with \(\sum _{t\in J_{X}} \sigma (t) \delta _t = \nu |_{(0,1)}\), where \(\sigma \in \{\pm 1\}\) denotes the sign of the \(e_d\) component of the jump. (Here we need to exclude jumps converging to 0 or 1, as they vanish from the jump set)
We now state some elementary properties of \(SBV_2^\div \).
Lemma 6.2
The notion of weak convergence in \(SBV_2^\div \) is metrizable. The underlying metric space is Polish, and \(SBV_2^0\) is a weakly closed subset. Given \(M>0\), the set
is weakly sequentially compact, with \(SBV_2^\div = \bigcup _{M\in {\mathbb N}} A_M\).
Proof
Since all of \(L^1([0,1;{\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\), \(L^2([0,1];{\mathbb R}^d)\) with the weak topology, and \({\mathcal M}([0,1])\) with the weak-\(*\) topology are metrizable and complete, these properties are inherited by \(SBV_2^\div \):
If \(X^k \rightarrow X\) in \(L^1([0,1];{\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\), \(\dot{X}^k \rightharpoonup V \in L^2([0,1];{\mathbb R}^d)\), and \(\sum _{t\in J_{X^k}} \sigma (t) \delta _t {\mathop {\rightharpoonup }\limits ^{*}}\nu \in {\mathcal M}((0,1))\) vaguely, then \(\dot{X} = V\), \(\# J_X = |\nu |((0,1))\), and \(\sum _{t\in J_X} \sigma (t) \delta _t = \nu |_{(0,1)}\).
This shows that weak convergence in \(SBV_2^\div \) is metrizable and complete. For separability, note that while \({\mathcal M}([0,1])\) is not separable, its subset \(\{\sum _{t\in J} \sigma (t) \delta _t\,:\, J\subset [0,1]\) finite\(, \sigma (t) \in \{\pm 1\}\}\) is. The fact that \(SBV_2^\div = \bigcup _{M\in {\mathbb N}} A_M\) follows from the definition. The weak sequential compactness of \(A_M\) also follows from the above argument. \(\square \)
In the presence of a membrane, we see that some – but not all – particles at the membrane, will jump between the upper and lower half spaces. We model this using a stochastic jump process with rate determined by the ratio of the flux f and the density of \(\rho ^\pm \).
Proposition 6.3
Let \((\rho _t^-,\rho _t^+)_{t\in [0,1]} \subset {\mathcal M}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\) be a curve with finite limit action and finite mass, with \(\partial _t \rho _t^\pm + {{\,\mathrm{div}\,}}V_t^\pm \pm f_t{\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm } = 0\). Then there exists a measure \(P\in {\mathcal M}_+(SBV_2^0)\) with mass \(P(SBV_2^0) = \rho _0^-({\mathbb R}^d_-) + \rho _0^+({\mathbb R}^d_+)\) such that the following hold:
-
\(X_t \sim (\rho _t^-, \rho _t^+)\) for every \(t\in [0,1]\).
-
\(E[\int _0^1 |\dot{X}_t|^2\,dt] \le \sum _{\pm } \int _0^1 \int _{{\mathbb R}^d_\pm }\left| \frac{dV_t^\pm }{d\rho _t^\pm }\right| ^2\,d\rho _t^\pm \,dt\).
-
The Borel measures \(F_\pm \in {\mathcal M}_+([0,1] \times \partial {\mathbb R}^d_\pm )\) defined as \(F_\pm (A) = E[\#\{t\in J_X\,:\,(t,X_{t^-})\in A\}]\) are absolutely continuous with respect to \(dt\otimes d{\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm }\) with densities \(g_t^\pm \) satisfying \(g_t^\pm ({{\tilde{x}}}) \le (f_t({{\tilde{x}}}))^\pm \) for almost every \((t,{{\tilde{x}}})\).
Note that for all nonnegative measures \(P\in {\mathcal M}_+(SBV_2^0)\) with \(E\left[ \int _0^1 |\dot{X}_t|^2\,dt\right] <\infty \) and \(\sum _\pm \int _0^1 \int _{\partial {\mathbb R}^d_\pm } |g_t^\pm |^2\,d{\mathcal H}^{d-1}\,dt< \infty \), the laws \( (\rho _t^-, \rho _t^+)=E[\delta _{X_t}]\) have finite limit action, with \(\partial _t \rho _t^\pm + {{\,\mathrm{div}\,}}V_t^\pm + (g_t^\pm - g_t^\mp \circ S){\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm }=0\), where \((V_t^-,V_t^+)=E[\dot{X}_t\delta _{X_t}]\), and
by Jensen’s inequality.
For the proof, we follow the argument in [1, Theorem 4.4].
Proof
Step 1 Instead of \((\rho _t^-, \rho _t^+)_{t\in [0,1]}\) we consider the mollified versions \(\rho _t^{\pm \varepsilon }(dx) {:}{=}\rho _t^\pm *\phi ^{\pm \varepsilon }(dx) + \varepsilon e^{-|x|^2}(dx)|_{{\mathbb R}^d_{\pm }}\), where \(\phi ^{\pm \varepsilon }\in \mathcal C_c^\infty (B(\pm \varepsilon e_d, \varepsilon ))\) is a Dirac sequence with \(\phi ^{-\varepsilon }\circ S = \phi ^{+\varepsilon }\).
We note that after the mollification, we have \(\rho _t^{\pm \varepsilon } \in \mathcal C^\infty ({\mathbb R}^d_{\pm })\), Lipschitz, and strictly positive. If \(\partial _t \rho _t^\pm + {{\,\mathrm{div}\,}}V_t^\pm \pm f_t{\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm }=0\), then setting \(V_t^{\pm \varepsilon } = V_t^\pm *\phi ^{\pm \varepsilon }\), \(v_t^{\pm \varepsilon } = V_t^{\pm \varepsilon }/\rho _t^{\pm \varepsilon }\), and \(g_t^{\pm \varepsilon } = \pm f_t{\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_{\pm }} *\phi ^{\pm \varepsilon }\), we have
with \(v_t^{\pm \varepsilon }\) locally Lipschitz and satisfying the boundary values \(v_t^{\pm \varepsilon } = 0\) on \(\partial {\mathbb R}^d_\pm \) since \(V_t^{\pm \varepsilon }=0\) on \(\partial {\mathbb R}^d_\pm \) and \(\rho _t^{\pm \varepsilon }>0\) in \({\mathbb R}^d_\pm \). By Jensen’s inequality and the convexity of \((V,\rho )\mapsto \frac{|V|^2}{\rho }\) in \({\mathbb R}^d\times (0,\infty )\) we may estimate
We note that \(g_t^{\pm \varepsilon }\) is no longer supported on the boundary but in a \(2\varepsilon \)-neighborhood of the same.
We now define a random curve \(X \in SBV_2^\div \). First, its starting point \(X_0\in {\mathbb R}^d_- \sqcup {\mathbb R}^d_+\) is distributed according to \((\rho _0^{-\varepsilon },\rho _0^{+\varepsilon })\). Independently of the starting point, take a random realization of the 1-Poisson process, yielding discrete times \({\mathcal T}= \{t_i\}_{i\in {\mathbb N}} \subset [0,\infty )\). Then define the random curve \((X_t,T_t):[0,1]\rightarrow {\mathbb R}^d_-\sqcup {\mathbb R}^d_+\times [0,\infty )\) as the solution to the ODE
Here \(\sigma :[0,\infty ) \rightarrow \{-1,1\}\) is the function indicating whether \(X_t\) is in the lower or upper half-space, with \(\sigma (0)\) determined by the starting half-space of \(X_0\) and jump set \(J_\sigma = {\mathcal T}\). Clearly \(X\in SBV_2^\div \) almost surely. In particular, if \(X_t\) is in the lower half-space, it jumps to the upper half-space whenever \(T_t=t_i\) and vice versa. Because its derivative is nonnegative, \(T_t\) is nondecreasing.
By using Itô’s formula for semimartingales with jumps (Sect. 2.1 in [21]) we see that the distribution \(X_t \sim (\mu _t^{-\varepsilon },\mu _t^{+\varepsilon })\) solves the Cauchy problem
as does \((\rho _t^{-\varepsilon },\rho _t^{+\varepsilon })\), since \((g_t^{\pm \varepsilon })_+ - (g_t^{\mp \varepsilon })_+\circ S = g_t^{\pm \varepsilon }\), and \((\rho _t^{-\varepsilon },\rho _t^{+\varepsilon })\) solves (67). Because the solution is unique by the Cauchy-Kovalevskaya theorem, we have \(\mu _t^{\pm \varepsilon } = \rho _t^{\pm \varepsilon }\) for every \(t\in [0,1]\). We take \(P^\varepsilon \in {\mathcal M}_+(SBV_2^\div )\) to be the law of X. Defining for a Borel \(A\subset [0,1]\times {\mathbb R}^d_\pm \) the nonnegative measure \(F^{\pm \varepsilon }(A) {:}{=}E^\varepsilon [ \# \{t\in J_X\,:\,(t,X_{t^-})\in A\}]\), we note that \(F^{\pm \varepsilon }\) is absolutely continuous with respect to \(dt\otimes dx\) with density \(g_t^{\pm \varepsilon }(x)\) according to the construction.
Step 2 The next step is to show that the \(P^\varepsilon \in {\mathcal M}_+(SBV_2^\div )\) are tight. To this end we use the weakly sequentially compact sets \(A_M\) from Lemma 6.2 and show that \(\lim _{M \rightarrow \infty } \sup _{\varepsilon > 0} P^\varepsilon (SBV_2^\div \setminus A_M) = 0\). We check each of the three conditions defining \(A_M\):
since the \((\rho ^\varepsilon _0)_{\varepsilon >0}\subset {\mathcal M}_+({\mathbb R}^d_- \sqcup {\mathbb R}^d_+)\) are tight, where \(\rho _0^\varepsilon =(\rho _0^{-\varepsilon },\rho _0^\varepsilon )\).
For the second condition, this follows from the finity of the transport part of the energy and Markov’s inequality:
For the third condition, this follows from the finity of the membrane part of the energy and Hölder’s and Markov’s inequalities. In order to use Hölder’s inequality, we note that if \(|X_0|\le M\) and \(\int _0^1 |\dot{X}_t|^2 \,dt\le M^2\), then \(|X_t|\le 2M\) for all t, independently of the jump set. Thus,
This shows that the \((P^\varepsilon )_{\varepsilon > 0} \subset {\mathcal M}_+(SBV_2^\div )\) are weakly tight, so that by Prokhorov’s theorem they have a weakly convergent subsequence \(P^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}P\in {\mathcal M}_+(SBV_2^0)\). It is easily seen that the law of \(X_t\) under P is \(X_t\sim (\rho _t^-,\rho _t^+)\). Because the pathwise energy is weakly-\(*\) lower semicontinuous, it follows from the Portmanteau theorem
For the membrane part, note that as \(P^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}P\), we have for any relatively open \(A\subset [0,1]\times {\mathbb R}^d_\pm \) that
since \(X\mapsto \# \left\{ t\in J_X\,:\,(t,X_{t^-})\in A\right\} \) is weakly sequentially lower semicontinuous. On the other hand, clearly \(F^{\pm \varepsilon } {\mathop {\rightharpoonup }\limits ^{*}}(\pm f_t({{\tilde{x}}}))_+ dt\otimes d{\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm }({{\tilde{x}}})\), so that \(F^\pm \) is absolutely continuous with density at most \((\pm f_t({{\tilde{x}}}))_+\). \(\square \)
Example 6.4
Take \(\rho ^\pm = \frac{1}{\omega _{d-1}R^{d-1}} {\mathcal H}^{d-1}|_{\partial {\mathbb R}^d_\pm \cap B(0,R)}\) and take \(\rho _t^- = (1-t)\rho ^-\), \(\rho _t^+ = t \rho ^+\). Then \(V_t^\pm = 0\), \(f_t({{\tilde{x}}}) = \frac{1}{\omega _{d-1}R^{d-1}} \mathbb {1}_{B(0,R)}({{\tilde{x}}})\) in the continuity equation. The probability measure \(P\in {\mathcal P}(SBV_2^0)\) is the uniform distribution on the curves
for \(t_0\in [0,1], x_0\in \partial {\mathbb R}^d_- \cap B(0,R)\). We see that there is no way to choose the jump times deterministically.
We now use this Lagrangian representation to prove the upper bound. Roughly, instead of having particles teleport across the membrane of width \(\varepsilon >0\), we replace a particle entering the membrane from one side with a different one exiting on the other side. This technique is inspired by the magical illusion “The Tranported Man" from the novel The Prestige [20], where instead of actually teleporting himself, a magician simply exits the stage as his identical twin brother enters it at the same time. The illusion is the difference between the Eulerian and the supposed Lagrangian formulation of the transport.
Proof
(Proof of the upper bound) Take a curve with finite limit action \((\rho _t^-, \rho _t^+)_{t\in [0,1]}\) and represent it using \(P\in {\mathcal M}_+(SBV_2^0)\) as in Proposition 6.3. We shall modify these paths to pay heed to the finite thickness of the membranes. To this end, we modify the curves in \({{\,\mathrm{supp}\,}}P\) as follows:
For any measure \(F^\pm \in {\mathcal M}_+([0,1]\times \partial {\mathbb R}^d_\pm )\) with absolutely continuous density \(dF^\pm = f_t^\pm ({{\tilde{x}}})\,(dt \otimes d{\mathcal H}^{d-1}({{\tilde{x}}}))\), define a stopping time \(\tau _F:SBV_2^0 \rightarrow [0,\infty ]\) through
Note that \(\tau _F\) is Borel-measurable and decreasing in F.
On the other hand, given a measurable stopping time \(\tau :SBV_2^0 \rightarrow [0,\infty ]\), define a Borel measure \(F_\tau ^\pm \in {\mathcal M}_+([0,1]\times \partial {\mathbb R}^d_\pm )\) through
where the expectation is taken with respect to P. Note that \(F_\tau \) is decreasing in \(\tau \) and \(F_\tau ^\pm \le F^\pm \). In particular, \(F_\tau ^\pm \) is absolutely continuous.
Define for every \(\varepsilon >0\) first \(\tau _0 {:}{=}\infty \), then \(F_k^\pm {:}{=}F_{\tau _k}^\pm \in {\mathcal M}_+([0,1]\times \partial {\mathbb R}^d_\pm )\) and \(\tau _{k+1} {:}{=}\tau _{F_k}\). Then \((\tau _k)_{k\in {\mathbb N}} \subset [0,\infty ]^{SBV_2^0}\) forms a nonincreasing sequence of Borel-measurable stopping times and converges pointwise to some Borel-measurable \(\tau _\varepsilon :SBV_2^0\rightarrow [0,\infty ]\). Likewise, \((F_k^\pm )_{k\in {\mathbb N}} \subset {\mathcal M}_+([0,1]\times \partial {\mathbb R}^d_\pm )\) forms a nonincreasing sequence and converges weakly-\(*\) to a a limit measure \(F^{\pm \varepsilon } \in {\mathcal M}_+([0,1]\times \partial {\mathbb R}^d_\pm )\) with density \(f_t^{\pm \varepsilon }({{\tilde{x}}}) \le f_t^\pm ({{\tilde{x}}})\) for every \((t,{{\tilde{x}}})\in [0,1]\times \partial {\mathbb R}^d_\pm \). By continuity, we then have
for P-almost every \(X\in SBV_2^0\), and
Now we define the stopped process \(SBV_2^0 \ni X \mapsto X^\varepsilon \in SBV([0,1];{\mathbb R}^d)\) through
We note that in the stopped process, the first \(\alpha \varepsilon ^2\) particles to attempt a jump across the membrane at \({{\tilde{x}}}\) are instead frozen inside the membrane. This allows us to easily construct the recovery sequence as follows:
We define the momentum field first as a measure \(V\in {\mathcal M}([0,1]\times {\mathbb R}^d;{\mathbb R}^d)\) and later show that V is absolutely continuous in time:
Here \([X_t^\varepsilon ]\in {\mathbb R}^d\) denotes the jump of \(X_t^\varepsilon \), which is always parallel to \(e_d\).
By the linearity of the continuity equation, it is clear that \(\partial _t \rho _t^\varepsilon + {{\,\mathrm{div}\,}}V^\varepsilon = 0\) in \({\mathcal D}'((0,1)\times {\mathbb R}^d)\).
Define \(U_t^\varepsilon \subset {\mathbb R}^{d-1}\times (0,\varepsilon )\) as the set
We claim that \(\rho _t^\varepsilon |_{{\mathbb R}^{d-1}\times (0,\varepsilon )} = \alpha \varepsilon {\mathcal L}^d|_{U_t^\varepsilon }\), see Fig. 4. We test this against cylindrical sets \({{\tilde{A}}} \times I\), with \({{\tilde{A}}} \subset {\mathbb R}^{d-1}\) and \(I\subset (0,\varepsilon )\) Borel:
Here we used (79), (80), Fubini’s theorem, and the change of variables formula. The claim is shown. In particular, \(\rho _t^\varepsilon \le h^\varepsilon \). It follows that \(\rho _t^\varepsilon |_{{\mathbb R}^{d-1}\times (-\infty ,0]} {\mathop {\rightharpoonup }\limits ^{*}}\rho _t^-\) and \(\rho _t^\varepsilon |_{{\mathbb R}^{d-1}\times (0,\infty ))} {\mathop {\rightharpoonup }\limits ^{*}}\rho _t^+\) for every \(\varepsilon > 0\), since \(P(\tau _\varepsilon (X)<\infty , |X_1^\varepsilon | < R) \le C(d)R^{d-1}\alpha \varepsilon ^2\), whereas by Prokhorov’s theorem \(P(|X_1^\varepsilon | > R) \rightarrow 0\) as \(R\rightarrow \infty \). All in all, \(|\rho _t^\varepsilon - \rho _t| \rightarrow 0\).
Finally, we have to estimate the action. Outside of the membrane, this is simply Jensen’s inequality:
Inside the membrane, we first note that \(V^\varepsilon \) is absolutely continuous with respect to (t, x), with density
so that
Combining (86) with (88) yields the upper bound
\(\square \)
Example 6.5
Consider \(d=1\) and set \(\rho _t^- = (1-t)\delta _0\) and \(\rho _t^+ = t\delta _0\). This is an optimal curve connecting its two end points. The flux is \(f(t) = 1\) and the cost is simply \(\frac{1}{\alpha }\).
Another optimal curve is given by \(\rho _t^- = \mathbb {1}_{[-1+t,0]}\), \(\rho _t^+ = \mathbb {1}_{[0,t]}\). This curve is also optimal, with the same flux \(f(t) = 1\) and cost \(1 + \frac{1}{\alpha }\).
For \(d>1\), the optimal curve between \(\rho _0 = (\delta _0, 0)\) and \(\rho _1 = (0,\delta _0)\) is supported on the curves
with \(t_0\in [0,1]\) and \({{\tilde{x}}}_0 \in \partial {\mathbb R}^d_-\). The distribution \(\mu (dt_0,d{{\tilde{x}}}_0) \in {\mathcal P}([0,1]\times \partial {\mathbb R}^d_-)\) of crossing coordinates \((t_0,{{\tilde{x}}}_0)\) then minimizes
among all probability measures. A simple calculation shows that
with \(c(d, \alpha ) > 0\) chosen uniquely so that \(\mu \) is a probability measure. We note that for \(d=1\), the only crossing point is \({{\tilde{x}}}_0 = 0\), and we recover \(\frac{d\mu }{dt_0} = 1\).
7 Homogenization
In this section we prove Theorem 1.2, i.e. we will show that \(E_{h_\varepsilon }\) \(\Gamma \)-converges to \(E_{\hom }\).
Let us start by collecting a few properties of the functional \(E_{\hom }\) defined in (10).
Lemma 7.1
The following properties hold:
-
(i)
For all \(m\in (0,\int _{{\mathbb T}^d} h(x)\, dx]\) there exist minimizers \(\nu (m,U)\in L^1({\mathbb T}^d)\) and \(W(m,U)\in L^2({\mathbb T}^d;{\mathbb R}^d)\) of \(f_{\hom }(m,U)\).
-
(ii)
The map \((m,U)\mapsto f_{\hom }(m,U)\) is convex, lower semicontinuous, and 2-homogeneous in U.
-
(iii)
\(E_{\hom }\) is convex and lower semicontinuous.
-
(iv)
There is a constant C depending only on \(\{h>0\}\) and \(\alpha \) such that \(\frac{|U|^2}{m} \le f_{\hom }(m,U) \le C \frac{|U|^2}{m}\) for all \(U\in {\mathbb R}^d\), \(m\in (0,\int _{{\mathbb T}^d} h(x)\,dx]\).
-
(v)
If \(m\le \inf _{{\mathbb T}^d} h\) then \(f_{\hom }(m,U)=\frac{|U|^2}{m}\).
-
(vi)
With C as above,
$$\begin{aligned} f_{\hom }(m,U+Z) \le f_{\hom }(m,U) + C\frac{|U+Z||Z|}{m} , \end{aligned}$$(93)for all \(U,Z\in {\mathbb R}^d\), \(m\in (0,\int _{{\mathbb T}^d} h(x)\,dx]\). In addition, \(f_{\hom }\) is locally Lipschitz in \((0,\int _{{\mathbb T}^d}h(x)\,dx]\times {\mathbb R}^d\).
Proof
- (i):
-
First note that \(f_{\hom }(m,U)\ge 0\). We take minimizing sequences \((\nu ^n)_{n\in {\mathbb N}} \subset L^\infty ({\mathbb T}^d)\), \((W_n)_{n\in {\mathbb N}} \subset L^2({\mathbb T}^d;{\mathbb R}^d)\). Then \(0\le \nu ^n(x) \le h(x)\) almost everywhere and \(\int \nu ^n(x)\, dx=m\). By the Banach-Alaoglu Theorem there exists a subsequence \(\nu ^n\) converging weakly-\(*\) in \(L^\infty ({\mathbb T}^d)\) to some \(\nu \) satisfying \(0\le \nu (x) \le h(x)\) almost everywhere and \(\int \nu (x)\, dx=m\). Since \(\int _{{\mathbb T}^d} |W_n(x)|^2\,dx \le \frac{1}{\alpha } \int \frac{|W_n(x)|^2}{\nu _n(x)}\,dx\), we also get a subsequence \(W_n \rightharpoonup W\) in \(L^2({\mathbb T}^d;{\mathbb R}^d)\), with \({{\,\mathrm{div}\,}}W = 0\) in \({\mathcal D}'({\mathbb T}^d)\) and \(\int _{{\mathbb T}^d} W(x)\,dx = U\). By the convexity and lower semicontinuity of the function \((m, U) \mapsto \frac{|U|^2}{m}\) and Mazur’s Lemma, we have
$$\begin{aligned} \int _{{\mathbb T}^d} \frac{|W(x)|^2}{\nu (x)}\,dx \le \liminf _{n \rightarrow \infty } \int _{{\mathbb T}^d} \frac{|W_n(x)|^2}{\nu _n(x)}\,dx, \end{aligned}$$(94)which shows that \((\nu , W)\) are minimizers.
- (ii):
-
These properties are inherited from the function \((\nu , W) \mapsto \frac{|W|^2}{\nu }\).
- (iii):
-
This is the result of Lemma 2.1.
- (iv):
-
The lower bound follows from Jensen’s inequality. For the upper bound, consider the vector field \(X_U\in L^2(\{h>0\};{\mathbb R}^d)\) from Lemma 7.2 below, and find \(\nu \in L^1({\mathbb T}^d)\) such that \(h(x) \ge \nu (x) \ge \min (m, \alpha )\) almost everywhere in \(\{h>0\}\), and \(\int _{{\mathbb T}^d} \nu (x) \,dx = m\). Then
$$\begin{aligned} \int _{{\mathbb T}^d} \frac{|X_U(x)|^2}{\nu (x)}\,dx \le \int _{\{h>0\}} \frac{|X_U(x)|^2}{\min (m,\alpha )}\,dx \le C(h) \frac{|U|^2}{m}. \end{aligned}$$(95) - (v):
-
The lower bound is shown in (iv). For the upper bound, take \(\nu (x) = m\) and \(W(x) = U\).
- (vi):
-
This follows from (ii) and (iv): Let \(p\in \partial _U^-f_{\hom }(m,U)\). Then
$$\begin{aligned} C\frac{|U|^2}{m} \ge f_{\hom }(m,U+\frac{|U|}{|p|}p) - f_{\hom }(m,U) \ge |p||U|, \end{aligned}$$(96)so that \(|p|\le C\frac{|U|}{m}\).
Now take \(U,Z\in {\mathbb R}^d\), \(m\in (0,\int _{{\mathbb T}^d} h(x)\,dx]\), \(p\in \partial _U^-f_{\hom }(m, U+Z)\). Then
which is (93). In addition, for \(0<m_1<m_2\le \int _{{\mathbb T}^d} h(x) \, dx\), we have
To see the first inequality, start with a minimizer \(\nu _1 = \nu (m_1,U), W_1 = W(m_1,U)\). Then \(\left( \nu _1 + (m_2 - m_1) \frac{h-\nu _1}{h-m_1}, W_1\right) \) is a competitor for \(f_{\hom }(m_2, U)\).
To see the second inequality, start with a minimizer \(\nu _2 = \nu (m_2,U), W_2 = W(m_2,U)\). Then \(\left( \frac{m_1}{m_2} \nu _2, W_2\right) \) is a competitor for \(f_{\hom }(m_1,U)\).
Together with the growth condition (iv) we obtain the local Lipschitz property on \((0,\int _{{\mathbb T}^d} h(x)\, dx]\times {\mathbb R}^d\). \(\square \)
The following lemma turns out to be crucial.
Lemma 7.2
There is a constant \(C>0\) depending only on \(\{h>0\}\) such that for every \(U\in {\mathbb R}^d\) there is a vector field \(X_U\in \mathcal C_c^\infty ({\mathbb T}^d \cap \{h>0\};R^d)\) such that \({{\,\mathrm{div}\,}}X_U = 0\) in \({\mathcal D}'({\mathbb T}^d)\), \(\int _{\{h>0\}} X_U(x)\,dx = U\), and \(\int _{\{h>0\}} |X_U(x)|^2\,dx \le C|U|^2\).
Proof
Let \(\gamma :[0,1] \rightarrow {\mathbb R}^d\) be a Lipschitz curve. Define the vector-valued measure \(M {:}{=}\gamma _\# ({{\dot{\gamma }}}\, dt) \in {\mathcal M}({\mathbb R}^d;{\mathbb R}^d)\). Then \({{\,\mathrm{div}\,}}M = \delta _{\gamma _1}-\delta _{\gamma _0}\) in \({\mathcal D}'({\mathbb R}^d)\), \( M({\mathbb R}^d) = \gamma (1) - \gamma (0)\), and \(|M|({\mathbb R}^d) \le \int _0^1 |\dot{\gamma }(t)|\,dt = L(\gamma )\).
Let \(x\in \{h>0\}\). By the conditions on \(\{h>0\}\), there are Lipschitz curves \(\gamma _j:[0,1]\rightarrow \{h>0\}\), \(j=1,\ldots ,d\), such that \(\gamma _j(0) = x\), \(\gamma _j(1) = x+e_j\), and \(\delta {:}{=}\min _j {{\,\mathrm{dist}\,}}(\gamma _j, \partial \{h>0\}) > 0\).
Define \(X_U = \sum _{z\in {\mathbb Z}^d} \sum _{j=1}^d U_j ((\gamma _j-z)_\# {{\dot{\gamma }}}_j) *\phi _\delta \in \mathcal C_c^\infty (\{h>0\};{\mathbb R}^d)\), where \(\phi _\delta \in \mathcal C_c^\infty (B(0,\delta ))\) is a standard mollifier. We note that \(X_U\) is \({\mathbb Z}^d\)-periodic, \(\int _{[0,1)^d} X_U(x)\,dx = U\), \({{\,\mathrm{div}\,}}X_U = 0\), and \(\Vert X_U\Vert _{L^2([0,1)^d)} \le C \Vert \phi _\delta \Vert _{L^2} \sum _{j=1}^d |U_j| L(\gamma _j)^{d+1} \le C(h) |U|\), where we used Young’s convolution inequality and the finite overlap of the curves \((\gamma _j - z)_{z\in {\mathbb Z}^d, j=1,\ldots ,d}\). The projection of \(X_U\) to \({\mathbb T}^d\) inherits all the relevant properties. \(\square \)
We need the following lemma to estimate corrector errors.
Lemma 7.3
(Local Poincaré-trace inequality) There are constants \(R>0\), \(C>0\) depending only on \(\{h > 0\}\) such that for any \(\varepsilon >0\), \(a\in {\mathbb R}^d\), \(u\in H^1_{\mathrm {loc}}(\{h_\varepsilon > 0\})\), we have
Here  .
.
This differs from the standard Poincaré-trace inequality (see e.g. Theorem 12.3 in [15]) in that the smaller cube is not connected, nor is either cube Lipschitz-bounded.
Left: Even though the unit cell is not connected we control the \(L^2\) variation through the \(L^2\)-norm of the gradient in the larger cell. Right: If \(\{h>0\}\) is not connected Theorem 1.2 fails. In this case mass may only move in the coordinate directions
Proof
The statement is independent of \(\varepsilon \). We only have to show it for \(\varepsilon = 1\) and \(a\in [0,1]^d\).
We take \(R>3\) as any number such that all \(y,y'\in [0,2]^d \cap \{h>0\}\) are connected by a rectifiable path in \((-R,R)^d \cap \{h>0\}\).
Assume that for this choice of R, no such C exists. Then there exists a sequence \((u_n)_{n\in {\mathbb N}} \subset H^1([-R,R]^d)\) and a sequence \((a_n)_{n\in {\mathbb N}} \subset [0,1]^d\) such that \(\int _{a_n+[0,1]^d} u_n\,dx = 0\), \(\int _{a_n+[0,1]^d} u^2\,dx + \int _{\partial (a_n + [0,1]^d)} u^2 \,d{\mathcal H}^{d-1} = 1\), and \(\int _{[-R,R]^d} |\nabla u_n|^2 \rightarrow 0\).
Because \(\{h>0\}\) is Lipschitz bounded, we can cover \(\partial \{h > 0\} \cap [0,2]^d\) with finitely many open rectangles \((R_i)_{i\in I}\) such that, up to a rigid motion, \(\{h>0\} \cap R_i = \{(\tilde{y}, y_d)\,:\,{{\tilde{y}}} \in {{\tilde{R}}}_i, 0<y_d<f_i({{\tilde{y}}})\}\), where \(f:{\mathbb R}^{d-1} \rightarrow (0,\infty )\) is Lipschitz.
From [15, Theorem 12.3], we infer that there exists a bounded linear extension operator \(E:H^1([-R,R]^d\cap \{h>0\}) \rightarrow H^1(([-R,R]^d \cap \{h>0\}) \cup \bigcup _{i\in I}R_i)\) such that \(Eu = u\) almost everywhere in \([-R,R]^d \cap \{h>0\}\) and
Note that only \(\nabla u\) appears on the right-hand side since we are not looking for a global extension.
Extending each \(u_i\) using this operator, we extract a subsequence (not relabeled) such that \(a_i \rightarrow a\), \(Eu_i \rightarrow u\) in \(L^2_{\mathrm {loc}}(([-R,R]^d \cap \{h>0\}) \cup \bigcup _{i\in I} R_i)\), and \(\nabla Eu_i \rightarrow 0\) in \(L^2(([-R,R]^d \cap \{h>0\}) \cup \bigcup _{i\in I} R_i)\). Also, the traces \(u_n|_{\partial (a_n+[0,1]^d)}\mathbb {1}_{\{h>0\}}\) converge in \(L^2(\partial ([0,1]^d))\) to the trace \(u|_{\partial (a+[0,1]^d)}\mathbb {1}_{\{h>0\}}\).
It follows that u is piecewise constant. Because any two points in \([0,2]^d\) are path-connected in the domain, u is constant in \([0,2]^d\cap \{h>0\}\). Because \(\int _{a+[0,1]^d} u \,dx = 0\), \(u=0\) almost everywhere in \([0,2]^d \cap \{h>0\}\). However, we have
a contradiction. \(\square \)
We note that this implies the usal Poincaré-trace inequality in particular for \(\varepsilon {\mathbb Z}^d\)-periodic functions in \(H^1(\{h_\varepsilon > 0\})\).
Finally we prove Theorem 1.2.
7.1 Proof of Theorem 1.2
Proof
(Proof of the lower bound) We start with a sequence of curves \((\rho _t^\varepsilon )_{t\in [0,1]} \subset L^\infty ({\mathbb T}^d)\) with \(0 \le \rho _t^\varepsilon (dx) \le h_\varepsilon (x)\,dx\), together with a sequence of momentum fields \((V_t^\varepsilon )_{t\in [0,1]} \subset L^2({\mathbb T}^d;{\mathbb R}^d)\), such that \(\partial _t \rho _t^\varepsilon + {{\,\mathrm{div}\,}}V_t^\varepsilon = 0\) in \({\mathcal D}'((0,1)\times {\mathbb T}^d)\) and
Step 1 We consider instead averaged versions \((\rho _t^{\delta ,\varepsilon })_t, (V_t^{\delta , \varepsilon })_t\) defined through

Here \(\rho _t^\varepsilon , V_t^\varepsilon \) are first extended for \(t\in {\mathbb R}\setminus [0,1]\) constantly and by 0 respectively, and \(H_\delta ^\varepsilon \) is the discrete heat kernel for \(\varepsilon {\mathbb Z}^d / {\mathbb Z}^d\) at time \(\delta \).
The averaged versions have the following properties:
We note that \(\rho _t^{\varepsilon ,\delta }(dx) \le h_\varepsilon (x)dx\) and \(\partial _t \rho _t + {{\,\mathrm{div}\,}}V_t^{\varepsilon ,\delta } = 0\) in \({\mathcal D}'((0,1)\times {\mathbb T}^d)\), and by the convexity of the function \((m,U)\mapsto \frac{|U|^2}{m}\), we have
Step 2 Define for \(x\in {\mathbb T}^d\) the cube \(Q_{x,\varepsilon } = (x + [0,\varepsilon )^d )/ {\mathbb Z}^d \subset {\mathbb T}^d\). Define  and
and  . Note that \(\partial _t m_t^{\varepsilon , \delta } + {{\,\mathrm{div}\,}}U_t^{\varepsilon ,\delta } = 0\) in \({\mathcal D}'((0,1)\times {\mathbb T}^d)\). We now find a competitor for \(f_{\hom }(m_t^{\varepsilon ,\delta }(x),U_t^{\varepsilon ,\delta }(x))\) for almost every x, t:
. Note that \(\partial _t m_t^{\varepsilon , \delta } + {{\,\mathrm{div}\,}}U_t^{\varepsilon ,\delta } = 0\) in \({\mathcal D}'((0,1)\times {\mathbb T}^d)\). We now find a competitor for \(f_{\hom }(m_t^{\varepsilon ,\delta }(x),U_t^{\varepsilon ,\delta }(x))\) for almost every x, t:
Consider the Hilbert space \(H^1_{\varepsilon \text {-per}}(\{h_\varepsilon > 0\})\) of \(\varepsilon {\mathbb Z}^d\)-periodic functions with mean 0, equipped with symmetric bilinear form \(\mathcal {A}(\phi ,\psi ) = \int _{Q_{x,\varepsilon } \cap \{h_\varepsilon >0\}} \nabla \phi \cdot \nabla \psi \,dy\), which is independent of \(x\in {\mathbb T}^d\) and positive definite by Lemma 7.3.
By the Lax-Milgram theorem, we may thus find for every \(x\in {\mathbb T}^d\) a weak solution \(\phi _{t,x}^{\varepsilon ,\delta } \in H^1_{\varepsilon \text {-per}}(\{h_\varepsilon > 0\})\) of
for every \(\psi \in H^1_{\varepsilon \text {-per}}(\{h_\varepsilon > 0\})\). Moreover, through integration by parts, using Hölder’s inequality and Lemma 7.3, we may estimate
where we used the fact that \(\psi \) is \(\varepsilon {\mathbb Z}^d\)-periodic and that \(V_t^{\varepsilon ,\delta }\cdot n = 0\) on \(\partial \{h_\varepsilon > 0\}\) in the sense of distributions.
Inserting the solution \(\phi _{t,x}^{\varepsilon ,\delta }\) into (107) and using the estimates in (104), we find through Fubini’s theorem and Hölder’s inequality that for every \(t\in [0,1]\) we have
Further, the vector field \(W_t^{\varepsilon ,\delta }=V_t^{\varepsilon ,\delta } +\nabla \phi _{t,x}^{\varepsilon ,\delta }\in L^2(Q_{x,\varepsilon }\cap \{h_\varepsilon >0\};{\mathbb R}^d)\) can be extended periodically to all of \(\{h_\varepsilon > 0\}\) and then by 0 in \(\{h_\varepsilon =0\}\), and the extension has zero distributional divergence in \({\mathbb T}^d\) by (106). It follows that

We also use inequality (vi) from Lemma 7.1 to obtain

Integrating over \({\mathbb T}^d \times [0,1]\) yields

where we used Jensen’s inequality and the convexity of the function \((m,U) \mapsto \frac{|U|^2}{m}\) for the first term, and the lower bound \(\rho _t^{\varepsilon ,\delta } \ge \delta \alpha \) in \(\{h_\varepsilon > 0\}\) for the second.
We can then comfortably bound the error terms by repeatedly applying Hölder’s inequality and (108).

Similarly,
Combine this with (105) to obtain
for every \(\delta > 0\). Using a diagonal sequence \(\delta (\varepsilon ) \rightarrow 0\), we see that \(m_t^{\varepsilon ,\delta (\varepsilon )} {\mathop {\rightharpoonup }\limits ^{*}}\rho _t\) for almost every \(t\in [0,1]\). The claim follows then from Lemma 2.1. \(\square \)
Proof
(Proof of the upper bound) We have to show that for all curves of measures \((\rho _t)_{t\in [0,1]}\subset {\mathcal M}_+({\mathbb T}^d)\) there exists for every \(\varepsilon =\frac{1}{n}\) a curve of measures \((\rho _t^\varepsilon )_{t\in [0,1]}\) such that as \(\varepsilon \rightarrow 0\) we have for all \(t\in [0,1]\) \(\rho ^\varepsilon _t{\mathop {\rightharpoonup }\limits ^{*}}\rho _t\) and
- Step 1:
-
We may assume that \((\rho _t)_{t\in [0,1]}\) has finite energy. We mollify in time and space with a standard mollifier. Let us call this curve \(({\tilde{\rho }}_t)_{t\in [0,1]}\in {\mathcal C}^\infty ([0,1]\times {\mathbb T}^d)\) and the corresponding optimal momentum vector field \(({{\tilde{V}}}_t)_{t\in [0,1]}\in {\mathcal C}^\infty ([0,1]\times {\mathbb T}^d,{\mathbb R}^d)\).
- Step 2:
-
We fix a number \(M\in {\mathbb N}\) of time steps satisfying \(\varepsilon \ll \frac{1}{M}\ll 1\). We define for \(t_i{:}{=}\frac{i}{M}\) and \(z\in (\varepsilon {\mathbb Z}^d)/ {\mathbb Z}^d\) the following objects
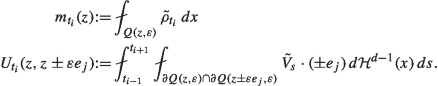 (116)
(116)Note that for \(t\in (t_i,t_{i+1})\) with \(m_t\) the linear interpolation between \(m_{t_i}\) and \(m_{t_{i+1}}\)
$$\begin{aligned} \partial _tm_t(z)+\varepsilon ^{-1}\sum _{j=1}^d\left( U_{t_i}(z,z+\varepsilon e_j)+U_{t_i}(z,z-\varepsilon e_j)\right) =0. \end{aligned}$$(117) - Step 3:
-
We insert the optimal microstructures \(\nu _{t_i,z}\in L^1(\{h>0\})\) and \(W_{t_i,z}\in L^2(\{h>0\};{\mathbb R}^d)\) for \(f_{\hom }(m_{t_i}(z),U_{t_i}(z))\), where
$$\begin{aligned} U_{t_i}(z)\cdot e_j {:}{=}U_{t_i}(z,z+\varepsilon e_j). \end{aligned}$$(118)Fix \(a\in [0,\varepsilon )^d/{\mathbb Z}^d\) to be chosen later, and define for \(x\in Q_{z+a,\varepsilon }\)
$$\begin{aligned} \begin{aligned} \rho _{t_i}^\varepsilon (x) {:}{=}&(1-\delta )\sum _{z'\in (\varepsilon {\mathbb Z}^d)/ {\mathbb Z}^d}H_\delta ^\varepsilon (z-z')\nu _{t,z'}\left( \frac{x}{\varepsilon }\right) +\delta \alpha \mathbb {1}_{\{h_\varepsilon >0\}}(x),\\ V_{t_i}^\varepsilon (x) {:}{=}&(1-\delta )\sum _{z'\in (\varepsilon {\mathbb Z}^d)/ {\mathbb Z}^d}H_\delta ^\varepsilon (z-z')W_{t,z'}\left( \frac{x}{\varepsilon }\right) ,\\ X_{t_i}^\varepsilon (x) {:}{=}&(1-\delta ) \sum _{z' \in (\varepsilon {\mathbb Z}^d) / {\mathbb Z}^d} H_\delta ^\varepsilon (z-z') X_{U_{t_i}(z') - U_{t_{i+1}}(z')}\left( \frac{x}{\varepsilon }\right) , \end{aligned} \end{aligned}$$(119)where \(\delta >0\), \(\alpha \) is the positive lower bound of the function h, \(H_\delta ^\varepsilon \) is the discrete heat flow on \((\varepsilon {\mathbb Z}^d)/ {\mathbb Z}^d\), and \(X_U\in L^2(\{h>0\};{\mathbb R}^d)\) is the vector field from Lemma 7.2.
- Step 4:
-
For \(t\in (t_i,t_{i+1})\) we define \(\rho ^\varepsilon _t\in L^\infty ({\mathbb T}^d)\) and \( V^\varepsilon _t\in L^2(\{h_\varepsilon >0\};{\mathbb R}^d)\) as the linear interpolations
$$\begin{aligned} \begin{aligned} \rho _t^\varepsilon (x){:}{=}&\frac{t_{i+1}-t}{t_{i+1}-t_i}\rho _{t_i}^\varepsilon (x)+\frac{t-t_i}{t_{i+1}-t_i}\rho _{t_{i+1}}^\varepsilon (x),\\ V_t^\varepsilon (x){:}{=}&\frac{t_{i+1}-t}{t_{i+1}-t_i} V_{t_i}^\varepsilon (x)+\frac{t-t_i}{t_{i+1}-t_i} \left( V_{t_{i+1}}^\varepsilon (x) + X_{t_i}^\varepsilon (x) \right) . \end{aligned} \end{aligned}$$(120)We see that
$$\begin{aligned} {{\,\mathrm{div}\,}}V_t^\varepsilon = \sum _{z\in (\varepsilon {\mathbb Z}^d)/{\mathbb Z}^d} \sum _{j=1}^d - [V_t^\varepsilon ]\cdot e_j {\mathcal H}^{d-1}|_{\partial Q_{z+a,\varepsilon } \cap \partial Q_{z + a - \varepsilon e_j, \varepsilon }} \end{aligned}$$(121)where \([V_t^\varepsilon ]\) denotes the jump of \(V_t^\varepsilon \) from \(Q_{z+a,\varepsilon }\) to \(Q_{z+a-\varepsilon e_j,\varepsilon }\). Note that since \(V_t^\varepsilon \in L^2({\mathbb T}^d;{\mathbb R}^d)\), by Fubini’s theorem the above is defined for almost every \(a\in [0,\varepsilon )^d/{\mathbb Z}^d\). Moreover, for every \(z\in (\varepsilon {\mathbb Z}^d)/{\mathbb Z}^d\) we have
$$\begin{aligned} \int _{Q_{z+a,\varepsilon }} V_t^\varepsilon (x) \,dx = (1-\delta ) \sum _{z'\in (\varepsilon {\mathbb Z}^d)/{\mathbb Z}^d} H_\delta ^\varepsilon (z-z') U_{t_i}(z'), \end{aligned}$$(122)and
$$\begin{aligned} \int _{Q_{z+a,\varepsilon }} \partial _t\rho _t^\varepsilon (x)\,dx = (1-\delta )\sum _{z'\in (\varepsilon {\mathbb Z}^d)/{\mathbb Z}^d} H_\delta ^\varepsilon (z-z') \frac{m_{t_{i+1}}(z') - m_{t_i}(z')}{t_{i+1}-t_i}. \end{aligned}$$(123)Combining the above with (117), we also obtain that
$$\begin{aligned} \int _{Q_{z+a,\varepsilon }} \partial _t\rho _t^\varepsilon (x)\,dx + \sum _{j=1}^d \int _{\partial Q_{z+a,\varepsilon } \cap \partial Q_{z + a - \varepsilon e_j, \varepsilon }}- [V_t^\varepsilon ]\cdot e_j \,d{\mathcal H}^{d-1} = 0, \end{aligned}$$(124)or more concisely
$$\begin{aligned} (\partial _t \rho _t^\varepsilon + {{\,\mathrm{div}\,}}V_t^\varepsilon ) (Q_{z+a,\varepsilon }) = 0, \end{aligned}$$(125)for every \(z\in (\varepsilon {\mathbb Z}^d)/{\mathbb Z}^d\), for almost every a. Note that in (125) it is imperative that \(Q_{z+a\varepsilon }\) be the half-open cubes.
- Step 5:
-
Let \(\phi _t^\varepsilon \in H^1(\{h_\varepsilon > 0\})\) be the weak solution to
$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta \phi _t^\varepsilon = -(\partial _t \rho _t^\varepsilon + {{\,\mathrm{div}\,}}V_t^\varepsilon )&{}\text {, in }\{h_\varepsilon> 0\}\\ \nabla \phi _t^\varepsilon \cdot n = 0 &{}\text {, on }\partial \{h_\varepsilon>0\}\\ \int _{\{h_\varepsilon > 0\}} \phi _t^\varepsilon (x)\,dx = 0, \end{array}\right. } \end{aligned}$$(126)i.e. the unique function in the Hilbert space
$$\begin{aligned} H^1_\varepsilon {:}{=}\left\{ \psi \in H^1(\{h_\varepsilon> 0\})\,:\,\int _{\{h_\varepsilon > 0\}} \psi (x)\,dx = 0\right\} \end{aligned}$$(127)with
$$\begin{aligned} \begin{aligned}&\int _{\{h_\varepsilon> 0\}} \nabla \phi _t^\varepsilon \cdot \nabla \psi \,dx \\ =&\sum _{z\in (\varepsilon {\mathbb Z}^d)/{\mathbb Z}^d} \int _{Q_{z+a,\varepsilon }\cap \{h_\varepsilon> 0\}} \partial _t\rho _t^\varepsilon \psi \,dx \\&+ \sum _{j=1}^d \int _{\partial Q_{z+a,\varepsilon } \cap \partial Q_{z + a - \varepsilon e_j, \varepsilon } \cap \{h_\varepsilon > 0\}}- [V_t^\varepsilon ]\cdot e_j \psi \,d{\mathcal H}^{d-1} \end{aligned} \end{aligned}$$(128)for all \(\psi \in H_\varepsilon ^1\). Note that after extending \(\nabla \phi _t^\varepsilon \) by 0 in \(\{h_\varepsilon =0\}\), (128) actually holds for all \(\psi \in H^1({\mathbb T}^d)\). By the Lax-Milgram Theorem, a unique such \(\phi _t^\varepsilon \) exists for almost every a. Testing with \(\psi = \phi _t^\varepsilon \) and using Lemma 7.3, we see that
$$\begin{aligned} \begin{aligned} \int _{\{h_\varepsilon> 0 \}} |\nabla \phi _t^\varepsilon |^2\,dx =&\sum _{z\in (\varepsilon {\mathbb Z}^d)/{\mathbb Z}^d} \bigg ( \int _{Q_{z+a,\varepsilon }} \partial _t\rho _t^\varepsilon (\phi _t^\varepsilon - \overline{\phi _t^\varepsilon }_z)\,dx\\&+ \sum _{j=1}^d \int _{\partial Q_{z+a,\varepsilon } \cap \partial Q_{z + a - \varepsilon e_j, \varepsilon }}- [V_t^\varepsilon ]\cdot e_j (\phi _t^\varepsilon - \overline{\phi _t^\varepsilon }_z) \,d{\mathcal H}^{d-1}\bigg )\\ \le&C(\{h_\varepsilon> 0\})\varepsilon \left( \Vert \partial _t \rho _t^\varepsilon \Vert _{L^2(\{h_\varepsilon> 0\})} + \frac{1}{\sqrt{\varepsilon }}\Vert [V_t^\varepsilon ]\Vert _{L^2(\bigcup _z \partial Q_{z+a,\varepsilon })}\right) \\&\times \Vert \nabla \phi _t^\varepsilon \Vert _{L^2(\{h_\varepsilon > 0\})}. \end{aligned} \end{aligned}$$(129)At this point we pick \(a\in [0,\varepsilon )^2/{\mathbb Z}^d\) such that \(\Vert [V_t^\varepsilon ]\Vert _{L^2\left( \bigcup _z \partial Q_{z+a,\varepsilon }\right) }^2 \le C(\delta ) \varepsilon \), which is possible by Fubini’s theorem and the regularity of the discrete heat flow. Of course, \(\Vert \partial _t \rho _t^\varepsilon \Vert _{L^\infty } \le CM\), so that
$$\begin{aligned} \int _{\{h_\varepsilon > 0\}} |\nabla \phi _t^\varepsilon |^2\,dx \le (C(\delta ) + CM^2)\varepsilon ^2. \end{aligned}$$(130)Further, taking \(W_t^\varepsilon = V_t^\varepsilon + \nabla \phi _t^\varepsilon \mathbb {1}_{\{h_\varepsilon > 0\}}\), we see by (128) that \(\partial _t \rho _t^\varepsilon + {{\,\mathrm{div}\,}}W_t^\varepsilon = 0\) in \({\mathcal D}'((0,1)\times {\mathbb T}^d)\).
- Step 6:
-
We estimate using (130) that
$$\begin{aligned} \begin{aligned} \int _{{\mathbb T}^d}\frac{|W^\varepsilon _t|^2}{\rho ^\varepsilon _t}\,dx\le&\int _{{\mathbb T}^d}\frac{ |V_t^\varepsilon |^2}{\rho _t^\varepsilon }\, dx+\frac{C}{\delta \alpha }\int _{{\mathbb T}^d} |\nabla \phi _t^\varepsilon ||V_t^\varepsilon + \nabla \phi _t^\varepsilon |\,dx\\ \le&\int _{{\mathbb T}^d}\frac{ |V_t^\varepsilon |^2}{\rho _t^\varepsilon }\, dx + \frac{C(\delta )\varepsilon }{\alpha }(1+\varepsilon )(1 + M)\\ \le&\int _{{\mathbb T}^d}\frac{ |V_t^\varepsilon |^2}{\rho _t^\varepsilon }\, dx + \frac{C(\delta )}{\alpha }M\varepsilon . \end{aligned} \end{aligned}$$(131)
Using the joint convexity of the function \((m,U)\mapsto \frac{|U|^2}{m}\) we find for \(t\in (t_i,t_{i+1})\) that
We estimate I using Lemma 7.2:
For the main term we find through exploiting the convexity and the definition of \(V_{t_i}^\varepsilon ,\rho _{t_i}^\varepsilon \) that
We now combine the estimates (131), (132), (133), (134) and integrate in time so that
Finally, we use the Lipschitz continuity of \(f_{\hom }\) from Lemma 7.1 and the Lipschitz continuity of \(({\tilde{\rho }}, {{\tilde{V}}})\) to estimate the Riemann sum above by the integral
Choosing \(M=\lfloor {\varepsilon ^{-1/2}}\rfloor \) and letting \(\varepsilon \rightarrow 0\) we otain the desired estimate
where we used the convexity of \(E_{\hom }\) in the last equality (Lemma 7.1). Finally take a diagonal sequence such that \(\rho _t^\varepsilon {\mathop {\rightharpoonup }\limits ^{*}}\rho _t\) for all \(t\in [0,1]\). \(\square \)
Remark 7.4
Finally, we note that we may add lower bounds on the density, in the form \(\rho _t(A) \ge \int _A l(x)\,dx\) for every closed set A, with a measurable lower density bound \(l\in L^1(\Omega )\), with \(l(x)\le h(x)\) almost everywhere. This is just another convex constraint.
In fact, Theorem 1.2 can be proved under the additional constraint for \(l^\varepsilon (x) = l(x/\varepsilon )\) with a few easy modifications. In (11), we take the infimum with the additional constraint that \(\nu (x)\ge l(x)\) almost everywhere, increasing the energy.
In Lemma 7.1, the upper bound in (iv) then has to be replaced by
Finally, in (103) and (119), the term \(\delta \alpha \mathbb {1}_{\{h_\varepsilon > 0\}}\) has to be replaced by \(\delta (\alpha \mathbb {1}_{\{h_\varepsilon > 0\}} \vee l_\varepsilon )\).
References
Ambrosio, Luigi, Crippa, Gianluca, De Lellis, Camillo, Otto, Felix, Westdickenberg, Michael: Transport equations and multi-D hyperbolic conservation laws, volume 5 of Lecture Notes of the Unione Matematica Italiana. Springer-Verlag, Berlin. UMI, Bologna: Lecture notes from the Winter School held in Bologna, January 2005. In: Ancona, Fabio, Bianchini, Stefano (eds.) Rinaldo M. Colombo, De Lellis, Andrea Marson and Annamaria Montanari (2008)
Ambrosio, Luigi, Fusco, Nicola, Pallara, Diego: Functions of bounded variation and free discontinuity problems Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2000)
Benamou, Jean-David., Brenier, Yann: A computational fluid mechanics solution to the Monge-Kantorovich mass transfer problem. Num. Math. 84(3), 375–393 (2000)
Benamou, Jean-David., Carlier, Guillaume, Santambrogio, Filippo: Variational mean field games. Act. Part. 1, 141–171 (2017)
Braides, Andrea.: Gamma-convergence for Beginners, volume 22. Clarendon Press (2002)
Braides, Andrea, Defranceschi, Anneliese: Homogenization of Multiple Integrals. Oxford University Press, Oxford (1998)
Braides, Andrea, Fonseca, Irene, Leoni, Giovanni: A-quasiconvexity: relaxation and homogenization. ESAIM: Control Opt. Cal. Variat. 5, 539–577 (2000)
Buttazzo, Giuseppe, Jimenez, Chloé, Oudet, Edouard: An optimization problem for mass transportation with congested dynamics. SIAM J. Control Opt. 48(3), 1961–1976 (2009)
Cardaliaguet, Pierre, Mészáros, Alpár R., Santambrogio, Filippo: First order mean field games with density constraints: pressure equals price. SIAM J. Control Opt. 54(5), 2672–2709 (2016)
Dal Maso, Gianni.: An introduction to \(\Gamma \)-convergence, volume 8. Springer Science & Business Media (2012)
Ford Jr, Lester Randolph, Fulkerson, Delbert Ray.: Flows in networks. Princeton university press (2015)
Friesecke, Gero, James, Richard D., Müller, Stefan: A theorem on geometric rigidity and the derivation of nonlinear plate theory from three-dimensional elasticity. Commun. Pure Appl. Math. 55(11), 1461–1506 (2002)
Jordan, Richard, Kinderlehrer, David, Otto, Felix: The variational formulation of the Fokker-Planck equation. SIAM J. Math. Anal. 29(1), 1–17 (1998)
Korman, Jonathan, McCann, Robert: Optimal transportation with capacity constraints. Trans. Am. Math. Soc. 367(3), 1501–1521 (2015)
Leoni, Giovanni.: A first course in Sobolev spaces. American Mathematical Soc. (2017)
Liu, Jian-Guo, Pego, Robert L, Slepčev, Dejan.: Euler sprays and Wasserstein geometry of the space of shapes. (2016) arXiv:1604.03387
Liu, Jian-Guo., Pego, Robert L., Slepčev, Dejan: Least action principles for incompressible flows and geodesics between shapes. Calc. Var. Part. Differ. Equ. 58(5), 179 (2019)
Moerbeke, Pierre: On optimal stopping and free boundary problems. Arch. Ration. Mech. Anal. 60(2), 101–148 (1976)
Otto, Felix.: The geometry of dissipative evolution equations: the porous medium equation (2001)
Priest, Christopher: The Prestige. Simon & Schuster, Touchstone (1995)
Protter, Philip E.: Stochastic differential equations. In: Stochastic integration and differential equations. Springer, Heidelberg (2005)
Smirnov, S.K.: Decomposition of solenoidal vector charges into elementary solenoids and the structure of normal one-dimensional currents. St. Petersburg Math. J. 5(4), 841–867 (1994)
Teorell, Torsten: Studies on the “Diffusion Effect’’ upon ionic distribution. Some theoretical considerations. Proc. Natl. Acad. Sci. U. S. A. 21(3), 152 (1935)
Vázquez, Juan Luis.: The porous medium equation: mathematical theory. Oxford University Press (2007)
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Malchiodi.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
P.G. is partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) 350398276. E.K. gratefully acknowledges support by the German Research Foundation through the Hausdorff Center for Mathematics and the Collaborative Research Center 1060.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gladbach, P., Kopfer, E. Limits of density-constrained optimal transport. Calc. Var. 61, 70 (2022). https://doi.org/10.1007/s00526-021-02163-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-02163-7