Shape Optimization of a Weighted Two-Phase Dirichlet Eigenvalue

Abstract

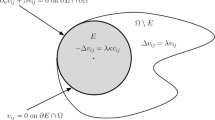
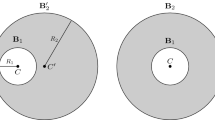
This article is concerned with a spectral optimization problem: in a smooth bounded domain ${\Omega }$, for a bounded function m and a nonnegative parameter $\alpha$, consider the first eigenvalue $\lambda _\alpha (m)$ of the operator ${\mathcal {L}}_m$ given by ${\mathcal {L}}_m(u)= -{\text {div}} \left( 1+\alpha m)\nabla u\right) -mu$. Assuming uniform pointwise and integral bounds on m, we investigate the issue of minimizing $\lambda _\alpha (m)$ with respect to m. Such a problem is related to the so-called “two phase extremal eigenvalue problem” and arises naturally, for instance in population dynamics where it is related to the survival ability of a species in a domain. We prove that unless the domain is a ball, this problem has no “regular” solution. We then provide a careful analysis in the case of a ball by: (1) characterizing the solution among all radially symmetric resources distributions, with the help of a new method involving a homogenized version of the problem; (2) proving in a more general setting a stability result for the centered distribution of resources with the help of a monotonicity principle for second order shape derivatives which significantly simplifies the analysis.

Proof of Lemma 1

We prove hereafter that the mapping $m\mapsto (u_{\alpha ,m}, \lambda _\alpha (m))$ is twice differentiable (and even $\mathscr {C}^\infty$) in the $L^2$ sense, the proof of the differentiability in the weak $W^{1,2}({\Omega })$ sense being similar. Let $m^*\in \mathcal M_{m_0,\kappa }({\Omega })$, $\sigma _\alpha {{:}{=}}1+\alpha m^*$, and $(u_0,\lambda _0)$ be the eigenpair associated with $m^*$. Let $h\in {\mathcal {T}}_{m^*}$ (see Definition 1). Let $m^*_h{{:}{=}}m^*+h$ and $\sigma _{m^*+h}{{:}{=}}1+\alpha (m^*+h).$ Let $(u_{h},\lambda _h)$ be the eigenpair associated with $m^*_h$. Let us introduce the mapping G defined by

$$\begin{aligned} G:\left\{ \begin{array}{ll} {\mathcal {T}}_{m^*}\times W^{1,2}_0({\Omega })\times \mathbb {R}\rightarrow W^{-1,2}({\Omega })\times \mathbb {R},&{} \\ (h, v, \lambda )\mapsto \left( -{\nabla }\cdot (\sigma _{m^*+h}{\nabla }v))-\lambda v-m^*_hv, \int _{\Omega }v^2-1\right) .&{} \end{array} \right. \end{aligned}$$

From the definition of the eigenvalue, one has $G(0,u_{0},\lambda _{0})=0$. Moreover, G is ${\mathscr {C}}^\infty$ in ${\mathcal {T}}_{m^*}\cap B\times W^{1,2}_0({\Omega })\times \mathbb {R}$, where B is an open ball centered at 0. The differential of G at $(0,u_0,\lambda _0)$ reads

$$\begin{aligned} D_{v,\lambda }G(0,u_0,\lambda _0)[w,\mu ]=\left( -{\nabla }\cdot (\sigma _\alpha {\nabla }w)-\mu u_0-\lambda _0 w-m^*w, \int _{\Omega }2u_0w\right) . \end{aligned}$$

Let us show that this differential is invertible. We will show that, if $(z,k)\in W^{-1,2}({\Omega })\times \mathbb {R}$, then there exists a unique pair $(w,\mu )$ such that $D_{v,\lambda }G(0,u_0,\lambda _0)[w,\mu ]=(z,k)$. According to the Fredholm alternative, one has necessarily $\mu =-\langle z,u_0\rangle _{L^2({\Omega })}$ and for this choice of $\mu$, there exists a solution $w_1$ to the equation

$$\begin{aligned} -{\nabla }\cdot (\sigma _\alpha {\nabla }w)-\mu u_0-\lambda _0 w-m^*w=z\quad \text {in }{\Omega }. \end{aligned}$$

Moreover, since $\lambda _0$ is simple, any other solution is of the form $w=w_1+tu_0$ with $t\in \mathbb {R}$. From the equation $2\int _{\Omega }u_0w=k$, we get $t=k/2-\int _{\Omega }w_1u_0$. Hence, the pair $(w,\mu )$ is uniquely determined. According to the implicit function theorem, the mapping $h\mapsto (u_h,\lambda _h)$ is ${\mathscr {C}}^\infty$ in a neighbourhood of $\mathbf {0}$.