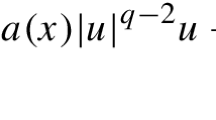Abstract
An optimal first-order global regularity theory, in spaces of functions defined in terms of oscillations, is established for solutions to Dirichlet problems for the p-Laplace equation and system, with the right-hand side in divergence form. The exact mutual dependence among the regularity of the solution, of the datum on the right-hand side, and of the boundary of the domain in these spaces is exhibited. A comprehensive formulation of our results is given in terms of Campanato seminorms. New regularity results in customary function spaces, such as Hölder, \(\text {BMO}\) and \({{\,\mathrm{VMO}\,}}\) spaces, follow as a consequence. Importantly, the conclusions are new even in the linear case when \(p=2\), and hence the differential operator is the plain Laplacian. Yet in this classical linear setting, our contribution completes and augments the celebrated Schauder theory in Hölder spaces. A distinctive trait of our results is their sharpness, which is demonstrated by a family of apropos examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We are concerned with the Dirichlet problem for the p-Laplace system
Here, the exponent \(p \in (1, \infty )\), \(\Omega \) is a bounded open set in \({\mathbb {R}^n}\), with \(n \geqq 2\), the function \(\mathbf {F}\,:\, \Omega \rightarrow \mathbb {R}^{N\times n}\), with \(N \geqq 1\), is given, \(\mathbf {u}\,:\, \Omega \rightarrow {\mathbb {R}^N}\) is the unknown, and \(\nabla \mathbf {u}: \Omega \rightarrow \mathbb {R}^{N\times n}\) denotes its gradient.
Under the assumption that \(\mathbf {F}\in L^{p'}(\Omega )\), where \(p'=p/(p-1)\), one has that \({{\,\mathrm{div}\,}}\mathbf {F}\) belongs to the dual of the Sobolev space \( W^{1,p}_0(\Omega )\). Hence, a weak solution \(\mathbf {u}\in W^{1,p}_0(\Omega )\) to problem (1.1) is well defined, and its existence and uniqueness follow via standard variational methods.
The present paper focuses on global—namely up to the boundary—higher regularity properties of \(\nabla \mathbf {u}\) inherited from those of \(\mathbf {F}\). A systematic study of the regularity, in Lebesgue spaces, of the gradient of solutions to equations like those in problem (1.1) was initiated in [35], a contribution that inspired numerous researches on this topic. Here, we offer a sharp global Schauder regularity theory for norms depending on oscillations of \(\nabla \mathbf {u}\). Campanato type norms provide a suitable framework for a unified formulation of such a theory. Membership of the gradient of the solution \(\mathbf {u}\) to problem (1.1) in Campanato type spaces depends on both the regularity of the datum \(\mathbf {F}\) and that of the boundary \(\partial \Omega \) in the same kind of spaces. Our results provide an exact description of the interplay among these three pieces of information, and show that the required balance among them is qualitatively independent of the dimensions n and N, and of p. Their optimality is demonstrated via a precise analysis of the behaviour of the solutions in suitable model problems. Proofs entail the development of new decay estimates on balls near the boundary, that rely upon an unconventional flattening technique exploiting local coordinates which depend on the radius of the balls.
Although our primary interest is in nonlinear problems, the conclusions to be presented are new, and the best possible, even in the linear case when \(p=2\), namely when the differential operator in (1.1) is just the Laplacian. Interestingly, since our results also admit a local version, they provide novel optimal gradient regularity properties up to the boundary also for harmonic functions vanishing on a subset of \(\partial \Omega \). This can be regarded as a counterpart, in the scale of norms depending on oscillations, of the sharp \(L^q\) gradient regularity theory for linear equations developed in [38], and of the \(L^\infty \) gradient bounds of [47].
As far as genuinely nonlinear problems—corresponding to \(p \ne 2\)—are concerned, global \(\text {BMO}\) regularity is an important new consequence of our general estimates, which actually cover the whole region between \(\text {BMO}\) and Hölder spaces. They include, for instance, spaces defined in terms of a general modulus of continuity. In fact, on providing sharp quantitative information, our results also enhance the classical global theory, where Hölder norms are employed to describe the regularity of \(\mathbf {F}\), \(\partial \Omega \) and \(\nabla \mathbf {u}\).
The local Hölder gradient regularity of solutions to the system in (1.1), in the homogeneous case when \(\mathbf {F}=0\) and for \(p \geqq 2\), goes back to the paper [55], after which systems involving differential operators depending only on the length of the gradient are usually called with Uhlenbeck structure. The same result in the scalar case (\(N=1\)) had been earlier established in [56] for every \(p \in (1,\infty )\). Solutions to nonlinear systems whose principal part does not depend on the gradient just through its length can lack regularity, as shown by well known counterexamples from [53]. By contrast, no special structure is needed for the regularity of solutions in the scalar case, as shown in the papers [18, 25, 45, 54]. The contribution [55] was extended to the situation when \(1<p<2\) in [1] and in [11], the latter paper also including non-vanishing right-hand sides and parabolic problems. The local \(\text {BMO}\) gradient regularity for solutions to (1.1) is proved, for \(p \geqq 2\), in [19]. A version of that result, which holds for every \(p \in (1, \infty )\), and for \(\mathbf {F}\) in more general Campanato type spaces, has recently been obtained in [21], but still in local form.
The global regularity theory is not as developed as the local one. The Hölder gradient regularity for equations of p-Laplacian type, in domains whose boundary has also Hölder continuous first-order derivatives, can be traced back to [46]. The result for systems (with Uhlenbeck structure) was achieved in [11] for domains of the same kind. However, we stress that our result provide us with the best possible Hölder exponent for first-order derivatives of the solution depending on the Hölder exponent of the first-order derivatives of the boundary. By contrast, the conclusions of [46] and [11] do not yield any explicit mutual dependence of these exponents. Moreover, the right-hand sides considered in [46] and [11] are not in divergence form, and hence the system in (1.1) cannot be reduced to the form of those papers in general. Right-hand sides in non-divergence form also appear in [12, 13], where \(L^\infty \) gradient estimates, under minimal boundary regularity assumptions, are established. Results on global \(\text {BMO}\) regularity seem to be still completely missing in the existing literature. Filling a gap in this major special instance was one of the original motivations for our research. some preliminary steps of which are contained in [51]
Further contributions on gradient regularity up to the boundary for systems and variational problems with Uhlenbeck structure, or perturbations of it, are [7, 26, 27, 33]. Partial boundary regularity, that is regularity at the boundary outside subsets of zero \((n-1)\)-dimensional Hausdorff measure, for nonlinear elliptic systems with general structure, is proved in [24, 42] (see also [34] for a special case). Related results on regular boundary points for \(\nabla u\) can be found in [3, 32]. The question of regular boundary points for u is of course a different issue. In particular, the continuity of u up to the boundary, even under non-homogeneous Dirichlet boundary conditions, is fully characterized thanks to the classical works [40] and [48] on a nonlinear version of the Wiener test.
2 Main Results
Our comprehensive result, stated in Theorem 2.1, is formulated in terms of Campanato type seminorms \({\Vert {\cdot }\Vert }_{\mathcal L ^{\omega (\cdot )} (\Omega )}\), associated with parameter-functions \(\omega : [0, \infty ) \rightarrow [0, \infty )\) which will be assumed to be continuous and non-decreasing in what follows. These seminorms are defined as

for a real, vector or matrix-valued integrable function \(\mathbf {f}\) in \(\Omega \). Here, \(B_r(x)\) denotes a ball of radius R and centered at x,  stands for averaged integral, and \(\langle {\mathbf {f}}\rangle _{E}\) for the mean value of \(\mathbf {f}\) over a set E. As hinted above, and will be specified below, the spaces \(\mathcal L ^{\omega (\cdot )} (\Omega )\) are a family of spaces that, depending on the choice of \(\omega \), may consist of continuous functions with modulus of continuity \(\omega \), of continuous functions with a slightly worse modulus of continuity, or also include discontinuous and unbounded functions, but with a degree of integrability depending on \(\omega \). In the borderline case corresponding to \(\omega (r)=1\), \(\mathcal L ^{\omega (\cdot )} (\Omega )\) agrees with the space \(\text {BMO}(\Omega )\) of functions of bounded mean oscillation in \(\Omega \). Observe that, as a consequence of the John-Nirenberg lemma for functions in \(\text {BMO}(\Omega )\), replacing the integral
stands for averaged integral, and \(\langle {\mathbf {f}}\rangle _{E}\) for the mean value of \(\mathbf {f}\) over a set E. As hinted above, and will be specified below, the spaces \(\mathcal L ^{\omega (\cdot )} (\Omega )\) are a family of spaces that, depending on the choice of \(\omega \), may consist of continuous functions with modulus of continuity \(\omega \), of continuous functions with a slightly worse modulus of continuity, or also include discontinuous and unbounded functions, but with a degree of integrability depending on \(\omega \). In the borderline case corresponding to \(\omega (r)=1\), \(\mathcal L ^{\omega (\cdot )} (\Omega )\) agrees with the space \(\text {BMO}(\Omega )\) of functions of bounded mean oscillation in \(\Omega \). Observe that, as a consequence of the John-Nirenberg lemma for functions in \(\text {BMO}(\Omega )\), replacing the integral  by
by  on the right-hand side of equation (2.1) results in an equivalent seminorm for every \(q > 1\).
on the right-hand side of equation (2.1) results in an equivalent seminorm for every \(q > 1\).
We denote by \(C^{0, \omega (\cdot )}(\Omega )\) the space of functions \(\mathbf {f}\) in \(\Omega \) endowed with the seminorm

Plainly, if \(\omega (0)=0\), then \(C^{0, \omega (\cdot )}(\Omega )\) is a space of uniformly continuous functions in \(\Omega \), with modulus of continuity not exceeding \(\omega \). If \(\omega (r)= r^\beta \) for some \(\beta \in (0, 1]\), then \(C^{0, \omega (\cdot )}(\Omega )\) coincides with the space of Hölder continuous functions with exponent \(\beta \), that will simply be denoted by \(C^{0,\beta }(\Omega )\), as customary. The space of functions obtained on replacing \(\mathbf {f}\) by \(\nabla \mathbf {f}\) in the definition of the seminorm (2.2) will be denoted by \(C^{1, \omega (\cdot )}(\Omega )\). The meaning of the notation \(C^{1,\beta }(\Omega )\) is analogous. Of course, when \(\Omega \) is bounded, only the behaviour of \(\omega \) near 0 is relevant in the definitions of \(C^{0, \omega (\cdot )}(\Omega )\) and \(C^{1, \omega (\cdot )}(\Omega )\).
It is easily seen that
for every parameter function \(\omega \), where the arrow \(`` \rightarrow "\) stands for continuous embedding. A reverse embedding holds if \(\omega (r) = r^\beta \), for any \(\beta \in (0, 1]\), provided that \(\Omega \) is regular enough—a bounded Lipschitz domain, for instance. However, the latter embedding may fail if \(\omega \) does not decay to 0 rapidly enough. In fact, functions in \(\mathcal L ^{\omega (\cdot )}(\Omega )\) need not even be (locally) bounded on \(\Omega \). We shall be more precise about this issue below.
In view of our applications, an additional property will be imposed on parameter functions \(\omega \). We shall assume that the function \(\omega (r)r^{-\beta _0}\) is almost decreasing for a suitable exponent \(\beta _0= \beta _0(n,N,p)\). Such an exponent depends on the optimal Hölder exponent for gradient regularity of p-harmonic functions, namely local solutions to the system in (1.1) with \(\mathbf {F}=0\). This amounts to requiring that
for some constant \(c_\omega \). Such an assumption is clearly undispensable, due to the maximal regularity enjoyed by p-harmonic functions. The explicit value of \(\beta _0\), in the case when \(n=2\) and \(N=1\), has been detected in [37].
When writing \(\partial \Omega \in X\) for some function space X, we mean that \(\Omega \) is a bounded open set, which, in a neighbourhood of each point of \(\partial \Omega \), agrees with the subgraph of a function of \((n-1)\) variables that belongs to X. Similarly, the notation \(\partial \Omega \in W^1X\) has to be understood in the sense that such function is weakly differentiable, and its weak derivatives belong to the space X.
Theorem 2.1, as well as the other results of this paper, are most neatly formulated in terms of the nonlinear expression \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\) appearing under the divergence operator in the system in (1.1). As shown in several recent contributions, this is a proper expression to use in the description of the regularity of solutions to p-Laplacian type equations and systems—see for example [2, 8, 14,15,16, 21, 43, 44].
Theorem 2.1
(Regularity in Campanato spaces) Let \(\Omega \) be a bounded open set in \({\mathbb {R}^n}\) such that \(\partial \Omega \in W^1{\mathcal {L}}^{\sigma (\cdot )} \cap C^{0,1}\) for some parameter function \(\sigma \). Let \(\omega \) be a parameter function satisfying condition (2.4). Assume that \(\mathbf {F}\in \mathcal L ^{\omega (\cdot )} (\Omega )\) and let \(\mathbf {u}\) be the solution to the Dirichlet problem (1.1). There exist constants \(\delta =\delta (p, N, \omega , \Omega )\) and \(C=C(p, N, \omega , \Omega )\) such that, if
then \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\in \mathcal L ^{\omega (\cdot )} (\Omega )\), and
Condition (2.5) in Theorem 2.1 is sharp, when
in the sense that not only the finiteness of the supremum in (2.5), but also its smallness cannot be dispensed with. This can be demonstrated yet in the simplest situation when \(n=2\), \(N=1\) and \(p=2\) to which we alluded above, namely for the scalar Dirichlet problem for the Poisson equation in the plane
This is the content of Theorem 2.2, that tells us that the conclusion of Theorem 2.1 may fail if the supremum on the left-hand side of equation (2.5), though finite, is not small enough.
On the other hand, if instead \(\omega (r)\) decays so fast to 0 as \(r \rightarrow 0^+\) that
then condition (2.5) can still be slightly relaxed, by requiring that its left-hand side is just finite, and hence allowing for the choice \(\omega = \sigma \). This is stated in Therorem 2.6 below, which also asserts that, under condition (2.9), the function \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\) is uniformly continuous, with a modulus of continuity depending on \(\omega \) and p.
Theorem 2.2
(Sharpness) Let \(\omega \in C^1(0, \infty )\) be any concave parameter function, satisfying conditions (2.4) and (2.7), and such that \(\lim _{r\rightarrow 0^+}\frac{r\omega '(r)}{\omega (r)}\) exists. Then there exist a parameter function \(\sigma \), a bounded open set \(\Omega \subset {\mathbb {R}}^2\), and a function \(\mathbf {F}\in \mathcal L ^{\omega (\cdot )} (\Omega )\) such that, if u is the solution to the Dirichlet problem (2.8), then
and
but
Remark 2.3
The result of Theorem 2.1 has a local nature. Indeed, it will be clear from its proof that, under the same assumptions on \(\mathbf {F}\) and \(\partial \Omega \), if \(B_R\) is a ball centered on \(\partial \Omega \), then \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\in \mathcal L ^{\omega (\cdot )} ( \Omega \cap B_R)\) for any solution of the system in (1.1) in \( \Omega \cap B_{2R}\) that fulfills the Dirichlet boundary condition on \(\partial \Omega \cap B_{2R}\). The sharpness of Theorem 2.1 can also be shown in its local version, as is apparent from the proof of Theorem 2.2. Indeed, a local formulation of Theorem 2.2 allows for the choice \(F\equiv 0\), and hence applies to scalar harmonic functions that just vanish on part of the boundary. The other results of this paper, that rely upon Theorem 2.1, also admit a local variant [57].
Remark 2.4
As announced in Section 1, condition (2.5) in Theorem 2.1 is qualitatively—namely up to the constant \(\delta \)—independent of the dimension n (and N) and of the exponent p. On the other hand, the optimality of this condition is shown in Theorem 2.2 under the presumably smoothest situation corresponding to the two-dimensional linear scalar case. Theorem 2.1 and Remark 2.3 thus tell us that global regularity properties of the gradient in Campanato type spaces hold in any dimension, and for any power-nonlinearity, under boundary conditions that are qualitatively sharp still for harmonic functions in the plane. The fact that an optimal boundary regularity assumption be dimension-free is a feature that our result shares with the linear gradient regularity theory for Lebesgue norms in Lipschitz domains developed in [38]. The contribution [9] generalizes, to some extent, that theory to nonlinear problems in the framework of Raifenberg-flat domains.
The conclusion of Theorem 2.1 corresponding to the special choice \(\omega (r)=1\) is enucleated in the next corollary. In this case, Theorem 2.1 implies that regularity in \(\text {BMO}(\Omega )\) of \(\mathbf {F}\) is reflected into the same regularity for \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\), provided that the derivatives of the functions describing \(\partial \Omega \) belong to a Campanato type space associated with a logarithmic parameter function \(\omega \). An additional argument ensures that a parallel conclusion holds if \(\text {BMO}(\Omega )\) is replaced with \( {{\,\mathrm{VMO}\,}}(\Omega )\), the space of functions of vanishing mean oscillation on \(\Omega \). Recall that a real, vector or matrix-valued integrable function \(\mathbf {f}\) in \(\Omega \) is said to belong to \({{\,\mathrm{VMO}\,}}(\Omega )\) if

These results are stated in the next corollary, whose sharpness is a consequence of Theorem 2.2.
Corollary 2.5
(BMO and VMO regularity) Let \(\Omega \) be a bounded open set in \({\mathbb {R}^n}\) such that \(\partial \Omega \in W^1{\mathcal {L}}^{\sigma (\cdot )} \cap C^{0,1}\) for some parameter function \(\sigma \) satisfying
Assume that \(\mathbf {F}\in \text {BMO}(\Omega )\) and let \(\mathbf {u}\) be the solution to the Dirichlet problem (1.1). Then \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\in \text {BMO}(\Omega )\), and there exists a constant \(C=C(p, N, \Omega )\) such that
Moreover, if \(\mathbf {F}\in {{\,\mathrm{VMO}\,}}(\Omega )\), then \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\in {{\,\mathrm{VMO}\,}}(\Omega )\) as well.
Our enhanced result under assumption (2.9) is the subject of Theorem 2.6. Embeddings of Campanato spaces into spaces of uniformly continuous functions, to which we alluded above, have a role in its proof. They go back to [52], and tell us that, if \(\Omega \) is a bounded Lipschitz domain, and the parameter function \(\omega \) fulfills condition (2.9), then
where \(\underline{\omega }\) is the parameter function defined by
Note that, as shown in [52], if the function \(\tfrac{\omega (r)}{r}\) is non-increasing, condition (2.9) is necessary even for the space \(\mathcal L ^\omega (\Omega )\) to be included in \(L^\infty (\Omega )\). Also, the function \(\underline{\omega }\) is optimal in (2.15).
Theorem 2.6
(Continuity estimates)
Let \(\Omega \) be a bounded open set in \({\mathbb {R}^n}\) such that \(\partial \Omega \in W^1{\mathcal {L}}^{\omega (\cdot )}\) for some parameter function \(\omega \) satisfying conditions (2.4) and (2.9). Assume that \(\mathbf {F}\in \mathcal L ^{\omega (\cdot )} (\Omega )\) and let \(\mathbf {u}\) be the solution to the Dirichlet problem (1.1). Then \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\in \mathcal L ^{\omega (\cdot )} (\Omega )\), and inequality (2.6) holds.
Moreover, if \(\underline{\omega }: [0, \infty ) \rightarrow [0, \infty )\) is the parameter function given by (2.16), then \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\in C^{0, {\underline{\omega }} (\cdot )}( \Omega )\), and there exists a constant \(C=C(p, N, \omega , \Omega )\) such that
In particular, the same conclusions hold if \(\mathbf {F}\in {C^{0, {\omega (\cdot )}} (\Omega )}\), and \({\Vert {\mathbf {F}}\Vert }_{ \mathcal L^{\omega (\cdot )} (\Omega )}\) is replaced with the stronger norm \({\Vert {\mathbf {F}}\Vert }_{C^{0, {\omega (\cdot )}} (\Omega )}\) in inequalities (2.6) and (2.17).
The specific choice \(\omega (t) = t^\beta \) in Theorem 2.6, with \(\beta <\beta _0\), yields the following Hölder continuity result.
Corollary 2.7
(Hölder continuity) Let \(\Omega \) be a bounded open set in \({\mathbb {R}^n}\) such that \(\partial \Omega \in C^{1,\beta }\) for some \(\beta \in (0, \beta _0)\). Assume that \(\mathbf {F}\in C^{0, \beta } ( \Omega )\) and let \(\mathbf {u}\) be the solution to the Dirichlet problem (1.1). Then \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\in C^{0, \beta }(\Omega )\), and there exists a constant \(C=C(p,N, \beta , \Omega )\) such that
Theorems 2.1 and 2.6, whose proofs are accomplished in Sections 5 and 6, respectively, are in fact consequences of stronger pointwise estimates, of diverse potential uses, between a sharp maximal function of \(|\nabla \mathbf {u}|^{p-2} \nabla \mathbf {u}\) and a sharp maximal function of \(\mathbf {F}\)—see Propositions 5.1 and 6.1.
Our approach to these estimates entails the choice of appropriate local coordinates, where the boundary of the domain is flat, in the sense that the domain is locally mapped into a half-ball, with a proper radius, after changing variables. Suitable decay oscillation estimates have to be established as the radii of the balls tend to zero. The relevant decay estimates for flat boundaries are the subject of Section 3, and, specifically, of Proposition 3.1.
Due to the minimal regularity required on \(\partial \Omega \), when considering general boundaries in Section 4 we have to develop a new strategy, based on the selection of ad hoc coordinate systems taylored for each scale of the radii. This is a pivotal step, which makes it possible to derive the sharp oscillation bounds stated in Proposition 4.2. This idea seems to be flexible enough for prospective implementations in other questions in the global regularity theory of elliptic boundary value problems. Thanks to a suitable continuation of the differential operator and of the solution beyond the flattened boundary, the problem is reduced to inner regularity. However, the new differential operator is not anymore the p-Laplacian, and, in particular, it is not of Uhlenbeck type and also depends on the space variables. Therefore, standard inner local regularity results cannot be applied. A subsequent task is thus to derive local estimates for perturbed systems. The point is that our regularity assumption on \(\partial \Omega \) allows for the perturbed differential operator to be locally still sufficiently close to the original one for the regularity of solutions not to be destroyed. The techniques proposed in the proof of Proposition 4.2 in this connection are also of possible independent interest.
A proof of the sharpness result contained in Theorem 2.2 is provided in the final Section 7. The two-dimensional nature of this result allows for benefiting from classical local asymptotic expansions for conformal transformations of special domains in the plane. These expansions yield sufficiently exact information on the behaviour of the solution near an irregular point on the boundary, but not on its gradient. The contradiction showing the optimality of the gradient regularity has then to be reached via an indirect argument. The latter combines the knowledge of the modulus of continuity of the solution at the boundary point in question with an embedding theorem for Sobolev type spaces of those functions whose gradients belongs to Campanato spaces, proved in Proposition 7.1.
Let us conclude this section by pointing out that gradient regularity of solutions to Dirichlet problems, for systems with space dependent coefficients, falls among the further issues hinted above, which are likely to be approachable via the methods developed here. For instance, systems of the form
can presumably be considered, where the function \(a: \Omega \rightarrow (0, \infty )\) is bounded and bounded away from 0, and has a prescribed modulus of continuity. In particular, the fact that we are able to treat perturbed systems with variable coefficients, obtained after changing variables in the plain p-Laplace system, is relevant here. One can conjecture, for example, that the balance condition (2.5) admits a still sharp extension as to also include the modulus of continuty of the function a. Parallel generalizations of the other results stated above can be speculated. These results would however require a nontrivial additional analysis, which goes beyond the scope of this work, and will be the object of future researches.
3 A Decay Estimate Near a Flat Boundary
The present section is devoted to a decay estimate for the gradient of solutions to the system in (1.1) satisfying the Dirichlet boundary condition locally on a flat boundary. This is the content of Proposition 3.1.
We begin our discussion by fixing a few notations and conventions. The relation \(`` \approx "\) between two real-vaued expressions means that they are bounded by each other, up to positive multiplicative constants depending on quantities to be specified.
Given \(m, n \in \mathbb N\), we denote by \({\mathbb {R}}^{m\times n}\) the space of \(m \times n\) matrices, by \(`` \cdot "\) the standard scalar product in \({\mathbb {R}}^{m \times n}\), and by \({|{\, \cdot \, }|}\) the induced norm on \({\mathbb {R}}^{m \times n}\).
A point \(x\in \mathbb R^n\) will be regarded as a column vector, namely an element of \({\mathbb {R}}^{n\times 1}\), although, for ease of notation, we shall write \((x_1, \dots , x_n)\) when its components have to be specified. We also set \(x'=(x_1, \dots , x_{n-1})\in \mathbb R^{n-1}\), whence \(x=(x', x_n)\) for \(x\in {\mathbb {R}}^n\). One has that
where the apex \(``\, t\, "\) stands for transpose, and \(`` \mathrm{tr}"\) for trace. More generally, if \(\mathbf {B}, \mathbf {C}\in \mathbb R^{m\times n}\), then
Also, if \(\mathbf {B}, \mathbf {C}\in \mathbb R^{m\times N}\) and \(\mathbf {P},\mathbf {Q}\in {\mathbb {R}}^{N\times n}\), then
Given a function
its gradient \(\nabla w\) is a row vector in \({\mathbb {R}}^n\), namely \(\nabla w \in {\mathbb {R}}^{1 \times n}\). More generally, if
then \(\nabla \mathbf {w}\) is the matrix in \({\mathbb {R}}^{N\times n}\) whose rows are the gradients of the components \(w^1, \, \dots \, , w^N\) of \(\mathbf {w}\). With these conventions in place, if \(\varvec{\psi }: {\mathbb {R}}^d \rightarrow {\mathbb {R}}^n\), then
where the product on the right-hand side is just the matrix product. In particular, if \(\mathbf {Q}\in {\mathbb {R}}^{d\times n}\), and
then \(\nabla \varvec{\psi }=\mathbf {Q}\), and
Notice also that, if \(\eta : {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) and \(\mathbf {w}: {\mathbb {R}}^n \rightarrow {\mathbb {R}}^N\), then
where \( \mathbf {w}\nabla \eta \in {\mathbb {R}}^{N\times n}\) is the matrix product between \(\mathbf {w}\in {\mathbb {R}}^{N\times 1}\) and \(\nabla \eta \in {\mathbb {R}}^{1\times n}\). Therefore, \( \mathbf {w}\nabla \eta \) agrees with the tensor product \(\mathbf {w}\otimes \nabla \eta \).
Given \(p >1\), define the function \(\mathbf {A}: {\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}^{N\times n}\) as
If \(\mathbf {T}\in {\mathbb {R}}^{n\times n}\) we also denote by \(\mathbf {A}_{\mathbf {T}} : {\mathbb {R}}^{N\times n} \rightarrow {\mathbb {R}}^{N\times n}\) the function defined by
Let us now recall a few notions of solutions. Let \(\mathbf {F}\in L^{p'}(\Omega )\). A function \(\mathbf {u}\in W^{1,p}_0(\Omega )\) is called a weak solution to problem (1.1) if
for every function \(\varvec{\varphi }\in W^{1,p}_0(\Omega )\).
Assume next that \(\mathbf {F}\in L^{p'}_\mathrm{loc}(\Omega )\). A function \(\mathbf {u}\in W^{1,p}_\mathrm{loc}(\Omega )\) is called a local weak solution to the system
if
for every function \(\varvec{\varphi }\in W^{1,p}_0(\Omega ')\) with \(\Omega ' \subset \subset \Omega \).
Let \(B_R\) be a ball centered on \(\partial \Omega \), with radius R, and let \(\mathbf {F}\in L^{p'}(\Omega \cap B_R)\). Assume that \(\mathbf {u}\) belongs to the closure in \(W^{1,p}(\Omega \cap B_R)\) of the space of those functions in \(C^\infty (\Omega \cap B_R)\) that vanish in a neighbourhood of \(\partial \Omega \). Then \(\mathbf {u}\) is called a weak solution to the problem
if
for every function \(\varvec{\varphi }\in W^{1,p}_0(\Omega \cap B_R)\).
Given a matrix \(\mathbf {T}\in {\mathbb {R}}^{n \times n}\), with \(\mathrm{det} \mathbf {T}\ne 0\), and a function \(\mathbf {w}: \Omega \rightarrow {\mathbb {R}}^N\), define the function
as
Therefore,
Let \(\mathbf {A}_{\mathbf {T}^{-1}}\) be function defined as in (3.3), with \(\mathbf {T}\) replaced by \(\mathbf {T}^{-1}\). Assume that \(\mathbf {u}\) is a local solution to the system
Let \(\overline{\mathbf {u}}\) and \(\overline{\mathbf {F}}\) be the functions built upon \( \mathbf {u}\) and \(\mathbf {F}\) as in (3.9). We claim that the function \(\overline{\mathbf {u}}\) is a local solution to the system
As a consequence, local results available for the p-Laplacian are translated to systems with constant coefficients of the form (3.10). Our claim follows from the following chain, that, owing to (3.1), holds for any function \(\varvec{\varphi }\in W^{1,p}_0(\Omega )\):
Now, assume that the matrix \(\mathbf {T}\in \mathbb R^{n\times n}\) is positive definite, with smallest eigenvalue \(\lambda \) and largest eigenvalue \(\Lambda \). In particular
for every \(r>0\). We consider solutions to systems of type (3.10) in a half-ball, subject to zero boundary conditions on the flat part of its boundary. Precisely, define
and
and let \(\mathbf {u}\) be a weak solution to the problem
Choosing \(\Omega = H^+\cap B_r(0)\) in (3.10) tells us that \( \overline{\mathbf {u}}\) is a weak solution to the problem
Since solutions are invariant under orthonormal transformations, we can make use of an even reflection with respect to the half-space \(H_{ \mathbf {T}^{-1}}\), and obtain a local solution in an entire ball. To this purpose, consider the linear map from \(H_{\mathbf {T}^{-1}}\) into \(H^+\) associated with an orthonormal matrix \(\mathbf {Q}\in \mathbb R^{n \times n}\). Also, we define \(\widehat{\mathbf {u}}\) and \(\widehat{\mathbf {F}}\) as the composition of the inverse of this transformation with \(\overline{\mathbf {u}}\) and \(\overline{\mathbf {F}}\), respectively. Namely, we define \(\widehat{\mathbf {u}}, \widehat{\mathbf {F}} : H^+\cap B_{\lambda r}(0) \rightarrow \mathbb R^N\) as
and
for \(z \in H^+\cap B_{\lambda r}(0)\) . On making use of the fact that \(\mathbf {Q}^t=\mathbf {Q}^{-1}\), the argument above implies that \(\widehat{\mathbf {u}}\) is a weak solution to the problem
Let \(\mathbf {R}\in {\mathbb {R}}^{N\times n}\) be the matrix given by \(\mathbf {R}=\text {diag}(1,\ldots ,1,-1)\). Set
The function \(\mathbf {v}: B_{\lambda r}(0) \rightarrow \mathbb R^N\), defined as
belongs to \(W^{1,p}_\mathrm{loc}(B_{\lambda r}(0))\), and
Let \(\mathbf {C}\in \mathbb {R}^{N\times n}\). We will show that, if \(\mathbf {G}: B_{\lambda r}(0) \rightarrow \mathbb R^{N\times n}\) is defined as
then \(\mathbf {v}\) is a local solution to the system
To verify this assertion, note that any function \(\varvec{\varphi }\in C^{\infty }_0(B_{\lambda r}(0))\) can be decomposed as

where we have set
for \((x', x_n) \in B_{\lambda r}(0)\). In particular,
for \((x', x_n) \in B_{\lambda r}(0)\). Also, \(\varvec{\varphi }_2 \in W^{1,p}_0(B_{\lambda r}^+(0))\). Hence,
Note that in this chain we have made use of (3.1), of the fact that \(\mathbf {R}=\mathbf {R}^t=\mathbf {R}^{-1}\), and of the equality
which holds since \(\mathbf {v}= \widehat{\mathbf {u}}\) in \(B_{\lambda r}^+\) and \(\widehat{\mathbf {u}}\) is a solution to problem (3.17). Consequently,
By the density of the space \(C^\infty _0(B_{\lambda r}(0))\) in \(W^{1,p} _0(B_{\lambda r}(0))\), this implies that \(\mathbf {v}\) is a local weak solution to system (3.18).
Let us now set
for \(s\in (0,\lambda r)\), whence \(D_s={\{{\mathbf {Q}^t z:z\in B_s^+(0)}\}}\). Also, define the matrix \(\overline{\mathbf {A}}_s\in {\mathbb {R}}^{N\times n}\) by
We are now ready to state and prove the main result of this section. In the statement, we keep in force the notations introduced above.
Proposition 3.1
Let \(p>1\), \(r>0\), and let \(\omega \) be a parameter function satisfying condition (2.4). Assume that \(\mathbf {F}\in L^{p'}(H^+ \cap B_r(0))\). Let \(\mathbf {u}\) be a local weak solution to problem (3.15) and let \(\overline{\mathbf {u}}\) be the corresponding weak solution to problem (3.16). There exist constants \(c>0\) and \(\theta \in (0,1)\), depending only on \(n,N,p,c_\omega ,\beta ,\lambda , \Lambda \), such that

for every \({\mathbf {F}}_0\in \mathbb {R}^{N\times n}\) and for \(s \in (0, \lambda r)\).
Proposition 3.1 will be derived from the following inner local decay estimate contained in [8, Inequality (3.11)]. Earlier estimates in a similar spirit can be traced back to [10, 29, 35].
Proposition 3.2
([8]) Let \(p>1\), and let \(\omega \) be a parameter function satisfying condition (2.4). Let \(\Omega \) be an open set in \(\mathbb R^n\). Assume that \(\mathbf {F}\in L^{p'}_\mathrm{loc}(\Omega )\). Let \(\mathbf {u}\) be a local weak solution to problem (3.5). There exist constants \(c>0\) and \(\theta \in (0,1)\), depending only on \(n,N,p,c_\omega ,\beta \), such that

for every \(\mathbf {F}_0\in \mathbb {R}^{N\times n}\) and every ball \(B_r \subset \subset \Omega \).
The following observations also play a role in the proof of Proposition 3.1. Assume that \(\mathbf {f}\) is a real, vector or matrix-valued function on \( B_r(0)\) such that \(\mathbf {f}\in L^q(B_r(0))\) for some \(q\geqq 1\). If \(\mathbf {f}(x',x_n)=\mathbf {f}(x',-x_n)\) for almost every \((x', x_n) \in B_r(0)\) , then

If \(\mathbf {f}(x',x_n)=-\mathbf {f}(x',-x_n)\) for almost every \((x', x_n) \in B_r(0)\), then, plainly, \(\langle {\mathbf {f}}\rangle _{B_r(0)}=0\). Thus,

Note that, in inequality (3.24), we have made use of the fact that, if E is a measurable subset of \({\mathbb {R}}^n\), and \(q \in [1, \infty ]\), then
for every measurable function \(\mathbf {f}: E \rightarrow {\mathbb {R}}^m\) such that \(\mathbf {f}\in L^q(E)\), where the minimum is extended over all \(\mathbf {c}\) in the range of \(\mathbf {f}\). This basic property will be repeatedly expolited in what follows.
Proof
Analogously to (3.21), for \(s\in (0,\lambda r)\) we define the matrix \(\widehat{\mathbf {A}}_s\in {\mathbb {R}}^{N\times n}\) as
Given \({\mathbf {F}}_0\in \mathbb {R}^{N\times n}\), choose \(\mathbf {C}={\mathbf {F}}_0 \mathbf {T}^t \mathbf {Q}\). From Proposition 3.2, applied to the solution \(\mathbf {v}\) to system (3.18), we deduce, via (3.17), that

Observe that a proof of inequality (3.28) also calls into play the property that \(\mathbf {A}(\nabla \widehat{\mathbf {u}})_{ki}\) is odd in the variable \(x_n\), and \((\widehat{\mathbf {A}}_s)_{ki}=0\) if \(k\in {\{{1,\ldots ,N}\}}\), \(i\in {\{{1,\ldots ,n-1}\}}\), whence (3.25) can be exploited, whereas \(\mathbf {A}(\nabla \widehat{\mathbf {u}})_{kn}\) is even, and hence (3.24) can be exploited. Now, since \(\mathbf {Q}\) is an orthonormal matrix,
Hence, inequality (3.23) follows from (3.28), via a change of variables.
4 A Decay Estimate Near a Non-flat Boundary
Our task in the present section is to establish an inequality in the spirit of (3.22) for local solutions \(\mathbf {u}\) to problem (3.7) in the case when \(\partial \Omega \cap B_R\) is not necessarily contained in a hyperplane. Decay estimates at the boundary for solutions to \(p\)-Laplacian type equations are available in the literature. For instance, they can be found in the paper [41], where the case of boundaries of class \(C^{1,\beta }\) is reduced, via a suitable change of cooordinates, to that of a flat boundary treated in [46]. A flattening technique, combined with a reflection argument, is also exploited in [11] to treat systems. Neither the approach of [41], nor that of [11], however, applies to deal with boundaries under as weak regularity assumptions as those imposed in this paper. We have thus to resort to a new method adapted to the situation at hand.
4.1 A Gehring Type Result Near the Boundary
One ingredient in our proof of the decay estimate near the boundary is a higher integrability result for the gradient of the solution to system (1.1). This is stated in the following proposition, that applies to any open bounded set \(\Omega \subset {\mathbb {R}}^n\) such that
for some constant \(C>0\) and every ball \(B\) centered at a point in \(\Omega \).
In what follows, given a ball \(B\) and a positive number \(\theta \), we denote by \(\theta B\) the ball with the same center as \(B\), whose radius is \(\theta \) times the radius of \(B\).
Proposition 4.1
Let \(\Omega \) be an open bounded subset of \({\mathbb {R}}^n\) fulfilling condition (4.1). Let \(p>1\) and let \(N \geqq 1\). There exist constants \(q_0>1\) and \(c>0\), depending on \(n\), \(N\), \(p\) and on the constant \(C\) appearing in (4.1), such that if \(q \in [1, q_0]\), \(\mathbf {F}\in L^{p'q}(\Omega )\) and \(\mathbf {u}\) is the solution to the Dirichlet problem (1.1), then

and

for every matrix \(\mathbf {F}_0\in {\mathbb {R}}^{N \times n}\) and every ball \(B\subset {\mathbb {R}}^n\). Here, \(\mathbf {F}\) and \(\mathbf {u}\) are extended by \(0\) outside \(\Omega \).
Proof
A key step in the proof of inequalities (4.2) and (4.3) is a reverse Hölder type inequality, which tells us that that

for some constant \(c\) depending on \(n\), \(N\), \(p\) and on the constant \(C\) in (4.1), and for every matrix \(\mathbf {F}_0\in {\mathbb {R}}^{N \times n}\) and every ball \(B\subset {\mathbb {R}}^n\). Here, \(\theta =\max \big \{ \frac{n}{n+p}, \frac{1}{p}\big \}\). In order to prove inequality (4.4), let us distinguish into some cases. If \(\frac{3}{2}B\subset \Omega \), inequality (4.4) follows from [30, Remark 6.12], via a standard covering argument. If \(\Omega \cap \frac{3}{2}B = \emptyset \) the result is trivial. It remains to consider the case when \({\partial \Omega }\cap \frac{3}{2}B\ne \emptyset \). Choose a function \(\eta \in C^\infty _0(2B)\) such that \(0 \leqq \eta \leqq 1\), \(\eta =1\) in \(B\) and \({|{\nabla \eta }|} \leqq \frac{c}{R}\) for some absolute constant \(c\), where \(R\) denotes the radius of \(B\). Let \(\alpha \geqq {p}\), whence \((\alpha -1){p}' \geqq \alpha \). Set \({\varvec{\xi }}= \eta ^{\alpha } \mathbf {u}\), and let \(\mathbf {F}_0\in \mathbb {R}^{N\times n}\). Making use of the function \({\varvec{\xi }}\) as a test function in the weak formulation (3.4) of system (1.1) yields
Thereby,

By Young’s inequality, there exist positive constants \(c\) and \(c'\) such that

for \(\delta >0\),

and

for \(\delta >0\). On the other hand, as a consequence of our current assumption that \(\frac{3}{2}B\cap \partial \Omega \ne \emptyset \) and of (4.1), the function \(\mathbf {u}\) vanishes on a subset of \(2B\) whose measure exceeds \(c|2B|\) for some positive constant \(c\). On choosing \(\delta \) small enough, exploiting the fact that \(\eta ^{(\alpha -1) p'}\leqq \eta ^\alpha \), and making use of a Poincaré–Sobolev inequality on balls for functions enjoying this property, one can deduce from inequalities (4.6)–(4.9) that

for some constants \(c\) and \(c'\). Inequality (4.4) is thus established. This inequality, via a version of Gehring’s lemma as in [36], implies that there exist an exponent \(q_0>1\) and a constant \(c\) such that

for every \(q\in [1,q_0]\). Inequalities (4.2) and (4.3) follow from (4.10), via [21, Lemma 3.3].
4.2 Change of Coordinates
Since the system in (3.7) and the estimate to be derived are invariant under translations and rotations, we may assume, without loss of generality, that \(0 \in \partial \Omega \), that \(B_R\) is centered at \(0\), and that the outer normal to \(\Omega \) at \(0\) agrees with the opposite of the \(n\)-th unit vector of the canonical basis in \(\mathbb R^n\).
Assume, for the time being, that \(\Omega \) is just a bounded Lipschitz domain, namely that \(\partial \Omega \in C^{0,1}\). Then, there exists \(R>0\), depending on the Lipschitz constant of \(\partial \Omega \), and a map \(\psi : {\mathbb {R}}^{n-1}\rightarrow {\mathbb {R}}\) such that
and
Also, we define \(\Psi : \overline{\Omega }\cap B_R(0)\rightarrow B_R^+(0)\) as
Observe that \(\Psi (\partial \Omega \cap B_R(0))\subset {\{{(x',x_n):x_n=0}\}}\) and \(\Psi (0)=0\). Moreover, the function \(\Psi : \overline{\Omega }\cap B_R(0) \rightarrow \Psi (\overline{\Omega }\cap B_R(0))\) is invertible, with a Lipschitz continuous inverse \(\Psi ^{-1} : \Psi (\overline{\Omega }\cap B_R(0)) \rightarrow \overline{\Omega }\cap B_R(0)\). Since, at this stage, we are merely assuming that \(\partial \Omega \in C^{0,1}\), no additional regularity on \(\Psi \) is available yet. Define \(\mathbf {J}: \overline{\Omega }\cap B_R(0)\rightarrow {\mathbb {R}}^{n\times n}\) as
Thus,
for \((x', x_n) \in \overline{\Omega }\cap B_R(0)\). Moreover, with some abuse of notation, we define \(\mathbf {J}^{-1} : \Psi (\overline{\Omega }\cap B_R(0)) \rightarrow {\mathbb {R}}^{n\times n}\) as \(\mathbf {J}^{-1}(y) = \nabla \Psi ^{-1} (y)\) for \(y \in \Psi (\overline{\Omega }\cap B_R(0)) \). Hence,
Therefore, \(\mathbf {J}^{-1}(y) \mathbf {J}(\psi ^{-1}(y)) =\mathbf {I}\), the identity matrix, for \(y \in \Psi (\overline{\Omega }\cap B_R(0)) \). Clearly \(\det \mathbf {J}(x)=1\) for \(x \in \overline{\Omega }\cap B_R(0)\) and \(\det \mathbf {J}^{-1} (y)=1\) for \(y \in \Psi (\overline{\Omega }\cap B_R(0)) \). Hence \({|{\Psi (E)}|}={|{E}|}\) for every measurable set \(E \subset \overline{\Omega }\cap B_R(0)\), and \({|{\Psi ^{-1}(E)}|}={|{E}|}\) or every measurable set \(E \subset \Psi (\overline{\Omega }\cap B_R(0)) \).
Owing to the Lipschitz continuity of \(\Psi \) and \(\Psi ^{-1}\), there exist constants
such that
if \(0<r \leqq R\), and
if \(B_r^+(0) \subset \Psi (\overline{\Omega }\cap B_R(0))\). Note that the constant \(C\) appearing in (4.1) only depends on a lower estimate for \(R\) and \(\lambda \) and on an upper estimate for \(\Lambda \).
Next, given a function \(\mathbf {f}\) on \(\overline{\Omega }\cap B_R(0)\), we define the function \(\widetilde{\mathbf {f}}\) on \( \Psi (\overline{\Omega }\cap B_R(0))\) as
Hence, if \(\mathbf {f}\) is differentiable, then
and
where \(\nabla _x\) and \(\nabla _y\) denote gradient with respect to the variables \(x\) and \(y\), respectively.
By the boundedness of \(\mathbf {J}\), we have that
up to multiplicative constants depending only the Lipschitz constants of \(\Psi \) and \(\Psi ^{-1}\).
Our aim is now to show that, if \(\mathbf {u}\) is a solution to problem (3.7), then the function \(\widetilde{\mathbf {u}}\), associated with \(\mathbf {u}\) as in (4.17), solves a similar problem, involving an elliptic system with variable coefficients. To this purpose, we define, for each \(y \in \Psi (\overline{\Omega }\cap B_R(0))\), the function \(\mathbf {A}_{\widetilde{\mathbf {J}}}: \mathbb R^{N\times n} \rightarrow \mathbb R^{N\times n}\) as in (3.3), with \(\mathbf {T}^{-1}\) replaced by \(\widetilde{\mathbf {J}}(y)\). Thereby,
Since \(\det {\mathbf {J}}^{-1}=1\), by (3.1) one has that
for every function \(\varvec{\varphi }\in C^\infty _0({\Omega }\cap B_R(0))\). A similar chain strarting wth the integral
for an arbitrary matrix \(\mathbf {F}_0\in {\mathbb {R}}^{N\times n}\), and the use of equation (3.8) imply that
Equation (4.18) tells us that the function \(\widetilde{\mathbf {u}}\) solves the following problem:
where we have set \(\widehat{\mathbf {F}}=(\widetilde{\mathbf {F}}-\mathbf {F}_0)\widetilde{\mathbf {J}}^t\) and exploited (4.15). Let us introduce the matrix \(\mathbf {J}_s \in {\mathbb {R}}^{n \times n}\) defined as
Our purpose is to apply inequality (3.22) to the solution \(\widetilde{\mathbf {u}}\) to system (4.19), that can be rewritten as
Choose \(\Lambda \) so large that, in addition to (4.15) and (4.16), one has that \(\mathbf {J}_s B_s(0)\subset B_{\lambda R}(0)\) for \(s\in (0,\lambda R)\). Following the approach of the previous section, we define \(\overline{\mathbf {u}} : H_{\mathbf {J}_s} \cap B_{\frac{\lambda }{\Lambda } R}(0) \rightarrow {\mathbb {R}}^N\) as
Hence,
Notice that, by the special form of \(\mathbf {J}\), and hence of \(\mathbf {J}_s\), given \(z \in {\mathbb {R}}^n\), we have that
Also, define accordingly \(\overline{\mathbf {F}} : H_{\mathbf {J}_s} \cap B_{\frac{\lambda }{\Lambda } R}(0) \rightarrow {\mathbb {R}}^{N}\) as
and \(\overline{\mathbf {J}} : H_{\mathbf {J}_s} \cap B_{\frac{\lambda }{\Lambda } R}(0) \rightarrow {\mathbb {R}}^{N\times n}\) as
An analogous argument as in the proof of equation (3.11) implies that \(\overline{\mathbf {u}}\) is a solution to the problem
where we have set
Thus,
for \(z \in H_{\mathbf {J}_s} \cap B_{\frac{\lambda }{\Lambda } R}(0)\).
4.3 Decay Near the Boundary
We are now in a postion to state and prove a crucial decay estimate at the boundary for the gradient of the solution \(\mathbf {u}\) to the Dirichlet problem (1.1). Given \(R>0\) and \(x \in \partial \Omega \), define \(\mathbf {A}_s \in {\mathbb {R}}^{N\times n}\), for \(s\in (0,R]\), as
Proposition 4.2
Let \(\Omega \) be a bounded open set in \({\mathbb {R}}^n\) and let \(x\in \partial \Omega \). Assume that there exists \(R>0\) and local coordinates in \(\Omega \cap B_R(x)\), as in Subsection 4.2, such that \(\psi \in W^1\mathcal L^{\sigma (\cdot )} \cap C^{0,1}\) for some parameter function \(\sigma \). Assume that \(\mathbf {F}\in L^{p'q}(\Omega )\) for some \(q>1\), and let \(\mathbf {u}\) be the weak solution to the Dirichlet problem (1.1). Then there exist constants \(c>0\) and \(\theta \in (0,1)\), depending on \(n,p,N, \omega , q, \Omega \) such that

for every matrix \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\) and every \(s\in [0,R]\).
The following algebraic inequality will be needed in the proof of Proposition 4.2.
Lemma 4.3
Assume that the matrices \(\mathbf {T}_i \in {\mathbb {R}}^{n\times n}\), \(i= 1,2\), are such that \(\lambda {|{\mathbf {Q}}|}\leqq {|{\mathbf {T}_i \mathbf {Q}}|}\leqq \Lambda {|{\mathbf {Q}}|}\), for some \(\Lambda>\lambda >0\), and every \(\mathbf {Q}\in {\mathbb {R}}^{N\times n}\). Let \(\mathbf {A}_{\mathbf {T}_i}\), \(i= 1,2\), be the functions defined as in (3.3). Then there exists a constant \(c = c(p,n,N,\lambda , \Lambda )\) such that
Proof
One has that
up to multiplicative constants depending on \(n,N,p\). Hence, there exist constants \(c\) and \(c'\) such that
for every \(\mathbf {Q}\in {\mathbb {R}}^{N\times n}\).
Proof of Proposition 4.2
Without loss of generality, we may assume that \(x=0\), and, for simplicity, we denote the ball \(B_r(0)\) by \(B_r\) throughout this proof. Assume, for the time being, that \(q\in (1,q_0]\), where \(q_0\) is the exponent appearing in the statement of Proposition 4.1. To begin with, note that, since \(\psi \in W^1\mathcal L^{\sigma (\cdot )}\), there exists a constant \(C\) such that

where \(\mathbf {J}\) is defined as in (4.12). This is a consequence of the definition of Campanato seminorms and of the observation following their definition in (2.1).
We want to apply Proposition 3.1, with \(\mathbf {T}^{-1}= \mathbf {J}_s\), to the solution \(\overline{\mathbf {u}}\), given by (4.22), to problem (4.25). To this purpose, define \(D_s\) as in (3.20), with this choice of \(\mathbf {T}^{-1}\). Namely,
Also, we set
for \(\theta \in (0,1]\). Next, define \(\overline{\mathbf {A}}_\tau \in {\mathbb {R}}^{N\times n}\) for \(\tau \in (0,s]\) by
An application of Proposition 3.1 then tells us that there exist \(\theta \in (0,1)\) and \(c>0\) such that

for every \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\) and every \(\tau \in (0,1)\). Given any \(\delta \in (0,1)\), let \(k\in {\mathbb {N}}\) be such that \(2^{-k}\leqq \delta \). Iterating inequality (4.32), with \(\tau = \theta ^j\), \(j={\{{0,1,\ldots ,k}\}}\), tells us that there exist \(\theta \in (0,1)\) and \(c>0\), depending on \(\delta \), such that

for every \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\).
Fix \(r\) such that \({\frac{\Lambda }{\lambda } r}=\theta s\). By property (3.26) applied to the \(n\)-th component, a change of variables, and the fact that \(\det (\nabla \Psi ^{-1} \mathbf {J}_s)=\det (\nabla \Psi ^{-1})\det (\mathbf {J}_s)=1 \cdot 1 = 1\), one has that

Observe that the second inequality holds since, by the second inclusion in (4.15) and the first inequality in (4.14),
Now, note the identities
and
for \(z \in D_R\), and the inequality
Owing to equations (4.35)–(4.37) and (4.29), the following chain holds:
for some constant \(c\). In the last inequality we have also made use of the fact that \(\mathbf {J}_s\) and \(\mathbf {J}^{-1}\) are bounded. Thus, one has that

for some constants \(c,c', c'', c'''\) and for every \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\). Notice that first inequality in (4.39) is due to (4.38) and (2.4) (and to Hölder’s inequality if \(p\in (1,2)\)), the second one to Hölder’s inequality and (2.4), the third one to (4.30), to a change of variable, to the boundedness of \(\mathbf {J}_s\), \(\mathbf {J}\) and \(\mathbf {J}^{-1}\) and to the fact that
and the last one to Proposition 4.1. Similarly, we have that

for some constants \(c,c'\) and for every \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\). By the very definition of \(\underline{\mathbf {F}}\) in (4.26), a change of variables and the boundedness of \(\mathbf {J}, \mathbf {J}^{-1}, \mathbf {J}_s\),

for some constants \(c,c'\) and for every \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\). Finally, observe that
for \(z \in H_{\mathbf {J}_s} \cap B_{\frac{\lambda }{\Lambda }R}\), where \(\mathbf {I}\) is the unit matrix in \({\mathbb {R}}^{(n-1) \times (n-1)}\), and \((\Psi ^{-1}(\mathbf {J}_s z))'\) denotes the vector in \(\mathbb R^{n-1}\) of the first \((n-1)\) components of \(\Psi ^{-1}(\mathbf {J}_s z)\). Thus, by Lemma 4.3,
Hence, via the last two inequalities in equation (4.39),

for some constant \(c\) and for every \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\). Combining inequalities (4.33), (4.34), (4.39), (4.40), (4.41) and (4.43) yields, on enlarging the domains of integration when necessary and making use of (2.4),

for some constant \(c\) and for every \(\mathbf {F}_0 \in {\mathbb {R}}^{N\times n}\). Hence, inequality (4.28) follows, by fixing \(\delta \) sufficiently small and then redefining \(\theta \) and \(c\) accordingly. The fact that (4.28) actually holds for every \(q>1\), and not just for \(q \in (1, q_0]\), is a consequence of Hölder’s inequality.
5 Proof of Theorem 2.1
A main step in our proof of Theorem 2.1 is a pointwise estimate for a sharp maximal function of the gradient of the weak solution \(\mathbf {u}\) to the Dirichlet problem (1.1). The relevant sharp maximal function operator has a local nature, and involves a parameter function \(\omega \). Assume that \(\Omega \) is a bounded open set satisfying condition (4.1). Let \(R>0\) and \(q \in [1, \infty )\). If \(\mathbf {f}\) is a real, vector or matrix-valued function in \(\Omega \) such that \(\mathbf {f}\in L^q(\Omega )\), we define the function \(M^{\sharp ,q}_{\omega ,\Omega , R} \mathbf {f}\) on \({\mathbb {R}}^n\) as

Proposition 5.1
Let \(\Omega \) be a bounded open set in \({\mathbb {R}}^n\) such that \(\partial \Omega \in W^1\mathcal L^{\sigma (\cdot )} \cap C^{0,1}\) for some parameter function \(\sigma \). Let \(\omega \) be a parameter function fulfilling condition (2.4). Assume that \(\mathbf {F}\in L^{p'q}(\Omega )\) for some \(q>1\), and let \(\mathbf {u}\) be the weak solution to the Dirichlet problem (1.1). Then there exist positive constants \(\varepsilon \), \(R_0\) and \(c\), depending on \(n,p,N,\omega , q, \Omega \), such that, if
then

for every \(x \in \partial \Omega \) and \(R\in (0,R_0)\).
Hence,

for every \(x \in \partial \Omega \) and \(R\in (0,R_0)\).
The following lemma will be needed in the proof of Proposition 5.1.
Lemma 5.2
Let \(\Omega \) be a bounded Lipschitz domain in \({\mathbb {R}}^n\). Let \(R\in (0,1)\) be such that, for every \(x \in \partial \Omega \) there exists a map \(\Psi : \Omega \cap B_R(x) \rightarrow {\mathbb {R}}^n\) as in (4.11), with \(\Psi \in C^{0,1}(\Omega \cap B_R(x))\). Assume that \(q\in [1,\infty )\) and \(\omega \) is a parameter function satisfying condition (2.4). Let \(\overline{\omega }: (0, 1) \rightarrow [0, \infty )\) be the function defined as
Then there exists a constant \(c=c(n,\beta ,c_\omega ,\lambda ,\Lambda ,q)\) such that

for every \(\mathbf {f}\in L^q(\Omega )\), \(x\in \partial \Omega \) and \(r \in (0,R]\).
Proof
Let us keep the notations of Subsection 4.2 in force. Moreover, we can assume that all balls are centered at \(0\). For simplicity, the center will thus be dropped in the notation.
Owing to properties (3.26) and (4.16), a change of variables and the fact that \(|\det \mathbf {J}|=1\), we have that

for some constants \(c\) and \(c'\). Next, let \(B_R\) be any ball in \({\mathbb {R}}^n\) and let \(\mathbf {g}\in L^q(B_R)\). We claim that

for \(r \in (0, R]\), and that inequality (5.8) contiunes to hold if balls are replaced by half-balls. To prove our claim, observe that

Let \(m \in {\mathbb {N}}\). By iterating the previous inequality, we obtain that

Given any \(\tau \in (2^{-m},2^{1-m}]\), property (3.26) ensures that

Consequently,

Moreover,

Given \(\theta \in (0, 1)\), choose \(m \in \mathbb N\) in such a way that \(\theta \in (2^{-m},2^{1-m}]\). Then, we deduce from (5.11), (5.9) and (5.10) that

Property (3.26) ensures that

for \(\tau \in (0,1]\). Inequality (5.12) (applied with \(\mathbf {g}\) replaced by \(|\mathbf {g}|\)), inequality (5.13) and Hölder’s inequality imply that

for every \(q \in [1,\infty )\). Given any \(r\in (0, {R}]\), the choice \(\theta = \frac{r}{R}\) in (5.14) and a change of variables in the last integral yield (5.8).
Having inequality (5.8) at disposal, we are ready to accomplish the proof of inequality (5.6). If \(r\in [\frac{\lambda R}{\Lambda },R]\), then inequality (5.6) follows by enlarging the domain of integration. Assume, next, that \(r\in [0,\frac{\lambda R}{\Lambda }]\). From a change of variables and inequality (5.8) in its version for half-balls, we deduce that there exist constants \(c\) and \(c'\) such that

Note that in the last inequality we have made use of the fact that \(\overline{\omega }(r) \geqq \int _{\Lambda r}^{\lambda R}\frac{\omega (\rho )d\rho }{\rho }\), thanks to assumption (4.14). Owing to inequalities (5.15), (5.7), (4.15) and to condition (2.4), there exist constants \(c\) and \(c'\) such that

namely (5.6).
Proof of Proposition 5.1
We keep the notations of the previous sections in force. Let \(R_0\) denote the minimum among \(1\) and the radii \(R\) for which the assumptions of Proposition 4.2 are fulfilled. Observe that \(R_0>0\), since \(\partial \Omega \) is compact. Our first aim is to estimate the quantity

where \(R\in (0, R_0)\), and \(\mathbf {A}_s\) is defined as in (4.27). Let \(\theta \in (0,1)\) be the parameter appearing in the statement of Proposition 4.2. First, assume that \(s\in [\frac{\theta R}{2},R]\). By enlarging the domain of integration, and exploiting condition (2.4), triangle inequality, inequality (4.3) (applied with \(\mathbf {F}_0=\langle {\mathbf {F}}\rangle _{ \Omega \cap B_{2R}}\) and \(q=1\)) and Hölder’s inequality, we infer that

for some constants \(c\) and \(c'\). Hence,

Assume next that \(s\in (0, \frac{\theta R}{2})\). By Proposition 4.2, there exists a constant \(c\) such that

Hence, via Lemma 5.2, there exists a constant \(c\) such that

Let \(c\) be the constant appearing in inequality (5.19). Let us choose \(\varepsilon \) so small in condition (5.2) that
By (2.4),

for some positive constant \(c\). By inequalities (5.20) and (5.21), there exists a constant \(c\) such that
From inequality (5.19) with \(\mathbf {F}_0=\langle {\mathbf {F}}\rangle _{ \Omega \cap B_s(x)}\), inequalities (5.20) and (5.22), and the boundedness of \(\sigma \), one deduces that

for some constant \(c\), provided that \(s \in (0, \frac{R}{2})\).
Inasmuch as \(\theta s \in (0, \tfrac{\theta R}{2})\) if and only if \(s\in (0, \tfrac{R}{2})\), inequality (5.23) implies that

Here, we have made use of the fact that \(\sup _{s \in (0, \frac{\theta R}{2})} \sup _{\rho \in (\frac{s}{\theta }, R)}{(\cdot )} = \sup _{\rho \in (0, R)}{(\cdot )}\). Since the last term on the right-hand side of (5.24) does not exceed \(M^{\sharp ,p'q}_{\omega ,\Omega ,{2}R}(\mathbf {F})(x)\) times a suitable constant, coupling inequalities (5.17) and (5.24) yields

for some constant \(c\). Absorbing the first term into the right-hand side of inequality (5.25) into the left-hand side tells us that

Now, let \(y \in B_{R/8}(x)\), and let \(r\leqq R/8\). Set \(s_y= \mathrm{dist}(y, \partial \Omega )\). Assume first that \(r < s_y/2\), whence \(B_{2r}(y) \subset \Omega \). By the local inner estimate of [8, Theorem 1.3 and Remark 1.4], there exists a constant \(c\) such that

Since \(B_{kr}(y) \subset B_{kR/8}(y) \subset B_{kR/4}(x)\) for \(k>0\), we infer from inequality (5.27) and condition (2.4) that

for some constant \(c\). Suppose next that \(r\geqq s_y/2\). Then there exists \(x_y \in \partial \Omega \cap B_{R/8}{(x)}\) such that \(B_{2r}(y) \subset B_{4r}(x_y)\). Therefore, by inequality (5.26) and condition (2.4) again,

for some constants \(c, c', c''\). Inequalty (5.3) follows from (5.28) and (5.29), via the very definition of sharp maximal function (5.1) and property (3.26). Inequality (5.4) is a consequence of inequality (5.3) and of the definition of Campanato seminorm.
We are now in a position to accomplish the proof of Theorem 2.1.
Proof of Theorem 2.1
A basic energy estimate obtained by choosing \(u\) as a test function in equation (3.4), and [22, Theorem 5.23] tell us that
for some constant \(c\). Let \(R_0\) be the radius provided by Proposition 5.1. Trivially,

If \(r\geqq R_0/16\), then, by (2.4), Hölder’s inequality and (5.30), there exist constants \(c\) and \(c'\) such that

If \(r \in (0,R_0/16)\), then, by (5.4), Hölder’s inequality and (5.30), there exist constants \(c\) and \(c'\) such that

Inequality (2.6) follows from (5.31)–(5.33).
Proof of Corollary 2.5
The assertion about the case when \(\mathbf {F}\in \text {BMO}(\Omega )\) is a straighforward consequence of Theorem 2.1, since the integral on the left-hand side of equation (2.5) agrees with \(\log \frac{1}{r}\) if \(\omega (r)=1\).
Assume next that \(\mathbf {F}\in {{\,\mathrm{VMO}\,}}(\Omega )\), and define the function \(\varrho : [0, \infty ) \rightarrow [0, \infty )\) as

and \(\varrho (0)=0\) Then \(\varrho \) is a non-decreasing bounded function, such that \(\lim _{r\rightarrow 0^+} \varrho (r)=0\). Now, let \(\omega : [0, \infty ) \rightarrow [0, \infty )\) be the function given by
for \(r\in (0,1]\), \(\omega (0)=0\), and \(\omega (r) =\omega (1)\) if \(r>1\). It is easily verified that \(\omega \) is a continuous parameter function fulfilling condition (2.4). The function \(\omega \) is also non-decreasing. This follows from an argument analogous to that employed in the proof of assertion (6.8) below. Moreover,
and hence,
for \(r \in (0,1)\). Thus, by assumption (2.14), condition (2.5) is fulfilled with \(\omega \) given by (5.34). An application of Theorem 2.1 tells us that \({|{\nabla \mathbf {u}}|}^{p-2}\nabla \mathbf {u}\in {\mathcal {L}}^\omega (\Omega )\) , whence, in particular, \({|{\nabla \mathbf {u}}|}^{p-2}\nabla \mathbf {u}\in {{\,\mathrm{VMO}\,}}(\Omega )\).
6 Proof of Theorem 2.6
A critical result in view of a proof of Theorem 2.6 is an analogue of the pointwise estimate for the gradient of solutions to problem (1.1) established in Proposition 5.1, but under condition (2.9) and the a priori assumption that the gradient is bounded. The punctum of this result, contained in the next proposition, is that the mere finiteness of the supremum on the left-hand side of equation (2.5) suffices under such an assumption.
Proposition 6.1
Let \(\Omega \), \(x, R, \sigma , \omega , q, \mathbf {F}\) and \(\mathbf {u}\) be as in Proposition 5.1, save that assumption (5.2) is replaced by
for some positive constant \(C\). Assume in addition, that \(\nabla \mathbf {u}\in L^\infty (\Omega )\). Then there exist positive constants \(c\) and \(R_0\), depending on \(n,N,p, \omega , q, \Omega \), such that
for every \(x \in \partial \Omega \) and \(R\in (0, R_0)\). Hence,
for every \(x \in \partial \Omega \) and \(R\in (0, R_0)\).
Proof
We employ the notations of Proposition 5.1. The proof of inequality (6.2) proceeds along the same lines as that of inequality (5.3) of Proposition 5.1. The situation is now actually simpler, owing to the boundedness assumption on the gradient. In fact, inequality (5.18) and assumption (6.1) immediately imply that

This inequality replaces (5.23). The rest of the argument in the proof of inequalities (6.2) and (6.3) is the same as that of inequalities (5.3) and (5.4) in Proposition 5.1.
Proof of Theorem 2.6
We begin by showing that \(|\nabla \mathbf {u}| \in L^\infty (\Omega )\). To this purpose, observe that, owing to assumption (2.9), there exists an increasing function \(\eta : (0, 1) \rightarrow (0, \infty )\) such that \(\lim _{r \rightarrow 0^+} \eta (r) =0\), and still
For instance, one can choose \(\eta (r) = {\underline{\omega }} (r)^{1-\gamma }\) for some \(\gamma \in (0,1)\). Next, define the non-decreasing function \(\omega _1 : (0, 1) \rightarrow (0,\infty )\) as
One has that
for some positive constant \(c\). In particular, the second inequality in (6.5) and condition (6.4) ensure that condition (2.9) is still satisfied with \(\omega \) replaced by \(\omega _1\), namely
Moreover, the first inequality in (6.5) tells us that \(\partial \Omega \in W^1 \mathcal L^{\omega _1(\cdot )}\). Now, consider the function \(\eta _1: (0, \infty ) \rightarrow [0, \infty )\) given by
and observe that
and
Also, we claim that
To verify this claim, note that there exists a (possibly empty) family \(\{(a_i, b_i)\}\), with \(i \in I \subset {\mathbb {N}}\), of disjoint intervals in \((0,1)\), with \(\lim _{i\rightarrow \infty } a_i =0\) if \(I\) is infinite, such that, if \(r \in (0,1)\), then either \(\omega _1(r) = \frac{\omega (r)}{\eta (r)}\), or \(r \in [a_i, b_i]\) for some \(i \in I\) and \(\omega _1(r) = \omega _1(s)= \frac{\omega (a_i)}{\eta (a_i)}\) for every \(s \in [a_i, b_i]\). Now, let \(r, s \in (0,1)\) be such that \(r<s\). If \(\omega _1(r) = \frac{\omega (r)}{\eta (r)}\) and \(\omega _1(s) = \frac{\omega (s)}{\eta (s)}\), then
since \(\eta \) is non-decreasing. If \(r, s \in [a_i, b_i]\) for some \(i\in I\), then
since \(\omega \) is non-decreasing. If \(r \in [a_i, b_i]\) for some \(i\in I\), \(s \geqq b_i\) and \(\omega _1(s) = \frac{\omega (s)}{\eta (s)}\), then
Finally, if \(s \in [a_i, b_i]\) for some \(i \in I\), \(r \leqq a_i\) and \(\omega _1(r) = \frac{\omega (r)}{\eta (r)}\), then
Property (6.8) is thus established. This property ensures that the function \(\omega _1\) fulfills assumtpion (2.4) with the same exponent \(\beta \) as \(\omega \), since
Next, we claim that
To verify this claim, assume, by contradiction, that (6.10) fails. Thus, there exists a positive number \(c\) such that
As a consequence of the properties of the family \(\{(a_i, b_i)\}\) introduced above, there exists a sequence \(\{r_k\}\), with \(\lim _{k\rightarrow \infty } r_k =0\), such that
for \(k \in \mathbb N\). From (6.11) with \(r=r_k\) we infer that
This contradicts the fact that \(\lim _{r\rightarrow 0^+}\eta (r) =0\).
By properties (6.10) and (6.6),
This fact ensures that assumption (2.5) is fulfilled with \(\sigma \) replaced by \(\omega \), and \(\omega \) replaced by \(\omega _1\). This property, combined with the properties of \(\omega _1\) established above, enables us to apply Theorem 2.1 with the same replacements for \(\sigma \) and \(\omega \). In particular, we infer that \(|\nabla \mathbf {u}|^{p-2}\nabla \mathbf {u}\in {\mathcal {L}}^{\omega _1(\cdot )}({\Omega })\), whence, by condition (6.6) and inclusion (2.15) with \(\omega \) replaced by \(\omega _1\), we have that \(|\nabla \mathbf {u}| \in L^\infty (\Omega )\).
We are now in a position to apply Proposition 6.1. Notice that condition (6.1) is satisfied, with \(\sigma = \omega \), owing to assumption (2.9). To be precise, from (2.9) one can deduce that condition (6.1) holds with \(\sigma = \omega \) and the quantity \(\int _0^1\tfrac{\omega (\rho )}{\rho }\, \mathrm{d} \rho \) on the right-hand side. Starting from inequality (6.3), and arguing as in the proof of Theorem 2.1 yields the conclusion.
7 Sharpness of Results
Our proof of Theorem 2.2 is based on precise information on conformal transformations of certain planar domains established in [57], coupled with the embedding theorem contained in the following proposition. In its statement, \(W^{1}_0\mathcal L ^{\omega (\cdot )}(\Omega )\) denotes the Sobolev type space of those functions in \(\Omega \) whose continuation by \(0\) outside \(\Omega \) belongs to \(W^{1}\mathcal L ^{\omega (\cdot )}({\mathbb {R}}^n)\).
Proposition 7.1
Let \(\Omega \) be a bounded open set in \(\mathbb R^n\), let \(\omega : (0,1) \rightarrow [0, \infty )\) be a parameter function fulfilling condition (2.7), and let \(\overline{\omega }\) be the function associated with \(\omega \) as in (5.5). Let \(\upsilon : (0,1) \rightarrow [0, \infty )\) be the function defined by
Then
Proof
Assume, without loss of generality, that \(|\Omega |=1\). Define the (increasing) function \(\varsigma : (0,1) \rightarrow [0, \infty )\) as
and denote by \(M^{\varsigma (\cdot )}(\Omega )\) the Marcinkiewicz space associated with \(\varsigma \), and consisting of those measurable functions \(\mathbf {f}\) on \( \Omega \) such that
Here, \(\mathbf {f}^*\) stands for the decreasing rearrangement of \(\mathbf {f}\), defined on \((0, 1)\) as
where \(|E|\) denotes Lebesgue measure of a set \(E \subset {\mathbb {R}}^n\). We claim that the supremum in (7.4) is equivalent, up to multiplicative constants independent of \(\mathbf {f}\), to the rearrangement-invariant norm—in the sense of Luxemburg (see [5])—defined as
where we have set \(\mathbf {f}^{**}(r) = \tfrac{1}{r} \int _0^r\mathbf {f}^*(s)\, \mathrm{d}s\) for \(r \in (0,1)\). Thus, \(M^{\varsigma (\cdot )}(\Omega )\) is a rearrangement-invariant space equipped with this norm. Since \(\mathbf {f}^* \leqq \mathbf {f}^{**}\), this equivalence will follow if we show that
for some constant \(C\) and for every measurable function \(g : (0,1) \rightarrow [0, \infty )\). A characterization of weighted Hardy type inequalities tells us that inequality (7.6) holds if (and only if)
for some constant \(C\)—see for example [49, Theorem 1.3.2/2]. Since the function \(\varsigma \) is increasing, it suffices to verify inequality (7.7) with the supremum extended to values of \(s\) in a sufficiently small right neighbourhood of \(0\). Given \(a>1\), one has that
provided that \(a>e^{\frac{1}{n}}\), and \(r\in (0, \tfrac{1}{{a^{n}}})\). Hence, the function \(\frac{\varsigma (r)}{r} \) is decreasing in \((0, \tfrac{1}{{a^{n}}})\). Therefore, inequality (7.7) will follow if we show that
for some constant \(C\) and for small \(r\). An application of Fubini’s theorem tells us that
The second addend on the right-hand side of (7.10) agrees with \( \frac{1}{\varsigma (r)}\). On the other hand,
Since the right-hand side of this inequality is bounded, whereas \(\frac{1}{\varsigma (r)}\) diverges to \(\infty \) as \(r \rightarrow 0^+\), inequality (7.9) follows via (7.10).
We have thus established that \(M^{\varsigma (\cdot )}(\Omega )\) is a rearrangement-invariant space. Now, recall that the fundamental function \(\varphi _{M^{\varsigma (\cdot )}}: [0, 1] \rightarrow [0, \infty )\) of \(M^{\varsigma (\cdot )}(\Omega )\) is defined as
where \(E\) is any measurable set contained in \(\Omega \) and such that \(|E|=r\), and \(\chi _{E}\) stands for its characteristic function. Since, by (7.8), the function \(\varsigma \) is quasi-concave, [5, Chapter 2, Proposition 5.8] tells us that
From [52, Theorem 1] one infers that
The associate space of \(M^{\varsigma (\cdot )}(\Omega )\) is the Lorentz space \(\Lambda (\Omega )\) equipped with the norm defined as
for a measurable function \(\mathbf {f}\) in \(\Omega \)—see [31, Corollary 1.9]. Owing to [17, Theorem 3.4],
where \(\nu : [0, \infty ) \rightarrow [0, \infty )\) is the function given by
and by \(\nu (r)=\nu (1)\) for \(r>1\), provided that the norm on the right-hand side of (7.14) is finite for \(r \in [0,1]\) and tends to \(0\) as \(r \rightarrow 0^+\). We have that
up to multiplicative constants independent of \(r\). Observe that the second equality holds by an integration by parts, owing to (7.11) and to the fact that
and the equivalence inasmuch as
On the other hand,
for \(r \in (0,1) \)where the second equality follows from Fubini’s theorem, and the equivalence by the fact that
as is easily seen via an application of De L’Hopital’s rule.
Embedding (7.2) is a consequence of (7.12), (7.13), (7.15) and (7.16).
Proof of Theorem 2.2
Let \(\overline{\omega }\) be the function associated with \(\omega \) as in (5.5). Define the parameter function \(\widehat{\sigma }\) as
\( \widehat{\sigma } (0)=0\) and \( \widehat{\sigma } (r)= \widehat{\sigma } (\tfrac{1}{2})\) if \(r >\tfrac{1}{2}\). Here, \(\gamma \) is a positive number to be chosen later. Note that \(\widehat{\sigma }\) is an increasing continuous, function, being the product of increasing continuous functions. Also, \(\widehat{ \sigma }\in C^1(0, \frac{1}{2} )\), since we are assuming that \(\omega \in C^1(0, \infty )\). We claim that the function \(\widehat{\sigma } (r)/r\) is non-increasing in \((0, \delta )\) for suffciently small \(\delta \). Indeed, if \(\omega (0) >0\), then we may assume, without loss of generality, that \(\omega (r) = 1\), and our claim follows trivially. Suppose next that \(\omega (0)=0\). As a preliminary observation, note that the existence of \(\lim _{r\rightarrow 0^+}\frac{r\omega '(r)}{\omega (r)}\), coupled with assumption (2.7), ensures that in fact
Indeed, the failure of (7.18) would imply that
for some positive constants \(c\) ad \(\delta \), thus contradicting (2.7). Now,
Since
an integration by parts tells us that
Equations (7.19) and (7.21) imply that
for \(r\in (0,\tfrac{1}{2})\). Thanks to (7.18), there exists \(\delta >0\) such that the right-hand side of equation (7.22) is negative for \(r \in (0, \delta )\). Our claim is thus verified.
The increasing monotonicity of the function \(\widehat{\sigma }(r)\) and the decreasing monotoncity of the function \(\widehat{\sigma } (r)/r \) ensure that \(\widehat{\sigma }\) is equivalent to a concave function \(\sigma \in C^1(0, \delta )\), in the sense that
One can choose, for instance, \(\sigma = \Xi ^{-1}\), where \(\Xi : [0, \delta ) \rightarrow {\mathbb {R}}\) is the function given by \(\Xi (r) = \int _0^r \frac{\widehat{\sigma } ^{-1}(s)}{s}\, ds\) for \(r \in [0, \delta )\). Let \(\sigma \) be extended to a continuously differentiable, concave increasing bounded function in \((0, \infty )\), still denoted by \(\sigma \). In particular, the function \(\frac{\sigma (r)}{r}\) is non-increasing.
Define the function \(\psi :\, [0,\infty ) \rightarrow [0,\infty )\) as
Then
where the first two inequalities hold since \(\sigma \) is increasing, and the last one owing to the monotonicity of the function \(\frac{\sigma (r)}{r}\). Inasmuch as \(\psi ' = \sigma \), and the latter is a concave function, one can verify that \(\psi \in C^{1, \sigma (\cdot )}\), and hence \(\psi \in W^1\mathcal L^{\sigma (\cdot )}\cap C^{0,1}\).
Let us identify \({\mathbb {R}}^2\) with \({\mathbb {C}}\), and define the domain \(\Omega \subset {\mathbb {R}}^2\) as
Let \(\zeta (\xi )\) denote the conformal map of \(\Omega \) onto the half-disc \(\mathbb {D}^+ = \{\zeta \,:\, \mathrm {Im}(\zeta )>0, |\zeta |<1\}\), with fixed point \(\xi =0\). Let \(\phi : [0, \infty ) \rightarrow [0, \infty )\) be the function such that \(\Omega \) is given in polar coordinates \((\rho , \theta )\) by
We need to describe the precise behaviour of the function \(\phi \) as \(\rho \rightarrow 0^+\). To this purpose, define the function \(\widetilde{\sigma } : (0, \infty ) \rightarrow [0, \infty )\) as
and observe that, thanks to equation (7.24), there exists a constant \(c>0\) such that
Moreover, the function \( \widetilde{\sigma } \in C^2(0, \infty )\), and \(\widetilde{\sigma }'\) is locally Lipschitz continuous in \((0, \infty )\), since \(\sigma \) is concave. In particular,
and
for \(r>0\). Notice also that
and hence \(\widetilde{\sigma } \) is concave, since \(\sigma \) so is.
For sufficiently small \(|\xi |\), one has that \(\xi \in \partial \Omega \) if and only if \(\tan \theta =\frac{\psi (|x_1|)}{|x_1|}\), or, equivalently,
By Taylor’s formula,
Here, then notation \(O(\varpi (r))\) as \(r\rightarrow 0^+\) for some function \(\varpi \) means that \(O(\varpi (r))\approx \varpi (r)\) near \(0^+\). Since \(|x_1|= \rho \cos \theta \),
for some \(\rho _\theta \in (\rho \cos \theta ,\rho )\) and for sufficiently small \(\rho \). Furthermore, from equation (7.26) and the fact that \(\rho _\theta \approx \rho \) one has that
for some constant \(c\), for sufficiently small \(\rho \) and \(\theta \). Finally, since \(\widetilde{\sigma }\) is increasing, equation (7.29) implies that \(\theta \leqq \,c\,\widetilde{\sigma }(\rho )\), and hence
Coupling equation (7.29) with (7.30), and recalling (7.25) yield
Next, on defining the function \(F: [0, \infty ) \times (-\pi , \pi ) \rightarrow {\mathbb {R}}\) as
equation (7.28) can be rewritten as
Therefore, the function \(\phi (\rho )\) agrees with the function \(\theta (\rho )\) implicitly defined by (7.32). One has that
for \((\rho , \theta ) \in [0, \infty ) \times (-\pi , \pi )\). Hence,
and
for sufficiently small \(\rho \). By equation (7.26) and the monotonicity of \(\sigma \),
for some constants \(c\) and \(c'\) and for sufficiently small \(\rho \).
Now,
for \((\rho , \theta ) \in [0, \infty ) \times (-\pi , \pi )\). Thus, on denoting \(\widetilde{\sigma }(\rho \cos \phi (\rho ))\), \(\widetilde{\sigma }'(\rho \cos \phi (\rho ))\) and \(\widetilde{\sigma }''(\rho \cos \phi (\rho ))\) simply by \(\widetilde{\sigma }\), \(\widetilde{\sigma }'\) and \(\widetilde{\sigma }''\), one infers from (7.34) and (7.38)–(7.40) that

for \(\rho \geqq 0\). On setting
and making use of (7.26), (7.27) and (7.31) and of the fact that \(\sigma \) and \(\widetilde{\sigma }\) are bounded, we deduce that
for some constants \(c\) and \(c'\) and for sufficiently small \(\rho \). Similar estimates tell us that
and
for some constant \(c\) and for sufficiently small \(\rho \). Since \(\sigma \) and \(\widetilde{\sigma } \) are concave, their derivatives ar non-increasing, and hence
for sufficiently small \(\rho \). From equations (7.41)–(7.45) one can infer that there exists \(\delta >0\) such that
Let us define the functions \(\Phi _-, \Phi _+, \Theta : (0, \delta ] \rightarrow {\mathbb {R}}\) as
and
for \(\rho \in (0, \delta ]\). Note that \(\Phi _+(\rho )+\Phi _-(\rho )=0\). Moreover, by (7.37), \(0\leqq \rho \Phi _+'(\rho )=\rho \phi '(\rho )\leqq c \sigma (\rho )\) for some constant \(c\) and for sufficiently small \(\rho \), whence
Similarly \(\lim _{\rho \rightarrow 0^+} \rho \Phi _-'(\rho )=0\). Thus the assumptions of [57, Thm. XI(B)] will be verified, if we show that, in addition,
Incidentally, let us note that the last integral is affected by a typo in the statement of [57, Thm. XI(B)], where the factor \(\rho \) is missing.
Since \(\phi ' \geqq 0\), by equation (7.46)
On the other hand, owing to (7.37),
for some constants \(c\) and \(c'\). Now,
whence, by (7.17) and (7.23), \(\sigma (\rho )\leqq \tfrac{\gamma }{\log (1/\rho )}\) for \(\rho \in (0, \delta ]\). Consequently, the integral on the leftmost side of equation (7.49) is finite. It follows from [57, Theorem (XI)(b)] that
for some positive constant \(c\). Note that
Let us define the function \(\mu : (0, \delta ] \rightarrow {\mathbb {R}}\) as
Consequently,
We have that \(\lim _{\rho \rightarrow 0^+} \mu (\rho ) <\infty \), since, by (7.31) and (7.25), there exist constants \(c\) and \(c'\) such that
Observe that the last but one equality holds thanks to the fact that \(\lim _{r \rightarrow 0^+}\overline{\omega }(r)=\infty \). Moreover, by (7.31), there exists a positive constant \(\kappa \) such that
Next,
for \(\rho \in (0, \tfrac{1}{2})\). Thus, there exists a positive constant \(c\) such that
for sufficiently small \(\rho \), where \(\kappa \) is the constant appearing in equation (7.52), and
for some constant \(C\). Define the function \(v : \Omega \rightarrow {\mathbb {R}}\) as
Since the function \(\zeta \) is holomorphic, the function \(v\) is harmonic, and vanishes on \(\{x_2= - \psi (|x_1|)\}\). Furthermore, by the Cauchy-Riemann equations,
where \(\mathrm{J}\zeta \) denotes the Jacobian matrix of the conformal map \(\zeta \). Let \(w \in C^\infty _0(B_{\frac{1}{2}}(0))\) be such that \(w=1\) in \(B_{\frac{1}{4}}(0)\). Denote by \(u: \Omega \rightarrow \mathbb R\) the function given by
Thanks to equation (7.55), the function \(u\in W^{1,2}_0(\Omega )\), and solves the Dirichlet problem (2.8), with \(\mathbf {F}= (w-1) \nabla v + v \nabla w\). We claim that \(\mathbf {F}\in C^{0, \omega (\cdot )}(\Omega )\) and hence, thanks to equation (2.3),
To verify out claim, notice that, owing to equation (7.18),
for every \(\varepsilon >0\). Thus, equation (7.56) will follow if we show that there exists \(\varepsilon \in (0, 1)\) such that
As observed above, one has that \(\psi \in C^{1, \sigma (\cdot )}\), whence \(\psi \in C^{1, 0}\). Thus, since \(v\) is harmonic in \(\Omega \), one has that \(v\in C^\varepsilon (\Omega )\) for some \(\varepsilon >0\). On the other hand, \(\sigma \) is concave in \((0, \infty )\), and consequently \(\sigma \in C^{0,1}(\tfrac{1}{8}, \infty )\). Thus, \(\psi \in C^{1,1}(\tfrac{1}{4}, \infty )\), and therefore \(\nabla v \in C^{0, \varepsilon }(\Omega {\setminus } B_{\frac{1}{8}}(0))\) for some \(\varepsilon >0\). Since the function \(1-w\) vanishes in \(B_{\frac{1}{4}}(0)\), there exists \(\varepsilon >0\) that renders equation (7.57) true .
In order to conclude the proof, it remains to show that
for a suitable choice of \(\gamma \). To prove this assertion, observe that, by inequality (7.54), there exists a positive constant \(c\) such that
for sufficiently small \(\rho \), provided that \(\mathrm{arg}\, \zeta (\xi ) = \tfrac{\pi }{2}\), namely if \(\theta =0\). Assume, by contradiction, that \(\nabla u \in \mathcal L ^{\omega (\cdot )}(\Omega )\,.\) Then, by Proposition 7.1, there exists a constant \(c\) such that
This contradicts inequality (7.59) if \(\gamma > \tfrac{\kappa \pi }{2}\).
References
Acerbi, E., Fusco, N.: Regularity for minimizers of nonquadratic functionals: the case \(1\le p \le 2\). J. Math. Anal. Appl. 140, 115–135, 1989
Avelin, B., Kuusi, T., Mingione, G.: Nonlinear Calderón–Zygmund theory in a limiting case. Arch. Ration. Mech. Anal. 227, 663–714, 2018
Beck, L.: Boundary regularity results for systems with sub-linear growth. Quart. J. Math. 62, 791–824, 2011
Beirão da Veiga, H., Crispo, F.: On the global \(W^{2, q}\) regularity for nonlinear \(N\)-systems of the \(p\)-Laplacian type in \(n\) space variables. Nonlinear Anal. 75, 4346–4354, 2012
Bennett, C., Sharpley, R.: Interpolation of operators. Academic Press (1988)
Breit, D., Stroffolini, B., Verde, A.: A general regularity theorem for functionals with \(\varphi \)-growth. J. Math. Anal. Appl. 383, 226–233, 2011
Buliček, M., Marinogová, E., Stroffolini, B., Verde, A.: A boundary regularity result for minimizers of variational integrals with nonstandard growth. Nonlinear Anal. 177, 153–168, 2018 part A
Breit, D., Cianchi, A., Diening, L., Kuusi, T., Schwarzacher, S.: Pointwise Calderón–Zygmund gradient estimates for the \(p\)-Laplace system. J. Math. Pures Appl. 114, 146–190, 2018
Byun, S., Wang, L.: Elliptic equations with BMO coefficients in Reifenberg domains Comm. Pure Appl. Math. 57, 1283–1310, 2004
Caffarelli, L.A., Peral, I.: On \(W^{1, p}\) estimates for elliptic equations in divergence form. Comm. Pure Appl. Math. 51, 1–21, 1998
Chen, Y., Di Benedetto, E.: Boundary estimates for solutions of nonlinear degenerate parabolic systems. J. Reine Angew. Math. 395, 102–131, 1989
Cianchi, A., Maz’ya, V.: Global Lipschitz regularity for a class of quasilinear elliptic equations. Comm. Part. Diff. Equat. 36, 100–133, 2011
Cianchi, A., Maz’ya, V.: Global boundedness of the gradient for a class of nonlinear elliptic systems. Arch. Ration. Mech. Anal. 212, 129–177, 2014
Cianchi, A., Maz’ya, V.: Gradient regularity via rearrangements for \(p\)-Laplacian type elliptic boundary value problems. J. Europ. Math. Soc. 16, 571–595, 2014
Cianchi, A., Maz’ya, V.: Second-order two-sided estimates in nonlinear elliptic problems. Arch. Ration. Mech. Anal. 229, 569–599, 2018
Cianchi, A., Maz’ya, V.: Optimal second-order regularity for the \(p\)-Laplace system, J. Math. Pures Appl., 132, 41–78, 2019
Cianchi, A., Randolfi, M.: On the modulus of continuity of weakly differentiable functions. Indiana Univ. Math. J. 60, 1939–1974, 2011
Benedetto, E.: \(C^{1+\alpha }\) local regularity of weak solutions of degenerate elliptic equations. Nonlinear Anal. 7, 827–850, 1983
Di Benedetto, E., Manfredi, J.: On the higher integrability of the gradient of weak solutions of certain degenerate elliptic systems. Amer. J. Math. 115, 1107–1134, 1993
Diening, L., Ettwein, F.: Fractional estimates for non-differentiable elliptic systems with general growth. Forum Math. 20, 523–556, 2008
Diening, L., Kaplický, P., Schwarzacher, S.: BMO estimates for the \(p\)-Laplacian. Nonlinear Anal. 75, 637–650, 2012
Diening, L., Ružička, M., Schumacher, K.: A decomposition technique for John domains. Ann. Acad. Sci. Fenn. Math. 35, 87–114, 2010
Diening, L., Stroffolini, B., Verde, A.: Everywhere regularity of functionals with \(\phi \)-growth. Manuscripta Math. 129, 449–481, 2009
Duzaar, F., Kristensen, J., Mingione, G.: The existence of regular boundary points for non-linear elliptic systems. J. Reine Angew. Math. 602, 17–58, 2007
Evans, L.C.: A new proof of local \(C^{1,\alpha }\) regularity for solutions of certain degenerate elliptic P.D.E.,. J. Diff. Equat. 45, 356–373, 1982
Foss, M.: Global regularity for almost minimizers of nonconvex variational problems. Ann. Mat. Pura Appl. 187, 263–321, 2008
Foss, M., Passarelli di Napoli, A., Verde, A.: Global Lipschitz regularity for almost minimizers of asymptotically convex variational problems. Ann. Mat. Pura Appl. 189, 127–162, 2010
Giaquinta, M.: A counter-example to the boundary regularity of solutions to quasilinear systems. Manuscripta Math. 24, 217–220, 1978
Giaquinta, M., Modica, G.: Remarks on the regularity of the minimizers of certain degenerate functionals. Manuscripta Math. 57, 55–99, 1986
Giusti, E.: Direct Methods in the Calculus of Variations. World Scientific Publishing Co. Inc., River Edge, 2003
Gogatishvili, A., Pick, L.: Embeddings and duality theorems for weak classical Lorentz spaces. Canad. Math. Bull. 149, 82–95, 2006
Grotowski, J.F.: Boundary regularity for nonlinear elliptic systems. Calc. Var. PDE 15, 353–388, 2002
Hamburger, C.: Regularity of differential forms minimizing degenerate elliptic functionals. J. Reine Angew. Math. 431, 7–64, 1992
Hamburger, C.: Partial boundary regularity of solutions of nonlinear superelliptic systems. Boll. Unione Mat. Ital. Sez. B 10, 63–81, 2007
Iwaniec, T.: Projections onto gradient fields and \(L^{p}\)-estimates for degenerated elliptic operators. Studia Math. 75, 293–312, 1983
Iwaniec, T.: The Gehring Lemma, pp. 181–204. Springer, Quasiconformal Mappings and Analysis (1998)
Iwaniec, T., Manfredi, J.J.: Regularity of p-harmonic functions on the plane. Rev. Mat. Iberoamericana 5, 1–19, 1989
Jerison, D., Kenig, C.E.: The inhomogeneous Dirichlet problem in Lipschitz domains. J. Funct. Anal. 130, 161–219, 1995
John, F., Nirenberg, L.: On functions of bounded mean oscillation. Comm. Pure. Appl. Math 14, 415–426, 1961
Kilpelainen, T., Maly, J.: The Wiener test and potential estimates for quasilinear elliptic equations. Acta Math. 172(1), 137–161, 1994
Kinnunen, J., Zhou, S.: A boundary estimate for nonlinear equations with discontinuous coefficients. Differ. Integral Equ. 14, 475–492, 2001
Kristensen, J., Mingione, G.: Boundary regularity in variational problems. Arch. Ration. Mech. Anal. 198, 369–455, 2010
Kuusi, T., Mingione, G.: Linear potentials in nonlinear potential theory. Arch. Ration. Mech. Anal. 207, 215–246, 2013
Kuusi, T., Mingione, G.: Vectorial nonlinear potential theory. J. Eur. Math. Soc. 20, 929–1004, 2018
Lewis, J.L.: Regularity of the derivatives of solutions to certain degenerate elliptic equations. Indiana Univ. Math. J. 32, 849–858, 1983
Lieberman, G.M.: Boundary regularity for solutions of degenerate elliptic equations. Nonlinear Anal. 12, 1203–1219, 1988
Maz’ya, V.G.: The boundedness of the first derivatives of the solution of the Dirichlet problem in a region with smooth nonregular boundary. Vestnik Leningrad. Univ. 24, 72–79 (Russian). English translation: Vestnik Leningrad. Univ. Math. 2(1975), 59–67, 1969
Maz‘ya, V.G.: The continuity at a boundary point of the solutions of quasi-linear elliptic equations, Vestnik Leningrad. Univ. Mat. Mekh. Astronom. 25, 42–55 (1970) (Russian) English translation Vestnik Leningrad. Univ. 3 (1976) 225-242 (1980).
Maz’ya, V.G.: Sobolev spaces with applications to partial differential equations. Springer, Berlin, 2011
Maz’ya, V.G., Shaposhnikova, T.: Theory of Sobolev Multipliers. Springer, Berlin, 2009
Schwarzacher, S.: Regularity for degenerate elliptic and parabolic equations. PhD thesis, LMU Munich, 2013
Spanne, S.: Some function spaces defined using the mean oscillation over cubes. Ann. Scuola Norm. Sup. Pisa 19, 593–608, 1965
Sverák, V., Yan, X.: Non-Lipschitz minimizers of smooth uniformly convex variational integrals. Proc. Natl. Acad. Sci. USA 99, 15269–15276, 2002
Tolksdorf, P.: Regularity for a more general class of quasilinear elliptic equations. J. Differ. Equ. 51, 126–150, 1983
Uhlenbeck, K.: Regularity for a class of non-linear elliptic systems. Acta Math. 138, 219–240, 1977
Uralc’eva, N.N.: Degenerate quasilinear elliptic systems, Zap. Naučn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 7, 84–222, 1968
Warschawski, S.E.: On conformal mapping of infinite strips. Trans. Am. Math. Soc. 51, 280–335, 1942
Acknowledgements
We wish to thank the referee for his careful reading of the paper and for his valuable comments and suggestions.
Funding
This research was partly funded by: (i) Grant LDS 2012-05 of Leopoldina (German National Academy of Science) (D. Breit); (ii) Research Project of the Italian Ministry of University and Research (MIUR) Prin 2015 “ Partial differential equations and related analytic-geometric inequalities" (Grant Number 2015HY8JCC) (A. Cianchi); (iii) GNAMPA of the Italian INdAM (National Institute of High Mathematics) (grant number not available) (A. Cianchi); (iv) Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB 1283/2 2021 – 317210226 (L. Diening); (v) Primus Research Programme of Charles University, Prague (grant number PRIMUS/19/SCI/01) (S. Schwarzacher); (vi) The programme GJ19-11707Y of the Czech national grant agency (GAČR). (S. Schwarzacher).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Communicated by G. Dal Maso.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
In memory of Jan Malý, distinguished mathematician and a special friend of ours.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Breit, D., Cianchi, A., Diening, L. et al. Global Schauder Estimates for the \(\mathbf {p}\)-Laplace System. Arch Rational Mech Anal 243, 201–255 (2022). https://doi.org/10.1007/s00205-021-01712-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00205-021-01712-w