Long-Time Behavior of Alfvén Waves in a Flowing Plasma: Generation of the Magnetic Island

Abstract

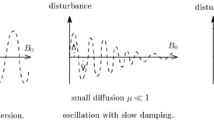
Magnetic islands are the regions enclosed by magnetic field lines and separated by reconnection points. In this paper, we study the long-time behavior of the solution for the linearized MHD system around the linearly stable, steady flowing plasma with sheared velocity and magnetic field. As a consequence, we prove that for a class of initial data, the magnetic islands appear at the final state.

Appendix

In this “Appendix”, let us complete the extension process for Case 2–9.

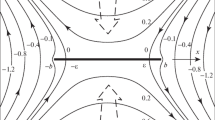
Case 2 $W_+(1)= W_-(-1)>0> W_-(1)>W_+(-1)$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_+(-1), W_+(1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r \in [W_+(-1), W_+(1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^{l}{\mathop {=}\limits ^{def}}\big \{c=W_+(-1)+\epsilon e^{i\theta }, \ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^{r}{\mathop {=}\limits ^{def}}\big \{c=W_+(1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^{l}\cup B_{\epsilon _0}^{r}.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_+(-1) \ \text {for} \ c\in B_{\epsilon _0}^{l}, \quad c_r=W_+(1) \ \text {for} \ c\in B_{\epsilon _0}^{r}. \end{aligned}$$

By Lemma 3.1, we can take a $C^5$ extension of $W_-$ to be $\widetilde{W}_-$ for $y\in [-1,\mathrm{{a}}_+]$ such that $\widetilde{W}_-(\mathrm{{a}}_+)=W_+(-1)$ and $\widetilde{W}'_-(y)<0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,\mathrm{{a}}_+]$ with $y_{c_+}=(\widetilde{W}_-)^{-1}(c_r)$ so that $\widetilde{W}_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_+(-1)=\widetilde{W}_-(\mathrm{{a}}_+)$, and we denote $y_{c_+}=\mathrm{{a}}_+$ and $y_{c_-}=-1$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_+(1)=W_-(-1)$, and we denote $y_{c_+}=1$ and $y_{c_-}=-1$.

We show the relationship between $y_{c_+}, y_{c_-}$ and $c_r$ in Fig. 6. We also take a $C^5$ extension of $W_+$ to be $\widetilde{W}_+$ for $y\in [-1,\mathrm{{a}}_+]$ so that $\widetilde{W}_+'(y)>0$.

Case 3 $W_-(-1)> W_+(1)>0> W_-(1)>W_+(-1)$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_+(-1), W_-(-1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r\in [W_+(-1), W_-(-1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^{l}{\mathop {=}\limits ^{def}}\big \{c=W_+(-1)+\epsilon e^{i\theta },\ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^{r}{\mathop {=}\limits ^{def}}\big \{c=W_-(-1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^{l}\cup B_{\epsilon _0}^{r}.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_+(-1) \ \text {for} \ c\in B_{\epsilon _0}^{l}, \quad c_r=W_-(-1) \ \text {for} \ c\in B_{\epsilon _0}^{r}. \end{aligned}$$

By Lemma 3.1, we can take a $C^5$ extension of $W_-$ to be $\widetilde{W}_-$ and $W_+$ to be $\widetilde{W}_+$ for $y\in [-1,\mathrm{{a}}_+]$ such that $\widetilde{W}_-(\mathrm{{a}}_+)=W_+(-1)$, $\widetilde{W}'_-(y)<0$ and $\widetilde{W}_+(\mathrm{{a}}_+)=W_-(-1)$, $\widetilde{W}'_+(y)>0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,\mathrm{{a}}_+]$ with $y_{c_+}=(\widetilde{W}_+)^{-1}(c_r)$ so that $\widetilde{W}_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,\mathrm{{a}}_+]$ with $y_{c_+}=(\widetilde{W}_-)^{-1}(c_r)$ so that $\widetilde{W}_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_+(-1)=\widetilde{W}_-(\mathrm{{a}}_+)$, and we denote $y_{c_+}=\mathrm{{a}}_+$ and $y_{c_-}=-1$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_-(-1)=\widetilde{W}_+(\mathrm{{a}}_+)$, and we denote $y_{c_+}=\mathrm{{a}}_+$ and $y_{c_-}=-1$.

We show the relationship between $y_{c_+}, y_{c_-}$ and $c_r$ in Fig. 7.

Fig. 6

Case 2

Fig. 7

Case 3

Case 4 $W_+(1)> W_-(-1)>0> W_-(1)=W_+(-1)$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_+(-1), W_+(1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r\in [W_+(-1), W_+(1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^{l}{\mathop {=}\limits ^{def}}\big \{c=W_+(-1)+\epsilon e^{i\theta },\ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^{r}{\mathop {=}\limits ^{def}}\big \{c=W_+(1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^{l}\cup B_{\epsilon _0}^{r}.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_+(-1) \ \text {for} \ c\in B_{\epsilon _0}^{l}, \quad c_r=W_+(1) \ \text {for} \ c\in B_{\epsilon _0}^{r}. \end{aligned}$$

By Lemma 3.1, we can take a $C^5$ extension of $W_-$ to be $\widetilde{W}_-$ for $y\in [\mathrm{{a}}_-,1]$ such that $\widetilde{W}_-(\mathrm{{a}}_-)=W_+(1)$ and $\widetilde{W}'_-(y)<0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [\mathrm{{a}}_-,0]$ with $y_{c_-}=(\widetilde{W}_-)^{-1}(c_r)$ so that $\widetilde{W}_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_+(-1)=W_-(1)$, and we denote $y_{c_+}=1$ and $y_{c_-}=-1$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_+(1)=\widetilde{W}_-(\mathrm{{a}}_-)$, and we denote $y_{c_+}=1$ and $y_{c_-}=\mathrm{{a}}_-$.

We show the relationship between $y_{c_+}, y_{c_-}$ and $c_r$ in Fig. 8. We also take a $C^5$ extension of $W_+$ to be $\widetilde{W}_+$ for $y\in [\mathrm{{a}}_-,1]$, so that $\widetilde{W}_+'(y)>0$.

Case 5 $W_+(1)> W_-(-1)>0> W_+(-1)>W_-(1)$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_-(1), W_+(1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r\in [W_-(1), W_+(1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^{l}{\mathop {=}\limits ^{def}}\big \{c=W_-(1)+\epsilon e^{i\theta },\ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^{r}{\mathop {=}\limits ^{def}}\big \{c=W_+(1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^{l}\cup B_{\epsilon _0}^{r}.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_-(1) \ \text {for} \ c\in B_{\epsilon _0}^{l}, \quad c_r=W_+(1) \ \text {for} \ c\in B_{\epsilon _0}^{r}. \end{aligned}$$

By Lemma 3.1, we can take a $C^5$ extension of $W_-$ to be $\widetilde{W}_-$ and $W_+$ to be $\widetilde{W}_+$ for $y\in [\mathrm{{a}}_-,1]$ such that $\widetilde{W}_-(\mathrm{{a}}_-)=W_+(1)$, $\widetilde{W}'_-(y)<0$ and $\widetilde{W}_+(\mathrm{{a}}_-)=W_-(1)$, $\widetilde{W}'_+(y)>0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [\mathrm{{a}}_-,0]$ with $y_{c_-}=(\widetilde{W}_-)^{-1}(c_r)$ so that $\widetilde{W}_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [\mathrm{{a}}_-,0]$ with $y_{c_-}=(\widetilde{W}_+)^{-1}(c_r)$ so that $\widetilde{W}_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_-(1)=\widetilde{W}_+(\mathrm{{a}}_-)$, and we denote $y_{c_+}=1$ and $y_{c_-}=\mathrm{{a}}_-$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_+(1)=\widetilde{W}_-(\mathrm{{a}}_-)$, and we denote $y_{c_+}=1$ and $y_{c_-}=\mathrm{{a}}_-$.

We show the relationship between $y_{c_+}, y_{c_-}$ and $c_r$ in Fig. 9.

Fig. 8

Case 4

Fig. 9

Case 5

Case 6 $W_+(1)=W_-(-1)>0> W_-(1)=W_+(-1)$. We do not extend $W_{\pm }$ due to $Ran\, W_+=Ran\, W_-$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_-(1), W_+(1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r\in [W_-(1), W_+(1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^l{\mathop {=}\limits ^{def}}\big \{c=W_-(1)+\epsilon e^{i\theta },\ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^r{\mathop {=}\limits ^{def}}\big \{c=W_+(1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^l\cup B_{\epsilon _0}^r.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_-(1) \ \text {for} \ c\in B_{\epsilon _0}^l, \quad c_r=W_+(1) \ \text {for} \ c\in B_{\epsilon _0}^r. \end{aligned}$$

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_-(1)=W_+(-1)$, and we denote $y_{c_+}=1$ and $y_{c_-}=-1$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_+(1)=W_-(-1)$, and we denote $y_{c_+}=1$ and $y_{c_-}=-1$.

We show the relationship between $y_{c_+}$, $y_{c_-}$ and $c_r$ in Fig. 10.

Case 7 $W_+(1)= W_-(-1)>0> W_+(-1)>W_-(1)$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_-(1), W_+(1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r\in [W_-(1), W_+(1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^{l}{\mathop {=}\limits ^{def}}\big \{c=W_-(1)+\epsilon e^{i\theta },\ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^{r}{\mathop {=}\limits ^{def}}\big \{c=W_+(1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^{l}\cup B_{\epsilon _0}^{r}.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_-(1) \ \text {for} \ c\in B_{\epsilon _0}^{l}, \quad c_r=W_+(1) \ \text {for} \ c\in B_{\epsilon _0}^{r}. \end{aligned}$$

By Lemma 3.1, we can take a $C^5$ extension of $W_+$ to be $\widetilde{W}_+$ for $y\in [\mathrm{{a}}_-,1]$ such that $\widetilde{W}_+(\mathrm{{a}}_-)=W_-(1)$, $\widetilde{W}'_+(y)>0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [\mathrm{{a}}_-,0]$ with $y_{c_-}=(\widetilde{W}_+)^{-1}(c_r)$ so that $\widetilde{W}_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_-(1)=\widetilde{W}_+(\mathrm{{a}}_-)$, and we denote $y_{c_+}=1$ and $y_{c_-}=\mathrm{{a}}_-$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_+(1)=W_-(-1)$, and we denote $y_{c_+}=1$ and $y_{c_-}=-1$.

We show the relationship between $y_{c_+}, y_{c_-}$ and $c_r$ in Fig. 11

Fig. 10

Case 6

Fig. 11

Case 7

We also take a $C^5$ extension of $W_-$ to be $\widetilde{W}_-$ for $y\in [\mathrm{{a}}_-,1]$ so that $\widetilde{W}_-'(y)<0$.

Case 8 $W_-(-1)> W_+(1)>0> W_-(1)=W_+(-1)$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_+(-1), W_-(-1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r\in [W_+(-1), W_-(-1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^{l}{\mathop {=}\limits ^{def}}\big \{c=W_+(-1)+\epsilon e^{i\theta },\ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^{r}{\mathop {=}\limits ^{def}}\big \{c=W_-(-1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^{l}\cup B_{\epsilon _0}^{r}.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_+(-1) \ \text {for} \ c\in B_{\epsilon _0}^{l}, \quad c_r=W_-(-1) \ \text {for} \ c\in B_{\epsilon _0}^{r}. \end{aligned}$$

By Lemma 3.1, we can take a $C^5$ extension of $W_+$ to be $\widetilde{W}_+$ for $y\in [-1,\mathrm{{a}}_+]$ such that $\widetilde{W}_+(\mathrm{{a}}_+)=W_-(-1)$, $\widetilde{W}'_+(y)>0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,\mathrm{{a}}_+]$ with $y_{c_+}=(\widetilde{W}_+)^{-1}(c_r)$ so that $\widetilde{W}_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_+)^{-1}(c_r)$ so that $W_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_+(-1)=W_-(-1)$, and we denote $y_{c_+}=1$ and $y_{c_-}=-1$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_-(-1)=\widetilde{W}_+(\mathrm{{a}}_+)$, and we denote $y_{c_+}=\mathrm{{a}}_+$ and $y_{c_-}=-1$.

We show the relationship between $y_{c_+}, y_{c_-}$ and $c_r$ in Fig. 12. We also take a $C^5$ extension of $W_-$ to be $\widetilde{W}_-$ for $y\in [-1, \mathrm{{a}}_+]$ so that $\widetilde{W}_-'(y)<0$.

Case 9 $W_-(-1)> W_+(1)>0> W_+(-1)>W_-(1)$. Let

$$\begin{aligned}&D_0{\mathop {=}\limits ^{def}}\big \{c\in [W_-(1), W_-(-1)]\big \},\\&D_{\epsilon _0}{\mathop {=}\limits ^{def}}\big \{c=c_r+i\epsilon , \ c_r \in [W_-(1), W_-(-1)], \ 0<|\epsilon |<\epsilon _0\big \},\\&B_{\epsilon _0}^{l}{\mathop {=}\limits ^{def}}\big \{c=W_-(1)+\epsilon e^{i\theta }, \ 0<\epsilon<\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \},\\&B_{\epsilon _0}^{r}{\mathop {=}\limits ^{def}}\big \{c=W_-(-1)-\epsilon e^{i\theta }, \ 0<\epsilon <\epsilon _0, \ \frac{\pi }{2}\leqq \theta \leqq \frac{3\pi }{2}\big \}, \end{aligned}$$

for some $\epsilon _0\in (0,1).$ We denote $\Omega _{\epsilon _0}{\mathop {=}\limits ^{def}}D_0\cup D_{\epsilon _0}\cup B_{\epsilon _0}^{l}\cup B_{\epsilon _0}^{r}.$ We define

$$\begin{aligned} c_r=Re\, c\ \text {for} \ c\in D_0\cup D_{\epsilon _0}, \quad c_r=W_-(1) \ \text {for} \ c\in B_{\epsilon _0}^{l}, \quad c_r=W_-(-1) \ \text {for} \ c\in B_{\epsilon _0}^{r}. \end{aligned}$$

By Lemma 3.1, we can take a $C^5$ extension of $W_+$ to be $\widetilde{W}_+$ for $y\in [\mathrm{{a}}_-,\mathrm{{a}}_+]$ such that $\widetilde{W}_+(\mathrm{{a}}_-)=W_-(1)$, $\widetilde{W}_+(\mathrm{{a}}_+)=W_-(-1)$ and $\widetilde{W}'_+(y)>0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\geqq 0$, we denote $y_{c_+}\in [0,\mathrm{{a}}_+]$ with $y_{c_+}=(\widetilde{W}_+)^{-1}(c_r)$ so that $\widetilde{W}_+(y_{c_+})-c_r=0$, and $y_{c_-}\in [-1,0]$ with $y_{c_-}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_-})-c_r=0$.

• For $c\in D_0\cup D_{\epsilon _0}$ and $c_r\leqq 0$, we denote $y_{c_+}\in [0,1]$ with $y_{c_+}=(W_-)^{-1}(c_r)$ so that $W_-(y_{c_+})-c_r=0$, and $y_{c_-}\in [\mathrm{{a}}_-,0]$ with $y_{c_-}=(\widetilde{W}_+)^{-1}(c_r)$ so that $\widetilde{W}_+(y_{c_-})-c_r=0$.

• For $c\in B_{\epsilon _0}^l$, then $c_r=W_-(1)=\widetilde{W}_+(a_-)$, and we denote $y_{c_+}=1$ and $y_{c_-}=\mathrm{{a}}_-$.

• For $c\in B_{\epsilon _0}^r$, then $c_r=W_-(-1)=\widetilde{W}_+(\mathrm{{a}}_+)$, and we denote $y_{c_+}=\mathrm{{a}}_+$ and $y_{c_-}=-1$.

We show the relationship between $y_{c_+}, y_{c_-}$ and $c_r$ in Fig. 13.

Fig. 12

Case 8

Fig. 13

Case 9

We also take a $C^5$ extension of $W_-$ to be $\widetilde{W}_-$ for $y\in [\mathrm{{a}_-}, \mathrm{{a}}_+]$ so that $\widetilde{W}_-'(y)<0$.

In the last step of Case 2, 4, 7, 8, 9, we only restrict the regularity and monotonicity of the extension.