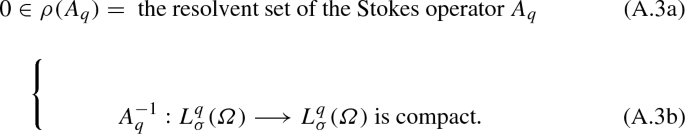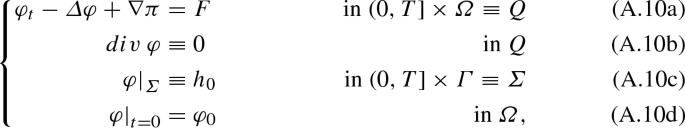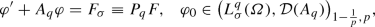Uniform Stabilization of 3D Navier–Stokes Equations in Low Regularity Besov Spaces with Finite Dimensional, Tangential-Like Boundary, Localized Feedback Controllers

Abstract

The present paper provides a solution in the affirmative to a recognized open problem in the theory of uniform stabilization of 3-dimensional Navier–Stokes equations in the vicinity of an unstable equilibrium solution, by means of a ‘minimal’ and ‘least’ invasive feedback strategy which consists of a control pair $\{ v,u \}$ (Lasiecka and Triggiani in Nonlinear Anal 121:424–446, 2015). Here v is a tangential boundary feedback control, acting on an arbitrary small part ${\widetilde{\varGamma }}$ of the boundary $\varGamma$; u is a localized, interior feedback control, acting tangentially on an arbitrarily small subset $\omega$ of the interior supported by ${{\widetilde{\varGamma }}}$. The ideal strategy of taking $u = 0$ on $\omega$ is not sufficient. A question left open in the literature is: can such feedback control v of the pair $\{ v,u \}$ be asserted to be finite dimensional also in dimension $d = 3$? We here give an affirmative answer to this question, thus establishing an optimal result. To achieve the desired finite dimensionality of the feedback tangential boundary control v, it is here then necessary to abandon the Hilbert-Sobolev functional setting of past literature and replace it with a “right" Besov space setting of lower regularity. These spaces are ‘close’ to $L^3(\varOmega )$ for $d = 3$. This functional setting is significant. It is in line with recent well-posedness results in the full space of the non-controlled N–S equations (Escauriaza et al. in Math Subj Classif 35K:76D, 1991; Rusin and Sverak in Minimal initial data for potential Navier–Stokes singularities. arXiv:0911.0500; Jia and Šverák in SIAM J Math Anal 45(3):1448–1459, 2013; Gallagher et al. in Math Ann 355(4):1527–1559, 2013). A double key feature of such Besov spaces with tight indices is that they do not recognize compatibility conditions while having a sufficiently high topological level to handle the 3d-nonlinearity in the analysis of well-posedness and uniform stabilization. The proof is constructive and is “optimal” also regarding the “minimal” number of tangential boundary feedback controllers needed. The new setting requires the solution of novel technical and conceptual issues. These include establishing maximal regularity up to $T = \infty$ in the required suitably identified “right" Besov setting for the overall closed-loop linearized problem with tangential feedback control applied on the boundary. This result is also a new contribution to the area of maximal regularity as the operator to which it applies incorporates a boundary feedback control term rather than homogeneous boundary conditions. It escapes direct use of perturbation theory. Finally, the very ability to stabilize even the finite dimensional unstable projected system is linked to a Unique Continuation Property of a suitably over-determined (adjoint) Oseen eigenproblem, which requires the presence of the interior tangential-like control u acting on $\omega$.

Appendices

Appendix A: Some Auxiliary Results for the Stokes and Oseen Operators: Analytic Semigroup Generation, Maximal Regularity, Domains of Fractional Powers

In this subsection we collect mostly known results to be used in the sequel.

• (a) The Stokes and Oseen operators generate strongly continuous analytic semigroups on $L^{q}_{\sigma }(\varOmega )$, $1< q < \infty$.

Theorem A.1

Let $d \ge 2, 1< q < \infty$ and let $\varOmega$ be a bounded domain in ${\mathbb {R}}^d$ of class $C^3$. Then

• (i) the Stokes operator $-A_q = P_q \varDelta$ in (2.14), repeated here as

  $$\begin{aligned} -A_q \psi = P_q \varDelta \psi , \quad \psi \in \mathcal {D}(A_q) = W^{2,q}(\varOmega ) \cap W^{1,q}_0(\varOmega ) \cap L^{q}_{\sigma }(\varOmega )\end{aligned}$$

  (A.1)

  generates a s.c analytic semigroup $e^{-A_qt}$ on $L^{q}_{\sigma }(\varOmega )$. See [37] and the review paper [39, Theorem 2.8.5 p 17], and [68].

• (ii) The Oseen operator ${\mathcal {A}}_q$ in (2.16)

  $$\begin{aligned} {\mathcal {A}}_q = - (\nu _o A_q + A_{o,q}), \quad {\mathcal {D}}({\mathcal {A}}_q) = {\mathcal {D}}(A_q) \subset L^{q}_{\sigma }(\varOmega )\end{aligned}$$

  (A.2)

  generates a s.c analytic semigroup $e^{{\mathcal {A}}_qt}$ on $L^{q}_{\sigma }(\varOmega )$. This follows as $A_{o,q}$ is relatively bounded with respect to $A^{{}^{1}\!/_{2}}_q$, to be formally defined in (A.6): thus a standard theorem on perturbation of an analytic semigroup generator applies [60, Corollary 2.4, p 81].

• (iii)

  

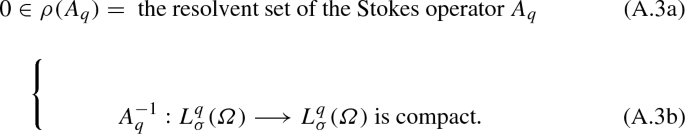
• (iv) The s.c. analytic Stokes semigroup $e^{-A_qt}$ is uniformly stable on $L^{q}_{\sigma }(\varOmega )$: there exist constants $M \ge 1, \delta > 0$ (possibly depending on q) such that

  $$\begin{aligned} \left\Vert e^{-A_qt}\right\Vert _{{\mathcal {L}}(L^{q}_{\sigma }(\varOmega ))} \le M e^{-\delta t}, \ t > 0. \end{aligned}$$

  (A.4)

• (b) Domains of fractional powers, ${\mathcal {D}}(A_q^{\alpha }), 0< \alpha < 1$ of the Stokes operator $A_q$ on $L^{q}_{\sigma }(\varOmega ), 1< q < \infty$,

Theorem A.2

For the domains of fractional powers ${\mathcal {D}}(A_q^{\alpha }), 0< \alpha < 1$, of the Stokes operator $A_q$ in (2.14) = (A.1), the following complex interpolation relation holds true [38, 39, Theorem 2.8.5, p 18]

$$\begin{aligned} {[} {\mathcal {D}}(A_q), L^{q}_{\sigma }(\varOmega )]_{1-\alpha } = {\mathcal {D}}(A_q^{\alpha }), \ 0< \alpha< 1, \ 1< q < \infty ; \end{aligned}$$

(A.5)

in particular, see (2.15)

$$\begin{aligned} {[} {\mathcal {D}}(A_q), L^{q}_{\sigma }(\varOmega )]_{\frac{1}{2}} = {\mathcal {D}}(A_q^{{}^{1}\!/_{2}}) \equiv W_0^{1,q}(\varOmega ) \cap L^{q}_{\sigma }(\varOmega ). \end{aligned}$$

(A.6)

Thus, on the space ${\mathcal {D}}(A_q^{{}^{1}\!/_{2}})$, the norms

$$\begin{aligned} \left\Vert \nabla \ \cdot \ \right\Vert _{L^q(\varOmega )} \text { and } \left\Vert \ \right\Vert _{L^q(\varOmega )} \end{aligned}$$

(A.7)

are equivalent via the Poincaré inequality.

• (c) The Stokes operator $-A_q$ and the Oseen operator ${\mathcal {A}}_q, 1< q < \infty$ generate s.c. analytic semigroups on the Besov space.

  Recall (1.15a, 1.15b)

  $$\begin{aligned} \Big ( L^{q}_{\sigma }(\varOmega ),\mathcal {D}(A_q) \Big )_{1-\frac{1}{p},p}&= \Big \{ g \in B^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega ): \text { div } g = 0, \ g|_{\varGamma } = 0 \Big \} \nonumber \\&\text {if } \frac{1}{q}< 2 - \frac{2}{p} < 2; \end{aligned}$$

  (A.8a)
  $$\begin{aligned} \Big ( L^{q}_{\sigma }(\varOmega ),\mathcal {D}(A_q) \Big )_{1-\frac{1}{p},p}&= \Big \{ g \in B^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega ): \text { div } g = 0, \ g\cdot \nu |_{\varGamma } = 0 \Big \} \nonumber \\&\quad \equiv {{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega ) \quad \text { if } 0< 2 - \frac{2}{p}< \frac{1}{q}, \text { or } 1< p < \frac{2q}{2q-1}. \end{aligned}$$

  (A.8b)

  In fact, Theorem A.1(i) states that the Stokes operator $-A_q$ generates a s.c analytic semigroup on the space $L^{q}_{\sigma }(\varOmega ), \ 1< q < \infty$, hence on the space ${\mathcal {D}}(A_q)$ in (A.1), with norm $\displaystyle \left\Vert \ \cdot \ \right\Vert _{{\mathcal {D}}(A_q)} = \left\Vert A_q \ \cdot \ \right\Vert _{L^{q}_{\sigma }(\varOmega )}$ as $0 \in \rho (A_q)$. Then, one obtains that the Stokes operator $-A_q$ generates a s.c. analytic semigroup on the real interpolation spaces in (A.8). Next, the Oseen operator ${\mathcal {A}}= -(\nu _o A_q + A_{o,q})$ likewise generates a s.c. analytic semigroup $\displaystyle e^{{\mathcal {A}}_q t}$ on $\displaystyle L^{q}_{\sigma }(\varOmega )$ by Theorem A.1(ii). Moreover ${\mathcal {A}}_q$ generates a s.c. analytic semigroup on $\displaystyle {\mathcal {D}}({\mathcal {A}}_q) = {\mathcal {D}}(A_q)$ (equivalent norms). Hence ${\mathcal {A}}_q$ generates a s.c. analytic semigroup on the real interpolation spaces (A.11). Here below, however, we shall formally state the result only in the case $\displaystyle 2-{}^{2}\!/_{p} < {}^{1}\!/_{q}$. that is $\displaystyle 1< p < {}^{2q}\!/_{2q-1}$, in the space $\displaystyle {{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )$, as this does not contain B.C. The objective of the present paper is precisely to obtain stabilization results on spaces that do not recognize B.C.

Theorem A.3

Let $1< q< \infty , 1< p < {}^{2q}\!/_{2q-1}$

• (i) The Stokes operator $-A_q$ in (A.1) generates a s.c analytic semigroup $e^{-A_qt}$ on the space ${{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )$ defined in (1.15b) which moreover is uniformly stable, as in (A.4),

  $$\begin{aligned} \left\Vert e^{-A_qt}\right\Vert _{{\mathcal {L}}\big ({{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )\big )} \le M e^{-\delta t}, \quad t > 0. \end{aligned}$$

  (A.9)

• (ii) The Oseen operator ${\mathcal {A}}_q$ in (A.2) generates a s.c. analytic semigroup $e^{{\mathcal {A}}_qt}$ on the space ${{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )$ in (1.15b).

• (d) Space of maximal $L^p$ regularity on $L^{q}_{\sigma }(\varOmega )$ of the Stokes operator $-A_q, \ 1< p< \infty , \ 1< q < \infty$ up to $T = \infty$. We shall use the notation of [24] and write $\displaystyle -A_q \in MReg (L^p \big ( 0,\infty ; L^{q}_{\sigma }(\varOmega )\big ))$. We return to the dynamic Stokes problem in $\{\varphi (t,x), \pi (t,x) \}$

  

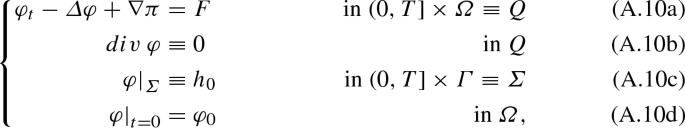
  rewritten in abstract form, after applying the Helmholtz projection $P_q$ to (A.10a) and recalling $A_q$ in (A.1) as

  

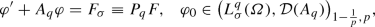  (A.11)

recall (A.8). Next, we introduce the space of maximal regularity for $\{\varphi , \varphi '\}$, that is for $-A_q$, as [39, p 2; Theorem 2.8.5.iii, p 17], [36, p 1404-5], with T up to $\infty$:

$$\begin{aligned} X^T_{p,q, \sigma } (A_q) = L^p(0,T;{\mathcal {D}}(A_q)) \cap W^{1,p}(0,T;L^{q}_{\sigma }(\varOmega )) \end{aligned}$$

(A.12)

(recall (2.14) for ${\mathcal {D}}(A_q)$) and the corresponding space for the pressure as

$$\begin{aligned} Y^T_{p,q} = L^p(0,T;{\widehat{W}}^{1,q}(\varOmega )), \quad {\widehat{W}}^{1,q}(\varOmega ) = W^{1,q}(\varOmega ) / {\mathbb {R}}. \end{aligned}$$

(A.13)

The following embedding, also called trace theorem, holds true [3, Theorem 4.10.2, p 180, BUC for $T=\infty$].

$$\begin{aligned} X^T_{p,q,\sigma }\subset X^T_{p,q}\equiv & {} L^p(0,T; W^{2,q}(\varOmega )) \cap W^{1,p}(0,T; L^q(\varOmega )) \nonumber \\&\hookrightarrow C \Big ([0,T]; B^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )\Big ). \end{aligned}$$

(A.14)

For a function g such that $div \ g \equiv 0, \ g|_{\varGamma } = 0$ we have $g \in X^T_{p,q}\iff g \in X^T_{p,q,\sigma }$, by (1.4).

The solution of Equation (A.11) is

$$\begin{aligned} \varphi (t) = e^{-A_qt} \varphi _0 + \int _{0}^{t} e^{-A_q(t-\tau )} F_{\sigma }(\tau ) \mathrm{d} \tau . \end{aligned}$$

(A.15)

The following is the celebrated result on maximal regularity on $L^{q}_{\sigma }(\varOmega )$ of the Stokes problem due originally to Solonnikov [70] reported in [39, 64, Theorem 2.8.5(iii) for $\varphi _0 = 0$ and Theorem 2.10.1 p24], [36, 61, Proposition 4.1 , p 1405]. See also [12, Theorem 3.1 p 31 for $p = q =2$ case]. See also [69, 71,72,73].

Theorem A.4

Let $1< p,q < \infty , T \le \infty$. With reference to problem (A.10), (A.11), assume

$$\begin{aligned} F_{\sigma }\in L^p(0,T;L^{q}_{\sigma }(\varOmega )), \ \varphi _0 \in \Big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q)\Big )_{1-\frac{1}{p},p}. \end{aligned}$$

(A.16)

Then there exists a unique solution $\varphi \in X^T_{p,q,\sigma }$ continuously on the data: there exist constants $C_0, C_1$ independent of $T, F_{\sigma }, \varphi _0$ such that via (A.14)

$$\begin{aligned} \begin{aligned} C_0 \left\Vert \varphi \right\Vert _{C \big ([0,T]; B^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )\big )}&\le \left\Vert \varphi \right\Vert _{X^T_{p,q,\sigma }} + \left\Vert \pi \right\Vert _{Y^T_{p,q}}\\&= \left\Vert \varphi '\right\Vert _{L^p(0,T;L^{q}_{\sigma }(\varOmega ))} + \left\Vert A_q \varphi \right\Vert _{L^p(0,T;L^{q}_{\sigma }(\varOmega ))} + \left\Vert \pi \right\Vert _{Y^T_{p,q}}\\&\le C_1 \bigg \{ \left\Vert F_{\sigma }\right\Vert _{L^p(0,T;L^{q}_{\sigma }(\varOmega ))} \\&\quad + \left\Vert \varphi _0\right\Vert _{\big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q)\big )_{1-\frac{1}{p},p}} + \left\Vert h_0\right\Vert _{L^p(0,\infty ; W^{1-{}^{1}\!/_{q},q}(\varGamma ))} \bigg \}.\nonumber \end{aligned}\\ \end{aligned}$$

(A.17)

In particular,

• (i) With reference to the variation of parameters formula (A.15) of problem (A.11) arising from the Stokes problem (A.10), we have recalling (A.12): the map

  $$\begin{aligned} F_{\sigma }&\longrightarrow \int _{0}^{t} e^{-A_q(t-\tau )}F_{\sigma }(\tau ) \mathrm{d}\tau : \ : \text {continuous} \end{aligned}$$

  (A.18)
  $$\begin{aligned} L^p(0,T;L^{q}_{\sigma }(\varOmega ))&\longrightarrow X^T_{p,q,\sigma }(A_q) \equiv L^p(0,T; {\mathcal {D}}(A_q)) \cap W^{1,p}(0,T; L^{q}_{\sigma }(\varOmega )). \end{aligned}$$

  (A.19)

• (ii) The s.c. analytic semigroup $e^{-A_q t}$ generated by the Stokes operator $-A_q$ (see (A.1)) on the space $\displaystyle \Big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q)\Big )_{1-\frac{1}{p},p}$ satisfies

  $$\begin{aligned}&e^{-A_q t}: \ \text {continuous} \quad \Big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q)\Big )_{1-\frac{1}{p},p} \longrightarrow \nonumber \\&\quad X^T_{p,q,\sigma }(A_q) \equiv L^p(0,T; {\mathcal {D}}(A_q)) \cap W^{1,p}(0,T; L^{q}_{\sigma }(\varOmega )). \end{aligned}$$

  (A.20a)

  In particular via (A.8b), for future use, for $1< q< \infty , 1< p < \frac{2q}{2q - 1}$, the s.c. analytic semigroup $\displaystyle e^{-A_q t}$ on the space $\displaystyle {{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )$, satisfies

  $$\begin{aligned} e^{-A_q t}: \ \text {continuous} \quad {{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )\longrightarrow X^T_{p,q,\sigma }. \end{aligned}$$

  (A.20b)

• (iii) Moreover, setting $\nabla \pi = (Id - P_q)(\varDelta + F)$, it follows that $\{ \varphi , \pi \} \in X^T_{p,q,\sigma }\times Y^T_{p,q}$, see (A.13), solves problem (A.10) and there is a constant $C>0$ independent of $T,F_{\sigma },\phi _0$ s.t.

  $$\begin{aligned} \left\Vert \varphi \right\Vert _{X^T_{p,q,\sigma }} + \left\Vert \pi \right\Vert _{Y^T_{p,q}} \le C \bigg \{ \left\Vert F_{\sigma }\right\Vert _{L^p(0,T;L^{q}_{\sigma }(\varOmega ))} + \left\Vert \varphi _0\right\Vert _{\big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q) \big )_{1-\frac{1}{p},p}} \bigg \}\nonumber \\ \end{aligned}$$

  (A.21a)

  while, for future use, for $1< q< \infty , 1< p < \frac{2q}{2q - 1}$, then (A.21a) specializes to

  $$\begin{aligned} \left\Vert \varphi \right\Vert _{X^T_{p,q,\sigma }} + \left\Vert \pi \right\Vert _{Y^T_{p,q}} \le C \bigg \{ \left\Vert F_{\sigma }\right\Vert _{L^p(0,T;L^{q}_{\sigma }(\varOmega ))} + \left\Vert \varphi _0\right\Vert _{{{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )} \bigg \}.\nonumber \\ \end{aligned}$$

  (A.21b)

• (e) Maximal $L^p$ regularity on $L^{q}_{\sigma }(\varOmega )$ of the Oseen operator $\displaystyle {\mathcal {A}}_q, \ 1< p< \infty , \ 1< q < \infty$: $\displaystyle {\mathcal {A}}_q \in MReg (L^p(0,T;L^{q}_{\sigma }(\varOmega )))$, T finite arbitrary. We next transfer the maximal regularity of the Stokes operator $(-A_q)$ on $L^{q}_{\sigma }(\varOmega )$-asserted in Theorem A.4 into the maximal regularity of the Oseen operator ${\mathcal {A}}_q = -\nu _o A_q - A_{o,q}$ exactly on the same space $X^T_{p,q,\sigma }$ defined in (A.12), except now only on $T < \infty$.

Thus, consider the dynamic Oseen problem in $\{ \psi (t,x), \pi (t,x) \}$ with equilibrium solution $y_e$, see Theorem 1.1 on (1.2) :

(A.23)

rewritten in abstract form, after applying the Helmholtz projector $P_q$ to (A.22a) and recalling ${\mathcal {A}}_q$ in (A.2)

$$\begin{aligned} \psi _t = {\mathcal {A}}_q \psi + P_q F = -\nu _o A_q \psi - A_{o,q} \psi + F_{\sigma }, \quad \psi _0 \in \big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q)\big )_{1-\frac{1}{p},p}\nonumber \\ \end{aligned}$$

(A.24)

whose solution is

$$\begin{aligned} \psi (t)= & {} e^{{\mathcal {A}}_qt} \psi _0 + \int _{0}^{t} e^{{\mathcal {A}}_q(t-\tau )} Fs(\tau ) \mathrm{d} \tau . \end{aligned}$$

(A.25)

$$\begin{aligned} \psi (t)= & {} e^{- \nu _o A_qt} \psi _0 + \int _{0}^{t} e^{-\nu _o A_q(t-\tau )} F_{\sigma }(\tau ) \mathrm{d} \tau - \int _{0}^{t} e^{- \nu _o A_q(t-\tau )} A_{o,q} \psi (\tau ) \mathrm{d} \tau .\nonumber \\ \end{aligned}$$

(A.26)

Theorem A.5

Let $1< p,q < \infty$, $0< T < \infty$. Assume (as in (A.16))

$$\begin{aligned} F_{\sigma }\in L^p \big ( 0, T; L^q_{\sigma } (\varOmega ) \big ), \quad \psi _0 \in \big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q) \big )_{1-\frac{1}{p},p}\end{aligned}$$

(A.27)

where ${\mathcal {D}}(A_q) = {\mathcal {D}}({\mathcal {A}}_q)$, see (A.2). Then there exists a unique solution $\psi \in X^T_{p,q,\sigma }$ of the dynamic Oseen problem (A.22), continuously on the data: that is, there exist constants $C_{0T}, C_{1T}$ independent of $F_{\sigma }, \psi _0$ such that (recall (A.14)):

$$\begin{aligned} C_{0T} \left\Vert \psi \right\Vert _{C \big ([0,T]; B^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )\big )}&\le \left\Vert \psi \right\Vert _{X^T_{p,q,\sigma }} + \left\Vert \pi \right\Vert _{Y^T_{p,q}} \nonumber \\&\equiv \left\Vert \psi '\right\Vert _{L^p(0,T;L^q(\varOmega ))} + \left\Vert A_q \psi \right\Vert _{L^p(0,T;L^q(\varOmega ))} + \left\Vert \pi \right\Vert _{Y^T_{p,q}} \end{aligned}$$

(A.28)

$$\begin{aligned}&\le C_{1T} \bigg \{ \left\Vert F_{\sigma }\right\Vert _{L^p(0,T;L^{q}_{\sigma }(\varOmega ))} + \left\Vert \psi _0\right\Vert _{\big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q) \big )_{1-\frac{1}{p},p}} \bigg \} \end{aligned}$$

(A.29)

Equivalently, for $1< p, q < \infty$

• i. The map

  $$\begin{aligned} \begin{aligned} F_{\sigma }\longrightarrow \int _{0}^{t} e^{{\mathcal {A}}_q(t-\tau )}F_{\sigma }(\tau ) \mathrm{d}\tau : \ : \text {continuous}&\\ L^p(0,T;L^{q}_{\sigma }(\varOmega ))&\longrightarrow L^p \big (0,T;{\mathcal {D}}({\mathcal {A}}_q) = {\mathcal {D}}(A_q) \big )\nonumber \end{aligned}\\ \end{aligned}$$

  (A.30)

  where then automatically, see (A.24)

  $$\begin{aligned} L^p(0,T;L^{q}_{\sigma }(\varOmega )) \longrightarrow W^{1,p}(0,T;L^{q}_{\sigma }(\varOmega )) \end{aligned}$$

  (A.31)

  and ultimately

  $$\begin{aligned} L^p(0,T;L^{q}_{\sigma }(\varOmega ))\! \longrightarrow \!X^T_{p,q,\sigma }(A_q) \!\equiv \! L^p \big (0,T;{\mathcal {D}}(A_q) \big ) \!\cap \! W^{1,p}(0,T;L^{q}_{\sigma }(\varOmega )).\nonumber \\ \end{aligned}$$

  (A.32a)

  Thus,

  $$\begin{aligned} {\mathcal {A}}_q \in MReg (L^p(0,T;L^{q}_{\sigma }(\varOmega ))), \ 1< T < \infty \end{aligned}$$

  (A.32b)

  and the operator $\displaystyle {\mathcal {A}}_q$ has maximal $L^p$ regularity on $L^{q}_{\sigma }(\varOmega )$.

• ii. The s.c. analytic semigroup $e^{{\mathcal {A}}_q t}$ generated by the Oseen operator ${\mathcal {A}}_q$ (see (A.2)) on the space $\displaystyle \big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q) \big )_{1-\frac{1}{p},p}$ satisfies for $1< p, q < \infty$

  $$\begin{aligned} e^{{\mathcal {A}}_q t}: \ \text {continuous} \quad \big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q) \big )_{1-\frac{1}{p},p}\longrightarrow L^p \big (0,T;{\mathcal {D}}({\mathcal {A}}_q) = {\mathcal {D}}(A_q) \big ) \nonumber \\ \end{aligned}$$

  (A.33)

  and hence automatically

  $$\begin{aligned} e^{ {\mathcal {A}}_q t}: \ \text {continuous} \quad \big ( L^{q}_{\sigma }(\varOmega ), {\mathcal {D}}(A_q) \big )_{1-\frac{1}{p},p}\longrightarrow X^T_{p,q,\sigma }. \end{aligned}$$

  (A.34)

  In particular, for future use, for $1< q< \infty , 1< p < \frac{2q}{2q - 1}$, we have that the s.c. analytic semigroup $\displaystyle e^{{\mathcal {A}}_q t}$ on the space $\displaystyle {{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )$, satisfies

  $$\begin{aligned} e^{{\mathcal {A}}_q t}: \ \text {continuous} \quad {{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )\longrightarrow L^p \big (0,T;{\mathcal {D}}({\mathcal {A}}_q) = {\mathcal {D}}(A_q) \big ), \ T < \infty , \nonumber \\ \end{aligned}$$

  (A.35)

  and hence automatically

  $$\begin{aligned} e^{ {\mathcal {A}}_q t}: \ \text {continuous} \quad {{\widetilde{B}}}^{2-{}^{2}\!/_{p}}_{q,p}(\varOmega )\longrightarrow X^T_{p,q,\sigma }(A_q), \ T < \infty . \end{aligned}$$

  (A.36)

• iii. An estimate such as the one in (A.21a) applies to the pressure $\pi$, where now $\displaystyle \nabla \pi (Id - P_q)(\varDelta - L_e + F)$.

A proof of Theorem A.5 is given in [50].

Appendix B: The Eigenvectors $\displaystyle \varphi ^*_{ij} \in W^{2,q'}(\varOmega ) \cap W^{1,q'}_0(\varOmega ) \cap L^{q'}_{\sigma }(\varOmega )$ of $\displaystyle {\mathcal {A}}^* (={\mathcal {A}}_q^*)$ in $\displaystyle L^{q'}(\varOmega )$ May Be Viewed Also as $\displaystyle \varphi ^*_{ij} \in W^{3,q}(\varOmega )$, so that $\displaystyle \frac{\partial \varphi ^*_{ij}}{\partial \nu } \bigg |_{\varGamma } \in W^{2-{}^{1}\!/_{q},q}(\varGamma ), \ q \ge 2$.

The eigenvectors $\displaystyle \varphi ^*_{ij}$ of $\displaystyle {\mathcal {A}}^* (={\mathcal {A}}_q^*)$, defined in (4.8a), are in $\displaystyle {\mathcal {D}}(({\mathcal {A}}_q^*)^n)$ for any n, so the are arbitrarily smooth in $L^{q'}_{\sigma }(\varOmega )$, say $\displaystyle \varphi ^*_{ij} \in W^{s,q'}(\varOmega )$, with s as large as we please. We seek to view $\displaystyle \varphi ^*_{ij}$ in an $\displaystyle L^q(\varOmega )$-based space. To this end, we recall a Sobolev embedding theorem.

Theorem B.1

[81, p328], For a more restricted version [1, p 97] Let $\varOmega$ be an arbitrary bounded domain, dim $\varOmega = d$. Let $0 \le t \le s < \infty$ and $\infty> q \ge {\widetilde{q}} > 1$. Then, the following embedding holds true:

$$\begin{aligned} W^{s,{\widetilde{q}}}(\varOmega ) \subset W^{t, q}(\varOmega ), \ s - \frac{d}{{\widetilde{q}}} \ge t - \frac{d}{q} \quad \end{aligned}$$

(B.1)

$\square$

Corollary B.2

With $\displaystyle 2 \le q < \infty , \ {}^{1}\!/_{q} + {}^{1}\!/_{q'} = 1$, so that $\displaystyle 1 < q' \le 2 \le q, \ 0 \le r$, we have

• (i)
  $$\begin{aligned} \varphi ^*_{ij} \in W^{r+m, q'}(\varOmega ) \subset W^{r,q}(\varOmega ), \quad m \ge d \left( \frac{1}{q} + \frac{1}{q'} \right) = \left\{ \begin{array}{ll} 0, &{} q' = q = 2 \\ d, &{} q' = 1, q = \infty \end{array}\right. \nonumber \\ \end{aligned}$$

  (B.2)
• (ii)
  $$\begin{aligned} \frac{\partial \varphi ^*_{ij}}{\partial \nu } \bigg |_{\varGamma } \in W^{r-1-{}^{1}\!/_{q},q}(\varGamma ), \quad r > 1 + \frac{1}{q} \quad \end{aligned}$$

  (B.3)

• (iii) With reference to the sub-space ${\mathcal {F}}$ based on $\varGamma$, as defined in (1.25), we have

  $$\begin{aligned} {\mathcal {F}}\equiv & {} \text{ span }\left\{ \frac{\partial }{\partial \nu } \varphi ^*_{ij}, \ i = 1,\ldots ,M; \ j = 1,\ldots ,\ell _i\right\} \nonumber \\\subset & {} W^{r-1-{}^{1}\!/_{q},q}(\varGamma ), \ r > 1 + \frac{1}{q} \end{aligned}$$

  (B.4)

  In particular, for our purposes, if will suffice to take $r=3$ in (B.2), so that (B.2)–(B.4) become

  $$\begin{aligned} \varphi ^*_{ij} \in W^{3,q}(\varOmega ), \quad \frac{\partial \varphi ^*_{ij}}{\partial \nu } \bigg |_{\varGamma } \in W^{2-{}^{1}\!/_{q},q}(\varGamma ), \quad {\mathcal {F}}\subset W^{2-{}^{1}\!/_{q},q}(\varGamma ). \end{aligned}$$

  (B.5)

• (iv) Thus, with reference to the boundary vector $v = v_N$ introduced in (5.1) = (6.10), we have

  $$\begin{aligned} v = \sum _{k=1}^{K} \nu _k(t) f_k \in W^{2-{}^{1}\!/_{q},q}(\varGamma ), \ f_k \in {\mathcal {F}}, \ f_k \cdot \nu |_{\varGamma } = 0, \ v \cdot \nu |_{\varGamma } = 0 \nonumber \\ \end{aligned}$$

  (B.6)

• (v) Recalling the Dirichlet map D introduced to describe the solution of problem (2.1), we have

  $$\begin{aligned} Dv \in W^{2,q}(\varOmega ), \quad 2 \le q < \infty \end{aligned}$$

  (B.7)

Proof

(i) Apply Theorem B.1 with $\displaystyle s = r + m \ge t = r, \ {\widetilde{q}} = q', \ {}^{1}\!/_{q} + {}^{1}\!/_{q'} = 1, \ q \ge 2$, so that $\displaystyle q' = {\widetilde{q}} \le q$, to verify that the required condition (B.1)

$$\begin{aligned} s - \frac{d}{{\widetilde{q}}} = r + m - \frac{d}{q'} \ge t - \frac{d}{q} = r - \frac{d}{q}, \ \text {or} \ m \ge d \left( \frac{1}{q'} - \frac{1}{q} \right) \ge 0 \end{aligned}$$

(B.8)

can always be satisfied by taking $m \ge 0$ suitable as in (B.8). This is possible, since $\displaystyle \varphi ^*_{ij}$ is arbitrarily smooth.

(ii) Then (B.3) follows by the usual trace theory [1].

Then, (iii)–(v) readily follow, as D improves regularity by ${}^{1}\!/_{q}$ from the boundary to the interior. $\square$

Next, we return to the operator $\displaystyle F: L^q(\varOmega ) \subset L^{q}_{\sigma }(\varOmega )\longrightarrow L^q(\varGamma )$ in (5.6). Its adjoint $F^*$ is

$$\begin{aligned} F^*g = \sum _{k = 1}^{K} (f_k, g)_{_{\varGamma }} p_k \in (W^u_N)^* \subset L^{q'}_{\sigma }(\varOmega ), \quad g \in L^q(\varGamma ) \end{aligned}$$

(B.9)

where we have seen in (2.64) that $\displaystyle D: L^q(\varGamma ) \supset U_q \longrightarrow W^{{}^{1}\!/_{q},q}(\varOmega ) \cap L^{q}_{\sigma }(\varOmega )\subset {\mathcal {D}}\Big ( A^{{}^{1}\!/_{2q} - \varepsilon }_q \Big )$

$$\begin{aligned} F^*D^*h = \sum _{k = 1}^{K} (f_k, D^*h)_{_{\varGamma }} p_k = \sum _{k = 1}^{K} \big < Df_k, h \big >_{_{W^u_N}} p_k \in (W^u_N)^* \end{aligned}$$

(B.10)

where we have conservatively: $\displaystyle f_k \in L^{q'}(\varGamma ), \ f_k \cdot \nu = 0$ on $\varGamma$, thus by (2.9), $\displaystyle Df_k \in W^{{}^{1}\!/_{q'},q'}(\varOmega ) = W^{{}^{1}\!/_{q'},q'}_0(\varOmega )$ by (2.63a) since $\displaystyle {}^{1}\!/_{q'} \le q'$ for $1 < q' \le 2$. Thus, in (B.10) we can take $\displaystyle h \in W^{-{}^{1}\!/_{q},q}(\varOmega )$. In particular

$$\begin{aligned} F^*D^* \in {\mathcal {L}}\big (L^{q'}(\varOmega )\big ), \quad 1 < q' \le 2. \end{aligned}$$

(B.11)

Appendix C: Relevant Unique Continuation Properties for Overdetermined Oseen Eigenvalue Problems

In this Appendix C, we assemble a comprehensive account of unique continuation problems for Oseen eigenproblems, as they pertain to the problem of controllability of finite dimensional projected system (4.8a, 4.8b) of the linearized w-problem (1.28) (with interior, tangential-like localized control $u \equiv 0$). Positive solution, or lack thereof, of this finite dimensional problem is a key step, or obstruction, for the uniform stabilization of the Navier Stokes equations. This issue has been known since the study of boundary feedback stabilization of a parabolic equation with Dirichlet boundary trace in the feedback loop, as acting on the Neumann boundary conditions [54]. We return to the bounded domain $\varOmega , \ d = 2,3,$ with boundary $\varGamma = \partial \varOmega$. As before, ${\widetilde{\varGamma }}$ is a subportion of $\varGamma$.

Problem #1 (over-determination only on a portion ${\widetilde{\varGamma }}$ of $\varGamma$) Let $\{\varphi , p\} \in W^{2,q}(\varOmega ) \times W^{1,q}(\varOmega )$ solve the over-determined problem

with over-determination only on the portion ${\widetilde{\varGamma }}$ of $\varGamma$. Does (C.1a, C.1b, C.1c) imply

(C.2)

The answer is negative even in the Stokes case: $L_e(\varphi ) \equiv 0$. This follows from [26], where the following counterexample is given in the 2-dimensional half-space $\varOmega = \{(x,y) : x \in {\mathbb {R}}^+, y \in {\mathbb {R}}\}$ with boundary $\varGamma = \{ x = 0 \}$. On $\varOmega$ take

$$\begin{aligned} u_1(x,y) \equiv 0, \quad u_2(x,y) = ax^2, \quad p = 2ay, \quad a \ne 0, \end{aligned}$$

(C.3)

so that with $u = \{u_1, u_2\}$, it follows that

$$\begin{aligned} \varDelta u = \nabla p \text { in } \varOmega , \quad u|_{\varGamma } = \nabla u|_{\varGamma } = 0, \end{aligned}$$

(C.4)

to obtain a nontrivial solution of the Stokes overdetermined eigenproblem with $\lambda = 0$. Such half-space example can then be transformed into a counterexample over the bounded domain $\varOmega$ where the over-determination is active on any subset ${\widetilde{\varGamma }}$ of the boundary $\varGamma = \partial \varOmega$.

Implications of failure of unique continuation under Problem #1: A negative consequence of the lack of unique continuation (C.1) $\implies$ (C.2) with over-determination only in a portion ${\widetilde{\varGamma }}$ of the boundary $\varGamma$ is as follows: that global uniform stabilization of the linearized w-problem (1.28) by means of a purely tangential (finite or infinite dimensional) feedback boundary control v (as given by (5.1) in the finite dimensional case) acting only on a small subportion ${\widetilde{\varGamma }}$ of the boundary $\varGamma$ (and thus with localized interior tangential-like control $u \equiv 0$) is not possible. This is so since the algebraic rank condition (4.11b) (with $u \equiv 0$) fails, as boundary traces

$$\begin{aligned} \left\{ \left. \frac{\partial \varphi ^*_{i1}}{\partial \nu }\right| _{{\widetilde{\varGamma }}}, \left. \frac{\partial \varphi ^*_{i2}}{\partial \nu }\right| _{{\widetilde{\varGamma }}}, \dots , \left. \frac{\partial \varphi ^*_{i \ell _i}}{\partial \nu }\right| _{{\widetilde{\varGamma }}} \right\} \text { fail to be linearly independent on } {\widetilde{\varGamma }} \end{aligned}$$

(C.5)

since, equivalently, the implication (C.1)$\implies$(C.2) fails. See Orientation.

Problem #2 (dual of the statement of Lemma 4.3): necessity to complement the localized control v on ${\widetilde{\varGamma }}$ with a localized interior tangential-like control u supported on $\omega$ in terms of ${\widetilde{\varGamma }}$. Let now $\{ \varphi , p \} \in W^{2,q}(\varOmega ) \times W^{1,q}(\varOmega )$ solve the problem

Then, [53, Theorem 6.2],

$$\begin{aligned} \varphi \equiv 0 \quad \text {and} \quad p \equiv \text {const} \quad \text {in } \varOmega . \end{aligned}$$

(C.7)

It is as a consequence of such unique continuation property that the Kalman algebraic rank conditions (6.28b) are satisfied. This is the basic result upon which the uniform stabilization of the present paper relies. Thus we can conclude that the results of the present paper (as in [53]) are optimal in terms of the required extra condition of the localized interior, tangential-like control needed to supplement the insufficient role of the localized tangential boundary control v on ${\widetilde{\varGamma }}$. Optimality is in terms of the smallness of the required control action for v and u.

Problem #3 (over-determination on the entire boundary $\varGamma = \partial \varOmega$). Let now $\{ \varphi , p \} \in W^{2,q}(\varOmega ) \times W^{1,q}(\varOmega )$ solve the over-determined problem

with over-determination on all of $\varGamma$. Then, does (C.8a, C.8b, C.8c) imply

(C.9)

It seems that a general definitive answer is not known at present. Only partial results are known.

The desired unique continuation (C.8)$\implies$(C.9) holds true, if the equilibrium solution $y_e \equiv 0$ (Stokes eigenproblem) or, more generally, if $y_e$ is sufficiently small in the $W^{1,q}(\varOmega )$-norm. Several different proofs are given in [79, 80].

The case $y_e \equiv 0$ is actually physically quite important as it occurs for instance when the forcing function in (1.1a) or (1.2a) is a conservative vector field (say an electrostatic or gravitational field) $f = \nabla g$. In this case, a solution (1.2a, 1.2b, 1.2c) is: $\displaystyle y_e \equiv 0, \ \pi _e = g$.

When $y_e \equiv 0$ (or $y_e$ small) the tangential boundary feedback control v alone, in the form such as (5.1), as acting on the entire boundary $\varGamma$ produces enhancement of stability at will for the linearized w-problem.

Of course, with $y_e \equiv 0$, the corresponding Oseen problems reduces to the Stokes problem. The Stokes semigroup is already uniformly stable, see (3.7), with margin of stability $\delta > 0$. When $y_e \equiv 0$ a most valuable variation of the problem under investigation of the present paper is to enhance the original margin of stability $\delta > 0$ of the original linearized uncontrolled w-problem (1.11) (with $u \equiv 0, \ v \equiv 0$) to obtain an arbitrary decay rate, say $k^2$, by means of only a tangential boundary finite dimensional feedback control, of the same form as the operator F in (5.6b) but applied to all of $\varGamma$. To this, it suffices to apply the procedure of the present paper to a finite dimensional projected space spanned by the eigenvectors of the Stokes operator corresponding to finitely many eigenvalues $\lambda _i, \ i = 1, \dots , I$,

$$\begin{aligned} -k^2 \le - Re \ \lambda _I \le \dots \le Re \ \lambda _1 \le -\delta \end{aligned}$$

(C.10)

Problem #4 over-determination on a portion of the boundary ${\widetilde{\varGamma }}$ involving also the pressure p. Let $\{\varphi , p\} \in W^{2,q}(\varOmega ) \cap W^{1,q}(\varOmega )$ solve the over-determined problem

Does this imply

(C.12)

This answer is in the affirmative. The argument, given in the [79] is along more classical elliptic arguments [45]. Here however the new condition in (C.11c) contains the pressure, which must be viewed as unknown in general. Application of this result to the present paper will result in substituting $\displaystyle \partial _{\nu } \varphi _{ij}^*|_{{\widetilde{\varGamma }}}$ with $\displaystyle [\partial _{\nu } \varphi _{ij}^* - p_i \nu ]|_{{\widetilde{\varGamma }}}$ in the matrix $W_i$ in (4.9), which then—with this modification—becomes full rank, as desired. Thus, the stabilizing control will be expressed in terms of the pressure on the boundary, which is typically unknown.