The Saturn Ring Effect in Nematic Liquid Crystals with External Field: Effective Energy and Hysteresis

Abstract

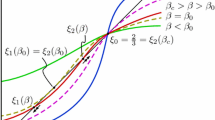
In this work we consider the Landau–de Gennes model for liquid crystals with an external magnetic field to model the occurrence of the Saturn ring effect under the assumption of rotational equivariance. After a rescaling of the energy, a variational limit is derived. Our analysis relies on precise estimates around the singularities and the study of a radial auxiliary problem in regions, where a continuous director field exists. Studying the limit problem, we explain the transition between the dipole and Saturn ring configuration and the occurence of a hysteresis phenomenon, giving a rigorous explanation of what was derived and simulated previously by [H. Stark, Eur. Phys. J. B 10, 311–321 (1999)].

Appendix

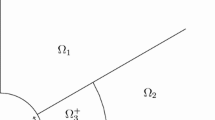
In this section we check that the two functions $g_1$ and $g_2$ as defined in (9) verify the assumptions on g, in particular (5), (6), (7) and (8). All calculations are straightforward.

Proposition A.1

(Properties of $g_1$) Let $g_1$ be given as in (9). Then

• 1. If $Q\in {\mathcal {N}}$ is given by $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})$ with ${\mathbf{n}}\in {\mathbb {S}}^2$, then

  $$\begin{aligned} g_1(Q) = s_*\left( 1 - {\mathbf{n}}_3^2\right) \, , \end{aligned}$$

  that is $c_*^2=s_*$.

• 2. There exists a constant $C>0$ such that for all $Q\in {\mathrm{Sym}}_{0}$

  $$\begin{aligned} |g_1(Q) - g_1({\mathcal {R}}(Q))| \leqq C\, {\mathrm{dist}}(Q,{\mathcal {N}})\, . \end{aligned}$$

  (68)

• 3. The function $g_1$ satisfies the growth assumptions (5),(6) and is invariant by rotations around the $e_3-$axis. For fixed |Q|, $g_1(Q)$ is minimal if ${\mathbf{e}}_3$ is the eigenvector corresponding to the maximal eigenvalue of Q. For $Q=s(({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}}) + r({\mathbf{m}}\otimes {\mathbf{m}}-\frac{1}{3}{\mathrm{Id}}))$ (using the notation of (4)), $g_1(Q)$ is minimized for $r=0$.

Proof

For $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})$ with ${\mathbf{n}}\in {\mathbb {S}}^2$ and $s_*\geqq 0$ one easily checks that

$$\begin{aligned} g_1(Q)&= \frac{2}{3}s_* - s_*\Big ({\mathbf{n}}_3^2-\frac{1}{3}\Big ) = s_* - s_*{\mathbf{n}}_3^2\, . \end{aligned}$$

For the second assertion, we take a $Q\in {\mathrm{Sym}}_{0}$ and use Proposition 2.3 to write

$$\begin{aligned} Q = s\left( \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) + r \left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \right) \, , \end{aligned}$$

with $s>0$, $0 \leqq r <1$ and ${\mathbf{n}},{\mathbf{m}}$ orthonormal eigenvectors of Q and ${\mathcal {R}}(Q) = s_* \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right)$. Then we can estimate

$$\begin{aligned} |g_1(Q) - g_1({\mathcal {R}}(Q))|&= \Big |s\Big ({\mathbf{n}}_3^2-\frac{1}{3}\Big ) + sr\Big ({\mathbf{m}}_3^2-\frac{1}{3}\Big ) - s_*\Big ({\mathbf{n}}_3^2-\frac{1}{3}\Big )\Big | \\&\leqq |s-s_*|\Big |{\mathbf{n}}_3^2-\frac{1}{3}\Big | + |sr|\Big |{\mathbf{m}}_3^2-\frac{1}{3}\Big |\, . \end{aligned}$$

On the other hand, as in (38),

$$\begin{aligned} {\mathrm{dist}}^2(Q,{\mathcal {N}})&= |Q - {\mathcal {R}}(Q)|^2 \geqq \frac{1}{3}|s-s_*|^2 + \frac{1}{3}|sr|^2\, . \end{aligned}$$

Combining these two expressions, we find that

$$\begin{aligned} |g_1(Q) - g_1({\mathcal {R}}(Q))|&\leqq \frac{4}{\sqrt{3}}\,{\mathrm{dist}}(Q,{\mathcal {N}})\, , \end{aligned}$$

which completes the proof of the second assertion for the choice $C=\frac{4}{\sqrt{3}}$.

The function $g_1$ is smooth and obviously satisfies (5) and (6). Furthermore, since $g_1$ only depends on $Q_{33}$, it is invariant under rotations around the ${\mathbf{e}}_3-$axis. Writing once again $Q\in {\mathrm{Sym}}_{0}$ in the form of Proposition 2.3, we get

$$\begin{aligned} g_1(Q) \ = \ \frac{2}{3}s_* - s \Big (\Big ({\mathbf{n}}_3^2 - \frac{1}{3}\Big ) + r\Big ({\mathbf{m}}_3^2-\frac{1}{3}\Big )\Big )\, . \end{aligned}$$

For fixed $s,r,{\mathbf{m}}$ this is minimized by ${\mathbf{n}}_3^2=1$, which corresponds to the principal eigenvector ${\mathbf{n}}$ equal to ${\mathbf{e}}_3$. We also see that for ${\mathbf{n}}={\mathbf{e}}_3$ and s fixed, g becomes minimal if $r=0$, since ${\mathbf{m}}\perp {\mathbf{n}}$. $\square$

Proposition A.2

(Properties of $g_2$) Let $g_2$ be given as in (9). Then

• 1. $g_2(Q)\geqq 0$ for all $Q\in {\mathrm{Sym}}_{0}$ with equality of and only if $Q=t({\mathbf{e}}_3\otimes {\mathbf{e}}_3 - \frac{1}{3}{\mathrm{Id}})$ for some $t\geqq 0$.

• 2. If $Q\in {\mathcal {N}}$ is given by $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})$ with ${\mathbf{n}}\in {\mathbb {S}}^2$, then

  $$\begin{aligned} g_2(Q) = \sqrt{\frac{3}{2}}\left( 1 - {\mathbf{n}}_3^2\right) \, , \end{aligned}$$

  that is $c_*^2=\sqrt{\frac{3}{2}}$.

• 3. There exist constants $\delta _1,C>0$ such that if $Q\in {\mathrm{Sym}}_{0}$ with ${\mathrm{dist}}(Q,{\mathcal {N}})\leqq \delta$ for $0<\delta <\delta _1$, then

  $$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))| \leqq C\, {\mathrm{dist}}(Q,{\mathcal {N}})\, . \end{aligned}$$

  (69)

• 4. The function $g_2$ satisfies the growth assumptions (5),(6) and is invariant by rotations around the $e_3-$axis. For fixed |Q|, $g_2(Q)$ is minimal if ${\mathbf{e}}_3$ is the eigenvector corresponding to the maximal eigenvalue of Q. For $Q=s(({\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}}) + r({\mathbf{m}}\otimes {\mathbf{m}}-\frac{1}{3}{\mathrm{Id}}))$ (using again the notation of (4)), $g_2(Q)$ is minimized for $r=0$.

Proof

Minimizing $g_2$ under the tracelessness constraint, we get the necessary conditions

$$\begin{aligned} -\frac{1}{|Q|}+\frac{Q_{33}^2}{|Q|^3}-\lambda = 0\, , \quad \frac{Q_{33}Q_{jj}}{|Q|^3}-\lambda = 0 \text { for } j=1,2\, , \quad \frac{Q_{33}Q_{ij}}{|Q|^3} = 0 \text { for }i\ne j \end{aligned}$$

for a Lagrange multiplier $\lambda$. For $Q=0$ the claim is clear by definition. So let $Q\in {\mathrm{Sym}}_{0}{\setminus }\{0\}$. If $Q_{33}=0$ we get a contradiction. Hence we can assume $Q_{33}\ne 0$. Then the third equation from above implies $Q_{ij}=0$ for $i\ne j$ and the second $Q_{11}=Q_{22}$. By ${\mathrm{tr}}(Q)=0$, we have $Q_{33}=-2Q_{11}$. Then the first equation reads $0=\frac{3}{2}Q_{33}^2 - |Q|^2$, that is $Q_{33}=\sqrt{2/3}|Q|$. Inserting this into $g_2$ we get $\min _{{\mathrm{Sym}}_{0}} g_2 = 0$. Our conditions also imply the claimed representation $Q=t({\mathbf{e}}_3\otimes {\mathbf{e}}_3 - \frac{1}{3}{\mathrm{Id}})$. Reversely, it is obvious that $g_2=0$ for such Q.

For the second claim, it is straightforward to check that for $Q=s_*({\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}})\in {\mathcal {N}}$ we have $|Q|^2=\frac{2}{3}s_*^2$. Thus

$$\begin{aligned} g_2(Q)&= \sqrt{\frac{2}{3}} - \frac{s_*({\mathbf{n}}_3^2-\frac{1}{3})}{\sqrt{\frac{2}{3}}s_*} = \sqrt{\frac{2}{3}} + \frac{1}{3}\sqrt{\frac{3}{2}} - \sqrt{\frac{3}{2}}{\mathbf{n}}_3^2 = \sqrt{\frac{3}{2}}\left( 1 - {\mathbf{n}}_3^2\right) \, . \end{aligned}$$

For the next property we use the same notation as before (from Proposition 2.3) to write

$$\begin{aligned} Q = s\left( \left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) + r \left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \right) \, , \end{aligned}$$

with $s>0$, $0 \leqq r <1$ and ${\mathbf{n}},{\mathbf{m}}$ orthonormal eigenvectors of Q. From the second part of this proposition, we infer that $g_2({\mathcal {R}}(Q)) = \sqrt{\frac{3}{2}}(1-{\mathbf{n}}_3^2)$. In order to calculate $g_2(Q)$, we note that

$$\begin{aligned} |Q|^2&= s^2 \left| {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right| ^2 + (sr)^2 \left| {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right| ^2 + 2 s^2r\\&\left( {\mathbf{n}}\otimes {\mathbf{n}}- \frac{1}{3}{\mathrm{Id}}\right) :\left( {\mathbf{m}}\otimes {\mathbf{m}}- \frac{1}{3}{\mathrm{Id}}\right) \\&= \frac{2}{3} s^2 \left( r^2 - r +1 \right) \, . \end{aligned}$$

This implies

$$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))|&= \left| \sqrt{\frac{2}{3}} - \frac{s(n_3^2 - \frac{1}{3}) + sr(m_3^2-\frac{1}{3})}{\sqrt{\frac{2}{3}} s \sqrt{1-r+r^2}}\right. \\&\left. - \sqrt{\frac{2}{3}} + \frac{s_*(n_3^2-\frac{1}{3})}{s_* \sqrt{\frac{2}{3}}} \right| \\&\leqq \frac{n_3^2-\frac{1}{3}}{\sqrt{\frac{2}{3}}} \left( \frac{1}{\sqrt{1-r+r^2}} - 1\right) + \frac{m_3^2-\frac{1}{3}}{\sqrt{\frac{2}{3}}} \frac{r}{\sqrt{1-r+r^2}}\, . \end{aligned}$$

Note, that the Taylor expansion at $r=0$ is given by $\displaystyle {\frac{1}{\sqrt{1-r+r^2}} - 1} = \frac{r}{2} + {\mathcal {O}}(r^2)$ and $\displaystyle {\frac{r}{\sqrt{1-r+r^2}} = r + {\mathcal {O}}(r^2)}$. Hence

$$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))| \leqq \frac{3}{2} r + {\mathcal {O}}(r^2)\, . \end{aligned}$$

(70)

As in Proposition A.1 we get that ${\mathrm{dist}}^2(Q,{\mathcal {N}})\geqq \frac{1}{3}|s-s_*|^2 + \frac{1}{3}|sr^2|$ and hence $|s-s_*|\leqq \sqrt{3}\,{\mathrm{dist}}(Q,{\mathcal {N}})$ and $\displaystyle {|r|\leqq \frac{\sqrt{3}\, {\mathrm{dist}}(Q,{\mathcal {N}})}{|s|}}$. We define $\displaystyle {\delta _1 = \frac{1}{2\sqrt{3}}s_*}$ and together with (70) we get

$$\begin{aligned} |g_2(Q) - g_2({\mathcal {R}}(Q))| \leqq C r \leqq \frac{\sqrt{3}{\mathrm{dist}}(Q,{\mathcal {N}})}{|s|} \leqq C\frac{2\sqrt{3}}{s_*} {\mathrm{dist}}(Q,{\mathcal {N}})\, . \end{aligned}$$

It remains to prove the last assertion. Again the growth assumptions (5) and (6) are trivially satisfied. With the same arguments as in Proposition A.1 (since |Q| is fixed), we get that $g_2(Q)$ is minimal for ${\mathbf{n}}={\mathbf{e}}_3$. Finally, we can compute

$$\begin{aligned} g_2\left( s\left( \left( {\mathbf{e}}_3\otimes {\mathbf{e}}_3-\frac{1}{3}{\mathrm{Id}}\right) + r\left( {\mathbf{m}}\otimes {\mathbf{m}}-\frac{1}{3}{\mathrm{Id}}\right) \right) \right) \ = \ \sqrt{\frac{2}{3}} - \frac{\frac{2}{3} s + sr\left( {\mathbf{m}}_3^2-\frac{1}{3}\right) }{\sqrt{\frac{2}{3}}s \sqrt{1-r+r^2}} \end{aligned}$$

and see that this is indeed minimal if $r=0$. $\square$