Symmetry and Rigidity of Minimal Surfaces with Plateau-like Singularities

Abstract

By employing the method of moving planes in a novel way we extend some classical symmetry and rigidity results for smooth minimal surfaces to surfaces that have singularities of the sort typically observed in soap films.

Appendix A. A Rigidity Result for Geodesic Nets

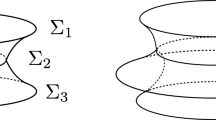
In the proof of the Removable Singularity lemma for Plateau minimal surfaces, see Lemma 2.1, we have used a rigidity lemma for geodesic nets on the unit sphere whose statement and proof are presented in this appendix. We say that $\Gamma \subset {\mathbb {S}}^2$ is a geodesic net if $\Gamma$ is a finite union $\Gamma =\bigcup _{i=1}^M\gamma _m$ of geodesic arcs $\gamma _i$ in ${\mathbb {S}}^2$ so that if $p\in \Gamma$, then, setting $I(p)=\{i:p\in \gamma _i\}$, one has that either $\#\,I(p)=1$ and $p\in \mathrm{int}\,\gamma _i$, or $\#\,I(p)\ge 2$, $p\in \partial \gamma _i$ for each $i\in I(p)$ and

$$\begin{aligned} \sum _{i\in I(p)}\nu ^{\mathrm{co}}_{\gamma _i}(p)=0\,, \end{aligned}$$

(A.1)

where $\nu ^{\mathrm{co}}_{\gamma _i}$ denotes the outer unit conormal to $\gamma _i$ in ${\mathbb {S}}^2$ at p. Of course, if $\#I(p)\ge 2$, then $\#I(p)\ge 3$. If $\Gamma$ is a geodesic net in ${\mathbb {S}}^2$, then the multiplicity one, 1-dimensional varifold $V_\Gamma$ associated to $\Gamma$ is stationary in ${\mathbb {S}}^2$. Moreover, a cone K in ${\mathbb {R}}^3$ with vertex at 0 induces a multiplicity one, 2-dimensional, stationary varifold $V_K$ in ${\mathbb {R}}^3$ if and only if $\Gamma =K\cap \partial B_1$ is a geodesic net in ${\mathbb {S}}^2\equiv \partial B_1$ thanks to [1]. Of course, any finite union of equatorial circles defines a geodesic net. Equatorial circles and Y-nets (three equatorial half-circles meeting at two common end-points at $2\pi /3$-angles) are examples of geodesic nets that are also locally length minimizing, in the sense that they minimize ${\mathcal {H}}^1$ with respect to Lipschitz deformations with sufficiently small support. The following lemma provides a rigidity statement which allows one to characterize these two length minimizing geodesic nets among all geodesic nets. The proof uses moving equatorial half-circles.

Lemma A.1

(Rigidity of geodesic nets) Let $\Gamma$ be a geodesic net in ${\mathbb {S}}^2$, let e be a unit vector and let $\varepsilon >0$. If $\Gamma$ agrees either with an equatorial circle or with a Y-net in the spherical cap $\{x\cdot e>-\varepsilon \}$, then $\Gamma$ is either an equatorial circle or a Y-net.

Proof

Without loss of generality let us assume that $e=e_3$, so that $\Gamma \cap \{x_3\ge 0\}$ is equal to a equatorial half-circle $\Gamma _0$ contained in $\{x_3\ge 0\}$ with endpoints $p_0$ and $-p_0$. In this way $\Gamma \cap \{x_3>-\varepsilon \}$ is either equal to $S_0\cap \{x_3>-\varepsilon \}$ or to $Y_0\cap \{x_3>-\varepsilon \}$, where $S_0=\Gamma _0\cup (-\Gamma _0)$ is the unique equatorial circle containing $\Gamma _0$ and $Y_0$ is the unique Y-net containing $\Gamma _0$.

Let $\{\Gamma (t)\}_{0\le t\le \pi }$ and $\{\Gamma '(t)\}_{0\le t\le \pi }$ denote the two distinct one-parameter families of equatorial half-circles obtained by rotating by t-radians $\Gamma _0$ around the axis defined by its endpoints $\pm p_0$ one clockwise the other counter-clockwise. In particular, $\Gamma (t)$ and $\Gamma '(t)$ have the same endpoints of $\Gamma _0$, $\Gamma (0)=\Gamma '(0)=\Gamma _0$, and $\Gamma (\pi )=\Gamma '(\pi )=-\Gamma _0$ is the equatorial half-circle antipodal to $\Gamma _0$. By assumption, there are maximal intervals $[0,\delta _0)$ and $[0,\delta _0')$ such that

$$\begin{aligned} \Gamma (t)\cap \Gamma {\setminus }\{\pm p_0\}=\emptyset \qquad \forall t\in (0,\delta _0)\,, \end{aligned}$$

(A.2)

and such that the same holds for $\Gamma '(t)$ in place of $\Gamma (t)$ if $t\in (0,\delta _0')$. Notice that as $\Gamma$ agrees with either an equatorial circle or a Y-net on $\{x_3>-\varepsilon \}$, then either $\delta _0$ or $\delta _0'$ must be strictly larger than $\pi /2$. We assume, without loss of generality, that $\delta _0>\pi /2$.

If $\delta _0=\pi$ but $\Gamma \cap \Gamma (\pi ){\setminus }\{\pm p_0\}=\emptyset$, then the validity of (A.2) for every $t\in (0,\pi )$ implies that $\Gamma \subset W$ where W is wedge given by the intersection of two different closed half-spaces. Therefore $\#I(p_0)\ge 2$ but (A.1) cannot hold at $p=p_0$. We deduce that if $\delta _0=\pi$, then $\Gamma \cap \Gamma (\pi ){\setminus }\{\pm p_0\}\ne \emptyset$. As a consequence, $\Gamma$ is touched by $\Gamma (\pi )$ at an interior point q, and locally near q $\Gamma$ lies on one side of $\Gamma (\pi )$ thanks to (A.2) with $\delta _0=\pi$: by the strict maximum principle we find that, locally near q, $\Gamma$ is equal to $\Gamma (\pi )$. Let I be the component of $\Gamma \cap \Gamma (\pi )$ containing q. As I is the intersection of closed sets it is closed. Moreover, for every $p\in I$, as $\Gamma$ lies on one side of $\Gamma (\pi )$ near p one has $\# I(p)\le 2$ and so $\Gamma$ is smooth near p. Hence, we may appeal to a unique continuation to see that $I=\Gamma (\pi )$. That is, $\Gamma (\pi )\subset \Gamma$. We have thus proved that

$$\begin{aligned} S_0\subset \Gamma \,,\qquad \Gamma \cap H_0=\emptyset \,, \end{aligned}$$

where $H_0$ is one of the two open half-spaces bounded by $S_0$. It is easily seen that (A.1) and $\Gamma \cap H_0=\emptyset$ imply that $\#\,I(p)=1$ for every $p\in S_0$. In particular, by a covering argument, $\Gamma$ is equal to $S_0$ in an open neighborhood of $S_0$, and since $\Gamma$ is connected, this implies that $\Gamma =S_0$.

We are left to discuss the case when $\delta _0\in (\pi /2,\pi )$. By the strict maximum principle, the regularity of points of $\Gamma$ lying on a $\Gamma (\delta _0)$ and the unique continuation principle we see that

$$\begin{aligned} \Gamma _0\cup \Gamma (\delta _0)\subset \Gamma \,,\qquad \Gamma \cap V=\emptyset \quad \text{ where }\quad V=\bigcup _{t\in (0,\delta _0)}\Gamma (t). \end{aligned}$$

The fact that $\delta _0<\pi$ implies that $\Gamma \cap \{x_3>-\varepsilon \}=S_0\cap \{x_3>-\varepsilon \}$ cannot hold. Therefore it must be $\Gamma \cap \{x_3>-\varepsilon \}=Y_0\cap \{x_3>-\varepsilon \}$, which gives $\delta _0=2\pi /3$, $\delta _0'=2\pi /3$, and thus that $Y_0\subset \Gamma$. Now pick let $V'$ denote the smaller wedge bounded by $\Gamma _0$ and $\Gamma '(2\pi /3)$, and notice that similarly V is the smaller wedge bounded by $\Gamma _0$ and $\Gamma (2\pi /3)$. If q is in the interior of $\Gamma (2\pi /3)$, then the fact that $V\cap \Gamma =\emptyset$ combined with (A.1) implies that $\Gamma (2\pi /3)$ is equal to $\Gamma$ in a neighborhood of q; similarly, $V'\cap \Gamma =\emptyset$ and (A.1) imply that $\Gamma '(2\pi /3)$ is equal to $\Gamma$ in a neighborhood of each of its points. Finally, $\Gamma$ and $Y_0$ agree in a neighborhood of $\{\pm p_0\}$ and in a neighborhood of $\Gamma _0$ thanks to $\Gamma \cap \{x_3>-\varepsilon \}=Y_0\cap \{x_3>-\varepsilon \}$, so that, in conclusion, by a covering argument, $\Gamma$ is equal to $Y_0$ in an open neighborhood of $Y_0$. This proves that $\Gamma =Y_0$, as claimed. $\square$