1 Introduction of load frequency control (LFC) problem

The electrical power system comprises interconnecting multiple control areas via tie lines, where generators within each area collectively adjust their speed—either accelerating or decelerating—to uphold preset frequency and corresponding power angle. Load frequency control (LFC) governs the adjustment of actual power output from generators in response to fluctuations in system frequency and power exchange across tie-lines, adhering to predefined thresholds. The LFC process ensures that the output of system generators stays within an acceptable range, aligning with the present system demand. Additionally, the exchange of electrical power between different power generation areas should adhere to agreed contractual values [1,2,3]. The amalgamation of frequency variations and tie-line power exchanges among control areas, represented in a linear format, is commonly termed as the area control error (ACE) and hence concept of LFC is to minimize or eliminate the ACE from the system by matching the minute by minute generation with present system demand and hence this necessitates precise tuning of controllers overseeing generation units within the electrical power system to maintain frequency deviations within a nominal range of ± 0.1 Hz.

1.1 Literature review and research gaps

Over the years, a multitude of LFC schemes have been introduced in the literature with the aim of offering effective designs to direct the LFC needs and the researchers have explored various models of LFC such as single-area [4], interconnected two-area [5], three-area LFC [6], four-area LFC [7], multi-area LFC [8], LFC models with time delay and nonlinearity [9], and LFC models with incorporation of renewable energy sources [10]. In the early stages, control techniques in this field were centered around traditional controllers, representing the initial forays into this domain [11]. However, this approach had inherent limitations, primarily because it lacked specific criteria for selecting controller gains. Instead, it heavily relied on the experience of plant operators, rendering it ineffective in meeting the stringent LFC standards, especially in the face of varying operational conditions. In recent times, bio-inspired optimization algorithms have emerged as crucial components of LFC owing to their effectiveness and efficiency in maintaining essential system parameters within specified ranges. The differential evolution (DE) algorithm has been proposed for LFC in multisource power systems [12]. Cuckoo Search Algorithm (CSA) was introduced for two-area power systems [13, 14], and the beta wavelet neural network (BWNN) approach has been employed for LFC in [15]. Teaching–learning-based optimization (TLBO) algorithm has been implemented in LFC [16, 17], and the hybrid particle swarm optimization-pattern search (hPSO-PS) technique has been applied for LFC in [18]. Non-dominated sorting genetic algorithm-II (NAGA-II)-based optimal control strategy has been implemented to improve frequency regulation [19], while the minority charge carrier-inspired algorithm has been applied to LFC in interconnected hydrothermal power systems [20]. A modified harmony search algorithm was proposed for LFC in [21] in nonlinear interconnected systems and a bat-inspired algorithm has been utilized for LFC in interconnected reheat thermal power systems [22]. The flower pollination algorithm was developed by Yang in [23] and its application to solve LFC issue of multi-area energy system with non-linearity was discussed in [24]. In [25], the application of FPA was tested on thermal system with dead-band limitations and the performance of FPA-oriented controller were assessed considering various loading conditions.

The literature review acknowledges the plethora of LFC techniques proposed, which have significantly evolved over time. However, it is observed that earlier studies on LFC predominantly focused on traditional power systems. With conventional resources dwindling and power demand on the rise, there is an increasing emphasis on integrating renewable energy sources (RESs). The utilization of RES offers numerous benefits, including zero carbon emissions, cleanliness, abundance, economic viability, and environmental friendliness [26,27,28,29]. The transition to occasional non-conventional energy sources such as solar PV [30,31,32,33,34] has a dual impact on interconnected power systems, mainly affecting frequency stability due to decreased system inertia and intermittent generation. As a result, the high penetration of RES may exacerbate specific challenges such as frequency deviations and uncontracted exchange of power between control areas and hence these challenges necessitate innovative perspectives and novel approaches to enhance the integration of RES into the existing power system.

An energy storage system presents itself as a feasible solution for alleviating the detrimental effects of inertia reduction resulting from RES. The energy storage module provides necessary power during sudden load fluctuations to uphold the stability of load frequency. The stored reserve power within the energy storage module has the potential to oversee both active and reactive power, thus enhancing the performance of energy systems, particularly when faced with sudden fluctuations in load demands. Additionally, they serve a pivotal role in guaranteeing the dependable supply of top-tier electrical energy to contemporary consumers. The redox flow battery (RFB) boasts an effectively instant time constant of zero seconds, allowing it to swiftly inject active power into the system and enhance the system's frequency profile. Conversely, the unified power flow controller (UPFC) stands as an inventive device, delivering a budget-friendly approach to enhancing the performance of electrical energy systems when integrated in series with tie-lines [35].

1.2 Motivation behind the present research work

Following the preceding discussions and research reviews, it is evident that researchers have primarily focused on conventional LFC methods. However, as lifestyles evolve and conventional energy sources deplete, coupled with changing supply–demand dynamics, the significance of integrating RES into the conventional system continues to rise to meet the escalating energy demand in a more environmentally friendly manner. Nevertheless, integrating RES, such as solar PV, poses significant challenges to system frequency due to their intermittent nature, necessitating the development of advanced control strategies to fulfill LFC requirements. Additionally, energy storage systems like RFB and devices such as UPFC can store or release surplus energy from the system, playing a crucial role in minimizing unnecessary frequency and tie-line power excursions, thus stabilizing system operation more efficiently and rapidly.

1.3 Objectives and contribution

Given the preceding discussion, this research article's unique contribution lies in its aim to:

  1. 1.

    A robust computational intelligence method, flower pollination algorithm (FPA), is utilized and proposed for the optimization of PID controller parameters in LFC systems.

  2. 2.

    The study focuses on a two-area thermal system and showcases the superiority of the proposed approach by contrasting the results with those obtained using GA-PID, PSO-PID, and HBFO-PID controllers.

  3. 3.

    In addition, the solar PV system, as a prolific renewable energy source, is integrated to each control area of the system to show its impact on the overall response of the system.

  4. 4.

    Further, the impact of UPFC and RFB is also checked individually with the PV integration using FPA-PID controller. The application results of the present research work are showcased to see the benefits of the advocated approach.

1.4 Paper organization

The remainder of the article is structured as follows: Sect. 2 presents the mathematical modeling of solar PV for LFC, while the mathematical modeling of UPFC and RFB is outlined in Sect. 3. Section 4 provides insight into the optimization approach, followed by result analysis in Sect. 5. Finally, Sect. 6 concludes the article.

2 Mathematical modeling of solar PV array for LFC

Incorporating a PV array into a LFC power system necessitates a strong grasp of power electronics principles and strict adherence to established guidelines [30, 31]. Once the power output from the PV array is acquired, the initial step in linking it with the LFC power system involves the utilization of a boost converter. This device raises the voltage to a suitable level, preparing it for use as the input in the subsequent stage, which is the inverter. The primary function of the inverter is to generate AC current to harmonize with the grid's AC power characteristics and synchronize with its voltage and current levels.

The input to the PV system connected to the grid is the output of the PV array, which is a DC current. This involves a system composed of 150 arrays, each capable of generating 30 kW of power, and these arrays are connected to a consistent voltage source of 6 kV on the PV array side [32]. The PV system operates at the lower end of the voltage and power spectrum, which is commonly found in inverter-based PV systems that are connected to grids with power capacities ranging from 1 kW to a few MW [33]. The maximum power point (MPP) represents the specific voltage value at which the highest output power is achieved, and it is a critical factor in solar array performance [34].

In this configuration of solar arrays, the MPP is located at which results in an MPP of 4.5 MW. The output generated by an array is inherently DC. When observed over longer time periods, such as hours, this output exhibits nonlinear behavior. However, when analyzed within shorter intervals, typically seconds (the relevant timeframe for designing system controllers), it manifests as a stable, constant DC voltage. Even in practical scenarios where voltage variations occur over extended periods due to factors like temperature fluctuations or changes in solar irradiance, these variations shift from one consistent DC value to another. First, the PV system can be linked to conventional power system with the utilization of a DC–DC boost converter to connect the PV system to the grid. In an ideal scenario, this converter essentially acts as an amplifier or gain device. To determine this required gain, it becomes crucial to understand the overall gain needed between the DC voltage and the desired amplitude of the final AC voltage, denoted as 'm' in Eq. (1).

$$ m = \frac{{V_{{{\text{dc}}}} }}{{V_{{{\text{ac}}}} }} $$
(1)

In this model, an optimal value for 'm' is considered to be below 0.866, and in this specific instance, it has been set at 0.7. The PV system operates with a consistent DC voltage, while the output current and power of the PV arrays fluctuate due to variations in solar irradiance and temperature. With this fixed DC voltage value and the selected 'm' value for this particular system, the amplitude of the AC voltage remains constant. Consequently, the AC current and power can vary in sync with changing conditions.

Now, we can employ the value of 'm' to determine the required voltage after the boost converter, denoted as 'V2' in Eq. 2. Further, the photovoltaic system is connected to the low-voltage side of the grid, and the root-mean-square (RMS) value of the grid line to line voltage in the conventional system under consideration is 11 kV. Thus, the grid phase to neutral voltage is 11 kV divided by the square root of 3. That is, it is calculated as 6.4 kV. We will use this value because in this photovoltaic system, only one phase (phase A) is taken into account, even though there are two other phases (B and C) contributing power to the system with a certain phase shift.

$$ \begin{gathered} V_{2} = \frac{{V_{m} }}{m} \hfill \\ V_{2} = \frac{{6.4\;{\text{kV}}}}{0.7} \hfill \\ V_{2} = 9.1\;{\text{kV}} \hfill \\ \end{gathered} $$
(2)

Hence, using the input DC voltage equal to 6 kV, we can compute the gain of the boost converter as follows.

$$ \begin{gathered} M_{1} = \frac{{V_{2} }}{{V_{1} }} \hfill \\ M_{1} = \frac{9.1}{6} \hfill \\ M_{1} = 1.52 \hfill \\ \end{gathered} $$
(3)

Therefore, the boost converter gain will be computed as.

$$ \begin{gathered} G_{1} = \frac{1}{{M_{1} }} \hfill \\ G_{1} = \frac{1}{1.52} \hfill \\ G_{1} = 0.66 \hfill \\ \end{gathered} $$
(4)

The subsequent step involves the DC–AC inverter, which transforms the DC current into AC current suitable for connection to the conventional AC-based power system. The transfer function can be derived by performing the Laplace transform on each term.

$$ {\text{Since}}\;{\text{AC}}\;{\text{current}}\;{\text{is}}\;{\text{given}}\;{\text{by:}}\;i_{{{\text{ac}}}} = I_{m} \cos \left( {\omega t} \right) $$
(5)

Laplace transform for Eq. (5) is given by.

$$ \frac{s}{{s^{2} + \omega^{2} }} $$
(6)

The output current of the boost converter which is \(I_{2}\), has a Laplace transform of \(\frac{1}{s}\). Since the second transfer function is inverting DC to AC current, then the equation is expressed as.

$$ G_{2} (s) = \frac{{i_{{{\text{ac}}}} (s)}}{{I_{2} (s)}} $$
(7)

By substituting (7) for (6), we obtain.

$$ G_{2} (s) = \frac{s}{{\frac{{s^{2} + \omega^{2} }}{\frac{1}{s}}}} $$
(8)

Finally, the Eq. (8) can be formalized to

$$ G_{2} (s) = \frac{{s^{2} }}{{s^{2} + \omega^{2} }} $$
(9)

The angular frequency \((\omega )\), is given by \(2\pi .50\;{\text{Hz}}\) which result updating (9) to

$$ G_{2} (s) = \frac{{s^{2} }}{{s^{2} + 98700}} $$
(10)

The third transfer function aims to convert \((I_{2} )\) into instantaneous power so that the output of the conventional system will match, since the energy from PV to power grid should be in terms of power.

$$ {\text{The}}\;{\text{gain}}\;{\text{is}}\;G_{3} = \frac{p}{{i_{{{\text{ac}}}} }} $$
(11)

then the instantaneous power is given by

$$ p = i_{{{\text{ac}}}}^{2} .Z_{m} $$
(12)

The impedance of a purely resistive load can be expressed as

$$ p = \frac{{V_{m} }}{{I_{m} }}.i_{{{\text{ac}}}}^{2} $$
(13)

Apply Eq. (5) to (13)

$$ p = \frac{{V_{m} }}{{I_{m} }}\left[ {I_{m} \cos \left( {\omega t} \right)} \right]^{2} $$
(14)

By applying Laplace transform in Eq. (14), we obtain,

$$ p(s) = \frac{{V_{m} I_{m} }}{2s} + \frac{{V_{m} I_{m} }}{2}\left( {\frac{s}{{s^{2} + 2\omega^{2} }}} \right) $$
(15)

Substitute Eq. (15) into (11)

$$ G_{3} (s) = \frac{p(s)}{{i_{ac} (s)}} = \frac{{V_{m} I_{m} }}{{\frac{2s}{{I_{m} \cos \omega t}}}} + \frac{{V_{m} I_{m} }}{2}\left( {\frac{s}{{s^{2} + 2\omega^{2} }}} \right) $$
(16)

Equation (16) may be rewritten as

$$ G_{3} (s) = \frac{{(s^{2} + \omega^{2} )(s^{2} + 4\omega^{2} )}}{{s^{2} (s^{2} + 16\omega^{2} )}} $$
(17)

From Eq. (3.10), \(\omega = 2\pi .50 = 314.16\;{\text{rad}}/{\text{sec}}\), the third transfer function which is capable to convert AC current into instantaneous power is given by.

$$ G_{3} (s) = \frac{{6351s^{4} + 1.88e9s^{2} + 1.237e14s^{2} }}{{s^{4} + 3.948e5s^{2} }} $$
(18)

By squared the inverted current in Eq. (12) to determine the instantaneous power, the frequency of the PV get doubled as seen in Eq. (18). The fourth transfer function of the PV is to transform the instantaneous power that was in frequency domain into average power in time domain. The gain is given by.

$$ G_{4} = \frac{{P_{{{\text{ave}}}} }}{p} $$
(19)

The average power is expressed as

$$ P_{{{\text{ave}}}} = \frac{1}{T}\int\limits_{0}^{T} {v_{{{\text{ac}}}} .i_{{{\text{ac}}}} {\text{d}}t} $$
(20)

Apply Eqs. (5) to (20), both voltage and current. Then (20) will be expressed as

$$ P_{{{\text{ave}}}} = \frac{1}{T}\int\limits_{0}^{T} {V_{m} \cos (\omega t).I_{m} \cos (\omega t){\text{d}}t} $$
(21)

Apply Eq. (15) into (21) and consider Laplace transform. We obtain.

$$ \begin{gathered} G_{4} (s) = \frac{{P_{{{\text{ave}}}} (s)}}{p(s)} \hfill \\ G_{4} (s) = \frac{{V_{m} I_{m} }}{2} \div \left( {\frac{{V_{m} I_{m} }}{2s} + \frac{{V_{m} I_{m} }}{2}.\frac{s}{{s^{2} + 2\omega^{2} }}} \right) \hfill \\ \end{gathered} $$
(22)

To obtain a transfer function that convert the instantaneous power to average power, use the same method used to obtain the \(G_{3} (s)\)

$$ G_{4} (s) = \frac{{s^{2} + 3.948e5}}{{2s^{2} + 3.948e5}} $$
(23)

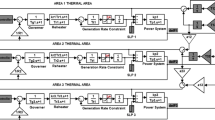
Figure 1 illustrates the LFC model incorporating solar PV integrated into the thermal power system.

Fig. 1
figure 1

Solar PV integrated LFC model of interconnected thermal–thermal power system

Full size image

3 Modeling of UPFC and RFB

The UPFC is recognized for its capacity to control power flow within interconnecting tie-lines, thereby enhancing system voltage stability. When there are abrupt changes in load demand, it significantly disrupts the performance of LFC systems. The shunt converter incorporated within UPFC injects adjustable shunt voltage to ensure that the real/active component of the current in the shunt branch matches the real power demanded by the series converter. The expression for the magnitude of complex power at the line's receiving end is denoted by [35]:

$$ P_{{{\text{real}}}} - jQ_{{{\text{reactive}}}} = \overline{{V_{r}^{*} }} I_{{{\text{line}}}} = \overline{{V_{r}^{*} }} \left\{ {\left( {\overline{{V_{s} }} + \overline{V}_{{{\text{se}}}} - \overline{V}_{r} } \right)/j(X)} \right\} $$
(24)
$$ {\text{Where}},\;\overline{V}_{{{\text{se}}}} = \left| {V_{{{\text{se}}}} } \right|\angle (\delta_{s} - \phi_{{{\text{se}}}} ) $$
(25)

In Eq. (25), Vse signifies the absolute value of the series voltage, whereas \(\phi_{{{\text{se}}}}\) represents the phase angle of the series voltage. Upon solving Eq. (24), the resulting real component is as follows:"

$$ \begin{aligned} P_{{{\text{real}}}} & = \frac{{\left| {V_{s} } \right|\left| {V_{r} } \right|}}{X}\sin \delta + \frac{{\left| {V_{s} } \right|\left| {V_{{{\text{se}}}} } \right|}}{X}\sin (\delta - \phi_{{{\text{se}}}} ) \\ & = P_{0} (\delta ) + P_{{{\text{se}}}} (\delta , \, \phi_{{{\text{se}}}} ) \\ \end{aligned} $$
(26)

In the equation mentioned, when Vse is set to 0, it signifies a lack of compensation for real power. Nevertheless, the UPFC series voltage magnitude can be finely tuned, ranging from 0 to Vse max. Moreover, the phase angle can be manipulated in the span of 0° to 360° at any given power angle. When performing LFC studies, the control design for UPFC can be depicted using the subsequent transfer function:

$$ \Delta P_{{{\text{UPFC}}}} (s) = \left\{ {\frac{1}{{1 + sT_{{{\text{UPFC}}}} }}} \right\}\Delta F(s) $$
(27)

In this context, TUPFC designates the time constant associated with the UPFC and Fig. 2 shows the schematic model of UPFC as used for present research studies.

Fig. 2
figure 2

Schematic model of UPFC

Full size image

3.1 RFB

An energy storage device known for its rapid response to frequency deviations is the Redox flow battery (RFB), which is one of the key technologies in this regard. In terms of response time, the RFB can adjust its operational parameters within a matter of seconds. The RFB storage system boasts a notable advantage in terms of efficiency, thanks to its robust charge and discharge capabilities. This design eliminates self-discharge in the RFB, ultimately enhancing its lifespan, which is considerably longer compared to other battery technologies. The electrolytes in the Redox flow battery consist of sulfuric acid solutions containing vanadium ions, which are housed in both positive and negative storage tanks as shown in Fig. 3. Moreover, the RFB, when operated at typical temperatures, is relatively safe, despite its reputation for rapid charge and discharge capabilities. Another notable feature attributed to the Redox flow battery is its ability to efficiently reestablish its set value following a load disturbance. This means that the RFB can swiftly return to its desired operational parameters after a disturbance, without causing delays in subsequent load changes. The RFB's set value and its power exchange with the system are contingent on the deviated frequency signal. The RFB is a rechargeable battery, and its lifespan remains unaffected even with multiple charging and discharging cycles, offering a rapid response to unforeseen load variations. The Redox flow battery is particularly valuable for load leveling, contributing to the maintenance of power quality. The RFB model is based on the representation provided in [35] and is illustrated in Fig. 3.

$$ \Delta P_{RFB} \left( s \right) = \left\{ {\frac{{K_{RFB} }}{{1 + sT_{RFB} }}} \right\}\Delta F\left( s \right) $$
(28)
Fig. 3
figure 3

Schematic model of RFB

Full size image

4 Optimization problem and details of flower pollination algorithm

The fundamental goal of LFC is to mitigate deviations in system frequency and fluctuations in tie-line power when abrupt changes in the power demand occur. This research initiative is motivated by the objective of evaluating LFC performance for a thermal–thermal power system. It seeks to propose an effective PID control design optimized through flower pollination algorithm (FPA). The aim is to assess the performance of this newly proposed control design across various operational scenarios within the system. In addition, the solar PV generating enough electrical energy is integrating to each area of thermal–thermal system. Furthermore, it is also checked and assessed that FPA-PID output and performance can improved significantly if solar PV is feeding the power to thermal–thermal system. Finally, further enhancement is possible by adding the UPFC and RFB in LFC model separately.

To address this challenge, PID controllers are connected in each area. The outputs controlled by PID controllers, with gains determined through FPA execution, are then inputted into the governors of the LFC system. Governor operations are restricted by incorporating dead bands. The presence of these dead-bands exerts a notable influence on the stability of the system, leading to changes in oscillation amplitudes and impacting the time required for the system's performance to reach a stable state. As a result, the system model introduces a form of nonlinearity, specifically a dead-band set at 0.02%. Furthermore, power generation is controlled within a specified generation rate constraint (GRC) to limit the rate of change in generation. Any power generation changes caused by the governor exceeding the prescribed GRC may result in damage to the equipment within the thermal power system.

FPA aims to achieve the minimum value of a user-defined objective function for the specific system model in question. In the context of LFC studies, the objective function is constructed based on the ACE of the system, and it is a combination of frequency of one of the areas and deviation over tie-line in a linear fashion. The ACE for LFC in the present study is considered using distinct performance criteria and set as objective function for FPA: Integral Time Absolute Error (ITAE), Integral Time Multiplied Square Error (ITSE) and Integral of Absolute Error (IAE). The performance index for the nth control areas is as follows:

$$ J_{n} = \int\limits_{0}^{Tsim} {(ACE} ). \, t.{\text{ d}}t $$
(29)

The optimization task at hand is to minimize the error value while ensuring compliance with the following constraints:

$$ K_{Pn}^{\min } \le K_{pn} \le K_{pn}^{\max } $$
(30)
$$ K_{{{\text{in}}}}^{\min } \le K_{{{\text{in}}}} \le K_{{{\text{in}}}}^{\max } $$
(31)
$$ K_{dn}^{\min } \le K_{dn} \le K_{dn}^{\max } $$
(32)

The \(K_{pn} , \, K_{in} \, and \, K_{dn}\) variables represent the parameters linked to the PID control design, with a permissible range spanning from − 5 to 5. Within this research analysis, an innovative FPA is utilized to achieve the optimal PID control gains, accounting for diverse operational scenarios and compared with results of GA-PID [24], PSO-PID [24], and HBFO-PID.

Flower Pollination Algorithm: The main objective of flower pollination is to achieve optimum reproduction of plants with respect to both quantity and fitness. It is a completely novel optimization that utilizes flower pollination features. The envisioned features of the FPA are [24, 25]:

  1. (1)

    Biological and cross-pollination are recognized as global pollination procedures, where pollinators carrying pollen engage in Levy flights.

  2. (2)

    Abiotic and self-pollination are categorized as pollination processes occurring on a smaller scale.

  3. (3)

    The concept of flower constancy pertains to the likelihood of reproduction being influenced by the similarity between the two flowers involved.

  4. (4)

    The switch probability p ∈ [0, 1] controls local as well as global pollination.

Because of closeness to one another along with other considerations including wind, local pollination can account for a large portion of global pollination activity. In fact, each plant might contain numerous flowers, and each flower patch frequently releases millions or billions of pollen gametes. For the sake of clarity, each plant has only one flower, which produces only one pollen gamete. There is no requirement to discriminate between a pollen gamete, a flower, a plant, or a solution to a problem. This simplicity implies that a solution \({y}_{i}\) is identical to a flower and/or a pollen gamete. There are two steps: global pollination and local pollination. In the global pollination step, flower pollens are transported by pollinators like insects, and pollens can travel a considerable distance because insects can frequently fly and travel over significantly greater distances. This assures pollination and reproduction for the fittest, thus we denote the fittest as \({f}^{*}\). The first rule and flower constancy can be stated numerically as

$${Y}_{i}^{t+1}={Y}_{i}^{t}+P\left({Y}_{i}^{t}-{f}^{*}\right)$$
(33)

where \({Y}_{i}^{t}\) is the solution vector of pollen \(i\) at tth iteration, and \({f}^{*}\) represents the optimal solution discovered thus far within all solutions at the current iteration. The parameter \(P\) determines the intensity of pollination, essentially functioning as a step size. Considering that insects can traverse varying distances with different step sizes, we can implement a Levy flight.

$$P\approx \frac{\gamma\Gamma \left(\gamma \right)sin\left(\prod \gamma /2\right)}{\Pi }\frac{1}{{s}^{1+\gamma }}$$
(34)

where \(\Gamma \left(\gamma \right)\) represents the standard gamma function, and this distribution is applicable for large steps \(s\) > 0. The feature 2 and 3 of local pollination can be governed as:

$${Y}_{i}^{t+1}={Y}_{i}^{t}+\varepsilon \left({Y}_{j}^{t}-{Y}_{k}^{t}\right)$$
(35)

where \({Y}_{j}^{t}\) and \({Y}_{k}^{t}\) represent pollen grains from different flowers of the same plant species. This effectively mirrors flower constancy within a specific region. In mathematical terms, if \({Y}_{j}^{t}\) and \({Y}_{k}^{t}\) are from the same species or population, we can select \(\varepsilon \) from a uniform distribution in the range [0, 1] to generate a local random walk. While flower pollination can occur at various scales, both globally and locally, flowers in close proximity or neighboring patches are more likely to receive pollen from nearby flowers than those further away. To simulate this phenomenon, we can employ a switching probability p to transition from widespread global pollination to concentrated local pollination and the complete process of FPA in form of flowchart is given in Fig. 4.

Fig. 4
figure 4

Flowchart of FPA

Full size image

5 Analysis of results from the proposed research study

At first, the output of PFA-PID is evaluated for 0.01 p.u. MW loading condition in area-1, and the performance of FPA-PID is compared with other optimization techniques, i.e., GA-PID [24], PSO-PID [24], HBFO-PID by calculating the gains of PID controller for each optimization technique and by calculating IAE, ITSE, and ITAE values. These values are listed in Table 1. From the results, it is observed that GA-PID offers IAE of 0.02251, ITSE of 0.0001394, and ITAE of 0.1108 which are significantly higher whereas PSO-PID offers IAE of 0.01775, ITSE of 8.87e−05, and ITAE of 0.05393. Under similar load disturbance, HBFO-PID shows IAE of 0.01231, ITSE of 3.641e−05 and ITAE of 0.04882. The error values obtained via FPA-PID are remarkable and significantly outperform these optimization techniques which are IAE of 0.008889, ITSE of 2.07e−05, and ITAE of 0.01839. All error values obtained are appreciable and significantly lesser than other comparable optimization techniques. The error values obtained via PSO-PID are much lesser than GA-PID, however worse than FPA-PID. Further, the computed distinct error values of HBFO-PID are better than GA-PID, PSO-PID under similar loading condition.

Table 1 Calculated gains of PID for thermal–thermal LFC utilizing various optimization techniques
Full size table

The graphical time response of LFC is shown through Fig. 5a–d. It is observed that PSO-PID offer higher overshoot and oscillations in various LFC responses. However, GA-PID and HBFO-PID shows reduced overshoot, still settling time of LFC responses are much higher. On other side, the FPA-PID shows higher first peak, still shows better and settling time of a few seconds with zero steady state error for all LFC responses which are not possible through other optimization techniques. An improvement in LFC responses is seen through FPA-PID under similar loading conditions with integration of solar PV in each area of the thermal–thermal system, and it is seen that solar PV has capability to inject the active power into the system resulting into reduction of first peak, enhanced settling time with zero steady-state error for LFC responses under similar load change conditions.

Fig. 5
figure 5

a–d Impact of PV with FPA-PID for LFC

Full size image

In the next step, a load change of 0.01 p.u. MW loading condition is imposed in area one of thermal–thermal system and the results of FPA-PID are matched with FPA-PID with solar PV and with FPA-PID + solar PV + UPFC installation in the interconnecting tie-line between two areas. The performance is obtained by calculating three distinct error values and by plotting graphical LFCs. The error values for this case in shown through Table 2. It is observed that PV integration in each area has reduced the IAE to 0.005376, ITSE to 7.872e−06, and ITAE to 0.008953 in comparison to error values obtained via FPA-PID only. Further reduction in these values is obtained by interlinking UPFC in series with the tie-line, and it is seen that IAE has further reduced to best possible value of 0.003475, ITSE to 2.6e−06 and ITAE to 0.008813 in comparison to error values obtained with FPA-PID and FPA-PID with PV integration. The LFC responses obtained for FPA-PID, FPA-PID + PV integration, and FPA-PID + PV integration + UPFC is shown through Fig. 6a–d. From the obtained results, it is very clear that FPA-PID has highest overshoots when matched with FPA-PID + PV and FPA-PID + PV + UPFC. The PV integration in each area has reduced the overshoot in time responses of LFC when matched with FPA-PID without PV integration for same LFC model. Further reduction in the first peak is observed when UPFC is installed with PV integration in each area of thermal–thermal system using FPA-PID. In addition, zero steady state error is observed for all LFC responses as well as settling time of LFC responses are appreciable and almost comparable.

Table 2 Computed performance of FPA-PID with PV and FPA-PID with PV + UPFC
Full size table
Fig. 6
figure 6

a–d Impact of FPA-PID + PV + UPFC for LFC

Full size image

The research is extended to see the impact of RFB in area one or simultaneously in both areas of the LFC model with solar PV contribution to improve the frequency, tie-line as well as ACE deviations. The computed values of IAE, ITSE, and ITAE is given in Table 3 for various possible scenarios. The results of Table 3 clearly shows that RFB has operating time of zero seconds and that is why quick enough to reduce the IAE to 0.004924 from 0.005376 whereas ITSE reduces to 7.057e−06 from 7.872e−06 and ITAE reduces finally to 0.006143 from 0.008953, higher error values are observed using FPA-PID with solar PV in each area. The performance of LFC improves largely by considering RFB in both areas simultaneously and RFB in both areas has significantly reduces three distinct error values to best possible lower value, however, it is not advisable to install RFB in each area of LFC due to financial reasons. The graphical comparison of FPA-PID, FPA-PID + PV, FPA-PID + PV + RFB, and FPA-PID + PV + RFB in both areas is shown through Fig. 7a–d. The results show the positive impact of PV and RFB in minimizing LFC deviations, and this combination is fast enough to match the power generation with the current load demand and hence after disturbance, system is coming back to original and reference value within couple of a second. It is also seen that RFB in both areas has reduced the three error values significantly in comparison to RFB installation in area one only. However, this change was very minor and the LFC responses obtained via FPA-PID + PV + RFB is almost like that obtained through FPA-PID + PV + RFB in both of the areas.

Table 3 Computed performance of FPA-PID, FPA-PID + PV, and PFA-PID + PV + RFB in single and in both areas
Full size table
Fig. 7
figure 7

a–d Impact of FPA-PID + PV + RFB for LFC

Full size image

6 Conclusions

In this paper, a novel approach is introduced where a PID controller is effectively fine-tuned using the flower pollination algorithm for the purpose of load frequency control (LFC) within an interconnected thermal–thermal power system. The performance of the designed PID controller is assessed under the influence of a step load disturbance occurring in the area one of the thermal–thermal system. The obtained results unequivocally establish the superiority of the FPA-PID when compared with others available in the literature like GA-PID, PSO-PID, and HBFO-PID. This superiority is demonstrated through the computation of PID gains and the evaluation of various performance metrics, including IAE, ITSE, and ITAE. From this research, several key conclusions can be drawn:

  • The FPA-PID exhibits improved time responses in terms of frequency and tie-line power deviations, with the advantage of reaching a zero steady-state value. This stands in contrast to the results obtained from GA-PID, PSO-PID, and HBFO-PID, especially when considering the nonlinearities associated with LFC.

  • Furthermore, when examining performance metrics, including IAE, ITSE, and ITAE, it becomes evident that GA-PID offers IAE of 0.02251, ITSE of 0.0001394, and ITAE of 0.1108 which are significantly higher, whereas PSO-PID offers IAE of 0.01775, ITSE of 8.87e−05, and ITAE of 0.05393. Under similar load disturbance, HBFO-PID shows IAE of 0.01231, ITSE of 3.641e−05, and ITAE of 0.04882. The error values obtained via FPA-PID are remarkable and significantly outperform other optimization techniques which are IAE of 0.008889, ITSE of 2.07e−05, and ITAE of 0.01839.

  • In the next step, a load change of 0.01 p.u. MW is imposed in area one and the results of FPA-PID are matched with FPA-PID + solar PV and with FPA-PID + solar PV + UPFC. It is observed that PV integration in each area has reduced the IAE to 0.005376, ITSE to 7.872e−06, and ITAE to 0.008953 in comparison to error values obtained via FPA-PID only.

  • Further reduction in these values is obtained by interlinking UPFC in series with the tie-line, and it is seen that IAE has further reduced to best possible value of 0.003475, ITSE to 2.6e−06, and ITAE to 0.008813 in comparison to error values obtained with FPA-PID and FPA-PID with solar PV integration.

  • This integration of solar PV with UPFC has resulted in a decrease in the initial peak values and an enhancement in the settling time of the LFC time responses.

  • The performance of the FPA-PID controller is evaluated in terms of how well it integrates with RFB in one or both regions and how well solar PV is incorporated. The results show that the addition of RFB can improve the dynamic performance of the system by improving the responses of LFC and reducing three particular error values.

  • As this study shows, it is still not as good as the output of FPA-PID + Solar PV + UPFC.