1 Introduction

1.1 Motivation

Distributed energy resources (DERs) such as renewable energy sources, electric vehicles, and energy storage devices are disruptive technologies in modern distribution networks [1]. These technologies are essential for achieving the Paris Agreement’s goals on climate change. However, their technical problems might outweigh the evident environmental benefits when implemented in real power distribution networks. It is well-known that DERs may jeopardize the system’s stability and reliability due to their high variability [2]. A paradigm shift is required to coordinate these active resources and achieve efficient and reliable system operation. The transformation is so significant that a new term has been coined: Active distribution networks, a.k.a. ADNs [3].

Unlike conventional networks, an ADN can operate in grid-connected and islanded modes. In the former, the primary grid can maintain an energy balance. However, the ADN requires adapting the operation according to the energy deficit or surplus in the former. Thus, it can disconnect loads or reduce generation if required. Conventionally, optimization models are tailored for each operation model. Nevertheless, a unified optimization framework may be favorable in this context. Such a framework also requires mathematical guarantees, including global optimum, solution uniqueness, and convergence in a worst-case scenario [4].

1.2 State of the art

Optimization models for operating ADNs are closely related to the optimal power flow (OPF) and the tertiary control in microgrids. The latter is responsible for the optimal operation by defining the set points of generators and battery energy storage systems to minimize an objective function, e.g., cost or power loss [5]. It also includes a set of technical constraints such as power balance, power capacity, and voltage limits [6]. These constraints lead to a complex nonlinear programming (NLP) model [7].

In this context, convex optimization is an effective technique with advantageous properties due to the guarantee of global optimum, uniqueness of the solution, and fast convergence of the numerical algorithm [8]. In addition, the convex-optimization framework makes the model solver-agnostic, meaning that the solution must be equal using any available solver. Unfortunately, many real-world problems are non-convex. In such cases, simplifications or approximations may be necessary to fit the problem into the convex-optimization framework. However, solving a convex relaxation of a non-convex problem can lead to a loss of precision. Hence, as presented in this work, a numerical study is required to evaluate the accuracy of a convex relaxation.

Convex optimization approaches aim to approximate the nonlinear equations from power flow into a convex equivalent, such as conic, quadratic, or affine constraints (see [9] for a complete review of these approximations). Most of the proposals above are designed in grid-connected mode. In this operation mode, the DERs can deliver power without caring about voltage or frequency regulation; nevertheless, under the islanded mode, DERs have to maintain a stable operation considering the deviation of frequency and voltage variables [10]. In that case, it is necessary to integrate the droop controls into the optimization model for the operational problem (OPF) [11, 12]. Furthermore, if the DERs cannot supply all the demand, it is required to match the available generation to the load, thus causing load shedding.

This problem has been studied under different approaches; for example, in the specialized literature, there are several proposals for studying the power flow under islanded operation. Authors in [13] proposed a modified backward-forward sweep algorithm for isolated radial grids, considering droop control. In [14], an approach based on the Newton–Raphson method that considers the effect of the frequency variation on the \(Y_\text {bus}\) was proposed. [15] proposed a Newton-trust region method to solve the power flow in islanded mode, considering droop controls, PV nodes, and PQ nodes. However, most of these proposals are hardly extendable to the OPF problem.

For the OPF case, authors in [16] proposed a mixed-integer nonlinear (MINLP) optimization model based on the branch-flow model equations for the OPF in islanded mode, which is linearized using piecewise functions. This model minimizes inhibited energy consumption, with the main problem of formulating the power flow in terms of the branch-flow model equations, and hence, it is not applicable for meshed grids. Whereas [17] extended the latter study using Monte-Carlo simulation to include the stochastic nature of the load and demand. Additionally, authors in [18] used heuristic methods such as the particle swarm algorithm to solve the OPF. On the other hand, [19] proposed a MINLP problem to operate the grid during the grid-connected mode and also aimed to maintain a secure operation during the grid-islanded mode; the problem with this proposal is the not incorporation of droop controllers (and hence, it does not consider the control over voltage and frequency; moreover, it does not incorporate frequency). [20] proposed a Heuristic approach that uses [14] to operate isolated microgrids while maximizing the total load coverage. Other approaches, such as [21,22,23], proposed an exact formulation in the equivalent nonlinear programming.

Linear programming methods have been proposed to operate islanded microgrids that could be easily extended to ADNs.Footnote 1 In [24], the authors proposed a MINLP BFM problem that was convexified by linearizing complex equations to obtain an affine equivalent; this work considered grid-connected and islanded modes with load shedding. In [25], the authors proposed a linearization of the power flow equations in the equivalent real and imaginary parts; however, the authors did not consider the load shedding and the grid-connected mode. In contrast, the authors in [26] proposed a linear approach based on Wirtinger’s calculus for the tertiary control, although the droop control was not included. It is, therefore, an inexact formulation for islanded operation. Each of the models mentioned above is associated with a single operation mode, requiring a model that can combine different operation modes that may occur in practice.

1.3 Contributions

This paper presents a linear convex approximation for the operation of droop-controlled islanded ADNs, The main benefit of the proposed linear approximation is the ability to transform the nonlinear/non-convex problem into a convex-optimization problem. Hence, it benefits from the convex-optimization framework, which guarantees properties such as the uniqueness of the solution, global optimum, and fast convergence of the state-of-the-art algorithms; however, the final optimization problem still approximates the exact formulation from the original nonlinear programming problem. The main advantages of the proposed framework are summarized below:

  • A simplified approach for a generalized operation of ADNs considering grid-connected and islanded mode with load shedding is proposed. This approach is based on convex optimization.

  • This approach considers the inclusion of the droop-controlled inverter into the operation model, which is more suitable in grids with a high r/x ratio and has been poorly explored in the operation problem.

  • Since this approach is based on bus injection-model (BIM) equations, it could be extended to meshed grids, contrary to formulations based on branch-flow model (BFM) equations.

Table 1 shows a comparison with previous works. These works can be classified into three main approaches: i) using linear approximations, ii) considering the NLP problem, and iii) using meta-heuristics. Furthermore, these approaches consider only the conventional droop control, ignoring that inverse droops are used in grids with a high r/x ratio. Moreover, most authors assumed the grid could operate correctly without considering possible mismatches in the available generation and load. An optimization model that considers the effect of the frequency control and that could be extendable to a meshed grid is required. Hence, this article proposes a generalized model that fills this research gap.

Table 1 Comparison with existing models in the scientific literature
Full size table

1.4 Outline

The rest of the paper is organized as follows: Sect. 2 presents the grid operation modes and the exact mathematical formulation of the optimization problem. Section 3 presents a concise introduction to Wirtinger’s Calculus and the linear approximations to transform the MINLP problem into a MILP problem. Section 4 presents the significant results, and finally, Sect. 5 presents the conclusions and future work.

2 Proposed framework

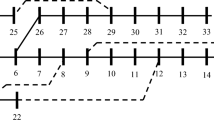
We consider an active distribution network as the one depicted in Fig. 1

Fig. 1
figure 1

Schematic representation of an active distribution network (ADN) on island operation

Full size image

The OPF aims for the optimal operation of the grid. It presents the slowest dynamics of the hierarchical control (usually considered as a stable state); for this reason, in studies related to the Optimal Power Flow (as well as in this study), it is usually depreciated the dynamics of the converters [27]. Furthermore, since the present work only aims for optimal grid operation, that is, the definition of optimal DG operating settings aimed to maintain the ADN frequency and voltage among their normal ranges of operations in islanded mode, we make the following assumptions:

  • Some DGs are grid-forming converters equipped with droop control capable of controlling frequency and voltage. Other sets of DGs (especially photovoltaic units) do not have droop control schemes and only deliver power (these are known as grid-following).

  • The dynamics produced by the disconnection and connection of loads (as well as the dynamics of the connection and disconnection from the main grid) are not modeled. The primary and secondary layers (widely discussed in other research works) are assumed to control such responses.

  • The proposed methodology only aims to optimally adjust power at distributed units to minimize operation costs and ensure operation with frequency and voltages in a feasible range.

For the unified OPF (operation either in grid-connected or grid-islanded mode), the operation modes described in Fig. 2 are considered. These operation modes are explained below:

Fig. 2
figure 2

Proposed operation modes

Full size image

  • Normal operation (grid-connected): Constitutes the system’s regular operation with a slack node that imposes frequency and voltage references. All the variables are within their normal operating range during this operation mode, and the generation meets the demand.

  • Islanded-mode: In this case, the ADN is disconnected from the primary grid; corrective actions are required since the system’s variables deviate from its normal operating range. Generators equipped with droop control (i.e., grid-forming converters) are in charge of correcting frequency and voltage. Two sub-operation modes could happen; the first, known as deficit mode, occurs when the generation does not meet the demand, and some load shedding is required to maintain frequency and voltage values; the second one is known as surplus mode, where the distributed energy resources have enough capacity to maintain stable the grid while feeding the load.

  • Floating-mode: In this operating mode, a slack node imposes frequency and voltage, but there is no power interchange between the main grid and the ADN. It has been defined as an islanded operation since the slack node does not send (or receive) power to the ADN [26]. The droop control model from the islanded mode is more general and could cover this operation.

Implementing an optimization model to deal with all the previously presented operating modes is required since the ADN could go into each mode during a day of operation. The specific demand, the available generation, and the presence of the slack node (which imposes frequency and voltage in the grid) at a particular instant provide the data to define the operating mode. Some DG contains a primary control, as depicted in Fig. 3; in this work, the inverse droop control is used since it has been demonstrated to be more suitable for grids with high r/x ratio such as the ADNs [11].

Fig. 3
figure 3

Type of droop control schemes (conventional above, and inverse below)

Full size image

The optimal operation of the active distribution network is mathematically modeled via the MINLP formulation described in (1)–(22). The objective function seeks to reduce the overall costs of operation; the first term refers to the costs of importing energy from the main grid, and the second term refers to the costs of generation of DGs.Footnote 2 Finally, the third term refers to the grid’s load-shedding costs.

Obj. function:

$$\begin{aligned} \min f_1 + f_2 + f_3 \end{aligned}$$
(1)

with

$$\begin{aligned} f_1&= \sum _{\begin{array}{c} t=1 \\ t \in {\mathcal {T}} \end{array}} c^s p_t^s (1-\alpha _t^s) \end{aligned}$$
(2)
$$\begin{aligned} f_2&= \sum _{\begin{array}{c} t=1 \\ t \in {\mathcal {T}} \end{array}} \sum _{\begin{array}{c} k=1 \\ k \in {\mathcal {G}} \end{array}}^n c_{k,t}^g p_{k,t}^g \end{aligned}$$
(3)
$$\begin{aligned} f_3&= \sum _{\begin{array}{c} t=1 \\ t \in {\mathcal {T}} \end{array}} \sum _{\begin{array}{c} k=1 \\ k\in {\mathcal {L}} \end{array}}^n c_{k,t}^d p_{k,t}^d(1-\alpha _{k,t}^d) \end{aligned}$$
(4)

Subject to:

$$\begin{aligned}{} & {} \begin{aligned} p_t^s \alpha _t^s +p^g_{k,t}-p^c_{k,t}+p^{sol}_k-(p_k^d-jq_k^d)\alpha _{k,t}^d + \\ +p^{dc}_{k,t} + j(-q_{k}^{cap}-q^g_{k,t})=\sum _{m\in {\mathcal {N}}}{\textbf{y}}_{km}{\textbf{v}}_k^*{\textbf{v}}_m \end{aligned} \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \Vert \mathbf {v_{k,t}} - 1 \Vert \ \le \delta \end{aligned}$$
(6)
$$\begin{aligned}{} & {} p_k^\textrm{min} \le p_{k,t}^g \le p_k^\textrm{max} \end{aligned}$$
(7)
$$\begin{aligned}{} & {} q_k^\textrm{min} \le q_{k,t}^g \le q_k^\textrm{max} \end{aligned}$$
(8)
$$\begin{aligned}{} & {} p_s^\textrm{min} \le p_{t}^s \le p_s^\textrm{max} \end{aligned}$$
(9)
$$\begin{aligned}{} & {} q_s^\textrm{min} \le q_{t}^s \le q_s^\textrm{max} \end{aligned}$$
(10)
$$\begin{aligned}{} & {} 0 \le pv_{k,t} \le pv^\textrm{max}_{k,t} \end{aligned}$$
(11)
$$\begin{aligned}{} & {} (x_t) pb^{\text {min}}\le pb_{k,t}^c \le pb^{\text {max}} (x_t) \end{aligned}$$
(12)
$$\begin{aligned}{} & {} (1-x_t) pb^{\text {min}}\le pb_{k,t}^{dc} \le pb^{\text {max}} (1-x_t) \end{aligned}$$
(13)
$$\begin{aligned}{} & {} E^{\text {min}}_{k} \le E_{k,t}\le E^{\text {max}}_k \end{aligned}$$
(14)
$$\begin{aligned}{} & {} 1-\Delta \omega \le \omega _t \ \le 1+\Delta \omega \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \omega _{k,t}-\omega _0 =K_{q,k}(q_{k,t}^g-q_k^{\text {max}}) \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \Vert \mathbf {v_k}\Vert -{\bar{u}}_k =-K_{p,k} (p_{k,t}^g-p_k^{\text {max}}) \end{aligned}$$
(17)
$$\begin{aligned}{} & {} E_{k,t}^b= E_{k,t-1}^b-\eta ^c pb^c_{k,t}\Delta _t - \frac{1}{\eta ^{dc}}pb^{dc}_{k,t} \end{aligned}$$
(18)
$$\begin{aligned}{} & {} E_{k,t=0} = E^{bf}_{k} \end{aligned}$$
(19)
$$\begin{aligned}{} & {} E_{k,t=24} = E^{bo}_{k} \end{aligned}$$
(20)
$$\begin{aligned}{} & {} \omega _{CI}=\frac{\sum _{k\in {\mathcal {N}}} K_q^{-1}\omega _k}{\sum _{k\in {\mathcal {N}}} K_q^{-1}} \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \alpha _s, \alpha _d, x_t \in \{0,1\} \end{aligned}$$
(22)

In this optimization problem, complex variables are represented using bold letters (such as \(\mathbf {v_k}\), which symbolizes the complex voltage at the node k). The optimization problem is also decomposed into rectangular variables, where the \(j = \sqrt{-1}\) is the imaginary operator. The remaining variables are real-valued. The sets of constraints are described as follows: (5) represents the power balance in each node of the system, where \(p_t^s\) represents the power injection of the slack, \(p_t^g\) power injection of the DG, \(p_t^c\) charging power of BESS, \(p_t^{dc}\) discharging power of BESS \(p_t^{sol}\) and power produced by the PV units. \(p_k^d\) and \(q_k^d\) correspond to the active and reactive power demanded, and \(\alpha _d\) is the binary variable associated with the connection or disconnection, \(q_k^{cap}\) and \(q_k^g\) correspond to the reactive power injection due to the capacitors and the DGs. Finally, the left-hand side of the equation corresponds to the power flow (which is nonlinear due to the bilinear nature of the equation).

Equation (6) represents the maximum voltage deviation \(\delta \) at each moment in the grid, which is set to 10% of its nominal voltage. (78910)–(11) represents the maximum active and reactive power from the DGs, slack node, and the maximum power of the photovoltaic unit available; it is essential to remark that PV units act as a constant power source with unitary factor. Equations (12)–(13) represent the maximum power of charge and discharge of the Battery Energy Storage system; it is essential to emphasize the presence of the binary variable \(x_t\) which indicates if a given BESS is charging or discharging for the time t, (14) indicates the maximum and minimum energy capacity of the BESS, (15) illustrates the maximum variation of the grid frequency (which is assumed to be \(\pm \Delta 0.1\) Hz). Equation (16) and (17) are the droop controls of each DG unit, where \(\omega _{k,t}\) is the frequency response for each DG unit, however, in the steady state, all DG units reach the same frequency and hence, the concept of the centroid is introduced to unify the frequency (see equation (21)). This centroid has been widely employed in the secondary layer of the hierarchical control [28], and studies related to small signal analysis for the first layer of control [29], it is introduced the concept for a study related to the tertiary layer of control. As discussed, inverse droop controllers are used since they have been demonstrated to be more suitable for grids with high r/x ratios (such as ADNs or microgrids). Finally, equations (18)–(20) represent the BESS’s state of charge, which depends on the previous state and the charge, the discharging process multiplied by their corresponding efficiency, and the initial and final state of charge.

As described above, the problem corresponds to a MINLP due to the binary variables associated with the load disconnection and the operation states of the BESS.

3 Convex approximation

This section presents the convex approximations employed for the MINLP problem described in Sect. 2, where the main idea is to transform it into a convex-optimization problem. In general, equality constraints must be affine to be convex, and as described before, Eq. (5) is nonlinear due to its bilinear nature; furthermore, the function is non-holomorphic since it does not meet the Cauchy–Riemann equations [26, 30] and a conventional derivative could not be handled. However, deriving these unique functions and making linear approximations using the Wirtinger Calculus is possible.

3.1 Wirtinger calculus

Wirtinger Calculus allows calculating the derivative of non-holomorphic functions. Given a complex variable \({\textbf{z}}=x+jy\) and a complex function \(f({\textbf{z}})=u+jv\), the derivative of f respect to the complex variable z and the conjugated complex variable \(z^*\) is obtained as (23) and (24).

$$\begin{aligned}{} & {} \frac{\hat{\partial f}}{\partial z}=\frac{1}{2}\left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) +\frac{j}{2}\left( \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y} \right) \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \frac{\hat{\partial f}}{\partial z^*}=\frac{1}{2}\left( \frac{\partial u}{\partial x} - \frac{\partial v}{\partial y} \right) +\frac{j}{2}\left( \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y} \right) \end{aligned}$$
(24)

Furthermore, Wirtinger calculus allows making linear approximations of f(z) around an operational point as follows:

$$\begin{aligned} f(z)= f(z_0)+\frac{\hat{\partial f}}{\partial z}\Delta z + \frac{\hat{\partial f}}{\partial z^*}\Delta z^* \end{aligned}$$
(25)

The previous formulation can be employed in the following subsection to transform the problem into a MILP problem.

3.1.1 Linear approximation

As described in the optimization problem, the first source of nonconvexity is the product of voltages in equation (5). This equation has the following structure.

$$\begin{aligned} f(v,v*)=vv^* \end{aligned}$$
(26)

And could be approximated employing equation (25) as follows:

$$\begin{aligned} f(v,v^*) \approx v_ov_o^* + v_o^*\Delta v + v_o \Delta v^* \end{aligned}$$
(27)

Which transforms the nonlinear constraint as an equivalent affine described below:

$$\begin{aligned} f(v,v^*) \approx -1 +v + v^* \end{aligned}$$
(28)

It is important to remark that all variables are treated per unity. Finally, the constraint related to the voltage magnitude presented in the droop scheme has to be approximated; this constraint has the following structure:

$$\begin{aligned} h(v,v*)=v_m=\Vert v\Vert \end{aligned}$$
(29)

Since v is a complex variable, this equation could be rewritten in terms of a product as follows:

$$\begin{aligned} h(v,v*)=\sqrt{vv^*} \end{aligned}$$
(30)

And could be approximated employing (25):

$$\begin{aligned} h(v,v*)\approx (v_ov_o^*)^{1/2}+\frac{v_o^*}{2(v_ov_o^*)^{1/2}}\Delta v +\frac{v_o}{2(v_ov_o^*)^{1/2}}\Delta v^* \end{aligned}$$
(31)

Which conduces to:

$$\begin{aligned} h(v,v*)\approx \frac{v+v^*}{2} \end{aligned}$$
(32)

Finally, taking into account the concept of the centroid described in constraint (21) and the droop control associated with the frequency (16), it is straightforward to derive the following modifications:

$$\begin{aligned}{} & {} \omega _o-\omega _{CI} =K_{q,k}(q_{k,t}^g-q_k^{\text {max}}) \end{aligned}$$
(33)
$$\begin{aligned}{} & {} \omega _{CI} = \frac{\sum _{k\in {\mathcal {N}}}q_k^{\text {max}}-q_k}{\sum _{k\in {\mathcal {N}}} K_q^{-1}} +\omega _o \end{aligned}$$
(34)

Considering the linear approximations and the modification of equations associated with the droop control and the frequency centroid, it is possible to deduce that the problem has been transformed into a MILP equivalent. The linear approximations developed during in this paper are synthesized in Table 2

Table 2 Linear approximations
Full size table

3.1.2 Power loss

The costs of power losses can be included in the optimization as presented in (35), where the power loss costs are defined as \(c_{km}\) and \({\mathcal {L}}\) as the set of lines.

$$\begin{aligned} P_l=\sum _{km \in {\mathcal {L}}} c_{km}r_{km}\mathbf {\Vert (v_k-v_m)y_{km}\Vert ^2} \end{aligned}$$
(35)

The expression (35) is a convex-quadratic equation that can be easily included in the proposed framework, maintaining the geometrical properties of the model (e.g., global optimum). However, a quadratic objective function transforms the problem into a MIQP (Mixed Integer Quadratic Programming) or a MISOC (Mixed Integer Second-Order Cone Optimization) due to the presence of both quadratic and binary variables. Hence, adding the power losses may increase the computational complexity, making it unsuitable for real-time operation. This aspect must be evaluated in practice, considering a trade-off between a power loss and the time calculation. The main objective of service continuity is keeping operative limits within a normal range (i.e., an accepted voltage deviation).

3.2 Tested network

The 33 nodes benchmark described in [31] is the network employed for testing the generic optimal power flow, and is illustrated in Fig. 4. This network has a rated voltage of 12.66 kV and a total rated load of 3.715 MW. To effectuate the optimal operation for a given day, the following modifications were carried: BESS, DG units, and PV information is supplied in Tables 3, 4 and 5, respectively. This test system was designed to evaluate the case in which BESS system are placed together with PV (i.e., nodes 21 and 24) and the case in which PV is directly connected to the grid without BESS. Other distribution generators, such as Diesel or Biomass placed in nodes 6, 18, and 33, lack BESS since these technologies are usually integrated without energy storage. The optimal placement of these BESS is an important planning problem beyond the objectives of this paper.

Furthermore, Fig. 5 represents the daily load and PV variations. Both Daily load and PV capacity variation have been obtained from [32], which shows data obtained from Empresas Publicas de Medellín, a local network operator in Colombia [33], and for the PV capacity by the National Aeronautics and Space Administration’s (NASA) database [34]. Since the considered ADN is urban, customers are concentrated, then a commonly accepted approximation is to employ a normalized PV capacity variation. Since the only measure available from the grid operator is the power at the beginning of the distribution feeder, all customers are characterized by the same load behavior. Results for the average curve are presented first for the sake of reproducibility and replicability of the model. Non-coincident maximum loads are included in the model by random deviation from this normalized curve, as given in Sect. 4.6.

Fig. 4
figure 4

33 node test system modified

Full size image
Fig. 5
figure 5

Normalized daily load and photovoltaic generation

Full size image
Table 3 BESS information
Full size table
Table 4 DGs information
Full size table
Table 5 PV units data
Full size table

The CIGRE MV benchmark described in [35] is used for the meshed case. This benchmark of 4.16 kV of nominal voltage contains 11 nodes; to include DGs, the following modifications were performed: since the load in the first node is roughly 2.2 times the sum of all the loads of the grid (without taking into account the first node), all loads (except those of first node) are multiplied by 5 to have more consistently (homogeneous) loads. The BESS, DG units, and PV information are given in Tables 6, 7 and 8, respectively. For the sake of simplicity, the load variation is the same as Fig. 5.

Table 6 BESS information
Full size table
Table 7 DGs information
Full size table
Table 8 PV units data
Full size table

For both benchmarks, the \(K_p\) and \(K_q\) constants of the DG units are calculated by modifying the equations presented in [16] as follows:

$$\begin{aligned} K_p= & {} \frac{\Delta v}{2p^{\text {max}}} \end{aligned}$$
(36)
$$\begin{aligned} K_q= & {} \frac{\Delta \omega }{q^{\text {max}}} \end{aligned}$$
(37)

The maximum deviation of the frequency allowed is \(\Delta \omega = 0.1\) Hz, and the maximum deviation of the voltage allowed is 10% of its nominal value (which depends on the test system).

4 Results

This section exposes the results of applying the Optimal power flow discussed above. The simulations were performed employing CvxPy [36], a software specialized in convex optimization, and were solved with Gurobi [37], a specialized convex solver. The versatility of the optimization model is demonstrated by the study cases next presented.

  • Grid connected during the day of operation.

  • Grid islanded during the day of operation.

    • Optimal Operation without BESS or PVs

    • Optimal Operation with BESS and PVs

  • Generic operation with two disconnections from the main grid (11:00 h - 13:00 h) and (18:00 h - 21:00 h)

4.1 Connected mode

For this operation mode, the main grid is always connected; hence, \(\alpha =1\) and the DGs operate without droop schemes, delivering their available power without restrictions. The dispatch of the DGs and BESS is illustrated in Fig. 6

Fig. 6
figure 6

Load and generation behavior while the slack node is connected to the main grid

Full size image

Since the fundamental objective is to reduce the total operation costs, DGs consistently deliver power because it is cheaper than importing it from the main grid. However, when the load demanded is much higher than the available DG capacity, some energy is imported from the main grid (18:00–22:00 h); furthermore, during this time, the BESS also delivers power since this does not have operation cost (since they are assumed to be ideal), and during these hours, the energy cost is much expensive. As observed in Fig. 7, the batteries retain the charge until 18:00 h (to discharge), where the energy cost is the highest during the horizon day. During this operating mode, it is not required to perform load shedding, and all the loads are supplied at the minimum cost of generation.

Fig. 7
figure 7

Energy of BESS during Grid Connected mode

Full size image

PV units act as a constant power source with a unity factor, delivering all their available power in all the operation modes. This happens since they do not count with droop schemes, and their representation in the charts is not depicted to make them legible (also due to their low contribution compared to the DGs).

4.2 Islanded mode

During grid islanding, there is no slack node, and some DGs require ceasing the constant generation to control and maintain stable frequency and voltage variables via droop schemes. In this case, it is also necessary to make load shedding and supply the maximum energy (since load shedding is more expensive than a generation). Any load may be disconnected to obtain a feasible operation in island mode. However, disconnection costs are different in each node; then, the model never disconnected some loads due to their high cost. As observed in Fig. 8, DGs and BESS attempt to supply the maximum amount of power; however, during some hours (notoriously rush hours 10:00–2:00 and 18:00–21:00), it is impossible to supply all the load, and some shedding \(p^{sd}\) (black dashed line) is required to maintain stable the grid. The DGs cease the constant power supply to control and maintain stable grid variables such as voltage and frequency; therefore, some DGs do not deliver their maximum available capacity.

Fig. 8
figure 8

Load and generation behavior while the slack node is disconnected from the main grid

Full size image

Furthermore, the BESS in Fig. 9 seeks to reduce the load shedding, especially when load disconnection supposes more cost (as discussed in previous sections). This situation is notorious since, for example, during some hours when the BESS are charging or in 100% of their capability (9:00–11:00 h), there is no supply of energy, holding until the first peak of demand (around 12:00 h), reducing its impact, and recharging once again in order to discharge in the final peak of consumption (17:00–21:00 h).

Fig. 9
figure 9

Energy of BESS during Grid-Islanded Mode

Full size image

The dashed gray line in Fig. 8 corresponds to the results obtained for the load shedding when no BESS are added. There is an increase in the amount of load shedding during the operation horizon, especially in peak hours, which is reflected in the operation costs (see Table 9); in this order, the integration of BESS for the operation of grid islanded reduces considerable the amount of load shedding and consequently the costs of operation. It is important to remark that the BESS does not contribute to the frequency control since it is controlled via the reactive power of DGs, and hence, the deviation remains fundamentally the same (see Fig. 12).

4.3 Generic operation

Figure 10 shows the optimal dispatch for the generic operation. As stated before, there are two periods when the grid is disconnected from the slack node (11:00–13:00 and 18:00–21:00, denoted for the semitransparent red box) during rush hours (considerably more expensive than the other hours). These periods were selected to obtain worst-case scenarios. The first case corresponds to the middle day when the energy production is higher than the demand, generating a surplus scenario. The second case corresponds to the peak load where the energy production is lower than the demand, generating a deficit scenario. As could be noted, the DGs supply most of the load during grid-connected mode (since the cost is cheaper than importing from the main grid) while charging the BESS during the first hours to discharge during the first disconnection; however, during the second disconnection the BESS and DGs are not able to provide all the load, and some shedding is required to maintain stable the grid.

Fig. 10
figure 10

Load and generation behavior while the slack node is disconnected, 11:00–13:00 and 18:00–21:00

Full size image

From Fig. 11, it is possible to note that BESS can supply all the load during the first disconnection since they may allow a depth discharge and can be once again charged thanks to the reconnection of the main grid. As observed in the grid-islanded case, this situation could not be possible in complete disconnection. Finally, BESS are fully discharged during the last peak of load to alleviate disconnection costs during these hours.

Fig. 11
figure 11

Energy of BESS during generic mode

Full size image

Figure 12 depicts the frequency response for the four studied cases. It is possible to observe that for islanded mode and the generic mode, the frequency remains between the stable limit of operation (\(\pm \Delta 0.1\)). Hence, the proposed optimization model ensures stable operation during the operation horizon and minimizes operation costs. Additionally, the frequency response during grid-islanded operating modes, with and without BESS, is almost the same; this situation is mainly due to the droop control type, where the reactive power of the DGs controls the frequency. Furthermore, Fig. 13 illustrates the voltages at the slack node for the three types of operation and Moreover Fig. 14 illustrates the voltage behavior at node 18 (which contains a DG); it is important to observe how during Grid-Islanded and Generic mode (specifically during the time of disconnection) the voltage is around 1 p.u. since during these times the voltage is regulated through inverse voltage droop control. Additionally, among disconnection periods, there is an increase in the nodal voltage (mainly because voltages are no longer regulated); as discussed for the frequency, both remain within the stable range of operation.

Fig. 12
figure 12

Frequency response during different operation schemes

Full size image
Fig. 13
figure 13

Voltage variation at the slack node

Full size image
Fig. 14
figure 14

Voltage variation at the 18 node

Full size image

Finally, the operating costs are given in Table 9. It is possible to observe how working during GI-mode is more expensive than working during GC-mode, due to the load shedding and how including BESS reduces the total operating costs.

Table 9 Cost for a daily operation of the different modes
Full size table

4.4 Extension to meshed grids

As discussed before, one of the main advantages of this proposal is the ability to be implemented in meshed grids. Figure 15 illustrates the power dispatch for the CIGRE test system discussed before. For the sake of simplicity, this case only considers the islanded operation (\(\alpha =1\)); as can be observed, this case needs even more disconnection to maintain the stable grid (due to the capacity of DGs and the amount of load demanded). Furthermore, contrary to the 33 case studies, after 8:00 h DGs are always at their maximum capacity, and BESS attempts to reduce the load disconnection from the peaks of demand (since it is expensive to disconnect during these hours).

Fig. 15
figure 15

Load and generation behavior while the slack node is connected to the main grid for CIGRE Test System

Full size image

Finally, Fig. 16 represents the frequency response for the CIGRE benchmark. As stated, there is not a great frequency deviation (the frequency is among its normal range of operation); this is thanks to the significant amount of load shedding presented in Fig. 15 (notice that when a load is disconnected, the reactive part is disconnected as well), which allows controlling the frequency properly by the reactive power of the DGs.

Fig. 16
figure 16

Frequency response for CIGRE meshed grid

Full size image

4.5 Power loss

Power losses may be included in the model as presented in (35). Results are presented in Table 10. According to the results, adding power loss into the objective function is reasonable for this test system, considering an increase in the time calculation. Hence, power loss can be included in the optimization model, maintaining convexity in the objective function; however, the calculation time increases since the model is transformed into a mixed-integer convex-quadratic optimization problem.

Table 10 Effect of including power loss \(p_l\) into the objective function
Full size table

4.6 Non-coincident loads and non-coincident generation

Previous results were obtained using normalized curves from load variation and photovoltaic generation. Although these normalized curves were taken from real data, it is unrealistic to consider all loads are coincident. To represent a more realistic picture of an active distribution network, industrial and commercial profiles were taken from [35] and are depicted in Fig. 17. Moreover, all loads were modified by adding normally distributed random noise with mean = 1 and standard deviation 0.1. Figure 17 shows the results for each node in this case (the same procedure was done for the PV capacity)

Fig. 17
figure 17

Type of loads

Full size image
Fig. 18
figure 18

Load profiles

Full size image

It is assumed that nodes 31, 19, and 23 are industrial loads; nodes 4, 12, 20, and 7 are commercial, and the rest are assumed to be residential. By employing these load profiles, the power dispatch is depicted in Fig. 18, where the load profile is slightly flatter compared to the normalized case due to industrial and commercial loads. Moreover, from an algorithm point of view, using load profile data for each node (or load) is irrelevant since the algorithm could handle these variations without problems; as stated before, the main reason for employing normalized curves was simplicity.

Fig. 19
figure 19

Load and generation behavior while the slack node is disconnected from the main grid

Full size image

On the other hand, when the power generation is not enough (energy deficit), load shedding is required; by comparing the previous figure with Fig. 8, it can be observed that the load shedding is higher, mainly due to two facts: (a) There is an increase in load demand, (b) due to constraints in operation. Comparing power generation at node 6 from Figs. 8 and 19, it could be observed that in the previous case, the generation was 1 MW from 8:00 a.m. Nevertheless, in a superavit situation, the system should do curtailment to maintain voltage between the normal range of operations.

5 Conclusions

This paper presented an optimization model for the optimal operation of active distribution networks under different operation modes. The model worked in grid-connected, grid-islanded, and generic modes (where the first two modes could be presented). As observed from the results, the model seeks firstly to maintain variables such as frequency and voltage among their stable operating range while reducing the total operating cost. The previous is reached by load shedding or power curtailment in islanded mode for energy deficit and surplus, respectively. Some distributed generators require working as grid forming to maintain grid stability. This demonstrates that the inverse droop controllers are suitable for controlling frequency and voltage for grids with a high r/x ratio (a common situation in power distribution networks). Furthermore, as discussed above, including battery energy storage systems reduces the noticeable load disconnected during peak demand, minimizing costs since those batteries (which are assumed to have costs of operation negligible) charge along the day and discharge during peak load to avoid load shedding, moreover, by comparing all study cases, it could be concluded that employing the generic operation is less expensive than operating the grid in fully islanded mode. DG’s were added into not only locations with bad voltage regulation but also some locations with good voltage profiles (such as node 6); as observed, certain DGs, to maintain voltage around 1 per unity perform load shedding, whereas some other DGs deliver all its available capacity to supply the maximum amount of load. Power loss can be included in the optimization model, maintaining convexity in the objective function. However, the time of calculation increases since the model is transformed into a mixed-integer convex-quadratic optimization problem. Further research includes implementing Hardware and communications in the loop, including unbalanced operation. This type of study may identify potential problems in introducing the proposed framework, including loss of communication and latencies. Stability constraints can be added to the model to obtain a better picture of the dynamic behavior of the active distribution network.