A self-oscillating series-none inductive power transfer system using a matrix converter

Abstract

Power density and conversion efficiency are two critical parameters of inductive power transfer (IPT) systems. These parameters are related to the number of components in the power conversion circuit as well as its modulation method. The combination of Midpoint Matrix Converter and pulse-density modulation (PDM) has a potential to improve these parameters, due to a low number of semiconductor switches utilization as well as constant efficiency at the maximum output and partial load operations . In this context, this paper analyzes the performance of a three-phase to single-phase Midpoint Matrix Converter using a Free-wheeling Switch (MMCFS) and the PDM in a high coupling factor series-none IPT application. This converter utilizes on–off control to manage power transfer, which automatically tracks the load resonant frequency. Dynamic and steady-state mathematical equations were derived to represent the converter and the IPT system characteristics. These equations show a relationship between the link efficiency, the link gain, the damping ratio and the coupling factor. A kick-start method and a multistep switching strategy were developed to start and operate the converter, respectively. Additionally, a 150 W MMCFS-based IPT prototype was built to verify the improvement, which demonstrated an efficiency of around 80% at the maximum output and partial load operations.

1 Introduction

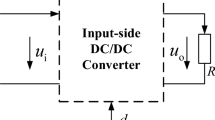
Inductive power transfer (IPT) is one approach for powering electric loads without any physical contact. IPT has been implemented in many fields, including land and sea transportations, robotics, and consumer electronics. IPT has many advantages in terms of reliability, safety and mobility. It has been explained that the absence of a direct contact between the source and the load decreases both the need for maintenance and the likelihood of electric spark, as well as provides freedom of movement during power transfer for the pickup circuit. Furthermore, in a high-power charging application, IPT can avoid lifting a heavy power cable [1,2,3,4,5]. A typical unidirectional or bidirectional IPT system connected to a three-phase AC power source is shown in Fig. 1. On the primary side, the power converter produces a single-phase AC voltage with a higher frequency than the AC source. Both the primary and secondary sides are magnetically coupled through $L_\textrm{p}$ and $L_\textrm{s}$ coils connected to their compensation circuits. These compensations are used to optimize power transfer. To improve power delivery at a partial load, the secondary-side power converter can be used for impedance matching. Additionally, an energy storage element typically functions as the system load [1,2,3,4,5,6,7,8,9].

Fig. 1

The layout of typical unidirectional or bidirectional IPT system

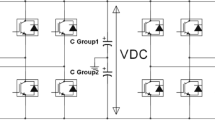
In the series–series compensation IPT system, the primary-side power converter in Fig. 1 usually consists of two conversion stages, namely rectification and inversion, as can be seen from Fig. 2. Figure 2a shows the two-level voltage back-to-back topology having these two conversion capabilities. The circuit is constructed from diodes and IGBTs, in which the three-phase and single-phase sides are connected through an intermediate capacitor. Since both sides utilize active switches, the role of rectification and inversion can be altered. Thus, this back-to-back topology possesses bidirectional power transfer capability. If only unidirectional power transfer is needed, a passive rectification with the diode bridge can replace the active switches on the three-phase side, as can be seen in Fig. 2b. In this case, the power can only be transferred from the three-phase to the single-phase side [7, 10, 11].

Fig. 2

Typical three-phase to single-phase AC–AC power converter topology. a Two-level voltage back-to-back topology. b Rectifier–inverter topology

The complexity of the primary-side power converter can be reduced by replacing the two-stage configuration with a matrix topology. This replacement can lead to an overall efficiency improvement and lower production cost [10,11,12,13,14]. The authors in [10, 15] proposed a Midpoint Matrix Converter using a Free-wheeling Switch (MMCFS), where the former uses a phase-shift modulation (PSM). The combination of MMCFS and PSM generally has a better overall efficiency than the unidirectional rectifier–inverter topology in an IPT application. However, the efficiency decreases significantly at a partial load due to switching loss [10]. This loss has also been observed in power converters utilizing the bridge topology [9, 16, 17]. Moreover, it is difficult to implement a variable-frequency controller that tracks the resonant frequency of the series–series IPT system in a high-power and high coupling factor setting (e.g., an electric bus charger), since this system exhibits frequency split behavior that makes the controller unstable [2, 8, 10, 18, 19]. In an attempt to maintain a constant efficiency of the MMCFS-based IPT system at the maximum output and partial load operations, this paper proposes a high coupling factor series-none IPT system utilizing the MMCFS with pulse-density modulation (PDM) on the primary side.

This paper is organized as follows. The MMCFS-based series-none IPT system (MMCFS-IPT) and its fundamental working principle are explained in Sect. 2. Section 3 derives steady-state and dynamic equations of the IPT system. Practical methods for starting and operating the converter as well as the experimental setup configuration of the MMCFS-IPT are described in Sect. 4. Section 5 elaborates the experimental waveforms and compares theoretical calculations with experimental data. Finally, the conclusions drawn from the paper are given in the last section.

2 System description

A circuit diagram of the MMCFS-IPT is given in Fig. 3. The primary side consists of a three-phase voltage source connected to a LC circuit ($L_\textrm{p}$ and $C_\textrm{p}$), through a switching network of the converter. The network consists of bidirectional switches constructed by two discrete IGBTs, which are {$\textrm{S}_\textrm{ap}$, $\textrm{S}_\textrm{an}$}, {$\textrm{S}_\textrm{bp}$, $\textrm{S}_\textrm{bn}$}, {$\textrm{S}_\textrm{cp}$, $\textrm{S}_\textrm{cn}$} and {$\textrm{S}_\textrm{dp}$, $\textrm{S}_\textrm{dn}$}. Three of these switches are connected in series with their corresponding input phase $v_\textrm{a}(t)$, $v_\textrm{b}(t)$, or $v_\textrm{c}(t)$. These switches also form a common connection to the inductance L. The fourth pair (i.e., {$\textrm{S}_\textrm{dp}$, $\textrm{S}_\textrm{dn}$}) provides free-wheeling current commutations. The common emitter configuration was selected for the bidirectional switch, since it can reduce the number of isolated power supplies of the gate drivers. Additionally, this configuration allows the implementation of $v_{CE}$ monitoring system for fault detection. On the secondary side, a coil $L_\textrm{s}$ is connected to a pickup circuit. The circuit usually contains a rectifier, and a power converter to maximize power transfer efficiency to the energy storage $v_\textrm{o}(t)$ [13, 14, 19, 20]. Although each switch is represented by an IGBT, a MOSFET can alternatively be used for this purpose.

Fig. 3

The schematic of the three-phase to single-phase MMCFS-IPT

For a low coupling IPT system, the transfer efficiency of the series-none configuration is poorer than the series–series due to the absence of compensation capacitor on the secondary side. However, in a high quality and high coupling factor IPT system, the efficiency difference is not significant. Thus, removing the secondary-side compensation capacitor can reduce the number of passive components and increase the overall power density of the system [1, 18, 19, 21, 22].

2.1 Current commutation

Injection and free-wheeling oscillation (FWO) are two types of commutation used on the primary side, which were previously introduced in [3, 23]. Both methods are depicted in Figs. 4 and 5, respectively. Injection is performed by connecting one of the input phases to the primary LC circuit, through their respective bidirectional switch. In this mode, the current $i_\textrm{p}(t)$ can flow either from or to the AC source. Injection is used to increase the amplitude of $i_\textrm{p}(t)$. Although Fig. 4 only shows injections using Phase A, the same principles are also valid for Phase B and Phase C. In contrast, FWO disconnects the LC circuit from the input three-phase voltage. It is performed by operating only $\textrm{S}_\textrm{dn}$ and $\textrm{S}_\textrm{dp}$. FWO is utilized to reduce the amplitude of $i_\textrm{p}(t)$ [13, 14].

Fig. 4

Injection modes of MMCFS using Phase A. a Positive injection. b Negative injection

Fig. 5

FWO modes of MMCFS. a Positive FWO. b Negative FWO

2.2 Modulation strategy

A modulation strategy based on the commutations given in Sect. 2.1 is used to operate the MMCFS. This modulation refers to the non-successive injection modulation (NIM) which is illustrated in Fig. 6, in which $v_\textrm{p}(t)$ and $i_\textrm{p}(t)$ are the voltage and current over the primary LC circuit, respectively, and $V_\textrm{amp}$ is the amplitude of the input three-phase voltage. For clarity, the $v_\textrm{p}(t)$ waveform is drawn with bold lines and its switching duration is exaggerated. This NIM utilizes the maximum absolute value of the three-phase source, which can be expressed as

$$\begin{aligned} \text {Max}(v) = \text {Max}(|v_{\text {a}}(t)|, |v_{\text {b}}(t)|, |v_{\text {c}}(t)|). \end{aligned}$$

(1)

Within this $\textrm{Max}(v)$ region, the injections and FWOs are performed sequentially at the zero-crossings of the $i_\textrm{p}(t)$ to reduce switching loss. Consequently, the switching frequency is equivalent to the converter load resonant frequency, and the converter is therefore self-oscillating. A more detailed illustration is shown in Fig. 7, in which the region of $\textrm{Max}(v) = v_\textrm{c}(t)$ is highlighted and the $v_\textrm{p}(t)$ is denoted by bars with dashed stripes. From the switching and current signals, it can be deduced that injections are performed by $s_\textrm{cn}(t)$, while FWOs are applied by $s_\textrm{dn}(t)$ and $s_\textrm{dp}(t)$. These commutations are forming the $v_\textrm{p}(t)$ over the primary LC circuit. Power flow from the primary to the secondary side can be adjusted by varying the ratio between the two commutations [1, 13, 14]. Since the modulation changes the density of injection with respect to FWO, it can be considered a type of PDM [9].

Fig. 6

NIM of the MMCFS performed on the three-phase input voltage

Fig. 7

NIM during $\textrm{Max}(v)$ equals $v_\textrm{a}(t)$ and $v_\textrm{c}(t)$

3 IPT circuit model

Steady-state and dynamic equations for the IPT system can be derived from equivalent circuit models given in Fig. 8. For the purpose of simplification, the MMCFS is replaced by an equivalent sinusoidal input $v_\textrm{eq}(t)$, while the secondary pickup circuit and $v_\textrm{o}(t)$ (see Fig. 3) are represented by a rectifier connected to a smoothing capacitor $C_\textrm{L}$ and a resistive load $R_\textrm{L}$ (marked by a gray area). The variables $R_\textrm{p}$ and $R_\textrm{s}$ denote the parasitic resistance of $L_\textrm{p}$ and $L_\textrm{s}$, respectively. The secondary side can be further simplified by replacing the components in the gray area with an AC load, namely $R_\textrm{eq}$, as was explained in [24]. In this model, all components are assumed to be ideal [25].

Fig. 8

The models of an IPT system equivalent to that shown in Fig. 3

3.1 Steady-state behavior

A set of equations can be formulated from the model given in Fig. 8. With the $R_\textrm{eq}$ simplification, the set becomes

$$\begin{aligned} \left\{ \begin{array}{l} V_\textrm{eq} = \frac{\mathbf {i_p}}{\textrm{j} \omega C\mathrm {_p}} + \mathbf {i_p} \textrm{j} \omega L\mathrm {_p} + \mathbf {i_p} R_{\text {p}}- \mathbf {i_s}\textrm{j}\omega M,\\ 0 = \mathbf {i_s} R\mathrm {_{eq}} + \mathbf {i_s} \textrm{j}\omega L\mathrm {_s} + \mathbf {i_s} R_{\text {s}}- \mathbf {i_p} \textrm{j}\omega M,\\ M = k \sqrt{L_\textrm{p} L_\textrm{s}}, \end{array} \right. \end{aligned}$$

(2)

where M is the mutual inductance of $L_\textrm{p}$ and $L_\textrm{s}$, k is the coupling factor, and $\omega$ is the switching frequency in rad/s. The equations can be combined to show a relationship between input voltage and circuit currents. The combination leads to [25]

$$\begin{aligned} V_\textrm{eq}= & {} \mathbf {i_{p}} Z_\textrm{t1} = \mathbf {i_s}Z_\textrm{t2}, \end{aligned}$$

(3)

$$\begin{aligned} Z_\textrm{t1}= & {} \frac{\omega ^2 M^2 (R_{\textrm{s}} + R_{\textrm{eq}})}{\omega ^2 L_{\textrm{s}}^2 + (R_{\textrm{s}} + R_{\textrm{eq}})^2} + R_\textrm{p}\nonumber \\{} & {} \quad + \textrm{j}\Bigg [\omega L_{\textrm{p}} - \frac{1}{\omega C_{\textrm{p}}} - \frac{\omega ^3 M^2 L_{\textrm{s}}}{\omega ^2 L_{\textrm{s}}^2 + (R_{\textrm{s}} + R_{\textrm{eq}})^2}\Bigg ], \end{aligned}$$

(4)

$$\begin{aligned} Z_\textrm{t2}= & {} \bigg (\frac{R_{\textrm{s}} + R_{\textrm{eq}} + \textrm{j}\omega L_{\textrm{s}}}{\textrm{j}\omega M}\bigg )\bigg (R_{\textrm{p}} + \frac{1}{\textrm{j}\omega C_{\textrm{p}}} + \textrm{j}\omega L_{\textrm{p}}\bigg )\nonumber \\{} & {} \quad - \textrm{j}\omega M. \end{aligned}$$

(5)

3.1.1 Resonant frequency

Since the IPT system is designed to be operated at the load $Z_\textrm{t1}$ resonant frequency, all electrical characteristics, such as current and power, need to be calculated at this particular frequency. During resonance where $\omega = \omega _0$, $Z_\textrm{t1}$ becomes purely resistive. The series-none resonant frequency can be obtained by setting the imaginary part of (4) to zero, which leads to

$$\begin{aligned} \omega _\text {0} L_\text {p} - \frac{1}{\omega _\text {0} C_\text {p}} = \frac{\omega _\text {0}^3 M^2 L_\text {s}}{\omega _\text {0}^2 L_\text {s}^2 + (R_\text {s} + R_{\textrm{eq}})^2}, \end{aligned}$$

(6)

and this equation can be arranged into a quartic form as follows:

$$\begin{aligned}&C_\text {p}(L_\text {p} L_\text {s}^2 - M^2 L_\text {s})\omega _\text {0}^4 + [L_\text {p} C_\text {p}(R_\text {s} + R_{\textrm{eq}})^2 - L_\text {s}^2]\omega _\text {0}^2\nonumber \\&\quad - (R_\text {s} + R_{\textrm{eq}})^2 = 0. \end{aligned}$$

(7)

The quartic equation has a biquadratic structure where its roots (which are a set of $\omega _0$) can be obtained by the following quadratic formula:

$$\begin{aligned} \omega _\text {0}&= \pm \sqrt{-\Theta \pm \Psi }, \end{aligned}$$

(8)

$$\begin{aligned} \Theta&= \frac{1}{2L_\text {p}^2}\Bigg [\frac{{\beta _1}^2(R_\text {s} + R_{\textrm{eq}})^2 - \beta _2}{1-k^2}\Bigg ], \end{aligned}$$

(9)

$$\begin{aligned} \Psi&= \sqrt{\Theta ^2 + \frac{\beta _2 {\beta _1}^2(R_\text {s} + R_{\textrm{eq}})^2}{L_\text {p}^4(1 - k^2)}}, \end{aligned}$$

(10)

$$\begin{aligned} \beta _1&= \frac{L_\text {p}}{L_\text {s}}, \quad \beta _2 = \frac{L_\text {p}}{C_\text {p}}. \end{aligned}$$

(11)

The root of $\omega _0$ with a positive and real value is the IPT resonant frequency, which is also represented by $f_0$ in Hertz [1, 2, 25]. From (8)–(11), it can be seen that $\omega _{0}$ depends on k.

3.1.2 Equivalent input voltage approximation

Figure 9 illustrates an approximation of the input voltage $v_\textrm{p}(t)$ required to obtain the $v_\textrm{eq}(t)$ in Fig. 8. This approximation is only applied to the maximum output power operation of the MMCFS, due to its repetitive pattern of the $v_\textrm{p}(t)$ and $i_\textrm{p}(t)$. The resonant frequency period is exaggerated for purposes of clarity. The approximation process involves two stages: conversion of $v_\textrm{p}(t)$ to a square voltage $v_\textrm{sqr}(t)$ and a fundamental extraction of $v_\textrm{eq}(t)$ from the $v_\textrm{sqr}(t)$. Variable $T_\textrm{0}$ is the resonant frequency period, which is equal to the switching frequency period. Furthermore, a region of two $\textrm{Max}(v)$ is marked by $T_\textrm{t}$.

Since power equality is used in the calculation, $v_\textrm{sqr}(t)$ must produce the same average power as $v_\textrm{p}(t)$ in a steady state. Therefore, it is assumed: only one frequency component of $v_\textrm{p}(t)$ and $i_\textrm{p}(t)$ contributes to active power, $T_\textrm{0} \ll T_\textrm{t}$ and $T_\textrm{t} = nT_\textrm{0}$, where $n \in \mathbb {Z}$. If the average power of $v_\textrm{p}(t)$ and $v_{\textrm{sqr}}(t)$ is equal, then the dashed area of $v_\textrm{p}(t)$ and $v_\textrm{sqr}(t)$ must be identical:

$$\begin{aligned} P_\textrm{p}&= \frac{1}{T_\textrm{t}}\int _{0}^{T_\textrm{t}}v_\textrm{p}(t)i_\textrm{p}(t)\textrm{d}t \end{aligned}$$

(12)

$$\begin{aligned}&\approx \frac{1}{T_\textrm{t}}\int _{0}^{T_\textrm{t}}v_\textrm{sqr}(t)i_\textrm{p}(t)\textrm{d}t = P_\textrm{sqr}, \end{aligned}$$

(13)

$$\begin{aligned} v_\textrm{p}(t)T_\textrm{t}&\approx v_\textrm{sqr}(t)T_\textrm{t}, \end{aligned}$$

(14)

where $T_\textrm{t} = 2 \pi /3 \omega _\textrm{l}$, and $\omega _\textrm{l}$ is the input line frequency in radian. The left side of (14) can be approximated by

$$\begin{aligned} v_\textrm{p}(t)T_\textrm{t} \approx&V_\textrm{amp}\Bigg [\sum _{k_1 = 0}^{k_1 = (N_1-1)}\textrm{sin} \Big (\omega _\textrm{l} k_1 \frac{T_\textrm{0}}{2} + \frac{\pi }{3}\Big ) \nonumber \\&\quad + \sum _{k_1 = N_1}^{k_1 = (N_2-1)}\textrm{sin}\Big (\omega _\textrm{l} k_1 \frac{T_\textrm{0}}{2} + \frac{4 \pi }{3}\Big )\Bigg ]\frac{T_\textrm{0}}{2}, \end{aligned}$$

(15)

$$\begin{aligned} k_1 =&\, 2\mathbb {Z}, \quad N_1 \approx \frac{T_\textrm{t}/2 - 0}{T_\textrm{0}/2}, \quad N_2 \approx \frac{T_\textrm{t} - T_\textrm{t}/2}{T_\textrm{0}/2}. \end{aligned}$$

(16)

The approximation symbols for $N_1$ and $N_2$ are an implication of the $n \in \mathbb {Z}$ assumption. If both Max(v) areas are assumed to have an equal pattern and size, both summations in (15) can be combined. The amplitude $V_\textrm{mag}$ becomes

$$\begin{aligned} v_\textrm{p}(t)T_\textrm{t} = 2V_\textrm{amp}\bigg [\sum _{k = 0}^{k = N_1}\textrm{sin}\Bigg (\omega _\textrm{l} k \frac{T_\textrm{0}}{2} + \frac{\pi }{3}\Bigg )\bigg ]\frac{T_\textrm{0}}{2}. \end{aligned}$$

(17)

On the right-hand side of (15), two summations correspond to the area of Max$(v) = v_\textrm{a}(t)$ and Max$(v) = v_\textrm{c}(t)$ correspondingly. Meanwhile, the right side of (14) can be expressed as

$$\begin{aligned} v_\textrm{sqr}(t)T_\textrm{t}\approx & {} V_\textrm{mag}\sum _{k_0 = 0}^{k_0 = (N_0-1)}\frac{T_\textrm{0}}{2} = V_\textrm{mag}T_\textrm{t}, \end{aligned}$$

(18)

$$\begin{aligned} k_0= & {} \mathbb {Z},\quad N_0 \approx \frac{T_\textrm{t} - 0}{T_\textrm{0}/2}, \end{aligned}$$

(19)

By combining equation (14), (17) and (18), the amplitude $V_\textrm{mag}$ becomes,

$$\begin{aligned} V_\textrm{mag} = 2V_\textrm{amp}\Bigg [\sum _{k = 0}^{k = N_1}\textrm{sin}\Big (\omega _\textrm{l} k \frac{T_\textrm{0}}{2} + \frac{\pi }{3}\Big )\Bigg ]\frac{T_\textrm{0}}{2T_\textrm{t}}, \end{aligned}$$

(20)

The peak value of $V_\textrm{eq}$ is obtained by extracting the fundamental harmonic of $v_{\textrm{sqr}}(t)$ as follows

$$\begin{aligned} V_\textrm{eq} = V_\textrm{mag} \frac{4}{\pi } \frac{1}{\sqrt{2}}, \end{aligned}$$

(21)

which has the RMS form due to $\sqrt{2}$ division [13].

Fig. 9

Equivalent voltage approximation of NIM modulation during Max(v) equals $v_\textrm{a}(t)$ and $v_\textrm{c}(t)$

The primary and secondary current equations can be derived from (3), which at resonance then becomes [14, 25]

$$\begin{aligned} \mathbf {i_{p\mathrm {(res)}}}= & {} V_\textrm{eq}/\Bigg [R_\textrm{p} + \frac{\omega _0^2 M^2 (R_{\textrm{eq}} + R_{\textrm{s}})}{\omega _0^2 L_{\textrm{s}}^2 + (R_{\textrm{eq}} + R_{\textrm{s}})^2}\Bigg ], \end{aligned}$$

(22)

$$\begin{aligned} \mathbf {i_{s\mathrm {(res)}}}= & {} V_\textrm{eq}/\Bigg \{\frac{R_{\textrm{p}}L_{\textrm{s}}}{M} + \frac{\omega _0^2 L_{\textrm{s}} M (R_{\textrm{s}} + R_{\textrm{eq}})}{(R_{\textrm{s}} + R_{\textrm{eq}})^2 + \omega _0^2 L_{\textrm{s}}^2}\nonumber \\{} & {} + \textrm{j}\Bigg [\frac{L_{\textrm{s}}}{M}\bigg (\omega _{0}L_\textrm{p}-\frac{1}{\omega _{0}C_\textrm{p}}\bigg ) \nonumber \\{} & {} - \frac{R_{\textrm{p}}(R_{\textrm{s}} + R_{\textrm{eq}}) + \omega _0^2 M^2}{\omega _0 M} \Bigg ]\Bigg \}. \end{aligned}$$

(23)

3.1.3 Link efficiency and gain

The transfer/link efficiency at resonance has the following form:

$$\begin{aligned} \eta _\textrm{link} = \frac{P_\textrm{s}}{P_\textrm{p}}, \quad P_\textrm{s} = {|\mathbf {i_\mathrm {s(res)}}|}^2 R_{\textrm{eq}}, \quad P_\textrm{p} = V_\textrm{eq}\mathbf {i_{p(\textrm{res})}} \end{aligned}$$

(24)

with variable $P_\textrm{p}$ representing the power applied to the primary LC circuit and $P_\textrm{s}$ denoting the power consumed by $R_\textrm{eq}$. The link efficiency can be derived further using the following equations:

$$\begin{aligned}&\eta _\text {link} = \frac{\bigg [\frac{\omega _{0}^2 M^2 (R_{\textrm{s}} + R_{\textrm{eq}})}{\omega _{0}^2 L_{\textrm{s}}^2 + (R_{\textrm{s}} + R_{\textrm{eq}})^2}\bigg ]}{\bigg [R_\textrm{p} + \frac{\omega _{0}^2 M^2 (R_{\textrm{s}} + R_{\textrm{eq}})}{\omega _{0}^2 L_{\textrm{s}}^2 + (R_{\textrm{s}} + R_{\textrm{eq}})^2}\bigg ]} \frac{R_\text {eq}}{(R_\text {s} + R_\text {eq})} \end{aligned}$$

(25)

$$\begin{aligned}&= \frac{\omega _\text {0}^2 M^2 R_\text {eq}}{\omega _\text {0}^2 M^2 (R_{\textrm{s}} + R_\text {eq}) + R_\text {p}\big [(R_{\textrm{s}} + R_\text {eq})^2 + \omega _\text {0}^2 L_\text {s}^2\big ]}, \end{aligned}$$

(26)

$$\begin{aligned}&= \frac{1}{1 + \frac{1}{Q_\text {s}\gamma } + \frac{\gamma }{k^2 Q_\text {p}} + \frac{2}{k^2 Q_\text {p} Q_\text {s}} + \frac{1}{k^2 Q_\text {p} Q_\text {s}^2 \gamma } + \frac{1}{k^2 Q_\text {p} \gamma }}, \end{aligned}$$

(27)

$$\begin{aligned} k&=\frac{M}{\sqrt{L_\text {p} L_\text {s}}}, Q_\text {p} = \frac{\omega _\text {0} L_\text {p}}{R_\text {p}}, Q_\text {s} = \frac{\omega _\text {0} L_\text {s}}{R_\text {s}}, \gamma = \frac{R_\text {eq}}{\omega _\text {0} L_\text {s}}. \end{aligned}$$

(28)

The variable $\gamma$ is load matching factor, while the variables $Q_\text {p}$ and $Q_\text {s}$ denote primary and secondary-side quality factors, respectively [1, 8, 25].

The link gain is an amplitude ratio between $v_\textrm{s}(t)$ and $v_\textrm{eq}(t)$ and can be expressed as [1, 25],

$$\begin{aligned} G&= \frac{V_\textrm{s}}{V_\textrm{eq}} = \frac{\sqrt{P_\text {p}\eta _\text {link}R_\text {eq}}}{V_\textrm{eq}}, \end{aligned}$$

(29)

$$\begin{aligned}&= \frac{\omega _\text {0} M R_\text {eq}\sqrt{(R_\text {eq} + R_\text {s})^2 + \omega _\text {0}^2 L_\text {s}^2}}{\omega _{\text {0}}^2 M^2 (R_\text {eq} + R_\text {s}) + R_\text {p}\big [(R_\text {eq} + R_\text {s})^2 + \omega _\text {0}^2 L_\text {s}^2\big ]}, \end{aligned}$$

(30)

$$\begin{aligned}&= \frac{\eta _\text {link}\sqrt{(R_\text {eq} + R_\text {s})^2 + \omega _\text {0}^2 L_\text {s}^2}}{\omega _\text {0} M}, \end{aligned}$$

(31)

$$\begin{aligned}&= \frac{\eta _\text {link}}{k}\sqrt{\frac{1}{\beta _1}\Bigg [\Bigg (\gamma + \frac{1}{Q_\text {s}}\Bigg )^2 + 1\Bigg ]}. \end{aligned}$$

(32)

The gain value is apparently affected by $\omega _{0}$ through $\eta _\textrm{link}$, $\gamma$ and $K_\textrm{s}$.

3.2 Dynamic behavior

Since the IPT is a self-oscillating system, it must be able to maintain a free-wheeling oscillation for a certain period of time, and hence, an underdamped characteristic is preferred. Oscillatory behavior can be determined through a damping ratio variable, which can be calculated using dynamic equations. The equations for the series-none IPT system are presented as follows:

(33)

In this case, $T_0$ is the resonant frequency period, $v_\textrm{p}(t)$ is the voltage over the primary LC circuit, and $v_\textrm{cp}(t)$ is a voltage over $C_\textrm{p}$. A state-space representation can then be constructed from (33) having the following form [26]:

(34)

$$\begin{aligned} \textbf{A} = \begin{bmatrix} 0 &{} \frac{1}{C_{\text {p}}} &{} 0 \\ -\frac{L_{\text {s}}}{L_{\text {p}}L_{\text {s}} - M^2} &{} -\frac{R_{\text {p}}L_{\text {s}}}{L_{\text {p}}L_{\text {s}} - M^2} &{} -\frac{M(R_{\text {s}} + R_{\text {eq}})}{L_{\text {p}}L_{\text {s}} - M^2} \\ -\frac{M}{L_{\text {p}}L_{\text {s}} - M^2} &{} -\frac{MR_{\text {p}}}{L_{\text {p}}L_{\text {s}} - M^2} &{} -\frac{L_{\text {p}}(R_{\text {s}} + R_{\text {eq}})}{L_{\text {p}}L_{\text {s}} - M^2} \end{bmatrix} \end{aligned}$$

(35)

The damping ratio is obtained through eigenvalues of the matrix $\textbf{A}$ that can be calculated using the determinant operation:

$$\begin{aligned}{} & {} |s\textbf{I} - \textbf{A}|= s^3 + \Bigg [ \frac{R_{\text {p}}L_{\text {s}} + L_{\text {p}}(R_{\text {s}} + R_{\text {eq}})}{L_{\text {p}}L_{\text {s}} - M^2} \Bigg ] s^2 \nonumber \\{} & {} + \Bigg [\frac{R_{\text {p}}(R_{\text {s}} + R_{\text {eq}})C_{\text {p}} + L_{\text {s}}}{C_{\text {p}}(L_{\text {p}}L_{\text {s}} - M^2)}\Bigg ]s + \frac{(R_{\text {s}} + R_{\text {eq}})}{C_{\text {p}}(L_{\text {p}}L_{\text {s}} - M^2)}. \end{aligned}$$

(36)

The eigenvalues are the roots of the cubic polynomial equation, as well as the poles of the system [27]. A system that has one real root and one pair of complex conjugate roots must have a discriminant of $D > 0$ [28]. By assuming that the discriminant value is met, the poles of (36) become

$$\begin{aligned} s_{1,2} = -\zeta \omega _\textrm{0} \pm \textrm{j}\omega _\textrm{0} \sqrt{1- \zeta ^2}, \qquad s_3 = c_3, \end{aligned}$$

(37)

where $\zeta$ denotes a damping ratio and $c_3$ denotes a real value constant [26].

A dominant pole (the closest one to the imaginary axis in a complex plane) can determine the behavior of a system. An output that exhibits oscillation occurs if the complex conjugate poles are the dominant ones. If $c_3$ is far enough on the negative side of the real axis, the third-order system can be approximated by its second-order part [29]. Assuming that the approximation can be applied, the $\zeta$ can be calculated as follows:

$$\begin{aligned} \zeta = \frac{|\text {Re}\{s_\text {1}\}|}{|s_\text {1}|} = \frac{|\text {Re}\{s_\text {2}\}|}{\vert s_\text {2}|}. \end{aligned}$$

(38)

A damping ratio value that is close to zero is preferred in order to prolong the free-wheeling oscillation [26, 27, 29].

4 Practical implementation

4.1 Kick-start method

Since the IPT is self-oscillating, it is necessary to trigger the initial current oscillation. One approach is to gradually charge the primary capacitor $C_\textrm{p}$ to a certain voltage level, followed by releasing the accumulated energy through the free-wheeling switch on the primary side. The process can be achieved by taking advantage of the MMCFS topology based on the DC resonant charging approach described in [30, 31]. This charging circuit is commonly used for power pulse generators in microwave radar applications. Figure 10 shows the positive and negative current injection paths of the Phase A extracted from the matrix topology. Note that the two circuit paths resemble the resonant charging circuit. If a quasi-square pulse is generated from the input using the IGBT with a duration greater than $2\pi \sqrt{L_\textrm{p}C_\textrm{p}}$, then the empty $C_\textrm{p}$ is charged to twice the input voltage. In this kick-start case, the $C_\textrm{p}$ is charged by one injection followed by the opposite one sequentially. The voltage of $C_\textrm{p}$ increases to a certain level after each injection pulse is applied. When this voltage level is sufficiently high, the free-wheeling path will be activated to generate a short burst $i_\textrm{p}(t)$ for triggering the steady-state operation of the matrix converter. The amplitude of generated $i_\textrm{p}(t)$ is proportional to the charging voltage [30,31,32].

Fig. 10

Injection current path from Phase A. a Positive injection path. b Negative injection path

Figure 11 illustrates the gradual charging process using positive and negative injections alternatingly to charge the $C_\textrm{p}$. In this illustration, the positive injections are performed by $s_\textrm{ap}(t)$ and $s_\textrm{bp}(t)$, while the negative injection is applied by $s_\textrm{cn}(t)$. These injections are applied at the beginning of each Max(v) cycle, where the turn-on duration $T_\textrm{d}$ should be greater than $T_\textrm{0}/2$. This $T_\textrm{0}$ denotes the resonant frequency period of the series-none IPT system. During this charging process, the capacitor voltage level is the same as $v_\textrm{p}(t)$ and their waveforms are indistinguishable. Since this voltage can be much higher than the input amplitude after the charging process, the voltage ratings of $C_\textrm{p}$ and the free-wheeling IGBTs should be able to handle the desired charging voltage. Nevertheless, this kick-start approach can trigger the MMCFS-IPT at a different resonant frequency configuration, as long as the resonant system is underdamped [32].

Fig. 11

Gradual capacitor charging illustration of the MMCFS-IPT

4.2 Multistep switching strategy

Since the ZCS cannot be realized in practice due to component non-ideality, a multistep switching strategy was developed. This approach maintains current conduction at any switching state to prevent converter destruction [10, 12]. Figure 12 describes the approach using Phase A. Variable $T_\textrm{b}$ is the blanking time. The signal duration $T_\textrm{d}$ and its position must be set properly, to prevent overlapping of $T_\textrm{b}$ and the zero-crossing transition of $i_\textrm{p}(t)$. The time variables $T_\textrm{asc}$ and $T_\textrm{des}$ are the periods corresponding to the turning on and off of injection with respect to the zero-crossings. The signal {$s_\textrm{ap}$, $s_\textrm{an}$} can be replaced by either {$s_\textrm{bp}$, $s_\textrm{bn}$} or {$s_\textrm{cp}$, $s_\textrm{cn}$}, in the case of Phase B or Phase C, respectively.

Fig. 12

Current-based multistep switching transitions. a Positive injection. b Negative injection

4.3 Controller structure

To adjust power delivery from the input to the load, a PDM-based on–off controller is implemented in the IPT system. This controller changes the ratio of injections and FWOs based on the level of $I_\textrm{p}$. The controller flowchart is given in Fig. 13. Initially, the existence of $i_\textrm{p}(t)$ is checked by comparing $I_\textrm{p}$ with a certain minimum value $I_\textrm{lim}$. If $I_\textrm{p} < I_\textrm{lim}$, then a kick-start process is carried out, which will produce a short burst of $i_\textrm{p}(t)$ to trigger a steady-state operation of the converter. During the steady state, the ON switch is constantly being monitored whether it is active or not. As long as this switch is active, $I_\textrm{p}$ is continuously compared with the $I_\textrm{ref}$ reference, so the controller can adjust the amount of injections with respect to FWOs. If $I_\textrm{p} < I_\textrm{ref}$, then the number of injection will be increased and vice versa. If the ON switch is deactivated, FWO is utilized to completely remove $i_\textrm{p}(t)$ in the primary and secondary coils [13].

Fig. 13

The on–off current control flowchart of a self-oscillating IPT system

This on–off control approach based on PDM is easy to implement, since it does not involve computationally demanding calculation. However, due to an irregularity of injection and the FWO pattern, a mathematical model of the equivalent voltage $v_\textrm{eq}(t)$ at a partial load operation becomes difficult to construct. As a consequence, theoretical equations of $\mathbf {i_\mathrm {p(res)}}$, $\mathbf {i_\mathrm {s(res)}}$, $\eta _\text {link}$ and G at this particular operation are not presented in this paper. If these values are needed, a simulation of the MMCFS-IPT can be used to approximate them.

In addition, this control approach can also be applied to the IPT system with series–series configuration, as long as the transmission coils’ coupling factor is below the critical coupling. Above this coupling limit, a frequency split occurs that will disrupt the operation of the PDM [2].

4.4 Experimental setup

Experimental setup and block diagram of the MMCFS-IPT are shown in Figs. 14 and 15, respectively. In Fig. 14, the entire setup is marked by two red boundaries, in which the big one consists of the input capacitors, MMCFS-IPT, AC load, a current processor and a controller, while the small one consists of a voltage processor. In Fig. 15, power flow is illustrated by thick arrows, while information flow is marked by thin arrows. The three-phase voltage was produced using Regatron TC50.480.72-ACS-14026, and each phase is connected to the neutral line by a 12 $\mu$F input film capacitor to nullify the effect of input line inductance on the MMCFS. The input capacitors are attached to a switching network consisting of discrete IGBTs (IKW40N120H3 from Infineon). This MMCFS switching network is connected to a primary capacitor bank, a coupled coil, and an AC load. The load contains a full-bridge rectifier (SemiQ GHXS030A060S-D1E), a smoothing film capacitor, and a resistor (Terco MV1100). Calculating the $\textrm{Max}(v)$ requires input voltage polarity provided by the voltage processor circuit. This circuit contains a resistor divider, an analog-to-digital converter and a phase-locked loop. Additionally, the amplitude of $i_\textrm{p}(t)$ and its zero-crossing information are calculated by the current processor, which utilizes a ZCD circuit (similar to that described in [33]), a precision rectifier, and a LEM CASR-6 current transducer. The voltage and current data are used by the DE10-nano-FPGA to modulate the switching network. TI UCC21521 and CUI VQA-S15-D15-SIP are the gate driver and its isolated power supply, respectively.

Fig. 14

The experimental setup of MMCFS-IPT

Fig. 15

The block diagram of MMCFS-IPT

The transmitting and receiving coils are identical in that they are planar and core-less. Each coil structure and its dimensions are presented in Fig. 16. The coil is constructed using Litz wire (1000 strands of 38 AWG) and a wooden platform. Coil dimensions were calculated based on the Wheeler approximation to produce an inductance value close to 200 $\upmu$H [34, 35].

Fig. 16

Diagonal and lateral illustration of the IPT coil. Circles with diagonal stripes represent wire cross sections

The electrical characteristics for the experimental setup of the series-none IPT system are given in Table 1, in which the structure of passive components can be seen in Fig. 8. All components were measured using a Fluke 28-II multimeter, a PM6306 RCL meter and Tektronix TPS 2014B oscilloscope. The input line frequency is represented by $f_\textrm{l}$ in Hertz. The parasitic resistances of the primary and secondary coils ($R_\textrm{p}$ and $R_\textrm{s}$) were obtained around $\omega _{0}$ of the IPT system. Additionally, the k value corresponds to a distance of 5.5 cm and was derived by connecting the coils in series. Using the measured value of $R_\textrm{L}$, variable $R_\textrm{eq}$ becomes 40.45 $\Omega$.

Table 1 Passive components’ values

5 Calculation and data analysis

5.1 Input voltage correction

Due to semiconductor voltage drops and multistep switching implementation, corrections need to be added to the square voltage equation given in (20). The voltage drops caused by the transistor–diode pair on the input side reduce the voltage amplitude $V_\textrm{p}$ over the primary LC circuit. Meanwhile, the existence of $T_\textrm{asc}$ and $T_\textrm{des}$ (see Fig. 12) reduces the area of $v_\textrm{sqr}(t)$. The equivalent square voltage amplitude thus becomes

$$\begin{aligned} V_\textrm{mag}= & {} 2V_\textrm{corr}\Bigg [\sum _{k = 0}^{k = N_1}\textrm{sin}\Big (\omega _\textrm{l} \Big [k \frac{T_\textrm{0}}{2} + T_\textrm{asc}\Big ] + \frac{\pi }{3}\Big )\Bigg ]\frac{T_\textrm{corr}}{T_\textrm{t}}, \end{aligned}$$

(39)

$$\begin{aligned} V_\textrm{corr}= & {} V_\textrm{amp} - V_\textrm{dt} - V_\textrm{dd},\quad T_\textrm{corr} = \frac{T_\textrm{0}}{2} - T_\textrm{asc} - T_\textrm{des}, \end{aligned}$$

(40)

where $V_\textrm{dt}$ and $V_\textrm{dd}$ represent the voltage drops of the IGBT and its antiparallel diode, respectively.

5.2 Gain and resonant frequency behaviors

The G and phase angle variations of the series-none IPT system can be observed by plotting these variables with respect to the switching frequency of the matrix converter. For the case of multiple k and single $R_\textrm{L}$, the plots are presented in Fig. 17. The G and phase angle equations to plot the graphs in this figure are taken from (29) and (3), respectively. This phase angle represents a shift between $v_\textrm{p}(t)$ and $i_\textrm{p}(t)$ on the input side, in which the zero value indicates the $f_0$ of the series-none IPT system. In this case, increasing the value of k leads to a decreasing shift of G and an increasing shift of $f_0$.

Fig. 17

Phase angle plot with respect to switching frequency when $R_{eq}$ is held constant

Alternatively, the gain and phase angle plots for the case of multiple $R_\textrm{L}$ and single k are given in Fig. 18. In this scenario, a high value of $R_\textrm{L}$ relates to a high value of G and a low value of $f_0$. Since each phase angle line in Figs. 17 and 18 only intersects the zero phase once, the series-none IPT system has no frequency split phenomenon in a high coupling and quality factor case, under the given passive components’ values.

Fig. 18

Phase angle plot with respect to switching frequency when k is held constant

5.3 Current damping characteristic

Figure 19 shows the relationship between k and the roots in (37) derived using both the dynamic model given in 3.2 and the components’ values listed in Table 1. The figure shows the eigenvalues position in a complex plane around $k = 0.53$. Since the complex poles are dominant, and D values are always greater than zero, a second-order system can be used to approximate $\zeta$. Thus, it can be seen that $\zeta$ is proportional to k. Since the free-wheeling duration of $i_\textrm{p}(t)$ becomes short at a high $\zeta$ value, the k must be limited to a certain range.

Fig. 19

The roots of characteristic equation plotted for different k values. The table shows the relationships between k, D and $\zeta$

5.4 Experimental data

Data for visualizing the behavior of the MMCFS-IPT were recorded using Tektronix TPS 2014B and MDO4104C oscilloscopes. Additionally, the Fluke Ti110 thermal camera was used to approximate the junction temperature of the semiconductor switches during a steady-state operation for estimating the voltage drops of the IGBT and its antiparallel diode. The end-to-end efficiency was calculated by measuring the output active power of the Regatron, and the DC voltage and current over the Terco resistive load. These DC values were measured using two Agilent 34410A multimeters. Some of the electrical quantities will be compared with calculation results to validate the model given in Sect. 3. The visual data from the oscilloscopes were re-plotted by MATLAB for a better presentation.

5.4.1 Turn-on stage

The kick-start process explained in Sect. 4.1 was used to trigger the steady state of MMCFS-IPT. The resulting experimental waveforms are shown in Fig. 20. The turn-on duration $T_\textrm{d}$ of the charging signal was set to 100 $\upmu$s. In this case, the capacitor $C_\textrm{p}$ was gradually charged to around 500 V, as can be deduced from the $v_\textrm{p}(t)$ plot. As shown in the figure, the stored energy is released at 0 ms through FWO, producing a short burst of $i_\textrm{p}(t)$ at the transient state to trigger a steady-state operation. During this transient state, $I_\textrm{p}$ grows and then shrinks due to the charging of an empty $C_\textrm{L}$ on the load side.

Fig. 20

Kick-start process of the MMCFS-IPT

5.4.2 Maximum output operation

Figures 21 and 22 present the converter waveform at the steady state, in which the former has a longer time scale than the latter. These figures consist of voltage and current waveforms on the primary and secondary sides of MMCFS-IPT driven by NIM. Due to circuit impedance, a phase shift between $i_\textrm{p}(t)$ and $i_\textrm{s}(t)$ can be observed in Fig. 22. The frequency components of the voltages and currents calculated using the fast Fourier transform are shown in Fig. 23. In this figure, two dominant peaks can be observed from the $\hat{v}_\textrm{p}/\hat{v}_\textrm{ph}$ plot at 150 Hz and 26.675 kHz. The latter peak represents the converter switching frequency, which is equal to the $f_0$. This is also a component that contributes to active power.

Fig. 21

Steady-state operation of the MMCFS-IPT with a long time scale

Fig. 22

Steady-state operation of the MMCFS-IPT with a short time scale

Fig. 23

Frequency component plots of the voltages and currents on the primary and secondary sides

The switching transitions of the experimental setup can be seen from Fig. 24. To avoid a short circuit, the turn-on of $s_\textrm{ap}$ and $s_\textrm{dn}$ must not overlap. Therefore, a blanking time of $1.1~\upmu s$ was introduced. Switching characteristics are also given in the table of the corresponding figure. Gate resistance is marked by $R_\textrm{g}$, while the remaining variables were described previously using Fig. 12. The gate voltages applied here were − 9 V and 15 V. Since the switching transitions of $v_\textrm{p}(t)$ were not executed at the zero-crossing of $i_\textrm{p}(t)$, the switching losses were present during the operation.

Fig. 24

Multistep switching waveform involving MMCFS switches. Injection is applied from Phase A through $s_\textrm{ap}$

Some electrical quantities of the operation can be seen in Table 2. They were obtained from the calculation results and experimental data recorded using the MDO oscilloscope. The calculation involved voltage corrections described in Sect. 5.1. The $V_\textrm{dt}$ and $V_\textrm{dd}$ were estimated from the IGBT datasheet, corresponding to roughly 1.52 V and 1.78 V, respectively. To estimate the $V_\textrm{dt}$ and $V_\textrm{dd}$, we used collector current and junction temperature of 10 A and $25^{\circ }$ C, which are the approximated values from the oscilloscope and thermal camera closest to those available in the IGBT manufacturer’s datasheet. In contrast, the experimental data were calculated from the FFT analysis of the experimental waveforms and correspond to the RMS value at the $f_0$ of the series-none IPT. However, the calculated values slightly differ from the experimental results. This discrepancy can be attributed to approximation error and limited measurement accuracy. Nevertheless, the experimental end-to-end efficiency is 81.68%. This efficiency is partly caused by the switching losses that is mentioned in the previous paragraph.

Table 2 Electrical quantities at maximum output

5.4.3 On–off control implementation

Figures 25 and 26 show the waveforms produced by implementing the control scheme explained in Sect. 4.3, in which the former has a longer time scale than the latter. Additionally, the extracted quantities of the waveforms are presented in Table 3. In this case, the ratio between injection and FWO was adjusted automatically by the controller to keep $I_\textrm{p}$ around 6 $A_\textrm{rms}$. As a result, not only injection voltages of NIM become sparse, but also the RMS values of voltages and currents are lower than the maximum output operation. This scenario was found to have an end-to-end efficiency of 79.23%.

Fig. 25

Steady-state operation with a current control (long time scale)

Fig. 26

Steady-state operation with a current control (short time scale)

Table 3 Electrical quantities at partial load

In this on–off control implementation, the number of injections that can be applied within one $\textrm{Max}(v)$ determines the control accuracy to regulate $i_\textrm{p}(t)$. Higher accuracy can be achieved by increasing the switching frequency, which means raising the $\omega _{0}$ of the IPT system. However, this form of power regulation is difficult to implement in a system with very high k, due to very high $\zeta$. In this very high $\zeta$ condition, few successive FWOs can quickly reduce $I_\textrm{p}$ to zero due to a very short free-wheeling duration characteristic, thus abruptly stopping the operation of the converter.

5.4.4 Input and ground currents

The input and ground currents of the MMCFS-IPT are analyzed at the turn-off, maximum output and partial load conditions. At the turn-off, the three-phase voltage source is turned-on, while the matrix converter remains off. Since each input capacitor is connected to the neutral line, the harmonics of the input three-phase go through these capacitors and appear in the neutral as can be seen in Fig. 27. In this figure, the input is represented by the Phase A, where variables $v_\textrm{a}$, $i_\textrm{a}$ and $i_\textrm{g}$ denote Phase A voltage, Phase A current and neutral/ground current, respectively. Additionally, the frequency components of the input and ground currents are depicted in Fig. 28, in which the harmonics in the input and neutral lines have a fundamental at 40 kHz and a DC component. The existence of these harmonics and DC affects the waveforms of the MMCFS during its maximum and partial load operations.

Fig. 27

Turn-off condition of the MMCFS-IPT

Fig. 28

Frequency component plot of the input and ground currents during the turn-off

At the maximum output and partial load operations, the voltage and current waveforms of the MMCFS-IPT driven by NIM can be seen in Figs. 29 and 30, respectively. Since the current injections of NIM are performed at the Max(v) of the input three-phase, the average of $i_\textrm{a}(t)$ is not sinusoid, in which there is a $120^{\circ }$ gap of zero input current. Additionally, the harmonics of the input three-phase are added to the waveforms. During the partial load operation, the amplitude of $i_\textrm{p}(t)$ is reduced. This reduction affects the amplitude of $i_\textrm{a}(t)$ and $i_\textrm{g}(t)$ and makes the input source harmonics more dominant.

Fig. 29

Maximum output operation of the MMCFS-IPT

Fig. 30

Partial load operation of the MMCFS-IPT

Due to the non-sinusoidal current waveforms of the NIM, lower-order harmonics exist in the input and neutral lines during the maximum output and partial load operations, as can be seen in Figs. 31 and 32, respectively. These harmonics are difficult to filter since they are close to the input line frequency of 50 Hz. In practice, the existence of these harmonics can disturb other electrical equipment connected to the same source as the MMCFS-IPT. In Fig. 32, the DC component in the neutral caused by the input source becomes apparent due to the low amplitude of $i_\textrm{g}(t)$.

Fig. 31

Frequency component plot of the input and ground currents during the maximum output

Fig. 32

Frequency component plot of the input and ground currents during the partial load

It is clear that the existence of the input source harmonics must be reduced or eliminated to avoid DC on the neutral line. Moreover, these harmonics also hinder further analysis of the input and neutral current behaviors of the MMCFS-IPT.

6 Conclusion

This paper has demonstrated the theoretical and experimental analyses of the MMCFS-IPT driven by a PDM, namely NIM. The converter not only requires fewer semiconductor switches than the VB2B topology, but also operates in a self-oscillating manner. This self-oscillation could be realized since the series-none configuration does not exhibit frequency split behavior. This behavior leads to a possibility of implementing a variable-frequency controller for a dynamic coupling factor application in the future.

In practice, a kick-start process is needed to generate an oscillating current, since the controller tracks the current zero-crossing to operate the NIM. This process produces a short burst of $i_\textrm{p}(t)$ to trigger a steady-state operation. In addition, this process has a possibility to trigger the steady state at different initial $f_0$ configurations, as long as the series-none IPT system is underdamped.

Regarding the coupled flat spiral coils, its k value is proportional to the damping ratio $\zeta$ of the $i_\textrm{p}(t)$. Thus, the lower bound of k is determined by the voltage and current ratings of the resonant tank, since the system is less damped at low k value. In contrast, as k increases, the $\zeta$ and $\omega _{0}$ of the $i_\textrm{p}(t)$ also increase, so the upper bound of k is determined by the accuracy of current transducer for measuring this $i_\textrm{p}(t)$, as well as maximum converter switching frequency. As a result, k value that produces a near critical damping behavior must be avoided.

During the steady state, the control accuracy of the PDM is determined by the value of $\omega _0$. Additionally, since the ZCS cannot be implemented due to non-ideality of the semiconductor devices, multistep switching is applied as an alternative for operating the MMCFS. If the damping of MMCFS-IPT is quite significant, the number of successive FWOs must be limited in order to prevent an abrupt stoppage of the converter. Nevertheless, the end-to-end efficiency between the maximum output power and partial load operations was maintained around 80%.

In terms of input current, the NIM produces a non-sinusoidal input. As a consequence, it contains lower-order harmonics that are difficult to filter. However, further harmonic analysis could not be performed due to an existence of another harmonics in the output of the three-phase voltage source.