1 Introduction

The interaction between two earth return circuits, e.g., high voltage alternating current (HVAC) transmission line and a neighboring pipeline, is an important theme in power systems engineering/electromagnetic compatibility. A consequence of electromagnetic interference (EMI) of power lines on buried pipelines is that AC voltages can be induced on the pipelines during ground fault conditions and normal conditions. The actual magnitude of the induced AC voltage depends on many factors, including the overall configuration of all the structures involved, soil resistivity, pipeline electrical parameters, magnitude of the line currents in the power circuit(s), and any current imbalance between the phases. Induced voltages and produced currents in the victim circuit can endanger the circuit’s normal operation by causing the malfunctioning of its control and protection equipment, can endanger human health, and may lead to the AC-enhanced corrosion phenomenon, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Predicting high voltage interference is a complex problem, with multiple interacting variables affecting the influence and impact. In recent decades, development of advanced calculation methods and computer-based tools for simulation of interference effects, analysis of faults, and development of mitigation methods has been significant. Computer-based numerical modeling can be utilized to examine the collocated pipeline’s susceptibility to HVAC interference, help identify locations of possible AC current discharge, and where necessary design appropriate mitigation systems to reduce the effects of AC voltage, fault currents, and AC current density to meet accepted industry standards. These numerical models are capable of analyzing the interacting contribution of multiple variables to the overall magnitude of AC interference. Typical standard software packages for calculation of the EMI and corresponding effects on buried pipelines were reviewed in the literature [10,11,12,13,14,15,16,17,18,19, 21,22,23,24,25,26].

Conventional methods used to analyze the inductive interference between HVAC power lines and pipelines are usually based on a circuit model approach. In the computation of the line parameters in the circuit model approach, the lines are assumed to be parallel and infinite in length. When they are not parallel, a piecewise parallelism approach is employed. It is shown in the literature that for a straight, parallel, homogenous collocation, induced potentials along pipelines having medium-quality insulating coating (resistance to dozens of k\(\Omega \)m\(^{2}\) or less) are highest at the ends of the collocated segment, and fall exponentially with distance past the point of divergence. For more complex collocations, voltage peaks may occur at geometric or electrical discontinuities, where there is an abrupt change in the collocation geometry or electromagnetic field. Specifically, voltage peaks commonly occur where the pipeline converges or diverges with the HVAC power line, separation distance or soil resistivity changes significantly; where isolation joints are present on the pipeline; or where the electromagnetic field varies such as at phase transpositions [8].

With the fast development of industry and urbanization, the demand for energy requires the construction of an increasing number of HVAC transmission lines, and the laying of large diameter, high-pressure transmission pipelines. The items related to the transmission pipeline that greatly affect the magnitude of induced voltage are the total length of electrically continuous pipeline, the pipeline length collocated in close proximity to power lines and the resistance of the pipeline coating. Pipelines should be electrically isolated from compressor stations, pump stations, well sites, offshore pipelines and structures, terminals and processing facilities. Isolation should be achieved by installation of monolithic (monoblock) isolation joints, isolating flange kits or non-conductive pipe sections. Coating resistance to ground is a function of the coating type, condition, thickness and local soil resistivity. Pipeline insulation resistance is in the range of \(10^{7}\) k\(\Omega \)m\(^{2}\) for polyethylene coatings or even higher. High-quality insulating coatings, diameters and lengths of pipelines have significant impact on equivalent unit-length pipeline electrical parameters: longitudinal resistance \(R'\) (\(\Omega \)/m), longitudinal inductance \(L'\) (H/m), shunt conductance \(G'\) (S/m) and shunt capacitance \(C'\) (F/m). The relationships between these parameters of main pipelines used in practice, buried in soil with typical conductivity, meet inequality \(R^{\prime }< \omega L^{\prime }\) and \(G^{\prime }<\omega C^{\prime } \) what significantly affects wave parameters—propagation coefficient and characteristic impedance of a transmission pipeline. The pipelines may not be farther treated as lossy transmission lines, and the distribution of induced potentials along the pipelines recalls the distribution of voltage standing wave in a lossless line.

Electromagnetic interference on earth return circuits—field phenomenon in nature, can also be modeled using circuit methods. The advantage of this approach is the ability to simulate earth return circuits using universal simulation programs type of SPICE (Simulation Program with Integrated Circuit Emphasis) [27] or similar, which greatly simplifies and speeds up the analysis. This is an alternative approach to the existing methods of earth return circuits analysis. At the same time allows you to extend the scope of the relevant issues and can be used where analytical methods fail. The main disadvantage to use the software, type of SPICE, is time-consuming to prepare the source file, the greater the larger the system is modeled. This also applies to other simulation programs. This is compensated by the short time simulation and a wide range of output data to which one can access.

In the literature, there is a lack of studies on the EMI on the pipelines with unit-length parameters \(R'<\omega L'\) and \(G' < \omega C'\). The purpose of this work is to take this problem and present a method for the analysis of inductive interference of power lines on transmission pipelines taking into account the wave nature of this phenomenon. Modeling of such impact shall be carried out using the simulation package SPICE. A comprehensive study of how various parameters influence the peak and distribution/shape of the induced potential will present.

2 General considerations

2.1 Equivalent circuit of a conductor with earth return

Equivalent model of an earth return circuit is essential to the computer simulation of effects of external electromagnetic excitation on the earth return circuit. The basic model subjected to the external (primary) electric field is shown in Fig. 1.

In Fig. 1, a single circuit of the differential length dx consists of a unit-length series impedance \(Z' \) and a unit-length shunt admittance \(Y'\). The driving voltage source \(E'\hbox {d}x\) represents the external excitation, producing a current I(x) and a potential V(x) along the circuit. Formulas for calculation of electrical parameters of a pipeline buried in the earth can be found, e.g., in [8, 9, 16].

Fig. 1
figure 1

Equivalent model of an elementary section of earth return circuit (pipeline) with external excitation

Full size image

The unit-length series impedance of the tubular conductor (pipe) with internal and external radii \(r_{1}\) and \(r_{2}\), buried at depth d in the earth with conductivity \(\sigma \), permeability \(\mu \) \(_{0}\) and dielectric constant \(\varepsilon \), consists of two terms: conductor internal impedance \({Z}'_\mathrm{i} \) and impedance of ground return \({Z}'_\mathrm{g} \):

$$\begin{aligned} {Z}'= & {} {Z'}_{\mathrm{i}} +{Z}_\mathrm{g}'\nonumber \\= & {} \frac{j\omega \mu {}\left[ {I_0 \left( {kr_2 } \right) K_1 \left( {kr_1 } \right) +I_1 \left( {kr_1 } \right) K_0 \left( {kr_2 } \right) } \right] }{2\pi {}kr_2 \left[ {I_1 \left( {kr_2 } \right) K_1 \left( {kr_1 } \right) -I_1 \left( {kr_1 } \right) K_1 \left( {kr_2 } \right) } \right] }+\nonumber \\&+\frac{j\omega \mu _0 }{2\pi }\ln \frac{1.85}{\sqrt{r_2^2 +4d^{2}}\sqrt{\gamma ^{2}+j\omega \mu _0 \left( {\sigma +j\omega \varepsilon } \right) }} \end{aligned}$$
(1)

where \(I_{0}\) and \(I_{1}\) are the modified Bessel functions of first kind, zero and first order, respectively, \( K_{0}\) and \(K_{1}\) are the modified Bessel functions of second kind, zero and first order, respectively, \(\mu \)—conductor permeability, \(\omega \)—angular frequency, \(\sigma _{\mathrm{c}}\)—conductor conductivity and

$$\begin{aligned} k^{2}=j\omega \mu \sigma _\mathrm{c} \end{aligned}$$
(2)

where \(j=\sqrt{-1}\).

The unit-length shunt admittance of the conductor consists of two terms: pipe insulation admittance \({Y}'_\mathrm{i} \) and spread admittance in the ground \({Y}'_\mathrm{g} \) and can be obtained from the relation:

$$\begin{aligned} Y'^{-1}= & {} {Y'}_\mathrm{i}^{-1}+{Y'}_\mathrm{g}^{-1}={Y'}_\mathrm{i}^{-1}\nonumber \\&+\frac{1}{\pi \left( {\sigma +j\omega \varepsilon } \right) }\ln \frac{1.12}{\gamma \sqrt{r_2^2 +4d^{2}}} \end{aligned}$$
(3)

and

$$\begin{aligned} {Y'}_\mathrm{i}= & {} G'_\mathrm{i} +j\omega C'_\mathrm{i} \end{aligned}$$
(4)
$$\begin{aligned} G'_\mathrm{i}= & {} \frac{\pi D}{r_u } \end{aligned}$$
(5)
$$\begin{aligned} \omega C'_\mathrm{i}= & {} \frac{\omega \pi D\varepsilon _o \varepsilon _\mathrm{r} }{t} \end{aligned}$$
(6)

where \({G}'_\mathrm{i} \)—unit-length conductance of pipeline insulation and \({C}'_\mathrm{i} \)—unit-length capacitance between the pipe and the earth, D—pipe diameter, \(r_{u}\)—pipe coating resistivity, t—insulation thickness, \(\varepsilon _{\mathrm{r}}\)—relative permittivity of the insulation material.

The propagation coefficient \(\gamma \) can be determined from the equation

$$\begin{aligned} \gamma =\sqrt{{Z}'{Y}'} \end{aligned}$$
(7)

whereas the characteristic impedance of the pipeline:

$$\begin{aligned} Z_{\mathrm{c}}=\sqrt{\frac{Z{'}}{Y{'}}} \end{aligned}$$
(8)

In the case of two coupled earth return circuits from which one is a buried pipeline and the other is an overhead conductor at height h, the unit-length mutual impedance is

$$\begin{aligned} {Z}'_\mathrm{m} =j\frac{\omega \mu _{0} }{2\pi }\ln \frac{1.85}{\sqrt{j\omega \mu _{0} \left( {\sigma +j\omega \varepsilon } \right) }\cdot \sqrt{\left( {d+h} \right) ^{2}+a^{2}}} \end{aligned}$$
(9)

where d—pipeline burial depth, h—height of the power line conductor, a—horizontal distance between the pipeline and the power line conductor, \(s=\sqrt{\left( {d+h} \right) ^{2}+a^{2}}\)—distance between the pipeline and the overhead conductor, \(\sigma \)—ground conductivity, \(\varepsilon \)—ground permittivity.

Generally, \(E'\), the primary electric field intensity impressed at every point of the circuit, is the sum of an induced and a static component

$$\begin{aligned} {\overrightarrow{E'}}={\overrightarrow{E'}}_\mathrm{i} +{\overrightarrow{E'}}_\mathrm{s}. \end{aligned}$$
(10)

The induced electric field is associated with the inductive, whereas the static electric field with the conductive and/or capacitive influence on the earth return circuit.

In the case of the inductive interference

$$\begin{aligned} \overrightarrow{{E}'}_\mathrm{i} =-j\omega {}\overrightarrow{A}, \end{aligned}$$
(11)

where \(\overrightarrow{A}\) is the vector potential along the earth return circuit due to the current in an external influencing source, \(\omega \)—angular frequency, \(j=\sqrt{-1}\).

In the case of the conductive interference

$$\begin{aligned} \overrightarrow{{E}'}_\mathrm{s} =- \hbox {grad } V_\mathrm{e}^0 , \end{aligned}$$
(12)

where \(V_\mathrm{e}^0 \) is the scalar potential of the primary electric flow field along the earth return circuit. It should be noted that the primary electric field is considered in the absence of the earth return circuits.

2.2 SPICE basic circuits

Assuming a segment of the length l of the earth return circuit to be homogeneous (e.g., \(Z', Y' = \hbox {const.}\)), it is possible [16] to model the circuit by a \(\pi \)-two port, as shown in Fig. 2a, with the series impedance

$$\begin{aligned} Z=Z_\mathrm{c} \hbox {sinh}\left( {\gamma l} \right) \end{aligned}$$
(13)

and the shunt admittance

$$\begin{aligned} Y=\frac{2\tanh \left( {\gamma \frac{l}{2}} \right) }{Z_\mathrm{c} } \end{aligned}$$
(14)

where \(\gamma \) is the propagation coefficient and \(Z_{c }\) is the characteristic impedance of the earth return circuit.

If the earth return circuit is subjected to the inductive or conductive effects of an external field with the intensity

\(E'= \hbox {const.}\), the passive model (Fig. 2a) has to be completed by the voltage source \(E=E'l\). This leads to a circuit representation for the inductive and (or) the conductive interference (Fig. 2b).

Fig. 2
figure 2

Model of an elementary segment of a single earth return circuit: a model of a segment of homogeneous line, b \(\pi \)-two port with external influence

Full size image
Fig. 3
figure 3

SPICE basic circuits of a section of the pipeline under steady-state conditions with: a inductive influence, b conductive influence

Full size image

After being divided into sections of quasi-uniform exposure, the earth return circuit can be composed of such basic two-ports which define the nodes and branches of the network model, which is well suited for computer-aided circuit analysis using simulation programs. The number of subdivisions of the earth return circuit can theoretically be as large as required, according to the wanted degree of discrimination in the potential and current computation.

SPICE basic circuits of a segment of homogeneous pipeline with external steady-state excitation are shown in Fig. 3.

The elements of the basic circuit are to determine from the relations:

$$\begin{aligned} R= & {} \hbox {Re}(Z),\nonumber \\ \quad \omega L= & {} \hbox {Im}(Z),\nonumber \\ \quad G= & {} \hbox {Re}\left( \frac{Y}{2}\right) ,\nonumber \\ \quad \omega C= & {} \hbox {Im}\left( \frac{Y}{2}\right) \end{aligned}$$
(15)

The voltage source E (Fig. 3a) in the case of inductive interference due to, e.g., current \(I_{0}\) in a power line overhead conductor:

$$\begin{aligned} E=I_{0} {Z}'_\mathrm{m} l \end{aligned}$$
(16)

where \({Z}'_\mathrm{m} \)—unit-length mutual impedance between the overhead conductor and the subjected pipeline is given by Eq. (9).

In the case of conductive interference, the voltage sources in Fig. 3b represent the scalar potential of the primary electric field in the earth, calculated or measured at end points of the affected pipeline segment. If the primary electric field in the earth is produced by, e.g., a current \(I_{0}\) flowing out of a point earth electrode, the scalar potential

$$\begin{aligned} V_{\mathrm{e}}^{0} (P)=\mathop \int \limits _s^\infty {E_\mathrm{r} \hbox {d}r} =\frac{I_{0} }{2\pi \sigma s} \end{aligned}$$
(17)

where \(E_{\mathrm{r}}\)—radial component of the electric field intensity \(\sigma \)—earth conductivity, s—distance between the point earth electrode and the observation point P.

3 Cases study

In this section, cases are studied using SPICE program in order to evaluate the effect of various parameters on wave phenomena (voltages and currents) in transmission pipeline buried in the vicinity with power line. Long-term inductive interference of power line on nearby pipeline is assumed.

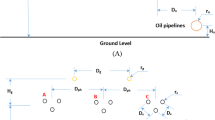
The layout of the power line and pipeline routes is shown in Fig. 4. The total length of the pipeline is \(l=180\) km. The pipeline with diameter 1.4 m is electrically continuous. There are isolation flanges at the two ends of the pipeline. A middle section of the pipeline with length 10 km is in parallel with the power line and distance between power line and pipeline is set as 10 m. Before and after the parallel section of the power line, it is perpendicular to the pipeline so that there is no inductive coupling between the power line and the pipeline. It is assumed that the equivalent influencing current in the equivalent overhead power line conductor is 1.0 A and the frequency \(f=50\) Hz. The soil resistivity \(\rho =100 \Omega \)m.

In order to simulate the inductive effects in the system shown in Fig. 4, the pipeline is modeled as a chain of 180 sections (basic \(\pi \) two-ports), symmetrically located with respect to the middle point of the pipeline, Fig. 5. The length of each section is 1 km. The segment (10 km) of the pipeline is inductive coupled to the power line and is represented by 10 active two-ports (as in Fig. 3a).

3.1 Pipeline leakage resistance

Coating resistance is a fundamental parameter because it affects the propagation coefficient \(\gamma \) and the characteristic impedance \(Z_{\mathrm{c}}\) of the pipeline. It can be shown using Eq. (7) that the principal effect of the pipeline coating is to decrease both Real(\(\gamma \)) and Im(\(\gamma \)) from the bare pipe values at any particular pipe diameter. Well-coated pipes (contrary to poorly coated pipes) having coating resistivities exceeding about 100 k\(\Omega \)m\(^{2}\) have values of the real part and the imaginary part of the propagation coefficient virtually unaffected by the conductivity of the surrounding soil. On the other hand, it follows from Eq. (8) that the principal effect of the pipeline coating is to increase both Real\((Z_{\mathrm{c}})\) and Im(\(Z_{\mathrm{c}})\) from the bare pipe values at any particular pipe diameter. Moreover, well-coated pipes, contrary to poorly coated ones, have values of \(Z_{\mathrm{c}}\) virtually unaffected by the conductivity of the surrounding soil.

First the system shown in Fig. 5 is simulated to evaluate the effects of pipeline leakage (coating) resistance on the voltage and current distributions along the affected pipeline. Tables 1 and 2 show the relevant pipeline parameters. It should be noted that the pipeline parameters (characteristic impedance \( Z_{\mathrm{c}}\) and complex propagation coefficient \(\gamma \)) are calculated according to formulas (7) and (8), whereas the parameters of the elements of the SPICE basic circuits are determined from the relations given in Sect. 2.2.

Four cases were considered—Table 1. In each case, only the value of the resistivity changed: from 10,000 k\(\Omega \)m\(^{2}\) (case 1—high-quality insulation) to 10 k\(\Omega \)m\(^{2}\) (case 4—low quality insulation). Such values of the pipeline coating resistivity exist in practice. It is assumed that in each case the soil resistivity \(\rho =100\,\Omega \hbox {m}\) (also a typical value). Using formulas given in Sect. 2, the values of the wave parameters ( \(\gamma \) and \(Z_{\mathrm{c}})\), electrical parameters (\({R^{\prime }, L^{\prime }, G^{\prime }, C^{\prime }}\)) of the pipeline being modeled and in addition the unit-length intensity of the induced electric field along the pipeline were calculated. Table 2 lists the parameters of the pipeline wave parameters calculated for above mentioned cases, including the wavelength \(\lambda \), phase velocity \(\upsilon \), attenuation coefficient \(\alpha \), phase coefficient \(\beta \) and the relationships between the parameters \(R^{\prime }, \omega L^{\prime }, G^{\prime }, \omega C^{\prime }\) for the frequency \(f= 50\) Hz.

Fig. 4
figure 4

Layout of the power line–pipeline collocation

Full size image
Fig. 5
figure 5

SPICE equivalent model of the power line (180 basic two-ports) in the collocation with a HVAC power line

Full size image
Table 1 Pipeline parameters for different values of pipeline leakage resistance \(r_{u}\)
Full size table
Table 2 Pipeline wave parameters for different values of pipeline leakage resistance \(r_{u}\) (\(\rho = 100~\Omega \)m)
Full size table

The effect of the pipeline leakage resistance is examined, and the calculation results are shown in Figs. 6, 7 and 8.

It can be observed from Fig. 6 that the maximum value (rms value) of the induced potential appears in end points of the pipeline parallel segment (\(-5\) and 5 km). The change in the induced potential on the pipeline is in direct proportion to the change in pipeline leakage resistance. It can be seen that with the increase in the leakage resistance, the value of the induced potential along the pipeline increases and the potentials are carried out outside of the pipeline parallel segment on long distances. Moreover, it can be stated that in case of very well coated pipelines (especially with \(r_{u}=10{,}000\) k\(\Omega \)m\(^{2})\), the wave propagation phenomenon occurs and the shape of potential along the pipeline tends to the distribution of standing wave in open circuit lossless transmission line (in Table 2: \(\omega L^{\prime }>R^{\prime }\) and \(\omega C^{\prime }>>G^{\prime })\). The potential varies along the pipeline in a periodic manner. The peaks and valleys of the potential are clearly present along the pipeline. In contrast to this case, in case of lower values of the coating resistance (\(r_{u}=100\) and 10 k\(\Omega \)m\(^{2})\) the magnitude of the signal is strongly attenuated, the potential decreases exponentially and tends very fast to zero, and the wave propagation effect is not observed.

Similar dependencies can be observed for the longitudinal current and leakage current density along the pipeline, Figs. 7 and 8. The maximum values of the current appear in the middle point of the parallel pipeline segment, whereas the values of the leakage current density in this point are zero. The change in the maximum excited current along the pipeline is in inverse proportion to the change in pipeline leakage resistance. It can be also stated that in case of very well coated pipeline the wave propagation phenomenon occurs and the shapes of current and leakage current density along the pipeline tend to the distribution of standing wave in lossless transmission line. In case of poorly coated pipeline, the current as well as the current density decrease exponentially and quickly tend to zero before they reach the pipeline endpoints.

Fig. 6
figure 6

Effect of leakage resistance on the potential distribution along the pipeline \(r_{u }\): (1) 10,000 k\(\Omega \)m\(^{2}\), (2) 1000 k\(\Omega \)m\(^{2}\), (3) 100 k\(\Omega \)m\(^{2}\), (4) 10 k\(\Omega \)m\(^{2}\) (\(\rho \) = 100 \(\Omega \)m)

Full size image
Fig. 7
figure 7

Effect of leakage resistance on the longitudinal current distribution along the pipeline \(r_{u }\): (1) 10,000 k\(\Omega \)m\(^{2}\), (2) 1000 k\(\Omega \)m\(^{2}\), (3) 100 k\(\Omega \)m\(^{2}\), (4) 10 k\(\Omega \)m\(^{2}\) (\(\rho \) = 100 \(\Omega \)m)

Full size image
Fig. 8
figure 8

Effect of leakage resistance on the leakage current distribution along the pipeline \(r_{u }\): (1) 10,000 k\(\Omega \)m\(^{2}\), (2) 1000 k\(\Omega \)m\(^{2}\), (3) 100 k\(\Omega \)m\(^{2}\), (4) 10 k\(\Omega \)m\(^{2}\) (\(\rho \) = 100 \(\Omega \)m)

Full size image

3.2 Pipeline length

The effect of the total length on the induced potential along the pipeline is examined. The simulations assume that the pipeline parameters are set as in Table 1—case 1 (very good insulation of the pipeline). As previously, the segment (\(-5\) to 5 km) of the pipeline is inductive coupled to the power line and is represented by 10 active two-ports. The model shown in Fig. 5 has been symmetrically shortened by disconnecting basic two-ports on the pipeline ends, so the number of basic two-ports has been changed from 180 to 30. Distributions of the pipeline potential as a function of the pipeline length are shown in Fig. 9. It can be observed from the figure that the wave phenomenon occurs when the length of the pipeline (measured from its center point) is greater than the length of a quarter wave (\(\lambda =82.07\) km). In such a case, the shape of potential along the pipeline tends to the distribution of standing wave in lossless transmission line. The peaks and valleys of the potential are clearly present along the pipeline. Otherwise, the potential does not change along the pipeline in a periodic manner, and the value of induced potential at the ends of the pipeline increases significantly as a result of potential wave reflection from the open ends of the pipeline.

Fig. 9
figure 9

Effect of pipeline length on the potential distribution along the pipeline l: 180 km, 164 km/2 = \(\lambda \), 122 km/2 = 3\(\lambda \)/4, 82 km/2 = \(\lambda \)/2, 40 km/2 = \(\lambda \)/4 (\(r_{u }= 10{,}000 \hbox {k}\Omega \hbox {m}^{2}\) and \(\rho = 100 \Omega \hbox {m}\))

Full size image

3.3 Pipeline potential as a function of time

The objective of the example is to present simulation of time domain responses (potentials) of the system considered in previous sections. Figure 10 presents SPICE simulation of potential waves calculated for two different values of pipeline coating resistance in two points: in distance 1.0 km—potential V(90), and in distance 90 km—potential V(1), both distances measured from the center of the inductively influenced pipeline segment. The initial conditions are set to zero. It should be mentioned that the steady state in the system is achieved after a period of 150 ms. From Fig. 10, the time \(t_{o}\) after which the potential signal appears on the end point of the pipeline can be read (the time interval between first maxima of signals V(90) and V(1), respectively). In Fig. 10a, b are shown the time value and the corresponding value of the potential for both the relevant pipeline points (for the first maximum of potential): (a) \(t_{V(1)}=23.403\) ms, \(t_{V(90)}=1.8056\) ms; (b) \(t_{V(1)}=23.542\) ms, \(t_{V(90)}=1.8056\) ms. The delay time \(t_{o}\) calculated as the difference of these values (\(t_{o}=t_{V(1)}-t_{V(90)})\): (a) \(t_{o}=23.403\)–1.8056 ms = 21.60 ms; (b) \(t_{o}=23.542\)–1.8056 ms = 21.74 ms). On the other hand, using formula \(t = l/v\) the time of the signal passage through a distance l (\(l=89\) km) with the phase velocity v can be calculated. Comparison of delay time of the potential wave at the end point of the pipeline with time of transition of the potential having a constant phase (for different values of coating resistance \(r_{u})\) is presented in Table 3. A large compliance of results may be stated.

Fig. 10
figure 10

Pipeline potential V(90) and V(1) versus time for different values of pipeline leakage resistance \(r_{u }\): a 10,000 k\(\Omega \)m\(^{2}\), b 1000 k\(\Omega \)m\(^{2}\), (\(\rho =100\; \Omega \)m)

Full size image
Table 3 Comparison of delay time of the potential wave at the end point of the pipeline with time of transition of the potential having a constant phase (\(l=89\) km)
Full size table

4 Conclusions

This paper presents a comprehensive study of the effect of different parameters on the induced voltage and current along a transmission pipeline. The use of the circuit simulation package SPICE permits the complex analysis of the EMI on transmission pipelines. In the approach presented, the pipeline is modeled as a large multinode electrical equivalent circuit. The circuit is a chain of basic circuits, which are equivalents of homogenous sections of the pipeline with uniform exposure to the primary interfering electric field associated with the inductive influence.

Due to the practice of applying at the ends of the transmission pipeline of monoblock isolation, the pipeline should be treated as a long transmission line with distributed excitation and open circuited at both ends. It can be concluded that the change in the coating resistance will change the shape of the induced potential distribution drastically. The wave propagation phenomenon can be observed. There are wave reflections at the ends of the pipeline. The potential and current waves propagate with delay in the positive and negative directions on the pipeline.

Moreover, a pipeline with high-quality insulating coating, with unit-length parameters \(R' < \omega L'\) and \(G'< \omega C'\), may not be farther treated as lossy transmission line, and the distribution of induced potentials along the pipelines recalls the distribution of voltage standing wave in a lossless line.

Time simulation conducted in SPICE for the most complex layout (180 basic two-ports—a total of 912 nodes and 1630 elements), while the analysis of AC and TRAN (with forced step simulation) ranged from 13.73 s (TRAN-scoped 400 ms) to 4.03 s (TRAN about the range of 100 ms). The calculations were carried out using a desktop computer with Intel Core i5 CPU 3.4 GHz and 8 GB memory. In general, for the duration of the simulation, the greatest impact has computer’s processor clock rate used in the simulations.

It should be noted that the case concerned is not real, but a legitimate from the point of view of physics. In the SPICE model presented, parameters of the pipeline are identical to the parameters of currently operated transmission pipeline. Power line parallel to the pipeline section has been replaced by an equivalent conductor suspended on high and at a distance from the pipeline found in practice. The value of the net current in the conductor is taken as a unit. Due to the proportionality of the induced signals (pipeline currents and pipeline potentials) and the net current, it is easy to convert results obtained for the unit net current in cases of other values of interfering current. In order to simulate the EMI from power lines on transmission pipelines during real long-term and short-term interferences, more refined approximation should be investigated. An advanced form of the model should consider any configuration and number of overhead power lines, pipelines, compensating earth return circuits, etc. Furthermore, field tests to verify the accuracy of the approach when applied to actual joint-use corridors should be carried out. This will be the subject of a future research