Magnetic field created by a conducting cylindrical shell of finite length

Abstract

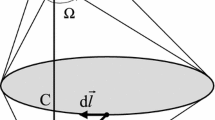
A conceptually simple result, which was recently derived for the circulation of the magnetic field created by a finite portion of wire carrying a slowly varying current, is used with the superposition principle and symmetry considerations to obtain an expression for the magnetic field of a thin cylindrical shell of finite length. This expression is combined with a new formula for an oblique solid angle, to obtain closed form solutions for the magnetic field created by the thin cylindrical shell segment in all regions of space. The solutions derived herein are applied in the limiting situations where the cylindrical shell’s length or radius is very large and compared to the known results for the magnetic field of a long conducting tube, and of an infinite plane, respectively. In addition, the use of physical principles of superposition and symmetry in this study is instructive from an educational perspective.

Appendix: Analytical solution for the solid angle defined by an oblique cone

In the context of spontaneous well-logging parameter identification, Li and Peng [20] derived an analytical solution for the solid angle $\omega$ defined by an oblique cone (in short ‘oblique solid angle’), which is only valid for $R_{\mathrm{C}} >R$. As far as is known to us, no solution is available in the literature for $R_{\mathrm{C}} <R$, the case shown in Fig. 6. In this Appendix, we derive a general analytical solution for the oblique solid angle $\omega$ valid for all values of $R_{\mathrm{C}}$ and R.

Fig. 6

Shows positive oblique solid angle $\omega$, $0\le \omega \le 2\pi$. For the xyz coordinate system chosen, $\omega$ is symmetrical about the xz-plane. Distances $\left( {R, \,H} \right)$, circle radius $\left( {R_{\mathrm{C}} } \right)$, polar coordinates $\left( {\,\rho ,\theta } \right)$, $\vec {r}$ being the position vector of elementary area $\rho \mathrm{d}\theta \mathrm{d}\rho$ relative to the vertex V. If H is allowed to become very small, $\omega \rightarrow 0$ for $R_{\mathrm{C}} <R$ and $\omega \rightarrow 2\pi$ for $R_{\mathrm{C}} >R$

From the definition of solid angle, for the choice of coordinate system in Fig. 6,

$$\begin{aligned} \mathrm{d}\omega =\frac{ \vec {r}\cdot \hat{{k}} \mathrm{d}S}{r^{3}}=\frac{H\rho \,\mathrm{d}\theta \,\mathrm{d}\rho }{r^{3}}, \end{aligned}$$

(18)

where $\hat{{k}}$ is the unit vector along z, $\mathrm{d}S=\rho \,\mathrm{d}\theta \,\mathrm{d}\rho$ is the infinitesimal area which subtends an elementary solid angle $d\omega$ with vertex at $\left( {-R,\;0,\;-H} \right)$, and $\vec {r}$ is given by:

$$\begin{aligned} \vec {r}= & {} \left( {\rho \,\,\cos \theta ,\;\rho \,\,\sin \theta ,\;0} \right) -\left( {-R,\;0,\;-H} \right) \nonumber \\= & {} \left( {\rho \,\,\cos \theta +R,\;\rho \,\,\sin \theta ,\;H} \right) . \end{aligned}$$

(19)

From (18) and (19), and the symmetry of the solid angle about the xz-plane (Fig. 6), we get:

$$\begin{aligned} \omega =2H\int _0^\pi {\mathrm{d}\theta } \int _0^{R_{\mathrm{C}} } {\frac{\rho \,\mathrm{d}\rho }{\left( {\rho ^{2}+2R\,\rho \cos \theta +R^{2}+H^{2}} \right) ^{{ 3}/2}}} . \end{aligned}$$

(20)

Equation (20) can be written as:

$$\begin{aligned} \omega =H\int _0^\pi {\mathrm{d}\theta } \int _0^{R_{\mathrm{C}} } {\frac{2\rho \,\mathrm{d}\rho }{\left[ {\left( {\rho +R\cos \theta } \right) ^{2}+H^{2}+R^{2}\sin ^{2}\theta } \right] ^{{\,3}/2}}} , \end{aligned}$$

(21)

and making the substitution $u=\rho +R\cos \theta$ gives:

$$\begin{aligned}&\omega =H\int _0^\pi {\mathrm{d}\,\theta } \int _{R\cos \theta }^{R_{\mathrm{C}} +R\cos \theta } {\frac{2u\,\mathrm{d}u}{\left( {\,u^{2}+H^{2}+R^{2}\sin ^{2}\theta } \right) ^{{\,3}/2}}}\nonumber \\&\quad ~~~~ -2RH\int _0^\pi {\cos \theta \,\mathrm{d}\theta } \int _{R\cos \theta }^{R_{\mathrm{C}} +R\cos \theta } {\frac{\mathrm{d}u}{\left( {\,u^{2}\,{+}\,H^{2}\,{+}\,R^{2}\sin ^{2}\theta } \right) ^{{\,3}/2}}} .\nonumber \\ \end{aligned}$$

(22)

Integrating with respect to u the two standard integrals in (22) gives:

$$\begin{aligned} \omega= & {} -2H\int _0^\pi {\mathrm{d}\theta \left. { \left( {u^{2}+H^{2}+R^{2}\sin ^{2}\theta } \right) ^{\,-1/2} } \right| _{\,u=R\cos \theta }^{\,u=R_{\mathrm{C}} +R\cos \theta } }\nonumber \\&~~ -2RH\int _0^\pi {\left. {\cos \theta \,\mathrm{d}\theta \frac{1}{H^{2}+R^{2}\sin ^{2}\theta } \frac{u}{\sqrt{u^{2}+H^{2}+R^{2}\sin ^{2}\theta }} } \right| } _{\,u=R\cos \theta }^{\,u=R_{\mathrm{C}} +R\cos \theta } ,\nonumber \\ \end{aligned}$$

(23)

which can be solved and rearranged as:

$$\begin{aligned} \omega= & {} \frac{2H}{\sqrt{H^{2}+R^{2}}}\int _0^\pi {\mathrm{d}\theta -} 2H\int _0^\pi {\frac{\mathrm{d}\theta }{\sqrt{H^{2}+R^{2}+R_{\mathrm{C}}^2 +2\,R\,R_{\mathrm{C}} \cos \theta }}} \nonumber \\&+\frac{2H}{\sqrt{H^{2}+R^{2}}}\int _0^\pi {\frac{R^{2}\cos ^{2}\theta }{H^{2}+R^{2}-R^{2}\cos ^{2}\theta } \mathrm{d}\theta }\nonumber \\&-2R\,H\int _0^\pi {\frac{\cos \theta \mathrm{d}\theta }{H^{2}+R^{2}\sin ^{2}\theta }\frac{R_{\mathrm{C}} +R\cos \theta }{\sqrt{H^{2}+R^{2}+R_{\mathrm{C}}^2 +2\,R\,R_{\mathrm{C}} \cos \theta }}}.\nonumber \\ \end{aligned}$$

(24)

The first integral in (24) is immediate. Since the integrand function in the third term in (24) is symmetrical about $\pi /2$ in the interval of integration, one can integrate it as:

$$\begin{aligned}&\frac{2\,H}{\sqrt{H^{2}+R^{2}}}\int _0^\pi {\frac{R^{2}\cos ^{2}\theta }{H^{2}+R^{2}-R^{2}\cos ^{2}\theta } \mathrm{d}\theta } \nonumber \\&\quad = \frac{4\,H}{\sqrt{H^{2}+R^{2}}} \left. {\left[ {-\theta +\sqrt{1+\frac{R^{2}}{H^{2}}}\tan ^{-1} \left( {\sqrt{1+\frac{R^{2}}{H^{2}}}\tan \theta } \right) } \right] } \right| _{\,0}^{{\,\pi }/2}\nonumber \\&\quad =2\pi \left( {1-\frac{H}{\sqrt{H^{2}+R^{2}}}} \right) . \end{aligned}$$

(25)

Inserting (25) into (24) gives the analytical solution for the oblique solid angle:

$$\begin{aligned} \omega =2\pi \left( {1-\frac{1}{\pi }\int _0^\pi {\frac{H \mathrm{d}\theta }{\sqrt{H^{2}+R^{2}+R_{\mathrm{C}}^2 +2\,R\,R_{\mathrm{C}} \cos \theta }}\frac{H^{2}+R^{2}+R\,R_{\mathrm{C}} \cos \theta }{H^{2}+R^{2}\sin ^{2}\theta }} } \right) , \end{aligned}$$

(26)

which is equivalent to Eqs. (7) and (8), being valid for all $R_{\mathrm{C}}$.

Figure 7 shows the value of $\omega$ as a function of H, for different values of $R/{R_{\mathrm{C}} }$. For ${0<R}/{R_{\mathrm{C}} }<1$, $\omega$ increases toward $2\pi$, while for $R/{R_{\mathrm{C}} }>1$, $\omega$ always increases initially, reaches a maximum, and then decreases towards zero. For $R/{R_{\mathrm{C}} }=1$, $\omega$ increases, reaching the value of $\pi$ when $H=0$. It also shows that for any $H\ne 0$, $\omega$ varies continuously from a maximum, at $R/{R_{\mathrm{C}} }=0$, toward 0 as $R/{R_{\mathrm{C}} }$ approaches $\infty$, whereas for $H=0$, $\omega$ exhibits a discontinuity of $2\pi$ at $R/{R_{\mathrm{C}} }=1$, where it has the value of $\omega =\pi$. A complementary analysis can be made using Fig. 8, which shows the variation in $\omega$ with $R/{R_{\mathrm{C}} }$ for different values of H.

Fig. 7

Plot of $\omega$ as a function of H, for different values of $R/{R_{\mathrm{C}} }$. For a given $R/{R_{\mathrm{C}} }$, $\omega$ is a continuous function of H. For a given $H\ne 0$, $\omega$ is a continuous function of $R/{R_{\mathrm{C}} }$, but for $H=0$, $\omega$ exhibits a discontinuity at $R=R_{\mathrm{C}}$

Fig. 8

Plot of $\omega$ as a function of $R/{R_{\mathrm{C}} }$, for different values ofH. As $H\rightarrow 0$, $\omega$ exhibits a discontinuity of $2\pi$ at $R=R_{\mathrm{C}}$