Capacitance of a finite cylinder

Abstract

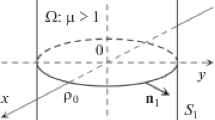
The aim of this paper is to present a new method of solving particular electrostatic problems. It is based on the superposition of the results obtained in the analysis of the single parts of the problem, to get the solution of a complex geometry. In particular, by means of the generalized solutions, dealing with the hollow cylinder and the end caps separately, the charge distribution, and therefore the capacitance, of a finite cylinder are evaluated.

Appendices

Appendix 1: Transforms of the Green functions

In this Appendix, a possible way to evaluate Fourier and Hankel transforms (with respect to x and r ₀ respectively) of Green's function

$$g\left( {r,r_0 ,x} \right) = {1 \over {2\pi }}\int\limits_0^{2\pi } {{{{\rm d}\Phi } \over {\sqrt {r^2 + r_0^2 - 2r\,r_0 \cos \Phi + x^2 } }}} $$

is shown.

The Fourier transform can be performed by means of the relevant integral [4]

$\int\limits_{ - \infty }^\infty {\exp \left( { - jwx} \right)H_0^{\left( 2 \right)} \left( {jwR} \right){\rm d}w = {{2j} \over {\sqrt {R^2 + x^2 } }}} ,$

(23)

and the Bessel functions addition theorem

$$ H_0^{\left( 2 \right)} \left( {mR} \right) = J_0 \left( {mr} \right)H_0^{\left( 2 \right)} \left( {mr_0 } \right) + 2\sum\limits_{k = 1}^\infty {J_k \left( {mr} \right)} H_k^{\left( 2 \right)} \left( {mr_0 } \right)\cos k\Phi $$

(24)

where $R = \sqrt {r^2 + r_0^2 - 2rr_0 \cos \Phi } \;{\rm and}\;r_0 > r.$ By integrating (24) with respect to Φ between 0 and 2π, it is easy to obtain

$$\int\limits_0^{2\pi } {H_0^{\left( 2 \right)} \left( {mR} \right){\rm d}\Phi = 2\pi J_0 \left( {mr} \right)} H_0^{\left( 2 \right)} \left( {mr_0 } \right)$$

(25)

The same passages applied to (23) lead to

$$\int\limits_{ - \infty }^\infty {\exp \left( { - jwx} \right)\left[ {\int\limits_0^{2\pi } {H_{\rm 0}^{\left( 2 \right)} \left( {jwR} \right){\rm d}\Phi } } \right]} {\rm d}w = \int\limits_0^{2\pi } {{{2j} \over {\sqrt {R^2 + x^2 } }}{\rm d}\Phi } $$

(26)

Substituting (25) in the previous equation, with m=jw, the following expression is obtained

$$\int\limits_{ - \infty }^\infty {\exp \left( { - jwx} \right)2\pi J_0 \left( {jwr} \right)H_0^{\left( 2 \right)} \left( {jwr_0 } \right){\rm d}w = \int\limits_0^{2\pi } {{{2j} \over {\sqrt {R^2 + x^2 } }}} } {\rm d}\Phi $$

(27)

namely

$$ {1 \over {2j}}J_0 \left( {jwr} \right)H_0^{\left( 2 \right)} \left( {jwr_0 } \right) = \int\limits_{ - \infty }^\infty {\left[ {\int\limits_0^{2\pi } {{{{\rm d}\Phi } \over {\sqrt {R^2 + x^2 } }}} } \right]} \exp \left( {jwx} \right){\rm d}x = G\left( {r,r_0 ,w} \right) $$

(28)

Remembering that [4]

$$ \matrix{ {{\rm I}_0 \left( z \right) = J_0 \left( {jz} \right),} & { - \pi < \arg z \leq {\pi \over 2}} \cr {K_0 \left( z \right) = - j{\pi \over 2}H_0^{\left( 2 \right)} \left( { - jz} \right),} & { - {\pi \over 2} < \arg z \leq \pi } \cr } $$

formula (28) becomes

$$G\left( {r,r_0 ,w} \right) = {1 \over \pi }{\rm I}_0 \left( {wr} \right)K_0 \left( {wr_0 } \right)$$

With reference to the Hankel transform of Green's function, interchanging the order of integration, it can be written as

$$G\left( {r,w,x} \right) = {1 \over {2\pi }}\int\limits_0^{2\pi } {\left[ {\int\limits_0^\infty {{{r_0 J_0 \left( {wr_0 } \right)} \over {\sqrt {r^2 + r_0^2 - 2rr_0 \cos \Phi + x^2 } }}{\rm d}r_0 } } \right]} {\rm d}\Phi $$

(29)

Now let r, r ₀ be vectors in the plane (x,y), r′=r ₀−r their difference and Φ and Φ′ the angles between r ₀ and r′ with x axis respectively.

Translating the axes as

$$x' = x + x_0 ,\,\,\,y' = y_0 $$

relation (29), after the variable change, becomes:

$$G\left( {r,w,x} \right) = {1 \over {2\pi }}\int\limits_0^{2\pi } {\left[ {\int\limits_0^\infty {{{r'J_0 \left( {w\sqrt {r'^2 + r^2 - 2r'r\cos \Phi ^, } } \right)} \over {\sqrt {r'^2 + x^2 } }}{\rm d}r'} } \right]{\rm d}\Phi '} $$

(30)

The integral in the square brackets in (30) can be evaluated using again the Gegenbauer addition theorem, in the Graf form [4]:

$$ \matrix{ {J_0 \left( {\sqrt {u^2 + v^2 - 2uv\cos \alpha } } \right) = \sum\limits_{k = - \infty }^\infty {J_k \left( u \right)J_k \left( v \right)\cos \left( {k\alpha } \right)} ,} & {u,v > 0,} & {\alpha \in \left[ {0,2\pi } \right]} \cr } $$

(31)

By means of the former relation, expression (30) becomes

$$G\left( {r,w,x} \right) = {1 \over {2\pi }}\sum\limits_{k = - \infty }^\infty {\left[ {\int\limits_0^{2\pi } {\cos \left( {k\Phi '} \right){\rm d}\Phi '\int\limits_0^\infty {{{r'J_k \left( {wr'} \right)J_k \left( {wr} \right)} \over {\sqrt {r'^2 + x^2 } }}{\rm d}r'} } } \right]} $$

(32)

Finally, remembering that

$$ \int\limits_0^{2\pi } {\cos \left( {k\Phi '} \right){\rm d}\Phi ' = 2\pi \delta _{k,0} } $$

relation (32) simplifies as [4]

$$ G\left( {r,w,x} \right) = \int\limits_0^\infty {{{r'J_k \left( {wr'} \right)J_k \left( {wr} \right)} \over {\sqrt {r'^2 + x^2 } }}} {\rm d}r' = J_0 \left( {wr_0 } \right){{\exp \left( { - w\left| x \right|} \right)} \over w} $$

Appendix 2: Capacitance of a disc of negligible thickness

In this Appendix, the capacitance with respect to infinity of a metallic disc of negligible thickness is analytically evaluated. The boundary conditions on the metallic disc lead to

$${1 \over {2\varepsilon }}\int\limits_0^a {r_0 } \sigma _{\rm B} \left( {r_0 } \right)g\left( {r,r_0 ,0} \right){\rm d}r_0 = V\,\,\,\,\forall r \in \left[ {0,a} \right]$$

(33)

V being the potential of the disc. Using (2) in the particular case p=1/2 to expand the charge distribution, and expressing Green's function in terms of Hankel transform, upon a projection onto the basis function themselves, the following algebraic system is obtained

$$\sum\limits_{n = 1}^\infty {D_{m,n} \,\,b_n = \sqrt {{2 \over \pi }} } \delta _{m,1} $$

where the coefficient matrix is defined as

$$D_{m,n} = D_{m,n} = \pi a\int\limits_0^\infty {{{J_{2n - 2 + 1/2} \left( {wa} \right)} \over {\left( {wa} \right)^{1/2} }}} {{J_{2m - 2 + 1/2} \left( {wa} \right)} \over {\left( {wa} \right)^{1/2} }}{\rm d}w = {\pi \over {4n - 3}}\delta _{n,m} $$

(34)

Since integral (34) is not zero only when m equals n, b ₁ can be analytically evaluated as

$$b_1 = {{\sqrt 2 } \over {\pi \sqrt \pi }},\;w{\rm ith}\;b_i = 0\,\,\,{\rm if}\;i \ge 2$$

and it is readily obtained

$$C_{{\rm DISC}} = {{4\pi ^2 \varepsilon a} \over {\sqrt 2 \;\Gamma \left( {1 + 1/2} \right)}}b_1 = 8\varepsilon a$$