The paint pot problem and common multiples in monoids

Abstract

Illustrated by a problem on paint pots that is easy to understand but hard to solve, we investigate whether particular monoids have the property of common right multiples. As one result we characterize generalized braid monoids represented by undirected graphs, being a subclass of Artin–Tits monoids. Stated in other words, we investigate to which graphs the old Garside result stating that braid monoids have the property of common right multiples, generalizes. This characterization also follows from old results on Coxeter groups and the connection between finiteness of Coxeter groups and common right multiples in Artin–Tits monoids. However, our independent presentation is self-contained up to some basic knowledge of rewriting, and also applies to monoids beyond the Artin–Tits format. The main new contribution is a technique to prove that the property of common right multiples does not hold, by finding a particular model, in our examples all being finite.

1 Introduction

Consider a finite sequence of paint pots. The following steps are allowed

• Two consecutive non-empty pots may be swapped.

• If the two neighbours of a non-empty pot are empty, then the paint in the middle pot may be divided over the two neighbours, after which these neighbours will be non-empty and the middle one will be empty. Also the reverse of this step is allowed: if the two neighbours of an empty pot contain paint of the same color, then this paint may be put in the middle pot after which the two neighbours will be empty.

In a picture:

Is it possible to start with a sequence in which the first four pots contain paint in four different colors, and by only applying steps of the above type end up in a sequence of which the first pot is empty?

Maybe the reader should stop reading now and try to solve this problem and experience its hardness.

As a notation for the problem write a for an empty pot and b, c, d, e for the initial colors of the first four pots. Maybe there are more colors, but these do not affect the problem and will be ignored. Now a sequence of paint pots is represented by a word over these five symbols. Let E be the following set of equations

$$\begin{aligned} \begin{array}{rcll} pq &{} = &{} qp &{} \text{ for } \text{ all }\ p,q \in \{b,c,d,e\}, p \ne q, \\ apa &{} = &{}pap &{} \text{ for } \text{ all }\ p \in \{b,c,d,e\}. \end{array}\end{aligned}$$

Now the problem boils down to the question whether words x, y exist such that $a x = bcde y$ in the monoid of words over $\{a,b,c,d,e\}$ modulo E.

In this paper we will prove that the answer on the question is negative, by showing that in the corresponding monoid the words a and bcde do not have a common right multiple.

In fact the topic of this paper is to investigate for a whole range of monoids whether any two words admit a common right multiple or not. A particular class of monoids that we consider are the Artin–Tits monoids, that is, monoids over a finite alphabet in which for every two distinct symbols p, q we have exactly one equation of one of the shapes

$$\begin{aligned} pq=qp, \; pqp=qpq, \; pqpq=qpqp, \; pqpqp = qpqpq, \; \ldots . \end{aligned}$$

We concentrate on the case containing only equations of the shape $pq=qp$ or $pqp=qpq$. These are called generalized braids, [9], and can be characterized by the undirected graph of which the nodes are the symbols and the edges are the pairs of symbols p, q for which the equation is $pqp=qpq$. So for symbols p, q not connected by an edge the equation is $pq=qp$. In case the graph consists of a single path, this corresponds exactly to the usual braids as already studied in [1]. A key question is to characterize for which graphs the corresponding generalized braid monoids have common right multiples. This has been solved long ago by the observation that having common right multiples in the Artin–Tits monoids is equivalent to finiteness of the corresponding Coxeter groups [2], Proposition 5.5 and Satz 5.6, based on results from Tits [13]. These Coxeter groups are obtained from the Artin–Tits monoids by adding the equations $pp = I$ for all symbols p. Finiteness of Coxeter groups has been fully analysed by Coxeter in 1935 [4]. So combining these results gives exactly the characterization we asked for. Our goal is to develop techniques to conclude this directly and self-contained, and also apply the techniques to other formats.

In order to achieve this we need two techniques: one for proving and the other for disproving that any two words admit a common right multiple. For the former we follow the basic idea of Garside who proved that braids have common right multiples in [8]. The key idea is the construction of a fundamental word $\varDelta$ (in later work also called Garside word) having particular properties from which the existence of common right multiples and more properties can be concluded. This concept of fundamental word is also central in the above mentioned result from [2]. This was the starting point of Garside theory, leading to an extensive text book [6]. In this paper we only consider the issue of common right multiples. By a short and elementary proof we show that to conclude the existence of common right multiples only two properties of the Garside word are needed, that we call init flexible and rotation flexible. In all our cases we have a straightforward way to construct an init flexible word, based on a rewriting method that is closely related to the word reversal technique as presented e.g. in [6], Chapter IX, Prop 1.33, and can be visualized as tiling. By the same tiling approach we are able to check that this constructed word is also rotation flexible. In this way we are able to conclude for these cases that any two words admit a common right multiple in a self-contained way, independent of the theory presented in [6]. A similar rewriting / tiling approach for braids was already elaborated in [7], however, without the notions of init and rotation flexibility..

For proving the converse, so proving that two words do not admit a common right multiple, our technique is completely different, and has not been considered before to our knowledge. For a set E of equations we define a model for E to be a non-empty set M, together with a mapping $a_M: M \rightarrow M$ for every symbol a, such that $u_M = v_M$ for every equation $u=v$ in E, where for a word $u = u_1 u_2 \ldots u_n$ the mapping $u_M: M \rightarrow M$ is defined by $u_M = u_{1M} \circ u_{2M} \circ \cdots \circ u_{nM}$. If we can find words u, v such that $u_M(m) \ne v_M(n)$ for all $m,n \in M$, then this proves that u, v have no common right multiple. This observation is not hard to prove, but the challenge is to find a corresponding model, finite or infinite. We prove that this method is not only sound but also complete: two words have no common right multiple if and only if such a (possibly infinite) model exists. For the paint pot problem we find such a model M with $|M| = 8$ in which b(c(d(e(m)))) is always one of two particular elements of M, while a(m) is always one of the remaining 6 elements. So indeed this gives the promised negative answer on the question we started with. For several other problems we find similar finite models, of up to 27 elements.

This paper is organized as follows. In Sect. 2 we give the basic definitions and present our results for Artin–Tits monoids. These results consist of positive results: for a particular graph the corresponding generalized braid monoid has common right multiples, and negative results: there are words in the corresponding generalized braid monoid not having common right multiples. Section 3 shows how the positive results are obtained from the notions init flexible and rotation flexible. Next in Sect. 4 it is shown how these properties can be checked by rewriting, covering all positive results except for one. The remaining positive result is obtained in Sect. 5, again exploiting the flexibility properties. Section 6 presents the negative results by the above mentioned technique of finding models. We conclude in Sect. 7.

2 Preliminaries and results for Artin–Tits monoids

We consider a finite alphabet $\varSigma$. The set of words over $\varSigma$ is denoted by $\varSigma ^*$. An equation is a pair of words, denoted by $u=v$. Equations applied in only one direction are also called rewrite rules, denoted by $u \rightarrow v$. For a set E of equations we write $\rightarrow _E$ for the relation on words defined by

$$\begin{aligned} x \rightarrow _E y \; \Longleftrightarrow \;\exists s=t \in E, u,v \in \varSigma ^*: x = usv \wedge y = utv. \end{aligned}$$

We write $=_E$ for the reflexive symmetric transitive closure of the relation $\rightarrow _E$, that is, $x =_E y$ if and only if there exists a natural number n and words $x_1,x_2,\ldots ,x_n$ such that $x_1 = x$, $x_n = y$ and either $x_i \rightarrow _E x_{i+1}$ or $x_{i+1} \rightarrow _E x_i$ for all $i = 1,2,\ldots ,n-1$.

The monoid $M_E$ of words over $\varSigma$ modulo E is defined to be $M_E = \varSigma ^* / {=_E}$.

In Garside theory the monoids $M_E$ are studied for various E, and equality in this monoid is just denoted by ’$=$’. As we will also consider rewriting and equational reasoning, we prefer to consider words as the first class citizens and denote ’$=$’ for word equality, where the just defined ’$=_E$’ corresponds to equality modulo E, being the equality in the monoid $M_E$.

Definition 1

In a monoid $M_E$ two words $u,v \in \varSigma ^*$ have a common right multiple if there exist $x,y \in \varSigma ^*$ such that $ux =_E vy$.

The monoid $M_E$ has common right multiples if every two words $u,v \in \varSigma ^*$ have a common right multiple.

2.1 Artin–Tits monoids

For two symbols a, b and a natural number m write $(a|b)^m$ for the prefix of length m of the infinite word $abab\cdots$. Formally, we define it inductively by $(a|b)^0 = \epsilon$ and $(a|b)^{m+1} = a (b|a)^m$ for all $m \ge 0$.

Definition 2

For n symbols $a_1,\ldots ,a_n$ and natural numbers $m_{ij} >1$ for $1 \le i < j \le n$ the corresponding Artin–Tits monoid is the monoid on the $n(n-1)/2$ equations $(a_i | a_j)^{m_{ij}} = (a_j | a_i)^{m_{ij}}$, for $1 \le i < j \le n$.

Definition 3

For an undirected graph on n nodes, numbered from 1 to n, the corresponding generalized braid monoid is the Artin–Tits monoid on n symbols where $m_{ij} = 3$ if i, j are connected by an edge, and $m_{ij} = 2$ otherwise.

For instance, the paint pot problem asks whether $a_1$ and $a_2 a_3 a_4 a_5$ have a common right multiple in the monoid obtained by taking $n =5$, $m_{1j} = 3$ for $j = 2,3,4,5$ and $m_{ij} = 2$ for $2 \le i < j \le 5$, being the generalized braid monoid corresponding to the graph

The case where the graph consists of a single path corresponds to the standard braid monoid as studied in [1], for which it was shown in [8] that it has common right multiples. The starting point of our work was a question posed by Jan Willem Klop:

For which graphs does the generalized braid have common right multiples?

His first guess was that this holds if and only if the graph contains no cycle, but this was refuted by our negative solution of the paint pot problem. At that moment, we were not aware of the fact that a full characterization for all graphs already follows from earlier results on Coxeter graphs and their relation to Artin–Tits monoids. Nevertheless, as our techniques are completely different, it makes sense to see what our techniques achieve in this direction.

For $i \ge j \ge k > 0$ let $[ 3^{i,j,k}]$ denote the graph consisting of a central node of degree 3 and three paths of lengths i, j, k starting from this central node. For instance, $[ 3^{4,2,1}]$ is the following graph:

The following theorem summarizes our negative answers on the question, and will be proved in Sect. 6.

Theorem 1

Consider a connected graph having at least one of the following four properties:

• The graph contains a cycle,

• The graph contains a node of degree $\ge 4$,

• The graph contains at least two nodes of degree 3,

• The graph has $[ 3^{2,2,2}]$ as a subgraph.

Then in the corresponding generalized braid monoid there are two words not having a common right multiple.

Note that all connected graphs that are not a single path and are not of the shape $[ 3^{k,j,i}]$ are covered by Theorem 1.

The following theorem gives our positive answers on the question, and will be proved in Sects. 3, 4 and 5.

Theorem 2

For the graphs $[ 3^{4,2,1}]$ and $[ 3^{n,1,1}]$ for any $n \ge 1$ the corresponding generalized braid monoid has common right multiples.

Together Theorems 1 and 2 cover all connected graphs except for $[ 3^{m,k,1}]$ for $3 \le k \le m$, and $[ 3^{k,2,1}]$ for $k \ge 5$, which are known not to have common right multiples, as a result from [2] as we already mentioned in the introduction, combined with the classification of finiteness of Coxeter groups in [4].

Single paths correspond to ordinary braids for which having common right multiples was proved in [8]; since they are subgraphs of $[ 3^{n,1,1}]$ this also follow from Theorem 2.

3 Proving common right multiples

The property of common right multiples coincides with confluence of a particular relation. In [14] a property called Z was introduced that implies confluence, and as an example it was shown that braids satisfy common right multiples. Extracting and polishing these observations leads to the following definition and theorem.

Definition 4

A word $\varDelta \in \varSigma ^*$ is called init flexible with respect to E if for every $a \in \varSigma$ there exists $y \in \varSigma ^*$ such that $\varDelta =_E a y$.

A word $\varDelta \in \varSigma ^*$ is called rotation flexible with respect to E if for every $a \in \varSigma$ there exists $y \in \varSigma ^*$ such that $a \varDelta =_E \varDelta y$.

In Sect. 7 we will see that the classical notion of Garside word implies both being init flexible and rotation flexible. Now we will show that these notions are sufficient to conclude common right multiples.

Lemma 1

Let $\varDelta \in \varSigma ^*$ be rotation flexible with respect to E. Then for every $x \in \varSigma ^*$ there exists $y \in \varSigma ^*$ such that $x \varDelta =_E \varDelta y$.

Proof

Induction on |x|. $\square$

Theorem 3

Assume that $\varDelta \in \varSigma ^*$ exists that is both init flexible and rotation flexible with respect to E. Then $M_E$ has common right multiples.

Proof

For arbitrary $u,v \in \varSigma ^*$ we have to construct $x,y \in \varSigma ^*$ such that $ux =_E vy$. We apply induction on |u|. For $|u| = 0$ the property holds by choosing $x = v$ and $y = \epsilon$. Next assume $u = a u'$ for $a \in \varSigma$. Then according to Lemma 1 and init flexibility we obtain $w,y \in \varSigma ^*$ such that $v \varDelta =_E \varDelta w =_E a y w$. According to the induction hypothesis for $u'$ we obtain $x,z \in \varSigma ^*$ such that $u' x =_E ywz$. Hence $ux = a u' x =_E a y w z =_E v \varDelta z$, proving the theorem. $\square$

Note that Theorem 3 does not require any condition on the shape of the equations in E.

When applying Theorem 3 to Artin–Tits monoids we have to construct a suitable string $\varDelta \in \varSigma ^*$. We do this by focussing only on init flexibility. Writing $\varSigma = \{a_1,a_2,\ldots ,a_n\}$ we start by $\varDelta _1 = a_1$, which trivially is init flexible over $\{ a_1 \}$. Next for $i = 2,\ldots ,n$ we try to construct $z_i \in \{a_1,\ldots ,a_i\}^*$ such that there exists $w \in \{a_1,\ldots ,a_i\}^*$ such that $\varDelta _{i-1} z_i =_E a_i w$. This is done by a tiling process based on rewriting that will be presented and illustrated in detail in Sect. 4. As long as this construction succeeds we define $\varDelta _i = \varDelta _{i-1} z_i$ for $i = 2,3,\ldots$. Note that $\varDelta _i$ is init flexible with respect to $a_1,\ldots ,a_i$: for $a_i$ this follows from $\varDelta _{i-1} z_i =_E a_i w$, and for $a_1,\ldots ,a_{i-1}$ this holds since $\varDelta _{i-1}$ is init flexible with respect to $a_1,\ldots ,a_{i-1}$. If this all succeeds, then $\varDelta = \varDelta _n$ is init flexible with respect to $\varSigma = \{a_1,a_2,\ldots ,a_n\}$. Next we check by again using the tiling / word reversing process whether rotation flexibility holds. In all cases we meet, this indeed could be checked, being sufficient for safely drawing our conclusions without a need to investigate rotation flexibility in general.

Tiling is a staple of rewrite theory since its inception [3, 10]. It takes centre stage, under the name of word reversal, in recent developments in algebra, cf. pp. 47–94 of [5] and (Chapter IX of) the book [6]. Links between both are given in Section 8.9 of [11] and in [7, 12]. Taking $\varDelta$ as least common multiple of all symbols we based on Lemma 8.7.35 of [11], the idea goes back to the Gross–Knuth strategy in rewriting, cf. [12], and Garside’s fundamental word in algebra [8].

The next example shows that outside the Artin–Tits format it does not hold that init flexibility implies rotation flexibility.

Example 1

Let E consist of the single equation $abb = baa$. Choose $\varDelta = abb$. Since $abb =_E abb$ and $abb =_E baa$ it is init flexible. But it is not rotation flexible, since $a \varDelta = aabb$ converts by E to no other words than aabb and abaa, none of which starting by abb. In Sect. 6 we will prove that $M_E$ has no common right multiples, in particular, aa and b have no common right multiple.

In the next section we develop a technique to systematically construct an init flexible word for particular monoids, and to check rotation flexibility. If this succeeds then by Theorem 3 the monoid has common right multiples.

Remark 1

In Example 1 we have not just chosen the word $\varDelta$, but in fact we systematically constructed it. In particular, using notation from the construction on page 6 and detailed below, $\varDelta _1 = a$ and $\varDelta _2 = abb = \varDelta$ with $\varDelta _2$ constructed by tiling starting with Ba with respect to the rules $R_E = \{ Aa \rightarrow \epsilon ,\; Bb \rightarrow \epsilon ,\; Ab \rightarrow bbAA \; Ba \rightarrow aaBB \}$. The normal form of Ba is aaBB, so the construction gives $\varDelta _2 = \varDelta _1bb = abb = \varDelta$.

4 Common right multiples by rewriting

In this section E is a set of equations over an alphabet $\varSigma$ in which for every equation $u=v$ in E both u and v are non-empty. For every $a \in \varSigma$ we introduce a fresh capitalized symbol A, and write $\varSigma ^C$ for $\{A \mid a \in \varSigma \}$. For a word $u = u_1 u_2 \cdots u_n \in \varSigma ^*$ we denote $U = U_n U_{n-1} \cdots U_1$, note that the symbols are not only capitalized but also reversed. We will use u, v, w, x, y, z to denote words over $\varSigma$ and U, V, W, X, Y, Z to denote words over $\varSigma ^C$, both to be extended by primes and indices when needed.

We define $R = R_E$ to be the set of the following rewrite rules over $\varSigma \cup \varSigma ^C$: $Aa \rightarrow \epsilon$ for all $a \in \varSigma$, and $Ba \rightarrow vU$ and $Ab \rightarrow uV$ for all equations $au = bv$ in E.

Theorem 4

Assume that for every $a \ne b \in \varSigma$ there is exactly one equation of the shape $au = bv$ or $bv = au$ in E, and E contains only these equations. Write $R = R_E$. If $Vu \rightarrow _R^* yX$, then $ux =_E vy$.

The power of this theorem is that finding common right multiples for v and u can now be done by rewriting a particular term. The rewrite system has been designed in order to achieve this result. Before giving the proof we observe that the assumptions for E in Theorem 4 hold for Artin–Tits monoids, and from these assumption it follows that for every $a,b \in \varSigma$ there is exactly one rule in R with left hand side Ab. By the shape of their left hand sides there are no critical pairs between such rules, and because in our case we only do string rewriting, Huet’s critical pair lemma [12, Lemma 2.7.15] specialises to that if $t \rightarrow _R u$ and $t \rightarrow _R v$, then either $u = v$, or a word w exists such that $u \rightarrow _R w$ and $v \rightarrow _R w$. Immediate consequences of that are the following, where words that cannot be rewritten are called normal forms as usual.

Lemma 2

Let E satisfy the assumptions of Theorem 4. Then

• 1. All normal forms of $R = R_E$ are of the shape uV.

• 2. For words s, t over $\varSigma \cup \varSigma ^C$ and a normal from n it holds that if $s \rightarrow _R^* n$ and $s \rightarrow _R^* t$, then $t \rightarrow _R^* n$.

• 3. If $s \rightarrow _R^* n$ for a normal form n, then there is no infinite reduction starting in s.

• 4. All reductions from any word s to a normal form have the same number of steps.

Item 1 follows by the shapes of the left hand sides of the rules, and items 2–4 are immediate consequences of that R has the so-called random descent property, by [11, Theorem  3] applied to the above instance of the critical pair lemma.

As we stated, the power of Theorem 4 is that it can be used for efficiently checking whether two words u, v have a common right multiple: just start by Vu and apply the rules of $R_E$ as long as possible. If this ends in a normal form, then this normal form should be of the shape yX according to Lemma 2 (1), and then the two words u, v have a common right multiple by Theorem 4. This will be the key procedure by which a word $\varDelta$ will be found systematically, proving that the monoid $M_E$ has common right multiples by Theorem 3.

Now we give the proof of Theorem 4.

Proof

Assume $Vu \rightarrow _R^k yX$. We will prove $ux =_E vy$ by induction on k. For $k=0$ we have $Vu = yX$ which is only possible if $V = X = \epsilon$ and $u=y$, or $V = X$ and $u=y=\epsilon$, for which $ux = vy$. For $k >0$ we observe that the first step of $Vu \rightarrow _R^k yX$ is of the shape

$$\begin{aligned}Vu = V' B a u' \rightarrow _R V' w_1 Z_1 u'\end{aligned}$$

for $u = a u'$ and $v = b v'$, and $a z_1 = b w_1$ an equation in E, yielding the rule $Ba \rightarrow w_1 Z_1$ in R. Next rewrite $Z_1 u'$ as long as possible. This does not go on forever, since an infinite reduction of $Z_1 u'$ would also yield an infinite reduction of $Vu \rightarrow _R V' w_1 Z_1 u'$, contradicting Lemma 2 (3) since Vu rewrites to the normal form yX. So $Z_1 u'$ rewrites to a normal form. According to Lemma 2 (2) this normal form is of the shape $w_2 Z_2$, and we have $Vu \rightarrow _R V' w_1 Z_1 u' \rightarrow _R^* V' w_1 w_2 Z_2$. Next we rewrite $V' w_1 w_2$ as long as possible, similarly rewriting to a normal form $w_3 Z_3$. Hence Vu rewrites to $w_3 Z_3 Z_2$. By Lemma 2 (2) we obtain $w_3 Z_3 Z_2 \rightarrow _R^* yX$. As $w_3 Z_3 Z_2$ is already a normal form, this is only possible if $w_3 = y$ and $Z_3 Z_2 = X$. By Lemma 2 (4) the reductions $Z_1 u' \rightarrow _R^* w_2 Z_2$ and $V' w_1 w_2 \rightarrow _R^* w_3 Z_3$ are shorter than k, hence by the induction hypothesis we obtain $u' z_2 =_E z_1 w_2$ and $w_1 w_2 z_3 =_E v' w_3$. Combining all yields $ux = a u' z_2 z_3 =_E a z_1 w_2 z_3 =_E b w_1 w_2 z_3 =_E b v' w_3 = vy$. $\square$

This process can be visualized by drawing the lower case symbols horizontally and the capitals vertically. Then the process filling the diagram starting from the top left is called tiling. Then the above proof is visualized as follows:

All small rectangles in this tiling picture are filled by applying R-steps, while all paths from the top left to the bottom right are E-convertible to each other.

Remark 2

We employ Theorem 4 as it is sufficient for our purposes here and its proof is easy. However, its assumptions are not always all necessary, as witnessed by:

• Let $E = \{ {a}\mathrel {{=}}{b}{b}{a}, {b}\mathrel {{=}}{c},{c}\mathrel {{=}}{a}\}$. Then $R = \{ Aa \rightarrow \epsilon ,\; Bb \rightarrow \epsilon ,\; Cc \rightarrow \epsilon ,\; Ba \rightarrow ba,\; Ab \rightarrow AB,\; Cb \rightarrow \epsilon ,\; Bc \rightarrow \epsilon , Ac \rightarrow \epsilon ,\; Ca \rightarrow \epsilon \}$, i.e. all local peaks except for Ba and Ab, rewrite to the empty word. For the words $u = {b}{a}$ and $v = {a}{a}$, tiling of $Vu = {A}{A}{b}{a}$ then (only) cycles as ${A}{A}{b}{a}\mathrel {{\rightarrow }_{R }}{A}{A}{B}{a}\mathrel {{\rightarrow }_{R }}{A}{A}{b}{a}$; the assumption of Theorem 4 that Vu rewrites to a normal form, does not hold. However, its conclusion does hold: $u = {b}{a}$ and $v = {a}{a}$ do have a common right multiple; in fact both are: ${b}{a}\mathrel {{=_E}}{c}{a}\mathrel {{=_E}}{a}{a}$. Thus, without more, one cannot conclude to the non-existence of common right multiples if tiling does not terminate.

• Let $\varSigma = \{ a,b \}$ and $E = \emptyset$ so that $R = \{ Aa \rightarrow \epsilon ,\; Bb \rightarrow \epsilon \}$. For the words $u = {a}{b}$ and $v = {a}$, tiling of $Vu = {A}{a}{b}$ terminates in a normal form ${A}{a}{b}\mathrel {{\rightarrow }_{R}}{b}$, so $x = \epsilon$ and $y = {b}$. Despite that the assumption of Theorem 4 that there is exactly one equation in E between words starting with a respectively b, does not hold, its conclusion does: $ux = {a}{b}= vy$.

• Similarly, having more than one such equation in E is harmless. For instance, for $E = \{ aa = b,\; a = bb \}$ we obtain $R = \{ Aa \rightarrow \epsilon ,\; Bb \rightarrow \epsilon ,\; Ba \rightarrow A,\; Ab \rightarrow a,\; Ba \rightarrow b,\; Ab \rightarrow B \}$. Then for words $u = ab$ and $v = b$, tiling of $Vu = {B}{a}{b}$ may proceed as ${B}{a}{b}\mathrel {{\rightarrow }_{R }}{A}{b}\mathrel {{\rightarrow }_{R }}{B}$, so $x = {b}$ and $y = \epsilon$. Accordingly, $ux = abb =_E aa =_E b = vy$ shows u and v have a common right multiple.

  Even stronger, in this example any pair of words has a common right multiple as a consequence of the following result, which we state without proof: for R over $\varSigma \cup \varSigma ^C$ having rules of shape $Ab \rightarrow wZ$, and S over $\varSigma$ having corresponding rewrite rules $aw \rightarrow bz$, if $Vu \rightarrow _R^* yX$, then $vy \rightarrow _S^* ux$. For example, for R and the diagram with legs abb and b as above, $S = \{ a \rightarrow a,\; b \rightarrow b,\; b \rightarrow aa,\; aa \rightarrow b,\; a \rightarrow bb,\; bb \rightarrow a \}$ and the result yields $abb \rightarrow _S aa \rightarrow _S b$, entailing $abb =_E b$.

Next we give a few examples of how to use Theorem 4 to prove that particular Artin–Tits monoids have common right multiples. We do this by focussing for $\varSigma = \{ a_1,a_2,\ldots ,a_n \}$ on the construction of init flexible words $\varDelta _1, \varDelta _2, \ldots , \varDelta _n$ in the way described on page 6. The algorithm starts by $\varDelta _1 = a_1$, trivially init flexible for $\{ a_1 \}$. Then if tiling $A_2\varDelta _1$ with respect to $R = R_E$ results in $y_2X_2$, we set $\varDelta _2 = \varDelta _1x_2$, which is init flexible for $\{ a_1,a_2 \}$ since $a_2y_2 =_E \varDelta _1x_2$ by Theorem 4. Then if tiling $a_3\varDelta _2$ results in $y_3X_3$, we set $\varDelta _3 = \varDelta _2x_3$, which is init flexible for $\{ a_1,a_2,a_3 \}$ since $a_3y_3 =_E \varDelta _2x_3$ by Theorem 4. Continuing like this, if this succeeds for all symbols in $\varSigma$ we have constructed a word $\varDelta _n$ init flexible for $\varSigma$.

In all cases we use a small program to rewrite particular strings to normal form with respect to $R = R_E$. This program (in fact written and executed independently by both authors) only constructs $R_E$ according its definition, and rewrites by searching for left hand sides and replacing by right hand sides as long as possible. Efficiency is no issue: in all cases yielding a normal form it is obtained instantaneously using the most straightforward implementation.

Example 2

Let E consist of the equations

$$\begin{aligned} aba = bab,\; aca = cac,\; ada = dad,\; bc=cb,\; bd=db,\; cd=dc. \end{aligned}$$

This corresponds to the generalized braid of the graph $[ 3^{1,1,1}]$, and can also be seen as the simplified version of the paint pot problem only having three colors. The following shows that bcd and a have a common right multiple:

$$\begin{aligned} \begin{array}{llllllll} &{}bc{\underline{dad}}cabacda &{}=&{}bcad{\underline{aca}}bacda &{}=&{}bcadca{\underline{cb}}acda &{}=&{} bcadcab{\underline{cac}}da \\ =&{}bcadcabac{\underline{ada}} &{}=&{}bcadc{\underline{aba}}cdad &{}=&{}bca{\underline{dc}}babcdad &{}=&{}b{\underline{cac}}dbabcdad \\ =&{}baca{\underline{db}}abcdad &{}=&{}bacabdab{\underline{cd}}ad&{}=&{} bacabda{\underline{bd}}cad &{}=&{}bacab{\underline{dad}}bcad \\ =&{}bac{\underline{aba}}dabcad &{}=&{}ba{\underline{cb}}abdabcad &{}=&{}{\underline{bab}}cabdabcad &{}=&{}abacabdabcad. \end{array} \end{aligned}$$

Next we show that not only bcd and a have a common right multiple, but every two words. In order to do so we systematically construct a word $\varDelta$ that is init flexible and rotation flexible, then the claim follows from Theorem 3. First we focus on init flexibility. Number the $n=4$ symbols by $a_1 = a$, $a_2 = b$, $a_3 = c$, $a_4 = d$. We start by $\varDelta _1 = a$. Next for $i = 2,3,4$ we construct $\varDelta _i$ for which for all $j = 1,2,\ldots ,i$ there exist $y_j$ such that $\varDelta _i =_E a_j y_j$. Then $\varDelta = \varDelta _n$ is init flexible by construction. To construct $\varDelta _2$ we take V to be the capitalized version B of $a_2$, and rewrite the word $V \varDelta _1 = Ba$ with respect to $R_E$ as long as possible. Note that $R_E$ consists of the following rules:

$$\begin{aligned} \begin{array}{rclrclrclrcl} Aa &{} \rightarrow &{} \epsilon &{} Ba &{}\rightarrow &{} abAB &{} Ca &{}\rightarrow &{} acAC &{} Da &{}\rightarrow &{} adAD \\ Ab &{} \rightarrow &{} baBA &{} Bb &{}\rightarrow &{} \epsilon &{} Cb &{}\rightarrow &{} bC &{} Db &{}\rightarrow &{} bD \\ Ac &{} \rightarrow &{} caCA &{} Bc &{}\rightarrow &{} cB &{} Cc &{}\rightarrow &{} \epsilon &{} Dc &{}\rightarrow &{} cD \\ Ad &{} \rightarrow &{} daDA &{} Bd &{}\rightarrow &{} dB &{} Cd &{}\rightarrow &{} dC &{} Dd &{}\rightarrow &{} \epsilon , \end{array} \end{aligned}$$

by which Ba rewrites in one step to abAB. By Theorem 4 we obtain $bab =_E aba$. Hence we define $\varDelta _2 = \varDelta _1 ba = aba$ for which indeed for $i = 1,2$ there exist $y_i$ such that $\varDelta _2 =_E a_i y_i$.

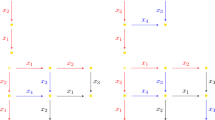
To construct $\varDelta _3$ we take V to be the capitalized version C of $a_3$, and rewrite the word $V \varDelta _2 = Caba$ with respect to $R_E$ as long as possible, resulting in acbacBAC. This rewriting can be visualized in a tiling diagram as follows

Here C in Caba corresponds to the leftmost vertical arrow, and aba in Caba corresponds to the top horizontal path. Every node with an arrow down and an arrow to the right is a peak, and a corresponding rewrite rule can be applied, creating a vertical arrow for every capital in the right hand side of the rule, and a horizontal arrow for every lower case letter in the right hand side of the rule. In case of an empty right hand side no such arrows are created, indicated by $\epsilon$ in the picture, to be ignored in processing next peaks. The resulting normal form acbacBAC is seen as the horizontal path at the bottom followed by the capitalized reversed path from the right top to the right bottom.

As Caba rewrites to acbacBAC, by Theorem 4 we obtain $abacab =_E cacbac$. Hence we define $\varDelta _3 = \varDelta _2 cab = abacab$ for which indeed for $i = 1,2,3$ there exist $y_i$ such that $\varDelta _3 =_E a_i y_i$: for $i =3$ due to $abacab =_E cacbac$, and for $i = 1,2$ since $\varDelta _3$ starts by $\varDelta _2$.

In the same way we construct $\varDelta _4$ by rewriting $D \varDelta _3$, resulting in $Dabacab \rightarrow _R^* adbadcabdacDACBAD$. By Theorem 4 we obtain $\varDelta _4 = \varDelta _3 dabcad = abacabdabcad =_E dadbadcabdac$, from which we conclude that $\varDelta _4 =_E a_i y_i$ for some $y_i$ for $i=4$, while the same holds for $i = 1,2,3$ since $\varDelta _4$ starts in $\varDelta _3$. Hence $\varDelta = \varDelta _4$ is init flexible.

It remains to check that $\varDelta$ is rotation flexible. Again we apply Theorem 4. Let ${\overline{\varDelta }}$ be the capitalized reversed version of $\varDelta$, so for this example ${\overline{\varDelta }} = DACBADBACABA$. Then rewrite ${\overline{\varDelta }} a_i \varDelta$ for $i = 1,2,3,4$. It turns out that ${\overline{\varDelta }} a \varDelta \rightarrow _R^* a$, ${\overline{\varDelta }} b \varDelta \rightarrow _R^* b$, ${\overline{\varDelta }} c \varDelta \rightarrow _R^* c$ and ${\overline{\varDelta }} d \varDelta \rightarrow _R^* d$. Hence by Theorem 4 we conclude that $a \varDelta =_E \varDelta a$, $b \varDelta =_E \varDelta b$, $c \varDelta =_E \varDelta c$ and $d \varDelta =_E \varDelta d$, so $\varDelta$ is rotation flexible, concluding the proof that for this particular set E any two words have a common right multiple.

Example 3

A more complicated example to which exactly the same approach applies is $[ 3^{4,2,1}]$. This proves one case of Theorem 2. This graph can be seen as an extension of Example 2 with a in the center, b, c, d around it, and four more nodes e, f, g, h around it organized as follows:

In order to construct an init flexible word $\varDelta$ we start by $\varDelta _1 = a$. Taking into account b, c, d yields $\varDelta _4 = abacabdabcad$ just like in Example 2. But now we continue by adding the symbols e, f, g, h consecutively, for which our rewriting program exploiting Theorem 4 yields

$$\begin{aligned} \varDelta = \varDelta _8 = abacabdabcadebadcabefcabedabcafcdabegfcabedabcafcgfdacbae\\ bdacfghgfcadbacfghebacfgdacfbacdabebadcabfcagfchgfdacbaebdacfgh, \end{aligned}$$

being a word of length 120 that is init flexible by construction. Just like in Example 2 rotation flexibility is checked by rewriting ${\overline{\varDelta }} p \varDelta$ to normal form for all symbols p. Indeed for all $p \in \{a,b,c,d,e,f,g,h\}$ the normal form is a single lower case symbol, from which by Theorem 4 we conclude that $\varDelta$ is rotation flexible. Hence by Theorem 3 we conclude that for the generalized braid of the graph $[ 3^{4,2,1}]$ the monoid $M_E$ has common right multiples.

In Example 2 and Example 3 for every symbol p the word ${\overline{\varDelta }} p \varDelta$ rewrites to the same symbol p. This is not always the case, for instance for C(1, 1, 2), obtained by removing the nodes f, g, h from the graph in Example 3 we obtain $\varDelta = abacabdabcadebadcabe$ for which for $p = a,b,c,d,e$ the word ${\overline{\varDelta }} p \varDelta$ rewrites to a, b, d, c, e respectively, so swapping c, d. But still this proves rotation flexibility by Theorem 4.

5 The case $[ 3^{n,1,1}]$

Theorem 2 consists of two parts. One part was proved in Example 3. It remains to prove that for every $n \ge 1$ the generalized braid monoid corresponding to the graph $[ 3^{n,1,1}]$ has common right multiples. We do this by constructing a word $\varGamma _n$ that is init flexible and rotation flexible and applying Theorem 3. In contrast to earlier examples we cannot apply Theorem 4 since now we need a result for every $n \ge 1$. Let the nodes of $[ 3^{n,1,1}]$ be $a,b,c,1,\ldots ,n$, where a is the node of degree 3, connected by edges to b, c and 1, and the remaining edges are from the path $1,\ldots ,n$. For $n = 4$ this looks as follows:

We will proceed by induction on n. To avoid clutter, we will simply write E, omitting the index n from the respective sets of equations $E_n$. This is harmless since $E_n \subseteq E_{n+1}$ and hence ${=_{E_n}} \subseteq {=_{E_{n+1}}}$, for all n. The word $\varGamma _{{n}}$ is inductively defined by

$$\begin{aligned} \begin{array}{rclrcl} \varGamma _{{0}} &{} \mathrel {{:}{=}}&{} {b}{a}{b}{c}{a}{b}\\ \varGamma _{{n}} &{} \mathrel {{:}{=}}&{} \varGamma _{{n}\mathbin {{-}}{1}}\mathbin {{\cdot }}\chi _{{n}} &{} \text {where}\ \chi _{{n}} \mathrel {{:}{=}}{n}\ldots {1}{a}{b}{c}{a}{1}\ldots {n}\end{array} \end{aligned}$$

and the bijection ${g}_{{n}}$ on $\varSigma \mathrel {{:}{=}}\{{a},{b},{c},{1},\ldots ,{n}\}$ is the identity, except that it swaps ${b},{c}$ if ${n}$ is even. In particular, $\chi _{{0}} = {a}{b}{c}{a}$, ${g}_{{0}}$ is the permutation $\begin{pmatrix} {a}&{} {b}&{} {c}\\ {a}&{} {c}&{} {b}\end{pmatrix}$, $\varGamma _{{1}} = {b}{a}{b}{c}{a}{b}{a}{b}{c}{a}$, $\chi _{{1}} = {1}{a}{b}{c}{a}{1}$, and ${g}_{{1}}$ is the identity on $\{{a},{b},{c},{1}\}$. We will show by induction on n that for all ${n}\ge 1$ and ${i}\mathbin {{\in }}\varSigma$ there is a ${w}$ such that

$$\begin{aligned} {i}{w}\mathrel {{=_E}}\varGamma _{{n}}\mathrel {{=_E}}{w}{g}_{{n}}({i}) \end{aligned}$$

(1)

Then for all ${i}\mathbin {{\in }}\varSigma$ there is a ${w}$ such that $iw =_E \varGamma _n$ and $i \varGamma _n =_E i w g_n(i) =_E \varGamma _n g_n(i)$, so $\varGamma _n$ is both init flexible and rotation flexible, and the graph $[ 3^{n,1,1}]$ has common right multiples by Theorem 3.

For the base case $n=1$ init flexibility and rotation flexibility was already proved in Example 2. The proof for the slightly stronger property () is given similarly by rewriting. In order to be able to capitalize we rename the symbol 1 to d, and have $\varGamma _1 = babcabdabcad$. (Note that $\varGamma _1 =_E \varDelta$ for $\varDelta = abacabdabcad$ as in Example 2.) Since $C \varGamma _1 = Cbabcabdabcad$ rewrites to bacbadabcad we obtain that for $i = c$ we get $w = bacbadabcad$, and since $CWcw = CDACBADABCABcbacbadabcad$ rewrites to the empty string this yields $cw =_E wc$ by Theorem 4, proving () for $i=c$; the claims for $i = a,b,d$ are proved similarly.

In case $n > 1$, we distinguish cases on ${i}\mathrel {{=}}{n}$ or not.

• Suppose ${i}\mathrel {{\ne }}{n}$. By the induction hypothesis we obtain a word ${w}'$ such that ${i}{w}'\mathrel {{=_E}}\varGamma _{{n}\mathbin {{-}}{1}}\mathrel {{=_E}}{w}'{g}_{{n}\mathbin {{-}}{1}}({i})$, and we claim ${j}\chi _{{n}} \mathrel {{=_E}^{(*)}} \chi _{{n}}{g}_{{0}}({j})$ for all ${j}\mathbin {{\in }}\varSigma \mathbin {{-}}\{{n}\}$ (which we will prove later). Therefore, setting ${w}\mathrel {{:}{=}}{w}'\chi _{{n}}$, we conclude to () by

  $$\begin{aligned} {i}{w}'\chi _{{n}} =_E \varGamma _{{n}\mathbin {{-}}{1}}\chi _{{n}} =_E {w}'{g}_{{n}\mathbin {{-}}{1}}({i})\chi _{{n}} =_E^{(*)} {w}'\chi _{{n}}{g}_{{0}}({g}_{{n}\mathbin {{-}}{1}}({i})) =_E {w}'\chi _{{n}}{g}_{{n}}({i}) \end{aligned}$$

  using that ${g}_{{0}}({g}_{{n}\mathbin {{-}}{1}}({i})) = {g}_{{n}}({i})$, which is seen to hold by cases on i and $n \bmod 2$.

• Suppose ${i}\mathrel {{=}}{n}$. We have to find a word ${w}$ such that ${n}{w}\mathrel {{=_E}}\varGamma _{{n}}\mathrel {{=_E}}{w}{n}$. We claim that $\chi _{{n}}\chi _{{n}\mathbin {{-}}{1}} \mathrel {{=_E}^{(**)}} \chi _{{n}\mathbin {{-}}{1}}\chi _{{n}}$. Setting ${w}\mathrel {{:}{=}}\varGamma _{{n}\mathbin {{-}}{2}}\chi _{{n}\mathbin {{-}}{1}}{n}\chi _{{n}\mathbin {{-}}{1}}$ we conclude, using ${n}$ commutes with letters $\mathrel {{\le }}{n}\mathbin {{-}}{2}$, by

  $$\begin{aligned} {n}{w}\mathrel {{=_E}}\varGamma _{{n}\mathbin {{-}}{2}}{n}\chi _{{n}\mathbin {{-}}{1}}{n}\chi _{{n}\mathbin {{-}}{1}} \mathrel {{=}}\varGamma _{{n}\mathbin {{-}}{2}}\chi _{{n}}\chi _{{n}\mathbin {{-}}{1}} \mathrel {{=_E}^{(**)}} \\ \mathrel {{=_E}^{(**)}} \varGamma _{{n}\mathbin {{-}}{2}}\chi _{{n}\mathbin {{-}}{1}}\chi _{{n}} \mathrel {{=_E}}\varGamma _{{n}\mathbin {{-}}{2}}\chi _{{n}\mathbin {{-}}{1}}{n}\chi _{{n}\mathbin {{-}}{1}}{n}\mathrel {{=}}{w}{n}. \end{aligned}$$

It remains to verify the two claims. For ($*$) we distinguish cases on ${j}\mathbin {{\in }}\varSigma \mathbin {{-}}\{{n}\}$:

• ${a}\chi _{{n}} \mathrel {{=_E}}{n}\ldots {a}{1}{a}{b}{c}{a}{1}\ldots {n}\mathrel {{=_E}}{n}\ldots {1}{a}{1}{b}{c}{a}{1}\ldots {n}\mathrel {{=_E}}{n}\ldots {1}{a}{b}{c}{a}{1}{a}\ldots {n}\mathrel {{=_E}}\chi _{{n}}{a}$;

• ${b}\chi _{{n}} \mathrel {{=_E}}{n}\ldots {1}{b}{a}{b}{c}{a}{1}\ldots {n}\mathrel {{=_E}}{n}\ldots {1}{a}{b}{c}{a}{c}{1}\ldots {n}\mathrel {{=_E}}\chi _{{n}}{c}$;

• ${c}\chi _{{n}} \mathrel {{=_E}}\chi _{{n}}{b}$ by symmetry and the previous item using ${b}{c}\mathrel {{=_E}}{c}{b}$, and

• ${j}\chi _{{n}} \mathrel {{=_E}}{n}\ldots {j}({j}\mathbin {{+}}{1}){j}\ldots {1}{a}{b}{c}{a}{1}\ldots {n}\mathrel {{=_E}}{n}\ldots {1}{a}{b}{c}{a}{1}\ldots {j}({j}\mathbin {{+}}{1}){j}\ldots {n}\mathrel {{=_E}}\chi _{{n}}{j}$ for ${j}\mathbin {{\in }}\{{1},\ldots ,{n}\mathbin {{-}}{1}\}$.

We show $(**)$ by induction on ${n}$.

• In the base case we must show $\chi _{{1}}\chi _{{0}} \mathrel {{=_E}}\chi _{{0}}\chi _{{1}}$. This is verified by:

  $$\begin{aligned} \underline{{1}{a}{b}{c}{a}{1}{a}}{b}{c}{a}\,\,&{=\;_E}&{a}\underline{{1}{a}{b}{c}{a}{1}{b}{c}}{a}\\&{=\;_E}&{a}{b}\underline{{1}{a}{b}{c}{a}{1}{b}}{a}\\&{=\;_E}&{a}{b}{c}\underline{{1}{a}{c}{b}{a}{1}{a}} \\&{=\;_E}&{a}{b}{c}{a}{1}{a}{b}{c}{a}{1}\end{aligned}$$

  where in each case the underlined subword is transformed by, repeatedly applying equations from E, starting on its right and working toward its left.

• In the step case we proceed as follows, using the induction hypothesis $\chi _{{n}\mathbin {{-}}{1}}\chi _{{n}\mathbin {{-}}{2}}\mathrel {{=_E}}\chi _{{n}\mathbin {{-}}{2}}\chi _{{n}\mathbin {{-}}{1}}$, where the changed parts are underlined:

  $$\begin{aligned} \chi _{{n}}\chi _{{n}\mathbin {{-}}{1}}&= {n}({n}\mathbin {{-}}{1})\chi _{{n}\mathbin {{-}}{2}}\underline{({n}\mathbin {{-}}{1}){n}({n}\mathbin {{-}}{1})}\chi _{{n}\mathbin {{-}}{2}}({n}\mathbin {{-}}{1}) \\& =_E {n}({n}\mathbin {{-}}{1})\underline{\chi _{{n}\mathbin {{-}}{2}}{n}}({n}\mathbin {{-}}{1})\underline{{n}\chi _{{n}\mathbin {{-}}{2}}}({n}\mathbin {{-}}{1}) \\& {=_E} \underline{{n}({n}\mathbin {{-}}{1}){n}}\chi _{{n}\mathbin {{-}}{2}}({n}\mathbin {{-}}{1})\chi _{{n}\mathbin {{-}}{2}}{n}({n}\mathbin {{-}}{1}) \\&{=_E}({n}\mathbin {{-}}{1}){n}\underline{({n}\mathbin {{-}}{1})\chi _{{n}\mathbin {{-}}{2}}({n}\mathbin {{-}}{1})\chi _{{n}\mathbin {{-}}{2}}}{n}({n}\mathbin {{-}}{1}) \\&{=_E}^{\text {induction hypothesis}}({n}\mathbin {{-}}{1}){n}\chi _{{n}\mathbin {{-}}{2}}({n}\mathbin {{-}}{1})\chi _{{n}\mathbin {{-}}{2}}({n}\mathbin {{-}}{1}){n}({n}\mathbin {{-}}{1}) \\&{=_E} \chi _{{n}\mathbin {{-}}{1}}\chi _{{n}} \end{aligned}$$

  and where the reasoning after the induction hypothesis is symmetrical to that before.

This concludes the proof that for every $n \ge 1$ the generalized braid monoid corresponding to the graph $[ 3^{n,1,1}]$ has common right multiples, and hence also the proof of Theorem 2.

6 Disproving common right multiples

Over the alphabet $\varSigma$ we define a model to be a non-empty set M, together with a mapping $a_M: M \rightarrow M$ for every symbol $a \in \varSigma$, so it is an algebra in which the symbols from $\varSigma$ are considered to be unary. For a word $w = w_1 w_2 \ldots w_n \in \varSigma ^*$ and such a model M we define $w_M: M \rightarrow M$ by $w_M(m) = w_{1\,M}(w_{2\,M}(\cdots (w_{nM}(m))\cdots ))$ for all $m \in M$. Note that in this notation in computing $w_M(m)$ the elements of w are processed from right to left, while in the closely related notion of automata the transition function $\delta$ is usually processed from left to right.

For a set E of equations over $\varSigma$ the model M is said to be a model for E if $v_M(m) = w_M(m)$ for all $m \in M$ and all $v=w \in E$. The following lemma states that equational reasoning ${=_E}$ is sound for such models. Its proof is straightforward and goes back to the soundness part of Birkhoff’s theorem, see [12, Theorem 7.1.15].

Lemma 3

Let M be a model for E, and let $v,w \in \varSigma ^*$ such that $v =_E w$. Then $v_M(m) = w_M(m)$ for all $m \in M$.

For a model M and a word $w \in \varSigma ^*$ write $M_w = \{ w_M(m) \mid m \in M \}$.

The following theorem states that non-existence of a common right multiple is equivalent to the existence of a particular model.

Theorem 5

For $u, v \in \varSigma ^*$ there exist no $x,y \in \varSigma ^*$ satisfying $ux =_E vy$ if and only if there exists a model M for E in which $M_u \cap M_v = \emptyset$.

Proof

Let M be a model for E in which $M_u \cap M_v = \emptyset$. Assume that $ux =_E vy$. Let $m \in M$ be arbitrary. Then according to Lemma 3 we have $(ux)_M(m) = (vy)_M(m)$. But $(ux)_M(m) = u_M(x_M(m)) \in M_u$ and $(vy)_M(m) = v_M(y_M(m)) \in M_v$, contradicting $M_u \cap M_v = \emptyset$.

Conversely, assume that no $x,y \in \varSigma ^*$ exist satisfying $ux =_E vy$. Consider the model $M = \varSigma ^*{/}{=_E}$, so M is the monoid corresponding to E, in which $a_M(w) = aw$ for every $a \in \varSigma$, $w \in \varSigma ^*$, identifying w with its class modulo $=_E$. By construction it is a model for E, and $u_M = \{ux \mid x \in \varSigma ^*\}$ and $v_M = \{vy \mid y \in \varSigma ^*\}$. From the assumption it follows that $M_u \cap M_v = \emptyset$. $\square$

If we can find a model M for E and words u, v such that $u_M(m) \ne v_M(n)$ for all $m,n \in M$, then this proves that u, v have no common right multiple. This observation is straightforward; but the challenge is to find a corresponding model, finite or infinite.

Finite models are closely related to automata, drawn by transition diagrams, being directed graphs with labeled edges. We draw the elements of M by nodes, and every arrow from m to n labeled by p means that the function $p_M$ is defined by $p_M(m) = n$.

Example 4

As a first example we consider $E = \{ abb=baa\}$ as in Example 1. We choose the following model $M = \{1,2,3\}$ of three elements:

For all nodes $n \in M$ we check that $a_M(b_M(b_M(n))) = 2 = b_M(a_M(a_M(n)))$, hence M is a model for $E = \{ abb=baa\}$. Moreover, $M_{aa} = \{1\}$ and $M_b = \{2,3\}$. As $M_{aa} \cap M_b = \emptyset$ by Theorem 5 we conclude that the strings aa and b have no common right multiple. This proves the claim of Example 1.

For more complicated finite models we introduce the convention to omit arrows from a node to itself, so for $p \in \varSigma$ the function $p_M$ is defined by $p_M(m) = n$ if there is an arrow from m to n labeled by p, and $p_M(m) = m$ if m has no outgoing p-arrow.

Example 5

Now we are ready to give the solution of the paint pot problem, and prove the second case of Theorem 1. So E consists of the equations $apa = pap$ for all $p \in \{b,c,d,e\}$, and $pq = qp$ for all $p,q \in \{b,c,d,e\}$, $p \ne q$. We consider the following model $M = \{1,2,3,4,5,6,7,8\}$:

One checks that the following holds for all $m \in M$:

• $a_M(p_M(a_M(m))) = p_M(a_M(p_M(m)))$ for all $p \in \{b,c,d,e\}$, and

• $p_M(q_M(m)) = q_M(p_M(m))$ for all $p,q \in \{b,c,d,e\}$, $p \ne q$.

So indeed this is a model for E. One also checks that $M_u = \{1,5\}$ for $u = bcde$ and $M_a = \{2,3,4,6,7,8\}$. Since $M_u \cap M_a = \emptyset$, from Theorem 5 we conclude that no $x,y \in \varSigma ^*$ exist satisfying $ux =_E ay$, solving the paint pot problem. More general, for any graph having a node of degree $\ge 4$ this shows that the corresponding generalized braid monoid does not have common right multiples: take the same model in which the symbols corresponding to other nodes than these 5 are interpreted as the identity.

This model was found by expressing the requirements of being a model for E and $M_a \cap M_{bcde} = \emptyset$ in an SMT formula for $|M| = n$. For $n = 2,3,4,\ldots$ the SMT solver Z3 was applied on this formula. For $n = 2,3,\ldots 7$ this yielded unsatisfiable, but for $n= 8$ this yielded satisfiable, and the corresponding satisfying assignment yielded the above model. This approach also shows that this model is the smallest possible.

In contrast to many solutions of other combinatorial problems found by SMT solving, this solution has some structure that may provide intuition why it works. Let’s first focus on the requirement of being a model with respect to all of the equations, starting by $pq=qp$ for $p,q \in \{b,c,d,e\}$. For the diamond on nodes 2,3,4,5 labeled by b and c, and the diamond on 1,6,7,8 labeled by b and c the requirements hold, and also for the rest since except for these diamonds, for every arrow labeled by b, c, d or e from a node n to a node $n'$, n has no incoming b, c, d, e-arrow and $n'$ has no outgoing b, c, d, e-arrow. For the equations of the shape $apa = pap$ for $p \in \{b,c,d,e\}$, the requirement is that for every a arrow from n to $n'$, n should have no incoming a-arrow and $n'$ should have no outgoing a-arrow, and for every $p \in \{b,c,d,e\}$ only an incoming p-arrow for n is allowed if $n'$ has no outgoing p-arrow. One checks that if all these properties hold, then the labeled graph indeed yields a model. Next there should be words u, v such that $M_u \cap M_v = \emptyset$. This is only possible if every node has at least one outgoing arrow. Moreover, we know that all symbols are essential, so for every $p \in \{a,b,c,d,e\}$ there should be at least one p arrow. Now playing around with these properties as requirements, it is feasible to find the above model M by hand. Once it has been found, it is not hard to find u, v such that $M_u \cap M_v = \emptyset$.

Example 6

For any connected graph with two nodes of degree $\ge 3$ we show that the corresponding generalized braid monoid does not have common right multiples. This will prove the third case of Theorem 1. Let $a_1,a_2,\ldots ,a_n$ be a path between these two nodes, then the graph contains the following subgraph:

Inspired by our solution for the paint pot problem we choose the following model M:

As always, for symbols p and $m \in M$ not having an outgoing p-arrow we have $p_M(m) = m$, so symbols corresponding to other nodes in the graph act as the identity on M. One checks that M is a model for E, that is, $p_M(q_M(p_M(m))) = q_M(p_M(q_M(m)))$ for all $m \in M$ and all p, q connected by an edge, and $p_M(q_M(m)) = q_M(p_M(m))$ for all $m \in M$ and all p, q not connected by an edge. Further, one checks that for $u = bcde$ and $v = a_1a_2 \cdots a _{n-1} a_n a_{n-1} \cdots a_2 a_1$ the set $M_v$ consists of the elements of the model marked by $*$ and the set $M_u$ consists of the elements of the model not marked by $*$. Since $M_u \cap M_v = \emptyset$ we conclude by Theorem 5 that u, v have no common right multiple.

Example 7

For any graph containing a cycle we show that the corresponding generalized braid monoid does not have common right multiples. This will prove the first case of Theorem 1. For the cycle $a_1,a_2,\ldots ,a_n$ depicted on the left we choose the model depicted on the right:

One checks that M is a model for E, that is, $p_M(q_M(p_M(m))) = q_M(p_M(q_M(m)))$ for all $m \in M$ and all p, q connected by an edge, and $p_M(q_M(m)) = q_M(p_M(m))$ for all $m \in M$ and all p, q not connected by an edge. Further one checks that for $u = a_1$ and $v = a_n a_{n-1} \cdots a_2$ the set $M_v$ consists of the element of the model marked by $*$ and the set $M_u$ consists of the elements of the model not marked by $*$. Since $M_u \cap M_v = \emptyset$ we conclude by Theorem 5 that u, v have no common right multiple.

Example 8

Our hardest example is the generalized braid monoid corresponding to the graph $[ 3^{2,2,2}]$, or more general, any graph having $[ 3^{2,2,2}]$ as a subgraph. For $[ 3^{2,2,2}]$ we choose the following names of the nodes:

We choose the following model of 27 elements / nodes and 42 arrows. The two nodes labeled by 1 should be identified, and similarly for the two nodes labeled by 2$*$.

One checks that M is a model for E. Further one checks that for $u = bcdefg$ the set $M_u$ consists of the 6 elements of the model marked by $*$ and the set $M_a$ consists of the remaining 21 elements of the model not marked by $*$. Since $M_u \cap M_a = \emptyset$ we conclude by Theorem 5 that u, v have no common right multiple. This proves the last case of Theorem 1.

To find this model first we tried SMT solving similar to the model of 8 elements for the paint pot problem. This failed, apparently 27 elements exceeds the power of this approach using current technology. Finally, exploiting properties observed from the model for the paint pot problem, this model was found by hand. Next, several of its properties were added to the SMT formula, and SMT solving succeeded, yielding the same model. In this way it was mechanically checked that the great number of requirements all hold.

Note that by these examples (Examples 7, 5, 6, 8) the full proof of Theorem 1 has been given.

We want to stress that this method of proving that particular words have no common right multiple is not restricted to a special format of rules. A simple example beyond the Artin–Tits format was already given in Example 4. Now we provide a more complicated example.

Example 9

Consider $E = \{ abb=baa, acb=caa, bcc=ccb\}$, for which we want to show that bb and cb have no common right multiple. We choose the following model $M = \{1,2,3,4\}$ of four elements:

One checks that this is a model for E, either by hand or by a program. One checks that $M_{bb} = \{3\}$ and $M_{cb} = \{2,4\}$, hence proving by Theorem 5 that bb and cb have no common right multiple.

The SMT solving approach shows that there are more compatible models of four elements, but that models of $< 4$ elements do not exist.

7 Conclusions

A main goal of this paper was to investigate for which graphs the corresponding generalized braid monoid has common right multiples, in a self-contained way that also applies to monoids of other formats. We were able to cover a great part of the known classification.

The positive results were strongly inspired by Garside theory, but in order to get short and self-contained proofs we introduced and exploited the new notions init flexible and rotation flexible. We presented a way to mechanically construct an init flexible word, and to check that it is also rotation flexible, both based on straightforward rewriting.

It is a natural question how these flexibility properties relate to the more standard notion of Garside word. Here a word $\varDelta$ is called a Garside word if for every $u \in \varSigma ^*$ it holds

$$\begin{aligned} \exists x \in \varSigma ^*: xu =_E \varDelta \; \Longleftrightarrow \;\exists y \in \varSigma ^*: uy =_E \varDelta , \end{aligned}$$

(2)

and the monoid $M_E$ is generated by the set of all $u \in \varSigma ^*$ satisfying $\exists x \in \varSigma ^*: xu =_E \varDelta$. We have the following:

Theorem 6

Every Garside word is both init flexible and rotation flexible.

Proof

Let $\varDelta$ be a Garside word. First we prove that $\varDelta$ is init flexible. Let $a \in \varSigma$ be arbitrary. Since $M_E$ is generated by $\{ u \in \varSigma ^*: \exists x \in \varSigma ^*: xu =_E \varDelta \}$ we conclude that a occurs in a word convertible to $\varDelta$, so we can write $\varDelta =_E u a v$. Then by () we obtain $\varDelta =_E u a v =_E a v y$ for some $y \in \varSigma ^*$, proving that $\varDelta$ is init flexible. For proving that $\varDelta$ is rotation flexible let $a \in \varSigma$. Since $\varDelta$ is init flexible there exists $x \in \varSigma ^*$ such that $\varDelta =_E ax$. Due to () there exists $y \in \varSigma ^*$ such that $xy =_E \varDelta$, yielding $a \varDelta =_E axy =_E \varDelta y$, proving that $\varDelta$ is rotation flexible. $\square$

The converse of Theorem 6 does not hold: for $E = \{ba = aa\}$ one easily checks that $\varDelta = aa$ is both init flexible and rotation flexible, but as $ba =_E \varDelta$ and no x exists such that $xb =_E \varDelta$, it is not a Garside word. It can even be shown similarly that in this example no Garside word exists at all.

A related question is whether the converse of Theorem 3 holds, that is, if $M_E$ has common right multiples, can we conclude that a word $\varDelta$ exists that is both init flexible and rotation flexible? On this question the answer is negative: one can show that for $E = \{ ba = abb \}$ every two words have a common right multiple, but every word $\varDelta$ that contains the symbol b is not rotation flexible, and every word $\varDelta$ that does not contain the symbol b it is not init flexible.

The main new contribution of this paper is the technique to disprove common right multiples by means of constructing a model. We showed that not having common right multiples is equivalent to the existence of such a model. Until now all our models were finite. However, there is no evidence that a finite model always exists; whether this is the case is a topic of further research.

Assume that E satisfies the conditions of Theorem 4. If $R_E$ is terminating, then from Theorem 4 it easily follows that $M_E$ has common right multiples. We conjecture that for generalized braids also the stronger result holds: $M_E$ has common right multiples if and only if $R_E$ is terminating. In view of Remark 2, it would be interesting to relate infinite reductions of $R_E$ to models disproving common right multiples, and also to have necessary conditions for Theorem 4 instead of the present sufficient ones.