Abstract
Let K be an arbitrary semi-cubical set that can be embedded in a standard cube. Using Discrete Morse Theory, we construct a CW-complex that is homotopy equivalent to the space \(\vec {P}(K)_v^w\) of directed paths between two given vertices v, w of K. In many cases, this construction is minimal: the cells of the constructed CW-complex are in 1–1 correspondence with the generators of the homology of \(\vec {P}(K)_v^w\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The spaces of directed paths on semi-cubical sets play an important role in Theoretical Computer Science [4, 5]. In the previous paper [13] the author constructed, for every bi-pointed semi-cubical set (K, v, w) satisfying certain mild assumptions, a regular CW-complex \(W(K)_v^w\) that is homotopy equivalent to the space of directed paths \(\vec {P}(K)_v^w\) on K from v to w. This construction is functorial, and even minimal amongst functorial constructions. The main goal of this paper is to provide a further reduction of this model.
We restrict our attention to semi-cubical sets that can be embedded into a standard cube, regarded as a semi-cubical complex. This special case is general enough to encompass most of interesting examples appearing in Concurrency. The main result of this paper is a construction of a discrete gradient field [6] \(\mathcal {W}_K\) on \(W(K)_v^w\). It is used to show that \(\mathcal {P}(K)_v^w\) is homotopy equivalent to an even smaller CW-complex X(K) whose cells correspond to the critical cells of \(\mathcal {W}_K\). Furthermore, explicit formulas describing the set of critical cells of \(\mathcal {W}_K\) are provided.
This construction allows to calculate the homology groups of \(\mathcal {P}(K)_v^w\), since the differentials in the cellular homology chain complex of X(K) can be recovered using methods from [9, Chapter 11]. We do not examine these differentials in detail. It appears that in many important cases it is not necessary since the differentials vanish for dimensional reasons. This way we reprove here the result of Björner and Welker [2], who calculate the homology of “no \((k+1)\)–equal’ configuration spaces on the real line, as well as a generalization due to Meshulam and Raussen [10].
We pay a special attention to the case when K is a Euclidean cubical complex, i.e., a union of cubes having integral coordinates in the directed Euclidean space \(\vec {\mathbb {R}}^n\). Since state spaces of PV-programs [3] are Euclidean cubical complexes, this case seems important for potential applications in concurrency. Since every finite Euclidean cubical complex can be embedded into a standard cube, our results apply in this case; also, a description of the critical cells of \(\mathcal {W}_K\) is given in this context.
2 Preliminaries
Let us recall some definitions and results obtained in [13].
A d-space [8] is a pair \((X,\vec {P}(X))\), where X is a topological space and \(\vec {P}(X)\subseteq P(X)={{\mathrm{map}}}([0,1],X)\) is a family of paths that contains all constant paths and is closed with respect to concatenation and non-decreasing reparametrizations. Paths that belong to \(\vec {P}(X)\) will be called directed paths or d-paths. For \(x,y\in X\), \(\vec {P}(X)_x^y\) denotes the space of d-paths starting at x and ending at y. Prominent examples of d-spaces are the directedn-cube\(\vec {I}^n=(I^n,\vec {P}(\vec {I}^n))\) and the directed Euclidean space\(\vec {\mathbb {R}}^n=(\mathbb {R}^n,\vec {P}(\vec {\mathbb {R}}^n))\), where \(\vec {P}(\vec {I}^n)\) and \(\vec {P}(\vec {\mathbb {R}}^n)\) are the spaces of all paths having non-decreasing coordinate functions.
A semi-cubical setK is a sequence of disjoint sets \((K[n])_{n\ge 0}\), equipped with face maps\(d^\varepsilon _i:K[n]\rightarrow K[n-1]\), where \(n\ge 0\), \(i\in \{1,\ldots ,n\}\) and \(\varepsilon \in \{0,1\}\), that satisfy the pre-cubical relations, i.e., \(d_i^\varepsilon d_j^\eta = d_{j-1}^\eta d_i^\varepsilon \) for \(i<j\). Elements of K[n] will be called cubes or n--cubes if one needs to emphasize their dimension; 0-cubes and 1-cubes will be called vertices and edges, respectively. The set of all cubes of a semi-cubical set K will be denoted by \({{\mathrm{Cell}}}(K)\) or by K if that does not lead to confusion. This set is partially ordered by inclusion, i.e. \(c\subseteq c'\) if c is the image of \(c'\) under some composition of face maps. Every cube \(c\in K[n]\) has the initial vertex\(d^0(c)=d^0_1\ldots d^0_1(c)\) and the final vertex\(d^1(c)=d^1_1\ldots d^1_1(c)\), where n face maps appear in both compositions.
The geometric realization of a semi-cubical set K is the d-space
where \(\delta ^\varepsilon _i(s_1,\ldots ,s_{n-1})=(s_1,\ldots ,s_{i-1},\varepsilon , s_i,\ldots ,s_{n-1})\). A path \(\alpha \in P(|K|)\) is directed if there exist numbers \(0=t_0<t_1<\cdots <t_l=1\), cubes \(c_i\in K[n_i]\) and directed paths \(\beta _i\) in \(\vec {I}^{n_i}\) such that \(\alpha (t)=(c_i,\beta _i(t))\) for \(t\in [t_{i-1},t_i]\).
For a semi-cubical set K and a pair of its vertices \(v,w\in K[0]\), a cube chain inKfromv to w in K is a sequence of cubes \(\mathbf {c}=(c_1,\ldots ,c_l)\), \(c_i\in K[n_i]\), \(n_i>0\), that satisfies the following conditions:
-
\(d^0(c_1)=v\),
-
\(d^1(c_l)=w\),
-
\(d^1(c_i)=d^0(c_{i+1})\) for \(i\in \{1,\ldots ,l-1\}\).
The set of all cube chains in K from v to w is denoted by \({{\mathrm{Ch}}}(K)_v^w\). There is a natural partial order on \({{\mathrm{Ch}}}(K)_v^w\) given by the refinement of cube chains, see [13, Definition 1.1] for details.
Assume that a semi-cubical set K is proper, i.e., if \(c\ne c'\) are cubes of K, then \(\{d^0(c),d^1(c)\}\ne \{d^0(c'),d^1(c')\}\). Under this assumption, the following holds:
Theorem 2.1
([13, Theorems 1.2 and 1.3]) Let \(v,w\in K[0]\) be vertices of K.
-
(a)
There is a homotopy equivalence
$$\begin{aligned} \vec {P}(|K|)_v^w\simeq |{{\mathrm{Ch}}}(K)_v^w|, \end{aligned}$$where \(|{{\mathrm{Ch}}}(K)_v^w|\) denotes the geometric realization of the nerve of \({{\mathrm{Ch}}}(K)_v^w\).
-
(b)
\(|{{\mathrm{Ch}}}(K)_v^w|\) carries a natural structure of a regular CW-complex with closed cells having the form \(|{{\mathrm{Ch}}}_{\le \mathbf {c}}(K)|\) for \(\mathbf {c}\in {{\mathrm{Ch}}}(K)_v^w\), where \({{\mathrm{Ch}}}_{\le \mathbf {c}}(K)\subseteq {{\mathrm{Ch}}}(K)_v^w\) is the subposet of cube chains that are finer than \(\mathbf {c}\), including \(\mathbf {c}\) itself. \(\square \)
In this paper we restrict to the case when K is a semi-cubical subset of the standard cube. The standardn-cube\(\square ^n\) is a semi-cubical set whose k-cubes \(\square ^n[k]\) are sequences \((e_1,\ldots ,e_n)\), \(e_i\in \{0,1,*\}\) having exactly k entries equal to \(*\). A face map \(d_i^\varepsilon \) converts the i-th occurrence of \(*\) into \(\varepsilon \). It is easy to see that the geometric realization of \(\square ^n\) is d-homeomorphic to the directed cube \(\vec {I}^n\). Furthermore, every semi-cubical subset of \(\square ^n\) is proper, so the results of [13] can be applied in this situation.
The majority of proofs in this paper is inductive with respect to the dimension of the ambient cube \(\square ^n\). Thus, for convenience, the coordinates will be indexed by an arbitrary finite ordered set A rather than by \(\{1,\ldots ,n\}\). In the case when A is non-empty, \(m\in A\) denotes its maximal element and \(A'=A{\setminus }\{m\}\).
Let \(\#X\) denote the cardinality of a finite set X.
Definition 2.2
The standardA-cube\(\square ^A\) is the semi-cubical set such that
-
\(\square ^A[k]\) is the set of all functions \(c:A\rightarrow \{0,1,*\}\) such that \(\#(c^{-1}(*))=k\).
-
For \(c\in \square ^A[k]\), if \(c^{-1}(*)=\{b_1<b_2<\cdots <b_k\}\), then
$$\begin{aligned} d^\varepsilon _i(c)(a)={\left\{ \begin{array}{ll} \varepsilon &{} \quad \hbox {if}\ a=b_i \\ c(a) &{} \quad \text {otherwise.} \end{array}\right. } \end{aligned}$$
AnA-cubical complex is a semi-cubical subset of \(\square ^A\).
We identify \(|\square ^A|\) with the directed A-cube \(\vec {I}^A\); thus, the geometric realization of an A-cubical complex is a subspace of \(\vec {I}^A\).
Let us introduce a notation for cubes of \(\square ^A\). For subsets \(B_1,B_*,B_0\subseteq A\) such that \(A=B_1\mathop {\dot{\cup }}B_* \mathop {\dot{\cup }}B_0\) is a partition of A, let \(c(B_1,B_*,B_0)\) be the cube of \(\square ^A\) satisfying
The dimension of \(c(B_1,B_*,B_0)\) equals \(\#B_*\), and \(c(B_0,B_*,B_1)\subseteq c(B'_0,B'_*,B'_1)\) if and only if \(B'_0\subseteq B_0\), \(B'_1\subseteq B_1\) and \(B_*\subseteq B'_*\).
For a subset \(B\subseteq A\) and \(\varepsilon \in \{0,1\}\), let \(K|_B^\varepsilon \subseteq \square ^B\) be the set of functions \(c:B\rightarrow \{0,1,*\}\) such that the function
belongs to K. Clearly, \(K|_B^\varepsilon \) is a B-cubical complex. After passing to geometric realizations, the restriction of K corresponds to the intersection with a particular face of the directed A-cube, i.e., there is a homeomorphism
3 Ordered partitions and cube chains in A-complexes
Definition 3.1
An ordered partition of a set A is a sequence \(\lambda =B_1|B_2|\cdots |B_{l(\lambda )}\) of non-empty disjoint subsets of A such that \(A=\bigcup _{i=1}^l B_i\). We say that an ordered partition \(\mu =C_1|\cdots |C_{l(\mu )}\) is finer than \(\lambda \) if there exists a sequence of integers
such that \(B_i=C_{r(i-1)+1}\cup C_{r(i-1)+2} \cup \cdots \cup C_{r(i)}\) for all \(i\in \{1,\ldots ,l(\lambda )\}\). Let \(\mathcal {P}_A\) be the poset of all ordered partitions of A, with the partial order given by \(\mu \le \lambda \) if and only if \(\mu \) is finer than \(\lambda \).
We will define an isomorphism between \(\mathcal {P}_A\) and the poset \({{\mathrm{Ch}}}(\square ^A)_{\mathbf {0}}^\mathbf {1}\), where \(\mathbf {0},\mathbf {1}\in \square ^A[0]\) stand for the constant functions having values 0 and 1 respectively. Pick a cube chain \(\mathbf {c}=(c_1,\ldots ,c_l)\in {{\mathrm{Ch}}}(\square ^A)_\mathbf {0}^\mathbf {1}\), and let \(B^\mathbf {c}_i=c_i^{-1}(*)\). For every cube \(c\in \square ^A\) and \(a\in A\) we have
Thus, from the condition \(d^1(c_i)=d^0(c_{i+1})\) follows that
-
\(c_i(a)=0\) implies \(c_{i-1}(a)=0\),
-
\(c_i(a)=1\) implies \(c_{i+1}(a)=1\),
-
\(c_i(a)=*\) implies \(c_{i-1}(a)=0\) and \(c_{i+1}(a)=1\).
Moreover,
-
\(c_1(a)\ne 1\) for all \(a\in A\), since \(d^0(c_1)=\mathbf {0}\),
-
\(c_l(a)\ne 0\) for all \(a\in A\), since \(d^1(c_l)=\mathbf {1}\).
Thus, for every \(a\in A\), the value \(*\) appears exactly once in the sequence \(\left( c_i(a)\right) _{i=1}^l\); all preceding elements are 0 and all succeeding ones are 1. As a consequence, \(\mathbf {c}\) determines the ordered partition \(\lambda ^\mathbf {c}:=B^\mathbf {c}_1|B^\mathbf {c}_2| \cdots | B^\mathbf {c}_l\) of A.
On the other hand, an ordered partition \(\lambda =B_1|\cdots | B_l\) determines a cube chain \(\mathbf {c}^\lambda =(c^\lambda _1,\ldots ,c^\lambda _l)\), where
It is easy to check that these operations are mutually inverse and that finer cube chains correspond to finer partitions. As a consequence, we obtain
Proposition 3.2
The map
is an isomorphism of posets.
This is a slight reformulation of [13, Proposition 8.1].
Now let K be an A-cubical complex. Define
This is the image of \({{\mathrm{Ch}}}(K)_\mathbf {0}^\mathbf {1}\) under the isomorphism in Proposition 3.2. As a consequence, there is a sequence of homotopy equivalences
The following criterion will be used later; it follows immediately from the definitions.
Proposition 3.3
Assume that \(A=C\mathop {\dot{\cup }}B_1 \mathop {\dot{\cup }}\cdots \mathop {\dot{\cup }}B_k \mathop {\dot{\cup }}D\) is a partition of A and \(\lambda \in \mathcal {P}_C\), \(\mu \in \mathcal {P}_D\). Then the following conditions are equivalent:
-
(a)
\(\lambda |B_1|\cdots |B_k|\mu \in \mathcal {P}_K\).
-
(b)
\(\lambda \in \mathcal {P}(K|^0_C)\), \(\mu \in \mathcal {P}(K|^1_D)\) and
$$\begin{aligned} c(C\cup B_1\cup \cdots \cup B_{i-1},B_i,B_{i+1}\cup \cdots \cup B_k\cup D)\in K \end{aligned}$$for every \(i\in \{1,\ldots ,k\}\).\(\square \)
In the remaining part of the paper we will examine the poset \(\mathcal {P}_K\) by means of Discrete Morse Theory.
4 Discrete Morse Theory for CW-posets
In this section we recall some basic facts from Discrete Morse Theory for regular CW-complexes. For detailed expositions of this topic see, for example, [6, 7, 9, Chapter 11].
Definition 4.1
([1]) A poset P is a CW-poset if, for every \(a\in P\), \(|P_{<a}|\) is homeomorphic to a sphere \(S^{d(a)-1}\). Elements of a CW-poset will be called cells and the integer d(a) will be called the dimension of a cell a. If \(a<b\in P\) and \(d(a)=d(b)-1\), then a will be called a facet ofb and we will write \(a\prec b\).
For a CW-poset P, |P| has a natural CW-structure; its closed k-cells have the form \(|P_{\le a}|\), for \(a\in P\) having dimension k. The cell poset C(W) of a regular CW-complex W is a CW-poset and |C(W)| is homeomorphic to W by a cell-preserving homeomorphism. In particular, the face poset of a convex polytope is a CW-poset.
Definition 4.2
Let P be a subposet of a finite CW-poset.
-
A discrete vector field \(\mathcal {V}\)onP is a set of pairwise disjoint pairs (called vectors) (a, b), \(a,b\in P\) such that a is a facet of b.
-
A flow of \(\mathcal {V}\) is a sequence of cells of P
$$\begin{aligned} (a_1,b_1,a_2,b_2,\ldots ,a_{k},b_k,a_{k+1}) \end{aligned}$$(4.1)such that, for all \(i\in \{1,\ldots ,k\}\),
-
\((a_i,b_i)\in \mathcal {V}\),
-
\((a_{i+1},b_i)\not \in \mathcal {V}\)
-
\(a_{i+1}\prec b_i\).
-
-
A cycle of \(\mathcal {V}\) is a flow (4.1) such that \(a_1=a_{k+1}\), \(k>0\).
-
A discrete vector field \(\mathcal {V}\) is a gradient field if it admits no cycle.
For a discrete vector field \(\mathcal {V}\) on a CW-poset P, let
be the set of regular cells of \(\mathcal {V}\), and let \({{\mathrm{Crit}}}(\mathcal {V})=P{\setminus }{{\mathrm{Reg}}}(\mathcal {V})\) be the set of critical cells of \(\mathcal {V}\). If \(P\subseteq Q\) and Q is a CW-poset, then \(\mathcal {V}\) can be regarded as a discrete vector field on Q. In such a case, we will write \({{\mathrm{Crit}}}_{P}(\mathcal {V})\) or \({{\mathrm{Crit}}}_Q(\mathcal {V})\) for the set of critical cells to emphasize which underlying poset we have in mind.
The importance of gradient fields follows from the following theorem:
Theorem 4.3
([9, Theorem 11.13]) Assume that P is a CW-poset and \(\mathcal {V}\) is a gradient field on P. Then there exists a CW-complex \(W(\mathcal {V})\) that is homotopy equivalent to |P|, whose d-dimensional cells are in 1–1 correspondence with the d-dimensional critical cells of \(\mathcal {V}\).
For convenience, we will use a notion of discrete Morse function which is slightly different from the original one.
Definition 4.4
Let \(\mathcal {V}\) be a discrete vector field on a finite CW-poset P. A (discrete) Morse function associated to \(\mathcal {V}\) is a function \(h:P\rightarrow H\), where H is an ordered set, such that, for every \(a\prec b\in P\),
-
(a)
\((a,b)\in \mathcal {V}\) implies that \(h(a)>h(b)\),
-
(b)
\((a,b)\not \in \mathcal {V}\) implies that \(h(a)\le h(b)\).
Lemma 4.5
Let \(\mathcal {V}\) be a discrete vector field on a finite CW-poset P. If there exists a Morse function associated to \(\mathcal {V}\), then \(\mathcal {V}\) is a gradient field.
Proof
If \((a_1,b_1,\ldots ,a_k,b_{k+1})\) is a flow in \(\mathcal {V}\), then
thus, \(a_1\ne a_{k+1}\). \(\square \)
We say that a subposet Q of a poset P is closed if, for \(x\le y\in P\), \(y\in Q\) implies that \(x\in Q\).
Lemma 4.6
Let P be finite CW-poset and let \(Q\subseteq P\) is a closed subposet. Let \(\mathcal {V}_Q, \mathcal {V}_{P{\setminus } Q}\) be discrete vector fields on Q and \(P{\setminus } Q\) respectively. Then every cycle of \(\mathcal {V}=\mathcal {V}_Q\cup \mathcal {V}_{P{\setminus } Q}\) is contained either in Q or in \(P{\setminus } Q\). In particular, if both \(\mathcal {V}_Q\) and \(\mathcal {V}_{P{\setminus } Q}\) are gradient fields, then \(\mathcal {V}\) is also a gradient field.
Proof
Let \((a_1,b_1,\ldots ,a_k,b_k,a_1)\) be a cycle. By the assumptions, \(a_i\in Q\) implies \(b_i\in Q\), and \(b_i\in Q\) implies \(a_{i+1}\in Q\), since \(a_{i+1}\prec b_i\). Thus, either all elements of the cycle are in Q or none is. \(\square \)
Now we will give some examples of gradient fields. While the first two examples are not crucial in proving the main results of this paper, they can be helpful in understanding similar constructions performed on permutahedra.
In all following examples, A is a non-empty finite ordered set, m is its maximal element and \(A'=A{\setminus } \{m\}\).
Example 4.7
(Simplices) The A-simplex is the poset \(\Delta ^A\) of non-empty subsets of A. The standard vector field on \(\Delta ^A\) is
This is a gradient field, since
is a Morse function. The only critical cell of \(\mathcal {S}^\Delta _A\) is \(\{m\}\).
Example 4.8
(Cubes) Here \(\square ^A={{\mathrm{Cell}}}(\square ^A)\) denotes the poset of cubes of the standard A-cube. Define \(\square ^{A,m}=\{c\in \square ^A:\; c(m)=0\}\) and \(\square ^{A,r}=\square ^A{\setminus } \square ^{A,m}\). Clearly, \(\square ^{A,m}\) is a closed subposet of \(\square ^A\), which is isomorphic to \(\square ^{A'}\). We define vector fields \(\mathcal {S}^{\square m}_A\), \(\mathcal {S}^{\square r}_A\) and \(\mathcal {S}^{\square }_A\) on the posets \(\square ^{A,m}\), \(\square ^{A,r}\) and \(\square ^A\), respectively, inductively as follows. We put
and for \(A\ne \emptyset \) let
-
(a)
\(\mathcal {S}^{\square m}_A=\{(f,g):\; (f|_{A'},g|_{{A'}})\in \mathcal {S}^\square _{{A'}}, \; f(m)=g(m)=0\}.\)
-
(cb)
\(\mathcal {S}^{\square r}_A=\{(f,g):\; f|_{{A'}}=g|_{{A'}},\; f(m)=1,\; g(m)=*\}\)
-
(c)
\(\mathcal {S}^{\square }_A=\mathcal {S}^{\square m}_A\cup \mathcal {S}^{\square r}_A\).
We will prove inductively that \(\mathcal {S}^\square _A\) is a gradient field. This is obvious for \(A=\emptyset \). By the inductive hypothesis, \(\mathcal {S}^{\square m}_A\simeq \mathcal {S}^\square _{A'}\) is a gradient field on \(\square ^{A,m}\simeq \square ^{A'}\), and \(\mathcal {S}^{\square r}_{A}\) admits the Morse function
and hence it is also a gradient field. Lemma 4.6 implies that \(\mathcal {S}^A_\square \) is a gradient field. The only critical cell of \(\mathcal {S}^\square _A\) is the 0-cell \(\mathbf {0}=(0,\ldots ,0)\).
Example 4.9
(Product of discrete vector fields) Let P, Q be finite CW-posets, and let \(\mathcal {V}\), \(\mathcal {W}\) be discrete vector fields on P and Q, respectively. Define a discrete vector field \(\mathcal {V}\times \mathcal {W}\) on \(P\times Q\) by
We have \({{\mathrm{Crit}}}(\mathcal {V}\times \mathcal {W})={{\mathrm{Crit}}}(\mathcal {V})\times {{\mathrm{Crit}}}(\mathcal {W})\). Notice that the gradient fields \(\mathcal {V}\times \mathcal {W}\) and \(\mathcal {W}\times \mathcal {V}\) do, in general, not agree.
Proposition 4.10
Assume that P, Q are finite CW-posets and \(\mathcal {V}\) and \(\mathcal {W}\) are gradient fields on P and Q, respectively. Then \(\mathcal {V}\times \mathcal {W}\) is a gradient field on \(P\times Q\).
Proof
Let
be a cycle of \(\mathcal {V}\times \mathcal {W}\), i.e., \(((p_{2i-1},q_{2i-1}),(p_{2i},q_{2i}))\in \mathcal {V}\times \mathcal {W}\), \((p_{2i+1},q_{2i+1})\prec (p_{2i},q_{2i})\). Assume that not all \(p_i\) are equal, and let
be an enumeration of all different values among the \(p_i\). For \(s\in \{1,\ldots ,r-1\}\), the dimensions of \(p_{i(s)}\) and \(p_{i(s+1)}\) differ by 1; if \(\dim (p_{i(s)})=\dim (p_{i(s+1)})-1\), then \((p_{i(s)},p_{i(s+1)})\in \mathcal {V}\) which implies that \((p_{i(s+1)},p_{i(s+2)})\not \in \mathcal {V}\), since no cell may belong to two different vectors, and then \(p_{i(s+2)}\prec p_{i(s+1)}\). As a consequence, either \((p_{i(1)},p_{i(2)},\ldots ,p_{i(r)}=p_{i(1)})\) or \((p_{i(2)},p_{i(3)},\ldots ,p_{i(r)}=p_{i(1)},p_{i(2)})\) is a cycle of \(\mathcal {V}\). If all \(p_i\)’s are equal, then \((q_1,\ldots ,q_{2k+1})\) is a cycle of \(\mathcal {W}\). In both cases we get a contradiction. \(\square \)
Notice that the standard gradient fields on cubes can be defined alternatively by formulas \(\mathcal {S}^\square _{\{x\}}=\{(1,*)\}\), \(\mathcal {S}^\square _A=\mathcal {S}^\square _{\{m\}}\times \mathcal {S}^\square _{A'}\).
5 Permutahedra
The main goal of this section is to construct “standard” gradient fields on permutahedra. As before, A is a finite ordered set, \(m\in A\) is a maximal element and \(A'=A{\setminus } \{m\}\). We will write \(A=B_1\mathop {\dot{\cup }}\cdots \mathop {\dot{\cup }}B_n\) when \(B_1,\ldots ,B_n\) are pairwise disjoint subsets of A such that \(\bigcup B_i=A\) and the order on every \(B_i\) is inherited from A.
Recall that \(\mathcal {P}_A\) denotes the poset of ordered partitions of A. \(\mathcal {P}_A\) is a CW-poset whose geometrical realization is a permutahedron on letters in A [12, p. 18]. For a cell \(\lambda =B_1|B_2|\cdots |B_l\in \mathcal {P}_A\), we have
Denote
Clearly, \(\mathcal {P}_A^m\) is a closed subposet of \(\mathcal {P}_A\), which is isomorphic to \(\mathcal {P}_{A'}\).
Define discrete vector fields \(\mathcal {V}^{r}_{A}\) on \(\mathcal {P}_A^r\), \(\mathcal {V}^{m}_{A}\) on \(\mathcal {P}_A^m\) and \(\mathcal {V}_{A}=\mathcal {V}^{r}_{A}\cup \mathcal {V}^{m}_{A}\) on \(\mathcal {P}_A\) inductively in the following way. We put \(\mathcal {V}^{r}_\emptyset =\mathcal {V}^{m}_\emptyset =\mathcal {V}_\emptyset =\emptyset \) and, for a \(A\ne \emptyset \),
Proposition 5.1
The only critical cell of \(\mathcal {V}_A\) is
having dimension 0.
Proof
It follows immediately from the definition that \({{\mathrm{Reg}}}(\mathcal {V}_A^r)=\mathcal {P}_A^r\) and
Thus, \({{\mathrm{Crit}}}_{\mathcal {P}_A}(\mathcal {V}_A)={{\mathrm{Crit}}}_{\mathcal {P}^m_A}(\mathcal {V}^m_A)\cup {{\mathrm{Crit}}}_{\mathcal {P}^r_A}(\mathcal {V}^r_A)=u_A\). \(\square \)
Proposition 5.2
\(\mathcal {V}_A\) is a gradient field.
Proof
This is obvious for \(A=\emptyset \), so assume otherwise. There is an isomorphism \((\mathcal {P}^m_A,\mathcal {V}^m_A)\cong (\mathcal {P}_{A'},\mathcal {V}_{A'})\); hence, by the inductive hypothesis, \(\mathcal {V}^m_A\) is a gradient field on \(\mathcal {P}^m_A\). By Lemma 4.6, it remains to prove that \(\mathcal {V}^r_A\) is a gradient field on \(\mathcal {P}^r_A\).
Define an order \({\dot{\le }}\) on the set \(H=\mathbb {Z}\times \mathbb {Z}_+\) in the following way: \((s,t)\mathrel {\dot{\le }} (s',t')\) if and only if one of the following conditions is satisfied:
-
\(s>s'\),
-
\(s=s'\) and \(1\ne t\le t'\),
-
\(s=s'\) and \(t'=1\).
This is the lexicographic order on the product, with the inverse order on \(\mathbb {Z}\) and the order
on \(\mathbb {Z}_+\). Every element \(\lambda \in \mathcal {P}^r_A\) can be written uniquely as
where \(m\in B\), \(\pi \in \mathcal {P}(C)\), \(\varrho \in \mathcal {P}(D)\), \(A=C\mathop {\dot{\cup }}B\mathop {\dot{\cup }}D\). Let
We will prove that \(h_A:\mathcal {P}^r_A\rightarrow H\) is a Morse function. Assume that \(\mu \prec \lambda \) and \(\lambda \) has the presentation (5.4). If \(\mu =\pi '|B|\varrho \) for \(\pi '\prec \pi \in \mathcal {P}_C\), or \(\mu =\pi |B|\varrho '\) for \(\varrho '\prec \varrho \in \mathcal {P}_D\), then \((\mu ,\lambda )\not \in \mathcal {V}^r_A\) and \(h_A(\lambda )=h_A(\mu )\). Assume otherwise, i.e., that \(\mu =\pi |B_1|B_2|\varrho \) for \(B_1\mathop {\dot{\cup }}B_2=B\), \(B_1,B_2\ne \emptyset \). Consider the following cases:
-
\(B_1=\{m\}\). Then \((\mu ,\lambda )\in \mathcal {V}^r_A\), and
$$\begin{aligned} h_A(\mu )=(\#C,1)\mathrel {\dot{>}}(\#C,\#B)=h_A(\lambda ). \end{aligned}$$ -
\(\{m\}\subsetneq B_1\). Then \((\mu ,\lambda )\not \in \mathcal {V}^r_A\) and
$$\begin{aligned} h_A(\mu )=(\#C,\#B_1)\mathrel {\dot{<}}(\#C,\#B)=h_A(\lambda ), \end{aligned}$$since \(\#B_1>1\).
-
\(m\in B_2\). Then \((\mu ,\lambda )\not \in \mathcal {V}^r_A\) and
$$\begin{aligned} h_A(\mu )=(\#C+\#B_1,\#B_2)\mathrel {\dot{<}}(\#C,\#B)=h_A(\lambda ). \end{aligned}$$
This proves that \(\mathcal {V}^r_A\) is a gradient field. \(\square \)
The following picture illustrates the gradient field \(\mathcal {V}_{A}\) for \(A=\{1,2,3\}\).

6 A gradient field on \(\mathcal {P}_K\)
In this Section, we construct a gradient field on \(\mathcal {P}_K\), for any finite ordered set A and an A-cubical complex \(K\subseteq \square ^A\). The starting point is the restriction of \(\mathcal {V}_K\) to \(\mathcal {P}_A\), i.e.,
In general, the discrete vector field \(\mathcal {V}_K\) has critical cells that are not critical cells of \(\mathcal {V}_A\): if \((\lambda ,\mu )\in \mathcal {V}_A\), \(\lambda \in \mathcal {P}_K\) and \(\mu \not \in \mathcal {P}_K\), then \(\lambda \in {{\mathrm{Crit}}}(\mathcal {V}_K)\). We will add some vectors to \(\mathcal {V}_K\) to reduce the number of critical cells.
Denote \(\mathcal {P}^r_K=\mathcal {P}_A^r\cap \mathcal {P}_K\), \(\mathcal {P}^m_K=\mathcal {P}_A^m\cap \mathcal {P}_K\). Note that \(\mathcal {P}^m_K\) is a closed subposet of \(\mathcal {P}_K\), which is empty if \(c(A',\emptyset ,m)\not \in K\) and otherwise there is an isomorphism of CW-posets
Definition 6.1
A cube \(c(C,B\cup \{m\},D)\in \square ^A\) is a branching cube of K if
-
\(c(C,m\cup B,D)\not \in K\),
-
\(c(C,m,B\cup D),c(C\cup m, B,D)\in K\).
These conditions imply that \(B\ne \emptyset \). Sequences (C, B, D) such that \(c(C,B\cup \{m\},D)\) is a branching cube of K will be called branching sequences of K. Let \({{\mathrm{Br}}}(K)\) be the set of all branching sequences of K.
For \((C,B,D)\in {{\mathrm{Br}}}(K)\) let
and let
Clearly, the posets \(\mathcal {R}_{(C,B,D)}\) are pairwise disjoint, and there is an isomorphism of posets
which shifts the dimensions of elements by \(\#B-1\).
Proposition 6.2
For an A-cubical complex K, we have \({{\mathrm{Crit}}}_{\mathcal {P}^r_K}(\mathcal {V}^r_K)=\mathcal {R}_K\).
Proof
If \(\lambda =\pi |m|B|\varrho \in \mathcal {R}_{(C,B,D)}\), then \((\pi |m|B|\varrho ,\pi |m\cup B |\varrho )\in \mathcal {V}^r_A\) and \(c(C,m\cup B,D)\not \in K\); as a consequence, \(\pi |m\cup B |\varrho \not \in \mathcal {P}^r_K\) and then \(\lambda \in {{\mathrm{Crit}}}_{\mathcal {P}^r_K}(\mathcal {V}^r_K)\). This proves that \(\mathcal {R}_K\subseteq {{\mathrm{Crit}}}_{\mathcal {P}^r_K}(\mathcal {V}^r_K)\).
Assume that \(\lambda \in {{\mathrm{Crit}}}_{\mathcal {P}^r_K}(\mathcal {V}^r_K)\). Since \({{\mathrm{Crit}}}_{\mathcal {P}^r_A}(\mathcal {V}^r_A)=\emptyset \), there exists \(\mu \in \mathcal {P}_A^r\) such that \((\lambda ,\mu )\in \mathcal {V}^r_A\) and \(\mu \not \in \mathcal {P}^r_K\). The definition of \(\mathcal {V}^r_A\) implies that
for \(A=C\mathop {\dot{\cup }}m \mathop {\dot{\cup }}B\mathop {\dot{\cup }}D\), \(\pi \in \mathcal {P}_C\), \(\varrho \in \mathcal {P}_D\). By 3.3, \(\lambda \in \mathcal {P}_K\) implies that \(\pi \in \mathcal {P}_{K|^0_C}\), \(\varrho \in \mathcal {P}_{K|^1_D}\) and \(c(C,m,B\cup D),c(C\cup m, B,D)\in K\). Thus, since \(\mu \not \in \mathcal {P}_{K}\), \(c(C,m\cup B,D)\) cannot belong to K. As a consequence, \((C,B,D)\in {{\mathrm{Br}}}(K)\) and then \(\lambda \in \mathcal {R}_{(C,B,D)}\subseteq \mathcal {R}_K\). \(\square \)
As a consequence, there is a decomposition
We will define inductively discrete vector fields on the components of this decomposition; they are empty if \(A=\emptyset \), and otherwise they are inductively defined by the following formulas:
-
On \(\mathcal {P}_K^m\):
$$\begin{aligned} \mathcal {W}^m_K=\mathcal {W}_{K|^0_{A'}}|m=\{(\lambda |m,\mu |m):\; (\lambda ,\mu )\in \mathcal {W}_{K|^0_{A'}}\} \end{aligned}$$if \(c(A', m, \emptyset )\in K\); otherwise, \(\mathcal {W}^m_K=\emptyset \). Notice that if \(\lambda |m\in \mathcal {P}^m_K\) and \(\mu \in \mathcal {P}_{K|^0_{A'}}\), then also \(\mu |m\in \mathcal {P}^m_K\), which guarantees that this definition is valid.
-
On \({{\mathrm{Reg}}}(\mathcal {V}^r_K)\) we take \(\mathcal {V}^r_K\).
-
For \((C,B,D)\in {{\mathrm{Br}}}(K)\), let \(\mathcal {Y}_{(C,B,D)}\) be the discrete vector field on \(\mathcal {R}_{(C,B,D)}\) given by
$$\begin{aligned}&\mathcal {Y}_{(C,B,D)}=\mathcal {W}_{K|_{C}^0}|m|B|\mathcal {W}_{K|_D^1}\\&\quad =\{(\pi |m|B|\varrho , \pi |m|B|\varrho '):\; \pi \in \mathcal {P}_{K|_C^0}, (\varrho ,\varrho ')\in \mathcal {W}_{K|_D^1}\}\\&\quad \cup \{(\pi |m|B|\varrho , \pi '|m|B|\varrho ):\; (\pi ,\pi ')\in \mathcal {W}_{K|_C^0}, \varrho \in {{\mathrm{Crit}}}(\mathcal {W}_{K|_D^1})\}. \end{aligned}$$This is isomorphic to the product discrete vector field \(\mathcal {W}_{K|_{C}^0}\times \mathcal {W}_{K|_D^1}\) on \(\mathcal {P}_{K|_{C}^0}\times \mathcal {P}_{K|_{D}^1}\) via the isomorphism
$$\begin{aligned} \mathcal {P}_{K|_{C}^0} \times \mathcal {P}_{K|_{D}^1}\ni (\lambda ,\mu ) \mapsto \lambda |m|B|\mu \in \mathcal {R}_{(C,B,D)} \end{aligned}$$of the underlying posets.
-
On \(\mathcal {R}_K\):
$$\begin{aligned} \mathcal {Y}_K=\bigcup \mathcal {Y}_{(C,B,D)}. \end{aligned}$$
Finally, we define \(\mathcal {W}^r_K=\mathcal {V}^r_K \cup \mathcal {Y}_K\) and
An easy inductive argument shows that \(\mathcal {V}_K\subseteq \mathcal {W}_K\).
Recall (5.5) that \(h_A:\mathcal {P}^r_A\rightarrow H\) is the weak Morse function associated to \(\mathcal {V}^r_A\).
Proposition 6.3
If \((\lambda ,\mu )\in \mathcal {Y}^r_K\), then \(h_A(\lambda )=h_A(\mu )\). As a consequence, \((\lambda ,\mu )\in \mathcal {W}^r_K\) implies that \(h_A(\lambda )\mathrel {\dot{\ge }} h_A(\mu )\).
Proof
We have \(h_A(\lambda )=h_A(\mu )=(\#C,1)\) for \((\lambda ,\mu )\in \mathcal {Y}_{(C,B,D)}\). \(\square \)
Proposition 6.4
\(\mathcal {W}_K\) is a gradient field.
Proof
Proof by induction with respect to the cardinality of A. By the inductive hypothesis, \(\mathcal {W}^m_K\simeq \mathcal {W}_{K|^0_{A'}}\) is a gradient field on \(\mathcal {P}^m_K\simeq \mathcal {P}_{K|^0_{A'}}\). Since \(\mathcal {P}^m_K\) is closed in \(\mathcal {P}_K\), by 4.6 it remains to prove that \(\mathcal {W}^r_K\) is a gradient field on \(\mathcal {P}^r_K\). Assume that
is a cycle of \(\mathcal {W}^r_K\). By 6.3, all values \(h_A(\lambda _i)\), \(h_A(\mu _i)\) are equal; thus, \((\lambda _i,\mu _i)\in \mathcal {Y}_K\) for all i, since \(h_A\) is a weak Morse function of \(\mathcal {V}^r_K\). For every i, \(\lambda _i\) and \(\mu _i\) must lie in the same component \(\mathcal {R}_{(C_i,B_i,D_i)}\). Moreover, \(C_{i+1}=C_i\) and \(B_{i+1}\subseteq B_i\); this implies that the triples \((C_i,B_i,D_i)\) are equal for all i. Thus, this cycle is a cycle of \(\mathcal {Y}_{(C,B,D)}\) for some \((C,B,D)\in {{\mathrm{Br}}}(K)\); this leads to a contradiction since \(\mathcal {Y}_{C,B,D}\) is isomorphic to \(\mathcal {W}_{K|^0_C}\times \mathcal {W}_{K|^1_D}\), which is a gradient field by the inductive hypothesis. \(\square \)
As a consequence of [13, Theorem 1.2] and Theorem 4.3 we obtain
Corollary 6.5
For an A-cubical complex \(K\subseteq \square ^A\), the space \(\vec {P}(K)_{\mathbf {0}}^\mathbf {1}\) is homotopy equivalent to a CW-complex whose k-cells correspond to the k-dimensional critical cells of \(\mathcal {W}_K\).
The following inductive formula for critical cells of \(\mathcal {W}_K\) is an immediate consequence of the definition of \(\mathcal {W}_K\):
Proposition 6.6
Let K be an A-cubical complex. If \(A=\emptyset \), then \({{\mathrm{Crit}}}_{\mathcal {P}_K}(\mathcal {W}_K)=\mathcal {P}_K\); if \(A\ne \emptyset \)
In the next section we will obtain an explicit formula for the critical cells of \(\mathcal {W}_K\).
7 Explicit formula for the critical cells
For any finite ordered set \(B=\{b_1<b_2<\cdots <b_l\}\) define \(\tau _B,\kappa _B\in \mathcal {P}_B\) by
for \(\kappa _B\) we require that B has at least two elements.
Definition 7.1
A critical sequence in an A-cubical complex K is a pair of sequences of subsets \(((E_j)_{j=1}^q,(F_j)_{j=0}^q)\) of A such that
-
(a)
\(A=E_1\mathop {\dot{\cup }}\cdots \mathop {\dot{\cup }}E_q\mathop {\dot{\cup }}F_0\mathop {\dot{\cup }}F_1\mathop {\dot{\cup }}\cdots \mathop {\dot{\cup }}F_q\).
-
(b)
The critical cell
$$\begin{aligned} \sigma ((E_j),(F_j)):=\tau _{F_0}|\kappa _{E_1}|\tau _{F_1}|\kappa _{E_2}|\cdots |\tau _{F_{q-1}}|\kappa _{E_q}|\tau _{F_q}\in \mathcal {P}_A \end{aligned}$$associated to \(((E_j),(F_j))\) belongs to \(\mathcal {P}_K\).
-
(c)
For every \(j\in \{1,\ldots ,q\}\), either \(F_{j-1}=\emptyset \) or \(\max (F_{j-1})<\max (E_j)\),
-
(d)
For every \(j\in \{1,\ldots ,q\}\), \(c(C_j,E_j,D_j)\not \in K\), where
$$\begin{aligned} C_j&= F_0\cup E_1\cup F_1 \cup E_2\cup \cdots \cup E_{j-1}\cup F_{j-1}\nonumber \\ D_j&= F_j\cup E_{j+1}\cup F_{j+1} \cup E_{j+2}\cup \cdots \cup E_{q}\cup F_{q} \end{aligned}$$(7.2)If (b) is satisfied, this is equivalent to the condition \(\tau _{F_0}|\kappa _{E_1}|\cdots |\tau _{F_{j-1}}|E_j|\tau _{F_j}|\cdots |\kappa _{E_q}|\tau _{F_q}\not \in \mathcal {P}_K\). Let \({{\mathrm{CrSeq}}}(K)\) be the set of all critical sequences in K.
We do not require that the sets \(F_j\) are non-empty but the conditions (b) and (d) imply that every \(E_j\) has at least two elements. The dimension of a critical sequence \(((E_j)_{j=1}^q,(F_j)_{j=0}^q)\) is
which is equal to the dimension of the associated critical cell. Let \({{\mathrm{CrSeq}}}^d(K)\) denote the set of d-dimensional critical sequences.
Let \({{\mathrm{CrCell}}}(K)\subseteq \mathcal {P}_K\) be the set of critical cells in K, i.e., the cells that are associated to a critical sequence, and let \({{\mathrm{CrCell}}}^d(K)\subseteq {{\mathrm{CrCell}}}(K)\) be the subset of d-dimensional cells. Notice that there are bijections
since every critical cell \(\lambda \) determines a unique critical sequence \(((E_j),(F_j))\in {{\mathrm{CrSeq}}}(K)\) such that \(\lambda =\sigma ((E_j),(F_j))\), and the dimensions of critical sequences and of the associated critical cells coincide.
Proposition 7.2
For every A-cubical complex K and \(d\ge 0\), we have
Proof
This is obvious if \(A=\emptyset \), so we assume otherwise and proceed inductively. Assume that \(((E_j)_{j=1}^q,(F_j)_{j=0}^q)\in {{\mathrm{CrSeq}}}(K)\); we will show that \(\lambda := \sigma ((E_j),(F_j))\in {{\mathrm{Crit}}}(\mathcal {W}_K)\). There are two cases to consider:
-
There existsrsuch that\(m\in E_r\). Then
$$\begin{aligned} \left( (E_j)_{j=1}^{r-1},(F_j)_{j=0}^{r-1}\right)&\in {{\mathrm{CrSeq}}}(K|^0_{C_j})\\ \left( (E_j)_{j=r+1}^q,(F_j)_{j=r}^q\right)&\in {{\mathrm{CrSeq}}}(K|^1_{D_j}) \end{aligned}$$where \(C_j, D_j\) are defined as in (7.2). From the inductive hypothesis,
$$\begin{aligned} \pi&:= \sigma \left( (E_j)_{j=1}^{r-1},(F_j)_{j=0}^{r-1}\right) \in {{\mathrm{Crit}}}(K|^0_{C_j}) \text { and} \\ \varrho&:= \sigma \left( (E_j)_{j=r+1}^{q},(F_j)_{j=r}^{q}\right) \in {{\mathrm{Crit}}}(K|^1_{D_j}). \end{aligned}$$The conditions (b) and (d) imply that \((C_j,E_j{\setminus }\{m\}, D_j)\in {{\mathrm{Br}}}(K)\). Therefore, it follows from 6.6 that
$$\begin{aligned} \lambda =\sigma ((E_j)_{j=1}^q,(F_j)_{j=0}^q)= \pi | \kappa _{E_j} |\varrho = \pi | m | E_j{\setminus }\{m\}| \varrho \in {{\mathrm{Crit}}}(\mathcal {W}_K). \end{aligned}$$ -
\(m\not \in E_r\)for everyr. Then the condition (c) guarantees that \(m\in F_q\). Let
$$\begin{aligned} \lambda '=\sigma ((E_j)_{j=1}^q, (F_0,F_1,\ldots , F_{q-1}, F_q{\setminus }\{m\})); \end{aligned}$$it is easy to check that \(\lambda '\in {{\mathrm{CrCell}}}(K|^0_{A'})\). As above, it follows from the inductive hypothesis and 6.6 that \(\lambda =\lambda '|m\in {{\mathrm{Crit}}}(\mathcal {W}_K)\).
Now assume that \(\lambda \in {{\mathrm{Crit}}}(\mathcal {W}_K)\). Again, by 6.6 there are two cases:
-
\(\lambda =\lambda '|m\)for\(\lambda '\in {{\mathrm{Crit}}}(\mathcal {W}_{K|^0_{A'}})\). By the inductive hypothesis, \(\lambda '\in {{\mathrm{CrCell}}}(K|^0_{A'})\) and then \(\lambda '=\sigma ((E_j)_{j=1}^q,(F_j)_{j=0}^q)\) for \(((E_j),(F_j))\in {{\mathrm{CrSeq}}}(K)\). Clearly,
$$\begin{aligned} ((E_j)_{j=1}^q, (F_0,\ldots ,F_{q-1},F_{q}\cup \{m\}))\in {{\mathrm{CrSeq}}}(K). \end{aligned}$$Thus, \(\lambda \in {{\mathrm{CrCell}}}(K)\), since it is the critical cell of the sequence above.
-
\(\lambda =\pi |m|B|\varrho \) for \((C,B,D)\in {{\mathrm{Br}}}(K)\), \(\pi \in {{\mathrm{Crit}}}(\mathcal {W}_{K|^0_{C}})\), \(\varrho \in {{\mathrm{Crit}}}(\mathcal {W}_{K|^1_{D}})\). By the inductive hypothesis,
$$\begin{aligned} \pi&=\sigma \left( (E^\pi _j)_{j=1}^q,(F^\pi _j)_{j=0}^q\right) ,\\ \varrho&=\sigma \left( (E^\varrho _j)_{j=1}^r,(F^\varrho _j\right) _{j=0}^r), \end{aligned}$$for \(((E^\pi _j),(F^\pi _j))\in {{\mathrm{CrSeq}}}(K|^0_C)\), \(((E^\varrho _j),(F^\varrho _j))\in {{\mathrm{CrSeq}}}(K|^1_D)\). Now \(\lambda \) is associated to a sequence
$$\begin{aligned} \left( (E_1^\pi ,\ldots ,E_q^\pi ,B\cup \{m\},E_1^\varrho ,\ldots ,E_r^\varrho ),(F_0^\pi ,\ldots ,F_q^\pi ,F_0^\varrho ,\ldots ,F^\varrho _r)\right) , \end{aligned}$$which is critical in K; the only non-trivial fact to check is that either \(E^\pi _q=\emptyset \) or \(\max (E^\pi _q)<\max (B\cup \{m\})\), which is guaranteed since m is a maximal element of A.
We have shown that \({{\mathrm{Crit}}}(\mathcal {W}_k)\cong {{\mathrm{CrSeq}}}(K)\) and it is clear that dimension is preserved. \(\square \)
Theorem 7.3
Let K be an A-cubical complex. Then \(|\mathcal {P}_K|\simeq \vec {P}(|K|)_\mathbf {0}^\mathbf {1}\) is homotopy equivalent to a CW-complex \(X_K\) that has exactly \(\# {{\mathrm{CrSeq}}}^d(K)\) cells of dimension d.
Proof
By 6.4, \(\mathcal {W}_K\) is a gradient field and by 7.2 the number of critical cells of dimension d equals to \(\# {{\mathrm{CrSeq}}}^d(K)\). The conclusion follows from 4.3. \(\square \)
8 Euclidean cubical complexes
Euclidean cubical complexes [11] constitute a class of semi-cubical sets which is especially important for applications in concurrency, since they include state spaces of PV-programs [3, 5, 14]. We recall the definition here and show that every finite Euclidean cubical complex can be embedded into the standard cube. Therefore, Euclidean cubical complexes can be regarded as A-cubical complexes.
Definition 8.1
An elementary cube in \(\vec {\mathbb {R}}^n\) is a subset of the form
where \(\mathbf {a}=(a_1,\ldots ,a_n),\mathbf {b}=(b_1,\ldots ,b_n)\in \mathbb {Z}^n\) and \(b_i-a_i\in \{0,1\}\) for all i. The integer \(|\mathbf {b}-\mathbf {a}|=\sum _{i=1}^n (b_i-a_i)\) is the dimension of the cube \([\mathbf {a},\mathbf {b}]\). The set
is the set of directions of the cube \([\mathbf {a},\mathbf {b}]\).
A Euclidean cubical complexK in \(\vec {\mathbb {R}}^n\) is a family of elementary cubes in \(\vec {\mathbb {R}}^n\) that is closed with respect to taking subsets. K can be regarded as a semi-cubical set: K[d] is the set of all d-dimensional elementary cubes of K, and the face maps are defined as follows. If \([\mathbf {a},\mathbf {b}]\in K[d]\) and \({{\mathrm{dir}}}([\mathbf {a},\mathbf {b}])=\{r(1)<\cdots <r(d)\}\), then
where \(\mathbf {e}_i=(0,\ldots ,0,1,0,\ldots ,0)\) and 1 stands at the i-th place. This corresponds to taking the lower or the upper face in the i-th direction of the cube.
Remark
The geometric realization of a Euclidean complex K regarded as a semi-cubical set is homeomorphic, in a canonical way, with the union of these cubes regarded as subsets of \(\mathbb {R}^n\).
We will define an embedding of the hyperrectangle \([\mathbf {0},\mathbf {k}]\subseteq \vec {\mathbb {R}}^n\), \(\mathbf {k}=(k_1,\ldots ,k_n)\in \mathbb {Z}^n\), in the standard cube. For \(n=1\), \(k\in \mathbb {Z}_{\ge 0}\) and an elementary cube \([a,b]\subseteq [0,k]\), define
This defines the semi-cubical embedding \(i_k:[0,k]\rightarrow \square ^k=\square ^{\{1<\cdots <k\}}\). For an arbitrary n, we will construct the embedding which is the product of the \(i_k\). Define the ordered set
For an elementary cube \([\mathbf {a},\mathbf {b}]\subseteq [\mathbf {0},\mathbf {k}]\) having dimension d, define \(i_\mathbf {k}([\mathbf {a},\mathbf {b}])\in \square ^{A_\mathbf {k}}[d]\) by
This definition makes sense since \(b_i-a_i\in \{0,1\}\) for all i, and defines the injective semi-cubical map \(i_\mathbf {k}:[\mathbf {0},\mathbf {k}]\rightarrow \square ^{A_\mathbf {k}}\); it is elementary to check that this map commutes with the face maps. Denote
Let K be a finite Euclidean cubical complex. Without loss of generality, we can assume that K is contained in the hyperrectangle \([\mathbf {0},\mathbf {k}]\), \(\mathbf {k}=(k_1,\ldots ,k_n)\in \mathbb {Z}^n\), since K can be shifted if necessary. We have
Thus, K can be regarded as an \(A_\mathbf {k}\)-cubical complex.
Remark
Instead of the order (8.1) we can use any order such that \((i,j)<(i,j')\) for \(j<j'\). This leads to a different vector field \(\mathcal {W}_{i_\mathbf {k}(K)}\), with possibly another set of critical cells.
The following observation is elementary but will be used frequently:
Proposition 8.2
Let \(\lambda =B_1|\cdots |B_l\in \mathcal {P}_{A_\mathbf {k}}\). The following conditions are equivalent:
-
(a)
\(\lambda \in \mathcal {P}_{{\boxplus }^\mathbf {k}}\).
-
(b)
For every \(i\in \{1,\ldots ,n\}\) and \(j<j'\in \{1,\ldots ,k_i\}\), if \((i,j)\in B_r\) and \((i,j')\in B_{r'}\), then \(r<r'\). \(\square \)
For a subset \({B}\subseteq A_\mathbf {k}\), let \({\bar{B}}\) be the multiset that contains only elements from \(\{1,\ldots ,n\}\), and every \(i\in \{1,\ldots ,n\}\) is contained in \(\bar{B}\) with multiplicity \(\#\{j\in \{1,\ldots ,k_i\}:\; (i,j)\in {B} \}\). \(\bar{B}\) is the image of B under the projection \(A_\mathbf {k}\ni (i,j)\mapsto i\in \{1,\ldots ,n\}\), with multiplicities preserved. In terms of characteristic functions, we have
Proposition 8.3
If \(\lambda =B_1|\cdots |B_l\in \mathcal {P}_{{\boxplus }^\mathbf {k}}\), then, for every \(r\in \{1,\ldots ,l\}\), \(\bar{B}_r\) is a set.
Proof
This follows from Proposition 8.2. \(\square \)
Let \([\mathbf {k}]\) denote the multiset having characteristic function \(\mathbf {k}\), i.e., such that it contains \(i\in \{1,\ldots ,n\}\) exactly \(k_i\) times. An ordered partition of\([\mathbf {k}]\) is a sequence \(\mu =C_1|C_2|\cdots |C_l\), where the \(C_i\) are multisets with all elements in \(\{1,\ldots ,n\}\), such that \(\sum _{i=1}^l \chi _{C_i}=\mathbf {k}\). An ordered partition \(\mu \) is proper if all multisets \(C_i\) are sets, i.e., \(\chi _{C_i}\le \mathbf {1}\). Let \(\mathcal {R}_\mathbf {k}\) be the poset of ordered partitions of \(\mathbf {k}\), ordered by refinement, and let \(\mathcal {R}_\mathbf {k}^{pr}\subseteq \mathcal {R}_\mathbf {k}\) be the subposet of proper partitions.
Proposition 8.4
If \(\lambda =B_1|\cdots |B_l\in \mathcal {P}_{{\boxplus }^\mathbf {k}}\), then \({{\bar{\lambda }}}=\bar{B}_1|\cdots |\bar{B}_l\in \mathcal {R}_\mathbf {k}^{pr}\).
Proof
For \(i\in \{1,\ldots ,n\}\) we have
Thus, \({{\bar{\lambda }}}\) is an ordered partition of \([\mathbf {k}]\), and by 8.3 this is proper. \(\square \)
Proposition 8.5
For every proper ordered partition \(E_1|E_2|\cdots |E_l\) of \([\mathbf {k}]\) there exists a unique ordered partition \(\lambda =B_1|\cdots |B_l\in \mathcal {P}_{{\boxplus }^\mathbf {k}}\) such that \(E_r=\bar{B}_r\) for all \(r\in \{1,\ldots ,l\}\).
Proof
Define
Clearly, \(\bar{B}_r=E_r\) and \(\lambda =B_1|\cdots |B_l\) is a partition of \(A_\mathbf {k}\), which satisfies condition 8.2(b). Thus, \(\lambda \in \mathcal {P}_{{\boxplus }^\mathbf {k}}\). On the other hand, if \(i\in E_r\), then \(B_r\) must contain a pair (i, j) and 8.2(b) enforces that \(j=1+\#\{s\in \{1,\ldots ,r-1\}\}\). \(\square \)
As a consequence, the formula
defines an isomorphism of posets. For a Euclidean cubical complex \(K\subseteq [\mathbf {0},\mathbf {k}]\) let
Proposition 8.6
For a Euclidean cubical complex \(K\subseteq [\mathbf {0},\mathbf {k}]\), we have
Proof
The definition of \(i_\mathbf {k}\) implies that
The conclusion follows. \(\square \)
Proposition 8.7
Assume that \((({E}_j)_{j=1}^q,({F}_j)_{j=0}^q)\in {{\mathrm{CrSeq}}}(i_\mathbf {k}(K))\). Then, for all j, \(\bar{E}_j\) is a set.
Proof
The associated critical cell \(\sigma (({E}_j),({F}_j))\) belongs to \(\mathcal {P}_{i_\mathbf {k}(K)}\) and has the form \(\lambda |(r,s)|E'_j|\mu \), where \((r,s)=\max (E_j)\), \(E'_j=E_j{\setminus }(r,s)\). Then, by 8.3, \(\bar{E}'_j\) is a set. If \(\max (\bar{E}'_j)=r\), then \((r,s')\in E'_j\) for some \(s'\). But 8.2 implies that \(s<s'\), which contradicts the assumption that \((r,s)=\max (E_j)\). Thus, \(r>\max (\bar{E}'_j)\) and then \(\bar{E}_j=\{r\}\cup \bar{E}'_j\) is a set. \(\square \)
For \(\mathbf {a}\le \mathbf {b}\in \mathbb {Z}^n\), the minimal line from\(\mathbf {a}\)to\(\mathbf {b}\) is a Euclidean cubical complex \(L_{\mathbf {a},\mathbf {b}}\) such that
Definition 8.8
A route to\(\mathbf {k}\), where \(0\le \mathbf {k}\in \mathbb {Z}^n\), is a pair of sequences \(((\mathbf {a}^j)_{j=1}^{q+1}, (\mathbf {b}^j)_{j=0}^{q})\) of points of \(\mathbb {Z}^n\) such that
-
(a)
\(\mathbf {b}^0=\mathbf {0}\)
-
(b)
\(\mathbf {a}^{q+1}=\mathbf {k}\),
-
(c)
\(\mathbf {b}^j\le \mathbf {a}^{j+1}\) for \(0\le j\le q\),
-
(d)
\(\mathbf {0}<\mathbf {b}^j - \mathbf {a}^j \le \mathbf {1}\) for \(0<j\le q\).
Let \(K\subseteq [\mathbf {0},\mathbf {k}]\) be a Euclidean complex. A critical route inK is a route to \(\mathbf {k}\) such that
-
(e)
\(L_{\mathbf {b}^{j},\mathbf {a}^{j+1}}\subseteq K\) for \(0\le j\le q\),
-
(f)
\([\mathbf {a}^j,\mathbf {b}^j]\not \in K\) for \(0<j\le q\),
-
(g)
\([\mathbf {a}^j,\mathbf {a}^j+\mathbf {e}_{m_j}], [\mathbf {a}^j+\mathbf {e}_{m_j},\mathbf {b}_j]\in K\) for \(0<j\le q\), where \(m_j=\max ({{\mathrm{dir}}}([\mathbf {a}^j,\mathbf {b}^j]))\).
We will prove that there is 1–1 correspondence between critical sequences in \(i_\mathbf {k}(K)\) and critical routes in K.
For \((({E}_j)_{j=1}^q,({F}_j)_{j=0}^q)\in {{\mathrm{CrSeq}}}(i_\mathbf {k}(K))\) define
We will check that \(((\mathbf {a}^j)_{j=1}^{q+1}, (\mathbf {b}^j)_{j=0}^{q})\) satisfies the conditions (a)–(g) of Definition 8.8. Points (a) and (c) and obvious, and (b) follows from 7.1. (a), since \(\chi _{\bar{A}_\mathbf {k}}=\mathbf {k}\). Points (e) and (g) follow from 7.1(b) and the definitions of \(\tau _{F_j}\) and \(\kappa _{E_j}\) (7.1), respectively. Finally, point (d) follows from 8.7 and (f) follows from 7.1(d). Thus, \(((\mathbf {a}^j),(\mathbf {b}^j))\) is a critical route in K.
On the other hand, if \(((\mathbf {a}^j)_{j=1}^{q+1}, (\mathbf {b}^j)_{j=0}^{q})\) is a critical route in K, then we define sequences of subsets of \(A_\mathbf {k}\):
An argument similar to the one above shows that \(((E_j)_{j=1}^q, (F_j)_{j=0}^q)\) is a critical sequence in the \(A_\mathbf {k}\)-cubical complex \(i_\mathbf {k}(K)\).
Both constructions preserve the dimension. Let \({{\mathrm{Rt}}}^d(K)\) be the set of critical routes in K having dimension d. By combining the argument above with Proposition 7.2, we obtain
Proposition 8.9
Let \(K\subseteq [\mathbf {0},\mathbf {k}]\) be a Euclidean cubical complex. For every \(d\ge 0\) there are bijections
\(\square \)
Here follows the main theorem of this Section.
Theorem 8.10
Let \(\mathbf {k}\in \mathbb {Z}^n_{\ge 0}\) and let \(K\subseteq [\mathbf {0},\mathbf {k}]\) be a Euclidean cubical complex. Then \(\vec {P}(|K|)_\mathbf {0}^\mathbf {k}\) is homotopy equivalent to a CW-complex \(X_K\) which has exactly \(\#{{\mathrm{Rt}}}^d(K)\) cells of dimension d.
Proof
This follows from Theorem 7.3 and Proposition 8.9. \(\square \)
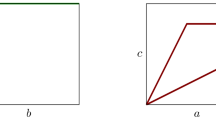
The following picture illustrates all critical routes in an example of a Euclidean cubical complex.

Each of these routes represents one of three components in the path space, each of which is contractible.
9 Applications
At first glance, it is not clear to which extent the description of the space of directed paths on an A-cubical complex provided in Theorems 7.3 and 8.10 can be used for actual calculations. In this section we describe three cases in which this description is optimal, i.e., the cells of the CW-complex \(X_K\) correspond to the generators of the homology of \(\vec {P}(|K|)_\mathbf {0}^\mathbf {1}\).
9.1 “No \((s+1)\)–equal” configuration spaces
For integers \(0<s<n\), the “no \((s+1)\)-equal” configuration space is
Homology groups of these spaces were calculated by Björner and Welker [2]. We will reprove their result here.
Theq-skeleton of a semi-cubical complex K is the cubical complex \(K_{(q)}\) such that
and the face maps of \(K_{(q)}\) are inherited from K.
Fix \(n>0\) and let \(A=\{1<2<\cdots <n\}\); we will write \(\square ^n\) instead of \(\square ^{\{1<2<\cdots <n\}}\).
Proposition 9.1
For \(0<s\le n\), the following spaces are homotopy equivalent:
-
(a)
\(\vec {P}(|\square ^n_{(s)}|)_\mathbf {0}^\mathbf {1}\),
-
(b)
\(|\mathcal {P}_{\square ^n_{(s)}}|\),
-
(c)
\({{\mathrm{Conf}}}_{n,s}(\mathbb {R})\).
Proof
This is a consequence of Sect. 2 and [10, Section 2.2]. \(\square \)
The space \(\vec {P}(|\square ^n_{(s)}|)_\mathbf {0}^\mathbf {1}\) plays an important role in concurrency, since it is the execution space of a PV-program consisting of n processes each of which using a resource of capacity s once.
Proposition 9.2
Fix \(s>1\). Then \({{\mathrm{CrSeq}}}^d(\square ^n_{(s)})=\emptyset \) if \((s-1)\) does not divide d; otherwise,
where \(E_1\mathop {\dot{\cup }}\cdots \mathop {\dot{\cup }}E_q\mathop {\dot{\cup }}F_0\mathop {\dot{\cup }}\cdots \mathop {\dot{\cup }}F_q=\{1,\ldots ,n\}\).
Proof
Condition (b) in Definition 7.1 implies that \(\# E_j\le s+1\), and condition (d) implies that \(\#E_j>s\) for all j. \(\square \)
As a consequence, we obtain
Proposition 9.3
For \(0<s\le n\), \(\vec {P}(\square ^n_{(s)})_\mathbf {0}^\mathbf {1}\) is homotopy equivalent to a CW-complex that has exactly \(\# {{\mathrm{CrSeq}}}^d(\square ^n_{(s)})\) cells of dimension d. If \(s>2\), then
where \(b(n,s,q):=\#{{\mathrm{Crit}}}^{q(s-1)}(\square ^n_{(s)})\).
Proof
The first statement follows from 7.3 and 9.2. If \(s>2\), no cells having consecutive dimensions appear, which implies the second statement. \(\square \)
For \(s=2\), a calculation of the homology groups requires checking the incidence numbers of cells having consecutive dimensions. This can be done using methods from, for example, [9, Chapter 11]. We omit these technical calculations here.
9.2 Generalized “no \((s+1)\)–equal” configuration spaces.
For \(\mathbf {k}=(k_1,\ldots ,k_n)\in \mathbb {Z}_+^n\) define the generalized “no \((s+1)\)–equal” configuration space:
This is a generalization of “no \((s+1)\)–equal” configuration spaces, since \({{\mathrm{Conf}}}_{n,s}(\mathbb {R})={{\mathrm{Conf}}}_{(1,\ldots ,1),s}(\mathbb {R})\).
The following proposition is an analogue of 9.1, and its proof is similar.
Proposition 9.4
For \(\mathbf {k}\in \mathbb {Z}_+^n\), the following spaces are homotopy equivalent:
-
(a)
\(\vec {P}([\mathbf {0},\mathbf {k}]_{(s)})_\mathbf {0}^\mathbf {k}\),
-
(b)
\(\vec {P}(|{\boxplus ^\mathbf {k}_{(s)}}|)_\mathbf {0}^\mathbf {1}\),
-
(c)
\(|\mathcal {P}_{{\boxplus }^\mathbf {k}_{(s)}}|\),
-
(d)
\({{\mathrm{Conf}}}_{\mathbf {k},s}(\mathbb {R})\).\(\square \)
In terms of PV-programs, the space \(\vec {P}([\mathbf {0},\mathbf {k}]_{(s)})_\mathbf {0}^\mathbf {k}\) is the execution space of a PV-program with a single resource of capacity s and n processes. The i-th process acquires the resource exactly \(k_i\) times.
Proposition 9.5
Fix \(s>0\). A route \(((\mathbf {a}^j)_{j=1}^{q+1}, (\mathbf {b}^j)_{j=0}^{q})\) to \(\mathbf {k}\) is a critical route in \([\mathbf {0},\mathbf {k}]_{(s)}\) if and only if \(\dim ([\mathbf {a}^j,\mathbf {b}^j])=s+1\) for \(j\in \{1,\ldots ,q\}\). In particular, the dimension of the critical route equals \(q(s-1)\).
Proof
The condition 8.8(e) is satisfied since \(s>0\), and the condition \(\dim ([\mathbf {a}^j,\mathbf {b}^j])=s+1\) is equivalent to the conditions 8.8(f)–(g). \(\square \)
Immediately from Theorem 8.10 follows the analogue of Proposition 9.3.
Proposition 9.6
Let \(b_\mathbf {k}(n,s,q)\) be the number of \(q(s-1)\)-dimensional routes in \([\mathbf {0},\mathbf {k}]_{(s)}\). Then \(\vec {P}([\mathbf {0},\mathbf {k}]_{(s)})_\mathbf {0}^\mathbf {k}\) is homotopy equivalent to a CW-complex that has exactly \(b_\mathbf {k}(n,s,q)\) cells of dimension \(q(s-1)\) and no cells having dimension non-divisible by \((s-1)\). As a consequence,
for \(s>2\).
This recovers results obtained by Meshulam and Raussen in [10, Section 5.3].
9.3 Directed path spaces on K for \([\mathbf {0},\mathbf {k}]_{(n-1)}\subseteq K\subseteq [\mathbf {0},\mathbf {k}]\)
This case was considered in [11].
Proposition 9.7
Assume that \(n\ge 2\), \(\mathbf {0}\le \mathbf {k}\in \mathbb {Z}^n\) and that K is a Euclidean cubical complex such that \([\mathbf {0},\mathbf {k}]_{(n-1)}\subseteq K\subseteq [\mathbf {0},\mathbf {k}]\). Then a route to \(\mathbf {k}\) given by \(((\mathbf {a}^j)_{j=1}^{q+1}, (\mathbf {b}^j)_{j=0}^{q})\) is a critical route in K if and only if \([\mathbf {a}^j,\mathbf {b}^j]\not \in K\) for \(j\in \{1,\ldots ,n\}\). In particular, this implies that \(\mathbf {a}^j=\mathbf {b}^j-\mathbf {1}\) for \(j\in \{1,\ldots ,n\}\) and that the dimension of the critical route equals \(q(n-2)\).
Proof
The conditions (e) and (g) in Definition 8.8 are trivially satisfied so only the condition (f) remains. \(\square \)
Note that there is 1–1 correspondence between critical routes in K and cube sequences in K defined in [11, Section 1.4]: if \(((\mathbf {a}^j)_{j=1}^{q+1}, (\mathbf {b}^j)_{j=0}^{q})\) is a critical route in K, then \([\mathbf {b}^1,\ldots ,\mathbf {b}^q]\) is a cube sequence and, inversely, a cube sequence \([\mathbf {b}^1,\ldots ,\mathbf {b}^q]\) determines the critical route \(((\mathbf {b}^j-\mathbf {1})_{j=1}^{q+1}, (\mathbf {b}^j)_{j=0}^{q})\) (where \(\mathbf {b}^0=\mathbf {0}\), \(\mathbf {b}^{q+1}=\mathbf {k}+\mathbf {1}\)).
Thus, the main theorem of [11] (Theorem 1.1) follows immediately from Theorem 8.10 if \(n\ne 3\) since there are no critical routes having consecutive dimensions. For \(n=3\), the homology calculation requires, as in the previous cases, some additional calculations we do not present here.
References
Björner, A.: Posets, regular CW-complexes and Bruhat order. Eur. J. Combin. 5, 7–16 (1984)
Björner, A., Welker, V.: The homology of “k-Equal” manifolds and related partition lattices. Adv. Math. 110, 277–313 (1995)
Dijkstra, E.W.: Co-operating Sequential Processes. Programming Languages, pp. 43–110. Academic Press, New York (1968)
Fajstrup, L., Goubault, E., Raussen, M.: Algebraic topology and concurrency. Theor. Comput. Sci. 357, 241–278 (2006)
Fajstrup, L., Goubault, E., Haucourt, E., Mimram, S., Raussen, M.: Directed Algebraic Topology and Concurrency. Springer, Berlin (2016)
Forman, R.: Morse theory for cell complexes. Adv. Math. 134, 90–145 (1998)
Forman, R.: A users guide to discrete Morse theory. Sém. Lothar. Combin. 48, Article B48c (2002)
Grandis, M.: Directed homotopy theory, I. The fundamental category. Cahiers Top. Geom. Diff. Categ 44, 281–316 (2003)
Kozlov, D.: Combinatorial Algebraic Topology. Algorithms and Computation in Mathematics. Springer, Berlin (2007)
Meshulam, R., Raussen, M.: Homology of Spaces of Directed Paths in Euclidean Pattern Spaces. In: Loebl, M., Nesetril, J., Thomas, R. (eds.) A Journey Through Discrete Mathematics: A Tribute to Jirí Matousek, pp. 593–614. Springer. https://doi.org/10.1007/978-3-319-44479-6_24
Raussen, M., Ziemiański, K.: Homology of spaces of directed paths on Euclidian cubical complexes. J. Homotopy Relat. Struct. 9, 67–84 (2014)
Ziegler, G.M.: Lectures on Polytopes. Springer, Berlin (1995)
Ziemiański, K.: Spaces of directed paths on pre-cubical sets AAECC (2017). https://doi.org/10.1007/s00200-017-0316-0
Ziemiański, K.: On execution spaces of PV-programs. Theor. Comput. Sci. 619, 87–98 (2016). https://doi.org/10.1016/j.tcs.2016.01.018
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ziemiański, K. Directed path spaces via discrete vector fields. AAECC 30, 51–74 (2019). https://doi.org/10.1007/s00200-018-0360-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00200-018-0360-4