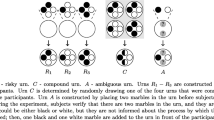
Abstract
We propose a model of learning when experimentation is possible, but unawareness and ambiguity matter. In this model, complete lack of information regarding the underlying data generating process is expressed as a (maximal) family of priors. These priors yield posterior inferences that become more precise as more information becomes available. As information accumulates, however, the individual’s level of awareness as encoded in the state space may expand. Such newly learned states are initially seen as ambiguous, but as evidence accumulates there is a gradual reduction of ambiguity.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Benavoli, A., Mangili, F., Ruggeri, F., et al.: Imprecise Dirichlet process with application to the hypothesis test on the probability that \(X\le Y\). J. Stat. Theory Pract. 9(3), 658–684 (2015)
Berti, P., Pratelli, L., Rigo, P.: Limit theorems for a class of identically distributed random variables. Ann. Probab. 32(3), 2029–2052 (2004)
Bewley, T.F.: Knightian decision theory. Part I. Decis. Econ. Finance 25(2), 79–110 (2002)
Billot, A., Gilboa, I., Samet, D., et al.: Probabilities as similarity-weighted frequencies. Econometrica 73(4), 1125–1136 (2005)
Blackwell, D., Dubins, L.: Merging of opinions with increasing information. Ann. Math. Stat. 33(3), 882–886 (1962)
Boole, G.: An Investigation of the Laws of Thought: On Which are Founded the Mathematical Theories of Logic and Probabilities. George Boole’s Collected Logical Works, Walton and Maberly (1854)
Crès, H., Gilboa, I., Vieille, N.: Aggregation of multiple prior opinions. J. Econ. Theory 146(6), 2563–2582 (2011)
Dominiak, A., Tserenjigmid, G.: Ambiguity under growing awareness. J. Econ. Theory 199, 105256 (2022)
Epstein, L.G., Schneider, M.: Learning under ambiguity. Rev. Econ. Stud. 74(4), 1275–1303 (2007)
Escobar, M.D., West, M.: Bayesian density estimation and inference using mixtures. J. Am. Stat. Assoc. 90(430), 577–588 (1995)
Ferguson, T.S.: A Bayesian analysis of some nonparametric problems. Ann. Stat. 1(2), 209–230 (1973)
Ferguson, T.S.: Prior distributions on spaces of probability measures. Ann. Stat. 2(4), 615–629 (1974)
Genest, C., Zidek, J.V.: Combining probability distributions: a critique and an annotated bibliography. Stat. Sci. 1(1), 114–135 (1986)
Ghosh, J.K., Ramamoorthi, R.V.: Bayesian Nonparametrics. Springer, Secaucus (2003)
Gilboa, I., Samet, D., Schmeidler, D.: Utilitarian aggregation of beliefs and tastes. J. Polit. Econ. 112(4), 932–938 (2004)
Gilboa, I., Macheroni, F., Marinacci, M., et al.: Objective and subjective rationality in a multiple prior model. Econometrica 78(2), 755–770 (2010)
Grant, S., Quiggin, J.: Inductive reasoning under unawareness. Econ. Theory 54, 717–755 (2013). https://doi.org/10.1007/s00199-012-0734-y
Grant, S., Guerdjikova, A., Quiggin, J.: Ambiguity and awareness: a coherent multiple priors model. BE J. Theor. Econ. 21(2), 571–612 (2021)
Halpern, J.Y., Rong, N., Saxena, A.: Mdps with unawareness. In: Proceedings of the Twenty-Sixth Conference on Uncertainty in AI, pp. 228–235 (2010)
Hylland, A., Zeckhauser, R.: The impossibility of Bayesian group decision making with separate aggregation of beliefs and values. Econometrica 47(6), 1321–1336 (1979)
Kalai, E., Lehrer, E.: Rational learning leads to Nash equilibrium. Econometrica 61(5), 1019–1045 (1993)
Kallenberg, O.: Spreading and predictable sampling in exchangeable sequences and processes. Ann. Probab. 16(2), 508–534 (1988)
Karni, E., Schmeidler, D.: Utility theory with uncertainty. In: Hildenbrand, W., Sonnenschein, H. (eds.) Handbook of Mathematical Economics, pp. 1763–1831. Elsevier Science, New York (1991)
Karni, E., Vierø, M.L.: “Reverse Bayesianism”: a choice-based theory of growing awareness. Am. Econ. Rev. 103(7), 2790–2810 (2013)
Karni, E., Vierø, M.L.: Awareness of unawareness: a theory of decision making in the face of ignorance. J. Econ. Theory 168, 301–328 (2017)
Kingman, J.F.C.: Uses of exchangeability. Ann. Probab. 6(2), 183–197 (1978)
Kochov, A.: A behavioral definition of unforeseen contingencies. J. Econ. Theory 175, 265–290 (2018)
Kopylov, I.: Subjective probability, confidence, and Bayesian updating. Econ. Theory 62(4), 635–658 (2016). https://doi.org/10.1007/s00199-015-0929-0
Kurz, M.: On the structure and diversity of rational beliefs. Econ. Theory 4(6), 877–900 (1994). https://doi.org/10.1007/BF01213817
Marinacci, M.: Learning from ambiguous urns. Stat. Pap. 43(1), 143–151 (2002)
Meier, M., Schipper, B.C.: Bayesian games with unawareness and unawareness perfection. Econ. Theory 56, 219–249 (2014). https://doi.org/10.1007/s00199-013-0788-5
Mongin, P.: Consistent Bayesian Aggregation. J. Econ. Theory 66, 313–351 (1995)
Morris, S.: The common prior assumption in economic theory. Econ. Philos. 11(02), 227–253 (1995)
Nehring, K.: imprecise probabilistic belief as a context for decision-making under ambiguity. J. Econ. Theory 144, 1054–1091 (2009)
Pivato, M.: Subject expected utility with a spectral state space. Econ. Theory 69, 249–313 (2020). https://doi.org/10.2139/ssrn.3232039
Raiffa, H., Schlaifer, R.: Applied Statistical Decision Theory. Graduate School of Business Administration, Harvard University, Division of Research (1961)
Shafer, G.: A Mathematical Theory of Evidence. Princeton University Press, Princeton (1986)
Walker, S.G., Damien, P., Laud, P.W., et al.: Bayesian nonparametric inference for random distributions and related functions. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 61(3), 485–527 (1999)
Walley, P.: Statistical Reasoning with Imprecise Probabilities. No. 42 in Monographs on Statistics and Applied Probability. Chapman and Hall (1991)
Walley, P.: Inferences from multinomial data: learning about a bag of marbles. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 58(1), 3–57 (1996)
Weerahandi, S., Zidek, J.V.: Multi-Bayesian statistical decision theory. J. R. Stat. Soc. Ser. A (Gen.) 144(1), 85–93 (1981)
Weerahandi, S., Zidek, J.V.: Elements of multi-Bayesian decision theory. Ann. Stat. 11(4), 1032–1046 (1983)
Zabell, S.L.: Predicting the unpredictable. Synthese 90(2), 205–232 (1992)
Zabell, S.L.: Symmetry and Its Discontents: Essays on the History of Inductive Probability. Cambridge University Press, Cambridge (2005)
Zidek, J.V.: Group decision analysis and its application to combining opinions. J. Stat. Plan. Inference 20(3), 307–325 (1988)
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank George Mailath, Larry Epstein, Larry Samuelson, and Marie-Louise Vierø for invaluable comments. We also thank participants of SAET 2015, ZiF Robust Finance & Beyond Conference 2016, FUR 2016, D-TEA 2017, and Virginia Tech Advances in Decision Theory Workshop 2018.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grant, S., Meneghel, I. & Tourky, R. Learning under unawareness. Econ Theory 74, 447–475 (2022). https://doi.org/10.1007/s00199-021-01408-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-021-01408-y