Financial intermediation and the welfare theorems in incomplete markets

Abstract

In production economies with incomplete markets, shareholders disagree about the objective of the firm. We show that a weak financial intermediary, who is unable to complete markets, can offer just enough spanning to resolve this disagreement. The intermediary is limited to offering one customized contract per consumer. Knowledge of demand functions is sufficient for offering the right contracts. Once agreement among shareholders is reached, productive efficiency is restored, which in turn permits a Pareto efficient market outcome. This result shows that the first welfare theorem does not depend on complete spanning, but merely on institutions that provide the right span. However, this cannot be said about the second welfare theorem: For some wealth distributions, equilibria with transfers fail to exist due to nonconvexities caused by market incompleteness.

1 Introduction

The welfare theorems provide a strong justification for organizing economic activity in the form of competitive markets. Efficient production is achieved when firms maximize profits, and efficient distribution is achieved when consumers trade. Even an omnipotent planner cannot achieve a Pareto improvement. This result is strong but limited to complete markets: Time and uncertainty must be spanned by an exogenous set of financial assets. However, financial assets are endogenous in nature as they are created by institutions, such as firms and financial intermediaries. If markets are incomplete, or at least potentially so, efficient spanning becomes a precondition for efficient distribution. The present paper argues that financial intermediaries are the right agents to pursue efficient spanning. Many problems in the previous literature on incomplete markets are due to the inability of firms to provide the right span, or to align spanning with productive efficiency. We show how these problems can be overcome if the responsibility for spanning is delegated from firms to an intermediary.

The intermediary can enlarge the asset span by providing additional assets. However, such financial innovation is not guaranteed to be socially desirable. There may be adverse welfare effects, and these can be particularly strong in economies with multiple future dates or commodities: Elul (1995) and Cass and Citanna (1998) show that enlarging the asset span may have any welfare effect, including a Pareto deterioration. The focus of the present paper is on two-date finance economies. In such economies the problem exists in a weaker form: Financial innovation cannot harm all consumers simultaneously, but its price effects may still make some consumers worse off. The positive aspect is that the set of assets whose introduction leads to a Pareto improvement is sizable. Therefore, an intermediary can always improve welfare by providing the right assets. This task would be trivial if the intermediary was very powerful. For example, if the intermediary could offer a complete set of contingent claims, we would be back in the Arrow and Debreu (1954) setting. We do not permit such ample contracts, but restrict the intermediary to one customized contract per consumer. This restriction places an upper bound on the dimension of the span.

The fundamental problem of production in incomplete markets is that consumers disagree about the valuation of production plans outside the asset span. Except for lower-dimensional production sets that are fully contained in the asset span, which is a special case studied by Ekern and Wilson (1974) and Radner (1974), this generates conflicts between shareholders about the objective of the firm. Even though our intermediary is too weak for spanning in the Ekern–Wilson–Radner sense, its services are sufficient for alleviating conflicts of interest between shareholders. We demonstrate this point in an introductory example with two consumers and two firms. Even though the example is simple, it is not clear what objective either firm should pursue if there is no intermediary. We consider two traditional objectives, but in either case the resulting equilibrium concept exhibits undesirable behavior.

The first objective is derived by Grossman and Hart (1979) from a criterion of unanimity with side payments among initial shareholders. This derivation is based on the assumption of competitive price perceptions, originally formulated by Gevers (1974) and Leland (1977): Each consumer believes that his personal valuation of a production plan agrees with its market value in the resulting equilibrium. The foundation of this assumption is questioned by Dierker and Dierker (2012), who present an example in which competitive price perceptions are everywhere incorrect. Our example seems to be much better suited for this criterion because competitive price perceptions are everywhere correct. Nevertheless, no Grossman–Hart equilibrium exists because the objective function of the firm exhibits a discontinuity when two firms choose identical production plans. Contrary to a similar problem in exchange economies discussed by Hart (1975), the nonexistence of Grossman–Hart equilibrium is robust to perturbations of consumer characteristics. At least the problem is not robust to perturbations of production technologies, which Magill and Quinzii (1991) prove with formal rigor.

The second objective is derived by Drèze (1974) from the first-order conditions for constrained efficiency. However, the first-order conditions are necessary but not sufficient, owing to nonconvexity of the constrained feasible set. This leads to problems: Dierker et al (2002) present an example with a unique but constrained inefficient Drèze equilibrium. To attain constrained efficiency in their example, an equilibrium with transfers is required. In our example the problem is more pronounced: By construction, any constrained optimum must satisfy both distributional efficiency and productive efficiency. However, firms cannot attain both simultaneously because the asset span collapses at all production-efficient plans. The unique Drèze equilibrium is Pareto dominated by market outcomes for nearby production plans. The source of this problem is explained by Zierhut (2019): There is a discontinuity in the feasible correspondence of the constrained planner. As a consequence, the Pareto problem of the planner has no solution and the set of constrained efficient allocations is empty.

In contrast to these difficulties, the present paper provides a positive result: All these problems disappear once the intermediary is introduced. The intermediary offers only contracts that are unanimously approved by its stakeholders. This idea is not entirely new: A criterion of unanimity with side payments is successfully used by Bejan (2020) for deriving an objective for a firm that may create new assets. The case of an intermediary who creates new assets is studied by Hara (2011), who highlights an important link between unanimity and welfare: If the intermediary proposes a sequence of span-enlarging contracts, and consumers must unanimously approve each proposal, then only Pareto improving financial innovation takes place. In either case, consumers must correctly anticipate the price effects of financial innovation, which is a demanding assumption. Our approach is different. We view unanimity as a cooperative solution concept. It can be explained by means of a thought experiment: Suppose consumers have the right to form coalitions, who can open their own members-only intermediary. Side payments at the present date can be used to reach agreement within a coalition. All these transactions take place after the market has closed and therefore no anticipations or perceptions of prices are necessary. Unanimity is reached if all consumers find it optimal to forgo their right. This solution concept is consistent with price-taking behavior and justifies that one single intermediary serves the entire economy.

Since this criterion is not based on a benevolent planner but on market outcomes in incomplete markets, there is no a priori reason to believe that it meets any efficiency standard. In fact, previous results are negative: In an incomplete market setting without intermediary, Zierhut (2017) shows that constrained efficiency and unanimity are generically incompatible. The present paper shows that the intermediary makes a difference:

• 1. In the presence of an intermediary, constrained efficiency, Pareto efficiency and unanimity are equivalent (Theorem 1).

This equivalence holds trivially when markets are complete but seems surprising when markets are incomplete. This result can be explained as follows: Even if markets were complete, all net transfers would be limited to a lower dimensional subspace. The dimension of this subspace is smaller than the number of consumers. It can therefore be spanned by the intermediary with only one contract per consumer. Since transfers outside this space are never demanded, such a span is sufficient for an efficient distribution, and marginal rates of substitution are equalized across consumers. As a consequence, all conflicts about the objective of the firm disappear and profit maximization with respect to any linear combination of marginal rates leads to efficient production. The resulting equilibria are Arrow–Debreu equivalent in spite of incomplete markets, and they exist generally:

• 2. Every economy has an equilibrium (Corollary 1).

This result is unusually strong for an incomplete market economy without short sale constraints. With insufficient spanning, existence is at best a generic property because the budget correspondence is discontinuous when firms choose redundant production plans. However, these discontinuities are patched up by the spanning service of the intermediary. All these equilibria are Pareto efficient—hence, the first welfare theorem holds. This raises hopes that market completeness can be dropped as a condition in the second welfare theorem as well. This would complement recent findings of Koutsougeras and Ziros (2015), who are able to drop the condition of price-taking behavior: Pareto efficient allocations can be decentralized in a strategic market game, but in addition to lump-sum transfers, a regulator must impose a tax policy on bids and offers. However, market completeness turns out to be crucial:

• 3. The second welfare theorem fails: Some Pareto efficient allocations cannot be decentralized as an equilibrium with transfers when markets are incomplete.

The problem can be summarized as follows: When markets are incomplete, Pareto efficient allocations are still price-supportable, but the set of feasible lump-sum transfers is not convex: For some wealth distributions, there exist Pareto optima but no equilibrium with transfers. This is contrary to the effect of nonconvex production sets documented by Guesnerie (1975): For some wealth distributions, there exist marginal cost pricing equilibria but no Pareto optimum. Both cases have in common that price-supportability is not sufficient for the desired result. The same limitations apply to the findings of Pan (1995), who shows that constrained efficient allocations are price-supportable. To conclude: The spanning service of an intermediary eliminates discontinuities but does not iron out nonconvexities.

The remainder of this paper is structured as follows. Section 2 presents the model and introduces our concept of intermediated financial market equilibrium. Section 3 explains the role of the intermediary in a simple example and shows how it eliminates the conflict between constrained efficiency and unanimity. Section 4 generalizes this result and derives the objective of the intermediary. Section 5 discusses the welfare theorems in incomplete markets and demonstrates the failure of the second theorem. Section 6 concludes.

2 Model

Consider a two-date finance economy with production. Uncertainty is represented by a finite state space ${\varvec{\varOmega }}$. The economy is populated by a finite number I of price-taking consumers, a finite number K of firms, and one intermediary. There is a single consumption good at date 0 and in each state at date 1. All decisions are made at date 0, and these determine the available consumption levels at date 1. We believe the most realistic case is a number of consumers much larger than the number of firms, and a number of states much larger than the number of consumers. As a minimal assumption we require that $K \le I < |{\varvec{\varOmega }}|$.

The following notation is used throughout: If x is a vector in Euclidean space, $x \ge 0$ means all components are non-negative, $x > 0$ means at least one component is greater than zero, and $x \gg 0$ means all components are greater than zero. Moreover, $\Vert x\Vert$ denotes the Euclidean norm, $x^\mathrm {N}$ denotes the normalization of x to unit length, $x\cdot y$ is the usual inner product, and $\mathbf {1}$ is the vector whose components are all one. For any set $\mathcal {X}$, denote by $N_\mathcal {X}[x]$ the (Clarke) normal cone at $x \in \mathcal {X}$. For any matrix M, denote by ${\left\langle M\right\rangle } = \mathrm {Im}(M)$ the column span and by ${\left\langle M\right\rangle }^\bot$ its orthogonal complement. Prices, gradients, and Lagrange multipliers are viewed as row vectors; all other variables are viewed as column vectors.

2.1 Consumers

Consumers are indexed by superscripts $i \in \{1,\ldots ,I\}$. Each of them chooses a consumption plan $c^i$ in $\mathbb {R}^{|{ {\varvec{\varOmega }}}|+1}$. Vectors in this space can be split $c^i = (c_0^i,c_{{\textit{1}}}^i)$, into their component $c_0^i$ at date zero and the subvector $c_{{{\textit{1}}}}^i$ at date 1. Within this subvector, $c_\omega ^i$ stands for consumption in a particular state $\omega \in {{\varvec{\varOmega }}}$. Since only non-negative quantities can be consumed, the consumption set is $\mathcal {C} = \mathbb {R}_+^{|{{\varvec{\varOmega }}}|+1}$. The preferences of consumer i are represented by a utility function $U^i:\mathcal {C}\rightarrow \mathbb {R}$ that satisfies the following assumption:

Assumption 1

(Preferences) For each consumer i, $U^i$ is continuous, strictly increasing, strictly concave, as well as twice continuously differentiable in $\mathbb {R}_{++}^{|{\varvec{\varOmega }}|+1}$, and $U^i(c^i) > U^i(0)$ implies $c^i \gg 0$.

Since $U^i$ is differentiable at any interior consumption plan $c^i \gg 0$, the marginal rates of substitution are well-defined as the normalized utility gradient

$$\begin{aligned} \nabla U^i[c^i] = \frac{DU^i[c^i]}{D_{c_0^i}U^i[c^i]}, \end{aligned}$$

and by strong monotonicity, $\nabla U^i[c^i] \gg 0$. The income of consumer i is represented by an endowment vector $e^i \in \mathcal {C}$. Whenever agent-specific variables are joined in a single vector, the superscript is omitted; e.g., $e = (e^1,\ldots ,e^I)$. Consumers have a positive endowment in each state:

Assumption 2

(Endowments) For each consumer i, $e^i \gg 0$.

2.2 Firms

Firms are indexed by superscripts $k \in \{1,\ldots ,K\}$. They are organized as corporations, owned by consumers who hold shares. The initial shareholdings of consumer i are represented by a vector $\delta ^i = (\delta _1^i,\ldots ,\delta _K^i) \ge 0$. For each firm k, the number of shares is normalized to one. Therefore, the initial ownership structure $\delta$ is an element of the set

$$\begin{aligned} \varDelta = \left\{ \delta \in \mathbb {R}_+^{IK}\left| \,\sum _{i=1}^I \delta ^i = \mathbf {1}\right. \right\} . \end{aligned}$$

At date 0, firm k chooses a production plan $Y^k \in \mathbb {R}^{|{\varvec{\varOmega }}|+1}$. Negative signs indicate input goods, positive signs indicate output goods. Profits from production are distributed pro rata among the initial shareholders. The production set $\mathcal {Y}^k$ consists of all production plans that are technologically feasible for firm k.

Assumption 3

(Production technology) For each firm k, $\mathcal {Y}^k$ is closed, convex, and satisfies $\mathcal {C} \subset -\mathcal {Y}^k$ (free disposal) and $\mathcal {C} \cap \mathcal {Y}^k = \{0\}$ (no free output). Moreover, aggregate production possibilities are bounded:

$$\begin{aligned} \mathcal {C} \cap \left( \bar{e} + \sum _{k=1}^K \mathcal {Y}^k\right) \text { is compact for any } \bar{e} \in \mathcal {C}. \end{aligned}$$

The production plan of each firm is divided among its shareholders. If there is a financial market for shares, ownership of firms may change through trade. In this case, payments at date 0 concern initial shareholders, whereas payments at date 1 concern final shareholders.

2.3 Economy

A production economy is a tuple $(\mathcal {Y},U,e,\delta )$ of production sets, utility functions, endowments, and initial shares that satisfies Assumptions 1, 2, and 3. This definition is institution-free in the sense that it does not specify how the economy is organized. Three different organizational forms are considered in the present paper: centrally planned economies, decentralized market economies, and regulated market economies.

In a centrally planned economy, all consumption and production plans are chosen by a planner, and consumption goods are allocated to consumers. There are not markets. An allocation c is feasible if it belongs to the set

$$\begin{aligned} \mathcal {F} = \left\{ c\in \mathcal {C}^I\left| \,\sum _{i=1}^I \left( c^i-e^i\right) \in \sum _{k=1}^K \mathcal {Y}^k\right. \right\} . \end{aligned}$$

(1)

A benevolent planner, who aims at meeting a welfare standard, serves as a normative benchmark. The most common welfare standard is Pareto efficiency.

Definition 1

An allocation $c\in \mathcal {F}$ is Pareto efficient if there is no other allocation $\hat{c}\in \mathcal {F}$ such that $U^i(\hat{c}^i)\ge U^i(c^i)$ for all consumers i with strict inequality for at least one consumer.

Every Pareto efficient allocation c is supported by some production plans Y. Pareto efficiency implies the following two properties: First, the aggregate production plan is efficiently distributed among the consumers. Second, no resources are wasted in production; that is to say, the aggregate production plan lies at the boundary of the aggregate production set. These properties are referred to as distributive efficiency and productive efficiency. An allocation $c \in \mathcal {F}$ is distribution-efficient for given production plans Y if there is no other allocation $\hat{c} \in \mathcal {F}$ that satisfies $\sum _{i=1}^I (\hat{c}^i-e^i) = \sum _{k=1}^K Y^k$ such that $U^i(\hat{c}^i)\ge U^i(c^i)$ for all consumers i with strict inequality for at least one consumer. Production plans $Y \in \mathcal {Y}$ are production-efficient if there are no other plans $\hat{Y} \in \mathcal {Y}$ such that $\sum _{k=1}^K (\hat{Y}^k-Y^k) > 0$.

In a decentralized market economy, consumption plans are chosen by consumers, production plans are chosen by firms, and markets are used to transfer income across time and between states of the world. We distinguish two market structures: The first market structure is contingent markets in the sense of Arrow–Debreu: For each state $\omega$, there is a contingent claim that delivers one unit of consumption in this state and zero in all other states. These contingent claims are traded at date 0 and enable arbitrary income transfers. There is no need for trade in corporate shares, and the entire production plan is paid to the initial shareholders. In particular, there is no need for an intermediary. The second market structure is financial markets: Contingent claims are not available, and trade in shares is the only method of income transfer. As some transfers are not feasible in incomplete financial markets, consumers may have demand for financial intermediation.

In a regulated market economy, decisions of consumers and firms are again decentralized, and markets are used for income transfers. However, a regulator may intervene in the market by enforcing lump-sum transfers between consumers. Such a regulator is less powerful than a central planner. The regulator may redistribute wealth, but consumers and firms make their own decisions at the given wealth levels. Moreover, since the regulator can only redistribute what is traded in the market, its set of transfers is limited by the market structure in the same way as consumers are limited in their transfers.

2.4 Contingent market equilibrium

Suppose there are contingent markets. The market prices of all claims are represented by a state-price vector $q \in \mathcal {C}$, in which $q_\omega$ stands for the price of the claim that delivers one unit of consumption in state $\omega$. Consumption at date 0 serves as the numéraire: $q_0 = 1$. There are no short-sale constraints. The contingent market budget correspondence $B:\mathcal {C}\times \mathcal {C}\times \mathbb {R}_+^K\times \mathcal {Y} \rightrightarrows \mathcal {C}$ specifies the set of attainable consumption plans for each consumer:

$$\begin{aligned} B(q,e^i,\delta ^i,Y) = \left\{ c^i\in \mathcal {C}\left| \,q\cdot (c^i-e^i) \le q\cdot Y\cdot \delta ^i\right. \right\} . \end{aligned}$$

(2)

This correspondence has a simple interpretation in terms of net transfers $z^i = c^i - e^i$ in contingent markets. Each such transfer is a bundle of state-contingent payments. A net transfer is attainable if its present value $q\cdot z^i$ does not exceed the consumer’s share in profits $q\cdot Y$ from production. Since utility functions are continuous, strictly increasing, and strictly concave under Assumption 1, there is a continuous solution function $c^{i*}(q)$ to the utility maximization problem

$$\begin{aligned} \max _{c^i} U^i(c^i) \quad \text {subject to} \quad c^i \in B(q,e^i,\delta ^i,Y), \end{aligned}$$

(3)

and thus the optimal net transfer $z^{i*}(q) = c^{i*}(q) - e^i - Y\cdot \delta ^i$ in contingent markets is also continuous. The economy is in equilibrium if consumers maximize utility, firms maximize profits, and all contingent markets clear. Profit maximization is well-defined because there is a unique state price vector.

Definition 2

A contingent market equilibrium (CM equilibrium) for the production economy $(\mathcal {Y},U,e,\delta )$ is a tuple $(q,c,Y) \in \mathcal {C}\times \mathcal {C}^I\times \mathcal {Y}$ of state prices, consumption plans, and production plans that satisfies

• 1. for each consumer i,

  $$\begin{aligned} c^i = \mathop {{\text {arg max}}}\limits _{\hat{c}^i} U^i(\hat{c}^i) \quad \text {subject to} \quad \hat{c}^i \in B(q,e^i,\delta ^i,Y) \end{aligned}$$

• 2. for each firm k,

  $$\begin{aligned} Y^k \in \mathop {{\text {arg max}}}\limits _{y} q\cdot y \quad \text {subject to} \quad y \in \mathcal {Y}^k \end{aligned}$$

• 3. market clearing,

  $$\begin{aligned} \sum _{i=1}^I c^i = \sum _{i=1}^I e^i + \sum _{k=1}^K Y^k. \end{aligned}$$

Under Assumptions 1 through 3, the existence proof of Arrow and Debreu (1954) applies and there is a contingent market equilibrium for every economy. Moreover, all equilibrium prices and allocations are positive: $(q,c) \gg 0$. The first welfare theorem states that contingent market equilibria are Pareto efficient. This can be verified easily: The first-order conditions of the utility maximization problem (3) imply that

$$\begin{aligned} \nabla U^i[c^i] = q \end{aligned}$$

(4)

for each consumer i. Thus, the marginal rates of substitution are equalized in equilibrium. The first-order conditions of the profit maximization problem imply that q is contained in the normal cone $N_{\mathcal {Y}^k}[Y^k]$ to the optimal production plan of each firm k. In combination with (4), this leads to

$$\begin{aligned} \nabla U^i[c^i] \in N_{\mathcal {Y}^k}[Y^k] \end{aligned}$$

(5)

for each consumer i and firm k. Thus, the equalized marginal rates of substitution are normal to individual production sets, and therefore normal to the aggregate production set. This is the classical characterization of Pareto efficiency by Debreu (1951) and others. If the economy is regulated, the endowments of consumers may be reallocated. The income levels attainable by means of lump-sum transfers in contingent markets are given by the transfer correspondence $\mathcal {T}:\mathcal {C}^I\rightrightarrows \mathcal {C}^I$,

$$\begin{aligned} \mathcal {T}(e) = \left\{ \hat{e}\in \mathcal {C}^I\left| \,\sum _{i=1}^I \left( \hat{e}^i-e^i\right) \le 0\right. \right\} , \end{aligned}$$

(6)

which is compact-convex-valued and has a closed, convex graph. The regulator takes production plans Y as given but may reallocate initial shares. Market outcomes that can be attained by such a regulator are called contingent market equilibria with transfers.

Definition 3

A CM equilibrium with transfers for the production economy $(\mathcal {Y},U,e,\delta )$ is a tuple $(q,c,Y) \in \mathcal {C}\times \mathcal {C}^I\times \mathcal {Y}$ which is a contingent market equilibrium for some other economy $(\mathcal {Y},U,\hat{e},\hat{\delta })$ with $(\hat{e},\hat{\delta })\in \mathcal {T}(e)\times \varDelta$.

It should be noted that the set of CM equilibria with transfers is rather large. In particular, it contains all CM equilibria.

2.5 Intermediated financial market equilibrium

Now suppose shares of firms are the only traded assets. Shares of firm k are traded at a price of $p^k$ and these share prices are collected in the share price vector $p = (p^1,\ldots ,p^K) \in \mathbb {R}^K$. There are no short-sale constraints. In addition, there is an intermediary with the ability to offer each consumer i one customized contract $X^i \in \mathbb {R}^{|{\varvec{\varOmega }}|+1}$ at no cost. Each contract is a complete specification of payments at date 0 and in each future state of the world: $X_\omega ^i > 0$ stands for the payoff to consumer i in state $\omega$; negative signs $X_\omega ^i < 0$ indicate payments to the intermediary. Future contract payments are collected in the vector $X_{{\textit{1}}}^i$; payments at date 0 are denoted by $X_0^i$. Markets are said to be complete if $\mathrm {rank}(X_{{\textit{1}}},Y_{{\textit{1}}}) = |{\varvec{\varOmega }}|$; that is, all future states are spanned by the payments of contracts and shares. Otherwise, if $\mathrm {rank}(X_{{\textit{1}}},Y_{{\textit{1}}}) < |{\varvec{\varOmega }}|$, markets are said to be incomplete.

At date 0, each consumer i chooses a quantity $\phi ^i \in \mathbb {R}$ of the contract being offered to him and a portfolio of final shares $\psi ^i \in \mathbb {R}^K$. Since each contract can be demanded in arbitrary quantities, there is no loss of generality in restricting the choice set of the intermediary to the unit sphere:

$$\begin{aligned} \mathcal {X} = \left\{ X^i\in \mathbb {R}^{|{\varvec{\varOmega }}|+1}\,\left| \,\left\| X^i\right\| = 1\right. \right\} \end{aligned}$$

The intermediary must maintain a balanced book: In each state $\omega$, incoming and outgoing payments must match; that is, $X_\omega ^1\phi ^1 + \cdots + X_\omega ^I\phi ^I = 0$. Such an intermediary does not make profits but cannot go bankrupt either. The choice set of consumers is defined by the financial market budget correspondence $\mathbb {B}:\mathbb {R}^K\times \mathcal {C}\times \mathbb {R}_+^K\times \mathcal {X}\times \mathcal {Y} \rightrightarrows \mathcal {C}$:

$$\begin{aligned}&\mathbb {B}(p,e^i,\delta ^i,X^i,Y) \nonumber \\&= \left\{ c^i\in \mathcal {C}\left| \,c^i-e^i \le \begin{pmatrix}-p\\ Y_{{\textit{1}}}\end{pmatrix}\cdot (\psi ^i-\delta ^i) + X^i\phi ^i + Y\cdot \delta ^i,\;(\phi ^i,\psi ^i) \in \mathbb {R}\times \mathbb {R}^K\right. \right\} . \end{aligned}$$

(7)

Consumers choose their portfolios of contracts and shares in such a way that the resulting consumption plan is a solution to their utility maximization problem

$$\begin{aligned} \max _{c^i} U^i(c^i) \quad \text {subject to} \quad c^i \in \mathbb {B}(p,e^i,\delta ^i,X^i,Y). \end{aligned}$$

(8)

Since utility functions are strictly increasing under Assumption 1, the budget constraint holds with equality, and the first-order conditions with respect to $\phi ^i$ and $\psi ^i$ are

$$\begin{aligned} \nabla U^i[c^i]\cdot X^i = 0,\quad \quad \nabla _{{\textit{1}}} U^i[c^i]\cdot Y_{{\textit{1}}} = p. \end{aligned}$$

(9)

These reveal that the vector of marginal rates of substitution is again a state price vector that assigns present values to bundles of state-contingent payments. In fact, any vector q that solves the linear equations $q\cdot X = 0$ and $q_{{\textit{1}}}\cdot Y_{{\textit{1}}} = p$ is a potential state price vector. The solution set to these linear equations is a nontrivial subspace whenever markets are incomplete. In this case, the set of state price vectors is a continuum, and profit maximization becomes an ambiguous concept. Therefore, a different objective of the firm is needed. In abstract terms, each firm must have a choice correspondence $Y^{k*}:\mathbb {R}^K\times \mathcal {C}^I\times \mathbb {R}^I\times \mathbb {R}^{IK}\times \mathcal {X}^I\times \mathcal {Y} \rightrightarrows \mathcal {Y}^k$ that associates optimal production plans with observable prices and actions of other agents $(p,c,\phi ,\psi ,X,Y)$. This choice correspondence may depend on shareholder characteristics, such as their utility functions, demand functions, or wealth levels. Two choice correspondences are of particular prominence in the literature on production in incomplete markets. Both extend the principle of profit maximization by selecting one particular state price vector from the continuum. The selection criterion proposed by Grossman and Hart (1979) is based on a share-weighted sum of marginal rates of substitution. Initial shares are used as weights:

$$\begin{aligned} Y^{k*} = \mathop {{\text {arg max}}}\limits _{y} \sum _{i=1}^I \delta _k^i \nabla U^i[c^i] \cdot y \quad \text {subject to} \quad y \in \mathcal {Y}^k. \end{aligned}$$

(10)

This criterion is based on positive considerations. It can be rationalized in terms of a condition of unanimity with side payments, provided that shareholders have competitive price perceptions—an assumptions we will discuss in Sect. 2.6. In Grossman–Hart equilibrium, consumers solve the utility maximization problem (8), firms employ the choice correspondence (10), and markets clear. A selection criterion that is justified on welfare grounds, rather than by price perceptions, is proposed by Drèze (1974): Final shares are used as weights for selecting a state price vector:

$$\begin{aligned} Y^{k*} = \mathop {{\text {arg\,max}}}\limits _{y} \sum _{i=1}^I \psi _k^i \nabla U^i[c^i] \cdot y \quad \text {subject to} \quad y \in \mathcal {Y}^k, \end{aligned}$$

(11)

This criterion is based on normative considerations. It aims at implementing the welfare standard of constrained efficiency in a decentralized market economy. In Drèze equilibrium, consumers solve the utility maximization problem (8), firms employ the choice correspondence (11), and markets clear. Both criteria can be viewed as a generalization of price taking behavior as found in the concept of contingent market equilibrium. Firms do not behave strategically and make their choices independently of the choices of their competitors. At the same level of abstraction as before, the behavior of the intermediary is specified by a choice correspondence $X^{i*}:\mathbb {R}^K\times \mathcal {C}^I\times \mathbb {R}^I\times \mathbb {R}^{IK}\times \mathcal {X}^I\times \mathcal {Y} \rightrightarrows \mathcal {X}$. Since the intermediary is the novel feature of the present paper, its choice correspondence must be derived rather than assumed. For this reason, we maintain the current level of abstraction in our definition of equilibrium, and leave the specifics of choice correspondences for Sect. 4.

Definition 4

An intermediated financial market equilibrium (IFM equilibrium) for given choice correspondences $(X^*,Y^*)$ and production economy $(\mathcal {Y},U,e,\delta )$ is a tuple $(p,c,\phi ,\psi ,X,Y) \in \mathbb {R}^K\times \mathcal {C}^I\times \mathbb {R}^I\times \mathbb {R}^{IK}\times \mathcal {X}^I\times \mathcal {Y}$ of prices, consumption plans, portfolios, contracts, and production plans that satisfies

• 1. for each consumer i,

  $$\begin{aligned} c^i = \mathop {{\text {argmax}}}\limits _{\hat{c}^i} U^i(\hat{c}^i) \quad \text {subject to} \quad \hat{c}^i \in \mathbb {B}(q,e^i,\delta ^i,X^i,Y) \end{aligned}$$

• 2. for each firm k,

  $$\begin{aligned} Y^k \in Y^{k*}(p,c,\phi ,\psi ,X,Y) \end{aligned}$$

• 3. the intermediary offers each consumer i,

  $$\begin{aligned} X^i \in X^{i*}(p,c,\phi ,\psi ,X,Y) \end{aligned}$$

• 4. market clearing,

  $$\begin{aligned} \sum _{i=1}^I X^i\phi ^i = 0,\quad \sum _{i=1}^I \psi ^i = \mathbf {1} . \end{aligned}$$

If a regulator intervenes in the market, it is restricted to transfers of date 0 consumption and shares. These restrictions are incorporated in the constrained transfer correspondence $\mathcal {T}_C:\mathcal {C}^I\times \mathcal {Y} \rightrightarrows \mathcal {C}^I$

$$\begin{aligned} \mathcal {T}_C(e,Y) = \left\{ \hat{e}\in \mathcal {T}(e)\left| \,\hat{e}^i-e^i \in {\left\langle \begin{pmatrix}1 &{} 0 \\ 0 &{} Y_{{\textit{1}}}\end{pmatrix}\right\rangle }\right. \right\} , \end{aligned}$$

(12)

which is compact-convex valued but need not have a closed or convex graph. Market outcomes that can be attained by the constrained regulator are referred to as intermediated financial market equilibria with transfers.

Definition 5

An IFM equilibrium with transfers for given choice correspondences $(X^*,Y^*)$ and production economy $(\mathcal {Y},U,e,\delta )$ is a tuple $(p,c,\phi ,\psi ,X,Y) \in \mathbb {R}^K\times \mathcal {C}^I\times \mathbb {R}^I\times \mathbb {R}^{IK}\times \mathcal {X}^I\times \mathcal {Y}$ which is an intermediated financial market equilibrium for $(X^*,Y^*)$ and some other economy $(\mathcal {Y},U,\hat{e},\hat{\delta })$ with $(\hat{e},\hat{\delta })\in \mathcal {T}_C(e,Y)\times \varDelta$.

Since contracts of the intermediary are customized, they cannot be transferred from one consumer to another. Put differently: The regulator cannot override the objective of the intermediary, just like it cannot override the objective of the firm. Clearly, these objectives should not be arbitrary but based on a form of unanimity, constrained efficiency, or ideally both.

2.6 Constrained efficiency and unanimity

The normative approach to defining choice correspondences aims at reaching a welfare standard. Welfare standards reflect the ethical standpoint of an outside observer. Pareto efficiency is typically a standard too high when markets are incomplete because the underlying planner can make transfers that are not feasible for consumers. Therefore, it has become customary to consider a constrained planner, who must use portfolio reallocations for transfers of future consumption. This planner has the power to define the asset span by choosing contracts $X \in \mathcal {X}^I$ and production plans $Y \in \mathcal {Y}$ but is then constrained to transfers within the chosen asset span as well as transfers $\upsilon \in \mathbb {R}^I$ of present consumption. An allocation c is constrained feasible if it can be implemented by such a planner. Any constrained feasible allocation is supported by choices $(\upsilon ,\phi ,\psi ,X,Y)$ that satisfy:

$$\begin{aligned}&c^i \le e^i + \begin{pmatrix}1\\ {{\textit{0}}}\end{pmatrix}\upsilon ^i+ X^i\phi ^i + Y\cdot \psi ^i\quad \forall i \end{aligned}$$

(13)

$$\begin{aligned}&\sum _{i=1}^I \upsilon ^i = 0 \end{aligned}$$

(14)

$$\begin{aligned}&\sum _{i=1}^I X^i\phi ^i = 0 \end{aligned}$$

(15)

$$\begin{aligned}&\sum _{i=1}^I \psi ^i = \mathbf {1} \end{aligned}$$

(16)

All such allocations are collected in the constrained feasible set $\mathcal {F}_C \subseteq \mathcal {F}$, defined as

$$\begin{aligned} \mathcal {F}_C = \left\{ c\in \mathcal {C}^I\left| \, \begin{matrix} \exists (\upsilon ,\phi ,\psi ,X,Y) \in \mathbb {R}^I\times \mathbb {R}^I\times \mathbb {R}^{IK}\times \mathcal {X}^I\times \mathcal {Y} \\ \text { such that (13) to (16) hold} \end{matrix} \right. \right\} . \end{aligned}$$

An allocation in this set is called constrained inefficient if the constrained planner can attain a Pareto improvement. By contrast, an allocation is called constrained efficient if it is a Pareto optimum in $\mathcal {F}_C$.

Definition 6

An allocation $c\in \mathcal {F}_C$ is constrained efficient if there is no other allocation $\hat{c}\in \mathcal {F}_C$ such that $U^i(\hat{c}^i)\ge U^i(c^i)$ for all consumers i with strict inequality for at least one consumer.

The positive approach to defining choice correspondences is based on a form of unanimity among consumers. Unanimity requires the approval of those consumers who hold a share in firms, and use the services of the intermediary. Since there is an abundance of unanimity criteria in the literature, it is worth introducing a categorization. Unanimity can be defined as an individual criterion, as a group criterion, or as a coalitional criterion; it can be defined as an ex ante criterion or as an ex post criterion. In either case, the market outcome under the given choice correspondences is taken as a status quo. Consumers, as individuals or as a group, are then given the chance to intervene and enforce a deviation from the status quo. Unanimity is reached if no interventions are made.

The difference between ex ante and ex post unanimity lies in the timing of interventions: Ex ante criteria allow consumers to intervene before the market opens. Such interventions affect market prices, and consumers must understand these price effects and take them into account. It should be stressed that such a deep understanding of the price mechanism is a demanding assumption for consumers. Moreover, even stronger assumptions are needed to justify that such sophisticated consumers are viewed as price takers who do not misreport their own preferences to the firm. No such complications arise in ex post criteria, which permit interventions only after the market has closed. Such interventions affect the payoffs of contracts and shares, but consumers can no longer rebalance their share portfolios, and prices can no longer change.

The difference between individual, group, and collective unanimity lies in the institutional details that are assumed. Individual criteria take institutions and their choice correspondences as given and test whether each consumer is satisfied with the resulting choices. There is no comparison with alternative decision criteria. Group criteria take the institutions of the firm and the intermediary as given and test whether a Pareto improvement among the members of a predetermined control group is possible. Side-payments in date 0 consumption can be used to reach an agreement among the members of the control group. Such a form of unanimity justifies the objective of the firm: The control group has no incentive to implement a different objective. A criterion of this kind is best suited when the control group has proprietary access to a non-imitable production technology. Coalitional criteria are similar, but the control group is not predetermined: The test is repeated for all coalitions of consumers as if they were the control group. Side-payments in date 0 consumption between the members of a coalition are allowed. Such a form of unanimity justifies the institutions themselves: No coalition has an incentive to organize production and intermediation differently. This is the strongest form of unanimity. Since individuals and fixed control groups are coalitions in their own right, individual unanimity and group unanimity are implied.

The original criterion of shareholder unanimity, as introduced by Ekern and Wilson (1974) and Radner (1974), is a criterion of ex post individual unanimity. Later contributions are based on group criteria: For example, Magill and Quinzii (1996, §31) consider ex post unanimity among the group of final shareholders and show that it can serve as an alternative foundation for the Drèze criterion, at least in partnership economies with constant returns to scale and no initial shares. Other authors consider ex ante group criteria. The criterion of unanimity with side payments employed by Grossman and Hart (1979) in order to justify their equilibrium concept is a criterion of ex ante unanimity among the group of initial shareholders. Since the unanimity test takes place before the market opens, shareholders must understand the mapping $p^*(Y)$ from production plans to resulting equilibrium prices. The assumption of competitive price perceptions reduces this understanding substantially: Each initial shareholder i correctly anticipates the prices at the status quo, but perceives that $p^*$ is linear in his own marginal rates of substitution at the status quo consumption plan $c^i$:

$$\begin{aligned} p^*(Y) = \nabla _{{\textit{1}}} U^i[c^i]\cdot Y_{{\textit{1}}}. \end{aligned}$$

Under such perceptions, changes in production scales result in proportional share price changes. If these perceptions are correct, the market impact of each firm is negligible as under perfect competition—hence the name competitive. Such perceptions do not turn unanimity with side payments into an ex post criterion: Price effects are still taken into account, but only perceived price effects instead of true price effects. A formulation of unanimity with side payments without perceptions is the criterion of C-efficiency proposed by Bejan (2020). It is a criterion of ex ante unanimity among a fixed control group, possibly the group of initial shareholders.

For defining the choice correspondence of an intermediary, a more natural criterion of unanimity is one without a fixed control group. Since the intermediary in IFM equilibrium operates under a balanced book condition, it makes no profits that have to be distributed and therefore has no need for shares or shareholders. However, there is a well-defined group of stakeholders, namely all consumers who make a contract with the intermediary. Nevertheless, the composition of this group is not institution-free: It depends on the assumption that there is only one intermediary that serves the entire economy. If there were two intermediaries who serve different consumers, there would be two separate groups of stakeholders, who might agree on two completely different objectives. Since a number of intermediaries equal to one seems quite arbitrary as an assumption, it should be backed by a strong form of agreement. The following coalitional criterion provides such support: There exists no subset of consumers, who would change anything if they were in charge. Consistent with price-taking behavior, unanimity is evaluated at the ex post stage.

Definition 7

An IFM equilibrium $(p,c,\phi ,\psi ,X,Y)$ satisfies unanimity with side payments if there is no coalition $C \subseteq \{1,\ldots ,I\}$ of consumers and no plan $(\hat{\upsilon },\hat{c},\hat{\phi },\psi ,\hat{X},\hat{Y})$ with $\hat{c} \in \mathcal {F}_C$ such that $U^i(\hat{c}^i)\ge U^i(c^i)$ for all members $i \in C$ with strict inequality for at least one member and $\hat{X}^i=X^i, \hat{\upsilon }^i=0, \hat{\phi }^i = \phi ^i$ for all outsiders $i \notin C$.

Two aspects of Definition 7 should be noted. First, deviations from the status quo are restricted to the constrained feasible set $\mathcal {F}_C$, which guarantees budget balancedness even if some coalition deviates from the status quo. Therefore, a deviating coalition can always be viewed as being served by a separate intermediary. Second, even though consumers who do not hold a share in some firm k, i.e. $\psi _k^i = 0$, are theoretically given the power to change its production plan $Y^k$, this does not happen in practice because the utility of this consumer is unaffected by the change. Therefore, unanimity with side payments can indeed be viewed as a criterion where shareholders of firm k decide about firm k, and stakeholders of the intermediary decide about the intermediary.

What sets apart the concept of intermediated financial market equilibrium from traditional equilibrium concepts, such as Drèze equilibrium or Grossman–Hart equilibrium, is the separation of production and spanning. Our main result is that such a separation is sufficient for closing the gap between normative and positive objectives: Constrained efficiency, Pareto efficiency, and unanimity with side payments are equivalent in an intermediated economy. Since Pareto efficiency implies that marginal rates of substitution are equalized across consumers, the criteria of Drèze and Grossman–Hart coincide, and equilibria exist generally. That these properties depend critically on the presence of an intermediary is demonstrated in a simple example in Sect. 3, which motivates our proposed choice correspondence. The reader whose interest lies mainly in the result and not in its motivation may skip this section and jump directly to its formal statement in Sect. 4.

3 Example

Consider an economy with three states of the world ${\varvec{\varOmega }}= \{\omega _1,\omega _2,\omega _3\}$, $K=2$ firms, and $I=2$ consumers with utility functions

$$\begin{aligned} U^1\left( c^1\right)&= \ln \left( c_0^1\right) + 3\ln \left( c_{\omega _1}^1\right) + \ln \left( c_{\omega _2}^1\right) + 2\ln \left( c_{\omega _3}^1\right) \\ U^2\left( c^2\right)&= \ln \left( c_0^2\right) + \ln \left( c_{\omega _1}^2\right) + 3\ln \left( c_{\omega _2}^2\right) + 2\ln \left( c_{\omega _3}^2\right) \end{aligned}$$

Relative to the other consumer, Consumer 1 prefers more consumption in state $\omega _1$, while Consumer 2 prefers more consumption in state $\omega _2$. The two consumers have identical endowments of $e_0^i = 4$ at date 0, and $e_\omega ^i = 0$ in each state $\omega \in {\varvec{\varOmega }}$ at date 1.¹ The two firms have identical production technologies but different initial ownership structures: Firm 1 is fully owned by Consumer 1, $\delta _1^1 = 1$, and Firm 2 is fully owned by Consumer 2, $\delta _2^2 = 1$. The production sets of both firms are of the form

$$\begin{aligned} \mathcal {Y}^k = \left\{ y\in \mathbb {R}^{|{\varvec{\varOmega }}|+1}\,\left| \, -y_0 \ge \sum _{\omega \in {\varvec{\varOmega }}}\max \{0,y_\omega \}^2 \right. \right\} . \end{aligned}$$

Note that $\mathcal {Y}^k$ represents a decreasing returns to scale production technology whose input is the good at date 0, and whose output is a combination of the state-contingent goods at date 1. The geometry of this set is simple: If $Y^k \in \mathcal {Y}^k$ maximizes profits with respect to some state price vector $q \gg 0$, then the output vector $Y_{{\textit{1}}}^k$ lies on the sphere with radius $\sqrt{-Y^k_0}$ and is strictly positive; that is, $Y_{{\textit{1}}}^k \gg 0$. In spite of its simplicity, the example challenges both traditional equilibrium concepts.

3.1 Nonexistence of Grossman–Hart equilibrium

As said above, the concept of Grossman–Hart equilibrium is rooted in positive theory. Its decision criterion is derived from unanimity with side payments among the group of initial shareholders. The present example seems to be ideal for this equilibrium concept because competitive price perceptions are always correct. Nevertheless, the positive properties of Grossman–Hart equilibrium in the example are rather undesirable: No equilibrium exists.

In search of an equilibrium, we consider two possible cases: First, suppose both firms choose identical production plans, which is plausible because they have identical production technologies. In this case, the function $p^*:\mathcal {Y}\rightarrow \mathbb {R}_+$ that maps each production plan to a market-clearing share price can be determined by solving the equation system

$$\begin{aligned}&p = \nabla _{{\textit{1}}} U^i\left[ e^i + \begin{pmatrix}-p\\ Y_{{\textit{1}}}\end{pmatrix}\cdot \psi ^i + \begin{pmatrix}p+Y_0\\ {{\textit{0}}}\end{pmatrix}\cdot \delta ^i\right] \cdot Y_{{\textit{1}}} \quad \forall i\in \{1,2\} \\&2 = \psi ^1 + \psi ^2, \end{aligned}$$

for $(p,\psi ^1,\psi ^2)$. Share supply is normalized to two, because both firms have shares with identical payoffs. In this case, the solution is $\psi ^1 = \psi ^2 = 1$ and $p^*(Y) = 6(4+Y_0)$. Thus, shares are never traded, each consumers receives the output of his own firm, and prices are linear in production scale. The marginal rates of substitution in this case are

$$\begin{aligned} \nabla _{{\textit{1}}} U^1&= \left( \frac{3(4+Y_0)}{Y_{\omega _1}}, \frac{(4+Y_0)}{Y_{\omega _2}}, \frac{2(4+Y_0)}{Y_{\omega _3}}\right) , \nonumber \\ \nabla _{{\textit{1}}} U^2&= \left( \frac{(4+Y_0)}{Y_{\omega _1}}, \frac{3(4+Y_0)}{Y_{\omega _2}}, \frac{2(4+Y_0)}{Y_{\omega _3}}\right) , \end{aligned}$$

(17)

and therefore competitive price perceptions are everywhere correct, which is easy to see when share prices are computed using the present-value formula:

$$\begin{aligned} p = \nabla _{{\textit{1}}} U^1\cdot Y_{{\textit{1}}} = \nabla _{{\textit{1}}} U^2\cdot Y_{{\textit{1}}} = 6(4+Y_0) \end{aligned}$$

There can be no Grossman–Hart equilibrium in this case: Under the conjecture that both firms choose identical production plans, marginal rates of substitution are never equalized, but then firms would never choose identical plans under the Grossman–Hart criterion.

Now suppose both firms choose different plans. By symmetry of the example, $Y_{\omega _1}^1 = Y_{\omega _2}^2$ and $Y_{\omega _2}^1 = Y_{\omega _1}^2$ are natural restrictions, and so is $Y_{\omega _3}^1 = Y_{\omega _3}^2$. These restrictions result in identical prices for both types of shares, and the solution is again $p^*(Y) = 6(4+Y_0)$, but this time with trade in shares

$$\begin{aligned} \psi _1^1 = \psi _2^2 = \frac{3Y_{\omega _1}-Y_{\omega _2}}{4(Y_{\omega _1}-Y_{\omega _2})} \quad \text {and}\quad \psi _2^1 = \psi _1^2 = \frac{3Y_{\omega _2}-Y_{\omega _1}}{4(Y_{\omega _1}-Y_{\omega _2})}, \end{aligned}$$

(18)

which results in marginal rates of substitution of the form

$$\begin{aligned} \nabla _{{\textit{1}}} U^1&= \left( \frac{4(4+Y_0)}{Y_{\omega _1}+Y_{\omega _2}}, \frac{4(4+Y_0)}{Y_{\omega _1}+Y_{\omega _2}}, \frac{2(4+Y_0)}{Y_{\omega _3}}\right) \, \nonumber \\ \nabla _{{\textit{1}}} U^2&= \left( \frac{4(4+Y_0)}{Y_{\omega _1}+Y_{\omega _2}}, \frac{4(4+Y_0)}{Y_{\omega _1}+Y_{\omega _2}}, \frac{2(4+Y_0)}{Y_{\omega _3}}\right) . \end{aligned}$$

(19)

As in the previous case, competitive price perceptions are correct, yet there can be no Grossman–Hart equilibrium: Under the conjecture that both firms choose different production plans, marginal rates of substitution are always equalized, but then firms would choose identical plans under the Grossman–Hart criterion. Since these two cases are exhaustive, there can be no such equilibrium in the example.

From a technical viewpoint, this nonexistence problem traces back to a discontinuity in the budget correspondence (7) when the rank of $Y_{{\textit{1}}}$ changes. Since this problem is in the consumer’s domain, it need not affect the firm. However, a puzzling feature of the Grossman–Hart criterion is that it translates a discontinuity in demand of the consumer into a discontinuity in the objective function of the firm. Contrary to the multi-period exchange economy of Hart (1975), the nonexistence problem is not triggered by exceptional price constellations, but it is hardwired into the objective function. Not surprisingly, but again contrary to exchange economies, the nonexistence problem survives perturbations of consumer characteristics.

From an economic viewpoint, the nonexistence problem is tightly connected to conflicts of interest between shareholders. The example is constructed in such way that whenever firms maximize profits with respect to some linear combination of marginal rates of substitution, these rates are not equalized in equilibrium. In other words: Conflicts of interest prevail. Contrary to the Drèze criterion, the Grossman–Hart criterion does not aim at a compromise between shareholders. There are only three initial ownership structures (out of the entire set $\varDelta$) for which a Grossman–Hart equilibrium exists: the two dictatorial economies with $\delta _1^1 = \delta _2^1 = 1$ and $\delta _1^1 = \delta _2^1 = 0$, where no compromise is necessary because one consumer controls all firms, and the economy with $\delta _1^2 = \delta _2^2 = \nicefrac {1}{2}$, where a compromise seems to be reached by coincidence of the Grossman–Hart criterion with the Drèze criterion. Existence is guaranteed in this case, because the objective function of the firm in Drèze equilibrium is continuous. It turns out, however, that the concept of Drèze equilibrium is problematic in its own right in the present example.

3.2 Constrained inefficiency of Drèze equilibrium

As said above, the concept of Drèze equilibrium is rooted in normative theory. Its decision criterion is derived from the first-order conditions of the planner associated with constrained efficiency. In the example, these are identical to the joint first-order conditions for distributional efficiency and productive efficiency. If a constrained efficient allocation is not attained at some Drèze equilibrium, it is not attainable in a decentralized market economy at all. Nevertheless, the normative properties of Drèze equilibrium in the example are rather undesirable: There is a unique equilibrium, but it is Pareto dominated by allocations that can also be attained in a decentralized market economy.

The unique Drèze equilibrium has been identified as a by-product of the discussion of Grossman–Hart equilibrium. It involves production plans of $Y^1 = Y^2 = (-3,1,1,1)$, which are feasible because they satisfy

$$\begin{aligned} -Y_0^k = \sum _{\omega \in {\varvec{\varOmega }}} \left( Y_\omega ^k\right) ^2 \qquad \forall k\in \{1,2\}, \end{aligned}$$

(20)

and these lead to prices of $p = (6,6)$. Final shareholdings are $\psi ^1 = \psi ^2 = (\nicefrac {1}{2},\nicefrac {1}{2})$ and these lead to consumption plans $c^1 = c^2 = (1,1,1,1)$. Using (17), it is easy to verify that the first-order conditions of both firms,

$$\begin{aligned} \sum _{i=1}^I \psi ^i \nabla U^i[c^i] \in N_{\mathcal {Y}^k}[Y^k] \qquad \forall k\in \{1,2\}, \end{aligned}$$

in which $N_{\mathcal {Y}^k}[Y^k] = {\left\langle (1,2,2,2)\right\rangle }$ is the normal cone to $\mathcal {Y}^k$ at $Y^k$, are indeed satisfied. The resulting utility levels are $U^1(c^1) = U^2(c^2) = 0$. This equilibrium is production-efficient: Since $Y^1$ lies at the boundary of $\mathcal {Y}^1$, and $Y^2$ lies at the boundary of $\mathcal {Y}^2$, aggregate production $Y^1 + Y^2$ lies at the boundary of the aggregate production set $\mathcal {Y}^1 + \mathcal {Y}^2$ because $Y^1 = Y^2$ and $\mathcal {Y}^1 = \mathcal {Y}^2$. However, the equilibrium is not distribution-efficient because the set of possible transfers is small. The dimension of the asset span is only $\mathrm {rank}(Y_{{\textit{1}}}) = 1$. The span can be enlarged by one dimension if firms are forced to choose different plans.

Consider a small deviation in production plans to $Y^1 = (-3.02, 1.1, 0.9, 1)$ and $Y^2 = (-3.02, 0.9, 1.1, 1)$, which maintains the aggregate output levels but leads to an asset span of dimension $\mathrm {rank}(Y_{{\textit{1}}}) = 2$. According to (18), these production plans result in final shareholdings of $\psi ^1 = (3,-2)$ and $\psi ^2 = (-2,3)$ and the market clears at a price of $p^*(Y) = 5.88$. The consumption plans are now $c^1 = (0.98, 1.5, 0.5, 1)$ and $c^2 = (0.98, 0.5, 1.5, 1)$. This allocation leads to utility levels of $U^1(c^1) = U^2(c^2) = 0.503$ and thus Pareto dominates the Drèze equilibrium. However, these production plans are not production-efficient because $Y^1+Y^2 = (-6.04,2,2,2)$. Thus, the aggregate production plan lies in the interior of $\mathcal {Y}^1+\mathcal {Y}^2$, below the boundary point $(-6,2,2,2)$.

Since Drèze equilibria are the only candidates for constrained efficient market outcomes, it is clear that this standard cannot be met in this decentralized market economy. However, the example is constructed in such a way that this welfare standard is even out of reach for the constrained planner. For the given production sets, all production-efficient plans are of the form $Y^1 = Y^2$ and therefore result in a 1-dimensional asset span. At the same time, a 1-dimensional asset span is always too small for an efficient distribution between two consumers with different preferences. As a consequence, the two conditions are generally at odds in the example, and a constrained efficient allocation does not exist. In technical terms, this nonexistence problem is due to a discontinuity in the transfer correspondence $\mathcal {T}_C$ from (12).

3.3 The role of financial intermediation

These problems can be overcome if an intermediary is introduced. Suppose the intermediary offers contract $X^1 = (0,2^{-0.5},-2^{-0.5},0)$ to Consumer 1 and $X^2 = (0,-2^{-0.5},2^{-0.5},0)$ to Consumer 2. Further, suppose both firms apply the Drèze criterion,

$$\begin{aligned} Y^{i*} = \mathop {{\text {argmax}}}\limits _{y \in \mathcal {Y}^k} \sum _{i=1}^I \psi ^i\,\nabla U^i[c^i]\cdot y. \end{aligned}$$

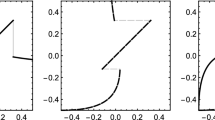
and production plans, prices, and final shares are $Y^1 = Y^2 = (-3,1,1,1)$, $p = (6,6)$, and $\psi ^1 = \psi ^2 = (\nicefrac {1}{2},\nicefrac {1}{2})$, as in the previously identified Drèze equilibrium. Productive efficiency is satisfied because both firms choose identical production plans that satisfy (20). At the same time, the dimension of the asset span is $\mathrm {rank}(X_{{\textit{1}}},Y_{{\textit{1}}}) = 2$. This case is illustrated in Fig. 1: The ball consists of all output vectors $Y_{{\textit{1}}}^k$ that are affordable for firm $k\in \{1,2\}$ given an input of $Y_0^k = -3$. Contract $X^1$ enables Consumer 1 to move from $Y_{{\textit{1}}}$ along the black line to the left. Contract $X^2$ enables Consumer 2 to move from $Y_{{\textit{1}}}$ along the black line to the right.

Fig. 1

Pareto efficiency in spite of incomplete markets: All transfers go from $Y_{{\textit{1}}}$ along ${\left\langle X_{{\textit{1}}}\right\rangle }$ (black line). The asset span ${\left\langle X_{{\textit{1}}},Y_{{\textit{1}}}\right\rangle }$ contains $\nabla _{{\textit{1}}} U^1 = \nabla _{{\textit{1}}} U^2$

Both consumers choose $\phi ^1 = \phi ^2 = 2^{-0.5}$ and the intermediary has a balanced book. The resulting consumption plans $c^1 = (1, 1.5, 0.5, 1)$ and $c^1 = (1, 0.5, 1.5, 1)$ lead to utility values of $U^1(c^1) = U^2(c^2) = 0.523$. Any deviation from (X, Y) within $\mathcal {X}^I\times \mathcal {Y}$ would lower utility for at least one consumer, and thus distributional efficiency is satisfied. Most notably, the marginal rates of substitution of both consumers agree, $\nabla U^1[c^1] = \nabla U^2[c^2] = (1,2,2,2)$, and the normality condition (5) is fulfilled for any consumer i and firm k because $N_{\mathcal {Y}^k}[Y^k] = {\left\langle (1,2,2,2)\right\rangle }$. Therefore, the attained allocation c is Pareto efficient. This strong welfare property is due to the fact that both consumers can make the same contractual transfers as in a contingent market equilibrium with state prices $q = (1,2,2,2)$; that is, $X^i\phi ^i = z^{i*}(q)$. The choice rule of the intermediary is simple: Take the marginal rates of substitution of some reference consumer as a state price vector, use these state prices to compute the hypothetical demand for contingent claims, and offer contracts that replicate the net transfers. If such transfers are possible, marginal rates are equalized across consumers and the choice of reference consumer becomes irrelevant. In this case, the criteria of Drèze and Grossman–Hart agree and the optimal production plans are well-defined. Since the market clearing and book balancedness conditions are satisfied, the tuple $(p,c,\phi ,\psi ,X,Y)$ just identified constitutes an intermediated financial market equilibrium.

From an economic viewpoint, two properties of this equilibrium should be emphasized: First, all shareholders unanimously agree on production plans even though the ex post spanning condition of Ekern and Wilson (1974) and Radner (1974), roughly $\mathcal {Y}^k \subseteq \mathbb {R}\times {\left\langle X_{{\textit{1}}},Y_{{\textit{1}}}\right\rangle }$, is not satisfied for any firm k. This is one role of the intermediary: It helps resolve conflicts of about the objective of the firm. Second, the equilibrium is Pareto efficient even though markets are incomplete and even though the ex ante spanning condition of Zierhut (2019), precisely $\mathcal {Y}^k \subseteq \mathbb {R}\times {\left\langle X_{{\textit{1}}}\right\rangle }$, is not satisfied for any firm k. This is another role of the intermediary: It helps resolve the conflict between distributional efficiency and productive efficiency. Both properties are easy to see in Fig. 1: The asset span ${\left\langle X_{{\textit{1}}},Y_{{\textit{1}}}\right\rangle }$ is the gray plane. Neither does it span the entire output set—that is, the ball and its multiples—nor does it cover the entire payoff space. Nevertheless, marginal rates of substitution are equalized. The intermediated financial market equilibrium exhibits properties that are thus far only known from complete markets.

From a technical viewpoint, this finding can be explained as follows: Even if consumers had access to complete contingent markets, all optimal transfers $z^i = c^i - e^i - Y\cdot \delta ^i$ would be contained in a subspace whose dimension is at most $I-1$. Spanning this subspace is sufficient for attaining a distribution-efficient allocation through trade. The first-order conditions for distributional efficiency imply that marginal rates of substitution are equalized across consumers, and therefore all firms have identical objective functions under any criterion that is based on a weighted sum of utility gradients. This guarantees that aggregate production lies at the boundary of the aggregate production set, and thus productive efficiency is satisfied as well. Therefore, to resolve the conflicts discussed above, it is not necessary to create complete markets, but sufficient to span a subspace of dimension less than I. This is exactly what the intermediary achieves through offering each consumer a suitable contract. The resulting equilibrium is equivalent to a contingent market equilibrium in the Arrow–Debreu sense.

4 Results

The purpose of this section is to generalize the insights from the example. If there were no intermediary, it would be unreasonable to expect that Pareto efficiency and unanimity with side payments hold simultaneously in equilibrium: As regards normative criteria, Pareto efficiency is a stronger condition than constrained efficiency. As regards positive criteria, unanimity in the sense of Definition 7 is a stronger condition than Ekern–Wilson–Radner shareholder unanimity. But even the weaker two are mutually exclusive in almost all economies. This is the impossibility theorem of Zierhut (2017), who shows that constrained efficiency and shareholder unanimity are generically incompatible. However, this discrepancy vanishes as soon as an intermediary is present in the economy. This is our main result and its proof can be found in “Appendix”.

Theorem 1

Let $(p,c,\phi ,\psi ,X,Y)$ be an IFM equilibrium for given choice correspondences $(X^*,Y^*)$. Then, the following statements are equivalent:

• (i) The equilibrium is constrained efficient.

• (ii) The equilibrium is Pareto efficient.

• (iii) The equilibrium satisfies unanimity with side payments.

Moreover, let $w \in \mathbb {R}_+^{I(K+1)}$ be arbitrary weights such that $\sum _{i=1}^I w_k^i = 1$ for each firm k and the intermediary with index $k=0$. If the choice correspondences are

$$\begin{aligned} X^{i*}&= z^{i*}\left( \sum _{i=1}^I w_0^i\nabla U^i[c^i]\right) ^\mathrm {N}\\ Y^{k*}&= \mathop {{\text {argmax}}}\limits _{y \in \mathcal {Y}^k} \sum _{i=1}^I w_k^i\,\nabla U^i[c^i]\cdot y, \end{aligned}$$

then every IFM equilibrium satisfies (i)–(iii).

The first part of Theorem 1 is an equivalence result formulated at a high level of abstraction: No matter how firms and the intermediary come to their decisions, the three conditions of constrained efficiency, Pareto efficiency, and unanimity with side payments are equivalent. Thus, when production and spanning are separated, there is no longer a discrepancy between normative and positive criteria. Unanimity among the stakeholders of the intermediary ensures distributive efficiency. Unanimity among the shareholders of each firm ensures productive efficiency. If the objectives of the firm and the intermediary are designed to reach unanimity, then Pareto efficiency is automatically achieved.

The second part of the theorem is more specific and presents a family of objectives for the firm and the intermediary that are unanimously approved. For firms, this family includes the Grossman–Hart criterion and the Drèze criterion. Each firm uses a weighted sum of marginal rates of substitution to compute profits, and the profit-maximizing production plan is chosen. The weights turn out to be irrelevant because all marginal rates are equalized in equilibrium. If one follows Drèze (1974) and Grossman and Hart (1979) in interpreting these weights as control rights, one has to conclude that the distribution of control rights becomes irrelevant when the intermediary enables agreement between consumers. For this purpose, the intermediary offers each consumers a contract that replicates his trade in hypothetical contingent claims markets. State prices in these hypothetical markets can be computed as a weighted sum of marginal rates of substitution. It is the presence of the intermediary that matters, not its choice of weights.

This result is close in spirit to the Coase theorem. Both theorems show that institutions can help overcome inefficiencies even when their source cannot be eliminated. In the Coase theorem, on the one hand, the source of inefficiency is externalities, and the proposed institution is a property right exchange. The inefficiency disappears because consumers come to agree on prices of property rights. For reaching Pareto efficiency, the allocation of property rights is irrelevant. In Theorem 1, on the other hand, the source of inefficiency is market incompleteness, and the proposed institution is the intermediary. The inefficiency disappears because consumers come to agree on prices of consumption in all relevant states. For reaching Pareto efficiency, the allocation of control rights is irrelevant.

From a technical viewpoint, the equivalence in Theorem 1 of constrained efficiency and Pareto efficiency can be explained as follows: The presence of the intermediary enlarges the constrained feasible set $\mathcal {F}_C$. This does not mean that this set becomes as large as the feasible set. In fact, unless the number of states is small relative to the number of agents, the set inclusion $\mathcal {F}_C \subset \mathcal {F}$ is proper. Nevertheless, all Pareto optima in $\mathcal {F}$ are also contained in the smaller set $\mathcal {F}_C$. In the terminology of LeRoy and Werner (2014), Chapter 16, markets are effectively complete. In economies with this property, constrained efficiency and Pareto efficiency are equivalent.² The unconstrained social planner would choose the same allocations as its constrained counterpart.

A similar relation holds in decentralized market economies. Under the choice correspondences from Theorem 1, the financial market budget set is contained in the contingent market budget set if state prices are computed as the weighted sum $q = \sum _{i=1}^I w_0^i \nabla U^i[c^i]$; that is, $\mathbb {B}(p,e^i,\delta ^i,X^i,Y) \subset B(q,e^i,\delta ^i,Y)$. When markets are incomplete, this set inclusion is proper. Nevertheless, the unique optimum of any consumer i in $B(q,e^i,\delta ^i,Y)$ is also contained in the smaller set $\mathbb {B}(p,e^i,\delta ^i,X^i,Y)$. Therefore, every resulting IFM equilibrium is equivalent to some CM equilibrium—consumption and production plans agree in both equilibrium concepts. As a consequence, the first welfare theorem holds in intermediated financial markets. That IFM equilibria with the properties from Theorem 1 exist follows from the converse relation: Every CM equilibrium is equivalent to an IFM equilibrium, which leads to the following existence result.

Corollary 1

Every production economy $(\mathcal {Y},U,e,\delta )$ has an IFM equilibrium with the properties from Theorem 1.

Proof

Under Assumptions 1, 2, and 3 a CM equilibrium (q, c, Y) exists by Theorem I of Arrow and Debreu (1954). It follows from (4) that q can be substituted for $\nabla U^i[c^i]$ in the choice correspondences from Theorem 1. Set $p = q\cdot Y_{{\textit{1}}}$; then, by comparison with Definition 2 it becomes clear that $Y = Y^*(p,c,\phi ,\psi ,X,Y)$. Thus, if $X = X^*(p,c,\phi ,\psi ,X,Y)$, any resulting IFM equilibrium is Pareto efficient by Theorem 1. Set $\phi ^i = \Vert z^{i*}(q)\Vert$ for each consumer i, and $\psi = \delta$; then, markets clear because

$$\begin{aligned} \sum _{i=1}^I X^i\phi ^i = \sum _{i=1}^I z^{i*}(q) = 0 \quad \text {and}\quad \sum _{i=1}^I \psi ^i = \sum _{i=1}^I \delta ^i = 1. \end{aligned}$$

The tuple $(p,c,\phi ,\psi ,X,Y)$ is thus an IFM equilibrium for the choice correspondences from Theorem 1 and therefore has the desired efficiency and unanimity properties. $\square$

For an incomplete market economy, this existence result is strong: Intermediated financial market equilibria as in Theorem 1 exist generally, not only generically. Since the spanning role is decoupled from production plans, the dimension of the asset span ${\left\langle X_{{\textit{1}}},Y_{{\textit{1}}}\right\rangle }$ becomes independent of the rank of $Y_{{\textit{1}}}$ for the right choices of $X_{{\textit{1}}}$. Therefore, discontinuities in the financial market budget correspondence that other existence proofs, such as in Magill and Shafer (1990) or Duffie and Shafer (1985), have to deal with are avoided. As a consequence, no such discontinuity is translated into the objective function of the firm, at least not in the relevant range. This also fixes the nonexistence problem inherent in Grossman–Hart equilibrium.

All these results would be trivial if markets were complete. It should therefore be emphasized that complete markets cannot be expected in IFM equilibrium. In fact, markets are never complete if the number of states is sufficiently large. The following proposition states this explicitly in the form of a sufficient condition for market incompleteness. The example from Sect. 3 underlines that this condition is not necessary.

Proposition 1

If the production economy $(\mathcal {Y},U,e,\delta )$ satisfies

$$\begin{aligned} I + K \le |{\varvec{\varOmega }}| \end{aligned}$$

then markets are incomplete at any IFM equilibrium.

Proof

Note that $\mathrm {rank}(X_{{\textit{1}}},Y_{{\textit{1}}}) \le \mathrm {rank}(X_{{\textit{1}}}) + \mathrm {rank}(Y_{{\textit{1}}})$. By the balanced book condition from Definition 4, there exists some nonzero $\phi \in \mathbb {R}^I$ that solves $X\cdot \phi = 0$, and thus $\mathrm {rank}(X) \le I-1$. Since all columns $X^1,\ldots ,X^I$ lie on the unit sphere, this is can be equivalently stated as $\mathrm {rank}(X_{{\textit{1}}}) \le I-1$. Moreover, $\mathrm {rank}(Y_{{\textit{1}}})$ is at most K. This implies that

$$\begin{aligned} \mathrm {rank}(X_{{\textit{1}}},Y_{{\textit{1}}}) \le I - 1 + K. \end{aligned}$$

(21)

Markets are incomplete if $\mathrm {rank}(X_{{\textit{1}}},Y_{{\textit{1}}}) < |{\varvec{\varOmega }}|$. A sufficient condition for incompleteness, according to (21), is therefore $I - 1 + K < |{\varvec{\varOmega }}|$. The condition from the proposition is obtained by dropping $-1$ in favor of a weak inequality. $\square$

5 Welfare theorems

The first welfare theorem states that every contingent market equilibrium gives rise to a Pareto efficient allocation. Theorem 1 extends this result to intermediated financial markets. If the objectives of the intermediary and the firm are based on unanimity, then every intermediated financial market equilibrium is Pareto efficient. This is a version of the first welfare theorem in an incomplete market environment—complete markets cannot be expected according to Proposition 1.

The second welfare theorem states that every Pareto efficient allocation can be decentralized as a contingent market equilibrium with transfers. The insight that the intermediary renders markets effectively complete raises hopes of an analogous decentralization result for intermediated financial markets. However, as will be demonstrated in the following example, such hopes are unfounded. The second welfare theorem does not hold when markets are incomplete.

As in Sect. 3, consider an economy with three states of the world ${\varvec{\varOmega }}= \{\omega _1,\omega _2,\omega _3\}$ and two dates. There are the same $I=2$ consumers with utility functions

$$\begin{aligned} U^1\left( c^1\right)&= \ln \left( c_0^1\right) + 3\ln \left( c_{\omega _1}^1\right) + \ln \left( c_{\omega _2}^1\right) + 2\ln \left( c_{\omega _3}^1\right) \\ U^2\left( c^2\right)&= \ln \left( c_0^2\right) + \ln \left( c_{\omega _1}^2\right) + 3\ln \left( c_{\omega _2}^2\right) + 2\ln \left( c_{\omega _3}^2\right) , \end{aligned}$$

but now consumption goods are initially available in all three future states. The endowment of Consumer 1 is $e^1 = (0,0,1,1)$, and the endowment of Consumer 2 is $e^2 = (1,1,0,0)$. To keep production as simple as possible, let there be only one firm with a constant returns to scale production technology

$$\begin{aligned} \mathcal {Y} = \left\{ y\in \mathbb {R}^{|{\varvec{\varOmega }}|+1}\,\left| \, -y_0 \ge \sum _{\omega \in {\varvec{\varOmega }}}\max \{0,y_\omega \} \right. \right\} . \end{aligned}$$

The firm index is omitted since there is only one firm. Both consumers hold equal shares $\delta ^1 = \delta ^2 = \nicefrac {1}{2}$ in the firm. Since the normal cone to $\mathcal {Y}$ is $N_{\mathcal {Y}}[Y] = {\left\langle \mathbf {1}\right\rangle }$ at any boundary production plan with $Y_{{\textit{1}}} \gg 0$, Pareto efficient allocations are easily identified by the condition $\nabla U^1[c^1] = \nabla U^2[c^2] = \mathbf {1}$. Since the supporting state price vector must always be $q = \mathbf {1}$, it is easy to associate wealth levels $w = (w^1,w^2) = q\cdot (c^1,c^2)$ with each Pareto efficient allocation $c \in \mathcal {F}$. These wealth levels must sum to four, because $q\cdot (e^1 + e^2) = 4$. Initial shares have no effect on wealth because profits are zero under constant returns to scale. There is one CM equilibrium with transfers for each wealth distribution.

For IFM equilibrium with transfers, this is no longer the case. Consider three different wealth distributions: $w_A = (2,2)$, $w_B = (1.75, 2.25)$, and $w_C = (1.5, 2.5)$. Consumer 2 becomes wealthier as one moves from A to C. The equal-wealth Pareto efficient allocation consists of $c_A^1 = (\nicefrac {2}{7},\nicefrac {6}{7},\nicefrac {2}{7},\nicefrac {4}{7})$ and $c_A^2 = (\nicefrac {2}{7},\nicefrac {2}{7},\nicefrac {6}{7},\nicefrac {4}{7})$, and it involves the production plan $Y_A = (-\nicefrac {3}{7},\nicefrac {1}{7},\nicefrac {1}{7},\nicefrac {1}{7})$. This allocation can be established by a regulator, as an IFM equilibrium with transfers, if there are some post-transfer endowments $\hat{e} \in \mathcal {T}_C(e,Y_A)$ corresponding to wealth levels $w_A$. This is clearly the case: The original endowments e already satisfy $q\cdot (e^1,e^2) = (2,2)$. Therefore, allocation $c_A$ can be established without transfers.

The Pareto efficient allocation with wealth levels $w_B = (1.75, 2.25)$ consists of $c_B^1 = (\nicefrac {1}{4},\nicefrac {3}{4},\nicefrac {1}{4},\nicefrac {2}{4})$ and $c_B^2 = (\nicefrac {9}{28},\nicefrac {9}{28},\nicefrac {27}{28},\nicefrac {18}{28})$, and it involves the production plan $Y_B = (-\nicefrac {3}{7},\nicefrac {1}{14},\nicefrac {3}{14},\nicefrac {1}{7})$. To decentralize this allocation as an IFM equilibrium with transfers, one would need post-transfer endowments $\hat{e}$ that satisfy $q\cdot (\hat{e}^1,\hat{e}^2) = (1.75, 2.25)$. However, such a vector does not exist in $\mathcal {T}_C(e,Y_B)$: No lump-sum transfer that satisfies $q\cdot (\hat{e}^1-e^1) = -0.25$ is feasible for the regulator, who is constrained to transfers of date 0 consumption and final shares. Transfers of consumption are not an option because Consumer 1 has no date 0 income that could be transferred. Transfers of final shares would deduct date 1 consumption in all three states, and this is again not feasible because Consumer 1 has no income in state $\omega _1$ that could be taken. As a consequence, an IFM equilibrium with wealth levels $w_B$ does not exist.

There is no such problem for wealth levels $w_C = (1.5, 2.5)$. The associated Pareto optimum is $c_C^1 = (\nicefrac {3}{14},\nicefrac {9}{14},\nicefrac {3}{14},\nicefrac {6}{14})$ and $c_C^2 = (\nicefrac {5}{14},\nicefrac {5}{14},\nicefrac {15}{14},\nicefrac {10}{14})$, and this allocation requires the production plan $Y_C = (-\nicefrac {3}{7},0,\nicefrac {2}{7},\nicefrac {1}{7})$. The regulator can realize this allocation through a transfer $\hat{e}^1 - e^1 = (0,0,-\nicefrac {2}{6},-\nicefrac {1}{6})$ from Consumer 2 to Consumer 1. This transfer is feasible by means of reallocating $\nicefrac {7}{6}$ units of final shares, and thus $\hat{e} \in \mathcal {T}_C(e,Y_C)$. The Pareto efficient allocation $c_C$ is therefore attainable as an IFM equilibrium with transfers.

From a technical viewpoint, the behavior observed in the example is due to a nonconvexity in the graph of the constrained transfer correspondence $\mathcal {T}_C$ from (12). By construction, the set of Pareto efficient allocations is linear in this example. Each wealth level $w^1$ of Consumer 1 corresponds to one point on this line segment. However, an entire interval on the line segment cannot be reached in IFM equilibrium with transfers: For each wealth level $w^1 \in (1.5, 2)$, no IFM equilibrium with transfers exists. In the interest of transparency, we deviate from Assumption 2 in the example, but this is not crucial. It should be clear that the nonconvexity does not disappear if there are small positive endowments in all states. Such a modification would only shrink the range of problematic wealth levels. There is no such problem for CM equilibrium with transfers because the graph of $\mathcal {T}$ from (6) is convex, and in particular it is a much larger set than the graph of $\mathcal {T}_C$. Every Pareto efficient IFM equilibrium with transfers is a CM equilibrium with transfers. However, the example shows that the converse does not hold. The set of Pareto efficient IFM equilibria with transfers is much smaller.

From an economic viewpoint, the asset span that consumers need in order to reach some Pareto optimum is smaller than the asset span required by the regulator to realize a particular Pareto optimum. It should be stressed that this is unrelated to the restriction that the regulator must not use contracts X for wealth transfers. In IFM equilibrium, the contracts chosen by the intermediary always have a present value of $q\cdot X = 0$, and thus they would not be suited for wealth transfers anyhow. For any given asset span with less than full dimension, it is possible to construct cases in which some Pareto efficient allocation can only be decentralized with wealth transfers that are not feasible in the available markets. Therefore, we conclude that the only plausible market structure for the second welfare theorem are complete markets.

One argument against this conclusion could be that the regulator requires at most an asset span of dimension $2(I-1)$, just like consumers require only an asset span of dimension $I-1$ to reach a Pareto optimum. However, we do not find this argument compelling. The first welfare theorem holds in IFM equilibrium because there is an intermediary who is guided by unanimity and offers the right contracts for consumers. By contrast, it is unclear what kind of agent is supposed to provide the right contracts for the regulator. If it were again an intermediary, it is not at all clear where its objective comes from. Unanimity among consumers cannot serve as a basis because the introduction of additional contracts cannot raise utility any further. Moreover, it would be unreasonable to assume that the regulator itself introduces contracts. If it had the ability to open new markets, its interventions would exceed simple lump-sum transfers by far. In fact, the power of such a regulator would be greater than what is considered appropriate for a central planner in the incomplete markets literature.

6 Conclusion

There is a widely-held belief that the welfare theorems depend on complete markets. As regards the first theorem, this belief is not true. The distinction between complete and incomplete markets matters only insofar as the nature of institutions is different. When markets are complete, there is no role for institutions other than firms, and the choices of firms are limited to input and output quantities. When markets are incomplete, there are more choices because the asset structure is endogenous. This leaves room for institutions beside firms. A necessary condition for Pareto efficiency, irrespective of whether markets are complete or incomplete, is that consumers agree on the objectives of institutions. If a financial intermediary is among the institutions, this condition is also sufficient. We have shown that the objective of the intermediary can be based on unanimity considerations, and that one customized contract per consumer is sufficient for achieving unanimity.

As regards the second theorem, the belief seems more than justified. The desired result is that any Pareto efficient allocation can be attained in a market economy after a suitable lump-sum transfer. When markets are complete, this statements boils down to price-supportability of Pareto efficient allocations because arbitrary wealth distributions can be realized by lump-sum transfers. When markets are incomplete, this is no longer true because some wealth distributions would require transfers outside the asset span. An intermediary of the kind considered in this paper cannot be expected to provide an asset span sufficiently large to enable arbitrary distributions. The second welfare theorem does not hold, at least not for the institutions in the present setting. Furthermore, if the intermediary were able to provide a larger asset span, it must be guided by objectives other than unanimity. We therefore doubt that any reasonable institution would provide the right span, unless it were sufficiently powerful to provide complete markets.

Appendix

Proof of Theorem 1

This proof consists of three parts: In the first part, the first-order conditions for constrained efficiency are derived for further reference. In the second part, the equivalence of the three statements is proven, implication by implication. In the third part, it is shown that the given choice correspondences imply that the smaller financial market budget set contains the utility maximum of the larger contingent market budget set. This implies that marginal rates of substitution are equalized in IFM equilibrium, leads back to one of the three equivalent statements, and completes the proof.

Every constrained efficient allocation c with supporting plan $(\upsilon ,\phi ,\psi ,X,Y)$ is a solution to the Pareto problem of a social planner,

$$\begin{aligned} \max _{c} \sum _{i=1}^I \alpha ^i U^i(c^i) \quad \text {subject to}\quad c\in \mathcal {F}_C, \end{aligned}$$

(22)

in which $\alpha \in \mathbb {R}_+^I$ is a vector of welfare weights. The system of first-order conditions consists of (13) to (16) as well as

$$\begin{aligned} \alpha ^i D_{c_0^i}U^i[c^i] - \kappa = 0 \quad&\forall i \end{aligned}$$

(23)

$$\begin{aligned} \left( \alpha ^i DU^i[c^i]-\lambda \right) \cdot X^i = 0 \qquad&\forall i\end{aligned}$$

(24)

$$\begin{aligned} \alpha ^i DU^i[c^i]\cdot Y - \mu = 0 \qquad&\forall i\end{aligned}$$

(25)

$$\begin{aligned} \left( \alpha ^i DU^i[c^i]-\lambda \right) \in N_{\mathcal {X}}[X^i] \qquad&\forall i\end{aligned}$$

(26)

$$\begin{aligned} \sum _{i=1}^I\alpha ^i\psi _k^i DU^i[c^i] \in N_{\mathcal {Y}^k}[Y^k] \qquad&\forall k \end{aligned}$$

(27)

in which $\kappa \in \mathbb {R}_+$, $\lambda \in \mathbb {R}_+^{|{\varvec{\varOmega }}|+1}$, and $\mu \in \mathbb {R}_+^K$ are the Lagrange multipliers associated with the constraints (14), (15), and (16). Since the system of equations (23) to (27) is homogeneous of degree 1 in the multipliers $(\alpha ,\kappa ,\mu ,\lambda )$, this vector can be normalized such that $\kappa = 1$. Then, (23) implies that $\alpha ^i = (D_{c_0^i}U^i[c^i])^{-1}$ for each consumer i. Note that non-negativity of consumptions need not be incorporated as an explicit constraints: Since the resulting welfare weights are positive, $\alpha ^i > 0$ for each consumer i, it follows from Assumptions 1 and 2 that (22) has only interior solutions. Now, the implications can be proven:

(i) $\implies$ (ii): Constrained efficiency implies that the above first-order conditions hold. After the normalization of multipliers, (24) can be equivalently stated as $(\nabla U^i[c^i] - \lambda ) \in {\left\langle X^i\right\rangle }^\bot$. In the same fashion, (26) can be equivalently stated as $(\nabla U^i[c^i] - \lambda ) \in {\left\langle X^i\right\rangle }$ because $\mathcal {X}$ is the unit sphere, and thus $N_\mathcal {X}[X^i] = {\left\langle X^i\right\rangle }$. By definition of the orthogonal complement, ${\left\langle X^i\right\rangle }^\bot \cap {\left\langle X^i\right\rangle } = \{0\}$, and thus $\nabla U^i[c^i] = \lambda$ for each consumer i; that is to say, marginal rates of substitution are equalized across consumers and Equation (4) holds with $q = \lambda$. Since $\sum _{i=1}^I \psi _k^i = 1$, this leads to a simplification of (27) to $\nabla U^i[c^i] \in N_{\mathcal {Y}^k}[Y^k]$ for arbitrary i, and thus Equation (5) holds. Since $c \in \mathcal {F}$ because $\mathcal {F}_C \subseteq \mathcal {F}$, the two equations (4) and (5) characterize Pareto efficiency and the allocation c is indeed Pareto efficient.

(ii) $\implies$ (i): This follows directly from Definitions 1 and 6 because $\mathcal {F}_C \subseteq \mathcal {F}$.

(ii) $\implies$ (iii): Suppose not; then, some coalition C could improve the utility of its members, either through alternative contracts $(\hat{X},\hat{\phi })$ or through alternative production $\hat{Y}$. Alternative contracts do not affect consumption of outsiders; i.e., $\hat{c}^i = c^i$ if $i \notin C$. For utility improvements within the coalition, $U(\hat{c}^i) \ge U^i(c^i)$ must hold for all members, with strict inequality for at least one member $i \in C$. But then c cannot be Pareto efficient—a contradiction. Alternative production can only lead to a utility improvement within C if $\nabla U^i[c^i]\cdot (\hat{Y}^k-Y^k)\psi _k^i > 0$ for some $i \in C$ and firm k. However, since $U^i$ is strictly concave and $\mathcal {Y}^k$ is closed and convex by Assumptions 1 and 3, this would require that $\nabla U^i[c^i] \notin N_{\mathcal {Y}^k}[Y^k]$. But Pareto efficiency implies that $\nabla U^i[c^i] \in N_{\mathcal {Y}^k}[Y^k]$ for each consumer i and firm k—again a contradiction.

(iii) $\implies$ (ii): Unanimity with side payments implies that no Pareto improvement is possible for the grand coalition $C = \{1,\ldots ,I\}$ when $\psi$ is fixed. This corresponds to a solution to the Pareto problem (22) when restricted to the smaller set

$$\begin{aligned} \hat{\mathcal {F}}_C(\psi ) = \left\{ c\in \mathcal {C}^I\left| \, \begin{matrix} \exists (\upsilon ,\phi ,X,Y) \in \mathbb {R}^I\times \mathbb {R}^I\times \mathcal {X}^I\times \mathcal {Y} \\ \text { such that (13) to (15) hold} \end{matrix} \right. \right\} . \end{aligned}$$

Let $\kappa \in \mathbb {R}_+$ and $\lambda \in \mathbb {R}_+^{|{\varvec{\varOmega }}|+1}$ be the Lagrange multipliers associated with (14) and (15); then, the system of first-order conditions includes (23), (24), and (26). This leads again to $(\nabla U^i[c^i] - \lambda ) \in {\left\langle X^i\right\rangle } \cap {\left\langle X^i\right\rangle }^\bot = \{0\}$, and thus $\nabla U^i[c^i] = \lambda$ for each consumer i. Therefore, (27) holds in the form $\nabla U^i[c^i] \in N_{\mathcal {Y}^k}[Y^k]$ for each consumer i. As a consequence, both (4) and (5) are satisfied and since $\hat{\mathcal {F}}_C(\psi ) \subseteq \mathcal {F}$, the allocation c must be Pareto efficient.

For the third part of the proof take arbitrary weights $w_0^1,\ldots ,w_0^I$. Recall that Walras’ law holds for any $q \in \mathcal {C}$; that is, $q\cdot z^{i*}(q) = 0$. It implies that $q\cdot z^{i*}(q)^\mathrm {N}= 0$. Set $q = \sum _{i=1}^I w_0^i \nabla U^i[c^i]$; then, for the choice correspondence $X^*$, this means that $q\cdot X^i = 0$ for any consumer i. Moreover, the first-order conditions (9) in IFM equilibrium imply that

$$\begin{aligned} w_0^i\nabla U^i[c^i] \cdot \begin{pmatrix}-p\\ Y_{{\textit{1}}}\end{pmatrix} = 0 \quad \quad \forall i, \end{aligned}$$

and summing up over all consumers results in

$$\begin{aligned} q \cdot \begin{pmatrix}-p\\ Y_{{\textit{1}}}\end{pmatrix} = 0 \end{aligned}$$

Taking the inner product with q on both sides of the financial market budget constraint in (7) leads to $q\cdot (c^i - e^i) \le q\cdot Y\cdot \delta ^i$, and thus $c^i \in \mathbb {B}(p,e^i,\delta ^i,X^i,Y)$ implies $c^i \in B(q,e^i,\delta ^i,Y)$, which is the contingent market budget set (2). Recall that the utility maximizing consumption plan $c^{i*}(q)$ from this set satisfies $c^{i*}(q) - e^i = z^{i*}(q) + Y\cdot \delta ^i$. Therefore, the choice correspondence $X^*$ implies that $c^{i*}(q) \in \mathbb {B}(p,e^i,\delta ^i,X^i,Y)$, but since this set is contained in $B(q,e^i,\delta ^i,Y)$, it follows that $c^{i*}(q)$ also solves the utility maximization problem (8) in intermediated financial market equilibrium. Since $c^{i*}$ fulfills the first-order conditions (4) in CM equilibrium, it follows that $\nabla U^i[c^i] = q$, and this holds for each consumer i. Thus, for arbitrary weights $w_k^1,\ldots ,w_k^I$, $\sum _{i=1}^I w_k^i \nabla U^i[c^i] = q$. Therefore, the choice correspondence $Y^*$ implies that (27) holds for any firm k. Set $\lambda = q$, then (24) and (26) hold as well. Set $\mu = p + Y_0$, then (25) is implied by the first-order conditions (9) in IFM equilibrium. Finally, (23) holds automatically after the normalization $\kappa = 1$. All first-order condition for constrained efficiency are thus fulfilled with $\upsilon = 0$, and since these have been shown to imply Pareto efficiency, the proof is complete. $\square$