Abstract
We adopt the notion of myopic-farsighted stable set to study the stability of networks when myopic and farsighted individuals decide with whom they want to form a link, according to some utility function that weighs the costs and benefits of each connection. A myopic-farsighted stable set is the set of networks satisfying internal and external stability with respect to the notion of myopic-farsighted improving path. We first provide conditions on the utility function that guarantee the existence of a myopic-farsighted stable set and we show that, when the population becomes mixed, the myopic-farsighted stable set refines the set of pairwise stable networks by eliminating some Pareto-dominated networks. In the end, when all players are farsighted, the myopic-farsighted stable set only consists of all strongly efficient networks. We next show that, in the case of a distance-based utility function, a tension between stability and efficiency is likely to arise when the population is homogeneous (either all myopic or all farsighted). But, once the population is mixed, the tension vanishes if there are enough farsighted individuals. In the case of a degree-based utility function, myopic and farsighted individuals may end up segregated with myopic individuals being overconnected and farsighted ones getting the socially optimal payoff.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The organization of individuals into networks plays an important role in the determination of the outcome of many social and economic interactions. For instance, a communication or friendship network in which individuals have very few acquaintances with whom they share information will result in different employment patterns than one in which individuals have many such acquaintances. A central question is predicting the networks that individuals will form. Up to now, it has been assumed that all individuals are either myopic or farsighted when they decide with whom they want to link. Jackson and Wolinsky (1996) propose the notion of pairwise stability to predict the networks that one might expect to emerge in the long run. A network is pairwise stable if no individual benefits from deleting a link and no two individuals benefit from adding a link between them. Pairwise stability presumes that individuals are myopic: they do not anticipate that other individuals may react to their changes. Farsighted individuals may not add a link that appears valuable to them as this can induce the formation of other links, ultimately lowering their payoffs.Footnote 1
However, recent experiments provide evidence in favor of a mixed population consisting of both myopic and farsighted individuals. Kirchsteiger et al. (2016) test the myopic and the farsighted models of network formation and compare the stability notions that are based on them. They find that most subjects are best classified as myopic but many others are limitedly farsighted.Footnote 2 So, the outcomes of real-life network formation problems are likely to be affected by the degree of farsightedness of the individuals. Consider the situation where the worth of link creation turns nonnegative after some threshold in the connectedness of the network is reached, both for the individuals and on aggregate, but the individual benefits are negative below this threshold. If network externalities take this form, myopic individuals can be stuck in insufficiently dense networks. Farsightedness may take care of this problem and achieve efficiency. In the presence of both myopic and farsighted individuals, their ability to pass the threshold will depend on the number of farsighted individuals. Only if there are enough farsighted individuals that, by linking among them, could pass the threshold, the myopic individuals would also start forming links achieving the efficient network.
Moreover, it is important to understand what happens when myopic players interact with farsighted players since, in general, some networks that are neither stable when all players are myopic nor stable when all players are farsighted could now emerge in the long run. Is turning myopic players into farsighted players beneficial for the society? Could it be that a heterogeneous society does better than a homogeneous society in terms of efficiency? And if yes, when?
To address those questions, we adopt the notion of myopic-farsighted stable set. This concept will help us to determine the networks that emerge when myopic and farsighted individuals decide with whom they want to form a link, according to some utility function that weighs the costs and benefits of each connection.Footnote 3 A myopic-farsighted stable set is the set of networks satisfying internal and external stability with respect to the notion of myopic-farsighted improving path. When all individuals are farsighted, the definition of a myopic-farsighted stable set boils down to the farsighted stable set.Footnote 4
We first provide general results that are useful for characterizing the myopic-farsighted stable set in applications. If a network is optimal for the farsighted players and pairwise stable for the myopic players, then it belongs to any myopic-farsighted stable set. A set of networks is the unique myopic-farsighted stable set if there is no myopic-farsighted improving path from any network within the set, and from any network outside the set there is a myopic-farsighted improving path leading to some network within the set. We next provide conditions on the utility function that guarantee the existence and uniqueness of a myopic-farsighted stable set. We find that, under the egalitarian utility function or in the presence of positive convex externalities or in the case of no externality, the unique myopic-farsighted stable set consists of all pairwise stable networks when all players are myopic. When the population is composed of myopic and farsighted players, the myopic-farsighted stable set refines the set of pairwise stable networks by eliminating some Pareto-dominated networks. In the end, when all players are farsighted, the unique myopic-farsighted stable set only consists of all strongly efficient networks. Hence, under the egalitarian utility function or in the presence of positive convex externalities or in the case of no externality, turning myopic players into farsighted players alleviates the tension between stability and efficiency. In addition, myopic players can only be better off by becoming farsighted since the least preferred pairwise stable networks are progressively discarded.
We then analyze two specific utility functions: distance-based utility function (where the formation of a link exerts positive externalities) and degree-based utility function (where the formation of a link exerts negative externalities).
First, we reconsider Bloch and Jackson (2007) model of network formation where individuals decide with whom they want to form a link, according to a distance-based utility function that weighs the costs and benefits of each connection. Benefits of a connection decrease with distance in the network, while the cost of a link represents the time an individual must spend with another individual for maintaining a direct link. Adding a link requires the consent of both individuals, while deleting a link can be done unilaterally. We now allow the population of individuals to include not only myopic individuals but also farsighted ones. Farsighted individuals are able to anticipate that once they add or delete some links, other individuals could add or delete links afterwards.
We focus on the range of costs and benefits such that a star network is the unique strongly efficient network.Footnote 5 When all individuals are myopic, Jackson (2008) shows that a conflict between stability and efficiency is likely to occur. In addition, starting from the empty network, a random process where pairs of players meet to add or to delete links becomes unlikely to reach a star network as the number of players increases (see Watts 2001; Jackson 2008). When the population consists of both myopic and farsighted individuals, we show that the conflict between stability and efficiency vanishes if there are enough farsighted individuals. Indeed, the set consisting of all star networks where the center of the star is a myopic individual is the unique myopic-farsighted stable set. However, once all individuals become farsighted, every set consisting of a star network encompassing all players is a myopic-farsighted stable set, but there may be other myopic-farsighted stable sets. For instance, the set of circles among four farsighted players can be a myopic-farsighted stable set.
One can then conclude that diversity guarantees the emergence in the long run of the efficient outcomes. When all individuals are myopic or all individuals are farsighted, a tension between stability and efficiency can occur. However, if the population is mixed, then this tension disappears. Farsighted individuals try to avoid ending up in the central position of the star, and so, if all of them are farsighted, this can lead to a worse inefficient outcome. But, if some individuals are myopic, farsighted individuals are able to place myopic individuals in positions where they have myopic incentives to move toward some star network where one of the myopic individuals ends up being the center of the star. However, if there are too many myopic individuals with respect to farsighted ones, farsighted individuals may fail to engage a path from some inefficient network toward a star network.Footnote 6
Second, we reconsider Morrill (2011) model of network formation where the individual’s utility from a link is a decreasing function of the number of links the other individuals maintain. Benefits of a link now decrease with the degree of the neighbors while costs of a link still represent the time an individual must spend with another individual for maintaining a link. Degree-based utility functions exhibit negative externalities. In general, there is a conflict between stability and efficiency. Morrill (2011) shows that when individuals are all myopic and are able to make transfers to their neighbors, then stable networks coincide with strongly efficient ones. When the population is mixed (and without transfers), we show that myopic and farsighted individuals may end up segregated with myopic individuals being overconnected and farsighted ones getting the socially optimal payoff. The more numerous farsighted individuals are, the less likely inefficient networks will emerge. In the limit, when all individuals are farsighted, the set of all strongly efficient networks is stable without the use of any transfers.
Finally, we study how networks evolve when myopic players may become farsighted over time. Players are initially unconnected to each other. Over time, pairs of players decide whether or not to form or cut links with each other. A link can be cut unilaterally, but agreement by both players is needed to form a link. All players are initially myopic and thus decide to form or cut links if doing so increases their current payoffs. The length of a period is sufficiently long so that the process can converge to some stable network. At the beginning of each period after the initial period, some myopic players become farsighted. The likelihood of becoming farsighted may be related to some endogenous factors (e.g., number of farsighted players in the neighborhood, average payoff of the neighbors, etc.) or some exogenous factors (e.g., a policy for improving individuals’ cognitive ability, etc.). Depending on their positions in the network, the process either stays at the same network or evolves to another stable network. For instance, in the distance-based utility model, the dynamic process first converges to some pairwise stable network. Once the number of myopic players who have become farsighted is large enough, the dynamic process evolves to a star network with some myopic player in the center. Such star network will be dismantled once the myopic player in the center of the star becomes farsighted. In this case, the process evolves next to another star network with one of the remaining myopic players in the center.
The paper is organized as follows: In Sect. 2, we introduce networks, myopic-farsighted improving paths, myopic-farsighted stable sets, and we provide general results for characterizing a myopic-farsighted stable set of networks. In Sect. 3, we consider distance-based utility functions and we characterize the myopic-farsighted stable sets when the population consists of a mixture of myopic and farsighted individuals. In Sect. 4, we consider degree-based utility functions. In Sect. 5, we study the evolution and the dynamics of networks and we discuss the robustness of our results with respect to deviations by groups and limited farsightedness. In Sect. 6, we conclude.
2 Network formation
2.1 Modeling networks
We study networks where players form links with each other in order to exchange information. The population consists of both myopic and farsighted players. The set of players is denoted by \(N=M\cup F\), where M is the set of myopic players and F is the set of farsighted players. Let n be the total number of players and \(m\ge 0\) (\(n-m\ge 0\)) be the number of myopic (farsighted) players. A network g is a list of pairs of players who are linked to each other and \(ij\in g\) indicates that i and j are linked under g. The complete network on the set of players \(S\subseteq N\) is denoted by \(g^{S}\) and is equal to the set of all subsets of S of size 2.Footnote 7 It follows in particular that the empty network is denoted by \(g^{\emptyset }\). The set of all possible networks on N is denoted by \(\mathcal {G}\) and consists of all subsets of \(g^{N}\). The network obtained by adding link ij to an existing network g is denoted \(g+ij\), and the network that results from deleting link ij from an existing network g is denoted \(g-ij\). Let \(N(g)=\{i\mid \)there is j such that \( ij\in g\}\) be the set of players who have at least one link in the network g. Let \(N_{i}(g)=\{j\in N\mid ij\in g\}\) be the set of neighbors of player i in g. The degree of player i in network g, denoted \(d_{i}(g)\), is the cardinality of i’s set of neighbors, \(d_{i}(g)=\#N_{i}(g)\). A star network is a network such that there exists some player i (the center) who is linked to every other player \(j\ne i\) (the peripherals) and that contains no other links (i.e., g is such that \(N_{i}(g)=N\setminus \left\{ i\right\} \) and \(N_{j}(g)=\left\{ i\right\} \) for all \(j\in N\setminus \left\{ i\right\} \)). A d-regular network is a network where all players have the same degree d. A path in a network g between i and j is a sequence of players \(i_{1},\ldots ,i_{K}\) such that \(i_{k}i_{k+1}\in g\) for each \(k\in \{1,\ldots ,K-1\}\) with \(i_{1}=i\) and \(i_{K}=j\). A network g is connected if for all \(i\in N\) and \(j\in N\setminus \{i\}\), there exists a path in g connecting i and j. A nonempty subnetwork \(h\subseteq g\) is a component of g, if for all \(i\in N(h)\) and \(j\in N(h)\setminus \{i\},\) there exists a path in h connecting i and j, and for any \(i\in N(h)\) and \(j\in N(g)\), \(ij\in g\) implies \(ij\in h\). The set of components of g is denoted by H(g).
A network utility function (or payoff function) is a mapping \(U_{i}:\mathcal { G\rightarrow \mathbb {R} }\) that assigns to each network g a utility \(U_{i}(g)\) for each player \( i\in N\). A network \(g\in \mathcal {G}\) is strongly efficient if \(\sum _{i\in N}U_{i}(g)\ge \sum _{i\in N}U_{i}(g^{\prime })\) for all \(g^{\prime }\in \mathcal {G}\). Let E be the set of strongly efficient networks. Jackson and Wolinsky (1996) propose the notion of pairwise stability to analyze the networks that one might expect to emerge in the long run when all players are myopic. A network \(g\in \mathcal {G}\) is pairwise stable if (i) for all \( ij\in g\), \(U_{i}(g)\ge U_{i}(g-ij)\) and \(U_{j}(g)\ge U_{j}(g-ij)\), (ii) for all \(ij\notin g\), if \(U_{i}(g)<U_{i}(g+ij)\) then \(U_{j}(g)>U_{j}(g+ij)\). Let P be the set of pairwise stable networks.
2.2 Myopic-farsighted improving paths and stable sets
We adopt the notion of myopic-farsighted stable set to determine the networks that are stable when some players are myopic while others are farsighted.Footnote 8 A set of networks G is said to be a myopic-farsighted stable set if it satisfies the following two types of stability. Internal stability: No network in G is dominated by any other network in G. External stability: Every network not in G is dominated by some network in G. A network \(g^{\prime }\) is said to be dominated by a network g if there is a myopic-farsighted improving path from \(g^{\prime }\) to g. Hence, a set of networks is a myopic-farsighted stable set if (internal stability) there is no myopic-farsighted improving path between networks within the set and (external stability) there is a myopic-farsighted improving path from any network outside the set to some network within the set.
A myopic-farsighted improving path is a sequence of distinct networks that can emerge when farsighted players form or delete links based on the improvement the end network offers relative to the current network while myopic players form or delete links based on the improvement the resulting network offers relative to the current network. Since we only allow for pairwise deviations, each network in the sequence differs from the previous one in that either a new link is formed between two players or an existing link is deleted. If a link is deleted, then it must be that either a myopic player prefers the resulting network to the current network or a farsighted player prefers the end network to the current network. If a link is added between some myopic player i and some farsighted player j, then the myopic player i must prefer the resulting network to the current network and the farsighted player j must prefer the end network to the current network.
Along a myopic-farsighted improving path, myopic players do not care whether other players are myopic or farsighted. They behave as if all players are myopic and they compare their resulting network’s payoff to their current network’s payoff for taking a decision. However, farsighted players know exactly who is farsighted and who is myopic and they compare their end network’s payoff to their current network’s payoff for taking a decision.Footnote 9
Definition 1
A myopic-farsighted improving path from a network g to a network \( g^{\prime }\) is a finite sequence of distinct networks \(g_{1},\ldots ,g_{K}\) with \(g_{1}=g\) and \(g_{K}=g^{\prime }\) such that for any \(k\in \{1,\ldots ,K-1\}\) either
- (i):
-
\(g_{k+1}=g_{k}-ij\) for some ij such that \( U_{i}(g_{k+1})>U_{i}(g_{k})\) and \(i\in M\) or \(U_{j}(g_{K})>U_{j}(g_{k})\) and \(j\in F\); or
- (ii):
-
\(g_{k+1}=g_{k}+ij\) for some ij such that \( U_{i}(g_{k+1})>U_{i}(g_{k})\) and \(U_{j}(g_{k+1})\ge U_{j}(g_{k})\) if \( i,j\in M\), or \(U_{i}(g_{K})>U_{i}(g_{k})\) and \(U_{j}(g_{K})\ge U_{j}(g_{k})\) if \(i,j\in F\), or \(U_{i}(g_{k+1})\ge U_{i}(g_{k})\) and \(U_{j}(g_{K})\ge U_{j}(g_{k})\) (with one inequality holding strictly) if \(i\in M,j\in F\).
If there exists a myopic-farsighted improving path from a network g to a network \(g^{\prime }\), then we write \(g\rightarrow g^{\prime }\). The set of all networks that can be reached from a network \(g\in \mathcal {G}\) by a myopic-farsighted improving path is denoted by \(\phi (g)\), \(\phi (g)=\left\{ g^{\prime }\in \mathcal {G}\mid g\rightarrow g^{\prime }\right\} \). When all players are myopic, our notion of myopic-farsighted improving path reverts to Jackson and Watts (2002) notion of improving path.Footnote 10 When all players are farsighted, our notion of myopic-farsighted improving path reverts to Herings et al. (2009) notion of farsighted improving path.
A set of networks G is a myopic-farsighted stable set if the following two conditions hold. Internal stability: for any two networks g and \(g^{\prime }\) in the myopic-farsighted stable set G there is no myopic-farsighted improving path from g to \(g^{\prime }\) (and vice versa). External stability: for every network g outside the myopic-farsighted stable set G there is a myopic-farsighted improving path leading to some network \( g^{\prime }\) in the myopic-farsighted stable set G (i.e., there is \( g^{\prime }\in G\) such that \(g\rightarrow g^{\prime }\)).
Definition 2
A set of networks \(G\subseteq \mathcal {G}\) is a myopic-farsighted stable set if: (IS) for every \(g,g^{\prime }\in G\) (\(g\ne g^{\prime }\)), it holds that \(g^{\prime }\notin \phi (g)\), and (ES) for every \(g\in \mathcal {G}\setminus G\), it holds that \(\phi (g)\cap G\ne \emptyset \).
When all players are farsighted, the myopic-farsighted stable set is simply the farsighted stable set as defined in Herings et al. (2009) or Ray and Vohra (2015). When all players are myopic, the myopic-farsighted stable set boils down to the pairwise CP vNM set as defined in Herings et al. (2017) for two-sided matching problems.Footnote 11
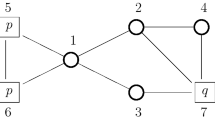
Example 1
Consider a situation where four players can form links. The utilities they obtained from different network configurations are as follows. For the empty network \(g^{\emptyset }\), \(U_{i}(g^{\emptyset })=8\) for all \(i\in N\). For the complete network \(g^{N}\), \(U_{i}(g^{N})=9\) for all \(i\in N\). For a line network \(g^{L4}\) with four players, \(U_{i}(g^{L4})=2+3d_{i}(g^{L4})\) for all \(i\in N\). For a line network \(g^{L3}\) with three players, \( U_{i}(g^{L3})=20-11d_{i}(g^{L3})\) for all \(i\in N(g^{L3})\) and \( U_{j}(g^{L3})=0\) for \(j\in N\setminus N(g^{L3})\). For all other networks g , \(U_{i}(g)=-d_{i}(g)\). Figure 1 gives some of the network configurations. Both the empty network and the complete network are pairwise stable networks. The complete network is also the Pareto-dominant network. When all players are farsighted, \(\{g^{N}\}\) is the unique myopic farsighted stable set since \(g^{N}\in \phi (g)\) for all \(g\ne g^{N}\) and \(\phi (g^{N})=\emptyset \). When all players are myopic, \(\{g^{N},g^{\emptyset }\}\) is the unique myopic farsighted stable set since \(g^{\emptyset }\in \phi (g)\) for all \(g\ne g^{N},g^{\emptyset }\), \(\phi (g^{\emptyset })=\emptyset \) and \(\phi (g^{N})=\emptyset \). Suppose now that players 1 and 3 are farsighted while players 2 and 4 are myopic. That is, \(M=\{2,4\}\) and \( F=\{1,3\}\). We still have \(\phi (g^{\emptyset })=\emptyset \) and \(\phi (g^{N})=\emptyset \). But now, there are no myopic-farsighted improving paths from the line networks \(\{12,13,34\}\) and \(\{14,13,23\}\) to the empty network since myopic players are worse off at the adjacent networks to \( \{12,13,34\}\) and \(\{14,13,23\}\) and farsighted players prefer \(\{12,13,34\}\) and \(\{14,13,23\}\) to the empty network. Obviously, there are no myopic-farsighted improving paths from the line networks \(\{12,13,34\}\) and \( \{14,13,23\}\) to the complete network since along any path toward the complete network utilities are decreasing before reaching the complete network. The external stability condition implies that both \(g^{\emptyset }\) and \(g^{N}\) have to belong to any myopic-farsighted stable set. One can easily check that \(\phi (g)\cap \{g^{\emptyset },g^{N}\}\ne \emptyset \) for all \(g\ne \{12,13,34\},\{14,13,23\},g^{\emptyset },g^{N}\), while \(\phi (\{12,13,34\})=\{\{12,13\},\{13,34\}\}\) and \(\phi (\{14,13,23\})=\{\{14,13\},\{13,23\}\}\). So, if \(\{12,13,34\}\) would not belong to a myopic-farsighted stable set, then either \(\{12,13\}\) or \( \{13,34\}\) has to be included in it. But, then the internal stability condition would be violated since \(\phi (\{12,13\})\supseteq g^{\emptyset }\) and \(\phi (\{13,34\})\supseteq g^{\emptyset }\). Hence, \(\{g^{\emptyset },g^{N},\{12,13,34\},\{14,13,23\}\}\) is the unique myopic farsighted stable set when \(M=\{2,4\}\) and \(F=\{1,3\}\). Thus, a mixed population can stabilize networks that are not stable when the population is homogeneous (i.e., where players are either all farsighted or all myopic).
In the external stability condition, it is implicitly assumed some optimism on behalf of the players. A network \(g^{\prime }\) is said to be dominated by a network g if there exists a myopic-farsighted improving path from \( g^{\prime }\) to g. But along the path from \(g^{\prime }\) to g, both farsighted and myopic players who are moving on the path may have a better alternative than the one prescribed by the path when they are called on to move. This is true not only for myopic players but also for farsighted players. However, Ray and Vohra (2019) show that every (farsighted) stable set satisfying some reasonable and easily verifiable properties is unaffected by the imposition of stringent maximality constraints. These constraints are satisfied by all (farsighted) stable sets consisting of networks with a single payoff.
In the definition of myopic-farsighted stable sets, it is implicitly assumed that myopic players stay myopic and cannot become farsighted. However, one could argue that a myopic player could learn and become less myopic overtime when interacting in an environment composed mainly of farsighted players. To address this issue, we look in Sect. 5 at the evolution and dynamics of networks when at the beginning of each period, some myopic player become farsighted. The likelihood of becoming farsighted may be random or may depend on the network (number of farsighted players in the neighborhood, average payoff of neighbors, ...).
2.3 General results
2.3.1 Existence and uniqueness
Let \(\phi ^{2}(g)=\phi (\phi (g))=\{g^{\prime \prime }\in \mathcal {G}\mid \exists g^{\prime }\in \phi (g)\) such that \(g^{\prime \prime }\in \phi (g^{\prime })\}\) be the set of networks that can be reached by a composition of two myopic-farsighted improving paths from g. We extend this definition and, for \(r\in \mathbb {N}\), we define \(\phi ^{r}(g)\) as those networks that can be reached from g by means of r compositions of myopic-farsighted improving paths. The transitive closure of \(\phi \) is denoted by \(\phi ^{\infty }\) and defined as \(\phi ^{\infty }(g)={\bigcup }_{r\in \mathbb {N} }\phi ^{r}(g)\). Since the set \(\mathcal {G}\) is finite, it holds that, for some \(r^{\prime }\in \mathbb {N}\), for every \(g\in \mathcal {G}\), \(\phi ^{\infty }(g)={\bigcup }_{r=1}^{r^{\prime }}\phi ^{r}(g)\). We now extend Jackson and Watts (2002) notions of cycle and closed cycle to myopic and farsighted players. A set of networks C forms a cycle if for any \(g\in C\) and \(g^{\prime }\in C\) there exists a sequence of myopic-farsighted improving paths connecting g to \(g^{\prime }\), i.e., \(g^{\prime }\in \phi ^{\infty }(g)\). A cycle C is a closed cycle if no network in C lies on a myopic-farsighted improving path leading to a network that is not in C, i.e., \(\phi ^{\infty }(C)=C\).
Proposition 1
Let G \(\subseteq \mathcal {G}\) be a myopic-farsighted stable set. If \(\phi (g)=\emptyset \), then \(g\in G\).
Proof
Take any g such that \(\phi (g)=\emptyset \). Then, g should belong to the myopic-farsighted stable set G. Otherwise, G would violate the external stability condition (ES). \(\square \)
Suppose that G \(\subseteq \mathcal {G}\) is a myopic-farsighted stable set. Proposition 1 tells us that if there is a network such that there is no myopic-farsighted improving path leaving it, then this network belongs to any myopic-farsighted stable set. In addition, each myopic-farsighted stable set and each closed cycle have a non-empty intersection. That is, if \(C^{1},\ldots ,C^{R}\) are the closed cycles, then \( C^{k}\cap G\ne \emptyset \) for \(k=1,\ldots ,R\). Indeed, if \(C^{k}\cap G=\emptyset \), then G would violate (ES) since for every \(g\in C^{k}\) we have \(\phi (g)\subseteq C^{k}\). The following result follows as a corollary of Proposition 1. If a network is optimal for the farsighted players and pairwise stable for the myopic players, then it belongs to any myopic-farsighted stable set.
Corollary 1
Let G \(\subseteq \mathcal {G}\) be a myopic-farsighted stable set. If there is \(g\in P\) such that for all \(g^{\prime }\in \mathcal {G}\setminus \{g\}\) it holds \(U_{i}(g)>U_{i}(g^{\prime })\) for all \(i\in F\), then \(g\in G\).
Proposition 2 tells us when a set of networks is the unique myopic-farsighted stable set. A set G \(\subseteq \mathcal {G}\) is the unique myopic-farsighted stable set if (i) there is no myopic-farsighted improving path from any network within the set and (ii) from any network outside the set there is a myopic-farsighted improving path leading to some network within the set.
Proposition 2
If G \(\subseteq \mathcal {G}\) is such that \((\mathbf {i})\) for every \(g\in \mathcal {G}\setminus G\), it holds that \(\phi (g)\cap G\ne \emptyset \), and \((\mathbf {ii})\) for every \(g\in G\), it holds that \(\phi (g)=\emptyset \), then G is the unique myopic-farsighted stable set.
Proof
From (i) the set G satisfies (ES) and from (ii ) the set G satisfies (IS). Hence, G is a myopic-farsighted stable set. We now show that it is the unique one. Suppose that \(G^{\prime }\ne G\) is a myopic-farsighted stable set. Since for every \(g\in G\), it holds that \(\phi (g)=\emptyset \), then \(G\subseteq G^{\prime }\). Otherwise, \( G^{\prime }\) violates (ES). But, if \(G\varsubsetneq G^{\prime }\), then \(G^{\prime }\) violates (IS). Hence, G is the unique myopic-farsighted stable set. \(\square \)
2.3.2 Characterization when all players are myopic
Suppose now that all players are myopic, i.e., \(F=\emptyset \). Lemma 1 in Jackson and Watts (2002) shows that there always exists at least one pairwise stable network or closed cycle of networks. Starting from any network, either it is pairwise stable (and no improving path leaves it) or it lies on an improving path to another network. Either the network reached is pairwise stable or the improving path can be continued forever and ends up running into a closed cycle. Using Lemma 1 of Jackson and Watts (2002) we provide a characterization of the (myopic-farsighted) stable set when all players are myopic. A set of networks is a (myopic-farsighted) stable set if and only if it consists of all pairwise stable networks and one network from each closed cycle.Footnote 12
Proposition 3
Suppose that all players are myopic, \(F=\emptyset \). Let \( C^{1},\ldots ,C^{R}\) be the set of closed cycles. A set of networks \(G\subseteq \) \(\mathcal {G}\) is a myopic-farsighted stable set if and only if \(G=P\cup \left\{ g^{1},\ldots ,g^{R}\right\} \) with \(g^{k}\in C^{k}\) for \(k=1,\ldots ,R\).
Proof
We first show that any \(G=P\cup \left\{ g^{1},\ldots ,g^{R}\right\} \) with \( g^{k}\in C^{k}\) for \(k=1,\ldots ,R\) satisfies (IS) and (ES). Since all players are myopic, the set G satisfies (IS) by definition of a pairwise stable network and of a closed cycle; i.e., for every \(g,g^{\prime }\in G\) we have that \(g\notin \phi (g^{\prime })\). From Lemma 1 in Jackson and Watts (2002), we have that, for every \(g\notin G\), \( \phi (g)\cap G\ne \emptyset \), and so G satisfies (ES).
Suppose now that G is a (myopic-farsighted) stable set. First, \(P\subseteq G\); otherwise, G would violate (ES). Second, \(C^{k}\cap G\ne \emptyset \) for \(k=1,\ldots ,R\); otherwise, G would violate (ES). Third, take any \(G,G^{\prime }\) such that \(G\varsupsetneq G^{\prime }=\) \( P\cup \left\{ g^{1},\ldots ,g^{R}\right\} \) with \(g^{k}\in C^{k}\) for \(k=1,\ldots ,R\) . Then, from Lemma 1 in Jackson and Watts (2002) we have that there is \( g,g^{\prime }\in G\) such that \(g\in \phi (g^{\prime })\) and G violates ( IS). \(\square \)
Since there always exists at least one pairwise stable network or closed cycle of networks (Jackson and Watts 2002), the existence of a myopic-farsighted stable set is guaranteed when all players are myopic.Footnote 13 When all players are myopic (i.e., \(N=M\)), if \((g,\ldots ,g^{\prime })\) and \((g^{\prime },\ldots ,g^{\prime \prime })\) are myopic-farsighted improving paths, then \( (g,..,g^{\prime },..,g^{\prime \prime })\) is also a myopic-farsighted improving path. However, when some players are farsighted (\(F\ne \emptyset \) ), if \((g,\ldots ,g^{\prime })\) and \((g^{\prime },\ldots ,g^{\prime \prime })\) are myopic-farsighted improving paths, then \((g,..,g^{\prime },..,g^{\prime \prime })\) may not be a myopic-farsighted improving path since some farsighted players who move along the first myopic-farsighted improving path \((g,\ldots ,g^{\prime })\) may now decide not to move once they look forward toward the end network \(g^{\prime \prime }\) of the second myopic-farsighted improving path. This is why it is much harder to analyze situations involving farsighted players.
2.3.3 Existence and characterization under the egalitarian utility function
Suppose that the utility function U is such that, for any given network, all players get the same payoff: \(U_{i}(g)=U_{j}(g)\) for all \(i,j\in N\). With the egalitarian utility function U, each player’s payoff depends on the network but not on the specific role she plays within the network. Proposition 4 shows that there is a unique myopic-farsighted stable set under the egalitarian utility function. Let \( G^{\emptyset }=\{g\in \mathcal {G}\mid \phi (g)=\emptyset \}\) be the set of networks such that there are no myopic-farsighted improving paths emanating from them.
Proposition 4
Take any U such that \(U_{i}(g)=U_{j}(g)\) for all \( i,j\in N\). The set \(G^{\emptyset }=\{g\in \mathcal {G}\mid \phi (g)=\emptyset \}\) is the unique myopic-farsighted stable set.
Proof
First, we show that for every \(g\in \mathcal {G}\setminus G^{\emptyset }\), it holds that \(\phi (g)\cap G\ne \emptyset \). Given the egalitarian utility function U, we have that, for \(0\le m\le n\), there are no closed cycles: for all \(g\in \mathcal {G}\) we have \(g\notin \phi ^{\infty }(g)\). Thus, all sequences of myopic-farsighted improving paths starting from any g such that \(\phi (g)\ne \emptyset \) will reach after a finite number of myopic-farsighted improving paths some network \(g^{\prime }\) such that \(\phi (g^{\prime })=\emptyset \). In addition, given the egalitarian utility function U, we have that \(U_{i}(g_{k})<U_{i}(g_{K})\) for all \(i\in N\), \( k=1,\ldots ,K-1\), along any myopic-farsighted improving path \((g_{1},\ldots ,g_{K})\) . It follows that if \(g^{\prime }\in \phi (g)\) and \(g^{\prime \prime }\in \phi (g^{\prime })\) then \(g^{\prime \prime }\in \phi (g)\). Hence, \(\phi (g)=\phi ^{\infty }(g)\). Thus, for any g such that \(\phi (g)\ne \emptyset \) we have \(\phi (g)\cap G^{\emptyset }\ne \emptyset \), and the set \( G^{\emptyset }\) satisfies (ES). Second, since \(\phi (g)=\emptyset \) for all \(g\in G^{\emptyset }\), the set \(G^{\emptyset }\) satisfies (IS ). Third, uniqueness follows from Proposition 2. \(\square \)
Let \(G_{\mid M,F}^{\emptyset }\) and \(G_{\mid M^{\prime },F^{\prime }}^{\emptyset }\) denote the set \(G^{\emptyset }\) when \(N=M\cup F\) and \( N=M^{\prime }\cup F^{\prime }\), respectively. Proposition characterizes the unique myopic-farsighted stable set under the egalitarian utility function. When all players are myopic, the unique myopic-farsighted stable set consists of all pairwise stable networks. When all players are farsighted, the unique myopic-farsighted stable set consists of all strongly efficient networks. When the population is mixed, the unique myopic-farsighted stable set is a subset of the set of pairwise stable networks. In fact, under the egalitarian utility function, turning myopic players into farsighted players improves efficiency by removing Pareto-dominated pairwise stable networks and in the end fully eliminates the tension between stability and efficiency.
Proposition 5
Take any U such that \(U_{i}(g)=U_{j}(g)\) for all \( i,j\in N\). The unique myopic-farsighted stable set is such that
- (i):
-
\(G^{\emptyset }=P\) for \(N=M\) (\(F=\emptyset \));
- (ii):
-
\(G_{\mid M^{\prime },F^{\prime }}^{\emptyset }\subseteq G_{\mid M,F}^{\emptyset }\) for \(M^{\prime }\varsubsetneq M\);
- (iii):
-
\(G^{\emptyset }=E\) for \(N=F\) (\(M=\emptyset \)).
Proof
- (i):
-
First, take \(N=M\) (\(F=\emptyset \)). Given the egalitarian utility function U, we have that there are no closed cycles. Hence, it follows from Proposition 3 that the set of pairwise stable networks P is the unique myopic-farsighted stable set and is equal to \( \{g\in \mathcal {G}\mid \phi (g)=\emptyset \}\).
- (ii):
-
Second, take the unique myopic-farsighted stable set \(G_{\mid M,F}^{\emptyset }=\{g\in \mathcal {G}\mid \phi (g)=\emptyset \}\) for \(N=M\cup F\). Now take \(N=M^{\prime }\cup F^{\prime }\) with \(M^{\prime }\varsubsetneq M \). We show that the unique myopic-farsighted stable set \(G_{\mid M^{\prime },F^{\prime }}^{\emptyset }\) for \(N=M^{\prime }\cup F^{\prime }\) is included in \(G_{\mid M,F}^{\emptyset }\), i.e., \(G_{\mid M^{\prime },F^{\prime }}^{\emptyset }\subseteq G_{\mid M,F}^{\emptyset }\) for \(M^{\prime }\varsubsetneq M\). Given the egalitarian utility function U, we have that along any myopic-farsighted improving path \((g_{1},\ldots ,g_{K})\), \( U_{i}(g_{k})<U_{i}(g_{K})\) for all \(i\in N\), \(k=1,\ldots ,K-1\). In particular, if \((g_{1},\ldots ,g_{K})\) is a myopic-farsighted improving path when all players are myopic (\(F=\emptyset \)), then we have \( U_{i}(g_{1})<U_{i}(g_{2})<\cdots <U_{i}(g_{K})\) for all \(i\in N\). Hence, if \( (g_{1},\ldots ,g_{K})\) is a myopic-farsighted improving path for \(N=M\cup F\), then \((g_{1},\ldots ,g_{K})\) remains a myopic-farsighted improving path for \( N=M^{\prime }\cup F^{\prime },M^{\prime }\varsubsetneq M\). Let \(\phi (g)_{\mid M,F}\) be the set of all networks that can be reached from g by a myopic-farsighted improving path given the set of players \(N=M\cup F\). It follows that \(\phi (g)_{\mid M,F}\subseteq \phi (g)_{\mid M^{\prime }\varsubsetneq M,F^{\prime }}\), and so \(G_{\mid M^{\prime },F^{\prime }}^{\emptyset }\subseteq G_{\mid M,F}^{\emptyset }\) for \(M^{\prime }\varsubsetneq M\).
- (iii):
-
Third, given the egalitarian utility function U, any strongly efficient network \(g\in E\) Pareto-dominates any network \(g^{\prime }\notin E\). That is, \(U_{i}(g)>U_{i}(g^{\prime })\) for all \(g\in E,g^{\prime }\notin E\), for all \(i\in N\). Hence, once all players are farsighted (\( N=F,M=\emptyset \)), we have that \(\phi (g)=\emptyset \) for all \(g\in E\) and \( \phi (g^{\prime })\cap E\ne \emptyset \) for all \(g^{\prime }\in \mathcal {G} \setminus E\).
\(\square \)
2.4 Externalities
2.4.1 No externality
Suppose that the utility function U exhibits no externality and is given by \(U_{i}(g)=a(d_{i})\) for all \(i\in N\). The function \(a(d_{i})\) is assumed to be single peaked: there exists an integer \(d^{*}\) such that \( a(d_{i})-a(d_{i}-1)>0\) for every \(d_{i}\le d^{*}\) and \( a(d_{i})-a(d_{i}-1)<0\) for every \(d_{i}>d^{*}\). For \(d^{*}=n-1\), each player wants to be linked to all players. For \(d^{*}=0\), each player does not want to form any link. Thus, \(d^{*}\) is the maximum number of links a player would like to form. If she has more than \(d^{*}\) links she will cut some of them. To guarantee the existence of d-regular networks (\(1\le d\le n-1\)), we restrict the analysis to an even number of players. Let \(G^{d^{*}}=\{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \( i\in N\}\) be the set of \(d^{*}\)-regular networks. Obviously, \(E=\) \( G^{d^{*}}\) when U exhibits no externality and is single peaked.
Proposition 6 tells us that, when all players are myopic, the unique myopic-farsighted stable set consists of all pairwise stable networks. Notice that \(d^{*}\)-regular networks are pairwise stable. In fact, in a pairwise stable network, each player has either \(d^{*}\) links or less than \(d^{*}\) links and those players who have less than \(d^{*}\) links are fully linked among themselves. When all players are farsighted, the unique myopic-farsighted stable set consists of all strongly efficient networks \(E=\) \(G^{d^{*}}\). When the population is mixed, a myopic-farsighted stable set consists not only of all \(d^{*}\)-regular networks, but also of all networks where farsighted players have \(d^{*}\) links and are not linked to myopic players, each myopic player has either \( d^{*}\) links or less than \(d^{*}\) links and those myopic players who have less than \(d^{*}\) links are fully linked among themselves. Hence, turning myopic players into farsighted players improves again efficiency by removing Pareto-dominated pairwise stable networks and in the end fully eliminates the tension between stability and efficiency.
Proposition 6
Take any U such that \(U_{i}(g)=a(d_{i})\) for all \(i\in N\) where \(a(d_{i})\) is single peaked. Suppose that the number of players n is even.
- (i):
-
If all players are farsighted (\(M=\emptyset \)), then the set \(G^{d^{*}}\) is the unique myopic-farsighted stable set.
- (ii):
-
If all players are myopic (\(F=\emptyset \)), then the set \(P=\{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\setminus S\), \( d_{j}<d^{*}\) for all \(j\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\) is the unique myopic-farsighted stable set.
- (iii):
-
If the population is mixed (\(M\ne \emptyset ,F\ne \emptyset \)) with \(n-m>d^{*}\) and \(n-m\) even, then the set \(G^{d^{*}}\cup \{g\in \mathcal {G}\mid \phi (g)\cap G^{d^{*}}=\emptyset \), \( d_{i}=d^{*}\) for all \(i\in F\), \(N_{j}(g)\cap F=\emptyset \) if \(j\in M\), \( d_{j}=d^{*}\) for all \(j\in M\setminus S\), \(d_{k}<d^{*}\) for all \( k\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\) is a myopic-farsighted stable set.
Proof
Since n is even, we have that \(G^{d^{*}}=\{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\}\ne \emptyset \).
- (i):
-
Take \(N=F\) (\(M=\emptyset \)). Take any \(g\notin G^{d^{*}}\). We will show that \(\phi (g)\cap G^{d^{*}}\ne \emptyset \). First, players who have more than \(d^{*}\) links successively cut their links to reach a network \(g^{\prime }\) where all players have at most \(d^{*}\) links. If \(g^{\prime }\in G^{d^{*}}\) we are done. Otherwise, players who have less than \(d^{*}\) links successively cut all their links looking forward some \(d^{*}\)-regular network \(g^{*}\in G^{d^{*}}\). We reach a network \(g^{\prime \prime }\) where players have either no links (they are isolated) or \(d^{*}\) links (they are part of a \(d^{*}\) -regular subnetwork). (*) From \(g^{\prime \prime }\), looking forward to \(g^{*}\), one isolated player, say i, build a link to some player j who has \(d^{*}\) links and belongs to some component \( h\subseteq g^{\prime \prime }\). Player j is indifferent between the current network \(g^{\prime \prime }\) and the end network \(g^{*}\) while player i strictly prefers the end network. From \(g^{\prime \prime }+ij\), player j cuts a link with another player k who has \(d^{*}\) links. At \(g^{\prime \prime }+ij-jk\), player k has \(d^{*}-1\) links and has now incentives to cut all her links looking forward to \(g^{*}\). Player k is now isolated. Next, players who were linked to player k have now less than \(d^{*}\) links and so have incentives to cut all their links looking forward to \(g^{*}\). They become isolated. Next, we repeat the process where all players who have less than \(d^{*}\) links cut all their links until we reach a network \(g^{\prime \prime \prime }\varsubsetneq g^{\prime }\) where all players of the component h have now become isolated (player i is again isolated). Next, we repeat the process (*) with another component where all players have \(d^{*}\) links, until we reach the empty network \(g^{\emptyset }\) where all players are isolated. From the empty network \(g^{\emptyset }\), players add successively links to form \(g^{*}\in G^{d^{*}}\). Hence, \(G^{d^{*}}=\{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\}\) satisfies (ES). Obviously, \( \phi (g^{\prime })=\emptyset \) for all \(g^{\prime }\in G^{d^{*}}\), and thus, this set satisfies (IS). Uniqueness follows from Proposition 2.
- (ii):
-
Take \(N=M\) (\(F=\emptyset \)). Take any \(g\notin \{g\in \mathcal { G}\mid d_{i}=d^{*}\) for all \(i\in N\setminus S\), \(d_{j}<d^{*}\) for all \(j\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\). We will show that \(\phi (g)\cap \{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\setminus S,d_{j}<d^{*}\) for all \(j\in S,\#S\le d^{*},g^{S}\varsubsetneq g\}\ne \emptyset \). First, players who have more than \( d^{*}\) links successively cut their links to reach a network \(g^{\prime } \) where all players have at most \(d^{*}\) links. If \(g^{\prime }\in \{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\setminus S\), \( d_{j}<d^{*}\) for all \(j\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\) we are done. (*) Otherwise, two players i and j who have less than \( d^{*}\) links build the link ij. We repeat this process (*) until we reach a network \(g^{\prime \prime }\in \{g\in \mathcal {G}\mid d_{i}=d^{*} \) for all \(i\in N\setminus S\), \(d_{j}<d^{*}\) for all \(j\in S\), \( \#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\) where players have either \( d^{*}\) links or less than \(d^{*}\) links with players who have less than \(d^{*}\) links being all linked to each other. Hence, \(\{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\setminus S\), \(d_{j}<d^{*}\) for all \(j\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\) satisfies (ES). Obviously, \(\phi (g^{\prime })=\emptyset \) for all \(g^{\prime }\in \{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\setminus S\), \( d_{j}<d^{*}\) for all \(j\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}=P\), and thus, this set satisfies (IS). Uniqueness follows from Proposition 2.
- (iii):
-
Take \(M\ne \emptyset ,F\ne \emptyset \) with \(n-m>d^{*}\) and \(n-m\) even. Take any \(g\notin G^{d^{*}}\cup G^{M,F}\) where \( G^{M,F}=\{g\in \mathcal {G}\mid \phi (g)\cap G^{d^{*}}=\emptyset \), \( d_{i}=d^{*}\) for all \(i\in F\), \(N_{j}(g)\cap F=\emptyset \) if \(j\in M\), \( d_{j}=d^{*}\) for all \(j\in M\setminus S\), \(d_{k}<d^{*}\) for all \( k\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\). First, players who have more than \(d^{*}\) links successively cut their links to reach a network \(g^{\prime }\) where all players have at most \(d^{*}\) links. If \( g^{\prime }\in G^{d^{*}}\cup G^{M,F}\) we are done. (*) Otherwise, two players i and j who have less than \(d^{*}\) links build the link ij . We repeat this process (*) until we reach a network \(g^{\prime \prime }\in \{g\in \mathcal {G}\mid d_{i}=d^{*}\) for all \(i\in N\setminus S\), \( d_{j}<d^{*}\) for all \(j\in S\), \(\#S\le d^{*}\), \(g^{S}\varsubsetneq g\}\) where players have either \(d^{*}\) links or less than \(d^{*}\) links, with players who have less than \(d^{*}\) links being all linked to each other. If \(g^{\prime \prime }\in G^{d^{*}}\cup G^{M,F}\) we are done. Otherwise, looking forward to some \(g^{*}\in G^{d^{*}}\cup G^{M,F}\), one farsighted player, say i, forms a link with some player j who has less than \(d^{*}\) links (player j may be farsighted or not but strictly improves, while player i is indifferent). Now, player i has more than \(d^{*}\) links. Next, looking forward to some \(g^{*}\in G^{d^{*}}\cup G^{M,F}\), player i has now strict incentives to build successively the missing links with the other farsighted players who are at \( g^{*}\) either strictly better off or equally off. (**) Next another farsighted player who has now \(d^{*}+1\) links after having linked to j (if any) forms successively the missing links with the other farsighted players who are at \(g^{*}\) either strictly better off or equally off. We repeat this process (**) until we reach a network where each farsighted player is linked to all other farsighted players. Next, farsighted players successively cut all their links with myopic players. We reach a network \( g^{\prime \prime \prime }\) where \(N_{j}(g)\cap F=\emptyset \) if \(j\in M\) and \(g^{F}\subseteq g^{\prime \prime \prime }\). From \(g^{\prime \prime \prime }\) , farsighted players successively delete links to form a \(d^{*}\)-regular subnetwork. Next, myopic players form links between myopic players until they reach a pairwise stable subnetwork. We reach a network \(\widehat{g}\) where \(d_{i}=d^{*}\) for all \(i\in F\), \(N_{j}(\widehat{g})\cap F=\emptyset \) if \(j\in M\), \(d_{j}=d^{*}\) for all \(j\in M\setminus S\), \( d_{k}<d^{*}\) for all \(k\in S\subseteq M\), \(\#S\le d^{*}\), \( g^{S}\varsubsetneq \widehat{g}\). If \(\phi (\widehat{g})\cap G^{d^{*}}=\emptyset \) we are done and \(g^{*}=\widehat{g}\). If \(\phi (\widehat{g} )\cap G^{d^{*}}\ne \emptyset \), from \(\widehat{g}\) to some \(g^{*}\in G^{d^{*}}\), there is a myopic-farsighted improving path that involves only farsighted players and myopic players who have less than \( d^{*}\) in \(\widehat{g}\). Notice that farsighted players are indifferent between \(\widehat{g}\) and \(g^{*}\in G^{d^{*}}\) while myopic players who have less than \(d^{*}\) links strictly prefers \(g^{*}\) to \( \widehat{g}\). Thus, the myopic-farsighted improving path from g to \( \widehat{g}\) followed by the myopic-farsighted improving path from \(\widehat{ g}\) to some \(g^{*}\in G^{d^{*}}\) constitutes a myopic-farsighted improving path from g to \(g^{*}\in G^{d^{*}}\). Hence, \(G^{d^{*}}\cup G^{M,F}\) satisfies (ES). Obviously, \(\phi (g)=\emptyset \) for all \(g\in G^{d^{*}}\cup G^{M,F}\), and thus, \(G^{d^{*}}\cup G^{M,F}\) satisfies (IS).
\(\square \)
2.4.2 Positive convex externalities
Suppose now that the utility function U is given by \(U_{i}(g)={\textstyle \sum }_{j\in N_{i}(g)}\alpha (d_{j})\) for all \(i\in N\) where the function \(\alpha (d_{j})\) exhibits positive convex externalities: (i) there exists an integer \(d^{*}\) such that \(\alpha (d_{j})>0\) for \(d_{j}\ge d^{*}\) and \(\alpha (d_{j})\le 0\) for \(d_{j}<d^{*}\), (ii) \(\alpha (d_{j}+2)-\alpha (d_{j}+1)>\alpha (d_{j}+1)-\alpha (d_{j})>0\) for \(d_{j}\ge d^{*}\). Once some player j has at least \(d^{*}-1\) links then each player who is not yet linked to j has incentives to form a link with j. Under positive convex externalities, we have that \(E=\{g^{N}\}\). Proposition 7 tells us that, under positive convex externalities, there is a threshold with respect to the number of farsighted players such that if the number of farsighted players is above the threshold then the set E is the unique myopic-farsighted stable set while if the number of farsighted players is below the threshold then the unique myopic-farsighted stable set consists of the empty network \(g^{\emptyset }\) and the complete networks \(g^{S}\) on the set of players S for all S large enough. Thus, under positive convex externalities, we do not need all the population to be farsighted to guarantee the emergence of the strongly efficient network.
Proposition 7
Take any U such that \(U_{i}(g)={\textstyle \sum }_{j\in N_{i}(g)}\alpha (d_{j})\) for all \(i\in N\) where \(\alpha (d_{j})\) exhibits positive convex externalities.
- (i):
-
Take \(d^{*}=1\). The set \(\{g^{N}\}\) is the unique myopic-farsighted stable set.
- (ii):
-
Take \(n-1\ge d^{*}>1\). If \(d^{*}\le n-m\), then \(\{g^{N}\}\) is the unique myopic-farsighted stable set. If \(d^{*}>n-m\), then \(\{g^{S}\mid \#S\ge d^{*}+1\}\cup \{g^{\emptyset }\}\) is the unique myopic-farsighted stable set.
Proof
- (i):
-
Take \(d^{*}=1\). From any \(g\ne g^{N}\), both myopic and farsighted players have incentives to add links to all other players. Thus, \( \phi (g)\cap \{g^{N}\}\ne \emptyset \). Obviously, \(\phi (g^{N})=\emptyset \) . Hence, the set \(\{g^{N}\}\) satisfies (ES) and (IS) and is the unique myopic-farsighted stable set from Proposition 2.
- (ii):
-
Take \(n-1\ge d^{*}>1\). (ii.a) Suppose \(d^{*}\le n-m\). Take any \(g\ne g^{N}\) we will show that \(\phi (g)\cap \{g^{N}\}\ne \emptyset \). First, looking forward to \(g^{N}\) farsighted players successively build links among themselves to reach a network \(g^{\prime }\supseteq g^{F}\). In \(g^{\prime }\) farsighted players have at least \(d^{*}-1\) links. Hence, myopic players have now incentives to link to all farsighted players. At the end of this process we reach a network \(g^{\prime \prime }\) where all myopic players have at least \( d^{*}-1\) links, and so now each myopic player has incentives to link to all other myopic players to finally reach the complete network \(g^{N}\). From \(g^{N}\) we have \(\phi (g^{N})=\emptyset \) since \(g^{N}\) Pareto dominates all other networks. Hence, the set \(\{g^{N}\}\) satisfies (ES) and ( IS) and is the unique myopic-farsighted stable set from Proposition 2. (ii.b) Suppose \(d^{*}>n-m\). Take any \(g\notin G^{M,F}=\{g^{S}\mid \#S\ge d^{*}+1\}\cup \{g^{\emptyset }\}\) we will show that \(\phi (g)\cap G^{M,F}\ne \emptyset \). Step 1. Myopic players successively cut the links they have to myopic and farsighted players who have less than \(d^{*}\) links (If there is no myopic or farsighted player who has at least one link but less than \(d^{*}\) links we go directly to Step 3). We repeat this process until we reach a network where myopic players have either at least \(d^{*}\) links or no link. Now, farsighted players who have less than \(d^{*}\) links can only be linked to farsighted players. Since the number of farsighted players is too small, \( d^{*}>n-m\), myopic players with no link and farsighted players with less than \(d^{*}\) links will never reach the threshold of \(d^{*}-1\) links so that other players (myopic or farsighted) would have incentives to link to them. Hence, all farsighted players will delete their links with those farsighted players who have less than \(d^{*}\) links and they become isolated. Step 2. If some other farsighted players now have less than \(d^{*}\) links, we repeat Step 1; otherwise, we go to Step 3. Step 3. We have reached a network where \(n-\#S\) players have no links and \( \#S\) players belong to a component where each player has at least \(d^{*}\) links. If \(\#S=0\), we end up at \(g^{\emptyset }\). Otherwise, the players belonging to S have now incentives to link to each other until they form the network \(g^{S}\), and we end up at \(g^{S}\). Obviously, \(\phi (g^{\emptyset })=\emptyset \) and \(\phi (g^{S})=\emptyset \). Hence, the set \( \{g^{S}\mid \#S\ge d^{*}+1\}\cup \{g^{\emptyset }\}\) satisfies ( ES) and (IS) and is the unique myopic-farsighted stable set from Proposition 2.
\(\square \)
3 Distance-based utility
Distance-based utility functions exhibit positive externalities as any player weakly benefits from any new link between any two other players. As in Bloch and Jackson (2007) or Jackson (2008), if player i is connected to player j by a path of t links, then player i receives a benefit of b(t) from her indirect connection with player j. It is assumed that \( b(t)\ge b(t+1)>0\) for any t.Footnote 14 Each direct link \(ij\in g\) results in a benefit b(1) and a cost c to both i and j. This cost can be interpreted as the time a player must spend with another player in order to maintain a direct link. Player i’s distance-based utility or payoff from a network g is given by
where t(ij) is the number of links in the shortest path between i and j (setting \(t(ij)=\infty \) if there is no path between i and j), \(c\ge 0\) is a cost per link, and b is a nonincreasing function. The symmetric connections model (\(b(t)=\delta ^{t}\)) and the truncated connections model of Jackson and Wolinsky (1996) are special cases of distance-based payoffs.Footnote 15
Proposition 4 in Bloch and Jackson (2007) tells us that the unique strongly efficient network is (i) the complete network \(g^{N}\) if \(c<b(1)-b(2)\), (ii) a star encompassing everyone if \(b(1)-b(2)<c<b(1)+((n-2)/2)b(2)\), and (iii) the empty network \(g^{\emptyset }\) if \(b(1)+((n-2)/2)b(2)<c\). Are the strongly efficient networks likely to arise when all players are myopic?
Jackson (2008) characterizes the pairwise stable networks. He shows that a conflict between pairwise stability and efficiency is likely to occur except if link costs are small. For \(c<b(1)-b(2)\), the unique pairwise stable network is the complete network \(g^{N}\). For \(b(1)-b(2)<c<b(1)\), a star encompassing all players is pairwise stable, but not necessarily the unique pairwise stable network. For \(b(1)<c\), any pairwise stable network which is nonempty is such that each player has at least two links and thus is inefficient. Only for \(c<b(1)-b(2)\), there is no conflict between efficiency and pairwise stability. When \(b(1)-b(2)<c<b(1)\), the efficient network is pairwise stable, but there are other pairwise stable networks that are not efficient. For \(b(1)<c<b(1)+((n-2)/2)b(2)\), the efficient network is never pairwise stable. And, finally, for \(b(1)+((n-2)/2)b(2)<c\), the efficient network is pairwise stable, but there could be other pairwise stable networks that are not efficient.
Hence, from Proposition 3, the concept of myopic-farsighted stable set confirms that, for a large range of parameter values, a conflict between stability and efficiency is likely to occur when all players are myopic.
We denote by \(g^{*i}\) the star network where player i is the center of the star. For intermediate linking costs, \(b(1)-b(2)<c<b(1)\), we next show that, if there are enough farsighted players, the set consisting of all star networks where the center of the star is a myopic player is the unique myopic-farsighted stable set.
Proposition 8
Consider the distance-based utility model in the case \( b(1)-b(2)<c<b(1)\). If \(n>\#F\ge 1+b(2)/(b(2)-b(3))\), then the set \(G^{*}=\left\{ g^{*i}\mid i\in M\right\} \) is the unique myopic-farsighted stable set.
Proof
We first show that \(G^{*}=\left\{ g^{*i}\mid i\in M\right\} \) satisfies both internal stability (i.e., condition (IS) in Definition 2) and external stability (i.e., condition (ES) in Definition 2).
IS Farsighted players are peripherals in all networks in \(G^{*} \) so that they always obtain the same payoff: \(U_{i}(g)=b(1)+(n-2)b(2)-c\) for all \(i\in F\), \(g\in G^{*}\). Myopic players who are peripherals have no incentive to delete their single link (\(b(1)+(n-2)b(2)-c>0\)) or to add a new link (\(2b(1)+(n-3)b(2)-2c<b(1)+(n-2)b(2)-c\) since \(b(1)-b(2)<c\)). The center who is myopic has no incentive to delete one link since \(c<b(1)\). Hence, for every \(g,g^{\prime }\in G^{*}\), it holds that \(g^{\prime }\notin \phi (g)\).
ES Take any network \(g\notin G^{*}\). We build in steps a myopic-farsighted improving path from g to some \(g^{*i}\in G^{*}\).
Step 1: Starting in g, farsighted players delete all their links successively looking forward to some \(g^{*i}\in G^{*}\), where they obtain their highest possible payoff given \(b(1)-b(2)<c\). Notice that if g is a star network where the center is a farsighted player, then the center starts by deleting all her links since only the center is better off in \( g^{*i}\) compared to g (and we go directly to Step 8). We reach a network \(g^{1}\) where all farsighted players have no link and myopic players only keep the links to myopic players they had in g.
Step 2: From \(g^{1}\), looking forward to \(g^{*i}\in G^{*}\), farsighted players build a star network \(g^{*jF}\) restricted to farsighted players with player j being the center (i.e., \(g^{*jF}\) is such that \(j\in F\), \(N_{j}(g^{*jF})=F\setminus \left\{ j\right\} \) and \( N_{k}(g^{*jF})=\left\{ j\right\} \) for all \(k\in F\setminus \left\{ j\right\} \)), and we obtain \(g^{2}=g^{1}\cup g^{*jF}\) where all farsighted players are still disconnected from the myopic ones.
Step 3: From \(g^{2}\), looking forward to \(g^{*i}\in G^{*}\), the farsighted player j who is the center of \(g^{*jF}\) adds a link to some myopic player, say player 1. Player j is better off in \(g^{*i}\) compared to \(g^{2}\), \(b(1)+(n-2)b(2)-c>(n-m-1)(b(1)-c)\), while player 1 is better in \(g^{2}+j1\) since \(b(1)>c\).
Step 4: From \(g^{2}+j1\), looking forward to \(g^{*i}\in G^{*} \), the farsighted player j adds a link successively to the myopic players who are neighbors of player 1 (if any), say player 2. Player 2 who is myopic and linked to player 1 has an incentive to add the link j2 if and only if \(b(2)+(n-m-1)b(3)<b(1)-c+(n-m-1)b(2)\). Thus, the necessary and sufficient condition for adding the link is
Since \(c<b(1)\), a sufficient condition is
where \(n-m\) is the number of farsighted players (\(\#F\)). In \( g^{2}+j1+\left\{ jl\mid l\in N_{1}(g^{2}+j1)\right. \left. \cap M\right\} \), player j is (directly) linked to all other farsighted players, player 1 and all neighbors of player 1.
Step 5: From \(g^{2}+j1+\left\{ jl\mid l\in N_{1}(g^{2}+j1)\cap M\right\} \), the myopic players who are neighbors of player 1 and have just added a link to the farsighted player j delete their link successively with player 1. They have incentives to do so since \( b(1)-b(2)<c<b(1)\) and we reach \(g^{2}+j1+\left\{ jl\mid l\in N_{1}(g^{2}+j1)\cap M\right\} -\left\{ 1l\mid l\in N_{1}(g^{2}+j1)\cap M\right\} \).
Step 6: Next, looking forward to \(g^{*i}\in G^{*}\), the farsighted player j adds a link successively to the myopic players who are neighbors of some \(l\in N_{1}(g^{2}+j1)\cap M\) and we proceed as in Step 4 and Step 5. We repeat this process until we reach a network \(g^{3}\) where there is no myopic player linked directly to the myopic neighbors of player j (i.e. \(N_{k}(g^{3})\cap M=\emptyset \) for all \(k\in N_{j}(g^{3})\cap M\)).
Step 7: From \(g^{3}\), player j adds a link to some myopic player belonging to another component (if any) as in Step 3 and we proceed as in Step 4 to Step 6. We repeat this process until we end up with a star network \(g^{*j}\) with player j (who is farsighted) in the center (i.e., \( N_{j}(g^{*j})=N\setminus \left\{ j\right\} \) and \(N_{k}(g^{*j})=\left\{ j\right\} \) for all \(k\in N\setminus \left\{ j\right\} \)).
Step 8: From \(g^{*j}\), looking forward to \(g^{*i}\in G^{*}\), the farsighted player j deletes all her links successively to reach the empty network \(g^{\emptyset }\). From \(g^{\emptyset }\), myopic and farsighted players have both incentives (since \(b(1)>c\)) to add links successively to build the star network \(g^{*i}\in G^{*}\) where some myopic player \(i\in M\) is the center.
Uniqueness We now show that \(G^{*}\) is the unique myopic-farsighted stable set. Farsighted players who are peripherals in all networks in \(G^{*}\) obtain their highest possible payoff. Myopic players who are peripherals have no incentive to delete their single link or to add a new link. The center who is myopic has no incentive to delete one link. Hence, \(\phi (g)=\emptyset \) for every \(g\in G^{*}\). Suppose that \(G\ne G^{*}\) is another myopic-farsighted stable set. (1) G does not include \(G^{*}\): \(G\nsupseteq G^{*}\). External stability would be violated since \(\phi (g)=\emptyset \) for every \(g\in G^{*}\). (2) G includes \( G^{*}\): \(G\varsupsetneq G^{*}\). Internal stability would be violated since for every \(g\in \mathcal {G}\setminus G^{*}\), it holds that \(\phi (g)\cap G^{*}\ne \emptyset \). \(\square \)
In fact, the set \(G^{*}\) satisfies a stronger external stability requirement: for every \(g\in \mathcal {G}\setminus G^{*}\), it holds that \( \phi (g)\supseteq G^{*}\). The internal stability condition is satisfied for \(G^{*}\) even when \(\#F<1+b(2)/(b(2)-b(3))\).Footnote 16
If \(b(1){-}b(2){<}c{<}b(1){-}b(3)\), then the sufficient condition for having external stability becomes \(b(1)-b(3)\le b(1)-b(2){+}(n{-}m{-}1)(b(2){-}b(3))\) or \(2\le n{-}m\). Thus, once linking costs are intermediate but not so high, it suffices to have two farsighted players to guarantee that only efficient networks are going to emerge in the long run.
Corollary 2
Consider the distance-based utility model in the case \(b(1)-b(2)<c<b(1)-b(3)\) . If \(n>\#F\ge 2\) then the set \(G^{*}=\left\{ g^{*i}\mid i\in M\right\} \) is the unique myopic-farsighted stable set.
What happens if \(\#F<1+b(2)/(b(2)-b(3))\) and (1) is not satisfied? If a myopic-farsighted stable set exists then \(G^{*}\) should be included in it. Otherwise, external stability would be violated since \(\phi (g)=\emptyset \) for all \(g\in G^{*}\).
Corollary 3
Consider the distance-based utility model in the case \(b(1)-b(2)<c<b(1)\). If \(1\le \#M\le 3\), then the set \(G^{*}=\left\{ g^{*i}\mid i\in M\right\} \) is the unique myopic-farsighted stable set.
Notice that in a society with only three players, a star network is the unique pairwise stable network. Hence, if the population is mixed but the number of myopic players is less or equal than 3, then our main result holds without any condition on the number of farsighted players: the set consisting of all star networks where the center of the star is a myopic player is the unique myopic-farsighted stable set. But, what happens if the population consists of only farsighted players?
Proposition 9
Consider the distance-based utility model in the case \(b(1)-b(2)<c<b(1)\). Suppose that all players are farsighted, \(N=F\). If g is a star network then \(\left\{ g\right\} \) is a myopic-farsighted stable set.
Proof
Since each set is a singleton set, internal stability (IS) is satisfied. (ES) Take any network \(g\ne g^{*i}\), we need to show that \(\phi (g)\ni g^{*i}\). (i) Suppose \(g\ne g^{*j}\) (\(j\ne i\)). From g, looking forward to \(g^{*i}\) (where they obtain their highest possible payoff), farsighted players (\(\ne i\)) delete all their links successively to reach the empty network. From \( g^{\emptyset }\), farsighted players have incentives (since \(b(1)>c\)) to add links successively to build the star network \(g^{*i}\) with player i in the center. (ii) Suppose \(g=g^{*j}\) (\(j\ne i\)). From g, looking forward to \(g^{*i}\), the farsighted player j deletes all her links successively to reach the empty network. From \(g^{\emptyset }\), farsighted players have incentives (since \(b(1)>c\)) to add links successively to build the star network \(g^{*i}\) with player i in the center.\(\square \)
Once all players become farsighted (i.e., \(N=F\)), for \(b(1)-b(2)<c<b(1)\), every set consisting of a star network encompassing all players is a myopic-farsighted stable set, but they are not necessarily the unique myopic-farsighted stable sets. For instance, when \(n=4\), the set of circles among the four farsighted players can be a myopic-farsighted stable set.Footnote 17
Example 2
Take \(N=F=\left\{ 1,2,3,4\right\} \) and \(b(1)-b(2)<c<b(1)-b(3)<b(1)\) in the distance-based utility model. Let \(G^{c,4}=\{\{12,23,34,14\},\{13,12,34,24 \},\{13,14,23,24\}\}\) be the set of circles among the four farsighted players. The set \(G^{c,4}\) is a myopic-farsighted stable set. It satisfies ( IS) since the four players obtain the same payoffs in all circle networks. We now show that (ES) is satisfied: for every \(g\notin G^{c,4}\), it holds that \(\phi (g)\cap G^{c,4}\ne \emptyset \). (i) Take any g such that there is \(g^{\prime }\in G^{c,4}\) and \(g\varsubsetneq g^{\prime }\). In g, looking forward to \(g^{\prime }\), players have incentives to add links successively to form \(g^{\prime }\) since \( c<b(1)-b(3) \), and so \(g^{\prime }\in \phi (g)\). (ii) Take any \(g^{S}\) such that \(\#S=3\). Players belonging to S have two links and are better off in any circle network \(g^{\prime }\in G^{c,4}\) than in \(g^{S}\): \( 2b(1)-2c<2b(1)-2c+b(2)\). Hence, from \(g^{S}\), looking forward to some circle network \(g^{\prime }\), some player deletes one of her links and we reach a network belonging to case (i) from which players have incentives to add links successively to form some circle network \(g^{\prime }\), and so \( g^{\prime }\in \phi (g^{S})\). (iii) Take any g such that at least one player has three links. Any star network \(g^{*i}\) is one of such network. Players who have three links are better off in any circle network \( g^{\prime }\) than in g: \(3b(1)-3c<2b(1)-2c+b(2)\) or \(b(1)-b(2)<c\). Hence, from g, looking forward to some circle network \(g^{\prime }\), players who have three links successively delete one of their links and we reach either a circle network or a network belonging to case (i) or case (ii) from which players have incentives to add links successively to form some circle network \(g^{\prime } \), and so \(g^{\prime }\in \phi (g)\).
We have focused on the range of costs and benefits such that a star network is the unique strongly efficient network. In the case of small (very large) link costs relative to benefits, there is no conflict between stability and efficiency. The set consisting of the complete (empty) network is the unique myopic-farsighted stable set whatever the mixture of myopic and farsighted individuals.Footnote 18
Remark 1
Consider the distance-based utility model in the case \(c<b(1)-b(2)\). The set \(\left\{ g^{N}\right\} \) is the unique myopic-farsighted stable set.
Suppose now that player i’s distance-based utility from a network g is given by \(U_{i}(g)={\textstyle \sum }_{j\ne i}b_{i}(t(ij))-d_{i}(g)c_{i}\) where \( c_{i}\ge 0\) and \(b_{i}\) is a nonincreasing function. Assume that \( b_{i}(1)-b_{i}(2)<c_{i}<b_{i}(1)\) for all \(i\in N\). If \(n>\#F\) and \(\#F\ge 1+b_{i}(2)/(b_{i}(2)-b_{i}(3))\) for all \(i\in M\), then the set \(G^{*}=\left\{ g^{*i}\mid i\in M\right\} \) is the unique myopic-farsighted stable set, and Proposition 8 still holds. However, such asymmetries in benefits and costs would imply that a conflict between stability and efficiency could again arise. For instance, the efficient network might even lie outside the set \(G^{*}\) if it is a star network with some farsighted player in the center. Transfers might then be a solution for avoiding any conflict.Footnote 19
4 Degree-based utility
Another common utility function in network formation is one where a player’s payoff from a link is a decreasing function of the number of links the other players maintain.Footnote 20 Degree-based utility functions exhibit negative externalities. If player i is linked to player j, then player i receives a benefit of \(\beta (d_{j}) \) from her link with player j. It is assumed that \(\beta (d_{j})\) is decreasing with \(d_{j}\), i.e., \(\beta (d_{j})>\beta (d_{j}+1)>0\) for any \( d_{j}\). Each direct link \(ij\in g\) results in a cost c to both i and j for maintaining this direct link. As in Morrill (2011), player i’s degree-based utility or payoff from a network g is given by
where \(d_{i}\) is player i’s degree, \(d_{j}\) is player j’s degree, \(c\ge 0\) is a cost per link, and \(\beta \) is a decreasing function. A special case of degree-based utility function is Morrill’s co-author model where \(\beta (d_{j})=\gamma ^{d_{j}}\) with \(0<\gamma <1\).Footnote 21 We assume as in Morrill (2011) that \(c\ne \beta (d)\) for any \(d\in \mathbb {N} \) and we let \(\overline{d}\) be such that \(\beta (\overline{d}+1)<c<\beta ( \overline{d})\).
To simplify the analysis, we focus on the case where the population consists of an even number of myopic players (\(m\ge 0\) is even) and an even number of farsighted players (\(n-m\ge 0\) is even). Morrill (2011) shows that a network g is strongly efficient if and only if for every player i, \( d_{i}\in \arg \max x(\beta (x)-c)\). It follows that, for any \(d\in \arg \max x(\beta (x)-c)\), all d-regular networks are strongly efficient. When all players are myopic, there is often a conflict between efficiency and stability for degree-based utility functions. For instance, take \(\beta (d_{j})=(1/2)^{d_{j}}\), \(n=10\), \(0<c<(1/2)^{9}\). Then, \(\overline{d}\ge 9\) and \(\arg \max x(\beta (x)-c)=1\). Hence, the strongly efficient networks are regular ones where every player has exactly one link. However, myopic players may have a tendency to form overconnected networks: the complete network is pairwise stable. Morrill (2011) shows that, although the strongly efficient and stable networks diverge in general, they coincide when players are able to make transfers to their partners.
What happens when myopic players coexist with farsighted ones? Could we stabilize the strongly efficient networks without transfers when the population is mixed?
Proposition 10
Consider the degree-based utility model with an even number of myopic players and an even number of farsighted players. Suppose \(d^{*}=\arg \max x(\beta (x)-c)\),Footnote 22\(m-1>d^{*}\), \(n-m>d^{*}\), \(\overline{d}\ge n-1\) and \( m\beta (m)+(x-m)\beta (x)-xc<d^{*}(\beta (d^{*})-c)\) for \( x=m+1,\ldots ,n-1\). If \(g^{s}\in G^{s}=\{g\in \mathcal {G}\mid d_{j}(g)=m-1\) if \( j\in M\), \(d_{i}(g)=d^{*}\) if \(i\in F\) and \(N_{j}(g)\cap F=\emptyset \) if \(j\in M\}\) then \(\left\{ g^{s}\right\} \) is a myopic-farsighted stable set.
Proof
We show that each \(\left\{ g^{s}\right\} \) such that \(g^{s}\in G^{s}\) satisfies both internal stability (i.e., condition (IS) in Definition 2) and external stability (i.e. condition (ES) in Definition 2). Since \(d^{*}=\arg \max x(\beta (x)-c)\), a network \(g^{e}\) is strongly efficient if and only if it is a \(d^{*}\) -regular network. We have \(U_{i}(g^{e})=U_{i}(g^{s})=d^{*}(\beta (d^{*})-c)\) for all \(i\in F\).
IS. Since each set \(\{g^{s}\}\), \(g^{s}\in G^{s}\), is a singleton set, internal stability (IS) is satisfied.
ES. Take any network \(g^{s}\in G^{s}\). Take any \(g\ne g^{s}\). We build in steps a myopic-farsighted improving path from g to \(g^{s}\). Let \( I(g)=\{i\in N\mid d_{i}(g)=d^{*}\) and \(d_{j}(g)=d^{*}\) for all \(j\in N_{i}(g)\}\) be the set of players who have \(d^{*}\) links in g and their neighbors have \(d^{*}\) links too.
1. Since \(\overline{d}\ge n-1\), we have that \(\beta (x)-c\) is positive for all \(x\le n-1\). Hence, myopic players have always incentives to form additional links. Starting from g, myopic players form successively the missing links between them to reach a network \(g^{\prime }\) where \(g^{M}\subseteq g^{\prime }\) (remember that \(g^{M}\) is the complete network on the set of myopic players M). Notice that \(d_{j}\ge m-1>d^{*}\) for all \(j\in M\).
2. Step (2.1) Take any farsighted player \(i\in F\) such that \(N_{i}(g^{\prime })\subseteq M\). That is, player i has only links with myopic players. Since \(U_{i}(g^{\prime })\le m(\beta (m)-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\), player i who looks forward toward \( g^{s}\) has incentives to cut successively her links with the myopic players. Player i becomes an isolated player. We proceed similarly with all other farsighted players who are only linked to myopic players. We end up with \( g^{\prime \prime }\). Step (2.2) Take any \(i\in F\) such that \( d_{i}(g^{\prime \prime })=1\) and \(i\notin I(g^{\prime \prime })\). We do have \(U_{i}(g^{\prime \prime })<U_{i}(g^{s})=U_{i}(g^{e})\). Player i (looking forward toward \(g^{s}\)) cuts her link to her neighbor j and we move back to step 2.1 with \(g^{\prime \prime }-ij\) replacing \(g^{\prime }\). If there is no \(i\in F\) such that \(d_{i}(g^{\prime \prime })=1\) and \(i\notin I(g^{\prime \prime })\), we move to step 2.3. Step (2.3) Take any \( i\in F\) such that \(d_{i}(g^{\prime \prime })=2\) and \(i\notin I(g^{\prime \prime })\). Player i gets at most \((\beta (m)-c)\) from her link with a myopic player and at most \(d_{i}(\beta (d_{i})-c)\) from her links with the farsighted players since all farsighted players \(j\in N_{i}(g^{\prime \prime })\cap F\) have \(d_{j}\ge d_{i}\). Since \(d_{i}\le m\) (\(m\ge 2\)) we have that all players \(j\in N_{i}(g^{\prime \prime })\) have \(d_{j}\ge d_{i}\), and so \(U_{i}(g^{\prime \prime })\le d_{i}(\beta (d_{i})-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\). Player i (looking forward toward \(g^{s}\)) cuts successively her links to j and k to obtain \(g^{\prime \prime }-ij-ik\) and we move back to step 2.1 with \(g^{\prime \prime }-ij-ik\) replacing \(g^{\prime }\). Her payoff along the sequence decreases. Hence, we do have \(U_{i}(g^{\prime \prime })<U_{i}(g^{s})=U_{i}(g^{e})\), \( U_{i}(g^{\prime \prime }-ij)<U_{i}(g^{s})=U_{i}(g^{e})\) and \(U_{i}(g^{\prime \prime }-ij-ik)<U_{i}(g^{s})=U_{i}(g^{e})\). If there is no \(i\in F\) such that \(d_{i}(g^{\prime \prime })=2\) and \(i\notin I(g^{\prime \prime })\), we move to step 2.4. Step (2.4) Take any \(i\in F\) such that \( d_{i}(g^{\prime \prime })=3\) and \(i\notin I(g^{\prime \prime })\). Player i gets at most \(2(\beta (m)-c)\) from her links with myopic players and at most \(d_{i}(\beta (d_{i})-c)\) from her links with the farsighted players since all players \(j\in N_{i}(g^{\prime \prime })\cap F\) have \(d_{j}\ge d_{i}\). If \(d_{i}\le m\) then \(U_{i}(g^{\prime \prime })\le d_{i}(\beta (d_{i})-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\) since all players \( j\in N_{i}(g^{\prime \prime })\) have \(d_{j}\ge d_{i}\). If \(d_{i}\ge m+1\) then the condition, \(m\beta (m)+(x-m)\beta (x)-xc<d^{*}(\beta (d^{*})-c)\) for \(x=m+1,\ldots ,n-1\),Footnote 23 guarantees that \(U_{i}(g^{\prime \prime })<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\). Player i (looking forward toward \(g^{s}\)) cuts successively her links to j, k and l to obtain \(g^{\prime \prime }-ij-ik-il\) and we move back to step 2.1 with \(g^{\prime \prime }-ij-ik-il\) replacing \(g^{\prime }\). Her payoff along the sequence decreases. If there is no \(i\in F\) such that \(d_{i}(g^{\prime \prime })=3\) and \(i\notin I(g^{\prime \prime })\), we move to step 2.5. ...If there is no \(i\in F\) such that \(d_{i}(g^{\prime \prime })=q-1\) and \(i\notin I(g^{\prime \prime })\) , we move to step 2.q. Step (2.q) Take any \(i\in F\) such that \(d_{i}(g^{\prime \prime })=q-1\) and \(i\notin I(g^{\prime \prime })\) . Player i gets at most \((q-2)(\beta (m)-c)\) from her links with myopic players and at most \(d_{i}(\beta (d_{i})-c)\) from her links with the farsighted players since all players \(j\in N_{i}(g^{\prime \prime })\cap F\) have \(d_{j}\ge d_{i}\). If \(d_{i}\le m\) then \(U_{i}(g^{\prime \prime })\le d_{i}(\beta (d_{i})-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\) since all players \(j\in N_{i}(g^{\prime \prime })\) have \(d_{j}\ge d_{i}\). If \( d_{i}\ge m+1\) then the condition, \(m\beta (m)+(x-m)\beta (x)-xc<d^{*}(\beta (d^{*})-c)\) for \(x=m+1,\ldots ,n-1\), guarantees that \( U_{i}(g^{\prime \prime })<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\). Player i (looking forward toward \(g^{s}\)) cuts successively her links to her neighbors to obtain \(g^{\prime \prime }\setminus \left\{ ij\mid j\in N_{i}(g^{\prime \prime })\right\} \) and we move back to step 2.1 with \( g^{\prime \prime }\setminus \left\{ ij\mid j\in N_{i}(g^{\prime \prime })\right\} \) replacing \(g^{\prime }\). Her payoff along the sequence decreases. If there is no \(i\in F\) such that \(d_{i}(g^{\prime \prime })=q-1\) and \(i\notin I(g^{\prime \prime })\), we move to step 2.\(q+1\). ...If there is no \(i\in F\) such that \(d_{i}(g^{\prime \prime })=n-2\) and \(i\notin I(g^{\prime \prime })\), we move to step 2.n. Step (2.n) Take any \(i\in F\) such that \(d_{i}(g^{\prime \prime })=n-1\) and \(i\notin I(g^{\prime \prime })\). Player i gets \((n-1)(\beta (n-1)-c)\) from her links. Since \(d^{*}<n-1\), we have that \(U_{i}(g^{\prime \prime })=(n-1)(\beta (n-1)-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\). Player i (looking forward toward \(g^{s}\)) cuts successively her links to her neighbors to obtain \(g^{\prime \prime }\setminus \left\{ ij\mid j\in N_{i}(g^{\prime \prime })\right\} \) and we move back to step 2.1 with \( g^{\prime \prime }\setminus \left\{ ij\mid j\in N_{i}(g^{\prime \prime })\right\} \) replacing \(g^{\prime }\). If there is no \(i\in F\) such that \( d_{i}(g^{\prime \prime })=n-1\) and \(i\notin I(g^{\prime \prime })\), then the process ends. Since n is finite this process stops after a finite number of steps. At the end of the process we reach a network \(g^{\prime \prime \prime }\) where every farsighted player \(i\in F\) is either isolated (i.e., \( d_{i}=0\)) or she has exactly \(d^{*}\) links and her neighbors are farsighted and have \(d^{*}\) links too (i.e., \(d_{j}=d^{*}\) for all \( j\in N_{i}(g^{\prime \prime \prime })\subseteq F\) and \( U_{i}(g^{e})=U_{i}(g^{\prime \prime \prime })=U_{i}(g^{s})\)) and every myopic player has exactly \(m-1\) links.
3. Start with \(g^{\prime \prime \prime }\). Take any farsighted player i such that \(d_{i}=d^{*}\) (if there is no such player, then go directly to 5). Player i looking forward to \(g^{s}\) (i is indifferent between her current payoff and the end payoff at \(g^{s}\)) builds a link with some myopic player j to form \(g^{\prime \prime \prime }+ij\). In \(g^{\prime \prime \prime }+ij\), we have \(U_{k}(g^{s})=U_{k}(g^{\prime \prime \prime })>U_{k}(g^{\prime \prime \prime }+ij)\) for all \(k\in N_{i}(g^{\prime \prime \prime })\). Next one farsighted player \(k\in N_{i}(g^{\prime \prime \prime })\) cuts her link with player i to form \( g^{\prime \prime \prime }+ij-ik\) looking forward to \(g^{s}\). Next player i who is farsighted cuts successively all her links, with her link ij being the last one to be deleted. We reach the network \(g^{\prime \prime \prime }\setminus \left\{ ij\mid j\in N_{i}(g^{\prime \prime \prime })\right\} \) where player i is isolated. Notice that \(U_{i}(g^{\prime \prime \prime }+ij)>U_{i}(g^{s})=d^{*}(\beta (d^{*})-c)>U_{i}(g^{\prime \prime \prime }+ij-ik)\) since \(d_{j}(g^{\prime \prime \prime }+ij-ik)\ge m>d^{*}=d_{i}(g^{\prime \prime \prime }+ij-ik)\), \(d_{l}(g^{\prime \prime \prime }+ij-ik)=d^{*}\) for all \(l\in N_{i}(g^{\prime \prime \prime }+ij-ik)\), \( l\ne k\), and \(d_{k}(g^{\prime \prime \prime }+ij-ik)=d^{*}-1\).
4. We repeat the process from 2 with \(g^{\prime \prime \prime }\setminus \left\{ ij\mid j\in N_{i}(g^{\prime \prime \prime })\right\} \) replacing \(g^{\prime }\) until we reach the network \(g^{M}\) where all farsighted players are isolated (\(d_{i}=0\) for all \(i\in F\)) and all myopic players have \(m-1\) links.
5. From the network \(g^{M}\), we build a sequence of networks \( g_{1},g_{2},\ldots ,g_{K}\) such that \(g_{1}=g^{M}\), \(g_{K}=g^{s}\) and \( \left| \#N_{i}(g_{k})-\#N_{j}(g_{k})\right| \le 1\), \(k=1,\ldots ,K\), for all \(i,j\in N(h)\), \(h\in H(g^{s})\) and h is \(d^{*}\)-regular. It guarantees that along such a sequence, farsighted players who look forward toward \(g^{s}\) do have incentives to build those links to form such \(g^{s}\) . Hence, \(\left\{ g^{s}\right\} \) satisfies (ES). \(\square \)
Proposition 10 tells us that once we have enough farsighted players in the population, myopic and farsighted players may end up segregated with overconnected myopic players and farsighted players who obtain the socially optimal payoff. The next example illustrates Proposition 10.
Example 3
Take the degree-based utility model with \(\beta (d_{j})=(1/2)^{d_{j}}\), \( 0<c<(1/2)^{9}\), \(M=\{1,2,3,4,5,6\}\) and \(F=\{7,8,9,10\}\). Thus, \(m=6\), \( n-m=4 \), and we have \(d^{*}=1\) and \(\overline{d}\ge 9\). Notice that the condition \(m\beta (m)+(x-m)\beta (x)-xc=6(1/2)^{6}+(x-6)(1/2)^{x}-xc<d^{*}(\beta (d^{*})-c)=(1/2)-c\) is clearly satisfied for \(x=7,8,9\). From Proposition 10, the singleton set \(\left\{ g\right\} \) is a myopic-farsighted stable set if the network g is such that (i) there are no links between farsighted and myopic players, (ii) every myopic player is linked to all other myopic players, and (iii) farsighted players form regular components where each farsighted player has exactly \(d^{*}\) links. Figure 2 illustrates such a network where the six myopic players and the four farsighted players are fully segregated with myopic players being overconnected (all of them have five links) and farsighted players having exactly one link.
When the cost for maintaining links increases, myopic players may stop having incentives to build links to all other players, i.e. \(\overline{d}\) becomes lower than \(n-1\). As a result, the path from some inefficient network \(g\notin G^{s}\) to some network \(g^{\prime }\in G^{s}\) becomes more tedious. For instance, suppose \(\beta (d_{j})=(3/5)^{d_{j}}\), \(c=1/5\), \( M=\{1,2,3,4\}\) and \(F=\{5,6\}\). Thus, \(m=4\), \(n-m=2\), and we have \(d^{*}=1\) and \(\overline{d}=3\). Take the network \(\{16,56,23,24,26,34,35,45\}\) depicted in Fig. 3. Player 1 who is myopic has no incentives to link to one of the other myopic players since they have exactly three links. Player 6 who is farsighted obtains more than the socially optimal payoff: \( (3/5)+2(3/5)^{3}-3c>(3/5)-c=U_{6}(g^{s})\). However, the other farsighted player, who has also three links, is worse off than at \(g^{s}\): \( 3(3/5)^{3}-3c<3/5-c=U_{5}(g^{s})\). Player 5 then cuts successively all her links and becomes isolated. Next player 1 has now incentives to link successively with players 3 and 4. We reach the network \( \{16,13,14,23,24,26,34\}\). Now player 6’s current payoff is equal to \( 2(3/5)^{3}-2c<3/5-c\). Hence, player 6 cuts successively all her links and becomes isolated. Next player 1 adds a link to player 2. Finally, player 5 builds a link to player 6 and we reach the network \( \{12,13,14,23,24,34,56\}\in G^{s}\).
Let \(G^{SYM}{=}\left\{ g\in \mathcal {G}\mid d_{i}(g){=}d_{j}(g)\text { for all } i,j\in F\text {, }d_{k}(g){=}d_{l}(g)\text { for all }l,k\in M\right\} \) be the set of symmetric networks where all myopic players have the same number of links and all farsighted players have the same number of links. Notice that \( d_{i}(g)\) might be different than \(d_{k}(g)\) for \(i\in F\), \(k\in M\). Since \( \phi (g^{s})\cap G^{SYM}=\emptyset \) for all \(g^{s}\in G^{s}\), any set \( \{g\} \) with \(g\in G^{SYM}\setminus G^{s}\) violates (ES) and cannot be a myopic-farsighted stable set. Hence, all \(g^{s}\in G^{s}\) are the only symmetric networks that can emerge in the long run as singleton myopic-farsighted stable sets.
Remark 2
Consider the degree-based utility model with an even number of myopic players and an even number of farsighted players. Suppose \(d^{*}=\arg \max x(\beta (x)-c)\), \(m-1>d^{*}\), \(n-m>d^{*}\), \(\overline{d}\ge n-1 \) and \(m\beta (m)+(x-m)\beta (x)-xc<d^{*}(\beta (d^{*})-c)\) for \( x=m+1,\ldots ,n-1\). If \(g\in G^{SYM}\setminus G^{s}\), then \(\left\{ g\right\} \) is not a myopic-farsighted stable set.
Remember that, when n is even, the set of \(d^{*}\)-regular networks \( G^{d^{*}}=\{g\in \mathcal {G}\mid d_{i}(g)=d^{*}\) for all \(i\in N\}\) is the set of strongly efficient networks E, and \(g^{e}\) denotes some strongly efficient network. Once all players are farsighted, the set \( G^{d^{*}}\) consisting of all strongly efficient networks is a myopic-farsighted stable set.
Proposition 11
Consider the degree-based utility model with an even number of players. Suppose all players are farsighted, \(N=F\), and \(d^{*}=\arg \max x(\beta (x)-c)\). The set \(G^{d^{*}}=\left\{ g\in \mathcal {G}\mid d_{i}(g)=d^{*}\text { for all }i\in N\right\} \) is a myopic-farsighted stable set.
Proof
We show that \(G^{d^{*}}=\left\{ g\in \mathcal {G}\mid d_{i}(g)=d^{*} \text { for all }i\in N\right\} \) satisfies both internal stability (i.e., condition (IS) in Definition 2) and external stability (i.e., condition (ES) in Definition 2). Since \(d^{*}=\arg \max x(\beta (x)-c)\), a network \(g^{e}\) is strongly efficient if and only if \(g^{e}\) is a \(d^{*}\)-regular network. So, \(G^{d^{*}}\) is the set of strongly efficient networks. Take any network \(g\notin G^{d^{*}}\) . There is always some player i such that \(U_{i}(g^{e})>U_{i}(g)\).
IS. Players obtain the same payoff in all networks in \(G^{d^{*}} \): \(U_{i}(g)=d^{*}(\beta (d^{*})-c)\) for all \(i\in N\), \(g\in G^{d^{*}}\). Hence, for every \(g,g^{\prime }\in G^{d^{*}}\), it holds that \(g^{\prime }\notin \phi (g)\).
ES. Take any network \(g\notin G^{d^{*}}\). We build in steps a myopic-farsighted improving path from g to some \(g^{e}\in G^{d^{*}}\). Remember that \(I(g)=\{i\in N\mid d_{i}(g)=d^{*}\) and \(d_{j}(g)=d^{*}\) for all \(j\in N_{i}(g)\}\).
1. Step (1.1) Take any \(i\in F\) such that \( d_{i}(g)=1\) and \(i\notin I(g)\). We do have \(U_{i}(g)<U_{i}(g^{e})\). Player i (looking forward toward \(g^{e}\)) cuts her link to her neighbor j and we move back to step 1.1 with \(g-ij\) replacing g. If there is no \(i\in F\) such that \(d_{i}(g)=1\) and \(i\notin I(g)\), we move to step 1.2. Step (1.2) Take any \(i\in F\) such that \(d_{i}(g)=2\) and \(i\notin I(g)\). Player i (looking forward toward \(g^{e}\)) cuts successively her links to j and k to obtain \(g-ij-ik\) and we move back to step 1.1 with \(g-ij-ik\) replacing g. In the sequence, player i first cuts all her links with players such that \(d_{j}\le \overline{d}\) (if any such j). It guarantees that her payoff along the sequence decreases or is negative. Hence, we do have \(U_{i}(g)<U_{i}(g^{e})\), \(U_{i}(g-ij)<U_{i}(g^{e})\) and \( U_{i}(g-ij-ik)<U_{i}(g^{e})\). Notice that \(U_{i}(g)\le d_{i}(\beta (d_{i})-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\) since all players \( j\in N_{i}(g)\) have \(d_{j}\ge d_{i}\). If there is no \(i\in F\) such that \( d_{i}(g)=2\) and \(i\notin I(g)\), we move to step 1.3. Step (1.3) Take any \(i\in F\) such that \(d_{i}(g)=3\) and \(i\notin I(g)\). Player i (looking forward toward \(g^{e}\)) cuts successively her links to j, k and l to obtain \(g-ij-ik-il\) and we move back to step 1.1 with \(g-ij-ik-il\) replacing g. In the sequence, player i first cuts all her links with players such that \(d_{j}\le \overline{d}\) (if any such j). It guarantees that her payoff along the sequence decreases or is negative. Notice that \( U_{i}(g)\le d_{i}(\beta (d_{i})-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\) since all players \(j\in N_{i}(g)\) have \(d_{j}\ge d_{i}\) . If there is no \(i\in F\) such that \(d_{i}(g)=3\) and \(i\notin I(g)\), we move to step 1.4. ...If there is no \(i\in F\) such that \(d_{i}(g)=q-1\) and \( i\notin I(g)\), we move to step 1.q. Step (1.q) Take any \(i\in F\) such that \(d_{i}(g)=q\) and \(i\notin I(g)\). Player i (looking forward toward \(g^{e}\)) cuts successively her links to her neighbors to obtain \(g\setminus \left\{ ij\mid j\in N_{i}(g)\right\} \) and we move back to step 1.1 with \(g\setminus \left\{ ij\mid j\in N_{i}(g)\right\} \) replacing g. In the sequence, player i first cuts all her links with players such that \(d_{j}\le \overline{d}\) (if any such j). It guarantees that her payoff along the sequence decreases or is negative. Notice that \( U_{i}(g)\le d_{i}(\beta (d_{i})-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\) since all players \(j\in N_{i}(g)\) have \(d_{j}\ge d_{i}\) . If there is no \(i\in F\) such that \(d_{i}(g)=q\) and \(i\notin I(g)\), we move to step 1.\(q+1\). ...If there is no \(i\in F\) such that \(d_{i}(g)=n-2\) and \( i\notin I(g)\) we move to step 1.\(n-1\). Step (\(1.n - 1\)) Take any \(i\in F\) such that \(d_{i}(g)=n-1\) and \(i\notin I(g)\). Notice that \( U_{i}(g)=(n-1)(\beta (n-1)-c)<d^{*}(\beta (d^{*})-c)=U_{i}(g^{e})\) since all players \(j\in N_{i}(g)\) have \(d_{j}=n-1\) and \(i\notin I(g)\). Player i (looking forward toward \(g^{e}\)) cuts successively her links to her neighbors to obtain \(g\setminus \left\{ ij\mid j\in N_{i}(g)\right\} \) and we move back to step 1.1 with \(g\setminus \left\{ ij\mid j\in N_{i}(g)\right\} \) replacing g. If there is no \(i\in F\) such that \( d_{i}(g)=n-1\) and \(i\notin I(g)\), then the process ends. Since n is finite this process stops after a finite number of steps. At the end of the process we reach a network \(g^{\prime }\) where every farsighted player \(i\in F\) is either isolated (i.e., \(d_{i}=0\)) or she has exactly \(d^{*}\) links and her neighbors too (i.e., \(d_{j}=d^{*}\) for all \(j\in N_{i}(g)\) and \( U_{i}(g^{e})=U_{i}(g^{\prime })\)).
2. (2a) \(d^{*}=1\). At \(g^{\prime }\), there is an even number of players who have just one link, so both \(\#N(g^{\prime })\) and \( n-\#N(g^{\prime })\) are even numbers. From \(g^{\prime }\), every player who has no links builds exactly one link to another player who has no links and we reach some \(g^{e}\in G^{d^{*}}\). (2b) \(d^{*}\ne 1\). (i) At \(g^{\prime }\), some isolated player i (i.e., \(d_{i}(g^{\prime })=0\)) forms a link with some player j who has \(d^{*}\) links looking forward to some \(g^{e}\in G^{d^{*}}\). Player i strictly prefers the end network \(g^{e}\) while player j is indifferent: \(U_{i}(g^{e})>U_{i}(g^{ \prime })=U_{i}(g^{\emptyset })\) and \(U_{j}(g^{e})=U_{j}(g^{\prime })=d^{*}(\beta (d^{*})-c)\). In \(g^{\prime }+ij\), we have \( U_{i}(g^{e})>U_{i}(g^{\prime }+ij)>U_{i}(g^{\prime })\) and \( U_{k}(g^{e})=U_{k}(g^{\prime })>U_{k}(g^{\prime }+ij)\) for all \(k\in N_{j}(g^{\prime })\). Next one \(k\in N_{j}(g^{\prime }+ij)\) (\(k\ne i,j\)) cuts successively all her links looking forward to some \(g^{e}\in G^{d^{*}}\). Each time she is cutting one of her links she is decreasing her current payoff and so she is always better off at the end network \(g^{e}\in G^{d^{*}}\). Next player i cuts her link to player j and player i is again isolated. In \(g^{\prime }+ij-\left\{ kl\mid l\in N_{k}(g^{\prime }+ij)\right\} \), we have \(U_{i}(g^{e})>U_{i}(g^{\prime }+ij-\left\{ kl\mid l\in N_{k}(g^{\prime }+ij)\right\} )\) since \(d_{i}(g^{\prime }+ij-\left\{ kl\mid l\in N_{k}(g^{\prime }+ij)\right\} )=1\ne d^{*}\) and \( d_{j}(g^{\prime }+ij-\left\{ kl\mid l\in N_{k}(g^{\prime }+ij)\right\} )=d^{*}\). We reach the network \(g^{\prime \prime }=g^{\prime }+ij-\left\{ kl\mid l\in N_{k}(g^{\prime }+ij)\right\} -ij\) where players k and i are isolated.
3. We repeat the process from step 1 with \(g^{\prime \prime }\) replacing g, and we proceed in this way until we reach the empty network \(g^{\emptyset }\).
4. From the empty network \(g^{\emptyset }\), we build a sequence of networks \(g_{1},g_{2},\ldots ,g_{K}\) such that \(g_{1}=g^{\emptyset }\), \( g_{K}=g^{e}\) and \(\left| \#N_{i}(g_{k})-\#N_{j}(g_{k})\right| \le 1\) , \(k=1,\ldots ,K\), for all \(i,j\in N(h)\), \(h\in H(g^{e})\). Along such a sequence, farsighted players who look forward toward some \(g^{e}\) do have incentives to build those links to form such \(g^{e}\). Hence \(G^{d^{*}}\) satisfies (ES). \(\square \)
The next example shows that, once all players become farsighted (i.e., \(N=F\) ), the set consisting of all strongly efficient networks is a myopic-farsighted stable set, but it is not necessarily the unique myopic-farsighted stable set.
Example 4
Take the degree-based utility model with \(\beta (d_{j})=(1/2)^{d_{j}}\), \( 1/16<c<1/8\), \(N=F=\{1,2,3,4\}\). We have \(d^{*}=1\) and \(\overline{d}=3\). From Proposition 11 the set of networks \(G^{d^{*}}\) such that all players have exactly one link is a myopic-farsighted stable set. However, the set \(\{\{12,23,34\}\), \(\{12,14,34\}\), \(\{14,24,23\}\), \( \{14,13,23\}\), \(\{13,34,24\}\), \(\{13,12,24\}\}\) composed of asymmetric networks where the two central players obtain a higher payoff than in \(g^{e}\) while the other two (loose-end) players get less than in \(g^{e}\) is a (myopic-)farsighted stable set. Similarly, the set \(\{\{13,23,24\}\), \( \{13,14,24\}\), \(\{12,24,34\}\), \(\{12,13,34\}\), \(\{14,34,23\}\), \( \{14,12,23\}\}\) is a (myopic-)farsighted stable set.
5 Discussion
5.1 Evolution and dynamics
To study how networks evolve when myopic players may become farsighted over time, we start with a group of players who are initially unconnected to each other. Over time, pairs of players decide whether or not to form or cut links with each other. A link can be cut unilaterally but agreement by both players is needed to form a link. All players are initially myopic and thus decide to form or cut links if doing so increases their current payoffs. The length of a period is sufficiently long so that the process can converge to some stable network. At the beginning of each period after the initial period, some myopic players become farsighted.Footnote 24 Depending on their positions in the network, the process either stays at the same network or evolves to another stable network.
Time is divided into periods and is modeled as a countable and infinite set, \(T=\{1,2,\ldots ,t,\ldots \}\). We denote by g(t) the network that exists at the end of period \(t\in T\) and by g(0) the initial network. The process of forming links starts from the empty network. Hence, \(g(0)=g^{\emptyset }\). We denote by M(t) (F(t)) the set of myopic (farsighted) players at the beginning of period \(t\in T\). The population dynamics of players is described by the following sequence \(\left\{ M(t),F(t)\right\} _{t=1}^{\infty }\) where \(M(t)=N\setminus F(t)\), \(M(1)=N\), \(M(t)\varsubsetneq M(t-1)\) for \(2\le t<\overline{t}\) and \(M(t)=\emptyset \) for \(t\ge \overline{t}\). A myopic-farsighted improving path in period \(t\in T\) from a network \(g(t-1)\) to a network \(g(t)\ne g(t-1)\) is a finite sequence of graphs \(g_{1},\ldots ,g_{K}\) with \(g_{1}=g(t-1)\) and \(g_{K}=g(t)\) such that for any \(k\in \{1,\ldots ,K-1\}\) either (i) \(g_{k+1}=g_{k}-ij\) for some ij such that \(U_{i}(g_{k+1})>U_{i}(g_{k})\) and \(i\in M(t)\) or \( U_{j}(g_{K})>U_{j}(g_{k})\) and \(j\in F(t)\); or (ii) \(g_{k+1}=g_{k}+ij\) for some ij such that \(U_{i}(g_{k+1})>U_{i}(g_{k})\) and \(U_{j}(g_{k+1})\ge U_{j}(g_{k})\) if \(i,j\in M(t)\), or \(U_{i}(g_{K})>U_{i}(g_{k})\) and \( U_{j}(g_{K})\ge U_{j}(g_{k})\) if \(i,j\in F(t)\), or \(U_{i}(g_{k+1})\ge U_{i}(g_{k})\) and \(U_{j}(g_{K})\ge U_{j}(g_{k})\) (with one inequality holding strictly) if \(i\in M(t),j\in F(t)\). We denote by \(\phi _{t}(g)\) the set of all networks that can be reached from g by a myopic-farsighted improving path in period t. We denote by \(\overline{G}\) the set of networks that belong to some myopic-farsighted stable set, \(\overline{G} =\{g\in G\mid G\subseteq \mathcal {G}\) is a myopic-farsighted stable set\(\}\), and we suppose that \(\overline{G}\ne \emptyset \) for all M, F such that \( N=M\cup F\).
Starting in period 1 from g(0) with \(M(1)=N\) and \(F(1)=\emptyset \), the dynamic process will evolve to some g(1) such that (i) there is a myopic-farsighted improving path from g(0) to g(1) and (ii) g(1) belongs to some myopic-farsighted stable set, i.e. \(g(1)\in \overline{G} (M(1),F(1))\). At the very beginning of period 2 some myopic players become farsighted, \(M(2)\varsubsetneq N\) and \(F(2)\ne \emptyset \). If g(1) is no longer stable (i.e. \(g(1)\notin \overline{G}(M(2),F(2))\)), then the dynamic process will evolve to some \(g(2)\ne g(1)\) such that (i) \(g(2)\in \phi _{2}(g(1))\) and (ii) \(g(2)\in \overline{G}(M(2),F(2))\). Otherwise, it remains where it was, i.e., \(g(2)=g(1)\). Given the population dynamics \( \left\{ M(t),F(t)\right\} _{t=1}^{\infty }\), we say that \(\left\{ g(t)\right\} _{t=1}^{\infty }\) is an evolution of stable networks if and only if (i) \(g(t)\in \overline{G}(M(t),F(t))\) and (ii) if \(g(t)\ne g(t-1)\) then \(g(t)\in \phi _{t}(g(t-1))\).
Consider again the network formation with utility function U such that \( U_{i}(g)={\textstyle \sum }_{j\in N_{i}(g)}\alpha (d_{j})\) for all \(i\in N\) where \(\alpha (d_{j})\) exhibits positive convex externalities. Take \(n-1\ge d^{*}>1\). Starting from the empty network \(g^{\emptyset }\) with a population consisting of only myopic players (\(M(1)=N\)), the dynamic process first remains at the empty network \(g^{\emptyset }\). In fact, the empty network will persist until some period \(t^{*}\) where \(\#F(t^{*}+1)\ge d^{*}>\#F(t^{*})\). At period \(t^{*}+1\), there are now enough farsighted players within the population to dismantle \(g^{\emptyset }\) and move the process toward the complete network \(g^{N}\) that Pareto dominates all other networks and will persist forever.
Since players do not interact in the empty network, it is not excluded that more time would be needed for a myopic player to become farsighted. Hence, if \(d^{*}\) is large, the empty network can persist many periods until the dynamic process moves away to the complete network. On the contrary, in the distance-based utility model with \(b(1)-b(2)<c<b(1)\), it is likely that the dynamic process will evolve faster from one star network to another star network since myopic players in the center interact closely with all farsighted players. Starting from the empty network, the dynamic process first converges to some pairwise stable network. Once the number of myopic players who have become farsighted is large enough, the dynamic process evolves to a star network with some myopic player in the center. Such star network will be dismantled once the myopic player in the center of the star becomes farsighted. In this case, the process evolves next to another star network with one of the remaining myopic players in the center.
Finally, consider the network formation under the egalitarian utility function. Starting from the empty network \(g^{\emptyset }\) with a population consisting of only myopic players (\(M(1)=N\)), the dynamic process first converges to some pairwise stable network \(g\in G^{\emptyset }=P\). If this pairwise stable network is strongly efficient (i.e., if \(g\in E\)), this network will persist forever. Otherwise, some myopic players become farsighted (\(M(2)\varsubsetneq M(1)=N\)) and the dynamic process either remains where it was (if \(g\in G_{\mid M(2),F(2)}^{\emptyset }\subseteq G_{\mid M(1),F(1)}^{\emptyset }\)) or evolves to some network \(g^{\prime }\in G_{\mid M(2),F(2)}^{\emptyset }\) that Pareto dominates g (if \(g\in G_{\mid M(1),F(1)}^{\emptyset }\setminus G_{\mid M(2),F(2)}^{\emptyset }\)). If this network is strongly efficient (i.e., if \(g^{\prime }\in E\)), it will persist forever. Otherwise, some remaining myopic players become now farsighted. In the end, the dynamic process always reaches some strongly efficient network that will persist forever.
5.2 Coalitions
In the notion of myopic-farsighted stable set, we only consider deviations by at most a pair of players at a time. It might be that some coalition of players could all be made better off by some complicated reorganization of their links, which is not accounted for under myopic-farsighted stable sets with pairwise deviations. Groupwise deviations make sense in situations where players have substantial information about the overall structure and potential payoffs and can coordinate their actions. Our definition of myopic-farsighted stable set can be extended to groupwise deviations.
A network \(g^{\prime }\) is obtainable from g via deviations by group \( S\subseteq N\) if (i) \(ij\in g^{\prime }\) and \(ij\notin g\) implies \( \{i,j\}\subseteq S\), and (ii) \(ij\in g\) and \(ij\notin g^{\prime }\) implies \( \{i,j\}\cap S\ne \emptyset \). A groupwise myopic-farsighted improving path from a network g to a network \(g^{\prime }\ne g\) is a finite sequence of networks \(g_{1},\ldots ,g_{K}\) with \(g_{1}=g\) and \(g_{K}=g^{\prime }\) such that for any \(k\in \{1,\ldots ,K-1\}\), (i) \(g_{k+1}\) is obtainable from \( g_{k}\) via deviations by \(S_{k}\subseteq N\), (ii) \(U_{i}(g_{k+1})\ge U_{i}(g_{k})\) for all \(i\in S_{k}\cap M\) and \(U_{j}(g_{K})\ge U_{j}(g_{k})\) for all \(j\in S_{k}\cap F\) (with one inequality holding strictly). For a given network g, let \(\Phi (g)\) be the set of networks that can be reached by a groupwise myopic-farsighted improving path from g. A set of networks \( G\subseteq \mathcal {G}\) is a myopic-farsighted stable set with groupwise deviations if: (IS) for every \(g,g^{\prime }\in G\) (\(g\ne g^{\prime }\)), it holds that \(g^{\prime }\notin \Phi (g)\), and (ES) for every \(g\in \mathcal {G}\setminus G\), it holds that \(\Phi (g)\cap G\ne \emptyset \).
For any given network g, we have \(\phi (g)\subseteq \Phi (g)\). Hence, if \( \phi (g)\cap G\ne \emptyset \) for all \(g\in \mathcal {G}\setminus G\), then \( \Phi (g)\cap G\ne \emptyset \) for all \(g\notin \mathcal {G}\setminus G\). Thus, if \(\{g\}\) is a myopic-farsighted stable set, then it is a myopic-farsighted stable set with groupwise deviations.Footnote 25 However, if G is a myopic-farsighted stable set, then G may become unstable with groupwise deviations since G might now violate ( IS).
In the case of network formation under the egalitarian utility function, groupwise deviations imply that the set of strongly efficient networks E is the unique myopic-farsighted stable whatever the number of farsighted and myopic players. Remember that all networks \(g\in E\) Pareto dominates all networks \(g^{\prime }\in \mathcal {G}\setminus E\). Hence, \(\Phi (g^{\prime })\cap E\ne \emptyset \) for all \(g^{\prime }\in \mathcal {G}\setminus E\) and \(\Phi (g)=\emptyset \) for all \(g\in E\). Similarly, in the case of positive convex externalities, we have that \(G=\{g^{N}\}\) is the unique myopic-farsighted stable with groupwise deviations. When there is no externality and the number of players is even, the set of \(d^{*}\)-regular networks is the unique myopic-farsighted stable with groupwise deviations. Indeed, in a \(d^{*}\)-regular network compared to any other network, players are at least as well off with at least one of them being strictly better off.
In the distance-based utility model, for \(b(1)-b(2)<c<b(1)\), the set consisting of all star networks where the center of the star is a myopic player, \(\left\{ g^{*i}\mid i\in M\right\} \), is still the unique myopic-farsighted stable set with groupwise deviations. However, we now only need that there is at least one farsighted player and one myopic player in the population to sustain this result. From any \(g^{\prime }\notin \left\{ g^{*i}\mid i\in M\right\} \), we can build a groupwise myopic-farsighted improving path leading to some \(g{\in } \left\{ g^{*i}\mid i\in M\right\} \) . First, \(S=N\) deviates from \(g^{\prime }\) to form in one step a star network \(g^{*j}\) with some farsighted player j in the center. Next, player j cuts all her links leading to the empty network \(g^{\emptyset }\). Finally, \(S=N\) deviates from \(g^{\emptyset }\) to form in one step a star network \(g^{*i}\) with some myopic player i in the center. Obviously, \( \Phi (g)=\emptyset \) for all \(g\in \left\{ g^{*i}\mid i\in M\right\} \).
5.3 Limited farsightedness
Pairwise stability requires that networks are immune to immediate deviations. On top of this requirement, one might look for networks that are also immune to deviations by myopic and farsighted players. A network \(g\in \mathcal {G}\) is myopic-farsighted pairwise stable if \(\phi (g)=\emptyset \) . The set of myopic-farsightedly pairwise stable networks is denoted by \( P_{MF}\). When \(N=F\) it reverts to Jackson (2008) set of farsightedly pairwise stable networks. Similar to pairwise stability, there is no guarantee that the set \(P_{MF}\) is non-empty. From the proofs of Propositions 5 and 7, we have that, under the egalitarian utility function or in the presence of positive convex externalities, each network belonging to the unique myopic-farsighted stable set is myopic-farsightedly pairwise stable. Consider now the distance-based utility model with \(b(1)-b(2)<c<b(1)\). From the proof of Proposition we have that, if \(n>\#F\ge 1+b(2)/(b(2)-b(3))\), then each network \( g\in G^{*}=\left\{ g^{*i}\mid i\in M\right\} \) is myopic-farsightedly pairwise stable, i.e., \(P_{MF}=G^{*}\). So, there are no myopic-farsighted deviations from networks in \(G^{*}\). In addition, myopic-farsighted deviations from networks outside \(G^{*}\) to networks inside \(G^{*}\) are credible since networks in \(G^{*}\) are stable.
The notion of myopic-farsighted stable set assumes that each player is either myopic or farsighted. But, it could be that each player is neither fully myopic nor fully farsighted. Herings et al. (2019) propose the concept of a horizon-K farsighted set to analyze which networks are going to emerge in the long run when players have an arbitrary homogeneous degree of farsightedness. A set of networks is a horizon-K farsighted set if three conditions are satisfied: (i) deviations to networks outside the set are horizon-K deterred, (ii) from any network outside the set there is a sequence of farsighted improving paths of length smaller than or equal to K leading to some network in the set, and (iii) there is no proper subset satisfying the conditions (i) and (ii). There is no general relationship between the myopic-farsighted stable set and the horizon-K farsighted set, except when all players are myopic. There is a unique horizon-1 farsighted set that consists of all pairwise networks and all networks belonging to the closed cycles. Hence, the horizon-1 farsighted set is equal to the union of all myopic-farsighted stable sets when all players are myopic.
6 Conclusion
We have adopted the notion of myopic-farsighted stable set to determine the networks that emerge when myopic and farsighted individuals decide with whom they want to form a link, according to some utility function that weighs the costs and benefits of each connection. We have provided conditions on the utility function that guarantee the existence and uniqueness of a myopic-farsighted stable set. We have shown that, under the egalitarian utility function or in the presence of positive convex externalities or in the case of no externality, the unique myopic-farsighted stable set consists of all pairwise stable networks when all players are myopic. When the population becomes mixed, the myopic-farsighted stable set refines the set of pairwise stable networks by eliminating some Pareto-dominated networks. In the end, when all players are farsighted, the unique myopic-farsighted stable set only consists of all strongly efficient networks. Hence, under the egalitarian utility function or in the presence of positive convex externalities or in the case of no externality, turning myopic players into farsighted players alleviates the tension between stability and efficiency. In addition, myopic players can only improve by becoming farsighted since the worst pairwise stable networks are progressively discarded.
It is important to understand what happens when myopic players interact with farsighted players since, in general, some networks that are neither stable when all players are myopic nor stable when all players are farsighted could emerge in the long run. In addition, turning myopic players into farsighted players might be costly for the society. Hence, a social planner would face a trade-off between the costs for increasing the number of farsighted players and the gains in terms of efficiency.
In the context of network formation with distance-based utilities (where links have positive externalities but diminishing with the distance), we have shown that, once the population of myopic and farsighted players is mixed, there is no tension between stability and efficiency. On the contrary, when all players are farsighted (or all players are myopic), a conflict is likely to arise. Hence, with distance-based utilities, once there are enough farsighted players in the population, there is no need for turning more myopic players into farsighted ones.
In the context of network formation with degree-based utilities (where links have negative externalities), we have shown that, in the case of a mixed population, segregation is likely to occur where myopic players tend to build too many links, while farsighted players coordinate for building the socially optimal number of links. Hence, with degree-based utilities, turning myopic players into farsighted ones improves continuously efficiency.
Finally, notice that farsighted players do better than myopic players under different models we have studied (egalitarian utility function, distance-based utility, degree-based utility, positive convex externalities, no externality). But this is not always the case. For instance, in R&D networks, some myopic firms may obtain a higher profit than some farsighted firms in a myopic-farsighted stable set (see Mauleon et al. 2018b).
Notes
Teteryatnikova and Tremewan (2020) compare the predictive power of myopic and farsighted stability concepts in a network formation experiment with a stream of payoffs. Their results show that there exist environments where farsighted stability concepts identify empirically stable networks that are not identified by myopic stability concepts.
See Chwe (1994), Herings et al. (2009), Mauleon et al. (2011), Ray and Vohra (2015, 2019), Roketskiy (2018) for definitions of the farsighted stable set. Alternative notions of farsightedness are suggested by Diamantoudi and Xue (2003), Dutta et al. (2005), Dutta and Vohra (2017), Herings et al. (2004, 2019), Page et al. (2005), Page and Wooders (2009), Xue (1998) among others.
In the case of intermediate link costs relative to benefits, individuals obtain their highest possible payoff when they are the peripherals in a star network. The center of the star is worse off compared to the peripherals.
Another strand of the literature that was initiated by Bala and Goyal (2000) studies the formation of two-way flow networks where individuals unilaterally form costly links in order to access the benefits generated by other individuals. Benefits flow in both directions, irrespective of who pays the cost of the link. In Galeotti et al. (2006), individuals are heterogeneous with respect to benefits and costs of forming links. In Bloch and Dutta (2009), individuals choose how much to invest in each link. See also Hojman and Szeidl (2008), Feri (2007), Kannan et al. (2007), Haller et al. (2007) among others.
Throughout the paper, we use the notation \(\subseteq \) for weak inclusion and \(\varsubsetneq \) for strict inclusion. Finally, \(\#\) will refer to the notion of cardinality.
Stability concepts have their roots in cooperative game theory. They predict which network will emerge independently of the network formation process, but they are silent on how a network architecture is expected to emerge through the strategic decisions of the players. As such, myopia and farsightedness are not models of individual strategic behavior, because strategic behavior is concealed in the stability approach.
The distinction between myopic players and farsighted players can be linked to their cognitive ability or their patience. For instance, Dutta et al. (2005) propose a dynamic approach with payoffs accruing in real time along with the network formation process. Players get a discounted stream of payoffs, and the discount factor becomes a natural proxy for the degree of farsightedness (discount factor close to 0 for myopic players and discount factor close to one for farsighted players).
The pairwise CP vNM set follows the approach by Page and Wooders (2009) who define the stable set with respect to path dominance, i.e., the transitive closure of \(\phi \).
Demuynck et al. (2019) propose the myopically stable set for social environments, which generalizes the pairwise myopically stable set introduced by Herings et al. (2009) for generic network problems. Theorem 1 of Herings et al. (2009) shows that the pairwise myopically stable set is the union of all pairwise stable networks and closed cycles.
van Deemen (1991) introduces the generalized stable set for abstract systems and shows its existence. Page and Wooders (2009) define it for abstract network formation game with the path dominance relation. It is not hard to see that the generalized stable set for abstract systems due to van Deemen (1991) coincides with the myopic-farsighted stable set for generic network problems when all players are myopic. For such network problems with myopic players, Theorem 2 in van Deemen (1991) and Theorem 3 in Page and Wooders (2009) are therefore equivalent to Proposition 3 that characterizes the myopic-farsighted stable sets as all pairwise stable networks and one network from each closed cycle.
In communication networks, players directly communicate with the players to whom they are linked. They benefit not only from direct communication but also from indirect communication from the players to whom their neighbors are linked. But, the benefit obtained from indirect communication decreases with the distance.
Johnson and Gilles (2000) extend the connection model by introducing a cost of creating a link that is proportional to the geographical distance between two individuals. In Jackson and Rogers (2005) or De Marti and Zenou (2017), individuals belong to two different communities, and the cost for creating links depends whether it is an intracommunity link or an intercommunity link.
In the symmetric connections model where \(b(t)=\delta ^{t}\), the lower bound on the number of farsighted players, \(1+b(2)/(b(2)-b(3))\), becomes \( 1+1/(1-\delta )\). Hence, the number of farsighted players needed for guaranteeing the emergence of the efficient networks increases with \(\delta \) .
Dutta and Vohra (2017) propose two related solution concepts: the rational expectations farsighted stable set (REFS) and the strong rational expectations farsighted stable set (SREFS) where they restrict coalitions (or pairs in our case) to hold common, history independent expectations that incorporate maximality regarding the continuation path. REFS and SREFS coincide with a farsighted stable set when the latter consists of networks with a single payoff (Theorem 1 of Dutta and Vohra 2017). Since every set consisting of a star network encompassing all players is a myopic-farsighted stable set, it is also a REFS and SREFS. When \(n=4\), the same holds for the set of circles among the four farsighted player.
Let \(\overline{c}(n)=\max \{c\in \mathbb {R} \mid \exists g\in \mathcal {G}\) such that \(g\ne g^{\emptyset }\) and \( U_{i}(g)\ge 0\) \(\forall i\in N\}\) be the highest cost such that the utility of all players is nonnegative in at least one network other than the empty network. For \(n>3\), it follows from the proof of Proposition 2 in Grandjean et al. (2011) that if \(b(1)<\overline{c} (n)<c<b(1)+((n-2)/2)b(2)\) then \(\{g^{\emptyset }\}\) is the unique myopic-farsighted stable set when all players are farsighted.
When all players are myopic, Bloch and Jackson (2007) show that peripheral players can subsidize the center of the star to keep their links formed. Any (efficient) star network is supportable as a pairwise equilibrium of the direct transfer game when \(b(1)-b(2)<c<b(1)+b(2)(n-2)/2\).
Möhlmeier et al. (2016) consider a utility function that incorporates both the effects of distance and of neighbors’ degree.
It is an alternative functional form to Jackson and Wolinsky (1996) original coauthor model. In the coauthor model a researcher benefits from having a coauthor as it increases her research output. But, if her coauthor works on a new project with someone else, she has less time to devote to their project and the benefit of the collaboration decreases.
Instead of assuming a unique \(d^{*}=\arg \max x\beta (x)\), Morrill (2011) imposes a stronger regularity condition for analyzing the network game with transfers: the social payoff function \(x\beta (x)\) is single peaked.
When the number of farsighted players is large, it might happen that the farsighted player with the smallest number of links has more links than the myopic players she is linked to. Remember that all myopic players are linked to each other. Hence, \(m\beta (m)\) is the maximal gain she can obtain from her links to myopic players and \((x-m)\beta (x)\) is the gain she obtains from being linked to other farsighted players who have at least the same number of links than her. The condition \(m\beta (m)+(x-m)\beta (x)-xc<d^{*}(\beta (d^{*})-c)\) guarantees that this farsighted player prefers being in the strongly efficient network. Hence, she is ready to cut her links looking forward to some network where she gets the socially optimal payoff.
For instance, a myopic player may become faster farsighted when interacting in an environment composed mainly of farsighted players (e.g., when it belongs to a component with a majority of farsighted players).
If \(\{g\}\) was the unique myopic-farsighted stable set, then it is not necessarily the unique myopic-farsighted stable set with groupwise deviations since now we could have \(\Phi (g)\ne \emptyset \) while \(\phi (g)=\emptyset \).
References
Bala, V., Goyal, S.: A noncooperative model of network formation. Econometrica 68, 1181–1229 (2000)
Bloch, F., Dutta, B.: Communication networks with endogenous link strength. Games Econ. Behav. 66, 39–56 (2009)
Bloch, F., Jackson, M.O.: The formation of networks with transfers among players. J. Econ. Theory 133, 83–110 (2007)
Chwe, M.S.: Farsighted coalitional stability. J. Econ. Theory 63, 299–325 (1994)
De Marti, J., Zenou, Y.: Segregation in friendship networks. Scand. J. Econ. 119, 656–708 (2017)
Demuynck, T., Herings, P.J.J., Saulle, R.D., Seel, C.: The myopic stable set for social environments. Econometrica 87, 111–138 (2019)
Diamantoudi, E., Xue, L.: Farsighted stability in hedonic games. Soc. Choice Welf. 21, 39–61 (2003)
Dutta, B., Ghosal, S., Ray, D.: Farsighted network formation. J. Econ. Theory 122, 143–164 (2005)
Dutta, B., Vohra, R.: Rational expectations and farsighted stability. Theor. Econ. 12, 1191–1227 (2017)
Feri, F.: Stochastic stability in networks with decay. J. Econ. Theory 135, 442–457 (2007)
Galeotti, A., Goyal, S., Kamphorst, J.: Network formation with heterogeneous players. Games Econ. Behav. 54, 353–372 (2006)
Grandjean, G., Mauleon, A., Vannetelbosch, V.: Connections among farsighted agents. J. Public Econ. Theory 13, 935–955 (2011)
Haller, H., Kamphorst, J., Sarangi, S.: (Non-)existence and scope of Nash networks. Econ. Theory 31, 597–604 (2007)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Rationalizability for social environments. Games Econ. Behav. 49, 135–156 (2004)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Farsightedly stable networks. Games Econ. Behav. 67, 526–541 (2009)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Stable sets in matching problems with coalitional sovereignty and path dominance. J. Math. Econ. 71, 14–19 (2017a)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Matching with myopic and farsighted players. CORE Discussion Paper 2017-14, UCLouvain (2017b)
Herings, P.J.J., Mauleon, A., Vannetelbosch, V.: Stability of networks under horizon-$K$ farsightedness. Econ. Theory 68, 177–201 (2019)
Hojman, D., Szeidl, A.: Core and periphery in networks. J. Econ. Theory 139, 295–309 (2008)
Jackson, M.O.: Social and Economic Networks. Princeton University Press, Princeton (2008)
Jackson, M.O., Rogers, B.W.: The economics of small worlds. J. Eur. Econ. Assoc. 3, 617–627 (2005)
Jackson, M.O., Watts, A.: The evolution of social and economic networks. J. Econ. Theory 106, 265–295 (2002)
Jackson, M.O., Wolinsky, A.: A strategic model of social and economic networks. J. Econ. Theory 71, 44–74 (1996)
Johnson, C., Gilles, R.P.: Spatial social networks. Rev. Econ. Des. 5, 273–299 (2000)
Kannan, R., Ray, L., Sarangi, S.: The structure of information networks. Econ. Theory 30, 119–134 (2007)
Kirchsteiger, G., Mantovani, M., Mauleon, A., Vannetelbosch, V.: Limited farsightedness in network formation. J. Econ. Behav. Organ. 128, 97–120 (2016)
Mauleon, A., Vannetelbosch, V.: Network formation games. In: Bramoullé, Y., Galeotti, A., Rogers, B.W. (eds.) The Oxford Handbook of the Economics of Networks, pp. 167–190. Oxford University Press, Oxford (2016)
Mauleon, A., Vannetelbosch, V., Vergote, W.: von Neumann Morgernstern farsightedly stable sets in two-sided matching. Theor. Econ. 6, 499–521 (2011)
Mauleon, A., Roehl, N., Vannetelbosch, V.: Constitutions and groups. Games Econ. Behav. 107, 135–152 (2018a)
Mauleon, A., Sempere-Monerris, J.J., Vannetelbosch, V.: R&D network formation with myopic and farsighted firms. CORE Discussion Paper 2018-26, UCLouvain (2018b)
Mauleon, A., Roehl, N., Vannetelbosch, V.: Paths to stability for overlapping group structures. J. Math. Econ. 83, 19–24 (2019)
Möhlmeier, P., Rusinowska, A., Tanimura, E.: A degree-distance-based connections model with negative and positive externalities. J. Public Econ. Theory 18, 168–192 (2016)
Morrill, T.: Network formation under negative degree-based externalities. Int. J. Game Theory 40, 367–385 (2011)
Page Jr., F.H., Wooders, M.: Strategic basins of attraction, the path dominance core, and network formation games. Games Econ. Behav. 66, 462–487 (2009)
Page Jr., F.H., Wooders, M., Kamat, S.: Networks and farsighted stability. J. Econ. Theory 120, 257–269 (2005)
Ray, D., Vohra, R.: The farsighted stable set. Econometrica 83, 977–1011 (2015)
Ray, D., Vohra, R.: Maximality in the farsighted stable set. Econometrica 87, 1763–1779 (2019)
Roketskiy, N.: Competition and networks of collaboration. Theor. Econ. 13, 1077–1110 (2018)
Song, Y., van der Schaar, M.: Dynamic network formation with incomplete information. Econ. Theory 59, 301–331 (2015)
Teteryatnikova, M., Tremewan, J.: Myopic and farsighted stability in network formation games: an experimental study. Econ. Theory 69, 987–1021 (2020)
van Deemen, A.M.A.: A note on generalized stable sets. Soc. Choice and Welf. 8, 255–260 (1991)
Watts, A.: A dynamic model of network formation. Games Econ. Behav. 34, 331–341 (2001)
Xue, L.: Coalitional stability under perfect foresight. Econ. Theory 11, 603–627 (1998)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank the editor, an associate editor and three anonymous referees for their valuable comments and suggestions to improve the paper. Ana Mauleon and Vincent Vannetelbosch are, respectively, Research Director and Senior Research Associate of the National Fund for Scientific Research (FNRS). Financial support from the Spanish Ministry of Economy and Competition under the Project ECO2015-64467-R, from the MSCA ITN Expectations and Social Influence Dynamics in Economics (ExSIDE) Grant No. 721846 (1/9/2017–31/8/2020), from the Belgian French speaking community ARC project 15/20-072 of Saint-Louis University - Brussels, and from the Fonds de la Recherche Scientifique - FNRS research grant T.0143.18 is gratefully acknowledged.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luo, C., Mauleon, A. & Vannetelbosch, V. Network formation with myopic and farsighted players. Econ Theory 71, 1283–1317 (2021). https://doi.org/10.1007/s00199-020-01288-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-020-01288-8
Keywords
- Networks
- Stable sets
- Myopic and farsighted players
- Egalitarian utility
- Positive convex externalities
- Distance-based utility
- Degree-based utility