Stag Hunt with unknown outside options

Abstract

We study the Stag Hunt game where two players simultaneously decide whether to cooperate or to choose their outside options (defect). A player’s gain from defection is his private information (the type). The two players’ types are independently drawn from the same cumulative distribution. We focus on the case where only a small proportion of types are dominant (higher than the value from cooperation). It is shown that for a wide family of distribution functions, if the players interact only once, the unique equilibrium outcome is defection by all types of player. Whereas if a second interaction is possible, the players will cooperate with positive probability and already in the first period. Further restricting the family of distributions to those that are sufficiently close to the uniform distribution, cooperation in both period with probability close to 1 is achieved, and this is true even if the probability of a second interaction is very small.

Appendix

1.1 Proof of Proposition 1

For any pair of pure strategies $(s_1,s_2)$, let

$$\begin{aligned} T_i=T_i(s_i)=\{d_i \in [0,B]|s_i(d_i)=C\}. \end{aligned}$$

That is, $T_i$ is the (Borel) set of all types of player i who cooperate under $s_i$. Since C is a weakly dominant strategy for i of type $d_i=0$ it is assumed that $0 \in T_i$, and hence $T_i\ne \emptyset$. Let $\lambda$ be the measure on [0, B] generated by the distribution function F. The measure of $T_i$ is therefore $\lambda (T_i)$.

If player i of type $d_i\le 1-\mu$ chooses C, his expected payoff is $\lambda (T_j)$. If he chooses D he obtains $d_i\big (1-\lambda (T_j) \big )+(d_i+\mu )\lambda (T_j) =d_i+\mu \lambda (T_j).$ Hence $d_i\in T_i$ implies $d_i \le (1-\mu )\lambda (T_j)$, $j \ne i$, and $d_i \notin T_i$ implies $d_i \ge (1-\mu )\lambda (T_j)$. Consequently, in equilibrium, both $T_1$ and $T_2$ are intervals starting from zero. Part (i) of Proposition 1 follows. We next turn to proof part (ii).

Suppose $B>1-\mu$. Let $s^*=(s^*_1,s^*_2)$ be an equilibrium of $G_1(F, \mu )$. By part (i), both $s_1^*$ and $s_2^*$ are threshold strategies. For $i=1, 2$, denote by $\widehat{d}_i$ the threshold in $s^*_i$. As argued above, player i chooses C only if $d_i\le (1-\mu )\lambda (T_j)$. Therefore, $\widehat{d}_i=\min [B, (1-\mu )\lambda (T_j)]=\min [B, (1-\mu ) F(\widehat{d}_j)]$. Since $B>1-\mu$, we have for all $i=1, 2$ and $j\ne i$,

$$\begin{aligned} \widehat{d}_i=(1-\mu ) F(\widehat{d}_j). \end{aligned}$$

(15)

Suppose w.l.o.g. $\widehat{d}_i \ge \widehat{d}_j$. Then

$$\begin{aligned} \widehat{d}_i = (1-\mu ) F(\widehat{d}_j ) \le (1-\mu ) F(\widehat{d}_i )=\widehat{d}_j, \end{aligned}$$

and hence $\widehat{d}_i =\widehat{d}_j$. Therefore, when $s^*$ is an equilibrium, the threshold in $s_i^*$ satisfies $\widehat{d}_i=(1-\mu )F(\widehat{d}_i)$.

We next verify that as long as $\widehat{d}$ is a fixed point of F, the strategy profile $(s^{\widehat{d}}_1,s^{\widehat{d}}_2)$ is an equilibrium of $G_1(F, \mu )$.

Suppose Player 1 plays $s^{\widehat{d}}_1$. Let us show that $s^{\widehat{d}}_2$ is best reply to $s^{\widehat{d}}_1$. If $d_2$ chooses C he obtains $F(\widehat{d})$, otherwise, he obtains $d_2+\mu F(\widehat{d})$. Hence $d_2$ prefers C iff $d_2 \le (1-\mu ) F(\widehat{d})=\widehat{d}$. This completes the proof of part (ii) in Proposition 1.

1.2 Proof of Proposition 2

Similar to Proposition 1, it can be verified that the second-period choice of each player is determined by thresholds. Namely, $s^*_i(d_i,h^1)$, $h^1 \in H^1$ is defined by (3) for some threshold $d_i^{h^1}$. We need to prove that this is also true for the first-period choice, namely, (3) also holds for $h=\emptyset$.

Let $X \in \{C,D\}$. Denote

$$\begin{aligned} E_2^{\emptyset }= & {} \{d_2 \in [0,B]|s^*_2(d_2,\emptyset )=C\},\\ \overline{E}_2^{\emptyset }= & {} [0,B] \setminus E_2^{\emptyset },\\ E_2^{C,X}= & {} [0,d_2^{C,X}] \text{ and } E_2^{D,X}=[0,d_2^{D,X}],\\ P^{\emptyset }_2= & {} Prob E^{\emptyset }_2. \end{aligned}$$

Suppose Player 1 of type $d_1$ chooses C in the first period. He obtains an expected payoff of $U_1(d_1,C)$, where

$$\begin{aligned} U_1(d_1,C)&=P^{\emptyset }_2+\delta P_2^{\emptyset } \left\{ \begin{array}{ll} Prob(E^{C,C}_2|E_2^{\emptyset })&{}\quad d_1 \le d_1^{C,C}\\ d_1+\mu \cdot Prob(E^{C,C}_2|E_2^{\emptyset }) &{}\quad d_1>d_1^{C,C} \end{array} \right. +\\&\quad +(1-P^{\emptyset }_2) \cdot 0+\delta (1-P_2^{\emptyset }) \left\{ \begin{array}{ll} Prob(E^{C,D}_2|\overline{E}_2^{\emptyset })&{}\quad d_1 \le d_1^{C,D}\\ d_1+\mu \cdot Prob(E^{C,D}_2|\overline{E}_2^{\emptyset }) &{}\quad d_1>d_1^{C,D}. \end{array} \right. \end{aligned}$$

Observe that if Player 2 chooses C in the first period then the updated probability distribution of Player 1 about Player 2’s type changes from $F_2(d_2)$ to $F_2(d_2|d_2 \in E_2^{\emptyset }$). If Player 2 chooses D in the first period the updated distribution of Player 1 is $F_2(d_2|d_2 \in \overline{E}_2^{\emptyset }$). Since $B>1-\mu$, the second-period thresholds satisfy $d_1^{h^1}<B$ for all $h^1 \in H^1$. By Proposition 1 for $X \in \{C,D\}$,

$$\begin{aligned} (1-\mu )\cdot Prob(E_2^{X,C}|E_2^{\emptyset })=d_1^{X,C} \end{aligned}$$

(16)

and

$$\begin{aligned} (1-\mu )\cdot Prob(E_2^{X,D}|\overline{E}_2^{\emptyset })=d_1^{X,D}. \end{aligned}$$

(17)

By (16) and (17)

$$\begin{aligned} U_1(d_1,C)&=P^{\emptyset }_2+\delta P_2^{\emptyset } \left\{ \begin{array}{ll} \frac{1}{1-\mu }\cdot d_1^{C,C}&{}\quad d_1 \le d_1^{C,C}\\ d_1+\frac{\mu }{1-\mu }\cdot d_1^{C, C} &{}\quad d_1>d_1^{C,C} \end{array} \right. \nonumber \\&+ \delta (1-P_2^{\emptyset }) \left\{ \begin{array}{ll} \frac{1}{1-\mu }\cdot d_1^{C,D}&{}\quad d_1 \le d_1^{C,D}\\ d_1+\frac{\mu }{1-\mu }\cdot d_1^{C, D} &{}\quad d_1>d_1^{C,D}. \end{array} \right. \end{aligned}$$

(18)

By (18), $U_1(d_1,C)$ is continuous in $d_1$ (as a sum of two continuous functions) and it is piecewise linear in $d_1$. Moreover, the slope of $U_1(d_1,C)$ with respect to $d_1$ is at most $\delta$.

Similarly, if Player 1 chooses D in the first period, he obtains

$$\begin{aligned} U_1(d_1,D)&=p_2^{\emptyset }\cdot (d_1+\mu )+\delta P_2^{\emptyset } \left\{ \begin{array}{ll} Prob(E^{D,C}_2|E_2^{\emptyset })&{}\quad d_1 \le d_1^{D,C}\\ d_1+\mu \cdot Prob(E^{D,C}_2|E_2^{\emptyset }) &{}\quad d_1>d_1^{D,C} \end{array} \right. \\&\quad +(1-p_2^{\emptyset })\cdot d_1+\delta (1-P_2^{\emptyset }) \left\{ \begin{array}{ll} Prob(E^{D,D}_2|\overline{E}_2^{\emptyset })&{}\quad d_1 \le d_1^{D,D}\\ d_1+\mu \cdot Prob(E^{D,D}_2|\overline{E}_2^{\emptyset }) &{}\quad d_1>d_1^{D,D}. \end{array} \right. \end{aligned}$$

Hence

$$\begin{aligned} U_1(d_1,D)&=p_2^{\emptyset }\cdot (d_1+\mu )+\delta P_2^{\emptyset }\left\{ \begin{array}{ll} \frac{1}{1-\mu }\cdot d_1^{D,C}&{}\quad d_1 \le d_1^{D,C}\\ d_1+\frac{\mu }{1-\mu }\cdot d_1^{D, C} &{}\quad d_1>d_1^{D,C} \end{array} \right. \nonumber \\&\quad +(1-p_2^{\emptyset })\cdot d_1+ \delta (1-P_2^{\emptyset })\left\{ \begin{array}{ll} \frac{1}{1-\mu }\cdot d_1^{D,D}&{}\quad d_1 \le d_1^{D,D}\\ d_1+\frac{\mu }{1-\mu }d_1^{D, D} &{}\quad d_1>d_1^{D,D}. \end{array} \right. \end{aligned}$$

(19)

The payoff $U_1(d_1,D)$ is also continuous and piecewise linear in $d_1$, and its slope is at least 1. Since $\delta <1$, it is easy to verify that $U_1(d_1,C)-U_1(d_1,D)$ is continuous in $d_1$ and has a negative slope everywhere in [0, B]. Namely, it is decreasing everywhere in [0, B] and if $U_1(d_1,C) \ge U_1(d_1,D)$ for some $d_1$, it certainly holds for any type below $d_1$. This implies that $s^*_1(d_1, \emptyset )$ is a threshold strategy and $d_1^{\emptyset }$ is the (unique) solution of $U_1(d,C)=U_1(d,D)$ in d, if a solution exists. If $U_1(d_1, C)<U_1(d_1, D)$ for all $d_1\in (0, B]$, then $d_1^{\emptyset }=0$ and if $U_1(d_1, C)>U_1(d_1, D)$ for all $d_1\in (0, B]$ then $d_1^{\emptyset }=B$.

1.3 Proof of Proposition 3

Since the game is symmetric and the strategy $s^*$ described in (4)–(5) is symmetric, to show that $s^*$ is an equilibrium, it is sufficient to show that $s_1^*$ is a best response to $s_2^*$. There are two key steps: (1) there exists some $d^*\in (0, 1-\mu )$ such that it is optimal for Player 1 to cooperate in the first period if and only if $d_1\le d^*$, and (2) after Player 1 cooperated and his counterpart defected in period 1, Player 1 of type $d_1\le d^*$ strictly prefers to continue cooperating.

By defecting rather than cooperating in period 1, Player 1 of type $d_1$ gains the value of his outside option $d_1$, but loses $1-\mu$ if his counterpart chooses to cooperate, which happens if his counterpart is of type $d_2\le d^*$. Therefore, by defecting rather than cooperating in period 1, the payoff of Player 1 of type $d_1$ changes by

$$\begin{aligned} d_1-F(d^*)\cdot (1-\mu ) \end{aligned}$$

(20)

Suppose the counterpart has cooperated in period 1, then the counterpart will continue cooperating in period 2 and and Player 1 of any non-dominant type will cooperate, regardless of Player 1’s period 1 action. So Player 1’s period 2 payoff does not depend on his own period 1 action, if the counterpart cooperated in period 1, which happens when the counterpart has type $d_2\le d^*$.

Suppose the counterpart has defected in period 1, which happens if and only if the counterpart’s type is above $d^*$. By defecting rather than cooperating in period 1 and then following the equilibrium strategy, two possible effects will change Player 1’s period 2 payoff: (1) he will defect rather than cooperate in period 2 if his type is $d_1\le m^*$ where $m^*>d^*$, and (2) his counterpart of type $d_2\in (d^*, 1-\mu )$ will defect rather than cooperate in period 2.

The own action change effect, effect (1), is present if and only if Player 1’s type is $d_1<m^*$. Recall that, conditional on defection by the counterpart in period 1, Player 1 believes that the counterpart’s type is above $d^*$. Suppose the counterpart acts as if Player 1 cooperated in period 1. Then, in period 2, the counterpart of type $d_2\in (d^*, 1-\mu ]$ will cooperate while the counterpart of type $d_2>1-\mu$ will defect. Given such behaviour from the counterpart, Player 1 of type $d_1$ gains his outside option value $d_1$, but loses $1-\mu$ if his counterpart cooperates, which happens with conditional probability $\frac{F(1-\mu )-F(d^*)}{1-F(d^*)}$. Conditional on the counterpart defecting in period 1, effect (1) changes type $d_1$ Player 1’s payoff by

$$\begin{aligned} d_1-(1-\mu )\cdot \frac{F(1-\mu )-F(d^*)}{1-F(d^*)} \end{aligned}$$

(21)

if $d_i<m^*$. Note that in the analysis of effect (1), we assume that the counterpart acts as if Player 1 cooperated in period 1. Therefore, the amount in (21) is exactly type $d_1$ Player 1’s gain from defection at history (C, D).

We next turn to effect (2). By defecting rather than cooperating in period 1, Player 1 causes the counterpart of type $d_2\in (d^*, 1-\mu )$ to defect rather than cooperate in period 2. Given that Player 1 defects in period 2, effect (2) causes Player 1’s period 2 payoff to go down by $\mu$ with conditional probability $\frac{F(1-\mu )-F(d^*)}{1-F(d^*)}$. So, by defecting rather than cooperating in period 1 and then following the equilibrium strategy, type $d_1$ Player 1’s period 2 payoff changes by

$$\begin{aligned} \big (1-F(d^*) \big )\cdot \left[ \left( \underbrace{d_1-(1-\mu )\cdot \frac{F(1-\mu )-F(d^*)}{1-F(d^*)}}_{\begin{array}{c} \text {effect of Player 1's own action change,}\\ \text {fixing the counterpart's action.} \end{array}} \right) \mathbb {1}_{d_1\le m^*}- \underbrace{\mu \cdot \frac{F(1-\mu )-F(d^*)}{1-F(d^*)}}_{\begin{array}{c} \text {effect on the counterpart's}\\ \text {action change}. \end{array}} \right] . \end{aligned}$$

(22)

Since the cut-off at history (C, D) is $m^*>d^*$, type $d^*$ player is indifferent between defecting and cooperating in period 1 and then following the equilibrium strategy if and only if

$$\begin{aligned} \begin{aligned} 0=&d^*-F(d^*)\cdot (1-\mu )\\&+\delta \cdot \big (1-F(d^*) \big )\cdot \left[ \left( \underbrace{d^*-(1-\mu )\cdot \frac{F(1-\mu )-F(d^*)}{1-F(d^*)}}_{\begin{array}{c} \text {Part M: type }d^*\text { Player 1's gain}\\ \text {by defecting rather than cooperation at history ({ C},\,{ D}).} \end{array}} \right) -\mu \cdot \frac{F(1-\mu )-F(d^*)}{1-F(d^*)} \right] . \end{aligned} \end{aligned}$$

(23)

It then follows that, the cut-off in the first period, $d^*$, is a solution to (23), which can be simplified to:

$$\begin{aligned} d^*=\frac{(1-\delta -\mu )F(d^*)+\delta F(1-\mu )}{1+\delta -\delta F(d^*)}, \end{aligned}$$

(24)

It can be verified that the RHS of (23) is strictly negative when $d^*=0$, and it is strictly positive when $d^*=1-\mu$. Since the RHS of (23) is continuous in $d^*$, equation (23) has a solution in $(0, 1-\mu )$, for any $\mu \in [0, 1)$. In case there are multiple solutions, we let $d^*$ be the minimum one in $(0, 1-\mu )$.

We now turn to prove that after Player 1 cooperated and his counterpart defected in period 1, Player 1 of type $d^*$ strictly prefers to continue cooperating. As shown in (23), by defecting rather than cooperating at history (C, D), by (6) the conditional payoff of Player 1 of type $d^*$ changes by

$$\begin{aligned} \begin{aligned}&d^*-(1-\mu )\cdot \frac{F(1-\mu )-F(d^*)}{1-F(d^*)}\\&\quad = \frac{-\frac{1}{\delta }\cdot \big (d^*-F(d^*)\big )+\big (F(1-\mu )-F(d^*) \big )-\frac{\mu }{\delta }\cdot F(d^*)}{1-F(d^*)} \\&\quad -(1-\mu )\cdot \frac{F(1-\mu )-F(d^*)}{1-F(d^*)}\\&\quad = \frac{1}{1-F(d^*)}\cdot \left\{ -\frac{d^*-F(d^*)}{\delta }+\mu \cdot \left[ F(1-\mu )-\left( 1+\frac{1}{\delta }\right) \cdot F(d^*) \right] \right\} . \end{aligned} \end{aligned}$$

(25)

Since $d>F(d)$ for all $d\in (0, 1]$ and since $d^*\in (0, 1]$, (25) is strictly negative for the case $\mu =0$. That is, for $\mu =0$, type $d^*$ of Player 1 is better off cooperating at history (C, D). Since following history (C, D), Player 1’s second period strategy is of the threshold form, the corresponding threshold, denoted $m^*$, then satisfies $m^*>d^*$ for the case $\mu =0$. The next lemma asserts that $d^*$ as a function of $\mu$ is continuous at $\mu =0$, and hence by continuity, formula (25) is negative for sufficiently small $\mu >0$, as desired.

Lemma 1

There exists $\tilde{\mu }>0$ and a function $d^*:[0, \tilde{\mu })\rightarrow (0, 1)$ such that $d^*(\mu )$ is a solution to (24) for all $\mu \in [0, \tilde{\mu })$, and $d^*(\mu )$ is continuous at $\mu =0$. Furthermore, for all $\mu \in [0, \tilde{\mu })$, $d^*(\mu )<1-\mu$.

Proof

Let

$$\begin{aligned} H(\mu , d):=\frac{(1-\delta -\mu )F(d)+\delta F(1-\mu )}{1+\delta -\delta F(d)}. \end{aligned}$$

(26)

Let $G: [0, 1]\times [0, 1]\rightarrow \mathbb {R}$ be

$$\begin{aligned} G(\mu , d):= H(\mu , d)-d. \end{aligned}$$

(27)

For $\mu =0$, let $d_0$ be the minimal solution to $G(0, d)=0$ on (0, 1). Here $d_0$ is well defined because (i) $G(0, d=0)>0$ and $G(0, d=1)<1$, and hence a solution to $G(0, d)=0$ on (0, 1) exists; (ii) the function G is continuous function on a compact set, hence the smallest solution exists.

Let $\mu >0$. Since $G(0, d_0)=0$ and $G(\mu , d)$ is decreasing in $\mu$, $G(\mu , d_0)<0$ for all $0<\mu <1$. Moreover, since $G(0, 0)>0$, and $G(\mu , d)$ is continuous in $\mu$, for sufficiently small $\mu >0$, $G(\mu , 0)>0$. Namely, there exists $\tilde{\mu }_1>0$ such that $G(\mu , 0)>0$ for all $\mu \in (0, \tilde{\mu }_1]$. Therefore, for $\mu \in (0, \tilde{\mu }_1]$, there exists a solution $d\in (0, d_0]$ to $G(\mu , d)=0$. Let $d^*(\mu )$ be the maximal solution in d to $G(\mu , d)=0$ in $(0, d_0]$. Here, again, $d^*(\mu )$ is well defined since G is continuous.

We next prove the continuity of $d^*(\mu )$ at $\mu =0$. We will show that for every sequence $(\mu _n)_{n\in \mathbb {N}}$ that converges to 0, the sequence $\big (d^*(\mu _n) \big )_{n\in \mathbb {N}}$ converges to $d_0$, where $d_0:=d^*(0)$.

Suppose to the contrary that there exists a sequence $(\mu _n)_{n\in \mathbb {N}}$ that converges to 0, under which the sequence $\big (d^*(\mu _n) \big )_{n\in \mathbb {N}}$ does not converge to $d_0$. Then there exists $\epsilon >0$ (without loss of generality we can assume that $\epsilon <3d_0$) such that for every $N\in \mathbb {N}$, there exists $n\ge N$ with $|d^*(\mu _n)-d_0|\ge \epsilon$. Since $G(0, 0)>0$ and $d_0$ is the minimal solution to $G(0, d)=0$, we have $G(0, d)>0$ for all $d\in [0, d_0)$. This, together with $\frac{\epsilon }{3}<d_0$, imply that $G(0, d_0-\frac{\epsilon }{3})>0$. Hence, for N sufficiently large, and for all $n\ge N$, we have $G(\mu _n, d_0-\frac{\epsilon }{3})>0$ and $G(\mu _n, d_0)<G(0, d_0)=0$. Therefore, the equation $G(\mu _n, d)=0$ has a solution in $[d_0-\frac{\epsilon }{3}, d_0]$. Since $d^*(\mu _n)$ is defined as the largest solution in $[0, d_0]$ to $G(\mu _n, d)=0$, we have $d^*(\mu _n)\in [d_0-\frac{\epsilon }{3}, d_0]$, contradicting $|d^*(\mu _n)-d_0|\ge \epsilon$. Hence for every sequence $(\mu _n)_{n\in \mathbb {N}}$ that converges to 0, the sequence $\big (d^*(\mu _n) \big )_{n\in \mathbb {N}}$ converges to $d_0$, as claimed.

We next argue that for small $\mu$, $d^*(\mu )< 1-\mu$. Indeed, since $d^*(\mu )+\mu$ is continuous in $\mu$ at $\mu =0$ and $d^*(0)+0<1$, there exists $\tilde{\mu }_2>0$ such that for all $\mu \in [0, \tilde{\mu }_2)$, we have $d^*(\mu )+\mu <1$. The proof of Lemma 1 is complete by letting $\tilde{\mu }=\min (\tilde{\mu }_1, \tilde{\mu }_2)$. $\square$

We have thus shown that for sufficiently small $\mu$, Player 1 of type $d^*$ is indifferent between cooperating and defecting in period 1, and he is better off continuing cooperation after the history (C, D). By (21) (resp. the effect of Player 1’s own action change in (22)), Player 1’s payoff change if he defects rather than cooperates in period 1 (resp. after the history (C, D)) is strictly decreasing in his type $d_1$. Hence (i) it is optimal for Player 1 to cooperate in the first period if and only if $d_1\le d^*$, and (ii) following (C, D), Player 1 of type $d_1\le d^*$ strictly prefers to continue cooperating.

To complete the proof that $s^*$ is an equilibrium, it is left to verify that Player 1 has no incentive to deviate from $s_1^*$ after histories (D, D), (C, C), and (D, C). If both players defect in period 1, then Player 2 must be of a type above $d^*$, and thus he defects for sure in period 2, making it optimal for Player 1 to defect. If Player 2 cooperated in period 1, then he must be of type $d_2\le d^*$, and thus continues cooperating in period 2, making it optimal for Player 1 to cooperate.

1.4 Proof of Proposition 4

Suppose $F_{1}\in \mathcal {G}_{1}$. By Definition 2, for every $B>1$, $\mu \ge 0$, and $x\in (0, 1]$, we have $(1-\mu )F_B(x)\le F_B(x)=F_{1}(\frac{x}{B})<F_{1}(x)\le x$. By Corollary 1, full defection is the unique equilibrium of $G_1(F_B, \mu )$.

Suppose $\mu$ is sufficiently small and it satisfies Proposition 3 (that is, $\mu \in [0, \widehat{\mu })$). Since $B>1$ and $F_B(x)<x$ for all $x\in (0, 1]$, by Proposition 3, the strategy profile $s^*$ defined in (4)–(5) is an equilibrium of $G_2(F_B, \mu )$.

We first analyze the case $\mu =0$. Define

$$\begin{aligned} \begin{aligned} H_{B}(x):=\frac{(1-\delta )F_B(x)+\delta \cdot F_B(1)}{1+\delta -\delta \cdot F_B(x)}. \end{aligned} \end{aligned}$$

(28)

By (24), the first-period threshold $d^*$ of $s^*$ in $G_2(F_B, \mu =0)$ is a fixed point of $H_B$.

Since $F_1$ satisfies (8) and since

$$\begin{aligned} H_{1}(x)>x \text { iff } F_{1}(x)>\frac{x-\delta (1-x)}{1-\delta (1-x)}, \end{aligned}$$

(29)

there exists $\widehat{x}\in (0, 1)$ such that $H_1(x)>x$ for all $x\in (\widehat{x}, 1)$. Let $\epsilon >0$. There exists $x_{\epsilon }\in (1-\frac{\epsilon }{2}, 1)$ such that $H_{1}(x_{\epsilon })>x_{\epsilon }$. By the uniform continuity of $H_B(x)$ as a bivariate function of (B, x) on $[1, 2]\times [0, 1]$, there exists $B_{\epsilon }>1$ such that for every $1<B<B_{\epsilon }$, $H_B(x_{\epsilon })>x_{\epsilon }$. Let $B\in (1, B_{\epsilon })$. By (28), $H_B(1)<1$. By the continuity of $H_B(x)$, the equation $H_B(d)=d$ has solutions in $(x_{\epsilon }, 1)$. Denote by $d^*_0$ the minimal solution to $H_B(d)=d$ in $(x_{\epsilon }, 1)$.

Similar to the proof of Lemma 1, there exists $\tilde{\mu }>0$ and a unique continuous function $d^*(\mu ):[0, \tilde{\mu })\rightarrow (0, 1-\mu )$ such that $d^*(0)=d_0^*$ and $d^*(\mu )$ satisfies (6). Therefore, there exists $\mu '$, $0<\mu '<\tilde{\mu }$, such that for all $\mu \in [0, \mu ')$, $d^*(\mu )-d_0^*<\frac{\epsilon }{2}$. Since $d_0^*\in (x_{\epsilon }, 1)$ and $x_{\epsilon }\in (1-\frac{\epsilon }{2}, 1)$, we have $d^*(\mu )\in (1-\epsilon , 1-\mu )$ for all $\mu \in [0, \mu ')$. That is, the two-period game $G_2(F_B, \mu )$ has an equilibrium $s^*$ defined in (4)–(5) where $d^*\in (1-\epsilon , 1-\mu )$, as claimed in Proposition 4.

1.5 Proof of Proposition 5

Let $F_B^u:[0,B] \rightarrow \mathbb {R}_{+}$ be the uniform distribution on [0, B], $B>1$. In this section we characterize all symmetric equilibrium of $G_2(F_B^u)$. We will use the following lemma, the proof of which is straightforward and hence omitted.

Lemma 2

Let $\mu =0$, and $F(x)=\frac{x}{B}$, $x\in [0, B]$.

• (i) Suppose $B<1$. Then $G_1(F, \mu )$ has exactly two equilibrium points: $(s_1^0, s_2^0)$ and $(s_1^B, s_2^B)$.

• (ii) Suppose $B=1$; then every $y \in [0,1]$ is a fixed point of $F(\cdot )$ and the set of equilibria of $G_1(F, \mu )$ is $\{(s_1^{y}, s_2^{y})|y \in [0,1]\}$.

• (iii) Suppose $B>1$. The only equilibrium of $G_1(F, \mu )$ is $(s_1^{0}, s_2^{0})$.

As shown in Proposition 2, all equilibria of $G_2(F_B^u)$ consist of threshold strategies. We will first show that given the second-period thresholds, the first-period threshold is uniquely determined. We then characterize the thresholds after any history. Then we go back to determine the first-period threshold. This procedure yields at most 4 different equilibrium points. The next lemma deals with all symmetric equilibria other than the fully defecting equilibrium.

Lemma 3

Except for the full-defection equilibrium, the game $G_2(F_B^u)$ has at most three symmetric equilibria. They are defined by the following thresholds:

• (i) For $1<B< 1+\delta$, $\gamma _1=(d^{\emptyset }=\frac{1+\delta -B}{\delta }, d_i^{C, C}=1, d_i^{X, Y}=0 \text { for all } (X, Y)\ne (C, C) )$.

• (ii) $\gamma _2=(d^{\emptyset }=\frac{2\delta }{b+\sqrt{b^2-4\delta ^2}} \text { where } b=(1+\delta )(B-1)+2\delta , d_i^{C, C}=d_1^{D, C}=d_2^{C, D}=1, d_1^{C, D}=d_2^{D, C}=\frac{1-d^{\emptyset }}{B-d^{\emptyset }}, d_i^{D, D}=0)$.

• (iii) For $1<B<1+\delta$, $\gamma _3=\Big (d^{\emptyset }=\frac{1}{2}\left[ B+\frac{\delta }{1+\delta -B} -\sqrt{\left( B+\frac{\delta }{1+\delta -B}\right) ^2-4}\right] , d_i^{C, C}=1, d_1^{C, D}=d_2^{D, C}=\frac{(1+\delta -B)d^{\emptyset }}{\delta }, d_1^{D, C}=d_2^{C, D}=\frac{1+\delta -B}{\delta }, d_i^{D, D}=0 \Big )$.

Proof

Let $s^*=(s_1^*,s_2^*)$ be an equilibrium of $G_2(F^u_B)$, where $F^u_B(x)=\frac{x}{B}$, $B>1$

Claim 1

Given the thresholds $d_i^{h^1}$, $h^1\in H^{1}$, $i=1, 2$, the first-period threshold, $d_i^{\emptyset }$, is uniquely determined.

Proof

The proof of Proposition 2 shows that if $s^*$ is an equilibrium of $G_2(F^u_B)$, $\Delta (d_i)\equiv U_i(d_i, C)-U_i(d_i, D)$ is strictly decreasing in $d_i$. Therefore the threshold $d_i^{\emptyset }$ is the unique solution of $\Delta (d_i)=0$. If $\Delta (d_i)<0$ for all $d_i\in [0, 1]$, then $d_i^{\emptyset }=0$ and $d_i^{\emptyset }=1$ if $\Delta d_i>0$ for all $d_i\in [0, 1]$. $\square$

Denote $d^{\emptyset }=d^*$. We next characterize the thresholds $d_i^{h^1}$, $h^1\in H^1$. Let us start with $h^1=(C, C)$. The updated belief of Player 1 over the types of Player 2 is $\widehat{F}^u_{\widehat{B}}(d_2)$ on $[0, \widehat{B}]$, and

$$\begin{aligned} \widehat{F}^u_{\widehat{B}}(d_2)=F^u_B(d_2|E_2^{\emptyset }), \quad \widehat{B}=d^*, \end{aligned}$$

where $E_2^{\emptyset }$ is the set of all types of 2 that choose C in the first period. By Proposition 2, $E_2^{\emptyset }=[0, d^*]$. By Lemma 2,

$$\begin{aligned} d_1^{C, C}=\min \big (\widehat{F}^u_{\widehat{B}}(d_2^{C, C}), B \big )=\widehat{F}^u_{\widehat{B}}(d_2^{C, C}) \end{aligned}$$

(30)

and

$$\begin{aligned} \widehat{F}^u_{\widehat{B}}(d_2^{C, C})=F^u_B(d_2^{C, C}|d_2\in [0, d^*]). \end{aligned}$$

Thus

$$\begin{aligned} d_1^{C,C}=\left\{ \begin{array}{ll} \frac{d_2^{C, C}}{d^*}&{}\quad \text{ if } d_2^{C, C}\le d^*\\ 1&{}\quad \text{ if } d_2^{C, C}\ge d^*.\\ \end{array} \right. \end{aligned}$$

(31)

Similarly,

$$\begin{aligned} d_2^{C,C}=\left\{ \begin{array}{ll} \frac{d_1^{C, C}}{d^*}&{}\quad \text{ if } d_1^{C, C}\le d^*\\ 1&{}\quad \text{ if } d_1^{C, C}\ge d^*.\\ \end{array} \right. \end{aligned}$$

(32)

By (30), (31), and (32), either $d^*=1$ and $0 \le d_1^{C,C}=d_2^{C,C} \le 1$ or $d^* <1$ and either $d_i^{C, C}=1$ or $d_i^{C, C}=0$.

Suppose next $h^1=(D, D)$. By Lemma 2,

$$\begin{aligned} d_1^{D, D}=F^u_B(d_2^{D, D}|d_2\notin E_2^{\emptyset })=\frac{Prob([0, d_2^{D, D}]\cap [d^*, B])}{Prob([d^*, B])}. \end{aligned}$$

(33)

Hence

$$\begin{aligned} d_1^{D, D}=\left\{ \begin{array}{ll} 0&{}\quad \text{ if } d_2^{D, D}\le d^*\\ \frac{d_2^{D, D}-d^*}{B-d^*}&{}\quad \text{ if } d_2^{D, D}\ge d^*.\\ \end{array} \right. \end{aligned}$$

(34)

Similarly,

$$\begin{aligned} d_2^{D, D}=\left\{ \begin{array}{ll} 0&{}\quad \text{ if } d_1^{D, D}\le d^*\\ \frac{d_1^{D, D}-d^*}{B-d^*}&{}\quad \text{ if } d_1^{D, D}\ge d^*.\\ \end{array} \right. \end{aligned}$$

(35)

Suppose $d_2^{D,D}>d^*$. By (34), $d_1^{D,D}>0$, and by (35), $d_1^{D,D}>d^*$. Hence (34) and (35) imply $d_1^{D,D}=d_2^{D,D} \equiv d$, where

$$\begin{aligned} d=\frac{d-d^*}{B-d^*}. \end{aligned}$$

Equivalently $d=\frac{d^*}{1+d^*-B}$. Since $B>1$, either $d<0$ or $d>1$, a contradiction. We conclude that $d_i^{D,D}=0$.

Suppose next $h^1=(C, D)$. Then by Lemma 2,

$$\begin{aligned} d_1^{C, D}=F^u_B(d_2^{C, D}|d_2\notin E_2^{\emptyset })=\frac{Prob([0, d_2^{C, D}]\cap [d^*, B])}{Prob([d^*, B])}. \end{aligned}$$

Consequently,

$$\begin{aligned} d_1^{C, D}=\left\{ \begin{array}{ll} 0&{}\quad \text{ if } d_2^{C, D}\le d^*\\ \frac{d_2^{C, D}-d^*}{B-d^*}&{}\quad \text{ if } d_2^{C, D}\ge d^*.\\ \end{array} \right. \end{aligned}$$

(36)

Similarly,

$$\begin{aligned} d_1^{D, C}=\left\{ \begin{array}{ll} 1&{}\quad \text{ if } d^*\le d_2^{D, C}\\ \frac{d_2^{D, C}}{d^*}&{}\quad \text{ if } d^*>d_2^{D, C}.\\ \end{array} \right. \end{aligned}$$

(37)

Let $d_1^{D, C}=d_2^{C, D}=x$ and $d_1^{C, D}=d_2^{D, C}=y$ (symmetric equilibrium). By (36) and (37),

$$\begin{aligned} y= & {} \left\{ \begin{array}{ll} 0&{}\quad \text{ if } x\le d^*\\ \frac{x-d^*}{B-d^*} &{}\quad \text{ if } x\ge d^*.\\ \end{array} \right. \end{aligned}$$

(38)

$$\begin{aligned} x= & {} \left\{ \begin{array}{ll} 1&{}\quad \text{ if } y\ge d^*\\ \frac{y}{d^*} &{}\quad \text{ if } y\le d^*.\\ \end{array} \right. \end{aligned}$$

(39)

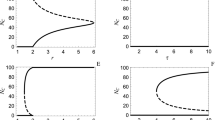
There are two cases (see Fig. 4):

Fig. 4

Graphs of (38) and (39)

In Case 1 of Fig. 4 the only solution is $x=y=0$. In Case 2 there are 3 solutions: (i) (0, 0); (ii) $\left( 1, \frac{1-d^*}{B-d^*} \right)$, where $\frac{1-d^*}{B-d^*}\in (0, 1)$ and (iii) $\left( \frac{d^*}{1-d^*(B-d^*)}, \frac{(d^*)^2}{1-d^*(B-d^*)} \right)$ provided $\frac{(d^*)^2}{1-d^*(B-d^*)} \le d^*$ and $\frac{d^*}{1-d^*(B-d^*)} \ge d^*$. It is easy to verify that the last two inequalities hold iff either $d^*=0$ or $d^* \le \frac{B+1-\sqrt{(B+1)^2-4}}{2}$. Hence $0 \le d^*<1$ must hold and either $d_i^{C,C}=0$ or $d_i^{C,C}=1$ (see the sentence below (32)). Let us examine these three cases.

Solutions (i) and (ii): Suppose $d_1^{X, Y}=d_2^{X, Y}=0$ for $X\ne Y$, $X,Y \in \{C,D\}$, $d_i^{D, D}=0$, and $d^*<1$. Then either $d_i^{C, C}=1$ or $d_i^{C,C}=0$. Suppose first that $d_i^{C,C}=1$. If Player 1 of type $d_1 \le 1$ chooses C in period 1 he obtains

$$\begin{aligned} \begin{aligned} U_1(C, d_1)&=\frac{d^*}{B}+\delta \big [Prob(d_2\le d^*)\cdot 1+Prob(d_2>d^*)\cdot d_1 \big ]\\&=(1+\delta )\frac{d^*}{B}+\frac{\delta (B-d^*)}{B}\cdot d_1. \end{aligned} \end{aligned}$$

(40)

If 1 chooses D in period 1 he obtains $U_1(D, d_1)=(1+\delta )d_1$. Hence $d^*$ is the solution to

$$\begin{aligned} (1+\delta )\frac{d^*}{B}+\frac{\delta (B-d^*)d^*}{B}=(1+\delta )d^*. \end{aligned}$$

There are two solutions to the last equation. The first one is $d^*=\frac{1+\delta -B}{B}$ and for $B<1+\delta$, $0<d^*<1$. In this case $d_i^{X,Y}=0$ for any $(X,Y) \ne (C,C)$ and $d_i^{C,C}=1$. The other solution is $d^*=0$ with $d_i^{D,D}=0$. On the equilibrium path every type of every player (except for type 0) defects in both periods. Since any history $h^1$ other than (D, D) is off the equilibrium path there are no restrictions on beliefs following $h^1$.

Suppose now $d_i^{C,C}=0$. Similarly to (40), $U_1(C,d_1)=\frac{d^*}{B}+\frac{\delta (B-d^*)}{B}d_1$ and $U_1(D,d_1)=(1+\delta )d_1$. Since $U_1(C,d_1) \ge U_1(D,d_1)$ iff $d_1 \le \frac{(1-\delta )d^*}{B}$ we must have $d^*=\frac{(1-\delta )d^*}{B}$ and again $d^*=0$.

To complete the analysis of solution (i) we prove that $d^*\ne 1$. Suppose that $d^*=1$ and $d_i^{C,C} \le 1$ (see the sentence below (32)):

$$\begin{aligned} U_1(C,d_1)= & {} \frac{d^*}{B}+\delta [Prob(d_2 \le d^*)Prob(d_2 \le d_2^{C,C}|d_2 \le d^*)+Prob(d_2>d^*)d_1],\\ U_1(C,d_1)= & {} \frac{d^*}{B}+\frac{\delta d_2^{C,C}}{B}+\frac{\delta (B-d^*)d_1}{B}, \end{aligned}$$

while

$$\begin{aligned} U_1(D,d_1)=(1+\delta )d_1. \end{aligned}$$

Since $d^*=1$, we have

$$\begin{aligned} \frac{1}{B}+\frac{\delta d_2^{C,C}}{B}+\frac{\delta (B-1) \cdot 1}{B}=1+\delta . \end{aligned}$$

Equivalently, $1+\delta d_2^{C,C}-\delta =B$, but this contradicts $B>1$.

The solution (ii) is essentially the strategy profile described in (4)–(5). Since it has been thoroughly studied in “Appendix A.3”, we omit the detailed analysis here.

Finally, let us analyze solution (iii) of Case 2 in Fig. 4. Let

$$\begin{aligned} \gamma _3&=(d^{\emptyset }=d^*, d_i^{C,C}=1, d_i^{D,D}=0, d_1^{D,C}=d_2^{C,D}=x=\frac{d^*}{(d^*)^2-Bd^*+1},\\&d_1^{C,D}=d_2^{D,C}=y=\frac{(d^*)^2}{(d^*)^2-Bd^*+1}). \end{aligned}$$

Note, that $0 <x \le 1$ iff

$$\begin{aligned} d^* \le \frac{B+1-\sqrt{(B+1)^2-4}}{2}. \end{aligned}$$

(41)

In this case, $y = d^* x \le d^* <x$. The last inequality holds since $B>1$. It can be easily verified that in this case (38) holds. Hence $\gamma _3$ defines an equilibrium iff (41) holds. Suppose that $d_1 \le 1$. Then,

$$\begin{aligned} U_1(C,d_1)&=(1+\delta )Prob(d_2 \le d^*)+\delta Prob(d_2>d^*)\nonumber \\&\quad \cdot \left\{ \begin{array}{ll} Prob(d_2 \le x|d_2>d^*)&{}\quad d_1 \le y\\ d_1 &{}\quad d_1>y\\ \end{array} \right. =\nonumber \\&=\frac{(1+\delta )d^*}{B}+\frac{\delta (B-d^*)}{B} \cdot \left\{ \begin{array}{ll} \frac{x-d^*}{B-d^*}&{}\quad d_1 \le y\\ d_1 &{}\quad d_1>y.\\ \end{array} \right. \end{aligned}$$

(42)

Next,

$$\begin{aligned} U_1(D,d_1)&=d_1+\delta [Prob(d_2 \le d^*)\cdot \nonumber \\&\quad \left\{ \begin{array}{ll} Prob(d_2 \le y|d_2 \le d^*)&{}\quad d_1 \le x\\ d_1 &{}\quad d_1>x\\ \end{array} \right. +d_1 Prob(d_2>d^*)] \nonumber \\&=d_1+\delta \left\{ \begin{array}{ll} \frac{y}{B}&{}\quad d_1 \le x\\ d_1 \frac{d^*}{B}&{}\quad d_1>x\\ \end{array} \right. +\frac{\delta (B-d^*)d_1}{B}. \end{aligned}$$

(43)

Subcase 1 Suppose $d_ 1 \le y$. Since $y \le x$, $U_1(C,d_1) \ge U_1(D,d_1)$ iff

$$\begin{aligned} \frac{(1+\delta )d^*}{B}+\frac{\delta (x-d^*)}{B} \ge d_1+\frac{\delta y}{B}+\frac{\delta (B-d^*)d_1}{B}. \end{aligned}$$

By the definition of $\gamma _3$, $y=d^*x$,

$$\begin{aligned} d_1[1+\frac{\delta (B-d^*)}{B}] \le \frac{(1+\delta )d^*}{B}+\frac{\delta (x-d^*)}{B}-\frac{\delta d^* x}{B} \end{aligned}$$

and

$$\begin{aligned} d_1 \le \frac{d^*+\delta (x-y)}{B(1+\delta )-\delta d^*} \equiv \widehat{d}. \end{aligned}$$

Next,

$$\begin{aligned} \widehat{d} \ge y \text{ iff } \frac{d^*+\frac{\delta d^* (1-d^*)}{(d^*)^2-Bd^*+1}}{B(1+\delta )-\delta d^*}>\frac{(d^*)^2}{(d^*)^2-B d^*+1} \end{aligned}$$

or, equivalently,

$$\begin{aligned} \widehat{d} \ge y \text{ iff } (1+\delta )(d^*)^2-\delta ^* ((2+\delta )B+\delta )+(1+\delta ) \ge 0. \end{aligned}$$

(44)

Note, that no equilibrium exists with $\widehat{d}<y$, since in equilibrium $y<d^*$ and $\widehat{d}=d^*$ must hold. So any candidate for an equilibrium of the next two subcases must have $\widehat{d} \ge y$.

Subcase 2 Suppose $y<d_1 \le x$. Then

$$\begin{aligned} U_1(C,d_1) \ge U_1(D,d_1) \text{ iff } d_1 \le \frac{(1+\delta )d^*-\delta y}{B} \equiv R_1. \end{aligned}$$

Subcase 3 Suppose $d_1 > x$. Then $U_1(C,d_1) \ge U_1(D,d_1)$ iff

$$\begin{aligned}&\frac{(1+\delta )d^*}{B}+\frac{\delta (B-d^*)d_1}{B} \ge d_1+\frac{\delta d_1d^*}{B}+\frac{\delta (B-d^*)d_1}{B}.\nonumber \\&d_1 \le \frac{(1+\delta ) d^*}{B+\delta d^*} \equiv R_2 \end{aligned}$$

(45)

It is easy to verify that $x \le R_2$ iff $x \le R_1$ and in this case $R_2 \le R_1$. Consequently, either $x \le R_2 \le R_1$ or $x \ge R_2 \ge R_1$.

There are four cases to check (recall that $y \le d^*<x$ must hold).

(1) $y<x \le R_2 \le R_1$. In this case, $d^*=R_2$ and $x \le d^*$, a contradiction. (2) $R_1 \le R_2 \le y \le x$. In this case, $d^*=y$ and $x=1$. That is, $\frac{d^*}{(d^*)^2-Bd^*+1}=1$ or $(d^*)^2-Bd^*+1=d^*$. But it is easy to verify from (44) that in this case $\widehat{d}<y$ and it yields no equilibrium. (3) $R_1 \le y \le R_2 \le x$. In this case again $d^*=y$. (4) $y \le R_1 \le R_2<x$. In this case, $d^*=R_1=\frac{(1+\delta )d^*-\delta y}{B}$. For $1<B<1+\delta$, $y=\frac{(1+\delta -B)d^*}{\delta }<d^*$ and $x=\frac{1+\delta -B}{\delta }$. It is easy to verify that (i) (41) holds, (ii) $x>R_1 \ge R_2=d^*$, and (iii) (44) holds. Since

$$\begin{aligned} x=\frac{d^*}{(d^*)^2-Bd^*+1}=\frac{1+\delta -B}{\delta } \end{aligned}$$

we have

$$\begin{aligned} d^*=\frac{2}{B+\frac{\delta }{1+\delta -B}+\sqrt{(B+\frac{\delta }{1+\delta -B})^2-4}}, \end{aligned}$$

where $d^*$ is decreasing in B and $\lim _{B \downarrow 1} d^* \nearrow 1$. This completes the proof of Lemma 3.

1.6 Proof of Proposition 6

Suppose $\mu =0$ and let $F_B\in \mathscr {F}(F_1)$, where $B>1$. It is shown in “Appendix A.4” that full defection is the unique equilibrium of $G_1(F_B)$ if $F_1\in \mathcal {G}_1$. We next deal with distributions in $\mathcal {G}_1$ and identify a subset of $\mathcal {G}_1$ for which $G_T(F_B)$ has an equilibrium where $d_T^*$ defined in (12) converges to 1, as the proportion of the dominant types decreases to 0.

Step 1: For every $T\ge 3$, $d_T^*< m^*_T$.

By the Mean Value Theorem, it can be verified that equation (12) has a solution $d_T^*$ in (0, 1). By (12),

$$\begin{aligned} \begin{aligned}&d_T^*\cdot \delta \cdot \big (1-F_B(d_T^*)\big )\\&\quad =-\big (d_T^*-F_B(d_T^*)\big )+\delta \cdot \big (F_B(1)-F_B(d_T^*)\big )+(1-d_T^*)\cdot \Delta \cdot \big (F_B(1)-F_B(d_T^*)\big ). \end{aligned} \end{aligned}$$

(46)

Since $F_1\in \mathcal {G}_1$ and since the function $F_B$ is generated by $F_1$ with $B>1$, by the definitions of $F_B$ and $\mathcal {G}_1$, we have $F_B(x)=F_1(\frac{x}{B})<F_1(x)\le x$. Hence

$$\begin{aligned} F_B(x)< x\quad \text {for all}\quad x\in (0, 1]. \end{aligned}$$

(47)

This observation, together with $d_T^*\in (0, 1)$, imply that $d_T^*>F_B(d_T^*)$. By (46),

$$\begin{aligned} \begin{aligned} d_T^*\cdot \delta \cdot \big (1-F_B(d_T^*)\big )< \delta \cdot \big (F_B(1)-F_B(d_T^*)\big )+(1-d_T^*)\cdot \Delta \cdot \big (F_B(1)-F_B(d_T^*)\big ). \end{aligned} \end{aligned}$$

(48)

This implies

$$\begin{aligned} \begin{aligned} d_T^*< \frac{\delta \cdot \big (F_B(1)-F_B(d_T^*)\big )}{\delta \cdot \big (1-F_B(d_T^*)\big )}+(1-d_T^*) \cdot \frac{\Delta \cdot \big (F_B(1)-F_B(d_T^*)\big )}{\delta \cdot \big (1-F_B(d_T^*)\big )}. \end{aligned} \end{aligned}$$

(49)

Equivalently,

$$\begin{aligned} \begin{aligned} d_T^*&<\frac{\delta \cdot \big (F_B(1)-F_B(d_T^*)\big )+\Delta \cdot \big (F_B(1)-F_B(d_T^*)\big )}{\delta \cdot \big (1-F_B(d_T^*)\big )+\Delta \cdot \big (F_B(1)-F_B(d_T^*)\big )}\\&=m_T^*. \end{aligned} \end{aligned}$$

(50)

Step 2: In this step we show that the strategy profile $s_T^*=(s_{T1}^*, s_{T2}^*)$ defined in Sect. 4 (see (9)–(10) for the first two periods) is an equilibrium of $G_T(F_B)$.

Let us show that $s_{T1}^*$ is a best response to $s_{T2}^*$. If Player 1 is of type $d>1$, then defect is a dominant strategy. Suppose next Player 1 is of type $d\le 1$.

If the pair of actions in period 2 is (C, C), then Player 2’s type must be below 1, and hence starting from period 3 Player 2 cooperates in every period. Therefore, cooperating in every period $t\ge 3$ is a best response for Player 1 of type $d\le 1$. If the pair of actions in period 2 is other than (C, C), then regardless of his type Player 2 defects in every period t, $t\ge 3$. Hence defecting in every period t, $t\ge 3$ is a best response to $s_{T2}^*$ for all types of Player 1.

Next consider period 2. Suppose the first-period pair of actions is (C, C). Then Player 2’s type must be below $d_T^*$, and Player 2 cooperates in period 2. Therefore, cooperate in period 2 is a best response of Player 1 of type $d\le 1$.

Suppose next the first-period pair of actions is (D, D), then regardless of his type Player 2 defects in period 2, and defecting in period 2 is a best response for all types of Player 1.

Suppose the first-period pair of actions is (D, C). Then Player 2’s type must be below $d_T^*$. Since $d_T^*<m_T^*$ (Step 1), Player 2 cooperates in period 2. Cooperating in period 2 is therefore a best response action for Player 1 of type $d\le 1$.

Suppose the first-period pair of actions is (C, D). If Player 1 cooperates in period 2, his expected payoff is

$$\begin{aligned} \begin{aligned} v_1(C)|_{(C, D)}:=\frac{F_B(1)-F_B(d_T^*)}{1-F_B(d_T^*)}\cdot 1&+\frac{F_B(1)-F_B(d_T^*)}{1-F_B(d_T^*)}\cdot \frac{\Delta }{\delta }\\&+\left( 1-\frac{F_B(1)-F_B(d_T^*)}{1-F_B(d_T^*)} \right) \cdot d_1\cdot \frac{\Delta }{\delta }, \end{aligned} \end{aligned}$$

(51)

where $\frac{F_B(1)-F_B(d_T^*)}{1-F_B(d_T^*)}$ is the conditional probability that Player 2 cooperates in period 2, given that he defected in period 1. If Player 1 of type $d_1$ defects in period 2, his expected payoff is

$$\begin{aligned} v_1(D)|_{(C, D)}:=d_1+d_1\cdot \frac{\Delta }{\delta }. \end{aligned}$$

(52)

It can be verified that $v_1(C)|_{(C, D)}\ge v_1(D)|_{(C, D)}$ if and only if

$$\begin{aligned} d_1\le \underbrace{\frac{\delta \cdot \big (F_B(1)-F_B(d_T^*)\big )+\Delta \cdot \big (F_B(1)-F_B(d_T^*)\big ))}{\delta \big (1-F_B(d_T^*) \big )+\Delta \cdot \big (F_B(1)-F_B(d_T^*) \big )}}_{m_T^*}. \end{aligned}$$

(53)

By (13), the RHS of (53) is equal to $m_T^*$. Therefore, if the first-period pair of actions is (C, D), it is a best response for Player 1 of type $d_1\le m_T^*$ to cooperate in period 2.

Next we examine the first period actions. If Player 1 of type $d_1$ plays C in the first period and follows $s_{T1}^*$ then after, his expected payoff (given that Player 2 plays $s_{T2}^*$) is

$$\begin{aligned} v_1(C):=F_B(d_T^*)+\delta \cdot F_B(1)\cdot 1+\Delta \cdot \big [F_B(1)\cdot 1+(1-F_B(1))\cdot d_1 \big ]. \end{aligned}$$

(54)

If Player 1 of type $d_1$ plays D in the first period and follows $s_{T1}^*$ then after, he obtains

$$\begin{aligned} v_1(D):=d_1+\delta \cdot \big [F_B(d_T^*)\cdot 1+\big (1-F_B(d_T^*)\big )\cdot d_1 \big ]+\Delta \cdot \big [F_B(d_T^*)\cdot 1+\big (1-F_B(d_T^*)\big )\cdot d_1 \big ]. \end{aligned}$$

(55)

By (54) and (55), it can be verified that $v_1(C)\ge v_2(D)$ if and only if

$$\begin{aligned} d_1\le \underbrace{\frac{F_B(d_T^*)+\delta \cdot \big (F_B(1)-F_B(d_T^*)\big )+\Delta \cdot \big (F_B(1)-F_B(d_T^*)\big ))}{1+\delta \big (1-F_B(d_T^*) \big )+\Delta \cdot \big (F_B(1)-F_B(d_T^*) \big )}}_{d_T^*}. \end{aligned}$$

(56)

Note that the RHS of (56) is $d_T^*$ given by (12).

We conclude that in the first period, it is a best response for Player 1 of type $d_1\le d_T^*$ to cooperate and all other types to defect. This completes the proof of Step 2.

Step 3: In this step we show that if $F_1$ satisfies (14), then for $F_B\in \mathscr {F}(F_1)$, $d_T^*$ converges to 1 as $B\downarrow 1$.

Suppose that $F_1\in \mathcal {G}_1$ and $F_1$ satisfies (14). Then there exists $\widehat{x}\in (0, 1)$ such that for all $x\in (\widehat{x}, 1)$,

$$\begin{aligned} F_1(x)>\overbrace{\frac{x-(\delta +\Delta )(1-x)}{1-(\delta +\Delta )(1-x)}}^{R_T(x)}. \end{aligned}$$

(57)

Let

$$\begin{aligned} H_1^T(x):=\frac{F_1(x)+(\delta +\Delta )\big (1-F_1(x)\big )}{1+(\delta +\Delta ) \big (1-F_1(x)\big )}. \end{aligned}$$

It can be verified that the condition $F_1(x)>R_T(x)$ is equivalent to $H_1^T(x)>x$. Let

$$\begin{aligned} H_B^T(x):=\frac{F_B(x)+\delta \big (F_B(1)-F_B(x)\big )+ \Delta \big (F_B(1)-F_B(x)\big )}{1+\delta \big (1-F_B(x) \big )+\Delta \big (F_B(1)-F_B(x) \big )}. \end{aligned}$$

(58)

By (12), the threshold for cooperation in the first period of $G_T(F_B)$, $d_T^*$, is a fixed point of $H_B^T$.

It can be verified that for $B>1$, $H_1^T(x)>H_B^T(x)$ for every $x\in (0, 1]$. By the uniform continuity of $H_B(x)$ as a bivariate function of (B, x) on $[1, 2]\times [0, 1]$, for every $\zeta$, there exists $B^{\zeta }>1$ such that for every $1<B\le B^{\zeta }$,

$$\begin{aligned} \max _{x\in [0, 1]}\left( |H^T_{1}(x)-H^T_{B}(x)|\right) <\zeta . \end{aligned}$$

(59)

To complete the proof of Proposition 6, let $0<\epsilon <1$. Since $F_1$ satisfies (14), there exists $x_{\epsilon }$, $1-\epsilon<x_{\epsilon }<1$ such that $H_1^T(x_{\epsilon })>x_{\epsilon }$. By (59), there exists $B_{\epsilon }$ such that for every $1<B<B_{\epsilon }$, $H^T_B(x_{\epsilon })>x_{\epsilon }$. By (58), $H^T_B(1)<F_B(1)<1$. Since $H^T_B(x)$ is continuous in x, the equation $H_B^T(x)=x$ has a solution $d_T^*\in (1-\epsilon , 1)$. Therefore, the first-period threshold $d_T^*$ given in (12), is in $(1-\epsilon , 1)$, as claimed.