Expected utility theory with probability grids and preference formation

Abstract

We reformulate expected utility theory, from the viewpoint of bounded rationality, by introducing probability grids and a cognitive bound; we restrict permissible probabilities only to decimal ($\ell$-ary in general) fractions of finite depths up to a given cognitive bound. We distinguish between measurements of utilities from pure alternatives and their extensions to lotteries involving more risks. Our theory is constructive from the viewpoint of the decision maker. When a cognitive bound is small, the preference relation involves many incomparabilities, but these diminish as the cognitive bound is relaxed. Similarly, the EU hypothesis would hold more for a larger bound. The main part of the paper is a study of preferences including incomparabilities in cases with finite cognitive bounds; we give representation theorems in terms of a 2-dimensional vector-valued utility functions. We also exemplify the theory with one experimental result reported by Kahneman and Tversky.

Introduction

We reconsider EU theory from the viewpoints of bounded rationality and preference formation. We restrict permissible probabilities to decimal ($\ell$-ary, in general) fractions up to a given cognitive bound $\rho ;$ if $\rho$ is a natural number k, the set of permissible probabilities is given as $\varPi _{\rho }=\varPi _{k}=\{\frac{0}{10^{k}},\frac{1}{10^{k}},\ldots , \frac{10^{k}}{10^{k}}\}$. The decision maker makes preference comparisons step by step using probabilities with small k to those with larger $k^{\prime }$ to obtain accurate comparisons. The derived preference relation is incomplete in general, but the EU hypothesis holds for some lotteries and it would hold more when there is no cognitive bound, i.e., $\rho =\infty$ and $\varPi _{\infty }=\cup _{k<\infty }\varPi _{k}$. However, our main concern is the case of finite and small $\rho$. Since the theory involves various entangled aspects, we first disentangle them.

The concepts of probability grids and cognitive bounds are introduced based on the idea of “bounded rationality.” The idea can be interpreted in many ways such as bounded logical inference, bounded perception ability, though Simon’s (1956) original concept meant a relaxation of utility maximization. The mathematical components involved in EU theory are classified into two types; object components used by the decision maker and meta-components used by the outside analyst and possibly by the decision maker himself. The former are primary targets in EU theory, and the latter such as highly complex rational as well as irrational probabilities are added for analytic convenience. A free use of the latter leads to a critique that the theory presumes “super rationality” (Simon 1983).

As a significance level for statistical hypothesis testing is typically $5\%$ or $1\%$, probability values $\frac{t}{10^{2}} (t=0,\ldots ,10^{2})$ are already quite accurate for ordinary people. However, the classical EU theory starts with the full real number theory and makes no separation between the viewpoints of the decision maker and the outside analyst for available probabilities. This appears to be a problem of degree, but it would be meaningful if they are separated in some manner. The concepts of probability grids and a cognitive bound $\rho$ make this separation.

Turing (1937) in his attempt to define computable numbers faced a similar situation: “...The differences from our point of view between the single and compound symbols is that the compound symbols, if they are too lengthy, cannot be observed at one glace. This is in accordance with experience. We cannot tell at a glance whether $\underline{0.}9999999999999999$ and $\underline{0.}999999999999999$ (the underlined parts by the author) are the same (1937, p. 250).”¹ In contrast, it is easy for us to distinguish between 0.999 and 0.99. Turing’s theory tried to abstract calculation in the human mind, but a built machine has no such problem since it reads each primitive symbol one by one. This is, so far, due to the difference in human and machine cognition. A cognitive bound $\rho$ is a bound on such distinguishability and also on how deep the decision maker cares about those probabilities.

The set of probability grids up to depth k is given as $\varPi _{k}=\{\frac{0 }{10^{k}},\frac{1}{10^{k}},\ldots ,\frac{10^{k}}{10^{k}}\}$. The decision maker thinks about his preferences with $\varPi _{k}$ from a small k to a larger k up to bound $\rho ;$ for example, when $\rho =2$, $\varPi _{0}$, $\varPi _{1}$, and $\varPi _{2}$ are only allowed. This is a constructive approach from the viewpoint of the decision maker in the sense that he finds/forms his own preferences.²$^{,}$³

We turn our attention to the development of our constructive EU theory. Construction needs a basis; we take a hint from Von Neumann and Morgenstern (1944), Section 3.3.2, p.17. They mentioned a separation of their argument into the following two steps, though this was not reflected in their mathematical development:

Step B::

measurements of utilities from pure alternatives in terms of probabilities;

Step E::

extensions of these measurements to lotteries involving more risks.

These steps differ in their natures: Step B is to measure a “satisfaction”, “desire”, etc. from a pure alternative, while Step E is to extend the measured satisfactions given by Step B to lotteries including more risks. An important difference is that Step B is to find the subjective preferences hidden in the mind of the decision maker, while Step E is to extend logically the preferences found in Step B to lotteries with more risks.

Fig. 1

Step B with the benchmark scale

We develop our theory based on the above two steps and also take two approaches in terms of preferences and numerical utilities; each approach consists of Steps B and E. In this introduction, we focus mainly on the former theory, and we give a brief explanation of the latter.⁴

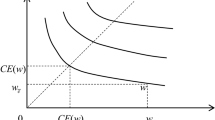
We assume two pure alternatives ${\overline{y}}$ and ${\underline{y}}$, called the upper and lower benchmarks;  these together with the probability grids $\varPi _{k}$ form the benchmark scale $B_{k}({\overline{y}}; {\underline{y}})$ in layer k. In Step B, pure alternatives are measured by this scale. Preferences are constructed in shallow to deeper layers, where preferences are incomplete in the beginning, except for benchmark lotteries as measurement units, and in deeper layers, more precise preferences may be found. In Fig. 1, the benchmark scale for layer k is depicted as the right broken line with dots; x is measured exactly by the scale, y need a more precise scale within $\rho$. However, z is not done within $\rho$.

Two different roles of probability grids appear for evaluation of a lottery:

• (i) probability grids used for measurement of a pure alternative in Step B;

• (ii) probability coefficients to pure alternatives.

By these, relevant cognitive depths of lotteries become more complex, especially with a finite cognitive bound; this leads to incomparabilities in preferences and a violation of the EU hypothesis. This is central in our development and is closely related to the issue of “bounded rationality”.

Let us illustrate (i) and (ii) via an example, which is a lottery for choice in the Allais paradox in Sect. 8. Consider one example with the upper and lower benchmarks ${\overline{y}}$, ${\underline{y}}$, and the third pure alternative y with strict preferences ${\overline{y}}\succ y\succ {\underline{y}}$. In Step B, the decision maker looks for a probability $\lambda$ so that y is indifferent to a lottery $[{\overline{y}},\lambda ; {\underline{y}}]=\lambda {\overline{y}}*(1-\lambda ){\underline{y}}$ with probability $\lambda$ for ${\overline{y}}$ and $1-\lambda$ for ${\underline{y}} ;$ this indifference is denoted by

$$\begin{aligned} y\sim [{\overline{y}},\lambda ;{\underline{y}}]. \end{aligned}$$

(1)

Suppose that this $\lambda$ is uniquely determined as $\lambda =\lambda _{y}=\frac{83}{10^{2}}\in \varPi _{2}$. Here, exact measurement of y is successful in layer 2, where Step B is enough here.

We have the other source of cognitive depths as mentioned in (ii). Consider lottery $d=\tfrac{25}{10^{2}}y*\tfrac{75}{10^{2}}{\underline{y}}$, which includes the third pure alternative y. The independence condition of the classical EU theory dictates that because of (1), $[{\overline{y}}, \frac{83}{10^{2}};{\underline{y}}]$ is substituted for y in d, and d is reduced to:

$$\begin{aligned} d=\tfrac{25}{10^{2}}y*\tfrac{75}{10^{2}}{\underline{y}}\sim \tfrac{25}{ 10^{2}}\left[ {\overline{y}},\tfrac{83}{10^{2}};{\underline{y}}\right] *\tfrac{75}{10^{2}} {\underline{y}}=\tfrac{2075}{10^{4}}{\overline{y}}*\tfrac{7925}{10^{4}} {\underline{y}}, \end{aligned}$$

(2)

where $\frac{2075}{10^{4}}=\frac{25}{10^{2}}\times \frac{75}{10^{2}}$ and $\frac{7925}{10^{4}}=1-\frac{2075}{10^{4}}$. Thus, y is evaluated as being indifferent to $[{\overline{y}},\frac{83}{10^{2}};{\underline{y}}]$ in Step B, but y also has a probability coefficient $\frac{25}{10^{2}}$ in d, which is taken into account in Step E. These steps lead to probability $\frac{2075}{10^{4}}$, which is much more precise than either of $\tfrac{83}{10^{2}}$ and $\tfrac{25}{10^{2}}$.

As indicated in (i) and (ii), lottery $d=\tfrac{25}{10^{2}}y*\tfrac{75}{ 10^{2}}{\underline{y}}$ has two types of cognitive depths; one is simply a probability coefficient $\frac{25}{10^{2}}$ and the other is $\lambda _{y}= \tfrac{83}{10^{2}}$ from (1). Although d itself is expressed as a lottery of depth 2, the total depths including these two are 4, which is beyond the cognitive bound $\rho =2$. One point is that the resulting probability may become more precise from lotteries of a relatively small bound, and the other is that this is intimately related to the EU hypothesis. When $\rho$ is small, the EU hypothesis does not hold typically, while it would hold more as $\rho$ is getting larger.

The preference formation by Steps B and E is formulated as a form of mathematical induction; Step B is the inductive base and Step E is the inductive step. Step B is spread out to layers of various depths, i.e., the induction base is spread, too. These steps are described in Table 1: the relation $\unrhd _{k}$ for layer k of row B expresses preferences measured in Step B . In layer k, $\succsim _{k}$ is derived from $\unrhd _{k}$ and $\succsim _{k-1};$ the former is a part of the inductive base and the latter is the inductive step. This is a weak form of “independence condition.”

Table 1 Measurement and extension

As stated earlier, we provide another approach in terms of a 2-dimensional vector-valued utility functions $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}=\langle [{\overline{\upsilon }}_{k},{\underline{\upsilon }} _{k}]\rangle _{k<\rho +1}$ and $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}=\langle [{\overline{u}}_{k},{\underline{u}}_{k}]\rangle _{k<\rho +1}$ with Fishburn’s (1970) interval order $\ge _{I}$. In each of Steps B and E, this approach is entirely equivalent to the preference approach, as depicted in Table 2. This may be interpreted as what Von Neumann and Morgenstern (1944), p.29, indicated. The approaches in terms of preferences and utilities enable us to view Steps B and E in different ways as well as they serve different analytic tools for studies of incomparabilities/comparabilities involved.

Table 2 Developments of the preference and utility theories

Our theory enjoys a weak form of the expected utility hypothesis. This will be discussed in Sect. 6. In the case of $\rho =\infty$, restricting our attention to the set of measurable pure alternatives, Sect. 7 shows that our theory exhibits a form of the classical EU theory. We provide a further extension of $\succsim _{\infty }$ to have the full form of the classical EU theory; this extension involves some unavoidable non-constructive step, which may be interpreted as the criticism of “super rationality” by Simon (1983).

A remark is on the relationship between k and $\rho$ exhibiting a layer and a cognitive bound. The former is a variable in our theory, and the latter is a parameter of the theory. We talk about the sequences $\langle \succsim _{k}\rangle _{k<\rho +1}$ and $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ describing the process of preference/utility formation, layer to layer, up to $\rho$. Nevertheless, the final target preferences and utilities are $\succsim _{\rho }$ and ${\varvec{u}}_{\rho }$. In the context of the quotation from Turing (1937), within the layers up to $\rho$, the decision maker can distinguish each probability as a single symbol, but beyond $\rho$, he would have a difficulty; here, it is assumed that he does not think about his decision problem beyond $\rho$. When $\rho =\infty$, he can treat any grid probability as a single entity. This remark leads to the view that our theory is a generalization of the classical EU theory, which is discussed in Sect. 7.

In Sect. 8, we apply our theory to the Allais paradox, specifically to an experimental result from Kahneman and Tversky (1979). We show that the paradoxical results remains when the cognitive bound $\rho \ge 3$. However, when $\rho =2$, the resultant preference relation $\succsim _{\rho }$ is compatible with their experimental result, where incomparabilities play crucial roles in explaining them.

The paper is organized as follows: Section 2 explains the concept of probability grids and other basic concepts. Section 3 formulates Step B in terms of preferences and utilities and states their equivalence. Section 4 discusses Step E in terms of preferences, and Sect. 5 does it in terms of utilities. Section 6 discusses the measurable/non-measurable lotteries and shows that the expected utility hypothesis holds for the measurable lotteries. Section 7 discusses the connection from our theory to the classical EU theory. In Sect. 8, we exemplify our theory with an experimental result in Kahneman and Tversky (1979). Section 9 concludes this paper with comments on further possible studies. Proofs of all the results in each section are given in a separate subsection; only proof of Lemma 2.1 is given in “Appendix.”

Preliminaries

Our theory is about preference formation in the context of EU theory. The classical EU theory is the reference point, but our theory deviates from it in various manners. To have clear relations between the classical EU theory and our development, we first mention the classical theory (cf. Herstein and Minor 1953; Fishburn 1982), and then, we start our development. In Sect. 2.2, we give various basic concepts for our theory and one basic lemma. In Sect. 2.3, we give definitions of preferences, indifferences, incomparabilities, and their counterparts in terms of vector-valued utility functions.

Classical EU theory

Let X be a given set of pure alternatives with cardinality $\left| X\right| \ge 2$. A lottery f is a function over X taking values in [0, 1] such that for some finite subset S of X, $\sum \nolimits _{x\in S}f(x)=1$, $f(x)>0$ if $x\in S$, and $f(x)=0$ if $x\in X-S$. This subset S is called the support of f. We define $L_{[0,1]}(X)= \{f:f:X\rightarrow [0,1]$ is a lottery$\}$. The set $L_{[0,1]}(X)$ is uncountable. We define compound lotteries: for any $f,g\in L_{[0,1]}(X)$ and $\lambda \in [0,1]$, $\lambda f*(1-\lambda )g$ is a lottery in $L_{[0,1]}(X)$ defined by $(\lambda f*(1-\lambda )g)(x)=\lambda f(x)+(1-\lambda )g(x)$ for all $x\in X$.

Let $\succsim _{E}$ be a binary relation over $L_{[0,1]}(X);$ we assume NM0 to NM2 on $\succsim _{E}$. This system is one among various equivalent systems.

• Axiom NM0 (Complete preordering): $\succsim _{E}$ is a complete and transitive relation on $L_{[0,1]}(X)$.

• Axiom NM1 (Intermediate value): For any $f, g, h\in L_{[0,1]}(X)$, if $f\succsim _{E}g\succsim _{E}h$, then $\lambda f*(1-\lambda )h\sim _{E}g$ for some $\lambda \in [0,1]$.

• Axiom NM2 (Independence): For any $f,g,h\in L_{[0,1]}(X)$ and $\lambda \in (0,1]$,

  • ID1: $f\succ _{E}g$ implies $\lambda f*(1-\lambda )h\succ _{E}\lambda g*(1-\lambda )h;$

  • ID2: $f\sim _{E}g$ implies $\lambda f*(1-\lambda )h\sim _{E}\lambda g*(1-\lambda )h$,

where the indifference part and strict preference part of $\succsim _{E}$ are denoted by $\sim _{E}$ and $\succ _{E};$ that is, $f\sim _{E}g$ means $f\succsim _{E}g$ & $g\succsim _{E}f;$ and $f\succ _{E}g$ does $f\succsim _{E}g$ & not $(g\succsim _{E}f)$.

The following two are the key theorems in the classical EU theory. For a fruitful development of our theory, we should be conscious of how they remain in our theory.

Theorem 2.1

(Classical EU theorem). A preference relation $\succsim _{E}$ satisfies Axioms NM0 to NM2 if and only if there is a function $u:X\rightarrow {\mathbb {R}}$ so that for any $f,g\in L_{[0,1]}(X)$,

$$\begin{aligned} f\succsim _{E}g\text { if and only if }E_{f}(u)\ge E_{g}(u), \end{aligned}$$

(3)

where the expected utility functional $E_{f}(u)$ is defined as:

$$\begin{aligned} E_{f}(u)=\sum _{x\in S}\text { }f(x)u(x)\text { for each }f\in L_{[0,1]}(X)\text { with its support }S. \end{aligned}$$

(4)

Theorem 2.2

(Uniqueness up to Affine transformations). Suppose that $\succsim _{E}$ satisfies Axioms NM0 to NM2. If two functions $u,v:X\rightarrow {\mathbb {R}}$ satisfy (3), then there are two real numbers $\alpha >0$ and $\beta$ such that $u(x)=\alpha v(x)+\beta$ for all $x\in X$.

This theory is silent about how a decision maker finds/forms his preferences and does not separate between object components and meta-components for decision making. The above two theorems are meta-components, and some structural components such as lotteries and a preference relation $\succsim _{E}$ in $(L_{[0,1]},\succsim _{E})$ are object components, but some include both such as highly complex probabilities. Another difficulty is the presumption that a well-formed preference relation $\succsim _{E}$ already exists somewhere in the mind of decision maker. Here, our theory studies a formation of such a preference relation by reflecting upon his mind (with past experiences) from the simplest case to complex cases. We target to describe this process; Sects. 2.2 and 2.3 prepare basic concepts for the description of the process. Using these basic concepts, Sect. 3 describes Measurement Step B and Sects. 4 and 5 describe Extension Step E.

Since we target a process of preference formation, a preference relation contains almost necessarily some or many incomparabilities at least in the beginning. In the literature, we find some studies on expected utility theory without the completeness axiom. Aumann (1962) and Fishburn (1971) considered one-way representation theorem [i.e., the only-if of (3)], dropping completeness. See Fishburn (1972) for further studies. Dubra and Ok (2002) and Dubra et al. (2004) developed representation theorems in terms of utility comparisons based on all possible expected utility functions for the relation without completeness. In this literature, incomparabilities are given in the preference relation. In contrast, in our approach, incomparabilities are changing with a cognitive bound and may disappear when there are no cognitive bounds.

Probability grids, lotteries, and decompositions

Let $\ell$ be an integer with $\ell \ge 2$. This $\ell$ is the base for describing probability grids; we take $\ell =10$ in the examples in the paper. The set of probability grids $\varPi _{k}$ is defined as

$$\begin{aligned} \varPi _{k}=\left\{ \tfrac{\nu }{\ell ^{k}}:\nu =0,1,\ldots ,\ell ^{k}\right\} \text { for any finite }k\ge 0. \end{aligned}$$

(5)

Here, $\varPi _{1}=\{\tfrac{\nu }{\ell }:\nu =0,\ldots ,\ell \}$ is the base set of probability grids for measurement, whereas $\varPi _{0}=\{0,1\}$ is needed for completeness of our discourse; Table 1 starts with layer 0 and continues up to layer $\rho$. Each $\varPi _{k}$ is a finite set, and $\varPi _{\infty }:=\cup _{k<\infty }\varPi _{k}$ is countably infinite. We use the standard arithmetic rules over $\varPi _{\infty }$; sum and multiplication are needed.⁵ We allow reduction by eliminating common factors; for example, $\tfrac{20}{10^{2}}$ is the same as $\tfrac{2}{10}$. Hence, $\varPi _{k}\subseteq \varPi _{k+1}$ for $k=0,1,\ldots$ The parameter k is the precision of probabilities that the decision maker uses. We define the depth of each $\lambda \in \varPi _{\infty }$ by: $\delta (\lambda )=k$ iff $\lambda \in \varPi _{k}-\varPi _{k-1}$. For example, $\delta (\tfrac{25}{10^{2}})=2$ but $\delta (\tfrac{20}{10^{2}} )=\delta (\tfrac{2}{10})=1$. The concept of a layer of probability grids up to a given depth k is well defined. The decision maker thinks about his preferences along probability grids from a shallow layer to a deeper one.

We use the standard equality $=$ and strict inequality > over $\varPi _{k}$. Then, trichotomy holds: for any $\lambda ,\lambda ^{\prime }\in \varPi _{k}$,

$$\begin{aligned} \text {either }\lambda >\lambda ^{\prime },\text { }\lambda =\lambda ^{\prime },\text { or }\lambda <\lambda ^{\prime }. \end{aligned}$$

(6)

Each element in $\varPi _{k}$ is obtained by taking the weighted sums of elements in $\varPi _{k-1}$ with the equal weights:

$$\begin{aligned} \varPi _{k}=\left\{ \sum _{t=1}^{\ell }\frac{1}{\ell }\lambda _{t}:\lambda _{1},\ldots ,\lambda _{\ell }\in \varPi _{k-1} \right\} \text { for any }k\text { }(1\le k<\infty ). \end{aligned}$$

(7)

This is basic for the connection between layer $k-1$ to the next. A proof of (7) is not given here, but an extension will be given in Lemma 2.1 with a proof in “Appendix.”

The union $\varPi _{\infty }=\cup _{k<\infty }\varPi _{k}$ is a proper and dense subset of $[0,1]\cap \mathrm {{\mathbb {Q}}}$, where ${\mathbb {Q}}$ is the set of rational numbers. For example, when $\ell =10$, $\varPi _{\infty }$ has no recurring decimals, but they are rationals. We also note that $\varPi _{\infty }$ depends upon the base $\ell ;$ for example, $\varPi _{1}$ with $\ell =3$ has $\frac{1}{3}$, but $\varPi _{\infty }$ with $\ell =10$ has no element corresponding to $\frac{1}{3}$.

For any $k<\infty$, we define $L_{k}(X)$ by

$$\begin{aligned} L_{k}(X)=\left\{ f: f\text { is a function from }X\text { to }\varPi _{k}\text { with } \sum _{x\in X}f(x)=1 \right\} . \end{aligned}$$

(8)

We identify each pure alternative x with the lottery having x as its support; so X is regarded as a subset of $L_{k}(X)$. Specifically, $L_{0}(X)=X$. Since $\varPi _{k}$ is a finite set, every $f\in L_{k}(X)$ has a finite support. Since $\varPi _{k}\subseteq \varPi _{k+1}$, it holds that $L_{k}(X)\subseteq L_{k+1}(X)$. We denote $L_{\infty }(X)= \cup _{k<\infty }L_{k}(X)$. As long as X is finite, $L_{k}(X)$ is also a finite set, but $L_{\infty }(X)$ is a countable set and is dense in $L_{[0,1]}(X)$.

We define the depth of a lottery f in $L_{\infty }(X)$ by $\delta (f)=k$ iff $f\in L_{k}(X)-L_{k-1}(X)$. We use the same symbol $\delta$ for the depth of a lottery and the depth of a probability. It holds that $\delta (f)=k$ if and only if $\max _{x\in X}\delta (f(x))=k$. This is relevant in Sect. 6. Lottery $d=\frac{25}{10^{2}}y*\frac{75}{10^{2}} {\underline{y}}$ of (2) is in $L_{2}(X)-L_{1}(X)$ and its depth $\delta (d)=2,$ but since $d^{\prime }=\frac{20}{10^{2}}y*\frac{80}{10^{2} }{\underline{y}}= \frac{2}{10}y*\frac{8}{10}{\underline{y}}\in L_{1}(X)$, we have $\delta (d^{\prime })=1$.

The decision maker thinks about and/or forms his own preferences from shallow layers to deeper ones. This stops at a cognitive bound $\rho ,$ which is a natural number or infinity $\infty$. If $\rho =k<\infty$, he eventually reaches the set of lotteries $L_{\rho }(X)=L_{k}(X)$, and if $\rho =\infty$, he has no cognitive limit; we define $L_{\rho }(X)=L_{\infty }(X)=\cup _{k<\infty }L_{k}(X)$.

We formulate a connection from $L_{k-1}(X)$ to $L_{k}(X);$ we say that ${\widehat{f}}=(f_{1},\ldots ,f_{\ell })$ in $L_{k-1}(X)^{\ell }=L_{k-1}(X)\times \cdots \times L_{k-1}(X)$ is a decomposition of $f\in L_{k}(X)$ iff for all $x\in X$,

$$\begin{aligned} f(x)=\sum _{t=1}^{\ell }\frac{1}{\ell }\times f_{t}(x)\text { and } \delta (f_{t}(x))\le \delta (f(x))\text { for all }t\le \ell . \end{aligned}$$

(9)

We denote this by $\sum _{t=1}^{\ell }\frac{1}{\ell }*f_{t}$, and letting ${\widehat{e}}=(\tfrac{1}{\ell },\ldots ,\tfrac{1}{\ell })$, it is written as ${\widehat{e}} \mathbf {*} {\widehat{f}}$. We can regard ${\widehat{e}} \mathbf { *} {\widehat{f}}$ as a compound lottery connecting $L_{k-1}(X)$ to $L_{k}(X)$ by reducing ${\widehat{e}} \mathbf {*} {\widehat{f}}$ to f in (9). Our theory allows only this form of compound lotteries and reduction with the depth constraint. The next lemma states that $L_{k}(X)$ is generated from $L_{k-1}(X)$ by taking all compound lotteries of this kind. It facilitates our induction method described in Table 1 reducing an assertion in layer k to layer $k-1$. A proof of Lemma 2.1 is given in “Appendix.”⁶

Lemma 2.1

(Decomposition of lotteries). Let $1\le k<\infty$. Then,

$$\begin{aligned} L_{k}(X)=\{f\in L_{k}(X):f\text { has a decomposition }{\widehat{f}}\}. \end{aligned}$$

(10)

Furthermore, for any $f\in L_{k}(X)$ with $\delta (f)>0$, there is a decomposition of ${\widehat{f}}$ of f so that

$$\begin{aligned} \delta (f_{t}(x))<\delta (f(x))\text { for any }x\in X\text { with }f(x)>0. \end{aligned}$$

(11)

The right-hand side of (10) is the set of composed lotteries from $L_{k-1}(X)$ with the equal weights. The inclusion $\supseteq$ states that the composed lotteries from $L_{k-1}(X)$ belong to $L_{k}(X)$. The converse inclusion $\subseteq$ is essential and means that each lottery in $L_{k}(X)$ is decomposed to an equally weighted sum of some $(f_{1},\ldots ,f_{\ell })$ in $L_{k-1}(X)^{\ell }$ with the depth constraint in (9). In the trivial case that $f=x\in L_{0}(X)$ is decomposed to ${\widehat{f}}=(x,\ldots ,x)$. This will be used in Lemma 4.2. The latter with (11) asserts the choice of a strictly shallower decomposition for f with $\delta (f)>0$.

Here, we give three remarks. One is that when f is a benchmark lottery in $B_{k}({\overline{y}};{\underline{y}})$, for its decomposition ${\widehat{f}} =(f_{1},\ldots ,f_{\ell })$, each $f_{t}$ is a benchmark lottery in $B_{k-1}( {\overline{y}};{\underline{y}})$. This fact will be used without referring. The second is that when $f\in L_{k-1}(X)$, ${\widehat{f}}=(f,\ldots ,f)$ is a decomposition of f. To allow this triviality, we require only the weak inequality in the depth constraint in (9). The third is that for any subset $X^{\prime }$ of X, we define $L_{k}(X^{\prime })=\{f\in L_{k}(X): f(x)>0$ implies $x\in X^{\prime }\}$. Hence, $L_{k}(X^{\prime })$ is a subset of $L_{k}(X)$. Lemma 2.1 holds for $L_{k}(X^{\prime })$ and $L_{k-1}(X^{\prime })$.

The lottery $d=[y,\frac{25}{10^{2}};{\underline{y}}]$ has three types of decompositions:

$$\begin{aligned} d=\tfrac{t}{10}*y+\tfrac{5-2t}{10}*[y,\tfrac{5}{10}; {\underline{y}}]+\tfrac{5+t}{10}*{\underline{y}}\text { for }t=0,1,2. \end{aligned}$$

(12)

Here, a decomposition ${\widehat{f}}= (f_{1},\ldots ,f_{10})$ is given as $f_{1}=\cdots =f_{t}=y$, $f_{t+1}=\cdots =f_{5-t}=[y,\frac{5}{10};{\underline{y}}]$, and $f_{5-t+1}=\cdots =f_{10}={\underline{y}}$. We use this short-hand expressions rather than a full specification of ${\widehat{f}}= (f_{1},\ldots ,f_{10})$. We should be careful about this multiplicity.

The reason for explicit considerations of layers for $L_{k}(X)$ and also preference relation $\succsim _{k}$ is to avoid collapse from a layer to a shallower one. Without them, we may have a difficulty in identifying the sources for preferences. For example, the weighted sum $\frac{5}{10}[\frac{25 }{10^{2}}y*\frac{75}{10^{2}}{\underline{y}}] *\frac{5}{10}[\frac{ 75}{10^{2}}y*\frac{25}{10^{2}}{\underline{y}}]$ is reduced to $\frac{5}{10} y*\frac{5}{10}{\underline{y}};$ preferences about $\frac{5}{10}y*\frac{ 5}{10}{\underline{y}}$ may possibly come from layer 2 or from layer 0. To prohibit such collapse, we take depths of layers explicitly into account in (9).

Incomplete preference relations and vector-valued utility functions

We consider two methods to express the decision maker’s desires: a preference relation and a utility function. We starts with an incomplete preference relation and then works on a vector-valued utility function with the interval order. These are the first departures from the classical EU theory.

Let $\succsim$ be a preference relation over a given set, say A. For $f,g\in A$, the expression $f \succsim g$ means that f is strictly preferred to g or is indifferent to g. We define the strict (preference) relation $\succ$, indifference relation $\sim$, and incomparability relation $\bowtie$ by

$$\begin{aligned}&f \succ g\text { if and only if }f\succsim g\text { and not }g\succsim f; \nonumber \\&f \sim g\text {if and only if}f\succsim g\text { and }g\succsim f; \nonumber \\&f \bowtie g\text { if and only if neither}f\succsim g\text { nor } g\succsim f. \end{aligned}$$

(13)

All the axioms are given on the relations $\succsim$, $\succ$, $\sim$, and the relation $\bowtie$ is defined as the residual part of $\succsim$. Although $\sim$ and $\bowtie$ are sometimes regarded as closely related (cf. Shafer 1986, p. 469), they are well separated in Theorem 6.2 in our theory.

In the classical theory in Sect. 2.1, the preference relation $\succsim _{E}$ is assumed to be complete. Since, however, we consider a formation of preferences, our theory should avoid this completeness assumption. Nevertheless, it appears as a result when a domain of lotteries is restricted.

Another method of measurement of desires is by a vector-valued function ${\varvec{u}}$ with the interval order introduced by Fishburn (1970). Let ${\varvec{u}}(f)=[{\overline{u}}(f),{\underline{u}}(f)]$ be a 2 -dimensional vector-valued function from its domain A to the set $\mathbb {Q }^{2}=\mathbb {Q\times Q}$ with ${\overline{u}}(f)\ge {\underline{u}}(f)$ for each $f\in A$. The components ${\overline{u}}(f)$ and ${\underline{u}}(f)$ are interpreted as the least upper and greatest lower bounds of possible utilities from f. We say that ${\varvec{u}}(f)$ is effectively single-valued iff ${\overline{u}}(f)={\underline{u}}(f);$ in this case, we write ${\overline{u}}(f)={\underline{u}}(f)=u(f)$, dropping the upper and lower bars. We use the interval order $\ge _{I}$ over the values of $\varvec{ u};$ for $f,g\in A$,

$$\begin{aligned} {\varvec{u}}(f)\ge _{I}{\varvec{u}}(g)\text {if and only if } {\underline{u}}(f)\ge {\overline{u}}(g). \end{aligned}$$

(14)

That is, f and g are ordered if and only if the greatest lower bound ${\underline{u}}(f)$ from f is larger than or equal to the least upper bound ${\overline{u}}(g)$ from g. This $\ge _{I}$ allows incomparabilities, for example, if ${\varvec{u}}(f)=[\frac{9}{10},\frac{7}{10}]$ and $\varvec{ u}(g)=[\frac{83}{10^{2}},\frac{83}{10^{2}}]$, then f and g are incomparable by $\ge _{I}$. The relation $\ge _{I}$ is transitive, but is not reflexive; ${\varvec{u}}(f)\ge _{I}{\varvec{u}}(g)$ and ${\varvec{u}}(g)\ge _{I}{\varvec{u}}(f)$ are equivalent to $u(f)= {\underline{u}}(f)={\overline{u}}(g)={\underline{u}}(g)$, i.e., this is the case only when the values ${\varvec{u}}(f)$ and ${\varvec{u}}(g)$ are effectively single-valued and identical.

Measurement Step B

We formulate Step B of measurement of pure alternatives up to cognitive bound $\rho$. This has two sides: in terms of preference relations $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ and in terms of vector-valued utility functions $\langle \varvec{\upsilon } _{k}\rangle _{k<\rho +1}$. We show the representation theorem on $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ by $\langle \varvec{\upsilon } _{k}\rangle _{k<\rho +1}$, and the uniqueness theorem on $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ up to positive linear transformations. Finally, we mention that these are well interpreted in terms of Simon’s (1956) satisficing/aspiration argument.

Base preference streams

The set of pure alternatives X is assumed to contain two distinguished elements ${\overline{y}}$ and ${\underline{y}}$, which we call the upper and lower benchmarks. Let $k<\infty$. We call an $f\in L_{k}(X)$ a benchmark lottery of depth (at most) k iff $f(\overline{ y})=\lambda$ and $f({\underline{y}})=1-\lambda$ for some $\lambda \in \varPi _{k}$, which we denote by $[{\overline{y}},\lambda ;{\underline{y}}]$. The benchmark scale of depth k is the set $B_{k}({\overline{y}};{\underline{y}} )=\{[{\overline{y}},\lambda ;{\underline{y}}]:\lambda \in \varPi _{k}\}$. In particular, $B_{0}({\overline{y}};{\underline{y}})=\{{\overline{y}},{\underline{y}} \}$. The grids (dots) in Fig. 1 express the benchmark lotteries. We define $B_{\infty }({\overline{y}};{\underline{y}})=\cup _{k<\infty }B_{k}({\overline{y}}; {\underline{y}})$. The depth of a benchmark lottery $[{\overline{y}},\lambda ; {\underline{y}}]$ is the same as the depth of $\lambda$, i.e., $\delta ([ {\overline{y}},\lambda ;{\underline{y}}])=\delta (\lambda )$.

We denote a cognitive bound by $\rho$, which is a natural number or $\rho =\infty$. We use k as a variable expressing a natural number of a layer, but $\rho \$as a constant parameter of the theory. Stipulating $\infty +1=\infty$, “$k<\rho +1$” expresses the two statements “$k\le \rho$ if $\rho <\infty$” and “$k<\rho$ if $\rho =\infty$”. This constant $\rho$ plays an active role as a small constraint such as $\rho =2$ or 3 in Example 5.1 and Sect. 8, and as $\rho =\infty$ in Sect. 7 for consideration of the expected utility hypothesis.

Let $\trianglerighteq _{k}$ be a subset of

$$\begin{aligned} D_{k}=B_{k}({\overline{y}};{\underline{y}})^{2}\cup \{(x,g),(g,x):x\in X\text { and }g\in B_{k}({\overline{y}};{\underline{y}})\}. \end{aligned}$$

(15)

Thus, $\trianglerighteq _{k}$ consists of the scale part of the benchmarks and the measurement part of pure alternatives. The scale part allows the decision maker to make comparisons between any grids of depth k. For a pure alternative $x\in X$, he thinks about where x is located in the benchmark scale $B_{k}({\overline{y}};{\underline{y}});$ it may or may not correspond to a grid, which is seen in Fig. 1. For example, if $(x,g)\in \trianglerighteq _{k}$ but $(g,x)\notin \trianglerighteq _{k}$, then x is strictly better than the grid g,  and if $(x,g)\notin \trianglerighteq _{k}$ and $(g,x)\notin \trianglerighteq _{k}$, then x and g are incomparable for him.

A stream of basic preference relations is expressed as $\langle \trianglerighteq _{k}\rangle _{k<\rho +1};$ when $\rho <\infty$, it is expressed as $\langle \trianglerighteq _{0},\trianglerighteq _{1},\ldots ,\trianglerighteq _{\rho }\rangle$, and when $\rho =\infty$, it is as $\langle \trianglerighteq _{0},\trianglerighteq _{1},\ldots \rangle$. We make four axioms on $\langle \trianglerighteq _{k}\rangle _{k<\rho +1};$ the first requires a property on measurement on layer 0, the second and third require properties on measurement on each layer k, and the fourth connects measurements in layers k and $k+1$.

Specifically, Axiom B0 requires pure alternatives to be between the upper and lower benchmarks ${\overline{y}}$, ${\underline{y}}$.

Axiom B0 (Benchmarks): ${\overline{y}}\trianglerighteq _{0}x$ and $x\trianglerighteq _{0}{\underline{y}}$ for all $x\in X$.

The next states that preferences over $B_{k}({\overline{y}};{\underline{y}})$ are the same as the natural order on $\varPi _{k}$.

Axiom B1 (Benchmark scale): For $\lambda ,\lambda ^{\prime }\in \varPi _{k}$, $[{\overline{y}},\lambda ;{\underline{y}}]\trianglerighteq _{k}[ {\overline{y}},\lambda ^{\prime };{\underline{y}}]$ if and only if $\lambda \ge \lambda ^{\prime }$.

It follows from Axiom B1 that for $\lambda ,\lambda ^{\prime }\in \varPi _{k}$,

$$\begin{aligned}{}[{\overline{y}},\lambda ;{\underline{y}}]\vartriangleright _{k}[\overline{ y},\lambda ^{\prime };{\underline{y}}]\text { if and only if }\lambda >\lambda ^{\prime }. \end{aligned}$$

(16)

Also, $\lambda =\lambda ^{\prime }$ if and only if $[{\overline{y}},\lambda ; {\underline{y}}]$ and $[{\overline{y}},\lambda ^{\prime };{\underline{y}}]$ are indifferent. Thus, $\trianglerighteq _{k}$ is a complete relation over $B_{k}({\overline{y}};{\underline{y}})$ by (6). This is the scale part of $\trianglerighteq _{k}$ and is precise up to $\varPi _{k}$. Since ${\overline{y}}=[{\overline{y}},1;{\underline{y}}]$ and ${\underline{y}} =[{\overline{y}},0;{\underline{y}}]$, it follows from (16) that ${\overline{y}}\vartriangleright _{0}{\underline{y}}$.

Measurement is required to be coherent with the scale part given by Axiom B1.

Axiom B2 (Monotonicity): For all $x\in X$ and $\lambda ,\lambda ^{\prime }\in \varPi _{k}$, if $[{\overline{y}},\lambda ;{\underline{y}} ]\trianglerighteq _{k}x$ and $\lambda ^{\prime }>\lambda$, then $[{\overline{y}},\lambda ^{\prime };{\underline{y}}]\vartriangleright _{k}x,$ and if $x\trianglerighteq _{k}[{\overline{y}},\lambda ;{\underline{y}}]$ and $\lambda >\lambda ^{\prime }$, then $x\vartriangleright _{k}[{\overline{y}},\lambda ^{\prime };{\underline{y}} ].$

This implies no reversals with Axiom B1; if $[{\overline{y}},\lambda ; {\underline{y}}]\trianglerighteq _{k}x$ and $x\trianglerighteq _{k}[\overline{y },\lambda ^{\prime };{\underline{y}}]$, then $\lambda \ge \lambda ^{\prime }$. Indeed, if $\lambda <\lambda ^{\prime }$, then $[{\overline{y}},\lambda ^{\prime };{\underline{y}}]\vartriangleright _{k}x$ by B2, which implies not $x\trianglerighteq _{k}[{\overline{y}},\lambda ^{\prime };{\underline{y}}]$. If we assume transitivity for $\trianglerighteq _{k}$ over $D_{k}$, B2 could be derived from B1, but we adopt B2 instead of transitivity, since B2 gives a more specific property to the measurement step.

The last requires the preferences in layer $k\$ to be preserved in the next layer $k+1$. This is expressed by the set-theoretical inclusion $\subseteq$ in Table 1.

Axiom B3 (Preservation): For all $f,g\in D_{k}$, $f\trianglerighteq _{k}g$ implies $f\trianglerighteq _{k+1}g$.

The above axioms still allow great freedom for base preference relations $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$. To see this fact and how the measurement step B of utilities from pure alternatives goes on, we consider vector-valued utility functions with the interval order $\ge _{I}$ in Sect. 3.2.

Base utility streams

Let $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}=\langle [{\overline{\upsilon }}_{k},{\underline{\upsilon }}_{k}]\rangle _{k<\rho +1}$ be a sequence of vector-valued functions, where $\langle \varvec{\upsilon } _{k}\rangle _{k<\rho +1}=\langle \varvec{\upsilon }_{0},\varvec{ \upsilon }_{1},\ldots ,\varvec{\upsilon }_{\rho }\rangle$ if $\rho <\infty$ and $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}=\langle \varvec{\upsilon }_{0},\varvec{\upsilon }_{1},\ldots \rangle$ if $\rho =\infty$. For each $k<\rho +1$, $\varvec{\upsilon }_{k} =[{\overline{\upsilon }}_{k},{\underline{\upsilon }}_{k}]$ is a function from $B_{k}( {\overline{y}};{\underline{y}})\cup X$ to ${\mathbb {Q}}^{2}\varvec{\ }$such that $\overline{\upsilon }_{k}(f)\ge {\underline{\upsilon }}_{k}(f)$ for all $f\in B_{k}({\overline{y}};{\underline{y}})\cup X$, which are intended to be the least upper utility and greatest lower utility from lottery f. Recall that when $\varvec{\upsilon }_{k}(f)$ is effectively single-valued, we write $\overline{\upsilon }_{k}(f)={\underline{\upsilon }}_{k}(f)=\upsilon _{k}(f)$. The following conditions on $\langle \varvec{\upsilon } _{k}\rangle _{k<\rho +1}$ are not exactly parallel to Axioms B0 to B3, but these two systems are equivalent, which is stated in Theorem 3.1 :

b0::

$\upsilon _{0}({\overline{y}} )>\upsilon _{0}({\underline{y}});$

b1::

for $k <\rho +1$, $\upsilon _{k}([ {\overline{y}},\lambda ;{\underline{y}}])=\lambda \upsilon _{k}({\overline{y}} )+(1-\lambda )\upsilon _{k}({\underline{y}})$ for all $[{\overline{y}},\lambda ;{\underline{y}}]\in B_{k}({\overline{y}};{\underline{y}});$

b2::

for $k <\rho +1$ and $x\in X$, ${\overline{\upsilon }}_{k}(x)=\upsilon _{k}([{\overline{y}},{\overline{\lambda }} _{x};{\underline{y}}])$ and ${\underline{\upsilon }}_{k}(x)=\upsilon _{k}([ {\overline{y}},{\underline{\lambda }}_{x};{\underline{y}}])$ for some ${\overline{\lambda }}_{x}$ and ${\underline{\lambda }}_{x}$ in $\varPi _{k};$

b3::

for $k<\rho$ and $x\in X$, ${\overline{\upsilon }}_{k}(x)\ge {\overline{\upsilon }}_{k+1}(x)\ge \underline{ \upsilon }_{k+1}(x)\ge {\underline{\upsilon }}_{k}(x).$

Condition b0 fixes the utility values from the upper and lower benchmarks ${\overline{y}}$ and ${\underline{y}}$, which corresponds to the implication of B0. Then, b1 means that for each benchmark lottery $[{\overline{y}},\lambda ; {\underline{y}}]\in B_{k}({\overline{y}};{\underline{y}})$, $\varvec{\upsilon }_{k}([{\overline{y}},\lambda ;{\underline{y}}])$ is effectively single-valued and takes the expected utility value of ${\overline{y}}$ and ${\underline{y}}$, which corresponds to B1. b2 states that for each pure alternative $x\in X$, the least upper and greatest lower utilities from x are measured by the benchmark scale $B_{k}({\overline{y}};{\underline{y}});$ this does not exactly correspond to B2, but it does an implication of B2 with the help of transitivity of the interval order $\ge _{I}$. Corresponding to B3, b3 states that ${\overline{\upsilon }}_{k}(x)$ and ${\underline{\upsilon }}_{k}(x)$ are getting more accurate as k increases.

We observe that by b3, $\overline{\upsilon }_{k}(x)={\underline{\upsilon }} _{k}(x)$ implies $\overline{\upsilon }_{k}(x)={\overline{\upsilon }}_{k+1}(x)= \underline{\upsilon }_{k+1}(x)={\underline{\upsilon }}_{k}(x)$, i.e., if $\varvec{\upsilon }_{k}(x)=[\overline{\upsilon }_{k}(x),{\underline{\upsilon }}_{k}(x)]$ is effectively single-valued, then $\varvec{\upsilon }_{k^{\prime }}(x)$ is constant and effectively single-valued for any $k^{\prime }>k$. In particular,

$$\begin{aligned} \upsilon _{0}({\overline{y}})=\upsilon _{k}({\overline{y}})\text { and }\upsilon _{0}({\underline{y}})=\upsilon _{k}({\underline{y}})\text { for all }k<\rho +1. \end{aligned}$$

(17)

This and b1 imply that a benchmark lottery takes the same utility value as long as it belongs $B_{k}({\overline{y}};{\underline{y}})$. Also, the values $\lambda _{{\overline{y}}}$ and $\lambda _{{\underline{y}}}$ given by b2 are 1 and 0, since ${\overline{y}}=[{\overline{y}},1;{\underline{y}}]$ and ${\underline{y}}=[{\overline{y}},0;{\underline{y}}]$. Hence,

$$\begin{aligned} \delta (\lambda _{{\overline{y}}})=\delta (\lambda _{{\underline{y}}})=0. \end{aligned}$$

(18)

These observations will be used later.

Now, we have Theorem 3.1. As stated, all proofs are given in separate subsections.

Theorem 3.1

(Representation in Step B). A base preference stream $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ satisfies Axioms B0 to B3 if and only if there is a base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ satisfying b0 to b3 such that for any $k<\rho +1$ and $(f,g)\in D_{k}$,

$$\begin{aligned} f\trianglerighteq _{k}g\text { if and only if }\varvec{\upsilon } _{k}(f)\ge _{I}\varvec{\upsilon }_{k}(g). \end{aligned}$$

(19)

Without difficulty, we can construct a sequence $\langle \varvec{ \upsilon }_{k}\rangle _{k<\rho +1}$ satisfying b0 to b3. Thus, by Theorem 3.1, there is a sequence $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ satisfying B0 to B3, which implies the consistency of Axioms B0 to B3.

We have the uniqueness theorem.

Theorem 3.2

(Uniqueness up to affine transformations). Let $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ satisfy Axioms B0 to B3. If $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ and $\langle \varvec{\upsilon }_{k}^{\prime }\rangle _{k<\rho +1}$ satisfying b0 to b3 represent $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ in the sense of (19), there are rational numbers $\alpha >0$ and $\beta$ such that $\varvec{\upsilon }_{k}^{\prime }(x)=\alpha \varvec{ \upsilon }_{k}(x)+\beta =[\alpha {\overline{\upsilon }}_{k}(x)+\beta ,\alpha {\underline{\upsilon }}_{k}(x)+\beta ]$ for all $x\in X$ and $k<\rho +1$.

Conditions b0 to b3 require $\varvec{\upsilon }_{k}(x)=[{\overline{\upsilon }}_{k}(x),\underline{\upsilon }_{k}(x)]$ to be represented essentially by two values ${\overline{\lambda }}_{x}$ and ${\underline{\lambda }}_{x}$ in $\varPi _{k}$ with $\upsilon _{0}({\overline{y}})$ and $\upsilon _{0}({\underline{y}} )$. However, $\upsilon _{0}({\overline{y}})$ and $\upsilon _{0}({\underline{y}})$ are allowed to take any values in ${\mathbb {Q}}$ only with $\upsilon _{0}( {\overline{y}})> \upsilon _{0}({\underline{y}})$. Hence, for two streams $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ and $\langle \varvec{\upsilon }_{k}^{\prime }\rangle _{k<\rho +1}$ representing the same $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$, one is expressed as a positive linear transformation of the other, which is the above uniqueness result.

The uniqueness up to a positive linear transformation plays a crucial role in the literature on bargaining such as Nash (1950) and also the Nash welfare function theory by Kaneko and Nakamura (1979). The rational number scalars are enough for the 2-person case (cf. Kaneko 1992) and the real-algebraic numbers are enough for the general n-person case . It is easy to generalize Theorem 3.2 for the real numbers scalars, but the problem is how much we can restrict the scalars. Theorem 3.2 is suggestive of how bounded rationality is incorporated to these theories.

The processes described in terms of $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ and/or $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ are regarded as thought experiments by the decision maker to search preferences/ utilities in his mind. These preference and utility comparisons are object components for the decision maker, but the above theorems belong to the level of meta-components. From the viewpoint of “bounded rationality”, he may stop his search when he is satisfied and/or tired. This is the same as Simon’s (1956) argument of satisficing/aspiration. We consider one example and exemplify the satisficing/aspiration argument.

Example 3.1

Let $X=\{{\overline{y}},y,{\underline{y}}\}$, $\varvec{\upsilon }_{0}({\overline{y}})=[1,1]$, $\varvec{\upsilon }_{0}( {\underline{y}})=[0,0]$, and $\varvec{\upsilon }_{0}(y)=[1,0]$. Also, let $\varvec{\upsilon }_{1}(y)=[\frac{9}{10},\frac{7}{10}]$. For $f=[ {\overline{y}},\frac{8}{10};{\underline{y}}]$, $\varvec{\upsilon }_{1}(f)=[ \frac{8}{10},\frac{8}{10}]$ by (17) and b1. Then $\varvec{ \upsilon }_{1}(y)\ngeq _{I}\varvec{\upsilon }_{1}(f)$ and $\varvec{ \upsilon }_{1}(f)\ngeq _{I}\varvec{\upsilon }_{1}(y);$ so y and f are incomparable with respect to $\trianglerighteq _{1}$ by (19). In Fig. 2, $\langle \varvec{\upsilon }_{k}(y)\rangle _{k<\rho +1}=\langle [{\overline{\upsilon }}_{k}(y),\underline{\upsilon }_{k}(y)]\rangle _{k<\rho +1}$ is described as solid lines in cases A, B, and C. Since $\varvec{\upsilon }_{0}(y)=[1,0]$, we have ${\overline{y}}\vartriangleright _{0}y\vartriangleright _{0}{\underline{y}}$ by (19). For $k=2$, in A, $\varvec{\upsilon }_{2}(y)=[\frac{77}{10^{2}}, \frac{77}{10^{2}}]$ and the decision maker prefers $f=[{\overline{y}},\frac{8}{ 10};{\underline{y}}]$ to y;  and in B, $\varvec{\upsilon } _{2}(y)=[\frac{83}{10^{2}},\frac{83}{10^{2}}];$ he prefers y to f. In C, $\varvec{\upsilon }_{k}(y)=[\frac{9}{10},\frac{7}{10}]$ is constant for $k\ge 2;$ he gives up comparisons between y and f after $k=1$.

Fig. 2

Upper and lower bounds of utilities

This example is interpreted in terms of Simon’s satisficing/aspiration. The decision maker starts evaluating the pure alternative y the benchmark scale $B_{0}({\overline{y}};\underline{y })$. Suppose that he finds $\varvec{\upsilon }_{0}(y)=[1,0]$, i.e., he attaches the upper value 1 and lower value 0 to y. When $\rho =0$, he immediately concludes that y is between ${\overline{y}}$ and ${\underline{y}}$ . When $\rho \ge 1$, he goes to layer 1 and uses the more precise scale $B_{1}({\overline{y}};{\underline{y}})$ to measure y. Since $\varvec{ \upsilon }_{1}(y)=[\frac{9}{10},\frac{7}{10}],\ y$ is better than $[ {\overline{y}},\frac{7}{10};{\underline{y}}]$ but worse than $[{\overline{y}}, \frac{9}{10};{\underline{y}}]$. Still, he has not reached an exact measurement. If $\rho =1$, he stops introspection and is satisfied with these evaluations of y. If $\rho \ge 2$, he goes to layer $k=2;$ in A of Fig. 2, he reaches the exact utility value $\varvec{\upsilon } _{2}(y)= [\frac{77}{10^{2}},\frac{77}{10^{2}}]$,⁷ but in C, he has still imprecise values ${\varvec{\upsilon }}_{2}(y)=[ \frac{9}{10},\frac{7}{10}]$ and does not improve them any more even for $k>2$.

Proofs

Proof of Theorem 3.1

(If): Suppose that $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ satisfies b0 to b3 and that (19) holds for $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ and $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$

B0: We have, by b0, b1, and b2, $\upsilon _{0}({\overline{y}} )\ge {\overline{\upsilon }}_{0}(x)$ and ${\underline{\upsilon }}_{0}(x)\ge \upsilon _{0}({\underline{y}})$, i.e., ${\overline{y}}\trianglerighteq _{0}x\trianglerighteq _{0}{\underline{y}}$. Thus, B0.

B1: By (19), b1, and b2, we have $[{\overline{y}},\lambda ; {\underline{y}}]\trianglerighteq _{k}[{\overline{y}},\lambda ^{\prime }; {\underline{y}}]$ if and only if $\varvec{\upsilon }_{k}([{\overline{y}} ,\lambda ;{\underline{y}}])\ge _{I} \varvec{\upsilon }_{k}([{\overline{y}} ,\lambda ^{\prime };{\underline{y}}])$ if and only if $\lambda \upsilon _{0}( {\overline{y}})+(1-\lambda )\upsilon _{0}({\underline{y}})\ge \lambda ^{\prime }\upsilon _{0}({\overline{y}})+(1-\lambda ^{\prime })\upsilon _{0}(\underline{y })$. By b0, this is equivalent to $\lambda \ge \lambda ^{\prime }$. That is, B1.

B2: Let $[{\overline{y}},\lambda ;{\underline{y}}]\trianglerighteq _{k}x$ and $\lambda ^{\prime }>\lambda$. By b2, (19), (17 ), and b0, we have $\lambda ^{\prime }\upsilon _{0}({\overline{y}} )+(1-\lambda ^{\prime })\upsilon _{0}({\underline{y}})> \lambda \upsilon _{0}({\overline{y}})+ (1-\lambda )\upsilon _{0}({\underline{y}}) \ge {\overline{\upsilon }}_{k}(x)$. Thus, $\upsilon _{k}([{\overline{y}},\lambda ^{\prime };{\underline{y}}])=\lambda ^{\prime }\upsilon _{k}({\overline{y}} )+(1-\lambda ^{\prime })\upsilon _{k}({\underline{y}})>{\overline{\upsilon }} _{k}(x)$. By (19), we have $[{\overline{y}},\lambda ^{\prime }; {\underline{y}}]\vartriangleright _{k}x$. The other case is symmetric.

B3: Let $f\trianglerighteq _{k}g$. By (19), we have ${\underline{\upsilon }}_{k}(f)\ge {\overline{\upsilon }}_{k}(g)$. Let $f=x\in X$ and $g=[{\overline{y}},\lambda ;{\underline{y}}]\in B_{k}({\overline{y}}; {\underline{y}})$. Then, by b3, we have ${\underline{\upsilon }}_{k+1}(f)\ge {\underline{\upsilon }}_{k}(f)\ge \upsilon _{k}(g)=\upsilon _{k+1}(g)$. By ( 19), $f\trianglerighteq _{k+1}g$. The case $f\in B_{k}({\overline{y}}; {\underline{y}})$, $g=x\in X$ is parallel. The case $f=[{\overline{y}},\lambda ; {\underline{y}}]$, $g=[{\overline{y}},\lambda ^{\prime };{\underline{y}}]\in B_{k}( {\overline{y}};{\underline{y}})$ is similar.

(Only-if): Suppose that $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ satisfying Axioms B0 to B3 is given. We construct a base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}=[ {\overline{\upsilon }}_{k},{\underline{\upsilon }}_{k}]$ satisfying (19 ), as follows: for any $f\in B_{k}({\overline{y}};{\underline{y}})\cup X$,

$$\begin{aligned} {\overline{\upsilon }}_{k}(f)= & {} \min \{\lambda \in \varPi _{k}:[{\overline{y}} ,\lambda ;{\underline{y}}]\trianglerighteq _{k}f\}; \nonumber \\ {\underline{\upsilon }}_{k}(f)= & {} \max \{\lambda \in \varPi _{k}:f\trianglerighteq _{k}[{\overline{y}},\lambda ;{\underline{y}}]\}. \end{aligned}$$

(20)

Note that when $f=[{\overline{y}},\lambda _{f};{\underline{y}}]\in B_{k}( {\overline{y}};{\underline{y}})$, we have ${\overline{\upsilon }}_{k}(f)= {\underline{\upsilon }}_{k}(f)=\lambda _{f}$ for $f\in B_{k}({\overline{y}}; {\underline{y}})$ by (20). Consider $f=[{\overline{y}},\lambda _{f}; {\underline{y}}],g =[{\overline{y}},\lambda _{g};{\underline{y}}]\in B_{k}( {\overline{y}};{\underline{y}})$. Then, $f\trianglerighteq _{k}g$ if and only if $[{\overline{y}},\lambda _{f};{\underline{y}}]\trianglerighteq _{k} [\overline{ y},\lambda _{g};{\underline{y}}]$ if and only if$\ \lambda _{f}\ge \lambda _{g}$, i.e., $\varvec{\upsilon }_{k}(f)\ge _{I}\varvec{\upsilon } _{k}(g)$ by B1. Let $f\in B_{k}({\overline{y}};{\underline{y}})$ and $g=x\in X$. Denote $\upsilon _{k}(f)=\lambda _{f}$ and ${\overline{\upsilon }}_{k}(x)= {\overline{\lambda }}_{x}$. Suppose $f\trianglerighteq _{k}x$. By (20 ), $[{\overline{y}},\lambda _{f};{\underline{y}}]=f \trianglerighteq _{k}[ {\overline{y}},{\overline{\lambda }}_{x};{\underline{y}}]$. By B1, $\lambda _{f}\ge {\overline{\lambda }}_{x}$, i.e., $\varvec{\upsilon }_{k}(f)\ge _{I}\varvec{\upsilon }_{k}(x)$. The converse is obtained by tracing this back. Thus, $f\trianglerighteq _{k}x$ if and only if$\ \varvec{\upsilon } _{k}(f)\ge _{I}\varvec{\upsilon }_{k}(x)$. The case $f=x\in X$, $g\in B_{k}({\overline{y}};{\underline{y}})$ is parallel.

By (16) and B0, we have b0. Consider b1. Since $\upsilon _{k}({\overline{y}})=1$ and $\upsilon _{k}({\underline{y}})=0$, it follows from the note immediately after (20) that $\upsilon _{k}(f)=\lambda =\lambda \upsilon _{k}({\overline{y}})+(1-\lambda )\upsilon _{k}({\underline{y}})$, which is b1. By (20), we have b2 and b3. $\square$

Proof of Theorem 3.2

Let $\alpha =(\upsilon _{0}^{\prime }({\overline{y}})-\upsilon _{0}^{\prime }({\underline{y}} ))/(\upsilon _{0}({\overline{y}})-\upsilon _{0}({\underline{y}}))$ and $\beta = (\upsilon _{0}({\overline{y}})\upsilon _{0}^{\prime }({\underline{y}})-\upsilon _{0}^{\prime }({\overline{y}})\upsilon _{0}({\underline{y}}))/(\upsilon _{0}( {\overline{y}})-\upsilon _{0}({\underline{y}}))$. By b1 and (17), we have $\varvec{\upsilon }_{k}^{\prime }({\overline{y}})=\alpha \varvec{ \upsilon }_{k}({\overline{y}})+\beta$ and $\varvec{\upsilon }_{k}^{\prime }({\underline{y}})=\alpha \varvec{\upsilon }_{k}({\underline{y}}) +\beta$ . For $[{\overline{y}},\lambda ;{\underline{y}}]\in B_{k}({\overline{y}}; {\underline{y}})$, we have $\varvec{\upsilon }_{k}^{\prime }([{\overline{y}} ,\lambda ;{\underline{y}}])=\lambda \varvec{\upsilon }_{k}^{\prime }( {\overline{y}})+ (1-\lambda )\varvec{\upsilon }_{k}^{\prime }({\underline{y}}) = \alpha \varvec{\upsilon }_{k}([{\overline{y}},\lambda ; {\underline{y}}]) +\beta$ by b1.

For $x\in X$, we have ${\overline{\lambda }}_{x}$ and ${\underline{\lambda }}_{x}$ in $\varPi _{k}$ by b2 for $\varvec{\upsilon } _{k}$ such that $\varvec{\upsilon }_{k}(x)= [\upsilon _{k}([\overline{ y},{\overline{\lambda }}_{x};{\underline{y}}]),\upsilon _{k}([{\overline{y}}, {\underline{\lambda }}_{x};{\underline{y}}])]$. Let ${\overline{\lambda }} _{x}^{\prime }$ and ${\underline{\lambda }}_{x}^{\prime }$ be given by b2 for $\varvec{\upsilon }_{k}^{\prime }$. Suppose ${\overline{\lambda }} _{x}\ne {\overline{\lambda }}_{x}^{\prime }$, say, ${\overline{\lambda }}_{x}> {\overline{\lambda }}_{x}^{\prime }$. Then, $\varvec{\upsilon }_{k}([ {\overline{y}},{\overline{\lambda }}_{x};{\underline{y}}])\ge _{I}\varvec{ \upsilon }_{k}(x)$, but ${\overline{\upsilon }}_{k}(x)=\upsilon _{k}([ {\overline{y}},{\overline{\lambda }}_{x};{\underline{y}}])> \upsilon _{k}([ {\overline{y}},{\overline{\lambda }}_{x}^{\prime };{\underline{y}}])$. Hence, $\varvec{\upsilon }_{k}([{\overline{y}},{\overline{\lambda }}_{x}^{\prime }; {\underline{y}}])\ngeq _{I}\varvec{\upsilon }_{k}(x)$. However, by definition of ${\overline{\lambda }}_{x}^{\prime }$, we have $\varvec{ \upsilon }_{k}^{\prime }([{\overline{y}},{\overline{\lambda }}_{x}^{\prime }; {\underline{y}}])\ge _{I}\varvec{\upsilon }_{k}^{\prime }(x)$. This is impossible since $\varvec{\upsilon }_{k}$ and $\varvec{\upsilon } _{k}^{\prime }$ represent the same $\trianglerighteq _{k}$. The case ${\overline{\lambda }}_{x}<{\overline{\lambda }}_{x}^{\prime }$ is parallel. Thus, ${\overline{\lambda }}_{x}^{\prime }={\overline{\lambda }}_{x}$, and similarly, ${\underline{\lambda }}_{x}^{\prime }={\underline{\lambda }}_{x}$. It was shown in the above paragraph that $\varvec{\upsilon }_{k}(f)= \alpha \varvec{\upsilon }_{k}^{\prime }(f)+\beta$ for any $f\in B_{k}( {\overline{y}};{\underline{y}})$. This together with ${\overline{\lambda }} _{x}^{\prime }={\overline{\lambda }}_{x}$ and ${\underline{\lambda }} _{x}^{\prime }={\underline{\lambda }}_{x}$ implies $\varvec{\upsilon } _{k}^{\prime }(x)= [\upsilon _{k}^{\prime }([{\overline{y}},\overline{ \lambda }_{x};{\underline{y}}])$, $\upsilon _{k}^{\prime }([{\overline{y}}, {\underline{\lambda }}_{x};{\underline{y}}])] = \alpha [\upsilon _{k}([{\overline{y}},{\overline{\lambda }}_{x};{\underline{y}}]),\upsilon _{k}([ {\overline{y}},{\underline{\lambda }}_{x};{\underline{y}}])]+\beta =\alpha [{\overline{\upsilon }}_{k}(x),{\underline{\upsilon }}_{k}(x)]+\beta =\varvec{ \upsilon }_{k}(x)+\beta$. $\square$

Extension Step E: preferences

Step B is an introspection process to find preferences hidden in the mind of the decision maker. On the other hand, Step E is a logical process to extend base preferences found in Step B; it involves a possible difficulty generated by a new type of probability depths, $\delta (f(x))$, interacting with a finite cognitive bound $\rho$. This requires our axiomatic system, Axiom E1 in particular, to take a certain specific form. Keeping this remark in mind, we present our axiomatic system for Step E. Throughout this section, let $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ be a given base preference stream satisfying Axioms B0 to B3.

Extended preference streams

We consider how $\trianglerighteq _{k}$ is extended to $L_{k}(X)$ for $k<\rho +1$. We formulate this derivation by a kind of mathematical induction from the base preferences $\trianglerighteq _{k}$ and the previously derived relation $\succsim _{k-1};$ this process starts at layer 0 to the last layer $\rho$ (or goes to any layer if $\rho =\infty$ ). These are formulated by three axioms; the first axiom E0 corresponds to the start, and the other two, E1 and E2, describe the extension process. It is shown by Theorem 4.1 that our formalism involves no logical difficulty. Then, we give one additional axiom to capture the central part determined by E0 to E2.

First, Axiom E0 is to convert base preferences $\trianglerighteq _{k}$ to $\succsim _{k}$ for each $k<\rho +1$, depicted as the vertical arrows in Table 1.

Axiom E0 (Extension)(i): For any $(f,g)\in D_{0}$, $f\trianglerighteq _{0}g$ if and only if $f\succsim _{0}g$.

(ii): For any $k (1\le k<\rho +1)$ and $(f,g)\in D_{k}$, if $f\trianglerighteq _{k}g$, then $f\succsim _{k}g$.

This states that $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ is the ultimate source for $\langle \succsim _{k}\rangle _{k<\rho +1}$ in Step E. For $k=0$, the base preferences are only the direct source for $\succsim _{0};$ thus, (i) has both directions. For $k\ge 1$, in addition to the base preferences, there is another source from the previous $\succsim _{k-1};$ (ii) requires only one direction. We will show that as long as the domain $D_{k}$ is concerned, the converse of (ii) holds for our intended preference stream $\langle \succsim _{k}\rangle _{k<\rho +1}$.

Now, we consider the connection between layers $k-1$ and k. For ${\widehat{f}}=(f_{1},\ldots ,f_{\ell })$ and ${\widehat{g}}=(g_{1},\ldots ,g_{\ell })$, we write ${\widehat{f}}\succsim _{k}{\widehat{g}}$ iff $f_{t}\succsim _{k}g_{t}$ for all $t=1,\ldots ,\ell$. Recall that a decomposition of $f\in L_{k}(X)$ is defined by (9)$\mathbf {.}$ We formulate a derivation of $\succsim _{k}$ from $\succsim _{k-1}$ as follows: let $1\le k<\rho +1$.

Axiom E1 (Derivation from the previous layer): Let $f\in L_{k}(X)$, $g\in B_{k}({\overline{y}};{\underline{y}})$, and ${\widehat{f}}$, ${\widehat{g}}$ their decompositions. If ${\widehat{f}} \succsim _{k-1}{\widehat{g}}$ or ${\widehat{g}} \succsim _{k-1}{\widehat{f}}$, then $f\succsim _{k}g$ or $g\succsim _{k}f$, respectively.

In layer $k-1$, each $f_{t}$ of ${\widehat{f}}=(f_{1},\ldots ,f_{\ell })$ is compared with the corresponding benchmark lottery $g_{t}$ of ${\widehat{g}} =(g_{1},\ldots ,g_{\ell })$. These preferences are extended to layer k. In Table 1, the horizontal arrows indicate this derivation. A lottery $f\in L_{k}(X)$ may involve the depth $\delta (f(x))$ of the probability value f(x) and the depths of $\delta ({\overline{\lambda }}_{x})$, $\delta ({\underline{\lambda }} _{x})$ of ${\overline{\lambda }}_{x}$, ${\underline{\lambda }}_{x}$ given in b2, for each pure alternative $x\in X$ with $f(x)>0$. In the lottery $d=\frac{25}{10^{2}}y*\frac{75}{ 10^{2}}{\underline{y}}$ in Example 3.1, the former is $\delta ( \frac{25}{10^{2}})=2$ and the latter is $\delta ({\overline{\lambda }} _{x})=\delta ({\underline{\lambda }}_{x})= \delta (\frac{77}{10^{2}})=2$ in case A. On the other hand, benchmark lotteries involve only the former depths since $\delta (\lambda _{{\overline{y}}})=\delta (\lambda _{ {\underline{y}}})=0$ by (18). In Axiom E1, extension is always made based on the benchmark scale. In fact, Lemma 4.1 does not take this constraint into account, but Theorem 4.1 does.

Preferences extended through the benchmark scale $B_{k}({\overline{y}}; {\underline{y}})$ in E1 are further extended by transitivity, which is the next axiom. Let $0\le k<\rho +1$.

Axiom E2 (Transitivity): For any $f,g,h\in L_{k}(X)$, if $f\succsim _{k}g$ and $g\succsim _{k}h$, then $f\succsim _{k}h$.

We interpret Axioms E1 and E2 as inference rules with Axiom E0 as the bases for $\succsim _{k}$. This means that the decision maker constructs $\succsim _{0},\succsim _{1},\ldots$, step by step, using these axioms. This may involve some subtlety; Axioms E0 to E2 may lead to new unintended preferences. We will show Theorem 4.1, implying that this is not the case for the constructed preference relations.

The following are strengthened versions of E0 and E1:

E0$^{*}:$ for all $k<\rho +1$ and $(f,g)\in D_{k}$, $f\trianglerighteq _{k}g$ if and only if $f\succsim _{k}g;$

E1$^{*}:$ E1 holds and if the premise of E1 includes strict preferences, so does the conclusion.

Condition E0$^{*}$ states that $\langle \succsim _{k}\rangle _{k<\rho +1}$ is a faithful extension of $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ as long as the pairs of lotteries in $D_{k}$ are concerned. The other, E1$^{*}$, is a strengthening of E1, too. Without these, some preferences would be added in the derivation process of $\succsim _{0},\succsim _{1},\ldots$ Note that E2 (transitivity) preserves strict preferences in the same way as E1$^{*}$.

To prove that our extended stream $\langle \succsim _{k}\rangle _{k<\rho +1}\$enjoys E0$^{*}$, E1$^{*}$, and E2, we first show the following lemma using the EU hypothesis, which is an auxiliary step to Theorem 4.1. A by-product is the consistency of E0$^{*}$, E1$^{*}$, and E2. For the lemma, a base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ satisfying (19) in Theorem 3.1 is given.

Lemma 4.1

(Direct application of the EU hypothesis). Let $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ be defined as follows: for all $k<\rho +1$,

$$\begin{aligned} f\succsim _{k}^{*}g\text { if and only if }E_{f}(\varvec{\upsilon } _{k})\ge _{I}E_{g}(\varvec{\upsilon }_{k}). \end{aligned}$$

(21)

Then, $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ satisfying Axioms E0$^{*}$, E1$^{*}$, and E2.

The right-hand side is given by comparisons of the expected values of the vector-valued utility function $\varvec{\upsilon }_{k}$. The point of the lemma is not the representation of expected utility values; instead, it is the consistency of E0$^{*}$, E1$^{*}$, and E2, which will be used in Theorem 4.1. The consistency of Axioms E0, E1, and E2 is straightforward since E0 takes only preferences given by B0 to B3, and E1 and E2 introduce new preferences from them. On the other hand, E0$^{*}\ \text { and E1}^{*}$ may generate strict preferences, including negations. Hence, the consistency implied by Lemma 4.1 is a basis of our development.

It will be argued in Sect. 7 that when $\rho =\infty$, the limit preference relation $\succsim _{\infty }^{*}$ is determined E0, E1, and E2 under some additional condition on $L_{\infty }(X)=\cup _{k<\infty }L_{k}(X)$.

Now, we prepare a few concepts for Theorem 4.1. Let $\langle \succsim _{k}\rangle _{k<\rho +1}$ be a stream satisfying E0 to E2. We say that $\langle \succsim _{k}\rangle _{k<\rho +1}$ is the smallest stream iff for any $\langle \succsim _{k}^{\prime }\rangle _{k<\rho +1}$ satisfying E0 to E2, and $f,g\in L_{k}(X)$, $k<\rho +1$,

$$\begin{aligned} f\succsim _{k}g\text { implies }f\succsim _{k}^{\prime }g. \end{aligned}$$

(22)

Also, the set of preferences over $L_{k}(X)$ derived from $\succsim _{k-1}$ by E1 is denoted by $(\succsim _{k-1})^{\text {E1}}$, and the set of transitive closure of $F\subseteq L_{k}(X)^{2}$ is denoted by $F^{tr}$, i.e., $(f,g)\in F^{tr}$ if and only if there is a finite sequence $f=h_{0}$, $h_{1},\ldots ,h_{m}=g$ such that $(h_{t},h_{t+1})\in F$ for $t=0,\ldots ,m-1$.

Using these concepts, we construct the smallest stream $\langle \succsim _{k}\rangle _{k<\rho +1}$, each of which is a binary relation on $L_{k}(X)$, and show, using Lemma 4.1, that it satisfies E0$^{*}$ and E1$^{*}$ as well as E2.

Theorem 4.1

(Smallest extended stream). The stream $\langle \succsim _{k}\rangle _{k<\rho +1}$ of the sets generated by the following induction:

$$\begin{aligned} \succsim _{0}= & {} (\trianglerighteq _{0})^{tr};\text { and } \nonumber \\ \succsim _{k}= & {} [(\succsim _{k-1})^{\text {E1}}\cup (\trianglerighteq _{k})]^{tr}\text { for each }k\text { }(1\le k<\rho +1) \end{aligned}$$

(23)

is the smallest stream satisfying E0 to E2. This $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies E0$^{*}$ and E1$^{*}$.

The construction of $\langle \succsim _{k}\rangle _{k<\rho +1}$ starts with $\succsim _{0} = (\trianglerighteq _{0})^{tr}$, which is well defined since $\trianglerighteq _{0}$ is a binary relation in $D_{0}$. Then, provided that $\succsim _{k-1}$ and $\trianglerighteq _{k}$ are already given, $\succsim _{k}$ is defined to be $[(\succsim _{k-1})^{\text {E1}}\cup (\trianglerighteq _{k})]^{tr}$. This is a subset of $L_{k}(X)^{2};$ thus, it is a binary relation. Thus, the stream $\langle \succsim _{k}\rangle _{k<\rho +1}$ is unique and is the smallest among the streams satisfying E0 to E2. Furthermore, it satisfies E0$^{*}$ and E1$^{*}$, where Lemma 4.1 is used. This assertion guarantees that the constructed stream $\langle \succsim _{k}\rangle _{k<\rho +1}$ is a faithful extension of $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$.⁸

The stream $\langle \succsim _{k}\rangle _{k<\rho +1}$ constructed in Theorem 4.1 differs from the stream $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ given in Lemma 4.1 in that the two types of depths, $\delta ({\overline{\lambda }}_{x})$, $\delta ({\underline{\lambda }}_{x})$ , and $\delta (f(x))$ are taken into account in the former, but for the latter, (21) defines the expected utility, ignoring them. These depths are interactive with cognitive bound $\rho$. When $\rho =\infty$, $\succsim _{\infty }=\cup _{k<\rho +1}\succsim _{k}$ and $\succsim _{\infty }^{*}=\cup _{k<\rho +1}\succsim _{k}^{*}$ coincide under some additional restriction on $L_{\infty }(X)$, which will be discussed in Sect. 7.1. In general, $\langle \succsim _{k}\rangle _{k<\rho +1}$ and $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ differ and coincide only in partial domains, which will be discussed in Sect. 6.

In the constructing process of $\langle \succsim _{k}\rangle _{k<\rho +1}$, E0 to E2 are all extension axioms, and the resulting stream of (23) is uniquely constructed, while there are multiple preference streams satisfying E0 to E2. It would be easier for various purposes to extract the essence of (23) by formulating one axiom. It is formulated as Axiom E3, which requires that a preference $f\succsim _{k}g$ be based on comparisons with the benchmark scale $B_{k}({\overline{y}};{\underline{y}})$ with either $\trianglerighteq _{k}$ or $\succsim _{k-1}$, that is, it eliminates preferences from other possible sources. Note that h in E3 may be the same as f or g.

Axiom E3.Let $k<\rho +1$ and $f,g\in L_{k}(X)$ with $f\succsim _{k}g$. Then $f\succsim _{k}h \succsim _{k}g$ for some $h\in B_{k}({\overline{y}};{\underline{y}})$. When $k\ge 1$, for the pair (f, h), $f\trianglerighteq _{k}h$ holds or f, h have decompositions ${\widehat{f}},{\widehat{h}}$ with ${\widehat{f}}\succsim _{k-1}{\widehat{h}}$; the same holds for the pair (h, g).

The stream $\langle \succsim _{k}\rangle _{k<\rho +1}$ given by (23) is characterized by adding E3 to E0 to E2.

Theorem 4.2

(Unique determination by E0 to E3). Any extended stream satisfying E0 to E3 is the same as the preference stream $\langle \succsim _{k}\rangle _{k<\rho +1}$ given by Theorem 4.1.

Throughout the following, the stream given by (23) is denoted by $\langle \succsim _{k}\rangle _{k<\rho +1}$. Other streams may have some additional superscripts such as $^{\prime }$, $*$.

Lemma 4.2 will be used in the subsequent analyses; (1) is the horizontal arrows in Table 1; and (2) means that $\succsim _{k}$ is bounded in $L_{k}(X)$ by the upper and lower benchmarks ${\overline{y}}$ and ${\underline{y}}$.

Lemma 4.2

Let $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies E0 to E3, and $1\le k<\rho +1$.

(1):

(Preservation of preferences): For any $f,g\in L_{k-1}(X)$, $f\succsim _{k-1}g$ implies $f\succsim _{k}g$.

(2):

${\overline{y}}\succsim _{k}f\succsim _{k}{\underline{y}}$ for any $f\in L_{k}(X)$.

The EU hypothesis is included in Axiom B1 and condition b1 along the benchmark scale $B_{k}({\overline{y}};{\underline{y}})$, and E1 is a weak form of Axiom NM2 (independence). It follows from Lemma 4.1 and Theorem 4.1 that there are possibly multiple preference streams satisfying E0 to E2, among which some satisfy the EU representation in (21) but not in general. This is caused by two types of depths included in a lottery. For example, lottery $d=\frac{25}{10^{2}}y*\frac{75}{10^{2}}{\underline{y}}$ involves the depths of coefficient $\frac{25}{10^{2}}$ and of evaluation $\lambda _{y}$. This is the reason for the EU hypothesis to hold only for some partial domain, which will be explicitly studied in Sect. 6.

Proofs

Proof of Lemma 4.1

We show that $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ given by (21) satisfies E0$^{*}$, E1$^{*}$, and E2. By Theorem 3.2, we can assume that $\upsilon _{k}({\overline{y}})=1$ and $\upsilon _{k}({\underline{y}})=0$.

Since $E_{f}({\underline{\upsilon }}_{k})=\lambda$ if $f=[{\overline{y}},\lambda ;{\underline{y}}]\in B_{k}({\overline{y}};{\underline{y}})$ and $E_{x}(\overline{\upsilon }_{k})={\overline{\upsilon }}_{k}(x)$ if $f=x\in X$. Hence, by (19) and b2, $f\trianglerighteq _{k}x$ if and only if $\lambda \ge {\overline{\upsilon }}_{k}(x)$ if and only if $E_{f}({\underline{\upsilon }}_{k})\ge E_{x}(\overline{\upsilon }_{k})$. The other cases are symmetric. Thus, E0$^{*}$ holds for any $(f,g)\in D_{k}$.

It remains to show that $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ satisfies E1$^{*}$ and E2. Since (21) gives the interval order over the set $\{[E_{f}({\overline{\upsilon }} _{k}),E_{f}({\underline{\upsilon }}_{k})]:f\in L_{k}(X)\}$, E2 holds. We show E1$^{*}$. Let $f\in L_{k}(X),g\in B_{k}[{\overline{y}};{\underline{y}}]$ and their decompositions ${\widehat{f}}$ and ${\widehat{g}}$ with ${\widehat{f}} \succsim _{k-1}^{*}{\widehat{g}}$. By (21), $E_{f_{t}}(\underline{ \upsilon }_{k})\ge E_{g_{t}}({\overline{\upsilon }}_{k})$ for all $t=1,\ldots ,\ell$. Then, $E_{f}({\underline{\upsilon }}_{k})=E_{{\widehat{e}}*{\widehat{f}}}({\underline{\upsilon }}_{k})=\sum _{t=1}^{\ell }\tfrac{1}{\ell } E_{f_{t}}({\underline{\upsilon }}_{k})\ge \sum _{t=1}^{\ell }\tfrac{1}{\ell } E_{g_{t}}({\overline{\upsilon }}_{k})=E_{{\widehat{e}}*{\widehat{g}}}( {\overline{\upsilon }}_{k})=E_{g}({\overline{\upsilon }}_{k})$. If strict preferences are included in the decompositions, the conclusion is strict; thus, we have E1$^{*}$. $\square$

Proof of Theorem 4.1

This has the three assertions: ( a) $\langle \succsim _{k}\rangle _{k<\rho +1}$ is a sequence of a binary relations satisfying Axioms E0 to E2; (b) it is the smallest in the sense of (22) among the streams $\langle \succsim _{k}^{\prime }\rangle _{k<\rho +1}$ satisfying E0 to E2; and (c) E0$^{*}$, E1$^{*}$ hold for $\langle \succsim _{k}\rangle _{k<\rho +1}$.

(a): E2 follows directly from (23). Consider E0. (ii) follows from (23). We show that $\succsim _{0} =(\trianglerighteq _{0})^{tr}$ satisfies that for any $(f,g)\in D_{0}$, $f\succsim _{0}g$ implies $f\trianglerighteq _{0}g$. Since $\succsim _{0} =(\trianglerighteq _{0})^{tr}$, there is a sequence $f=h_{0}\trianglerighteq _{0}\ldots \trianglerighteq _{0}h_{m}=g$. If $h_{t}\in X-B_{0}({\overline{y}}; {\underline{y}})$, then $h_{t-1}\in B_{0}({\overline{y}};{\underline{y}})$ and $h_{t+1}\in B_{0}({\overline{y}};{\underline{y}})$. By B2, $\lambda _{t-1}\ge \lambda _{t+1}$, where $h_{t-1}=[{\overline{y}};\lambda _{t-1},{\underline{y}}]$ and $h_{t+1}=[{\overline{y}};\lambda _{t+1},{\underline{y}}]$. If $h_{t},h_{t+1}\in B_{0}({\overline{y}};{\underline{y}})$, then $\lambda _{t}\ge \lambda _{t+1}$. Hence, we can shorten the sequence to $f=h_{0} \trianglerighteq _{0}h_{m}=g$. Thus, $f\trianglerighteq _{0}g$.

Consider E1. Suppose that $f\in L_{k}(X)$ and $g\in B_{k}[{\overline{y}};{\underline{y}}]$ have decompositions ${\widehat{f}},{\widehat{g}}$ with ${\widehat{f}}\succsim _{k-1}{\widehat{g}}$. By (23), we have $f=e*{\widehat{f}}\succsim _{k}e*{\widehat{g}}=g$. This causes no difficulty, even if $f\in B_{k}(X)$ and $g\in B_{k}[{\overline{y}};{\underline{y}}]$. The symmetric case ${\widehat{g}}\succsim _{k-1}{\widehat{f}}$ is similar.

(b): We prove by induction on k that $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies (22) for any $\langle \succsim _{k}^{\prime }\rangle _{k<\rho +1}$ satisfying E0 to E2. When $k=0$, we have $\succsim _{0} = (\trianglerighteq _{0})^{tr}$ by (23). Let $f\succsim _{0}g$, i.e., $f (\trianglerighteq _{0})^{tr}g$, which implies that there is a sequence $f=h_{0}\trianglerighteq _{0}h_{1}\trianglerighteq _{0}\ldots \trianglerighteq _{0}h_{m}=g$. By E0.(i), we have $f=h_{0}\succsim _{0}^{\prime }h_{1}\succsim _{0}^{\prime }\ldots \succsim _{0}^{\prime }h_{m}=g$. By E2 for $\succsim _{0}^{\prime }$, we have $f\succsim _{0}^{\prime }g$.

Now, we assume that (22) holds for $k-1$. Let $f\succsim _{k}g$. By (23), there is a sequence $f=h_{0}\succsim _{k}\ldots \succsim _{k}h_{m}=g$ such that each $h_{t}\succsim _{k}h_{t+1}$ is a consequence of E1 or $h_{t}\succsim _{k}h_{t+1}$ is $h_{t}\trianglerighteq _{k}h_{t+1}$. In the first case, there are decompositions ${\widehat{h}}_{t}, {\widehat{h}}_{t+1}$ of $h_{t},h_{t+1}$ such that ${\widehat{h}}_{t}\succsim _{k-1}{\widehat{h}}_{t+1}$. By the induction hypothesis, we have ${\widehat{h}} _{t}\succsim _{k-1}^{\prime }{\widehat{h}}_{t+1}$. Thus, $h_{t}\succsim _{k}^{\prime }h_{t+1}$ by E1 for $\succsim _{k}^{\prime }$. In the second case, $h_{t}\trianglerighteq _{k}h_{t+1}$ implies $h_{t}\succsim _{k}^{\prime }h_{t+1}$ by E0.(ii) for $\succsim _{k}^{\prime }$. Hence, $f\succsim _{k}^{\prime }g$ by E2 for $\succsim _{k}^{\prime }$.

(c): Take $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ given by Lemma 4.1. Since $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ satisfies E0 to E2, it holds by (b) that for all $k<\rho +1$ and $f,g\in L_{k}(X)$,

$$\begin{aligned} f\succsim _{k}g\text { implies }f\succsim _{k}^{*}g. \end{aligned}$$

(24)

E0$^{*}$: Since E0$^{*}$ holds for $\succsim _{k}^{*}$ by Lemma 4.1, for any $(f,g)\in D_{k}$, $f\succsim _{k}^{*}g$ implies $f\trianglerighteq _{k}g$. Thus, if $f\succsim _{k}g$, then $f\succsim _{k}^{*}g$ by (24), which implies $f\trianglerighteq _{k}g$. For the converse, $f\trianglerighteq _{k}g$ implies $f\succsim _{k}g$ by (23).

$E1^{*}$: First, we prove by induction on k that for all $k<\rho +1$ and $f,g\in L_{k}(X)$,

$$\begin{aligned} f\succ _{k}g\text { implies }f\succ _{k}^{*}g. \end{aligned}$$

(25)

We make the induction hypothesis that (25) holds for $k-1$. Now, let $f,g\in L_{k}(X)$ with $f\succ _{k}g$. By (23), there are $h_{0}=f,h_{1},\ldots ,h_{m}=g$ in $L_{k}(X)\$such that $(h_{l},h_{l+1})\in (\succsim _{k-1})^{\text {E1}}$ or $(h_{l},h_{l+1})\in (\trianglerighteq _{k})$ for each $l=0,\ldots ,m-1$.

Consider case $(i): (h_{l},h_{l+1})\in (\trianglerighteq _{k})$. Then by E0$^{*}$ for $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$, it holds that $h_{l}\succsim _{k}^{*}h_{l+1}$, and also, if the premise is strict, it follows from E0$^{*}$ for $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ that $h_{l}\succ _{k}^{*}h_{l+1}$. Now, consider case $(ii): (h_{l},h_{l+1})\in (\succsim _{k-1})^{\text {E1}}$. Let ${\widehat{h}}_{l},{\widehat{h}}_{k+1}$ be decompositions of $h_{l},h_{l+1}$ so that ${\widehat{h}}_{l}\succsim _{k-1} {\widehat{h}}_{l+1}$ with/without strict preferences for some components. Hence, by (24) and (25) (the induction hypothesis), the same holds for $\succsim _{k-1}^{*}$. By E1$^{*}$ for $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$, we have $h_{l}\succsim _{k}^{*}h_{l+1}$ and $h_{l}\succ _{k}^{*}h_{l+1}$ if strict preferences hold for some components. At least one of $l=0,\ldots ,m-1$, we have strict preferences for $(h_{l},h_{l+1})\in (\trianglerighteq _{k})$ or ${\widehat{h}} _{l}\succsim _{k-1}{\widehat{h}}_{l+1}$, because of $f\succ _{k}g$. This and the above assertions in (i) and (ii) imply $f\succ _{k}^{*}g$.

Finally, we verify E1$^{*}$ for $\langle \succsim _{k}\rangle _{k<\rho +1}$. Let $f\in L_{k}(X)$ and $g\in B_{k}({\overline{y}}; {\underline{y}})$, and let their decompositions be ${\widehat{f}},{\widehat{g}}$ with ${\widehat{f}}\succsim _{k-1}{\widehat{g}}$. Suppose that one of these preferences is strict. By E1, we have $f\succsim _{k}g$. It suffices to show not $g\succsim _{k}f$. However, ${\widehat{f}}\succsim _{k-1}{\widehat{g}}$ implies ${\widehat{f}}\succsim _{k-1}^{*}{\widehat{g}}$ by (24), and some components of the latter hold strictly by (25). By E1$^{*}$ for $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$, we have $f\succ _{k}^{*}g$, implying not $g\succsim _{k}^{*}f$. By the contrapositive of (24), we have not $g\succsim _{k}f$. $\square$

Proof of Theorem 4.2

Let $\langle \succsim _{k}^{*}\rangle _{k<\rho +1}$ be any extended stream satisfying E0 to E3. We prove by induction on $k<\rho +1$ that for any $f,g\in L_{k}(X)$,

$$\begin{aligned} f\succsim _{k}^{*}g\text { if and only if }f\succsim _{k}g. \end{aligned}$$

(26)

Since $\langle \succsim _{k}\rangle _{k<\rho +1}$ is the smallest stream satisfying E0 to E2 by Theorem 4.1, the if part holds for any $k<\rho +1$.

Consider the only-if part. Let $k=0$. Let $f,g\in L_{0}(X)$ with $f\succsim _{0}^{*}g$. Then, by E3 for $\succsim _{0}^{*}$, we have an $h\in B_{0}({\overline{y}};{\underline{y}})$ with $f\succsim _{0}^{*}h\succsim _{0}^{*}g$. Thus, $f\trianglerighteq _{0}h\trianglerighteq _{0}g$ by E0 for $\succsim _{0}^{*}$. Hence, $f (\trianglerighteq _{0})^{tr}g$, i.e., $f\succsim _{0}g$ by (23). Now, we make the induction hypothesis that the only-if part holds for $k-1.$ Let $f\succsim _{k}^{*}g$. Then, by E3, we have $h_{0}:=f\succsim _{k}^{*}h_{1}\succsim _{k}^{*}h_{2}:=g$ for some $h_{1}\in B_{k}({\overline{y}};{\underline{y}})$. Let $h_{0}=x\in X$. If $h_{0}\trianglerighteq _{k}h_{1}$, then $h_{0}\succsim _{k}h_{1}$ by E0$^{*}$ for $\succsim _{k}$. Suppose ${\widehat{h}}_{0}\succsim _{k-1}^{*}{\widehat{h}}_{1}$ for some decompositions ${\widehat{h}}_{0}$, ${\widehat{h}}_{1}$ of $h_{0}$, $h_{1}$. By the induction hypothesis, we have ${\widehat{h}}_{0}\succsim _{k-1}{\widehat{h}}_{1}$. Thus, by E1 for $\succsim _{k}$, we have $h_{0}\succsim _{k}h_{1}$. In the above two cases, we have $h_{0}\succsim _{k}h_{1}$. By the same argument, we have $h_{1}\succsim _{k}h_{2}$. Thus, by E2 for $\succsim _{k}$, we have $f=h_{0}\succsim _{k}h_{2}=g$, i.e., $f\succsim _{k}g$. $\square$

Proof of Lemma 4.2

(1): Let $f\in L_{k-1}(X)$ and $g\in B_{k-1}({\overline{y}};{\underline{y}})$. Suppose $f\succsim _{k-1}g$. Then, $f,g\in L_{k-1}(X)\subseteq L_{k}(X)$. Let $f_{1}=\cdots =f_{\ell }=f$ and $g_{1}=\cdots =g_{\ell }=g$. Then, $f=\sum \nolimits _{t=1}^{\ell }\frac{1}{\ell } *f_{t}$ and $g=\sum \nolimits _{t=1}^{\ell }\frac{1}{\ell }*g_{t}$. By E1, we have $f\succsim _{k}g$. The case $g\succsim _{k-1}f$ is similar.

Let $f,g\in L_{k-1}(X)$ with $f\succsim _{k-1}g$. Then, by E3 for k, $f\succsim _{k-1}h\succsim _{k-1}g$ for some $h\in B_{k-1}({\overline{y}};{\underline{y}})$. It follows from the conclusion of the above paragraph that $f\succsim _{k}h\succsim _{k}g$. By E2, we have $f\succsim _{k}g$.

(2): Let $f\in L_{0}(X)=X$. By B0 and $\succsim _{0} = \trianglerighteq _{0}$, we have the assertion for $k=0$. Suppose the induction hypothesis that ${\overline{y}}\succsim _{k-1}f\succsim _{k-1} {\underline{y}}$ for any $f\in L_{k-1}(X)$. Consider $f\in L_{k}(X)$. Then, by Lemma 2.1, there is a vector ${\widehat{f}}\in L_{k-1}(X)^{\ell }$ such that $f={\widehat{e}}*{\widehat{f}}\mathbf {.}$ By the induction hypothesis, ${\overline{y}}\succsim _{k-1}f_{t}\succsim _{k-1}{\underline{y}}$ for any $t\le \ell$. By E1, ${\overline{y}}={\widehat{e}}*{\overline{y}} \succsim _{k} f={\widehat{e}}*{\widehat{f}} \succsim _{k} {\widehat{e}} *{\underline{y}}={\underline{y}}$. $\square$

Extension Step E: utilities

We extend a base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ to $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ so that each ${\varvec{u}}_{k}$ is a function over $L_{k}(X)$ to ${\mathbb {Q}}^{2}$. We show that this approach is equivalent to that given in Sect. 4. It provides clear-cut interpretations and mathematical tractability of the entire theory.

Extended utility streams

Let a base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ satisfying b0 to b3 be given. Consider a stream of functions $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ so that each ${\varvec{u}}_{k}=[{\overline{u}}_{k},{\underline{u}}_{k}]$ is a function from $L_{k}(X)$ to ${\mathbb {Q}}^{2}$ with ${\overline{u}}_{k}(f)\ge {\underline{u}} _{k}(f)$ for all $f\in L_{k}(X)$. As for a base utility stream, the values ${\overline{u}}_{k}(f)$ and ${\underline{u}}_{k}(f)$ are interpreted as the least upper and greatest lower bounds of possible utilities from f. Recall that when ${\varvec{u}}_{k}=[{\overline{u}}_{k},{\underline{u}}_{k}]$ is effectively single-valued for f, we drop the upper and lower bars from ${\overline{u}}_{k}(f)={\underline{u}}_{k}(f)$ as $u_{k}(f)$. For ${\widehat{f}} =(f_{1},\ldots ,f_{\ell })$, we write ${\overline{u}}_{k}({\widehat{f}})= ( {\overline{u}}_{k}(f_{1}),\ldots ,{\overline{u}}_{k}(f_{\ell }))$ and ${\underline{u}} _{k}({\widehat{f}})=({\underline{u}}_{k}(f_{1}),\ldots ,{\underline{u}}_{k}(f_{\ell }))$. For ${\widehat{f}}$, ${\widehat{g}}$, we write ${\underline{u}}_{k}({\widehat{f}})\ge {\overline{u}}_{k}({\widehat{g}})$ to mean “${\underline{u}}_{k}(f_{t})\ge {\overline{u}}_{k}(g_{t})$ for $t\le \ell$ ”.

We assume the following four conditions on $\langle {\varvec{u}} _{k}\rangle _{k<\rho +1}:$ for each $k<\rho +1$,

$\varvec{e0}\mathbf {:}$:

The restriction of ${\varvec{u}}_{k}$ to $B_{k}({\overline{y}};{\underline{y}})\cup X$ coincides with $\varvec{\upsilon }_{k}$.

$\varvec{e1}\mathbf {:}$:

Let $f\in L_{k}(X)-B_{k}( {\overline{y}};{\underline{y}})\cup X$, $g\in B_{k}({\overline{y}};{\underline{y}})$, and ${\widehat{f}}$, ${\widehat{g}}$ their decompositions. If $u_{k-1}(\widehat{g }) \ge {\overline{u}}_{k-1}({\widehat{f}})$ or ${\underline{u}}_{k-1}({\widehat{f}})\ge u_{k-1}({\widehat{g}})$, then $u_{k}(g)\ge {\overline{u}}_{k}(f)$ or ${\underline{u}}_{k}(f)\ge u_{k}(g)$, respectively.

$\varvec{e2}\mathbf {:}$:

For any $f\in L_{k}(X)-B_{k}({\overline{y}};{\underline{y}})\cup X$, there are decompositions ${\widehat{f}},{\widehat{f}}^{\prime }$ of f such that ${\overline{u}}_{k}(f)={\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}})$ and ${\underline{u}}_{k}(f)=\ {\widehat{e}}*\underline{u }_{k-1}({\widehat{f}}^{\prime })$.

$\varvec{e3}\mathbf {:}$:

For any $f\in L_{k}(X)-B_{k}({\overline{y}};{\underline{y}})\cup X$, there are g, h in $B_{k}( {\overline{y}};{\underline{y}})$ such that ${\overline{u}} _{k}(f)=u_{k}(g)$ and ${\underline{u}}_{k}(f)=u_{k}(h)$.

Conditions e0 and e1 correspond to E0 and E1. By b1 and e0, ${\varvec{u}}_{k}$ is effectively single-valued for $g\in B_{k}({\overline{y}} ;{\underline{y}})$, i.e., $u_{k}(g)=\upsilon _{k}(g)$. Since the interval order $\ge _{I}$ satisfies transitivity, no condition corresponding to E2 is assumed. Instead, e2 requires that the least upper and greatest lower utilities ${\overline{u}}_{k}(f)$ and ${\underline{u}}_{k}(f)$ come from those of some decompositions. Condition e3 requires ${\overline{u}}_{k}(f)$ and ${\underline{u}}_{k}(f)$ be measured by the benchmark scale $B_{k}({\overline{y}} ;{\underline{y}})$ of the same depth k, which is a depth constraint corresponding to Axiom E3. Under e0, b1, and b2, this is equivalent to

$\varvec{e3}^{*}\mathbf {:}$:

For any $f\in L_{k}(X)$, there are g, h in $B_{k}({\overline{y}};{\underline{y}})$ such that ${\overline{u}}_{k}(f)=u_{k}(g)$ and ${\underline{u}} _{k}(f)=u_{k}(h)$.

We may use either e3 or $e3^{*}$ whichever is more convenient.

Also, it holds that

$$\begin{aligned}&\text {If }g\in B_{k}({\overline{y}};{\underline{y}}) \text { and } g={\widehat{e}} *{\widehat{g}}\text { for some }{\widehat{g}}\in B_{k-1}({\overline{y}}; {\underline{y}})^{\ell },\nonumber \\&\text {then } u_{k}(g)={\widehat{e}}*u_{k-1}( {\widehat{g}}). \end{aligned}$$

(27)

That is, if a benchmark lottery g is decomposed into ${\widehat{g}}$, then the utility value $u_{k}(g)$ is obtained from the weighted sum of $u_{k-1}( {\widehat{g}})$. This will be proved in Sect. 5.2.

First, we present the unique determination of a possible utility stream $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ extended from a given base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$.

Theorem 5.1

(Unique extension). Let $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ be an extended utility stream satisfying e0 to e3. Then, it holds that for any $f\in L_{k}(X)$ with $k\ge 0$,

$$\begin{aligned} {\overline{u}}_{k}(f)=\left\{ \begin{array}{l} {\overline{\upsilon }}_{k}(f)\text { if }f\in B_{k}({\overline{y}};{\underline{y}})\cup X \\ \min \{{\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}}):{\widehat{f}}\text { is a decomposition of }f\}\text { otherwise} \end{array} \right. \end{aligned}$$

(28)

$$\begin{aligned} {\underline{u}}_{k}(f)=\left\{ \begin{array}{l} \text { }{\underline{\upsilon }}_{k}(f)\text { if }f\in B_{k}({\overline{y}};{\underline{y}})\cup X \\ \max \{{\widehat{e}}*{\underline{u}}_{k-1}({\widehat{f}}):{\widehat{f}}\text { is a decomposition of }f\}\text { otherwise.} \end{array} \right. \end{aligned}$$

(29)

Conversely, when a base utility stream $\langle \varvec{\upsilon } _{k}\rangle _{k<\rho +1}$ is given, an extended utility stream $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ is uniquely determined from $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ by (28) and (29), and it satisfies e0 to e3.

Since $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ representing $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ is uniquely determined up to positive linear transformations, stated in Theorem 3.2, and since the extended utility stream $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ is uniquely determined by $\langle \varvec{\upsilon } _{k}\rangle _{k<\rho +1}$, the stream of pair $\langle \varvec{\upsilon } _{k},{\varvec{u}}_{k}\rangle _{k<\rho +1}$ is unique determined up to positive linear transformations.

The existence of $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ representing $\langle \succsim _{k}\rangle _{k<\rho +1}$ is guaranteed by the next theorem. Recall that $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ with B0 to B3 is assumed behind $\langle \succsim _{k}\rangle _{k<\rho +1}$ by E0 and that $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ with b0 to b3 is assumed behind $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ by e0. These $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ and $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ are connected by (19) in Theorem 3.1. Axiom E3 and condition e3 are separately treated in Theorem 5.2, because this separation will be needed for Theorem 7.1.

Theorem 5.2

(Representation of $\langle \succsim _{k}\rangle _{k<\rho +1}$by $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$). A preference stream $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies E0 to E2 (and E3, respectively) if and only if there is a utility stream $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ satisfying e0 to e2 (and e3) such that for any $k<\rho +1$ and $f,g\in L_{k}(X)$,

$$\begin{aligned} f\succsim _{k}g\text { if and only if }{\varvec{u}}_{k}(f)\ge _{I} {\varvec{u}}_{k}(g). \end{aligned}$$

(30)

Table 2 summarizes the results in Sects. 3 to 5; here E3 and e3 are included 5.2. Section 3 is started with the theory of a base preference stream $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ and of a base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$. In Sect. 4, $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ is extended to $\langle \succsim _{k}\rangle _{k<\rho +1};$ Theorems 4.1 and 4.2 show the unique existence of $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfying E0 to E3, relative to $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$. Correspondingly, Theorem 5.1 implies that $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ is uniquely determined relative to $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$. Theorem 5.2 states the existence of an extended utility stream $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ when $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies E0 to E3.

The above theorems can be regarded as a substantiation of the indication, by Von Neumann and Morgenstern (1944), p. 29, of a possibility of a representation of a preference relation involving incomparabilities in terms of a higher-dimensional vector-valued function.

The utility stream $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ given by Theorem 5.2 with E3 and e3 differs from the EU representation in Lemma 4.1. This causes some difficulty in practical calculation of $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ for the case $\rho <\infty ,$ but Theorem 5.1 is useful for practical purpose. We show how to calculate ${\overline{u}}_{k}$ and ${\underline{u}}_{k}$ in Example 3.1, which will be used in Sect. 8.

Example 5.1

Consider A and B of Example 3.1 with $X=\{{\overline{y}},y,{\underline{y}}\}$. Recall $\varvec{\upsilon }_{0}({\overline{y}})=\varvec{\upsilon }_{1}( {\overline{y}})=[1,1]$, $\varvec{\upsilon }_{0}({\underline{y}})=\varvec{ \upsilon }_{1}({\underline{y}})=[0,0]$, $\varvec{\upsilon }_{0}(y)=[1,0]$, $\varvec{\upsilon }_{1}(y)=[\frac{9}{10},\frac{7}{10}]$. These values are the same as ${\varvec{u}}_{0},{\varvec{u}}_{1}$ by e0. Also, we have:

$$\begin{aligned} A:\varvec{\upsilon }_{2}(y)={\varvec{u}}_{2}(y)=\left[ \tfrac{77}{10^{2}}, \tfrac{77}{10^{2}}\right] \text { and }B:\text { }\varvec{\upsilon }_{2}^{\prime }(y)={\varvec{u}}_{2}^{\prime }(y)=\left[ \tfrac{83}{10^{2}},\tfrac{83}{10^{2}}\right] . \end{aligned}$$

(31)

Consider how to calculate ${\varvec{u}}_{2}(d)$ and ${\varvec{u}}_{3}(d)$ for $d=\frac{25}{10^{2}}y*\frac{75}{10^{2}}{\underline{y}}$. We mainly consider case A and will adjust the calculation for case B.

The lottery d has the three types of decompositions $\tfrac{t}{10}*y+\tfrac{5-2t}{10}*[y,\tfrac{5}{10};\underline{ y}]+\tfrac{5+t}{10}*{\underline{y}}$ for $t=0,1,2$ in (12). Among these, the one with $t=2$ gives ${\varvec{u}}_{2}$ and ${\varvec{u}}_{3}$ ; since y is evaluated in a shallower layer through $\tfrac{5-2t}{10}*[y,\tfrac{5}{10};{\underline{y}}]$ than $\tfrac{t}{10}*y$, it is more accurate to use $\tfrac{t}{10}*y$ than $\tfrac{5-2t}{10}*[y,\tfrac{5}{10};{\underline{y}}]$. Thus, we take the largest weight $t=2$ to $\tfrac{t}{10}*y$ for the min and max operators in (28) and (29).

The second term $[y,\tfrac{5}{10};{\underline{y}}]= \tfrac{5}{10}y*\tfrac{5}{10}{\underline{y}}$ itself is regarded as a unique decomposition; we have, by (28) and (29),

$$\begin{aligned} {\varvec{u}}_{1}\left( \tfrac{5}{10}y*\tfrac{5}{10}{\underline{y}}\right) =\tfrac{5}{ 10}\varvec{\upsilon }_{0}(y)+\tfrac{5}{10}\varvec{\upsilon }_{0}( {\underline{y}})=\left[ \tfrac{5}{10},0\right] . \end{aligned}$$

(32)

Plugging these to the decomposition $\tfrac{2}{10}y*\tfrac{1}{10}(\tfrac{ 5}{10}y*\tfrac{5}{10}{\underline{y}})*\tfrac{7}{10}{\underline{y}}$, we have, by e1,

$$\begin{aligned} {\varvec{u}}_{2}(d)= & {} {\varvec{u}}_{2}\left( \tfrac{2}{10}y*\tfrac{1}{10}\left( \tfrac{5}{10}y*\tfrac{5}{10}{\underline{y}}\right) *\tfrac{7}{10}{\underline{y}} \right) \nonumber \\= & {} \tfrac{2}{10}{\varvec{u}}_{1}(y)+\tfrac{1}{10}{\varvec{u}}_{1}\left( \tfrac{5 }{10}y*\tfrac{5}{10}{\underline{y}}\right) +\tfrac{7}{10}{\varvec{u}}_{1}\left( {\underline{y}}\right) \nonumber \\= & {} \tfrac{2}{10}\left[ \tfrac{9}{10},\tfrac{7}{10}\right] +\tfrac{1}{10}\left[ \tfrac{5}{10},0\right] + \tfrac{1}{10}[0,0]=\left[ \tfrac{23}{10^{2}},\tfrac{14}{10^{2}}\right] . \end{aligned}$$

(33)

This is compared with ${\varvec{u}}_{2}(c)={\varvec{u}}_{2}(\tfrac{2}{10} {\overline{y}}*\tfrac{8}{10}{\underline{y}})=[\tfrac{2}{10},\tfrac{2}{10}]$, and thus, by Theorem 5.2, c and d are incomparable with respect to $\succsim _{2}$.

In the same as (32), we have ${\varvec{u}} _{2}(\tfrac{5}{10}y*\tfrac{5}{10}{\underline{y}})=\tfrac{5}{10}\varvec{ \upsilon }_{1}(y)+\tfrac{5}{10}\varvec{\upsilon }_{1}({\underline{y}})=[ \tfrac{45}{10^{2}},\tfrac{35}{10^{2}}]$. Then, we calculate ${\varvec{u}} _{3}(d)$ for case $\rho =3:$

$$\begin{aligned} {\varvec{u}}_{3}(d)= & {} {\varvec{u}}_{3}\left( \tfrac{2}{10}y*\tfrac{1}{10}\left( \tfrac{5}{10}y*\tfrac{5}{10}{\underline{y}}\right) *\tfrac{7}{10}{\underline{y}} \right) \nonumber \\= & {} \tfrac{2}{10}{\varvec{u}}_{2}(y)+\tfrac{1}{10}{\varvec{u}}_{2}\left( \tfrac{5 }{10}y*\tfrac{5}{10}{\underline{y}}\right) +\tfrac{7}{10}{\varvec{u}}_{2}( {\underline{y}}) \nonumber \\= & {} \tfrac{2}{10}\left[ \tfrac{77}{10^{2}},\tfrac{77}{10^{2}}\right] +\tfrac{1}{10}\left[ \tfrac{ 45}{10^{2}},\tfrac{35}{10^{2}}\right] +\tfrac{7}{10}[0,0]=\left[ \tfrac{199}{10^{3}}, \tfrac{189}{10^{3}}\right] . \end{aligned}$$

(34)

Here, c is strictly preferred to d, since ${\varvec{u}}_{3}(c)= {\varvec{u}}_{3}(\tfrac{2}{10}{\overline{y}}*\tfrac{8}{10}{\underline{y}} )=[\tfrac{2}{10},\tfrac{2}{10}]$. For $k\ge 4$, since ${\varvec{u}} _{k}(d)=[\tfrac{1925}{10^{4}},\tfrac{1925}{10^{4}}]$, c is strictly preferred to d.

Consider case B :  ${\varvec{u}}_{2}^{\prime }(y)=[ \frac{83}{10^{2}},\frac{83}{10^{2}}]$ for $\rho =2$. Then, the above calculation (33) for ${\varvec{u}}_{2}(d)$ remains the same for ${\varvec{u}}_{2}^{\prime }(d)$ with ${\varvec{u}}_{2}^{\prime }(d)=[ \tfrac{23}{10^{2}},\tfrac{14}{10^{2}}]$, but for $\rho =3,\ {\varvec{u}} _{3}^{\prime }(d)$ is calculated as follows:

$$\begin{aligned} {\varvec{u}}_{3}^{\prime }(d)= & {} {\varvec{u}}_{3}^{\prime }\left( \tfrac{2}{10} y*\tfrac{1}{10}\left( \tfrac{5}{10}y*\tfrac{5}{10}{\underline{y}}\right) *\tfrac{7}{10}{\underline{y}}\right) \nonumber \\= & {} \tfrac{2}{10}{\varvec{u}}_{2}(y)+\tfrac{1}{10} {\varvec{u}}_{2}\left( \tfrac{5}{10}y*\tfrac{5}{10}{\underline{y}}\right) +\tfrac{7}{ 10}{\varvec{u}}_{2}({\underline{y}}) \nonumber \\= & {} \tfrac{2}{10}\left[ \tfrac{83}{10^{2}},\tfrac{83}{10^{2}}\right] +\tfrac{1}{10}\left[ \tfrac{ 45}{10^{2}},\tfrac{35}{10^{2}}\right] +\tfrac{7}{10}[0,0]=\left[ \tfrac{211}{10^{3}}, \tfrac{201}{10^{3}}\right] \end{aligned}$$

(35)

Here, d is strictly preferred to c. This holds for $k\ge 4$ since ${\varvec{u}}_{k}^{\prime }(d)$ is calculated as $[\tfrac{2075}{10^{4}}, \tfrac{2075}{10^{4}}]$.

Proofs

Proof of (27)

Suppose $g=[{\overline{y}},\lambda ;{\underline{y}}]\in B_{k}({\overline{y}};{\underline{y}})$. Let $g_{t}=[{\overline{y}},\lambda _{t};{\underline{y}}]$ for $t\le \ell$. Since $g={\widehat{e}}*{\widehat{g}} ,$ we have $\lambda =\sum _{t\le \ell }\frac{1}{\ell }\lambda _{t}$. Since $\lambda _{t}\in \varPi _{k-1}\subseteq \varPi _{k}$ for $t\le \ell$, we have $\upsilon _{k-1}(g_{t})=\lambda _{t}\upsilon _{0}({\overline{y}})+(1-\lambda _{t})\upsilon _{0}({\underline{y}})= \upsilon _{k}(g_{t})$ by (17). Since $\upsilon _{k}(g)=\lambda \upsilon _{0}({\overline{y}})+(1-\lambda )\upsilon _{0}({\underline{y}})=(\sum _{t\le \ell }\frac{1}{\ell }\lambda _{t})\upsilon _{0}({\overline{y}})+(1-(\sum _{t\le \ell }\frac{1}{\ell } \lambda _{t})\upsilon _{0}({\underline{y}})= \sum _{t\le \ell }\frac{1}{ \ell }(\lambda _{t}\upsilon _{0}({\overline{y}})+ (1-\lambda _{t})\upsilon _{0}({\underline{y}}))=\sum _{t\le \ell }\frac{1}{\ell }u_{k-1}(g_{t})= {\widehat{e}}*u_{k-1}({\widehat{g}})$. $\square$

Proof of Theorem 5.1

Since (28) and (29 ) are dual, we consider only (28). Let $f\in B_{k}({\overline{y}}; {\underline{y}})\cup X$. Then, by e0, ${\overline{u}}_{k}(f)={\overline{\upsilon }}_{k}(f)$. Consider the case where $f\in L_{k}(X)- B_{k}( {\overline{y}};{\underline{y}})\cup X$. We prove ${\overline{u}}_{k}(f)=\min \{ {\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}}):{\widehat{f}}$ is a decomposition of $f\}$. By e2, there is a decomposition ${\widehat{f}}$ of f such that ${\overline{u}}_{k}(f)={\widehat{e}}*{\overline{u}}_{k-1}( {\widehat{f}})$. Let $\widehat{f^{\prime }}$ be any decomposition of $f.\$We show ${\widehat{e}}*{\overline{u}}_{k-1}(\widehat{f^{\prime }})\ge {\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}})$. By e3, for each $t\le \ell$, there is a benchmark lottery $g_{t}^{\prime }\in B_{k-1}({\overline{y}}; {\underline{y}})$ such that ${\overline{u}}_{k-1}(f_{t}^{\prime })=u_{k-1}(g_{t}^{\prime })$. Let $\widehat{g^{\prime }}=(g_{1}^{\prime },\ldots ,g_{\ell }^{\prime })$, which is a decomposition of $g^{\prime }:= {\widehat{e}}*\widehat{g^{\prime }}$. By applying e1 to $u_{k-1}( \widehat{g^{\prime }})={\overline{u}}_{k-1}({\widehat{f}}^{\prime })$, we obtain $u_{k}(g^{\prime })\ge {\overline{u}}_{k}(f)$. Since ${\widehat{e}}*u_{k-1}( \widehat{g^{\prime }})= u_{k}(g^{\prime })$ by (27), we have ${\widehat{e}}*{\overline{u}}_{k-1}(\widehat{f^{\prime }})={\widehat{e}}*u_{k-1}(\widehat{g^{\prime }})= u_{k}(g^{\prime })\ge {\overline{u}}_{k}(f) ={\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}})$.

For the latter assertion, we construct inductively $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ from $k=0$ by (28) and (29). It is easy to see that $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ satisfies e0 to e2. We need an inductive proof for e3. $\square$

Proof of Theorem 5.2

(If): Let $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ be the extended utility stream satisfying e0 to e2 (and/or e3). Let $\succsim _{k}$ be the binary relation over $L_{k}(X)$ defined by (30) and let its restriction to $D_{k}$ be $\trianglerighteq _{k}$. Since $\varvec{ \upsilon }_{k}$ the restriction of ${\varvec{u}}_{k}$ to $B_{k}(\overline{y };{\underline{y}})\cup X$ for each $k<\rho +1$, $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$ satisfies b0 to b3 by Theorem 3.1 . Thus, we have E0. It remains to show that $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies E1 to E2 (and/or E3). Since the relation $\ge _{I}\$over $\{{\varvec{u}}_{k}(f):f\in L_{k}(X)\}$ is transitive, E2 is satisfied.

Consider E1. Let ${\widehat{f}}\in L_{k-1}(X)^{\ell }$ and ${\widehat{g}}\in B_{k-1}({\overline{y}};{\underline{y}})^{\ell }$ be decompositions of $f\in L_{k}(X)$ and $g\in B_{k}({\overline{y}};{\underline{y}} )$. Suppose that ${\widehat{f}}\succsim _{k-1}{\widehat{g}}$, which implies ${\varvec{u}}_{k-1}({\widehat{f}})\ge _{I}{\varvec{u}}_{k-1}({\widehat{g}})$ by (30).

Suppose $f\in B_{k}({\overline{y}};{\underline{y}} )\cup X$. Let $f=x\in X$. Then ${\widehat{f}}=(x,\ldots x)$. Then, ${\underline{\upsilon }}_{k-1}(x)\ge u_{k-1}(g_{t})$ for all $t\le \ell$, which, b3, implies ${\underline{\upsilon }}_{k}(x)\ge {\underline{\upsilon }}_{k-1}(x)\ge u_{k-1}(g_{t})$ for all $t\le \ell$. Thus, $\underline{ \upsilon }_{k}(x)\ge \sum _{t\le \ell }\frac{1}{\ell }u_{k-1}(g_{t})= {\widehat{e}}*{\overline{u}}_{k-1}({\widehat{g}})$. By (27), $\widehat{e }*{\overline{u}}_{k-1}({\widehat{g}})=u_{k}(g)$. Hence, by b0, ${\underline{u}}_{k}(x)={\underline{\upsilon }}_{k}(x)\ge u_{k}(g)$. Thus, $f\succsim _{k}g$ by (30).

Suppose $f\in B_{k}({\overline{y}};{\underline{y}})$. By (27), $u_{k}(f)={\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}})$, and again, by (27), ${\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}} )=u_{k}(g)$. Since $u_{k-1}(g_{t})\ge u_{k-1}(g_{t})$ for $t\le \ell$, we have $u_{k}(f)\ge u_{k}(g)$. Thus, $f\succsim _{k}g$ by (30).

Finally, consider the case $f\in L_{k}(X)-B_{k}({\overline{y}};{\underline{y}})\cup X$. Thus, ${\widehat{e}}*{\underline{u}}_{k-1}({\widehat{f}})\ge {\widehat{e}}*u_{k-1}({\widehat{g}}) = u_{k-1}({\widehat{e}}*{\widehat{g}}) =u_{k}(g)$ by (27). By e1, we have ${\underline{u}}_{k}(f)\ge {\widehat{e}}*u_{k-1}({\widehat{f}} )\ge u_{k}(g)$. Hence, ${\varvec{u}}_{k}(f)\ge _{I}{\varvec{u}} _{k}(g);$ thus, $f\succsim _{k}g$ by (30). The other case of ${\widehat{g}}\succsim _{k-1}{\widehat{f}}$ is symmetric.

To prove Axiom E3, we prove the following assertion. Then, we obtain Axiom E3 from E3$(\langle {\varvec{u}}_{k}\rangle _{k<\rho +1})$ by translating it in terms of the preference stream $\langle \succsim _{k}\rangle _{k<\rho +1}$.

E3:

$(\langle u_{k}\rangle _{k< \rho +1})$: Let $k<\rho +1$ and $f,g\in L_{k}(X)$ with ${\varvec{u}}_{k}(f)\ge _{I} {\varvec{u}}_{k}(g)$. There is an $h\in B_{k}({\overline{y}};{\underline{y}})$ such that ${\varvec{u}}_{k}(f)\ge _{I}{\varvec{u}}_{k}(h)\ge _{I}{\varvec{u}}_{k}(g)$. When $k\ge 1$, $\varvec{\upsilon }_{k}(f)\ge _{I}\varvec{\upsilon }_{k}(h)$ or f, h have decompositions ${\widehat{f}},{\widehat{h}}$ with ${\varvec{u}}_{k-1}({\widehat{f}})\ge _{I}{\varvec{u}}_{k-1}({\widehat{h}})$ , and the same holds for h, g.

Since ${\underline{u}}_{k}(f)\ge {\overline{u}}_{k}(g)$, by $e3^{*}$, there is an $h\in B_{k}({\overline{y}};{\underline{y}})$ such that ${\underline{u}} _{k}(f)=u_{k}(h)$. Hence, ${\underline{u}}_{k}(f)=u_{k}(h)\ge {\overline{u}} _{k}(g)$, i.e., ${\varvec{u}}_{k}(f)\ge _{I}{\varvec{u}}_{k}(h)\ge _{I} {\varvec{u}}_{k}(g)$.

Let $k\ge 1$. Let $f\in B_{k}({\overline{y}};{\underline{y}})\cup X$. By e0, ${\varvec{u}}_{k}(f)=\varvec{\upsilon }_{k}(f)$ and ${\varvec{u}}_{k}(h)=\varvec{\upsilon }_{k}(h)$ since $h\in B_{k}( {\overline{y}};{\underline{y}})$. Hence, ${\varvec{u}}_{k}(f)\ge _{I} {\varvec{u}}_{k}(h)$ implies $\varvec{\upsilon }_{k}(f)\ge _{I} \varvec{\upsilon }_{k}(h)$. Now, suppose f, $g\notin B_{k}({\overline{y}} ;{\underline{y}})\cup X$. We show that f, h have decompositions ${\widehat{f}}$, ${\widehat{h}}$ such that ${\varvec{u}}_{k-1}({\widehat{f}})\ge _{I} {\varvec{u}}_{k-1}({\widehat{h}})$. By e2, there is a decomposition of ${\widehat{f}}$ of f such that ${\widehat{e}}*{\underline{u}}_{k-1}({\widehat{f}})={\underline{u}}_{k}(f)$. By e3, there are ${\underline{\lambda }} _{f_{1}},\ldots ,\underline{\lambda }_{f_{\ell }}$ in $\varPi _{k}$ such that ${\underline{u}}_{k-1}(f_{t})={\underline{\lambda }}_{f_{t}}$ for $t\le \ell$. Let $h_{t}=[{\overline{y}},\underline{\lambda }_{f_{t}};{\underline{y}}]$ for $t\le \ell$ and let ${\widehat{h}}=(h_{1},\ldots ,h_{\ell })$. Since ${\widehat{f}} \in L_{k-1}(X)^{\ell -1}$, ${\widehat{h}}=(h_{1},\ldots ,h_{\ell })$ belongs to $L_{k-1}(X)^{\ell -1}$. Since $\underline{\lambda }_{f}={\underline{u}}_{k}(f)= {\widehat{e}}*{\underline{u}}_{k-1}({\widehat{f}})=\sum \frac{1}{\ell }\cdot {\underline{\lambda }}_{f_{t}}$, we have $h=[{\overline{y}},{\underline{\lambda }} _{f};{\underline{y}}]=\sum _{t}\frac{1}{\ell }*h_{t}$. Hence, ${\widehat{h}}$ is a decomposition of h with ${\underline{u}}_{k-1}({\widehat{f}})=u_{k-1}( {\widehat{h}})$. This implies ${\varvec{u}}_{k-1}({\widehat{f}})\ge _{I} {\varvec{u}}_{k-1}({\widehat{h}}).$

(Only-if): Suppose that $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies Axioms E0 to E2 (and/or E3) with its base preference stream $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$. Then, $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ satisfies B0 to B3 by E0. Although this part can be proved using Theorem 5.1, the following direct proof is clearer.

We define $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}=\langle [{\overline{u}}_{k},{\underline{u}}_{k}]\rangle _{k<\rho +1}$ as follows: for each $f\in L_{k}(X)$,

$$\begin{aligned} {\overline{u}}_{k}(f)= & {} \min \{\lambda \in \varPi _{k}:[{\overline{y}},\lambda ; {\underline{y}}]\succsim _{k}f\}; \nonumber \\ {\underline{u}}_{k}(f)= & {} \max \{\lambda \in \varPi _{k}:f\succsim _{k}[\overline{ y},\lambda ;{\underline{y}}]\}. \end{aligned}$$

(36)

By Lemma 4.1.(2), these are well defined. Let $f,g\in L_{k}(X)$, ${\underline{u}}_{k}(f):={\underline{\lambda }}_{f}$, and ${\overline{u}}_{k}(g):= {\overline{\lambda }}_{g}$. Then, ${\varvec{u}}_{k}(f)\ge _{I}{\varvec{u}} _{k}(g)$ if and only if ${\underline{\lambda }}_{f}\ge {\overline{\lambda }} _{g}$. It holds that ${\varvec{u}}_{k}(f)\ge _{I}{\varvec{u}}_{k}(g)$ if and only if $f\succsim _{k}g;$ indeed, if ${\varvec{u}}_{k}(f)\ge _{I} {\varvec{u}}_{k}(g)$, then $f\succsim _{k}[{\overline{y}},\underline{\lambda }_{f};{\underline{y}}]\succsim _{k}[{\overline{y}},{\overline{\lambda }}_{g}; {\underline{y}}]\succsim _{k}g$, i.e., $f\succsim _{k}g$ by E2, and conversely, if $f\succsim _{k}g$, then ${\underline{u}}_{k}(f)\ge {\overline{u}} _{k}(g)$ by (36).

When $f\in B_{k}({\overline{y}};{\underline{y}})$, we have ${\overline{u}}_{k}(f)=\lambda _{f}=\upsilon _{k}(f)$. Thus, e0 holds. Consider e1 to e2(and e3).

$\varvec{e1}:$ Let ${\widehat{f}}\in L_{k-1}(X)^{\ell }$. By (36) for $k-1$, ${\overline{u}}_{k-1}(f_{t})$ is written as $\lambda _{t}\in \varPi _{k-1}$ for all $t=1,\ldots ,\ell$. Let ${\widehat{\lambda }}=(\lambda _{1},\ldots ,\lambda _{\ell })$. Then, ${\widehat{e}}*{\overline{u}}_{k-1}( {\widehat{f}})={\widehat{e}}*{\widehat{\lambda }}\in \varPi _{k}$. By (36 ) for k, it holds that ${\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}})= {\widehat{e}}*{\widehat{\lambda }} \ge {\overline{u}}_{k}({\widehat{e}}*{\widehat{f}})$. The other assertion that ${\underline{u}}_{k}({\widehat{e}}*{\widehat{f}})\ge {\widehat{e}}*u_{k-1}({\widehat{f}})$ is similarly proved.

$\varvec{e2}:$ Let $f\in L_{k}(X)-B_{k}({\overline{y}};{\underline{y}})\cup X$. We prove that ${\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}})= {\overline{u}}_{k}(f)$ for some decomposition ${\widehat{f}}$ of f. The other half can be proved in the dual manner. By (36), we have $\overline{ u}_{k}(f)={\overline{\lambda }}_{f}\in \varPi _{k}$. Let $g:=[{\overline{y}}, {\overline{\lambda }}_{f};{\underline{y}}]$. By (36) and B1, g is the least preferred among $g^{\prime }\in B_{k}({\overline{y}};{\underline{y}})$ with $g^{\prime }\succsim _{k}f$, that is,

$$\begin{aligned} g^{\prime }\succsim _{k}g\text { for any }g^{\prime }\in B_{k}({\overline{y}}; {\underline{y}})\text { with }g^{\prime }\succsim _{k}f. \end{aligned}$$

(37)

Consider the preference $g\succsim _{k}f$. By (23), there are lotteries $g=h_{0},h_{1},\ldots ,h_{m}=f$ such that each $(h_{l},h_{l+1})$ either belongs to $\trianglerighteq _{k}$ or is derived by E1. Since $h_{m}=f\in L_{k}(X)-B_{k}({\overline{y}};{\underline{y}})\cup X$, the preference $h_{m-1}\succsim _{k}h_{m}=f$ is derived by E1, which implies $h_{m-1}\in B_{k}({\overline{y}};{\underline{y}})$. Since $g=h_{0}\succsim _{k}h_{m-1}$ and $g\in B_{k}({\overline{y}};{\underline{y}})$, we have ${\overline{\lambda }} _{f}=\lambda _{0}\ge \lambda _{m-1}$. However, since ${\overline{\lambda }} _{f}$ is given by the minimization (36), it is impossible that ${\overline{\lambda }}_{f}=\lambda _{0}>\lambda _{m-1}$. Thus, $\lambda _{0}= {\overline{\lambda }}_{f}=\lambda _{m-1}$, i.e., $h_{0}=g=h_{m-1}$.

Since $h_{0}=g=h_{m-1}\succsim _{k}f$ is derived by E1, there are decompositions ${\widehat{g}},{\widehat{f}}$ of g, f such that ${\widehat{g}}\succsim _{k-1}{\widehat{f}}$ and $g={\widehat{e}}*{\widehat{g}} \succsim _{k}{\widehat{e}}*{\widehat{f}}=f$. Then, by (36), each component $f_{t}$ of ${\widehat{f}}$ has $g_{t}^{\prime }\in B_{k-1}(\overline{ y};{\underline{y}})$ such that ${\overline{u}}_{t-1}(f_{t})= u_{t-1}(g_{t}^{\prime })=\lambda _{g_{t}^{\prime }}$. Since $g_{t}\succsim _{k-1}f_{t}$, we have $g_{t}\succsim _{k-1}g_{t}^{\prime }$ by (36), which implies $u_{k-1}(g_{t})=\lambda _{g_{t}}\ge \lambda _{g_{t}^{\prime }}=u_{t-1}(g_{t}^{\prime })={\overline{u}}_{t-1}(f_{t})$. Since this holds for all $t\le \ell$, we have

$$\begin{aligned} u_{k}(g)={\widehat{e}}*u_{k-1}({\widehat{g}})\ge {\widehat{e}}*u_{k-1}( \widehat{g^{\prime }})={\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}}). \end{aligned}$$

(38)

On the other hand, each $g_{t}^{\prime }$ satisfies $g_{t}^{\prime }\succsim _{k-1}f_{t}$ for all $t\le \ell$ by definition. By E1, ${\widehat{e}}*\widehat{g^{\prime }}\succsim _{k}{\widehat{e}}*{\widehat{f}} =f$. By (37), ${\widehat{e}}*\widehat{g^{\prime }}\succsim _{k}g$. This implies ${\widehat{e}}*u_{k-1}(\widehat{g^{\prime }})=u_{k}({\widehat{e}}*\widehat{g^{\prime }})\ge u_{k}(g)$, which implies that all the terms in ( 38) are identical. Thus, ${\overline{u}}_{k}(f)=u_{k}(g)={\widehat{e}} *{\overline{u}}_{k-1}({\widehat{f}})$.

$\varvec{e3}:$ By (36), ${\overline{u}}_{k}(x)=\lambda \in \varPi _{k}$ and ${\underline{u}}_{k}(x)=\lambda ^{\prime }\in \varPi _{k}$ for some $\lambda$ and $\lambda ^{\prime }$ in $\varPi _{k}$. Hence, ${\overline{u}} _{k}(x)=u_{k}([{\overline{y}},\lambda ;{\underline{y}}])$ and ${\underline{u}} _{k}(x)=u_{k}([{\overline{y}},\lambda ^{\prime };{\underline{y}}])$. This is the conclusion of e3. $\square$

Measurability, comparability, and the EU hypothesis

Here, we study the concepts of measurable and non-measurable lotteries. Comparability and the EU hypothesis hold for measurable lotteries, while incomparability is intimately related to non-measurable lotteries. We assume that $\langle \succsim _{k}\rangle _{k<\rho +1}$ satisfies E0 to E3, relative to a base preference stream $\langle \trianglerighteq _{k}\rangle _{k<\rho +1}$ satisfying B0 to B3.

Measurable and non-measurable lotteries

We define the set $M_{k}\$for $k<\rho +1$ by

$$\begin{aligned} M_{k}=\{f\in L_{k}(X):f\sim _{k}g\text { for some }g\in B_{k}({\overline{y}}; {\underline{y}})\}. \end{aligned}$$

(39)

Each $f\in M_{k}$ is precisely measured by the benchmark scale $B_{k}( {\overline{y}};{\underline{y}})$, while measurement of $f\in L_{k}(X)-M_{k}$ contains some indeterminacy. We call $f\in M_{k}$measurable and $f\in L_{k}(X)-M_{k}$non-measurable. Here, we study measurability and non-measurability. We use the fact that $f\in M_{k}$ is equivalent to that $f\sim _{k}g$ for some $g\in M_{k}$.

Under our axioms, it holds that

$$\begin{aligned} \text {for each }f\ \in M_{k},\text { the probability weight }\lambda \ \text { with }f\sim _{k}[{\overline{y}},\lambda ;{\underline{y}}]\text { is unique}, \end{aligned}$$

(40)

which we denote by $\lambda _{f}$. In $M_{k}$, no incomparabilities are observed; that is, if $f,g\in M_{k}$ with $\lambda _{f}\ge \lambda _{g}$, then $f\sim _{k}[{\overline{y}},\lambda _{f};{\underline{y}}]\succsim _{k}[ {\overline{y}},\lambda _{g};{\underline{y}}]\sim _{k}g$. It also holds by Lemma 4.2.(1) that

$$\begin{aligned} M_{k}\subseteq M_{k+1}\text { for all }k<\rho +1. \end{aligned}$$

(41)

To analyze the structure of $M_{k}$, we define $Y_{k}=M_{k}\cap X$ for all $k<\rho +1$. Then, $Y_{k}\subseteq Y_{k+1}$ for all $k<\rho +1$. It follows from E0$^{*}$ that $y\in Y_{k}$ if and only if y and $[{\overline{y}} ,\lambda _{y};{\underline{y}}]$ are indifferent with respect to $\trianglerighteq _{k};$ pure alternative $y\in Y_{k}$ is precisely measured by the benchmark scale $B_{k}({\overline{y}};{\underline{y}})$. Measurability for a pure alternative is a property of the base preference relation $\trianglerighteq _{k}$. In Example 3.1, $Y_{0}=Y_{1}=\{\overline{ y},{\underline{y}}\}$ and $Y_{2}=X=\{{\overline{y}},y,{\underline{y}}\}$ in A and B of Fig. 2, but in C, $Y_{k}=\{{\overline{y}},\underline{y }\}$ even when $\rho =\infty$, i.e., y becomes never measurable.

Let $Y=\cup _{k<\infty }Y_{k}$. Each lottery $f\in L_{\infty }(Y)=\cup _{k<\infty }L_{k}(Y)=\cup _{k<\infty }L_{k}(Y_{k})$ involves two types of depths, i.e., the measurement depth $\delta (\lambda _{y})$ of $y\in Y_{k}$ with $f(y)>0$ and the depth $\delta (f(y))$ of the probability value f(y). The sum of these two types gives a criterion for measurability, which is given in Theorem 6.1. Before it, we need Lemma 6.1. The first implies that any lottery $f\in M_{k}$ has a support in $Y_{k}$, which is the second.

Lemma 6.1

(1):If $f\in M_{k}$, then $f(y)=0$ or 1 for all $y\in Y_{k}-Y_{k-1},\$ where $Y_{-1}=\emptyset$, and $f(y)=0$ for all $y\in X-Y_{k}$.

(2): $M_{k}\subseteq L_{k}(Y_{k})$ for all $k<\rho +1$.

For any $f\in L_{\infty }(X)$, we define $k_{f}$ by

$$\begin{aligned} k_{f}=\left\{ \begin{array}{ll} \max \{\delta (\lambda _{y})+\delta (f(y)):f(y)>0\}&{}\quad \text { if }f\in L_{\infty }(Y)\\ \infty &{}\quad \text { if }f\notin L_{\infty }(Y). \end{array} \right. \end{aligned}$$

(42)

That is, if $f\in L_{\infty }(Y)$, then $k_{f}$ is the maximum of the sum of $\delta (\lambda _{y})$ and $\delta (f(y))$ over the support of f, and if $f\in L_{\infty }(X)-L_{\infty }(Y)$, then $\lambda _{y}$ is undefined and $k_{f}$ is assumed to take the value $\infty$.

Theorem 6.1

(Measurability criterion). Let $k<\rho +1$ and $f\in L_{\infty }(X)$. Then,

$$\begin{aligned} f\in M_{k}\text { if and only if }k_{f}\le k. \end{aligned}$$

(43)

A lottery $f\in L_{\infty }(X)-L_{\infty }(Y)$ is neither measurable because of Lemma 6.1.(2), nor the right-hand side of (43) holds. When $f\in L_{\infty }(Y)$, (43) can be read in two ways. One is to fix a lottery $f\in L_{\infty }(Y)$ but to change (increase) k. Lottery f becomes measurable when k is large enough. For example, when $f=\frac{25 }{10^{2}}y*\frac{75}{10^{2}}{\underline{y}}$ and $y\sim _{2}[{\overline{y}}, \frac{83}{10^{2}};{\underline{y}}]$, we have $k_{f}=\delta (\frac{83}{10^{2}} )+\delta (\frac{25}{10^{2}}) =4;$ by (43), $f\in M_{k}$ if and only if $4\le k$. The other reading is to fix a k and to change f. If $\delta (\lambda _{y})>0$ for some $y\in Y_{k}$, there is an $f\in L_{k}(Y_{k})$ such that $\delta (\lambda _{y})+\delta (f(y))>k;$ so $f\notin M_{k}$ by (43). Thus, non-measurable lotteries exist as long as $\{ {\overline{y}},{\underline{y}}\}\subsetneq Y_{k}$.

Incomparability $\bowtie _{k}$ and indifference $\sim _{k}$ may appear similar: indeed, Shafer (1986), p. 469, discussed whether $\bowtie _{k}$ and $\sim _{k}$ could be defined together and pointed out a difficulty from the constructive point of view. Theorem 6.2 gives a clear distinction between $\sim _{k}$ and $\bowtie _{k}$. By E2, $\sim _{k}$ is transitive, but $\bowtie _{k}$ is not; indeed, we have distinct $f,h\in M_{k}$ with $f\sim _{k}h$, but by Theorem 6.2, for any $g\notin M_{k}$, $f\bowtie _{k}g$ and $g\bowtie _{k}h$. Also, reflexivity holds for the measurable domain $M_{k}$ but not at all for $L_{k}(X)-M_{k}$.

Theorem 6.2

Let $f,g\in L_{k}(X)$.

(1) (No indifferences outside $M_{k}$): If $f\notin M_{k}$, then $f\not \sim _{k}g$.

(2) (Reflexivity): $f\sim _{k}f$ if and only if $f\in M_{k}$.

EU hypothesis for measurable lotteries

Our theory is closely related to the expected utility hypothesis. It is explicitly assumed for the benchmark scale, i.e., B1 and b1. For the other part, it is only partially observed by looking at conditions e1, e2 for $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ as well as Axiom E1 for preference relations $\langle \succsim _{k}\rangle _{k<\rho +1}$. In fact, the EU hypothesis holds for the measurable domain $M_{k}$, which is now shown.

Let $\langle {\varvec{u}}_{k}\rangle _{k<\rho +1}$ be the extended utility stream satisfying e0 to e3, given Theorem 5.2, relative to a base utility stream $\langle \varvec{\upsilon }_{k}\rangle _{k<\rho +1}$. It follows from Theorem 6.2.(2) and (30) that for any $f\in L_{k}(X)$,

$$\begin{aligned} {\overline{u}}_{k}(f)={\underline{u}}_{k}(f)\text { if and only if }f\in M_{k}. \end{aligned}$$

(44)

Following our convention, we drop the upper and lower bars and write $u_{k}(f)$ for $f\in M_{k}$. In fact, $u_{k}(f)$ is expressed as the expected utility value of the base utility function $\upsilon _{k};$ recall $\upsilon _{k}=\overline{\upsilon }_{k}={\underline{\upsilon }}_{k}$ over $Y_{k}$ because $Y_{k}=M_{k}\cap X.$

Theorem 6.3

(EU hypothesis in the measurable domain). For each $k<\rho +1$, $u_{k}(f)=E_{f}(\upsilon _{k})$ for all $f\in M_{k}$.

Thus, the EU hypothesis holds for measurable lotteries, which gives a simple method of calculation of $u_{k}(f)$. On the other hand, by Theorem 6.2.(2) and (30), it holds that

$$\begin{aligned} {\overline{u}}_{k}(f)>{\underline{u}}_{k}(f)\text { if and only if }f\in L_{k}(X)-M_{k}. \end{aligned}$$

(45)

Thus, the EU hypothesis does not hold for non-measurable lotteries.

Proofs

Proof of Lemma 6.1

As mentioned, the latter assertion of (1) implies that any $f\in M_{k}$ has a support in $Y_{k}$, which is (2). We show (1) by induction on $k\ge 0$. Let $k=0$. Since $Y_{0}=M_{0}$, we have $f\in M_{0}=Y_{0}=L_{0}(Y_{0})$, which implies (1) for $k=0$. Suppose the induction hypothesis that (1) hold for k. Now, we take any $f\in M_{k+1}$.

Suppose, on the contrary, that $0<f(y_{o})<1$ for some $y_{o}\in Y_{k+1}-Y_{k}$ or $0<f(y_{o})\le 1$ for some $y_{o}\in X-Y_{k+1}$. If $f(y_{o})=1$ and $y_{o}\in X-Y_{k+1}$, there is no $g\in B_{k+1}( {\overline{y}};{\underline{y}})$ with $f\sim _{k+1}g$, a contradiction to $f\in M_{k+1}$. Hence, $0<f(y_{o})<1$. By $f\in M_{k+1}$, we have a $g\in B_{k+1}( {\overline{y}};{\underline{y}})$ with $f\sim _{k+1}g$. Since $0<f(y_{o})< 1$, it holds that $f\in L_{k+1}(X)-X$. Hence, E3 is applied to $f\sim _{k+1}g$ with the middle $h=g\in B_{k+1}({\overline{y}};{\underline{y}});$ we have decompositions ${\widehat{f}}$, ${\widehat{g}}$ of f, g with ${\widehat{f}} \succsim _{k}{\widehat{g}}$. If one preference was strict, then $f\succ _{k+1}g$ by E1$^{*}$, which is impossible; hence, ${\widehat{f}}\sim _{k} {\widehat{g}}$, which implies $f_{t}\in M_{k}$ for each t. Applying the induction hypothesis to $f_{t}$, we have ${\widehat{f}}\in L_{k}(Y_{k})^{\ell }$, and by E1, $f={\widehat{e}}*{\widehat{f}}\in L_{k+1}(Y_{k})$. This is impossible since $0<f(y_{o})<1$ and $(y_{o}\in Y_{k+1}-Y_{k}$ or $y_{o}\in X-Y_{k+1})$. Hence, $f(y)=0$ or 1 if $y\in Y_{k+1}-Y_{k}$ and $f(y)=0$ if $y\in X-Y_{k+1}$. Now, we have (1) for $k+1$. $\square$

Proof of Theorem 6.1

By (42) and Lemma 6.1.(2), it suffices to prove (43) for any $f\in L_{\infty }(Y)$. We prove (43) by induction on $k\ge 0$. Let $k=0$. Since $Y_{0}=L_{0}(Y_{0})=M_{0}$, it holds that $\delta (\lambda _{f})=\delta (f(y))=0$ for all $f\in L_{0}(Y_{0})=M_{0}$. Thus, (43) holds for $k=0$. Now, suppose the induction hypothesis that (43) holds for k. We prove (43) for $k+1$. In the following, let $f\in L_{k+1}(Y)$ with $\delta (f)>0$.

Suppose $k_{f}\le k+1$. By the latter assertion of Lemma 2.1, there is a decomposition ${\widehat{f}}$ of f so that $\delta (f_{t}(x))<\delta (f(x))$ for all x with $\delta (f(x))>0$. Hence, $k_{f_{t}}=\max \{\delta (\lambda _{x})+\delta (f_{t}(x)): \delta (f_{t}(x))>0\} <\max \{\delta (\lambda _{x})+\delta (f(x)): \delta (f(x))>0\} \le k_{f}$ for all t;  so, $k_{f_{t}}<k_{f}\le k+1$, which implies $k_{f_{t}}\le k$ for all t. By the induction hypothesis, it holds that $f_{t}\in M_{k}$ for all t. Thus, for each t, we have $g_{t}\in B_{k}({\overline{y}},{\underline{y}})$ such that $f_{t}\sim _{k}g_{t}$. By E1, $f={\widehat{e}}*{\widehat{f}}\sim _{k+1}{\widehat{e}}*{\widehat{g}}\in B_{k+1}({\overline{y}};{\underline{y}})$, which implies $f\in M_{k+1}$.

Consider the converse. Let $f\in M_{k+1}$. If $f\in M_{k}$, we have $k_{f}\le k<k+1$ by the induction hypothesis. Consider the case $f\in M_{k+1}-M_{k}$. Then, $f\sim _{k+1}g$ for some $g\in B_{k+1}( {\overline{y}};{\underline{y}})$. By E3, there are decompositions ${\widehat{f}}$, ${\widehat{g}}$ of f, g such that ${\widehat{f}}\sim _{k}{\widehat{g}}$. Thus, ${\widehat{f}}\in (M_{k})^{\ell }\subseteq L_{k}(Y_{k})^{\ell }$ by Lemma 6.1.(2). By the induction hypothesis, we have $\delta (\lambda _{y})+\delta (f_{t}(y))\le k_{f_{t}}\le k$ for all $y\in Y_{k}$ with $f_{t}(y)>0$ and $t\le \ell$. Since $f={\widehat{e}}\mathbf {*}{\widehat{f}} ,$ it holds that $\delta (f(y))\le \max _{t\le \ell }\delta (f_{t}(y))+1$ for all $y\in Y_{k}$ with $f(y)>0$. Thus, for $y\in Y_{k}$ with $f(y)>0$, $\delta (\lambda _{y})+ \delta (f(y)) \le \delta (\lambda _{y})+\max _{t\le \ell }\delta (f_{t}(y))+1\le \max _{t\le \ell }k_{f_{t}}+1\le k+1$. Since $\delta (f(y))=0$ for $y\in Y_{k+1}-Y_{k}$ by Lemma 6.1.(1), we have $k_{f}=\max \{\delta (\lambda _{y})+\delta (f(y)): f(y)>0\}\le k+1$. This means $k_{f}\le k+1$. $\square$

Proof of Theorem 6.2

(1): Let $f\notin M_{k}$. Suppose $f\sim _{k}g$. By E3, $f\succsim _{k}h\succsim _{k}g$ for some $h\in B_{k}({\overline{y}};{\underline{y}})$. By E2 (transitivity), $f\sim _{k}h\sim _{k}g$. This is impossible since $f\notin M_{k}$. Hence, $f\not \sim _{k}g$.

(2): The if part is by (39) and E2. The only-if part (contrapositive) follows from (1). $\square$

Proof of Theorem 6.3

Let $f\in M_{k}$. When $f\in B_{k}({\overline{y}};{\underline{y}})\cup X$, we have, by e0, ${\overline{u}} _{k}(f)={\underline{u}}_{k}(f)=\upsilon _{k}(f);$ if $f=[{\overline{y}},\lambda ; {\underline{y}}]\in B_{k}({\overline{y}};{\underline{y}})$, then, by b1, $\upsilon _{k}(f)= \lambda \upsilon _{k}({\overline{y}})+(1-\lambda )\upsilon _{k}({\underline{y}})=E_{f}(\upsilon _{k});$ and if $f=x\in X$, then $\upsilon _{k}(f)=1\times \upsilon _{k}(x)=E_{f}(\upsilon _{k})$. Now, let $f\notin B_{k}({\overline{y}};{\underline{y}})\cup X$. We show the assertion by induction on $k<\rho +1$. The case $k=0$ is included in the case $f\in B_{k}({\overline{y}};{\underline{y}})\cup X$, $k<\rho +1$. Suppose that the assertion holds for $k-1$. Let $f\in M_{k}$. Then, $\delta (f)>0$, and by Lemma 6.1, $x\in Y_{k-1};$ so, $\upsilon _{k}(x)=\upsilon _{k-1}(x)$. Since $f\in M_{k}$, we have $f\sim _{k}h$ for some $h\in B_{k}({\overline{y}};{\underline{y}})$. By (23), this $f\sim _{k}h$ is derived by E1 from the decompositions ${\widehat{f}}$, ${\widehat{h}}$ of f, h. By E1$^{*}$, it holds that ${\widehat{f}} \sim _{k-1}{\widehat{h}}$. Hence, ${\widehat{f}} \in (M_{k-1})^{\ell }$. By the induction hypothesis, we have ${\overline{u}} _{k-1}(f_{t})= {\underline{u}}_{k-1}(f_{t}) =E_{f_{t}}(\upsilon _{k-1})$ for $t\le \ell$. By e1, ${\widehat{e}}*{\overline{u}}_{k-1}({\widehat{f}} )\ge {\overline{u}}_{k}(f)\ge {\underline{u}}_{k}(f)\ge {\widehat{e}}*{\underline{u}}_{k-1}({\widehat{f}});$ thus, these are all equal. Now, we have $u_{k}(f)={\widehat{e}}*{\underline{u}}_{k-1}({\widehat{f}})= \sum _{t}\frac{1 }{\ell }E_{f_{t}}(\upsilon _{k-1})=E_{f}(\upsilon _{k})$. $\square$

Toward the classical EU theory

We have focused on our theory from the constructive point of view. In particular, Theorem 4.1 reflects this constructiveness, which is extracted by Axiom E3 as well as condition b3. These are constraints on depths and interact with a finite cognitive bound. When we delete this bound, we go toward the classical EU theory. We have still two steps. The first step is to go to the case $\rho =\infty$, where the EU hypothesis holds in the exact form when the set of pure alternatives is restricted to $Y=\cup _{k<\infty }Y_{k}$, where $Y_{k}=M_{k}\cap X$ for $k<\infty$. The second is to allow all real number probabilities for lotteries, i.e., we take lotteries in $L_{[0,1]}(Y)$. There, the classical EU theory is a unique extension of our theory, while it contains highly non-constructive components.

Two steps to the classical EU theory

Throughout this section, we assume $\rho =\infty$. Let $\langle \succsim _{k}\rangle _{k<\infty }$ be a preference stream satisfying E0 to E2, relative to a base preference stream $\langle \trianglerighteq _{k}\rangle _{k<\infty }$ satisfying B0 to B3. Also, let $\langle \varvec{\upsilon } _{k}\rangle _{k<\infty }$ be a base utility stream satisfying (19) of Theorem 3.1, where $\langle \varvec{\upsilon }_{k}\rangle _{k<\infty }$ satisfies conditions b0 to b3. In this section, Axiom E3 and condition e3 are unnecessary.

We assume that for any $x\in X$, there is a k such that for any $k^{\prime }\ge k$,

$$\begin{aligned} {\overline{\upsilon }}_{k}(x)={\overline{\upsilon }}_{k^{\prime }}(x)\text { and }\underline{\upsilon }_{k}(x)={\underline{\upsilon }}_{k^{\prime }}(x). \end{aligned}$$

(46)

That is, the upper and lower evaluations of x become constant after some k.⁹

Now, the limit preference relation of $\langle \succsim _{k}\rangle _{k<\infty }$ is defined to be $\succsim _{\infty } = \cup _{k<\infty }\succsim _{k};$ that is, the decision maker can go to any layer k for his preference comparisons. In parallel, the limit utility function of $\langle \varvec{\upsilon }_{k}\rangle _{k<\infty }$ is defined by, for each $x\in X$,

$$\begin{aligned} {\overline{\upsilon }}_{\infty }(x)=\lim _{k\rightarrow \infty }\overline{ \upsilon }_{k}(x)\text { and }{\underline{\upsilon }}_{\infty }(x)=\lim _{k\rightarrow \infty }{\underline{\upsilon }}_{k}(x). \end{aligned}$$

(47)

By (46), for each $x\in X$, there is a $k_{x}$ such that ${\overline{\upsilon }}_{k}(x)$ and ${\underline{\upsilon }}_{k}(x)$ are constant for $k\ge k_{x}$. Also, we define ${\varvec{u}}_{\infty }(f)=\lim _{k\rightarrow \infty }{\varvec{u}}_{k}(f)=\lim _{k\rightarrow \infty }[{\overline{u}}_{k}(f),{\underline{u}}_{k}(f)]$ for any $f\in L_{\infty }(X)$.

We have the following theorem.

Theorem 7.1

(EU hypothesis without cognitive bounds).

(1): For all $f\in L_{\infty }(X)$, ${\varvec{u}}_{\infty }(f)=E_{f}(\varvec{\upsilon }_{\infty }).$

(2): For all $f,g\in L_{\infty }(X)$, $f\succsim _{\infty }g$ if and only if $E_{f}(\varvec{\upsilon }_{\infty })\ge _{I}E_{g}( \varvec{\upsilon }_{\infty })$.

This theorem corresponds to Lemma 4.1 for $\rho <\infty$. Under (46), the limit preference relation $\succsim _{\infty }$ is represented by the expectation of the vector-valued utility $\varvec{ \upsilon }_{\infty }$. Thus, without the cognitive restriction, the EU hypothesis holds for the limit relation $\succsim _{\infty }$ even without completeness. Here, focusing on the limit utility function $\varvec{ \upsilon }_{\infty }$ with (46), condition e3 becomes unnecessary and so does E3.

Let us restrict the set of pure alternatives X to $Y=\cup _{k<\rho +1}Y_{k}$. For each $x\in Y$, we can write $\overline{\upsilon }_{\infty }(x)={\underline{\upsilon }}_{\infty }(x)=\upsilon _{\infty }(x)$ for $x\in Y$. Theorem 7.1.(2) is written as: for all $f,g\in L_{\infty }(Y)$,

$$\begin{aligned} f\succsim _{\infty }g\text { if and only if }E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty }). \end{aligned}$$

(48)

This is exactly the EU hypothesis in the classical sense.

The final step is to jump to $L_{[0,1]}(Y)$ and to extend the relation $\succsim _{\infty }$ to $L_{[0,1]}(Y)$. The extension is uniquely determined and it is a relation in the classical theory. However, this extension involves non-constructive components; $L_{[0,1]}(Y)$ is uncountable but $L_{\infty }(Y)$ is countable. First, we have the following lemma.

Lemma 7.1

$L_{\infty }(Y)$ is a dense subset of $L_{[0,1]}(Y)$.

Now, we define a binary relation $\succsim _{E}$ over $L_{[0,1]}(Y)$ by: for any $f,g\in L_{[0,1]}(Y)$,

$$\begin{aligned} f\succsim _{E}g\text { if and only if }E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty }). \end{aligned}$$

(49)

We have the following theorem.

Theorem 7.2

(Unique extension). The relation $\succsim _{E}$ defined by (49) is a unique extension of $\succsim _{\infty }$ to $L_{[0,1]}(Y)$ with NM0 to NM2;  that is,

(1): for any $f,g\in L_{\infty }(Y)$, $f\succsim _{\infty }g$ if and only if $f\succsim _{E}g$.

(2): $\succsim _{E}$ satisfies NM0 to NM2.

This theorem is proved by the denseness of $L_{\infty }(Y)$ in $L_{[0,1]}(Y)$ and the continuity of $E_{f}(\upsilon _{\infty })$ with respect to f relative to point-wise convergence, where $E_{f}(\upsilon _{\infty })$ is continuous iff for any sequence $\{f^{\nu }\}$ in $L_{[0,1]}(Y)$ and $f\in L_{[0,1]}(Y)$, if $f^{\nu }(y)\rightarrow f(y)$ for each $y\in Y$, then $\lim _{\nu \rightarrow \infty }E_{f^{\nu }}(\upsilon _{\infty }) =E_{f}(\upsilon _{\infty })$. The proof of the theorem may appear to be constructive, but the last extension step to $\succsim _{E}$ is non-constructive, since probabilities newly involved in $f\in L_{[0,1]}(Y)-L_{\infty }(Y)$ may be given only in a non-constructive manner.¹⁰

Proofs

Proof of Theorem 7.1

(1):We show only ${\overline{u}}_{\infty }(f)=E_{f}(\overline{\upsilon }_{\infty })$ and the other is parallel. Take an $f\in L_{\infty }(X)$, i.e., $f\in L_{k^{\prime }}(X)$ for some $k^{\prime }$. Let S be the support of f, which is a finite set. We choose a $k\ge k^{\prime }$ by (46) such that for all $x\in S$, ${\overline{\upsilon }}_{k^{\prime \prime }}(x)= \overline{\upsilon }_{k}(x)$ for all $k^{\prime \prime }\ge k$. It holds that for $l=0,\ldots$,

$$\begin{aligned} {\overline{u}}_{k+l}(h)=E_{h}({\overline{\upsilon }}_{k+l})\text { for any }h\in L_{l}(S). \end{aligned}$$

(50)

Once this is proved, this implies ${\overline{u}}_{\infty }(f)=E_{f}(\overline{ \upsilon }_{\infty });$ indeed, both sides become constant for large l;  so, we can choose one large $k^{\prime \prime }$ such that ${\overline{u}} _{k^{\prime \prime }}(h)=E_{h}({\overline{\upsilon }}_{k^{\prime \prime }})$ for any $h\in L_{k^{\prime \prime }}(S)$. The above chosen f belongs to $L_{k^{\prime \prime }}(S)$. Hence, ${\overline{u}}_{\infty }(f)=E_{f}( {\overline{\upsilon }}_{\infty })$.

Now, we show (50) by induction on $l=0,\ldots$ Let $l=0$. Then, any $h\in L_{0}(S)$ is expressed as $h=x$ for some $x\in S$. By e0, ${\overline{u}}_{k}(h)={\overline{\upsilon }}_{k}(x)=E_{h}(\overline{ \upsilon }_{k});$ so, (50) holds for $l=0$. Suppose that (50 ) holds for l. Consider it for $l+1$. Take $h\in L_{l+1}(S)$. By e2, there is a decomposition ${\widehat{h}}$ of h such that ${\overline{u}} _{k+l+1}(h)={\widehat{e}}*{\overline{u}}_{k+l}({\widehat{h}})$. Since each $h_{t}$ belongs to $L_{l}(X)$, we have, by the induction hypothesis, ${\overline{u}}_{k+l}(h_{t})=E_{h_{t}}({\overline{\upsilon }}_{l})$. Thus, ${\overline{u}}_{k+l+1}(h)={\widehat{e}}*{\overline{u}}_{k+l}({\widehat{h}})= \sum _{t=1}^{\ell }\frac{1}{\ell }*E_{h_{t}}({\overline{\upsilon }}_{l}) =E_{h}({\overline{\upsilon }}_{l})$. Since ${\overline{\upsilon }}_{l+1}(x)= {\overline{\upsilon }}_{l}(x)$ for all $x\in S$. Thus, we have ${\overline{u}} _{k+l+1}({\widehat{h}})=E_{h}({\overline{\upsilon }}_{l+1})$.

(2): By Theorem 5.2, for each k, we have some ${\varvec{u}}_{k}$ representing $\succsim _{k}$. Let $f,g\in L_{\infty }(X).$ By definitions, $f\succsim _{\infty }g$ if and only if $f\succsim _{k}g$ for large k. Thus, ${\varvec{u}}_{k}(f)\ge _{I}{\varvec{u}} _{k}(g)$, which implies ${\varvec{u}}_{\infty }(f)\ge _{I}{\varvec{u}} _{\infty }(g)$. Tracing this argument back, we have the converse that ${\varvec{u}}_{\infty }(f)\ge _{I}{\varvec{u}}_{\infty }(g)$ implies $f\succsim _{\infty }g$. By (1) of this theorem, $E_{f}(\varvec{\upsilon } _{\infty })={\varvec{u}}_{\infty }(f)\ge _{I}{\varvec{u}}_{\infty }(g)=E_{g}(\varvec{\upsilon }_{\infty })$. Hence, $f\succsim _{\infty }g$ if and only if $E_{f}(\varvec{\upsilon }_{\infty })\ge _{I}E_{g}( \varvec{\upsilon }_{\infty })$. $\square$

Proof of Lemma 7.1

Take any $f\in L_{[0,1]}(Y)$. This f has a support $S=\{y_{0},y_{1},\ldots ,y_{m}\}$ in Y with $f(y_{t})>0$ for $t\le m$. We construct a sequence $\{g^{\nu }\}_{\nu =\nu _{o}}^{\infty }$ so that $g^{\nu }\in L_{\infty }(Y)$ for $\nu \ge \nu _{0}$, and for each $y\in Y$, $g^{\nu }(y)\rightarrow f(y)$ as $\nu \rightarrow \infty$. When $m=0$, let $g^{\nu }=f$ for all $\nu \ge 0$. Now, we assume $m\ge 1$.

For any natural number $\nu$, let $z_{\nu ,t}=\max \{\pi _{t}\in \varPi _{\nu }:\pi _{t}\le f(y_{t})\}$ for all $t\le m$. There is a $\nu _{o}$ such that for all $\nu \ge \nu _{o}$, $\frac{1}{\ell ^{\nu } }\le z_{\nu ,t}\le 1-\frac{1}{\ell ^{\nu }}$ for all $t=0,\ldots ,m-1$ and $\frac{1}{\ell ^{\nu }}\le 1-\sum \nolimits _{t^{\prime }<m}z_{\nu ,t^{\prime }}\le 1-\frac{m}{\ell ^{\nu }}$. Also, we define $u_{\nu ,0},\ldots ,u_{\nu ,m}$ by

$$\begin{aligned} u_{\nu ,t}=\left\{ \begin{array}{c} z_{\nu ,t}\text {if }t<m \\ 1-\sum \nolimits _{t^{\prime }<m}z_{\nu ,t^{\prime }}\text {if }t=m. \end{array} \right. \end{aligned}$$

Then, $\sum \nolimits _{t\le m}u_{\nu ,t}=1$ and $u_{\nu ,t}\in \varPi _{\nu }$ for all $t\le m-1$. Since $\frac{1}{\ell ^{\nu }}\le 1-\sum \nolimits _{t^{\prime }<m}z_{\nu ,t^{\prime }}=u_{\nu ,m}\le 1- \frac{m}{\ell ^{\nu }}$, we have $u_{\nu ,m}\in \varPi _{\nu }$.

We define $\{g^{\nu }\}_{\nu =\nu _{o}}^{\infty }$ by

$$\begin{aligned} g^{\nu }(y)=\left\{ \begin{array}{c} 0\text { if }y\in Y-S \\ u_{\nu ,t}\text {if }y=y_{t}\in S. \end{array} \right. \end{aligned}$$

Each $g^{\nu }$ belongs to $L_{\nu }(Y)$. For $t\le m-1$, since $g^{\nu }(y_{t})=u_{\nu ,t}\le f(y_{t})< u_{\nu ,t}+\frac{1}{\ell ^{\nu }} =g^{\nu }(y_{t})+\frac{1}{\ell ^{\nu }}$ for all $\nu \ge \nu _{o}$, we have $\lim _{\nu \rightarrow \infty }g^{\nu }(y_{t})=f(y_{t})$. Since $g^{\nu }(y_{m})-\frac{m}{\ell ^{\nu }}= 1-\sum \nolimits _{t^{\prime }<m}g^{\nu }(y_{t^{\prime }}) -\frac{m}{\ell ^{\nu }} \le 1-\sum \nolimits _{t^{\prime }<m}f(y_{t^{\prime }}) =f(y_{m})\le 1-\sum \nolimits _{t^{\prime }<m}g^{\nu }(y_{t^{\prime }})=g^{\nu }(y_{m})$ for all $\nu \ge \nu _{o}$. Thus, $\lim _{\nu \rightarrow \infty }g^{\nu }(y_{m})=f(y_{m})$. $\square$

Proof of Theorem 7.2

(1): Let $f,g\in L_{\infty }(Y)$. Then, if k is large enough, then $f,g\in L_{k}(Y_{k})$ and $\upsilon _{k}(x)=\upsilon _{\infty }(x)$ for all $x\in Y_{k}$. Now, suppose $f\succsim _{\infty }g$. Then $f\succsim _{k}g$, equivalently, $E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty })$, which implies $f\succsim _{E}g$. Conversely, if $f\succsim _{E}g$, then $E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty })$, equivalently, $f\succsim _{k}g$ for a large enough k. Thus, $f\succsim _{\infty }g$.

(2): The relation $\succsim _{E}$ is a complete preordering, i.e., it satisfies NM0. Let us see NM1; let $f\succsim _{E}h\succsim _{E}g$. Then, $E_{f}(\upsilon _{\infty })\ge E_{h}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty })$. Choose a $\lambda \in [0,1]$ so that $E_{h}(\upsilon _{\infty })=\lambda E_{f}(\upsilon _{\infty })+ (1-\lambda )E_{g}(\upsilon _{\infty })$. Then, $E_{\lambda f+(1-\lambda )g}(\upsilon _{\infty })=\lambda E_{h}(\upsilon _{\infty })+(1-\lambda )E_{g}(\upsilon _{\infty })=E_{h}(\upsilon _{\infty })$. Finally, we can see NM2-ID1: let $f\succsim _{E}g$, i.e., $E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty })$. Hence, for any $\lambda \in [0,1]$ and $h\in L_{[0,1]}(Y)$, we have $E_{\lambda f+(1-\lambda )h}(\upsilon _{\infty })= \lambda E_{f}(\upsilon _{\infty })+(1-\lambda )E_{h}(\upsilon _{\infty })\ge \lambda E_{g}(\upsilon _{\infty })+(1-\lambda )E_{h}(\upsilon _{\infty })=E_{\lambda g+(1-\lambda )h}(\upsilon _{\infty })$, i.e., $\lambda f+(1-\lambda )h\succsim _{E} \lambda g+(1-\lambda )h$. Similarly, we can verify NM2-ID2.

Finally, we show that $\succsim _{E}$ is uniquely determined. Suppose that $\succsim _{E}^{\prime }$ is an extension of $\succsim _{\infty }$ in the sense of (1) and satisfies NM0 to NM2. Then, for any $f,g\in L_{\infty }(Y)$, $f\succsim _{E}g$ if and only if $f\succsim _{\infty }g$, and by the supposition, $f\succsim _{\infty }^{\prime }g$ if and only if $E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty })$. Hence, for any $f,g\in L_{\infty }(Y)$, $f\succsim _{E}^{\prime }g$ if and only if $E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty })$.

Now, let $f,g\in L_{[0,1]}(Y)$ with $f\succsim _{E}^{\prime }g$. By Lemma 7.1, there are sequences $\{f^{\nu }\}$ and $\{g^{\nu }\}$ in $L_{\infty }(Y)$ such that they point-wise converge to f and g. As stated above, $E_{h}(\upsilon _{\infty })$ is continuous with respect to h. Then, $E_{f}(\upsilon _{\infty })=\lim _{\nu \rightarrow \infty }E_{f^{\nu }}(\upsilon _{\infty }) \ge \lim _{\nu \rightarrow \infty }E_{g^{\nu }}(\upsilon _{\infty })=E_{g}(\upsilon _{\infty })$. We have shown that that for any $f,g\in L_{[0,1]}(Y)$, $E_{f}(\upsilon _{\infty })\ge E_{g}(\upsilon _{\infty })$ if and only if $f\succsim _{E}^{\prime }g$. Thus, $f\succsim _{E}g$ if and only if $f\succsim _{E}^{\prime }g$. $\square$

An application to a Kahneman–Tversky Example

We apply our theory to an experimental result reported in Kahneman and Tversky (1979). The experimental instance is formulated as Examples 3.1 and 5.1 , and the relevant lotteries are $c=[ {\overline{y}},\frac{2}{10};{\underline{y}}]$ and $d=\frac{25}{100}y*\frac{75 }{100}{\underline{y}}$, which are incomparable for people with $\rho =2$. It is the key how the observed behaviors are connected to the incomparabilities predicted in our theory. First, we look at the Kahneman–Tversky example, and then we make a certain postulate to have such a connection.

In the Kahneman–Tversky example, 95 subjects were asked to choose one from lotteries a and b, and one from c and d. In the first problem, $20\%$ chose a, and $80\%$ chose b. In the second, $65\%$ chose c;  the remaining chose d.

$$\begin{aligned} a= & {} \left[ 4000,\tfrac{80}{10^{2}};0\right] \ (20\%)\ \ \text {vs.}\ \ \ b=3000\text { with probability }1\ (80\%) \\ c= & {} \left[ 4000,\tfrac{20}{10^{2}};0\right] \ (65\%)\ \ \text {vs.}\ \ \ d=[3000,\tfrac{25 }{10^{2}};0]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (35\%). \end{aligned}$$

The case of modal choices, denoted by $b\wedge c$, contradicts the classical EU theory. Indeed, these choices are expressed in terms of expected utilities as:

$$\begin{aligned} 0.80u(4000)+0.20u(0)< & {} u(3000) \nonumber \\ 0.20u(4000)+0.80u(0)> & {} 0.25u(3000)+0.75u(0). \end{aligned}$$

(51)

Normalizing $u(\cdot )$ with $u(0)=0$, and multiplying 4 to the second inequality, we have the opposite inequality of the first, a contradiction. The other case violating the classical EU theory is $a\wedge d$. It predicts the outcomes $a\wedge c$ and $b\wedge d$, depending upon the value u(3000). This is a variant of “common ratio effect” discussed in the literature, which is briefly discussed in Remark 8.1.

In Kahneman and Tversky (1979), no more information is mentioned other than the above percentages. Consider three possible distributions of the answers in terms of percentages over the four cases. In Table 3, the first, second, or third entry in each cell is the percentage derived by assuming $65\%$, $52\%$, or $45\%$ for $b\wedge c$. The first $65\%$ is the maximum possibility for $b\wedge c$, which leads to $0\%$ for $a\wedge c$, and these determine the $20\%$ for $a\wedge d$ and $15\%$ for $b\wedge d$. The second entries are based on the assumption that the choices of b and c are stochastically independent, for example, $52=(0.80\times 0.65)\times 100$ for $b\wedge c$. In the third entries, $45\%$ is the minimum possibility for $b\wedge c$. We interpret this table as meaning that each cell was observed at a significant level.

Table 3 Three possible distributions

Let ${\overline{y}}=4000$, ${\underline{y}}=0$, $y=b=3000$, and $\rho \ge 2$. Consider two cases A: $\varvec{\upsilon }_{2}(y)={\varvec{u}} _{2}(y)= [\frac{77}{10^{2}},\frac{77}{10^{2}}]$ and B: $\varvec{\upsilon }_{2}(y)={\varvec{u}}_{2}(y)=[\frac{83}{10^{2}},\frac{ 83}{10^{2}}]$ in Example 3.1, and recall that ${\varvec{u}} _{2}(a)= {\varvec{u}}_{2}([{\overline{y}},\tfrac{80}{10^{2}};{\underline{y}} ]) =[\frac{80}{10^{2}},\frac{80}{10^{2}}]$. Our theory predicts the choice a (or b) in case A (B), independent of $\rho$. We assume that the distribution of subjects over A and B is the same as that given in Table 3, i.e.,

$$\begin{aligned} \text {A }:\text {B }=20\%:80\%. \end{aligned}$$

(52)

We calculate the distribution of choices c and d based upon (52) and the distribution of $\rho$.

Comparisons between c and d depend upon $\rho$. In case $\rho \ge 4$, it follows from the calculation results in Example 5.1 that in case A, $c=[{\overline{y}},\tfrac{2}{10};{\underline{y}}]\succ _{4} [ {\overline{y}},\tfrac{1925}{10^{4}};{\underline{y}}]\sim _{4} [y,\tfrac{25}{ 10^{2}};{\underline{y}}] =d;$ so c is chosen, and in case B, $d=[y,\tfrac{25}{10};{\underline{y}}]\sim _{4}[{\overline{y}},\tfrac{2075}{10^{4}} ;{\underline{y}}]\succ _{4} [{\overline{y}},\tfrac{20}{10^{2}};{\underline{y}} ]=c;$ so d is chosen. In sum, our theory predicts only the diagonal cells $a\wedge c$ and $b\wedge d$ for cases A and B, which are the same as the predictions of the classical EU theory. Thus, if all subjects have their cognitive bounds $\rho \ge 4$, our theory is inconsistent with the experimental result.

Let $\rho =3$. In case A$,$ (34) states ${\varvec{u}} _{3}(c)=[\tfrac{2}{10},\tfrac{2}{10}]\ge _{I}{\varvec{u}}_{3}(d)=[\tfrac{ 199}{10^{3}},\tfrac{189}{10^{3}}],$ and in case B$,$ (35) states ${\varvec{u}}_{3}(d)=[\tfrac{211}{10^{3}},\tfrac{201}{ 10^{3}}]\ge _{I}{\varvec{u}}_{3}(c)=[\tfrac{2}{10},\tfrac{2}{10}]$. Hence, people with $\rho =3$ behave in the same manner as those with $\rho \ge 4$, though d is non-measurable.

In case $\rho =2$. (33) states that people in cases A and B show the same base utility evaluation of d, i.e., ${\varvec{u}} _{2}(d)=[\tfrac{23}{10^{2}},\tfrac{14}{10^{2}}]$. Since ${\varvec{u}} _{2}(c)=[\tfrac{2}{10},\tfrac{2}{10}]$, c and d are incomparable for these people.

Here, we find a conflict between our theory and the reported experimental result in that every subject chose one lottery in each of the above choice problems, while our theory states that c and d are incomparable for people with $\rho =2$. The issue is how a subject behaves for the choice problem when the lotteries are incomparable for him. In such a situation, a person would typically be forced (e.g., following social customs) to make a choice.¹¹ Here, we assume the following postulate for choice behavior for a subject having incomparabilities:

Postulate BH: each subject makes a random choice between c and d, following the probabilities proportional to the distances from $u_{2}(c)$ to ${\underline{u}}_{2}(d)$ and from ${\overline{u}}_{2}(d)$ to $u_{2}(c)$.

Since ${\varvec{u}}_{2}(d)=[\tfrac{23}{10^{2}},\tfrac{14}{10^{2}}]$ and ${\varvec{u}}_{2}(c)=[\tfrac{2}{10},\tfrac{2}{10}]$, the probabilities for the choices c and d are $\tfrac{2}{10}-\tfrac{14}{10^{2}}: \tfrac{23}{ 10^{2}}-\tfrac{2}{10}=2:1$.

Table 4 Ratios of choices c and d

Table 4 summarizes the above calculated results. To see the relationship between Tables 3 and 4, we specify the distribution of people over $\rho =2,3,\ldots$ We consider two distributions of $\rho$

$$\begin{aligned} r_{2}:r_{+3}=9:1\text { and }r_{2}:r_{+3}=8:2, \end{aligned}$$

where $r_{3+}$ is the ratio of subjects with ${ \rho \ge 3.}$ These are adopted based on the idea that $\rho =3$ is already quite precise, and the portion of people with $\rho \ge 3$ is already small.

In the case $r_{2}:r_{+3}=9:1$, the percentage of the choices $a\wedge c$ is calculated as ${ 100\times }\frac{2}{10}{\small \times (}\frac{9}{10} {\small \times }\frac{2}{3} {\small +}\frac{1}{10}{\small \times 1}) =14\%{\small .}$ The corresponding percentages $b\wedge c$ is calculated as ${\small 100\times }\frac{8}{10}{\small \times (}\frac{9}{10}{\small \times } \frac{2}{3} {\small +}\frac{2}{10}{\small \times 0})=48{\small \%.}$ Thus, we obtain Table 5. Table 6 is based on $r_{2}:r_{+3}=8:2$.

Table 5 $r_{2}:r_{+3}=9:1$

Table 6 $r_{2}:r_{+3}=8:2$

The results in Tables 5 and 6 are quite compatible with Table 4. Perhaps, we should admit that this is based upon our specifications of parameter values as well as Postulate BH. To make stronger assertions, we need to think about more cases of parameter values and different forms of BH. Nevertheless, this study may lead to observations on new aspects on bounded rationality that $\rho$ seems quite small.

Remark 8.1

(Common ratio effect). The anomaly mentioned in (51) is often called the “common ratio effect” (cf. Prelec 1998; van de Kuilen and Wakker 2006, and their references). It refers to the observation such as the fact that the opposite of the second inequality in (51) is obtained from the first with multiplication of $1/4=25/10^{2}$. In our theory for case B with $\rho =2$, $b\$is strictly preferred to a, but c and d, which are obtained by the multiplication, are incomparable, and the independence condition, NM2, is violated. We made the additional postulate BH to connect incomparability to the observed behavior in the experiment. The postulate shows a bigger tendency to choose c. In this sense, our result shows the “common ratio effect”. However, Postulate BH does not directly take depths for the choice behavior of agents. Perhaps, there are different postulates taking depths of lotteries to explain the “common ratio effect” more directly. This is an open problem (see also Sect. 9, [c]).

Conclusions

We have developed the EU theory with probability grids and preference formation. The permissible probabilities are restricted to the form of $\ell$-ary fractions up to a given cognitive bound $\rho$. We divide the argument into the measurement step of preferences and utilities on pure alternatives in terms of the benchmark scale and the extension step to lotteries with more risks. We take the constructive view point of the decision maker for our theory. The development includes the approach in terms of vector-valued utilities with the interval order due to Fishburn (1970). The connections between the preference approach and the utility approach are shown to be equivalent in Sects. 3 to 5. These approaches are complementary; each may give better interpretations as well as some technical merits over the other.

To study the resultant preference relation $\succsim _{\rho }$ over $L_{\rho }(X)$, we divide $L_{\rho }(X)$ into the set $M_{\rho }$ of measurable lotteries and its complement $L_{\rho }(X)-M_{\rho }$. The resultant $\succsim _{\rho }$ is complete over $M_{\rho }$, while it involves incomparabilities in $L_{\rho }(X)-M_{\rho }$. In Sect. 6, we studied the relationship between non-measurability and incomparability. When there is no cognitive bound, our theory gives a complete preference relation over $L_{\infty }(Y)$, enjoying the expected utility hypothesis. However, our main concern is still the bounded case $\rho <\infty$.

In Sect. 8, we applied the incomparability results to the Allais paradox, specifically to an experimental example in Kahneman and Tversky (1979). Our theory is compatible with their experimental result; incomparabilities involved for $\rho =2$ are crucial in interpreting their result.

We considered a few aspects of bounded rationality in terms of probability grids and cognitive bounds for EU theory; bounded rationality is more salient with shallow $\rho$. When, however, we consider a specific decision problem, other aspects of bounded rationality may manifest themselves. We should have more researches on the aspects of bounded rationality in various directions. Here, we give a few possible research agenda.

The first three are related to bounded rationality.

[a] Constructive method of particular preferences: We presented our theory following Table 1 to derive all the preferences in a layer from the previous layer. However, the decision maker may think about his preferences more locally focusing only on the target lotteries and involved pure alternatives and relevant probabilities. This question could enable us to think about complexities of preference formation. It may give a better understanding of how much bounded rationalities are involved when only target lotteries are concerned.

[b] Preference formation in inductive game theory (IGT): This theory studies experimental sources for individual knowledge/belief about the structure of the society (cf. Kaneko and Matsui 1999). Our approach has some parallelism to the constructive approach to IGT, due to Kline et al. (2019). In particular, Kaneko and Kline (2015) study the other person’s preferences from experiences of the other’s position through role-switching. However, since it is assumed that experiences include numerical utility values, their treatment does not capture the partial understanding/non-understanding of the other’s preferences/desires. Perhaps, lack of full experiences is closely related to incomparability in our theory.

This is also related to the case-based decision theory by Gilboa (2001) as well as to the frequentist interpretation of probability in the context of the classical EU theory (cf., Hu 2013). The former concerns evaluations of probabilities for causality (course-effect) from experiences, and the latter is about probability as frequency of an event. Bounded memory capacity of a person is relevant for both. Our theory with probability grids and cognitive bounds may give a suggestion to analyze such problems.

[c]: Behavior under incomparability: When two lotteries are incomparable, our theory is silent about a choice by the decision maker. In Section 8, we adopted postulate BH for choices by subjects for incomparable lotteries c and d. These lotteries have different depths, i.e., $\delta (c)=1$ and $\delta (d)=2$. BH did not directly take depths into account. A different postulate should take depths into account. Then, we may discuss “common ratio effect” (Remark 8.1) in a more direct manner and possibly Ellesberg’s paradox, too. This remains an open problem.

The other three comments are on possible generalizations of our theory.

[d]: Extensions of choices of benchmarks: In this paper, the benchmarks ${\overline{y}}$ and ${\underline{y}}$ are fixed. The choice of the lower ${\underline{y}}$ could be natural, for example, the status quo. The choice of ${\overline{y}}$ may be more temporary in nature. In general, there could be different benchmarks than the given ones. We could consider two possible extensions of choices of the benchmarks.

One is a vertical extension: we take another pair of benchmarks $\overline{{\overline{y}}}$ and $\underline{{\underline{y}}}$ such as $\overline{{\overline{y}}}\trianglerighteq _{0}{\overline{y}} \trianglerighteq _{0} {\underline{y}}\trianglerighteq _{0}\underline{ {\underline{y}}}$. The relation between the original system and the new system is not simple. In the case of measurement of temperatures, the grids for the Celsius system do not exactly correspond to those in the Fahrenheit system. We need multiple bases $\ell$ for probability grids and may have multiple preference systems even for similar target problems.

The other extension is horizontal: For example, ${\underline{y}}$ is the present status quo for a student facing a choice problem between the alternative ${\overline{y}}$ of going to work for a large company and the alternative $\overline{{\overline{y}}}$ of going to graduate school. He may not be able to make a comparison between ${\overline{y}}$ and $\overline{{\overline{y}}}$, while he can make a comparison between detailed choices after the choice of ${\overline{y}}$ or $\overline{{\overline{y}}}$. This involves incomparabilities different from those considered in this paper. These possible extensions are open problems of importance.

[e]: Extensions of the probability grids $\varPi _{\rho }$: The above extensions may require more subtle treatments of probability grids. A possibility is to extend $\varPi _{\rho }$ to $\cup _{\ell =2}^{{\overline{\ell }} }\varPi _{\ell };$ that is, probability grids having the denominators $\ell \le {\overline{\ell }}$ are permissible. Then, the Celsius and Fahrenheit systems of measuring temperatures are converted from each to the other. A question is how large ${\overline{\ell }}$ is required for such classes of problems.

[f]: Subjective probability: Our theory is almost directly applied to Anscombe and Aumann’s (1963) theory of subjective probability and subjective utility. An event E such as tomorrow’s weather is evaluated asking an essentially the same question as (1) in Sect. 1. We could have an extension of our theory including the subjective probability theory. It could be difficult to have an extension corresponding to Savage (1954), since no benchmark scale is assumed; perhaps, Savage’s theory is not in our scope.

Appendix

We prepare the extension $\delta ^{*}$ of the depth measure $\delta$ to $\varPi _{k}^{*}=\{\pi :\pi =\nu /\ell ^{k}$ and $\nu$ is a nonnegative integer$\}$, where $\nu$ may be larger than $\ell ^{k}$. This $\varPi _{k}^{*}$ is closed with respect to $+$. For $\pi \in \varPi _{k}^{*}$, we define $\delta ^{*}(\pi )=k$ iff $k\in \varPi _{k}^{*}-\varPi _{k-1}^{*}$. Then, $\delta ^{*}(\pi )=\delta (\pi )$ if $\pi \in \varPi _{k}$. The following facts will be used in the proof of Lemma 2.1:

$$\begin{aligned}&\text {if }\pi =s+\nu ^{\prime }/\ell ^{k}\text { for an integer }s\text { and } \nu ^{\prime }<\ell ^{k},\text { then }\delta ^{*}(\pi )=\delta ^{*}(\nu ^{\prime }/\ell ^{k}); \end{aligned}$$

(53)

$$\begin{aligned}&\text {if }\delta ^{*}(\pi ),\delta ^{*}(\pi ^{\prime })\le k,\text { then }\delta ^{*}(\pi +\pi ^{\prime })\le k. \end{aligned}$$

(54)

Proof of Lemma 2.1

¹² Let $k\ge 1$. We show that if $f\in L_{k}(X)$, then $f={\widehat{e}}\mathbf { *}{\widehat{f}}$ for some ${\widehat{f}}\in L_{k-1}(X)^{\ell }$ with the depth constraint $\delta (f(x))>\delta (f_{t}(x))$ for all $t\le \ell$ and $x\in X$ with $\delta (f(x))>0$. We assume $\delta (f)=k$. Let $\{x_{1},\ldots ,x_{m}\}$ be the support of f with $f(x_{t})>0$ for $t=1,\ldots ,m$. Since $\delta (f)=k\ge 1$, we have $m\ge 2$.

Notice that f is regarded as the list $(x_{1},\nu _{1}/\ell ^{k},\ldots ,x_{m},\nu _{m}/\ell ^{k})$ with $0\le \nu _{t}<\ell ^{k}$ for all $t\le m$ and $\sum \nolimits _{t=1}^{m}\nu _{t}=\ell ^{k}$. This is expressed as:

$$\begin{aligned} f=(\overset{\nu _{1}\text { times}}{\overbrace{x_{1},1/\ell ^{k},\ldots ,x_{1},1/\ell ^{k}}},\text { }\ldots ,\text { }\overset{\nu _{m}\text { times}}{\overbrace{x_{m},1/\ell ^{k},\ldots ,x_{m},1/\ell ^{k}}}), \end{aligned}$$

(55)

i.e., each $x_{t}$ occurs $\nu _{t}$ times with the same weight $1/\ell ^{k}.$ Since $\ell ^{k}=\ell \times \ell ^{k-1}$, the list $[x_{1},\ldots ,x_{1},\ldots$, $x_{m},\ldots ,x_{m}]$ of the length $\ell ^{k}$ can be rewritten as the concatenation of $\ell$ sublists of length $\ell ^{k-1}:$

$$\begin{aligned}{}[[y_{1}^{1},\ldots ,y_{\ell ^{k-1}}^{1}],\ldots ,[y_{1}^{\ell },\ldots ,y_{\ell ^{k-1}}^{\ell }]]. \end{aligned}$$

(56)

Associating weight $1/\ell ^{k-1}$ to each component, we regard these as lotteries $f_{1},\ldots ,f_{\ell }$ in $L_{k-1}(X):$

$$\begin{aligned} f_{1}= & {} [y_{1}^{1},1/\ell ^{k-1},\ldots ,y_{\ell ^{k-1}}^{1},1/\ell ^{k-1}],\nonumber \\&\vdots&\nonumber \\ f_{\ell }= & {} [y_{1}^{\ell },1/\ell ^{k-1},\ldots ,y_{\ell ^{k-1}}^{\ell },1/\ell ^{k-1}]. \end{aligned}$$

(57)

Then, it holds that ${\widehat{e}}*(f_{1},\ldots ,f_{\ell })=f;$ thus, $f\in L_{k}(X)$ is decomposed into $(f_{1},\ldots ,f_{\ell })\in L_{k-1}(X)^{\ell }$.

To show the depth constraint (11), we need a few concepts; first, we denote the list $[x_{1},\ldots ,x_{1}$, $x_{2},\ldots ,x_{2}, \ldots$, $x_{m},\ldots ,x_{m}]$ as $z=[z_{\xi }:1\le \xi \le \ell ^{k}]$ and ${\overline{\nu }}_{t}=\sum \nolimits _{s\le t}\nu _{s}$ for $t=1,\ldots ,m$. Then, $f(x_{t})$ is regarded as a segment of z, given as

$$\begin{aligned}{}[z_{\xi }:{\overline{\nu }}_{t-1}<\xi \le {\overline{\nu }}_{t}]\text { with weight }1/\ell ^{k}. \end{aligned}$$

(58)

This corresponds to the fragment with $x_{t}$ in (55). Thus, z is partitioned in two ways: $[[y_{1}^{1},\ldots ,y_{\ell ^{k-1}}^{1}] ,\ldots ,[y_{1}^{\ell },\ldots ,y_{\ell ^{k-1}}^{\ell }]]$ of (56) and $[[z_{\xi }:{\overline{\nu }}_{t-1}<\xi \le {\overline{\nu }}_{t}]:t=1,\ldots ,m]$ of (58); we call $[y_{1}^{t^{\prime }},\ldots ,y_{\ell ^{k-1}}^{t^{\prime }}]$ and $[z_{\xi }:{\overline{\nu }}_{t-1}<\xi \le {\overline{\nu }}_{t}]$fragments. The fragments of these partitions may have three types of non-empty intersections:

• (a): $[y_{1}^{t^{\prime }},\ldots ,y_{\ell ^{k-1}}^{t^{\prime }}]$ is a subfragment of $[z_{\xi }:{\overline{\nu }} _{t-1}<\xi \le {\overline{\nu }}_{t}]$;

• (b): $[y_{1}^{t^{\prime }},\ldots ,y_{\ell ^{k-1}}^{t^{\prime }}]$ is a superfragment of $[z_{\xi }:{\overline{\nu }} _{t-1}<\xi \le {\overline{\nu }}_{t}]$;

• (c): one of them starts inside the other but does not stop in it.

In (a), $f_{t^{\prime }}(x_{t})=1$, since $y_{1}^{t^{\prime }}=\cdots =y_{\ell ^{k-1}}^{t^{\prime }}=x_{t}$. Hence, $\delta (f_{t^{\prime }}(x_{t}))=0<\delta (f(x_{t}))$. In (b), since the length of $[z_{\xi }: {\overline{\nu }}_{t-1}<\xi \le {\overline{\nu }}_{t}]$ is $\nu _{t}$, we have $f_{t^{\prime }}(x_{t})=\nu _{t}/\ell ^{k-1}$ and $f(x_{t})=\nu _{t}/\ell ^{k}$. Since $\delta (\nu _{t}/\ell ^{k-1})<\delta (\nu _{t}/\ell ^{k})$, we have $\delta (f_{t^{\prime }}(x_{t}))<\delta (f(x_{t}))$.

Consider (c), which is neither (a) nor (b). Suppose that $[z_{\xi }:{\overline{\nu }}_{t-1}<\xi \le {\overline{\nu }}_{t}]$ ends inside $[y_{1}^{t^{\prime }},\ldots ,y_{\ell ^{k-1}}^{t^{\prime }}]$ but it starts in a previous fragment. Then, $f_{t^{\prime }}(x_{t})=\nu _{t}^{\prime }/\ell ^{k-1}$ for some $\nu _{t}^{\prime }$ with $0<\nu _{t}^{\prime }<\ell ^{k-1}$. In fact, $\sum \nolimits _{s\le t}\nu _{s}=(t^{\prime }-1)\ell ^{k-1}+\nu _{t}^{\prime }$. By (53) and (54),

$$\begin{aligned} \delta ^{*}(\nu _{t}/\ell ^{k-1})\ge \delta ^{*}(\sum \nolimits _{s\le t}\nu _{s}/\ell ^{k-1})=\delta ^{*}((t^{\prime }-1)+\nu _{t}^{\prime }/\ell ^{k-1})=\delta ^{*}(\nu _{t}^{\prime }/\ell ^{k-1}). \end{aligned}$$

Hence, $\delta (f_{t^{\prime }}(x_{t}))=\delta (\nu _{t}^{\prime }/\ell ^{k-1})\le \delta (\nu _{t}/\ell ^{k-1})<\delta (\nu _{t}/\ell ^{k})=\delta (f(x_{t}))$. The other case of (c) where $[z_{\xi }:{\overline{\nu }} _{t-1}<\xi \le {\overline{\nu }}_{t}]$ starts in $[y_{1}^{t^{\prime }},\ldots ,y_{\ell ^{k-1}}^{t^{\prime }}]$ but ends in a later fragment is similar. $\square$