Abstract
Some stylized facts about transactions among banks are not easily reconciled with coinsurance of short-term liquidity risks. In our model, interbank markets play a different role. We argue that lending to another bank can reduce a bank’s overall portfolio risk through diversification. If insolvency is costly, this diversification improves the interbank lender’s funding liquidity, boosting credit supply to nonbanks. However, diversification comes at an endogenous cost that depends on bank-specific factors of interbank borrower and lender. The model provides a framework for understanding the importance of interbank lending for aggregate credit supply and the stability of banking systems. The model’s predictions are consistent with evidence documented in the literature that other theories cannot consistently explain.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Interbank markets are traditionally considered to be dominated by overnight deposits and repos. These are short-term instruments traded on rather risk-intolerant markets. Motivated by this, the academic literature has explored the role of such contracts as instruments for banks to coinsure short-term liquidity risks (e.g., Allen and Gale 2000; Castiglionesi et al. 2014).
While the importance of such coinsurance as a driver for interbank transactions is widely accepted, this notion cannot be easily reconciled with three other stylized facts about interbank markets, especially in Europe. First, the size of banks’ interbank assets and liabilities is substantially larger than their average deposit and credit fluctuations (Bluhm et al. 2016). Second, although the flows among banks are predominantly short-term transactions, a substantial part of the stock of interbank claims is long term (European Central Bank 2015). Third, the average net position of many participants in the interbank market is substantially different from zero and persistent (Roengpitya et al. 2017). These observations suggest that there is a need for a theory of interbank markets which complements the established theory of interbank deposits or repos.Footnote 1 Such theory should also take into account that interbank transactions are to a large extent conducted bilaterally over the counter (Craig and von Peter 2014) and that interbank lenders tend to be better capitalized and have better credit ratings than interbank borrowers (Angelini et al. 2011).
We shall argue in this paper that there are economic environments where profit-maximizing banks have an incentive to engage in interbank transactions that capture these features. In these environments, a bank can lend funds to another bank that may default at a later date. As long as the correlation of the two banks’ earnings is not equal to one, assuming such counterparty risk can help the interbank lender to better diversify its overall exposure to insolvency risk. If insolvency creates losses, a reduction in risk will reduce the cost of external, nonbank funding sources, hence easing the external funding constraint of the interbank lender and allowing for an expansion of credit supply. Such diversification may be costly, though. To fully reap the potential diversification benefits, an interbank lender may have to lend more funds than the borrower wants to raise. In this case, the lender will have to offer a discounted interbank lending rate, i.e., the borrower’s expected repayment will fall short of the lender’s cost of raising the additional funds used to make the interbank loan. As a result, interbank loans come at an expected loss to the lender, making diversification costly. The benefits of diversification (in terms of improved access to external finance from nonbank investors) and its cost (in terms of expected losses from granting loans to another bank) are determined jointly in equilibrium as an interbank lender decides how much to lend to another bank.
With a focus on the capacity of the banking sector to borrow from nonbank investors, the present paper contributes to three related branches in the literature. The first concerns the role of interbank markets for banks’ credit supply to nonbank borrowers. In models where interbank markets facilitate the coinsurance of short-term liquidity risks, a fixed amount of liquid assets held in the banking sector is reallocated on interbank markets.Footnote 2 Accordingly, dysfunctional interbank markets result in liquidity hoarding and idle lending capacities, as loanable funds no longer flow to the most profitable lending opportunities, both within and across banks (Freixas and Holthausen 2005; Gertler and Kiyotaki 2010; Acharya and Skeie 2011; Diamond and Rajan 2011).Footnote 3 In our paper, the scope for banks to diversify risks shrinks if interbank markets become dysfunctional. As a consequence, an interbank lender’s financial constraint tightens which impairs its ability to grant loans to nonbanks. The interbank borrower may also curtail lending as it has to resort to nonbank investors who may provide funds either at higher costs or not at all.
A second strand of the literature studies the terms of interbank transactions, in particular how they depend on risk (Furfine 2001; King 2008) and other borrower-specific characteristics (Craig and von Peter 2014; Vollmer and Wiese 2014). Our model suggests that the characteristics of the interbank lender are also key for the terms of interbank transactions, in a way consistent with recent evidence (Angelini et al. 2011; Affinito 2012). For example, an interbank lender with fewer internal funds faces a tighter funding constraint. Hence, the lender has to gain more from diversification and would want to grant a larger loan. However, for the interbank borrower to accept the larger loan, the interest rate has to be smaller.
Finally, our paper is also related to a body of research on interbank linkages and financial stability, with a particular focus on probabilities of joint bank failures. The literature has identified contagion as one possible reason for joint failures. Since Allen and Gale (2000), it has been argued that incomplete interbank networks are more susceptible to contagion than complete networks because the former do not allow for as much coinsurance of risks (see also Afonso and Lagos 2015; Craig and von Peter 2014; Craig et al. 2015).Footnote 4 An alternative explanation of joint bank failures refers to systemic risk-shifting incentives according to which banks may gain from holding similar portfolios (Acharya and Yorulmazer 2008; Acharya 2009). We show that although diversification is generally beneficial for a financially constrained interbank lender, it may be better for the bank to make itself vulnerable to the failure of a counterparty holding not identical but similar assets. Diversification benefits will be smaller, but so will be the costs of diversification. This shows that banks do not necessarily seek a perfectly diversified exposure on interbank markets and that incentives for banks to hold somewhat similar assets exist beyond systemic risk-shifting.
The remainder of the paper has the following structure. In Sect. 2, we provide an overview of the environment in which banks benefit from diversification via interbank exposures. Having thus motivated our assumptions, we present in detail the formal model setup in Sect. 3. In Sect. 4, we characterize the equilibrium and its implication for credit supply. In Sect. 5, we extend the model to study the role of diversification and associated stability issues. In Sect. 6, we discuss some empirical implications of the model. Section 7 concludes.
2 Overview of the environment
The environment we consider in this paper has three features. These features are well established in the literature. Importantly, they are not rival to those environments in which banks seek to coinsure short-term liquidity risks.
Banks are financially constrained Banks’ equity capital is limited because building up internal funds is a costly process that takes time (Bucher et al. 2013) and raising funds on equity markets is subject to frictions, such as market segmentation (Allen et al. 2015). The resulting constraints on bank loan supply can be further aggravated by capital regulation (Behn et al. 2016). Tapping on alternative sources of funding is also hampered. For example, the pool of insured retail deposits, although usually a stable funding source (Martin et al. 2018), is rather fixed in size for a bank (Billett et al. 1998), and asymmetric information generally limits the willingness of investors to provide external funding (Stiglitz and Weiss 1981).
In our model, a bank has only a limited amount of funds at its immediate disposal, for example as a result of the above-mentioned frictions in equity and deposit markets. Furthermore, a bank’s ability to borrow more funds is impaired by asymmetric information about its solvency. We consider a reduced form of a model in which investors can enforce the promised payment from the bank only if they incur the costs of verifying the bank’s earnings. Under these circumstances, the literature has identified contracts as optimal if they specify a fixed repayment obligation and creditors get to verify the state of the bank if it defaults (Gale and Hellwig 1985; Krasa and Villamil 2000).Footnote 5 While this contract lessens the incentive for a bank to misreport the true state, it implies that investors incur verification costs when the bank is truly unable to repay, which reduces their willingness to lend to the bank in the first place. In such circumstances, any possible way to lower the probability of default, and thus of wasting resources when a bank fails, potentially helps banks to mitigate their financial constraints.
Diversifying and hedging risk is costly One way to reduce the probability of default is through diversification (Diamond 1984). However, banks are typically not fully diversified. One piece of evidence for diversification being imperfect is the substantial home bias in banks’ international asset allocations (García-Herrero and Vázquez 2013). For the Euro area, there is strong evidence that banks wishing to diversify their loan portfolio internationally are still hesitant to engage in direct cross-border lending in the retail market. Instead, they prefer cross-border interbank lending in the wholesale market. Despite a gradual increase in the share of direct cross-border loans to total loans for nonfinancial corporations and households to approximately 10% in 2018, the ratio of direct cross-border retail lending to wholesale interbank lending is still considerably below 30% (European Central Bank 2018, Charts 17 and 19). Such patterns can be the result of credit market segmentation due to asymmetric information problems. Typically, local banks have informational advantages over foreign banks, which would face adverse selection problems that leave them with a pool of the least creditworthy or even unworthy borrowers. In those environments, entry by foreign banks in regional loan markets can reduce the screening incentives for banks through increased competition (Gehrig 1998) or imply a lower resilience of foreign banks to liquidity shocks (Dietrich and Vollmer 2010).
Other means of reducing risks are also costly. For example, contingent contracts such as credit derivatives cause additional incentive problems (Hakenes and Schnabel 2010; Ahn and Breton 2014). Suppose the debt a bank issues and its loans suffer both from costly verification problems, i.e., a bank can enforce loan repayments only if it verifies the borrower’s income. In this scenario, buying a credit derivative will destroy the bank’s incentive to incur any verification costs as it will be compensated anyway when a borrower defaults. Having not been in any contractual relationship at all with the borrower, the seller of the credit derivative has a natural disadvantage in verifying the borrower’s true state. The borrower, in turn, will then not report the true earnings. Such problems do not arise if the bank seeks to reduce risks through diversification as a bank’s interest in enforcing loan repayments is maintained.
Taken together, a bank has different options to reduce risks and thus ease its financial constraint. As each instrument comes at a cost, optimal risk management will balance marginal costs and benefits across those instruments. Interbank lending belongs to the set of such instruments. It allows banks to reinsure their idiosyncratic credit risk, but has its own cost. In our model, these costs are endogenous. They exist even in the absence of regulation, such as capital requirements for term loans to other banks, provided the number of counterparties for interbank transactions is limited. The literature has identified lending relationships (Affinito 2012; Bräuning and Fecht 2017) and search costs (Afonso and Lagos 2015) as reasons for such limitations.
Information-sensitive investors exist For a bank to expect that by lowering its risk exposure it can improve the willingness of investors to provide funds, there have to be investors who are sensitive to information about the bank. Hence, investors should exist who are reasonably well informed about a bank and who care about whether the bank can fail. These characteristics usually do not apply to retail depositors, who may not care enough about the risk of a bank failure as they are covered by some sort of investor protection or deposit insurance scheme.
Real-world wholesale investors, such as insurance companies, pension funds or hedge funds, however, fit well in this description (Calomiris and Kahn 1991; Huang and Ratnovski 2011). They are professional investors who are in the business of monitoring prices of bank shares and credit derivatives. Like banks, they are able to infer banks’ individual probabilities of default from market data, and they do research into the different business models and risk exposures of banks. For our diversification argument, investors would only need to be able to assess a bank’s probability of default in equilibrium. In order to capture this ability of investors while keeping the analysis simple and tractable, however, investors in our model observe interbank transactions and their terms and know also the correlation of loan returns.Footnote 6
3 Setup
In this section, we present the baseline model. We consider a one-period economy, populated by two banks n ∈ {1,2} and a continuum of investors. Bank n enters the period with some liquid endowment Ωn ≥ 0 called internal funds. Investors as a group have plenty of funds, although an individual investor’s endowment may be infinitesimal. Everyone is risk neutral, lives the whole period, has no time preference and is protected by limited liability.
At the beginning of the period, each investor can use her funds to hold a portfolio of safe assets and claims on banks. Banks can also invest in safe assets, grant risky business loans and lend funds to each other. The potential interbank lender is called bank 1, and the potential interbank borrower is called bank 2.
Investors’ claims on bank n are characterized by the amount dn ≥ 0 the investors provide to the bank at the beginning of the period and a face value δn the bank has to repay at the end (all face values are per unit). Similarly, an interbank loan contract will stipulate the amount b ≥ 0 to be lent by bank 1 to bank 2 and a face value β that bank 2 promises to repay. Claims on banks held by investors rank pari passu with interbank loans.
Let an ≥ 0 be the amount bank n invests in safe assets and ln ≥ 0 be the amount invested in risky business loans. Then, the budget constraints at the beginning of the period read
While access to safe assets is free, granting business loans is associated with nonpecuniary, nonverifiable costs c(ln) arising from, e.g., processing applications, screening borrowers and negotiating loan contracts. These costs are increasing and convex; to simplify the exposition, we also assume c(0)=c′(0)=0. One interpretation is that business loans differ in their complexity and banks add the least complex loans first to their portfolios.
To pay out its creditors, a bank can use its portfolio returns generated at the end of the period. Returns on business loans are state-dependent and not freely observable. The success of a bank’s loans can be described as a random variable that takes the value H if loan earnings are high (success) and the value L if they are low (failure). Denote a high return of bank n’s business loans by λn, H, a low return by λn, L (all returns are per unit), and let pn be the probability of a low return. While business loans do not dominate the safe assets, which yield a risk-free return α > 0, the expectation of high loan earnings alone already exceeds the risk-free return, i.e.,
For now, we assume that business loans granted by bank 1 are a success if and only if business loans granted by bank 2 are a failure, i.e., there are two states of the world. Let s = LH be the state in which loan earnings for bank 1 are low, s = HL be the state in which loan earnings for bank 2 are low, and denote the set of all states by 𝕊 = {LH,HL}.Footnote 7 The probability of state s is ps, and the return on bank n’s business loans in state s is λn, s implying
As realized loan earnings are not freely observed by investors, a bank could pretend that it is unable to repay what it owes. However, if the bank does not repay, it goes into bankruptcy which triggers a costly state verification process. All creditors of such a failing bank, i.e., investors and potentially an interbank lender, then equally share the value of the bank’s assets net of any costs arising from bankruptcy. Therefore, a simple debt contract minimizes expected bankruptcy costs. To simplify matters, we assume that the net returns the creditors of a failing bank can expect after bankruptcy are infinitesimal, regardless of the state. Hence, while ensuring that a bank repays its debts whenever it can, nobody gets anything meaningful if loan earnings are too low to cover the bank’s payment obligations in full.
We formalize these assumptions by defining an indicator variable In, s, which is 1 when bank n suffers from bankruptcy in state s and 0 otherwise. A bank will be forced into bankruptcy whenever its end-of-period book value πn, s in state s is negative, i.e.,
For the sake of simplifying the exposition, we introduce the following definition:
Definition 1
Bank n operates in a safe mode\(m_n = {{\mathscr {S}}}\) if πn, s ≥ 0 for all s ∈ 𝕊 and in a risky mode\(m_n = {{\mathscr {R}}}\) if πn, s < 0 for all s ∈ 𝕊 with λn, s = λn, L and πn, s ≥ 0 for all s ∈ 𝕊 with λn, s = λn, H.
Accordingly, a bank chooses to either go bankrupt in those states in which loan earnings are small or to survive regardless which state materializes.Footnote 8
Contracting at the beginning of the period takes place as follows. Banks negotiate an interbank loan contract (b,β) in a simple noncooperative game. In this game, bank 1 makes a take-it-or-leave-it offer (b⋆,β⋆) to bank 2. If accepted, the offer will be implemented, i.e., (b,β) = (b⋆,β⋆). If bank 2 declines the offer, no interbank transaction takes place, i.e., (b,β) = (0,0).Footnote 9
Each bank n will also decide on the details of the contract (dn,δn) offered to investors taking their participation constraint into account. The latter requires the face value δn of claims on bank n to satisfy
that is, the expected repayments to investors at least cover the value of their next best alternative. As investors have plenty of funds and no better option than to invest in safe assets, their supply of funds to the banks is perfectly elastic. They are willing to provide any volume of funds provided the face value δn satisfies
The objective of a bank is to maximize expected profits subject to its constraints. These constraints are somewhat different for the interbank borrower and the interbank lender. For any given interbank loan contract (b,β), the optimization problem of the interbank borrower reads
Let P2(b, β) denote the associated indirect expected profits for the interbank borrower as a function of the terms of the interbank loan. Then, the optimization problem of the interbank lender is
We consider equilibria in pure strategies and without sunspots. Due to the information asymmetry, the equilibrium allocation can differ from the first-best, which is characterized by a loan volume lnfb satisfying (E[λn, s]−α) − c′(lnfb)=0.
4 Analysis
In the present section, we analyze the optimization problem of a bank and its implications. In Sect. 4.1, we start with a bank that does not form financial links to the other bank. This defines the outside options in the negotiations of the terms of the interbank loan which we analyze in Sect. 4.2. We then discuss the costs associated with interbank lending in Sect. 4.3 and draw conclusions regarding structure and volume of the supply of business loans in Sect. 4.4. We discuss the nonnegativity constraints on the interbank borrower’s internal funds and on the expected NPV of its business loans in Sect. 4.5. We conclude this section with a remark on the choice between holding a diversified portfolio of business loans and diversifying through interbank lending.
4.1 Without interbank loans
If the two banks are not linked via interbank loans (b = 0), each bank chooses between the safe and the risky mode. The advantage of the safe mode is that a bank can always collect all earnings. The disadvantage of the safe mode is that a bank has to ensure that it can pay investors the full face value of their claims even in the ‘bad’ state when earnings are low. Therefore, the total amount a bank owes has to satisfy
implying an upper limit on the funds a bank can obtain from investors. Together with the budget constraint (3.1) and the face value of investor claims on the bank (3.7), it implies that granting business loans is subject to a financial constraint, which reads
Given assumption (3.2), a bank cannot fully refinance business loans externally because it cannot repay investors a sufficiently large amount. There is a gap, which depends on the amount the bank plans to lend out. If the present value of this gap cannot be covered by internal funds, granting this amount of loans is not feasible. In short, since internal funds are limited, the volume of business loans is limited too in the safe mode.
In the risky mode, investors are repaid only in the state when returns are high. Hence,

Combining (4.3) with (3.1) and (3.7) gives
Restriction (4.4) states that the bank must grant a sufficiently large volume of risky business loans to be actually exposed to the risk of bankruptcy. Restriction (4.5) looks similar to (4.2). However, because of assumption (3.2), there is no funding gap in the risky mode, which is the advantage over the safe mode. The disadvantage of the risky mode is that business loans are less valuable, for bankruptcy will drive all values down to (almost) zero in the bad state.
Without interbank loans, a bank’s optimal investment and financing decision has the following properties.
Proposition 1
Let ϕn(ln):=(E[λn, s]−α)ln − c(ln). Provided b = β = 0, banks maximize expected profits if

with \(l_n^{{{\mathscr {R}}}}\) and \({\bar{{\Upomega }}}_n\) being defined by
Proof
See “Appendix”. \(\square \)
Proposition 1 shows that a bank, whose capacity to raise funds does not impose a binding constraint on business loans, grants the first-best loan volume. If the bank’s endowment implies that its financial constraint is binding in the safe mode, the bank operates either in the safe mode, with loan volumes being smaller, the tighter the constraint is, or in the risky mode. If the financial constraint in the safe mode is not too tight, the deviation from the first-best is not too large and the bank prefers the safe mode over the risky mode. Only if the financial constraint is sufficiently tight, i.e., a bank’s endowment is below \({\bar{{\Upomega }}}_n\), it prefers the risky mode because the benefits of shaking off a relatively tight financial constraint outweigh loan earnings forgone in the bad state.
4.2 With interbank loans
From the analysis so far, we know what happens if bank 2 does not agree to the terms of the interbank loan contract offered by bank 1. When making a take-it-or-leave-it offer to bank 2, bank 1 not only takes this into account but also that, if its offer is accepted, the interbank loan affects the funding liquidity of both banks. A necessary condition for a bank to face a financial constraint on its volume of business loans is to operate in the safe mode. With interbank loans, these constraints are
which differ from (4.2) with respect to the second term on the RHS. For bank 1, any dollar raised from investors at a cost of α and lent to bank 2 increases the amount collectible in the bad state by β. If β > α, the bank can use the difference β − α to increase the amount it can promise to repay to its investors in the safe mode. For this effect to work, bank 1 does not rely on how much it can collect from bank 2 in the other state, when earnings of bank 1 are high anyway. In fact, even if bank 1 takes the risk of being unable to collect its claims on bank 2 in that state, making an interbank loan to bank 2 will still offset the risk associated with its own business loans. Assuming such counterparty risk lowers the bank’s total portfolio risk, enabling it to commit to a higher face value of claims held by investors. Hence, bank 1 can attract additional funds from investors and refinance additional business loans.
Bank 2 will have scope for additional business loans only if β < α. However, bank 1 would never agree on interbank loans with β < α, as they neither cover their refinancing costs nor do they help to grant more business loans. This raises the question why bank 2 would accept an interbank loan with β > α. If bank 2 operated in the safe mode, such a loan would be more expensive than accepting funds directly from investors. However, if bank 2 is in the risky mode, it repays β only with probability 1 − p2 = p1. Hence, bank 2 accepts β > α as long as it will operate in the risky mode and the expected costs of the interbank loan are not higher than those of funds from investors, i.e., p1β ≤ α.
These insights already allow to draw two important conclusions. First, there is no benefit to bank 1 from diversifying its portfolio with claims on bank 2 if the former is not financially constrained even without interbank lending, i.e., if \({\Upomega }_1\ge \tfrac{\alpha - \lambda _{1,L}}{\alpha }l_1^{\text {fb}}\). Accordingly, provided diversification is the only reason for banks to trade in our context, there is no need for bank 1 to lend to bank 2 although doing so would not harm anyone either. The interbank lender would simply become an investor just like any other investor of bank 2.Footnote 10
Second, there is also no reason for interbank loans unless the interbank lender will be safe and the interbank borrower risky. For the sake of brevity and clarity, we henceforth focus on situations in which already in the absence of interbank markets, the endowments of banks Ωn imply that both banks would face external funding constraints, but while bank 1 would operate in the safe mode, bank 2 would operate in the risky mode.Footnote 11 That is,  and
and  .
.
The optimal interbank loan contract has the following properties.
Proposition 2
Suppose  and
and  .
.
-
1.
For \(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1 \le \tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \) the contract (b⋆,β⋆) satisfies
$$\begin{aligned} \beta ^{*}&= \tfrac{\alpha }{p_1}, \end{aligned}$$(4.10)$$\begin{aligned} b^{*}&\in \left[ \tfrac{p_1}{p_2}\left( \tfrac{\alpha - \lambda _{1,L}}{\alpha } l_1^{\text {fb}} - \varOmega _1 \right) , l_2^{{{\mathscr {R}}}} - \varOmega _2 \right] , \end{aligned}$$(4.11)implying
$$\begin{aligned} \begin{aligned} l_1^{*}&= l_1^{\text {fb}},\\ l_2^{*}&= l_2^{{{\mathscr {R}}}}. \end{aligned} \end{aligned}$$(4.12) -
2.
For \(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1 >\tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \), the contract (b⋆,β⋆) satisfies
$$\begin{aligned} \beta ^{*}&= \tfrac{\alpha }{p_1} -\tfrac{\left( \left( p_1 \lambda _{2,H} - \alpha \right) l_2^{{{\mathscr {R}}}} - c\left( l_2^{{{\mathscr {R}}}}\right) \right) -\left( \left( p_1 \lambda _{2,H} - \alpha \right) {\tilde{l}}_2 - c({\tilde{l}}_2 ) \right) }{p_1 ({\tilde{l}}_2 - \varOmega _2)}, \end{aligned}$$(4.13)$$\begin{aligned} b^{*}&= {\tilde{l}}_2 - \varOmega _2, \end{aligned}$$(4.14)implying
$$\begin{aligned} \begin{aligned} l_1^{*} = {\tilde{l}}_1, \\ l_2^{*} = {\tilde{l}}_2, \end{aligned} \end{aligned}$$(4.15)with
 and \({\tilde{l}}_2 >l_2^{{{\mathscr {R}}}}\) being jointly determined by $$\begin{aligned} \begin{aligned} \tfrac{ \alpha - \lambda _{1,L} }{ \alpha } {\tilde{l}}_1 - \varOmega _1&= \tfrac{p_2}{p_1} \left( {\tilde{l}}_2 - \varOmega _2 \right) - \tfrac{1}{p_1 \alpha } \int ^{ {\tilde{l}}_2 }_{ l_2^{{{\mathscr {R}}}} } {\left( p_2 \lambda _{2,L} - \phi ^\prime _2 ( l_2 ) \right) \mathrm{d} l_2 },\\ \phi ^\prime _1 ( {\tilde{l}}_1 )&= p_{1}\left( \alpha -\lambda _{1,L}\right) \tfrac{p_{2}\lambda _{2,L}-\phi _2 ^{\prime }( {\tilde{l}}_{2}) }{p_{2}\alpha -\left( p_{2}\lambda _{2,L}-\phi _2 ^{\prime }( {\tilde{l}}_{2}) \right) } . \end{aligned} \end{aligned}$$(4.16)
and \({\tilde{l}}_2 >l_2^{{{\mathscr {R}}}}\) being jointly determined by $$\begin{aligned} \begin{aligned} \tfrac{ \alpha - \lambda _{1,L} }{ \alpha } {\tilde{l}}_1 - \varOmega _1&= \tfrac{p_2}{p_1} \left( {\tilde{l}}_2 - \varOmega _2 \right) - \tfrac{1}{p_1 \alpha } \int ^{ {\tilde{l}}_2 }_{ l_2^{{{\mathscr {R}}}} } {\left( p_2 \lambda _{2,L} - \phi ^\prime _2 ( l_2 ) \right) \mathrm{d} l_2 },\\ \phi ^\prime _1 ( {\tilde{l}}_1 )&= p_{1}\left( \alpha -\lambda _{1,L}\right) \tfrac{p_{2}\lambda _{2,L}-\phi _2 ^{\prime }( {\tilde{l}}_{2}) }{p_{2}\alpha -\left( p_{2}\lambda _{2,L}-\phi _2 ^{\prime }( {\tilde{l}}_{2}) \right) } . \end{aligned} \end{aligned}$$(4.16)
Proof
See “Appendix”. \(\square \)
According to the proposition, two cases are to be distinguished, which differ with respect to the relative weight of two factors. One factor is the funding gap faced by bank 1 if it plans to grant the first-best volume of business loans, i.e., \(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1\). The other factor is the maximum amount bank 1 can raise from investors if it diversifies its portfolio with an interbank loan that is as costly for bank 2 as funds raised from investors. This amount has two components. First, as interbank loans cost bank 2 the same as funds from investors if α = p1β, each unit of interbank loans contributes to close the funding gap of bank 1 by \(\tfrac{ \beta - \alpha }{ \alpha } = \tfrac{p_2}{p_1}\). Second, bank 2 needs no more than \(l_2^{{{\mathscr {R}}}} - {\Upomega }_2\) from external sources to refinance its favored volume of business loans \(l_2^{{{\mathscr {R}}}}\) in the risky mode. Hence, provided that the interbank loan costs the same as funds from investors, \(l_2^{{{\mathscr {R}}}} - {\Upomega }_2\) is also the largest amount bank 2 is willing to accept from bank 1. Together this means that the highest amount, which bank 1 can raise externally if the interbank loan is to cost bank 2 as much as other external funds, is \(\tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \).
The first case in Proposition 2 refers to situations in which the funding gap of bank 1 \(\left( \tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1\right) \) is small relative to what this bank can potentially raise by diversifying its portfolio with an interbank loan that costs as much as funds from investors \(\left( \tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \right) \). In this case, bank 1 diversifies its portfolio such that the first-best volume of business loans becomes financially feasible, while bank 2 acts just like without an interbank market. It operates in the same mode and grants the same loan volume \(l_2^{{{\mathscr {R}}}}\) because, from the perspective of bank 2, the interbank loan merely crowds out funds from investors.
In the other case, bank 1 would still be financially constrained with an interbank loan of \( l_2^{{{\mathscr {R}}}} - {\Upomega }_2\) and would therefore benefit from granting a larger loan to bank 2. However, bank 2 is unwilling to accept more funds than necessary to refinance \(l_2^{{{\mathscr {R}}}}\), unless it receives compensation for granting otherwise inefficient business loans. Hence, bank 1 has to offer a contract with a lower repayment obligation β, making the interbank loan cheaper for bank 2 than funds from investors. In that sense, diversification becomes costly for bank 1 because expected returns on the interbank loan do not cover their own refinancing cost. Trading off this cost of diversification with its benefit, the optimum for bank 1 is given by (4.16). The LHS of the first equation in (4.16) reflects the funding gap of bank 1. According to the RHS, the compensation for bank 2 (second term) reduces the amount by which bank 1 could close its funding gap with the help of a costless interbank loan (first term). According to the second equation in (4.16), the gains from granting one more unit of business loans (LHS) just offsets the marginal cost of compensating bank 2 (RHS). To discuss further implications of the optimal arrangement between bank 1 and bank 2, we now take a closer look at the determinants of these costs.
4.3 Bank-specific characteristics and diversification costs
Our discussion of the determinants of diversification costs begins with the definition of these costs as a function K2 of the loan volume l1.
Definition 2
For any given l1, let
with \({\bar{l}}_2\) being implicitly defined by
and let
Financial endowments and credit risks of the interbank lender as well as the interbank borrower are key determinants of the diversification costs. Regarding endowments, a higher Ω1 eases the interbank lender’s own financial constraint, making it less dependent on diversification as a means to mitigate its financial constraint. The interbank loan is smaller and so is the compensation payable to the interbank borrower. By contrast, diversification is more expensive for the interbank lender if Ω2 is higher because the interbank borrower will require a higher compensation. The reason is that the interbank borrower would need less external funds. To be still willing to accept an interbank loan that makes the interbank lender’s portfolio sufficiently diversified, the interbank borrower asks for a higher compensation.
As regards risk, we operationalize it by introducing a mean-preserving spread to a bank’s loan earnings. Let \(\varDelta _n := \lambda _{n,H} - \lambda _{n,L}\) implying \(\lambda _{n,L} = E[\lambda _{n,s}]- \left( 1 - p_n \right) \varDelta _n\) and \(\lambda _{n,H}=E[\lambda _{n,s}] + p_n \varDelta _n\). By definition, a higher \(\varDelta _n\) increases the variance of loan earnings without changing E[λn, s]. According to (4.9), a higher credit risk \(\varDelta _1\) comes with a tighter financial constraint for the interbank lender. In order to have sufficient funds for maintaining a volume l1 of business loans, the interbank borrower has to be convinced to accept a larger interbank loan. As a larger interbank loan drives up \({\bar{l}}_2\), the interbank borrower requires a higher compensation. Similarly, the interbank borrower’s total loan earnings in its good state are higher with a higher \(\varDelta _2\). Holding everything else equal, this implies that the interbank borrower forgoes less in profits by investing in a larger than efficient loan portfolio. Hence, the required compensation can be smaller too.
The marginal costs of diversification K′2(l1) are defined as the change in compensation required if the interbank lender wants to marginally increase its business loans. If they are strictly positive, the properties of the function c imply that it is optimal for the interbank lender to remain financially constrained. Proposition 2 has shown that, although an interbank lender could potentially escape its financial constraint entirely, the interbank loan chosen by the interbank lender may be too small to achieve this. The characteristics of diversification costs in equilibrium are summarized in the following lemma.
Lemma 1
Let  and
and  .
.
-
1.
For \(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1 \le \tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \), and hence l1⋆ ≥ l1fb and \(l^\star _2 \le l_2^{{\mathscr {R}}}\), we have K2(l1⋆) = K2′(l1⋆) = 0.
-
2.
For \(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1 >\tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \), and hence l1⋆ < l1fb and \(l^\star _2 >l_2^{{\mathscr {R}}}\), we have
-
(a)
K2(l1⋆) > 0 and \(\tfrac{\mathrm {d}K_2 \left( l^\star _1 \right) }{\mathrm {d}{\Upomega }_1} < 0\), \(\tfrac{\mathrm {d}K_2 \left( l^\star _1 \right) }{\mathrm {d}{\Upomega }_2} >0\), \(\tfrac{\mathrm {d}K_2 \left( l^\star _1 \right) }{d \varDelta _1} >0\) and \(\tfrac{\mathrm {d}K_2 \left( l^\star _1 \right) }{\mathrm {d} \varDelta _2} < 0\);
-
(b)
K′2(l1⋆) > 0 and \(\tfrac{\mathrm {d}K^{\prime }_2 \left( l^\star _1 \right) }{\mathrm {d}{\Upomega }_{1}} < 0\), \(\tfrac{\mathrm {d}K^{\prime }_2 \left( l^\star _1 \right) }{\mathrm {d}{\Upomega }_{2}} >0\), \(\tfrac{\mathrm {d}K^{\prime }_2 \left( l^\star _1 \right) }{\mathrm {d} \varDelta _{1}} >0\) and \(\tfrac{\mathrm {d}K^{\prime }_2 \left( l^\star _1 \right) }{\mathrm {d} \varDelta _{2}} < 0\).
-
(a)
Proof
See “Appendix”. \(\square \)
The costs of diversification, and thus the bank-specific characteristics, have two implications. The first refers to the volume of business loans a bank wishes to grant, henceforth credit supply for short. Applying the general implicit function theorem to (4.16) and taking Lemma 1 into account, we obtain the following results.
Corollary 1
If the interbank lender’s credit supply depends on its own financial endowment Ω1 and credit risk \(\varDelta _1\), then
-
1.
credit supply of the interbank lender is negatively correlated with the interbank borrower’s endowment Ω2 and positively correlated with the interbank borrower’s credit risk \(\varDelta _2\);
-
2.
credit supply of the interbank borrower is negatively correlated with the interbank lender’s endowment Ω1 and varies with the interbank lender’s credit risk \(\varDelta _1\), but with an unclear sign.
Otherwise, the bank-specific characteristics of its interbank trading partner are irrelevant for a bank’s credit supply.
That lower internal funds and higher credit risk tend to tighten a bank’s own financial constraint is a rather standard result. In fact, the model has qualitatively similar implications when we abstract from any interbank linkages (i.e., setting b = 0, see Proposition 1). The novelty in our model is that bank-specific characteristics of the interbank borrower also matter for the credit supply of the interbank lender. Both, a better endowment Ω2 and a lower credit risk \(\varDelta _2\) increase the marginal costs of diversification, inducing a lower credit supply by the interbank lender. In addition, bank-specific characteristics of the interbank lender also have an effect on the interbank borrower’s credit supply. With a higher Ω1, an interbank lender relies less on diversification to maintain its credit supply. In order to economize on diversification costs, it reduces the interbank loan, leading to a lower credit supply by the interbank borrower. A higher credit risk \(\varDelta _1\) has two effects. In order to maintain a specific volume of business loans, the interbank lender would have to lend more to the interbank borrower. However, since the marginal costs of diversification are higher, the interbank lender does not want to leave the loan volume unchanged but prefers to grant fewer loans. The first effect increases credit supply by the interbank borrower, the second effect decreases it.
The second implication of diversification costs refers to the substitutability of interbank and nonbank wholesale funding.
Corollary 2
If the interbank lender’s credit supply does not depend on its own financial endowment Ω1 and/or credit risk \(\varDelta _1\), interbank loans and funds provided by nonbanks are perfect substitutes for the interbank borrower. Otherwise, they are not.
The reasons behind this corollary are the following. For K2(l1⋆) = 0, interbank loans are as costly for the interbank lender as funds from investors. If the interbank lender would reduce the volume of the interbank loan, the interbank borrower could easily replace them at no additional costs with funds from investors. For K2(l1⋆) > 0, the interbank loan comes at a lower unit cost and crowds out funding from other investors. Therefore, these two funding sources are not perfect substitutes for the interbank borrower, as a marginal reduction in interbank lending would not be offset by more funds from investors.
At times, a limited substitutability of funding sources causes worries among central banks and regulators. A major concern during the world financial crisis was that a freeze in interbank lending or the failure of a major interbank lender would cut off some other banks entirely from their funding sources, triggering a further blow to the banking sector and aggregate credit supply. We now turn to these issues.
4.4 Interbank markets and credit intermediation
The previous analysis suggests that to understand the role of interbank loans for credit supply, it is key to consider them as complements on the aggregate level. This is because the banking sector as a whole can raise more funds from nonbanks when banks trade with each other. Such a more-money effect of transactions among banks indicates that tensions in interbank markets have the potential to harm the real economy even more seriously than it is commonly thought. In particular, as the following comparison of credit supply in economies with and without an interbank market reveals, not only interbank borrowers but also interbank lenders supply less credit if interbank transactions cannot take place.
Corollary 3
A breakdown of interbank markets will lead to a drop in the interbank lender’s credit supply which
-
1.
is independent from bank-specific characteristics of the interbank borrower if the interbank lender’s credit supply before the market breakdown does not depend on its own financial endowment Ω1 and credit risk \(\varDelta _1\);
-
2.
tends to be more pronounced for a lower financial endowment Ω2 or higher credit risk \(\varDelta _2\) of the interbank borrower if the interbank lender’s credit supply depends on its own financial endowment Ω1 and credit risk \(\varDelta _1\).
Credit supply of a potential interbank lender, i.e., bank 1, will be different in economies with and without interbank markets. For example, if the interbank market allows the bank to completely escape its financial constraint at no further costs, i.e., K2(l1⋆) = 0, the bank will supply credit according to its first-best loan volume l1fb. In economies without interbank markets, however, this bank will face a binding financial constraint and supply only \({\hat{l}}_1 = \tfrac{\alpha }{\alpha -\lambda _{1,L}}{\Upomega }_1\). The percentage drop in credit supply will be \( 1-\tfrac{\alpha }{\alpha - \lambda _{1,L}} \tfrac{{\Upomega }_1}{l^{\text {fb}}_1}\), which depends on the aforementioned bank-specific characteristics Ω1 and \(\varDelta _1\) of the interbank lender. The less an interbank lender can refinance its optimal credit supply with internal funds, i.e., the smaller is Ω1/l1fb, the more important are interbank markets for aggregate credit supply. In a similar vein, interbank markets will boost aggregate credit supply the stronger, the higher the credit risk for the interbank lender is. A higher \(\varDelta _1\) implies a lower λ1, L and thus a tighter financial constraint for the bank if it cannot ease its funding constraint through diversification.Footnote 12
The more interesting insight, however, refers to the role of the interbank borrower’s characteristics. Corollary 1, Part 1 suggests that, if K2(l1*)>0, credit supply of the interbank lender depends negatively on the borrower’s endowment Ω2 and positively on its credit risk \(\varDelta _2\). Accordingly, the effect of a market breakdown on the interbank lender’s credit supply depends on these characteristics too.
Finally, the interbank borrower’s credit supply may also depend on whether there is an interbank market.
Corollary 4
A breakdown of interbank markets
-
1.
has no impact on the interbank borrower’s credit supply if the interbank lender’s credit supply does not depend on its own financial endowment Ω1 and/or credit risk \(\varDelta _1\);
-
2.
leads to a drop in the interbank borrower’s credit supply if the interbank lender’s credit supply depends on its own financial endowment Ω1 and credit risk \(\varDelta _1\). This drop is more pronounced if the financial endowment of the interbank lender Ω1 is low.
According to Proposition 1, a potential borrower on interbank markets, i.e., bank 2, may face a substantial external funding constraint in economies without an interbank market. From Proposition 2, we know that there are two cases. One refers to situations in which the interbank borrower wants to raise more externally than what the interbank lender, i.e., bank 1, needs for achieving a degree of diversification that would allow to refinance its first-best loan volume. Interbank loans and funds from investors are perfect substitutes, and the interbank borrower’s credit supply does not depend on whether or not there is an interbank market. Accordingly, an exogenous freeze of interbank markets would not have an effect on this bank’s ability to grant business loans.
In the other case, the interbank lender wants to lend more to the interbank borrower. The interbank borrower is funded entirely by the other bank, and interbank loans are not a perfect substitute for funds from investors. A freeze of the interbank market implies that the interbank borrower’s credit supply will be lower. Instead of \({\tilde{l}}_2\), as given in (4.16), the credit supply will be only \(l_2^{{{\mathscr {R}}}}\). The reason that this bank’s credit supply is higher in an economy with an interbank market is not that it is dependent on interbank borrowing, but that its business loans provide additional benefits to other banks which are internalized only through interbank transactions.
4.5 Debt overhang and business loans with negative NPV
Next, we remove the restrictions on bank 2’s internal funds and let Ω2 ≶ 0. We also ease the restriction on loan returns and assume merely α < λ2, H. In the absence of interbank lending, i.e., b = 0, bank 2 would still operate as described in Proposition 1, but with two qualifications. First, if Ω2 < 0, the bank would start with a negative endowment which could be the result of a debt overhang. If the debt overhang problem is bad enough such that \({\Upomega }_2 < - \tfrac{1}{\alpha }\left( \phi _2 \left( l_2^{{{\mathscr {R}}}}\right) -p_2 \lambda _{2,L} l_2^{{{\mathscr {R}}}}\right) \), bank 2 is better off closing down right at the beginning of the period as expected profits would not cover the existing debt overhang. Second, if α > p1λ2, H, the bank will not operate in the risky mode because expected loan earnings may not even cover their cost of finance. If bank 2’s endowment is positive, it will opt for the safe mode in the absence of interbank markets and credit supply will be l2max := αΩ2/(α−λ2, L). If its endowment is negative, the best it can do is to fail outright.
The major difference to the previously considered cases is that the costs of diversification comprise not only an element that depends on the deviation of the induced loan volume \({\tilde{l}}_2\) from the loan volume \(l^{{{\mathscr {R}}}}_2 \) the bank would grant in the risky mode. It also contains a lump sum. If bank 1 wants to take advantage of potential diversification benefits through interbank loans, it has to make bank 2 operate in the risky mode in the first place. Doing so requires a compensation C2 for bank 2 to not go bankrupt or operate in the safe mode, if either would be preferred by bank 2 over the risky mode, i.e.,
with \( l_2^{{{\mathscr {S}}}} := \min \left\{ l_2^{\text {fb}}, \max \left\{ 0, l_2^{\max } \right\} \right\} \). Hence, the total costs of diversification are C2 + K2(l1) with
and \({\bar{l}}_2\) satisfying
It follows that, although the cost of diversification can be higher, it does not necessarily render interbank loans meaningless as an instrument to relax funding constraints for the interbank lender. Even structurally weak banks with a debt overhang and lending opportunities with negative NPV may still offer a diversification benefit to an interbank lender which can outweigh its cost. Since the weak bank would not grant any loans in the absence of interbank markets, a loan from another bank would thus appear to be the only, life-sustaining funding source for this bank. Such a loan has to be less costly than any other funding alternative as the interbank lender has to compensate the interbank borrower for not going bankrupt. However, interbank loans will not be cheap enough to allow the interbank borrower to regain sufficient financial strength and a sound capital structure, for otherwise the interbank borrower would not offer any diversification benefits to the interbank lender.
4.6 Diversified loan portfolios versus diversification through interbank lending
We conclude this section with a remark on the endogenous choice between investing in a diversified portfolio of business loans and seeking diversification on the interbank loan market. As discussed in Sect. 2, there is evidence for regional fragmentation in European retail banking markets (European Central Bank 2018), which is considered to be linked to local information advantages of banks.
Our model helps to shed some further light on this phenomenon. Suppose that bank 1 can choose between two loan portfolios, A and B. There are again two states. In one state, both portfolios are a success, and in the other state, they are both a failure. However, compared to portfolio A, portfolio B is associated with higher marginal costs, c′, lower expected returns, E[λ1, s], and a lower variance, \(\varDelta _1\). One could interpret portfolio A as a portfolio solely consisting of business loans granted in the bank’s home country and portfolio B as a portfolio of loans the bank grants at home as well as abroad. The differences between portfolios then reflect both the informational disadvantage the bank has abroad and the higher degree of diversification achievable through direct cross-border lending. Importantly, these characteristics of the portfolios imply that the financial constraint for the bank is tighter if it invests only in domestic loans. This is not only because the lower costs and the higher expected return imply a higher first-best loan volume, but also due to the higher volatility which lowers the bank’s ability to repay investors regardless of whether the portfolio returns are high or low. Provided the bank wants to operate in the safe mode, this financial constraint may be so tight that the bank prefers the more diversified portfolio B over the more productive portfolio A.Footnote 13
However, instead of seeking diversification through direct cross-border lending, the bank can also choose to invest in loan portfolio A and lend to another bank which has a better expertise in the foreign market. Then, the benefit of interbank lending is given by the additional expected profit due to a looser financial constraint, net of any diversification costs payable to the interbank borrower. If this benefit is sufficiently high, the bank prefers diversification through interbank markets over direct diversification of its loan portfolio.
5 Imperfect correlation of loan portfolios
So far, we analyzed interbank loans as an instrument for a bank to reduce its probability of default provided that perfect diversification is possible, even though it may choose not to become perfectly diversified due to the associated costs. However, business loans granted by banks may be exposed to systematic risks, for example due to business cycle factors. In this section, we set out to explore two related questions. First, how does the correlation of banks’ business loans affect the benefits and costs of interbank lending, and hence the terms of interbank loans? Second, what are the stability implications if an interbank lender has to choose between counterparties with access to different borrower pools?
5.1 Modeling correlation
With the aim of controlling for changes in the correlation of loan portfolios for a given risk–return structure of business loans, we generalize the space of possible states 𝕊 in the following way.
As the success of a bank’s loans can be described as a random variable that takes the value L if loan earnings are low (failure) and the value H if they are high (success), the success of both banks follows a bivariate two-point distribution with four possible states 𝕊 = {LL,LH,HL,HH}. Let pLL, pLH, pHL and pHH denote the respective probabilities of these states so that we have
Thus, {LL,LH} is the set of states in which loan earnings for bank 1 are low, while {LL,HL} is the set of states in which loan earnings for bank 2 are low. As before, pn denotes the unconditional probability that earnings of the loan portfolio of bank n are low, i.e.,
Expected loan earnings of bank n are E[λn, s] = pnλn, L + (1−pn)λn, H with variance  . The covariance of the banks’ loan earnings is
. The covariance of the banks’ loan earnings is  with a correlation coefficient
with a correlation coefficient  .
.
In order to isolate the implications of the correlation of loan portfolios, we start off from unconditional probabilities of failure, p1 and p2, for which p1 = 1 − p2, and consider changes to ρ that do not affect p1 and p2. The probabilities of states hence read
implying that changes in the correlation of loan portfolios leave the risk-return profile of each bank’s business loans unchanged. As nonnegativity of pLH and pHL implies an upper bound on the correlation coefficient, given by min{p1/(1 − p1),(1 − p1/p1)} ∈ ]0, 1], we cover all negative correlation coefficients as well as a range of positive coefficients although not necessarily very large ones.Footnote 14
Note that pLL can serve as an indicator of the degree of correlation of loan portfolios. Obviously, pLL = 0 indicates perfect negative correlation while an increase in pLL indicates that the correlation of portfolios increases.
5.2 Correlation and the terms of interbank loans
To understand the role of correlation for the terms of interbank loans, we need to adjust the definition of a bank’s mode of operation.
Definition 3
Let ℚn be the set of states in which bank n is bankrupt. Bank n operates in a failure mode\(m_n{:=} {\mathscr {F}}\) if ℚn = 𝕊, in a safe mode\(m_n{:=} {\mathscr {S}}\) if ℚn = ∅, and in a risky mode\(m_n{:=} {\mathscr {R}}\left( {\mathbb {Q}}_n\right) \) otherwise.
We conclude:
Lemma 2
For ρ > −1 and thus pLL > 0, interbank loans imply ℚ1 = {LL} and ℚ2 = {LL, HL}.
Proof
See “Appendix”. \(\square \)
Naturally, there is no scope for interbank loans as a means to ease a financial constraint if the correlation coefficient is ρ = 1. For ρ ∈ ] − 1, 1[, interbank loans will be made only if the interbank borrower operates in the risky mode, just like for ρ = −1. However, if there is interbank lending, the interbank lender necessarily assumes also some risk of bankruptcy for ρ ∈ ] − 1, 1[. The lender will be bankrupt in state LL, in which earnings of its own business loans are low and the interbank borrower defaults.
Given that ℚ1 = {LL}, bank 1’s budget constraint together with the upper bound on funds from investors implies a funding constraint similar to (4.9). This constraint is now given by
Bankruptcy of bank 1 in state LL implies that investors will insist on a higher repayment promise α/(1 − pLL)>α. This has two immediate consequences. First, the funding liquidity of the bank’s business loans will be smaller as can be seen by comparing the first terms on the RHS in (4.9) and (5.3). Second, bank 1 can ease its financial constraint by lending to bank 2 only if β > α/(1 − pLL), see the second term on the RHS of (5.3).
How business loans are correlated does not affect the banks’ optimal portfolio choice in the absence of interbank lending. Hence, Proposition 1 still applies, i.e., provided their endowments satisfy \({\Upomega }_1 \in [{\bar{{\Upomega }}}_1, \tfrac{\alpha - \lambda _{1,L}}{\alpha }l_1^{\text {fb}}[\) and \({\Upomega }_2 \in [0, {\bar{{\Upomega }}}_2[\), bank 1 would operate in the safe mode without interbank lending and bank 2 in the risky mode. However, with interbank loans, correlation has an effect on bank 1’s funding constraint. Taking this into account, the interbank loan contract has the following properties.
Proposition 3
Suppose \({\Upomega }_1 \in [{\bar{{\Upomega }}}_1, \tfrac{\alpha - \lambda _{1,L}}{\alpha }l_1^{\text {fb}}[\) and \({\Upomega }_2 \in [0, {\bar{{\Upomega }}}_2[\) and recall that pLL = 0 for ρ = −1 and dpLL/dρ > 0. Provided bank 1 grants an interbank loan to bank 2, the interbank loan contract satisfies:
-
1.
For \(\tfrac{\alpha -\left( 1- p_{LL} \right) \lambda _{1,L}}{\alpha }l_{1}^{{\mathscr {R}}\left( {\mathbb {Q}}_1\right) }-{\Upomega }_{1}\le \tfrac{ p_2 - p_{LL} }{p_1}\left( l_{2}^{{\mathscr {R}}\left( {\mathbb {Q}}_2\right) }-{\Upomega }_{2}\right) \),
$$\begin{aligned} \beta ^{*}&=\tfrac{\alpha }{p_1}, \end{aligned}$$(5.4)$$\begin{aligned} b^{*}&\in \left[ \tfrac{ p_1 }{ p_2 - p_{LL} } \left( \tfrac{ \alpha - \left( 1- p_{LL} \right) \lambda _{1,L} }{ \alpha } l_{1}^{{\mathscr {R}}\left( {\mathbb {Q}}_1\right) }- \varOmega _{1} \right) ,l_{2}^{{\mathscr {R}}\left( {\mathbb {Q}}_2\right) }-\varOmega _{2}\right] , \end{aligned}$$(5.5)implying
$$\begin{aligned} l_{1}^{*}&=l_{1}^{{\mathscr {R}}\left( {\mathbb {Q}}_1\right) }, \end{aligned}$$(5.6)$$\begin{aligned} l_{2}^{*}&=l_{2}^{{\mathscr {R}}\left( {\mathbb {Q}}_2\right) }, \end{aligned}$$(5.7)with \(l_{1}^{{\mathscr {R}}\left( {\mathbb {Q}}_1\right) }\) and \(l_{2}^{{\mathscr {R}}\left( {\mathbb {Q}}_2\right) }\) being defined by
$$\begin{aligned} \phi _1^{\prime }\left( l_{1}^{{\mathscr {R}}\left( {\mathbb {Q}}_1\right) }\right)&= p_{LL} \lambda _{1,L} , \end{aligned}$$(5.8)$$\begin{aligned} \phi _2^{\prime }\left( l_{2}^{{\mathscr {R}}\left( {\mathbb {Q}}_2\right) }\right)&= p_2 \lambda _{2,L} . \end{aligned}$$(5.9) -
2.
For \(\tfrac{\alpha -\left( 1- p_{LL} \right) \lambda _{1,L}}{\alpha }l_{1}^{{\mathscr {R}}\left( {\mathbb {Q}}_1\right) }-{\Upomega }_{1} >\tfrac{ p_2 - p_{LL} }{p_1}\left( l_{2}^{{\mathscr {R}}\left( {\mathbb {Q}}_2\right) }-{\Upomega }_{2}\right) \),
$$\begin{aligned} \beta ^{*}&=\tfrac{\alpha }{p_{1}} - \tfrac{\left( ( p_{1}\lambda _{2,H}-\alpha ) l_{2}^{{\mathscr {R}}({\mathbb {Q}}_2)}-c\left( l_{2}^{{\mathscr {R}}({\mathbb {Q}}_2)}\right) \right) -\left( \left( p_{1} \lambda _{2,H} - \alpha \right) \check{l}_{2}-c(\check{l}_{2})\right) }{p_{1}(\check{l}_{2}-\varOmega _{2})} , \end{aligned}$$(5.10)$$\begin{aligned} b^{*}&=\check{l}_{2}-\varOmega _{2}, \end{aligned}$$(5.11)implying
$$\begin{aligned} l_{1}^{*}&=\check{l}_{1}, \end{aligned}$$(5.12)$$\begin{aligned} l_{2}^{*}&=\check{l}_{2} , \end{aligned}$$(5.13)with
 and \(\check{l}_{2}>l_{2}^{{\mathscr {R}}({\mathbb {Q}}_2)}\) being jointly determined by $$\begin{aligned} \begin{aligned}&\tfrac{\alpha - \left( 1 - p_{LL} \right) \lambda _{1,L} }{\alpha } \check{l}_{1} - \varOmega _{1} = \tfrac{ p_2 - p_{LL} }{ p_{1} } \left( \check{l}_{2}{-}\varOmega _{2}\right) \\&\quad -\tfrac{ 1{-} p_{LL} }{p_{1}\alpha } \displaystyle \int _{l_{2}^{{\mathscr {R}}({\mathbb {Q}}_2)}}^{\check{l}_{2}}{\left( p_2 \lambda _{2,L}{-}\phi _{2}^{\prime }({l_2}) \right) \mathrm{d}l_2} \end{aligned} \end{aligned}$$(5.14)
and \(\check{l}_{2}>l_{2}^{{\mathscr {R}}({\mathbb {Q}}_2)}\) being jointly determined by $$\begin{aligned} \begin{aligned}&\tfrac{\alpha - \left( 1 - p_{LL} \right) \lambda _{1,L} }{\alpha } \check{l}_{1} - \varOmega _{1} = \tfrac{ p_2 - p_{LL} }{ p_{1} } \left( \check{l}_{2}{-}\varOmega _{2}\right) \\&\quad -\tfrac{ 1{-} p_{LL} }{p_{1}\alpha } \displaystyle \int _{l_{2}^{{\mathscr {R}}({\mathbb {Q}}_2)}}^{\check{l}_{2}}{\left( p_2 \lambda _{2,L}{-}\phi _{2}^{\prime }({l_2}) \right) \mathrm{d}l_2} \end{aligned} \end{aligned}$$(5.14)and
$$\begin{aligned} \phi _{1}^{\prime }(\check{l}_{1})- p_{LL} \lambda _{1,L} = \frac{p_1 \left( \alpha - \left( 1 - p_{LL} \right) \lambda _{1,L} \right) \left( p_2 \lambda _{2,L} - \phi _{2}^{\prime }(\check{l}_{2}) \right) }{ \left( p_2 - p_{LL} \right) \alpha - \left( 1 - p_{LL} \right) \left( p_2 \lambda _{2,L}-\phi _{2}^{\prime }(\check{l}_{2})\right) }. \end{aligned}$$(5.15)
Proof
The proof follows the proof for Proposition 2. \(\square \)
Provided bank 1 grants a loan to bank 2, there are again two cases to distinguish. The first is when the interbank lender’s own funding gap is small. As the lender fails if both banks’ loan earnings are low, this funding gap now refers to the volume of business loans \(l_{1}^{{\mathscr {R}}\left( {\mathbb {Q}}_1\right) }\) that is optimal conditional on its failure in state LL. This volume is equal to the first-best only for pLL = 0 and thus ρ = −1, lower than the first-best for all pLL > 0 (ρ > −1) and decreasing in the degree of correlation. This is because an increase in correlation will increase the probability of bank 1 to fail and therefore lower the profitability of its business loans. The first part of Proposition 3 also shows that the interbank rate, or repayment obligation of bank 2, does not depend on the correlation of banks’ loan portfolios and that the interbank loan can be as large as with perfect diversification. The reason is that correlation does not affect bank 2’s behavior when there are no interbank links. Accordingly, it will also not affect the terms of an interbank loan acceptable to bank 2. To conclude, in case of the interbank lender facing a small funding gap, its volume of business loans is lower if correlation is higher while the volume of business loans granted by the interbank borrower will be the same as in the case of perfect diversification.
If the funding gap of the interbank lender is large, the second case in Proposition 3 applies. In this case, the volume \(\check{l}_{2}\) of business loans made by the interbank borrower depends on the volume of the interbank loan, which in turn depends on the volume \(\check{l}_1\) of business loans the interbank lender wishes to make. Applying the general implicit function theorem to Eqs. (5.14) and (5.15), we find that \(\mathrm {d}\check{l}_1 /\mathrm {d}\rho < 0\) while the sign of \(\mathrm {d}\check{l}_2 /\mathrm {d}\rho \) is not clear.Footnote 15 To understand this, consider Eq. (5.15). Clearly, higher correlation lowers the marginal returns (on the LHS) for a given volume of business loans \(\check{l}_{1}\) as the interbank lender’s probability of default (and thus of not collecting loan earnings) increases. In addition, an increase in correlation results in an increase of the marginal cost (on the RHS) of business loans \(\check{l}_{1}\). The budget constraint (5.3) suggests that this is for two reasons. First, maintaining the same loan volume \(\check{l}_{1}\) implies a tighter funding constraint for the interbank lender. To ease the additional pressure, a larger interbank loan is needed so that the interbank borrower would have to grant more business loans, for which marginal costs are higher. Second, a larger degree of correlation will impair the effectiveness of interbank loans as a means to ease the lender’s funding constraint, due to a rise in the minimum repayment promise β. Again, this implies that the interbank lender needs to increase the volume of the interbank loan to maintain a certain volume of business loans. Hence, the interbank lender will respond to an increase in correlation by reducing its business loans until marginal returns and costs of these loans are balanced. Whether this reduction in the lender’s business loans results in an increase or decrease in the volume of interbank loans and the interbank borrower’s business loans then depends on the extent to which the lender cuts its provision of business loans.
While we cannot specify how the terms of the interbank loan depend on the correlation of loan portfolios in general as the sign of \(\mathrm {d}\check{l}_2 /\mathrm {d}\rho \) is not clear, we can pinpoint these terms for correlation coefficients for which interbank loans are (almost) meaningless in terms of relaxing the interbank lender’s financial constraint.
Corollary 5
Suppose p1 ≥ 0.5. Provided interbank lending takes place, the terms of interbank loans converge to \(b=l_{2}^{{\mathscr {R}}\left( {\mathbb {Q}}_2\right) }-{\Upomega }_{2}\) and β = α/p1, respectively, if ρ converges to (1 − p1)/p1.
To understand this result, recall that bank 2 will under no circumstance accept an interbank loan with a repayment obligation β above α/(1−p2) = α/p1 as such a loan would be more expensive for bank 2 than funds from investors. Also, recall from the funding constraint (5.3) that an interbank loan helps to mitigate the interbank lender’s financial constraint only if (1 − pLL)β > α. Combining these bounds on β implies that an interbank loan cannot improve the lender’s ability to make business loans unless 1 − pLL > p1. If ρ converges to (1 − p1)/p1, the difference 1 − pLL will converge to p1. Consequently, it makes less and less sense to bank 1 to offer an interbank loan with a repayment obligation β below α/p1, which would be needed to compensate bank 2 whenever it was supposed make business loans in excess of \(l_2^{{\mathscr {R}}({\mathbb {Q}}_2)}\). Accordingly, for ρ → (1 − p1)/p1, bank 2’s volume of business loans will be equal to or only marginally higher than \(l_2^{{\mathscr {R}}({\mathbb {Q}}_2)}\) and the interbank loan will stipulate that the amount loaned is equal to or only marginally higher than \(l_2^{{\mathscr {R}}({\mathbb {Q}}_2)}-{\Upomega }_2\) and that the interbank rate β is equal to or only marginally below α/p1.
Given the changes in the terms of interbank loans, we also draw the following conclusion.
Corollary 6
There is a \({\bar{\rho }}< 1\) such that interbank lending breaks down if the coefficient of correlation between banks’ business loans is larger than \({\bar{\rho }}\).
The reason behind this finding is as follows. Bank 2 makes the same expected profit with and without interbank loans. Therefore, whether or not there is an active market for interbank loans depends on the profits bank 1 expects. Without interbank lending, these profits are determined by Proposition 1, and with interbank lending they follow from Proposition 3. Two cases are to be distinguished. The first is if p1 ≥ 0.5. As argued above, the RHS in Eq. (5.14) is arbitrarily close to zero if ρ is close to (1 − p1)/p1, which implies that \(\tfrac{\alpha {-}p_1 \lambda _{1,L} }{\alpha } \check{l}_{1}\approx {\Upomega }_{1}\) and thus \(\alpha {\Upomega }_1/(\alpha - \lambda _{1,L})>\check{l}_{1}\). Hence, the volume of business loans bank 1 would grant without interbank loan is larger than with interbank loan. Interbank lending therefore implies that bank 1 faces a tighter funding constraint and cannot realize loan earnings in state LL. Bank 1 is thus strictly better off without granting a loan to bank 2. The second case is if p1 < 0.5. The LHS in Eq. (5.15) converges to \( \phi _{1}^{\prime }(\check{l}_{1})-p_1\lambda _{1,L}\) if ρ converges to p1/(1 − p1). Given that the RHS in Eq. (5.15) is positive, the volume of business loans with an interbank loan, \(\check{l}_{1}\), is smaller than the respective volume if bank 1 would operate in a risky mode without granting any interbank loans, \(l_n^{{\mathscr {R}}}\). Yet, bank 1’s probability of survival is (almost) the same because pLH is arbitrarily close to zero. However, given that the safe mode is already better for bank 1 than the risky mode without interbank loans, interbank lending only makes bank 1 worse off. To conclude, since granting an interbank loan is always more profitable than not granting such loans provided the correlation coefficient is ρ = −1, and since granting no interbank loans makes bank 1 better off if ρ is close to (1 − p1)/p1 for p1 ≥ 0.5 and close to p1/(1 − p1) for p1 < 0.5, there is a critical value of the correlation coefficient \({\bar{\rho }}{\in ]-1,\min \{p_1/(1-p_1),(1-p_1)/p_1\}[}\) such that it is not profitable to make an interbank loan for \(\rho >{\bar{\rho }}\).
5.3 Stability implications
Suppose a bank can choose to lend either to a bank that would allow for perfect diversification, or to a bank that would expose the interbank lender to the risk that the failure of the counterparty can trigger its own failure. In both cases, the possibility that the counterparty fails to repay its interbank loan is what makes interbank lending profitable in the first place. However, why and under which circumstances is it profitable for the interbank lender to expose itself to the risk of its own bankruptcy?
To address this question, suppose there are three banks n ∈ {1, 2, 3}. As before, the potential interbank lender is bank 1. This bank can lend either to bank 2 or to bank 3, but not to both. Business loans of bank 2 are a success if and only if those by bank 1 are a failure. Business loans of bank 3 are imperfectly correlated with those granted by bank 1. Following the spirit of the previous notation, the relevant states are now 𝕊 = {LHL,LHH,HLL,HLH} with probabilities of states as in Eq. (5.2), i.e.,
Accordingly, {LHL, LHH} is the set of states in which loan earnings for bank 1 are low, {HLL, HLH} is the set of states in which loan earnings for bank 2 are low and {LHL, HLL} is the respective set of states for bank 3. As before, pn denotes the unconditional probability of low loan earnings of bank n, with p1 = 1 − p2 = 1 − p3. For all banks, loan earnings satisfy assumption (3.2).
The only interesting case is where the coefficient of correlation is sufficiently small such that granting a loan to bank 3 is better than granting no interbank loan at all, i.e., \(\rho \in ]-1,{\bar{\rho }}[\). According to Proposition 1, bank 1 operates in the safe mode and banks 2 and 3 operate in the risky mode in the absence of interbank lending if endowments satisfy  and
and  and
and  .
.
Lemma 3
Let Pk be the probability of at least k banks failing at the same time. For \({\Upomega }_1 \in \left[ {\bar{{\Upomega }}}_1, \tfrac{\alpha - \lambda _{1,L}}{\alpha }l_1^{\text {fb}}\right) \), \({\Upomega }_2 \in \left[ 0, {\bar{{\Upomega }}}_2\right) \) and \({\Upomega }_3 \in \left[ 0, {\bar{{\Upomega }}}_3\right) \), we have
Lemma 3 states that if bank 1 trades with bank 2, the probability of two banks being simultaneously in default equals the probability of those states in which bank 2 and bank 3 jointly fail. The joint bank failure is just the result of a common shock in the sense that both banks suffer low loan earnings in state HLL. If, however, bank 1 is better off by lending funds to bank 3, there is a spillover effect from bank 3 to bank 1 in state LHL. Without interbank loans, bank 1 would have operated in the safe mode and hence would survive in this state. By granting a loan to bank 3, however, bank 1 will not survive in this state according to Lemma 2. It has exposed itself to the risk that its counterparty will not repay in a state in which earnings will be already low anyway. The interbank lender has chosen to add interbank loans to its loan portfolio, although they are to some extent subject to the same shock as its own business loans.
The question about whether and under which conditions the interbank lender prefers bank 3 over bank 2 can be answered by looking at the respective costs of diversification, K2(l1) and K3(l1), associated with interbank loans to bank 2 and 3, respectively. Costs K2(l1) have been defined in Definition 2. According to Definition 3, the set of states in which bank 2 is bankrupt ℚ2 = {(1, 0, 0),(1, 0, 1)} and for bank 3 the respective set is ℚ3 = {(0, 1, 0),(1, 0, 0)}. Costs K3(l1) can thus be defined as follows.
Definition 4
Let
and
with \({\bar{l}}_3\) being implicitly defined by
Diversification costs K3(l1) have qualitatively similar properties as K2(l1) with respect to bank 3’s endowment Ω3 and credit risk \(\varDelta _3\). Bank 1 makes its decision about with whom to trade on interbank markets by comparing expected profits. Expected profits of bank 1 from trading with bank 2 are
and expected profits associated with lending to bank 3 are
When comparing expected profits, Proposition 2 implies that bank 1 prefers lending to bank 2 over holding no interbank claims at all if  . This is because it would operate in the safe mode regardless, but some b⋆ > 0, and not b = 0, actually maximizes expected profits. Another implication is that transactions with bank 2 will allow bank 1 to refinance the first-best loan volume l1fb already at no cost, i.e., \(K_2({\tilde{l}}_1)=0\), if \({(\alpha - \lambda _{1,L})l_1^{\text {fb}}}/{\alpha }-{\Upomega }_1 \le \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) (1-p_1)/p_1\). Trading with bank 3, however, would in any case at least imply to forfeit loan earnings in state HLL. Therefore, bank 2 will be the preferred transaction partner if \(K_2 ({\tilde{l}}_1) =0\).
. This is because it would operate in the safe mode regardless, but some b⋆ > 0, and not b = 0, actually maximizes expected profits. Another implication is that transactions with bank 2 will allow bank 1 to refinance the first-best loan volume l1fb already at no cost, i.e., \(K_2({\tilde{l}}_1)=0\), if \({(\alpha - \lambda _{1,L})l_1^{\text {fb}}}/{\alpha }-{\Upomega }_1 \le \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) (1-p_1)/p_1\). Trading with bank 3, however, would in any case at least imply to forfeit loan earnings in state HLL. Therefore, bank 2 will be the preferred transaction partner if \(K_2 ({\tilde{l}}_1) =0\).
Given that expected profits for the interbank lender are strictly decreasing in Ωn and increasing in \(\varDelta _n\) for n ∈ {2,3}, we come to the following conclusion.
Corollary 7
An interbank lender is more likely to lend to bank 3, and the probability of more banks going bankrupt at the same time tends to be higher, the larger are Ω2 and \(\varDelta _3\) and the smaller are Ω3 and \(\varDelta _2\).
To sum up, the answer to the question of which bank is the better alternative for bank 1 to trade with depends inter alia on bank-specific factors of the potential interbank borrowers. A larger endowment of a counterparty implies that the costs of diversification for the interbank lender are higher. By contrast, a larger risk makes a counterparty more attractive as it offers diversification at lower costs. The interbank lender shies away from perfect diversification if the funding gap of the interbank borrower, who operates in the risky mode and offers scope for perfect diversification, is relatively small.
6 Theory and evidence
While a full-fledged empirical test of our theory is beyond the scope of this paper, our framework matches a number of stylized facts about Europe’s interbank markets, and the mechanism we have described generates several empirical predictions that are consistent with recent empirical findings.
One stylized fact is that the size of interbank claims can be substantially larger than the average deposit and credit fluctuations of banks. For example, since 2002, the yearly average sum of interbank assets and liabilities in Germany has persistently exceeded the average fluctuations of deposits and credit (measured by the yearly standard deviation) by a factor of five to ten (Bluhm et al. 2016, Figure 1). This observation is economically significant for the Euro area as the German interbank market is the largest segment of the European interbank market where, according to Bluhm et al. (2016, Figure 4), total interbank lending exceeded 40% of total bank assets before the financial crisis and 30% afterward.Footnote 16
Another stylized fact refers to the maturity and risk structure of interbank transactions. According to Alves et al. (2013, Table 3), long-term (at least 1 year) interbank exposures of a median bank in 2011 accounted for more than half of total exposures for a sample of 53 large banks in the Euro area. In Germany, more than one-third of banks’ domestic interbank liabilities between 2002 and 2014 had a maturity of more than 1 year and the average maturity of interbank claims is well above 1 year (Bluhm et al. 2016, Figure 7). In terms of cross-border interbank loans, data from the Bank for International Settlement suggest that the average maturity of loans granted between 1997 and 2012 is close to 3 years.Footnote 17 The recent increase in the importance of long-term transactions among banks has sometimes been attributed to regulatory changes. The argument is that regulations such as the liquidity coverage ratio and the net stable funding ratio push banks to long-term maturities in the market for wholesale funding. But this argument is incomplete. If a bank wants to grant long-term loans and, because of the regulation, approaches another bank for a loan with a matching maturity, the problem of having to find long-term funding will not disappear. Instead, it will only shift from the interbank borrower to the lender, which will now have to find long-term funding to cover its additional long-term interbank loan. Accordingly, the interbank lender will agree to the transaction only if it can realize another benefit that is unavailable to the borrower. The diversification argument developed in our paper can explain such benefit.
As regards risks, Neal and García-Iglesias (2013, Table 1) report for the five largest economies in Europe (France, Germany, Italy, UK and Spain) that in 2011, the share of unsecured interbank liabilities in total liabilities ranged from 6.4 to 11.3%. In the UK, unsecured lending among banks accounts for more than a quarter of risk entailed in the interbank network, both in terms of credit risk and funding risk. Moreover, about one-third of unsecured lending is with a maturity of more than three months (Langfield et al. 2014).Footnote 18 In Italy, domestic credit exposures in the interbank market have shifted away from short-term to longer-term transactions. For example, based on consolidated data excluding intragroup lending, the figure for unsecured longer-term transactions in 2012 was more than twice as large as that of short-term transactions, whereas in 2008 the ratio was less than a quarter (Bargigli et al. 2015, Table 1).
A third stylized fact relates to the average net positions of interbank market participants. Not only are they substantially different from zero, their sign is also quite persistent over time (Ayadi et al. 2016; Martín-Oliver et al. 2017; Roengpitya et al. 2017). This suggests that there are banks which seldom switch from being interbank borrowers to interbank lenders or vice versa, which is at odds with the notion of interbank markets providing predominantly coinsurance of temporary idiosyncratic liquidity risks. For coinsurance of liquidity risk to explain this pattern, it would require that some banks are hit time and time again by a series of negative short-term liquidity shocks, while others are in a same way struck repeatedly by a series of positive short-term liquidity shocks. However, rather than referring to a series of bad luck or good luck, one would instead point to a structurally funding position of banks. Moreover, Ayadi et al. (2016, Table 3.1) report for a large sample of banks in the European Economic Area and Switzerland that compared to interbank borrowers, lending banks have a higher tangible common equity-to-assets ratio. Similarly, Martín-Oliver et al. (2017, Tables 3 and 5) find that Spanish interbank lenders tend to outperform borrowers in terms of solvency and liquidity measures, while Angelini et al. (2011, Tables 1 and 2) show that in Italy interbank lenders tend to have a higher (risk-weighted) capital ratio and a higher ratio of liquid assets to total assets than borrowers, especially during a crisis when financial constraints on banks tighten.
Altogether, these stylized facts suggest that the framework developed in this paper is appropriate to study interbank lending activities. Our framework also fits with the notion that the characteristics of counterparties seem to matter for interbank transactions (Afonso et al. 2011). The empirical literature indicates that banks rely heavily on decentralized, bilateral over-the-counter transactions where transaction partners know each other before entering a contract (Craig and von Peter 2014). However, even for trades not carried out over the counter, counterparty characteristics are key (Temizsoy et al. 2015). For example, an important alternative to OTCs is trading platforms such as e-MID which make the identity of the counterparty public (Angelini et al. 2011).Footnote 19 Another view is that banks overcome informational asymmetries by maintaining longer-term relationships (Bräuning and Fecht 2017). However, asymmetric information about counterparty risk alone cannot easily explain why worse performing banks increased the number of their counterparties right after the collapse of Lehman in September 2008 as documented by Afonso et al. (2011) who suggest that this could be the result of those banks seeking to diversify their exposure to interbank borrowers. The mechanism we present in the present paper analyzes such a motive for diversification and its implications.
As for the predictions of our model, the findings in Bluhm et al. (2016) are particularly interesting. They suggest that especially long-term transactions with nonbank customers can explain observed changes in a bank’s interbank accounts as predicted by our model. In Table 4, Bluhm et al. (2016) report that 1 percentage point more long-term liabilities to nonbanks (relative to total assets) is associated with 0.39 percentage points more gross long-term interbank assets (relative to total assets), while interbank liabilities are virtually unchanged. This finding fits with the results for our interbank lender who channels additional funds from nonbanks only partly to other banks and partly to finance other bank assets. In Table 5, Bluhm et al. (2016) report that a larger supply of long-term loans to nonbanks by 1 percentage point (relative to total assets) is associated with more gross long-term interbank liabilities by 0.84 percentage points (relative to total assets).Footnote 20 This observation suggests, first, that it matters for an interbank borrower how to fund loans to nonbanks and, second, that interbank borrowing is, to a large extent, the preferred way of funding. This fits with the results for an interbank borrower in our model to whom interbank loans and other types of finance tend to be imperfect substitutes.
The evidence documented in Iyer et al. (2014) also confirms predictions of our model. Focusing on the Portuguese banking sector, they investigate how the supply of credit to nonbanks was affected by the interbank market freeze in August 2007. Before the market freeze, Portuguese banks were consistently and persistently net borrowers on interbank markets, being funded to large extents by foreign banks.Footnote 21 Given that cross-border lending to firms and households in the Euro area has been traditionally low compared to cross-border interbank lending (European Central Bank 2018, Chart 19), Portuguese banks may thus have provided foreign banks with an opportunity to diversify their assets geographically. Against this background, our model predicts that a freeze in the interbank market causes a drop in credit supply which is stronger the more funds the interbank borrower has raised prior to the market freeze. Indeed, Iyer et al. (2014, Table 2) report that firms obtaining loans from banks with a higher interbank borrowing ratio before the freeze suffered from a sharper fall in credit supply from these banks. Our model also predicts that the credit supply of interbank borrowers to firms will respond more strongly to a freeze of the interbank market the larger the (marginal) cost of diversification is. This (marginal) cost depends positively on the ability of those banks to finance their loans with own funds (see Lemma 1). Accordingly, we would expect that banks with lower capital will reduce their credit supply less when interbank markets freeze (Corollary 4). This expectation is confirmed as banks with higher capital ratios tended to reduce credit supply more strongly in response to the market freeze in 2007 (Iyer et al. 2014, Table 7).
7 Conclusion
In this paper, we have developed an argument for transactions among banks that are not deposits or repos. In a nutshell, if a bank lends to another bank, the interbank lender assumes some counterparty risk. Taking on such risk can help to further diversify a bank’s overall exposure to risk, and a better diversified portfolio improves the cost and availability of external funding for a financially constrained bank. Then, interbank trades have effects on aggregate credit supply and the stability of the banking sector. These effects depend on the potential benefits of diversification as well as on its associated, endogenous cost. The latter are a function of a multitude of bank-specific characteristics of both, interbank lender and borrower.
Notes
We will discuss these stylized facts in detail in Sect. 6.
On contagion among banks in a dynamic setting, see Tsomocos et al. (2007).
The relevance of wholesale investors for banks is well documented in the literature. In 2012, wholesale funding accounted for 61% of total liabilities of large European banks, while the respective levels for Asia, emerging economies and large US banks ranged between 30 and 40% (Le Leslé 2012, Figure 2). See also Oura et al. (2013, Figure 3.1 and Box 3.1).
To study the case with correlated loan earnings, we will consider a larger set of states in Sect. 5.
Clearly, the option to go bankrupt regardless of which state materializes is not relevant when Ωn ≥ 0.
Assuming a take-it-or-leave-it structure for this bargaining game rules out that interbank market transactions foster aggregate credit supply by merely lowering the average cost of lending (c(l1)+c(l2))/(l1 + l2) in the banking sector.
For example, if the endowment Ω1 exceeds the first-best loan volume, bank 1 could lend its excess wealth to bank 2. To empirically assess the validity of this result, one would need to solve an endogeneity problem. Observing a bank which operates as interbank lender although it is not financially constrained does not need to be in contradiction with our results. The bank may be financially unconstrained because it lends to other banks. Therefore, the counterfactual question whether the bank would be financially constrained if it did not lend to other banks is to be answered.
Note that gains from trade exist for banks with other endowments, but the exposition would be more complex. We attend to a more general discussion in Sect. 4.5.
The existence of a functioning interbank market has qualitatively the same effect on bank 1’s credit supply if diversification is costly.
The bank may also prefer to operate in the risky mode holding portfolio A over the safe mode with portfolio B.
For details see “Appendix”.
See “Appendix”.
For the Euro area as a whole, the share is smaller but still substantial. Its pre- and post-crisis level was above 20% and between 18 and 21%, respectively.
According to calculations by Hale et al. (2019, Fn. 14).
In Figure 4, they report the maturity breakdown of the UK interbank market. According to Panel A, 20% of unsecured lending by UK banks is with a maturity between 3 and 12 months, and another 14% with a maturity of more than 1 year.
OTCs may become more important with the recent regulatory push toward centralized clearing (Bargigli et al. 2015).
All figures reported here are significant at the 1% level.
Between 2006 and 2009, borrowing from (only 34) foreign banks actually accounted for 27% of total bank assets (Iyer et al. 2014, Table 1).
References
Acharya, V.V.: A theory of systemic risk and design of prudential bank regulation. J. Financ. Stab. 5(3), 224–255 (2009)
Acharya, V.V., Skeie, D.: A model of liquidity hoarding and term premia in inter-bank markets. J. Monet. Econ. 58(5), 436–447 (2011)
Acharya, V.V., Yorulmazer, T.: Information contagion and bank herding. J. Money Credit Bank. 40(1), 215–231 (2008)
Affinito, M.: Do interbank customer relationships exist? And how did they function in the crisis? Learning from Italy. J. Bank. Finance 36(12), 3163–3184 (2012)
Afonso, G., Lagos, R.: Trade dynamics in the market for federal funds. Econometrica 83(1), 263–313 (2015)
Afonso, G., Kovner, A., Schoar, A.: Stressed, not frozen: the federal funds market in the financial crisis. J. Finance 66(4), 1109–1139 (2011)
Ahn, J.H., Breton, R.: Securitization, competition and monitoring. J. Bank. Finance 40, 195–210 (2014)
Allen, F., Gale, D.: Financial contagion. J. Polit. Econ. 108(1), 1–33 (2000)
Allen, F., Carletti, E., Marquez, R.: Deposits and bank capital structure. J. Financ. Econ. 118(3), 601–619 (2015)
Alves, I., Ferrari, S., Franchini, P., Heam, J.C., Jurca, P., Langfield, S., Laviola, S., Liedorp, F., Sánchez, A., Tavolaro, S., Vuillemey, G.: The structure and resilience of the European interbank market. ESRB Occasional Paper Series 03, European Systemic Risk Board (2013)
Angelini, P., Nobili, A., Picillo, C.: The interbank market after August 2007: what has changed, and why? J. Money Credit Bank. 43(5), 923–958 (2011)
Ayadi, R., De Groen, W.P., Sassi, I., Mathlouthi, W., Rey, H., Aubry, O.: Banking Business Models Monitor 2015 Europe. Discussion Paper 8764, International Research Centre on Cooperative Finance (2016)
Bargigli, L., di Iasio, G., Infante, L., Lillo, F., Pierobon, F.: The multiplex structure of interbank networks. Quant. Finance 15(4), 673–691 (2015)
Behn, M., Haselmann, R., Wachtel, P.: Procyclical capital regulation and lending. J. Finance 71(2), 919–956 (2016)
Billett, M.T., Garfinkel, J.A., O’Neal, E.S.: The cost of market versus regulatory discipline in banking. J. Financ. Econ. 48(3), 333–358 (1998)
Bluhm, M., Georg, C.P., Krahnen, J.P.: Interbank intermediation. Discussion Paper 16/2016, Deutsche Bundesbank (2016)
Bräuning, F., Fecht, F.: Relationship lending in the interbank market and the price of liquidity. Rev. Finance 21(1), 33–75 (2017)
Bucher, M., Dietrich, D., Hauck, A.: Business cycles, bank credit and crises. Econ. Lett. 120(2), 229–231 (2013)
Bucher, M., Hauck, A., Neyer, U.: Interbank market friction-induced holdings of precautionary liquidity: implications for bank loan supply and monetary policy implementation. Econ. Theory (2019). https://doi.org/10.1007/s00199-019-01207-6
Calomiris, C.W., Kahn, C.M.: The role of demandable debt in structuring optimal banking arrangements. Am. Econ. Rev. 81(3), 497–513 (1991)
Castiglionesi, F., Feriozzi, F., Lóránth, G., Pelizzon, L.: Liquidity coinsurance and bank capital. J. Money Credit Bank. 46(2–3), 409–443 (2014)
Craig, B., von Peter, G.: Interbank tiering and money center banks. J. Financ. Intermed. 23(3), 322–347 (2014)
Craig, B.R., Fecht, F., Tümer-Alkan, G.: The role of interbank relationships and liquidity needs. J. Bank. Finance 53, 99–111 (2015)
Diamond, D.W.: Financial intermediation and delegated monitoring. Rev. Econ. Stud. 51(3), 393–414 (1984)
Diamond, D.W., Rajan, R.G.: Fear of fire sales, illiquidity seeking, and credit freezes. Q. J. Econ. 126(2), 557–591 (2011)
Dietrich, D., Vollmer, U.: International banking and liquidity allocation. J. Financ. Serv. Res. 37(1), 45–69 (2010)
European Central Bank: Money Market Survey. European Central Bank, Frankfurt a.M (2015)
European Central Bank: Financial Integration in Europe. European Central Bank, Frankfurt a.M (2018)
Freixas, X., Holthausen, C.: Interbank market integration under asymmetric information. Rev. Financ. Stud. 18(2), 459–490 (2005)
Freixas, X., Martin, A., Skeie, D.: Bank liquidity, interbank markets, and monetary policy. Rev. Financ. Stud. 24(8), 2656–2692 (2011)
Furfine, C.H.: Banks as monitors of other banks: evidence from the overnight federal funds market. J. Bus. 74(1), 33–57 (2001)
Gale, D., Hellwig, M.: Incentive-compatible debt contracts: the one-period problem. Rev. Econ. Stud. 52(4), 647–663 (1985)
García-Herrero, A., Vázquez, F.: International diversification gains and home bias in banking. J. Bank. Finance 37(7), 2560–2571 (2013)
Gehrig, T.: Screening, cross-border banking, and the allocation of credit. Res. Econ. 52(4), 387–407 (1998)
Gertler, M., Kiyotaki, N.: Financial intermediation and credit policy in business cycle analysis. In: Friedman, B.M., Woodford, M. (eds.) Handbook of Monetary Economics, vol. 3, pp. 547–599. Elsevier, Amsterdam (2010)
Hakenes, H., Schnabel, I.: Credit risk transfer and bank competition. J. Financ. Intermed. 19(3), 308–332 (2010)
Hale, G., Kapan, T., Minoiu, C.: Shock transmission through cross-border bank lending: credit and real effects. Finance and Economics Discussion Series (FEDS) 2019-052, Board of Governors of the Federal Reserve System (2019)
Huang, R., Ratnovski, L.: The dark side of bank wholesale funding. J. Financ. Intermed. 20(2), 248–263 (2011)
Iyer, R., Peydró, J.L., da Rocha-Lopes, S., Schoar, A.: Interbank liquidity crunch and the firm credit crunch: evidence from the 2007–2009 crisis. Rev. Financ. Stud. 27(1), 347–372 (2014)
King, T.B.: Discipline and liquidity in the interbank market. J. Money Credit Bank. 40(2–3), 295–317 (2008)
Krasa, S., Villamil, A.P.: Optimal multilateral contracts. Econ. Theory 4(2), 167–187 (1994). https://doi.org/10.1007/BF01221199
Krasa, S., Villamil, A.P.: Optimal contracts when enforcement is a decision variable. Econometrica 68(1), 119–134 (2000)
Krasa, S., Sharma, T., Villamil, A.P.: Debt contracts and cooperative improvements. J. Math. Econ. 41(7), 857–874 (2005)
Krasa, S., Sharma, T., Villamil, A.P.: Bankruptcy and firm finance. Econ. Theory 36(2), 239–266 (2008). https://doi.org/10.1007/s00199-007-0267-y
Langfield, S., Liu, Z., Ota, T.: Mapping the UK interbank system. J. Bank. Finance 45(Supplement C), 288–303 (2014)
Le Leslé, V.: Bank Debt in Europe: “Are Funding Models Broken?”. IMF Working Papers 12/299, International Monetary Fund (2012)
Martin, C., Puri, M., Ufier, A.: Deposit inflows and outflows in failing banks: the role of deposit insurance. Working Paper 24589, National Bureau of Economic Research (2018)
Martín-Oliver, A., Ruano, S., Salas-Fumás, V.: The fall of Spanish cajas: lessons of ownership and governance for banks. J. Financ. Stab. 33, 244–260 (2017)
Näther, M.: The effect of the central bank’s standing facilities on interbank lending and bank liquidity holding. Econ. Theory (2018). https://doi.org/10.1007/s00199-018-1134-8
Neal, L., García-Iglesias, M.C.: The economy of Spain in the euro-zone before and after the crisis of 2008. Q. Rev. Econ. Finance 53, 336–344 (2013)
Oura, H., González-Hermosillo, B., Chan-Lau, J.A., Gudmundsson, T., Valckx, N.: Changes in Bank Funding Patterns and Financial Stability Risks. IMF Global Financial Stability Report Chapter 3, International Monetary Fund (2013)
Roengpitya, R., Tarashev, N., Tsatsaronis, K., Villegas, A.: Bank business models: popularity and performance. BIS Working Papers 682, Bank for International Settlement (2017)
Stiglitz, J.E., Weiss, A.: Credit rationing in markets with imperfect information. Am. Econ. Rev. 71(3), 393–410 (1981)
Temizsoy, A., Iori, G., Montes-Rojas, G.: The role of bank relationships in the interbank market. J. Econ. Dyn. Control 59(Supplement C), 118–141 (2015)
Tsomocos, D.P., Bhattacharya, S., Goodhart, C.A.E., Sunirand, P.: Banks, relative performance, and sequential contagion. Econ. Theory 32(2), 381–398 (2007). https://doi.org/10.1007/s00199-006-0190-7
Upper, C., Worms, A.: Estimating bilateral exposures in the German interbank market: is there a danger of contagion? Eur. Econ. Rev. 48(4), 827–849 (2004)
Vollmer, U., Wiese, H.: Explaining breakdowns in interbank lending: a bilateral bargaining model. Finance Res. Lett. 11(3), 247–253 (2014)
Acknowledgements
We thank two referees, Mich Tvede and seminar participants at Deutsche Bundesbank, University of Vienna and University of York, for their thoughts, questions and suggestions. Financial support from Leverhulme Trust is gratefully acknowledged (Grant No. SG122193).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Proof of Proposition 1
Combining (3.8) with (3.7) and either (4.1) and (4.2) or (4.3), we obtain a bank’s expected profits in the safe mode, \({\Uppi }_n^{{{\mathscr {S}}}}\), and in the risky mode \({\Uppi }_n^{{{\mathscr {R}}}} \), respectively. In reduced form, they read
Since \(\tfrac{\partial {\Uppi }_n^{{{\mathscr {S}}}} \left( l_n, {\hat{a}}_n \right) }{\partial l_n} \le 0\) only if ln ≥ lnfb, \(\tfrac{\partial {\Uppi }_n^{{{\mathscr {R}}}} \left( l_n, 0\right) }{\partial l_n} \le 0\) only if \(l_n \ge l_n^{{{\mathscr {R}}}}\), and \({\Uppi }_n^{{{\mathscr {S}}}} \left( l_n, {\hat{a}}_n \right) \ge {\Uppi }_n^{{{\mathscr {R}}}} \left( l_n, 0\right) \) for all \(l_n \le \tfrac{ \alpha {\Upomega }_n }{ \alpha - \lambda _{n,L} }\), expected profits Πn of bank n can be written as a piecewise function
so that its optimization problem reads
The solution to this problem satisfies
Moreover, for ln > lnmax, a bank sets an = 0 because then \(\tfrac{\partial {\Uppi }_n \left( l_n, a_n \right) }{\partial a_n} < 0\). For ln < Ωn, a bank sets an = Ωn − ln > 0. And for ln ∈ [Ωn, lnmax], a bank is indifferent with regard to holding the safe asset. Finally, since \(\tfrac{\partial {\hat{{\Uppi }}}_n^{{{\mathscr {S}}}} }{\partial {\Upomega }_n} \ge \alpha = \tfrac{\partial {\hat{{\Uppi }}}_n^{{{\mathscr {R}}}} }{\partial {\Upomega }_n}\), we obtain Proposition 1.
Proof of Proposition 2
We start with a characterization of the banks’ optimization problems. Bank 2’s expected profits in reduced form depend on exogenous parameters and on (b, β).
-
If \({\Upomega }_{2}+b \le l_{2}^{{\mathscr {R}}}\), expected profits \({\Uppi }_{2}^{{{\mathscr {R}}}}\left( l_{2},a_{2}\right) \) are obtained from (3.8) taking into account (3.1) and (3.7), which gives
$$\begin{aligned} \varPi _{2}^{{{\mathscr {R}}}}\left( l_{2},a_{2}\right) =\left( p_{1}\lambda _{2,H}-\alpha \right) l_{2}-\left( 1-p_{1}\right) \alpha a_{2}+\alpha \varOmega _{2}+\left( \alpha -p_{1}\beta \right) b-c\left( l_{2}\right) , \end{aligned}$$(B.1)for which the optimization problem is
$$\begin{aligned}&\max _{l_2,a_2} \quad \left( p_{1}\lambda _{2,H}-\alpha \right) l_{2}-\left( 1-p_{1}\right) \alpha a_{2}+\alpha \varOmega _{2}+\left( \alpha -p_{1}\beta \right) b-c\left( l_{2}\right) . \nonumber \\&\quad \mathrm{s.t.} \nonumber \\&\quad l_{2}\ge 0, \nonumber \\&\quad a_{2}\ge \max \left\{ 0,\varOmega _{2} + b -l_{2}\right\} . \end{aligned}$$(B.2) -
If \({\Upomega }_{2}+b >l_{2}^{{\mathscr {R}}}\), we have ϕ2′<p2λ2, 2, i. e. the bank will not raise any additional funds from investors, i. e. d2 = 0. The budget constraint (3.1) implies that the only decision left is about allocating Ω2 + b across l2 and a2, and expected profits are
$$\begin{aligned} \varPi _{2}^{{{\mathscr {R}}}}\left( l_{2},a_2\right) =p_{1}\left( \lambda _{2,H} l_{2} + \alpha a_2 -\beta b\right) -c\left( l_2 \right) \end{aligned}$$(B.3)and the optimization problem is
$$\begin{aligned}&\max _{l_2, a_2} \quad p_{1}\left( \lambda _{2,H} l_{2} + \alpha a_2 -\beta b\right) -c\left( l_2 \right) \nonumber \\&\quad \text {s.t.} \nonumber \\&\quad l_{2} + a_2 =\varOmega _2 + b. \nonumber \\&\quad l_{2}\ge 0, \nonumber \\&\quad a_{2}\ge 0 . \end{aligned}$$(B.4)Let L2 be defined by ϕ2′(L2) = p2(λ2−α). Then, the bank sets a2 = Ω2 + b − L2 if Ω2 + b > L2 and a2 = 0 if \(l_{2}^{{\mathscr {R}}}< {\Upomega }_{2}+b \le L_{2}\).
Let \(\left( \breve{l}_{2},\breve{a}_{2}\right) \) denote the solution to problems (B.2) and (B.4) and note that (i) if \({\Upomega }_{2}+b \notin \left( l_{2}^{{\mathscr {R}}}, L_{2} \right] \) then \(\tfrac{\mathrm {d} \breve{l}_2}{\mathrm {d} b} = 0\) and else \(\tfrac{\mathrm {d} \breve{l}_2}{\mathrm {d} b} = 1\), (ii) if Ω2 + b > L2 then \(\tfrac{\mathrm {d} \breve{a}_2}{\mathrm {d} b} = 1\) and else \(\tfrac{\mathrm {d} \breve{a}_2}{\mathrm {d} b} = 0\), and (iii) neither \(\breve{l}_{2}\) nor \(\breve{a}_{2}\) depend on β.
As regards bank 1, expected profits are again derived from (3.8) taking into account (3.1) and (3.7)
so that its optimization problem is
Constraint (B.11) is to ensure that bank 1 operates within its financial means and (B.12) that bank 2 is not better off by rejecting an interbank loan.
The proof is for each of the two cases made in the proposition separately.
Case 1\(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1 \le \tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \).
-
(a)
Equation (4.11) implies that budget constraint (3.1) is met for bank 2 if \(l_2=l_2^{{{\mathscr {R}}}}\). As for bank 1, assume that it chooses the highest possible volume of interbank loans according to (4.11), i.e., \(b^{*}=l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \), for which (4.9) becomes
$$\begin{aligned} l_1 \le \tfrac{\alpha \varOmega _1 + \left( \tfrac{\alpha }{p_1} -\alpha \right) \left( l_2^{{{\mathscr {R}}}} - \varOmega _2 \right) }{(\alpha -\lambda _{1,L})}. \end{aligned}$$(B.13)Rearranging terms shows that RHS is at least l1fb. For \(b^{*}=\tfrac{p_1}{p_2}\left( \tfrac{\alpha - \lambda _{1,L}}{\alpha } l_1^{\text {fb}} - {\Upomega }_1 \right) \), RHS is equal to l1fb. Hence, for any b* satisfying (4.11) bank 1 is not financially constrained if l1 = l1fb. Therefore, the solution (4.11) to (4.12) is feasible.
-
(b)
With interbank loans according to (4.10) and (4.11), bank 2 can raise the same amount of funds for the same total funding costs as in the absence of interbank trade. Choosing the same portfolio thus generates the same expected profits. Moreover, as any additional funds come at the same marginal costs, deviating from \(l_2^{{{\mathscr {R}}}}\) does not increase profits.
-
(c)
Bank 1 is not better off by asking for any \(\beta \ne \tfrac{\alpha }{p_1}\). If \(\beta >\tfrac{\alpha }{p_1}\), bank 2 would reject the contract. If \(\beta < \tfrac{\alpha }{p_1}\), the expected returns on interbank loans would not cover their financing costs. Moreover, the financial constraint of bank 1 would be tighter unless bank 1 increases b. However, for any \(b \in \left( \tfrac{p_1}{p_2}\left( \tfrac{\alpha - \lambda _{1,L}}{\alpha } l_1^{\text {fb}} - {\Upomega }_1 \right) , l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \) bank 1 could marginally increase b anyway if needed even without incurring the loss on interbank loans. Hence, \(\beta ^{*} = \tfrac{\alpha }{p_1}\).
-
(d)
The (b*, β*) implies for bank 1 that internal funds and external funds raised by borrowing against claims on bank 2 can be as high as \(\omega _1 :={\Upomega }_1 + \left( \tfrac{1}{p_1} -1\right) \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \) which is independent from l1. Hence, replacing Ω1 with ω1 and adapting the arguments made in Proposition 1 imply that bank 1, which at the margin would no longer be financially constrained, cannot be better off by deviating from l1fb. Since l1fb is optimal regardless of the degree of slack in (4.9), the bank is indifferent between volumes of interbank loans as long as l1fb is feasible.
To sum up, (a) and (b) show that the solution (4.10) to (4.12) is feasible, while (c) and (d) prove that bank 1 cannot be made (strictly) better off by choosing any other arrangement given that bank 2 is indifferent.
Case 2\(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1 >\tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \). For the time being, assume that l1* and l2*—as defined by (4.15) and (4.16)—are optimal, implying \(b\ge l_2^{{{\mathscr {R}}}}-{\Upomega }_2\).
-
(a)
Equation (4.14) directly implies that the budget constraint of bank 2 is met if d2 = 0. Furthermore, (4.14) and (4.16) imply that the budget constraint of bank 1 is met.
-
(b)
With (4.13) and (4.14), bank 2 gets more funds than it would raise in the absence of interbank trade. The associated increase in loans \({\tilde{l}}_2 - l_2^{{{\mathscr {R}}}}>0\) will cause expected profits being lower by \(( ( p_1 \lambda _{2,H} - \alpha ) l_2^{{\mathscr {R}}} - c(l^{{\mathscr {R}}}) ) - ( (p_1 \lambda _{2,H} - \alpha ) {\tilde{l}}_2 - c({\tilde{l}}_2 ))\). A per unit reduction in the cost of funds of
$$\begin{aligned} \tfrac{\left( \left( p_1 \lambda _{2,H} - \alpha \right) l_2^{{\mathscr {R}}} - c\left( l^{{\mathscr {R}}}\right) \right) -\left( \left( p_1 \lambda _{2,H} - \alpha \right) {\tilde{l}}_2 - c({\tilde{l}}_2 ) \right) }{p_1 ({\tilde{l}}_2 - \varOmega _2)} \end{aligned}$$compensates bank 2 for this drop in profits. Hence, expected profits are the same for bank 2 as for b = 0 and \(l=l_2^{{{\mathscr {R}}}}\). Moreover, any additional funds come at the same marginal costs as for b = 0. Hence, granting more loans than \({\tilde{l}}_2 \) by raising additional funds from investors is not increasing profits. This follows from \({\tilde{l}}_2 >l_2^{{{\mathscr {R}}}}\) and the FOC stated in Proposition 1. Similarly, granting fewer loans and investing in the safe asset does not increase profits.
-
(c)
For an arrangement to be optimal, it has to satisfy the FOC (4.16). The proof is by contradiction. Assume it would be optimal to increase/decrease loans l1 by some ε. Given that bank 2 needs to be compensated according to (4.14), it follows from the first equation in (4.16) that bank 2 would change its loans by \(\tfrac{\alpha -\lambda _{1,L}}{\tfrac{\alpha p_{2}}{p_{1}}-\tfrac{1}{p_{1}}\left( \left( p_{1}\lambda _{2,H}-\alpha \right) -c^{\prime }\left( {\tilde{l}}_{2}\right) \right) }\varepsilon \). The associated change in compensation then is
$$\begin{aligned} \left( p_2 \lambda _{2,L} - \phi ^\prime _2 \left( {\tilde{l}}_2 \right) \right) \tfrac{\alpha -\lambda _{1,L}}{\tfrac{\alpha p_{2}}{p_{1}}-\tfrac{1}{p_{1}}\left( \left( p_{1}\lambda _{2,H}-\alpha \right) -c^{\prime }\left( {\tilde{l}}_{2}\right) \right) }\varepsilon \end{aligned}$$while the change in profits for bank 1 due to changes in l1 would be \(\phi \prime _1 ({\tilde{l}}_1)\varepsilon \). Hence, if (4.16) holds, such changes do not increase expected profits. Note that (4.16) implies \(b>l_2^{{{\mathscr {R}}}}-{\Upomega }_2\) because any marginal changes in l1 would otherwise only affect the financial constraint of bank 1 without changing the costs of diversification, for the compensation payable to bank 2 cannot be further lowered (it is already nil).
To sum up, (a) and (b) show that the solution (4.13) to (4.16) is feasible, while (c) shows that it is also maximizing expected profits for bank 1.
Proof of Lemma 1
If \(\tfrac{ \alpha - \lambda _{1,L} }{ \alpha } l_1^{\text {fb}} - {\Upomega }_1 >\tfrac{p_2}{p_1} \left( l_2^{{{\mathscr {R}}}} - {\Upomega }_2 \right) \), then K2(l1⋆) > 0. Moreover, condition (4.16) then implies p2α − (p2λ2, L−ϕ2′(l2⋆)) > 0 and thus K′2(l1⋆) > 0. Write Eqs. (4.17) and (4.18) as
According to the general implicit function theorem, we obtain
with  , i.e.,
, i.e.,
and further by Young’s Theorem
Probability distribution with imperfect correlation
From  ,
,  and p1 = 1 − p2, it follows that
and p1 = 1 − p2, it follows that
while p1 = 1 − p2 and (5.1) imply
Combining (D.1) with (D.2) then results in (5.2).
Proof of Lemma 2
If ℚ2 = ∅, interbank loans would be safe and bank 2 would accept any b > 0 only if β ≤ α. Hence, from bank 1’s perspective, they would be weakly dominated by the safe asset. For interbank loans to offer any potential benefits to bank 1, it must be that β > α, which in turn requires {LL, HL}⊂ℚ2. However, as repayments are the same in states LH and HH, it follows {LH, HH}∉ℚ2 because otherwise bank 2 would never repay any interbank loan. Hence, ℚ2 = {LL, HL}.
Bank 1’s loan earnings are low in states LH and LL. In state LH, bank 1 has to survive to be able to collect interbank loans. Else, since it would not survive in state LL either and not gain anything in state HL, interbank loans would be at best useless. Hence, {LH}∉ℚ1. If {LH}∉ℚ1, then ℚ2 = {HL, LL} implies that bank 1’s financial constraint would be the same in the safe mode with b = 0. Hence, whether b > 0 or b = 0 would not matter. Therefore, {LL}⊂ℚ1. Finally, assumption (3.2) implies {HL}∉ℚ1, which leaves ℚ1 = {LL}.
Comparative statics
Write Eqs. (5.14) and (5.15) as
By the general implicit function theorem, we obtain
with
where Ξ = α(1 − p1)(1 − p1(1 + ρ)) − (1 − p1(1 − p1)(1 + ρ))((1 − p1)λ2, L − ϕ2′(l2)). The sign of ∂E1/∂l2 follows because if it would be positive in equilibrium it meant that bank 1 could ease its funding constraint and lower the compensation payable to bank 2 by making a smaller interbank loan such that bank 2 grants fewer loans.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dietrich, D., Hauck, A. Interbank borrowing and lending between financially constrained banks. Econ Theory 70, 347–385 (2020). https://doi.org/10.1007/s00199-019-01220-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-019-01220-9



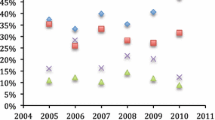
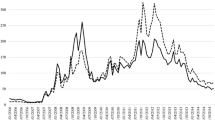
 and
and  and
and