Abstract
Non-recourse borrowing leaves no room for Ponzi schemes, as shown by Araujo et al. (Econometrica 70:1613–1638, 2002). This is not the case with recourse loans, for which, in the event of default and on top of the foreclosure of the collateral, the debtor’s estate can be seized or (in a way common in the GE literature) the debtor can suffer utility penalties. We focus on the latter and show that infinite horizon equilibrium with recourse exists in some interesting cases: (1) if utility penalties are low enough and the collateral does not yield utility (for example, when it is a productive asset or a security) or (2) for a nominal promise backed by real collateral (such as mortgages, whose payments are not tied to a commodity price index).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The modern general equilibrium literature on default evolved mainly from two seminal contributions, the Dubey et al. (2005) paper on utility penalties and the Geanakoplos and Zame (1997) work on non-recourse borrowing. In an infinite horizon setup, non-recourse loans have the appealing feature of being incompatible with Ponzi schemes, at least for time- and state-separable preferences, as shown by Araujo et al. (2002). Non-recourse is the rule for mortgages in thirteen states in the USA, but in all the other states and in many countries mortgages are treated as recourse loans. Other types of secured loans tend to be recourse: Collateralized borrowing for the purchase of equipment usually requires a default insurance, while in the case of credit for the purchase of securities default triggers personal bankruptcy.
Recourse means that the defaulter’s personal estate can be seized by the creditors, either entirely or in proportion to the outstanding debts that were not covered by the value of the collateral at the time the default occurred. There may be other types of default penalties, such as reputational effects, difficulties in applying for credit in the future or even criminal consequences, that we can also see as a form of recourse that ends up affecting the defaulter’s welfare. Utility penalties, introduced by Shubik and Wilson (1977) and more recently modeled by Dubey et al. (2005) in a GE framework, attempt to capture in utility terms the impact of all forms of recourse.
In the presence of utility penalties, collateral may not avoid a Ponzi game. In fact, the penalties may induce agents to repay above the minimum of the promised payment and the collateral value. Then, non-arbitrage cannot rule out that, at the borrowing date, the secured loan would have a negative haircut (the collateral cost would be lower than the loan). The resulting cash flow in an open end setting would give rise to a Ponzi scheme. This is actually what happens when the promise is traded in the examples by Páscoa and Seghir (2009) for utility penalties that make the maximal default prohibitive. However, the argument that also ruled out no-trade outcomes in Páscoa and Seghir (2009) was not correct and, as was pointed out by Martins-da-Rocha and Vailakis (2012a), a no-trade equilibrium could be found by setting the delivery rate at the minimal level, even though such expectation about the delivery rate is not consistent with the harsh penalty. Once the equilibrium is refined, along the lines of the refinement in Dubey et al. (2005), nonexistence of equilibrium prevails.
Our first contribution is to observe that the absence of pecuniary Ponzi schemes is not enough for existence of equilibrium. The net gain that the borrower can have at the borrowing moment consists of the loan net of collateral costs plus the utility from consumption of the collateral. Such direct utility effect may allow for an infinite horizon improvement strategy even when collateral costs outweigh the loan (as our Example 1 illustrates). Under non-recourse, the whole current benefit had to be non-positive, by non-arbitrage, as at the immediate next nodes new collateral values net of effective repayment were always nonnegative.
In our second contribution, we find an upper bound on utility penalty coefficients that make the collateral cost never fall below the promise price and existence of equilibrium is, therefore, guaranteed, under these moderate penalties, provided that the collateral does not give any utility (say it is a durable commodity with no utility yields, as in Fostel and Geanakoplos (2008), a productive asset or a share in it, as in Kubler and Schmedders (2003), or any real security in positive net supply that cannot be short-sold, as in Fostel and Geanakoplos 2015). Actually, the recourse feature that a utility penalty tries to capture is often observed in collateralized borrowing for the purchase of equipment or securities.
Our third contribution allows for harsher penalties and for utility yields from the consumption of the collateral. Moderate penalties are a strong condition as it makes agents give maximal default (as in the model where utility penalties were absent). However, equilibrium is compatible with partial default or no default, as illustrated in Example 2, where the sum, across next nodes, of the marginal penalty effects is dominated by the sum of the marginal income effects. The problem is that this dominance depends on relative prices and there might be no room to choose relative spot prices if these are already pinned down by market clearing.
There is, nevertheless, an important case where there are degrees of freedom in market clearing prices. It is the case where the promise is nominal, but the collateral is a real asset. This case is relevant for mortgages, which should be regarded as loans whose promised repayments are not adjusted by commodity price indices, and also for credit for the purchase of shares. In finite-horizon economies, there is indeterminacy in equilibrium with respect to the inflation rates. Now, high inflation rates across all the next nodes devalue the promised payments but not the collateral and, therefore, reduce the real value of default on which the penalty is applied. Our Example 3 illustrates such equilibria with nominal promises.
Example 2 and our two existence results do not collide with the result by Ferreira and Torres-Martinez (2010) on impossibility of recourse. Their result depends on collateral costs being lower than the deflated value of recourse (the repayment in excess of the minimal one) at the next nodes. It is interesting to note that such a condition had to be introduced to make recourse impossible. In Example 2, collateral coefficients do not satisfy such inequality and the haircut is zero (rather than negative as in Ferreira and Torres-Martinez 2010), which does not allow for a Ponzi scheme (or generalized version of it, since the collateral does not yield utility in this example). In Theorem 2, borrowers’ repayment is always the minimal one, while in Theorem 3 it might not be, but the promise is nominal and the result by Ferreira and Torres-Martinez (2010) does not apply.
One may wonder how do our existence results stand in the face of the possibility that trivial no-trade equilibria might be found. Dubey et al. (2005) showed that for unsecured promises subject to utility penalties on default, a trivial equilibrium always exists by setting promises prices, delivery rates and financial trades equal to zero. Martins-da-Rocha and Vailakis (2012a) found a no-trade incomplete markets equilibrium in an example with secured promises by setting the delivery rate at the minimal level. When the horizon is finite or markets are complete, such no-trade equilibria are trivially found but in infinite horizon incomplete markets that is not always the case, as we illustrate in a companion paper (Páscoa and Seghir 2019). There we also propose a refinement of equilibrium, which is milder than the straightforward extension to secured loans of the one in Dubey et al. (2005). Even so, the no-trade outcome in Martins-da-Rocha and Vailakis (2012a) still fails to meet this refinement but there exist refined versions for the equilibria we found in the main results of the current paper.
The next section presents the model. Section 3 addresses individual optimality. Section 4 presents the existence results. Proofs are presented in the Appendix.
2 The model
Consumers trade collateralized promises over a countably infinite tree D with finitely many branches at each node. Let \({\mathbb {N}}_0=\{0, 1, \ldots \}\) be the set of dates and \(\xi _0\) be the root of the tree D. Given a node \(\xi \in D\), let \(t(\xi ) \in {\mathbb {N}}_0\) be the date of node \(\xi \). We denote by \(D(\xi )\) the sub-tree that starts at \(\xi \). We write \(\xi ^{\prime } > \xi \) if \(\xi ^{\prime } \in D(\xi )\) and \(\xi ^{\prime } \ne \xi \). The immediate successors of node \(\xi \) constitute the set \(\xi ^+ \equiv \{\eta > \xi : t(\eta )=t(\xi )+1 \}\) while its immediate predecessor is denoted by \(\xi ^-\). We will also use the notation \(D_T \equiv \{\xi \in D: t(\xi )=T \}\) and \(D^T \equiv \bigcup \nolimits _{t=0}^{T} D_t\). For any real sequence \((a_n)\), the notation \(a \ggg 0\) (or \(a \lll 0\)) stands for \((a_n)\) being a positive (negative, respectively) sequence uniformly bounded away from zero.
At each node \(\xi \) a finite number G of commodities is traded together with a finite set J of one-period promises. Let us start by assuming that promises have real returns. This assumption will be modified later, in Sect. 4.3.
Let \(A_{j\xi } \in {\mathbb {R}}^G\) be the vector of promised real returns, per unit of the promise, at node \(\xi \).
Sales of promises are secured by collateral. For each promise j, we introduce collateral requirements at each node \(\xi \) by specifying a vector \(C^j_{\xi } \in {\mathbb {R}}^G\) of quantities of the commodities that have to be pledged when selling one unit of promise j.
Actually, we would like to allow collateral to be not necessarily a durable good, but possibly also a productive asset or a security in positive net supply that pays real returns and cannot be short sold. This can be accommodated by treating securities as if they were commodities that do not yield utility but transform into others at the following nodes.
Formally, we define at each node \(\xi \) a transformation matrix\(Y_{\xi }\), of type G.G, indicating how commodities of the previous node convert into commodities of the node \(\xi \).
If commodities are not just durable goods, we may have a non-diagonal transformation matrix. If g is a durable good, the only non-null element in column \((Y_{\xi })^g\) is \((Y_{\xi })_{gg}\), equal to the depreciation factor. If g is a security, \((Y_{\xi })_{gg}=1\) and, its nonnegative dividends are given, for \(g^\prime \ne g\), by \((Y_{\xi })_{g^{\prime } g}\). We allow also for productive assets [as in Kubler and Schmedders (2003)] which can be treated formally as commodities whose non-null columns in \(Y_\xi \) matrices represent their productive returns on other commodities.
Formally, the assumption on promises returns and collateral is the following.
-
Assumption [R].
-
(i)
Promised returns are given by \(A_{j\xi } \in {\mathbb {R}}^G_+\), \(\forall j \in J, \xi > \xi _0\).
-
(ii)
At each node \(\xi \), collateral must be posted in at least one \(g \in G\) for which the column \(Y_{\eta }^g\) is non-null at every node \(\eta \in \xi ^+\).
-
(i)
There is a finite set I of consumers whose endowments and preferences verify the following assumptions.
-
Assumption [E]. Endowments of consumer i of commodity g at node \(\xi \), denoted by \(\omega ^i_{g\xi }\), satisfy
-
(i)
\( \exists W \in {{\mathbb {R}}}_{++}:\)\(\forall i \in I, \ \forall \xi \in D, \ \sum \nolimits _{g \in G} {\omega }^{i}_{g\xi } \le W.\)
-
(ii)
\(\omega _{\xi _0}\gg 0\) and, for \(\xi > \xi _0\) and any g, \(\omega _{g\xi }>0\) whenever the \(g-\)th row of \(Y_{\xi }\) is null.
-
(i)
Let \(Y_{\xi _0, \xi _n}=Y(\xi _n) Y(\xi _{n-1}) \ldots Y(\xi _1)\) for \(\xi _{k+1} \in {\xi _k}^+\). The aggregate physical resources available at node \(\xi \) are given by \(\Omega _\xi =\sum \nolimits _{i} W^i_\xi ,\) where \(W^i_\xi =\sum \nolimits _{\eta \in \{\xi _0, \ldots , \xi ^-, \xi \}} \, Y_{\eta ,\xi } \ \omega ^i_{\eta }.\)
We say that good g is perishable at node \(\xi \) if the g-th column of \(Y_{\eta }\) is null for any \(\eta \in \xi ^+\).
-
Assumption [U].\(\forall i \in I\), preferences over consumption are described by a time and state separable utility \(U^i\) with instantaneous utility \(v^i_\xi : {\mathbb {R}}^G_+ \longrightarrow {\mathbb {R}}_+\) such that
-
(i)
\(v^i_\xi \) is monotone and concave,
-
(ii)
\(v^i_\xi \) is differentiable on \({\mathbb {R}}^G_{++}\),
-
(iii)
\(\forall \alpha \in {{\mathbb {R}}}^{G}_{+}\) we have \(\sum \nolimits _{\xi \in D}v^i_{\xi }(\alpha )< \infty \) and
-
(iv)
\(\sum \nolimits _{\xi \in D} v^i_\xi (\Omega _\xi ) < \infty \).Footnote 1
-
(i)
Consumers take as given prices p for goods, prices q for promises and delivery rates K on the promises. As in Dubey et al. (2005), these delivery rates are impersonal expectations about the ex post repayment of the promise. In equilibrium, \(1-K_{j\xi }\) is the default rate on promise j in node \(\xi \) by the aggregate sellers of that promise [as will be required in item (v) of Definition 1].
A choice variable is a nonnegative plan \((x, \theta , \varphi , \psi )\) consisting of purchases of goods not for collateral purposes, promises purchases, promises sales and defaults, respectively. We denote \({\tilde{x}}^i_{\xi }=x^i_{\xi }+C_{\xi }{\varphi }^{i}_{\xi }\). Budget constraints at the initial node or at subsequent nodes \(\xi \in D {\setminus } \{\xi _0 \},\) are given, respectively, by:
To shorten the notations, we define \(M_{j\xi }=\min \{p_{\xi } A_{j\xi }, p_{\xi } Y_{\xi } C^j_{\xi ^-} \},\) for each node \(\xi \) and for each promise \(j \in J_{\xi ^-}.\) The minimal repayment constraint requires consumers to repay at least \(M_{j\xi }\varphi ^i_{j\xi ^-}\), that is,
The right-hand side of inequality (3) is the maximal default and the one that would be given under non-recourse. Utility penalties may discourage consumers from defaulting that maximal value.
Utility penalties are assumed to be linear on default. The marginal penalty on nominal default in promise j is specified at each node \(\xi \) by \(\lambda ^i_{j\xi }\). The marginal penalty on real default in promise j at node \(\xi \) is given by \({\tilde{\lambda }}^i_{j\xi }=\frac{\lambda ^i_{j\xi }}{p_{\xi } \, e_{\xi }},\) where \(e_{\xi } \in {\mathbb {R}}^G_{++}\) is a reference bundle. The entire payoff of consumer i is
where \([a]^+ =\max \limits \{a,0 \}\), for any  . Observe that, by the way the penalty is written, there is no need to impose a nonnegativity constraint on \(\psi \). Consumer i problem consists in maximizing \({\Pi }^i\) subject to (1), (2) and (3) and the following nonnegativity constraint
. Observe that, by the way the penalty is written, there is no need to impose a nonnegativity constraint on \(\psi \). Consumer i problem consists in maximizing \({\Pi }^i\) subject to (1), (2) and (3) and the following nonnegativity constraint
Definition 1
An equilibrium is a process \((p,q,K,(x^{i},\theta ^{i},\varphi ^{i},\psi ^{i})_{i \in I})\) such that \(p_{\xi } >0\)Footnote 2 at any node \(\xi \in D\) and verifying:
-
(i)
\(\forall i \in I\), \((x^{i},\theta ^{i},\varphi ^{i},\psi ^{i}) \in {{\,\mathrm{argmax}\,}}\ \Pi ^i(x,\theta , \varphi ,\psi ;p,q,K)\) subject to (1), (2), (3) and (4).
-
(ii)
\(\sum \nolimits _{i \in I} [x^{i}(\xi _0) +C(\xi _0) \varphi ^{i}(\xi _0)]=\sum \nolimits _{i \in I} {\omega }^{i}(\xi _0),\)
-
(iii)
\(\sum \nolimits _{i \in I} [x^{i}_{\xi } +C_{\xi } \varphi ^{i}_{\xi }] =\sum \nolimits _{i \in I} [{\omega }^{i}_{\xi }+ Y_{\xi } x^i({\xi }^{-})+Y_{\xi } C({\xi }^{-}) \varphi ^{i}({\xi }^{-})], \ \forall \xi \in D {\setminus } \{\xi _0\},\)
-
(iv)
\(\sum \nolimits _{i \in I} \theta ^{i}= \sum \nolimits _{i \in I} \varphi ^{i},\)
-
(v)
\(\forall j,\xi \in D {\setminus } \{\xi _0 \}, \ p_{\xi } A_{j\xi }(1-K^{j}_{\xi } ) \sum \nolimits _{i \in I} \theta ^{i}_{j}({\xi }^{-})=\sum \nolimits _{i \in I} \psi ^{i}_{j\xi }.\)
3 Infinite horizon individual optimality
3.1 Necessary conditions: Euler and transversality conditions
If agent i were optimizing over a finite horizon H, a plan \((\psi ^{iH}_{j\xi },\varphi ^{iH}_{j\xi },\theta ^{iH}_{j\xi },x^{iH}_{g\xi })\) that satisfies (1), (2) and (3) is optimal if and only if it satisfies the Kuhn–Tucker conditions for some nonnegative multipliers together with some \(d^i_{j\eta } \in [0,1]\) supergradient of the function \(\max \{0, \cdot \}\) evaluated at \(\psi ^i_{j\xi }\). These conditions induce the analogous Euler conditions for the infinite horizon problem, as we report next.
Definition 2
Given prices (p, q, K) and a plan \(Z^i:=(x^i,\theta ^i,\phi ^i,\psi ^i)\) that verifies at these prices the constraints (1), (2), (3) and (4), we say that\(Z^i\)satisfies the Euler conditions at (p, q, K) if there exist supergradients \((d^i_j)_{j\in J}\) of the function \(\max \{0, \cdot \}\) evaluated at \(\psi ^i_{j\xi }\) and a nonnegative process \((\gamma ^i, (\rho ^i_j,)_{j\in J})\) of multipliers such that, for any promise \(j \in J\) and any node \(\xi \), the following hold
-
(i)
$$\begin{aligned}&{\tilde{\lambda }}^i_{j\xi } d^i_{j\xi }+ \rho ^i_{j\xi }= \gamma ^i_{\xi } \end{aligned}$$(5)$$\begin{aligned}&\gamma ^i_{\xi } \big (p_{\xi }C_{j\xi }-q^j_{\xi } \big ) - {v^i_\xi }^{\prime } ({\tilde{x}}_{\xi }) C_{j\xi } \ge \sum \limits _{\eta \in \xi ^+} \Big [ \gamma ^i_{\eta } \Big (p_{\eta } Y_{\eta } C_{j\xi }- M_{j\eta } \Big ) \nonumber \\&\quad -\,{\tilde{\lambda }}^i_{j\eta } d^i_{j\eta } \Big (p_{\eta } A_{j\eta }- M_{j\eta } \Big ) \Big ] \end{aligned}$$(6)$$\begin{aligned}&\gamma ^i_{\xi } q^j_{\xi } \ge \sum \limits _{\eta \in \xi ^+} \gamma ^i_{\eta } K_{j\eta } p_{\eta } A_{j\eta } \end{aligned}$$(7)$$\begin{aligned}&\forall g \in G, \ \ \ \gamma ^i_{\xi } p_{g\xi } \ge v^{i\prime }_{\xi }({\tilde{x}}_{\xi },g) + \sum \limits _{\eta \in \xi ^+} \gamma ^i_{\eta } p_{\eta } {(Y_{\eta })}^g, \end{aligned}$$(8)
-
(ii)
equalities in (6), (7) or (8) hold when \(\varphi _{j\xi }>0, \ \theta _{j\xi }>0\) or \(x_{g\xi }>0,\) respectively.
-
(iii)
\(\rho ^i_{j\xi }[\psi ^i_{j\xi }-(p_{\xi } A_{j\xi }- M_{j\xi })\varphi ^i_{j\xi ^-}]=0\)
As in any infinite horizon problem, Euler conditions are not the only necessary conditions for infinite horizon optimality, a transversality condition must also hold. For the problem described in Sect. 2, we say that a plan \((x^i,\theta ^i,\varphi ^i,\psi ^i)\) satisfies the transversality condition at (p, q, K) when for \({v^i_{\xi }}^{\prime }\) evaluated at \({\tilde{x}}^i\) we have
Proposition
Under assumption [U], if the plan \((x^i,\theta ^i,\phi ^i,\psi ^i)\) is a maximizer of \(\Pi ^i(x,\theta , \varphi ,\psi )\) subject to (1), (2), (3) and (4) at prices (p, q, K), then this plan satisfies the Euler conditions and the transversality condition (9) at (p, q, K).
Remark 1
(a) Actually, under (5), (7) and (8), we have that (9) implies the following transversality condition specifically on borrowing,
(b) The converse, (10) implying (9), might not hold.Footnote 3 See Appendix 6.1.
Remark 2
Notice that any sequence of equilibria \((p^H,q^H,K^H,(x^{iH},\theta ^{iH},\varphi ^{iH},\psi ^{iH})_{i \in I})\) of economies with increasing finite horizon H has a cluster point \((p,q,K,(x^{i},\theta ^{i},\varphi ^{i},\psi ^{i})_{i \in I})\) such that \((x^{i},\theta ^{i},\varphi ^{i},\psi ^{i})\) satisfies Euler conditions and transversality condition (9) at (p, q, K), for each agent i (see Appendix 6.1 ).
3.2 A sufficient condition
However, Euler conditions together with the transversality condition (9) usually fail to be sufficient in infinite horizon optimization problems. This is the case for the optimization problem described in Sect. 2, as we will illustrate in the next section. A sufficient condition can be provided by adding to Euler conditions and transversality condition (9) the requirement that all budget-feasible plans should satisfy the converse to condition (10). More precisely,
Theorem 1
(Sufficient condition for optimality) Let \((x^i,\theta ^i,\varphi ^i,\psi ^i)\) be a plan for consumer i that satisfies at (p, q, K) constraints (1), (2), (3) and (4), together with Euler conditions and the transversality condition (9). Suppose that any promises sales trajectory \({\hat{\varphi }}\) which is part of a plan \(({\hat{x}}, {\hat{\theta }}, {\hat{\varphi }}, {\hat{\psi }})\) satisfying constraints (1), (2), (3) and (4) at (p, q, K) is such that for \({v^i_\xi }^{\prime }\) evaluated at \(x^i_{\xi }+C_{\xi }\varphi ^i_{\xi }\), we have
then, under assumptions [U], [E] and [R], the plan \((x^i,\theta ^i,\varphi ^i,\psi ^i)\) is optimal for i at (p, q, K).
To put it in another way, as the horizon truncation goes to infinity, equilibria of finite-horizon economies have a cluster point which is actually an equilibrium for the infinite-horizon economy if (11) holds for any budget-feasible plan.
In the next section, we give some intuition on the role of condition (11) and provide an example where it does not hold and a plan satisfying Euler and transversality fails to be individually optimal. It is also an example where a limit of finite horizon equilibria is not an infinite horizon equilibrium.
3.3 Generalized Ponzi schemes
In the absence of utility penalties, one period non-arbitrage implies that, at each node \(\xi \) and for each promise \(j_{\xi }\), collateral costs \(p_{\xi } C^{j_{\xi }}_{\xi }\) cannot be lower than the promise price \(q^{j_{\xi }}\); this inequality rules out Ponzi schemes and guarantees existence of equilibrium for the infinite horizon economy (see Araujo et al. 2002). When utility penalties are introduced, this inequality does not follow anymore from non-arbitrage and Ponzi schemes may reappear (see Páscoa and Seghir 2009). Furthermore, as we show now, even if penalties were low enough so that Ponzi schemes could be avoided (as will be the case in Sect. 4.1), there might not exist optimal solutions to the consumers’ problems.
Let us be more precise. A Ponzi scheme consists in increasing the sale position in promise j at node \(\xi \) and then accommodate this by increasing the sale position in another promise at the following nodes. As shown in Páscoa and Seghir (2009), Section 4.1, a Ponzi scheme exists when there is a node \(\tilde{\xi }\) such that at all nodes \(\xi \) in the sub-tree starting at \(\tilde{\xi }\) we have \(p_{\xi } C^{j_{\xi }} _{\xi }-q^{j_{\xi }} _{\xi }<0\), for some promise \(j_{\xi }\).
There may exist nevertheless an extended form of Ponzi schemes, compatible with \(p_{\xi } C^{j_{\xi }} _{\xi }-q^{j_{\xi }} _{\xi } \ge 0\) holding for any promise j and at any node \(\xi \). This consists in increasing the sale position in some promise \(j_{\xi }\) at nodes \(\xi \) where the marginal utility of collateral consumption outweighs the disutility resulting from the haircut \(p_{\xi } C^{j_{\xi }} _{\xi }-q^{j_{\xi }} _{\xi }\). For such change to be budget-feasible, that cost has to be compensated by the reduction in another expenditure, say a decrease in consumption of a perishable good. Now, the utility impact at nodes that immediately follow \(\xi \) cancels out the utility gain that occurred at \(\xi \), provided the consumer was already shorting the promise \(j_{\xi }\) (so that the Euler condition on shorting holds as an equality). For this reason, the increase in a sale position in a promise at a certain node does not need to be related to what was the increase in a previous node; it just needs to be affordable by how much the perishable consumption may be cut.
However, for any finite horizon truncation T of such process, we are left with the gain that may occur at date T. In the open end setting, letting \(T \rightarrow \infty \), there may be a persistent gain (analogous to the limiting gains occurring in Ponzi schemes done in the case of unsecured unbounded promises or in the case of secured recourse promises with a negative haircut).
By definition, the improvement consisting in a generalized Ponzi scheme is done in spite of the absence of finite horizon arbitrage opportunities (ruled out by Euler conditions) and, therefore, the set of nodes where short positions are being increased must be an infinite set. When a generalized Ponzi scheme can be done upon a cluster point of finite horizon equilibria, the latter is not an infinite horizon equilibrium. Let us give an example.
Example 1
Two consumers, a and b, trade one promise in a deterministic setting. The promise pays in a perishable good, fruit, and is secured by a productive asset, fruit tree. The former is the numeraire and also the reference good in the real default penalty. We assume that consumer a just cares about fruit, with linear preferences, while consumer b has quasi-linear preferences, linear in fruit and strictly concave in the shade provided by the fruit tree.
Formally, \(U^{a}(x)=\sum \nolimits _{t=1}^{\infty }\beta _a^tx_{1t}\) and \(U^{b}(x)=\sum \nolimits _{t=1}^{\infty }\beta _b^t(x_{1t}+n_t(x_{2t}))\), where \(n_t(.)\) is a strictly concave function to be specified below. The utility that agent b gets at time t from the shade is \(v_t(x_{2t})=\beta _b^tn_t(x_{2t})\). We have \(\gamma ^{a}_t=\beta ^t_a\) when \(x^{a}_{1t}>0\) and, for \(x^{b}_t>>0\), we have also \(\gamma ^{b}_t=\beta _b^t\). We construct finite horizon equilibria where both agents consume fruit at every date in spite of the linearity of preferences in fruit.
Fruit trees just last from one date to the next. Trees take one period to yield fruit, at a rate \(y<1\) that is constant over time, and then die. The transformation matrix Y has a first row given by [0y] and a null second row. At each date, new fruit trees are born in the orchards of each consumer, in the amounts \(\omega ^i_{2t}\). We assume that, for both consumers, the sequence\((\omega ^i_{2t})_t\)converges and\(\omega ^i_2 \ggg 0\). The aggregate supply of fruit at date t is given by \((\omega ^{a}_{2,t-1}+\omega ^{b}_{2,t-1})y\). Let \(p_t\) and \(q_t\) be the tree and the promise prices, at date t.
We assume \(\beta _a>\beta _b\) and that the default penalty coefficient of agent b is \(\lambda ^{b}_t=\beta ^t_b \sigma _t\) where \(\sigma _t\) is lower than one. Now, \(\tilde{\lambda }^{b}_t=\lambda ^{b}_t<\gamma ^{b}_t\), so that this agent would always give maximal default when selling the promise. We suppose each unit of a promise traded at date t has a fruit yield \(A_{t+1}=\eta yC_{t}\), with \(\eta >1\), so that the minimal delivery of the promise becomes \(M_{t+1}=yC_{t}\). Let \(K_{t+1}=yC_t/A_{t+1}=1/\eta \).
We set the promise price equal to the willingness to pay of agent 1, \(q_t=\beta _1yC_t\), and also to the reservation price of agent b as a seller of the promise, \(q_t=p_tC_t-n'_tC_t+\beta _b\sigma _{t+1}d_{t+1}(A_{t+1}-yC_t)\), where \(d_{t+1}\in [0,1]\) is a supergradient of the function \(\max \{0, \cdot \}\) evaluated at the default. If the promise is actually traded, agent a will buy it and agent b will sell it. The price of a tree must satisfy \(p_t \ge \beta _a y\) and \(p_t \ge \beta _b y+n'_t(x^{b}_{2t})\), holding with equalities if the collateral constraint (\(x^{i}_{2t} \ge C_t\varphi _t^{i}\)) has null shadow value for the respective agent. Let us look for an equilibrium where the promise is traded, and these shadow values are positive for agent a and null for agent b. This is compatible with \(x^{a}_2\) and \(\varphi ^{a}\) both zero, while agent b could be consuming trees in excess of the collateral requirement but actually will not, as we will see. Then, \(\beta _{a}y<p_t = \beta _b y+n'_t(x^{b}_{2t})\). This implies \(p_tC_t-q_t=[n'_t-(\beta _a-\beta _b)y]C_t>0\).
Market clearing requires \(\theta _t^{a}=\varphi _t^{b}\), \(C_t\varphi ^{b}_t=\omega ^{a}_{2t}+\omega ^{b}_{2t}\) and \(x_{1t}^{a}+x_{1t}^{b}=(\omega ^{a}_{2,t-1}+\omega ^{b}_{2,t-1})y\). The promise short position is then given by \(\varphi ^{b}_t=(\omega ^{a}_{2t}+\omega ^{b}_{2t})/C_t\).
Our specification of \(C_t\) and \(n_t\) will allow for agent b to construct a generalized Ponzi scheme upon the limit \((p,q,K,\theta ,\varphi ,x)\) of finite horizon equilibrium plans.
Let agent b increase the sale of the promise by \(\alpha _t\) at each date and give maximal default on \(\alpha _t\) at the next date. The extra expenditure \((p_tC_t-q_t)\alpha _t\) is accommodated in the budget set by decreasing the consumption of the numeraire.
Claim
1(i): Suppose \(x^{b}_1 \ggg 0\). For \(s\in (0,1)\), let \(\alpha _t=s x^{b}_{1t}/(p_tC_t-q_t)\). For s close enough to 0, consumer b can improve upon \((x^{b}_1,\varphi ^{b})\) provided that \(\alpha \) is a bounded sequence satisfying the following condition
In fact, for \(x^b_1 \ggg 0\) there exists \({\tilde{s}} \in (0,1)\) such that for any \({\hat{s}} \in (0,{\tilde{s}})\) and \(\alpha ({\hat{s}})_t \equiv {\hat{s}} x^{b}_{1t}/(p_tC_t-q_t)\) the plan resulting from increasing sales by \(\alpha ({\hat{s}})\), giving maximal default on \(\alpha ({\hat{s}})\) and reducing consumption of good 1 to \((1-{\hat{s}})x^b_1\) is budget feasible. Let us evaluate the impact on the payoff.
The net utility gain at date t has a first-order approximation given by \([v'_tC_t-\gamma ^{b}_t(p_tC_t-q_t)]\alpha ({\hat{s}})_t\equiv B_t\), where \(v'_t\) is evaluated at \(C_t\varphi ^{b}_t\). Now, since agent b has the Euler condition on sales holding with equality, this gain will cancel out with the utility impact (including penalty impact) that such date t changes will have on date \(t+1\) utility, \([\gamma ^{b}_{t+1}(yC_t-M_t)-\tilde{\lambda }^{b}_td_t(A_{t+1}-M_{t+1})]\alpha ({\hat{s}})_t \equiv {\tilde{B}}_{t+1}\).
Then, up to date T the accumulated utility gain has a first-order approximation given by \(B_T\). As \(T \rightarrow \infty \), the first-order estimate of the utility gain remains positive if \(\limsup _T [v'_TC_T-\gamma ^{b}_T(p_TC_T-q_T)]\alpha ({\hat{s}})_T >0\).
To be more precise, consider the direction \(\alpha _{Z}({\hat{s}})\) consisting, at each date t, of a change in \(x_{1t}\) given by \(\alpha _{x_1}({\hat{s}})_t=-{\hat{s}}x^b_{1t}\), a change in sales given by \(\alpha ({\hat{s}})_t\), a change in default \(\alpha _{\psi }({\hat{s}})_t=(\eta -1)yC_t\alpha ({\hat{s}})_t\) and null changes \(\alpha _{\theta }({\hat{s}})_t\) and \(\alpha _{x_2}({\hat{s}})_t\) in \(\theta _t\) and \(x_{2t}\), respectively. The above estimate of the utility gain is actually the right-hand side directional derivative \(\delta ^+ \Pi ^{b}(Z^{b};\alpha _Z({\hat{s}}))\) of \(\Pi \) at \(Z^b\) along the direction \(\alpha _Z({\hat{s}})\) if \(\alpha _Z({\hat{s}})\) is a bounded sequence.Footnote 4 Agent b can improve upon if \(\delta ^+ \Pi ^{b}(Z^{b};\alpha _Z({\hat{s}}))>0\).
For a small enough step \(h>0\), consumer b becomes better off when replacing \(\varphi ^{b}\) by \(\varphi ^{b}+h\alpha ({\hat{s}})\), giving maximal default on \(h\alpha ({\hat{s}})\) and reducing \(x^b_1\) to \((1-{\hat{s}})x^b_1\). Let \(s=h{\hat{s}}\) we get the result. \(\square \)
Claim
1(ii): \(\alpha \) is a bounded sequence if \(C_t=1/\beta _b^t\) and the function \(n_t\) is defined by \(n_t(x_{2t})=(\beta _a-\beta _b)y x_{2t}+\beta _b^t\sqrt{x_{2t}}\) (that is, the instantaneous utility from fruit trees is becoming less strictly concave as times goes by).
In fact, \(\alpha \) is bounded if \((p_tC_t-q_t)_t \ggg 0\), that is, if \(((n'_t-(\beta _a-\beta _b)y)C_t)_t \ggg 0\). Now, \(p_tC_t-q_t=\beta _b^tC_t/[2\sqrt{\omega ^{a}_{2t}+\omega ^{b}_{2t}}]\), where \(\omega ^i_2\) are bounded sequences. \(\square \)
Claim
1(iii): inequality (12) holds, for \(x^{b}_1 \ggg 0\) and under the assumptions in 1.(ii) (where the limsup is actually the limit, due to 1(ii)).
This requires \(\lim \limits _{t \rightarrow \infty }\frac{s x^{b}_{1t} (\beta _a-\beta _b)y\beta ^t_b}{n'_t-(\beta _a-\beta _b)y} >0\), that is, \(\lim \limits _{t \rightarrow \infty }s x^{b}_{1t} (\beta _a-\beta _b)2y\sqrt{\omega ^{a}_{2t}+\omega ^{b}_{2t}} >0\), which holds if \(\omega ^{i}_2 \ggg 0\) for \(i=a,b\) and \(x^{b}_1 \ggg 0\). \(\square \)
Claim
1(iv): \(x^{b}_1 \ggg 0\), under the assumptions in 1.(ii).
In fact, \(x^{b}_{1t}=p_t\omega ^{b}_{2t}-(p_tC_t-q_t)\varphi ^{b}_t\) where \(p_t\) tends to \(\beta _{a}y\), while \(\varphi _t\) goes to zero and \(p_tC_t-q_t=1/[2\sqrt{\omega ^{a}_{2t}+\omega ^{b}_{2t}}]\), where \(\omega ^{i}_{2t} \ggg 0\). \(\square \)
Actually, the example illustrates more than a failure of cluster points of finite horizon equilibria to become infinite horizon equilibria. It illustrates that a budget-feasible plan satisfying Euler and transversality conditions may fail to be individually optimal.
In fact, in Example 1, the portfolio \(\varphi ^{b}+\alpha \) together with the perishable good consumption \(x^{b}_1(1-s)\) satisfy budget constraints and Euler conditions at prices (p, q) and \(K_t=1/\eta \). Notice that \(\varphi ^{b}\) satisfies also the transversality condition \(\lim \limits _{t \rightarrow \infty } [v'_tC_t-\gamma ^{b}_t(p_tC_t-q_t)]\varphi ^{b}_t=0\), since \(v'_tC_t-\gamma ^{b}_t(p_tC_t-q_t)=(\beta _a-\beta _b)y\) and \(\lim \limits _{t \rightarrow \infty } \varphi ^{b}_t=0\). Now, (11) fails for \({\hat{\varphi }}=\varphi ^{b}+\alpha \).
Examples 1 and 2 in Páscoa and Seghir (2009) illustrated why finite horizon equilibria may fail to induce infinite horizon equilibria for another reason. Utility penalties were high enough to discourage maximal default (there is no default in the former and default below the maximal one in the latter). An equality in (6) for the short, made the haircut \(p_tC_t-q_t\) become negative in finite horizon equilibria with trade (as shown in steps I and A of those examples, respectively). That allowed for a Ponzi scheme upon a cluster of finite horizon equilibria with trade. The novelty in the example we just described is that a negative haircut is not necessary to allow the short to improve upon such cluster point.
If utility penalties were absent, generalized Ponzi schemes could never be done. Constituting collateral and short-selling generates in this case nonnegative returns (\(\sum \nolimits _{\eta \in \xi ^+} \gamma ^i_{\eta } \Big (p_{\eta } Y_{\eta } C^j_{\eta }- M_{j\eta } \Big )\)) which, by non-arbitrage [see (6)], must induce a nonnegative promise cost \(\gamma ^i_{\xi } \big (p_{\xi } C^{j_{\xi }}_{\xi } -q^{j_{\xi }} _{\xi } \big )-{v^i_\xi }^{\prime } C^{j_{\xi }} _{\xi }\) (net of utility gains).
In Sect. 4, we present existence results in contexts where (11) holds.
4 Existence results
4.1 Moderate penalties
Let \(r^i_{\xi }(e_{\xi })\) be the minimum of the derivative \((v^i_\xi )'(z)e_{\xi }\), of \(v^i_\xi \) along the direction of the reference bundle \(e_{\xi }\) (used in the definition of penalties), taken over all feasible bundles z. This minimum is well defined, by Lemma 3 in Appendix 6.2.
Theorem 2
(Moderate penalties) Under assumptions [R], [E] and [U], if for every promise \(j \in J\) we have (a) \(\lambda ^i_{j\xi } <r^i_\xi \), then \(p_{\xi } C_{\xi } \ge q_{\xi }\) in equilibrium of finite-horizon economies and Ponzi schemes, in stricto sensu, are avoided. Equilibrium for the infinite-horizon economy exists if, in addition, (b) the collateral does not yield utility (say, it is a productive asset or a security in positive net supply that cannot be short sold).
Our moderate penalties assumption is in marginal terms (compares penalty coefficients and marginal utilities), whereas the moderation assumption contemplated in Páscoa and Seghir (2009) was in total terms: for each node \(\xi \) and each agent i, it assumed (1) \({\tilde{\lambda }}^i_{j\eta } [ p_{\eta }A_{j\eta }-M_{j\eta } ] \varphi ^i_{j\xi } < \textit{v}^i_\eta (\omega ^i_{\eta }), \ \forall \eta \in \xi ^+\), whenever (2) \(C^j _{\xi } \varphi ^i_{j\xi } \le \sum \nolimits _{i} W^i_{\xi }\). That total terms condition only suffices to get existence of equilibrium in infinite-horizon economies, if promises sales plans are required to satisfy (2) as a borrowing constraint (alternatively, (1) alone should be imposed). In fact, condition (11) holds in this case since \( \limsup _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} \Big ({v^i_\xi }^{\prime }({{\overline{Z}}}^i) C_{\xi }- \gamma ^i_{\xi } \, (p_{\xi }C_{\xi }-q_{\xi })\Big ) \varphi _{\xi } < \limsup _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} v^i(\omega ^i)\), which is zero since \(U^i(\omega ^i) < \infty .\)
4.2 Equilibrium without maximal default
However, the above low penalties, implying maximal default when the promises are traded, are not necessary for equilibrium existence. Partial default or even full repayment are compatible with equilibrium and may occur under higher penalty coefficients. In fact, generalized Ponzi schemes are obviously avoided when, for all i and all j, we have \(\gamma ^{i}_{\xi } (p_{\xi } C_{j\xi } -q^j_{\xi }) -{v_\xi ^i}^{\prime } \cdot C_{j\xi } \ge 0, \ \forall i\), at all nodes far away in the event tree [as this implies inequality (11) in Theorem 1]. By (6) it suffices to have, for all i, all \(\xi \) and all j, the following
where \(d^i_{j\eta }\) satisfies (5). We can state condition (5) in a more suggestive way. In market parlance, the consumer’s home equity is the difference between the collateral liquidation value and the repayment due on the loan. Let \(EQ^{j}_{\eta }:= p_{\eta } Y_{\eta } C_{j\xi }-p_{\eta } A_{j\eta }\). Home equity is linear on \(\varphi ^i_j\) with an impersonal coefficient \(EQ^{j}_{\eta }\) that determines what the sign of home equity will be. We name \(EQ^{j}_{\eta }\)the equity per unit of promisejat node\(\eta \).
Condition (13) can be equivalently written as follows
which says that, for each promise j and summing over all immediate successors of node \(\xi \), the marginal utility gains from positive per unit equity should outweigh default penalties on negative per unit equity. In the non-recourse case, the former occurred exclusively and were responsible for \(p_\xi C^j_\xi \) never being below than \(q_{j\xi }\), which ruled out Ponzi schemes.
Moreover, by (5), we see that (13) holds if (but not only if)
is satisfied for all i and for all \(\xi .\) Moreover, when the collateral does not yield utility gains, it is enough to have the inequality in (13) [or in (15)] satisfied, at each node \(\xi \), for some agent \(i_{\xi }\), as this implies \(p_{\xi } C_{j\xi } \ge q^j_{\xi }.\)
The difficulty is that condition (15) depends on relative spot prices \(p_{\eta }\) and on the marginal utilities of income \(\gamma ^i_{\eta }\), and, in general, it is not possible to guarantee that the market clearing spot prices (and the induced multiplier \(\gamma ^i\)) are such that (15) is satisfied, for an arbitrary combination of returns \((A^j)\) and collateral yields \(Y \, C^j.\) Let us give, nevertheless, an example where (15) holds for arbitrary penalty coefficients. This example will motivate our next result.
Example 2
(partial default or full repayment)
There are two infinite-lived agents, a and b. The event tree has two branches at each node \(\xi \) (up \((u_\xi )\) and down \((d_\xi )\)). There is one consumption good, and preferences are given by \(U^i(x)=\sum \nolimits _{\xi \in D} \beta ^{t_{\xi }} \, \nu _\xi ^i \, x_\xi \), where \(\nu ^i_{u_\xi } +\nu ^i_{d_\xi }=\nu ^i_{\xi }, \ \sum \nolimits _{\xi : \, t_{\xi }=t} \nu ^i_\xi =1, \ \forall t\). There is one promise paying in the consumption good and using as collateral a real security (or a productive asset) that is short-lived but is issued (or endowed) at each node. Formally, this collateral instrument can be treated as a second commodity that transforms into the consumption good at the next date and then disappears. Denote by \(A_\xi \) the promised returns and by \(y_\xi \) the collateral yields. The collateral coefficient is \(C_\xi =1\), and we take the perishable consumption good (\(g=1\)) as the numeraire.
Let the reference bundle in the penalty function be \(e_{\xi }=(1,0)\). Each agent i has a penalty coefficient \(\sigma ^i_\xi \) to be specified below. The penalty is then given by \(\sum \nolimits _{\xi \in D} \beta ^{t_{\xi }} \sigma ^i_\xi \nu _\xi {[A_\xi \, \varphi _{\xi ^-} - \Delta _{\xi }]}^+\), where \(\Delta _{\xi }\) stands for the delivery (\(\Delta _{\xi }=A_{\xi }\varphi _{\xi ^-}-\psi _{\xi }\)).
Given endowments \(\omega ^i_{\xi }=\Big ( \omega ^i_{1\xi }, \omega ^i_{2\xi } \Big )\) of the consumption good and the collateral instrument, we write consumers’ constraints as usual, denoting by \(p_{\xi }\) the collateral price and by \(q_{\xi }\) the promise price. Suppose \(\nu ^{a}_{u_\xi }=\nu ^{a}_{d_\xi }= {\frac{1}{2}}^{t_{\xi }+1},\) whereas \(\nu ^{b}_{u_\xi }=\frac{2}{3} \nu ^{b}_\xi \) and \(\nu ^{b}_{d_\xi }=\frac{1}{3} \nu ^{b}_\xi .\) We will construct equilibria where both agents consume the perishable good at every node, which implies that \(\gamma ^i_{\xi }=\beta ^{t(\xi )}\nu ^i_{\xi }\)
Claim
2(i): If \(A_{u_{\xi }}=2, \ A_{d_\xi }=1, \ y_{u_{\xi }}=1\) and \( y_{d_\xi }=2, \ \forall \xi \), then a cluster point of finite horizon equilibria is an infinite horizon equilibrium.
In fact, the equity at each node is such that (15) holds with equality for agent a (and therefore (13) holds with equality for this agent, for any penalty coefficients \(\sigma ^{a}_\xi \)). As the collateral does not yield utility, (11) holds for both agents. \(\square \)
Let us look for equilibrium prices and delivery rates for some possible configurations of default penalties of the two agents. For agent b, we assume \(\sigma ^{b}_{\xi } \ge 1\) (i.e., \(\lambda ^{b}_{\xi } \ge \gamma ^{b}_{\xi }, \ \forall \xi \)) and, for both agents, we take \(\rho ^{i}_{\xi }=0\), implying that (5) holds for \(d^{i}_{\xi }=\frac{1}{\sigma ^{i}_\xi }.\) Observe that if \(\beta \le 2/3\) then (8) holds, for both agents.
Suppose first that \(\sigma ^{a}_\xi =1\) (i.e., \(\lambda ^{a}_\xi = \gamma ^{a}_\xi ) \ \forall \xi \). Then \(K_{u_\xi }=0.9, \ p_{\xi }=q_{\xi }=\frac{4.6}{3} \, \beta \) and \(K_{d_\xi }=1\) satisfy Euler conditions (5) through (7), with agent a on-the-verge of selling and agent b on-the-verge of buying.
If \(\sigma ^{a}_\xi >1\) instead (i.e., \(\lambda ^{a}_\xi > \gamma ^{a}_\xi ) \ \forall \xi \), we see that \(K_{u_\xi }=K_{d_\xi }=1\) and \(p_{\xi }=q_{\xi }=\frac{5}{3} \, \beta \) satisfy Euler conditions (5) through (8), with agent a on-the-verge of selling and agent b on-the-verge of buying.
It remains to specify agents’ endowments and construct the equilibrium allocation of consumption plans and portfolios. Taking \(\omega ^{a}_\xi =(1,0)\) and \(\omega ^{b}_\xi =(1,w), \ \forall \xi \), let \(\theta ^{b}_\xi =w, \ \varphi ^{a}_\xi =w, \ \theta ^{i}_\xi \varphi ^{i}_\xi =0\) and \(x^{i}_{2 \, \xi }=0\) (no purchase of commodity 2 beyond what might be used as collateral).
Claim
2(ii): if \(w < 1,\) we can accommodate both \(\sigma ^{a}_\xi =1\) and \(\sigma ^{a}_\xi >1\) in equilibrium.
In the first case, where \(\sigma ^{a}_\xi =1,\) we obtain \(\Delta ^{a}_{u_{\xi }}= 0.9 A_{u_{\xi }} \, w=1.8 w, \ \Delta ^{a}_{d_{\xi }}= A_{d_\xi } \, w= w.\) Take \(x^{i}_{1\xi }=\omega ^{i}_{1\xi }+Y_{\xi } C_{\xi ^-} \varphi ^i_{\xi ^-} - \Delta ^{i}_{\xi }+K_{\xi } A_\xi \, \theta ^i_{\xi ^-}.\) Then, \(x^{a}_{1 \, u_\xi }=1-0.8 w, \ x^{a}_{1 \, d_\xi }=1+ w, \ x^{b}_{1 \, u_\xi }=1+1.8 w, \ x^{b}_{1 \, d_\xi }=1+ w.\) Market clearing follows \((\sum \nolimits _{i} x^i_{1\xi }=\sum \nolimits _{i} \omega ^i_{1\xi }+ y_\xi \, w)\) and we assume \(w < 1.25\) to obtain an equilibrium.
In the second case, where \(\sigma ^{a}_\xi >1, \ \forall \xi \) (that is \(\lambda ^{a}_\xi = \gamma ^{a}_\xi \ \forall \xi \)), the equilibrium allocation is given by the same promise allocation, \(\Delta ^{a}_{u_\xi }= 2 w, \ \Delta ^{a}_{d_\xi }= w, \ x^{a}_{1 \, u_\xi }=1 - w, \ x^{a}_{1 \, d_\xi }=1+ w, \ x^{b}_{1 \, u_\xi }=1+2 w, \ x^{b}_{1 \, d_\xi }=1+ w.\)\(\Box \)
Remark 3
on the result by Ferreira and Torres-Martinez (2010) on impossibility of recourse.
Example 2 shows that recourse can actually occur in infinite horizon equilibria. The borrower (agent a) repays more than the minimum between the promise and the collateral value. But recourse does not open up room for Ponzi schemes: the haircut does not become negative, it is just zero.
This seems to collide with the claim by Ferreira and Torres-Martinez (2010) that recourse is impossible in infinite horizon equilibria but a closer look shows that their assumption on collateral bounds is not satisfied.
As in Ferreira and Torres-Martinez (2010), we write \(K_{j\xi }=M_{j\xi }+Q_{j\xi }(p_{\xi }A_{j\xi }-Y_{\xi }C_{j\xi ^-})^{+}\), where \(Q_{j\xi } \in [0,1]\) measures the repayment above the minimal one (that is, the degree of recourse). Ferreira and Torres-Martinez (2010) showed that the haircut \(p_{\xi }C_{j\xi }-q_{j\xi }\) becomes negative if \(\sum \nolimits _{g}C_{jg\xi }<<\sum \nolimits _{\eta \in \xi ^+} Q_{j\xi }\underline{\pi }_{\eta }A_{j\eta }/\overline{\pi }_{\eta }\)\(\equiv \Psi _{\xi }\), where \(\underline{\pi }_{g\xi }\) and \(\overline{\pi }_{\xi }\) are lower and upper (over all goods) bounds, respectively, for \(\gamma ^i_{\xi }p_{g\xi }\).
In Example 2, there is just one promise and two cases. In case 1 (for \(\sigma ^{a}=1\)), we have \(Q_{u\xi }=0.8\) while \(Q_{d\xi }\) takes any value in [0, 1]. In case 2 (when \(\sigma ^{a}>1\)), we have \(Q_{u\xi }=1\) while \(Q_{d\xi }\) takes any value in [0, 1]. We actually know what \(\gamma ^i_{\xi }p_{g\xi }\) is. For the numeraire (the perishable good), it is \(\beta ^{t(\xi )}\nu ^{i}_{\xi }\) while for the commodity that serves as collateral it is \(\beta ^{t(\xi )}\nu ^{i}_{\xi }p_{\xi }\). Let \(\Psi ^{i}_{\xi }\equiv \sum \nolimits _{\eta \in \xi ^+} Q_{j\xi }\gamma ^i_{\eta }A_{\eta }/\gamma ^i_{\xi }p_{\xi } \ge \Psi _{\xi }\). Even for \(Q_{d\xi }=1\), we see that in case 1, \(\Psi ^{b}_{\xi }=4.2/4.6\) while in case 2, \(\Psi ^{b}_{\xi }=1\). As \(C=1\), it follows that the condition in Ferreira and Torres-Martinez (2010) is not satisfied. The haircut is actually zero and Ponzi schemes cannot be done (neither can generalized ones as the collateral does not yield any utility).
4.3 Nominal contracts
The above example where both the promise and the collateral are numeraire assets could be redone with both being nominal assets (say, the promise is a loan, with exogenous yields, whose purpose is the purchase of a bond). This leads us to study what happens when this promise or the collateral are nominal assets. In both cases, collateralized borrowing is not inflation proof.
Formally, we replace assumption [R] by
-
Assumption [N].
We allow for nominal promises or nominal collateral. A promise j not satisfying items (i) and (ii) of [R] is such that
-
(i)
its returns are nominal given by \(F^j_{\eta } \in {\mathbb {R}}_+\) at \(\eta \in \xi ^+\), for \(j \in J\).
-
(ii)
its collateral may be real as in [R (ii)] or nominal. In the latter, the collateral requirement at \(\eta \in \xi ^+\) is \(c^j_{\eta } \in {\mathbb {R}}_{++}\) and the collateral has an exogenous nominal return \({\tilde{y}}^j_{\eta } \in {\mathbb {R}}_{++}\) at any node \(\eta \in \xi ^+\).
-
(i)
As usual, given a promise with nominal returns \(F^{j_\xi }\), we let  where \(S_\xi \) stands for \(\Vert p_{\xi } \Vert _{1}\) and
where \(S_\xi \) stands for \(\Vert p_{\xi } \Vert _{1}\) and  . Analogously, in the case of nominal collateral, we make
. Analogously, in the case of nominal collateral, we make  . Equilibrium is still given by Definition 1.
. Equilibrium is still given by Definition 1.
Recall that for unsecured nominal assets, we had a homogeneity of commodity demand with respect to \({(S_\eta )}_{\eta \in \xi ^+}:\) if we multiply \(S_\eta \) by \(\tau >0, \ \forall \eta \in \xi ^+\), and adjust the portfolio (multiplying by \(\tau \)) and asset prices (dividing by \(\tau \)), we can maintain the original bundle at the same relative spot prices. However, that homogeneity does not hold for promises secured by exogenous collateral requirements.
The indeterminacy with respect to inflation rates,Footnote 5 at finite horizon equilibria with nominal promises or nominal collateral, may allow us to pick an equilibrium where marginal penalty effects \(\Big ({\tilde{\lambda }}^i_{j\eta } d^i_{j\eta } [EQ^j_\eta ]^- \Big )\) may become dominated by marginal income effects \(\Big (\gamma ^i_{\eta } [EQ^j_\eta ]^+ \Big ).\) If that is the case, (13) holds (and, therefore, (11) holds at the cluster point).Footnote 6
Theorem 3
Let \(J^{\star }\) be the set of promises for which assumptions (a) or (b) of Theorem 2 fail. Under assumptions [E] and [U], equilibrium exists, if every \(j \in J^*\) is a nominal promise backed by real collateral, as in [N].
For a nominal promise j backed by real collateral, (13) holds if:
Theorem 3 allows for direct utility gains from collateral in the case of nominal promises backed by real collateral, by showing that (16) holds for every agent. If the inequality in (16) held for just one agent and there were no utility gains from collateral, then the condition in Theorem 1 would still be verified and there would exist an equilibrium for the infinite horizon economy. The next example illustrates this case, actually in an economy where the nominal promise/real collateral contract coexists with a nominal promise/nominal collateral contract with endogenous margins.
For a nominal promise backed by a nominal collateral, (13) holds if:
Example 3
For the economy of Example 2 take agent a and the pair of contracts: one nominal-real with \(F^1_{u_\xi }=1, \ F^1_{d_\xi }=2\) and \(Y_{u_{\xi }}=(1,0), \ Y_{d_{\xi }}=(1,0), \ C^1=(0,1)\) and another nominal-nominal with \(F^2_{u_{\xi }}=1, \ F^2_{d_{\xi }}=3\) and \({{\tilde{y}}}_{u_{\xi }}={{\tilde{y}}}_{d_{\xi }}=1, \ c^2\) to be determined. For \(\lambda ^{a}_{j\eta }=\beta ^{t_{\eta }} {(\frac{1}{2})}^{t_{\eta }} \sigma ^{a \, j}_\eta ,\) let \(\sigma ^{a \, j}_{u_{\xi }}=2\) and \(\sigma ^{a \, j}_{\eta }=1\) otherwise \((j=1, \ 2).\)
Claim
3(i): conditions (16) and (17) hold (for \(j=1\) and \(j=2\), respectively), with an exogenous collateral requirement for \(j=1\) and endogenous ones for \(j=2.\)
These conditions are:
Holding as equalities for \(S_{u_\xi }^{-1}=S_{d_\xi }^{-1}=0.5\) and \(c^2=2.5\), implying that at \(u_\xi \), both promises are above collateral values (with opportunity for default, which will not be used as \(\lambda ^{a j}_{u_\xi } > \gamma ^{a}_{u_\xi } )\) while at \(d_\xi \) the first promise matches the collateral values whereas the second one falls below it. \(\square \)
5 Concluding remarks
Non-recourse loans have the beauty of eliminating Ponzi schemes and, therefore, the infinite-horizon economy has an equilibrium under the same costless assumptions that made the finite-horizon economy avoid the well-known Hart’s problem. There are, however, many credit contracts that are recourse and arguments that may explain why for some particular contracts recourse is more appealing, but we should ask ourselves why do they hold on in an open end framework. Our paper addresses this question.
Apart from the cases of mortgages in Europe and in most (37) of the US states, there are other examples of recourse collateralized loans. The most important are the security financing transactions (SFT), which take either the form of repo or security lending. In the former, a security serves as collateral for a cash loan (possibly for the purchase of the security itself), whereas in the latter a security is being lent against a collateral that can be either cash or another security. In both types of SFT, failure to redeliver the lent object constitutes an event of default and triggers bankruptcy. More precisely, the lender of cash in repo or the lender of the security who are both holding the collateral can dispose of it (there is no automatic stay) and then the remaining value of the loan (not covered by the current collateral value) will be claimed from the defaulter’s liquidated estate. There was only a brief exception to this, when the Fed allowed repo to be non-recourse in a short period in the aftermath of Lehman Brothers bankruptcy.
Our model is quite general and abstracts from institutional details that different recourse loans may have.Footnote 7 It is, however, a first step toward understanding why is recourse borrowing compatible with open end equilibrium (where either successive term loans become chained or an open end loan is present). We focus on the case of recourse due to the presence of a utility penalty on default. This case tries to capture non-explicit pecuniary, reputational or credit access penalties and is sometimes regarded as an approximate proxy for more elaborate forms of recourse. Our results show that while open end equilibrium does not exist in the same straightforward way as it did in non-recourse, there are nevertheless interesting cases, relevant for observed recourse contracts, where equilibrium exists, such as the case of moderate utility penalties combined with non-consumed collateral (as in the above STFs or in loans for the purchase of equipment) and the case of nominal promises backed by real collateral (as in most mortgages, where payments are not indexed to commodity prices).
Moreover, in our work, recourse is not just an ex ante scenario. We illustrate (in Example 2) how harsh utility penalties induce actual recourse (debts repayments above the minimal repayment) while still allowing for nonnegative haircuts, as desired to avoid Ponzi schemes, and equilibrium is shown to exist. We illustrate also (in Example 1) why absence of such schemes is not enough to ensure infinite horizon equilibrium when there are direct utility gains from the consumption of the collateral.
Notes
When Y is diagonal with elements uniformly bounded away from one, the assumptions that endowments are uniformly bounded and that the utility of a bounded plan is finite are sufficient to ensure \(\sum \nolimits _{\xi \in D} v^i_\xi (\Omega _\xi ) < \infty \) (see Páscoa and Seghir 2009).
The reason why we require \(p_{\xi } >0\) to be an equilibrium condition has to do with the fact that the default penalty coefficient \({\tilde{\lambda }}^i_{j\xi } \equiv \frac{\lambda ^i_{j\xi }}{p_{\xi } \, e_{\xi }}\) is only well defined in this case.
It does if \(\theta ^i=0\) and i does not consume any durable good in excess of the collateral bundle.
\(U^{b}\), being \((l^{\infty },l^1)\) Mackey continuous, has at \((x_1^{b},C\varphi ^{b}) \ggg 0\) a Gateaux derivative in \(l^1\) (see Lemma 1 in Araujo et al. 2011a) and \(\Pi \) has a Gateaux derivative \(D \Pi ^{b}(Z^{b}) \in l^1\) at \(Z^{b}\). If \(\alpha ({\hat{s}}) \in l^{\infty }\), then \(\alpha _Z ({\hat{s}}) \in l^{\infty }\) also and we have \(\delta ^+ \Pi ^{b}(Z^{b};\alpha _Z({\hat{s}}))\equiv \lim _{h \rightarrow 0+} [\Pi ^{b}(Z^b+h \alpha _Z({\hat{s}}))-\Pi ^{b}(Z^{b}]/h\) exists and is equal to \(D\Pi ^{b}(Z^{b})\alpha _Z({\hat{s}})=\sum \nolimits _{t=1}^{\infty }(B_t+{\tilde{B}}_{t+1})=\lim _T [v'_TC_T-\gamma ^{b}_T(p_TC_T-q_T)]\alpha ({\hat{s}})_T\).
We are not interested in checking whether the degree of freedom in the choice of inflation rates implies real indeterminacy of equilibria.
Given a nominal promise \(F^{j_\xi }\), the condition that ruled out recourse in Ferreira and Torres-Martinez (2010) will not hold for the real returns analog
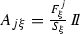 , for an appropriate choice of inflation rates \(S_\xi =\Vert p_{\xi } \Vert _{1}.\)
, for an appropriate choice of inflation rates \(S_\xi =\Vert p_{\xi } \Vert _{1}.\)
References
Araujo, A., Páscoa, M.R.: Bankruptcy in a model of unsecured claims. Econ. Theory 20, 455–481 (2002)
Araujo, A., Páscoa, M.R., Torres-Martínez, J.P.: Collateral avoids Ponzi schemes in incomplete markets. Econometrica 70, 1613–1638 (2002)
Araujo, A., Novinski, R., Páscoa, M.R.: General equilibrium, wariness and efficient bubbles. J. Econ. Theory 146, 785–811 (2011a)
Araujo, A., Páscoa, M.R., Torres-Martínez, J.P.: Long lived collateralized assets and bubbles. J. Math. Econ. 47, 260–271 (2011b)
Dubey, P., Geanakoplos, J., Shubik, M.: Default and punishment in general equilibrium. Econometrica 73, 1–37 (2005)
Ferreira, R., Torres-Martinez, J.P.: The impossibility of effective enforcement mechanisms in collateralized credit markets. J. Math. Econ. 46, 332–342 (2010)
Fostel, A., Geanakoplos, J.: Leverage cycles and the anxious economy. Am. Econ. Rev. 98, 1211–1244 (2008)
Fostel, A., Geanakoplos, J.: Leverage and default in binomial economies: a complete characterization. Econometrica 83, 2191–2229 (2015)
Geanakoplos, J.: Promises, promises. In: Arthur, W.B., Durlauf, S., Lane, D. (eds.) The Economy as an Evolving Complex System, pp. 285–320. Addison-Wesley, Reading (1997)
Geanakoplos, J., Zame, W.: Collateral, Default and Market Crashes. Cowles Foundation discussion paper (1997)
Geanakoplos, J., Zame, W.: Collateral equilibrium I: a basic framework. Econ. Theory 56, 443–492 (2014)
Kubler, F., Schmedders, K.: Stationary equilibria in asset-pricing models with incomplete markets and collateral. Econometrica 71, 1767–1793 (2003)
Martins-da-Rocha, V.F., Vailakis, Y.: Harsh default penalties lead to Ponzi schemes: a counter-example. Games Econ. Behav. 75, 277–282 (2012a)
Martins-da-Rocha, V.F., Vailakis, Y.: On Ponzi schemes in infinite horizon collateralized economies with default penalties. Ann. Finance 8, 455–488 (2012b)
Páscoa, M.R., Seghir, A.: Harsh default penalties lead to Ponzi schemes. Games Econ. Behav. 65, 270–286 (2009)
Páscoa, M.R., A. Seghir: No-trade and Refined equilibria for secured loans in infinite horizon. University of Surrey Discussion Papers in Economics DP09-2019, https://www.surrey.ac.uk/school-economics. ISSN: 1749-5075 (2019). Accessed 17 July 2019
Poblete-Cazenave, R., Torres-Martinez, J.P.: Equilibrium with limited-recourse collateralized loans. Econ Theory 53, 181–211 (2013)
Rockafellar, R.T.: Convex analysis. Princeton University Press, Princeton (1997)
Shubik, M., Wilson, C.: The optimal bankruptcy rule in a trading economy using fiat money. Zeitschrift fur Nationalokonomie 37, 337–354 (1977)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 On Sect. 3
Proof of the Proposition:
For each node \(\xi \), we define the Lagrangian function for agent i as:
For \(L^i_{\xi _0}\) to be well defined, we set \(Z_{\xi ^-_0}=(0,0,0,0)\).
(1) The claim in Proposition 1 on Euler conditions is as in Páscoa and Seghir (2009) and can be proven using the Kuhn–Tucker conditions of finite horizon truncated problems and making the horizon go to infinity (as in Araujo et al. 2011b). In fact, for each node, the sequence of Kuhn–Tucker multipliers has a cluster point, as the next lemma establishes.
A finite horizon Htruncated problem is defined by imposing on the optimization problem described in Sect. 2 the additional constraints \((\theta _{\xi },\varphi _{\xi })=0\) for \(t(\xi ) \ge H\) and \((x_{\xi },\psi _{\xi })=0\) for \(t(\xi )>H\).
Let us start by recalling the saddle point property [see Rockafellar (1997), Theorem 38.3]. For any finite horizon H truncated problem, at an optimal plan \((Z^{iH},p,q,K)\) and for any nonnegative plan \((Z_{\xi })_{\xi \in D^H}\) we have
By appropriately choosing the plan \((Z_{\xi })_{\xi \in D^H}\), we get the following result.
Lemma 1
For each node \(\xi \in D\) and for any economy with finite horizon \(H \ge t_{\xi }\), one has: \(0 \le \gamma ^{iH}_{\xi } < \frac{U^i(\Omega )}{{\underline{W}}^i_{\xi } \, \Vert {p}_{\xi } \Vert _1 }\).
Proof
For \(t \le H,\) let \(Z={(Z_{\xi })}_{\xi \in D^H}\) be such that \(Z_{\xi }=\Big (\mathcal{{W}}^i_{\xi },0,0,0 \Big )\) if \(\xi \in D^{t-1}\) and \(Z_{\xi }=0\) otherwise. By (18) we get
Hence, \(\sum \limits _{\xi \in D_t} \gamma ^{iH}_{\xi } p_{\xi } \mathcal{{W}}^i_{\xi } \le \sum \limits _{\xi \in D^H} v^i_{\xi } ({\tilde{x}}^{iH}_{\xi })\), where \(v^i_{\xi }({\tilde{x}}^{iH}_{\xi }) \le v^i_\xi (\Omega _{\xi })\). \(\square \)
It follows from Lemma 1 that multipliers \(\gamma ^{iH}_{\xi }\) have upper bounds \(\overline{\gamma }^{i} _{\xi }\) that are independent of the terminal horizon H of the economy, since \(\underline{W}^i_{\xi } >0\) by Assumption [E]. Moreover, it follows from Eq. (5) that \(\rho ^{iH}_{\xi }\) also has an upper bound independent of H. Letting \(H \rightarrow \infty \), we can find cluster points, for the product topology of the countable event tree, of the sequences \((\gamma ^{iH}_{\xi },\rho ^{iH}_{\xi },(Z^{iH}_{\xi })_i)\). Denote these cluster points by \((\gamma ^{i}_{\xi },\rho ^i_{\xi },(Z^{i}_{\xi })_i))\). We still have \(\gamma ^{i}_{\xi } < \frac{U^i(\Omega )}{{\underline{W}}^i_{\xi } \, \Vert {p}_{\xi } \Vert _1 }\).
Now, let the vectors \(L^i_{1 \, \xi }\) and \(L^i_{2 \, \xi }\) be partial supergradients of \(L^i_{\xi }(Z^i, \gamma ^i,p,q,K)\) with respect to the current and past decision variables, respectively.
The proof that Euler conditions hold at an optimal plan for the infinite horizon problem then follows as in Araujo et al. (2011b), proof of item (i) of Proposition 1. We get the following relations,
which are equivalent to the Euler conditions.
(2) The fulfillment of the transversality condition (9) follows from the saddle point property:
Claim
\(\sum \limits _{\xi : \, t_{\xi } = T} \sum \limits _{\eta \in \xi ^+} L^i_{2 \, \eta }({{\overline{Z}}}^i) {{\overline{Z}}}^i_\xi \le \sum \limits _{\xi \in D {\setminus } D^{T-1}} v^i_\xi ({{\overline{Z}}}^i_{\xi })\).
This claim can be established using (18) where for \(T \le H\) we let \((Z_{\xi })_{\xi \in D^T}\) be such that \(Z_{\xi }={\overline{Z}}^{iH}_{\xi } \chi _{D^{T-1}}(\xi )\). Then \(\sum \nolimits _{\xi : \, t_{\xi } = T} \sum \nolimits _{\eta \in \xi ^+} L^i_{2 \, \eta }({{\overline{Z}}}^{iH}) {{\overline{Z}}}^{iH}_\xi + \sum \nolimits _{\xi \in D^H {\setminus } D^{T-1}} \gamma ^{iH}_{\xi }p_{\xi }\omega ^i_{\xi } \le \sum \nolimits _{\xi \in D^H {\setminus } D^{T-1}} (v^i_\xi ({{\overline{Z}}}^{iH}_{\xi })-v^i_\xi (0))\). We let \(H \rightarrow \infty \) and get the claimed inequality. \(\square \)
The claim implies that
Claim
(9) holds if and only if (22) holds.
In fact,
\(\sum \nolimits _{\eta \in \xi ^+} L^i_{2 \, \eta }({{\overline{Z}}}^i) {{\overline{Z}}}^i_\xi \!=\!-\![L^i_{1x \, \xi }({{\overline{Z}}}^i) {{\overline{x}}}^i_\xi +L^i_{1\theta \, \xi }({{\overline{Z}}}^i) {\overline{\theta }}^i_\xi +L^i_{1\varphi \, \xi }({{\overline{Z}}}^i) {\overline{\varphi }}^i_\xi +L^i_{1\psi \, \xi }({{\overline{Z}}}^i) {\overline{\psi }}^i_\xi ]\). where \(L^i_{1\psi \, \xi }({\overline{\psi }}^i) {\overline{\psi }}^i_\xi =0\) by (5). Then, (22) is equivalent to (9). \(\square \)
This concludes the proof of Proposition 1.
On Remark 1:
Condition (10) holds if and only if \(\liminf \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} \big (L^i_{1\varphi \, \xi }({{\overline{Z}}}^i) {\overline{\varphi }}^i_\xi \big )\ge 0\).
(a) To see that (9) implies (10), let us show that
\(\liminf \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} (L^i_{1\varphi \, \xi }({{\overline{Z}}}^i) {\overline{\varphi }}^i_\xi ) \ge \liminf \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T}(L^i_{1 \, \xi }({{\overline{Z}}}^i) {{\overline{Z}}}^i_\xi )\)
It is enough to show that \(\liminf \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} (L^i_{1\varphi \, \xi }({{\overline{Z}}}^i) {\overline{\varphi }}^i_\xi -L^i_{1 \, \xi }({{\overline{Z}}}^i) {{\overline{Z}}}^i_\xi ) \ge 0\),
which by (5) is equivalent to \(\limsup \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} \big (L^i_{1x \, \xi }({{\overline{Z}}}^i) {{\overline{x}}}^i_\xi +L^i_{1\theta \, \xi }({{\overline{Z}}}^i) {\overline{\theta }}^i_\xi \big )\le 0\).
The latter follows from \(L^i_{1x \, \xi }({{\overline{Z}}}^i) {{\overline{x}}}^i_\xi \) and \(L^i_{1\theta \, \xi }({{\overline{Z}}}^i) {\overline{\theta }}^i_\xi \) being both non-positive [by (21) since at \(\eta \in \xi ^+\) we have \(L^i_{2x \, \eta }({{\overline{Z}}}^i) {{\overline{x}}}^i_\xi \ge 0\) and \(L^i_{2\theta \, \eta }({{\overline{Z}}}^i) {\overline{\theta }}^i_\xi \ge 0\)].
(b) Let us see that (10) implies (9) when \(\theta ^i=0\) and consumer i does not consume more of any durable good than the collateral bundle. These two assumptions imply that \(L^i_{1x \, \xi }({{\overline{Z}}}^i) {{\overline{x}}}^i_\xi =0\) and \(L^i_{1\theta \, \xi }({{\overline{Z}}}^i) {\overline{\theta }}^i_\xi =0\). So, \(\limsup \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} (-L^i_{1\varphi \, \xi }({{\overline{Z}}}^i) {\overline{\varphi }}^i_\xi ) = \limsup \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} L^i_{1\varphi \, \xi }({{\overline{Z}}}^i) {\overline{\varphi }}^i_\xi \).
On Remark 2:
The existence of a cluster point follows from the fact that equilibrium allocations \(Z^{iH}\equiv (x^{iH},\theta ^{iH},\varphi ^{iH},\psi ^{iH})\) of finite horizon economies have upper bounds, uniformly on the horizon H (for portfolios this follows from the collateral requirements and assumption [E]). Actually, equilibrium prices and the associated equilibrium multipliers also have uniform upper bounds: we normalize prices by placing \((p_{\xi },q_{\xi })\) in the \(G+J_{\xi }-1\) dimensional simplex and multipliers \((\gamma ^i_{\xi },\rho _{j\xi })\) have upper bounds that are independent of prices and of the terminal horizon T, as established in Remark A.1 in the Appendix. So, node by node, equilibrium variables (prices, delivery rates, allocations, multipliers and the above supergradients) of all finite-horizon economies have common upper bounds.
Then the sequence \(\Big (p^H, q^H, K^H, (Z^{iH}, \gamma ^{iH}, \rho ^{iH} , d^{iH})_{i} \Big )\) of equilibrium prices, allocations, multipliers and supergradients of the functions \(\max \{0, \cdot \}\) verify the Kuhn–Tucker conditions, for the truncated economies. This sequence has, node by node, a cluster point \(\Big (p,q,K, (Z^i, \gamma ^i, \rho ^i, d^i) _{i} \Big )\) satisfying Euler conditions. Observe that at the price cluster point p, the payoff functions are well defined, as \(p_{\xi }>0\) at any node \(\xi \), by the following lemma.
Lemma 2
At each node, the sum of spot prices is bounded away from zero, uniformly in the finite horizon H and, therefore, also bounded away from zero in the infinite-horizon economy.
This follows from Lemma 3 as in part (b) of Lemma A.2 in Páscoa and Seghir (2009). We have  and \(\sum \nolimits _{g} p_{\xi g} \ge (1+\sum \nolimits _{j} m^j_{\xi })^{-1}\). \(\square \)
and \(\sum \nolimits _{g} p_{\xi g} \ge (1+\sum \nolimits _{j} m^j_{\xi })^{-1}\). \(\square \)
Observation 1: if C, A and \(\lambda \) are uniformly bounded on the event tree, \(\underline{b} \ggg 0\) and the instantaneous utility \(v^i_{\xi }\) is node-invariant, then the positive lower bound refereed to in Lemma 2 is uniform across nodes, denoted by \(\underline{p}\in {\mathbb {R}}_++\).
Observation 2: under the conditions in Observation 1, \(\gamma ^i_{\xi }\) has a uniform upper bound on the event tree, provided that \(\mathcal{{\underline{W}}}^i_{\xi } \ggg 0\).
Proof of Theorem 1
To shorten the notation, we omit in this proof the dependence of the Lagrangian on prices (as these are fixed in this proof) and write \(L^i_{\xi }(Z) \equiv L^i_{\xi }(Z_\xi , Z_{\xi ^-}, \gamma , p,q,K)\).
Let \({\Pi }^{iT}({{x}}^i,{\theta }^i,{\varphi }^i,{\psi }^i):= \sum \nolimits _{\xi \in D^T} v^i_{\xi }({{\tilde{x}}}^i_{\xi })-\sum \nolimits _{\xi \in D^T {\setminus } \{xi_0\}} \sum \nolimits _{j \in J({\xi }^{-})} {\tilde{\lambda }}^{i}_{j\xi } [\psi ^i_{j\xi }]^+\).
Then, \(\Pi ^{iT}(Z)-\Pi ^{iT} ( {{\overline{Z}}}^i) \le \sum \nolimits _{\xi : \, t_{\xi } \le T} \Big ( L^i_\xi (Z)-L^i_\xi ( {{\overline{Z}}}^i) \Big ) \le \)
Now, the transversality condition (9) implies \(\limsup \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} \sum \nolimits _{\eta \in \xi ^+} L^i_{2 \, \eta }({{\overline{Z}}}^i) {{\overline{Z}}}^i_\xi \le 0. \) Thus, by (20) and (21), \(\limsup \limits _{T} \Big (\Pi ^{iT}(Z)-\Pi ^{iT} ({{\overline{Z}}}^i)\Big ) \le \limsup \limits _{T} \sum \nolimits _{\xi : \, t_{\xi }=T} L^i_{1 \, \xi }( {{\overline{Z}}}^i) Z_\xi .\)
Now, \(L^i_{1 \, \xi } ({\overline{Z}}) Z_\xi = \Big ( {v^i_\xi }^{\prime } ( {\overline{Z}}) -\gamma ^i_{\xi } p_{\xi } \Big ) x_{\xi }- \gamma ^i_{\xi } q_{\xi } \theta _{\xi } + \Big ( {v^i_\xi }^{\prime } ( {\overline{Z}}) C_{\xi }-\gamma ^i_{\xi } (p_{\xi }C_{\xi }-q_{\xi } \Big ) \varphi _{\xi } -\Big ({\tilde{\lambda }}^i_{j\xi } d^i_{j\xi }+\rho _{j\xi }-\gamma ^i_{\xi } \Big ) \psi ^i_{j\xi }\). Here, \( {v^i_\xi }^{\prime } ( {\overline{Z}}) -\gamma ^i_{\xi } p_{\xi } \le - \sum \nolimits _{\eta \in \xi ^+} \gamma ^i_{\eta } p_{\eta } Y_{\eta } \le 0\) and \({\tilde{\lambda }}^i_{j\xi } d^i_{j\xi }+\rho _{j\xi }-\gamma ^i_{\xi }= 0.\)\(\square \)
1.2 On Sect. 4
Lemma 3
Let \(\mathcal{{W}}_\xi =\sum \limits _{i} \mathcal{{W}}^i_{\xi }\). Given any bundle \(\kappa _\xi \in {\mathbb {R}}^G_{++}\), the directional derivative \((v^i_\xi )'(.) \kappa _\xi \) has a positive lower bound \(r^i(\kappa _\xi )\) on the set of bundles \(\{z \in {\mathbb {R}}^G_{++}: z \le \mathcal{{W}}_\xi \} \).
We can take  or \(\kappa _\xi = e_{\xi }\) or even \(\kappa _\xi \) being the \({\hat{g}}\)-th canonical vector.
or \(\kappa _\xi = e_{\xi }\) or even \(\kappa _\xi \) being the \({\hat{g}}\)-th canonical vector.
Proof
Denote by S(0, h) the sphere with center 0 and radius h and let B(0, h) be the open ball bounded by S(0, h). For any \(\epsilon >0\) let \({\tilde{S}}\) be the translation of \(S(0, \mathcal{{W}}_\xi ) \cap {\mathbb {R}}^G_+\) by the vector \(\varepsilon \kappa _\xi \in {\mathbb {R}}^G_{++}\), that is, \({\tilde{S}}:= S(0, \mathcal{{W}}_\xi ) \cap {\mathbb {R}}^G_+ + \varepsilon \kappa _\xi \), which is a compact set.
For \(y \in S(0, \mathcal{{W}}_\xi ) \cap {\mathbb {R}}^G_+\), let \(T_y\) be the affine set that runs through y in the direction of \(\kappa _\xi \), that is, \(T_y=\{z \in {\mathbb {R}}^G: \ z=a \kappa _\xi + y, \ \text{ for } \text{ some } \ a\}\). Let \(z_y\) be the point where the line \(T_y\) hits the spherical sector \({\tilde{S}}\). Actually, \({\tilde{S}}\) is the set of such points \(z_y\).
Now, the concavity of \(v^i\) implies the monotonicity of the directional derivative \((v^i_\xi )'(.) \kappa _\xi \) on \(T_y\). Hence, for any \(z \in T_y \cap B(0, \mathcal{{W}}_\xi ) \cap {\mathbb {R}}^G_{++}\), we have \((v^i_\xi )'(z) \kappa _\xi \ge (v^i_\xi )'(z_y) \kappa _\xi \). We know that \((v^i_\xi )'(z_y) \kappa _\xi >0\) by monotonicity of \(v^i\). Concavity implies the continuity of directional derivatives and, therefore, we can say that the set \({\hat{S}}:=\{(v^i_\xi )'(z_y) \kappa _\xi , \ \text{ for } \text{ some } \ y\}\) is a continuous image of the compact set \({\tilde{S}}\). Then, \({\hat{S}}\) is a compact set of positive real numbers, hence it has a positive lower bound, which we denote by \(r^i_\xi (\kappa _\xi ).\)\(\square \)
Observation 3: If \(\mathcal{{W}}_{g\xi }\) has a uniform upper bound \(\mathcal{{\overline{W}}}_g\) for each good g and the instantaneous utility \(v^i_{\xi }\) is node-invariant, then, given a bundle \(\kappa \in {\mathbb {R}}^G_{++}\), the positive lower bound referred to in Lemma A.1 is uniform across nodes, denoted by \(r^i(\kappa )\). This follows by adapting the proof of the lemma using \(\mathcal{{\overline{W}}}\) instead of \(\mathcal{{W}}_{\xi }\).
Proof of Theorem 2
Both along the sequence of finite economies equilibrium and at the limit point of the relevant subsequence, we have, by (8), that \(\lambda ^i_{j\xi } <r^i_\xi (e_{\xi })\) implies \({\tilde{\lambda }}^i_{j\xi } < \gamma ^i_{\xi }\). It follows, by (5), that \(\rho ^i_{j\xi }>0\) and, therefore, the delivery is \(M_{j\xi } \varphi ^i_{j \xi ^-}.\) Suppose that for any agent (6) cannot hold with \(d_{j\eta }=0, \ \forall \eta \in \xi ^+\) [otherwise we get immediately \(p_{\xi } C_{j\xi } \ge q^j_{\xi }\), by (6)].
If promise j is traded at \(\xi \), we get \(K_{j\eta }=\frac{M_{j\eta }}{ p_{\eta } A_{j\eta }}\) for \(\eta \in \xi ^+\) (along that subsequence and at its limit point) and (7) holds as equality for some agent. Combining with (8), we get \(p_{\xi } C_{j\xi } \ge q^j_{\xi },\) as for this agent we have:
If promise j is not traded, but was traded along a subsequence (of the above subsequence), the above argument still applies. Otherwise, we can reset \(K_{j\eta }=\frac{M_{j\eta }}{p_{\xi } A_{j\xi }}\) [in fact, (7) remains true as we just lower the right hand side]. Now, if (7) holds with strict inequality for every agent, with \(K_{j\eta }=\frac{M_{j\eta }}{p_{\xi } A_{j\xi }}\), we lower \(q^j_{\xi }\), until \(q^j_{\xi }=\max \limits _{i} \sum \nolimits _{\eta \in \xi ^+} \frac{\gamma ^i_{\eta }}{\gamma ^i_{\xi }} \, M_{j\eta }\) [notice that (6) still holds, as we just raise the left-hand side]. The agent(s) for whom this maximum occurs will have (23) satisfied and, therefore, \(p_{\xi } C_{j\xi } \ge q^j_{\xi }.\)
Actually the above resetting of \(q^j_{\xi }, \ K_{j\eta }\) and \(d_{j\eta }\) (for \(\eta \in \xi ^+)\) when asset j is not traded at node \(\xi \), along any subsequence of truncated economies equilibria, could be done already along the relevant converging subsequence (rather than by modifying the limit point), so we are back in the exact setting addressed by Theorem 1, knowing that \(p_{\xi } C_{j\xi } \ge q^j_{\xi }.\)
When the collateral does not yield any utility gains, condition (11) holds. \(\square \)
It can be seen from the proof of Theorem 2 that agents who have (7) holding with equality, for every promise, beyond some node \(\xi \), will have (23) satisfied at these nodes for all promises and, therefore, have no opportunities for doing generalized Ponzi schemes. So, only agents that do not purchase some promise at each node would have an opportunity to do a generalized Ponzi scheme.
Proof of Theorem 3
For the finite-horizon economy, we adapt the proof of Theorem 1 in Dubey et al. (2005). As in their proof the relative prices set is \(P_\xi =\Big \{(p_{\xi }, q_{\xi }) : \, \sum \nolimits _{g} p(\xi , g)=1, \ p(\xi , g) \ge s, \ q^j_{\xi } \in [0, 1/s]\Big \}.\) The correspondence that picks at each node the relative prices is defined by
Step 1. Now, we select the outcome that makes marginal penalty effects be dominated by marginal income effects [actually we make (16) hold as an equality]. We do this by creating a correspondence that defines what the inverse \(\iota _{\eta }\) of the absolute spot commodity prices sum \(S_{\eta }\) should be,
where \(E=\{(\iota _{\eta })_{\eta \in \xi ^+}:\iota _{\eta } \in [0, \chi _{\xi }]\}\) and \(\chi _{\xi }=\frac{ \max \limits _{j} \sum \nolimits _{\eta \in \xi ^+} \min \limits _{i} \min \{\lambda ^i_{j\eta }, \gamma ^i_{\eta }\} p_{\eta } Y_{\eta } C_{j\xi }}{ \min \limits _{j} \sum \nolimits _{\eta \in \xi ^+} \max \limits _{i} \max \{\lambda ^i_{j\eta }, \gamma ^i_{\eta }\} F^j_\eta }. \)
Step 2. We accommodate nominal promises in the real promises framework using the function \((\iota _{\xi }, F^j_{\xi }) \longmapsto A^j_{\xi \, g}= \iota _{\xi } F^j_{\xi }.\)
The correspondence that picks the repayment rates is defined as
Step 3. Consumers have the standard constrained demand correspondence \(\tau ^h_s={{\,\mathrm{argmax}\,}}_{Z_\xi } \Big \{ \Pi ^i(Z): (1), (2) \text{ and } (3) \text{ hold } \text{ at } (p,q,K), \ \text{ given } \ A, \ \text{ for } Z =(x, \theta , \varphi , \psi ) \text{ such } \text{ that } \ x_{\xi } \le \mathcal{{W} }_\xi (1+\epsilon ), \ \varphi ^i_{j\xi } \le \frac{\mathcal{W} (1+\epsilon )}{\max \limits _{g} C^j_{g\xi }} \equiv L^j_\xi , \ \theta ^i_{j\xi } \le (\# I) L^j_\xi , \ \psi ^i_{j\xi } \le (\max \limits _{g} A^j_{g\xi }) L^j_\xi , \ \text{ for } \text{ some } \ \epsilon \ \text{ relatively } \text{ small } \Big \}.\)
Step 4. Lagrange multipliers are constructed through correspondence  where
where 
Final step. For each \(s>0\), a fixed point of  exists, as \(\tau ^{\iota }_{s\xi }\) is nonempty valued (take \(\iota _\eta =\iota , \ \forall \eta \in \xi ^+,\) with \(\iota \le \frac{ \min \limits _{j \in J^*} \sum \nolimits _{\eta \in \xi ^+} \min \limits _{i} \min \{\lambda ^i_{j\eta }, \gamma ^i_{\eta }\} p_{\eta } Y_{\eta } C_{j\xi }}{ \max \limits _{j \in J^*} \sum \nolimits _{\eta \in \xi ^+} \max \limits _{i} \max \{\lambda ^i_{j\eta }, \gamma ^i_{\eta }\} F^j_\eta }\)) and upper hemicontinuous.
exists, as \(\tau ^{\iota }_{s\xi }\) is nonempty valued (take \(\iota _\eta =\iota , \ \forall \eta \in \xi ^+,\) with \(\iota \le \frac{ \min \limits _{j \in J^*} \sum \nolimits _{\eta \in \xi ^+} \min \limits _{i} \min \{\lambda ^i_{j\eta }, \gamma ^i_{\eta }\} p_{\eta } Y_{\eta } C_{j\xi }}{ \max \limits _{j \in J^*} \sum \nolimits _{\eta \in \xi ^+} \max \limits _{i} \max \{\lambda ^i_{j\eta }, \gamma ^i_{\eta }\} F^j_\eta }\)) and upper hemicontinuous.
As in the proof of Theorem 1 in Dubey et al. (2005), when \(s \longrightarrow 0,\) aggregate excess demand goes to zero, \(p(\eta ,g)\) does not go to zero and \(q_{\xi }\) stays bounded. Moreover, \(\iota _\eta \) stays both bounded from above and bounded away from zero. Passing to subsequences, we obtain a limit point which is an equilibrium for the finite-horizon economy and satisfying condition (13), for any \((\eta , j) \in D \times J^*\), since at \(S_\eta =\lim \iota _\eta ^{-1}\) we have (16) satisfied.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Páscoa, M.R., Seghir, A. Recourse loans and Ponzi schemes. Econ Theory 70, 527–550 (2020). https://doi.org/10.1007/s00199-019-01218-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-019-01218-3





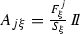 , for an appropriate choice of inflation rates
, for an appropriate choice of inflation rates