Abstract
We study games with almost perfect information and an infinite time horizon. In such games, at each stage, the players simultaneously choose actions from finite action sets, knowing the actions chosen at all previous stages. The payoff of each player is a function of all actions chosen during the game. We define and examine the new condition of individual upper semicontinuity on the payoff functions, which is weaker than upper semicontinuity. We prove that a game with individual upper semicontinuous payoff functions admits a subgame perfect \(\epsilon \)-equilibrium for every \(\epsilon >0\), in eventually pure strategy profiles.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Games with almost perfect information play a prominent role in the theory of dynamic games. In these games, at each stage, the players simultaneously choose actions, knowing the actions chosen at all previous stages. The payoff of each player is determined by the sequence of actions that have been chosen during the entire game. The notion of subgame perfect equilibrium and the weaker notion of subgame perfect \(\epsilon \)-equilibrium, where \(\epsilon >0\) is an error term, are two main solution concepts in these games. We continue the discussion of these games under the assumptions that the number of players is finite and the payoffs are bounded.
A major body of the literature on games with almost perfect information examines the existence of subgame perfect equilibrium while assuming some kind of continuity of the payoff functions and compactness of the action spaces. Fudenberg and Levine (1983) showed that if the payoff functions are continuous and the action spaces are finite, then there exists a subgame perfect equilibrium. With infinite but compact action spaces, the existence question becomes very subtle, see, for instance, Harris et al. (1995), Mertens and Parthasarathy (2003), or Maitra and Sudderth (2007). For a detailed overview, we refer the reader to the recent survey by Jaśkiewicz and Nowak (2016).
In this paper, we continue the investigation of the existence of subgame perfect \(\epsilon \)-equilibria in games with almost perfect information. We assume that the set of available actions is finite. The sequence of actions chosen in the game is referred to as a play. The contribution of this paper is twofold. First, we introduce a new condition, called individual upper semicontinuity, on the payoff functions. Individual upper semicontinuity is reminiscent of upper semicontinuity, but it uses a new notion of convergence on the set of plays for each player separately.
Consider a player i. We say that a sequence of plays \((p_m)_{m\in \mathbb {N}}\) is i-convergent to a play p if (1) the length of the common history between the play \(p_m\) and p tends to infinity, and (2) for large \(m\in \mathbb {N}\), either \(p_m=p\) or the first deviation from p to \(p_m\) involves only player i. This notion of convergence of plays is stronger than the conventional notion, which would only require property (1). That is, each i-convergent sequence of plays is also convergent in the conventional sense, but not vice versa. Based on the notion of i-convergence, we say that the payoff function of player i is i-upper semicontinuous if for each sequence of plays \((p_m)_{m\in \mathbb {N}}\) that is i-convergent to a play p, player i weakly prefers the payoff along p compared to the payoff along \(p_m\) for large m. If player i’s payoff function is upper semicontinuous in the conventional sense, then it is also i-upper semicontinuous, but not vice versa. We analyze the topological properties of i-convergence and the properties of i-upper semicontinuous payoff functions in detail.
Secondly, we show that if each player i’s payoff function is i-upper semicontinuous, then the game admits a subgame perfect \(\epsilon \)-equilibrium for every \(\epsilon >0\). Moreover, these strategy profiles are eventually pure, meaning that in each subgame randomization is only used at finitely many stages with probability 1. The proof of our existence result is constructive. The key idea is that if each player i’s payoff function is i-upper semicontinuous, then each play eventually reaches a history after which no player has an incentive to deviate from this play. This enables us to essentially cut the time horizon of the game at some finite stages and to apply backward induction on the earlier stages. This existence result generalizes the result of Purves and Sudderth (2011), who study perfect information games with upper semicontinuous payoff functions, in two directions. We reduce the topological restrictions on the payoff functions of the players, and we allow the players to move simultaneously.Footnote 1 Using the new concept of i-convergence, we can weaken the topological structure on the game while still maintaining sufficient conditions that guarantee the existence of a subgame perfect \(\epsilon \)-equilibrium. In normal form games with totally ordered compact strategy spaces, Prokopovych and Yannelis (2017) show that it is possible to ensure the existence of a pure Nash equilibrium, while significantly relaxing the requirements relating to the upper semicontinuity and single crossing properties of the payoff functions. Alós-Ferrer and Ritzberger (2017) study the problem of finding minimal topological conditions needed to guarantee the existence of a subgame perfect equilibrium in an extensive form game with continuous payoff functions.
Games with perfect information are an important special case of games with almost perfect information. Conditions related to semicontinuity of the payoff functions play an important role in several results for perfect information games. Not only do perfect information games where every player has an upper semicontinuous payoff function admit a subgame perfect \(\epsilon \)-equilibrium for every \(\epsilon >0\) (Purves and Sudderth 2011), so do perfect information games where every player has a lower semicontinuous payoff function as proven in Flesch et al. (2010). Moreover, these results were extended and unified in Flesch and Predtetchinski (2016). Questions related to semicontinuity are also studied in Le Roux and Pauly (2016) and Bruyère et al. (2017). A counterexample by Flesch et al. (2014) shows that perfect information games with finite action sets and Borel measurable payoff functions do not always have subgame perfect \(\epsilon \)-equilibria. This further illustrates the importance of topological properties of payoff functions in equilibrium analysis. For an overview on subgame perfect \(\epsilon \)-equilibria in perfect information games, we refer to Jaśkiewicz and Nowak (2016) and Bruyère (2017). We remark that it follows from a result of Secchi and Sudderth (2001) that if the players have upper semicontinuous payoff functions in a stochastic game with a countable state space, then the game admits a Nash \(\epsilon \)-equilibrium for every \(\epsilon >0\).
The remainder of this paper is structured as follows: In Sect. 2, we describe the model and introduce the notions of i-convergence for plays and i-upper semicontinuity for payoff functions of player i. In Sect. 3, we present four illustrating examples. In Sect. 4, we prove the above-mentioned existence result for subgame perfect \(\epsilon \)-equilibria. In Sect. 5, we study the topology induced by i-convergence in detail. Finally, in Sect. 6, we provide some concluding remarks.
2 The model
In this section, we describe the model and define the notion of individual upper semicontinuity of payoff functions. Let \(\mathbb {N}=\{1,2,\ldots \}\) and \(\mathbb {N}^{*}=\{0,1,2,\ldots \}\).
The game We consider games with almost perfect information and an infinite time horizon. We assume that the set of players and the sets of available actions are finite. Such a game is given by a tuple \(G=\{I,(A_i)_{i\in I},H,(u_i)_{i\in I}\}\), where
-
1.
I is a non-empty and finite set of players.
-
2.
For each player \(i\in I\), \(A_i\) is a non-empty finite set of actions. Let \(A=\times _{i\in I}A_i\). The set A corresponds to the set of stage game outcomes.
-
3.
\(H\subseteq \cup _{t\in \mathbb {N}^{*}} A^t\) is a non-empty set of histories, where \(A^0\) is the singleton
 . At each history \(h\in H\), let \(A(h)=\{a\in A|ha\in H\}\) and for each player \(i\in I\) let \(A_i(h)\) denote the projection of A(h) on \(A_i\). The set A(h) corresponds to the set of stage game outcomes at history h and \(A_i(h)\) to the set of available actions for player i at history h. We assume that: (i) H is closed under initial segments: if for some \(t\in \mathbb {N}^{*}\) and \(ha\in A^{t+1}\) we have \(ha\in H\), then we also have \(h\in H\), (ii) for each history \(h\in H\) and each player \(i\in I\), the set \(A_i(h)\) is non-empty, (iii) the set of stage game outcomes at history h is a product set: for each \(h\in H\) it holds that \(A(h)=\times _{i\in I}A_i(h)\).
. At each history \(h\in H\), let \(A(h)=\{a\in A|ha\in H\}\) and for each player \(i\in I\) let \(A_i(h)\) denote the projection of A(h) on \(A_i\). The set A(h) corresponds to the set of stage game outcomes at history h and \(A_i(h)\) to the set of available actions for player i at history h. We assume that: (i) H is closed under initial segments: if for some \(t\in \mathbb {N}^{*}\) and \(ha\in A^{t+1}\) we have \(ha\in H\), then we also have \(h\in H\), (ii) for each history \(h\in H\) and each player \(i\in I\), the set \(A_i(h)\) is non-empty, (iii) the set of stage game outcomes at history h is a product set: for each \(h\in H\) it holds that \(A(h)=\times _{i\in I}A_i(h)\). -
4.
Let P denote the set of all sequences \((a^1,a^2,\ldots )\in A^\mathbb {N}\) such that for every \(t\in \mathbb {N}\) we have \((a^1,\ldots ,a^t)\in H\). The set P is called the set of plays.Footnote 2 For each \(i\in I\), \(u_i:P\rightarrow \mathbb {R}\) is the payoff function of player i.
The game is played at stages in \(\mathbb {N}\). At stage 1, each player \(i\in I\) chooses an action \(a^1_i\) from the set  , independently of the other players. This yields a stage game outcome \(a^1=(a_i^1)_{i\in I}\). At a general stage \(t \in \mathbb {N}\), knowing the previous stage game outcomes \(a^1,\ldots ,a^{t-1}\), each player \(i\in I\) chooses an action \(a^t_i\) from the set \(A_i(a^1,\ldots ,a^{t-1})\), independently of the other players. This yields a stage game outcome \(a^t=(a_i^t)_{i\in I}\). The payoff of each player \(i\in I\) is given by \(u_i(a^1,a^2,\ldots )\).
, independently of the other players. This yields a stage game outcome \(a^1=(a_i^1)_{i\in I}\). At a general stage \(t \in \mathbb {N}\), knowing the previous stage game outcomes \(a^1,\ldots ,a^{t-1}\), each player \(i\in I\) chooses an action \(a^t_i\) from the set \(A_i(a^1,\ldots ,a^{t-1})\), independently of the other players. This yields a stage game outcome \(a^t=(a_i^t)_{i\in I}\). The payoff of each player \(i\in I\) is given by \(u_i(a^1,a^2,\ldots )\).
Notations for histories and plays For every \( t \in \mathbb {N}^{*}, \) for every history \( h = (a^1,\ldots , a^t) \in H, \) let \(\Vert h\Vert =t\) denote the number of stage games played during h. We refer to \(\Vert h\Vert \) as the length of history h. For \( k \in \mathbb {N}^{*} \) such that \(k\le t, \) let \(h_{\vert k}=(a^1,\ldots ,a^k)\) denote the truncated history available after stage game k. If \(h,h'\in H\) are such that there exists \(t\in \mathbb {N}^{*}\) for which \(h'_{\vert t}=h, \) then h is called an initial segment of \(h', \) denoted by \(h\preceq h'\). We write \(h\prec h'\) if \(h\preceq h'\) and \(h\ne h'\). Furthermore if \(h\preceq h'\), then we can define the maximum of these histories as \(\max (h,h')=h'\) and the minimum of these histories as \(\min ( h,h')=h\).
For every \(t\in \mathbb {N}^{*}\), let \(p_{\vert t}\) denote the history that arises by restricting p to the first t stages. Let \(p_{[t],i}=a_i^t\) denote the action that player i played at stage t along the play p. For a history \(h\in H\) and a play \(p\in P\) we write \(h\prec p\) if p is an extension of h, i.e., for some \(t\in \mathbb {N}^{*}\) we have \(p_{\vert t}=h\). We call h a prefix of p. For any two distinct plays \(p,q\in P\), let \(\min (p,q)\) denote the longest common history shared by those plays and let \(\ell (p,q)\) denote its length. Furthermore, define \(\min (p,p)=p\) and \(\ell (p,p)=\infty \). For any two distinct plays \(p,q\in P\), let \(I(p,q)\subseteq I\) denote the subset of players who deviated first from the play p to the play q, i.e., if \(\ell (p,q)=t\), then \(I(p,q)=\lbrace i\in I\vert p_{[t+1],i}\ne q_{[t+1],i}\rbrace \). We formally define \(I(p,p)=\emptyset \). Note that \( I, \ell , \) and \(\min \) are all symmetric in their two arguments.
Strategies A mixed action for player \(i\in I\) at history \(h\in H\) is a probability measure on \(A_i(h)\). A strategy for player \(i\in I\) is a mapping \(\sigma _i\) that assigns to each history \(h\in H\) a mixed action \(\sigma _i(h)\) for player i at history h. Let \(\mathcal {S}_i\) denote the set of all strategies of player i. If for every history \(h\in H\) the mixed action \(\sigma _i(h)\) places probability 1 on one action, then \(\sigma _i\) is called a pure strategy.
A tuple of strategies \(\sigma =(\sigma _i)_{i\in I}\) is called a strategy profile. The set of strategy profiles is denoted by \( \mathcal{S} = \times _{i \in I} \mathcal{S}_{i}\). For each player \( i \in I\), let \(\sigma _{ -i}=(\sigma _j)_{j\in I {\setminus } \{i\}}\) denote the profile of strategies of player i’s opponents. The strategy profile \(\sigma \) is called pure if each player i’s strategy \(\sigma _i\) is pure.
A pure strategy profile \( \sigma \in \mathcal{S} \) induces a unique play from every history h, which we denote by \(\pi (\sigma ; h)\). For a general strategy profile \(\sigma \in \mathcal{S}\), let \(H_\sigma \) denote the set of histories h with the following property: there is a play \( p=(h,a^{\ell (h)+1},a^{\ell (h)+2},\ldots )\) such that for each stage \( k\ge \ell (h) \) and for each player \(i\in I, \) the mixed action \(\sigma _i(h,a^{\ell (h)+1},\ldots ,a^{k})\) places probability 1 on action \(a^{k+1}_i\). Intuitively, this means that at history h, the strategy profile \(\sigma \) induces the play p with probability 1. The strategy profile \(\sigma \) is called eventually pure in every subgame if for each history \(h\in H\) and each play \(p\succ h\) there is a history \(h'\) such that \(h\preceq h'\prec p\) and \(h'\in H_\sigma \). This means that starting at any history, any continuation play reaches a history after which the strategy profile \(\sigma \) induces a unique play.
Topology on the set of plays We now define the standard cylinder topology on the set of plays P.Footnote 3 For each history \(h\in H\), let P(h) denote the set of all plays extending h, i.e., \(P(h)=\lbrace p\in P\vert p\succ h\rbrace \). Let \(\mathcal {T}\) denote the topology on the set of plays P induced by the collection \(\lbrace P(h)\vert h\in H\rbrace \). It is easy to see that the collection \(\lbrace P(h)\vert h\in H\rbrace \) forms a basis of the topology \(\mathcal {T}\). That is, for a set \(Q\subseteq P\), we have \(Q\in \mathcal {T}\) exactly when Q can be written as a union of sets belonging to \(\lbrace P(h)\vert h\in H\rbrace \). The topological space \((P,\mathcal {T})\) is metrizable. For example, the metric \(d:P\times P\rightarrow [0,\infty )\) defined by \(d(p,q)=2^{-\ell (p,q)}\) induces the topology \(\mathcal {T}\). Moreover, \(\mathcal {T}\) coincides with the relative topology inherited from the product topology on \(A^\mathbb {N}\). Since the latter space is compact and P is a closed subset of it, we conclude that \((P,\mathcal {T})\) is compact.
Let \(\Sigma \) denote the Borel sigma-algebra corresponding to the topology \(\mathcal {T}\). Then, \(( P,\Sigma )\) is a measurable space. Similarly, for every history \(h\in H\), we can construct the measurable space \(( P(h),\Sigma _h)\), where \(\Sigma _h\) is the sigma-algebra generated by all sets \( P(h')\) with \(h'\succeq h\). We have \(\Sigma _h=\{Q\cap P(h)|Q\in \Sigma \}\).
As a consequence of the Ionescu Tulcea extension theorem, every strategy profile \( \sigma \in \mathcal{S} \) induces for every history \(h\in H\) a probability measure \(\mathbb {P}_{h,\sigma }\) on the measurable space \(( P(h),\Sigma _h)\). Note that \(\sigma \) is pure exactly when for each history \(h\in H\), \(\mathbb {P}_{h,\sigma }\) is a Dirac measure. Also, \(\sigma \) is eventually pure in every subgame exactly when for each history \(h\in H\) and each play \(p\succ h\) there exists a history \(h'\) such that \(h\preceq h'\prec p\) and \(\mathbb {P}_{h',\sigma }\) is a Dirac measure.
Convergence and upper semicontinuity In the topology \(\mathcal {T}\), a sequence of plays \((p_m)_{m\in \mathbb {N}}\) is convergent to the play p if \(\lim _{m\rightarrow \infty } \ell (p_m,p)=\infty \). The payoff function \(u_i\) of player i is called upper semicontinuous if for each play \(p\in P\) and each sequence \((p_m)_{m\in \mathbb {N}}\) that is convergent to p, we have \(\limsup _{m\rightarrow \infty } u_i(p_m)\le u_i(p)\). If \(u_i\) is upper semicontinuous, then it is also Borel measurable.
We now strengthen the notion of convergence. Consider a player \(i\in I\). We say that a sequence of plays \((p_m)_{m\in \mathbb {N}}\) is i-convergent to the play p and write \({\lim _{m\rightarrow \infty }}^{(i)}p_m=p\) if \(\lim _{m\rightarrow \infty } \ell (p_m,p)=\infty \) and there exists \(M\in \mathbb {N}\) such that for every \(m\ge M\), \(I(p_m,p) \subseteq \lbrace i\rbrace \). The notion of i-convergence thus strengthens the notion of convergence by additionally imposing that eventually, if the plays \(p_m\) and p differ, player i is the only player who causes the first difference between \(p_m\) and p. Clearly, if a sequence of plays is i-convergent, then it is also convergent.
In turn, this leads to a weakening of upper semicontinuity that we refer to as individual upper semicontinuity. The payoff function \(u_i\) of player i is called i-upper semicontinuous if for each play \(p\in P\) and each sequence \((p_m)_{m\in \mathbb {N}}\) that is i-convergent to p, i.e., \({\lim _{m\rightarrow \infty }}^{(i)} p_m=p\), we have \(\limsup _{m\rightarrow \infty } u_i(p_m)\le u_i(p)\). As each i-convergent sequence of plays is also convergent, it holds that each upper semicontinuous payoff function is also i-upper semicontinuous. The converse, however, is not true and there are even i-upper semicontinuous payoff functions that are not Borel measurable. These issues are illustrated by Example 1 in Sect. 3.
Subgame perfect \(\epsilon \)-equilibrium Assume that for every player \( i \in I \) the payoff function \(u_i\) is bounded and Borel measurable. Then, for \(\epsilon \ge 0\), a strategy profile \( \sigma \in \mathcal{S} \) is called a subgame perfect \(\epsilon \)-equilibrium if for each history \(h\in H\), each player \(i\in I, \) and each strategy \(\sigma '_i\in \mathcal {S}_i,\) we have
In other words, \(\sigma \) is a subgame perfect \(\epsilon \)-equilibrium if at each history \( h \in H \) it induces a Nash \(\epsilon \)-equilibrium. When \(\epsilon =0\), the concept of subgame perfect 0-equilibrium coincides with the usual concept of subgame perfect equilibrium.
3 Examples
In this section, we discuss a few illustrative examples.
The first example demonstrates that i-upper semicontinuity of \(u_i\) does not imply that \(u_i\) is upper semicontinuous. In fact, it does not even imply that \(u_i\) is Borel measurable.
Example 1
Consider the following game with two players. At each stage, player 1 chooses an action from the set \(\{1,2\}\). Player 2 is a dummy player, who can only choose action 0 at each stage. The set of plays is thus \(P=(\{1,2\}\times \{0\})^\mathbb {N}\). Let Q be a non-Borel set of P.Footnote 4 Let the payoff function \(u_2\) of player 2 be defined as \(u_2(p)=1\) if \(p\in Q \) and \(u_2(p)=0\) if \(p\in P{\setminus } Q\).
The payoff function \(u_2\) is clearly not Borel measurable and hence not upper semicontinuous either. However, \(u_2\) is 2-upper semicontinuous. Indeed, take any sequence of plays \((p_m)_{m\in \mathbb {N}}\) that is 2-converging to a play p. Since player 2 is a dummy player, we have \(p_m=p\) for large m. Hence, \(u_2(p_m)=u_2(p)\) for large m, proving that \(u_2\) is 2-upper semicontinuous.
Of course, as long as the payoff function \(u_1\) is bounded and Borel measurable, the game admits a subgame perfect \(\epsilon \)-equilibrium for each \(\epsilon >0\).
The next example belongs to the class of so-called quitting games, see, for instance, Flesch et al. (1997) and Solan and Vieille (2001).
Example 2
Consider the following game with two players. The set of actions is \(\{c_1,q_1\}\) for player 1 and \(\{c_2,q_2\}\) for player 2, with \(c_1\) and \(c_2\) standing for “continue” and \(q_1\) and \(q_2\) for “quit”. The players choose actions simultaneously. For a play \(p \in P\), let \(K_1(p)\) denote the first stage at which player 1 chooses action \(q_1\). If player 1 always chooses action \(c_1,\) then \(K_1(p)=\infty \). We define \(K_2(p)\) similarly for player 2. The payoffs \((u_1(p),u_2(p))\) for the players are defined as follows: They are equal to (0, 0) if \(K_1(p)=K_2(p)=\infty \), i.e., if the players always choose “continue,” \((-1,1)\) if \(K_1(p)<K_2(p)\), \((1,-1)\) if \(K_1(p)>K_2(p)\), and (2, 2) if \(K_1(p)=K_2(p) < \infty \). Note that \(u_1\) and \(u_2\) are symmetric and continuous everywhere, except at the play \(p^c=((c_1,c_2),(c_1,c_2),\ldots )\).
We focus on player 1. The payoff function \(u_1\) is not upper semicontinuous. Indeed, for each \(m\in \mathbb {N}\), consider the play \(p_m\) in which \((c_1,c_2)\) is chosen at the first m stages and \((q_1,q_2)\) at stage \(m+1\). The payoff for player 1 is 2 at each \( p_m\). However, the sequence \((p_m)_{m\in \mathbb {N}}\) converges to the play \(p^c\), which only gives payoff 0 to player 1.
Nevertheless, \(u_1\) is 1-upper semicontinuous. Indeed, consider a sequence of plays \((p_m)_{m\in \mathbb {N}}\) that is 1-convergent to the play \(p^c\). Then for large m we have either \(p_m=p^c\) or \(K_1(p_m)<K_2(p_m)\). Hence, for large m we obtain \(u_1(p_m)\le 0=u_1(p^c)\). So, \(u_1\) is 1-upper semicontinuous.
A subgame perfect equilibrium in the game is obtained if player 1 always chooses action \(q_1\) and player 2 always chooses action \(q_2\). Another subgame perfect equilibrium is, for example, to always choose actions \(c_1\) and \(c_2\).
We now illustrate the usefulness of i-upper semicontinuity by examining a class of games that includes the game in Example 2 as a special case.
Example 3
Consider the two-player game of Example 2, where the action sets for players 1 and 2 are given by \(\lbrace c_1,q_1 \rbrace \) and \(\lbrace c_2,q_2\rbrace \), respectively. At every stage, both players pick an action from their action space. The game ends when at least one player picks quit. Let \(u^t_{i,\lbrace j\rbrace }\) denote the payoff of player i when player j unilaterally decides to quit at stage \(t\in \mathbb {N}\), and let \(u_{i,\emptyset }\) denote the payoff player i receives when quitting never takes place. For the sake of simplicity, assume that all payoffs are integers. Note that a payoff function of this game is continuous everywhere, except possibly at the play \(p^c=((c_1,c_2),(c_1,c_2),\ldots )\).
The payoff function \(u_i\) of player i is i-upper semicontinuous in this game if the payoff player i receives when being the only one who quits at a late stage is at most the payoff player i would receive if the game goes on indefinitely, i.e., if there exists a stage \(K\in \mathbb {N}\) such that for each \( k \ge K \) we have \(u^k_{i,\lbrace i\rbrace } \le u_{i,\emptyset }\). This follows from the fact that the play \(p^c\) is the only possible point of discontinuity of \(u_i\) and the assumption that all payoffs are integers.
We now explain why the game admits a subgame perfect equilibrium, provided that for each player \(i \in I\) the payoff function \(u_i\) is i-upper semicontinuous. A generalization of the main idea behind the construction constitutes the basis for the proof of Theorem 5. Assume that for each player \(i \in I\) the payoff function \(u_i\) is i-upper semicontinuous and define a strategy profile \( \sigma \in \mathcal{S} \) as follows. Since for each player \(i \in I \) the payoff function \(u_i\) is i-upper semicontinuous, there exists a stage K such that, for each stage \(k\ge K,\) for each player \(i \in I,\) we have \(u^k_{i,\lbrace i\rbrace }\le u_{i,\emptyset }\). Consequently, after stage K, there is a play that is most preferred by both players: the play \(p^c\). Thus, after stage K, we define \(\sigma _1\) and \(\sigma _2\) to continue indefinitely with probability 1. This implies that if stage no one quits before stage K, \(\sigma \) gives player i a payoff of \(u_{i,\emptyset }\). We complete the strategy profile \(\sigma \) by a backward induction argument on the stages \(K-1,K-2,\ldots ,1\). By construction, \(\sigma \) constitutes a subgame perfect equilibrium of the game.
The following example shows that games with bounded and upper semicontinuous payoff functions may have no subgame perfect equilibrium. This motivates the use of the concept of subgame perfect \( \epsilon \)-equilibrium.
Example 4
Consider the two-player centipede game depicted in Fig. 1. Before we proceed, we spell out some of our notational conventions.
First, whenever an action is taken from a singleton action set, it will be omitted from our notation. Notice that, the game in Fig. 1 having perfect information, at any given history only one of the players has a non-singleton action set. In accordance with our convention, we will only be recording the action taken by the active player. Thus, for each \(t \in \mathbb {N}^{*}\) we write \(c^{t}\) to denote the history of length t obtained if the players, whenever it is their turn to move, take the action c. In particular, \(c^{0}\) is the empty history. The symbol \(c^{t}q\) denotes the history of length \(t+1\) obtained if the action q is chosen for the first time in period \(t+1\).
Second, we assume that, once either player takes the action q, both players’ action sets become singletons for the rest of the game. This implies that the game only has countably many plays, which we denote by \(c^{0}q, c^{1}q, c^{2}q, \ldots \) and \(c^\infty \). Here \(c^{t}q\) denotes the play where action q is chosen for the first time in period \(t+1\). The symbol \(c^{\infty }\) is the play such that no one ever plays q. With these conventions in place, we turn to the analysis of the game.
The payoff function of player 1 is upper semicontinuous and the payoff function of player 2 is continuous. We show that the game does not have a subgame perfect equilibrium.
Suppose that \(\sigma =(\sigma _1,\sigma _2)\) is a subgame perfect equilibrium. For each \(t\in \mathbb {N}^{*}\), let \(\mathbb {P}_{c^t,\sigma }(c^\infty )\) denote the probability that, in the subgame at history \(c^t\), under \(\sigma \) the play \(c^\infty \) is realized. We distinguish two cases and derive a contradiction in each of them.
Assume first that for each \(t\in \mathbb {N}^{*}\) we have \(\mathbb {P}_{c^t,\sigma }(c^\infty )=0\). As \(\sigma \) is a subgame perfect equilibrium, it follows that at each history where player 1 is active, \(\sigma _1\) must place probability 1 on action q. This implies that, at each history where player 2 is active, \(\sigma _2\) places probability 1 on action c. But then player 1 would have a profitable deviation from \(\sigma _1\) by always choosing the action c, which is a contradiction.
Assume now that for some \(t\in \mathbb {N}^{*}\) we have \(\mathbb {P}_{c^t,\sigma }(c^\infty )>0\). Then, \(\mathbb {P}_{c^k,\sigma }(c^\infty )\) converges to 1 as \(k\rightarrow \infty . \)
So there exists \(K\in \mathbb {N}^{*}\) such that, for each \(k\ge K\), player 1’s expected payoff at history \(c^k\) is strictly more than 1, \(\mathbb {E}_{c^k,\sigma }[u_1]>1\). As \(\sigma \) is a subgame perfect equilibrium, \(\sigma _1\) places probability 1 on action c at each history where player 1 is active beyond stage K. This implies that \(\sigma _2\) places probability 1 on action q at each history where player 2 is active beyond stage K. But this contradicts \(\mathbb {P}_{c^t,\sigma }(c^\infty )>0\). Consequently, the game does not have a subgame perfect equilibrium.
Note, however, that for each \(\epsilon >0\) there exists a pure subgame perfect \(\epsilon \)-equilibrium. Indeed, fix \(\epsilon >0\). Then there is \( K \in \mathbb {N}\) such that if neither player quits before stage K then all feasible payoffs for player 2 are at most \(\epsilon \). Now the following pure strategy profile constitutes a subgame perfect \(\epsilon \)-equilibrium: player 1 quits at each history, whereas player 2 continues at each history before stage K and quits at each history after stage K. Note that this strategy profile can be found as follows: let player 2 quit at each history after stage K and, given this, use backward induction at the various parts of the game tree. This is in line with the construction that we provide in the proof of Theorem 5.
4 Existence of a subgame perfect \(\epsilon \)-equilibrium
The goal of this section is to present and prove the existence result, Theorem 5, for subgame perfect \(\epsilon \)-equilibria in games with almost perfect information as defined in Sect. 2.
Section 4 is structured as follows: In the first subsection, we present and discuss this existence result. In the second subsection, we examine some implications of individual upper semicontinuity in more detail. In the third subsection, we provide the proof.
4.1 The existence result
The main result of this section is the following theorem.
Theorem 5
Consider a game G with almost perfect information as defined in Sect. 2. If for every player \( i \in I \) the payoff function \(u_i\) is bounded, Borel measurable, and i-upper semicontinuous, then, for each \(\epsilon >0\), the game admits a subgame perfect \(\epsilon \)-equilibrium, which is eventually pure.
Theorem 5 generalizes the result of Purves and Sudderth (2011) on the existence of subgame perfect \(\epsilon \)-equilibria in perfect information games with upper semicontinuous payoff functions in two directions. First, as each upper semicontinuous function \(u_i\) is also Borel measurable and i-upper semicontinuous, we reduce the topological restrictions on the payoff functions of the players. Second, we allow the players to move simultaneously.
We provide a constructive proof for Theorem 5 in the next subsections. We remark that our proof is different from the one in Purves and Sudderth (2011), who after discretization of the payoffs, make use of an induction argument on the cardinality of the available payoffs in the subgames.
We discuss extensions of Theorem 5 and the necessity of the conditions in Sect. 6. Note Example 4 demonstrates that the conditions in Theorem 5 do not guarantee the existence of a subgame perfect equilibrium.
4.2 Optimal plays
Consider a player \(i\in I\). For every play \(p\in P\) and stage \(t\in \mathbb {N}^{*}\), we define the set \(O_i(p,t)\) as the set consisting of the play p and all other plays \(q\ne p\) such that q coincides with p until at least stage t and the first deviation from p to q is caused by player i alone. That is,
Note that \(O_i(p,t)\) is non-empty as it contains the play p.
Now we formulate a condition such that a player does not wish to deviate from a play after a certain stage.
Definition 6
Consider a player \(i\in I\) and some \(\epsilon >0\). A play \(p\in P\) is \((\epsilon ,i)\)-optimal after stage t if for each play \(q\in O_{i}(p,t)\)
A play \(p\in P\) is \(\epsilon \)-optimal after stage t if it is \((\epsilon ,i)\)-optimal after stage t for each player \(i\in I\). A play \(p\in P\) is \(\epsilon \)-optimal after history h if \(h\prec p\) and p is \(\epsilon \)-optimal after stage \(\Vert h\Vert \).
The concept of \(\epsilon \)-optimality is defined as a property of a play and not as a property of a strategy profile. Further, if the play p is \(\epsilon \)-optimal after stage t then, for each \( k \ge t\), the play p is also \(\epsilon \)-optimal after stage k.
Lemma 7 and Corollary 8 relate individual upper semicontinuity and \( \epsilon \)-optimality.
Lemma 7
Consider a player \(i\in I\) and assume that player i’s payoff function \(u_i\) is bounded. Then \(u_i\) is i-upper semicontinuous if and only if for each play \(p\in P\) and for each \(\epsilon >0\), there exists a stage \(t\in \mathbb {N}^{*}\) such that the play p is \((\epsilon ,i)\)-optimal after stage t.
Proof
Assume that the payoff function \(u_i\) is i-upper semicontinuous. Take a play \(p\in P\) and some \(\epsilon >0\).
Suppose that for each \(t\in \mathbb {N}^{*}\) there exists a play \(q_t\in O_i(p,t)\) such that
By construction, the sequence of plays \((q_t)_{t\in \mathbb {N}^{*}}\) is i-convergent to p and \(u_i(p) \le \limsup _{t\rightarrow \infty } u_i(q_t)-\epsilon \). This contradicts the assumption that \(u_i\) is i-upper semicontinuous.
For the other direction, fix a play \(p\in P\) and some \(\epsilon >0\). Then, by assumption there exists a stage \( t \in \mathbb {N}^{*} \) such that for every play \( q_t \in O_i(p,t)\), \(u_i(p)\ge u_i(q_t)-\epsilon \). Take any sequence of plays \((p_m)_{m\in \mathbb {N}}\) that i-converges to the play p. Then there exists \( M \in \mathbb {N}\) such that for every \( m \ge M\), \(p_m \in O_i(p,t). \) Consequently, for every \( m \ge M\), \( u_i(p) \ge u_i(p_m) - \epsilon . \) We conclude that \(u_i(p) \ge \limsup _{m \rightarrow \infty } u_i(p_m)-\epsilon \). Since this holds for any play \(p\in P\) and any \(\epsilon >0, \) it follows that \( u_{i} \) is i-upper semicontinuous. \(\square \)
Since the set of players is finite, we have the following corollary.
Corollary 8
Assume that, for each player \(i\in I\), the payoff function \(u_i\) is bounded and i-upper semicontinuous. Then, for each play \(p\in P\) and for each \(\epsilon >0\), there exists a stage \( t \in \mathbb {N}^{*} \) such that the play p is \(\epsilon \)-optimal after stage t.
The next definition presents the notion of an \(\epsilon \)-optimal history.
Definition 9
Let \(\epsilon >0\). A history \(h\in H\) is \(\epsilon \)-optimal if there exists a play \(p\in P\) which is \(\epsilon \)-optimal after history h.
In our construction of a subgame perfect \( \epsilon \)-equilibrium, strategy profiles will be such that in a subgame corresponding to an \(\epsilon \)-optimal history h, an \( \epsilon \)-optimal play after history h is followed.
For \( \epsilon > 0, \) the number of times a history \( h \in H \) has an initial segment which is \( \epsilon \)-optimal is denoted by \( n_{\epsilon }(h), \) so
Next, for \( m \in \mathbb {N}, \) the stopping time \( \tau ^m_\epsilon \) is defined by
In words, \(\tau ^m_\epsilon (p)\) is the stage at which it occurs for the m-th time that a prefix of p is \(\epsilon \)-optimal. Note that this does not mean that the play p needs to be \(\epsilon \)-optimal from this prefix.
The following lemma claims that all these stopping times are uniformly bounded.
Lemma 10
For every \(\epsilon >0, \) for every \(m\in \mathbb {N}\), there exists \(K^m_\epsilon \in \mathbb {N}^{*}\) such that for each play \(p\in P\) we have \(\tau ^m_\epsilon (p)\le K^m_\epsilon \).
Proof
Let some \(\epsilon >0\) and some \(m\in \mathbb {N}\) be given.
Suppose that \(\sup _{p\in P}\tau ^m_\epsilon (p)=\infty \). Then, by finiteness of the set  of possible stage game outcomes at stage 1, there is
of possible stage game outcomes at stage 1, there is  such that \(\sup _{p\succ (a^1)}\tau ^m_\epsilon (p)=\infty \). Then, for the same reason, there is \(a^2\in A(a^1)\) such that \(\sup _{p\succ (a^1,a^2)}\tau ^m_\epsilon (p)=\infty \). Continuing this way, we obtain a play \(p=(a^1,a^2, \ldots )\) for which \(\tau ^m_\epsilon (p)=\infty \). This is, however, in contradiction with Corollary 8. \(\square \)
such that \(\sup _{p\succ (a^1)}\tau ^m_\epsilon (p)=\infty \). Then, for the same reason, there is \(a^2\in A(a^1)\) such that \(\sup _{p\succ (a^1,a^2)}\tau ^m_\epsilon (p)=\infty \). Continuing this way, we obtain a play \(p=(a^1,a^2, \ldots )\) for which \(\tau ^m_\epsilon (p)=\infty \). This is, however, in contradiction with Corollary 8. \(\square \)
Example 11
Consider again the two-player centipede game depicted in Fig. 1 and discussed in Example 4. For the remainder of the example, take \(\epsilon =1/5\). We will now compute the stopping times \(\tau ^m_{1/5}(p)\) for all \(m\in \mathbb {N}\) and all plays \(p\in P\). To do this, we start by finding all 1 / 5-optimal histories.
Part 1: All histories \(h\notin \lbrace \emptyset , c^2 \rbrace \) are 1 / 5-optimal.
First note that all histories which contain a quitting action are clearly 1 / 5-optimal. All other histories have the form \(c^t\) for some \(t\in \mathbb {N}^{*}\).
The history \(c^0=\emptyset \) is not 1 / 5-optimal. Indeed, the only (1 / 5, 1)-optimal play after \(\emptyset \) is \(c^{\infty }\). However, \(c^{\infty }\) is not an (1 / 5, 2)-optimal play after \(\emptyset \) because the play cq gives player 2 a payoff strictly higher than 1 / 5. Likewise the history \(c^2\) is not 1 / 5-optimal: \(c^{\infty }\) is the only (1 / 5, 1)-optimal play after history \(c^{2}\), but it is not (1 / 5, 2)-optimal after \(c^{2}\), because the play \(c^{3}q\) gives player 2 a payoff strictly higher than 1 / 5.
The history c is 1 / 5-optimal because the play cq is 1 / 5-optimal after history c. To see this, notice that player 1 cannot profitably deviate from cq after history c since history c is controlled by player 2. And any deviation from the play cq by Player 2 after history c can increase player 2’s payoff by no more than \(1/2 - 1/3 < 1/5\). Using an analogous argument, one can easily show that history \(c^3\) is 1 / 5-optimal as the play \(c^3q\) is 1 / 5-optimal after this history.
All histories \(c^t\) with \(t\ge 4\) are 1 / 5-optimal because the play \(c^\infty \) becomes 1 / 5-optimal after history \(c^4\). Indeed, once history \(c^4\) has occurred neither player can gain an additional payoff of more than 1 / 5 by quitting.
Part 2: The stopping times \(\tau ^m(p)\).
From part 1, it now easily follows that \(\tau ^m_{1/5}(p)=m\) if \(m=1\) or if \(p\in \lbrace q,cq \rbrace \). While \(\tau ^m_{1/5}(p)=m+1\) if \(m\ge 2\) and \(p\notin \lbrace q,cq\rbrace \).
4.3 The proof of Theorem 5
In this subsection, we prove Theorem 5. Assume that for every player \( i \in I \) the payoff function \(u_i\) is bounded, Borel measurable, and i-upper semicontinuous. Fix \(\epsilon >0\). Our goal is to construct a subgame perfect \(\epsilon \)-equilibrium \(\sigma . \) The construction is illustrated graphically in Fig. 2. The trees \( T^{k}_{h} \) are defined in the proof.
Step 1: We start from the root of the game, at history  . Along each play \(p\in P\), the first \(\epsilon \)-optimal history is given by \(p_{\vert \tau ^1_\epsilon (p)}\). Let \(H^1\) denote the set of all these \(\epsilon \)-optimal histories:
. Along each play \(p\in P\), the first \(\epsilon \)-optimal history is given by \(p_{\vert \tau ^1_\epsilon (p)}\). Let \(H^1\) denote the set of all these \(\epsilon \)-optimal histories:
For each history \(h\in H^1\), choose a play \(p^h\) that is \(\epsilon \)-optimal after h.
Let  denote the subtree that consists of all the histories that can occur at or before this stopping time \(\tau ^1_\epsilon \), so
denote the subtree that consists of all the histories that can occur at or before this stopping time \(\tau ^1_\epsilon \), so

In view of Lemma 10, the tree  is finite. That is, the set of non-terminal nodes of
is finite. That is, the set of non-terminal nodes of  is the finite set
is the finite set
and the terminal histories of  are exactly the histories in \(H^1\). At each terminal history \( h^{1} \in H^1\), for each player \(i \in I\), we define the terminal payoff of
are exactly the histories in \(H^1\). At each terminal history \( h^{1} \in H^1\), for each player \(i \in I\), we define the terminal payoff of  to be \(u_i(p^{h^{1}})\). Intuitively, if \(h^{1}\) is reached, then player i receives the payoff corresponding to the \(\epsilon \)-optimal play \(p^{h^{1}}\) extending \( h^{1}. \) Given these terminal payoffs, we can find a subgame perfect equilibrium
to be \(u_i(p^{h^{1}})\). Intuitively, if \(h^{1}\) is reached, then player i receives the payoff corresponding to the \(\epsilon \)-optimal play \(p^{h^{1}}\) extending \( h^{1}. \) Given these terminal payoffs, we can find a subgame perfect equilibrium  for
for  by backward induction. Note that
by backward induction. Note that  is not necessarily pure, due to the potential presence of simultaneous moves.
is not necessarily pure, due to the potential presence of simultaneous moves.
For each \( h^{1} \in H^1\), let \( W^1(h^{1}) \) denote the prefixes of the play \( p^{h^{1}} \) after the subtree  :
:
Define
We now define the strategy profile \(\sigma \) for histories belonging to \(Z^1\) and \(W^1. \) The strategy profile \(\sigma \) equals  at histories in \(Z^1\) and follows the \(\epsilon \)-optimal plays at histories in \(W^1\). Thus, for every \(h\in Z^1\) we define
at histories in \(Z^1\) and follows the \(\epsilon \)-optimal plays at histories in \(W^1\). Thus, for every \(h\in Z^1\) we define  and, for every \(h^{1} \in H^{1}, \) for every \( h \in W^1(h^{1})\), \(\sigma (h)\) puts probability 1 on \( p^{h^{1}}_{[\Vert h\Vert +1]}\).
and, for every \(h^{1} \in H^{1}, \) for every \( h \in W^1(h^{1})\), \(\sigma (h)\) puts probability 1 on \( p^{h^{1}}_{[\Vert h\Vert +1]}\).
Step 2: Now we proceed by considering the minimal histories outside \(Z^1\cup W^1\). These are the histories that arise outside  when along a play \(p^{h^{1}}\) with \( h^{1} \in H^1\) a deviation occurs from \( p^{h^{1}}. \) That is, we are considering the set of histories
when along a play \(p^{h^{1}}\) with \( h^{1} \in H^1\) a deviation occurs from \( p^{h^{1}}. \) That is, we are considering the set of histories
For each history \( h^{\circ } = ha \in R^2, \) we execute the following. Similarly to step 1, by using the boundedness of stopping times, we let \( H^{2}(h^{\circ }) \) be the set of minimal \(\epsilon \)-optimal histories \( h^{2} \) with the initial segment \(h^{\circ } \) such that \( n_{\epsilon }(h^{2}) = n_{\epsilon }(h)+1\), so
Let \( T^2_{h^{\circ }} \) denote the finite subtree with root \(h^{\circ }\) that consists of all histories that can occur at or before the stopping time \( \tau ^{n_{\epsilon }(h)+1}_{\epsilon }\), so
Let \(Z^2(h^{\circ })\) denote the set of non-terminal histories belonging to \(T^2_{h^{\circ }}\). The terminal histories of \(T^{2}_{h^{\circ }} \) are precisely the histories in \(H^{2}(h^{\circ }). \) For each history \(h^{2} \in H^2(h^{\circ })\), choose a play \(p^{h^{2}}\) that is \(\epsilon \)-optimal after \(h^{2}\). At each terminal history \( h^{2} \in H^2(h^{\circ }), \) for each player \( i \in I\), we define the terminal payoff of \(T^2_{h^{\circ }}\) to be \(u_i(p^{h^{2}})\). Given these terminal payoffs, we can find a subgame perfect equilibrium \(\sigma ^2_{h^{\circ }}\) for \( T^2_{h^{\circ }}\) by backward induction. Once again, \(\sigma ^2_{h^{\circ }}\) is not necessarily pure.
Just like in step 1, for each \( h^{2} \in H^2(h^{\circ })\), let \(W^2(h^{\circ },h^{2})\) denote the histories along the play \(p^{h^{2}}\) after the subtree \(T^2_{h^{\circ }}\), and let \(W^2(h^{\circ })\) be the union of these sets. We define the strategy profile \(\sigma \) at histories belonging to \(Z^2(h^{\circ })\) and \(W^2(h^{\circ })\): the strategy profile \(\sigma \) equals \(\sigma ^2_{h^{\circ }}\) at histories in \(Z^2(h^{\circ })\) and follows the \(\epsilon \)-optimal plays at histories in \(W^2(h^{\circ })\).
All further steps, and conclusion: By repeating this construction with steps in \(\mathbb {N},\) we eventually consider each history of the game: certain histories belong to a finite subtree and certain histories are \(\epsilon \)-optimal. This yields a fully specified strategy profile \(\sigma \). By construction, \(\sigma \) is a subgame perfect \(\epsilon \)-equilibrium. Indeed, a player cannot gain more than \( \epsilon \) by deviating along an \(\epsilon \)-optimal play, and given this, it is never profitable to deviate at histories belonging to a finite subtree.
Moreover, as the prescription for \(\sigma \) along the \(\epsilon \)-optimal plays does not use randomization, \(\sigma \) is eventually pure in every subgame. This completes the proof of Theorem 5.
5 The topology induced by i-convergence
In this section, we examine the topology induced by the notion of i-convergence. We give criteria for metrizability, compactness, and separability for this topology.
5.1 The topological space \(( P,\mathcal {T}_i)\)
In this subsection, we fix a player \(i \in I\) and define a topology \(\mathcal {T}_i\) on the set of plays and show that a sequence of plays converges to a play p with respect to this topology \(\mathcal {T}_i\) exactly when this sequence of plays i-converges to p. We also examine the relationship between the topology \(\mathcal {T}_i\) and the topology \(\mathcal {T}\).
For every play \(p\in P\) and stage \(t\in \mathbb {N}^{*}\), the set \(O_{i}(p,t) \) is defined in (1). Let \(\mathcal {T}_i\) be the topology on P that is induced by the collection of sets \(\mathcal {O}_i=\lbrace O_i(p,t) \vert p\in P, t\in \mathbb {N}^{*} \rbrace \). That is, \(\mathcal {T}_i\) is the smallest topology on P that contains each set belonging to \(\mathcal {O}_i\). As the next lemma shows, the collection \(\mathcal {O}_i\) forms a basis of the topology \(\mathcal {T}_i\). This means that for a set \( O \subseteq P\), we have \( O \in \mathcal {T}_i\) exactly when O can be written as a union of sets belonging to \(\mathcal {O}_i\).
Lemma 12
The collection \(\mathcal {O}_i\) is a basis for the topology \(\mathcal {T}_i\).
Proof
We only need to show (cf. Aliprantis and Border, page 25) that, for any two sets \(O_i(p,s)\in \mathcal {O}_i\) and \(O_i(q,t)\in \mathcal {O}_i\), the intersection \(O_i(p,s)\cap O_i(q,t)\) can be written as a union of sets in \(\mathcal {O}_i\). Let \( O =O_i(p,s)\cap O_i(q,t)\). We can assume without loss of generality that \( s \le t\). We distinguish a number of cases and show in each case that O is indeed such a union.
-
Case 1: \( p = q\). In this case, \( O = O_i(q,t)\), so we are done.
-
Case 2: \( p \ne q\). Then \(\ell (p,q)<\infty \). We divide this case into three subcases.
-
Subcase 2.1: \( \ell (p,q) < s \le t. \) This case is trivial, as \( O = \emptyset \).
-
Subcase 2.2: \( s \le \ell (p,q) < t\). If \(I(p,q)=\{i\}\), then \( O = O_i(q,t)\). If \(I(p,q)\ne \{i\}\) then \( O = \emptyset \).
-
Subcase 2.3: \( s \le t \le \ell (p,q)\). If \(I(p,q)=\{i\}\), then \( O = O_i(q,t)\). If \(I(p,q)\ne \{i\}\), then O is the union of the sets P(ha) where the history \(h\in H\) and the stage outcome \(a\in A\) have the properties: (a) h is a common prefix of p and q with length \(t\le \Vert h\Vert \le \ell (p,q)-1\), (b) \(ha\in H\), (c) at the history h, the stage game outcome \(a\in A\) deviates from the common prefix of p and q, but the only difference is caused by player i. Note that each such set P(ha) is a union of sets in \(\mathcal {O}_i\), hence we are done. \(\square \)
The next lemma gives some basic properties of the topological space \((P,\mathcal {T}_i)\).
Lemma 13
The topological space \(( P,\mathcal {T}_i)\) is:
-
1.
Hausdorff.
-
2.
First countable.
-
3.
Sequential.
Proof
-
1.
If \(p\ne q\), then \(\ell (p,q)<\infty \) and hence \(O_i(p,\ell (p,q)+1)\) and \(O_i(q,\ell (p,q)+1)\) are disjoint open sets containing p and q, , respectively.
-
2.
Take a play \(p\in P\). Then, the sequence \( O_i(p,1) \supseteq O_i(p,2)\supseteq \ldots \) is a countable neighborhood basis for p.
-
3.
Follows immediately from (2). \(\square \)
Because the topological space \((P,\mathcal {T}_i)\) is sequential, it is fully determined by its convergent sequences. In the following lemma, we show that the convergent sequences of \((P,\mathcal {T}_i)\) are precisely the i-convergent sequences, thereby proving that \(\mathcal {T}_i\) is indeed the topology induced by i-convergence.
Lemma 14
A sequence of plays \((p_m)_{m\in \mathbb {N}}\) converges to the play p in the topological space \(( P,\mathcal {T}_i)\) if and only if the sequence \((p_m)_{m \in \mathbb {N}}\ i\)-converges to the play p.
Proof
Take a sequence of plays \((p_m)_{m\in \mathbb {N}}\) that converges to the play p in the topological space \(( P,\mathcal {T}_i)\). For each \( t \in \mathbb {N}^{*}\), the set \( O_i(p,t)\) is an open neighborhood of the play p, i.e., \(p\in O_i(p,t)\in \mathcal {T}_i\). Hence, for each \(t\in \mathbb {N}^{*}\), there exists a constant \( M_t\in \mathbb {N} \) such that for all \( m \ge M_t \) we have \( p_m \in O_i(p,M_t)\). Therefore, \(\lim _{m\rightarrow \infty } \ell (p_m,p)=\infty \), and for all \( m \ge M_1 \) we have \(I(p_m,p)\subseteq \lbrace i\rbrace \). This means that the sequence \((p_m)_{m\in \mathbb {N}}\ i\)-converges to the play p.
Conversely, take a sequence of plays \((p_m)_{m \in \mathbb {N}}\) that i-converges to the play p. Consider an open neighborhood O of the play p, i.e., \(p \in O \in \mathcal {T}_i\). By Lemma 12, there exists \( t \in \mathbb {N}^{*} \) such that \(O_i(p,t) \subseteq O. \) Since we assumed that \( (p_m)_{m \in \mathbb {N}} \) is i-convergent to p, there exists \( M \in \mathbb {N}\) such that for each \( m \ge M \) we have (a) \( \ell (p_m,p) \ge t \) and (b) \( I(p_m,p) \subseteq \{i\}. \) Thus, for each \( m \ge M \) we have \( p_m \in O_i(p,t)\) and in particular \(p_m\in O\). Therefore, \((p_m)_{m\in \mathbb {N}}\) converges to p in the topological space \(( P,\mathcal {T}_i)\). \(\square \)
Local basis of the play \(p=(00)^\infty \) in the topology \(\mathcal {T}_1\), \(\mathcal {T}_2\), \(\mathcal {T}_1\cap \mathcal {T}_2\) and \(\mathcal {T},\) respectively, for a 2-player multistage game where, for every \( h \in H, \) for \( i = 1,2\), \(A_i(h)=\lbrace 0, 1 \rbrace . \) The Euclidean distance between any play and the play p is inversely related to the length of the longest common history, while the circle sector indicates the subset of players who first deviated
Figure 3 illustrates the topologies \(\mathcal{T}_{1}, \mathcal{T}_{2},\mathcal{T}_{1} \cap \mathcal{T}_{2},\) and \(\mathcal{T}\) for a 2-player multistage game.
Lemma 15
The topology \(\mathcal {T}_i\) is finer than the topology \(\mathcal {T}\), that is, \(\mathcal {T}_i\supseteq \mathcal {T}\).
Proof
For every history \( h \in H \) and for each play \(p\in P(h)\), it holds that \(p\in O_i(p,\Vert h\Vert )\subseteq P(h)\), and hence, we have that \(P(h)=\cup _{p\in P(h)}O_i(p,\Vert h\Vert )\). Therefore, we have that \(\mathcal {T}_i\) contains each set P(h). As the topology \(\mathcal {T}\) is induced by these sets, we obtain \(\mathcal {T}_i\supseteq \mathcal {T}\). \(\square \)
Note that \(\mathcal {T}_i\) is strictly larger than \(\mathcal {T}\) in certain games. Consider the game in Example 4. The set \(O_1(c^\infty ,1)\) belongs to \(\mathcal {T}_1\), and it contains the play \(c^\infty \) and all plays in which player 1 quits at stage 3 or later. However, \(O_1(c^\infty ,1)\) does not belong to \(\mathcal {T}\) for the following reason. There is no history \(h\in H\) such that \(c^\infty \in P(h)\subseteq O_1(c^\infty ,1)\). As the sets P(h), where \(h\in H\), form a basis of the topology \(\mathcal {T}\), we conclude that \(O_1(c^\infty ,1)\notin \mathcal {T}\).
Now we turn to the question when \(\mathcal {T}_i\) coincides with \(\mathcal {T}\). The answer, and also the answer to many other questions, depends on the size of the action sets along each play. For this purpose, we introduce the notions of i-finiteness and i-cofiniteness of a play.
Definition 16
A play \( p \in P \) is i-finite if there exists a stage \( K \in \mathbb {N}^{*} \) such that at every prefix of p with length at least K the set of available actions to player i is a singleton, so for every \( k \ge K\), \( \vert A_i(p_{\vert k})\vert = 1\).
Thus, if a play p is i-finite, then after finitely many stages, it is not within the power of player i to deviate from p. Let \(F_i=\lbrace p\in P\vert p\text { is i-finite} \rbrace \) denote the subset of i-finite plays of the P.
Definition 17
A play \(p\in P\) is i-cofinite if there exists a stage \( K \in \mathbb {N}^{*} \) such that at every prefix of p with length at least K the set of available actions to every player \(j\ne i\) is a singleton, so for every \( k \ge K, \) for every \( j \ne i\), \(\vert A_j(p_{\vert k}) \vert =1\).
Thus, if a play p is i-cofinite, then after finitely many stages, player i has full control over the realization of the play p. Let \(C_i=\lbrace p\in P\vert p\text { is i-cofinite} \rbrace \) denote the subset of i-cofinite plays of the P.
Note that there can be plays that are neither i-finite nor i-cofinite and that a play can be both i-finite and i-cofinite.
As it turns out, \(\mathcal {T}_i=\mathcal {T}\) holds if and only if the topological space \((P,\mathcal {T}_i)\) is compact if and only if each play is i-cofinite.
Proposition 18
The following statements are equivalent:
-
(1)
\(\mathcal {T}_i=\mathcal {T}\).
-
(2)
The topological space \((P,\mathcal {T}_i)\) is compact.
-
(3)
Each play \(p\in P\) is i-cofinite, i.e., \(P=C_i\).
Proof
We prove that (1) and (2) are equivalent and that (1) and (3) are equivalent as well.
(1) implies (2): This is immediate because \((P,\mathcal {T})\) is compact.
(2) implies (1): As we know, \((P,\mathcal {T})\) is a compact Hausdorff space. By assumption, \((P,\mathcal {T}_i)\) is compact as well and by Lemma 13 it is Hausdorff too. Because \(\mathcal {T}_i\supseteq \mathcal {T}\) due to Proposition 15, the maximality principle of compact Hausdorff spaces implies that \(\mathcal {T}_i=\mathcal {T}\).Footnote 5
(1) implies (3): Suppose there exists a play \( p \in P \) which is not i-cofinite. Then there is an infinite set \( T \subseteq \mathbb {N}^{*} \) of stages such that at each prefix of p with length \(t\in T \) there is a player \(j_{t} \ne i\) with an action set containing at least two alternatives, so \(\vert A_{j_{t}}(p_{\vert t}) \vert \ge 2\). For each \(t\in T\), let \(p_t\) be a play in which the first difference from p is caused by the action of player \(j_t\) at stage t. Then, the sequence of plays \((p_t)_{t\in T}\) is convergent to the play p, but not i-convergent. Because both \(\mathcal {T}_i\) and \(\mathcal {T}\) are fully determined by the convergent sequences, this contradicts the assumption that \(\mathcal {T}_i= \mathcal {T}\). Consequently, it follows that every play \( p \in P \) is i-cofinite.
(3) implies (1): Because both \(\mathcal {T}_i\) and \(\mathcal {T}\) are determined by their convergent sequences, it is sufficient to show that if all plays are i-cofinite, then every convergent sequence is also i-convergent. To this end, fix a play \(p\in P\) and a sequence \((p_m)_{m\in \mathbb {N}}\) that converges to the play p, i.e., \(\lim _{m\rightarrow \infty } p_m=p\). Because the play p is i-cofinite, there exists a time \(t^{*}\) such that for every player \(j\ne i\) and every \(t\ge t^{*}\ \vert A_j(p_{\vert t})\vert =1\). Because the sequence \((p_m)_{m\in \mathbb {N}}\) is convergent to the play p, we have that there exists an \(M\in \mathbb {N}^{*}\) such that, for all \(m\ge M\), \(\ell (p_m,p)\ge t^{*}\). Furthermore, we have that \(I(p_m,p)\subseteq \lbrace i\rbrace \) for all \(m\ge M\). We can conclude that \({\lim _{m\rightarrow \infty }}^{(i)}p_m=p\). \(\square \)
A topological space is called separable if it contains a countable dense subset. The separability of \( (P,\mathcal {T}_i) \) depends on the cardinality of the set of plays which are i-finite. The reason is that each i-finite play, as a singleton, is open in \(\mathcal {T}_i\).
Proposition 19
The topological space \(( P,\mathcal {T}_i)\) is separable if and only if the subset of i-finite plays \(F_i\) is countable.
Proof
First notice that, for every \( p \in F_i, \) the singleton \( \{p\} \) is open in \(\mathcal {T}_i\). Indeed, as p is i-finite, there is a stage t such that at any prefix of p with length at least t player i’s action set is a singleton. It follows that \(\{p\}=O_i(p,t)\in \mathcal {T}_i\).
Part 1: Assume that \(( P,\mathcal {T}_i)\) is separable and let D be a countable dense subset of P. For each \( p \in F_i, \) the singleton \(\{p\}\) is open in \(\mathcal {T}_i\), so we have \( F_i \subseteq D. \) It follows that \(F_i \) is countable.
Part 2: Assume that \( F_i \) is countable. We show that \(( P,\mathcal {T}_i)\) is separable by constructing a countable dense subset of P.
For every history \(h\in H\), fix a play \(p^h\in P(h)\). Because the set H of histories is countable and because \(F_i\) is countable by assumption, the set \(D=\lbrace p^h\vert h\in H \rbrace \cup F_i\) is countable too. We claim that D is dense in P with respect to \(\mathcal {T}_i\).
It suffices to show that, for every \(p\notin D, \) for every stage \(t\in \mathbb {N}^{*}\), \( O_i(p,t)\cap D \ne \emptyset \). Take a play \(p\notin D\) and a stage \( t \in \mathbb {N}^{*}\). As \(p\notin D\) we also have \(p\notin F_i\), and hence, there exists a prefix h of p such that \( \Vert h\Vert \ge t \) and \( \vert A_i(h) \vert \ge 2. \) Consider a history \(h'\) of length \(\Vert h\Vert +1\) such that (a) \(h'\) coincides with h at the first \(\Vert h\Vert \) stages and (b) at stage \(\Vert h\Vert +1\), \(h'\) differs from the play p only by the action of player i. Then, \(p^{h'}\in O_i(p,t)\cap D\). \(\square \)
The following proposition shows that \( (P,\mathcal{T}_{i}) \) is not metrizable under mild conditions.
Proposition 20
If the set \(F_i\cup C_i\) is finite and \(P {\setminus } (F_i\cup C_i)\) is infinite, then the topological space \((P,\mathcal {T}_i)\) is not metrizable.
Proof
Suppose \(d_i: P \times P \rightarrow [0,\infty )\) is a metric which induces the topology \(\mathcal {T}_i\).
Step 1: Construction of two sequences of plays \((p_m)_{m \in \mathbb {N}}\) and \((q_m)_{m \in \mathbb {N}}\).
In this step, we inductively construct two sequences of plays \((p_m)_{m \in \mathbb {N}}\) and \((q_m)_{m\in \mathbb {N}}\) as illustrated in Fig. 4.
Start with any play \(p_1\) which is not i-finite. Because the play \(p_1\) is not i-finite and there are infinitely many plays which are not i-cofinite there exists a play \(q_1\) with the following three properties (1) \( I(p_1, q_1) = \{i\}, \) (2) \(q_1\) is not i-cofinite, and (3) \(d_i(p_1,q_1)< 1/2\). Indeed, the fact that the play \(p_1\) is not i-finite guarantees that there exists an eventually non-constant sequence of plays which i-converges to the play \(p_1. \) This guarantees that this sequence of plays contains an element \( q_{1} \) having all the desired properties.
Now assume that for some \( m \in \mathbb {N} \) the plays \(p_m\) and \(q_m\) are defined such that \(p_m\) is not i-finite and \(q_m\) is not i-cofinite. Take any play \(p_{m+1}\) that is not i-finite such that \(p_{m+1}\) coincides with the play \(q_m\) on a longer history than the play \(p_m\) and such that the first time the play \(p_{m+1}\) differs from \(q_m\) is not solely due to player i, so
Because the play \(p_{m+1}\) is not i-finite, it is possible to choose the play \(q_{m+1}\) in such a way that \(q_{m+1}\) is not i-cofinite and
Step 2: Finding a contradiction
For \( m \in \mathbb {N}, \) let \( h_m = \min (p_{m},q_m) \) denote the longest common history between the play \( p_{m} \) and the play \( q_{m}\). Notice that by construction we have \(h_1\prec h_2\prec \cdots \). Therefore, there exists a unique play p extending all histories \(h_m\). Note that for every \(m\in \mathbb {N}\) we have that
It follows that \( \lim _{m \rightarrow \infty } \ell (p, p_m) =\infty \). Furthermore, we have that \(I(p,p_{m})=I(p_{m}, q_m) =\lbrace i\rbrace \). Therefore, we can conclude that \({\lim _{m\rightarrow \infty }}^{(i)}p_{m}=p\) and hence \(\lim _{m\rightarrow \infty }d_i(p,p_{m})=0\). Furthermore, we have by construction that \(\lim _{m\rightarrow \infty } d_i(p_{m}, q_{m})=0\). It follows from the triangle inequality that, for every \(m\in \mathbb {N}\), \(d_i(p,q_m)\le d_i(p,p_{m})+d_i(p_{m},q_m)\). This yields that \(\lim _{m\rightarrow \infty }d_i(p,q_m)=0\) and consequently \({\lim _{m\rightarrow \infty }}^{(i)} q_m=p\). However, by construction we have that, for every \(m\in \mathbb {N}\), \(I(p,q_m)=I(p_{m},q_m)\nsubseteq \lbrace i\rbrace , \) so we have obtained a contradiction. \(\square \)
Example 21
Proposition 20 implies that the topological space \((P,\mathcal {T}_i)\) induced by an infinitely repeated stage game in which all players have at least two actions is not metrizable. Indeed, every play in such a game is neither i-finite nor i-cofinite and there are infinitely many plays.
Even though in general the topological space \((P,\mathcal {T}_i)\) is not metrizable, there are games for which the associated topological space is metrizable.
Lemma 22
If \(P=F_i\cup C_i\), then the topological space \((P,\mathcal {T}_i)\) is metrizable.
Proof
Let \(F_{i,k}\) denote the set of i-finite plays such that \(A_{i}(p_{|{t}})\) is a singleton for each \(t \ge k\). Thus, \(F_{i,1},F_{i,2},\dots \) is a non-decreasing sequence of sets converging to the set of i-finite plays \(F_{i}\). Let \(\delta (p) = 0\) for each \(p \notin F_{i}\) and let \(\delta (p) = 2^{-k}\) for each \(p \in F_{i,k} {\setminus } F_{i,k-1}\).
Define \(d_{i}(p,p) = 0\) for each \(p\in P\), and for two distinct plays \(p,q\in P\) we let \(d_{i}(p,q) = \max \{d(p,q),\delta (p),\delta (q)\}\), where d is the usual ultrametric defined by \(d(p,q)=2^{-\ell (p,q)}\). We now show that because d is an ultrametric, \(d_{i}\) is as well. By definition, we have that \(d_i(p,p)=0\) for all \(p\in P\); furthermore, it is trivial to see that \(d_i\) is nonnegative and symmetric. It remains to show that \(d_i(p,q)\le \max \{d_{i}(p,r),d_{i}(r,q)\}\) for any \(p,q,r\in P\). We have
We now show that the metric \(d_i\) induces the topology \(\mathcal {T}_i\) of i-convergence.
Part 1: If \(\lim _{m\rightarrow \infty } d_i(p_m,p)=0\) then the sequence \((p_m)_{m\in \mathbb {N}} \ i\)-converges to p.
Suppose the sequence \((p_{m})_{m\in \mathbb {N}}\) converges to p under the metric \(d_{i}\). First assume that \(p\in F_i\) then because p is i-finite there exists \(M\in \mathbb {N}\) such that \(p_m=p\) for all \(m\ge M\), which implies that \(I(p_m,p)=\emptyset \) and \(\ell (p_m,p)=\infty \) for all \(m\ge M\). We can conclude that \((p_m)_{m\in \mathbb {N}}\ i\)-converges to p. Now assume that \(p\in C_i\) and note that because \(d\le d_i\) we have that the sequence \((p_m)_{m\in \mathbb {N}}\) converges to p under the metric d. Furthermore, observe that any sequence of plays that converges to \(p \in C_{i}\) under the metric d also i-converges to p.
Part 2: If the sequence \((p_m)_{m\in \mathbb {N}} \ i\)-converges to p then \(\lim _{m\rightarrow \infty } d_i(p_m,p)=0\)
If the sequence \((p_{m})_{m\in \mathbb {N}}\ i\)-converges to p, then \(\lim _{k\rightarrow \infty } d(p_k,p)=0\) and there exists an \(M\in \mathbb {N}\) such that \(I(p_m,p)\subseteq \lbrace i\rbrace \) for every \(m\ge M\). Let \(n_m=\ell (p_m,p)\). Then, for each \(m\ge M\) we have that either \(p_m=p\) or the set \(A_i(p_{m\vert n_k})=A_i(p_{\vert n_m})\) is not a singleton. From this, we can conclude that p and \(p_{m}\) are not elements of \(F_{i,n_{m}}\). Therefore, \(\delta (p) \le 2^{-n_{m}}\) and \(\delta (p_{m}) \le 2^{-n_{m}}\). Because \(\lim _{m\rightarrow \infty } n_{m}=\infty \) and \(\lim _{m\rightarrow \infty } d(p_m,p)=0\) we conclude that \(p_{m}\) converges to p under the metric \(d_{i}\). \(\square \)
5.2 The topological space \( (P,\cap _{i\in I} \mathcal {T}_{i})\)
In this section, we take a closer look at the collection \(\cap _{i\in I} \mathcal {T}_{i}\) of sets which are open in every topological space \(( P,\mathcal {T}_i)\). By Proposition 15, we have \(\mathcal {T}_i\supseteq \mathcal {T}\) and hence \(\cap _{i\in I}\mathcal {T}_i\supseteq \mathcal {T}\). It is now a natural question to ask whether in fact \(\cap _{i\in I} \mathcal {T}_i=\mathcal {T}\). As we will see, this is the case for perfect information games, but not in general.
For every play \( p \in P \) and stage \( t \in \mathbb {N}^{*}, \) let
Let \(\mathcal {T}^{*}\) be the topology on P that is induced by the collection \(\mathcal {B}^{*}=\lbrace O^{*}(p,t)\vert p\in P, t\in \mathbb {N}^{*} \rbrace \). That is, \(\mathcal {T}^{*}\) is the smallest topology on P that contains each set belonging to \(\mathcal {B}^{*}\). As the next lemma shows, the collection \(\mathcal {B}^{*}\) forms a basis of the topology \(\mathcal {T}^{*}\). This means that for a set \( O \subseteq P\), we have \( O \in \mathcal {T}^{*} \) exactly when O can be written as a union of sets in \(\mathcal {B}^{*}\).
Lemma 23
The collection \(\mathcal {B}^{*}\) is a basis for the topology \(\mathcal {T}^{*}\).
Proof
The proof is similar to that of Lemma 12. We only need to show (cf. Aliprantis and Border, page 25) that, for any two sets \( O^{*}(p,s) \in \mathcal {B}^{*} \) and \( O^{*}(q,t) \in \mathcal {B}^{*}, \) the intersection \( O^{*}(p,s) \cap O^{*}(q,t) \) can be written as a union of sets in \(\mathcal {B}^{*}\). Let \( O^{*} = O^{*}(p,s) \cap O^{*}(q,t). \) We can assume that without loss of generality \( s \le t. \) We distinguish a number of cases and prove in each case that \( O^{*} \) is indeed such a union.
-
Case 1: \( p=q. \) In this case, \( O^{*} = O^{*}(q,t) \) and we are done.
-
Case 2: \( p \ne q. \) It follows that \( \ell (p,q) < \infty . \) We divide this case into three subcases.
-
Subcase 2.1: \( \ell (p,q) < s \le t. \) In this case, it holds that \( O^{*} = \emptyset \).
-
Subcase 2.2: \( s \le \ell (p,q) < t. \) If I(p, q) is a singleton, then \( O^{*} = O^{*}(q,t). \) If I(p, q) is not a singleton, so multiple players cause the first difference between p and q, then \( O^{*} = \emptyset \).
-
Subcase 2.3: \( s \le t \le \ell (p,q). \) If I(p, q) is a singleton, then \( O^{*} = O^{*}(p,s) = O^{*}(q,t). \) If I(p, q) is not a singleton, then \( O^{*} \) is the union of the sets P(ha) where the history \(h\in H\) and the stage outcome \(a\in A\) have the properties: (a) h is a common prefix of p and q with length \( t \le \Vert h\Vert \le \ell (p,q) - 1, \) (b) \(ha\in H\), (c) at the history h, the stage game outcome \(a\in A\) deviates from the common prefix of p and q and the difference is caused by exactly one player. Because for every history \(h\in H\), we have \(P(h)=\cup _{p\in P(h)}O_i(p,\Vert h\Vert )\), each such set P(ha) is a union of sets in \(\mathcal {B}^{*}\), and hence, we are done. \(\square \)
We now show that the topologies \(\mathcal {T}^{*}\) and \(\cap _{i\in I} \mathcal {T}_i\) coincide. Hence, \(\mathcal {B}^{*}\) is a basis for the topology \(\cap _{i\in I} \mathcal {T}_i\).
Lemma 24
\(\mathcal {T}^{*}=\cap _{i\in I} \mathcal {T}_i\).
Proof
Part 1: \(\mathcal {T}^{*}\supseteq \cap _{i\in I}\mathcal {T}_i\).
Let \( O \in \cap _{i \in I} \mathcal{T}_{i} \) be given. It is sufficient to show that for every \( p \in O \) there exists \( t \in \mathbb {N}^{*} \) such that \( O^{*}(p,t) \subseteq O. \) Let some \( p \in O \) be given. For every \( i \in I \), there exists \( t_{i} \in \mathbb {N}^{*} \) such that \( O_{i}(p,t_{i}) \subseteq O. \) For \( t = \max _{i \in I} t_{i} \) it holds that, for every \( i \in I\), \(O_{i}(p,t) \subseteq O. \) It follows that \( O^{*}(p,t) = \cup _{i \in I} O_{i}(p,t) \subseteq O. \)
Part 2: \(\mathcal {T}^{*}\subseteq \cap _{i\in I} \mathcal {T}_i\).
Fix a play \(p\in P\) and a time \( t \in \mathbb {N}^{*}\). It is sufficient to prove that, for every \( i \in I\), \( O^{*}(p,t) \in \mathcal {T}_i. \) Fix some player \( i \in \mathcal {I}. \) Let some \( q \in O^{*}(p,t) \) be given. It is sufficient to show that there exists \( k \in \mathbb {N}^{*} \) such that \( O_i(q,k) \subseteq O^{*}(p,t)\). If \( q = p, \) then let \( k = t, \) so we have that \(O_i(p,t) \subseteq \cup _{j \in I} O_j(p,t) = O^{*}(p,t) \) and we are done. If \( q \ne p, \) then there exists \( k \in \mathbb {N} \) such that \( k > \ell (p,q) \ge t. \) It is immediate that \( O_i(q,k) \subseteq O^{*}(p,t)\). \(\square \)
Because in perfect information games at every stage only one player can deviate from a given play, we obtain the following result.
Proposition 25
Consider a game G as defined in Sect. 2 with perfect information. It holds that \( \mathcal {T}^{*} = \mathcal {T}\).
Proof
Because G has perfect information, we have for every play \(p\in P\) and stage \( t \in \mathbb {N}^{*} \) that \(O^{*}(p,t)=\{q\in P|\ell (p,q)\ge t\}=P(p_{\vert t})\). Hence, \( \mathcal{T}^{*} \) and \( \mathcal {T} \) have the same basis and the statement follows. \(\square \)
Corollary 26
If a sequence of plays is convergent in \( \mathcal {T}^{*}, \) then it is convergent in \(\mathcal {T}\) as well. The converse holds for perfect information games.
6 Discussion
6.1 Perfect information games
In Theorem 5, we assumed that the set of available actions is always finite. This has two consequences. First, when applying backward induction in the proof of Theorem 5, we were guaranteed to have a subgame perfect equilibrium in each finite tree. Second, each stopping time \(\tau ^k_\epsilon \) is bounded.
The second consequence is not essential. Even with unbounded, but finite, stopping times we would obtain subtrees in the proof of Theorem 5 that have no infinite branches. Hence, it would still be possible to apply backward induction by the following idea. Start at the root of a subtree. If there is a child history that is non-terminal, then take this history and repeat this process as long as it is possible to choose a non-terminal child history. Since there is no infinite branch, this process will eventually stop at a history such that all of its children are terminal histories. Then, apply a step of backward induction at this history. By means of a transfinite procedure, applying a step of backward induction at each iteration step, we finally end up with a complete strategy profile for this subtree, and this strategy profile is thus a subgame perfect equilibrium for this subtree.
The first consequence is important though. Still, it would be enough to have a one-shot \( \epsilon \)-equilibrium in each possible stage game, for every \(\epsilon >0\). In particular, this would be the case if the game under consideration has perfect information, even if the set of available actions is not finite. To be more precise, this leads to the following statement.
Consider a perfect information game that satisfies the assumptions of Sect. 2, without the requirement that the set of available actions of each player is finite. If the payoff function \(u_i\) of every player \( i \in I \) is bounded and i-upper semicontinuous, then for each \(\epsilon >0\), the game admits a pure strategy profile such that in any subgame, no player can gain more than \(\epsilon \) by unilaterally deviating to another pure strategy.
This statement generalizes the corresponding result in Purves and Sudderth (2011), by relaxing the topological condition on the payoff functions.
6.2 Necessity of the conditions in Theorem 5
In this subsection, we discuss to which extent the conditions assumed in Theorem 5 are necessary for the existence of a subgame perfect \(\epsilon \)-equilibrium, for every \(\epsilon >0\).
The assumption that the set of available actions is always finite was already discussed in the previous subsection.
We also assumed in Theorem 5 that the payoffs are bounded. This is a standard assumption, and without this assumption even very simple 1-player games fail to have \(\epsilon \)-optimal solutions.
The assumption of individual upper semicontinuity is of course the main condition on the payoffs and is heavily used.
We also assumed that the payoffs are Borel measurable. The subgame perfect \(\epsilon \)-equilibria that we constructed in Theorem 5 are eventually pure in every subgame. Hence, the calculation of the expected payoffs for these strategy profiles, or even if a player deviates to a pure strategy, does not require the payoffs to be Borel measurable. Rather, Borel measurability is needed to be able to calculate the expected payoffs when a player deviates to a non-pure strategy.
The assumption that the number of players is finite was used to obtain the crucial Corollary 8.
6.3 Payoff functions that are i-lower semicontinuous
It is not known whether all games as defined in Sect. 2, where each player’s payoff function is bounded and lower semicontinuous admits an \(\epsilon \)-equilibrium, for every \(\epsilon >0\).Footnote 6
Nevertheless, using i-convergent sequences we can define the notion of i-lower semicontinuity. A payoff function \(u_i\) is i-lower semicontinuous if for every play p and every sequence \((p_m)_{m\in \mathbb {N}}\) of plays that is i-convergent to p we have \(\liminf _{m\rightarrow \infty } u_i(p_m)\ge u_i(p)\). With this concept, for perfect information games we can conclude the following statement. Flesch et al. (2010) showed that in every perfect information game, with arbitrary action spaces, if each player’s payoff function is bounded and lower semicontinuous, then there exists a pure strategy profile such that in any subgame, no player can gain more than \(\epsilon \) by unilaterally deviating to another pure strategy. After a careful look at the proof, the only place where the lower semicontinuity of the payoff functions is used is on page 750 in order to prove that Equation (18) follows from Equation (19). Since the sequence of plays considered there is not only convergent but also i-convergent, the result of Flesch et al. (2010) remains valid even if lower semicontinuity is relaxed to i-lower semicontinuity.
6.4 Stochastic transitions
It is a natural question whether or not Theorem 5 can be extended to games with stochastic transitions. Even if this is possible, the proof would be substantially more complex, as we would not be able to work with \(\epsilon \)-optimal plays any more.
Notes
Properties (3.i) and (3.ii) mean that H is a pruned tree on A. Thus, P can be seen as the set of all infinite branches of H.
For further reading, we refer to Kechris (1995).
The set P is an uncountable Polish space (essentially the Cantor space \(\{1,2\}^\mathbb {N}\)), so P contains a non-Borel set, see Corollary 6.7.11 in Bogachev (2007).
If \((X,\mathcal {V})\) is a compact Hausdorff space and \(\mathcal {W}\) is another topology on X such that \(\mathcal {W}\) strictly includes \(\mathcal {V}\), then the topological space \((X,\mathcal {W})\) is not compact. Indeed, take a set \(U\in \mathcal {W}{\setminus } \mathcal {V}\). As U is not open in \(\mathcal {V}\), the set \(X{\setminus } U\) is not closed in \(\mathcal {V}\). Because \((X,\mathcal {V})\) is Hausdorff, \(X{\setminus } U\) is not compact in \(\mathcal {V}\) and hence \(X{\setminus } U\) is not compact in \(\mathcal {W}\). However, by the choice of U, the set \(X{\setminus } U\) is closed in \(\mathcal {W}\). Hence, \((X,\mathcal {W})\) cannot be compact.
It is not even known in the context of quitting games, see for instance Solan and Solan (2017) and the references therein.
References
Alós-Ferrer, C., Ritzberger, K.: Characterizing existence of equilibrium for large extensive form games: a necessity result. Econ. Theory 63(2), 407–430 (2017)
Bogachev, V.: Measure Theory. Springer, Berlin (2007)
Bruyère, V.: Computer aided synthesis: a game-theoretic approach. In: Charlier, E., Leroy, J., Rigo, M. (eds.) International Conference on Developments in Language Theory, Lecture Notes in Computer Science, vol. 10396, pp. 3–35. Springer (2017)
Bruyère, V., Le Roux, S., Pauly, A., Raskin, J.F.: On the existence of weak subgame perfect equilibria. In: International Conference on Foundations of Software Science and Computation Structures, pp. 145–161. Springer, Berlin (2017)
Flesch, J., Predtetchinski, A.: Subgame-perfect \(\varepsilon \)-equilibria in perfect information games with common preferences at the limit. Math. Oper. Res. 41(4), 1208–1221 (2016)
Flesch, J., Thuijsman, F., Vrieze, K.: Cyclic Markov equilibria in stochastic games. Int. J. Game Theory 26(3), 303–314 (1997)
Flesch, J., Kuipers, J., Mashiah-Yaakovi, A., Schoenmakers, G., Solan, E., Vrieze, K.: Perfect-information games with lower-semicontinuous payoffs. Math. Oper. Res. 35(4), 742–755 (2010)
Flesch, J., Kuipers, J., Mashiah-Yaakovi, A., Schoenmakers, G., Shmaya, E., Solan, E., Vrieze, K.: Non-existence of subgame-perfect \(\varepsilon \)-equilibrium in perfect information games with infinite horizon. Int. J. Game Theory 43(4), 945–951 (2014)
Fudenberg, D., Levine, D.: Subgame-perfect equilibria of finite and infinite horizon games. J. Econ. Theory 31(2), 251–268 (1983)
Harris, C., Reny, P., Robson, A.: The existence of subgame-perfect equilibrium in continuous games with almost perfect information: a case for public randomization. Econometrica 63(3), 507–544 (1995)
Jaśkiewicz, A., Nowak, A.S.: Non-zero-sum stochastic games. In: Başar, T., Zaccour G. (eds.) Handbook of Dynamic Game Theory. Springer, Cham (2016)
Kechris, A.: Classical Descriptive Set Theory. Springer, Berlin (1995)
Le Roux, S., Pauly, A.: Equilibria in multi-player multi-outcome infinite sequential games. Preprint: Retrieved from arXiv:1401.3325 (2016)
Maitra, A.P., Sudderth, W.D.: Subgame-perfect equilibria for stochastic games. Math. Oper. Res. 32(3), 711–722 (2007)
Mertens, J.F., Parthasarathy, T.: Equilibria for discounted stochastic games. In: Neyman, A., Sorin, S. (eds.) Stochastic Games and Applications. NATO Science Series (Series C: Mathematical and Physical Sciences), vol. 570. Springer, Dordrecht (2003)
Prokopovych, P., Yannelis, N.C.: On strategic complementarities in discontinuous games with totally ordered strategies. J. Math. Econ. 70, 147–153 (2017)
Purves, R.A., Sudderth, W.D.: Perfect information games with upper semicontinuous payoffs. Math. Oper. Res. 36(3), 468–473 (2011)
Secchi, P., Sudderth, W.D.: \(N\)-Person stochastic games with upper semi-continuous payoffs. Int. J. Game Theory 30(4), 491–502 (2001)
Solan, E., Solan, O.: Quitting games and linear complementarity problems. Preprint: Retrieved from arXiv:1707.02598 (2017)
Solan, E., Vieille, N.: Quitting games. Math. Oper. Res. 26(2), 265–285 (2001)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Jérôme Renault, whose remarks inspired us to investigate this research question.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Flesch, J., Herings, P.JJ., Maes, J. et al. Individual upper semicontinuity and subgame perfect \(\epsilon \)-equilibria in games with almost perfect information. Econ Theory 73, 695–719 (2022). https://doi.org/10.1007/s00199-019-01201-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-019-01201-y
Keywords
- Almost perfect information
- Infinite game
- Subgame perfect \(\epsilon \)-equilibrium
- Individual upper semicontinuity


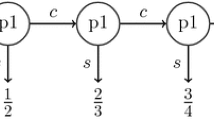
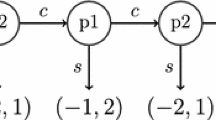

 . At each history
. At each history 


