Abstract
We investigate an adaptive learning model which nests several existing learning models such as payoff assessment learning, valuation learning, stochastic fictitious play learning, experience-weighted attraction learning and delta learning with foregone payoff information in normal form games. In particular, we consider adaptive players each of whom assigns payoff assessments to his own actions, chooses the action which has the highest assessment with some perturbations and updates the assessments using observed payoffs, which may include payoffs from unchosen actions. Then, we provide conditions under which the learning process converges to a quantal response equilibrium in normal form games.


Similar content being viewed by others
Notes
In this paper, we focus on the case in which the probability of choosing an action depends on and is proportional to the past performance of the action. Hart and Mas-Colell (2000) provide a model of adaptive players each of whom regrets the foregone payoffs and the probability of changing his decision depends on his regret. One important difference between this model and their model is that in their model, the probability of each player choosing one action depends on what he is currently choosing: whether each adaptive player changes his current action or not depends on the regret that he has experienced from the action, so that the probability of one action profile being chosen depends on which action profile is currently chosen. As a result, this dependency allows the convergence to a correlated equilibrium. In this paper, we do not allow the dependency and focus on the convergence to a non-correlated equilibrium.
For details, see Funai (2016a).
When it is obvious, we omit the index set and denote the sequence by \(\{ {\mathcal {F}}_{n}\}\). This rule is also applied to the other sequences with index set \({\mathbb {N}}_{0}\).
The formal description of each player’s decision rule is further specified in Sect. 2.2.2.
Note that when \(\gamma =0\), players do not take into account the foregone payoff information and thus there is no distortion on the foregone payoffs. Mathematically, note that \(\gamma _{n,i,s_{i}}{\tilde{\pi }}_{n,i,s_{i}}= {\mathbb {1}}_{n,s_{i}} \pi _{n,s_{i}} \) if \(\gamma =0\) and thus \(\delta \) does not affect the payoffs. Therefore, we impose this technical assumption for analytical convenience in Sect. 4.2.
Therefore, \({\mathbb {1}}_{n,s_{i}}\) is also \({\mathcal {F}}_{n+1}\)-measurable for each i and \(s_{i}\).
Also, the perturbations can be interpreted as random payoffs. In the SFPL model, players experience some random payoffs in addition to the payoffs from the game. Then, after the realisation of the random payoffs, each player chooses the action with the highest total value of the random payoff and the expected payoff with the empirical distribution over opponent actions. Here, the expected payoff and the random payoff of each action correspond to the payoff assessment and the perturbation, respectively.
Property (i) holds due to the (conditional) dominated convergence theorem and the assumption that there exists a positive density for the perturbation profile.
Another widely acknowledged choice rule is the linear choice rule
$$\begin{aligned} C_{i,s_{i}}(Q_{n,i}) =\frac{Q_{n, i,s_{i}}}{\sum _{t_{i} \in S_{i}}Q_{n, i,t_{i}}}, \end{aligned}$$which is adopted by Beggs (2005), Erev and Roth (1998) and Roth and Erev (1995). In this paper, the choice rule is not considered, as it cannot be obtained by the perturbed assessment maximisation. For example, see Proposition 2.3 of Hofbauer and Sandholm (2002).
In this paper, players use the joint empirical distribution on their opponents’ actions, rather than the marginal distribution on each individual opponent’s actions, which is a widely accepted version of stochastic fictitious play. Note that if there exist only two players, the two versions are equivalent; however, if there exist more than two players, then the joint empirical distribution can be correlated in the variant of this paper. Note that the original model of Fudenberg and Kreps (1993) allows the correlation.
\(\overline{D}\) can be a random variable.
Note that since \(\delta =1\) if \(\gamma \in [0,1)\), for each n, i and \(s_{i}\),
-
1.
if \(\gamma =1\), \(\frac{\lambda _{n,i,s_{i}} \gamma _{n,i,s_{i}} }{\alpha _{n,i,s_{i}}} {\tilde{\pi }}_{n,i,s_{i}} ={\tilde{\pi }}_{n,i,s_{i}}\);
-
2.
if \(\gamma \in [0,1)\), \({\tilde{\pi }}_{n,i,s_{i}}=\pi _{n,i,s_{i}}\) and \(\frac{\lambda _{n,i,s_{i}} \gamma _{n,i,s_{i}} }{\alpha _{n,i,s_{i}}} {\tilde{\pi }}_{n,i,s_{i}} = \frac{{\mathbb {1}}_{n,i,s_{i}} + (1-{\mathbb {1}}_{n,i,s_{i}}) \gamma }{ x_{n,i,s_{i}} + (1-x_{n,i,s_{i}}) \gamma } \pi _{n,i,s_{i}}\).
Therefore, \(E[M_{n,i,s_{i}} \mid {\mathcal {F}}_{n}]=0.\)
-
1.
Note that we ignore some aspects such as the noise term and stochastic nature of the learning process. To show the convergence formally, we adopt the stochastic approximation method.
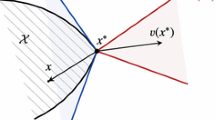
If F is a contraction mapping, then there exists \(k \in [0,1)\) such that for any \(Q,Q' \in {\mathbb {R}}^{|{\mathcal {S}}|}\),

Since \(F(Q^{*})=Q^{*}\) for the fixed point, by replacing \(Q'\) by \(Q^{*}\) in the inequality, we obtain condition (5).
We show in the following argument that if \(\delta =1\), \(x^{*}\) corresponds to a quantal response equilibrium. In addition, if \(\max _{i} \tau _{i}\) approaches 0, then \(x^{*}\) corresponds to a Nash equilibrium.
If \(\gamma =0\), the model coincides with the PAL model.
For instance, see Corollary 2.3 of Hall and Heyde (1980).
The quantal response equilibrium of the prisoner’s dilemma game approaches the unique Nash equilibrium (R, R) as \(\tau _{i} \rightarrow 0\) for each i.
For example, consider two close assessment profiles such that under one payoff assessment profile, one player’s assessment of L is greater than that of R, and under the other payoff assessment profile, his assessment of R is greater than that of L. In this case, his choice probability of L is close to one under the first assessment profile, while the choice probability is close to zero under the other assessment profile. Then, his opponent’s expected payoffs from L (and R as well) under the assessment profiles have a distance of almost 2, which is equal to \(\theta \).
In detail, for the random process \(\{ Q_{n} \}\), which is defined recursively by
$$\begin{aligned} Q_{n+1} = Q_{n} + \lambda _{n}(h(Q_{n}) + M_{n} + \eta _{n}) \end{aligned}$$(13)where (i) \(h: {\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^{m}\) is Lipschitz; (ii) \(\{\lambda _{n} \}\) satisfies condition (2); (iii) \(\{ M_{n}\}\) is a martingale difference with respect to \(\{{\mathcal {F}}_{n} \}\) and square-integrable with
$$\begin{aligned} E[||M||^{2}_{n+1} \mid {\mathcal {F}}_{n}] < K \ a.s., \ n \ge 0 \end{aligned}$$for some \(K>0\); and (iv) \(\sup _{n} ||Q_{n}|| < \infty \), a.s.,
$$\begin{aligned} \lim _{s \rightarrow \infty } \sup _{t \in [s,s+T]} || \overline{Q}_{t} - Q^{s}_{t} || = 0 \ a.s. \end{aligned}$$where the process \(\overline{Q}_{t}\) is a continuous interpolated trajectory of \(\{ Q_{n} \}\) and \(Q^{s}_{t} \) is the unique solution starting at s of the ordinary differential equation \(\dot{Q}_{t} = h (Q^{s}_{t})\), \(t \ge s\) with \(Q^{s}_{s} = \overline{Q}_{s}\).
References
Beggs, A.W.: On the convergence of reinforcement learning. J. Econ. Theory 122, 1–36 (2005)
Benaïm, M.: Dynamics of stochastic approximation algorithms. In: Azéma, J., Émery, M., Ledoux, M., Yor, M. (eds.) Séminaire De Probabilités, XXXIII. Lecture Notes in Mathematics, vol. 1709, pp. 1–68. Springer, Berlin (1999)
Benaïm, M., Hirsch, M.: Mixed equilibria and dynamical systems arising from fictitious play in perturbed games. Games Econ. Behav. 29, 36–72 (1999)
Borkar, V.S.: Stochastic Approximation: A Dynamical Systems Viewpoint. Cambridge University Press, Cambridge (2008)
Camerer, C., Ho, T.H.: Experience-weighted attraction learning in normal form games. Econometrica 67, 827–874 (1999)
Chen, Y., Khoroshilov, Y.: Learning under limited information. Games Econ. Behav. 44, 1–25 (2003)
Cominetti, R., Melo, E., Sorin, S.: A payoff-based learning procedure and its application to traffic games. Games Econ. Behav. 70, 71–83 (2010)
Conley, T.G., Udry, C.R.: Learning about a new technology: pineapple in Ghana. Am. Econ. Rev. 100, 35–69 (2010)
Duffy, J., Feltovich, N.: Does observation of others affect learning in strategic environments? An experimental study. Int. J. Game Theory 28, 131–52 (1999)
Erev, I., Roth, A.E.: Predicting how people play games: reinforcement learning in experimental games with unique mixed strategy equilibria. Am. Econ. Rev. 88, 848–881 (1998)
Fudenberg, D., Kreps, D.M.: Learning mixed equilibria. Games Econ. Behav. 5, 320–367 (1993)
Fudenberg, D., Takahashi, S.: Heterogeneous beliefs and local information in stochastic fictitious play. Games Econ. Behav. 71, 100–120 (2011)
Funai, N.: An adaptive learning model with foregone payoff information. B.E. J. Theor. Econ. 14, 149–176 (2014)
Funai, N.: A unified model of adaptive learning in normal form games. Working paper (2016a)
Funai, N.: Reinforcement learning with foregone payoff information in normal form games. Working paper (2016b)
Grosskopf, B., Erev, I., Yechiam, E.: Foregone with the wind: indirect payoff information and its implications for choice. Int. J. Game. Theory 34, 285–302 (2006)
Hall, P., Heyde, C.C.: Martingale Limit Theory and Its Application. Academic Press, New York (1980)
Hart, S., Mas-Colell, A.: A simple adaptive procedure leading to correlated equilibrium. Econometrica 68, 1127–1150 (2000)
Heller, D., Sarin, R.: Adaptive learning with indirect payoff information. Working paper (2001)
Hofbauer, J., Hopkins, E.: Learning in perturbed asymmetric games. Games Econ. Behav. 52, 133–152 (2005)
Hofbauer, J., Sandholm, W.H.: On the global convergence of stochastic fictitious play. Econometrica 70, 2265–2294 (2002)
Hopkins, E.: Two competing models of how people learn in games. Econometrica 70, 2141–2166 (2002)
Hopkins, E., Posch, M.: Attainability of boundary points under reinforcement learning. Games Econ. Behav. 53, 110–125 (2005)
Ianni, A.: Learning strict Nash equilibria through reinforcement. J. Math. Econ. 50, 148–155 (2014)
Jehiel, P., Samet, D.: Learning to play games in extensive form by valuation. J. Econ. Theory 124, 129–148 (2005)
Laslier, J.F., Topol, R., Walliser, B.: A behavioural learning process in games. Games Econ. Behav. 37, 340–366 (2001)
Leslie, D.S., Collins, E.J.: Individual q-learning in normal form games. SIAM J. Control Optim. 44, 495–514 (2005)
McKelvey, R.D., Palfrey, T.R.: Quantal response equilibria for normal form games. Games Econ. Behav. 10, 6–38 (1995)
Rustichini, A.: Optimal properties of stimulus-response learning models. Games Econ. Behav. 29, 244–273 (1999)
Roth, A.E., Erev, I.: Learning in extensive-form games: experimental data and simple dynamic models in the intermediate term. Games Econ. Behav. 8, 164–212 (1995)
Sarin, R., Vahid, F.: Payoff assessments without probabilities: a simple dynamic model of choice. Games Econ. Behav. 28, 294–309 (1999)
Sarin, R., Vahid, F.: Predicting how people play games: a simple dynamic model of choice. Games Econ. Behav. 34, 104–122 (2001)
Tsitsiklis, J.N.: Asynchronous stochastic approximation and q-learning. Mach. Learn. 16, 185–202 (1994)
Watkins, C.J.C.H., Dayan, P.: Q-learning. Mach. Learn. 8, 279–292 (1992)
Wu, H., Bayer, R.: Learning from inferred foregone payoffs. J. Econ. Dyn. Control 51, 445–458 (2015)
Yechiam, E., Busemeyer, J.R.: Comparison of basic assumptions embedded in learning models for experience-based decision making. Psychon. Bull. Rev. 12, 387–402 (2005)
Yechiam, E., Busemeyer, J.R.: The effect of foregone payoffs on underweighting small probability events. J. Behav. Dec. Mak. 19, 1–16 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper was initially circulated under the title “A Unified Model of Adaptive Learning in Normal Form Games”. I am grateful to Andrea Collevecchio, Marco LiCalzi and Massimo Warglien for their support at the Department of Management, Ca’ Foscari University of Venice. I also thank Rajiv Sarin, Farshid Vahid, Ikuo Ishibashi and seminar audiences at Monash University and UECE Game Theory Lisbon Meetings for suggestions and helpful comments. The comments from the anonymous referees and associate editor also greatly improved the paper. Financial support from the MatheMACS project (FP7-ICT, # 318723), the COPE project (supported by a Sapere Aude grant from the Danish Research Council for Independent Research) and Ca’ Foscari University of Venice is gratefully acknowledged. All remaining errors are mine.
Appendices
Appendices
1.1 The Proof of Proposition 4
The following argument is an extension of the proof of Proposition 5 in Cominetti et al. (2010) when players observe foregone payoff information and there exists a discount factor for the foregone payoff information. In the argument, we provide a condition under which F is a contraction mapping.
Now for Q, \(Q'\), \(x=(C_{i,s_{i}}(Q_{i}))_{i,s_{i}}\) and \(x'=(C_{i,s_{i}}(Q'_{i}))_{i,s_{i}}\), let i and \(s_{i}\) be such that
Consider a telescopic series \(y_{0},\ldots ,y_{N}\) such that \(y_{N}= x\), \(y_{0}=x'\) and
for \(n \notin \{0,N\}\). Then, equation (A.1) is expressed as follows:
Now, the summand for \(l = i\) is expressed as follows:
whereas the summand for \(l \ne i\) is expressed as follows:
where \(\overline{s}_{l}\) is fixed. Note that
for some \(Q^{*}_{l}\). For the last equality, we use the result of Lemma 1, which we show later. Therefore, for the summand of \(l =i\), we have
where \(K := \frac{(1-\delta )}{4}\max _{i,s_{i},s_{-i}} |\pi _{i}(s_{i},s_{-i})|\), whereas for the summand of \(l \ne i\), we have
where \(\theta := \max _{i,s_{i},s_{j},s'_{j}} | \pi _{i}(s_{i},s_{j},s_{-(i,j)}) - \pi _{i}(s_{i},s'_{j},s_{-(i,j)}) |\). Therefore,
where \(\theta ':=\max \{ \theta , K \}\) and \(\beta := \sum _{l \in {\mathcal {N}}} \frac{1}{\tau _{l}}\). Hence, if \((\tau _{l})\) is large enough, that is, \(2 \theta ' \beta <1\), F is a contraction mapping. \(\square \)
Lemma 1
For the logit choice rule, we have
and
for each i, \(Q_{i}\), \(s_{i}\) and \(t_{i}\).
Proof
and
\(\square \)
1.2 The Proof of Proposition 6
As we focus on a symmetric \(2 \times 2\) game, for actions, the set of actions and the payoff function, we omit the subscript referring to players. Since only two actions are available and the weighting parameters of the actions are equivalent for each player, it is enough for the following convergence analysis to focus on the assessment difference. In the following argument, without confusion, let \(Q_{n,i}\) denote the difference of player i’s assessments in period n: for \(s, t \in S\) and \(s \ne t\),
Let \(Q_{n}=(Q_{n,i}, Q_{n,-i})\) be the assessment difference profile. Note that each player’s choice rule can be expressed as a function of the difference: let \(C_{i}: {\mathbb {R}} \rightarrow {\mathbb {R}}\) be the choice rule of player i such that
and \(x_{n,i,s}=C_{i}(Q_{n,i})\).
Now, we express the updating rule of the assessment differences in the following manner: for each n and i,
where
-
1.
\(M'_{n,i} := M_{n, i, t} - M_{n, i, s}\), which is still a martingale difference noise;
-
2.
\(G=(G_{i}, G_{-i}): {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^{2}\) is defined in the following manner: for each i and \(Q=(Q_{i},Q_{-i}) \in {\mathbb {R}}^{2}\),
$$\begin{aligned} G_{i}(Q) :=\,&\big ( \pi (t, x_{-i}) - \pi (s, x_{-i}) \big ) \\ =\,&bx_{-i, s}+ c \end{aligned}$$where
-
(a)
\(x_{i, s}:=C_{i}(Q_{i})\), \(x_{i,t}:= 1-x_{i,s}\) and \(x_{i}:=(x_{i,s}, x_{i,t})\) for each i;
-
(b)
\(b:=( \pi (t, s)- \pi (s, s)) - (\pi (t, t) - \pi (s, t))\);
-
(c)
\(c:= \pi (t, t)- \pi (s, t)\).
-
(a)
By applying the asynchronous stochastic approximation method of Tsitsiklis (1994) to the assessment difference process, we show the convergence to a quantal response equilibrium, at which the following equations hold: for each i,
Without loss of generality, let s be the strictly dominant action of the game. Then, \(Q^{e}_{i}<0\) and \(C_{i}(Q^{e}_{i})> \frac{1}{2}\), as \(Q^{e}_{i} = (\pi (t, s) -\pi (s, s) )x^{e}_{-i, s} +(\pi (t, t) -\pi (s, t) )(1-x^{e}_{-i, s}) <0\). Note also that \(x^{e}_{i,s} \rightarrow 1\) as \(\tau _{i} \rightarrow 0\), which means that the quantal response equilibrium approaches the dominant strategy equilibrium of the game.
Now consider
where
Since \(C_{i}\) is decreasing, concave on the negative domain and convex on the positive domain for each i, we know that
for \(Q^{e}_{i}<0\) and \(C_{i}(Q^{e}_{i})>0\). Also, note that for each i,
and thus
Therefore, if \(b'<1\), we know that \(x_{n}\) converges to the quantal response equilibrium by the asynchronous stochastic approximation method.
Note that for symmetric \(2 \times 2\) games with a strictly dominant action,
and thus we obtain the convergence for the game. \(\square \)
Rights and permissions
About this article
Cite this article
Funai, N. Convergence results on stochastic adaptive learning. Econ Theory 68, 907–934 (2019). https://doi.org/10.1007/s00199-018-1150-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-018-1150-8