Abstract
This paper characterizes a model of reference dependence, where a state-contingent contract (act) is evaluated by its expected value and its expected gain–loss utility. The expected utility of an act serves as the reference point; hence, gains (resp., losses) occur when the act provides an outcome that is better (worse) than expected. The utility representation is characterized by a belief regarding the state space and a degree of reference dependence; both are uniquely identified from behavior. We establish a link between this type of reference dependence and attitudes toward uncertainty. We show that loss aversion and reference dependence are equivalent to max–min and concave expected utility.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In many circumstances, a decision maker (DM) may evaluate an uncertain prospect not only in absolute terms but also in relative relation to some reference point. Kahneman and Tversky (1979) first introduced the notion of reference dependence, in the seminal Prospect theory, to explain experimental violations of expected utility. Within Prospect theory, deviations from the reference point are weighted by a gain–loss value function, which has the feature, referred to as loss aversion, that losses have more negative value than equal sized gains have positive value.
A different resolution for empirical deviations from expected utility proposes models of multiple priors, in particular MaxMin Expected Utility (MMEU). MMEU, axiomatized by Gilboa and Schmeidler (1989) as an explanation of the Ellsberg Paradox,Footnote 1 considers a DM who holds a family of beliefs regarding the likelihood of events. She evaluates uncertain prospects by the minimum expected utility consistent with any of her beliefs. As such, a MMEU DM displays uncertainty aversion (or, ambiguity aversion), the feature that she prefers to minimize her exposure to uncertainty.
At a purely intuitive level, there seems to be a connection between loss aversion and uncertainty aversion; both behaviors characterize some form of pessimism in comparison with a subjective expected utility (SEU) maximizer. A loss averse DM places more weight on the utility of “bad” events but leaves the probabilities undistorted, whereas an uncertainty averse DM places more weight on the probability of “bad” events but leaves the utilities undistorted. We show in this paper that this connection is more than superficial; there exists a formal connection between reference dependence and attitude toward uncertainty. In particular, we axiomatize a simple class of reference-dependent preferences, called asymmetric gain–loss (AGL) preferences, which can be equivalently represented by a MMEU functional. Within our framework, loss aversion and uncertainty aversion produce identical choice data.
1.1 AGL preferences
In addition to formalizing the connection between reference dependence and ambiguity aversion, AGL preferences provide a simple model of endogenous reference dependence. Our object of choice is a state-contingent contract, or act, which is an assignment of consumption (in utility terms) to each state of the world. AGL preferences evaluate an act according to two components: consumption utility and gain–loss utility. The expected consumption utility of an act is as in the standard SEU model, where the decision maker holds a subjective belief, \(\mu \), over the state space. Her expected consumption utility of an act \(f: S \rightarrow {{\mathbb {R}}}\) is
where S is the state space and \(s\in S\) is a generic state. The AGL DM takes this assessment of acts both as the reference point by which gains and losses are measured, and as the baseline level of utility on which gains and losses act as distortions. The main result of this paper is the behavioral characterization of asymmetric gain–loss preferences, which are preferences that can be represented by the functional
The first term is the DM’s subjective expected utility without any reference considerations, and the second is the gain–loss utility. The gain–loss term captures the reference effects. When \(\lambda < 0\), the DM is loss averse and receives a utility penalty when the realized utility falls short of her expectation. This utility penalty is linearly scaled by \(\lambda \). In our representation results, all the elements are identified from choice behavior: \(\mu \) and \(\lambda \) are identified uniquely.Footnote 2
1.2 Reference point formation
There are two alternative views on the formation of endogenous reference points. In the first, the DM forms a reference point before making a choice, based on the set of options that she faces.Footnote 3 As such, her beliefs about her own actions will affect the reference point, leading these papers to generally require an equilibrium condition to account for the mutual relationship between reference points and choices.
In the second, the DM’s chosen action completely determines the reference point. Thus, each element of a choice set is associated with its own reference point.Footnote 4 AGL preferences fall into this second category. In particular, the AGL representation is closely related to the notion of choice acclimating personal equilibrium defined by Kőszegi and Rabin (2007), excepting that there the domain of uncertainty is objective risk. A main contribution of our paper is that, by considering the case where probabilities are subjective, we show how it is possible to simultaneously identify both the reference attitude and the beliefs of the DM.
It is worth noting that when the reference point is defined using equilibrium conditions, as in Kőzsegi and Rabin (2006), the joint identification of beliefs and reference effects is generally not possible. The feedback loop between choices and the reference point can lead to intransitivity of the revealed preference, as shown in Gul and Pesendorfer (2006).
Because of this identification problem, and the intrinsic complexity surrounding equilibrium conditions, the latter notion or reference point determination has proved more suitable for applications. Indeed, many applications use AGL preferences: Lange and Ratan (2010) explore how reference dependence can increase the optimal bid in sealed bid auctions (to be more in line with empirical evidence); Herweg et al. (2010) show that loss aversion can explain prevalence of binary incentive schemes (i.e., bonuses) in moral hazard environments; Abeler et al. (2011) show that, in an effort provision experiment, expectations-based reference dependence best explains their data; Karle and Peitz (2014) consider the competition of differentiated firms when buyers exhibit loss aversion. Each of the above-mentioned papers assumed a kinked, piecewise linear gain/loss function and assumed the reference point was the expected consumption utility—exactly the characterization given here. Our work provides the foundational restrictions for such consumer behavior, and shows that beliefs regarding uncertainty and reference effects can be jointly identified.
1.3 A simple example of AGL preferences
We employ the following numerical example to explain the intuition behind the representation, and show how asymmetric gain–loss preferences can explain different types of behavior regarding uncertainty.
Consider the environment of a seller selling a single good to a buyer who makes a take-it-or-leave-it offer. The value to the seller is \(\hat{v}\) which the buyer believes takes the values \(\{5,3,2\}\), with probability .2, .3, and .5, respectively. The buyer has an independent private value for the object given by \(v = 10\). The buyer will submit her offer, b, and the seller will accept or reject the offer. The seller will accept any offer which (weakly) exceeds her value. The buyer’s utility associated with the bid b is given by
It is obvious that the optimal bid will always be in \(\{5,3,2\}\). If the buyer is a risk neutral expected utility maximizer, her optimal bid solves
The optimal bid is \(b^{RN} = 3\), which has an expected utility of 5.6 before the bid is placed.
Now suppose that the buyer has gain–loss preferences: in addition to the expected value she wants to avoid losses, so she subtracts any expected losses from the expected consumption utility to determine the valuation (this corresponds to the parametrization \(\lambda = -1\)). A loss for her is any outcome where her ex-post utility is worse than the expected value; therefore, outcomes in which she does not obtain the item are considered losses.
Her expected AGL utility, taking into account her gain–loss preferences, of making the bid \(b = 3\) is given by:
which is equal to 4.48. The optimal AGL bid, however, is \(b^{AGL} = 5\), which provides a constant utility, and hence an AGL utility of 5.
When the buyer in this simple take-it-or-leave-it example takes into consideration expected gains and losses in addition to the standard expected utility, she is better off increasing her bid. Intuitively, she sacrifices her payoff in good outcomes (where she obtains the item) in order to decrease the chance of bad outcomes (not obtaining the item). While her payoff is smaller contingent on obtaining the good, the outcome is favorable more often and she increases her ex-ante utility.
A similar behavior could be captured by a buyer who was averse to ambiguity. To see this, assume that the buyer, instead of having AGL preferences, has MMEU preferences. Further, the buyer believes that the distribution of the seller’s valuation is contained in the following set of distributions over \(\{5,3,2\}\):
As such, the buyer chooses a bid according to:
It is straightforward to check that the optimal bid is \(b^{MMEU} = 5\). Therefore, a AGL bidder with \(\mu = [.2, .3,.5]\) and \(\lambda =-1\) and a MMEU bidder with multiple priors given by C will make the same optimal bid. While at first glance this connection may seem contrived, in fact, the AGL and MMEU DMs choose identically not only in this bidding game but in all decision problems—they have identical preferences.Footnote 5 We show in Sect. 3 that AGL behavior can always be equivalently described by a MMEU decision maker.
1.4 Structure of the paper
The rest of the paper is structured as follows. Section 2 provides an axiomatic characterization of the preferences, discusses the concept of the alignment of acts, which is instrumental for the endogenous determination of a reference point, and formally defines the utility representation. Section 3 explores the link between gain–loss and ambiguity attitudes. Section 4 puts forth comparative statics results. Section 5 contains a literature review. All proofs are contained in the “Appendices.”
2 Axiomatization
In this section, we formally present the choice environment and a set of axioms which prove to be necessary and sufficient for the representation presented later in this section.
Let \(S = \{s_1,s_2,\ldots ,s_n\}\) be a finite set of states of the world that represent all possible payoff-relevant contingencies for the DM; any \(E\subseteq S\) is called an event. Define \(\mathcal {E} = \mathcal {P}(S){\setminus }\{\emptyset , S\}\) as the set of all non-trivial events. Denote by \(\mathcal {F} = {{\mathbb {R}}}_{+}^S\) the set of all acts, that is, functions \(f:S\rightarrow {{\mathbb {R}}}_{+}\) (endowed with the standard Euclidean topology). We interpret the act f as providing the payoff f(s) in state \(s \in S\) and assume it is the utility received by the DM when f is chosen and s is realized.Footnote 6
Take the mixture operation on \(\mathcal {F}\) as the standard pointwise mixture, where for any \({\alpha }\in [0,1]\), \({\alpha }f+(1-{\alpha })g\in \mathcal {F}\) gives \({\alpha }f(s)+(1-{\alpha })g(s)\in {{\mathbb {R}}}_{+}\) for any \(s\in S\). Abusing notation, any \(c \in {{\mathbb {R}}}_{+}\) can be identified with the constant act \(c(s) = c\) for all \(s\in S\). Let \(\mathcal {F}_c \cong {{\mathbb {R}}}_{+}\) be the set of constant acts. Preferences on \(\mathcal {F}\) are denoted by the binary relation \(\succsim \); \(\succ \) and \(\sim \) represent, respectively, the asymmetric and symmetric components of \(\succsim \). For each \(f\in \mathcal {F}\), if there is some \(c_f \in \mathcal {F}_c\), such that \(f\sim c_f\), then call \(c_f\) the certainty equivalent of f. Before we can specify the behavioral restrictions on preference that correspond to the AGL utility representation, we need to consider some particular structures in the choice domain.
2.1 Balanced pairs of acts
A particularly important type of act to study AGL preference is given by those that provide perfect hedges against uncertainty. Hedging gets rid of uncertainty, and therefore, it also removes all possible gain–loss considerations from the act. Call a pair of acts \((f,\bar{f})\)balanced if they provide a perfect hedge and are indifferent to each other.Footnote 7 The importance of balanced acts is that eliminating subjective gain–loss considerations allows an analyst to identify beliefs from preferences.
Definition 1
Two acts f and \(\bar{f}\) are balanced if \(f\sim \bar{f}\), and for any states \(s, s'\in S\)
If there exists \(e_f\in \mathcal {F}_c\) such that \(e_f = \frac{1}{2}f(s)+\frac{1}{2}\bar{f}(s)\) for all \(s\in S\), we call \(e_f\) the hedge of f. \((f,\bar{f})\) is referred to as a balanced pair, and \(\bar{f}\) is a balancing act of f (and vice-versa).
When the notation \(\bar{f}\) is used, it is always in reference to the balancing act of \(f\in \mathcal {F}\). The conditions imposed on preferences below guarantee that \(c_f\) and \(e_f\) are unique and well defined for each f.
2.2 Act alignment: separating positive and negative states
Balanced acts will provide a behavioral way of separating gains and losses. We require that when the outcome in state s is considered a gain for f, the outcome on state s is considered a loss for \(\bar{f}\). This is a natural requirement given that f and \(\bar{f}\) provide a perfect hedge to the DM. Hence, \(\bar{f}\) has the exact opposite gain–loss composition of f. For an act, define positive states as those states that deliver gains, and negative states as those states that deliver losses.
Definition 2
Let \((f,\bar{f})\) be a balanced pair. Say \(s\in S\) is a positive state for f if \(f(s) \ge \bar{f}(s)\), and a negative state for f if \(\bar{f}(s) \ge f(s)\). If a state is both positive and negative (i.e., \(f(s) = \bar{f}(s)\)) say s is a neutral state for f.
Any balanced pair of acts induces a set of partitions, each of which splits the state space into two events: one event that contains only positive states for f (\(\{s\in S|f(s) \ge \bar{f}(s)\}\)) and one event that contains only negative states for f (\(\{s\in S|\bar{f}(s)\ge f(s)\}\)). We use the convention that neutral states can be labeled as either positive or negative (but not both).Footnote 8 When there are no neutral states, each act has a unique way of partitioning the states into positive and negative. These partitions associated with each act are called the alignment of the act. We use the convention that the alignment of the act is represented by the event that includes the positive states E (the complement is the negative states) rather than saying that the alignment is represented by the partition \(\{E,E^c\}\).
Definition 3
Let \((f,\bar{f})\) be a balanced pair. For any \(f\in \mathcal {F}\), say f is aligned with the event \(E\in \mathcal {E}\) if for all \(s\in E\), \(f(s)\ge \bar{f}(s)\) and for all \(s\in E^c\), \(\bar{f}(s) \ge f(s)\).
For every \(E\in \mathcal {E}\), there is a set of acts that is aligned with E.
Definition 4
Given any event \(E\subset S\), define \(\mathcal {F}^E\) be the set of acts where the positive states are contained in E, i.e.,
where \(\bar{f}\) is the balancing act to f.
Note that any constant act is its own balancing act, and therefore, constant acts are aligned with all partitions of the state space. It is useful to consider acts that have only one alignment, which are called single-alignment acts. These acts are important because they are acts where small perturbations on outcomes do not change the alignment.
Definition 5
Let \((f,\bar{f})\) be a balanced pair. Then, f is single-alignment act if for no \(s\in S\), \(f(s) = \bar{f}(s)\).
If the event E represents an alignment of f, every subset of E or \(E^c\) is called a non-overlapping event. These are the events where all the states are either all positive or all negative for f, so there is no overlap between positive and negative states for f. Non-overlapping events provide a way of specifying situations where there is no tradeoff between positive and negative states, only across one type of state.
Definition 6
Given \(f\in {\mathcal {F}}\), event \(F\subset S\) is a non-overlapping event for f if every state in F is aligned in the same way.
If follows that F is non-overlapping for \(f \in {\mathcal {F}}^E\) if
Abusing terminology, we say that F is non-overlapping for E whenever F is non-overlapping for all \(f\in {\mathcal {F}}^E\).
With these definitions in mind, we can now specify the behavioral restrictions that are necessary and sufficient to be represented by the AGL functional, as given by Eq. (1.2).
2.3 Standard axioms
The first 3 conditions, A1–A3, are standard axioms in the literature of choice under uncertainty.Footnote 9
-
A1. (Weak Order). \(\succsim \) is complete and transitive.
-
A2. (Continuity). For all \(f\in \mathcal {F}\), the sets \(\{g\in \mathcal {F}: g\succsim f\}\) and \(\{g\in \mathcal {F}: f\succsim g\}\) are closed.
-
A3. (Strict Monotonicity). If for all s, \(f(s) \ge g(s)\) then \(f \succsim g\). If \(f(s) > g(s)\) for some s and \(f(s) \ge g(s)\) for all s, then \(f\succ g\).
2.4 New axioms: mixture conditions
The standard subjective expected utility model from Anscombe and Aumann (1963) is characterized by some version of A1–A3, plus the independence axiom. Independence requires that \(f\succsim g\) if and only if \({\alpha }f + (1-{\alpha }) h \succsim {\alpha }g + (1-{\alpha }) h\) for any \(h\in \mathcal {F}\), and any \({\alpha }\in (0,1)\).
The independence axiom does not hold for AGL preferences because it does not allow for gains and losses to be evaluated differently; convex combinations of acts can change the gain–loss composition of acts, therefore changing the assessments as well. AGL preferences relax independence, but impose three consistency requirements for mixtures of acts.
The first new axiom states that as long as the alignment of acts remains the same when mixing, then independence is preserved. If two acts have the same alignment, taking any mixture of them does not change the composition of gains and losses, so the tradeoff between gains and losses should not change.
-
A4. (Alignment Independence). If \(f,h\in {\mathcal {F}}^E\) and \(g,h \in {\mathcal {F}}^F\) for some \(E,F \in \mathcal {E}\), then \(f\succsim g\) if and only if \({\alpha }f+ (1-{\alpha })h \succsim {\alpha }g + (1-{\alpha })h\) for all \({\alpha }\in [0,1]\).
When considering the families of acts that have the same alignment, Axiom 4 implies the regular independence axiom holds, imposing an expected utility representation over such acts. Further, because constant acts are mutually aligned with all other acts, this provides a connection between the different expected utility representations.
Under the full independence axiom, the preference between an \(\alpha \) mixture of f and h or f and \(h'\) would depend only on the preference between h and \(h'\). Here, on the other hand, mixing acts may change valuations in nonlinear ways: This could happen if either (i) the mixture changes the alignment of states, or (ii) the mixture provides an opportunity to hedge by improving loss states and worsening gain states (or the opposite, if the DM is gain seeking).
The next axiom, Local Mixture Consistency, states that these are the only two reasons for the nonlinearity; Axiom A5 states that the effect of adding a small amount of noise, entirely contained within the positive or negative alignment of an act, depends only on the expected consumption utility of the noise. Because of continuity, a sufficiently small amount of noise will not change the alignment of a single-alignment act. Moreover, if the noise is added only to states that are positive or states that are negative, the mixture does not allow for the possibility of hedging (since any decreasing in loss utility in one negatively aligned state must be added to another negatively aligned state).
-
A5. (Local Mixture Consistency). For any single-alignment acts \(f \in {\mathcal {F}}^E\) and \(g\in {\mathcal {F}}^{E'}\), any event F, which is non-overlapping for bothE and \(E'\), and any \(h,h'\in \mathcal {F}\) such that \(h(s) = \bar{h}(s) = h'(s) = \bar{h}'(s)\) for all \(s\not \in F\), there exists \(\alpha ^* < 1\) such that
$$\begin{aligned} {\alpha }f + (1-{\alpha })h\succsim {\alpha }f + (1-{\alpha })h' \ \Longleftrightarrow {\alpha }g + (1-{\alpha }) h \succsim {\alpha }g + (1-{\alpha }) h', \end{aligned}$$for all \({\alpha }\in ({\alpha }^*,1)\).
To see how the mechanics capture the intuition above: because h and \(h'\) are equal to their hedge—except on a subset of \(E \cap E'\)—they do not contribute any gain/loss considerations except on F. Since all of the variation of h and \(h'\) take place within F, \({\alpha }f + (1-{\alpha })h\) and \({\alpha }f + (1-{\alpha })h'\) will all be aligned the same way for any state \(s \notin F\). Of course, we might still worry that mixing f with h or \(h'\) will alter the alignment differently within F. However, because \(F \subset E\) and f was a single-alignment act, for \(s \in F\), f(s) is strictly better than the expected consumption utility of f. Hence, mixing with very little weight on h or \(h'\) will still not distort the alignment. All of the same considerations hold for g, indicating that the final preference over mixtures depends only on h and \(h'\).
The last axiom imposes a consistency condition on mixtures of acts when reversing the role of gains and losses. Intuitively, the condition requires that the effect of mixing h and f is the opposite to the effect of mixing h and \(\bar{f}\). This condition is called Antisymmetry.
-
A6. (Antisymmetry). For any acts f and g such that \(f\sim g\), for every \(h\in \mathcal {F}\), and for any \(\alpha \in (0,1)\), \( \alpha h + (1-\alpha ) f \succsim \alpha h + (1-\alpha )g\) implies
-
(i)
\( \alpha h + (1-\alpha ) \bar{f} \precsim \alpha h + (1-{\alpha }) \bar{g}\), and,
-
(ii)
\({\alpha }\bar{h} + (1-{\alpha }) f \precsim {\alpha }\bar{h} + (1-{\alpha }) g\),
where \(\bar{f}\), \(\bar{g}\), and \(\bar{h}\) are balancing acts of f, g, and h, respectively.
-
(i)
Since f is indifferent to g, the DM has a strict preference between the mixtures only if h is changing the gain–loss component of utility. Consider the case where the DM is loss-biased. Then, \( \alpha h + (1-\alpha ) f \succsim \alpha h + (1-\alpha )g\) whenever f “smooths” out consumption of h more than g does—f provides a better hedge against the loss states of h. Of course, when f and g are replaced with \(\bar{f}\) and \(\bar{g}\), the losses and gains are reversed, and so, \(\bar{f}\) now exaggerates the loss states of h, breaking the indifference between f and g in the opposite direction. The same intuition applies when h is replaced with \(\bar{h}\). Notice, when h is constant, there is no room for hedging, and so, the mixtures with f and g will be indifferent (as dictated by Alignment Independence).
2.5 Representation results
This section provides the main representation results of the paper. Theorem 2.1 introduces the AGL representation as characterized by the above axioms. This section also outlines important preliminary results that highlight the role of particular axioms and elucidate the relation between the AGL representation and other decision theoretic models.
Theorem 2.1
The preference \(\succsim \) satisfies A1–A6 if and only if there exists a probability distribution \(\mu \in \Delta (S)\) such that \(\mu (s) > 0\) for all \(s \in S\), and a real number \(\lambda \in {{\mathbb {R}}}\) such that \(f \succsim g \iff V(f) \ge V(g)\) where \(V: {\mathcal {F}}\rightarrow {{\mathbb {R}}}\) is defined by
Moreover, (i) \(\mu \) is a unique probability distribution, (ii) \(\lambda \in {{\mathbb {R}}}\) is unique, and \(|\lambda | < \min _{s \in S} \frac{1}{1-\mu (s)}\).
The bound on \(\lambda \) is a consequence of strict monotonicity: Increasing the payoff in any state must increase the valuation of the act. The bound on \(\lambda \) ensure that the marginal increase in consumption utility outweighs any negative marginal decrease in gain/loss utility. The parameter \(\lambda \) captures the difference between the weight placed on gains and the weight placed on losses, which for the representation is unique. An important application of the representation result from Theorem 2.1 is that it provides an index for reference dependence (\(\lambda \)) that is decoupled from risk attitudes, and can be easily estimated. The fact that \(\mu \) lies in the interior \(\Delta (S)\) is also a consequence of strict monotonicity.
2.5.1 Sketch of the proof and preliminary results
The result is proven in two steps. First, Lemma 2.2 provides a SEU representation on \(\mathcal {F}^E\) established by Axioms A1–A4 (that is, excluding Local Mixture Consistency and Antisymmetry), which can be extended to aggregate preferences across families of mutually aligned acts. Then, we utilize the properties of Axioms A5 and A6 to generate the final result.
Lemma 2.2
The preference \(\succsim \) satisfies A1–A4 if and only if there exists a set of probability distributions over S, \(\{\mu _E\}_{E\in \mathcal {E}}\), such that for \(f\in {\mathcal {F}}^F\) and \(g\in {\mathcal {F}}^{F'}\),
Moreover the set \(\{\mu _E\}_{E\in \mathcal {E}}\) is unique.
Every prior in \(\{\mu _E\}_{E\in \mathcal {E}}\) is different, and Alignment Independence does not imply any structure on the priors. To derive the main result from the representation of Lemma 2.2, Local Mixture Consistency and Antisymmetry are used to guarantee that every prior in the set \(\{\mu _E\}_{E\in \mathcal {E}}\) can be written as functions of one unique prior \(\mu \).
If we mix f with a small amount of noise (either the act h or \(h'\)), where the noisy acts exhibit variation only on F non-overlapping with E, then Local Mixture Consistency guarantees that the preference over the two mixtures depends only on the expected consumption utility of the noise. Hence, for all \(E\in \mathcal {E}\), the conditional distributions—conditioned on F non-overlapping with E—are the same for all \(\mu _E\). That is, for E and \(E'\in \mathcal {E}\), \(\mu _E(\cdot |F) = \mu _{E'}(\cdot |F)\) whenever F is non-overlapping for E and \(E'\). In fact, there is a single \(\mu \) such that \(\mu (s | F) = \mu _{E}(s | F)\), keeping the condition of F.
Since E is non-overlapping with itself, this last point implies that for any \(s,s'\in E\), \(\frac{\mu (s)}{\mu (s')} = \frac{\mu _E(s)}{\mu _E(s')}\), which holds only if for all \(s\in E\), \(\mu (s)= \gamma \mu _E(s)\), \(\gamma \in {{\mathbb {R}}}_{++}\). So on E, \(\mu _E\) is just a constant perturbation of the original prior \(\mu \). Since \(E^{c}\) is non-overlapping with E the same holds for \(E^{c}\).
Then, the distribution \(\mu _E\) can be written in the following way
where \(\gamma _E^+\) represents how the original prior is perturbed on the positive states (i.e., E), and \(\gamma _E^-\) represents how the original prior is modified on the negative states. Both \(\gamma _E^+\) and \(\gamma _E^-\) are positive numbers from monotonicity of \(\succsim \), where \(\gamma _E^+ \ge 1 \Leftrightarrow \gamma _E^- \le 1\) for every E because \(\mu _E\) is a probability distribution.
Antisymmetry implies a particular relationship between distributions indexed by complementary alignments, which is that for any \(E,F \in \mathcal {E}\),
Using this observation, we show that for \(s\in E\) the distributions on \(\mu _E\) and \(\mu _{E{\setminus } s}\) depend only on s. In particular, whenever \(s\in E\cap F\),
Then, using these conditions about the family \(\{\mu _E\}_{E\in \mathcal {E}}\) we show that the difference between the distortion on negative states and positive states is always constant, thus \(\gamma _E^+ - \gamma _E^- = \lambda \) for all \(E\in \mathcal {E}\). Therefore, it is possible to characterize any \(\mu _E\), as functions of \(\mu \), and this constant \(\lambda \) that captures the difference between the negative and positive distortions. That is,
Finally, this representation of \(\mu _E\) is used to rewrite the representation from Lemma 2.2 in terms of \(\mu \), which yields the desired result.
3 Relation to ambiguity attitude
3.1 Maxmin expected utility
According to Theorem 2.1, the DM who abides by the AGL axioms is probabilistically sophisticated but displays some reference effect. That is, she holds some unique belief, \(\mu \), regarding the state space, and evaluates each act according to this belief and her preferences for outcomes. Nonetheless, Lemma 2.2 states that the same preferences can be represented by a family of distributions, \(\{\mu _E\}_{E\in \mathcal {E}}\), each of which is a distortion of the original belief, \(\mu \). This alludes to a possible relationship between reference effects and attitudes toward uncertainty, which has classically been modeled by a DM who considers a (non-singleton) set of priors.
Definition 7
\(\succsim \) has an MMEU representation if there exists a convex set of priors \(C \subseteq \Delta (S)\) such that
represents \(\succsim \).
MMEU, axiomatized by Gilboa and Schmeidler (1989), is characterized by two key conditions: certainty independence and uncertainty aversion. Certainty independence requires that \(f\succsim g\) if and only if for all \({\alpha }\in [0,1]\), \({\alpha }f + (1-{\alpha }) c \succsim {\alpha }g + (1-{\alpha }) c\) where \(c\in \mathcal {F}_c\). Mixing two acts with a common constant act does not reverse the preference between them. Since constant acts are aligned with every \(E\in \mathcal {E}\), Alignment Independence implies certainty independence.
Uncertainty aversion requires that for all f, g such that \(f\sim g\) for any \({\alpha }\in (0,1)\), \({\alpha }f + (1-{\alpha }) g \succsim f\). If uncertainty aversion is changed for uncertainty seeking preferences,Footnote 10 then the representation is a Maxmax representation, where the DM evaluates an act according to the prior that maximizes her expectations. It is clear from the representation that if \(\lambda \le 0\) then the DM is uncertainty averse, and if \(\lambda \ge 0\) then she is uncertainty seeking.
Uncertainty aversion can be characterized as a preference for hedging, as hedging reduces the exposure to uncertainty. Moreover, hedging reduces the exposure to negative states. Pushing the utility value in each state closer to the average has more effect on the negative states (because of the loss bias) and hence weakly improves the act.
The formal connection is captured by the following result, which states that asymmetric gain–loss preferences always admit a Maxmin or Maxmax representation and that the set of priors C has a specific structure that is related to the distortion of the (unique) beliefs of the DM.
Theorem 3.1
Suppose \(\succsim \) admits an AGL representation \((\mu , \lambda )\), with \(\lambda < 0\), then \(\succsim \) admits a MMEU representation. Moreover, \(C ={\text {conv}}(\{\mu _E\}_{E\in \mathcal {E}})\), as defined in Lemma 2.2.
Theorem 3.1 has several implications. First, it shows that this form of reference dependence is always tied to a particular attitude toward uncertainty.Footnote 11 So, preferences studied in this paper will always be either uncertainty averse or uncertainty seeking. Second, it gives a precise form to the belief distortion that takes place when gain–loss consideration affect a probabilistically sophisticated DM.
While every AGL representation can be faithfully captured within the MMEU framework, the converse is not true. In the AGL framework, the distorted beliefs keep the relative likelihood of states among gains and among losses unchanged, but, depending on the sign of \(\lambda \), increase or decrease the total weight given to gains (and losses) proportional to the baseline belief. This distortion is a function only of the degree of reference dependence, \(\lambda \), and the baseline prior \(\mu \). In addition, Antisymmetry implies the set of priors is symmetric with respect to all hyperplanes (in the \(|S| - 1\) dimensional simplex) which divide the state space into positive and negative states and which pass through the baseline prior. See Fig. 1; the dashed lines show such symmetries.
Intuitively, this additional symmetric structure imposed on MMEU stems from the fact the reference effects distort utility relative to a reference point. Hence, when translating the utility distortions in the AGL model into the equivalent probabilistic distortions, the symmetries around some reference point is preserved. An arbitrary convex set of priors would not necessarily admit such a baseline prior, and so, could not be translated into a model of reference effects.
3.2 Concave expected utility
Alignment Independence imposes more structure than certainty independence, and therefore, AGL also shares a connection to a class of ambiguity models outside of MMEU. In particular, any loss adverse AGL preference is also a concave expected utility (cavEU) preference. CavEU is a capacity-based model, which considers all possible decompositions of an act into bets over events (where a bet of magnitude \(a_{E} \in {{\mathbb {R}}}_{++}\) on E, is an act that is constant on E and 0 off E, i.e., \(a_{E}\mathbb {1}_{E}\) where \(\mathbb {1}_{E}\) is the characteristic function on E). The preference \(\succsim \) is cavEU if it can be represented by a concave integral introduced by Lehrer (2009).
Definition 8
\(\succsim \) has a cavEU representation if there exists a capacity \(v: 2^{S} \rightarrow [0, 1]\) such that
represents \(\succsim \).
The concave integral returns the maximum value of all possible decompositions, when aggregated according to the capacity v. Lehrer and Teper (2015) show that \(\succsim \) is cavEU if and only if it satisfies A1–A3 plus uncertainty aversion, independence with respect to the constant act 0, and co-decomposable independence. This last requirement states, for every non-bet act f, there exist a bet \(a_{E}\) and an act \(f'\) such that (i) \(f = \alpha a_{E} + (1-\alpha )f'\) for \(\alpha \in (0,1)\), and (ii) \(\succsim \) satisfies independence over \(\{\alpha a_{E} + \beta f' | \alpha ,\beta \in {{\mathbb {R}}}_{+}\}\).
Theorem 3.2
Suppose \(\succsim \) admits an AGL representation \((\mu , \lambda )\), with \(\lambda < 0\), then \(\succsim \) admits a cavEU representation with \(v: \mathcal {P}(S) \rightarrow [0,1]\) defined by \(v: E \mapsto \min _{F \in \mathcal {E}}\mu _F(E)\).
The property that AGL preference admits cavEU representations stems from the fact that each act, \(f \in \mathcal {F}^{E}\) can always be decomposed into a bet on E and another act in \(\mathcal {F}^{E}\). Since all these acts share the same alignment, independence holds within the convex-cone generated thereby. As with the set of priors in the MMEU representation, the capacity v is characterized by the lower envelope of the distorted beliefs arising themselves from Lemma 2.2. Of course, this must be, since these functionals represent the same preferences! Note, cavEU and MMEU are not nested models; AGL preferences reside in the non-trivial intersection.Footnote 12
4 Comparative gain/loss attitudes
This section advances comparative statics results relating behavior to elements of the AGL representation. For an act f, recall the hedge, \(e_{f}\), is the constant act which provides the expected consumption utility in every state; the constant equivalent, \(c_{f}\), is the constant act which provides the expected total utility in every state, in other words taking into account gain/loss considerations.
A natural measure for the degree and direction of reference effects is the gap between \(e_f\) and \(c_f\), the hedge and the certainty equivalent. For a loss averse DM, the difference between the hedge and the constant equivalent is how much, in utility terms, she is will sacrifice to avoid having to feel a loss. In the standard SEU model, \(e_f = c_f\), so the SEU model is the baseline case for reference effects.
Definition 9
Let \(\succsim \) be a preference over \(\mathcal {F}\). Say \(\succsim \) is gain-biased if for all \(f\in \mathcal {F}\), \(c_f \succsim e_f\). Say \(\succsim \) is loss-biased if for all \(f\in \mathcal {F}\), \(e_f \succsim c_f\).
Remark 1
An AGL decision maker is gain-biased (respectively, loss-biased) if and only if she is uncertainty seeking (resp., uncertainty averse) if and only if \(\lambda \ge 0\). (resp., \(\lambda \le 0\)).
Remark 1 follows immediately from the observation that \({{\mathbb {E}}}_{\mu }[f] = e_{f}\) and examination of the representing functionals.
Problematically, however, the hedge and constant equivalent of an act depend on the DM’s beliefs, so if we want to be able to compare two DM’s degree of reference dependence we want to disentangle reference dependence from beliefs. To do this, we define \(f\vee \bar{f}\), the join of a balanced pair \((f,\bar{f})\), as the act that gives the DM the best outcome between f and \(\bar{f}\) for each \(s\in S\).
Definition 10
Given any balanced pair \((f,\bar{f})\), define the act \(f\vee \bar{f}\), the join of\((f,\bar{f})\) as
From the AGL representation, gain–loss utility depends on how much the act deviates state by state from \(e_f\). \(f\vee \bar{f}\) provides the absolute value of the state by state deviations of f from \(e_f\). Thus, the hedge of the join, \(e_{f\vee \bar{f}}\), is the average deviation of f from \(e_{f}\). Then, to capture reference dependence behaviorally across DMs, we focus on acts that have the same hedge: If acts have different hedges, the reference effects can be confounded by the beliefs.
The intuition behind our comparative notion of “more loss biased” is that, holding the hedge constant, the DM prefers an act f with smaller expected losses. Conversely, a DM with gain–bias prefers acts with larger gains. Since we want to consider acts that have the same hedge, the comparative notions of “more gain-biased” and “more loss-biased” depend on a possibly different act for each DM: f for DM 1 and g for DM 2. We use the notation where \(e_f^i\) denotes the hedge of f for DM i. If, in addition, \(e^{1}_{f\vee \bar{f}} = e^{2}_{g\vee \bar{g}}\), then g (evaluated according to \(\mu _{1}\)) has the same variance as g (according to \(\mu _{2}\)). So we say DM 1 is more loss-biased than DM 2, if the exposure to the same variance, keeping the expected consumption utility the same, produces a harsher utility penalty.
Definition 11
Given two preference orders \(\succsim _1\) and \(\succsim _2\), say that \(\succsim _1\) is more loss-biased than \(\succsim _2\) (and \(\succsim _2\) is more gain-biased than \(\succsim _1\)) if for any f, g with \(e_f^1 = e_g^2\) and \(e^1_{f\vee \bar{f}} = e^2_{g\vee \bar{g}}\), then for any \(c\in \mathcal {F}_c\), \(f \succsim _1 c\) implies \(g \succsim _2 c\) and \(f \succ _1 c\) implies \(g \succ _2 c\).
Theorem 4.1
Let \(\succsim _i\) admits an AGL representation given by \((\mu _i,\lambda _i)\) for \(i=1,2\). Then, \(\succsim _1\) is more loss-biased than \(\succsim _2\) if and only if \(\lambda _1 \le \lambda _2\).
When \(\mu _1 = \mu _2\), we can say more than Theorem 4.1.
Remark 2
Let \(\succsim _i\) admits an AGL representation given by \((\mu ,\lambda _i)\) for \(i=1,2\). Further assume \(\lambda _{1} \le \lambda _{2} \le 0\). Then, (i) \(f \succsim _1 c\) implies \(f\succsim _2 c\), for all acts f and constant acts c, and (ii) \(C_2 \subseteq C_1\) for the equivalent Maxmin/Maxmax representation from Theorem 3.1.
These addition equivalences stem from the fact that when DMs have the same belief, then for any \(f\in \mathcal {F}\), \(e_f^1 = e_f^2\). In such circumstances, the degree of loss bias is equivalent to the comparative notion of ambiguity aversion from Ghirardato and Marinacci (2002). Remark 2 furthers this link: Whenever \(\succsim _i\) is gain-biased or loss-biased for both DMs, the notion of loss bias is consistent with the representation of comparative ambiguity aversion derived from Gilboa and Schmeidler (1989) (that the more ambiguity averse DM should have a larger set of priors). This observation establishes a clear connection between the idea of “loss aversion” that has been prevalent since Prospect theory, and uncertainty aversion.
These comparative statics results establish an unexplored link between the absolute and comparative notions of gain or loss bias, and existing notions of uncertainty aversion which is worth further exploring. The initial motivation for studying uncertainty was due to the Ellsberg (1961) idea that DMs are not able to formulate unique probabilities over uncertain events. Many models with multiple priors have been developed to capture what is considered “Ellsbergian behavior.” Nonetheless, even if the DM is able to form a unique prior, having gain–loss considerations can appear to contaminate her prior in a way that gives rise to behavior embodied by some multiple priors model. Hence, for AGL preference a probabilistically sophisticated DM can appear to have multiple priors due to gain–loss asymmetry.
5 Related literature
This paper links reference dependence and attitudes toward ambiguity. We show the notion of choice acclimating personal equilibrium (CPE) from Kőszegi and Rabin (2007)—where the reference point is the expectation of consumption utility—provides a clean way to link these two concepts in the domain of choice under uncertainty. Bell (1985), Loomes and Sugden (1986) and Kőzsegi and Rabin (2006) also provide various models where the DM is loss averse with respect to a reference point given by her expected consumption utility of an uncertain prospect.
In many decision theory models, the status quo has been interpreted as a reference point. Giraud (2004a), Masatlioglu and Ok (2005), Sugden (2003), Sagi (2006), Rubinstein and Salant (2007), Apesteguia and Ballester (2009), Ortoleva (2010), Riella and Teper (2014) and Masatlioglu and Ok (2013) provide models of reference dependence, where the reference point is exogenously given. Along with Kőzsegi and Rabin (2006) and Kőszegi and Rabin (2007), other papers that tackle the problem of endogenous reference point determination are Giraud (2004b), Sarver (2011), Ok et al. (2014), and Werner and Zank (2017). The approach in Ok et al. (2014) investigates reference point determination problem under a very general framework, where they do not need an equilibrium condition to characterize reference dependence. Nonetheless in their framework it is impossible to identify reference points and reference effects uniquely.
In Gul (1991), outcomes of a (n objective) lottery are considered either a disappointment or an elation depending on whether they are less than or more than the certainty equivalent. The DM suffers a utility penalty when an outcome is considered disappointing. In contrast, we assume an outcome is disappointing if it is dispreferred to the hedge, rather than the certainty equivalent. Blavatskyy (2010) extends this to a domain where certainty equivalents need not exist.
Dillenberger (2010) shows that Gul’s disappointment averse preferences satisfy negative certainty independence and so admit a cautious expected utility representation a la Cerreia-Vioglio et al. (2015). The later paper also shows that cautious expected utility is, in the objective risk domain, the analogy to MMEU in the subjective uncertainty domain. The connection between AGL and MMEU is therefore the subjective counterpart to the connection between disappointment aversion and cautious EU. AGL preferences (with \(\lambda < 0\)) satisfy negative certainty independence.Footnote 13
In a similar spirit to our paper, Masatlioglu and Raymond (2016) provide an complete characterization of CPE within the domain of objective risk. They show that CPE is exactly the intersection of quadratic preferences and rank-dependent expected utility preferences.
For AGL preferences, the evaluation of acts depends on the state by state variation of the act. Although some papers have studied attitudes toward variation in the context of risk and uncertainty, none relates such attitudes to reference dependence. In the risk domain, Quiggin and Chambers (1998, 2004) measure attitudes toward risk, which depend on the expectation of the lottery and a risk index of the lottery that depends on the variation of the distribution.
From the vantage of attitudes toward ambiguity, AGL preferences are a clear special case of mean-dispersion preferences: Grant and Polak (2013) axiomatize a very general model of mean-dispersion preferences, where an act is evaluated by the representation \(V(f) = \mu -\rho (d)\), where \(\mu \) is the expected consumption utility of f with respect to a given probability, d is the vector of state-by-state utility deviations from the mean, and \(\rho (\cdot )\) is a measure of (aversion to) dispersion.
Many well-known families of preferences such as Choquet EU (Schmeidler 1989), Maxmin EU (Gilboa and Schmeidler 1989), invariant biseparable preferences (Ghirardato et al. 2004), variational preferences (Maccheroni et al. 2006), and Vector EU (Siniscalchi 2009) belong to this family of preferences. Our paper (under loss aversion) corresponds to the specification where \(\rho = \lambda {{\mathbb {E}}}(\min \{d(s),0\})\). The interest in studying this special case is twofold. First, mean-dispersion preferences are so general that it is predominantly not possible to identify the DM’s baseline prior. (Although some authors do provide various additional restrictions that facilitate identification.) The additional structure imposed in this paper precipitates not only the identification of beliefs, but also the comparative statics results presented in Sect. 4. By taking a stand on way dispersion affects utility (i.e., via linear loss aversion), we can more thoroughly relate the parameters of the representation to behavioral patterns. The second motivation is the ubiquity of AGL (or very similar) preferences in applications. As outlined in Sect. 1.2, linear loss aversion with respect to expected consumption utility has proven to be a popular way of representing reference dependence in applied work. This paper, therefore, precisely outlines the tacit assumptions made in such applications.
Notes
Because it is well established in the literature, we refer the reader to Gilboa and Schmeidler (1989) for a formal discussion of the Ellsberg Paradox and its resolution by MMEU.
When \(\lambda >0\), the DM is gain seeking and receives a utility bonus. At first glance, it may seem counterintuitive that a utility bonus occurs in states where the outcome is below the reference utility. However, because gains and losses are relative to the expectation, expected gains must equal expected losses. Exploiting this symmetry of gains and losses, the above expression is equivalent to having the utility bonus occur in states that surpass the expectations. The equivalent expression given by Eq. (1.3) more clearly illustrates the role of the gain–loss term when \(\lambda \) is positive.
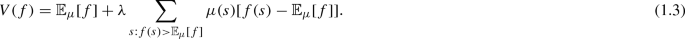
Note, we are tacitly assuming the decision makers cardinal utility has already been identified via standard means, i.e., the examination of preferences over objective lotteries. We could just as easily add a second stage of objective randomization into acts, à la Anscombe and Aumann (1963), but this would require additional notation, and the elicitation of utility values is not central to our model.
Siniscalchi (2009) calls a pair of acts that provide perfect hedging as complementary acts. We strengthen the definition of complementary acts to further require the acts to be indifferent.
We do not allow the neutral states to be labeled both positive and negative, instead when there are neutral states a balanced pair induces more than one partition.
Strict monotonicity implies non-triviality, state-independence, and that no state is null, i.e., the DM puts positive probability on every state occurring.
For all \(f,g\in \mathcal {F}\), \(f\sim g\) implies for all \({\alpha }\in (0,1)\)\(f\succsim {\alpha }f + (1-{\alpha }) g\).
Of course, if \(\lambda > 0\), then Theorem 3.1 holds when Maxmin is replaced with Maxmax.
AGL is a strict subset of the intersection of MMEU and cavEU. A6 implies a specific form to the set of distributions (or, the capacity) in the equivalent representations.
Negative Certainty Independence (adapted to our domain):
$$\begin{aligned} f \succsim c \implies \alpha f + (1-\alpha )g \succsim \alpha c + (1-\alpha )g \end{aligned}$$(NCI)for \(f,g \in {\mathcal {F}}\), \(c \in {\mathcal {F}}_{c}\) and \(\alpha \in (0,1)\). Assume \(f \succsim c\). Notice that when \(\lambda \le 0\) the AGL functional is concave. So we have
$$\begin{aligned} V(\alpha f + (1-\alpha )g)&\ge \alpha V(f) + (1-\alpha )V(g) \\&\ge \alpha V(c) + (1-\alpha )V(g) \\&=V(\alpha c + (1-\alpha )g) \end{aligned}$$where the last equality is a consequence of A4 (that independence is preserved over similarly aligned acts, and in particular, constant acts).
This cannot be violated in case (iii), and in case (ii), E must have more than two elements. Further, note that if \(|F| =1\), \(\gamma _{\emptyset }\) would not be defined, but in that case if \(|S|\ge 3\), \(|F^c| = n-1\) and the result can follow from reversing the roles of F and E, with \(E^c\) and \(F^c\) and Proposition A.3.
References
Abeler, J., Falk, A., Goette, L., Huffman, D.: Reference points and effort provision. Am. Econ. Rev. 101, 470–492 (2011)
Anscombe, F.J., Aumann, R.J.: A definition of subjective probability. Ann. Math. Stat. 34, 199–205 (1963)
Apesteguia, J., Ballester, M.: A theory of reference-dependent behavior. Econ. Theory 40(3), 427–455 (2009)
Bell, D.E.: Disappointment in decision making under uncertainty. Oper. Res. 33(1), 1–27 (1985)
Blavatskyy, P.R.: Expected utility-mean absolute semideviation model of individual decision making under risk. Mimio (2010)
Cerreia-Vioglio, S., Dillenberger, D., Ortoleva, P.: Cautious expected utility and the certainty effect. Econometrica 83(2), 693–728 (2015)
Dillenberger, D.: Preferences for one-shot resolution of uncertainty and allais-type behavior. Econometrica 78(6), 1973–2004 (2010)
Ellsberg, D.: Risk, ambiguity, and the savage axioms. Q. J. Econ. 75(4), 643–669 (1961)
Ghirardato, P., Marinacci, M.: Ambiguity made precise: a comparative foundation. J. Econ. Theory 102(2), 251–289 (2002)
Ghirardato, P., Maccheroni, F., Marinacci, M.: Differentiating ambiguity and ambiguity attitude. J. Econ. Theory 118(2), 133–173 (2004)
Gilboa, I., Schmeidler, D.: Maxmin expected utility with non-unique prior. J. Math. Econ. 18(2), 141–153 (1989)
Giraud, R.: Reference-dependent preferences: rationality, mechanism and welfare implications. Mimeo (2004a)
Giraud, R.: Framing under risk : endogenizing the reference point and separating cognition and decision. Cahiers de la maison des sciences economiques (2004b)
Grant, S., Polak, B.: Mean-dispersion preferences and constant absolute uncertainty aversion. J. Econ. Theory 148(4), 1361–1398 (2013)
Gul, F.: A theory of disappointment aversion. Econometrica 59(3), 667–686 (1991)
Gul, F., Pesendorfer, W.: The revealed preference implications of reference dependent preferences. Mimeo (2006)
Herstein, I.N., Milnor, J.: An axiomatic approach to measurable utility. Econometrica 21(2), 291–297 (1953)
Herweg, F., Müller, D., Weinschenk, P.: Binary payment schemes: moral hazard and loss aversion. Am. Econ. Rev. 100(5), 2451–2477 (2010)
Kahneman, D., Tversky, A.: Prospect theory: an analysis of decision under risk. Econometrica 47(2), 263–291 (1979)
Karle, H., Peitz, M.: Competition under consumer loss aversion. Rand J. Econ. 45(1), 1–31 (2014)
Kőszegi, B., Rabin, M.: Reference-dependent risk attitudes. Am. Econ. Rev. 97(4), 1047–1073 (2007)
Kőzsegi, B., Rabin, M.: A model of reference-dependent preferences. Q. J. Econ. 121(4), 1133–1165 (2006)
Lange, A., Ratan, A.: Multi-dimensional reference-dependent preferences in sealed-bid auctions-how (most) laboratory experiments differ from the field. Games Econ. Behav. 68(2), 634–645 (2010)
Lehrer, E.: A new integral for capacities. Econ. Theory 39(1), 157–176 (2009)
Lehrer, E., Teper, R.: Subjective independence and concave expected utility. J. Econ. Theory 158, 33–53 (2015)
Loomes, G., Sugden, R.: Disappointment and dynamic consistency in choice under uncertainty. Rev. Econ. Stud. 53(2), 271–282 (1986)
Maccheroni, F., Marinacci, M., Rustichini, A.: Ambiguity aversion, robustness, and the variational representation of preferences. Econometrica 74(6), 1447–1498 (2006)
Masatlioglu, Y., Ok, E.A.: Rational choice with status quo bias. J. Econ. Theory 121(1), 1–29 (2005)
Masatlioglu, Y., Ok, E.A.: A canonical model of choice with initial endowments. Rev. Econ. Stud. 81(2), 851–883 (2013)
Masatlioglu, Y., Raymond, C.: A behavioral analysis of stochastic reference dependence. Am. Econ. Rev. 106(9), 2760–2782 (2016)
Ok, E.A., Ortoleva, P., Riella, G.: Revealed (p) reference theory. Am. Econ. Rev. 105(1), 299–321 (2014)
Ortoleva, P.: Status quo bias, multiple priors and uncertainty aversion. Games Econ. Behav. 69, 411–424 (2010)
Quiggin, J., Chambers, R.G.: Risk premiums and benefit measures for generalized–expected-utility theories. J. Risk Uncertain. 17(2), 121–137 (1998)
Quiggin, J., Chambers, R.G.: Invariant risk attitudes. J. Econ. Theory 117(1), 96–118 (2004)
Riella, G., Teper, R.: Probabilistic dominance and status quo bias. Games Econ. Behav. 87, 288–304 (2014)
Rubinstein, A., Salant, Y.: \((a,f)\) choice with frames. Technical report, Mimeo (2007)
Sagi, J.S.: Anchored preference relations. J. Econ. Theory 130(1), 283–295 (2006)
Sarver, T.: Optimal anticipation. Mimeo (2011)
Schmeidler, D.: Subjective probability and expected utility without additivity. Econometrica 57(3), 571–587 (1989)
Shalev, J.: Loss aversion equilibrium. Int. J. Game Theory 29(2), 269–287 (2000)
Siniscalchi, M.: Vector expected utility and attitudes toward variation. Econometrica 77(3), 801–855 (2009)
Stiemke, E.: Über positive Lösungen homogener linearer Gleichungen. Math. Ann. 76, 340–342 (1915)
Sugden, R.: Reference-dependent subjective expected utility. J. Econ. Theory 111(2), 172–191 (2003)
Werner, K.M., Zank, H.: A revealed reference point for prospect theory. Econ. Theory (2017). https://doi.org/10.1007/s00199-017-1096-2
Author information
Authors and Affiliations
Corresponding author
Additional information
We would like to thank David Ahn, Haluk Ergin, Shachar Kariv, Jian Li, Omar Nayeem, Luca Rigotti, Chris Shannon, and seminar participants at UC Berkeley, Pitt, NC State, FSU, and CMU for helpful discussion and comments. We are particularly grateful to Roee Teper for constant discussions and comments throughout all stages of this project.
Appendices
Appendix: Proofs of the main results
This section provides proofs for the main results. The proofs for the auxiliary lemmas and propositions are in Appendix B.
Proof of Lemma 2.2
This is an obvious consequence of the Herstein and Milnor (1953) Mixture Space Theorem. Fix \(E\in \mathcal {E}\). \(\succsim \) satisfies Alignment Independence, \({\mathcal {F}}^E\) is convex, and it includes all the constant acts. Therefore, \(\succsim _E\) and \(\mathcal {F}^E\) define a mixture space, so by the Mixture Space Theorem, the conditions for a SEU representation of \(\succsim _E\) are satisfied. Therefore, there exists a cardinally unique expected utility function \(U_E: {{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\), and an unique probability distribution \(\mu _E: 2^S\rightarrow [0,1]\), such that for any \(f,g\in {\mathcal {F}}^E\),
Where
By strict monotonicity, \(\mu _E(s)> 0\) for all s, so every state is non-null. Moreover, by strict monotonicity, \(U_{E} = id_{{{\mathbb {R}}}}\) clearly represents \(\succsim _{E}\) over the constant acts, and therefore, such a normalization is without loss.
Since any constant \(c\in {\mathcal {F}}_c\) is in \({\mathcal {F}}^E\) for all \(E\in \mathcal {E}\), and every \(f\in {\mathcal {F}}\) has a certainty equivalence \(c_f\), (and \(\succsim \) is complete and transitive), we have, for any \(f\in {\mathcal {F}}^E\), \(g\in {\mathcal {F}}^{E'}\), \(f\succsim g\), if and only if \(c_f \succsim c_g\), if and only if \(V_E(f) \ge V_F(g)\), if and only if
proving the result. \(\square \)
Proof of Theorem 2.1
Start with the representation of Lemma 2.2, which is guaranteed by A1–A4. Hence, there is a set of probability distributions over S, indexed by \(\mathcal {E}\), \(\{\mu _E\}_{E\in \mathcal {E}}\).
Step 1: Show that for every \(E, E'\) the conditional distributions of \(\mu _E\) and \(\mu _{E'}\)- conditional on any event F which is non-overlapping for E and \(E'\), are the same. And show that there is a unique distribution \(\mu \) over S that generates all the conditionals.
Proposition A.1
Suppose \(\{\mu _E\}_{E\in \mathcal {E}}\) constitute SEU representations for \(\succsim _E\) on \({\mathcal {F}}^E\) for all \(E\in \mathcal {E}\). If \(\succsim \) satisfies A1–A6, then there exists a unique distribution \(\mu : 2^S\rightarrow [0,1]\), such that for any \(F, E \in \mathcal {E}\) such that \(F\subseteq E\) or \(F\cap E = \emptyset \), \(\mu _E(\cdot |F)= \mu (\cdot |F)\), where for all \(s\in F\), \(\mu (s|F)= \frac{\mu (s)}{\mu (F)}\).
Proof
In Appendix B. \(\square \)
By Proposition A.1, given \(E\in \mathcal {E}\), for any \(s,s'\in E\), \(\frac{\mu (s)}{\mu (s')} = \frac{\mu _E(s)}{\mu _E(s')}\). This holds if for all \(s\in E\), \(\mu (s)= \gamma \mu _E(s)\), where \(\gamma \in {{\mathbb {R}}}_{++}\). Then, the distribution \(\mu _E\) can be written in the following way
where \(\gamma _E^+\) represents how the original prior is perturbed on the positive states (i.e., E), and \(\gamma _E^-\) represents how the original prior is modified on the negative states (both positive by monotonicity).
Lemma A.2
Given \(E\ne E'\in \mathcal {E}\). Suppose \(\mu _E(s) = \mu _{E'}(s) \) for some s, then \(\mu _E = \mu _{E'}\).
Proof
In Appendix B. \(\square \)
Step 2: Adding Antisymmetry yields some consistency between the distributions induced on \(\mathcal {F}^E\) and \(\mathcal {F}^{E^c}\). In which the average probability attached to each s is always the same for the pair \(\mu _{E}, \mu _{E^c}\), or in other words the distortions on E and \(E^c\) exactly balance out.
Proposition A.3
Let \(\succsim \) satisfy A1–A6, then for any \(E,F\in \mathcal {E}\),
Proof
In Appendix B. \(\square \)
Lemma A.4
Let \(\succsim \) satisfy A1–A6, then for all \(E\in \mathcal {E}\),
where \(\mu _E\) is the distribution from Lemma 2.2 that represents preferences over \({\mathcal {F}}^E\).
Proof
This is an immediate consequence of Propositions A.1 and A.3. \(\square \)
From Lemma A.4, further conclude that \(\gamma _E^{+} + \gamma _{E^c}^- = 2\) for all \(E\in \mathcal {E}\). A more relevant implication is that \(\mu \), uniquely defines \(e_f\) for all \(f\in \mathcal {F}\). Recall that \(e_f\) is defined as the constant where \(e_f = \frac{1}{2} f(s) + \frac{1}{2} \bar{f}(s) \) for all \(s\in S\). Let \(f\in \mathcal {F}^E\) and hence \(\bar{f} \in \mathcal {F}^{E^c}\).
Proposition A.5
Let \(\succsim \) satisfy A1–A6, then for every \(f\in \mathcal {F}\), \(e_f\in \mathcal {F}_c\) is an act such that \(e_f = {{\mathbb {E}}}_{\mu }[f]\).
Proof
In Appendix B. \(\square \)
Step 3: Show that the distribution induced on \(\mathcal {F}^E\) and \(\mathcal {F}^{F}\) only depend on the states they do not have in common.
Proposition A.6
Let \(\succsim \) satisfy A1–A6, then for any \(E,F\in \mathcal {E}\) such that \(|E|, |F| \ge 2\) and \( s \in E\cap F\),
Proof
In Appendix B. \(\square \)
Step 4: Based on the previous results, provide a characterization of the distortions \(\gamma _E^+\) and \(\gamma _E^-\), as functions of \(\mu \) and \(\mu _E\). Further, show that for any particular \(E\in \mathcal {E}\), the difference between the negative and the positive distortion is always constant.
Proposition A.7
If \(\succsim \) satisfies A1–A6, then for any \(E,F\in \mathcal {E}\), \(\gamma _E^+ - \gamma _E^- = \gamma _F^+ - \gamma _F^-\), where \(\gamma _E^+, \gamma _E^-\) are defined as
Proof
In Appendix B. \(\square \)
Therefore, \(\gamma _E^{+} -\gamma _E^{-}\) is a constant (independent of E), which can de defined as
The next step is to characterize \(\lambda \).
Proposition A.8
If \(\gamma _E^{+} -\gamma _E^{-} = \lambda \) for all \(E\in \mathcal {E}\), then for any \(E\in \mathcal {E}\),
Proof
In Appendix B. \(\square \)
Step 5: Use the definition of \(\mu _E\) from Proposition A.8 into the representation from Lemma 2.2.
For any \(f\in \mathcal {F}^E\), then \(V(f) = {{\mathbb {E}}}_{\mu _E}[f]\) which is equivalent to
The representation follows from the observation that \(E^c = \{s \in S | f(s) < e_{f} = {{\mathbb {E}}}_{\mu }[f]\}\).
Step 6: Establish the claims on \(\mu \) and \(\lambda \).
The uniqueness of \(\mu \) and of every \(\mu _E\) follows from the uniqueness in the SEU model. \(\lambda = \gamma _E^{+} -\gamma _E^{-}\) is unique as well from the definition of \(\gamma \)’s from (B.13) and (B.13). Finally, the bound is given by the following proposition.
Proposition A.9
The functional given by (AGL) is monotone if and only if \(|\lambda | \le \min _{s} \frac{1}{1-\mu (s)}\).
Proof
In Appendix B. \(\square \)
\(\square \)
Proof of Theorem 3.1
Let \((\{\mu _E\}_{E\in \mathcal {E}}, \lambda )\) be an AGL representation. Let \(C ={\text {conv}}(\{\mu _E\}_{E\in \mathcal {E}})\). Then, from Eq. (A.3), we know, for any \(f \in \mathcal {F}\) and \(E \in \mathcal {E}\),
Hence, if \(\lambda < 0\), the functional, \({{\mathbb {E}}}_{\mu _{E}}[f]\), for a fixed f, is minimized at \(E = \{s \in S | f(s) < {{\mathbb {E}}}_{\mu }[f]\}\), and if \(\lambda > 0\) is maximized at \(E = \{s \in S | {{\mathbb {E}}}_{\mu }[f] < f(s)\}\). In either case, this is exactly (AGL). \(\square \)
Proof of Theorem 3.2
That \(\succsim \) satisfies A1–A3, uncertainty aversion and independence with respect to the constant act 0 is immediate. So it remains to show \(\succsim \) satisfies co-decomposable independence. Fix some non-bet act \(f \in {\mathcal {F}}^{E}\) and assume without loss of generality that E includes all neutral states for f. It is clear that the bet \(a_{E} = e_{f}\) (that is equals \(e_{f}\) on E and 0 otherwise) is also in \(\mathcal {F}^{E}\). For each \(\alpha \in (0,1)\) denote \(f'\) as the bet \(2f - a_{E}\), so \(f' = \frac{1}{2}f + \frac{1}{2}a_{E}\). Now, let \(g = \alpha a_{E} + \beta f'\) with \(\alpha ,\beta \in {{\mathbb {R}}}_{+}\). Then, for each \(s \in E\), \(g(s) = \alpha f'(s) + \beta a_{E}(s) = \alpha (\frac{1}{2}f(s) + \frac{1}{2}a_{E}(s)) + \beta a_{E}(s) \ge \alpha (\frac{1}{2}e_{f} + \frac{1}{2}e_{a_{E}}) + \beta e_{a_{E}} = \alpha e_{f'} + \beta e_{a_{E}} = e_{g}\). Likewise, for \(s \in E^{c}\), \(g(s) < e_{g}\). Hence, \(g \in \mathcal {F}^{E}\). So by Alignment Independence \(\succsim \) satisfies independence over \(\{\alpha a_{E} + \beta f' | \alpha ,\beta \in {{\mathbb {R}}}_{+}\}\).
Finally, to characterize v, notice that the capacity is fully determined by its valuation over all bets and that it is unique. Further, by Theorem 3.1, \(V^{MM}(a_{E}) = \min _{F \in \mathcal {E}}\mu _F(E)a_{E}\), for any bet \(a_{E}\). Hence, \(v: E \mapsto \min _{F \in \mathcal {E}}\mu _F(E)\) induces that same ranking over bets as \(V^{MM}(\cdot )\), and therefore represents \(\succsim \). \(\square \)
Proof of Theorem 4.1
Use the notation that superscripts denote the DM, e.g., \(e_f^i\) is the hedge of f for DM i.
(i) \(\Rightarrow \) (ii). Let \(\succsim _1\) be more loss-biased than \(\succsim _2\). Consider any \(f,g\in \mathcal {F}\) such that \(e^1_f = e^2_g\) and \(e_{f\vee \bar{f}}^1 = e_{g\vee \bar{g}}^2 \). So, by Proposition A.5, \({{\mathbb {E}}}_{\mu _{1}}[f\vee \bar{f}] = {{\mathbb {E}}}_{\mu _{1}}[g\vee \bar{g}]\). Now observe, by definition \(f\vee \bar{f} = e_{f} + |f - e_{f}|\):
Since, \(e^1_f = e^2_g\), this implies
Suppose further, \(f\succsim _1 c\) for any \(c\in \mathcal {F}_c\), implies that \(g\succsim _2 c\). Clearly, this is true if and only if \(V_{2}(g) \ge V_{1}(f)\). We can write \(V_{2}(g) \ge V_{1}(f)\) as defined in (AGL) as,
Canceling according to (A.4) and \({{\mathbb {E}}}_{\mu _{1}}[f] = e_{f}^{1} = e_{g}^{2} = {{\mathbb {E}}}_{\mu _{2}}[g]\) we see \(\lambda _2 \ge \lambda _1\).
(ii) \(\Rightarrow \) (i). Let \(\lambda _2 \ge \lambda _1\). Let \(f,g\in \mathcal {F}\) be such that \(e_f^1 = e_g^2\), and \(e_{f\vee \bar{f}}^1 = e_{g\vee \bar{g}}^2\). Suppose for some \(c\in \mathcal {F}_c\), \(f\succsim _1 c\). Therefore, using the associate given by Proposition A.5,
Since \(e_{f\vee \bar{f}}^1 = e_{g\vee \bar{g}}^2\), \({{\mathbb {E}}}_{\mu _{1}}[|f - e^{1}_{f}|] = {{\mathbb {E}}}_{\mu _{2}}[|g - e^{2}_{g}|]\) by the same logic of (A.4). So,
Therefore, \(V_2(g) \ge c\), as desired. \(\square \)
Proofs of lemmas and propositions
Proof of Proposition A.1
Consider any \(E,E'\in \mathcal {E}\), and single-alignment acts \(f\in {\mathcal {F}}^E\), \(g\in {\mathcal {F}}^{E'}\). Let F be a non-overlapping event for both E and \(E'\). Consider two distinct \(h,h' \in \mathcal {F}\), such that \(h(s) = \bar{h}(s) = h'(s) = \bar{h'}(s)\) for all \(s\not \in F\), which means that their alignment is neutral in \(F^c\). Moreover suppose that for every \(s\in F\), \(h(s) > \bar{h}(s)\) or \(h(s) < \bar{h}(s)\), and \(h'(s) > \bar{h'}(s)\) or \(h'(s) < \bar{h'}(s)\), so that on every state in F, h and \(h'\) are either strictly considered positive or negative. Further assume that for all \(s\in F\), \(0< h(s) < h'(s) \) or \(0< h'(s) < h(s)\) (hence on F the acts are always different in terms of preferences). By Strong Monotonicity and Continuity, there is always possible to find such acts h and \(h'\).
Local Mixture Consistency guarantees for f, g, h there exists some \(\alpha _{hh'}\) such that for any \(\alpha \in ({\alpha }_{hh'}, 1)\),
Moreover, since f and g are single-aligned continuity of preferences, it implies that alignment does not change for small perturbations around f and g. Hence, the for \({\alpha }\) close to one, \({\alpha }f + (1-{\alpha }) h\in \mathcal {F}^E\), and \({\alpha }g + (1-{\alpha }) h\in \mathcal {F}^{E'}\). From the representation of 2.2, (B.1) implies
Which by linearity and the fact that \(h(s) = h'(s)\) for all \(s\not \in F\), reduces to
Normalize \(\mu _E\) and \(\mu _{E'}\) conditional on F to be probability distributions over F, then Eq. (B.2) becomes
Since all states are non-null, \(\mu _E(\cdot |F)\) and \( \mu _{E'}(\cdot |F)\) are strictly positive |F|-dimensional vectors. These vectors are normal to \((h - h') \in {{\mathbb {R}}}^{|F|}\), which consists of nonzero elements by the assumption that h and \(h'\) are different for all \(s\in F\). Therefore, \(\mu _E(\cdot |F)\) and \( \mu _{E'}(\cdot |F)\) are collinear vectors in \({{\mathbb {R}}}^{|F|}\), with norm 1. Then, for all \(s\in F\),
It remains to show that if (B.3) holds there exists a unique distribution \(\mu \) that generates the conditional distributions, i.e., such that for all \(E\in \mathcal {E}\) and non-overlapping F,
Consider the events \(E_i = \{s_i, s_{i+1}\}\) for \(i = 1,\ldots ,n-1\). If such a \(\mu \) exists it follows from (B.4) that for \(E_i\),
If such a \(\mu \) exists and it is unique for the set \(\{E_i\}_{i=1,\ldots ,n-1}\), then by (B.3), it will hold for any \(E\in \mathcal {E}\). This is because the set \(\{E_i\}_{i=1,..n}\) can be used to find the conditional distributions for any other \(E\in \mathcal {E}\) using the results from the first part of the proof. To see this suppose that there is a unique \(\mu \) such that for all \(\{E_i\}_{i=1,\ldots ,n-1}\), (B.4) holds. Now consider some \(E\not \in \{E_i\}_{i=1,\ldots ,n-1}\). \(E \subset \bigcup _{i=m}^M E_i := E_m^M\) for some \(m< M\), where \(m \ge 1\) and \(M \le n\). Then, for any \(s_t,s_{k}\in E\), \(t< k\) and \(t,k\in \{m,\ldots ,M\}\), \(\frac{\mu _E(s_t)}{\mu _E(s_{k})} = \frac{\mu _{E^M_m}(s_t)}{\mu _{E^M_m}(s_{k})}\) from (B.3). Moreover,
Hence, it suffices to show that for the set \(\{E_i\}_{i=1,\ldots ,n}\), a unique distribution exists such that (B.4) holds. Note that (B.5) implies that for any \(i=1,2,\ldots n-1\),
These \(n-1\) equations, along with the necessary condition to be a probability distribution:
gives n equations and n unknowns (the \(\mu (s_i)\)’s), which can be written in the following form:
Equation (B.6) has a unique solution if and only if the matrix \(A_n\) is invertible. We will prove the stronger condition that \({\text {det}}(A_n)> 0\) instead, by induction on |S|. Let \(|S|=3\), then need to show that \({\text {det}}(A_3) \ne 0\). Let \(a_{ij} = \frac{\mu _{E_i}(s_i)}{\mu _{E_i}(s_{j})} >0\). \(a_{ij} \in (0,\infty )\) because every state is non-null so \(\mu _{E_i}(s_j) > 0\) for all i, j. We have,
Suppose now that \({\text {det}}(A_k) > 0\) for all \(k< m\). Then

Hence \({\text {det}}(A_k) = {\text {det}}(A_{m-1}) + a_{12} {\text {det}}(B_k)\) where \(B_k\) is defined as

Therefore, \({\text {det}}(A_k) = {\text {det}}(A_{m-1}) + a_{12} (a_{23} {\text {det}}(A_{m-3})) > 0\), from the induction hypothesis that for all \(k<m\), \(\det (A_k ) > 0\). Hence, the system from Eq. (B.6) has a unique solution, \(\mu \). From the previous result, for any \(E\in \mathcal {E}\) such that \(|E|>2\), \(\mu _E\) is also generated by \(\mu \). Hence, there exists a unique \(\mu :2^S\rightarrow [0,1]\) such that every conditional distribution of \(\mu \) (conditional on event F), is the same as the conditional distribution of \(\mu _E\) provided that F and E are non-overlapping. \(\square \)
Proof of Lemma A.2
Suppose there exists \(s\in S\) such that \(\mu _E(s) = \mu _{E'}(s)\) for some \(E\ne E'\). Then, by Proposition A.1, there are two cases:
-
(i.)
\(s\in E\cap E'\) (or \(s\in E^c \cap {E'}^c\)).
-
(ii.)
\(s\in E \cap (E')^c\) (or \(s\in E'\cap E^c\)).
For case (i) by Proposition A.1, for every \(s'\in E\cup E'\), \(\mu _E(s') = \mu _{E'}(s)\) since \(\mu _E(s) = \gamma _E^+ \mu (s)\) and \(\mu _E(s) = \gamma _{E'}^+\mu (s)\). In addition, for any \(t\in E\cap (E')^c\), \(\mu _E(t) = \mu _{E'}(t)\) by the same argument, which implies that for all \(s\in (E')^c\), \(\mu _{E'}(s) = \gamma _{E'}^+ \mu (s)\), which can only be true if \(\gamma _E^+ = \gamma _{E'}^+ = 1\). Hence, \(\mu _E = \mu _{E'} = \mu \). For the second case, the argument is symmetric (replacing \(\gamma _{E'}^+\) for \(\gamma _{E'}^-\)). \(\square \)
Proof of Proposition A.3
Consider some single alignment \(f\in \mathcal {F}^E\), and \(g\in \mathcal {F}^F\) such that \(f\sim g\), where \(\bar{f}\in \mathcal {F}^{E^c}\) and \(\bar{g}\in \mathcal {F}^{F^c}\) are the respective balancing acts. Given \(s\in S\), consider some \(h\in \mathcal {F}\) such that \(h(t) = 0\) for all \(t\ne s\) and \(h(s) > 0 \).
Suppose \({\alpha }f + (1-{\alpha })h \succ {\alpha }g+ (1-{\alpha }) h\), then by Antisymmetry \({\alpha }\bar{f} + (1-{\alpha })h \prec {\alpha }\bar{g}+ (1-{\alpha }) h\). From the definition of alignment and continuity of \(\succsim \), for \({\alpha }\) close to 1, then \({\alpha }f + (1-{\alpha })h\in \mathcal {F}^E\) and \({\alpha }g+ (1-{\alpha }) h \in \mathcal {F}^F\); likewise \({\alpha }\bar{f} + (1-{\alpha })h\in \mathcal {F}^{E^c}\) and \({\alpha }\bar{g}+ (1-{\alpha }) h\in \mathcal {F}^{F^c}\). Therefore, by the representation result from Lemma 2.2, from Antisymmetry \(\mu _E(s) > \mu _F(s)\) if and only if \(\mu _{F^c}(s) > \mu _{E^c}(s)\).
Suppose \(\mu _E+\mu _{E^c}\ne \mu _F+\mu _{F^c}\). It must be the case that the following two conditions hold:
Let \(h' \in \mathcal {F}\) be such that \(h'(t) = 0\) for all \(t\ne s,s'\), and \(h'(s),h'(s') \ne 0\). According to the above argument, for single alignment \(f\in \mathcal {F}^E\) and \(g\in \mathcal {F}^{F}\) where \(f\sim g\), for \({\alpha }\) close to 1, we can appeal to Antisymmetry and to obtain,
In other words, there is no solution to the system obtained from Eqs. B.7 and B.8.
Since there is no solution to (B.9), there exists some \(p > 0\) (Stiemke’s Alternative (Stiemke 1915)) such that
which implies that \(\left( \mu _{F^c}(s)-\mu _{E^c}(s)\right) \left( p_1\theta - p_2 \right) = 0\) and \(\left( \mu _{F^c}(s')-\mu _{E^c}(s')\right) (p_1\theta ' - p_2) = 0\), where \(p > 0\). Since \(\left( \mu _{F^c}(s)-\mu _{E^c}(s)\right) \ne 0\) and \(\left( \mu _{F^c}(s')-\mu _{E^c}(s')\right) \ne 0\), it must be the case that \((p_1\theta ' - p_2) = (p_1\theta - p_2) = 0\), which never holds when at least \(p_1 \) or \(p_2\) are nonzero, and \(\theta> 1 > \theta '\). A contradiction. Therefore, for any \(E,F\in \mathcal {E}\),
\(\square \)
Proof of Proposition A.5
Recall \(e_f\) is defined as the constant such that for a balanced pair, \((f,\bar{f})\), \(\frac{1}{2} f(s) + \frac{1}{2} \bar{f}(s) = e_f\) for all \(s\in S\). From lemma A.4 and the representation from Lemma 2.2,
\(\square \)
Proof of Proposition A.6
We will prove the claim in steps. First, for all such E and F such that \(E \cup F = S\) and \(E \cap F^{c} \ne \emptyset \) and \(F \cap E^{c} \ne \emptyset \) and \(E \cap F = I \ne \emptyset \), we claim \(\mu _E-\mu _{E{\setminus } I} = \mu _F - \mu _{F{\setminus } I}\). Indeed, by definition \(F{\setminus } I = E^c \ne \emptyset \) and \(E{\setminus } I = F^c \ne \emptyset \). So,
Also, from Proposition A.3, \(\mu _E + \mu _{E^c} = \mu _F + \mu _{F^c}\) for all \(E,F\in \mathcal {E}\). This and the above observation imply \(\mu _E-\mu _{E{\setminus } I} = \mu _F - \mu _{F{\setminus } I}\).
Next, we claim, for all such E and F such that \(E \cap F^{c} \ne \emptyset \) and \(F \cap E^{c} \ne \emptyset \) and \(E \cap F = I \ne \emptyset \), \(\mu _E-\mu _{E{\setminus } I} = \mu _F - \mu _{F{\setminus } I}\). To see this, notice that \((E, E^{c} \cup I)\), \((E^{c} \cup I, F^{c} \cup I)\), and \((F^{c} \cup I, F)\) all satisfy (as pairs of subsets), the conditions to apply the first claim. So, \(\mu _E-\mu _{E{\setminus } I} = \mu _{(E^{c} \cup I)}-\mu _{E^{c}} = \mu _{(F^{c} \cup I)}-\mu _{F^{c}}= \mu _F - \mu _{F{\setminus } I}\), as desired.
Finally, we use this second claim to prove the proposition. Let E and F be such that \(s \in E \cap F\). Notice, if \(E \cap F = s\) we can apply the second claim directly. So assume \(s \subsetneq E \cap F\). There are two cases. (i) \(E^{c} \cap F^{c} \ne \emptyset \). Then, \((E, (E^{c} \cap F^{c}) \cup s)\), and \(((E^{c} \cap F^{c}) \cup s, F)\), satisfy the conditions of the second claim so, \(\mu _E-\mu _{E{\setminus } s} = \mu _{(E^{c} \cap F^{c}) \cup s}-\mu _{E^{c} \cap F^{c}} = \mu _F-\mu _{F{\setminus } s}\). (ii) \(E^{c} \cap F^{c} = \emptyset \). Then, \((E,E^{c} \cup s)\) satisfy the conditions for the second claim: \(\mu _E-\mu _{E{\setminus } s} = \mu _{(E^{c} \cup s)}-\mu _{E^{c}}\). Now notice that it must be that \(E^{c} \cup s \subset F\), hence \((E^{c} \cup s)^{c} \cap F^{c} \ne \emptyset \). Applying case (i) provides \(\mu _{(E^{c} \cup s)}-\mu _{E^{c}} = \mu _F-\mu _{F{\setminus } s}\). This completes the proof. \(\square \)
Proof of Proposition A.7
Consider 3 different cases, (i) \(E =F^c\), (ii) \(F\subsetneq E\) and (iii) \(E\cap F \ne \emptyset \) and \(E^c \cap F\ne \emptyset \), and \(E \cap F^c \ne \emptyset \). It suffices to consider these three conditions since whenever \(E\cap F = \emptyset \), and \(E^c\cap F^c \ne \emptyset \), Lemma A.4 will get the result for E and F, from \(E^c\) and \(F^c\).
First note that the case where \(E = F^c\) the result follows straightforwardly from Proposition A.3. For cases (ii) and (iii) notice that there exists some \(s \in E \cap F\). It is without loss of generality to assume that \(|E|, |F| \ge 2\),Footnote 14 for this s and any \(t \in S\), we can divide (A.1) (from proposition A.6) by \(\mu (t) > 0\) and obtain
Now, consider the case where \(F\subsetneq E\). By the definition of \(\gamma _E^+= \frac{\mu _E(s)}{\mu (s)}\) for \(s\in E\), and \(\gamma _E^-= \frac{\mu _E(s)}{\mu (s)}\) for \(s\in E^c\). Suppose \(s \in E\cap F\), then using (B.10) and the definition of states as positive or negative (when viewed from \(E,F,E{{\setminus }}s\), and \(F{{\setminus }}s\)). Since \(F \subsetneq E\), there exists some \(s\in E\cap F\) and \(t\in E^{c} \cap F^{c}\).
Subtracting (B.11b) from (B.11a) yields \(\gamma _E^+ - \gamma _E^- = \gamma _F^+ - \gamma _F^-\).
Now consider the cases where \(E\cap F \ne \emptyset \) and \(E^c \cap F\ne \emptyset \), and \(E \cap F^c \ne \emptyset \). Define \(G = E \cap F\), so, \(G \subsetneq E\) and \(G \subsetneq F\). Applying case (ii) twice (i.e., \(\gamma _E^+ - \gamma _E^- = \gamma _G^+ - \gamma _G^- = \gamma _F^+ - \gamma _F^-\)), proves the claim. \(\square \)
Proof of Proposition A.8
By definition \(\mu _E(s)= \gamma _E^+ \mu (s)\) if \(s\in E\) and \(\mu _E(s) = \gamma _E^- \mu (s)\) if \(s\in E^c\). Since \(\gamma _E^+\) is the same for all \(s\in E\), it follows that for any \(E'\subseteq E\), then \(\mu _E(E') = \gamma _E^+ \mu (E')\) as well. Then, \(\gamma _E^{+} -\gamma _E^{-} = \lambda \) implies that
Solving for \(\mu _E(E)\) yields \(\mu _E(E) =\mu (E)\left( 1+ \lambda (1-\mu (E))\right) \), hence
Likewise we can solve for \(\gamma _E^-\) to get
The fact that \(\frac{\mu _E(E)}{\mu (E)} = \frac{\mu _E(s)}{\mu (s)}\) for all \(s\in E\), and \(\frac{\mu _E(E^c)}{\mu (E^c)}= \frac{\mu _E(s)}{\mu (s)}\) for all \(s\in E^c\) follows from Proposition A.1. Therefore
This proves the result. \(\square \)
Proof of Proposition A.9
We prove the case where \(\lambda > 0\), the opposite case is a clear analogy. Only if: assume to the contrary that \(\lambda \) exceeds this bound. Let \(s' = \text {argmin}_{S} \mu (s)\). Let \(y < 1\) and let f be the act defined by \(f(s) = 1\) for all \(s \ne s'\) and \(f(s') = y\). Then
Thus, V violates monotonicity. If: assume \(\lambda \) meets such a bound.
Define \(\phi : {{\mathbb {R}}}\rightarrow {{\mathbb {R}}}\) as \(\phi = \max \{0,x\}\). Since \(\phi \) is the maximum of two linear, hence convex, functions, it is convex. Notice we can rewrite \(V(f) = {{\mathbb {E}}}_{\mu }[f] + \lambda {{\mathbb {E}}}_{\mu }\phi (f - {{\mathbb {E}}}_\mu [f])\), so V is convex. From this perspective, we will show that every element of \(\partial V(f)\), the sub-differential at f, is strictly positive (for f in the interior of \({{\mathbb {R}}}^{n}_{+}\)). We have \(\partial V(f) = \partial ({{\mathbb {E}}}_{\mu }[f]) + \lambda \sum _{s}\mu (s) \partial \big (\phi (f(s) - {{\mathbb {E}}}_\mu [f])\big )\). So let \(d \in \partial V(f)\) and consider the s-wise component of d. Then, we have
where \(\phi '_{+} = 1\) and \(\phi '_{-} = 0\) are the maximum and minimum s-components of \(\partial \phi \), respectively. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lleras, J.S., Piermont, E. & Svoboda, R. Asymmetric gain–loss reference dependence and attitudes toward uncertainty. Econ Theory 68, 669–699 (2019). https://doi.org/10.1007/s00199-018-1138-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00199-018-1138-4
Keywords
- Reference-dependent preferences
- Endogenous reference points
- Gain–loss attitudes
- Subjective expected utility
- Belief distortion