Divide and rule: redistribution in a model with differentiated candidates

“...and the result which follows in democracies is that the poor are more sovereign than the rich, for they are in a majority, and the will of the majority is sovereign.”

Aristotle (Politics VI.2, 1317a40)

Abstract

We study an electoral competition model in which each voter is characterized by income level and non-economic characteristics, and where two vote share maximizing candidates, with fixed non-economic characteristics (differentiated candidates), strategically promise a level of redistribution. We prove existence of a unique Nash equilibrium which is characterized by policy convergence or divergence depending on whether candidates redistribution technologies are symmetric or not. Perhaps more importantly, we show that, independently of whether the equilibrium is convergent or divergent, there are three predominant effects on equilibrium tax rates: the group-size effect (the larger an income group, the larger its influence on equilibrium tax rate), the income effect (poor voters are more responsive to a redistributive transfer) and the within-group homogeneity effect (the degree to which voters of the same income group have similar non-economic characteristics). The latter drags redistribution toward the preferred level of redistribution of the less “divided”—in terms of non-economic characteristics—income group and may dominate over the other two.

1 Introduction

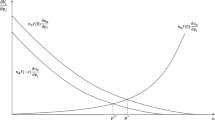
Over the past three decades, income inequality has steadily risen in many democracies and the middle class has become relatively poorer (Piketty and Saez 2003; Atkinson et al. 2011). Yet, in contrast with the predictions of economic theory of democracy (Downs 1957) that the democratic process will eventually reflect the preferences of the majority, rich voters’ preferences for less redistribution seem to be better represented. As many observers note (e.g., Bonica et al. 2013), while the majority of voters has become poorer (in relative terms) one does not observe majority’s preferences over taxation and redistribution being met by politicians (Fig. 1).¹ But how is it possible that democratic politics end up in such representation gaps? Since politicians compete for votes why is it not the case that they converge to promising the level of redistribution that the majority of voters prefers?

Fig. 1

a Fractile income shares in the US: 1968–2010. b Effective tax rates and top quintile income share in the US: 1968–2010

Standard models of redistributive politics (Meltzer and Richard 1981; Cox and McCubbins 1986; Alesina and Rodrik 1994; Persson and Tabellini 2001; Roemer 2005; Benhabib and Przeworski 2006) cannot explain the empirical puzzle described above as they predict median-preferred equilibrium levels of redistribution: as the median becomes poorer, redistribution is predicted to increase. In all those models, the relative size of poor versus rich voters drives the result as politicians will always pander to the relatively larger group—we call this the group-size effect. Models of special interest politics, on the other hand, consider that parties use redistribution in order to “woo those [poor] voters who are relatively more responsive to generous transfers” (Dixit and Londregan 1996). We call this the income effect. Thus both groups of models predict that the equilibrium redistribution level will reflect the preferences of poor voters. In the opposite direction, models assuming that rich voters are more involved in politics or finance candidates’ campaigns (e.g., Campante 2011) may indeed explain part of the phenomenon, but they cannot fully account for the sharp decline in redistribution (taxation) that is observed since the income share of most of the engaged voters is decreasing as well.²

In this study, we provide an alternative explanation to this paradox by the means of a two-dimensional electoral competition model with differentiated candidates:³ voters are characterized by income and a fixed non-economic characteristic (which can be thought of as ethnic, religious or cultural identity) and two candidates with also fixed non-economic characteristics strategically choose redistribution schemes in order to maximize their expected vote shares. In the main part of the paper, we focus on a case in which candidates have symmetric redistribution technologies. In specific, we consider that each candidate proposes a Meltzer and Richard (1981) balanced-budget redistribution scheme and we prove existence of a unique Nash equilibrium—conditional on candidates being sufficiently differentiated in non-economic characteristics—which is characterized by policy convergence.⁴ We then focus on understanding how different elements of the model affect this unique equilibrium tax rate. In our equilibrium, both described effects (the group-size effect and the income effect) are present but a third—and potentially dominant over the other two—factor appears: the within-group homogeneity effect.

Consider a simple example in which voters of two income groups (poor and rich) have preferences over a unidimensional non-economic issue: for example, the darkness of the skin of the candidate.⁵ If poor voters are many but divided in this dimension (say half prefer darker skins to paler ones and half prefer paler skins to darker), if rich voters are few but homogeneous and moderate in this dimension and one candidate is very dark while the other candidate is very pale, then the following force appears: the dark candidate knows that by offering a redistribution scheme slightly less generous than the pale candidate makes all rich voters vote for her (since rich voters do not have strong preferences about skin color) at the cost of losing the votes of very few poor voters (since poor voters have very strong feelings about the color, a marginal difference between the proposed redistribution schemes is not enough to make them switch their votes). This within-group homogeneity effect drives the equilibrium level of redistribution closer to the preferences of the more homogeneous group—in this example the rich voters’ group—despite the fact that poor voters constitute a majority.

We are particularly interested in studying the interaction between the three effects. We initially show that when candidates’ fixed non-economic characteristics are identical, then the group-size effect is dominant: consistent with previous literature (e.g., Meltzer and Richard 1981) candidates pander to the interests of the majority. This implies that redistribution will be high (low) when the majority of the society is poor (rich). We further show that when candidates are sufficiently differentiated in the non-economic dimension and when the degree of within-group homogeneity in the non-economic dimension is identical across income groups, a representation gap appears in favor of the poor voters: independently of the size of the group of poor voters, candidates promise a large level of redistribution. In this case, the income effect is dominant.

But more strikingly, we find that the direction of the representation gap can be quickly reversed in favor of the rich group when poor voters become more heterogeneous in the non-economic dimension. That is, by maintaining the assumption of sufficient candidate differentiation, we show that even if poor voters are only slightly more heterogeneous than the rich ones in the non-economic dimension, the equilibrium redistribution scheme will better reflect the interests of the rich. Candidates, in general, are found to pander to the interests of the most homogenous group, as the relative ratio of the densities of the swing voters of the two income groups on the non-economic dimension is found to be more relevant in determining equilibrium redistribution than the ratio of the sizes of these groups. Hence the within-group homogeneity effect is much stronger than the other two and presents itself as a possible explanation for the paradox that we described in the beginning.

After analyzing the interplay between the three effects, we consider a generalization of the model to a wide range of redistribution schemes, including asymmetric ones. That is, we consider a general framework in which candidates are not only differentiated in terms of their non-economic characteristics but also in terms of their redistribution technologies. Consider, for example, the case in which candidates have different abilities to provide different public goods that are more beneficial to the poor or the rich, or the case in which one of the candidates can credibly promise to increase voters’ welfare through outside funding.⁶ We show that, for a quite general class of such asymmetries in redistribution technologies, a (possibly) divergent equilibrium—with features similar to the ones in the main part of the paper—is guaranteed to exist when candidates’ non-economic characteristics are sufficiently different. In particular, we are able to prove that the within-group homogeneity effect is robust to candidates being characterized by distinct redistribution technologies: as the poor become more divided in non-economic characteristics compared to the rich, the tax rates proposed in equilibrium by both candidates become lower. This finding unambiguously strengthens the empirical relevance of the analysis as it establishes that the described effect is not an artifact of considering symmetric redistribution technologies.

Even though this paper merely aims to make a theoretical argument, real-world observations seem to back existence of this within-group homogeneity effect. In the USA, for example, the degree of polarization and heterogeneity in a series of non-economic matters (e.g., ethnicity, religion, culture and social ideology) has been documented to have risen—both at the political elite level, especially across parties and candidates in Congress (Poole and Rosenthal 1984, 1985, 2000; McCarty et al. 2006) and also among voters (Abramowitz and Saunders 2008; Harbridge and Malhotra 2011; Krasa and Polborn 2014b), especially among the poorer ones.⁷ In turn, this has further shifted the axis of political competition from class to identity. It is exactly this interplay between increased candidate differentiation and greater within-poor heterogeneity that incentivizes parties to pander to the relatively more homogenous rich voters—in the absence of any of those two elements our model predicts that redistribution should have been higher. Moreover our theoretical findings can speak to the literature of ethnic politics by supplementing recent empirical findings (Alesina et al. 1999, 2001; Alesina and Glaeser 2004) which suggest that there is more redistribution in ethnically (or culturally) more homogenous societies despite the fact that in the latter inequality—and the number of poor voters—might be smaller. Thus our findings offer a new insight that future empirical research can explore in greater detail: it appears that relative ethnic homogeneity within income groups is potentially a more relevant determinant of redistribution than the overall (aggregate) level of ethnic homogeneity in a society.

In terms of modeling assumptions, there are two papers which are very close to ours. The first one is Lindbeck and Weibull (1987). In the standard text-book redistribution problem in which two candidates are free to propose any balanced-budget redistribution scheme—even ones that upset the income ordering of citizens—no equilibria exist: for each redistribution scheme, there is another one which is preferred by a majority. In the framework of this problem, Lindbeck and Weibull (1987) make the following seminal observation: if voters care not only about the redistribution scheme but also about other characteristics of candidates and if candidates are sufficiently uncertain about how each voter evaluates their other characteristics, then a convergent equilibrium may exist. The equilibrium existence conditions that they provide are very stringent and the equilibrium redistribution scheme is such that the less politically biased income group receives transfers from all other income groups. That is, not only could it be the case that there is redistribution in favor of the rich—something which is at odds with bare-eye empirical observations—but it could further be that the total redistribution in favor of the rich, in a case in which rich are the less biased group, exceeds the total redistribution in favor of the poor in a case in which the poor are the less biased group. Thereafter no clear inference may be drawn from these results regarding the relationship between voters’ preferences on non-economic issues and total equilibrium redistribution. The second paper whose formal setup is very close to ours is a recent one by Krasa and Polborn (2014a). In their paper, they consider that candidates, who are differentiated in social ideology, strategically decide a flat tax rate in order to provide a public good. Their analysis is of predominant importance for our work as it was the first one that demonstrated that economic policy does not only depend on the distribution of income but also on the distribution of social preferences. Its aim was more to establish the existence of this effect between social preferences and economic outcomes, rather than to investigate the degree to which this effect creates the described representation gap.

There are a number of other papers which also explore the link between voter diversity and redistribution. Roemer (1998), for example, by analyzing a model with two policy-motivated candidates who strategically decide both a level of taxation and a social policy points to the intuitive idea that when the social issue is significantly more important for the voters than the economic issue, candidates policy platforms will converge to the ideal policy of the median of the social issue dimension. To obtain these results though, he introduces and applies a non-conventional equilibrium concept since such two-dimensional models rarely admit a Nash equilibrium in pure strategies. Moreover Austen-Smith and Wallerstein (2006), Lizzeri and Persico (2001, 2004), Levy (2004), Fernández and Levy (2008) and Huber and Ting (2013) also explore how diversity among the voters affects the size of government and the type of redistribution. But in all these papers, preference diversity among voters is considered to be of economic nature (some prefer general interest policies while others prefer specialized transfers) and not in relation to some non-economic issue as in this paper or as in Krasa and Polborn (2014a).

In what follows we first present the formal model and the results considering symmetric redistribution technologies. Then we provide a generalization of the model and we show that our results are robust to introducing possibly asymmetric redistribution technologies and efficiency costs of taxation. Finally, we comment on the implications of our results on issues of applied interest.

2 The model

We model electoral competition between two candidates, A and B, taking place in a two-dimensional space. We name those two dimensions non-economic characteristics and redistribution, respectively. Following the literature of electoral competition between differentiated candidates (Krasa and Polborn 2010a, 2012, 2014a; Dziubiński and Roy 2011), we assume that the two candidates have fixed non-economic characteristics, while in the second dimension they strategically choose a redistribution scheme to maximize expected vote shares. We, moreover, consider a unit mass of heterogeneous voters that differ both in terms of their non-economic characteristics and also in terms of their incomes.

We formally denote the platform of a candidate $J\in \{A,B\}$ by $(s_{J},t_{J})\in {\mathbb {R}} \times [0,1]$ where $s_{J}\in {\mathbb {R}}$ is the fixed non-economic characteristic of candidate J and $t_{J}\in [0,1]$ is a flat tax rate strategically chosen by the vote share maximizing candidate J (without loss of generality we consider that $s_{A}\le s_{B}$). That is, unlike Cox and McCubbins (1986) where candidates could use practically any redistribution scheme, in our setup candidates are allowed to promise only standard balanced-budget redistribution schemes which belong to the class defined by Meltzer and Richard (1981).

Each voter is characterized by her non-economic characteristic, $x\in {\mathbb {R}}$, and her income $y\in \{m,M\}$, with $0\le m<M.$ We denote by $q\in (0,1)$ the mass of poor voters (voters who have income m) and by $(1-q)$ the mass of rich voters (voters who have income M). The non-economic characteristics of the poor voters are distributed on ${\mathbb {R}}$ according to an absolutely continuous distribution function $F_{p}$ with a strictly positive density denoted by $f_{p}$, while the non-economic characteristics of the rich voters are distributed on ${\mathbb {R}}$ according to an absolutely continuous distribution function $F_{r}$ with a strictly positive density denoted by $f_{r}$.⁸ Each voter votes for the candidate whose platform, once implemented, offers the highest utility. In case of indifference a voter splits her vote. The distribution of income and the distributions of non-economic characteristics for each of the two groups of voters is common information. The utility of a voter with non-economic characteristic $x\in {\mathbb {R}}$ and income $y\in \{m,M\}$ when the elected candidate has non-economic characteristic $s\in {\mathbb {R}}$ and implements a flat tax rate $t\in [0,1]$ is given by:

$$\begin{aligned} U_{(x,y)}(s,t)=v(|x-s|) + w(y(1-t)+T(t)) \end{aligned}$$

where T(t) is the average revenue raised:

$$\begin{aligned} T(t)=t[qm+(1-q)M] \end{aligned}$$

and in a Meltzer and Richard (1981) redistribution scheme it coincides with the flat individual redistributive transfer.

Notice that preferences on flat individual redistributive transfers are always monotonic (independently of the number of distinct income groups): an income group with income smaller (larger) than the mean income prefers a higher (lower) tax rate to a lower (higher) one. That is, in our case, the distribution of voters’ ideal tax rates is always a Bernoulli one with support $\{0,1\}$ and parameter q.

We consider that $v:[0,+\infty )\rightarrow {\mathbb {R}}$ is twice differentiable, strictly decreasing, strictly concave everywhere with $v(0)=v^{\prime }(0)=0, \lim _{x\rightarrow +\infty }v^{\prime }(x)=-\infty$ and $\lim _{x\rightarrow +\infty }v^{\prime \prime }(x)-v^{\prime \prime }(x-c)\ne \pm \infty$ for a fixed $c\in {\mathbb {R}}$.⁹ That is, a voter has symmetric and single-peaked preferences on the non-economic dimension; the more similar the elected candidate’s non-economic characteristic to hers, the better. As far as the economic dimension is concerned, we assume that $w:[0,+\infty )\rightarrow {\mathbb {R}}$ is a twice differentiable, strictly increasing, strictly concave function with $w(0)=0$.

We consider a voting game with three stages. All information is publicly available and known ex ante to all agents. The solution concept we employ is Nash equilibrium. The three stages of the game are as follows:

Stage 1: Candidates announce simultaneously their platforms $(s_{A},t_{A})$ and $(s_{B},t_{B})$ which become common information.

Stage 2: Each voter votes for the candidate whose platform, once implemented, offers the highest utility.

Stage 3: Each candidate $J\in \{A,B\}$ receives her payoffs which coincide with her vote share.

Given that the behavior of voters is trivial in such two-candidate voting games (they vote for the platform they prefer), we focus on the two-player game between the candidates. To do that we first need to investigate voters’ optimal behavior when candidates announce platforms $(s_{A},t_{A})$ and $(s_{B},t_{B})$. For any fixed $s_{A}<s_{B}$ our assumptions regarding $v(\cdot )$ imply that there exists a single-valued, continuous and twice-differentiable $i_{p}(t_{A},t_{B}):[0,1]^{2}\rightarrow {\mathbb {R}}$ which denotes the indifferent poor voter when candidates choose $(t_{A},t_{B})\in [0,1]$ and it is such that:

$$\begin{aligned}&v\left( \left| i_{p}\left( t_{A},t_{B}\right) -s_{A}\right| \right) + w\left( m\left( 1-t_{A}\right) +T\left( t_{A}\right) \right) \nonumber \\&\quad =v\left( \left| i_{p}\left( t_{A},t_{B}\right) -s_{B}\right| \right) + w\left( m\left( 1-t_{B}\right) +T\left( t_{B}\right) \right) \end{aligned}$$

which can be written as:¹⁰

$$\begin{aligned}&v\left( \left| i_{p}\left( t_{A},t_{B}\right) -s_{A}\right| \right) -v\left( \left| i_{p}\left( t_{A},t_{B}\right) -s_{B}\right| \right) \nonumber \\&\quad = w\left( m\left( 1-t_{B}\right) +T\left( t_{B}\right) \right) -w\left( m\left( 1-t_{A}\right) +T\left( t_{A}\right) \right) . \end{aligned}$$

Obviously, when $t_{A}=t_{B}$ monotonicity of $v(\cdot )$ implies that $i_{p}(t_{A},t_{B})=\frac{s_{A}+s_{B}}{2}$. When $t_{A}>t_{B}$ we observe that $i_{p}(t_{A},t_{B})>\frac{s_{A}+s_{B}}{2}$ and when $t_{A}<t_{B}$ we have that $i_{p}(t_{A},t_{B})<\frac{s_{A}+s_{B}}{2}$. Equivalently, there exists a single-valued, continuous and twice-differentiable $i_{r}(t_{A},t_{B}):[0,1]^{2}\rightarrow {\mathbb {R}}$ which denotes the indifferent rich voter when candidates choose $(t_{A},t_{B})\in [0,1]$ and it is such that:

$$\begin{aligned}&v\left( \left| i_{r}\left( t_{A},t_{B}\right) -s_{A}\right| \right) + w\left( M\left( 1-t_{A}\right) +T\left( t_{A}\right) \right) \nonumber \\&\quad =v\left( \left| i_{r}\left( t_{A},t_{B}\right) -s_{B}\right| \right) + w\left( M\left( 1-t_{B}\right) +T\left( t_{B}\right) \right) \end{aligned}$$

which can be written as:

$$\begin{aligned}&v\left( \left| i_{r}\left( t_{A},t_{B}\right) -s_{A}\right| \right) -v\left( \left| i_{r}\left( t_{A},t_{B}\right) -s_{B}\right| \right) \nonumber \\&\quad = w\left( M\left( 1-t_{B}\right) +T\left( t_{B}\right) \right) -w\left( M\left( 1-t_{A}\right) +T\left( t_{A}\right) \right) . \end{aligned}$$

When $t_{A}=t_{B}$ monotonicity of $v(\cdot )$ implies that $i_{r}(t_{A},t_{B})=\frac{s_{A}+s_{B}}{2}$. When $t_{A}>t_{B}$ we have that $i_{r}(t_{A},t_{B})<\frac{s_{A}+s_{B}}{2}$ and when $t_{A}<t_{B}$ we have that $i_{r}(t_{A},t_{B})>\frac{s_{A}+s_{B}}{2}$. That is, for fixed $s_{A}<s_{B}$ and candidates choosing $(t_{A},t_{B})\in [0,1]$ we have that all the poor voters with non-economic characteristics to the left of $i_{p}(t_{A},t_{B})$ vote for A and all poor voters with non-economic characteristics to the right of $i_{p}(t_{A},t_{B})$ vote for B. Equivalently, all the rich voters with non-economic characteristics to the left of $i_{r}(t_{A},t_{B})$ vote for A and all rich voters with non-economic characteristics to the right of $i_{r}(t_{A},t_{B})$ vote for B . Consequently, the payoff functions of the two candidates when $s_{A}<s_{B}$ are given by:

$$\begin{aligned} \pi _{A}\left( t_{A},t_{B}\right) =q\times F_{p}\left( i_{p}\left( t_{A},t_{B}\right) \right) +\left( 1-q\right) \times F_{r}\left( i_{r}\left( t_{A},t_{B}\right) \right) \end{aligned}$$

and

$$\begin{aligned} \pi _{B}\left( t_{A},t_{B}\right) =q\times \left[ 1-F_{p}\left( i_{p}\left( t_{A},t_{B}\right) \right) \right] +\left( 1-q\right) \times \left[ 1-F_{r}\left( i_{r}\left( t_{A},t_{B}\right) \right) \right] \end{aligned}$$

When $s_{A}=s_{B}$ the payoff functions of the two candidates are:

3 Analysis

We start by providing two general formal results which offer a solid foundation to our subsequent, more detailed, analysis.

Proposition 1

For every $q\in (0,1)$, every $M>0$, every $m\in [0,M)$, every admissible $F_{p}$ and $F_{r}$ and every $s_{A}<s_{B}$ the game admits an equilibrium in mixed strategies.¹¹

This trivially follows from the fact that when $s_{A}<s_{B}$ we have that $i_{p}(t_{A},t_{B})$ and $i_{r}(t_{A},t_{B})$ are continuous in every $(t_{A},t_{B})\in [0,1]^{2}$ and, hence, $\pi _{A}(t_{A},t_{B})$ and $\pi _{B}(t_{A},t_{B})$ are continuous in every $(t_{A},t_{B})\in [0,1]^{2}$. Therefore the two conditions of Glicksberg (1952) are satisfied (compactness of the strategy space and continuity of the payoff function in own strategies) and an equilibrium in mixed strategies exists. Next we provide the most general formal result of the paper.

Proposition 2

For every $q\in (0,1)$, every $M>0$, every $m\in [0,M)$ and for every admissible $F_{p}$ and $F_{r}$ the game admits an equilibrium in pure strategies if candidates are sufficiently differentiated, that is, if $s_{B}-s_{A}$ is sufficiently large. This equilibrium is unique, symmetric, that is, $t_{A}=t_{B}=t^{*}$, and it is such that: (a) $t^{*}=1$ when $f_{p}(\frac{s_{A}+s_{B}}{2})\ge f_{r}(\frac{s_{A}+s_{B}}{2})$, (b) $t^{*}<1$ when $f_{p}(\frac{s_{A}+s_{B}}{2})<f_{r}(\frac{s_{A}+s_{B}}{2})$ and (c) $\frac{\Delta t^{*}}{\Delta q}\ge 0$, $\frac{\Delta t^{*}}{\Delta f_{p}(\frac{s_{A}+s_{B}}{2})}\ge 0$, $\frac{\Delta t^{*}}{\Delta f_{r}( \frac{s_{A}+s_{B}}{2})}\le 0$ and $\frac{\Delta t^{*}}{\Delta (s_{B}-s_{A})}=0$ for $\Delta (s_{B}-s_{A})$ sufficiently small.

This proposition states that a unique equilibrium tax rate is guaranteed to exist as long as candidates are sufficiently differentiated. No restrictions on voters’ utility functions or on all other parameters of the model were necessary to obtain this result. That is, unlike Lindbeck and Weibull (1987) whose equilibrium existence conditions are very difficult to be satisfied and unlike Krasa and Polborn (2014a) who focus only on local equilibria,¹² our framework allows us to establish existence of a unique Nash equilibrium under very mild assumptions. Moreover we were able to retrieve important qualitative features of this unique equilibrium tax rate even in the general case: the equilibrium tax rate is increasing in the size of the group of poor voters (group-size effect), it becomes one when the densities of the swing voters of both income groups are the same (income effect) and it is increasing in the ratio of the density of poor swing voters over the density of rich swing voters (within-group homogeneity effect).¹³ Finally, we show that the degree of candidate differentiation in the non-economic issue, despite it being an important determinant of whether an equilibrium exists or not, does not affect the equilibrium tax rate once an equilibrium exists.

In the analysis that follows, we elaborate on these qualitative features of our equilibrium: (a) by offering a few more general results and (b) by discussing in more detail some representative parametrization of our general model that will allow us to assess in an analytical way the relative prevalence of each one of those three forces.

3.1 Group-size effect dominance

As we saw above when candidates are sufficiently differentiated, a unique equilibrium exists and it is such that $\frac{\Delta t^{*}}{\Delta q} \ge 0$. This means that the groups’ relative sizes reflect on the equilibrium tax rate. We will now argue that when candidates are similar, this group-size effect is further amplified. In particular, we will show that it becomes the predominant determinant of the equilibrium tax rate when candidates are not differentiated at all.

Proposition 3

For every $q\in (0,1)-\{\frac{1}{2}\}$, every $M>0$, every $m\in [0,M)$, every admissible $F_{p}$ and $F_{r}$ and $s_{A}=s_{B}$ the game admits a unique equilibrium which is $(t_{A},t_{B})=(0,0)$ when $q<\frac{1}{2 }$ and $(t_{A},t_{B})=(1,1)$ when $q>\frac{1}{2}$. When $q=\frac{1}{2}$ any strategy profile is an equilibrium.

Naturally, in this case, as candidates are not differentiated in the non-economic dimension the only relevant policy for all voters is redistribution. Then, the resulting utility of income of a poor voter, given tax rate $t\in (0,1)$ is given by:

$$\begin{aligned} w\left( m(1-t)+qmt+(1-q)Mt\right) =w\left( m+(1-q)(M-m)t\right) >w(m) \end{aligned}$$

whereas, for a rich one it is:

$$\begin{aligned} w(M(1-t)+qmt+(1-q)Mt)=w(M-q(M-m)t)<w(M) \end{aligned}$$

By monotonicity of $w(\cdot )$ it follows that a poor voter strictly prefers a flat tax rate ${\hat{t}}$ to another flat tax rate ${\tilde{t}}$ if and only if ${\hat{t}}>{\tilde{t}}$. On the contrary, a rich voter strictly prefers a flat tax rate ${\hat{t}}$ to another flat tax rate ${\tilde{t}}$ if and only if ${\hat{t}}<{\tilde{t}}$.¹⁴ These dynamics trivially lead to the above result. Here the only relevant factors for the determination of the equilibrium tax rate are the relative sizes of the two income groups: the group-size effect is the dominant force. The intuition behind this result is straightforward. Suppose that 49 % of the population are poor and 51 % are rich. If both candidates pander to the rich, they each get one half of the votes. Proposing a higher tax rate is attractive only to the poor, and a candidate who does so receives only 49 % of the votes. As a result, this is not an optimal deviation.

But, how does the importance of this effect vary as a function of the degree of candidates’ differentiation? As we have just seen, when candidates are not differentiated, relative group size is the only thing that matters for the determination of equilibrium tax rate. Moreover by Proposition 2 we know that when candidates are sufficiently differentiated and a pure strategy Nash equilibrium exists, it is true that the equilibrium tax rate does not depend on the exact degree of candidate differentiation and that factors other than groups’ sizes affect equilibrium tax rate. Hence the importance of the group-size effect is present but not predominant when candidates are sufficiently differentiated and becomes predominant when candidates are not differentiated. Roughly speaking, this implies that as candidates become less differentiated, the importance of the group-size effect becomes greater.

3.2 Income effect dominance

Proposition 2 also pointed to another feature of the equilibrium tax rate when candidates are sufficiently differentiated; it tends to favor the poor voters. In particular, when the distributions of the non-economic characteristics of the two income groups coincide (that is when $F_{p}=F_{r}$ )¹⁵ it is the case that $t^{*}=1$ independently of what is the exact size of the group of poor voters. The reason behind this equilibrium feature is that, ceteris paribus, poor voters—due to concavity of the component of the utility function which relates to income—are relatively more willing than rich voters to switch their votes in response to tiny increases in the level of promised redistribution by one of the candidates. And, since the non-economic characteristics of these two income groups in this case are identical, this income effect becomes dominant.

But how strong is this result? That is, when $F_{p}=F_{r}$, is there a $\delta >0$ such that if $s_{B}-s_{A}>\delta$ the equilibrium tax rate is $t^{*}=1$ for any $q\in (0,1)$ (if this is the case, then the income effect finding would prove to be dominant) or is it the case that when $q\rightarrow 0$ it must be that $s_{B}-s_{A}\rightarrow +\infty$ (if this is the case, then the income effect finding would prove to be weak)? In other words, can we find a degree of candidate differentiation that guarantees that when the non-economic characteristics of both groups are identical, relative group size will not affect equilibrium tax rate and candidates will always pander to the group of poor voters?

In what follows we attempt to provide a positive answer to this last question and, hence, show that the income effect dominates all others when $F_{p}=F_{r}$ and candidates are sufficiently differentiated. To this end, we specifically assume that $m=0$, $M=1$ and that $v(\xi )=-\xi ^{2}$ and $w(\xi )=\sqrt{\xi }$.¹⁶ For our next result, we consider that $F_{p}$ and $F_{r}$ are both uniform distributions on [0, 1] and that $s_{A}\le \frac{1}{2}\le s_{B}=1-s_{A}$.¹⁷

Proposition 4

The strategy profile $(t_{A},t_{B})=(1,1)$ is the unique Nash equilibrium: (a) for any $s_{A}\in [0,\frac{1}{2}]$ when $q>\frac{1}{2}$ and (b) for $s_{A}\in [0,g(q)]$ when $q\le \frac{1}{2}$, where $g(q)=\frac{-1+2q }{2q}+\frac{1}{2}\sqrt{\frac{1-3q+3q^{2}-q^{3}}{q^{2}}}$. For $q\le \frac{1 }{2}$ and $s_{A}\in (g(q),\frac{1}{2})$ there is no equilibrium in pure strategies.

Notice that $g(0)=\frac{1}{4}$ and $g(1/2)=\frac{1}{2\sqrt{2}}$. Hence when $s_{A}<\frac{1}{4}$ candidates pander to the group of poor voters for any $q\in (0,1)$, that is, independently of the size of that group. When there are many poor voters (that is, when q is relatively large), the intuition behind the result is clear: candidates target the poor since they are more responsive to redistributive transfers compared to the rich. But why do candidates propose maximum redistribution even when the poor are very few (that is, even when q is relatively small)? When q is very small: (a) the difference between the pre- and post-redistribution income of a rich voter is very small, independently of the applied tax rate, and (b) the difference between the pre- and the post-redistribution income of a poor voter is very large (small) when the applied tax rate is large (small). As a result, a candidate still has incentives to propose more redistribution than her opponent: by doing so she effectively takes with her all the poor voters (whose utility varies a lot in tax rate), while at the same time she loses very few rich voter—their utility is relatively invariant in changes in the tax rate and, hence, they vote mainly on the basis of their preferences on the non-economic dimension.

As we argued above, the quality of all the above results does not depend on our specific assumptions regarding $v(\cdot )$ and $w(\cdot )$. What is, perhaps, more important to stress here is that the income effect dominance result qualifies to a case in which there are more than two income groups; even for a case in which there is a continuum of income groups. That is, we can relax the assumption that the support of the income distribution consists of only two points, m and M (the choice of $m=0$ and $M=1$ is obviously without any loss of generality), and assume instead a continuous distribution of income. For instance, we can construct an example with a uniform distribution of incomes on [0, 1] (as in Krasa and Polborn 2014a) considering that the distribution of non-economic characteristics of voters of each income level is uniform. In this case, one can validate (see Fig. 2) that when candidates are sufficiently differentiated, the strategy profile $(t_{A},t_{B})=(1,1)$ is the unique Nash equilibrium of the game.

Fig. 2

Payoffs of candidate A, $\pi _A \left( {t_A ,1} \right)$—height—as a function of $t_A \left[ {0,1} \right]$—length—and $s_A =1-s_B \left[ {0,0.14} \right]$—width—when: (i) the income distribution is given by a uniform distribution on [0, 1] and (ii) B is expected to play $t_B =1$

Moreover by Proposition 2 we know that the game exhibits the same qualitative features for any $F_{r}=F_{p}$. Hence when distribution of non-economic characteristics across income groups is identical and candidates are sufficiently differentiated, the income effect dominance result is really robust. To get a sense of the relative importance of the income effect, we present below computational results from the case in which $s_{B}=-s_{A}$ and $F_{r}=F_{p}=N(0,1)$.

Table 1 Equilibria for $F_{r}=F_{p}=N(0,1)$

As we see in Table 1, the sufficiently large degree of candidate differentiation, which was found in Proposition 2 to be necessary for the existence of a pure strategy equilibrium, need actually be very small. If the majority of voters is poor ($q>\frac{1}{2}$) then any degree of candidate differentiation above 0.08 is enough to guarantee equilibrium existence.

3.3 Within-group homogeneity effect dominance

We now move to what we consider to be the most important determinant of the equilibrium tax rate: the relationship between the densities of the swing voters of the two groups. By maintaining the parametrization of voters’ preferences and income levels that we introduced above and by assuming that $F_{r}$ and $F_{p}$ is any admissible pair of distributions, we can state the result that follows.

Proposition 5

If the density of poor swing voters is larger than the density of rich swing voters ($f_{p}(\frac{s_{A}+s_{B}}{2})\ge f_{r}(\frac{s_{A}+s_{B}}{2})$) then for any $q\in (0,1)$ and any $s_{B}-s_{A}$ sufficiently large we have that $(t_{A},t_{B})=(1,1)$ is the unique Nash equilibrium of the game. If the density of the rich swing voters is larger than the density of the poor swing voters ($f_{r}(\frac{s_{A}+s_{B}}{2})>f_{p}(\frac{s_{A}+s_{B}}{2})$) then for any $q\in (0,1)$ and any $s_{B}-s_{A}$ sufficiently large we have that the unique Nash equilibrium of the game is $(t_{A},t_{B})=(t^{*},t^{*})$, where $t^{*}=\frac{f_{p}(\frac{s_{A}+s_{B}}{2})^{2}}{ qf_{p}(\frac{s_{A}+s_{B}}{2})^{2}+(1-q)f_{r} (\frac{s_{A}+s_{B}}{2})^{2}}$.

Given Proposition 2, this result is quite straightforward. It suggests that not only the size of a group but, most importantly, the density of swing voters of a group can affect the equilibrium outcome in the direction preferred by that group. We, moreover, observe that this equilibrium tax rate does not depend on the degree of differentiation of the two candidates in the non-economic dimension. As in the case when $F_{r}$ and $F_{p}$ were identical (see Proposition 4), here, as well, by bringing candidates very close to each other we can only end up without any pure strategy equilibrium rather than smoothly affecting the taxation levels in a pure strategy equilibrium.¹⁸

Notice that the density of a distribution F which belongs to any general family, at its mean [denoted by $f(\frac{s_{A}+s_{B}}{2})$ if we assume that the mean of F is at $\frac{s_{A}+s_{B}}{2}$] is usually negatively related to its variance. That is, the relationship between $f_{p}(\frac{ s_{A}+s_{B}}{2})$ and $f_{r}(\frac{s_{A}+s_{B}}{2})$ can be viewed as a rough, but fair in many cases, approximation of the relationship between the levels of within-group homogeneity of the two income groups.

We further observe that, for $f_{r}(\frac{s_{A}+s_{B}}{2})>f_{p}(\frac{ s_{A}+s_{B}}{2})$, it is true that:

$$\begin{aligned} \frac{\partial t^{*}}{\partial f_{r}\left( \frac{s_{A}+s_{B}}{2}\right) }<0, \quad \frac{ \partial t^{*}}{\partial f_{p} \left( \frac{s_{A}+s_{B}}{2}\right) }>0 \quad \hbox { and } \quad \frac{ \partial t^{*}}{\partial q}>0. \end{aligned}$$

That is, the more divided the group of poor voters in terms of non-economic characteristics, the smaller the level of the equilibrium tax rate.

Note that to obtain this result we need not assume anything about $F_{r}$ and $F_{p}$—such as they are symmetric about $\frac{s_{A}+s_{B}}{2}$ or any other point for that matter—other than being twice differentiable. Hence our model fully incorporates the case in which one income group can lean toward a specific candidate in the non-economic dimension. For instance, going back to the example presented in the introduction, it can be that poor voters are leaning toward the darker candidate while rich voters are relatively more pale or vice versa. That is, the two dimensions can be correlated.

Moreover by specifically assuming that $s_{B}=-s_{A}=1$, $F_{p}=N(0,z)$ and $F_{r}=N(0,1)$ we can computationally show that this pure strategy Nash equilibrium exists for any standard deviation $z>0$. Hence even if the degree of within-group homogeneity of poor voters becomes very low compared to that of the rich voters (that is, z takes large values), candidate differentiation does not need to be immensely large for our equilibrium to exist.

Proposition 6

If $F_{p}=N(0,z)$ and $F_{r}=N(0,1)$ for $z>0$ and $s_{B}=-s_{A}=1$ then for any $q\in (0,1)$ we have that: (a) when the density of poor swing voters is larger than the density of rich swing voters ($f_{p}(0)\ge f_{r}(0)\iff z\le 1$), then $(t_{A},t_{B})=(1,1)$ is the unique Nash equilibrium of the game and (b) when the density of rich swing voters is larger than the density of poor swing voters ($f_{r}(0)>f_{p}(0)\iff z>1$), then $(t_{A},t_{B})=(t^{*},t^{*})$ where $t^{*}=\frac{1}{q+(1-q)z^{2}}$ is the unique Nash equilibrium of the game.

Observe that, for $q\in (0,1)$, $t^{*}$ is strictly decreasing in z. Therefore when candidates are sufficiently differentiated in the non-economic dimension, the ratio of the densities of the swing voters of the two income groups is more relevant in determining equilibrium redistribution than the ratio of the sizes of these groups. In such cases, the within-group homogeneity effect dominates, or in other words becomes stronger than both the group-size and the income effect: candidates will always pander to the relatively more homogenous group, irrespective of its size. That is, the larger z is from 1 (poor are relatively less homogenous) the lower $t^{*}$ will be and vice versa.

It should be stressed that the within-group homogeneity effect extends to the case in which there are more than two income groups. By following the proof of Proposition 2, one notices that the equilibrium existence and uniqueness results hold independently of how many income groups are assumed to exist. The complexity of equilibrium characterization, though, increases in several orders of magnitude. Despite this, it is still clear that homogeneous—in terms of non-economic characteristics—income groups exhibit larger influence on the equilibrium tax rate than heterogeneous ones. For example, if we have three income groups (rich, median, poor) such that everybody except the rich were in favor of more redistribution¹⁹ and if rich voters were more homogeneous than each of the other two groups, then again the equilibrium tax rate would reflect the preferences of the rich voters.

Finally, we would like to note that certainly we are not the first who argue that solid—in terms of non-economic preferences—income groups are more powerful compared to more heterogeneous ones. In particular, Lindbeck and Weibull (1987) consider a probabilistic voting model and show that income groups which are not biased toward any of the candidates should expect to receive transfers from income groups who lean toward one of the candidates. The probabilistic model that they consider is a special case of the differentiated candidates model, if one assumes that the only source of differentiation is a fixed characteristic and preferences are additively separable.²⁰ That is, their model employs a structure, as far as non-economic issues are concerned, which does not distinguish between objective candidates’ differences in non-economic issues and differences in voters’ evaluation of candidates’ platforms that are driven by voters’ preferences on those issues. As a consequence: (a) their main characterization result (Theorem 1), which describes a convergent equilibrium, and the discussion that follows is silent about the interaction between the within-group homogeneity effect and the group-size effect and (b) their main equilibrium existence result (Theorem 2) describes a technical condition that is very hard to be satisfied—if, for example, the involved distributions are normal ones, then the described condition is not satisfied by any utility function. In addition, we would like to stress that even when the described condition is satisfied, it remains a technical condition: it does not provide an intuitive description of the real-world cases in which one should expect stable outcomes in electoral competition regarding redistribution. On the other hand, in the differentiated candidates’ model one can isolate objective candidate differences from differences that depend only on voters’ preferences, and, as we saw in this paper so far, this allows us to describe intuitive conditions for equilibrium existence. Perhaps more importantly, it also allows us to study the interplay between the three effects on equilibrium tax rates. Moreover as we will see in the next section, the differentiated candidates’ model allows us to extend both the existence and the characterization results to frameworks in which different candidates have different redistribution technologies and, hence, propose in equilibrium different tax rates—this is never the case in most probabilistic voting models, including Lindbeck and Weibull (1987).

4 Generalization

In this section, we explore whether our results are robust in a number of dimensions. Primarily, we wish to investigate whether the analysis that we have conducted is relevant in settings that are more general than the one considered above. Sometimes, candidates are asymmetric not only in a fixed characteristic but also in their redistribution technology (one is referred to Krasa and Polborn 2014a for a discussion of the relevance and an analysis of such a model). It could be, for example, that candidate A’s redistribution technology favors the rich while candidate B is known to be biased toward the poor (class asymmetries). Or, it could be the case that the election is held for a local office (e.g., a mayor or regional governor) and that candidate A is supported by the party that controls the national government. That is, candidate A is aligned with the ruling party while candidate B is either independent or supported by an opposition party. In many countries, it is observed that local officials that are supported by ruling parties receive more funds from central government compared to local officials that are not aligned with ruling parties (alignment asymmetries).²¹ Of course, there can be many interesting ways to model asymmetries between candidates’ redistribution technologies. Since our aim is to be as general as possible, we will not attempt to study particular examples of asymmetries but to show that our equilibrium existence result holds for a general class of asymmetric technologies and, more importantly, that its main qualitative features remain intact as well. While doing that, though, we will be referring to the two examples that we discussed above (class and alignment asymmetries) in order for the analysis to be as less abstract as possible.

Secondarily, we are interested in studying the effect of enriching our main model (symmetric redistribution technologies) with more realistic elements. In specific, we wish to explore whether introducing efficiency costs of taxation upsets equilibrium existence and the direction of our results. Redistribution is hardly ever a zero-cost procedure as we model it here. Transferring wealth from one individual to another usually involves a welfare loss that needs to be taken into account. Hence for the preceding analysis to have empirical relevance one should make sure that its results qualify the introduction of such costs.

4.1 Asymmetric technologies

We consider here the same model as in the main part of our paper, with the only difference that the effect of a redistribution scheme on a voters’ utility may be both class- and candidate-specific. Namely, we consider that the utility of a voter with non-economic characteristic $x\in {\mathbb {R}}$ and income $y\in \{m,M\}$ when the elected candidate is $J\in \{A,B\}$ is given by:

$$\begin{aligned} U_{(x,y)}(s,t)=v(|x-s_{J}|) + w_{J,y}(t_{J}). \end{aligned}$$

All the other assumptions remain the same as before (e.g., candidates maximize vote share, voters vote for the candidate they like best) and are not repeated for economy of space. Notice that we may have up to four distinct $w_{J,y}$’s. In our main model, the quadruplet $W= \{w_{A,m},w_{A,M},w_{B,m},w_{B,M}\}$ was such that $w_{A,y}(t)=w_{B,y}(t)=w(y(1-t)+T(t))$, for each $y\in \{m,M\}$. Here no element of W needs to be identical to an other element of W. In line with our assumptions regarding the function w, we only assume that $w_{J,y}:[0,1]\rightarrow {\mathbb {R}}$ is a twice differentiable, strictly increasing (strictly decreasing) and strictly concave function, for every $J\in \{A,B\}$ and $y=m$ ($y=M$).²²

Given that the general setting that we consider here complicates the analysis in several orders of magnitude—mainly as far as the description of the qualitative features of an equilibrium are concerned— we fix $v(\xi )=-\xi ^{2}$.²³ Hence for any $s_{A}<s_{B}$ and $(t_{A},t_{B})\in [0,1]$, the indifferent poor voter is defined by:

$$\begin{aligned} \mathring{i}_{p}(t_{A},t_{B})=\frac{ s_{B}^{2}-s_{A}^{2}+w_{A,m}(t_{A})-w_{B,m}(t_{B})}{2(s_{B}-s_{A})} \end{aligned}$$

and the indifferent rich voter is defined by:

$$\begin{aligned} \mathring{i}_{r}(t_{A},t_{B})=\frac{ s_{B}^{2}-s_{A}^{2}+w_{A,M}(t_{A})-w_{B,M}(t_{B})}{2(s_{B}-s_{A})}. \end{aligned}$$

That is, the payoff functions of the two differentiated candidates ($s_{A}<s_{B}$) are given by:

$$\begin{aligned} \pi _{A}(t_{A},t_{B})=q\times F_{p}\left( \mathring{i}_{p}\left( t_{A},t_{B}\right) \right) +(1-q) \times F_{r}\left( \mathring{i}_{r}\left( t_{A},t_{B}\right) \right) \end{aligned}$$

and

$$\begin{aligned} \pi _{B}(t_{A},t_{B})=q\times \left[ 1-F_{p}\left( \mathring{i} _{p}\left( t_{A},t_{B}\right) \right) \right] +(1-q)\times \left[ 1-F_{r}\left( \mathring{i} _{r}\left( t_{A},t_{B}\right) \right) \right] . \end{aligned}$$

This general formulation allows us to consider at the same time both preferences that satisfy Uniform Candidate Ranking (UCR) and non-UCR ones. In the present setup, a voter’s preferences satisfy UCR when, for example, $w_{A,y}(t)=w_{B,y}(t)$ for each $y\in \{m,M\}$. UCR²⁴ essentially requires that if a voter prefers A to B when both candidates propose t, then she should also prefer A to B when both candidates propose $t^{\prime }$, for any $(t,t^{\prime })\in [0,1]^{2}$. It is straightforward that the voters’ preferences in the main model satisfy UCR and that the voters’ preferences in the two examples sketched above (class and alignment asymmetries) violate UCR. To make the latter clear, we formally define the described examples of asymmetric redistribution technologies by:

$$\begin{aligned} W^{\mathrm{Class}}= & {} \left\{ w\left( m(1-t)+\psi _{A,m}T(t)\right) ,w\left( M(1-t)+\psi _{A,M}T(t)\right) ,w\left( m(1-t) \right. \right. \nonumber \\&\left. \left. +\psi _{B,m}T(t)\right) ,w\left( M(1-t)+\psi _{B,M}T(t)\right) \right\} \end{aligned}$$

and

$$\begin{aligned} W^{\mathrm{Alignment}}= & {} \{w(m(1-t)+T(t)+\chi ),w(M(1-t)+T(t)\nonumber \\&+\chi ),w(m(1-t)+T(t)),w(M(1-t)+T(t))\} \end{aligned}$$

where $\frac{m}{qm+(1-q)M}<\psi _{A,m}<1<\psi _{A,M}<\frac{M}{qm+(1-q)M}$ ($\psi _{B,m}>1>\psi _{B,M}>0$) and $q\psi _{J,m}+(1-q)\psi _{J,M}=1$ for both $J\in \{A,B\}$; and $\chi >0$. Hence in the first (second) case, a rich voter with a non-economic characteristic equal to $\frac{s_{A}+s_{B}}{2} +\varepsilon$ ($\frac{s_{B}^{2}-s_{A}^{2}+w(M+\chi )-w(M)}{2(s_{B}-s_{A})} +\varepsilon$), for $\varepsilon >0$ sufficiently small, prefers candidate B to candidate A when they both propose $t_{A}=t_{B}=0$, but she prefers candidate A to candidate B when both candidates propose $t_{A}=t_{B}=1$ –both scenarios are non-UCR.²⁵

We proceed now to the equilibrium existence result.

Proposition 7

For every $q\in (0,1)$, every $M>0$, every $m\in [0,M)$ and for every admissible $F_{p}$, $F_{r}$ and W the game admits an equilibrium in pure strategies, $(t_{A}^{*},t_{B}^{*})$, if candidates are sufficiently differentiated, that is, if $s_{B}-s_{A}$ is sufficiently large. This equilibrium is unique and, when interior, it is such that $\frac{ w_{A,m}^{\prime }(t_{A}^{*})}{w_{A,M}^{\prime }(t_{A}^{*})}=\frac{ w_{B,m}^{\prime }(t_{B}^{*})}{w_{B,M}^{\prime }(t_{B}^{*})}$.

That is, when redistribution technology is both class- and candidate-specific, the unique equilibrium of the game need not be symmetric. In fact, the presented condition, which must hold in an interior equilibrium, indicates that when candidates’ redistribution technologies are asymmetric we should generically have $t_{A}^{*}\ne t_{B}^{*}$. This complicates the analysis of the qualitative features of the equilibrium for a generic W: when candidates use symmetric strategies, $t_{A}^{*}=t_{B}^{*}=t^{*}$, then we have $\mathring{i}_{p}(t_{A}^{*},t_{B}^{*})=\mathring{i}_{r}(t_{A}^{*},t_{B}^{*})=\frac{ s_{A}+s_{B}}{2}$; and this makes the comparative statics analysis of $t^{*}$ with respect to q (group-size effect) and to $f_{r}(\frac{ s_{A}+s_{B}}{2})/f_{p}(\frac{s_{A}+s_{B}}{2})$ (within-group homogeneity effect) straightforward.²⁶ When $t_{A}^{*}\ne t_{B}^{*}$, though, it is not as straightforward to study how $t_{A}^{*}\$ and $t_{B}^{*}$ respond to changes in q and $f_{r}(\frac{s_{A}+s_{B}}{2})/f_{p}(\frac{s_{A}+s_{B}}{ 2})$. Despite this apparent complication, we can prove that both the group-size effect and the within-group homogeneity effect are present in this general model, conditional on the two candidates being sufficiently differentiated.

Proposition 8

Consider society one, ($F_{p}$, $F_{r}$, q) and society two, (${\hat{F}}_{p}$ , ${\hat{F}}_{r}$, ${\hat{q}}$) and fix $s_{A}$, $s_{B}$, $M>0$, $m\in [0,M)$, and W (all common for both societies) such that an interior equilibrium, $(t_{A}^{*},t_{B}^{*})$, exists for society one and an interior equilibrium, $({\hat{t}}_{A}^{*},{\hat{t}}_{B}^{*})$, exists for society two. The following statements hold: (a) if candidates are sufficiently differentiated and $q={\hat{q}}$, then $t_{J}^{*}<{\hat{t}} _{J}^{*}$ if and only if $f_{r}(\frac{s_{A}+s_{B}}{2})/f_{p}(\frac{ s_{A}+s_{B}}{2})>{\hat{f}}_{r}(\frac{s_{A}+s_{B}}{2})/{\hat{f}}_{p}(\frac{ s_{A}+s_{B}}{2})$, for each $J\in \{A,B\}$; (b) if candidates are sufficiently differentiated and $f_{r}(\frac{s_{A}+s_{B}}{2})/f_{p}(\frac{ s_{A}+s_{B}}{2})={\hat{f}}_{r}(\frac{s_{A}+s_{B}}{2})/{\hat{f}}_{p}(\frac{ s_{A}+s_{B}}{2})$, then $t_{J}^{*}<{\hat{t}}_{J}^{*}$ if and only if $q<{\hat{q}}$, for each $J\in \{A,B\}$.

This proposition extends the qualitative findings of our analysis to more general settings. If candidates are sufficiently differentiated in their non-economic characteristics, then they may be proposing the same redistribution scheme if their technologies are symmetric and different redistribution schemes if their technologies are asymmetric, but in all cases the proposed tax rates should react positively to an increase in q and negatively to an increase in $f_{r}(\frac{s_{A}+s_{B}}{2} )/f_{p}(\frac{s_{A}+s_{B}}{2})$ . In other words, both the group-size effect and the within-group homogeneity effect on redistribution are proven to be robust to candidates having asymmetric redistribution technologies.

In Fig. 3, we present the equilibria of the class-asymmetries and the alignment-asymmetries examples and, as expected, they are indeed diverging. In the first case, the candidate that is expected to favor the rich proposes greater redistribution compared to the candidate that is expected to favor the poor, and in the second case the aligned candidate proposes a smaller tax rate compared to the nonaligned candidate. In accordance with the last proposition, all candidates’ proposed tax rates are decreasing in the ratio of the density of rich swing voters over the density of poor swing voters.

Fig. 3

Interior equilibrium strategies of candidate A (blue) and candidate B (red) for the class-asymmetries case (left) and the alignment-asymmetries case (right) as a function of $f_r \left( {\frac{s_B +s_A }{2}} \right) /f_p \left( {\frac{s_B +s_A }{2}} \right)$, considering $s_B =-s_A =s\rightarrow +\infty , w\left( x \right) =\sqrt{x}, q=0.6, m=0, M=1$, $\psi _{A,M} =\psi _{B,m} =1.1$ and $\chi =0.1$ (color figure online)

4.2 Efficiency costs of taxation

It is true that redistribution is not an absolutely zero-cost procedure. It can involve efficiency costs; economic agents probably face less incentives to generate income when taxation is high compared to when taxation is low. In this part of the paper, we briefly address this issue by incorporating in the original version of our model the following assumption: we now consider that the pre-redistribution income of all individuals depends on the applied tax rate. Formally, we assume that the pre-redistribution income of an individual is $y(1-ct)$ where, as before, $y\in \{m,M\}$ and $t\in [0,1]$ and, moreover, now $c\in [0,1]$ denotes the so-called efficiency costs. When c is large these costs are large and suggest that an increase in the tax rate is a strong counter incentive for income generation while when c is small these counter incentives are weak. The original version of our model obviously corresponds to the case of $c=0$.

Without entering into unnecessary formalities and focusing on the most frequent parametrization of our main model,²⁷ we will now argue that introducing efficiency costs in our analysis unambiguously reinforces our main results: we find that the equilibrium tax rate is decreasing in c. That is, not only it can be the case, as before, that poor voters constitute a majority and the tax rate is very low (representation gap) but now, with the efficiency costs of taxation, the equilibrium tax rate is even lower. This is quite intuitive as introduction of these costs makes poor voters be less in favor of redistribution. Even in the case in which $m=0$ and, hence, these costs do not affect the pre-redistribution income of poor voters, poor voters realize that if a very high tax rate is implemented rich voters will generate less income. Moreover rich voters are now hurt from taxes in two ways and, hence, their reaction to an increasing tax rate is stronger than before. These forces are clear and in the same direction thus pushing redistribution toward lower levels.

Using a same line of arguments as the one in the main model, one can show that when candidates are sufficiently differentiated there exists a unique equilibrium tax rate, $t^{**}$, and it is such that

$$\begin{aligned} t^{**}=1 \quad \hbox { if } \quad c\le & {} \frac{qf_{p}\left( \frac{s_{A}+s_{B}}{2}\right) -qf_{r} \left( \frac{s_{A}+s_{B}}{2}\right) }{f_{r} \left( \frac{s_{A}+s_{B}}{2}\right) +2q\left[ f_{p} \left( \frac{ s_{A}+s_{B}}{2}\right) -f_{r}\left( \frac{s_{A}+s_{B}}{2}\right) \right] } \quad \hbox { and } \quad \nonumber \\&f_{p}\left( \frac{s_{A}+s_{B} }{2}\right) \ge f_{r} \left( \frac{s_{A}+s_{B}}{2}\right) \end{aligned}$$

and

$$\begin{aligned} t^{**}\in & {} (0,1)\hbox { such that }\frac{q(-1+2ct^{**})f_{p}\left( \frac{ s_{A}+s_{B}}{2}\right) }{\sqrt{(-1+q)t^{**}(-1+ct^{**})}} +\frac{ (c+q-2cqt^{**})f_{r}\left( \frac{s_{A}+s_{B}}{2}\right) }{\sqrt{(-1+ct^{**})(-1+qt^{**})}} \nonumber \\= & {} 0\hbox { otherwise}. \end{aligned}$$

In Fig. 4, we depict these equilibrium tax rates as a function of the efficiency costs of taxation, $c\in [0,1]$ for, $q=0.8$, $f_{p}(\frac{ s_{A}+s_{B}}{2})=1$ and $f_{r}(\frac{s_{A}+s_{B}}{2})\in \{0.5,0.75,1,1.25,1.5\}$ and in Fig. 5 we depict them as a function of the size of the group of poor voters $q\in [0,1]$ for $f_{p}(\frac{ s_{A}+s_{B}}{2})=1$, $f_{r}(\frac{s_{A}+s_{B}}{2})=0.75$ and $c\in \{0.1,0.2,0.6\}$.

Fig. 4

Interior equilibrium tax rates as a function of $c\in \left[ {0,1} \right]$ when $q=0.8$ and $f_r \left( {\frac{s_B +s_A }{2}} \right) /f_p \left( {\frac{s_B +s_A }{2}} \right) =r$, for various values of r

Fig. 5

Interior equilibrium tax rates as a function of $q\in \left[ {0,1} \right]$ when $f_r \left( {\frac{s_B +s_A }{2}} \right) /f_p \left( {\frac{s_B +s_A }{2}} \right) =0.75$, for various values of c

As we can see in these two figures, when taxation involves efficiency costs ceteris paribus the rich are taxed even less. In a sense, we find that efficiency costs of taxation are a fourth distinct determinant of equilibrium tax rate which does not upset the existence and direction of the other three effects.

5 Discussion

The main point that this paper makes is to relate equilibrium levels of redistribution and taxation with candidate differentiation and voter homogeneity on non-economic matters (e.g., culture, identity, religion etc.). Our results show that when candidates are sufficiently differentiated in non-economic dimensions, then it is possible for a relatively less divided and more homogenous—in terms of non-economic characteristics—group to have it its way, irrespective of its size, thus driving equilibrium taxes and redistribution in the direction favored by it. That is, candidate differentiation is a sine qua non condition for observing such an anti-majoritarian outcome. The characterization of this interplay between voter homogeneity on non-economic matters, candidate differentiation and redistribution is the first element that our analysis adds.

In addition, by returning to the parametrization of the model used for the statement of Proposition 6, we can study how the direction of this representation gap varies with the degree of relative within-group homogeneity (Fig. 6). While, starting from $z\le 1$, candidate differentiation seems to initially favor the poor, the situation can be quickly reversed in favor of the rich voters if polarization spills over from candidates to poor voters: equilibrium tax rate becomes very small. Hence our findings can help understanding the current patterns of inequality and redistribution in the USA where a strong relationship between non-economic polarization and inequality has been documented (McCarty et al. 2006).

Fig. 6

Presence and the direction of the representation gap when candidates are differentiated $(s_B =-s_A =1)$, as a function of the size of poor voters $q\in \left( {0,1} \right)$—width—and relative within-rich homogeneity $z\in \left( {0,10} \right]$—height

While we defer for future work a more detailed discussion of the policy implications of our model, in the remaining part of this paper we briefly touch upon some of them. First, our results suggest that increasing inequality need not be detrimental for growth. That is, unlike previous studies (e.g., Alesina and Rodrik 1994; Persson and Tabellini 1994; Banerjee and Duflo 2003; Barro and Redlick 2011) that highlighted the negative effects of inequality on growth –operating via increased taxation—our work suggests that this need not be the case: the group-size effect is not always dominant and, hence, more inequality does not lead always to more taxation and redistribution. Moreover since voter polarization over non-economic matters and candidate differentiation have significant spillover effects on economic issues, our work suggests that mechanisms which can unbundle those issues—either via fiscal policy decentralization (e.g., introducing referenda on spending and taxes) or by introducing constitutional constraints (e.g., upper and lower bounds on tax rates or independent tax authorities)—could mitigate those effects. Thus our work extends in another direction previous findings (Lockwood 2002) on the inefficiency of fiscal policy centralization.

Furthermore, if one interprets the non-economic dimension in terms of racial or ethnic identity, then our main result—candidates propose relatively less redistribution when the group of high-income voters is ethnically or racially more homogenous—also can be applied to examine the nature of redistribution in environments where ethnic tensions are present. In fact, our model supplements existing empirical literature on the relationship between ethnic homogeneity and preferences for redistribution (e.g., Alesina et al. 2001; Alesina and Glaeser 2004; Dahlberg et al. 2012) in the following two ways. Firstly, it can provide a theoretical explanation to recent empirical findings (e.g., Alesina et al. 1999, 2001; Alesina and Glaeser 2004) linking less (ethnically or racially) homogenous societies with lower levels of redistribution and higher inequality than more homogenous ones: given that the group of poor voters is usually ethnically more diverse and divided, (ethnically) differentiated candidates have stronger incentives to pander to the economic interests of the relatively more homogenous rich elite. Secondly, it points to a new direction that needs to be explored further: it is relative within-group ethnic homogeneity that might be responsible for those patterns. Hence our work provides a framework to link economic inequality (and aversion to redistribution) with the salience of issues of race, ethnicity and other forms of identity (e.g., religion and culture).

A natural way to extend our work further would be to examine how issue salience arises endogenously. In line with Esteban and Ray (2008), our work can provide an additional insight on the incentives that relatively more homogenous rich elites have to support candidates or parties that campaign along the lines of ethnic, religious or racial identity in many ethnically divided and polarized societies in order to increase the salience of ethnic cleavages and to shift the axis of political competition from class (redistribution) to identity. Assuming that parties or elites have preferences over redistribution and are able to choose the social issue over which they campaign, what would their choice be? Should the social issue be correlated or completely orthogonal to the economic one? Our findings suggest that the answer to this question is not always straightforward. What seems to matter the most is how divided are (in relative terms) the different income groups over any particular issue. In general, while answering those questions will help us shed some more light in the relationship between ethnic (or cultural) heterogeneity and inequality, their analysis goes beyond the scope of this present study. Thus we defer them for future empirical and theoretical research.

Appendix: Proofs

Proof of Proposition 1

Existence of an equilibrium in mixed strategies for any admissible parameters is guaranteed since the players’ payoff functions satisfy Glicksberg’s (1952) conditions (continuous and bounded payoff functions, compact strategy sets). $\square$

Proof of Proposition 2. Step 1

(Existence of a pure strategy equilibrium) Given the continuity of $\pi _{A}(t_{A},t_{B})$ and $\pi _{B}(t_{A},t_{B})$ in every $(t_{A},t_{B})\in [0,1]^{2}$ it follows that if we could find conditions which would guarantee that $\pi _{A}(t_{A},t_{B})$ is strictly quasiconcave in $t_{A}$ for every $t_{B}\in [0,1]$ (equivalently, that $\pi _{B}(t_{A},t_{B})$ is strictly quasiconcave in $t_{B}$ for every $t_{A}\in [0,1]$), we would establish existence of an equilibrium in pure strategies (see Debreu 1952). To this end, we will characterize conditions which guarantee that $\pi _{A}(t_{A},t_{B})$ is strictly concave in $t_{A}$ for every $t_{B}\in [0,1]$ and hence that it is strictly quasiconcave in $t_{A}$ for every $t_{B}\in [0,1]$. An analysis of the concavity of $\pi _{B}(t_{A},t_{B})$ is equivalent and hence omitted.

Notice that when $s_{A}<s_{B}$ we have

$$\begin{aligned} \pi _{A}(t_{A},t_{B})=q\times F_{p}(i_{p}(t_{A},t_{B}))+(1-q)\times F_{r}(i_{r}(t_{A},t_{B})) \end{aligned}$$

and hence that

$$\begin{aligned} \frac{\partial ^{2}\pi _{A}(t_{A},t_{B})}{\partial t_{A}^{2}}= & {} q\times \left[ \frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})^{2}}\left( \frac{\partial i_{p}(t_{A},t_{B})}{\partial t_{A}} \right) ^{2}\right. \nonumber \\&\left. +\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})} \frac{\partial ^{2}i_{p}(t_{A},t_{B})}{\partial t_{A}^{2}}\right] \nonumber \\&+(1-q)\times \left[ \frac{\partial ^{2}F_{r}(i_{r}(t_{A},t_{B}))}{\partial i_{r}(t_{A},t_{B})^{2}}\left( \frac{\partial i_{r}(t_{A},t_{B})}{\partial t_{A}} \right) ^{2} \right. \nonumber \\&\left. +\frac{\partial F_{r}(i_{r}(t_{A},t_{B}))}{\partial i_{r}(t_{A},t_{B})} \frac{\partial ^{2}i_{r}(t_{A},t_{B})}{\partial t_{A}^{2}}\right] . \end{aligned}$$

We will argue that when $s_{B}-s_{A}$ is sufficiently large, the expression $\frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})^{2} }(\frac{\partial i_{p}(t_{A},t_{B})}{\partial t_{A}})^{2}+\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})}\frac{\partial ^{2}i_{p}(t_{A},t_{B})}{\partial t_{A}^{2}}$ is strictly negative for any $(t_{A},t_{B})\in [0,1]^{2}$.

Implicit differentiation of

$$\begin{aligned}&v(|i_{p}(t_{A},t_{B})-s_{A}|) + w(m(1-t_{A})+T(t_{A}))\nonumber \\&\quad =v(|i_{p}(t_{A},t_{B})-s_{B}|) + w(m(1-t_{B})+T(t_{B})) \end{aligned}$$

with respect to $t_{A}$ yields

$$\begin{aligned}&\frac{\partial i_{p}(t_{A},t_{B})}{\partial t_{A}}\\&\quad =\frac{(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})}{-sgn(i_{p}(t_{A},t_{B})-s_{A})\times v^{\prime } (|i_{p}(t_{A},t_{B})-s_{A}|)+sgn(i_{p}(t_{A},t_{B})-s_{B})\times v^{\prime } (|i_{p}(t_{A},t_{B})-s_{B}|)} \end{aligned}$$

which is always positive because the numerator is positive and: (a) if $t_{A}>t_{B}$ we have that $i_{p}(t_{A},t_{B})>\frac{s_{A}+s_{B}}{2}>s_{A}$, implying $sgn(i_{p}(t_{A},t_{B})-s_{A})=1$ and $|i_{p}(t_{A},t_{B})-s_{A}|>|i_{p}(t_{A},t_{B})-s_{B}|$ and, hence, by strict concavity of $v(\cdot )$ it follows that the denominator is positive independently of the value of $sgn(i_{p}(t_{A},t_{B})-s_{B})$, (b) if $t_{A}=t_{B}$ we have that $i_{p}(t_{A},t_{B})=\frac{s_{A}+s_{B}}{2}$, implying $sgn(i_{p}(t_{A},t_{B})-s_{A})=1$, $sgn(i_{p}(t_{A},t_{B})-s_{B})=-1$ and $|i_{p}(t_{A},t_{B})-s_{A}|=|i_{p}(t_{A},t_{B})-s_{B}|$ and, hence, the denominator is positive and (c) if $t_{A}<t_{B}$ we have that $i_{p}(t_{A},t_{B})<\frac{s_{A}+s_{B}}{2}<s_{B}$, implying $sgn(i_{p}(t_{A},t_{B})-s_{B})=-1$ and $|i_{p}(t_{A},t_{B})-s_{A}|<|i_{p}(t_{A},t_{B})-s_{B}|$ and, hence, by strict concavity of $v(\cdot )$ it follows that the denominator is positive independently of the value of $sgn(i_{p}(t_{A},t_{B})-s_{A})$.

Hence for every $(t_{A},t_{B})\in [0,1]^{2}$ it is true that $\frac{ \partial i_{p}(t_{A},t_{B})}{\partial t_{A}}>0$. In a similar manner, one can show that for every $(t_{A},t_{B})\in [0,1]^{2}$ it is true that $\frac{\partial i_{p}(t_{A},t_{B})}{\partial t_{B}}<0$. That is, it is true that $i_{p}(t_{A},t_{B})$ takes its maximal value at (1, 0) and its minimal value at (0, 1). We write these maximal and minimal values as a function of the pair $(s_{A},s_{B})$; that is we consider that $i_{p}^{\max }(s_{A},s_{B})=i_{p}(1,0)$ and $i_{p}^{\min }(s_{A},s_{B})=i_{p}(0,1)$. Obviously, $i_{p}^{\max }(s_{A},s_{B})>\frac{s_{A}+s_{B}}{2}>i_{p}^{\min }(s_{A},s_{B})$.

Given that $w(\cdot )$ is continuous, strictly increasing and concave it follows that there exists $\theta >0$ such that if $s_{B}-s_{A}>\theta$, then it is the case that $i_{p}(t_{A},t_{B})\in (s_{A},s_{B})$ for every $(t_{A},t_{B})\in [0,1]^{2}$. One can actually show that $\theta =v^{-1}(-w(qm+(1-q)M)+w(m))$ by considering that candidate A chooses $t_{A}=0$, that candidate B chooses $t_{B}=1$ and that $s_{A}$ and $s_{B}$ are such that $i_{p}(t_{A},t_{B})=s_{A}$. Hence assuming that: (a) $s_{B}-s_{A}$ is sufficiently large and (b) without loss of generality that $s_{B}=-s_{A}=s>0$, we implicitly differentiate

$$\begin{aligned}&v\left( i_{p}^{\max }(-s,s)+s\right) + w(m(1-1)+T(1))\nonumber \\&\quad =v\left( s-i_{p}^{\max }(-s,s)\right) + w(m(1-0)+T(0)) \end{aligned}$$

with respect to s and we get

$$\begin{aligned} \frac{\partial i_{p}^{\max }(-s,s)}{\partial s}=\frac{v^{\prime } \left( s-i_{p}^{\max }(-s,s)\right) -v^{\prime } \left( s+i_{p}^{\max }(-s,s)\right) }{v^{\prime } \left( s-i_{p}^{\max }(-s,s)\right) +v^{\prime } \left( s+i_{p}^{\max }(-s,s)\right) }<0. \end{aligned}$$

In a similar manner, we can show that $\frac{\partial i_{p}^{\min }(-s,s)}{ \partial s}>0$.

These two derivatives help us see that by moving simultaneously $s_{A}$ and $s_{B}$ away from a fixed point, the segment from which $i_{p}(t_{A},t_{B})$ takes its values shrinks about this fixed point.

Since, when $s_{B}-s_{A}$ is sufficiently large, it is the case that $i_{p}(t_{A},t_{B})\in (s_{A},s_{B})$ we have

$$\begin{aligned} \frac{\partial i_{p}(t_{A},t_{B})}{\partial t_{A}}=\frac{(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})}{-v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})-v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))} \end{aligned}$$

and by further differentiating with respect to $t_{A}$ we get

$$\begin{aligned}&\frac{\partial ^{2}i_{p}(t_{A},t_{B})}{\partial t_{A}^{2}}\nonumber \\&\quad =\frac{ -(m-M)^{2}(-1+q)^{2}w^{\prime \prime } (m+(m-M)(-1+q)t_{A})+\left( v^{\prime \prime } (s_{B}-i_{p}(t_{A},t_{B}))-v^{\prime \prime } (-s_{A}+i_{p}(t_{A},t_{B}))\right) \left( \frac{\partial i_{p}(t_{A},t_{B})}{ \partial t_{A}}\right) ^{2}}{v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))+v^{\prime } (-s_{A}+i_{p}(t_{A},t_{B}))}. \end{aligned}$$

Therefore

$$\begin{aligned}&\frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})^{2}} \left( \frac{\partial i_{p}(t_{A},t_{B})}{\partial t_{A}} \right) ^{2}+\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})} \frac{\partial ^{2}i_{p}(t_{A},t_{B})}{\partial t_{A}^{2}}\nonumber \\&\quad =\frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})^{2}} \left( \frac{(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A}) }{-v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})-v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))} \right) ^{2}\nonumber \\&\qquad +\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})} \nonumber \\&\qquad \frac{-(m-M)^{2}(-1+q)^{2}w^{\prime \prime } (m+(m-M)(-1+q)t_{A})+\left( v^{\prime \prime } (s_{B}-i_{p}(t_{A},t_{B}))-v^{\prime \prime } (-s_{A}+i_{p}(t_{A},t_{B}))\right) \left( \frac{\partial i_{p}(t_{A},t_{B})}{ \partial t_{A}}\right) ^{2}}{v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))+v^{\prime } (-s_{A}+i_{p}(t_{A},t_{B}))}\nonumber \\&\quad =\frac{1}{v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))+v^{\prime } (-s_{A}+i_{p}(t_{A},t_{B}))}\nonumber \\&\qquad \times \left[ \frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B}))}{ \partial i_{p}(t_{A},t_{B})^{2}}\frac{[(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})]^{2}}{v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})+v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))}\right. \nonumber \\&\qquad +\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})} \left[ -(m-M)^{2}(-1+q)^{2}w^{\prime \prime } (m+(m-M)(-1+q)t_{A})\right. \nonumber \\&\qquad \left. \left. +\left( v^{\prime \prime } (s_{B}-i_{p}(t_{A},t_{B}))-v^{\prime \prime } (-s_{A}+i_{p}(t_{A},t_{B}))\right) \left( \frac{\partial i_{p}(t_{A},t_{B})}{ \partial t_{A}}\right) ^{2}\right] \right] . \end{aligned}$$

We first notice that $\frac{1}{v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))+v^{\prime } (-s_{A}+i_{p}(t_{A},t_{B}))}<0$ for every $(t_{A},t_{B})\in [0,1]^{2}$ when $s_{B}-s_{A}$ sufficiently large. So the whole expression above is strictly negative if and only if the expression

$$\begin{aligned}&\left[ \frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})^{2}}\frac{[(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})]^{2}}{v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})+v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))}\right. \nonumber \\&\qquad +\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})} \left[ -(m-M)^{2}(-1+q)^{2}w^{\prime \prime } (m+(m-M)(-1+q)t_{A})\right. \nonumber \\&\left. \left. \qquad +\left( v^{\prime \prime } (s_{B}-i_{p}(t_{A},t_{B}))-v^{\prime \prime } (-s_{A}+i_{p}(t_{A},t_{B}))\right) \left( \frac{\partial i_{p}(t_{A},t_{B})}{ \partial t_{A}}\right) ^{2}\right] \right] \end{aligned}$$

is strictly positive.

Considering that $s_{A}=\frac{s_{A}+s_{B}}{2}-c$ and $s_{A}=\frac{s_{A}+s_{B} }{2}+c$ we further observe that

$$\begin{aligned} \lim _{c\rightarrow +\infty }\frac{[(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})]^{2}}{v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})+v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))}=0, \end{aligned}$$

because as we demonstrated when $s_{B}-s_{A}$ increases, $i_{p}(t_{A},t_{B})$ remains close to $\frac{s_{A}+s_{B}}{2}$ for every $(t_{A},t_{B})\in [0,1]^{2}$ and hence both $v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})$ and $v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))$ converge to minus infinity,

$$\begin{aligned} \lim _{c\rightarrow +\infty }\frac{\partial i_{p}(t_{A},t_{B})}{\partial t_{A}}=\lim _{c\rightarrow +\infty }\frac{(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})}{-v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})-v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))}=0, \end{aligned}$$

for the same reason, and therefore when $c\rightarrow +\infty$ the expression under study converges to

$$\begin{aligned} \frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})} \left[ -(m-M)^{2}(-1+q)^{2}w^{\prime \prime } (m+(m-M)(-1+q)t_{A})\right] >0 \end{aligned}$$

which is true for every admissible parameter values.

That is, when $s_{B}-s_{A}$ is sufficiently large, $\frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})^{2}}(\frac{ \partial i_{p}(t_{A},t_{B})}{\partial t_{A}})^{2}+\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})}\frac{\partial ^{2}i_{p}(t_{A},t_{B})}{\partial t_{A}^{2}}<0$ for every $(t_{A},t_{B})\in [0,1]^{2}$. Similar arguments guarantee that that when $s_{B}-s_{A}$ is sufficiently large, the expression $\frac{\partial ^{2}F_{r}(i_{r}(t_{A},t_{B}))}{\partial i_{r}(t_{A},t_{B})^{2}}(\frac{ \partial i_{r}(t_{A},t_{B})}{\partial t_{A}})^{2}+\frac{\partial F_{r}(i_{r}(t_{A},t_{B}))}{\partial i_{r}(t_{A},t_{B})}\frac{\partial ^{2}i_{r}(t_{A},t_{B})}{\partial t_{A}^{2}}<0$ for every $(t_{A},t_{B})\in [0,1]^{2}$ too. Hence when $s_{B}-s_{A}$ is sufficiently large $\pi _{A}(t_{A},t_{B})$ is strictly concave in $t_{A}$ for every $t_{B}\in [0,1]$ (equivalently, $\pi _{B}(t_{A},t_{B})$ is strictly concave in $t_{B}$ for every $t_{A}\in [0,1]$) and an equilibrium in pure strategies is guaranteed to exist.

Step 2 (Uniqueness of the equilibrium) Notice that the game is a constant-sum game and consider that $(t_{A},t_{B})$ and $({\hat{t}}_{A},{\hat{t}} _{B})$ are both equilibria of the game. These two strategy profiles to be distinct it should either be the case that $t_{A}\ne {\hat{t}}_{A}$ or that $t_{B}\ne {\hat{t}}_{B}$ - or both. Assume without loss of generality that $t_{A}\ne {\hat{t}}_{A}$. Since the game is constant-sum it follows that the equilibrium set is convex and hence that $({\hat{t}}_{A},t_{B})$ is an equilibrium of the game too. But for $s_{B}-s_{A}$ sufficiently large we have seen that $\pi _{A}(t_{A},t_{B})$ is strictly concave in $t_{A}$ for every $t_{B}\in [0,1]$ and it is thus impossible that both $t_{A}$ and ${\hat{t}}_{A}$ are best responses of A to B playing $t_{B}$. That is, when $s_{B}-s_{A}$ sufficiently large an equilibrium in pure strategies exists and it is unique.

Step 3 (Characterization of the unique equilibrium) We take the derivative of the payoff function of player A with respect to $t_{A}$,

$$\begin{aligned} \frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}= & {} q\times \frac{ \partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})}\frac{ \partial i_{p}(t_{A},t_{B})}{\partial t_{A}}+(1-q)\\&\times \frac{\partial F_{r}(i_{r}(t_{A},t_{B}))}{\partial i_{r}(t_{A},t_{B})}\frac{\partial i_{r}(t_{A},t_{B})}{\partial t_{A}}, \end{aligned}$$

and we observe that for $s_{B}-s_{A}$ sufficiently large it may be written as

$$\begin{aligned} \frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}= & {} q\times \frac{ \partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})}\nonumber \\&\times \frac{ (m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})}{-v^{\prime } (i_{p}(t_{A},t_{B})-s_{A})-v^{\prime } (s_{B}-i_{p}(t_{A},t_{B}))}\nonumber \\&+(1-q)\times \frac{\partial F_{r}(i_{r}(t_{A},t_{B}))}{\partial i_{r}(t_{A},t_{B})}\nonumber \\&\times \frac{(m-M)q\times w^{\prime } (M+(m-M)qt_{A})}{-v^{\prime } (i_{r}(t_{A},t_{B})-s_{A})-v^{\prime } (s_{B}-i_{r}(t_{A},t_{B}))}. \end{aligned}$$

Then,

$$\begin{aligned} \frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}|_{t_{A}=t_{B}}= & {} q \times f_{p}\left( \frac{s_{A}+s_{B}}{2}\right) \nonumber \\&\times \frac{(m-M)(-1+q)\times w^{\prime } (m+(m-M)(-1+q)t_{A})}{-2v^{\prime } \left( \frac{s_{B}-s_{A}}{2}\right) }\nonumber \\&+(1-q)\times f_{r}\left( \frac{s_{A}+s_{B}}{2}\right) \frac{(m-M)q\times w^{\prime } (M{+}(m{-}M)qt_{A})}{{-}2v^{\prime } \left( \frac{s_{B}{-}s_{A}}{2}\right) }\nonumber \\= & {} \frac{(m-M)q(1-q)}{-2v^{\prime } \left( \frac{s_{B}-s_{A}}{2}\right) } \left[ f_{r}\left( \frac{ s_{A}+s_{B}}{2}\right) w^{\prime } (M+(m-M)qt_{A})\right. \nonumber \\&\left. -f_{p}\left( \frac{s_{A}+s_{B}}{2}\right) w^{\prime } (m+(m-M)(-1+q)t_{A})\right] . \end{aligned}$$

Notice that

$$\begin{aligned} \frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}|_{t_{A}=t_{B}=1}= & {} \frac{(m-M)q(1-q)}{-2v^{\prime } \left( \frac{s_{B}-s_{A}}{2}\right) }w^{\prime } (M+(m-M)q)\left[ f_{r}\left( \frac{s_{A}+s_{B}}{2}\right) \right. \nonumber \\&\left. -f_{p}\left( \frac{s_{A}+s_{B}}{2}\right) \right] . \end{aligned}$$

Hence $f_{r}(\frac{s_{A}+s_{B}}{2})\le f_{p}(\frac{s_{A}+s_{B}}{2})$ implies that $\frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}} |_{t_{A}=t_{B}=1}\ge 0$ (one can also show that $f_{r}(\frac{s_{A}+s_{B}}{2} )\le f_{p}(\frac{s_{A}+s_{B}}{2})$ implies that $\frac{\partial \pi _{B}(t_{A},t_{B})}{\partial t_{B}}|_{t_{A}=t_{B}=1}\ge 0$). This, along with strict concavity of the players’ payoff functions in own strategies, suggests that (1, 1) is the unique equilibrium.

Similarly, $f_{r}(\frac{s_{A}+s_{B}}{2})w^{\prime } (M)\ge f_{p}(\frac{ s_{A}+s_{B}}{2})w^{\prime } (m)$ implies that $\frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}|_{t_{A}=t_{B}=0}\le 0$ (one can also show that $f_{r}(\frac{s_{A}+s_{B}}{2})w^{\prime } (M)\ge f_{p}(\frac{ s_{A}+s_{B}}{2})w^{\prime } (m)$ implies that $\frac{\partial \pi _{B}(t_{A},t_{B})}{\partial t_{B}}|_{t_{A}=t_{B}=0}\le 0$). As above, this, along with strict concavity of the players’ payoff functions in own strategies, suggests that (0, 0) is the unique equilibrium.

If none of these two inequalities hold, we observe that there exists a unique $t^{*}\in (0,1)$ such that $\frac{\partial \pi _{A}(t_{A},t_{B})}{ \partial t_{A}}|_{t_{A}=t_{B}=t^{*}}=0$ and $\frac{\partial \pi _{B}(t_{A},t_{B})}{\partial t_{B}}|_{t_{A}=t_{B}=t^{*}}=0$. This is because, $w^{\prime } (M+(m-M)qt)$ is positive and increasing in t while $w^{\prime } (m+(m-M)(-1+q)t)$ is positive and decreasing in t. This $t^{*}\in (0,1)$ should be such that $f_{r}(\frac{s_{A}+s_{B}}{2})w^{\prime } (M+(m-M)qt^{*})=f_{p}(\frac{s_{A}+s_{B}}{2})w^{\prime } (m+(m-M)(-1+q)t^{*})$.

Observing that $t^{*}$ is actually a function of the parameters of the model, implicit differentiation of the latter expression gives us $\frac{ \partial t^{*}}{\partial q}>0$, $\frac{\partial t^{*}}{\partial f_{p}(\frac{s_{A}+s_{B}}{2})}>0$, and $\frac{\partial t^{*}}{\partial f_{r}(\frac{s_{A}+s_{B}}{2})}<0$. Finally, we observe that the equilibrium tax rate does not depend on the exact values of $s_{A}$ and $s_{B}$. Hence it is true that as long as the degree of candidate differentiation $s_{B}-s_{A}$ remains large enough for our equilibrium to exist, variations in that degree do not affect equilibrium tax rate; $\frac{\Delta t^{*} }{\Delta (s_{B}-s_{A})}=0$ for $\Delta (s_{B}-s_{A})$ sufficiently small. $\square$

Proof of Proposition 3

When $s_{A}=s_{B}$ a voter with income y votes for A when $w(y(1-t_{A})+T(t_{A}))>w(y(1-t_{B})+T(t_{B}))$, for B when $w(y(1-t_{B})+T(t_{B}))>w(y(1-t_{A})+T(t_{A}))$ and splits her vote between the two candidates if $w(y(1-t_{A})+T(t_{A}))=w(y(1-t_{B})+T(t_{B}))$ . By the fact that $w(\cdot )$ is strictly increasing, it follows that if $y=m$ we have

$$\begin{aligned}&w(m(1-t_{A})+T(t_{A}))>w(m(1-t_{B})+T(t_{B}))\Longleftrightarrow t_{A}>t_{B} \\&w(m(1-t_{B})+T(t_{B}))>w(m(1-t_{A})+T(t_{A}))\Longleftrightarrow t_{B}>t_{A} \\&w(m(1-t_{A})+T(t_{A}))=w(m(1-t_{B})+T(t_{B}))\Longleftrightarrow t_{A}=t_{B} \end{aligned}$$

while if $y=M$ we have

$$\begin{aligned}&w(M(1-t_{A})+T(t_{A}))>w(M(1-t_{B})+T(t_{B}))\Longleftrightarrow t_{A}<t_{B}\\&w(M(1-t_{B})+T(t_{B}))>w(M(1-t_{A})+T(t_{A}))\Longleftrightarrow t_{B}<t_{A}\\&w(M(1-t_{A})+T(t_{A}))=w(M(1-t_{B})+T(t_{B}))\Longleftrightarrow t_{A}=t_{B} . \end{aligned}$$

That is all poor voters vote for the candidate who offers the highest tax rate and all rich voters vote for the candidate who offers the lowest tax rate. Hence if $q>\frac{1}{2}$ both candidates offer in equilibrium the highest possible tax rate, when $q<\frac{1}{2}$ both candidates offer in equilibrium the lowest possible tax rate and when $q=\frac{1}{2}$ any strategy profile is an equilibrium. $\square$

Proof of Proposition 4

To show why this proposition is true we start by studying how $i_{p}(t_{A},t_{B})$ and $i_{r}(t_{A},t_{B})$ behave when the proposed tax rates change. Here one can show that:

$$\begin{aligned} i_{p}(t_{A},t_{B})=\frac{1}{2}+\frac{-\sqrt{(1-q)t_{A}}+\sqrt{(1-q)t_{B}}}{ 2(-1+2s_{A})} \end{aligned}$$

and that

$$\begin{aligned} i_{r}(t_{A},t_{B})=\frac{1}{2}+\frac{-\sqrt{1-qt_{A}}+\sqrt{1-qt_{B}}}{ 2(-1+2s_{A})}. \end{aligned}$$

In the special case in which $t_{B}=1$ we have that $i_{p}(t_{A},1)\in [0,1]$ if and only if:

$$\begin{aligned} t_{A}\ge t_{p}=\max \left\{ 0,\,\frac{-2+q+4s_{A}-4s_{A}^{2}}{-1+q}-2 \sqrt{-\frac{1-4s_{A}+4s_{A}^{2}}{-1+q}}\right\} \end{aligned}$$

and $i_{r}(t_{A},1)\in [0,1]$ if and only if:

$$\begin{aligned} t_{A}\ge t_{r}= & {} \max \left\{ 0,\,\frac{-1+q+4s_{A}-4s_{A}^{2}}{q}\right. \nonumber \\&\left. -2 \sqrt{-\frac{-1+q+4s_{A}-4qs_{A}-4s_{A}^{2}+4qs_{A}^{2}}{q^{2}}}\right\} . \end{aligned}$$

We observe that for $q\le \frac{1}{2}$ it is always the case that $t_{r}\le t_{p}$.

This suggests that the payoff function of candidate A when candidate B is expected to announce a tax rate $t_{B}=1$ is given by:

$$\begin{aligned}&\pi _{A}(t_{A},1)\\&\quad =\left\{ \begin{array}{lll} (1-q)&{} \quad \text { if }t_{A}<t_{r} \\ (1-q)\times \left( \frac{1}{2}+\frac{-\sqrt{1-qt_{A}}+\sqrt{1-q}}{2(-1+2s_{A})}\right) &{} \quad \text { if }t_{r}\le t_{A}<t_{p} \\ (1-q)\times \left( \frac{1}{2}+\frac{-\sqrt{1-qt_{A}}+\sqrt{1-q}}{2(-1+2s_{A})}\right) +q\times \left( \frac{1}{2}+\frac{-\sqrt{(1-q)t_{A}}+\sqrt{1-q}}{2(-1+2s_{A})}\right) &{} \quad \text { if }t_{A}\ge t_{p} \end{array} \right. \end{aligned}$$

We observe that $\pi _{A}(t_{A},1)$ is continuous and that $\frac{\partial \pi _{A}(t_{A},1)}{\partial t_{A}}<0$ for $t_{r}<t_{A}<t_{p}$ and that $\frac{\partial \pi _{A}(t_{A},1)}{\partial t_{A}}>0$ for $t_{A}>t_{p}$; candidates for maxima are $t_{A}\in [0,t_{r}]$ and $t_{A}=1$. We compute $\pi _{A}(0,1)$ and $\pi _{A}(1,1)$ and by routine algebra we establish that $\pi _{A}(0,1)<\pi _{A}(1,1)$ if and only if $s_{A}<\frac{ -1+2q}{2q}+\frac{1}{2}\sqrt{\frac{1-3q+3q^{2}-q^{3}}{q^{2}}}$. We can do the same process for player B and show that $\pi _{B}(1,t_{B})<\pi _{B}(1,1)$ for any $t_{B}\in [0,1)$ if and only if $s_{A}<\frac{-1+2q}{2q}+\frac{ 1}{2}\sqrt{\frac{1-3q+3q^{2}-q^{3}}{q^{2}}\text {. }}$This proves why the strategy profile $(t_{A},t_{B})=(1,1)$ is a Nash equilibrium when $s_{A}< \frac{-1+2q}{2q}+\frac{1}{2}\sqrt{\frac{1-3q+3q^{2}-q^{3}}{q^{2}}}$ and $q\le \frac{1}{2}$.

When $q>\frac{1}{2}$ it is not always true that $t_{r}\le t_{p}$. If $s_{A}$ and q are such that $t_{r}\le t_{p}$ then the payoff function of A, when B is expected to play $t_{B}=1$, is the same as before. We compute again $\pi _{A}(0,1)$ and $\pi _{A}(1,1)$ and by routine algebra we establish that $\pi _{A}(0,1)<\pi _{A}(1,1)$ for any $s_{A}\in [0, \frac{1}{2})$. As before this is enough to establish that $(t_{A},t_{B})=(1,1)$ is a Nash equilibrium. When $s_{A}$ and q are such that $t_{r}>t_{p}$ then the payoff function of A, when B is expected to play $t_{B}=1$, becomes:

$$\begin{aligned}&\pi _{A}(t_{A},1)\\&\quad =\left\{ \begin{array}{l} (1-q)\quad \text { if }t_{A}<t_{p} \\ (1-q)+q\times \left( \frac{1}{2}+\frac{-\sqrt{(1-q)t_{A}}+\sqrt{1-q}}{2(-1+2s_{A})}\right) \quad \text { if }t_{p}\le t_{A}<t_{r} \\ (1-q)\times \left( \frac{1}{2}+\frac{-\sqrt{1-qt_{A}}+\sqrt{1-q}}{2(-1+2s_{A})}\right) +q\times \left( \frac{1}{2}+\frac{-\sqrt{(1-q)t_{A}}+\sqrt{(1-q)}}{2(-1+2s_{A})}\right) \quad \text { if }t_{A}\ge t_{r} \end{array} \right. \end{aligned}$$

We observe that $\pi _{A}(t_{A},1)$ is continuous and that $\frac{\partial \pi _{A}(t_{A},1)}{\partial t_{A}}>0$ for $t_{p}\le t_{A}<t_{r}$ and that $\frac{\partial \pi _{A}(t_{A},1)}{\partial t_{A}}>0$ for $t_{A}>t_{r}$; the unique candidate for maximum is $t_{A}=1$. Hence even if $t_{r}>t_{p}$, $(t_{A},t_{B})=(1,1)$ is a Nash equilibrium of the game. Notice that when $q> \frac{1}{2}$ we have that $\pi _{A}(0,1)<\pi _{A}(1,1)$ for any $s_{A}<\frac{ 1}{2}$.

To show that this is the unique equilibrium of the game, notice that our game is a zero-sum game. That is, every equilibrium strategy is also a minimaximizer strategy. But we have proved that for the cases (i) $q\le \frac{1}{2}$ and $s_{A}<\frac{-1+2q}{2q}+\frac{1}{2}\sqrt{\frac{ 1-3q+3q^{2}-q^{3}}{q^{2}}}$ and (ii) $q>\frac{1}{2}$ and $s_{A}<\frac{1}{2}$ the payoff function $\pi _{A}(t_{A},1)$ (and $\pi _{B}(1,t_{B})$) has a unique maximum at $t_{A}=1$ ($t_{B}=1$). That is, no other minimaximizer strategy exists for any of our players and, hence, no other (pure or mixed) equilibrium exists. The same holds true for the corner case $q\le \frac{1}{2 }$ and $s_{A}=\frac{-1+2q}{2q}+\frac{1}{2}\sqrt{\frac{1-3q+3q^{2}-q^{3}}{ q^{2}}}$. But, an extra argument is needed here in order for the uniqueness argument to be complete.

What is left to be proven is that for the rest of the parameter values, that is for $q\le \frac{1}{2}$ and $s_{A}\in (g(q),\frac{1}{2})$, there is no equilibrium in pure strategies. Notice that when $f_{r}(x)=f_{r}(s_{A}+s_{B}-x)$ and $f_{p}(x)=f_{p}(s_{A}+s_{B}-x)$ (when the density of each of the two distributions is symmetric about $\frac{ s_{A}+s_{B}}{2}$) we have that the game is symmetric in game-theoretic terms. That is, $\pi _{A}({\dot{t}},{\ddot{t}})=\pi _{B}({\ddot{t}},{\dot{t}})$ for any $({\dot{t}},{\ddot{t}})\in [0,1]^{2}$. This is obviously the case here where both $F_{r}$ and $F_{p}$ are assumed to be uniform in [0, 1]. In a symmetric zero-sum game, it is true that if an equilibrium in pure strategies exists then a symmetric equilibrium in pure strategies exists too. For $q\le \frac{1}{2}$ and $s_{A}\in (g(q),\frac{1}{2})$ we already know that $\pi _{A}(0,1)>\pi _{A}(1,1)$ and thus it follows that $(t_{A},t_{B})=(1,1)$ is not a Nash equilibrium of the game. But can it be that $(t_{A},t_{B})=({\hat{t}},{\hat{t}})$ is an equilibrium for ${\hat{t}}<1$? Since $s_{A}=1-s_{B}$ it should be true that in any profile $(t_{A},t_{B})=( {\hat{t}},{\hat{t}})$ it must hold that $i_{p}({\hat{t}},{\hat{t}})=\frac{1}{2}$ and that $i_{r}({\hat{t}},{\hat{t}})=\frac{1}{2}$ and that for $(t_{A},t_{B})\in ( {\hat{t}}-\varepsilon ,{\hat{t}}+\varepsilon )$, for $\varepsilon >0$ sufficiently small, it should be the case that:

$$\begin{aligned} \pi _{A}(t_{A},t_{B})= & {} (1-q)\times \left( \frac{1}{2}+\frac{-\sqrt{1-qt_{A}}+ \sqrt{1-qt_{B}}}{2(-1+2s_{A})}\right) \nonumber \\&+\,\,q\times \left( \frac{1}{2}+\frac{- \sqrt{(1-q)t_{A}}+\sqrt{(1-q)t_{B}}}{2(-1+2s_{A})}\right) . \end{aligned}$$

We notice that for any ${\hat{t}}<1$ it is true that $\frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}|_{t_{A}=t_{B}={\hat{t}}}>0$ for any $q\in (0,1)$. Hence no pure strategy equilibrium can exist for any $s_{A}\in [0,\frac{1}{2})$ and any $q\in (0,1)$ apart from the strategy profile $(t_{A},t_{B})=(1,1)$. But as we argued for $q\le \frac{1}{2}$ and $s_{A}\in (g(q),\frac{1}{2})$ it is never the case that $(t_{A},t_{B})=(1,1)$ is an equilibrium. That is, for these parameter values the game does not admit a Nash equilibrium in pure strategies. This completes the proof. $\square$

Proof of Proposition 5

The first part of this proposition is a direct corollary of Proposition 2. When $f_{r}(\frac{s_{A}+s_{B}}{2})>f_{p}( \frac{s_{A}+s_{B}}{2})$ we know from Proposition 2 and its proof that a Nash equilibrium may exist only where $\frac{\partial \pi _{A}(t_{A},t_{B})}{ \partial t_{A}}|_{t_{A}=t_{B}}=0$. By routine algebra, we find that $(t_{A},t_{B})$ such that $t_{A}=t_{B}$ can satisfy this condition if and only if $t_{A}=t_{B}=t^{*}=\frac{f_{p}(\frac{s_{A}+s_{B}}{2})^{2}}{ qf_{p}(\frac{s_{A}+s_{B}}{2})^{2}+(1-q)f_{r}(\frac{s_{A}+s_{B}}{2})^{2}}$ which is strictly larger than zero and strictly smaller than one for any $f_{r}(\frac{s_{A}+s_{B}}{2})>f_{p}(\frac{s_{A}+s_{B}}{2})$ and any $q\in (0,1)$. And because we know that when $s_{B}-s_{A}$ is large enough a unique equilibrium exists, the identified symmetric strategy profile must be the unique equilibrium of the game. $\square$

Proof of Proposition 6

To prove this proposition, we complement formal arguments with computational results. First notice that when $F_{p}=N(0,z)$ and $F_{r}=N(0,1)$, $f_{p}(0)\ge f_{r}(0)$ is equivalent to $z\le 1$. Now, for any value of z we have that $\pi _{A}(1,1)=\frac{1}{2}$ (due to symmetry of the game) and that $\pi _{A}(t_{A},1)$ is continuous. Moreover for any pair $(q,z)\in (0,1)\times (0,1]$ we have that $\pi _{A}(t_{A},1)<\frac{1}{2}$.²⁸ Hence when $(q,z)\in (0,1)\times (0,1]$ it is the case that $\pi _{A}(t_{A},1)$ admits a unique global maximum at $t_{A}=1$. The symmetric and zero-sum nature of the game ensures that for $z\le 1$ the strategy profile $(t_{A},t_{B})=(1,1)$ is the unique Nash equilibrium of the game.

When $z>1$, that is when $f_{r}(0)>f_{p}(0)$, it is the case that $\frac{ \partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}|_{t_{A}=t_{B}=1}<0$ and that $\frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}}|_{t_{A}=t_{B}=0}>0$. It is, moreover, true that $\frac{\partial \pi _{A}(t_{A},\frac{1}{ q+(1-q)z^{2}})}{\partial t_{A}}|_{t_{A}=\mathring{t}_{A}(q,z)}=0$ if and only if $\mathring{t}_{A}(q,z)=\frac{1}{q+(1-q)z^{2}}.$ Finally, computational results suggest that when $z>1$, it is the case that $\pi _{A}(t_{A},\frac{1}{q+(1-q)z^{2}})$ admits a unique global maximum and no local minimum. That is, for $z>1$ the strategy profile $(t_{A},t_{B})=(\frac{ 1}{q+(1-q)z^{2}},\frac{1}{q+(1-q)z^{2}})$ is the unique Nash equilibrium of the game. $\square$

Proof of Proposition 7

In Step 1 of the proof of Proposition 2 we establish that, when candidates are sufficiently differentiated, the payoff function of each candidate is strictly concave in own strategies for every strategy of the other candidate and, hence, an equilibrium is guaranteed to exist. To this end we show that $\frac{\partial ^{2}F_{p}(i_{p}(t_{A},t_{B})) }{\partial i_{p}(t_{A},t_{B})^{2}}(\frac{\partial i_{p}(t_{A},t_{B})}{ \partial t_{A}})^{2}+\frac{\partial F_{p}(i_{p}(t_{A},t_{B}))}{\partial i_{p}(t_{A},t_{B})}\frac{\partial ^{2}i_{p}(t_{A},t_{B})}{\partial t_{A}^{2}} <0$ for every $(t_{A},t_{B})\in [0,1]^{2}$ when $s_{B}-s_{A}$ is sufficiently large. In this generalized framework, we can establish equilibrium existence following the same strategy. That is, we can establish equilibrium existence by showing that, when $s_{B}-s_{A}$ is sufficiently large, then:

$$\begin{aligned}&\frac{\partial ^{2}F_{p}(\mathring{i}_{p}(t_{A},t_{B}))}{\partial \mathring{ i}_{p}(t_{A},t_{B})^{2}}\left( \frac{\partial \mathring{i}_{p}(t_{A},t_{B})}{ \partial t_{A}}\right) ^{2}+\frac{\partial F_{p}(\mathring{i}_{p}(t_{A},t_{B}))}{ \partial \mathring{i}_{p}(t_{A},t_{B})}\frac{\partial ^{2}\mathring{i} _{p}(t_{A},t_{B})}{\partial t_{A}^{2}}\nonumber \\&\quad <0\hbox { for every } (t_{A},t_{B})\in [0,1]^{2}. \end{aligned}$$

Considering without loss of generality that $s_{B}=-s_{A}=s>0$, we have that $\mathring{i}_{p}(t_{A},t_{B})=\frac{w_{A,m}(t_{A})-w_{B,m}(t_{B})}{4s}$. This suggests that:

$$\begin{aligned} \frac{\partial \mathring{i}_{p}(t_{A},t_{B})}{\partial t_{A}}=\frac{ w_{A,m}^{\prime }(t_{A})}{4s}\hbox { and }\frac{\partial ^{2}\mathring{i} _{p}(t_{A},t_{B})}{\partial t_{A}^{2}}=\frac{w_{A,m}^{^{\prime \prime }}(t_{A})}{4s}. \end{aligned}$$

Hence we have:

$$\begin{aligned}&\frac{\partial ^{2}F_{p}(\mathring{i}_{p}(t_{A},t_{B}))}{\partial \mathring{ i}_{p}(t_{A},t_{B})^{2}} \left( \frac{\partial \mathring{i}_{p}(t_{A},t_{B})}{ \partial t_{A}}\right) ^{2}+\frac{\partial F_{p}(\mathring{i}_{p}(t_{A},t_{B}))}{ \partial \mathring{i}_{p}(t_{A},t_{B})}\frac{\partial ^{2}\mathring{i} _{p}(t_{A},t_{B})}{\partial t_{A}^{2}}\nonumber \\&\qquad =\frac{1}{s}\left[ \frac{\partial ^{2}F_{p}( \mathring{i}_{p}(t_{A},t_{B}))}{\partial \mathring{i}_{p}(t_{A},t_{B})^{2}} \frac{(w_{A,m}^{\prime }(t_{A}))^{2}}{16s}+\frac{\partial F_{p}(\mathring{i} _{p}(t_{A},t_{B}))}{\partial \mathring{i}_{p}(t_{A},t_{B})}\frac{ w_{A,m}^{^{\prime \prime }}(t_{A})}{4}\right] . \end{aligned}$$

By the fact that $w_{A,m}^{\prime }(t)$ is bounded form above and from below for every $t\in [0,1]$, it follows that:

$$\begin{aligned}&\lim _{s\rightarrow +\infty }\left[ \frac{\partial ^{2}F_{p}(\mathring{i} _{p}(t_{A},t_{B}))}{\partial \mathring{i}_{p}(t_{A},t_{B})^{2}}\frac{ (w_{A,m}^{\prime }(t_{A}))^{2}}{16s}+\frac{\partial F_{p}(\mathring{i} _{p}(t_{A},t_{B}))}{\partial \mathring{i}_{p}(t_{A},t_{B})}\frac{ w_{A,m}^{^{\prime \prime }}(t_{A})}{4}\right] \nonumber \\&\qquad =\frac{\partial F_{p}(\mathring{i} _{p}(t_{A},t_{B}))}{\partial \mathring{i}_{p}(t_{A},t_{B})}\frac{ w_{A,m}^{^{\prime \prime }}(t_{A})}{4}. \end{aligned}$$

We observe that the latter is strictly negative for every $(t_{A},t_{B})\in [0,1]^{2}$. In other words, when $s_{B}-s_{A}$ is sufficiently large, the desired inequality holds and, subsequently, an equilibrium is guaranteed to exist. The uniqueness argument is identical to Step 2 of the proof of Proposition 2.

In an interior equilibrium, $(t_{A}^{*},t_{B}^{*})$, we should have $\frac{\partial \mathring{\pi }_{A}(t_{A},t_{B})}{\partial t_{A}} |_{t_{A}=t_{A}^{*},t_{B}=t_{B}^{*}}=0$ and $\frac{\partial \mathring{ \pi }_{A}(t_{A},t_{B})}{\partial t_{B}}|_{t_{A}=t_{A}^{*},t_{B}=t_{B}^{*}}=0$. Simple algebraic manipulations of these two equalities yield $\frac{w_{A,m}^{\prime }(t_{A}^{*})}{w_{A,M}^{\prime }(t_{A}^{*})}=\frac{w_{B,m}^{\prime }(t_{B}^{*})}{w_{B,M}^{\prime }(t_{B}^{*})}$. $\square$

Proof of Proposition 8

In the equilibrium of the first society, we should have that $\frac{\partial \pi _{A}(t_{A},t_{B})}{\partial t_{A}} |_{t_{A}=t_{A}^{*},t_{B}=t_{B}^{*}}=0$ which is equivalent to:

$$\begin{aligned} \frac{w_{A,m}^{\prime }(t_{A}^{*})}{w_{A,M}^{\prime }(t_{A}^{*})}= \frac{(-1+q)f_{r}(\mathring{i}_{r}(t_{A}^{*},t_{B}^{*}))}{qf_{p}( \mathring{i}_{p}(t_{A}^{*},t_{B}^{*}))} \end{aligned}$$

and in the equilibrium of the second society we should have that $\frac{\partial {\hat{\pi }}_{A}(t_{A},t_{B})}{\partial t_{A}}|_{t_{A}={\hat{t}} _{A}^{*},t_{B}={\hat{t}}_{B}^{*}}=0$ which is equivalent to:

$$\begin{aligned} \frac{w_{A,m}^{\prime }({\hat{t}}_{A}^{*})}{w_{A,M}^{\prime }({\hat{t}} _{A}^{*})}=\frac{(-1+{\hat{q}}){\hat{f}}_{r}(\mathring{i}_{r}({\hat{t}} _{A}^{*},{\hat{t}}_{B}^{*}))}{{\hat{q}}{\hat{f}}_{p}(\mathring{i}_{p}(\hat{ t}_{A}^{*},{\hat{t}}_{B}^{*}))}. \end{aligned}$$

We notice that:

$$\begin{aligned} \frac{\partial \frac{w_{A,m}^{\prime }(t)}{w_{A,M}^{\prime }(t)}}{\partial t }=\frac{w_{A,m}^{^{\prime \prime }}(t)w_{A,M}^{\prime }(t)-w_{A,m}^{^{\prime }}(t)w_{A,M}^{^{\prime \prime }}(t)}{(w_{A,M}^{\prime }(t))^{2}}>0,\hbox { for every }t\in [0,1] \end{aligned}$$

because $w_{A,m}$ is a strictly increasing and strictly concave function and $w_{A,M}$ is a strictly decreasing and strictly concave function; and that:

$$\begin{aligned} \lim _{s_{B}-s_{A}\rightarrow +\infty }\mathring{i}_{r}(t_{A},t_{B})= \lim _{s_{B}-s_{A}\rightarrow +\infty }\mathring{i}_{p}(t_{A},t_{B})=\frac{ s_{B}+s_{A}}{2}\hbox { for every } (t_{A},t_{B})\in [0,1]^{2}. \end{aligned}$$

Hence $\lim _{s_{B}-s_{A}\rightarrow +\infty }t_{A}^{*}<\lim _{s_{B}-s_{A}\rightarrow +\infty }{\hat{t}}_{A}^{*}$ holds if and only if $\frac{(-1+q)f_{r}(\frac{s_{B}+s_{A}}{2})}{qf_{p}(\frac{s_{B}+s_{A}}{ 2})}<\frac{(-1+{\hat{q}}){\hat{f}}_{r}(\frac{s_{B}+s_{A}}{2})}{{\hat{q}}{\hat{f}} _{p}(\frac{s_{B}+s_{A}}{2})}$. That is, if $q={\hat{q}}$, $\lim _{s_{B}-s_{A} \rightarrow +\infty }t_{A}^{*}<\lim _{s_{B}-s_{A}\rightarrow +\infty } {\hat{t}}_{A}^{*}$ holds if and only if $\frac{f_{r}(\frac{s_{B}+s_{A}}{2}) }{f_{p}(\frac{s_{B}+s_{A}}{2})}>\frac{{\hat{f}}_{r}(\frac{s_{B}+s_{A}}{2})}{ {\hat{f}}_{p}(\frac{s_{B}+s_{A}}{2})}$ and if $\frac{f_{r}(\frac{s_{B}+s_{A}}{2 })}{f_{p}(\frac{s_{B}+s_{A}}{2})}=\frac{{\hat{f}}_{r}(\frac{s_{B}+s_{A}}{2})}{ {\hat{f}}_{p}(\frac{s_{B}+s_{A}}{2})}$, $\lim _{s_{B}-s_{A}\rightarrow +\infty }t_{A}^{*}<\lim _{s_{B}-s_{A}\rightarrow +\infty }{\hat{t}}_{A}^{*}$ holds if and only if ${\hat{q}}>q$. The argument for candidate B is symmetric. $\square$