Abstract
Summary
A fracture risk assessment tool (FRAX™) is developed based on the use of clinical risk factors with or without bone mineral density tests applied to the UK.
Introduction
The aim of this study was to apply an assessment tool for the prediction of fracture in men and women with the use of clinical risk factors (CRFs) for fracture with and without the use of femoral neck bone mineral density (BMD). The clinical risk factors, identified from previous meta-analyses, comprised body mass index (BMI, as a continuous variable), a prior history of fracture, a parental history of hip fracture, use of oral glucocorticoids, rheumatoid arthritis and other secondary causes of osteoporosis, current smoking, and alcohol intake 3 or more units daily.
Methods
Four models were constructed to compute fracture probabilities based on the epidemiology of fracture in the UK. The models comprised the ten-year probability of hip fracture, with and without femoral neck BMD, and the ten-year probability of a major osteoporotic fracture, with and without BMD. For each model fracture and death hazards were computed as continuous functions.
Results
Each clinical risk factor contributed to fracture probability. In the absence of BMD, hip fracture probability in women with a fixed BMI (25 kg/m2) ranged from 0.2% at the age of 50 years for women without CRF’s to 22% at the age of 80 years with a parental history of hip fracture (approximately 100-fold range). In men, the probabilities were lower, as was the range (0.1 to 11% in the examples above). For a major osteoporotic fracture the probabilities ranged from 3.5% to 31% in women, and from 2.8% to 15% in men in the example above. The presence of one or more risk factors increased probabilities in an incremental manner. The differences in probabilities between men and women were comparable at any given T-score and age, except in the elderly where probabilities were higher in women than in men due to the higher mortality of the latter.
Conclusion
The models provide a framework which enhances the assessment of fracture risk in both men and women by the integration of clinical risk factors alone and/or in combination with BMD.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Several multi-factorial diseases (e.g., diabetes, hypertension) are defined on the basis of important risk factors for the clinical outcome. Hypertension, for example, is defined from the measurement of blood pressure that provides information on the likelihood of stroke. Hypercholesterolaemia and osteoporosis are also examples. In the case of osteoporosis, bone mineral density (BMD) is measured both to provide a diagnosis, and to yield information on fracture risk [1].
Many well-controlled prospective studies with dual energy X-ray absorptiometry (DXA), particularly in elderly women, indicate that the risk of fracture about doubles for each SD reduction in BMD [2, 3]. The measurement of a risk factor for diagnostic use, however, can only capture one aspect of the likelihood of the outcome when the disease is multifactorial, and in osteoporosis, assessment with BMD captures a minority of the fracture risk. For example, the annual incidence of hip fracture increases approximately 30-fold between the ages of 50 and 90 years; but, from the known relationship between BMD and fracture risk and the loss of bone with age, it is expected that hip fracture risk would rise only fourfold [4–6]. Thus, the increase in risk with age is approximately sevenfold greater than can be explained on the basis of BMD alone.
The imperfect capture of risk with BMD alone poses several problems for the clinical assessment of fracture risk. In the context of population screening with BMD alone, the performance characteristics of the test are less than optimal in terms of the trade-off between sensitivity and specificity [1, 7, 8]. Thus, osteoporotic fractures affect a substantial minority of the population, but intervention thresholds based on BMD alone lack sensitivity over most reasonable assumption, i.e., the detection rate is low. For example, at the age of 50 years the proportion of women with osteoporosis is approximately 5% [4]. The proportion of these who will fracture in the next 10 years (i.e., positive predictive value) is about 20%. The detection rate for these fractures (sensitivity) is, however, low, and 96% of fragility fractures would arise in women without osteoporosis given a test like BMD where the fracture risk doubled for each SD decrease [9]. Low sensitivity is one of the reasons why wide-spread population screening is not widely recommended in women at the menopause [1]. Moreover, a normal BMD measurement is no guarantee that a fracture will not occur.
The use of risk factors that add information on fracture risk independently of BMD improves the sensitivity of the assessment for any specificity [8, 9]. Over the past several years, we have undertaken a series of meta-analyses to identify clinical risk factors for fracture that provide independent information on fracture risk [3, 10–16]. The analyses were based on the primary data from prospective population based studies. This permits the inter-dependence of each of the candidate risk factors to be examined so that they can be accurately combined for clinical use. In the case of the clinical risk factors, BMI is used as a continuous variable, so that its distribution is preserved by the addition of dichotomous variables [8]. For hip fracture prediction, the gradient of risk (increase in fracture risk per standard deviation increase in risk score) for the CRFs is comparable to the use of DXA alone, and the gradient of risk is further enhanced by the addition of BMD to the CRFs [17]. These inter-relationships, assessed from multiple populations and validated in independent cohorts, permit the more accurate identification of individuals who will fracture, so that the average risk in any given proportion of the population identified for treatment will be higher [8].
These considerations indicate that assessment can be improved by the integration of clinical risk factors with or without BMD. In other words, treatment should be directed not only on the basis of T-score for BMD, but also on the independent contribution of other validated risk factors. However, the use of different metrics (the T-score, gradients of risk, risk ratios, etc) is confusing for clinicians and patients alike. For this reason, there has been interest in the development of algorithms that express absolute risk, or the probability of fracture within a given time period [18–20], as has been done for cardiovascular and other diseases [21–25]. The aim of the present study was to develop a model for the clinical assessment of fracture probability in men and women based on the epidemiology of the UK.
Methods
Cohorts
In order to identify the relevant risk factors, we used baseline and follow-up data from nine prospective population-based cohorts comprising the Rotterdam Study, The European Vertebral Osteoporosis Study (later the European Prospective Osteoporosis Study (EVOS/EPOS), The Canadian Multicentre Osteoporosis Study (CaMos), Rochester, Sheffield, Dubbo, a cohort from Hiroshima and two cohorts from Gothenburg. Details of each of the cohorts have been recently published elsewhere [10–16].
Baseline and outcome variables
Height and weight were measured using standard techniques in all cohorts. Body mass index (BMI) was calculated as weight divided by height squared (kg/m2) and used as a continuous variable. BMD was assessed at the femoral neck by DXA with the exception of the two Gothenburg cohorts in which BMD was measured elsewhere. Femoral neck BMD was used as a continuous variable (cohort-specific Z-scores excluding the two cohorts from Gothenburg). The clinical risk factors utilised were those identified from the previous meta-analyses [3, 10–16]. These comprised a parental history of hip fracture, exposure to systemic glucocorticoids, a prior history of fragility fracture, current smoking, high intake of alcohol (3 or more units daily on average) and the presence of rheumatoid arthritis as an indicator for secondary osteoporosis.
Fracture ascertainment in the primary cohorts was undertaken by self-report (Sheffield, EVOS/EPOS, Hiroshima) and/or verified from hospital or central data-bases (Gothenburg, CaMos, DOES, Sheffield, EVOS/EPOS, Rochester, Rotterdam).
Models used
Four models were constructed from the risk factor analysis to compute fracture probabilities. These comprised the probability of hip fracture, with and without BMD, and the probability of other major osteoporotic fractures (clinical spine, forearm and proximal humerus), with and without BMD. For each model, fracture and death as continuous hazard functions were computed using a Poisson regression [26, 27] and detailed in the Appendix. In brief, for each risk factor, all significant interactions terms that were identified by meta-analysis were entered (with age, time, sex and the risk factor) with and without BMD [17]. Interactions that were significant for hip fracture risk were also entered into the model for other osteoporotic fractures, and also included in the model for death. Where interactions noted in the “mega-analyses” were no longer significant for both hip fracture and other osteoporotic fractures, these were omitted in a step-wise manner by dropping the interaction with the largest p value. For the death hazard, all significant interactions for fracture risk were included and thereafter omitted if appropriate in a step-wise manner, as described for the fracture hazard.
Epidemiology
The incidence of hip, forearm and proximal humerus fractures in the UK was taken from Singer et al. [28]. Vertebral fractures can be classified as clinically overt fracture, that is, a symptomatic fracture that comes to clinical attention, or a morphometric fracture, which includes both symptomatic and asymptomatic fractures. For the purposes of this study the clinical definition of a vertebral fracture was used. Because data on vertebral fracture risk in the UK are scarce, with a great deal of variation in reported rates [29], the clinical vertebral fracture incidence was calculated by assuming that the ratio of clinical vertebral fracture to hip fracture would be similar in the UK compared to Sweden [30]. The validity of the assumption cannot be directly tested, but in the case of long bone fractures, there is a close concordance of relative incidence at different fracture sites despite marked differences in absolute risk [31]. Swedish fracture risk data were taken from Kanis et al. [32]. The models were then calibrated so that the mean hazard functions of fracture (and death) equalled that of the UK, as detailed in the Appendix.
Input and output variables
Individual patient details comprise age (50 to 90 years), sex, weight (in kg) and height (in cm). BMI is automatically computed from height and weight. Dichotomised risk variables are then entered:
-
A prior fragility fracture (yes/no)
-
Parental history of hip fracture (yes/no)
-
Current tobacco smoking (yes/no)
-
Ever long-term use of oral glucocorticoids (yes/no)
-
Rheumatoid arthritis (yes/no)
-
Other causes of secondary osteoporosis (yes/no)
-
Daily alcohol consumption of three or more units daily (yes/no)
A distinction is made between rheumatoid arthritis and other secondary causes of osteoporosis. Rheumatoid arthritis carries a fracture risk over and above that provided by BMD [11]. Whereas this may hold true for other secondary causes of osteoporosis, the evidence base is weak. Of the many secondary causes of osteoporosis, the following have been consistently documented to be associated with a significant increase in fracture risk:
-
Untreated hypogonadism in men and women, e.g., bilateral oophorectomy or orchidectomy, anorexia nervosa, chemotherapy for breast cancer, hypopituitarism [33–40]
-
Inflammatory bowel disease, e.g., Crohn’s disease and ulcerative colitis [41–43]. It should be noted that the risk is in part dependent on the use of glucocorticoids, but an independent risk remains after adjustment for glucocorticoid exposure [44].
-
Prolonged immobility, e.g., spinal cord injury, Parkinson’s disease, stroke, muscular dystrophy, ankylosing spondylitis [45–50]
-
Thyroid disorders, e.g., untreated hyperthyroidism, over-treated hypothyroidism [59–63]
Whereas there is strong evidence for the association of these disorders and fracture risk, the independence of these risk factors from BMD is uncertain. It was conservatively assumed, therefore, that the fracture risk was mediated via low BMD, but with a risk ratio similar to that noted in rheumatoid arthritis. From an operational view, where the field for rheumatoid arthritis is entered as ‘yes’, a risk is computed with and without BMD. If the field for other secondary osteoporosis is also filled as ‘yes’ this does not contribute to the calculation of fracture probability. Conversely, where the field for rheumatoid arthritis entered as ‘no’, and the field for secondary osteoporosis is ‘yes’, the same β coefficients as used for rheumatoid arthritis contribute to the computation of probability where BMD is not entered. In the presence of BMD, however, no additional risk is assumed in the presence of secondary osteoporosis, since its independence of BMD is uncertain.
If any of the fields for dichotomous variables is not completed, a negative response is assumed. Fractures probability can then be calculated. The output (without BMD) comprises the 10-year probability of hip, clinical spine, shoulder or wrist fracture and the 10-year probability of hip fracture (Fig. 1).
Femoral neck BMD can additionally be entered either as a Z-score or a T-score. The transformation of Z- to T-score and vice versa is derived for the NHANES III database for female Caucasians aged 20–29 years [64]. When entered, calculations give the 10-year probabilities as defined above with or without the inclusion of BMD.
Results
Clinical risk factors
The contribution of single clinical risk factors is shown in Table 1 for men and women aged 65 years. In the example, the BMI is set at 25 kg/m2. In the absence of BMD, hip fracture probabilities were higher in women than in men. Each clinical risk factor had a different significance for hip fracture probability, with a family history having the least and a prior fracture the greatest weight in the absence of BMD. The rank order of weighting differed for the major osteoporotic fractures. For example, a parental history of hip fracture was a strong risk factor, close to that provided by a prior fragility fracture. The contribution of age to the assessment of probability is shown in Table 2. In both men and women, there was greater than 100-fold difference in hip fracture probability between the age of 50 years (no risk factors) and 80 years (parental history of hip fracture).
The presence of more than one risk factor increased fracture probability in an incremental manner. For example, in women aged 65 years with a BMI of 25 kg/m2, the 10-year hip fracture probability was 1.3%. With one clinical risk factor, the probability ranged from 1.7% to 3.2%, depending on the risk factor. With two risk factors, the range was 2.5–6.6%, and with 3, 4 and 5 risk factors the ranges were 3.8–11%, 6.7–17% and 13–24%, respectively. In the presence of all six clinical risk factors, the 10-year probability of hip fracture was 30%.
The effect of several clinical risk factors on the 10-year probability of a major osteoporotic fracture is shown in Fig. 2 for a woman aged 65 years and a BMI of 25 kg/m2. In women with rheumatoid arthritis, there was a 33% increase in fracture probability compared with those without rheumatoid (from 9% to 12%). When women additionally took oral glucocorticoids and had a prior fracture there was a fourfold increase in fracture probability.
A higher or lower BMI had a marked effect on fracture probability (Fig. 3). For example, in women at the age of 65 years the 10-year hip fracture probability in the absence of risk factors was 2.3% with a BMI of 20 kg/m2, but was fourfold lower (0.6%) at a BMI of 40 kg/m2. At each level of BMI, fracture probability increased with an increasing number of clinical risk factors.
Ten-year probability of hip fracture (%) in women aged 65 years according to the number of clinical risk factors with a BMI of 20 kg/m2 (left-hand panels) and a BMI of 40 kg/m2 (right-hand panels). The intervals reflect the different weights afforded by different risk factors and provide a range of probabilities. [05Ca070]
Bone mineral density
The relationship between fracture probability and BMD is shown in Table 3. In general, fracture risk increased with increasing age and decreasing T-score. At low T-scores, however, fracture probabilities decreased with age, a phenomenon more marked in men than in women. For example, at the age of 50 years, the 10-year probability of hip fracture was 16.0% in men with a T-score of −4 SD and this fell progressively with age, so that at the age of 70 years, the probability was 12.9% and at the age of 90 years was 8.3%.
The differences in probabilities between men and women were much less marked for any given age and T-score than the differences seen with the use of clinical risk factors alone. At a fixed BMD (−2.5 SD in Table 1), the difference in probability between men and women was less evident. For example, the hip fracture probability ratio (women/men) with glucocorticoid use was 1.8 in the absence of BMD but 0.9 at a T-score of −2.5 SD. In the case of all major osteoporotic fractures, probabilities remained higher in women than in men at a T-score of −2.5 SD but the difference in probabilities between men and women was less marked.
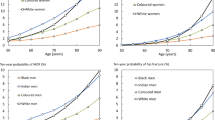
Figure 4 compares the probability of hip fracture in men and women with a prior fracture according to age. In the absence of BMD there was approximately a twofold difference in probability between men and women. When the BMD was set at an average for women (Z-score = 0), there was little difference in probabilities up to the age of 75 years. Thereafter, men had a lower probability than women due to the higher death hazard.
Ten-year hip fracture probability (%) in men and women with a prior fracture according to age. The left-hand panel gives probabilities in the absence of BMD. In the right-hand panel probabilities are shown at an average BMD for women at each specific age (i.e., a Z-score = 0). A BMI is set at 24 kg/m2. [05Ca065]
The clinical risk factors added to the information provided by BMD. Isopleths for 10-year fracture probability are shown in Fig. 5 for the combination of several of the clinical risk factors. The clinical risk factors were somewhat less predictive in the presence of BMD in the models. For example, in women aged 65 years and a BMI of 20 kg/m2, the 10-year hip fracture probability in the absence of BMD ranged from 2.3% in the absence of clinical risk factors to 27.9% with four risk factors. When BMD was set constant at a T-score of −2.5 SD, the range was from 2.8% with no clinical risk factor to 19.7% with four risk factors (Fig. 6). The effect of variations in BMI was even more markedly affected by BMD. For example, in women aged 65 years the 10-year hip fracture probability was 2.3% at a BMI of 20 kg/m2 and decreased progressively at higher levels of BMI to 0.6% with a BMI of 40 kg/m2. When BMD was fixed, hip fracture probability remained constant irrespective of BMI (Fig. 7).
Ten-year probability of hip fracture (%) in women aged 65 years, according to the number of clinical risk factors. The left-hand panel shows the probabilities without BMD at a BMI fixed at 20 kg/m2. The right-hand panel illustrates the effects with BMD fixed at the threshold for osteoporosis. [05Ca073]
Discussion
The present study provides a model for the assessment of fracture probability in men and women. The model (FRAX™) uses data derived from nine cohorts from around the world, including centres from North America, Europe, Asia and Australia and has been validated in 11 independent cohorts with a similar geographic distribution [17]. The use of primary (but anonymized) data for the model construct permits the interaction of each of the risk factors to be determined to improve the accuracy whereby fracture probability can be computed. The large sample permitted the examination of the general relationship of each risk factor by age, sex, duration of follow up and, for continuous variables (BMD and BMI), the relationship of risk with the variable itself in a manner hitherto not possible. The use of primary data also eliminates the risk of publication bias. The validity of the clinical risk factors identified are supported by the expected relationships between BMD and fracture risk [3].
In the present study, the FRAX™ model has been calibrated to the epidemiology of the UK, but could be calibrated to any country where the epidemiology of fracture and death is known (see Appendix). FRAX™ models for the UK and some other countries are available through the web (http://www.shef.ac.uk/FRAX/index.htm). The approach uses easily obtained clinical risk factors to estimate risk. The estimate can be used alone or with BMD to enhance fracture risk prediction.
Several previous studies have developed models to predict fracture risk from the combination of clinical risk factors and BMD [18, 65–78]. The risk factors used include activities of daily living, impaired cognition, liability to falls, poor overall health, history of stroke, seizure disorder and several different medications. A limitation of many of these studies is that, with the exception of the SOF study [18], and one of the GPRD studies [76], they have not been tested in other cohorts. The model described in this paper has been validated in 11 independent prospectively studied cohorts with in excess of one million patient years [17].
The use of risk factors for case finding presupposes that the risk so identified is responsive to a therapeutic intervention. To test this hypothesis, it would be necessary to recruit patients selected on the basis of the risk factor(s) to a randomised controlled trial (RCT). The risk factor that is best evaluated in this way is BMD, and indeed the vast majority of therapeutic studies have recruited patients on the basis of low BMD as recommended by regulatory agencies in the US and Europe [79, 80]. In recent years, other trials have recruited patients on the basis of age, gender, a prior vertebral fracture and current exposure to glucocorticoids irrespective of BMD, and have shown therapeutic effects similar to those noted in RCT’s based on BMD selection [14, 81–83].
For other risk factors, comparable data are lacking. In the absence of empirical data, an alternative approach is to demonstrate that the presence (or absence) of a risk factor does not adversely influence therapeutic efficacy against fractures. Several studies have shown no significant interaction between response to treatment and the presence or absence of the risk factors used in the present study including age, height, family history of fracture, low body weight or BMI, smoking, alcohol intake or prior non-vertebral fracture [84–88]. In contrast, some risk factors may be associated with less therapeutic efficacy. For example, patients selected on the basis of risk factors for falling may respond less completely to agents that preserve bone mass than patients selected on the basis of low BMD [89]. This concern is greatest in models that omit BMD, because pharmacological agents may not be equally effective across the entire range of BMD [90].
The present model has several unique features. FRAX™ uses Poisson regression to derive hazard functions of death and fracture. Such hazard functions are continuous as a function of time, unlike Cox’s regression for which the corresponding hazard functions are zero except at the time points of a fracture or death. There are also several advantages of the Poisson model over logistic regression analysis. Logistic regression does not take account of when a fracture occurred, nor whether individuals without a fracture died or when death occurred. Secondly, for the assessment of 10-year probabilities by logistic regression, the observation period should be for 10 years. Moreover, information longer than the 10-year period cannot be used for analysis. The cost of ignoring information when fractures occur and whether and when deaths occur is on the precision of the estimate. In simulation experiments, the Poisson model gives the same precision as logistic regression with fewer numbers of individuals. In our own simulations in the present context (data on file), the Poisson model gave the same precision as logistic regression with half the number of individuals. Finally, the Poisson model allows adjustments to be made for time trends. The ability to use several Poisson models permits the use of data from different sources to integrate fracture and death hazards, and to calibrate to different countries.
A further feature of the FRAX™ model is that it takes account of deaths from all causes. In several recent models of disease probability, this has not been accounted for [23–25]. For example, the probability of stroke has been determined as a function of age, race, smoking, body mass index, atrial fibrillation, HbA1c, systolic blood pressure, ratio of total to HDL cholesterol and duration of diabetes [25], but the risk of dying from other reasons was not taken into account. In the context of osteoporosis, fracture probabilities are markedly underestimated when no account is taken of the competing death hazard [27, 35, 36]. For example, in a study of men followed after orchidectomy, the cumulative incidence of fractures was 19% after 15 years, but the figure was 40% when deaths were considered as a competing event [36].
FRAX™ also takes account of the impact of risk factors on the death hazard. For example, smoking and low BMD are risk factors for fracture but also significant risk factors for death. Thus, at very low T-scores for BMD, hip fracture probabilities decrease with age (see Table 3), in part related to the higher mortality associated with the lower values for BMD.
There are several limitations that should be mentioned. As with nearly all randomly drawn populations, non-response bias may have occurred. The effect is likely to exclude sicker members of society, and may underestimate the absolute fracture risk for example by age. The analyses also have significant limitations that relate to the outcome variables and the characterisation of risk factors. The definition of what was considered to be an osteoporotic fracture was not the same in all cohorts, but the effect of this inconsistency is likely to weaken rather than strengthen the associations that were found. For the hip fracture outcome, the definition was similar in all cohorts, and may explain in part the higher risk ratios associated for this fracture rather than for osteoporotic fracture. Also, the analyses were confined to clinical fractures, and the results might differ from vertebral fractures diagnosed by morphometry or as an incidental radiographic finding.
There are also limitations with the risk factors themselves. In the case of BMI, this was chosen rather than weight as the measure for body composition. This has the advantage that there is less variability across countries and between sexes. A potential drawback is that BMI can be influenced by height loss associated with vertebral deformities. Therefore, in individuals with important loss of height, the risk conferred through BMI could be underestimated [91]. The use of maximal attained height, rather than current height, might be a solution in the future, if it were shown that fracture risk prediction could be improved.
Further problems relate to the construct of the questions to elicit the presence or absence of risk factors, which varied between cohorts. These included questions on family history, prior fracture, smoking and glucocorticoid use. The effect of this heterogeneity is likely to weaken rather than strengthen the associations found. Recall is also subject to errors and was not validated in any of these cohorts. This is particularly problematic in the elderly. In addition, the validity of self-reported alcohol intake is notoriously unreliable [92]. Indeed, alcohol consumption was significantly less in both men and women than that assessed in the UK [93]. Given that these studies were prospective, however, much of this error (with the exception of alcohol intake) should be random, giving rise to non-directional misclassification. Thus, the associations may actually be stronger than reported here. Any underestimate may have limited consequences for case-finding, since the populations to be tested are similar to the populations interrogated. Biases that arise have more significance where causality is inferred.
A further limitation is that several of the clinical risk factors identified take no account of dose-response, but give risk ratios for an average dose or exposure. By contrast, there is good evidence that the risk associated with excess alcohol consumption and the use of glucocorticoids is dose-responsive [14, 94]. In addition, the risk of fracture increases progressively with the number of prior fractures [95]. These limitations are nearly all conservative.
It should be acknowledged that there are many other risk factors that might be considered for incorporation into assessment algorithms. These include BMD at other skeletal sites, ultrasonography, quantitative computed tomography and the biochemical indices of bone turnover. The available information was too sparse to provide a meta-analytic framework, but they should be incorporated into risk assessment algorithms when they are more adequately characterised. Notwithstanding, the present model provides a mechanism to enhance patient assessment by the integration of clinical risk factors alone and/or in combination with BMD.
The application of this methodology to clinical practice will demand a consideration of the fracture probability at which to intervene, both for treatment (an intervention threshold) and for BMD testing (assessment thresholds). These are currently being developed for the UK, based on cost-effectiveness analyses [96]. Intervention thresholds developed for the United Kingdom may not be applicable to other countries. The 10-year probability of fracture varies markedly in different countries [97]. For countries with low hip fracture rates, as found in developing countries, the relative risk at which intervention is cost-effective will be higher, though the absolute risk at which intervention is cost-effective would not change assuming comparable costs. Intervention thresholds would, however, change with differences in costs, particularly fracture costs, which vary markedly world wide. There is also the issue of affordability or willingness to pay for a strategy. The gross domestic product (GDP) per capita provides an index of affordability. The GDP varies markedly in different regions of the world. In the UK, the GDP per capita is estimated at US$ 25,300 in 2002, as compared with US$ 7,000 in Turkey. Thus, for the same fracture risk and the same costs, treatment will be less affordable (at least to health services) in Turkey than in the UK. Nevertheless, individuals in Turkey, rather than society as a whole, may be willing to pay “United Kingdom prices” for health care. There is also a marked heterogeneity in the proportion of GDP devoted to health care, and in the proportion of the population at risk from osteoporotic fracture (i.e., elderly people) [98, 99]. For all these reasons, it is important to define intervention and assessment thresholds on a country by country basis that takes into account the setting for service provision and willingness to pay, as well as considerations of absolute costs.
References
World Health Organization (1994) Assessment of fracture risk and its application to screening for postmenopausal osteoporosis. WHO Technical Report Series 843. WHO, Geneva
Marshall D, Johnell O, Wedel JJ (1996) Meta-analysis of how well measures of bone mineral density predict occurrence of osteoporotic fractures. Br Med J 312:1254–1259
Johnell O, Kanis JA, Oden A, Johansson H et al (2005) Predictive value of bone mineral density for hip and other fractures. J Bone Miner Res 20:1185–1194
Kanis JA, Johnell O, Oden A, Jönsson B, De Laet C, Dawson A (2000) Risk of hip fracture according to World Health Organization criteria for osteopenia and osteoporosis. Bone 27:585–590
Hui SL, Slemenda CW, Johnston CC (1988) Age and bone mass as predictors of fracture in a prospective study. J Clin Invest 81:1804–1809
De Laet CEDH, van Hout BA, Burger H, Hofman A, Pols HAP (1997) Bone density and risk of hip fracture in men and women: cross sectional analysis. Br Med J 315:221–225
Kanis JA, Johnell O, Oden A, Jönsson B, Dawson A, Dere W (2000) Risk of hip fracture derived from relative risks: an analysis applied to the population of Sweden. Osteoporos Int 11:120–127
De Laet C, Oden A, Johansson H, Johnell O, Jonsson B, Kanis JA (2005) The impact of the use of multiple risk indicators for fracture on case-finding strategies: a mathematical approach. Osteoporos Int 16:313–318
Kanis JA, Johnell O, Oden A, De Laet C, Jonsson B, Dawson A (2002) Ten-year risk of osteoporotic fracture and the effect of risk factors on screening strategies. Bone 30:251–258
Kanis JA, Johansson H, Oden A et al (2004) A family history of fracture and fracture risk. Bone 35:1029–1037
Kanis JA, Johansson H, Oden A et al (2004) A meta-analysis of prior corticosteroid use and fracture risk. J Bone Miner Res 19:893–899
Kanis JA, Johnell O, De Laet C et al (2004) A meta-analysis of previous fracture and subsequent fracture risk. Bone 35:375–382
De Laet C, Kanis JA, Oden A et al (2005) Body mass index as a prediction of fracture risk. A meta-analysis. Osteoporos Int 16:1330–1338
Kanis JA, Johansson H, Johnell O et al (2005) Alcohol intake as a risk factor for fracture. Osteoporos Int 16:737–742
Kanis JA, Johansson H, Oden A et al (2005) A meta-analysis of milk intake and fracture risk: low utility for case finding. Osteoporos Int 16:799–804
Kanis JA, Johnell O, Oden A et al (2005) Smoking and fracture risk: a meta-analysis. Osteoporos Int 16:222–228
Kanis JA, Oden A, Johnell O et al (2007) The use of clinical risk factors enhances the performance of BMD in the prediction of hip and osteoporotic fractures in men and women. Osteoporos Int 18:1033–1046
Black DM, Steinbuch M, Palermo L et al (2001) An assessment tool for predicting fracture risk in postmenopausal women. Osteoporos Int 12:519–528
Kanis JA, Gluer C-C, for the Committee of Scientific Advisors, International Osteoporosis Foundation (2000) An update on the diagnosis and assessment of osteoporosis with densitometry. Osteoporos Int 11:192–202
Kanis JA (2002) Diagnosis of osteoporosis and assessment of fracture risk. Lancet 359:1929–1936
Ramsay LE, Haq IU, Jackson PR, Yeo WW, Pickin DM, Payne JN (1996) Targeting lipid-lowering drug therapy for primary prevention of coronary artery disease: an updated Sheffield table. Lancet 348:387–388
Ramsay LE, Haq IU, Jackson PR, Yeo WW (1996) The Sheffield table for primary prevention of coronary heart disease. Corrected. Lancet 348:1251–1252
Conroy RM, Pyörälä K, Fitzgerald AP et al (2003) Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Europ Heart J 11:987–1003
UKPDS Group (2001) The UKPDS Risk Engine: a model for the risk of coronary heart disease in type 2 diabetes (UKPDS 56). Clin Sci 101:671–679
UKPDS Group (2002) Risk of Stroke in Type 2 Diabetes Estimated by the UK Prospective Diabetes Study Risk Engine (UKPDS 60). Stroke 33:1776–1781
Breslow NE, Day NE (1987) Statistical methods in cancer research, vol 2. IARC Scientific Publications, no 32, Lyon 131–135
Oden A, Dawson A, Dere W, Johnell O, Jonsson B, Kanis JA (1988) Lifetime risk of hip fracture is underestimated. Osteoporos Int 8:599–603
Singer BR, McLauchlan GJ, Robinson CM, Christie J (1998) Epidemiology of fractures in 15,000 adults. The influence of age and gender. J Bone Joint Surg 80B:243–248
DeLusignan S, Valentin T, Chan T et al (2004) Problems with primary care data quality: Osteoporosis as an exemplar. Informatics in Primary Care 12:147–156
Kanis J, Brazier J, Stevenson M, Calvert W, Jones ML (2002) Treatment of established osteoporosis: a systematic review and cost-utility analysis. Health Technol Ass 6:1–146
Kanis JA, Oden A, Johnell O, Jonsson B, de Laet C, Dawson A (2001) The burden of osteoporotic fractures: a method for setting intervention thresholds. Osteoporos Int 12:417–427
Kanis JA, Johnell O, Oden A et al (2000) Long-term risk of osteoporotic fracture in Malmö. Osteoporos Int 11:669–674
Tuppurainen M, Kroger H, Honkanen R et al (1995) Risks of perimenopausal fractures - a prospective population-based study. Acta Obstetr Gynecol Scand 74:624–628
Kanis JA, McCloskey EV, Powles T, Paterson AH, Ashley S, Spector T (1999) A high incidence of vertebral fracture in women with breast cancer. Br J Cancer 79:1179–1181
Melton LJ III, Khosla S, Malkasian GD, Achenbach SJ, Oberg AL, Riggs BL (2003) Fracture risk after bilateral oophorectomy in elderly women. J Bone Miner Res 18:900–905
Melton LJ III, Alothman KI, Khosla S, Achanbach SJ, Oberg AL, Zinake H (2003) Fracture risk following bilateral orchidectomy. J Urol 169:1747–1750
Stanley I II, Selmatt BP, Poses RM, Deiss WP (1991) Does hypogonadism contribute to the occurrence of a minimal trauma hip fracture in elderly men? J Amer Geriatric Soc 39:766–771
Wuster C, Abs R, Bengtsson BA, Benmarker H, Feld B, Rasmussen U et al (2001) The influence of growth hormone deficiency, growth hormone replacement therapy, and other aspects of hypopituitarism on fracture rate and bone mineral density. J Bone Miner Res 16:398–405
Rigotti NA, Neer RM, Skates SJ, Herzog DB, Nussbaum SR (1991) The clinical course of osteoporosis in anorexia nervosa. A longitudinal study of cortical bone mass. JAMA 265:1133–1138
Gillberg C, Rastam M, Gillberg IC (1994) Anorexia nervosa: physical health and neurodevelopment at 16 and 21 years. Dev Med Child Neurol 36:567–575
Vestergaard P, Mosekilde L (2002) Fracture risk in patients with celiac disease, Crohn’s disease, and ulcerative colitis: a nationwide follow-up study of 16,416 patients in Denmark. Am J Epidemiol 156:1–10
Bernstein CN, Blanchard JF, Leslie W, Wajda A, Yu BN (2000) The incidence of fracture among patients with inflammatory bowel disease: a population-based cohort study. Ann Intern Med 133:795–799
Loftus EV, Crowson C, Sandborn WJ, Tremaine WJ, O’Fallon WM, Melton LJ III (2000) Long-term fracture risk in patients with Crohn’s disease: a population-based study in Olmsted County, Minnesota. Gastroenterol 123:468–475
Van Staa T-P, Cooper C, Brusst LS, Leufkens H, Javaid MK, Arden NK (2003) Inflammatory bowel disease and the risk of fracture. Gastroenterol 125:1591–1597
Vestergaard P, Krogh K, Rejnmark L, Mosekilde L (1998) Fracture rates and risk factors for fractures in patients with spinal cord injury. Spinal Cord 36:790–796
Vestergaard P, Glerup IT, Steffensen BF, Rejnmark I, Rabbek J, Mosekilde I (2001) Fracture risk in patients with muscular dystrophy and spinal muscular atrophy. J Rehabilitation Med 33:150–155
Johnell O, Melton LJ III, Atkinson EJ, O’Fallon WM, Kurland LT (1992) Fracture risk in patients with Parkinsonism: a population-based study in Olmsted County, Minnesota. Age Ageing 21:32–38
Dennis MS, Lo KM, McDowall M, West T (2002) Fractures after stroke: frequency, types and associations. Stroke 33:728–734
Kanis JA, Oden A, Johnell O (2001) Acute and long-term increase in fracture risk after hospitalisation for stroke. Stroke 32:702–706
Donnelly S, Doyle DV, Denton A, Roffe I, McCloskey EV, Spector TD (1994) Bone mineral density and vertebral compression fracture rates in ankylosing spondylitis. Ann Rheum Dis 53:117–121
Royal College of Physicians (2002) Glucocorticoid-induced osteoporosis. Guidelines on prevention and treatment. Bone and Tooth Society of Great Britain, National Osteoporosis Society and Royal College of Physicians. Royal College of Physicians London UK
Ramsey-Goldman R, Dunn JE, Dunlop DD (1999) Increased risk of fracture in patients receiving solid organ transplants. J Bone Miner Res 14:456–463
Vantour LM, Melton LJ 3rd, Clarke I, Achenbach SJ, Oberg AL, McCarthy JT (2004) Long-term fracture risk following renal transplantation: a population-based study. Osteoporos Int 15:160–167
Shane E, Papadoupoulos A, Staron RB et al (1999) Bone loss and fracture after lung transplantation. Transplantation 68:220–227
Nicodemus KK, Folsom AR, Iowa Women’s Health Study (2001) Type 1 and type 2 diabetes and incident hip fractures in postmenopausal women. Diabetes Care 24:1192–1197
U.S. Department of Health and Human Services (2004) Bone health and osteoporosis: a report of the Surgeon General. Rockville, MD, U.S. Department of Health and Human Services, Office of the Surgeon General
Vestergaard P, Rejnmark L, Mosekilde L (2005) Relative fracture risk in patients with diabetes mellitus, and the impact of insulin and oral antidiabetic medication on relative fracture risk. Diabetologia 48:1292–1299
Schwartz AV, Sellmeyer DE, Ensrud KE et al (2001) Older women with diabetes have an increased risk of fracture: a prospective study. J Clin Endocrinol Metab 86:32–38
Vestergaard P, Mosekilde L (2003) Hyperthyroidism, bone mineral, and fracture risk - a meta-analysis. Thyroid 13:585–593
Vestergaard P, Rejnmark L, Weeke J, Mosekilde L (2000) Fracture risk in patients treated with hyperthyroidism. Thyroid 10:341–348
Vestergaard P, Mosekilde L (2002) Fractures in patients with hyperthyroidism and hypothyroidism: a nationwide follow-up study in 16,249 patients. Thyroid 12:411–419
Melton LJ 3rd, Ardila E, Crowson CS, O’Fallon WM, Khosla S (2000) Fractures following thyroidectomy in women: a population-based cohort study. Bone 27:695–700
Bauer DC, Ettinger B, Nevitt MC, Stone KL, Study of Osteoporotic Fractures Research Group (2001) Risk for fracture in women with low serum levels of thyroid-stimulating hormone. Ann Intern Med 134:561–568
Looker AC, Wahner HW, Dunn WL, Calvo MS, Harris TB, Heyse SP (1998) Updated data on proximal femur bone mineral levels of US adults. Osteoporos Int 8:468–486
Burger H, de Laet CE, Weel AE, Hofman A, Pols HA (1999) Added value of bone mineral density in hip fracture risk scores. Bone 25:369–374
Albrand G, Munoz F, Sornay RE, Duboeuf F, Delmas PD (2001) Independent predictors of all osteoporosis-related fractures in healthy postmenopausal women: The OFELY Study. Bone 32:78–85
Carroll J, Testa M, Erat K, LeBoff M, Fuleihan G-EH (1997) Modelling fracture risk using bone density, age, and years since menopause. Am J of Preventive Med 13:447–452
Dargent-Molina P, Douchin MN, Cormier C, Meunier PJ, Bréart G (2002) Use of clinical risk factors in elderly women with low bone mineral density to identify women at higher risk of hip fracture: The EPIDOS prospective study. Osteoporos Int 13:593–599
Girman CJ, Chandler JM, Zimmerman S et al (2002) Prediction of fracture in nursing home residents. J Am Geriatr Soc 50:1341–1347
Honkanen RJ, Honkanen K, Kroger H, Alhava E, Tuppurainen M, Saarikoski S (2000) Risk factors for perimenopausal distal forearm fracture.Osteoporos Int 11:265–270
Leslie WD, Metge C, Salamon EA, Yuen CK (2002) Bone mineral density testing in healthy postmenopausal women. The role of clinical risk factor assessment in determining fracture risk. J Clin Densitom 5:117–130
Miller PD, Barlas S, Brenneman SK et al (2004) An approach to identifying osteopenic women at increased short-term risk of fracture. Arch Int Med 164:1113–1120
Westfall G, Littlefield R, Heaton A, Martin S (2001) Methodology for identifying patients at high risk for osteoporotic fracture. Clin Therap 23:1570–1588
Colón-Emeric CS, Pieper CF, Artz MB (2002) Can historical and functional risk factors be used to predict fractures in community-dwelling older adults? Development and validation of a clinical tool. Osteoporos Int 13:955–961
van Staa TP, Leufkens H-GM, Cooper C (2002) Utility of medical and drug history in fracture risk prediction among men and women. Bone 31:508–514
Van Staa T-P, Geusens P, Pols HAP, De Laet C, Leufkens HCM, Cooper C (2005) A simple score for estimating the long-term risk of fracture in patients using oral glucocorticoids. Quart Jl Med 98:191–198
McGrother CW, Donaldson M-MK, Clayton D, Abrams KR, Clarke M (2002) Evaluation of a hip fracture risk score for assessing elderly women: the Melton Osteoporotic Fracture (MOF) study. Osteoporos Int 13:89–96
Walter LC, Lui LY, Eng C, Covinsky KE (2003) Risk of hip fracture in disabled community-living older adults. J Am Geriatr Soc 51:50–55
Food and Drug Administration (1994) Guidelines for preclinical and clinical evaluation of agents used in the prevention or treatment of postmenopausal osteoporosis. Division of Metabolism and Endocrine Drug Products, Rockville, MD
Committee for Medicinal Products for Human Use (CHMP) (2006) Guideline on the evaluation of medicinal products in the treatment of primary osteoporosis. Ref CPMP/EWP/552/95Rev.2. London, CHMP, Nov
Saag KG, Emkey R, Schnitzer TJ et al (1998) Alendronate for the prevention and treatment of glucocorticoid-induced osteoporosis. Glucocorticoid-induced Osteoporosis Intervention Study Group. N Engl J Med 339:292–299
Adachi JD, Saag KG, Delmas PD et al (2001) Two year effects of alendronate on bone mineral density and vertebral fracture in patients receiving glucocorticoids: a randomised, double-blind, placebo-controlled extension trial. Arthr Rheum 44:202–211
Reginster JY, Minne HW, Sorensen OH et al (2000) Randomized trial of the effects of risedronate on vertebral fractures in women with established postmenopausal osteoporosis. Vertebral efficacy with risedronate therapy (VERT) study group. Osteoporos Int 11:83–91
Kanis JA, Barton I, Johnell O (2005) Risedronate decreases fracture risk in patients selected solely on the basis of prior vertebral fracture. Osteoporos Int 16:475–482
McCloskey EV, Selby P, Davies M et al (2004) Clodronate reduces vertebral fracture risk in women with post-menopausal or secondary osteoporosis: results of a double blind placebo-controlled 3 year study. J Bone Miner Res 19:728–736
Roux C, Reginster JY, Fechtenbaum J et al (2006) Vertebral fracture risk reduction with strontium ranelate in women with post-menopausal osteoporosis is independent of baseline risk factors. J Bone Miner Res 21:536–542
Marcus R, Wang O, Satterwhite J et al (2003) The skeletal response to teriparatide is largely independent of age, initial bone mineral density and prevalent vertebral fractures in postmenopausal women with osteoporosis. J Bone Miner Res 18:18–23
Johnell O, Kanis JA, Black DM et al (2004) Association between baseline risk factors and vertebral fracture risk in the Multiple Outcomes of Raloxifene Evaluation (MORE) study. J Bone Miner Res 19:764–772
McClung MR, Geusens P, Miller PD et al (2001) Effect of risedronate on the risk of hip fracture in elderly women. Hip Intervention Program Study Group. New Engl J Med 344:333–340
Cummings SR, Black DM, Thompson D et al (1998) Effect of alendronate on risk of fracture in women with low bone density but without vertebral fractures: results from the Fracture Intervention Trial. JAMA 280:2077–2082
Davison KS, Siminoski K, Chik C, Jen H, Warshawski R, Lee K (2003) Impact of height loss due to vertebral fractures on body mass index. J Bone Miner Res 18(Suppl 2):S243
Midanik LT (1988) Validity of self-reported alcohol use: a literature review and assessment. Br J Addict 83:1019–1030
Standing Medical Advisory Committee to the Secretaries of State for Health and for Wales (1989) Drinking problems. A challenge for every doctor. HMSO, London
Van Staa TP, Leufkens HGM, Abenhaim L, Zhang B, Cooper C (2000) Fracture and oral corticosteroids: relationship to daily and cumulative dose. Rheumatol 39:1383–1389
Delmas PD, Genant HK, Crans GG et al (2003) Severity of prevalent vertebral fractures and the risk of subsequent vertebral and nonvertebral fractures: results from the MORE trial. Bone 33:522–532
Kanis JA, Adams J, Borgström B et al (2008) The cost-effectiveness of alendronate in the management of osteoporosis. Bone, (in press)
Kanis JA, Johnell O, De Laet C, Jonsson B, Oden A, Oglesby A (2002) International variations in hip fracture probabilities: implications for risk assessment. J Bone Miner Res 17:1237–1244
World Health Organization (2008) Assessment of osteoporosis at the primary health care level. WHO, Geneva (in press)
Kanis JA, on behalf of the World Health Organization Scientific Group (2008) Assessment of osteoporosis at the primary health-care level. Technical Report. WHO Collaborating Centre, University of Sheffield, UK (in press)
Acknowledgements
We are grateful to the Alliance for Better Bone Health, Amgen, Hologic, IGEA, Lilly, Lunar, Novartis, Pfizer, Roche, Wyeth, the EU (FP3/5; QLK6-CT-2002-00491) for supporting this study and the International Osteoporosis Foundation, the International Society for Clinical Densitometry and the National Osteoporosis Foundation for their unrestricted support of this work.
Conflicts of interest
None.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors acknowledge the huge contribution of Olof Johnell, who died unexpectedly in April 2006.
Appendix
Appendix
The estimated hazard functions were of the form
where the betas were coefficients and x1, … , xk were the values of the variables.
The hazard functions were estimated as continuous functions by Poisson regression [26, 27].
A separate Poisson regression was performed for each cohort with men and women included together. Sex was a variable included in the model. The beta coefficients of the different variables were merged by the calculation of a weighted sum. The weights were chosen to give the smallest variance of the sum. Let vari denote the variance of βi, and s=Σ (βi/vari), z = Σ (1/vari). Then the merged beta was β = s/z, and the standard deviation SD of β was SD=√(1/z). Several variables and their interaction (products) with time, age or sex are included in the model. For some variables like BMI the change of risk was allowed to have a different increase or decrease below or above a pre specified limit.
The hazard functions were estimated by use of many cohorts from different countries and the data calibrated to the epidemiology of the UK, assuming that the relative importance of the variables was approximately the same for different countries. However, the risk of fracture and the risk of death at a certain age differ from country to country. By considering all variables except age, a risk score was calculated by multiplying each variable by the corresponding beta coefficient and adding the products. The hazard functions are then calibrated to a specified country so that the relative importance of the variables except age is preserved, but the mean hazard function (mean taken over all values of the risk score) equals the mean risk of the country. The adjusted hazard function is a product between three factors. The first factor is the natural number e to the linear combination obtained from the cohorts, i.e., e to the risk score. The second factor is calculated from the general fracture risk among the general population as described below. The third factor is a normalising factor making the mean risk equal to the second factor for each age. Let us denote the third factor z(age). If a random variable Y has a normal distribution with the mean μ and standard deviation σ then the expected value E[exp(Y)] = exp(μ+σ2/2). In this application Y is a risk score. By linear regression (in the simplest case) we determine E[Y∣age] = a + b × age and the standard deviation σ around the regression line. Then the third factor z(age), the calibrating one, can be put equal to 1/exp(a + b × age + σ2/2).
With regard to the relationship between probability and hazard functions, let h(t) denote the hip fracture hazard function, d(t) the death hazard function and g(t) the hazard function of the combined event hip fracture or death. Though the functions in typical applications contain several variables, only a time variable is given in order to simplify the notations. The hazard function g of having the first event of death or hip fracture is well approximated (see discussion) by d + h. From the general and well-known relationship between survival and hazard functions we know that the probability of being free from any of the two types of events at the end of the period (0,t) is
The probability p of a hip fracture event before t is, therefore, given by
The basic relationship between 10-year probability and the hazard functions of death and of hip fracture includes an approximation. The hazard function of hip fracture or death, g(x), is approximately equal to the sum of the hazard functions of hip fractures and of death, g(x) ≈ h(x) + d(x). Indeed g(x) is somewhat less than the sum of the two functions because when a hip fracture causes death, both will contribute to the right side of the relationship but only the hip fracture to the left side, so the approximation gives an underestimation of the probability.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial 2.0 International License, which permits any non-commercial use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by-nc/2.0/.
About this article
Cite this article
Kanis, J.A., Johnell, O., Oden, A. et al. FRAX™ and the assessment of fracture probability in men and women from the UK. Osteoporos Int 19, 385–397 (2008). https://doi.org/10.1007/s00198-007-0543-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00198-007-0543-5