Fully resolved coupled solid-fluid simulations of shock interaction with a layer of deformable aluminum particles

Abstract

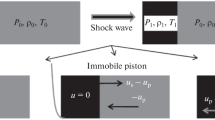
This work describes particle-resolved simulations of a single aluminum particle within a larger layer of particles that is interacting with a strong nitromethane shock. The objective is to observe how varying the particle’s volume fraction within a planar particle curtain changes the deformation of the particles as well as the fluid dynamics around them. First the isolated particle limit, when the distance between the neighbors is very large, is simulated; this is followed by simulating a single-layer of particles subjected to a planar shock propagating normal to the layer. Several initial particle volume fractions of the curtain are considered, and the results are compared and discussed. The results show that the presence and proximity of neighboring particles influence the shape and magnitude of the particle’s plastic deformation. The presence of neighboring particles also increases the initial average pressure within the particle during shock interaction as well as the average velocity of the particle afterwards. The strength of the reflected shock from the curtain of particles increases in magnitude and becomes more planar as the volume fraction increases due to neighboring particles’ individual reflections that coalesce to form a singular planar shock. The results obtained provide valuable insight into the microscale physics of shock interaction with an array of deformable particles.

Appendices

Appendix 1: Mesh resolution

To ensure the computational mesh size of 40 cells through the diameter of the particle was sufficient, a mesh resolution study was performed with the $\alpha = 0.33$ particle layer. Both the finite volume (fluid) and element (particle) meshes were varied to the same computational cell sizes for the study. The average particle pressure and velocity obtained with various grid resolutions are plotted in Fig. 16. From the results, it appears that 40 cells through the diameter of the particle is more than sufficient towards attaining a converging solution.

Fig. 16

Averaged states over time of the aluminum particle using various mesh/element sizes. Solid lines are pressure and dotted lines are velocity

Appendix 2: Computational methods

The computational methods used in this paper are well established in the literature. The purpose of this appendix is to present the basic governing equations and material models, briefly describe the solution method, and provide references for interested readers.

1.1 Lagrangian finite element solution

Solid materials are represented within an explicit finite element framework developed and maintained by Lawrence Livermore National Laboratory (LLNL) [49]. The general finite element method applied for transient analysis is presented in [37, 55, 56]. The governing equations for mass, momentum, and energy, cast in the Lagrangian framework, are:

$$\begin{aligned} \rho V= & {} \rho _\mathrm {0} \end{aligned}$$

(3)

$$\begin{aligned} \rho {\dot{u}}_{i}= & {} \sigma _{ij,j} + \rho f_{i} \end{aligned}$$

(4)

$$\begin{aligned} \rho {\dot{e}}= & {} \sigma _{ij}{\dot{\epsilon }}_{ij} + \rho f_{i} u_{i}. \end{aligned}$$

(5)

Here $\rho _\mathrm {0}$ is the initial density, $\rho$ is the density, V is the volume of the element relative to its initial volume, u is the velocity, $\sigma$ is the Cauchy stress tensor, f is a body or external force per unit mass, e is the internal energy per unit mass, and ${\dot{\epsilon }}$ is the strain rate tensor. The dot above a variable represents the total derivative: $\dot{( )}=D( )/Dt$.

For large deformation calculations, the stress tensor is separated into a deviatoric stress (s) and pressure (P) components:

$$\begin{aligned} \sigma _{ij} =s_{ij} + \delta _{ij} P, \end{aligned}$$

(6)

where $\delta$ is the Kronecker delta. Pressure is calculated via an equation of state, and the deviatoric stress rate is defined using the Jaumann rate:

$$\begin{aligned} {\dot{s}}_{ij} = 2 \mu {\dot{\epsilon }}'_{ij} + s_{ip} \omega _{pj} + s_{jp} \omega _{pi}. \end{aligned}$$

(7)

Here $\mu$ is the shear modulus, $\omega$ is the spin tensor, ${\dot{\epsilon }}$ is the strain rate tensor, and ${\dot{\epsilon }}'$ is the deviatoric strain rate tensor:

$$\begin{aligned} \omega _{ij}= & {} \frac{1}{2} \Big ( \frac{\partial u_{i}}{\partial x_{j}} - \frac{\partial u_{j}}{\partial x_{i}} \Big ) \end{aligned}$$

(8)

$$\begin{aligned} {\dot{\epsilon }}_{ij}= & {} \frac{1}{2} \Big ( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} \Big ) \end{aligned}$$

(9)

$$\begin{aligned} {\dot{\epsilon }}'_{ij}= & {} {\dot{\epsilon }}_{ij} - \frac{1}{3}{\dot{\epsilon }}_{ij}\delta _{ij} \end{aligned}$$

(10)

For elastic-plastic materials, the integration of (7) results in an elastic estimate ($s^{\mathrm {est}}$) which may exceed the yield condition imposed by the constitutive model. If so, a radial return method is used to return the stress to the yield surface. To assess this, the effective stress is calculated as:

$$\begin{aligned} s_\mathrm {eff} = \Big ( \frac{3}{2} s_{ij}^{\mathrm {est}} s_{ij}^{\mathrm {est}} \Big )^{1/2}. \end{aligned}$$

(11)

Finally, the effective stress is compared to the yield stress, $\sigma _\mathrm {y}$, and the stress tensor is scaled if necessary:

$$\begin{aligned} s_{ij} = {\left\{ \begin{array}{ll} \frac{\sigma _{y}}{s_\mathrm {eff}} s^\mathrm {est}_{ij} &{}\quad \text {if } s_\mathrm {eff} \ge \sigma _\mathrm {y}, \\ s^\mathrm {est}_{ij} &{}\quad \text {otherwise.} \end{array}\right. } \end{aligned}$$

(12)

Additional information on the stress update methodology and radial return algorithms can be found in [55, 57, 58].

Transient integration is accomplished using a central difference scheme in which velocity is saved at the half-step. Spatial derivatives are computed via central differencing, with the application of artificial viscosity to avoid numerical oscillations near discontinuities. See [37, 55, 59] for presentation of these methods.

1.2 Eulerian finite volume solution

The fluid domain is modeled using an Eulerian finite volume method. The fluid is compressible and assumed to be inviscid, so that the Euler equations apply. The governing equations are solved with dimensional splitting [60] via a series of 1D sweeps. The one-dimensional Euler equations are:

$$\begin{aligned} \frac{\partial {\varvec{M}}}{\partial t} + \frac{\partial {\varvec{N}}}{\partial r} = 0 \end{aligned}$$

(13)

where

$$\begin{aligned} {\varvec{M}}=\begin{bmatrix} \rho \\ \rho u \\ \rho E \\ \rho \nu \end{bmatrix},\quad {\varvec{N}} = \begin{bmatrix} \rho u \\ \rho u^{2} + P \\ \rho u E + P u \\ \rho u \nu \end{bmatrix}, \end{aligned}$$

where E is the total energy per unit mass and $\nu$ is a convected variable. Off-sweep velocities are treated as convected variables in this methodology.

A Monotonic Upwind Scheme for Conservation Laws (MUSCL) method is applied. The specific scheme used was proposed by Collela [61] and applied by Wardlaw [62]. This is a higher-order scheme that attains second order accuracy in both time and space in smooth flow regions, but reduces to first order accuracy at shocks. Interested readers are directed to [60, 63, 64] for further information.

1.3 Fluid-solid coupling

The finite element and finite volume solutions are coupled at the fluid-solid interface. A mechanical coupling consistent with the goverining equations for the solid and fluid are applied. Momentum and energy are exchanged due to pressure and the associated work, while viscous effects, heat and mass transfer are assumed to be negligible during the early times of shock-particle interaction. Coupling of the solvers at the solid-fluid interface is accomplished with an embedded boundary approach. The finite volume solver employs a ghost-fluid method to account for the boundary conditions at the solid particle surface while pressures from the fluid are mapped onto the exposed interface segments of the finite element mesh. Methods of this type are common in the literature [43,44,45,46, 65,66,67].

The external fluid applies a force boundary condition to the solid surface. The finite element solver calculates internal forces based on stress gradients and body forces. For the subset of nodes existing on the solid-fluid interface, coupling forces exerted from fluid pressure ($f^\mathrm {cpl}$) augment any other forces (e.g., body forces) existing in solution ($f^\mathrm {fem}$). The momentum, (4) and energy, (5) become:

$$\begin{aligned} \rho {\dot{u}}_{i}= & {} \sigma _{ij,j} + \rho \left( f^\mathrm {fem}_{i} + f^\mathrm {cpl}_{i} \right) \end{aligned}$$

(14)

$$\begin{aligned} \rho {\dot{e}}= & {} \sigma _{i,j}{\dot{\epsilon }}_{ij} + \rho \left( f^\mathrm {fem}_{i} + f^\mathrm {cpl}_{i} \right) u_{i}. \end{aligned}$$

(15)

A ghost-fluid method [43] is used to represent the solid body within the finite volume solver. Internal ghost cells are inserted into the dimensional sweeps. State values are assigned to enforce the cutting element velocity and position, in a manner consistent with MUSCL limited slopes. As discussed by Fedkiw [43], the interface normal velocity is defined as the finite element node velocity. Pressure equilibrium is not rigourously enforced at the interface, rather pressure differences in the Eulerian and Lagrangian solutions drive interface motion through (14), which leads to pressure equilibration. Further details of ghost fluid state construction and the overall coupling scheme are given in [62].

1.4 Steinberg-Guinan constitutive model

The constitutive model utilized for the aluminum particle was the Steinberg-Guinan high rate elastic-plastic model [48,49,50]. This model is applicable to metals at high strain rates, where plastic strain and pressure hardening, as well as thermal softening, may occur. The yield stress is defined as:

$$\begin{aligned} \sigma _{y}= & {} \sigma _\mathrm {0} \Big [ 1 + \beta \Big ( \gamma _\mathrm {i} + \epsilon ^\mathrm {p}_\mathrm {eff} \Big ) \Big ]^{n} \nonumber \\&\Big [ 1 + b P V^{\frac{1}{3}} - h \Big ( \frac{e - e_\mathrm {c}}{3 R \text {/} \mathrm {Aw} } - 300 \Big ) \Big ] \mathrm {e}^{\frac{f e}{e_\mathrm {m} - e }}. \end{aligned}$$

(16)

Equation (16) is applicable for when the material’s internal energy, e, has not exceeded the melting energy, $e_\mathrm {m}$, which is a function of the cold compression energy, $e_\mathrm {c}$, and the melting temperature of the material. In the above, $\gamma _\mathrm {i}$ is the initial plastic strain of the material, and $\sigma _\mathrm {0}$ is the base yield stress. $\beta , n, h, b,$ and f are constant parameters of the material model that define the yield stress as a function of effective plastic strain, $\epsilon ^\mathrm {p}_\mathrm {eff}$, pressure and energy. R is the universal gas constant and $\mathrm {Aw}$ is the atomic weight of the material. Model parameters used in this study are defined in Table 3.

1.5 Mie–Gruneisen EOS

The Mie–Gruneisen equation of state assumes separate forms for compression and tension [49]. The excess compression is defined as: $\mu =\rho / \rho _\mathrm {0} -1$. For compressed material ($\mu \ge 0$):

$$\begin{aligned} p = \frac{ \rho _\mathrm {0} C^{2} \mu \Big [1+\Big (1- \frac{\gamma _\mathrm {0}}{2} \Big ) \mu \Big ] }{ \Big [ 1-(S_\mathrm {1} -1)\mu -S_\mathrm {2} \frac{\mu ^{2}}{\mu +1} \Big ]^{2} } + \gamma _\mathrm {0} \rho e. \end{aligned}$$

(17)

For an expanded material ($\mu < 0$):

$$\begin{aligned} p = \rho _{0} C^{2} \mu + \gamma _{0} \rho e. \end{aligned}$$

(18)

The material parameters $\rho _\mathrm {0}$, C, $\gamma _\mathrm {0}$, $S_\mathrm {1}$, and $S_\mathrm {2}$ are defined in Table 2.