Experimental investigation of shock–shock interactions with variable inflow Mach number

Abstract

Experiments on shock–shock interactions were conducted in a transonic–supersonic wind tunnel with variable free-stream Mach number functionality. Transition between the regular interaction (RI) and the Mach interaction (MI) was induced by variation of the free-steam Mach number for a fixed interaction geometry, as opposed to most previous studies where the shock generator angles are varied at constant Mach number. In this paper, we present a systematic flow-based post-processing methodology of schlieren data that enables an accurate tracking of the evolving shock system including the precise and reproducible detection of RI$\rightleftarrows$MI transition. In line with previous experimental studies dealing with noisy free-stream environments, transition hysteresis was not observed. However, we show that establishing accurate values of the flow deflections besides the Mach number is crucial to achieve experimental agreement with the von Neumann criterion, since measured flow deflections deviated significantly, up to $1.2^{\circ }$, from nominal wedge angles. We also report a study conducted with a focusing schlieren system with variable focal plane that supported the image processing by providing insights into the three-dimensional side-wall effects integrated in the schlieren images.

1 Introduction

Interactions between two shock waves of opposite families (i.e., deflecting the flow in opposite directions) can be classified as regular interactions (RIs) or Mach interactions (MIs), as shown in Fig. 1a, b, respectively. The former type consists of four shock waves ($\mathrm {i_1}$, $\mathrm {i_2}$, $\mathrm {r_1}$, and $\mathrm {r_2}$) and one slip line ($\mathrm {s}$), while the latter includes an additional quasi-normal shock segment ($\mathrm {m}$), known as the Mach stem, and two slip lines ($\mathrm {s_1}$ and $\mathrm {s_2}$). We prefer to refer to either shock system as interaction and not reflection to allow for an asymmetric arrangement of incident shock waves, since the (inviscid) reflection of a shock wave on a solid surface compares to the symmetric case only.

Steady gas dynamics theory characterizes these shock interactions in terms of the free-stream Mach $M_\mathrm {0}$, the flow deflections $\vartheta _\mathrm {1}$ and $\vartheta _\mathrm {2}$ imposed by the incident shocks, and the gas thermodynamic properties. This is often visualized graphically in the form of the so-called shock polars [1]. Assuming constant gas properties, stability boundaries for the different interaction types can be calculated in terms of $M_\mathrm {0}$ for fixed flow deflections, or in terms of one of the flow deflections while keeping the other and the free-stream flow properties unchanged [2]. The stability boundary of the MI originates from the necessity of the slip line pair to be convergent so that the subsonic flow after the Mach stem can accelerate. The limit, usually referred to as the von Neumann criterion, defines an upper bound of flow deflection in the $\vartheta _\mathrm {1}$–$\vartheta _\mathrm {2}$ plane (in the case of fixed $M_\mathrm {0}$) and generally a lower $M_\mathrm {0}$ bound in the $M_\mathrm {0}$–$\vartheta _{\mathrm {1(2)}}$ plane (for fixed $\vartheta _{\mathrm {2(1)}}$). The stability condition of the RI is purely geometrical, based on whether the shock system is capable of satisfying all flow deflection boundary conditions. The limit, referred to as the detachment condition, defines a lower bound of flow deflection or an upper $M_\mathrm {0}$ bound. Of particular interest is the fact that von Neumann and detachment conditions do not necessarily coincide and so a region exists in the ${M}_{\mathrm {0}}{-}{\vartheta }_{\mathrm {1}}{-}{\vartheta }_{\mathrm {2}}$ parameter space, the so-called dual-solution domain (DSD), in which the regular and Mach interactions are both realizable, as shown in Fig. 2.

Fig. 1

Schematic representation of a the regular interaction and b the Mach interaction. $\phi _{k}$ denote shock angles of the incident shocks $\mathrm {i}_{k}$, and $\vartheta _{k}$ denote the corresponding flow deflections. The free-stream Mach number is referred to as $M_\mathrm {0}$. Reflected shocks are labeled as $\mathrm {r}_{k}$, slip lines are labeled as $\mathrm {s}$ or $\mathrm {s}_{k}$, and $\vartheta _{k\mathrm {n}}$ denote nominal shock generator angles. The interaction point in a is labeled as I, while triple points and the Mach stem in b are, respectively, labeled as $\hbox {T}_{k}$ and $\mathrm {m}$. The subscripts ${k}=1$ and ${k}=2$ relate quantities to the upper and lower incident shocks, respectively

Based on the existence of such dual-solution domain, Hornung, Oertel, and Sandeman [3] speculated about the possibility of hysteresis in the RI$\rightarrow$MI$\rightarrow$RI cycle. For steady flows, they anticipated the occurrence of RI$\rightarrow$MI transition according to the detachment condition, while the MI$\rightarrow$RI transition should abide the von Neumann criterion. This hypothesized hysteresis phenomenon turned out to be much easier to be reproduced numerically than experimentally. While numerical works provided unambiguous evidence [4, 5], different experimental investigations [6,7,8] yielded different RI$\rightarrow$MI transition conditions, all scattered across the theoretical DSD. Ivanov et al. [9] attributed the wide spread of experimental results to the different level of free-stream disturbances in each flow facility, which seemed to trigger premature RI$\rightarrow$MI transition and thus partially or totally prevent the hysteresis. The same research group later confirmed this hypothesis by successfully observing hysteresis in a low-noise wind tunnel facility [10]. Three-dimensional edge effects in wind tunnel studies and their impact on transition data were documented by Skews [11]. Additional works on shock interactions [12,13,14,15,16,17,18] further confirmed the sensitivity of the RI$\rightarrow$MI transition to flow disturbances and unambiguously identify the MI as more robust under these conditions.

Despite the physical phenomenon being well understood, there is a critical need for improvement in the measurement techniques and post-processing strategies adopted in the experimental investigations of shock interaction transition, as well as in assessing the agreement with theoretical stability boundaries. As means to control the shock generator pitch, electric motors are often used together with pre-calibrated digital transducers to measure the relative position of the model geometry with respect to the free-stream flow. These measurements, generally assumed to be representative of the flow direction, are taken at the location where the device is fixed, which is often at the model supports or at the sting (far away from the shock generators), and disregard potential model deformation induced by the aerodynamic loading. The same holds true for the influence of the boundary-layer growth along the shock generator geometry, which is also commonly disregarded. If such effects are not properly accounted for, either with a suitable feedback compensation technique or during post-processing, a non-negligible mismatch between nominal shock generator angle and effective flow deflection appears. Although this mismatch may not alter the main conclusions of the experiment in a qualitative sense, it certainly has an impact on the quantitative results, particularly on the effective flow deflections at transition and the Mach stem height evolution. The importance of providing high-fidelity experimental datasets of such quantities should not be taken lightly, as the validation of numerical simulations as well as reduced-order models and analytical descriptions of the phenomenon rely on them.

In this paper, we therefore propose a flow-based post-processing approach of the experimental data that accounts for the aforementioned effects. Parameters such as flow deflections and Mach stem height are quantified from schlieren visualizations of the shock system, in combination with associated free-stream pressure measurements from which the instantaneous value of the free-stream Mach number is determined. The analysis is complemented with the calculation of the stability boundaries consistent with the actual interaction conditions to properly assess hysteresis effects. While most experimental investigations on shock interactions have targeted the flow-deflection-induced hysteresis, that is, homogeneous free-stream conditions and varying shock generator deflections, we perform our analysis for the complimentary case, i.e., the Mach-number-induced hysteresis. Here, the shock generators remain fixed, while the free-stream Mach number varies. To our knowledge, there is only one reported experimental work using a similar approach [19]. Schlieren visualization was used as the main flow diagnostics tool, and a focusing schlieren system was additionally employed to investigate three-dimensional side-wall effects. The combination of these techniques enabled the accurate measurement of transition conditions, which was found crucial to achieve agreement with theoretical predictions. We show that RI$\rightleftarrows$MI transition, while apparently occurring outside the stability boundaries when their evaluation is based on nominal conditions, either occurs within the DSD or satisfies the von Neumann criterion corresponding to the measured flow deflections, which were found to differ noticeably, up to $1.2^{\circ }$, from nominal wedge angles.

The paper is organized as follows. In Sect. 2, we present our methodology, including the experimental facility, the shock generator setup, flow measurement techniques, and the proposed analysis procedure of the schlieren images. Results are presented and discussed in Sect. 3, with emphasis on the focusing schlieren data, the Mach stem height dependence on $M_\mathrm {0}$, and the detected transition conditions. The paper is concluded in Sect. 4.

2 Methodology

2.1 Experimental facility

The experiments were conducted in the transonic–supersonic blow-down wind tunnel (TST-27) of the Aerodynamics Laboratory at TU Delft. The facility has a rectangular test section of $280\times 272\,\hbox {mm}$ and is equipped with a flexible convergent–divergent nozzle that allows the Mach number to be continuously varied during testing. For the current experiments, the total pressure in the settling chamber ranged from 4 to $6\,\hbox {bar}$, depending on the start-up requirements for each model geometry. The total temperature was approximately $280\,\hbox {K}$ in all cases.

2.2 Setup

A schematic representation of the test model assembly is shown in Fig. 3. It consists of two opposing wedges with equal hypotenuse w that span the complete width of the test section ($b=272\,\hbox {mm}$) in order to minimize the influence of corner effects on the interaction region [11, 20]. Trailing edges of both wedges are located at the same stream-wise location and separated vertically by a distance 2g. Each wedge is rigidly connected to the side walls by means of a pair of horizontal supports. All wedges used in this study were manufactured out of stainless steel and mechanically polished. To distinguish between nominal wedge angles and measured flow deflections, subscripts $\mathrm {n}$ and $\mathrm {m}$ are used, respectively. Thus, we refer to the nominal upper wedge angle as $\vartheta _{\mathrm {1n}}$ and the nominal lower wedge angle as $\vartheta _{\mathrm {2n}}$.

Fig. 2

$M_\mathrm {0}$–$\vartheta _\mathrm {2}$ plane for $\vartheta _\mathrm {1} = 17^{\circ }$. The theoretical dual-solution domain (DSD) is shaded in gray. The dotted line corresponds to the von Neumann criterion, the dashed line corresponds to the detachment condition, and the attached shock boundaries for $\vartheta _\mathrm {1}$ and $\vartheta _\mathrm {2}$ are shown as dash-dotted lines. The free-stream Mach number ranges used in the experiments are also included as red horizontal segments

A parametric study based on gas dynamics theory was conducted to select the values of w, 2g, $\vartheta _{\mathrm {1n}}$, and $\vartheta _{\mathrm {2n}}$ and the ranges of $M_\mathrm {0}$, such as to maximize the width of the DSD while preventing wind tunnel start-up issues and the expansion fans from intersecting the incident shocks. Based on this analysis, w was chosen to be $42\,\hbox {mm}$, 2g was set to $1.79w=75\,\hbox {mm}$, and $\vartheta _{\mathrm {1n}}$ was set to $17^{\circ }$. The selection of $\vartheta _{\mathrm {1n}}$ unambiguously determines the shape of the von Neumann and detachment criteria in the $M_\mathrm {0}$–$\vartheta _{\mathrm {2n}}$ plane and thus the associated DSD, as shown in Fig. 2. The selected values of $\vartheta _{2n}$, namely $10^{\circ }$, $17^{\circ }$, $19^{\circ }$, and $21^{\circ }$, include the nominally symmetric interaction and three different asymmetric cases. The chosen $M_\mathrm {0}$ ranges, ensuring RI$\rightleftarrows$MI transition within the capabilities of the experimental facility, are indicated in Fig. 2 by the red horizontal lines.

Fig. 3

Schematic representation of the assembled model with its characteristic dimensions. The wedge hypotenuse w and span b are equal for all wedges. All dimensions are in mm

Tests were conducted as follows. First, the wind tunnel was started at the highest $M_\mathrm {0}$ value within the range associated with a specific wedge arrangement. As observed in Fig. 2, this unambiguously results in a RI. After steady flow conditions were established, $M_\mathrm {0}$ was continuously reduced toward the lowest value of the considered range. This enforced transition toward the MI. Once the lowest value had been reached, $M_\mathrm {0}$ was then again increased toward its starting value to enforce transition back to the RI. The ratio of the time rate of change of the Mach number $\mathrm {d}M_\mathrm {0}/\mathrm {d}t$ to the characteristic flow time scale $u_{\infty }/w$ was in the order of $10^{-5}$ in all cases, thus confirming the quasi-steady nature of the interactions [18]. Each wedge arrangement was tested five times in order to increase the statistical significance of the results.

2.3 Flow measurement techniques

The time evolution of the free-stream Mach number was obtained from total and static pressure measurements assuming an isentropic expansion. A pressure sensor located in the settling chamber provided the total pressure readings, while two sensors placed on the side walls of the test section, sufficiently upstream of the model, ensured a precise static pressure measurement. All pressure sensor data were recorded at a sampling rate of $5\,\hbox {kHz}$.

Schlieren visualization was used as the main flow visualization tool. A continuous white-light beam was collimated with a parabolic mirror (focal length $f=4000\,\hbox {mm}$) to create a parallel beam that traversed the test section. This beam was converged using a second parabolic mirror on a vertical knife edge and then recorded with a digital camera. A LaVision High-Speed 4M camera at a rate of 125 fps was used during testing of the wedge arrangements involving $\vartheta _{\mathrm {2n}} = 10^{\circ }$, $17^{\circ }$, and $19^{\circ }$. For the remaining geometry, that is, $\vartheta _{\mathrm {2n}} = 21^{\circ }$, due to equipment availability a LaVision Imager sCMOS at a frame rate of 50 fps was used instead. Both systems are essentially similar in optical performance and provided a spatial resolution of approximately $24\,\hbox {pixel/mm}$. All schlieren recordings were synchronized with the pressure readings so that a value of the free-stream Mach number could be assigned to every image.

Fig. 4

Schematic of the focusing schlieren setup

Table 1 Summary of relevant parameters of the focusing schlieren setup

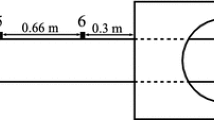
Conventional schlieren visualizations have an infinite depth of focus and therefore show the integrated effect of all density gradients present along the optical path, hence, in the spanwise direction of the test section. This results in undesirable features such as three-dimensional edge effects near the side walls obscuring the target flow features. In order to assess the impact of these effects and to facilitate the correct interpretation of the schlieren data, we additionally set up a focusing schlieren system, which provides sharp images of its focal plane, and examined multiple planes along the optical path. A schematic of the focusing schlieren setup is shown in Fig. 4 with all relevant parameters summarized in Table 1. The reader is referred to Weinstein [21] for additional details on the particular design used. A relay lens was added to the setup in order to adapt the image size to the camera sensor. The camera used to record the focusing schlieren images was a LaVision Imager sCMOS operated at a frame rate of 50 fps.

2.4 Image processing

We developed a flow-based post-processing methodology where accurate instantaneous flow deflection values are extracted from the flow measurement data instead of using the nominal shock generator geometry. This is followed by a consistent calculation of the stability boundaries to properly assess hysteresis effects. The main steps of the proposed methodology are detailed in the following.

2.4.1 Preprocessing

A preprocessing routine is applied to the raw schlieren images, consisting of cropping and background subtraction. Cropping is performed in order to reduce the image size and zoom into the region of interest, while subtracting the background reduces noise and removes unwanted artifacts, such as dust particles on the camera sensor or imperfections in the windows, from the images. A background image is defined as the average of a series of wind-off images of the test section recorded prior to every experimental run. An example of a preprocessed image compared to the raw counterpart is shown in Fig. 5. Notice that both wedges do not completely disappear after preprocessing, which highlights the non-negligible deformation of the model due to the aerodynamic loads.

Fig. 5

Comparison of a MI a before preprocessing (raw image) and b after preprocessing ($\vartheta _{\mathrm {1n}}=17^{\circ }$ and $\vartheta _{\mathrm {2n}}=21^{\circ }$ at $M_\mathrm {0}=2.3$)

2.4.2 Incident shock angle computation

Next, incident shock angles are computed from the preprocessed images. For this, a search area is defined for each incident shock. We use search windows containing 100 horizontal pixel lines and located such that the closest distance to the corresponding wedge tip (as seen in the background image) is 0.3w in the direction perpendicular to the free-stream flow. The horizontal positioning of each window depends on the corresponding incident shock line fit defined in the previous frame; each horizontal pixel row includes 120 pixels toward the free-stream flow from the shock line fit and 30 pixels toward the post-shock region.

Fig. 6

a Light intensity I along the search line and b corresponding gradient $\mathrm {d}I/\mathrm {d}x$ normalized with the maximum value. The profile after filtering is included in a as a dashed red line, whereas search window limits and the detected shock location are indicated in both figures with dash-dotted lines and red squares, respectively

For every window, the evolution of the light intensity is examined along each horizontal pixel line in search of the shock wave. A typical light intensity profile is shown in Fig. 6a. Even though the sudden decrease in light intensity is clearly related to the incident shock, the dark appears too wide to infer with sufficient accuracy the exact shock location at the mid-plane of the test section (where the shock interaction is two dimensional). Examination of the focusing schlieren data, which is discussed in detail in Sect. 3.1, revealed that the trailing edge of the dark region is representative of the true shock location, while most of the remaining thickness can be associated with shock-wave/boundary-layer interactions at the side windows. Therefore, we identify the incident shock by searching for the trailing edge of the dark region. This is done by first computing the gradient of the measured light intensity profile and then searching for the maximum value. In view of the noticeable oscillations, a median filter is applied prior to the gradient computation (dashed red line in Fig. 6a). As shown in Fig. 6b, the trailing edge location of the shock wave on the search line appears now as a sharp peak. We further seek for subpixel resolution of the location of extrema by performing a local parabolic reconstruction of the intensity gradient distribution.

Applying the above-mentioned procedure to all horizontal pixel lines within the search window results in a set of shock location points. An iterative least-square line fitting routine is employed on this set to reduce the number of outliers and optimize the coefficient of determination. We discard all points located beyond three times the RMS of the Euclidean point-to-line distance and recalculate the fit iteratively until convergence. The true incident shock angles $\phi _{\mathrm {1m}}$ and $\phi _{\mathrm {2m}}$ are finally determined by computing the angle between the corresponding line fit and the longitudinal direction of the wind tunnel. Figure 7 illustrates the key elements of the above-mentioned procedure applied to the upper incident shock and superimposed on the preprocessed schlieren image.

2.4.3 Flow deflection computation

Once the incident shock angles have been determined, the associated flow deflections follow in a straightforward manner. Due to the synchronous pressure measurements, each schlieren image has an associated free-stream Mach number value. Considering the ith image in a sequence with a corresponding $M^i_\mathrm {0}$ value, if $\phi ^i_{k\mathrm {m}}$ denotes the incident shock angle measured with the procedure outlined in Sect. 2.4.2 (with ${k}=1$ representing the upper incident shock and ${k}=2$ the lower one), then the corresponding flow deflection $\vartheta ^i_{k\mathrm {m}}$ follows from the oblique shock relation

$$\begin{aligned} \begin{aligned} \vartheta ^i_{k\mathrm {m} }&= f(M_\mathrm {0}, \phi , \gamma ) \\&= \tan ^{-1} \left( \dfrac{2}{\tan {\phi ^i_{k\mathrm {m} } }} \dfrac{ (M^i_\mathrm {0} \sin {\phi ^i_{k\mathrm {m} }} )^2 - 1}{{M^i_\mathrm {0}}^2(\gamma + \cos {2 \phi ^i_{k\mathrm {m} } })+2} \right) , \end{aligned} \end{aligned}$$

(1)

Fig. 7

Main features of the shock detection and shock angle $\phi _{\mathrm {1m}}$ calculation process. Dashed and dash-dotted lines indicate, respectively, the search window limits and the longitudinal direction of the wind tunnel, the orange $\times$ markers depict the detected shock location on each horizontal pixel line, and the green solid line illustrates the resulting shock line fit

with the specific heat ratio taken as $\gamma =1.4$.

We consider the propagation of errors in $M_\mathrm {0}$ and $\phi _{k\mathrm {m}}$ in (1) as means to assess the uncertainty associated with the resulting flow deflections $\vartheta _{k\mathrm {m}}$. For each test run, flow data over a short initial interval corresponding to nominally constant free-stream flow conditions were available (more than 100 visualizations and corresponding pressure measurements). From these data, we estimate the uncertainties on $M_\mathrm {0}$ and $\phi _{k\mathrm {m}}$, namely $\varDelta M_\mathrm {0}$ and $\varDelta \phi _{k\mathrm {m}}$, as twice the average RMS of the resulting $M_\mathrm {0}$ and $\phi _{k\mathrm {m}}$ values ($95.4\%$ statistical confidence limit). Since these are independent measurements, i.e., instantaneous errors in $M_\mathrm {0}$ and $\phi _{k\mathrm {m}}$ are uncorrelated, we approximate the uncertainty in $\vartheta _{k\mathrm {m}}$, namely $\varDelta \vartheta _{k\mathrm {m}}$, as the norm

$$\begin{aligned} \varDelta \vartheta _{k\mathrm {m} } \approx \sqrt{ \left( \left. \frac{\partial f}{\partial M_0}\right| _{\mathrm {max}} \varDelta M_\mathrm {0} \right) ^2 + \left( \left. \frac{\partial f}{\partial \phi _{k\mathrm {m}} } \right| _{\mathrm {max}} \varDelta \phi _{k\mathrm {m} } \right) ^2 },\nonumber \\ \end{aligned}$$

(2)

where the magnitude of the partial derivatives is taken as the maximum recorded in the run. Resulting uncertainties are reported in Table 2 per geometry.

Table 2 Estimated uncertainties

Recall that, in order to avoid confusion with nominal conditions, measured quantities are referred with the subscript $\mathrm {m}$, e.g., $\vartheta _{\mathrm {1n}}$ and $\vartheta _{\mathrm {2n}}$ denote nominal wedge angles, while $\vartheta _{\mathrm {1m}}$ and $\vartheta _{\mathrm {2m}}$ indicate measured flow deflections.

2.4.4 Intersection point determination

The intersection point is defined as the point where the linear fits for the upper and lower incident shocks intersect, which should coincide with the interaction point in case of a RI (point I in Fig. 1a). In order to determine whether or not the current shock configuration agrees with a regular interaction pattern, a horizontal line segment is defined that extends from a distance 0.1w downstream of the intersection point in the upstream direction toward the free-stream flow. The light intensity along this line is examined as explained in Sect. 2.4.2, and the true shock location is determined accordingly. The current shock configuration corresponds to a RI when the shock location R along the horizontal line is located at the intersection point $\hbox {I}_\mathrm {p}$, as shown in Fig. 8a. Conversely, as depicted in Fig. 8b, if R is sufficiently far upstream of $\hbox {I}_\mathrm {p}$, the shock system unambiguously corresponds to a MI. The exact occurrence of transition that segregates the RI from the MI, however, is determined according to Mach stem height considerations. This is explained in detail in Sect. 2.4.6, while the procedure to calculate the actual height of the Mach stem is described in the following.

2.4.5 Mach stem height determination

We define the Mach stem height $h_{\mathrm {ms}}$ as the distance between the triple points of the MI, points $\hbox {T}_\mathrm {1}$ and $\hbox {T}_\mathrm {2}$ in Fig. 1b, in the direction perpendicular to the free-stream flow. Recalling Fig. 8b, it can be seen that the true shock location R along the horizontal search line lies on the Mach stem. For shock configurations where the Mach stem is essentially a normal shock wave, as shown in Fig. 9a, a good approximation of its height is given by the length of the line segment $\overline{\text {P}_\mathrm {1}\text {P}_\mathrm {2}}$, where $\hbox {P}_\mathrm {1}$ and $\hbox {P}_\mathrm {2}$ result from intersecting the incident shock fits with the line perpendicular to the free-stream passing through R.

Fig. 8

Intersection point location $\hbox {I}_\mathrm {p}$ and true shock location R for a a RI and b a MI. Incident shock line fits are included as solid green lines

Fig. 9

Relevant auxiliary parameters for the Mach stem height determination: a straight line approach, b parabolic approach

However, if the Mach stem has non-negligible curvature, as in Fig. 9b, the straight line approach becomes inaccurate. For this reason, the Mach stem is instead approximated with a quadratic function, requiring two additional points lying on it besides R. These points, labeled as $\hbox {R}_\mathrm {2}$ and $\hbox {R}_\mathrm {3}$ in Fig. 9b, are obtained by applying the gradient-based method outlined in Sect. 2.4.2 to the light intensity profile over the horizontal lines passing through the midpoints of the line segments $\overline{\text {RP}}_\mathrm {1}$ and $\overline{\text {RP}}_\mathrm {2}$, respectively. The unique parabola resulting from the set of points {R, $\hbox {R}_\mathrm {2}$, $\hbox {R}_\mathrm {3}$} thus approximates the Mach stem curvature, and the distance in the direction perpendicular to the free-stream between points $\hbox {Q}_\mathrm {1}$ and $\hbox {Q}_\mathrm {2}$, the intersections of the parabola with each incident shock-fitted line, defines the Mach stem height.

For the investigated interactions, we measured deviations between the linear and the parabolic approach of up to $10\%$ in the large Mach stem height range ($h_{\mathrm {ms}}>0.3w$). Therefore, and for the sake of consistency, we use the parabolic approach to approximate the Mach stem height in all cases.

2.4.6 Transition detection

Although very close to each other, in view of measurement uncertainty, points $\hbox {I}_\mathrm {p}$ and R will never perfectly coincide in case of a RI, as shown in Fig. 8a. This leads to a finite nonzero value of the Mach stem height being determined also for these shock patterns. The resulting $h_{\mathrm {ms}}$ signal, however, is observed to have a close to zero mean value, which suggests that the measuring procedure, although affected by measurement uncertainty (noise), is not introducing any bias. The computed RMS variation of the $h_{\mathrm {ms}}$ signal, of the order of $10^{-2}w$, is used to define the threshold value to determine the occurrence of RI$\rightleftarrows$MI transition. That is, transition is detected when the $h_{\mathrm {ms}}$ signal of an image sequence exceeds or falls below $h_{\mathrm {ms}}/w = 2\times 10^{-2}$, and the corresponding $\vartheta _{\mathrm {1m}}$, $\vartheta _{\mathrm {2m}}$, and $M_\mathrm {0}$ values are thus recorded. In case $h_{\mathrm {ms}}/w = 2\times 10^{-2}$ is crossed multiple times due to a local small oscillation, an average value of the aforementioned quantities over the extent of the oscillation is considered instead. It was verified that the transition detection did not critically depend on the threshold value used: The magnitude of the recorded quantities varies by less than one percent when the $h_{\mathrm {ms}}$ threshold value is doubled.

2.4.7 Consistent stability boundary calculation

In order to properly assess hysteresis effects, the remaining step is to calculate the actual RI and MI stability boundaries, based on the recorded $\vartheta _{\mathrm {1m}}$ at transition, to allow for a consistent comparison between measurements and theory.

3 Results and discussion

3.1 Focusing schlieren diagnostics

As means to investigate the potential impact of three-dimensional effects in our setup, we used the focusing schlieren system presented in Sect. 2.3. Visualizations for different focal plane locations were achieved by mounting the camera on a rail allowing it to be moved forward or backward along the optical path. The plane of focus was initially located at the center of the test section, and after a stable shock interaction was generated, the camera was gradually moved such as to shift the image plane toward one of the wind tunnel windows.

Fig. 10

Focusing schlieren visualizations of a MI during a variable focal plane study. The focus plane is located at: a the center of the test section, d the wind tunnel window, and b–c intermediate locations. The corresponding geometry setup is $\vartheta _{\mathrm {1n}}=17^{\circ }$ and $\vartheta _{\mathrm {2n}}=21^{\circ }$ at constant $M_\mathrm {0}=2.26$

Fig. 11

Comparison between focusing schlieren and regular schlieren visualizations of a–b a RI and c–d a MI, resulting from the wedge arrangement $\vartheta _{\mathrm {1n}}=17^{\circ }$ and $\vartheta _{\mathrm {2n}}=21^{\circ }$ at $M_\mathrm {0}=3.0$ and $M_\mathrm {0}=2.41$, respectively

An example of the resulting focusing schlieren visualizations is shown in Fig. 10a, d for a MI corresponding to $\vartheta _{\mathrm {1n}}=17^{\circ }$ and $\vartheta _{\mathrm {2n}}=22^{\circ }$ at $M_\mathrm {0}=2.26$. Even though traces from out-of-focus features are still present in the image, it is clear that the MI appears the sharpest when the focal plane is located at the center of the test section, as shown in Fig. 10a. All characteristic elements, including the concave Mach stem, the expansion fans, and the curved slip lines, can be unambiguously recognized, while the shock waves appear considerably thinner than in the regular schlieren visualizations. As the image plane is moved away from the center, the aforementioned features become progressively blurred, as shown in Fig. 10b, c. At the same time, a considerable thickening of the shock regions is observed, which is attributed to shock-wave/boundary-layer interactions on the side-wall windows. The adverse pressure gradient imposed by the shock wave induces a boundary-layer thickening that affects the flow upstream of the impingement point through the subsonic layer [22]. This results in a series of compression waves generated upstream of the impinging shock that contribute to the apparent shock thickening in the visualizations. Such three-dimensional effects appear most predominant when the focal plane is located nearest to the side window, as shown in Fig. 10d. Notice also the considerable upstream motion of the quasi-normal shock associated with the Mach stem and the disappearance of the slip lines. An animation corresponding to Fig. 10 is available in our data repository [23].

Fig. 12

Quantitative results obtained with the presented post-processing methodology for all five experimental runs conducted with the wedge arrangement $\vartheta _{\mathrm {1n}}=17^{\circ }$ and $\vartheta _{\mathrm {2n}}=19^{\circ }$: a–b upper shock angle $\phi _{\mathrm {1m}}$ and flow deflection $\vartheta _{\mathrm {1m}}$ signals, c–d lower shock angle $\phi _{\mathrm {2m}}$ and flow deflection $\vartheta _{\mathrm {2m}}$ signals, and e normalized Mach stem height $h_{\mathrm {ms}}/w$ dependency on $M_\mathrm {0}$. Four of the five signals (semi-transparent lines) have been offset $+1^{\circ }$ vertically from each other in a–d and $+0.05$ horizontally in e for illustration purposes. Theoretical evolution of shock and flow deflection based on nominal conditions is also included as dashed red lines

When examining MI configurations, we never found a trace of a RI at any position along the span-wise direction; Mach stem and the slip-line pair were present in all planes of the optical path except very near the windows. The same holds true in the opposite case; traces of a MI were never found during examination of the span-wise variation of a RI. In addition, the sharp incident shocks recognized with the image plane at the test section center, as shown in Fig. 10a, appear in all remaining visualizations of the variable focal plane test, as shown in Fig. 10b–d. This confirms that the shock interactions generated with our setup are two-dimensional along most of the wind tunnel width.

It is relevant to note that the incident shocks in the focusing schlieren visualizations, where they appear as dark lines, are always located close to the rear of the blurred regions surrounding them. This observation agrees with the proposed effect of the shock-wave/boundary-layer interactions at the side walls, suggesting that most of the thickening of the incident shocks in schlieren visualizations results from the upstream influence effect. Figure 11 includes a direct comparison between focusing schlieren and regular schlieren visualizations of a RI and MI. As observed, the trailing edges associated with the shock regions appear as sharp discontinuities in the regular schlieren visualization, while the leading edges clearly fade out. These findings justify the approach described in Sect. 2.4 of searching for the trailing edge of the incident shock-wave footprint during post-processing, as being representative of the actual shock location.

3.2 Post-processing results

A total set of 20 schlieren visualization experiments with synchronous pressure readings were conducted as described in Sect. 2.2. The resulting image sequences were analyzed according to the procedure presented in Sect. 2.4. Figure 12a–e shows the results for shock angles, flow deflections, and corresponding Mach stem height dependency on $M_\mathrm {0}$ for the nominal wedge arrangement $\vartheta _{1\mathrm {n}}=17^{\circ }$ and $\vartheta _{\mathrm {2n}}=19^{\circ }$. They contain data from all five runs corresponding to this arrangement, with four of the five signals on each figure accordingly offset for illustration purposes (see the caption for details). The evident similarities between the different recordings highlight the robustness of the processing methodology. The spreading of each signal over the whole $M_\mathrm {0}$ range is also found to be in close agreement with the estimated uncertainties reported in Table 2.

The theoretical evolution of shock angle and flow deflection based on nominal conditions is also included in Fig. 12a–d (dashed red lines), revealing the mismatch between nominal and effective wedge angles. The largest shock angle deviation from nominal conditions in Fig. 12a is $1.36^{\circ }$, which translates into a $1.2^{\circ }$ flow deflection mismatch with the nominal wedge angle $\vartheta _{\mathrm {1n}}=17^{\circ }$, the maximum recorded in this work. This mismatch originates from the additional flow displacement through the viscous boundary layers over the wedge surfaces, manufacturing and mounting uncertainties, as well as deformations under high-pressure load. Interestingly, the aerodynamic loading on a two-dimensional wedge geometry reaches its maximum at the lowest $M_\mathrm {0}$ value. For a constant total pressure, the free-stream static pressure monotonically increases with decreasing $M_\mathrm {0}$ and this effect dominates over the corresponding decrease in pressure gradient across the shock waves. However, the largest deviations from nominal conditions in our experiments do not agree with the aforementioned. This evidences the complexity of the off-design interaction geometry and justifies the proposed flow-based post-processing methodology.

3.3 Mach stem height dependence on $M_\mathrm {0}$

The evolution of the Mach stem height in Fig. 12e appears insensitive to the increase or decrease in $M_\mathrm {0}$ in all five runs, which already indicates the absence of hysteresis for this wedge arrangement. The average normalized Mach stem height $h_{\mathrm {ms}}/w$ dependence on $M_\mathrm {0}$ for all geometries is included in Fig. 13. A distinction has been made for the data corresponding to a decreasing $M_\mathrm {0}$ and that for an increasing $M_\mathrm {0}$, but the almost perfect overlap between the two confirms the repeatability, as well as the absence of any measurable hysteresis effects in our experiments. The latter is consistent with past experimental works in noisy facilities [6,7,8, 19]. Data shown in Fig. 13 together with the corresponding shock angles and flow deflections are also available in our data repository [23].

Fig. 13

Average normalized Mach stem height $h_{\mathrm {ms}}/w$ dependence on the free-stream Mach number $M_\mathrm {0}$ for all wedge arrangements

The observed growth of the Mach stem height is clearly nonlinear in $M_\mathrm {0}$ with a sharp growth rate increase when approaching the RI$\leftrightarrows$MI transition, for all geometries besides $\vartheta _{\mathrm {2n}}=10^{\circ }$. We consider this effect to be related to the fact that a particular inlet-to-throat ratio in the convergent–divergent slip-line duct behind the Mach stem needs to form for the MI to be stable [18]. After RI$\rightarrow$MI transition, this requirement results in a rapid growth of the Mach stem until the mass flow through it can be swallowed at sonic conditions at the throat. In the opposite case, right before MI$\rightarrow$RI transition, this translates into a sudden collapse of the finite Mach stem. Whether this abrupt increase in the Mach stem growth rate can be observed or not, i.e., whether $h_{\mathrm {ms}}$ is finite in the vicinity of the RI$\leftrightarrows$MI transition, depends on the geometrical ratio 2g/w. As first suggested by Hornung and Robinson [6] for the symmetric MI, $h_{\mathrm {ms}}/w = f^+(M_{\mathrm {0}},\gamma ,\vartheta _\mathrm {1},\vartheta _\mathrm {2},2g/w)$, where $f^{+}$ is probably a universal non-dimensional function and 2g/w the only scaling parameter.

Fig. 14

Theoretical DSD and resulting RI$\rightarrow$MI transition ($\lhd$) and MI$\rightarrow$RI transition ($\rhd$) data based on nominal deflections (gray) and based on measured deflections (blue). a–b correspond to $\vartheta _{\mathrm {2n}}=21^{\circ }$, c–d to $\vartheta _{\mathrm {2n}}=19^{\circ }$, e–f to $\vartheta _{\mathrm {2n}}=17^{\circ }$, and g–h to $\vartheta _{\mathrm {2n}}=10^{\circ }$. Dotted and dashed lines indicate the corresponding von Neumann and detachment criteria, respectively. The average of the measured upper flow deflection $\vartheta _{\mathrm {1m}}$ used to recalculate the DSD is indicated at the top of each figure

3.4 Remarks on the RI$\leftrightarrows$MI transition

The final step in the analysis is to determine to what extent the RI$\rightleftarrows$MI transition observed in our experiments corresponds to the stability boundaries that enclose the DSD. The quantities (flow deflections and Mach number) at transition follow from the Mach stem height evolution as explained in Sect. 2.4.6, and the results are summarized in Table 3 and visualized in Fig. 14a–h in the $M_\mathrm {0}$–$\vartheta _\mathrm {2}$ plane. The DSD based on the nominal shock generator angles is indicated in the figure (gray) together with the DSD based on the average measured upper flow deflection $\vartheta _{\mathrm {1m}}$ (blue) which accounts for the off-design interaction geometry.

It becomes evident that transition in our experiments would appear inconsistent with the theoretical DSD based on the nominal deflections $\vartheta _{\mathrm {1n}}$ and $\vartheta _{\mathrm {2n}}$. However, consistency between experiments and theory is recovered by considering instead the measured deflections $\vartheta _{\mathrm {1m}}$ and $\vartheta _{\mathrm {2m}}$ together with the corresponding DSD, which also confirms that transition in our facilities occurs at (or close to) the von Neumann criterion. A very good overlap of the measured transition conditions was found within the expected uncertainty (which is about $0.1^{\circ }$–$0.2^{\circ }$, as given in Table 2). The wedge arrangement involving $\vartheta _{\mathrm {2n}}=19^{\circ }$ is the only geometry for which the detected RI$\rightleftarrows$MI transition seems to occur beyond the von Neumann criterion but still close to this boundary and within the corresponding DSD.

Table 3 Average transition data for all geometries

4 Conclusions

Experiments on shock–shock interactions were conducted in a transonic–supersonic wind tunnel with variable free-stream Mach number functionality. Transition between the regular interaction (RI) and the Mach interaction (MI) was induced by variation of the free-stream Mach number. In order to account for possible deformations of the model geometry and other off-design effects, we applied a systematic flow-based post-processing methodology of schlieren visualizations and synchronous pressure readings that enabled accurate tracking of the evolving shock system and precise detection of RI$\rightleftarrows$MI transition with high reproducibility. In line with previous works dealing with noisy experimental environments, no transition hysteresis was observed. Due to the measured deviations of the flow deflections from the nominal shock generator angles (of up to $1.2^{\circ }$), calculation of the theoretical dual-solution domain (DSD) consistent with the actual flow conditions was required to confirm that the measured transition data satisfy the von Neumann criterion in our experiments. Furthermore, different planes along the optical path were investigated using a focusing schlieren system to assess three-dimensional side-wall effects in the experimental setup. The analysis confirmed that the considerable shock thickening observed in regular schlieren visualizations is caused by shock-wave/boundary-layer interactions at the side walls and that the trailing edge of the incident shock footprint is a reliable indicator of the two-dimensional incident shock locations at the mid-plane of the test section.