Adjoint-based optimisation of detonation initiation by a focusing shock wave

Abstract

An optimisation study of a shock-wave-focusing geometry is presented in this work. The configuration serves as a reliable and deterministic detonation initiator in a pulsed detonation engine. The combustion chamber consists of a circular pipe with one convergent–divergent axisymmetric nozzle, acting as a focusing device for an incoming shock wave. Geometrical changes are proposed to reduce the minimum shock wave strength necessary for a successful detonation initiation. For that purpose, the adjoint approach is applied. The sensitivity of the initiation to flow variations delivered by this method is used to reshape the obstacle’s form. The thermodynamics is described by a higher-order temperature-dependent polynomial, avoiding the large errors of the constant adiabatic exponent assumption. The chemical reaction of stoichiometric premixed hydrogen-air is modelled by means of a one-step kinetics with a variable pre-exponential factor. This factor is adapted to reproduce the induction time of a complex kinetics model. The optimisation results in a 5% decrease of the incident shock wave threshold for the successful detonation initiation.

1 Introduction

The predictions for constant-pressure gas turbines foresee a convergence in terms of thermodynamic efficiency [1]. It is therefore necessary to fundamentally change the concept to allow a substantial increase in the turbine’s performance.

Pressure-gain combustion technology is one such candidate. Among the implementation strategies of this approach, the pulse detonation engine (PDE) has received significant attention [2]. The use of detonative combustion in this type of configuration brings the thermodynamic cycle closer to the constant-volume cycle (Humphrey cycle), making it more efficient than the constant-pressure cycle (Brayton cycle) [3]. However, the large amount of energy and high deposition rate required for direct detonation initiation prohibits its use in practical implementations. Instead, the detonation regime is initiated indirectly via the low-energy ignition of shock-to-detonation transition (SDT) [4], see [5] for a PDE chamber utilising this principle.

A robust and reliable detonation transition is a must for the viability of the engine in real applications with detonative burning. Consequently, previous studies were devoted to examine the effectiveness of low-energy detonation initiation for its integration into PDEs. The work of Smirnov et al. [6] discusses the influence of the cross section ratio, volume, and cavity separation on the pre-detonation length in round tubes equipped with cavities. The results indicate a bounded range within which the pre-detonation length decreases, while the transition is inhibited above an upper limit. The related publications of Smirnov et al. [7, 8] were aimed at studying the self-sustaining waves in metastable systems. The sensitivity of the transition mechanisms to changes in the external governing parameters, such as the initial temperature of the mixture, the fuel concentration, the number of cavities, and the ignition energy, is reported. The results describe a highly inhomogenous flow where the detonation initiation is located on contact surfaces originating from shock wave interactions.

In Jackson et al. [9], imploding annular shock waves were experimentally tested as initiator for different hydrocarbon mixtures. There, the minimum shock strength necessary for a successful detonation initiation was estimated. The theoretical investigation of Nikitin et al. [10] makes use of converging shock waves to promote the transmission of detonation into large chambers for hydrogen-air gases. Smirnov et al. [11] addressed the detonation onset by the reflection of a shock wave inside a wedge. The results describe two different initiation mechanisms, depending on the incoming shock strength: either by the focusing of a strong shock through an overdriven detonation mode or after a weak shock reflection by an intermediate transient regime with successive growth of instability on the front of a wrinkled flame. Frolov et al. used one shock-wave-focusing nozzle to accomplish SDT in propane-air [12] and natural gas-air [13]. The results present an alternative to conventional turbulising obstacles such as Shchelkin spirals, which suffer from significant thrust losses [2]. The understanding of SDT in the nozzle geometry is enhanced by the numerical investigation of Semenov et al. [14]. Also, a geometrical modification of the nozzle is proposed to promote SDT in pulsed detonative burners, see Semenov et al. [15].

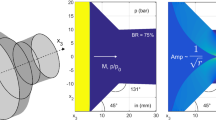
In the experimental and numerical work of Gray et al. [16] and Bengoechea et al. [5], a cylindrical pulse detonation chamber obstructed by a single convergent–divergent axisymmetric nozzle, similar to the one proposed by Frolov et al. [12], is studied. Figure 1 gives a detailed schematics of the overall device. The premixed mixture is injected on the left wall of the pre-chamber upstream of the nozzle. A low-energy spark plug ignites the reaction also on the left wall. The resulting turbulent flame induces the formation of a leading shock wave by the piston effect. In view of this, the successful detonation initiation can be decomposed in two elements: (1) an accelerating flame to form a strong leading shock wave, and (2) the focusing of this leading shock wave caused by the reflection at the obstacle geometry. Each of them can be analysed separately.

The focusing at the nozzle of the leading (or incoming) shock wave is further examined in Bengoechea et al. [4]. In particular, the effect on the detonation initiation by varying the strength of the incoming shock wave is investigated in this publication. As found by Smirnov et al. [11], the initiation mechanism is shown to be strongly dependent on the incoming shock wave strength, since two different mechanisms (direct or mild) were observed. In the direct (or strong) initiation, the high energy concentration at the focal point directly triggers the detonation. For weaker incoming shock waves, the detonation initiation occurs by the mild mechanism. Here, the process is not just dominated by the energy deposition at the focal area, but also by the resonance (or coupling) between a sequence of shock-wave-focusing events and a progressing reaction front. The temporal rate of these sequential focusing events is defined by the curvature of the imploding shock wave, resulting from the reflection at the nozzle. This curvature is determined by the geometry, proving the existence of a complex relation between the obstacle’s shape and the final combustion regime.

In the present paper, the optimisation potential of the shock-focusing nozzle of [4] is explored. The main goal is to reduce the SDT initiation threshold, guaranteeing the detonation outcome for weaker incoming shock waves. To this end, the obstacle’s shape is accordingly modified. Note that the incoming shock wave is formed by the pushing of an accelerating flame, see Fig. 1. For this reason, the amplitude of this incoming shock is proportional to the amount of burned gas upstream of the nozzle [5]. It is thus of great interest to minimise this amplitude and with it the fuel consumption in this type of configuration. Also, the proposed geometry changes can be applied to less reactive compounds, in which the onset of detonation is difficult to obtain. To this extent, the results shown here pave the way for the development of a new-generation chambers using pulse detonation combustion.

The workflow steps are listed next. First, the baseline geometry as the starting point of the optimisation is defined with a blockage ratio (BR) of 75%, a converging angle $\phi$ of $45^\circ$, and a diverging angle $\theta$ of $131^\circ$, as sketched in Fig. 1. This geometry parameters replicate the optimal SDT geometry with a minimum in the incoming shock wave strength proposed by Semenov et al. [14, 15]. Second, the detonation initiation threshold is identified for this baseline geometry. For that, a preliminary series of simulations are conducted with several incoming shock wave strengths. Third, the adjoint approach is applied to reveal the sensitivity (or gradient) of the detonation initiation process. This information is used to fine-tune the obstacle in order to decrease the initiation threshold.

The paper is organised in the following manner. The description of the numerical model is included in Sect. 2. Section 3 contains the discussion and analysis of the results. In Sect. 4, the conclusions of the study are drawn. The final appendices summarise detailed aspects of both the model and the adjoint equations. The validation and verification of the in-house code is also presented in these appendices.

Fig. 1

Upper left: overall schematics of the detonation chamber with the formation of the incoming shock (IS) by an accelerating turbulent flame (TF) in the pre-chamber [5]; MI–mixture injection, SP–spark plug. Lower left: baseline geometry of the shock-focusing nozzle [4]. Center: baseline geometry with the initial conditions. Right: baseline geometry with the formation of the imploding shock wave after the reflection; pressure (upper image) and temperature (lower image) contours are shown. The dashed white rectangle indicates the spatial subdomain $\varOmega$ where the adjoint method acts

2 Numerical methods

In this work, the compressible reactive Navier–Stokes equations

$$\begin{aligned}&\sqrt{\rho } \frac{\partial \sqrt{\rho }}{\partial t} + \frac{1}{2} \frac{\partial (\rho u_{i})}{\partial x_{i}} = 0 \end{aligned}$$

(1a)

$$\begin{aligned}&\sqrt{\rho } \frac{\partial (\sqrt{\rho } u_{i})}{\partial t} + \frac{1}{2} \left( \frac{\partial (\rho u_{j} u_{i})}{\partial x_{j}} + \rho u_{j} \frac{\partial u_{i}}{\partial x_{j}} \right) + \frac{\partial p}{\partial x_{i}} = \frac{\partial \tau _{ij}}{\partial x_{j}} \end{aligned}$$

(1b)

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \frac{p}{\gamma -1} \right) + \frac{\partial }{\partial x_{i}} \left( \frac{\gamma }{\gamma -1} u_{i} p \right) - u_{i} \frac{\partial p}{\partial x_{i}} \nonumber \\&\quad = \frac{\partial (u_{i}\tau _{ij})}{\partial x_{j}} - u_{j}\frac{\partial \tau _{ji}}{\partial x_{i}} + \frac{\partial }{\partial x_{i}} \left( \lambda \frac{\partial T}{\partial x_{i}} \right) + \dot{\omega }_{\text {T}} \end{aligned}$$

(1c)

$$\begin{aligned}&\frac{\partial (\rho Y)}{\partial t} + \frac{\partial ( \rho u_{i} Y)}{\partial x_{i}} = \frac{\partial }{\partial x_{i}} \left( \rho D_{\text {f}}\frac{\partial Y}{\partial x_{i}} \right) + \dot{\omega } \end{aligned}$$

(1d)

$$\begin{aligned}&\tau _{ij} = \mu \left( \left( \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} \right) - \delta _{ij} \frac{2}{3} \frac{\partial u_k}{\partial x_{k}}\right) \end{aligned}$$

(1e)

are solved numerically. In the set of equations, $x_{i}$ (or $x_{j}$, $x_{k}$) stands for the ith (or jth, kth) spatial dimension, t the temporal variable, $\rho$ the density, $u_{i}$ (or $u_{j}$, $u_{k}$) the ith (or jth, kth) velocity component, p the pressure, $\tau _{ij}$ the viscous stress tensor, T the temperature, and $\delta _{ij}$ the Kronecker symbol.

The cylindrical-like geometry displayed in an Fig. 1 allows to write the equations in an axial-symmetric form, effectively resulting in a two-dimensional domain. Only the longitudinal ($x_1$) and the radial ($x_2$) dimensions are simulated. Hence, the summation convention applies with i, j, $k = 1,2$. The physical coordinates of the axial-symmetric geometry are mapped onto an equidistant mesh space $\xi _i$. Therefore, the divergence and gradient operators need to account for arbitrarily distorted grids. These are denoted with the geometrical factors $m_{ji}$ and the functional determinant $F_{\text {d}}$ as $\frac{\partial u_i}{\partial x_i} = \nabla \cdot u = \frac{1}{F_{\text {d}}}\frac{\partial ( m_{ji} u_j)}{\partial \xi _i}$ and $\frac{\partial p}{\partial x_i} = \nabla p = \frac{1}{F_{\text {d}}}\frac{\partial (m_{ji} p)}{\partial \xi _i}$, respectively. The radial information ($x_2$) is contained in $F_{\text {d}}$ and $m_{ji}$. For a detailed description of $m_{ji}$ and $F_{\text {d}}$, refer to Appendix 5.

The momentum equation (1b) is given in the skew-symmetric formulation [17], ensuring the conservation properties for finite difference schemes [5]. Considering this, the computational variables are converted to $[\sqrt{\rho }$, $\sqrt{\rho }u_{i}$, p, $\rho Y]^{\text {T}}$.

The dynamic viscosity $\mu$ is calculated with the temperature-dependent Sutherland’s law [18]. The Fick’s law with $D_{\text {f}}= \frac{\mu }{\rho \, \text {Pr}\,\text {Le}}$, a constant Prandtl number $\text {Pr} = \frac{\mu c_{p}}{\lambda }= 0.71$, and the Lewis number $\text {Le}= 1$ describes the mass diffusion coefficient. The mass-specific heat capacity at constant pressure $c_{p} = \frac{\gamma (T) R_{\text {s}}}{\gamma (T) - 1}$ is also dependent on the temperature. The thermal conduction coefficient $\lambda$ is determined by $c_{p}$, Le, Pr, and $\mu$. The universal gas constant R and the mean molecular weight of the mixture W define the specific gas constant as $R_{\text {s}} = \frac{R}{W}$. The parameter values are stated in Table 3, Appendix 1.

2.1 Thermodynamics model

The sensible (non-chemical) energy $e_{\text {s}}$ is directly related to the thermodynamic quantities of p and T by means of the adiabatic exponent $\gamma$. For an ideal gas mixture, $e_{\text {s}}$ is described here as

$$\begin{aligned} e_{\text {s}}(T) = \int _{T_0}^{T} c_v \text {d}T - R_{\text {s}} T_0 = \frac{p}{\rho (\gamma (T) - 1)} + \text {const} \, \text {,} \end{aligned}$$

(2)

with the mass-specific heat capacity at constant volume $c_v$ [19]. The $\gamma (T)$ function of temperature in (2) is built with a seventh-order polynomial, so that $e_{\text {s}}$ approximates the one specified in the CHEMKIN database [20]. The polynomial coefficients of the resultant $\gamma (T)$ function are given in Table 4, Appendix 1. Figure 10, also in Appendix 1, depicts the $\gamma (T)$ function, together with the deviation made by this interpolation approach with the maximum absolute and relative errors of 0.41 K and 0.099%, respectively.

Equation (1c) takes into account the temporal change of the sensible energy density $\frac{\partial }{\partial t} \left( \frac{p}{\gamma (T)-1}\right)$. The numerical integration of this equation does not deliver per se the thermodynamic quantities of the flow (p and T) for the subsequent discrete time. Therefore, p and T must be extracted implicitly for each time integration substep, increasing the numerical effort considerably. For sufficiently small integration time step $\Delta t$, the assumption of $\gamma (T)^{t^{n+1}} \approx \gamma (T)^{t^n}$ is adopted. The temporal term in (1c) can be then rewritten as $\frac{\partial }{\partial t} \left( \frac{p}{\gamma (T)-1} \right) \approx \frac{1}{\gamma (T)-1} \frac{\partial p}{\partial t}$. The validity of this assumption is verified successfully on-the-fly; Fig. 10 in Appendix 1 contains the results.

2.2 Chemical kinetics model

The explosive mixture used in the numerical experiments is stoichiometric hydrogen-air ($2\text {H}_{2} + \text {O}_{2} + 3.76\text {N}_{2}$). An irreversible one-step kinetics with one effective species Y, varying from one (unburned) to zero (burned), models the global reaction. The source terms in (1) describing the reaction changes are the mass reaction rate $\dot{\omega }$ and the heat release due to combustion $\dot{\omega }_{\text {T}}$, namely

$$\begin{aligned} \dot{\omega } = - K_{\text {f}} \rho Y \, \text { and } \, \dot{\omega }_{\text {T}} = - Q \dot{\omega } . \end{aligned}$$

(3)

The reaction rate constant $K_{\text {f}}$ is defined by the Arrhenius law $K_{\text {f}} = A_{\text {f}}(T,p) \text {e}^{-\frac{T_{\text {a}}}{T}}$. The $\text {H}_{2}\text {O}$ mass formation enthalpy $\Delta h^{o}_{\text {f}}$ and the $\text {H}_{2}\text {O}$ stoichiometric mass fraction $Y^{\text {st}}_{\text {H}_{2}\text {O}}$ form the heat release per unit mass of fuel $Q = \Delta h^{o}_{\text {f}}\cdot Y^{\text {st}}_{\text {H}_{2}\text {O}}$ in (3) [21].

The available degrees of freedom of the chemical model are the pre-exponential factor $A_{\text {f}}(T,p)$ and the activation temperature $T_{\text {a}}$. These model parameters are chosen to match the induction time $\tau _{\text {c}}$ of the detailed San Diego kinetics mechanism with 21 reactions (in the following referred to as $\tau _{\mathrm {c_{ref}}}$) [22]. For this purpose, $A_{\text {f}}(T,p)$ is allowed to be pressure and temperature dependent with a linear interpolation function, parametrised with 7 discretisation points in pressure and 13 in temperature. The values of $A_{\text {f}}(T,p)$ are iteratively selected to replicate the behaviour of $\tau _{\mathrm {c_{ref}}}$ in the zero-dimensional isochoric reaction with the mentioned complex kinetics [4]. With this approach, the non-monotonous nature of $\tau _{\text {c}}$ with pressure in the hydrogen-air mixture is captured [23]. The model parameters and the adjusted $A_{\text {f}}(T,p)$ are reported in Tables 3 and 5, respectively (see Appendix 1). The induction time $\tau _{\text {c}}$ after the parameter fitting is depicted in Fig. 9 in Appendix 1. Good performance of the adjusted one-step model in $\tau _{\text {c}}$ terms is evident from this figure.

The correctness of the CJ detonation velocity and CJ state computed by the chemical model is also illustrated in Table 3, Appendix 1. Further code validations can be found in Appendix 2 and 3.

The use of one-step kinetics must be considered with caution. This type of models do not describe well the endothermic-exothermic character of the reaction, since they treat all temperatures as exothermic [24]. Nonetheless, the large pressure and temperature intervals appearing at the focal point (above 500 bar and 1700 K) set the ignition point below the crossover temperature $T_{\text {cross}}=2250$ K for 500 bar [25]. At the conditions relevant for this investigation, the chain branching endothermic stage is particularly shortened [24]. The present case is then less sensitive to the radical building phase, making the endothermic induction phase negligible [26]. With a precise calibration, the one-step kinetics is adequate to accurately reproduce the detonation initiation process in exothermic-(termination-recombination)-dominated reactions [26]. Based on this principle, the use of the optimised one-step kinetics is justified.

2.3 Adjoint optimisation method

The derivation of the adjoint method builds on the linearisation of the governing equations with respect to a small perturbation $\delta q_{\beta }$ in the system solution $q_{\beta } = {q_{0}}_{\beta } + \delta q_{\beta }$ [27]. Under this approach, the optimisation adjustments are applied to the start perturbation $\delta q(t_0) = \delta s$.

The linearisation steps are imposed to the Euler equations in a divergence form:

$$\begin{aligned}&\frac{\partial }{\partial t} \begin{pmatrix} \rho \\ \rho u_{i} \\ \frac{p}{\gamma - 1} \\ \rho Y \end{pmatrix} + \frac{\partial }{\partial x_{j}} \begin{pmatrix} \rho u_{j} \\ \rho u_{j} u_{i} + p \delta _{ij} \\ \frac{\gamma }{\gamma - 1} u_{j} p \\ \rho u_{j} Y \end{pmatrix} \nonumber \\&\quad - \frac{u_{j}\partial }{\partial x_{j}} \begin{pmatrix} 0 \\ 0 \\ p \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \dot{\omega }_{\text {T}} \\ \dot{\omega } \end{pmatrix}. \end{aligned}$$

(4)

The summation convention also applies here with i, $j = 1,2$. With the introduction of the vector-matrix notation, the system in (4) transforms into a compact expression, such as

$$\begin{aligned} \frac{\partial }{\partial t} a + \frac{\partial }{\partial x_{j}} b_{j} + C_{j} \frac{\partial }{\partial x_{j}} c = d . \end{aligned}$$

(5)

The linear Euler equations then take the form of

$$\begin{aligned}&\frac{\partial }{\partial t} \underbrace{ \frac{\partial a_{\alpha }}{\partial q_{\beta }}}_{{{A}}} \delta q_{\beta } + \frac{\partial }{\partial x_{j}} \underbrace{ \frac{\partial {b_{j}}_{\alpha }}{\partial q_{\beta }}}_{{{B}}_{j}} \delta q_{\beta } +C_{j} \frac{\partial }{\partial x_{j}} \underbrace{ \frac{\partial c_{\alpha }}{\partial q_{\beta }}}_{\widetilde{{{C}}}} \delta q_{\beta } \nonumber \\&\qquad + \delta C_{j} \frac{\partial }{\partial x_{j}} c = \overbrace{\frac{\partial d_{\alpha }}{\partial q_{\beta }}}^{{{D}}} \delta q_{\beta } , \end{aligned}$$

(6)

with $q = [\rho ,u_{i},p,Y]^{\text {T}}$, $\delta q = [\delta \rho ,\delta u_{i},\delta p,\delta Y]^{\text {T}}$, $\delta C_j=-\delta _{(4\alpha -12) \beta }\delta q_{j+1}$, the linear Jacobian matrices A, $B_j$, $\widetilde{C}$, D, and the summation convention $\alpha$, $\beta = 1,2,3,4, {\hbox {and}}~5$. For the sake of clarity, the exact entries of the matrices and vectors of this section are included in Appendix 4.

Apart from the linearisation, the definition of the objective function J(q) is a crucial aspect in each optimisation problem. The objective function J(q) is a scalar value which quantifies the distance in the vector space from the current system state q to a predetermined goal $q_{\text {ref}}$. This objective function is defined as the integral difference between q and $q_{\text {ref}}$:

$$\begin{aligned} J(q) = \frac{1}{2} ( q - q_{\text {ref}} )^{\text {T}}( q - q_{\text {ref}} ) . \end{aligned}$$

(7)

Here, the integration over time and space, $\int _{t} \int _{\varOmega } \frac{1}{2} ( q - q_{\text {ref}} ) \, \text {d}\varOmega \text {d}t$, is abbreviated by the scalar product. In order to consider the effect the perturbation $\delta q$ has on J(q), the objective function is also linearised with respect to the system solution $q = q_{0} + \delta q$, leading to $J = J_0 + \delta J$ with $\delta J = g^{\text {T}} \delta q$ and $g=q - q_{\text {ref}}$.

The purpose of the method is to minimise J by bringing the solution q closer to $q_{\text {ref}}$ without recalculating q for each modification separately. To this end, the adjoint equations are derived by adding to the objective function variation $\delta J$ the Lagrange multipliers (or adjoint solutions) $q^*$ and $s^*$ with the additional constraints of (6), and the initial conditions of the perturbation $\delta s = \delta q(t_0)$, respectively. The variation of the objective function $\delta J$ is afterwards integrated by parts:

(8)

The additional terms in the partial integration where the antiderivative is evaluated at the boundaries of the definite integral are omitted here. Only the terms ${\delta q}^{\text {T}} A^{\text {T}} q^*|_{t_0} - {\delta q}^{\text {T}} A^{\text {T}} q^*|_{t_{\text {end}}}$ from the partial time integration of ${q^*}^{\text {T}} \frac{\partial A}{\partial t}\delta q$ are discussed as representative example. Note that ${\delta q}^{\text {T}} A^{\text {T}} q^*|_{t_0}$ is combined with ${s^*}^{\text {T}} ( \delta q(t_0) - \delta s )$ in (8). For a detailed description of the rest of the omitted terms, see [27].

The variation of the objective function $\delta J$ can be determined without solving the linearised equation (6), if the dependency of $\delta J$ on the temporal development of the system perturbation $\delta q$ vanishes. That is the case when: first, $q^*$ is calculated by equalising the adjoint equations to zero; second, $q^*$ and $A^{\text {T}}$ at $t_0$ are deployed to find $s^*$; and third, $q^*|_{t_{\text {end}}}= 0$ as a means to eliminate the boundary term ${\delta q}^{\text {T}} A^{\text {T}} q^*|_{t_{\text {end}}}$ of the partial integration. This last demand imposes the initial condition for $q^*$ at the final time $t_{\text {end}}$, which implies that the adjoint equation must be integrated in reverse time-marching. The physical interpretation of that is the relation between cause and effect. The variation $\delta q$ (the cause) responsible for changes in J at certain time $t_n$ (the effect) occurred at a previous time in the past $t_{n-m}$. If the algorithm seeks for that previous variation, the information has to travel backwards in time or otherwise the causality principle will be broken.

Given the three above-mentioned conditions, the variation in J is then directly related to the initial form of the perturbation $\delta q(t_0)=\delta s$ via $s^*$. In other words, the adjoint solution $s^*$ provides the sensitivity of J to $\delta q(t_0)$, since $\frac{\partial J}{\partial q(t_0)} = \frac{\partial J}{\partial s} \approx \frac{\delta J}{\delta s}=s^*$. In this study, the minimum of J is sought by translating this computed gradient $\nabla _{\delta s} J$ into the modification of the obstacle’s shape, see Sect. 3.3. For completeness, the linear adjoint equations are fully expanded in Appendix 4.

2.4 Simulation details

The in-house code, fully MPI parallelised by a layer decomposition of the computational domain [28], is employed to numerically solve the set of differential equations (1). The code is validated and verified against exact analytical solutions (such as a steady shock wave and a classical Sod shock tube problem [29]) and benchmark problems (such as a laminar premixed flame and a detonation front). The precision based upon error accumulation in successive time integration steps is also estimated, as proposed by Smirnov et al. [30]. The results can be found in Appendices 2 and 3.

The solver equally integrate in space and time with fourth-order explicit schemes. Finite-difference central stencils, to prevent artificial dissipation, and the Runge–Kutta time integration are used for that purpose. The inflow–outflow (west–east) boundaries are assigned to be non-reflecting by the method of characteristics, while the north–south ones are designated as non-slip adiabatic walls. The appearance of discretisation errors, intrinsic to the finite representation of discontinuities, requires special treatment. Within this context, a sixth-order explicit filter [31] and an adaptive high-order shock-capturing filter [32] operate to handle this side effect. The grid consists of $n_1 , n_2 = 1024, \, 2048$ $\approx$ 2.1 million nodes, computed on 32 CPU units. The discretisation nodes fulfil $\{x_1,x_2|0 \, \le \, x_1 \, \le \, L_{x_1}, -L_{x_2} \, \le \, x_2 \, \le \, L_{x_2}, {\hbox {and}}\; x_2 \ne 0\}$, with the domain lengths $L_{x_1}$ and $L_{x_2}$. In this set of points, the geometrical singularity $\lim \nolimits _{x_2 \rightarrow 0} 1/x_2$ is avoided by excluding the pole ($\text {radius} = 0$) from the discretisation. The grid independence of the results is demonstrated in Appendix 2.

The performed simulations analyse the detonation initiation through the implosion of reflected shock waves with different incident strengths. The contemplated pressure ratios of the incoming shock wave are $p/p_0 = 4.5$, 4.75, 4.8, 4.9, 5.0, 5.5, and 6.0 with the corresponding Mach numbers of $M = 2.02$, 2.08, 2.09, 2.11, 2.13, 2.23, and 2.33. Figure 1 gives an overview of the configuration under study. Further details of the post-shock initial conditions are listed in Table 1. The quiescent pre-shock initial state is held constant for all the cases with $p_{0} = 1.01330$ bar and $T_{0} = 298.15$ K.

Table 1 Post-shock and Mach number initial conditions

3 Results

Initially, the incoming (or incident) shock wave is reflected at the converging part of the nozzle. This reflection develops into an imploding (or converging) shock wave, see right plot in Fig. 1. In this type of waves, the ever-decreasing radius forces the post-shock gas into a smaller area, creating an additional compression. The implosion process produces extremely high pressures and temperatures at the focusing point. Close to this focal point, the flow has a negligible gradient in the $x_1$-direction, similar to imploding cylindrical shock waves. The self-similar solution for inward-travelling cylindrical shocks approximates the amplitude increases to be proportional to $1/\sqrt{x}_2$.

3.1 Baseline geometry lower threshold

The minimum incident shock strength required for a successful detonation initiation in the baseline geometry is investigated. The interaction of several incoming shocks with the geometry of Fig. 1 is examined. The incident shock amplitudes ($p/p_0$) cover the range from 4.5 to 6.0, see the list of sampled $p/p_0$ in Table 1. The analysis is restricted to the focal area of the domain.

The results for $p/p_0 = 6.0$ are discussed first. The left column in Fig. 2 contains the temporal evolution of the pressure and temperature fields for this case. At $t = 26.86$ $\upmu$s, the imploding shock wave is about to collapse at the centre. The initial focusing reaches values over 800 bar and 2300 K during the process. Immediately after the implosion, a coupled pressure-reaction front emerges in the results for $t = 26.98$ $\upmu$s. The detonation origin coincides with the initial focusing spot. The mixture is heated by the strong compression, materialising the spontaneous ignition of detonation. The amount and rate of energy released at the focusing event is the underlying cause for this direct (or strong) initiation mechanism.

Fig. 2

Left column: pressure (upper images) and temperature (lower images) temporal evolution of the direct detonation initiation process, $p/p_0 = 6.0$. Right column: pressure (upper images) and temperature (lower images) temporal evolution of the mild detonation initiation process, $p/p_0 = 5.0$. The $x_2$ plot interval goes from $-1$ to 1 mm

The onset of detonation for an incoming shock of $p/p_0 = 5.0$ presents a different scenario. The right column in Fig. 2 describes this evolution towards the formation of a self-sustained detonation front. The spatial curvature ($\eta$) induces the imploding (or converging) shock wave to focus at different points for different times. As a result, the consecutive sequence of focusing events along the longitudinal direction ($x_1$) can be interpreted as two collapsing points travelling forwards and backwards. The temporal rate at which the focusing events occur is proportional to the inverse gradient of the curvature, $| \partial \eta /\partial x_1 |^{-1}$, see [4] for details. Therefore, these travel-collapsing points suffer a deceleration as the converging progresses and the spatial curvature increases. At $t=29.7$ $\upmu$s, the reaction is ignited at the initial focusing stage. Unlike in the previous case ($p/p_0 = 6.0$), the ignited reaction does not undergo detonation straight away at this time. The focusing alone does not suffice to trigger the detonation directly. Instead, the continuous deceleration of the backwards travel-collapsing point enables its interaction with the ignited reaction front. At this stage, the heat release due to combustion supports the increase in the temperature and pressure amplitudes in this travel-collapsing point. This, in turn, further enhances the burning rate of the reaction, releasing higher amounts of heat. The positive feedback mechanism leads to the mutual reinforcement of both the progressing reaction front and the backwards travel-collapsing point. This resonance amplification culminates with the travel-collapsing point restructured into a coupled pressure-combustion front, as shown for $t=30.93$ $\upmu$s in the right column of Fig. 2. This mild detonation initiation mechanism constitutes the intermediate regime from direct initiation to no-initiation at the lower threshold. A detailed analysis of the different detonation initiation mechanisms in the current SDT configuration is given in [4].

The results for incoming shock waves from $p/p_0=4.5$ to $p/p_0=4.9$ evince non-successful initiations. The case of $p/p_0=4.75$ is visualised in Fig. 3 as an illustrative outcome. The formation of the travel-collapsing points due to the curvature of the imploding shock ($\eta$) is also identified in this figure. The feedback mechanism in the backward point resembles the previous discussed case ($p/p_0 = 5.0$), although the reaction’s ignition takes place at a later stage of the feedback. The amplification process is not established completely. Subsequent to the decoupling of the reaction from the focusing events, just the deflagration front remains. No isochoric combustion develops, since the pre-detonation energy concentration at the focusing is lower than the initiation threshold.

In accordance with these results, the incident shock wave strength of $p/p_0 = 5.0$ is selected as the lower detonation initiation threshold. These physical fields define then $q_{\text {ref}} = [\rho ,u_{i},p,Y]^{\text {T}}_{p/p_0 = 5.0}$ in the objective function J (7) and the adjoint equations (21).

3.2 Adjoint results

In the current work, incident shock waves weaker than the reference value of $p/p_0 = 5.0$ are of interest. For this reason, $p/p_0 = 4.75$ is chosen as the case of study with $q = [\rho ,u_{i},p,Y]^{\text {T}}_{p/p_0 = 4.75}$. The adjoint solutions deliver the necessary changes in the initial conditions $q(t_0)$ in order to near the actual system solution q to the reference (or target) solution $q_{\text {ref}} = [\rho ,u_{i},p,Y]^{\text {T}}_{p/p_0 = 5.0}$. The target $q_{\text {ref}}$ serves as the sought-after solution by the adjoint method for q fields other than $q_{\text {ref}}$. In essence, the optimisation procedure pursues to push the detonation initiation limit from $p/p_0 = 5.0$ down to $p/p_0 = 4.75$.

Fig. 3

Pressure (upper images) and temperature (lower images) temporal evolution of the failed initiation, $p/p_0 = 4.75$. The $x_2$ plot interval goes from $-1$ to 1 mm

The solution $q(x_i,t)$ of the Navier–Stokes equations (1) enters the matrices $A^{\text {T}}$, ${B_j}^{\text {T}}$, ${C_j}^{\text {T}}$, $D^{\text {T}}$, and the vector c, for the adjoint time interval $[t_0, t_{\text {end}}]$, see (21) in Appendix 4. This implies that to solve the adjoint equations, q needs to be known beforehand $\forall t \in [t_0, t_{\text {end}}]$. By this means, the information of the $p/p_0 = 4.75$ case is introduced into the system of adjoint equations (21). The desired system state, $q_{\text {ref}}$ (as the solution for $p/p_0 = 5.0$), is included in the source term g of these same equations, and it has also to be calculated previously. The simulations of $p/p_0 = 4.75$ and $p/p_0 = 5.0$ for the baseline geometry then supply the terms in the adjoint equations. The results at the adjoint temporal boundaries $t_0$ and $t_{\text {end}}$ are depicted in Fig. 4. These span from the arrival of the imploding shock wave at the center line until the establishment of the resulting combustion regime, either the detonation for the reference case ($p/p_0 = 5.0$) or the deflagration for the optimisation case ($p/p_0 = 4.75$).

The adjoint equations are only considered for the part of the domain where the focusing-initiation process originates. This spatial subdomain $\varOmega$ is marked with a dashed white rectangle in the right image of Fig. 1. Note that the adjoint solution is not tracked down to the obstacle reflection due to the expensive I/O data-fetching of q and $q_{\text {ref}}$ into the system of adjoint equations [27]. Instead, the sensitivity results are extrapolated to the obstacle’s shape.

Fig. 4

Left column: pressure (upper images) and temperature (lower images) conditions in the adjoint spatial subdomain $\varOmega$ at the adjoint initial time ($t_0$) and the adjoint final time ($t_{\text {end}}$) for the case to optimise $p/p_0 = 4.75$. Right column: pressure (upper images) and temperature (lower images) conditions in the adjoint spatial subdomain $\varOmega$ at the adjoint initial time ($t_0$) and the adjoint final time ($t_{\text {end}}$) for the reference (or target) case $q_{\text {ref}}$ ($p/p_0 = 5.0$). The $x_2$ plot interval goes from $-3$ to 3 mm

Fig. 5

The adjoint solutions $s^*$ in the adjoint spatial subdomain $\varOmega$ at $t_0$. Left: ${s_1}^*$ in $10^7$ units (upper image) and ${s_4}^*$ in $10^2$ units (lower image) denote the changes suggested by the adjoint method on $\rho$ and p at $t_0$, respectively. Right: ${s_2}^*$ in $10^5$ units (upper image) and ${s_3}^*$ in $10^5$ units (lower image) denote the changes suggested by the adjoint method on $u_1$ and $u_2$ at $t_0$, respectively. Dotted lines signalise the original imploding shock wave curvature $\eta$ for $p/p_0 = 4.75$ in the baseline geometry. The black dashed line signalises the optimised imploding shock wave curvature $\eta _{\text {3B}}$ for $p/p_0 = 4.75$ in the Geom 3B case. ER: energy release spot, SW: secondary imploding shock wave. The $x_2$ plot interval goes from $-3$ to 3 mm

The adjoint solution $s^*$ shown on the left plot of Fig. 5 indicates the sensitivity of the detonation initiation to $\rho$ and p at $t_0$. On the right plot of this figure, the sensitivity to $u_1$ and $u_2$, also for $t_0$, is given. In these results, the importance of the energy released at the focal point is highlighted in all $s^*$ fields, marked with ER in Fig. 5. A highly concentrated focal event on $q(t_0)$ is suggested by the adjoint method to minimise the objective function J. Variations on the curvature of the imploding shock wave ($\eta$) are also detected by the method, marked with SW in Fig. 5. This reveals the detonation initiation sensitivity to the imploding shock curvature. Although the amplitude of this adjoint structure (SW in Fig. 5) is lower than the one observed at the focal point (ER in Fig. 5), its potential can be exploited fully by altering the form of the imploding shock.

The adjoint method provides the optimal direction of change in the degree of freedom $\delta q(t_0)$. These sensitivity conclusions are translated into the obstacle’s shape to influence the resulting combustion regime. The adjoint fields $s^*$ confirm that the energy release at the focusing dominates the detonation initiation. The direct geometrical approach to fulfil this adjoint guideline is to increase the BR of the obstacle. Additionally, the adjoint results also identify the sensitivity of the detonation initiation on the imploding shock curvature ($\eta$). This second finding proposes an alternative way of reducing the detonation initiation threshold. Having said that, the double strong nonlinearities in the system (stiff chemical reaction and imploding shock waves) make its geometrical interpretation difficult. Therefore, the adopted strategy applies a parametric study to a parabolic-like profile at the nozzle wall’s corner. The two geometrical proposals based on the adjoint results (increase of the BR and parametric study of the parabolic focusing) are studied in combination in the next section.

3.3 Geometrical variations

Changes to the original (baseline) geometry are first introduced by increasing the BR to 4.7, 5.84, 6.94, and 8.02%. The cases are named as Geom 2, Geom 3, Geom 4, and Geom 5, respectively. The upper part of Table 2 lists these four geometries with its modifications in the converging and diverging angles, $\phi$ and $\theta$. The central plot of Fig. 6 displays the resulting cases together with the baseline one for direct comparison.

The detonation initiation threshold for the four variations of the baseline geometry (Geom 2–5) is investigated. The detonation initiation success depending on the geometry type and the strength of the incident shock wave ($p/p_0$) is summarised in the left plot of Fig. 6. From the results of this figure, the minimum shock wave strength needed for initiation decays monotonically with increasing the BR. The $p/p_0 = 4.75$ threshold is achieved with an approximately 8% increment in the BR, see the solid blue line on the left-hand side of Fig. 6.

Table 2 Geometrical variations

In the four variations of the baseline geometry (Geom 2–5), six different parabolic profiles were included in the last quarter of the ascending (converging) slope. For clarity, only the modifications for successful detonation outcomes are presented in this paper. These are the second- and third-order parabolas, referred to as A and B, respectively, constructed with the polynomial function $y = \zeta x ( \kappa x - \chi )\;( x - \sqrt{2} )$. The BR and the $\phi$, $\theta$ angles remain constant, and only the downstream corner of the nozzle wall changes. The right-hand side of Fig. 6 exemplifies the A and B functions for the Geom 3 case. The lower part of Table 2 tabulates the parabolic profile parameters.

The inclusion of profiles A and B has a positive impact on diminishing the initiation threshold. The $p/p_0 = 4.75$ initiation limit is achieved with the profile A plus approximately 7% increase in the BR and with the profile B combined with an approximately 6% increment in the BR (see the red and yellow solid lines in the left plot of Fig. 6). The results of this figure show the amplification of the monotonic decrease in the incident shock wave strength with the addition of the A and B geometrical modifications.

Fig. 6

Left: detonation initiation success as a function of the incident shock strength ($p/p_0$) and the geometrical variation. Full symbols indicate Go, open symbols–NO-Go. Shading areas cover the successful detonation initiation range. Left axis registers the incident shock wave strength ($p/p_0$). Bottom axis indicates the BR. Top axis gives the geometry case. Center: BR variation without parabolic profile. Right: Geom 3 geometry, and Geom 3A and Geom 3B geometries with the A and B parabolic profiles at the nozzle wall’s corner

The parabolic profiles at the nozzle’s corner induce substantial changes in the reflection of the incoming shock wave. To illustrate this, the left-hand side of Fig. 7 depicts the imploding shock at the verge of collapsing for the Geom 3B case. The strength of the incoming shock wave corresponds to $p/p_0 = 4.75$, the lowest detonation initiation threshold for this geometry. In these results, a secondary imploding shock front is detected. The effect on the initiation process is made clear in the center and the right-hand side of Fig. 7.

The results presented in the central plot of Fig. 7 are discussed first. There, the chemical energy released in the baseline, Geom 3, and Geom 3B cases for an incident shock wave with $p/p_0= 4.75$ is quantified. The study of these cases encapsulates how the different geometries affect the chemical energy release at the focal point. The temporal change of the chemical energy $e_{\text {chem}}$ is integrated over $\varOmega$, the dashed rectangle in Fig. 1, i.e., $e_{\text {chem}}(t)= \int _{\varOmega } Q (Y|_{t^{n-1}}-Y|_{t^{n}}) |F_{\text {d}}| \text {d}\varOmega$. For ease of comparison, the resulting temporal evolutions in the center of Fig. 7 are aligned to the initial time of implosion $t_0$. The curves for all the studied cases clearly start with an exponential rapid increase due to the reaction ignition by the initial collapsing shock. The modified geometries (Geom 3 and Geom 3B) present a higher chemical energy release at this point with the highest value assigned to Geom 3B, see $\circ$ symbols in Fig. 7. The initial focusing activates the feedback stage. The presence of the inflection point in the temporal development of the chemical energy implies the acceleration of this feedback process, marked with $\square$. The energy release rate converges towards the end of the feedback stage for the baseline and the Geom 3 cases. This relaxation signalises an incipient decoupling of the combustion-pressure wave, showing the non-successful detonation initiation. In contrast, the results for Geom 3B indicate the coupling process concludes with the establishment of the detonation, marked with $\triangle$. After that, the self-sustained detonation wave is formed, releasing larger amounts of chemical energy as the front travels.

Fig. 7

Left: imploding shock wave at the verge of collision for Geom 3B. The $x_2$ interval goes from $-20$ to 20 mm. Center: temporal change of the chemical energy ($e_{\text {chem}}$) integrated over the spatial subdomain $\varOmega$. Results are aligned to the initial time of implosion $t_0$. The time interval between $\circ$ and $\triangle$ markers gives the feedback stage duration. Right: $V_{\text {tc}}$, velocity of the backward travel-collapsing point, i.e., the focusing events rate. For the ease of comparison, the velocity curves are aligned in $x_1$ to the initial implosion. The incoming shock strength is $p/p_0 = 4.75$ for all the cases

Fig. 8

Left column: pressure (upper images) and temperature (lower images) temporal evolution of the mild detonation initiation process for Geom 3A, $p/p_0 = 4.8$. Right column: pressure (upper images) and temperature (lower images) temporal evolution of the mild detonation initiation process for Geom 3B, $p/p_0 = 4.75$. The $x_2$ plot interval goes from $-1$ to 1 mm

The curves in the central plot of Fig. 7 demonstrate the augment of the chemical energy release by increasing the BR. The focusing is then reinforced for the Geom 3 and Geom 3B geometries, and as a result, the feedback stage is energy-richer compared with the baseline case. In the parametric study, the Geom 3B profile is found as a partial concave mirror. This is another strategy to increment the implosion process by redirecting part of the reflection into the focal point. The secondary imploding shock wave in the left plot of Fig. 7 confirms that, with a stronger shock towards the center. The inclusion of the parabolic-like profile at the nozzle’s corner of Geom 3B finally serves as an amplitude magnifier at the symmetry line. This enables the detonation initiation for a weaker incident shock wave, decreasing the threshold to $p/p_0=4.75$.

The right-hand side of Fig. 7 contains $V_{\text {tc}}$, the velocity of the backward travel-collapsing points (or the sequence of focusing events) for the baseline, Geom 3, and Geom 3B cases with an incident shock strength of $p/p_0=4.75$. The increase in the BR is associated with a steeper slope of the ascending nozzle’s wall, see the geometry sketch in the center of Fig. 6. As a consequence, an imploding shock with higher curvature ($\eta$) emerges from the reflection of the incoming shock wave at the obstacle. Since the spatial curvature $\eta$ determines the temporal rate at which the sequence of focusing events develops, $V_{\text {tc}} \sim | \partial \eta /\partial x_1 |^{-1}$, the Geom 3 and Geom 3B results present a rise in the deceleration of the focusing process compared with the baseline case, as the right part of Fig. 7 shows. This expands the feedback period, preceding the detonation onset in the mild initiation mechanism. In this particular mode, the resonance between the focusing process and the progressing reaction constitutes the underlying cause of the successful initiation [4]. By altering the curvature of the imploding shock wave ($\eta$), a delay manifests in the development of the focusing events, facilitating its coherent interaction with the chemical reaction.

The results drawn in the right-hand side of Fig. 7 ascribe the lowest measured velocity $V_{\text {tc}}$ to the Geom 3B geometry. This geometry case induces the highest deceleration effect, implying that the parabolic profile modification in Geom 3B affects the curvature $\eta$. In this context, the ability of the modified curvature for Geom 3B ($\eta _{\text {3B}}$) to match accurately the sensitivity curvature suggested by the adjoint method is noteworthy, see the right plot of Fig. 5. As indicated by the adjoint solution in this figure, the mild detonation initiation mechanism can be manipulated by enlarging either the energy release at the focusing or the curvature of the imploding shock wave ($\eta$). The Geom 3B configuration is proven to provide both of these elements to result in a successful detonation initiation. It ensures not only the boost of energy at the focal point, see the central part of Fig. 7, but also it slows down the focusing rate by the increase in the imploding shock curvature $\eta _{\text {3B}}$, see the right part of Fig. 7. The outcome is a delayed focusing sequence with a higher energy release, the best scenario for the SDT to succeed [4].

For the sake of completeness, further numerical results with the geometrical variations are given to confirm the outcome of the detonation. The temporal development of the pressure and temperature fields for the lower initiation threshold in the Geom 3A and the Geom 3B cases is presented in Fig. 8. The incident shock wave strengths equal $p/p_0 = 4.8$ and $p/p_0 = 4.75$, respectively. These results identify the mild initiation mode where the feedback stage appears prior to the detonation onset. The scenario resembles the one for the baseline geometry with an incoming shock wave of $p/p_0 = 5.0$ in the right column of Fig. 2.

4 Conclusions

The potential for optimisation of the nozzle-focusing geometry in a detonation-based engine is evaluated. The applied adjoint method deals only with linear variations of the governing equations (6) and the objective function (J). In consequence, the strong nonlinear character of the detonation initiation impedes the convergence to the optimum in the vector space. Despite this constraint, the method delivers an optimal sensitivity gradient, which leads to a deficit in the detonation initiation threshold of 5% or $p/p_0 = 0.25$ in absolute values.

In the detonation chamber under investigation, the strength of the incoming shock wave ($p/p_0$) is proportional to the amount of burned gas in a pre-chamber upstream of the nozzle. Therefore, it is of great interest and relevance to minimise the $p/p_0$ threshold while still obtaining a reliable detonation transition. The proposed geometry improvements achieve that purpose, allowing to cut the length of the shock wave-generator pre-chamber. An optimised design with a shorter chamber volume reduces the premixed fuel consumption, increasing the cycle thermal efficiency.

These conclusions could be extended for the use of less reactive compounds (or lean mixtures) in detonative technical applications.

Appendices

Appendix 1: Physical–chemical model

The physical–chemical model parameters, the seventh-order polynomial coefficients of $\gamma (T)$, and the adjusted pre-exponential values of the one-step kinetics are given in Tables 3, 4, and 5, respectively (Figs. 9, 10).

Table 3 Physical–chemical model parameters and CJ detonation values for stoichiometric $2\text {H}_{2} + \text {O}_{2} + 3.76\text {N}_{2} \rightarrow 2\text {H}_{2}\text {O} + 3.76\text {N}_{2}$

Table 4 The polynomial coefficients of $\gamma (T)=\sum _{n=0}^7 b_n T^n$

Table 5 The adjusted pre-exponential coefficients of $A_{\text {f}}(T,p) = \upsilon (T,p) T + \psi (T,p)$ in $10^{8}/\text {s}$

Appendix 2: Code validation and verification

The code is initially validated against a steady shock wave and the classical Sod shock tube problem in a one-dimensional domain [29]. The conservation laws of the applied numerical scheme are also tested. For that, the temporal changes in mass, momentum, and total energy in successive time steps $t^{n}$ to $t^{n+1}$ are calculated in the form: $\frac{\partial m_{\text {a}} }{\partial t}=\int _{x_{\text {1D}}} ( \rho ^{t^{n+1}}- \rho ^{t^{n}}) \text {d}x_{\text {1D}}$, $\frac{\partial m_{\text {o}} }{\partial t}=\int _{x_{\text {1D}}} ( \rho u ^{t^{n+1}}- \rho u ^{t^{n}}) \text {d}x_{\text {1D}}$, and $\frac{\partial e_{\text {tot}}}{\partial t}=\int _{x_{\text {1D}}} (e_{\text {tot}}^{t^{n+1}}- e_{\text {tot}}^{t^{n}}) \text {d}x_{\text {1D}}$.

The left plot of Fig. 11 contains the pressure for a steady shock wave of $p/p_0 = 4.0$ computed with 128, 256, 512, 1024, and 2048 spatial points. The inset of this plot shows the conservation properties for the coarsest discretisation (128 points). The temporal changes in mass, momentum, and total energy reach maximum absolute values of $7\cdot 10^{-19}$, $9\cdot 10^{-14}$, and $3\cdot 10^{-11}$, respectively. These small errors in the conservation prove the convergence of the shock wave to its steady solution.

The right plot of Fig. 11 shows the density for the Sod shock tube problem computed with the same number of points as the previous case. The initial conditions for this case are summarised in Table 6. The simulations are compared with the exact analytical solution with good results. The finer discretisations indicate the convergence of the computed results to the exact solution. The inset plot depicts again the conservation laws for the coarsest discretisation (128 points). The maximum absolute error presents values of $1\cdot 10^{-17}$, $3\cdot 10^{-15}$, and $1\cdot 10^{-12}$ in mass, momentum, and total energy, respectively. These results verify the correct operation of the code.

Fig. 9

Induction time $\tau _{\text {c}}$ (isochoric) for stoichiometric hydrogen-air ($2\text {H}_{2} + \text {O}_{2} + 3.76\text {N}_{2}$) specified by the time scale of the maximum reaction rate [24], i.e., $\tau _{\text {c}}=\frac{\partial T}{\partial t} \bigr |_{\text {max}}$. Solid line: San Diego mechanism, 21 reactions. Empty markers: adjusted one-step model. Maximum relative error 0.09978%

Fig. 10

Sensible energy $e_{\text {s}}$ and T relation for different $\gamma$ definitions (upper left); $\gamma (T)$ polynomial used in this study (upper right). Relative and absolute error in T of the seventh-order polynomial with respect to the CHEMKIN database [20] (lower left). The deviation $\gamma (T_{\text {max}}^{t^{n+1}}) - \gamma (T_{\text {max}}^{t^n})$ over time with a maximum error of $2.75\cdot 10^{-3}$ (lower right)

Fig. 11

Left: refinement test for pressure p of a steady shock wave of $p/p_0 = 4.0$ after 0.1 ms. Right: refinement test for density $\rho$ of the Sod shock tube problem after 1 ms. Inset left and right: conservation properties with 128 computational points. Both cases are computed with 128, 256, 512, 1024, and 2048 points

The mesh independence of the results is studied by applying the same five successively finer grids to a laminar premixed flame and a detonation front in a one-dimensional domain with a mixture of stoichiometric hydrogen-air. The results are presented in Fig. 12 relative to the flame thickness $\delta _{\text {o}}$ for the flame and to the half of the reaction length $L_{1/2}$ for the detonation. The left plot of this figure shows that the flame temperature is well resolved already with 8 points per $\delta _{\text {o}}$. The lower inset of this plot depicts the convergence of the burned state with 15 points per $\delta _{\text {o}}$. In the upper inset of this plot, the conservation properties for the coarsest discretisation ($\delta _{\text {o}}/\Delta x$ = 8) are given. The maximum absolute errors in the conservation of mass, momentum, and total energy for the flame are substantially low being $5\cdot 10^{-18}$, $1\cdot 10^{-16}$, and $6\cdot 10^{-10}$, respectively.

The right plot of Fig. 12 contains the discretised pressure in a detonation front. As in the previous case, the front is fairly well captured even with the lowest refinement of 4 points per $L_{1/2}$. The inset of this plot gives the conservation properties for the discretisation $L_{1/2}/\Delta x$ = 6 with maximum absolute errors of the order of $8\cdot 10^{-19}$, $7.6\cdot 10^{-12}$, and $1.6\cdot 10^{-9}$ for mass, momentum, and total energy, respectively.

The discretisation in the numerical experiments of this work ranges between a minimum of 20 and a maximum of 61 points per $\delta _{\text {o}}$, equivalently, between a minimum of 4.5 and a maximum of 13 points per $L_{1/2}$. These results demonstrate that the reactive fronts are well resolved with the used refinement.

The conducted validations confirm satisfactorily the convergence of the simulated results to the exact analytical solution, the fulfilment of the conservation laws by the numerical method, and the mesh independence of the results presented in the current numerical investigation.

Table 6 Sod shock tube problem initial conditions, $\gamma = 1.3$

Table 7 Precision based upon error accumulation for the $p/p_0 = 4.5$ case: $k_{\text {or}} = 4$, $L_{x_1} = 30$   mm, $L_{x_2} = 40.3$   mm, ${d}_{x_1}\bigr |_{\text {max}} =2.93 \cdot 10^{-2}$   mm, $\text {d}_{x_2}\bigr |_{\text {max}} =1.97 \cdot 10^{-2}$   mm

Fig. 12

Left: refinement test for temperature T of a stoichiometric hydrogen-air laminar premixed flame after 0.2 ms. Computed with 8, 15, 30, 61, and 121 computational points per flame thickness $\delta _{\text {o}}$. Inset upper left: conservation properties with 8 computational points per $\delta _{\text {o}}$. Inset lower left: convergence and accuracy test. Right: refinement test for pressure p of a stoichiometric hydrogen-air detonation front. Computed with 4, 6, 8, 17, and 27 computational points per half reaction length $L_{1/2}$. Inset right: conservation properties with 6 computational points per $L_{1/2}$

Appendix 3: Precision estimates

The discretisation error accumulates for $n_{\text {t}}$ successive time integration steps. Assuming that the numerical strategy is free of systematic errors, the stochastic error still remains. The latter sums up proportional to $\sqrt{n_{\text {t}}}$ [30].

The maximum relative error of integration for ith-dimensional domains is approximated with $S_{\mathrm {err_{max}}} \approx \sum _{i} \left( \frac{ \text {max} ( \text {d}x_i ) }{ L_{x_i} }\right) ^{k_{\text {or}}+1}$, where $\text {d}x_i$ stands for the mesh spacing, $L_{x_i}$ the domain size, and $k_{\text {or}}$ the integration order of accuracy [30]. The final stochastic accumulation of error for $n_{\text {t}}$ steps produces $S_{\mathrm {err_{max}}} \cdot \sqrt{n_{\text {t}}}$.

The simulation for the incident shock wave of $p/p_0=4.5$ takes the longest physical time. The error estimation for this worst case scenario is given in Table 7. The high-order integration scheme and the fine space discretisation induce an extremely low error accumulation. This indicates a high reliability of the numerical results presented in this investigation.

Appendix 4: Adjoint equations

Vector-matrix notation of  (5), (6), (7), and (8):

$$\begin{aligned}&a = \begin{bmatrix} \rho \\ \rho u_{i} \\ \frac{p}{\gamma -1} \\ \rho Y \end{bmatrix} ; \; b_{j} = \begin{bmatrix} \rho u_{j} \\ \rho u_j u_i + p\delta _{ij} \\ \frac{\gamma }{\gamma -1} u_j p \\ \rho u_j p \end{bmatrix} ; \nonumber \\&c = \begin{bmatrix} 0 \\ 0 \\ p \\ 0 \end{bmatrix} ; \; d = \begin{bmatrix} 0 \\ 0 \\ \dot{\omega }_{\text {T}} \\ \dot{\omega } \end{bmatrix} ; \; \end{aligned}$$

(9)

$$\begin{aligned}&q = \begin{bmatrix} \rho \\ u_i \\ p \\ Y \end{bmatrix} ; \; \delta q = \begin{bmatrix} \delta \rho \\ \delta u_i \\ \delta p \\ \delta Y \end{bmatrix} ; \; q^* = \begin{bmatrix} \rho ^* \\ {u_i}^* \\ p^* \\ Y^* \end{bmatrix} ; \nonumber \\&s^* = A^{\text {T}} q^*(t_0) \end{aligned}$$

(10)

$$\begin{aligned} \dot{\omega }&= -A_{\text {f}}(T,p) \text {e}^{\frac{-T_{\text {a}}}{T}} \rho Y = -(\upsilon T + \psi ) \text {e}^{\frac{-T_{\text {a}}}{T}} \nonumber \\&\rho Y = -\left( \upsilon \frac{p}{\rho R_{\text {s}}} + \psi \right) \text {e}^{\frac{ -T_{\text {a}} \rho R_{\text {s}}}{p} } \rho Y \end{aligned}$$

(11)

$$\begin{aligned}&A = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ u_1 &{} \rho &{} 0 &{} 0 &{} 0 \\ u_2 &{} 0 &{} \rho &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \frac{1}{\gamma -1} &{} 0 \\ Y &{} 0 &{} 0 &{} 0 &{} \rho \end{array}\right] ; \nonumber \\&B_{1} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} u_1 &{} \rho &{} 0 &{} 0 &{} 0 \\ {u_1}^2 &{} 2 \rho u_1 &{} 0 &{} 1 &{} 0 \\ u_1 u_2 &{} \rho u_2 &{} \rho u_1 &{} 0 &{} 0 \\ 0 &{} \frac{\gamma p}{\gamma - 1} &{} 0 &{} \frac{\gamma u_1}{\gamma - 1} &{} 0 \\ u_1 Y &{} \rho Y &{} 0 &{} 0 &{} \rho u_1 \end{array}\right] \end{aligned}$$

(12)

$$\begin{aligned}&B_{2} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} u_2 &{} 0 &{} \rho &{} 0 &{} 0 \\ u_1 u_2 &{} \rho u_2 &{} \rho u_1 &{} 0 &{} 0 \\ {u_2}^2 &{} 0 &{} 2 \rho u_2 &{} 1 &{} 0 \\ 0 &{} 0 &{} \frac{\gamma p}{\gamma - 1} &{} \frac{\gamma u_2}{\gamma - 1} &{} 0 \\ u_2 Y &{} 0 &{} \rho Y &{} 0 &{} \rho u_2 \end{array}\right] ; \nonumber \\&C_{j} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -u_j &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] \end{aligned}$$

(13)

$$\begin{aligned}&\widetilde{C} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] ; \; \delta C_{j} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\delta u_j &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] ; \end{aligned}$$

(14)

$$\begin{aligned}&\frac{\delta C_{j}}{\delta q} \approx \frac{\partial C_{j}}{\partial q} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] \end{aligned}$$

(15)

$$\begin{aligned}&D = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ d_{4,1} &{} 0 &{} 0 &{} d_{4,4} &{} d_{4,5} \\ d_{5,1} &{} 0 &{} 0 &{} d_{5,4} &{} d_{5,5} \end{array}\right] {\hbox {e}}^{\frac{-T_{\text {a}} \rho R_{\text {s}}}{p}} \end{aligned}$$

(16)

$$\begin{aligned}&d_{4,1}= - Q d_{5,1} \;;\; d_{4,4}= - Q d_{5,4} \;;\; d_{4,5}= - Q d_{5,5} \end{aligned}$$

(17)

$$\begin{aligned} d_{5,1}&= - \frac{T_{\text {a}} R_{\text {s}} \rho Y \left( \frac{p \upsilon }{R_{\text {s}} \rho } + \psi \right) }{p} - \frac{ p \upsilon Y }{R_{\text {s}} \rho }\nonumber \\&\qquad \quad + Y \left( \frac{p \upsilon }{R_{\text {s}} \rho } + \psi \right) \end{aligned}$$

(18)

$$\begin{aligned} d_{5,4}&= \frac{ T_{\text {a}} R_{\text {s}} {\rho }^2 Y \left( \frac{p \upsilon }{R_{\text {s}} \rho } + \psi \right) }{p^2} + \frac{ \upsilon Y }{R_{\text {s}}} \end{aligned}$$

(19)

$$\begin{aligned} d_{5,5}&= \rho \left( \frac{ p \upsilon }{R_{\text {s}} \rho } + \psi \right) \end{aligned}$$

(20)

The two-dimensional adjoint equations fully expanded:

$$\begin{aligned}&\frac{\partial q^*}{\partial t} + \underbrace{{A^{\text {T}}}^{-1}{B_{j}}^{\text {T}}}_{=X_j} \frac{\partial q^*}{\partial x_{j}} + \underbrace{{A^{\text {T}}}^{-1}\widetilde{C}^{\text {T}}}_{=Y} \frac{\partial {C_{j}}^{\text {T}}}{\partial x_{j}} q^*\nonumber \\&\quad + {A^{\text {T}}}^{-1} \left( c^{\text {T}} \frac{\partial }{\partial x_j} \underbrace{\left( \frac{\delta C_j}{\delta q} \right) ^{\text {T}} q^*}_{=z} \right) \nonumber \\&\quad - \underbrace{{A^{\text {T}}}^{-1} D^{\text {T}}}_{H} q^* - {A^{\text {T}}}^{-1}g = 0 \end{aligned}$$

(21)

$$\begin{aligned}&{A^{\text {T}}}^{-1} = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} \frac{-u_1}{\rho } &{} \frac{-u_2}{\rho } &{} 0 &{} \frac{-Y}{\rho } \\ 0 &{} \frac{1}{\rho } &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{1}{\rho } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \gamma - 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{1}{\rho } \end{array}\right] \end{aligned}$$

(22)

$$\begin{aligned}&X_1 = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} -{u_1}^2 &{} -u_1 u_2 &{} \frac{-\gamma p u_1}{\rho (\gamma -1)} &{} -u_1 Y \\ 1 &{} 2 u_1 &{} u_2 &{} \frac{\gamma p}{\rho (\gamma - 1)} &{} Y \\ 0 &{} 0 &{} u_1 &{} 0 &{} 0 \\ 0 &{} \gamma -1 &{} 0 &{} \gamma u_1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} u_1 \end{array}\right] \end{aligned}$$

(23)

$$\begin{aligned}&X_2 = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} -u_1 u_2 &{} -{u_2}^2 &{} \frac{-\gamma p u_2}{\rho (\gamma -1)} &{} -u_2 Y \\ 0 &{} u_2 &{} 0 &{} 0 &{} 0 \\ 1 &{} u_1 &{} 2 u_2 &{} \frac{\gamma p}{\rho (\gamma -1)} &{} Y \\ 0 &{} 0 &{} \gamma - 1 &{} \gamma u_2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} u_2 \end{array}\right] \end{aligned}$$

(24)

$$\begin{aligned}&Y = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \gamma -1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] \end{aligned}$$

(25)

$$\begin{aligned}&{C_1}^{\text {T}} q^* = \begin{bmatrix} 0 \\ 0 \\ 0 \\ p^*u_1 \\ 0 \end{bmatrix}; \; {C_2}^{\text {T}} q^* = \begin{bmatrix} 0 \\ 0 \\ 0 \\ p^*u_2 \\ 0 \end{bmatrix}; \; z = \begin{bmatrix} 0 \\ 0 \\ 0 \\ -p^* \\ 0 \end{bmatrix} \end{aligned}$$

(26)

$$\begin{aligned}&H = \left[ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 &{} h_{1,4} &{} h_{1,5} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} h_{4,4} &{} h_{4,5} \\ 0 &{} 0 &{} 0 &{} h_{5,4} &{} h_{5,5} \end{array}\right] {\hbox {e}}^{\frac{-T_{\text {a}} \rho R_{\text {s}}}{p}} \end{aligned}$$

(27)

$$\begin{aligned}&h_{1,4} = - Q h_{1,5} \; ; \; h_{4,4} = -(\gamma - 1) \frac{\rho }{p} h_{1,4} \; ; \nonumber \\&h_{4,5} = -(\gamma - 1) \frac{\rho }{p} h_{1,5} \; ; \; h_{5,4} = -Q h_{5,5} \end{aligned}$$

(28)

$$\begin{aligned}&h_{1,5} = \frac{-T_{\text {a}} \rho Y R_{\text {s}} \left( \frac{p \upsilon }{\rho R_{\text {s}}} + \psi \right) }{p} - \frac{p \upsilon Y}{R_{\text {s}} \rho } \end{aligned}$$

(29)

$$\begin{aligned}&h_{5,5} = \frac{p \upsilon }{\rho R_{\text {s}}} + \psi \end{aligned}$$

(30)

$$\begin{aligned}&{A}^{\text {T}} q^*|_{t_0} = s^* = \begin{bmatrix} {\rho }^* + u_1{u_1}^* + u_2{u_2}^* + YY^*|_{t_0} \\ \rho {u_1}^*|_{t_0} \\ \rho {u_2}^*|_{t_0} \\ \frac{p^*}{\gamma - 1}|_{t_0} \\ \rho Y^*|_{t_0} \end{bmatrix} \end{aligned}$$

(31)

Appendix 5: Axial-symmetric geometrical factors for arbitrarily distorted grids

$$\begin{aligned} \frac{\partial u_{i}}{\partial x_{i}}&= \nabla \cdot u = \frac{1}{F_{\text {d}}} \frac{\partial ( m_{ji} u_j)}{\partial \xi _{i}}\nonumber \\&= \frac{1}{F_{\text {d}}} \left( \frac{\partial }{\partial \xi _{1}} ( m_{11} u_1 + m_{21} u_2 ) \right. \nonumber \\&\quad \quad \left. + \frac{\partial }{\partial \xi _{2}} ( m_{12} u_1 + m_{22} u_2 ) \right) \end{aligned}$$

(32)

$$\begin{aligned}&\nabla p = \frac{1}{F_{\text {d}}} \frac{\partial (m_{ji} p)}{\partial \xi _{i}} = \frac{1}{F_{\text {d}}} \begin{pmatrix} \frac{\partial (m_{11} p) }{\partial \xi _1} + \frac{\partial ( m_{12} p) }{\partial \xi _2} \\ \frac{\partial ( m_{21} p) }{\partial \xi _1} + \frac{\partial (m_{22} p) }{\partial \xi _2} \end{pmatrix} \end{aligned}$$

(33)

$$\begin{aligned}&m_{ij} = \begin{pmatrix} x_2 \frac{\partial x_2}{\partial \xi _2} &{} -x_2 \frac{\partial x_2}{\partial \xi _1} \\ -x_2 \frac{\partial x_1}{\partial \xi _2} &{} x_2 \frac{\partial x_1}{\partial \xi _1} \end{pmatrix} \end{aligned}$$

(34)

$$\begin{aligned}&F_{\text {d}} = x_2 \bigg ( \frac{\partial x_1}{\partial \xi _1} \frac{\partial x_2}{\partial \xi _2}-\frac{\partial x_1}{\partial \xi _2} \frac{\partial x_2}{\partial \xi _1} \bigg ) \end{aligned}$$

(35)