Structure–property linkage in shocked multi-material flows using a level-set-based Eulerian image-to-computation framework

Abstract

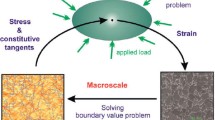
Morphology and dynamics at the mesoscale play crucial roles in the overall macro- or system-scale flow of heterogeneous materials. In a multi-scale framework, closure models upscale unresolved sub-grid (mesoscale) physics and therefore encapsulate structure–property (S–P) linkages to predict performance at the macroscale. This work establishes a route to S–P linkage, proceeding all the way from imaged microstructures to flow computations in one unified level-set-based framework. Level sets are used to: (1) define embedded geometries via image segmentation; (2) simulate the interaction of sharp immersed boundaries with the flow field; and (3) calculate morphological metrics to quantify structure. Mesoscale dynamics is computed to calculate sub-grid properties, i.e., closure models for momentum and energy equations. The S–P linkage is demonstrated for two types of multi-material flows: interaction of shocks with a cloud of particles and reactive meso-mechanics of pressed energetic materials. We also present an approach to connect local morphological characteristics in a microstructure containing topologically complex features with the shock response of imaged samples of such materials. This paves the way for using geometric machine learning techniques to associate imaged morphologies with their properties.

Appendices

Appendix 1

1.1 Governing equations and numerical method for mesoscale computations

The hyperbolic conservation laws for mass, momentum, and energy are solved:

$$ \begin{aligned} & \frac{\partial \rho }{\partial t} + \frac{{\partial \left( {\rho u_{i} } \right)}}{{\partial x_{i} }} = 0 \\ & \frac{{\partial \left( {\rho u_{i} } \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{i} u_{j} + \sigma_{ij} } \right)}}{{\partial x_{j} }} = 0 \\ & \frac{{\partial \left( {\rho E} \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{i} E + \sigma_{ij} u_{i} } \right)}}{{\partial x_{i} }} = \dot{\varepsilon } \\ \end{aligned} $$

(34)

Here, the density and velocity components of the material are denoted by $\rho$ and $u_{i}$, respectively. The total specific energy is $E = e + \frac{1}{2}u_{i} u_{i}$, where $e$ is the specific internal energy. The source term $\dot{\varepsilon }$ in (34) is the rise in specific internal energy of the system due to heat released in the decomposition of solid HMX into gaseous reaction products. The quantity $\sigma_{ij}$ is the Cauchy stress tensor and is given differently for the particle-laden gas flow computations and pressed energetic materials.

The stress tensor $\sigma_{ij}$ is:

$$ \sigma_{ij} = \varSigma_{ij} - p\delta_{ij} $$

(35)

where $p$ is the pressure and $\varSigma_{ij}$ refers to the deviatoric components of the stress tensor. For the gas, the deviatoric components $\varSigma_{ij}$ of the stress tensor are zero and an ideal gas equation of state is used to calculate the pressure:

$$ p = \rho e(\gamma - 1) $$

(36)

where $\gamma$ is the specific heat ratio with a value of 1.4. For the solid energetic materials, the deviatoric stress tensor $S_{ij}$ is evolved using the following evolution equation:

$$ \frac{{\partial \left( {\rho S_{ij} } \right)}}{\partial t} + \frac{{\partial \left( {\rho S_{ij} u_{k} } \right)}}{{\partial x_{k} }} + \rho S_{ik} \varOmega_{kj} - \rho \varOmega_{ik} S_{kj} = \rho G\left( {D_{ij}^{\text{d}} - D_{ij}^{\text{d,p}} } \right) $$

(37)

where $D_{ij}^{\text{d}}$ is the deviatoric component of the strain rate tensor, $\varOmega_{ij}$ is the spin tensor, $D_{ij}^{{{\text{d}},{\text{p}}}}$ is the plastic component of the deviatoric strain rate tensor, and G is the shear modulus of the material. The component $D_{ij}^{{{\text{d}},{\text{p}}}}$ is obtained using the radial return algorithm [41].

Pressure is obtained from the Birch–Murnaghan equation of state [105], which can be written in the general Mie-Gruneisen form as:

$$ p\left( {\rho ,e} \right) = p_{k} \left( \rho \right) + \rho \varGamma_{s} \left[ {e - e_{k} \left( \rho \right)} \right], $$

(38)

where

$$\begin{aligned} p_{k} \left( \rho \right) &= \frac{3}{2}K_{T0} \left[ {\left( {\frac{\rho }{{\rho_{0} }}} \right)^{ - 7/3} - \left( {\frac{\rho }{{\rho_{0} }}} \right)^{ - 5/3} } \right]\times\\ & \qquad\left[ 1 + \frac{3}{4}\left( {K_{T0}^{{\prime }} - 4} \right)\left[ {\left( {\frac{\rho }{{\rho_{0} }}} \right)^{ - 2/3} } - 1 \right] \right],\end{aligned} $$

(39)

The Birch–Murnaghan equation of state is solved to obtain the dilatational response, and the deviatoric response of HMX is obtained by modeling perfectly plastic response under shock loading (Table 3) [105]. Thermal softening caused due to melting of HMX under shock loading is modeled using the Kraut–Kennedy relation [105], $T_{\text{m}} = T_{\text{m}0} \left( {1 + a\frac{{\Delta V}}{{V_{0} }}} \right)$, with model parameters provided in the work of Menikoff et al. [105]. Once the temperature exceeds the melting point of HMX, the deviatoric strength terms are set to zero. Furthermore, the specific heat of HMX is known to change significantly with temperature. The variation of specific heat is modeled as a function of temperature as suggested in [105]. The specific heat as a function of temperature is obtained from [105]. A three-step chemical decomposition model is applied for the chemical reaction of HMX [2]. A detailed description of the implementation is presented in the previous work [93]. Here, a brief overview of the reaction model and its implementation is provided.

Table 3 Constitutive properties of HMX used for the [105] for the mesoscale void collapse simulations

Chemical decomposition of HMX takes place in three steps involving four different species:

$$ \begin{aligned}& {\text{Reaction}}\,1\!: {\text{HMX}}\,\left( {{\text{C}}_{4} {\text{H}}_{8} {\text{N}}_{8} {\text{O}}_{8} } \right)\\ &\quad\to {\text{fragments}}\,\left( {{\text{CH}}_{2} {\text{NNO}}_{2} } \right) \end{aligned}$$

(40)

$$\begin{aligned} &{\text{Reaction}}\, 2\!:\\ &\quad {\text{fragments}}\,\left( {{\text{CH}}_{2} {\text{NNO}}_{2} } \right)\\ &\quad \to {\text{intermediate}}\,{\text{gases}}\, \left( {{\text{CH}}_{2} {\text{O}},{\text{N}}_{2} {\text{O}},{\text{HCN}},{\text{HNO}}_{2} } \right)\end{aligned} $$

(41)

$$\begin{aligned} &{\text{Reaction}}\, 3\!:\\ &\quad 2 \times {\text{intermediate}}\,{\text{gases}}\, \left( {{\text{CH}}_{2} {\text{O}},{\text{N}}_{2} {\text{O}},{\text{HCN}},{\text{HNO}}_{2} } \right)\\ &\quad \to {\text{final}}\,{\text{gases}}\, \left( {{\text{N}}_{2} ,{\text{H}}_{2} {\text{O}},{\text{CO}}_{2} ,{\text{CO}}} \right)\end{aligned} $$

(42)

The solid HMX (species 1, mass fraction $Y_{1}$) under high temperature decomposes into fragments (species 2, $Y_{2}$). The fragments are further decomposed to intermediate gases (species 3, $Y_{3}$) which are later converted to the final gases (species 4, $Y_{4}$) through exothermic reactions leading to high temperatures in the hotspot. In the absence of information about the equations of state for the intermediate and the final products, in this work, it is assumed that these intermediates and the products follow the same cold curves as the bulk material.

Species formed by the chemical decomposition of HMX are evolved in time using the following species conservation equation:

$$ \frac{{\partial \left( {\rho [Y_{k} ]} \right)}}{\partial t} + \frac{{\partial \left( {\rho u_{i} [Y_{k} ]} \right)}}{{\partial x_{i} }} = \dot{Y}_{k} $$

(43)

where $Y_{k}$ corresponds to the mass fraction and $\dot{Y}_{k}$—to the mass production rate of the kth species. The change in temperature because of the chemical decomposition of HMX is calculated by solving the evolution equation:

$$ \rho C_{p} \dot{T} = \dot{Q}_{\text{R}} + k\Delta T $$

(44)

where $\rho$ is the density of HMX, $C_{p}$ is the specific heat of HMX, $T$ is the temperature, $k$ is the thermal conductivity of HMX, and $\dot{Q}_{\text{R}}$ is the total heat release rate because of the chemical reaction. The values of $C_{p}$, λ, and $\dot{Q}_{\text{R}}$ are obtained from the work of Tarver et al. [2]. The source term in (34) is computed by setting $\dot{\varepsilon } = C_{v} \dot{T}$, where $C_{v}$ is the specific heat of HMX at constant volume.

Spatial discretization of the governing equations is performed on a fixed Cartesian grid using a third-order essentially non-oscillatory (ENO) scheme [106]. A third order Runge–Kutta scheme is used for explicit time marching. The computational domain contains objects in the form of particles in the case of gas–particle flows and voids in the case of pressed energetic materials. All interfaces between materials are delineated by a signed distance function or the level-set function $\varphi \left( {\varvec{x},t} \right)$. The level set $\varphi \left( {\varvec{x},t} \right) < 0$ for regions in the interior of the objects and $\varphi \left( {\varvec{x},t} \right) > 0$ in the exterior and is defined in a narrow band for each interface [26]. If there are a total of $N_{\text{obj}}$ objects in the domain, the level-set field for the $l{\text{th}}$ object is given by a separate narrowband level-set field $\varphi_{l} (\varvec{x},t)$. No-penetration boundary conditions are applied at interfaces between the gas and solid using the modified ghost fluid method (GFM) [107]; appropriate boundary conditions on free surfaces and crystal–crystal contact conditions for the pressed HMX problem are prescribed [108]. A detailed explanation of the numerical framework used for the mesoscale simulations can be found in previous works [10, 23, 29,30,31, 49].

Appendix 2

2.1 Spatial and temporal homogenization of QoIs for gas–particle flow

The spatially averaged drag $\overline{{F_{\text{D}} }} (t^{*} )$ is the mean drag experienced by all the particles in the domain. Details of the averaging methods can be found in previous work [86]. Here, $t^{*} = \frac{t}{{t_{\text{ref}} }}$ and reference timescale $t_{\text{ref}} = \frac{{l_{\text{ref}} }}{{u_{\text{s}} }}$, where $l_{\text{ref}}$ is the reference length scale, and its value is 1.0 based on the dimensions of the square that contains the particle cluster (Fig. 9). The velocity $u_{\text{s}}$ is the incident particle velocity of the shock. The spatially averaged drag coefficient $\overline{{C_{\text{D}} }} (t^{*} )$ in the cluster is:

$$ \overline{{C_{\text{D}} }} (t^{*} ) = \frac{{\overline{{F_{\text{D}} }} (t^{*} )}}{{\frac{1}{2}\rho_{\text{s}} u_{\text{s}}^{2} d_{\text{eq}} }} $$

(45)

where $\rho_{\text{s}}$ is the density of static unshocked fluid, $u_{\text{s}}$ is the particle velocity, and $d_{\text{eq}}$ is the equivalent diameter of the particle cluster $d_{\text{eq}} = \sqrt {\frac{4}{\pi }\varOmega \phi }$ in the domain with area $\varOmega$ and volume fraction $\phi$. The velocity fluctuations cause stresses in the gas phase, which appear as the pseudo-turbulent stress tensor, $S_{ij}$, given by:

$$ S_{ij} (\varvec{x},t^{*} ) = \frac{{u_{i}^{{\prime }} (\varvec{x},t^{*} )\,u_{j}^{{\prime }} (\varvec{x},t^{*} )}}{{u_{\text{s}}^{2} }} $$

(46)

where $u_{i}^{\prime } (\varvec{x},t^{*} )$ is the velocity fluctuation field:

$$ u_{i}^{{\prime }} \left( {\varvec{x},t^{*} } \right) = u_{i} \left( {\varvec{x},t^{*} } \right) - \widetilde{u}_{\text{g} }\left( {t^{*} } \right) $$

(47)

and the Favre-averaged gas slip velocity $\widetilde{u}_{\text{g}} (t^{*} )$ is calculated as follows:

$$ \widetilde{u}_{\text{g} }\left( {t^{*} } \right) = \frac{{\mathop \int \nolimits_{\varOmega }^{ } \rho u_{\text{g}} {\text{d}}\varOmega }}{{\mathop \int \nolimits_{\varOmega }^{ } \rho {\text{d}}\varOmega }} $$

(48)

where $\rho$ and $u_{\text{g}}$ are the fluid phase density and velocity component, respectively.

The spatially-averaged pseudo-turbulent stress tensor $\tilde{S}_{ij} (t^{*} )$ is:

$$ \tilde{S}_{ij} \left( {t^{*} } \right) = \frac{{\mathop \int \nolimits_{\varOmega }^{ } \rho S_{ij} {\text{d}}\varOmega }}{{\mathop \int \nolimits_{\varOmega }^{ } \rho {\text{d}}\varOmega }} $$

(49)

The spatially averaged pseudo-turbulent kinetic energy (PTKE [86]), i.e., $\widetilde{\text{PTKE}}(t^{*} )$, is:

$$ \widetilde{\text{PTKE}}(t^{*} ) \equiv \tilde{S}_{ii} \left( {t^{*} } \right) $$

(50)

The temporal homogenization is performed over a time $T^{*}$ beginning with the shock entering the cluster until the entire incident shock wave leaves the particle cluster. The spatiotemporally-averaged drag coefficient $\left\langle {\overline{{C_{\text{D}} }} } \right\rangle$ is obtained as:

$$ \left\langle {\overline{{C_{\text{D}} }} } \right\rangle = \frac{{\mathop \int \nolimits_{{t^{*} = 0}}^{{t^{*} = T^{*} }} \overline{{C_{\text{D}} }} \left( {t^{*} } \right){\text{d}}t^{*} }}{{\mathop \int \nolimits_{{t^{*} = 0}}^{{t^{*} = T^{*} }} {\text{d}}t^{*} }} $$

(51)

The spatiotemporally-averaged pseudo-turbulent stress tensor $\tilde{S}_{ij}$ is given by:

$$ \left\langle {\tilde{S}_{ij} } \right\rangle = \frac{{\mathop \int \nolimits_{{t^{*} = 0}}^{{t^{*} = T^{*} }} \tilde{S}_{ij} \left( {t^{*} } \right){\text{d}}t^{*} }}{{\mathop \int \nolimits_{{t^{*} = 0}}^{{t^{*} = T^{*} }} {\text{d}}t^{*} }} $$

(52)

And the spatiotemporal average of the PTKE, $\left\langle {\widetilde{\text{PTKE}}} \right\rangle$, is defined as follows:

$$ \left\langle {\widetilde{\text{PTKE}}} \right\rangle \equiv \left\langle {\tilde{S}_{ii} } \right\rangle $$

(53)

Appendix 3

3.1 Spatial homogenization of QoIs in shocked HMX

The product species mass fraction is denoted by $Y_{4} (x,t)$ and is evolved using the conservation equations for species (43). The rate of chemical decomposition of HMX within the entire domain is calculated by accumulating the mass of the final gaseous products via:

$$ M_{\text{reacted}} (t) = \mathop \int \limits_{{\varOmega_{ } }}^{ } \rho (\varvec{x},t) Y_{4} (\varvec{x},t) {\text{d}}\varOmega $$

(54)

$M_{\text{reacted}}$ is calculated for the entire domain of area $\varOmega$, and $\rho$ is the local density. The burned fraction of HMX, $F$, is the mass of the solid converted to reaction product gaseous species denoted by $F$ which is useful to study the long-term behavior for a field of voids. The fraction of fully burned HMX to the total mass of HMX in the control volume is:

$$ F(t) = \frac{{M_{\text{reacted}} (t)}}{{M_{\text{HMX}} }} $$

(55)

where $M_{\text{HMX}}$ is the total mass of HMX present in the control volume $\varOmega_{ }$ prior to the start of chemical reactions.