Skip to main content
SpringerLink
Log in

On the propagation of decaying planar shock and blast waves through non-uniform channels

  • Original Article
  • Published:
Shock Waves Aims and scope Submit manuscript

Abstract

The propagation of planar decaying shock and blast waves in non-uniform channels is investigated with the use of a two-equation approximation of the generalized CCW theory. The effects of flow non-uniformity for the cases of an arbitrary strength decaying shock and blast wave in the strong shock limit are considered. Unlike the original CCW theory, the two-equation approximation takes into account the effects of initial temporal flow gradients in the flow properties behind the shock as the shock encounters an area change. A generalized order-of-magnitude analysis is carried out to analyze under which conditions the classical area–Mach (A–M) relation and two-equation approximation are valid given a time constant of decay for the flow properties behind the shock. It is shown that the two-equation approximation extends the applicability of the CCW theory to problems where flow non-uniformity behind the shock is orders of magnitude above that for appropriate use of the A–M relation. The behavior of the two-equation solution is presented for converging and diverging channels and compared against the A–M relation. It is shown that the second-order approximation and A–M relation have good agreement for converging geometries, such that the influence of flow non-uniformity behind the shock is negligible compared to the effects of changing area. Alternatively, the two-equation approximation is shown to be strongly dependent on the initial magnitude of flow non-uniformity in diverging geometries. Further, in diverging geometries, the inclusion of flow non-uniformity yields shock solutions that tend toward an acoustic wave faster than that predicted by the A–M relation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

a :

Sound speed (m/s)

A :

Channel cross-sectional area (m2)

\(h_0\) :

Starting channel height (m)

M :

Mach number

n :

Geometric index

p :

Pressure (N/m2)

\(Q_1\) :

\(\partial p / \partial t + \rho a \partial u / \partial t\) (kg/m s\(^3\))

\(Q_2\) :

\(\partial Q_1/ \partial t\) (kg/m s\(^4\))

t :

Time coordinate (s)

u :

Velocity (m/s)

W :

Shock wave velocity (m/s)

x :

Axial coordinate (m)

\(\alpha \) :

Coefficient function

\(\beta \) :

Coefficient function

\(\gamma \) :

Ratio of specific heats

\(\theta \) :

Channel half-angle

\(\rho \) :

Density (kg/m3)

\(\tau \) :

Time constant of flow property decay (s)

0:

Initial or undisturbed gas state

s:

Property on the shock

References

  1. Chester, W.: The quasi-cylindrical shock tube. Philos. Mag. 45(371), 1293–1301 (1954). https://doi.org/10.1080/14786441208561138

    Article  MathSciNet  MATH  Google Scholar 

  2. Chisnell, R.F.: The motion of a shock wave in a channel, with applications to cylindrical and spherical shock waves. J. Fluid Mech. 2(3), 286–298 (1957). https://doi.org/10.1017/S0022112057000130

    Article  MathSciNet  MATH  Google Scholar 

  3. Whitham, G.B.: On the propagation of shock waves through regions of non-uniform area or flow. J. Fluid Mech. 4(4), 337–360 (1958). https://doi.org/10.1017/S0022112058000495

    Article  MathSciNet  MATH  Google Scholar 

  4. Russell, D.A.: Shock-wave strengthening by area convergence. J. Fluid Mech. 27(2), 305–314 (1967). https://doi.org/10.1017/S0022112067000333

    Article  Google Scholar 

  5. Setchell, R.E., Storm, E., Sturtevant, B.: An investigation of shock strengthening in a conical convergent channel. J. Fluid Mech. 56(3), 505–522 (1972). https://doi.org/10.1017/S0022112072002484

    Article  MATH  Google Scholar 

  6. Nettleton, M.A.: Shock attenuation in a ‘gradual’ area expansion. J. Fluid Mech. 60(2), 209–5223 (1973). https://doi.org/10.1017/S0022112073000121

    Article  Google Scholar 

  7. Igra, O., Elperin, T., Falcovitz, J., Zmiri, B.: Shock wave interaction with area changes in ducts. Shock Waves 3(3), 233–238 (1994). https://doi.org/10.1007/BF01414717

    Article  MATH  Google Scholar 

  8. Whitham, G.B.: A new approach to problems of shock dynamics. Part I. Two dimensional problems. J. Fluid Mech. 2(2), 145–171 (1957). https://doi.org/10.1017/S002211205700004X

    Article  MathSciNet  MATH  Google Scholar 

  9. Ridoux, J., Lardjane, N., Monasse, L., Coulouvrat, F.: Comparison of geometrical shock dynamics and kinematic models for shock-wave propagation. Shock Waves 28(2), 401–416 (2017). https://doi.org/10.1007/s00193-017-0748-2

    Article  Google Scholar 

  10. Best, J.P.: A generalization of the theory of geometrical shock dynamics. Shock Waves 1(4), 251–273 (1991). https://doi.org/10.1007/BF01418882

    Article  MATH  Google Scholar 

  11. Kirkwood J.G., Bethe H.A.: The pressure wave produced by an underwater explosion. Office of Scientific Research and Development Report No. 588 (1942)

  12. Sharma, V.D., Ram, R., Sachdev, P.L.: Uniformly valid analytical solution to the problem of a decaying shock wave. J. Fluid Mech. 185, 153–170 (1987). https://doi.org/10.1017/S0022112087003124

    Article  MATH  Google Scholar 

  13. Sedov, L.I.: Similarity and Dimensional Methods in Mechanics, Chapter IV, “One-Dimensional Unsteady Motion of a Gas”. Academic Press, New York (1959). https://doi.org/10.1016/B978-1-4832-0088-0.50011-6

    Book  Google Scholar 

  14. Bethe, H.A., Fuchs, K., Hirschfelder, J.O., Magee, J.L., Peierls, R.E., von Neumann, J.: Blast waves. Los Alamos Scientific Laboratory Report LA-2000 (1947)

  15. Taylor, G.I.: The formation of a blast wave by a very intense explosion. Proc. R. Soc. Lond. A 201, 159–174 (1950). https://doi.org/10.1098/rspa.1950.0049

    Article  MATH  Google Scholar 

  16. Han, Z., Yin, X.: Shock Dynamics, Chapter 1, “Relation Between M and A for a Uniform Quiescent Gas Ahead of a Shock Wave”. Kluwer, Beijing (1993). https://doi.org/10.1007/978-94-017-2995-6_2

    Book  Google Scholar 

  17. Kamm J.R.: Evaluation of the Sedov–von Newman–Taylor blast wave solution. Los Alamos Scientific Laboratory Report LA-UR-00-6055 (2000)

  18. Takayama, K., Kleine, H., Grönig, H.: An experimental investigation of the stability of converging cylindrical shock waves in air. Exp. Fluids 5(5), 315–322 (1987). https://doi.org/10.1007/BF00277710

    Article  Google Scholar 

  19. Zha, Z., Si, T., Luo, X., Yang, J., Liu, C., Tan, D., Zou, L.: Parametric study of cylindrical converging shock waves generated based on shock dynamics theory. Phys. Fluids 24, 026101 (2012). https://doi.org/10.1063/1.3682376

    Article  Google Scholar 

  20. Liverts, M., Apazidis, N.: Limiting temperatures of spherical shock wave implosion. Phys. Rev. 116, 014501 (2016). https://doi.org/10.1103/PhysRevLett.116.014501

    Article  Google Scholar 

  21. Friedlander, F.G.: The diffraction of sound pulses I. Diffraction by a semi-infinite plane. Proc. R. Soc. A 186(1006), 322–343 (1946). https://doi.org/10.1098/rspa.1946.0046

    Article  MathSciNet  MATH  Google Scholar 

  22. Milton, B.E.: Mach reflection using ray-shock theory. AIAA J. 13(11), 1531–1533 (1975). https://doi.org/10.2514/3.60566

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Aerodynamics Research Center, Mechanical and Aerospace Engineering Department, University of Texas at Arlington, Arlington, TX, 76019, USA

    J. T. Peace & F. K. Lu

Authors
  1. J. T. Peace
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. K. Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. T. Peace.

Additional information

Communicated by D. Zeitoun and A. Higgins.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

An abridged version of this paper was presented at the 22nd International Shock Interaction Symposium, July 4–8, 2016, Glasgow, UK.

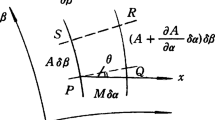
Appendix

Appendix

See Figs. 17, 18, 19, 20, 21, 22 and 23.

Fig. 17
figure 17

\(g(M_\mathrm {s})\) versus shock Mach number

Full size image
Fig. 18
figure 18

\(a_0 p_0 |f(M_\mathrm {s})|\) versus shock Mach number

Full size image
Fig. 19
figure 19

\(|\alpha _1(M_\mathrm {s})|\) versus shock Mach number

Full size image
Fig. 20
figure 20

\(|\alpha _2(M_\mathrm {s})|\) versus shock Mach number

Full size image
Fig. 21
figure 21

\(|\alpha _3(M_\mathrm {s})|/a_0 p_0\) versus shock Mach number

Full size image
Fig. 22
figure 22

\(|\alpha _4(M_\mathrm {s})|/a_0 p_0\) versus shock Mach number

Full size image
Fig. 23
figure 23

\(|\alpha _5(M_\mathrm {s})|/a_0 p_0\) versus shock Mach number

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peace, J.T., Lu, F.K. On the propagation of decaying planar shock and blast waves through non-uniform channels. Shock Waves 28, 1223–1237 (2018). https://doi.org/10.1007/s00193-018-0818-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00193-018-0818-0

Keywords

Search

Navigation