Diversity and mechanisms of economic evolution

Abstract

In the paper, we examine the relationship between the diversity of a competitive economy and the mechanisms that appear within economic development. We use the concept of transformation of the economic system to analyze innovation in the economy. A properly defined diversity function allows us to measure the diversity of the production system of a given economy as well as to relate the obtained value to certain properties of the mechanisms of economic evolution defined in the Hurwicz conceptual apparatus. We show that innovative mechanisms and eco-mechanisms can increase the diversity of the analyzed economic system. The conclusions are the results of mathematical theorems.

1 Introduction

Economic mechanisms understood as a set of rules and regularities governing the economic life play, along with innovations, entrepreneurship and competitiveness, a major role in Schumpeter’s approach to economic development (Schumpeter 1912, 1982). The concepts of innovation and economic mechanism and their importance in economic evolution are the subject of study in some subfields of economic theory, primarily the theory of economic development (Nelson and Winter 1982; Day 2007), theory of economic growth (Solow 1956; Aghion and Howitt 1992, 1998), competitiveness theory (Garud 1994; Bukowski et al. 2021), theory of entrepreneurship (Alchian 1950; Hessels and van Stel 2011), organizational theory (Aldrich 1999) and mechanism design theory (Lipieta and Malawski 2016; Lipieta and Ćwięczek 2020).

In his approach, Schumpeter (1950) assigned a special role to the mechanism clarifying the structure of the economic development process called creative destruction. Creative destruction, by Schumpeter, is the coexistence of two opposing processes: innovation resulting in the introduction of new commodities, new technologies and new organizational structures, etc., and processes of elimination of existing, outdated solutions. Thus, innovations are the result of some kinds of mechanisms, and the study of the mechanisms revealing within the evolution of the economy is essential for a comprehensive analysis of the Schumpeterian economic development.

The concept of diversity has been present in the theory of economic development from its beginnings (see Malerba 1992; Metcalfe 1994), however, there is no explicit definition of a diversity of the economy as a whole. The lack of a properly studied “theory of diversity” in the theory of economic development can be filled up by the contribution of Nehring and Puppe (2002). Their practical but strongly theoretically founded, definition of the diversity function for a collection of objects was adapted by Pliś (2020) to the case of the economic system. Having a properly defined value of diversity for the subsets of l-dimensional space of commodities, Pliś (2020) provided a definition of the diversity of a production system, as the value of diversity of the set of all production possibilities at a given stage of economic development. These production possibilities refer to the production plans available to the producers due to their state of knowledge and technological level at the time considered. Thanks to the operative definition of diversity, it was possible to study the causal relationship between the occurrence of innovation and the increase in the diversity of the economic system (Pliś 2020).

In this context, the paper aims at analyzing a relationship between some properties of economic mechanisms revealing within economic evolution, formalized by the use of mathematical apparatus borrowed from the theory of general equilibrium (Arrow and Debreu 1954; Mas-Colell et al. 1995), and the diversity of economic systems understood as in the paper by Pliś (2020).

The mathematical approach to mechanism design was initiated by Leonid Hurwicz (1960). Such an approach enables to formalize, compare and potentially drive economic processes to get desired goals. Hurwicz mechanism is a relational system (see Adamowicz and Zbierski 1997) consisted of a message space, a message correspondence and an outcome function (Hurwicz and Reiter 2006). Determining of an economic mechanism in the sense of Hurwicz begins with defining the so-called economic environment. The economic environment is a set of characteristics that determine individuals and firms as economic agents in the considered economic system. In any environment, economic agents, consciously or unconsciously, send signals about their market activities. The link between economic environments and the set of messages is described by the message correspondence. Formally, it assigns to every environment, hence indirectly to economic entities, the signals (information) that can be identified and analyzed by economic agents. These signals can be interpreted by agents and influence their actions in the future. Hence, to study the relationship between observable signals and market activities, in the full or partial access to information, makes sense. Therefore, the outcome function, which assigns to every message the outcome of activities of economic agents undertaken as a result of this message, is defined. The concept of Hurwicz mechanisms has been widely researched and used in many areas of life, above all, economics (for example Maskin and Riley 1984), medicine (see for example Roth et al. 2004), and logistics (for instance Abdulkadiroǧlu and Sönmez 2003).

When analyzing the agents’ behavior on non-equilibrium markets, the structure of information plays a central role. As we study macroeconomics mechanisms resulting from the specific behavior of market participants, our consideration can be seen as a part of the research on the microfoundations of macroeconomics (see for example: Weintraub 1979, van den Bergh and Gowdy 2003, Hoover 2010). In his classic book on microfoundations, Weintraub (1979) outlined the main paths to move economic analyses from mainstream micro to mainstream macro-models. Our approach can be classified as an example of what Weintraub called the Edgeworthian general interaction model (Weintraub 1979; Hurwicz et al. 1975), being “one of the various ways in which general equilibrium theory can be modified to provide a conceptual base for the formulation of macroeconomic concerns”. In our model the variety of mechanisms can be the source of economic diversity.

We extend the analysis of the diversity of the competitive economy (Section 3) initiated by Pliś (2020). By applying the concept of the Hurwicz mechanism, we formalize the relationship between the properties of the mechanism revealing within economic evolution and the diversity of the economic system under study. As a result, we prove that the increase of diversity of the economy is caused by innovative mechanisms (Theorem 1, Corollary 1). Moreover, we show that eco-innovation, and hence eco-mechanism connected with the process of creative destruction, can increase the diversity of the private ownership economy (Theorem 2, Corollary 7).

The remainder of the paper is organized as follows. Section 2 provides a brief literature review. In Section 3 we describe various transformations of the economic system and analyze associated changes in diversity. Section 4 indicates the relationship between diversity and the type of economic mechanism and illustrates the change of diversity connected with eco-innovation. Section 5 contains a discussion. The paper ends with a conclusion.

2 Literature review

In the book "Die Theorie der wirtschaftlichen Entwicklung" Joseph Schumpeter, for the first time, presented his theory of economic development. He distinguished the fundamental forms of economic life, identified innovations as well as the essential innovative changes, and pointed to the innovators-entrepreneurs as the major driving forces of the evolution of the economy (Schumpeter 1912). A few years later, Schumpeter explained the possible effects of innovative changes and defined a mechanism of creative destruction as the coexistence of two opposite processes: innovations resulting in the introduction of new commodities, new technologies, new organizational structures, etc., and the processes of elimination of the existing, outdated solutions (Schumpeter 1950).

In the early eighties of the XX century, the neoschumpeterian research program was initiated by the publication of the book by Richard R. Nelson and Sidney G. Winter (1982). Despite the significant development of Schumpeter’s ideas (see for example Freeman 1982, Dosi and Nelson 1994, Malerba and Orsenigo 1995, Witt 1996, Hanusch and Pyka 2007, Andersen 2009, Saviotti et al. 2009, Safarzyńska and van den Bergh 2010, Foster 2011, Cantner 2016 and Nelson 2016, Fontana et al. 2021), the qualitative changes resulting from creative destruction and the actions of innovators-entrepreneurs remain in the center of interest of this mainstream’s researchers.

At about the same time as the book (Nelson and Winter 1982) was published, Philippe Aghion and Peter Howitt studied creative destruction in the article "A Model of Growth Through Creative Destruction" (1992). It gave rise to the theory of the endogenous economic growth, and in the next years, many models of economic growth were created (Aghion and Howitt 1998; Acemoglu 2009; Aghion et al. 2015), as well as macroeconomic formal models (Dosi et al. 2010; Assenza et al. 2015; Almudi et al. 2020, Dawid et al. 2019; Almudi and Fatás-Villafranca 2021) focused on the quantitative properties of economic processes defined on the basis of Schumpeter’s premises.

The Hurwicz’s mechanism was first used as a modeling tool for evolutionary processes in a competitive economy by Lipieta and Malawski (2016), who identified two types of mechanisms: price and qualitative, which can occur within economic evolution. It enabled them to model two types of the economic life distinguished by Schumpeter i.e., circular flow and economic development. Based on the results of the paper (Lipieta and Malawski 2016), the model of economic evolution was defined and investigated (Lipieta and Lipieta 2017). The results of a comparative analysis of innovative and adopting mechanisms can be found in (Lipieta and Malawski 2018), while a study of the role of the imitative mechanism in economic evolution was presented in (Lipieta 2018). In the latter, a long-run equilibrium (see in Mas-Colell et al. 1995) mechanism was also defined and examined (see Lipieta and Lipieta 2021). Recently, a study on eco-mechanisms was presented (Lipieta and Malawski 2021), which showed that eco-mechanisms as a part of sustainable development, can result in equilibrium on real markets. There is also an analysis of such mechanisms that may result in an equilibrium in real and financial markets (Lipieta and Ćwięczek 2020) under certain natural assumptions, but different from those considered by Arrow and Debreu (1954).

Diversity, formalized in a number of different ways, is a term widely used in the evolutionary approach. Saviotti and Mani (1995) defined diversity as the number of distinguishable actors, activities, and objects required to characterize an economic system which analytically represents the qualitative change taking place in the economic system. Industrial diversity can be a source of future economic growth (Tisdell 1999). Diversity is considered in the context of innovation (Kwasnicki 2021) and stimulating the generation of diversity through innovation is the goal of technology policy (Metcalfe 1994). Dosi, Silverberg and Orsenigo (1988) noticed that diversity between firms consists of technological asymmetries, technological variety and behavioral diversity and is a fundamental and permanent feature of industrial environments undergoing technical change. A heterogeneous population (consisting of diverse elements or members) is crucial for any evolutionary model (Safarzyńska and van den Bergh 2010), but the importance of the notion of variety was confirmed by economists representing various approaches to economic analysis. In Romer’s contribution (1986, 1992a), the variety of technologies implies the diffusion of innovation and, consequently, an increase of the output variety of economic system, which is a necessary requirement for long-term world economic development (Saviotti 2002; Nelson et al. 2018; Pyka et al. 2020). In the literature on regional economic development related and unrelated variety is distinguished (Frenken et al. 2007): the former is concerned with the concentration of industries that present some form of similarity (Asheim et al. 2011; Boschma 2014), the latter concerns sectors that have no substantial complementary competences (Neffke et al. 2011; Content et al. 2016). Although the role of related and unrelated variety has not been definitively clarified, most studies show that regional economic systems need to diversify to grow (Content and Frenken 2016). In some more recent formal evolutionary studies, in which co-evolution is considered, the role of variety as a cause or a result of economic processes is also revealed. The reader can find the details in the papers by Fatás-Villafranca et al. (2009), Dosi et al. (1988), Almudi et al. (2020), and Almudi and Fatás-Villafranca (2021).

The concept of the diversity of a collection of objects owes its origin to ecology (for more on diversity in ecology see: Magurran 2013), where the discussion continues on how it should be measured. Many authors use the term in its colloquial (Abascal and Baldassarri 2020) or strict sense of heterogeneity, in which case different entropy indices are used (Frenken et al. 2007, Tomezsko et al. 2020). Weitzman (1992) defined a diversity function in which a value of diversity can be recursively obtained from the information about dissimilarity distance between any pair of objects in the set. Stirling (2007) suggested that no existing diversity indices are sufficient and proposed a heuristic in which he incorporated aggregations of subordinate properties called variety, disparity and dissimilarity to capture the essence of the notion.

We owe the proper definition of diversity for any set of objects endowed with different features to Nehring and Puppe. In 2002 they presented a seminal paper “A theory of diversity” (Nehring and Puppe 2002) with an original “multi-attribute” approach to diversity for a finite set of objects. This concept was further developed in a series of articles (Nehring and Puppe 2003, 2004a, 2004b, 2008, 2009). Nehring and Puppe generalized in fact the theory of products by Lancaster (1966b), in which he departed from the traditional approach that goods are the direct objects of utility, and instead assumed that it is the properties or characteristics of the goods from which utility is derived. Lancaster not only assumed that utility or preference orderings rank collections of characteristics (Lancaster 1966b) but also that a producer is ultimately selling characteristics collections rather than goods (Lancaster1966a). His approach was later used by Berry (1994) to consider methods for estimating product differentiation models in the presence of unobserved product characteristics. Since taking preferences over characteristics collections, the introduction of new goods varieties does not require new preferences, what Lancaster noticed, when constructing an index of quality change (Lancaster 1977).

The diversity function defined by Nehring and Puppe (2002) was used by Pliś (2020) to analyze the relationship between innovation and the diversity of the production system under evolution. Pliś applied the concept of a diversity function to the product and prices space R^l, and measured the diversity value of the firms’ input-output possibility sets characterized by different attributes. It enabled to define the diversity of the production system as a whole and to analyze the technological change in terms of diversity.

3 Diversity and transformations of the economy

In this section, we provide a brief overview of how the diversity function can characterize different types of economic transformation. We reformulate and complete the results presented by Pliś (2020).

3.1 A model of economy

There are n firms and m consumers operating on the market of l-goods:

$$\mathbf{R}^{l}=\{(x_{1},x_{2},...):x_{k}\in \mathbb{R},\forall_{k>l}\; x_{k}=0\},$$

where prices of commodities are given by a vector p ∈ R^l. Every firm of the set B = {b¹,..., bⁿ} is given by a production set $Y^{b^{j}}$ of possible production plans (input-output vectors), according to the mapping

$$y:B\ni b^{j}\mapsto Y^{b^{j}}\subset \mathbf{R}^{l}.$$

At the given prices, every producer chooses a production plan to realize from his/her set of input-output possibilities.

A two-range relational system $P=(B,\mathbf{R}^{l},\,y,\,p)$ is called a production system.

Every consumer aⁱ of the set H = {a¹, ..., a^m} is characterized by

• his/her preference relation (i.e. a reflexive, transitive and complete relation $\preceq _{a^{i}}$ in $\mathbf{R}^{l}_{+}$) given by

  $$\varepsilon: H\ni a^{i}\mapsto \preceq_{a^{i}}\subset \mathbf{R}^{l}_{+}\times \mathbf{R}^{l}_{+};$$

• a vector ωⁱ of his/her initial endowments due to the mapping

  $$\epsilon: H\ni a^{i}\mapsto\omega^{i}\in \mathbf{R}^{l}_{+}.$$

A three-range relational system $C=(H,\mathbf{R}^{l},\epsilon,\varepsilon ,p)$is called a consumption system.

Firms are owned by consumers, whose shares profits are given by a mapping $\theta :H\times B\rightarrow [0,1]$ satisfying

$$\sum\limits_{i=1}^{m}\theta (a^{i},b^{j})=1,\; j=1,...,n.$$

The budget set of a consumer aⁱ ∈ H has the form

$${\upbeta}_{a^{i}}(p):=\{x\in \mathbf{R}^{l}_{+}:p\cdot x\leq p\cdot \omega^{i}+\sum\limits_{j=1}^{n}\theta (a^{i},b^{j})(p\cdot y^{b^{j}})\}.$$

Every consumer realizes his/her the best (i.e. the most preferred) consumption plan on his/her budget set, if only such a plan exists.

Let a price vector p R^l be given.

Definition 1

A relational system $\mathcal {E}=(\mathbf{R}^{l},P,C,\theta , \omega )$, where

• $P=(B,\mathbf{R}^{l},y,p)$is a production system,

• $C=(H,\mathbf{R}^{l},\epsilon,\varepsilon ,p)$is a consumption system,

• $\omega ={\sum }_{i=1}^{m}\omega ^{i}$

is called the economy.

For more details on how the economy works, see for example Lipieta and Malawski (2018) and Pliś (2020).

3.2 Transformations of the economy (Lipieta and Lipieta 2017)

Let price vectors $p,\, p^{\prime }\in \mathbf{R}^{l}$ be given. Assume that $\mathcal {E}=(\mathbf{R}^{l},P,C,\theta , \omega )$ is an economy considered at time t ∈{1,2,...}. Let$P=(B,\mathbf{R}^{l},y,p)$be the production system and $C=(H,\mathbf{R}^{l},\epsilon,\varepsilon ,p)$- the consumption system of the economy $\mathcal {E}$.

Assume that at time $t^{\prime }\in \{2,3,...\}$, $t<t^{\prime }$ the economy $\mathcal E$ is transformed into the economy ${E^{\prime }}=({R}^{l},P^{\prime },C^{\prime }, \theta ^{\prime }, \omega ^{\prime })$, in such a way that the components of the production system P are transformed into the components of production system $P^{\prime }=(B^{\prime },\mathbf{R}^{l},y^{\prime },p^{\prime })$ and the components of the consumption system C are transformed into the components of $C^{\prime }=(H^{\prime },\mathbf{R}^{l},\epsilon ^{\prime },\varepsilon ^{\prime },p^{\prime })$. We denote the correlation between the two economies by $\mathcal {E}\subset \mathcal {E}^{\prime }$ and refer to $\mathcal E^{\prime }$ as a transformation of the economy $\mathcal E$. We write $P\subset P^{\prime }$ and call $P^{\prime }$ a transformation of P and, analogically, $C^{\prime }$ is called a transformation of C with notation $C\subset C^{\prime }$.

Economic transformations connected with changes in the production system are of our particular interest. Let $B=B^{\prime }$, $H=H^{\prime }$. Let Y^b be closed for every b ∈ B. Denote:

$$Y:=\bigcup_{b\in B} Y^{b},\;\;\;\;\;\;\;\;\;\;\; Y^{\prime}:=\bigcup_{b\in B} Y^{{\prime}b}.$$

In case of introducing a new commodity or new technology to the economy, we have the following definition.

Definition 2

A production system $P^{\prime }$ is called an innovative transformation of P, shortly $P\subset _{in} P^{\prime }$, if there exists at least one innovative production plan in $P^{\prime }$ with respect to P, i.e.

$$there\, exists\; b\in B \; and\; y^{{\prime}b}\in Y^{{\prime}b} \; such \, that\; y^{{\prime}b}\notin Y.$$

(1)

The definition above is equivalent to the condition $Y^{\prime }\backslash Y\neq \emptyset$. We refer to a producer b ∈ B, who realizes an input-output vector $y^{{\prime }b}\in Y^{{\prime }b}\backslash Y$ as an innovator. We do not assume that $Y\subset Y^{\prime }$ in the case of innovative transformation, therefore, innovative transformation allows for some kind of destruction in the production system, which we consider below.

If there is no producer-innovator in $P^{\prime }$, then $Y^{\prime }\subset Y$ and we have the following.

Definition 3

A production system $P^{\prime }$ is called an imitative transformation of P, shortly $P\subset _{im} P^{\prime }$, if $P^{\prime }$ is a transformation of P but not an innovative one.

For $Y=Y^{\prime }$, we deal with a special case of an imitative transformation.

Definition 4

An imitative transformation $P^{\prime }$ of a production system P is called its cumulative transformation and denoted shortly by $P\subset _{c} P^{\prime }$, if for every producer b ∈ B:

• (i) the previously available technologies remain so, i.e. $Y^{b}\subset Y^{{\prime }b}$;

• (ii) no producer’s profit decreases, i.e. for all y^b ∈ Y^b there exists $y^{{\prime }b}\in Y^{{\prime }b}$ such that $p\cdot y^{b}\leq p^{\prime }\cdot y^{{\prime }b}.$

Regardless of whether we deal with imitative or innovative transformation, the production system may be damaged in the process of evolution.

Definition 5

A production system $P^{\prime }$ is called a destructive transformation of the system P, shortly $P\subset _{d} P^{\prime }$, if some commodity disappears from the market, some technology is used no longer (i.e. $Y\backslash Y^{\prime }\neq \emptyset$) or an activity of some producer ceases (i.e. for some b ∈ B such that $Y\,^{b}\neq\{0\}$there is $Y^{{\prime }b}=\{0\}$).

A special case of an innovative transformation is creative destruction of a production system.

Definition 6

A transformation $P^{\prime }$ of a production system P is called its creative destruction and denoted by $P\subset _{cd} P^{\prime }$, if $P^{\prime }$ is both innovative and destructive transformation of P.

3.3 A function of diversity

We follow Nehring and Puppe (2002) in defining a diversity value of a set as the total weight of all attributes realized by this set. We however assume that in the case of an infinite set of objects, there is only a finite family of relevant attributes considered.

Let X be a non-empty set and let $2^{\mathbf x}\;:=\;\left\{S\;:\;\subset\;\mathbf X\right\}$ be a family of subsets of X. We call a subset A ⊂ X an attribute. An object x ∈ X possesses attribute A, if x ∈ A. A set S ⊂ X realizes attribute A, if there is x ∈ S such that x possesses attribute A, i.e. $A\;\cap\;S\neq\emptyset$. An attribute A can be seen as a set of such objects that possess some family of features on an exclusive basis.

To every attribute A ⊂ X we assign a number of its relative importance λ_A ≥ 0 and call it the weight of the attribute A. The family of relevant attributes, i.e. the family of attributes with positive weights, is denoted by

$${\Lambda}:=\{ A\subset \mathbf X: \lambda_ A\neq 0\}.$$

If X is finite, there are as many as 2^#X − 1 potentially relevant attributes. If X is an infinite set, then we assume that the family of relevant attributes is finite, i.e $\#{\Lambda } <+\infty$.

We adapt the following definition from Nehring and Puppe (2002).

Definition 7

A function $v:2^{\mathbf {X}}\rightarrow \mathbb {R}$ is called a diversity function, if there is an attribute weighting function $\lambda :2^{\mathbf {X}} \ni A\mapsto \lambda _{A}\in \mathbb {R}_{+}$ such that $\#{\Lambda }=\#\{ A\subset \mathbf X: \lambda _ A> 0\} <+\infty$ and for all S ⊂ X

$$v(S)={\sum}_{A\subset \mathbf X: A\cap S\neq\emptyset}\; \lambda_{A},$$

(2)

where $v\left(\varnothing\right)\;:=0$.

One can observe that each attribute occurs at most once in the sum (2). Each element x ∈ X contributes to the diversity of a set S weights of all attributes not possessed by any already existing objects in S (Nehring and Puppe 2002).

Example 1

Consider a grocery and a set of products

X = {a glass bottle of spring water, a plastic bottle of sparkling water, a plastic bottle of spring water, a glass bottle of orange juice}.

In this case, a possible attribute may be for example:

• “containing spring water” connected to the set A₁ = {a plastic bottle of spring water, a glass bottle of spring water},

• “having a glass container” corresponding to A₂ = {a glass bottle of spring water, a glass bottle of orange juice},

• “containing something different from water”, i.e. A₃ = {a glass bottle of orange juice},

• “containing water”, “containing sparkling water”, etc.

Assume that there is an eco-consumer who chooses glass cover instead of plastic one. If also such a consumer prefers spring water to anything else, then “containing spring water” and “having a glass container” can be considered as the only relevant attributes. Assign weights equal to 1 to each of them and calculate

• $v(\{ \textrm {a glass bottle of orange juice}\})=\lambda_{A_{2}}= 1$; 

• $v(\{\textrm {a plastic bottle of spring water}\})=\lambda _{A_{1}}= 1$;

• $v(\{\textrm {a glass bottle of orange juice, a plastic bottle of spring water}\})=v(\{\textrm {a glass bottle of spring water}\}) = \lambda _{A_{1}}+\lambda _{A_{2}}= 2$;

• $v(\{\textrm{a plastic bottle of sparkling water}\}=0, \, etc$

.

Remark 1

Nehring and Puppe (2002) Let $v:2^{\mathbf X}\rightarrow \mathbb {R}$ be a diversity function. Then

• $\mathcal v$ determines uniquely an underlying attribute weighing function $\lambda :2^{\mathbf X}\rightarrow \mathbb {R}_{+}$;

• $\mathcal v$ is monotonic, i.e. if S ⊂ T, then $v\left(S\right)\leq v\left(T\right)$, for S, T ⊂X;

• a marginal diversity decreases in the size of the set, i.e. $v\left (S\cup \{x\}\right )-v(S)\geq v\left (T\cup \{x\}\right )-v(T)$ for S, T ⊂X, S ⊂ T, x ∈X.

A function of diversity used in a model of economy

Let $\mathcal {E}=(\mathbf{R}^{l},P,C,\theta , \omega )$ be an economy at time t. Consider a diversity function $v:2^{\mathbf{R}^{l}}\rightarrow \mathbb {R}$ with a (finite) family of relevant attributes Λ.

We refer to the diversity value of the set $Y:=\bigcup _{b\in B} Y^{b}$ as the diversity of the production system $P=(B,\mathbf{R}^{l},y,p)$. The diversity of the production system depends only on the form of a given family of relevant attributes.

How do various transformations of the production system affect its diversity?

Let ${E^{\prime }}=({R}^{l},P^{\prime },C^{\prime }, \theta ^{\prime }, \omega ^{\prime })$ be a transformation of $\mathcal {E}$ at time $t^{\prime }$ ($t<t^{\prime }$). From the monotonicity of a diversity function, we have the following (Pliś 2020).

Proposition 1

Without innovation diversity of the production system does not grow (the occurrence of innovation is a necessary condition for an increase of diversity of a production system), i.e. if $v(Y) < v(Y^{\prime })$, then $P\subset _{in} P^{\prime }$.

The above can also be reformulated in the following way.

Remark 2

In case of an imitative transformation, a diversity value of a production system does not rise, i.e. if $P\subset _{im} P^{\prime }$, then $v(Y) \geq v(Y^{\prime })$.

For $Y=Y^{\prime }$, we have the following conclusion.

Remark 3

In a cumulative transformation, a diversity value of a production system does not change, i.e. if $P\subset _{c}P^{\prime }$, then $v(Y) = v(Y^{\prime }).$

Below, we note the connection between the loss of diversity and a destructive transformation of the production system.

Remark 4

Let $P\subset _{in} P^{\prime }$. If there is a loss of diversity in the production system, then the transformation of the production system is destructive, i.e. if $v(Y^{\prime }) < v(Y)$, then $P\subset _{d} P^{\prime }$.

Is the reverse theorem true? Does destruction always entail a loss of diversity? What is the relationship between creative destruction and diversity?

Definition 8

Let $P\subset _{cd} P^{\prime }$ and let $v:2^{\mathbf{R}^{l}}\rightarrow \mathbb {R}$ be a diversity function with a family of relevant attributes $\Lambda\;=\;\left\{A\;\subset\mathbf X\;:\;\lambda_A>0\right\}$ such that $\#{\Lambda } <+\infty$. We call a production system $P^{\prime }$ the ${v}\textbf {-creative destruction}$ of P, shortly $P\subset _{v} P^{\prime }$, if for every $A\;\in\Lambda$ the following condition is satisfied

$$if \; Y\cap A\neq \emptyset ,\; then \; Y^{\prime}\cap A\neq \emptyset.$$

(3)

Condition (3) means that for a given Λ any attribute which is relevant in P, remains so in $P^{\prime }$.

In the case of the $\mathcal v$-creative destruction of the production system, all the relevant attributes are preserved during the innovative change. As an example of such an attribute consider “being a tool for washing”. Although the washboard is no longer used in Europe, the attribute “being a tool for washing” has been taken over by the washing machine, and as such, it is stored in the economic system.

The $\mathcal v$-creative destruction of a production system transfers the essential features and valuable functions of the disappearing products or technologies to the new ones during the evolution of the economic system. One can argue then, that the $\mathcal v$-creative destruction is actually creative destruction as Schumpeter understood it.

Let a diversity function $v:2^{\mathbf{R}^{l}}\rightarrow \mathbb {R}$ with a finite family Λ of relevant attributes be given.

Remark 5

In the $\mathcal v$-creative destruction, diversity value of a production system does not decrease, i.e. if $P\subset _{v} P^{\prime }$, then $v(Y) \leq v(Y^{\prime }).$

In the case of the $\mathcal v$-creative destruction, if the attribute connected with an innovative production plan is both: relevant and new, we deal with an increase of the diversity value of the production system.

Definition 9

(compare to Nehring and Puppe 2002) An input-output vector $y^{\prime }\in Y^{\prime }$ is a relevantly innovative production plan, if

$$d(y^{\prime},Y):=v(Y\cup \{y^{\prime}\})-v(Y)>0.$$

Remark 6

If there is a relevantly innovative production plan in the $\mathcal v$-creative destruction $P^{\prime }$ of P, then $v(Y)<v(Y^{\prime })$.

4 Mechanisms and diversity

In the present section, we focus on the analysis of a diversity of mechanisms that may occur within economic evolution and we study the relationship between a diversity of mechanisms and an innovativeness of the economic system.

Economic evolution can be modeled as a composition of a finite or a countable number of adjustment processes. We use the model defined in (Lipieta and Lipieta 2017) and examined in (Lipieta and Malawski 2021), while the source definition of the adjustment process can be found in (Hurwicz 1986). As in the case of Schumpeter’s theory, economic mechanisms play a major role in this model. In the presented approach, the economic mechanism is understood as a mathematical structure defined by the conceptual apparatus of Leonid Hurwicz (Hurwicz 1960; Hurwicz and Reiter 2006). Below, for the purposes of our research, we recall the formal definition of the economic mechanism borrowed from (Hurwicz and Reiter 2006).

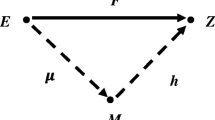
Let E, M and Z be non-empty sets. Assume that the set E consists of the considered characteristics of economic agents, M is the set of all signals (messages) sent by economic agents in the market, which can be observed and analyzed by other economic agents, and Z consists of the outcomes of activities undertaken as a result of knowledge (full or partial) on the messages sent.

Definition 10

A relational system Γ = (M, μ, h), where:

• $\mu : E \rightarrow M$ is a message correspondence which to every economic environment assigns the messages (signals) sent by market participants,

• $h: M \rightarrow Z$ is an outcome function which to every message assigns the outcomes of activities undertaken as the result of the knowledge on this message,

is called the economic mechanism determined in the set of environments E with messages from the set M and the outcomes from the set Z.

From now on, the structure defined above will be briefly referred to as the Hurwicz mechanism (compare to Hurwicz and Reiter 2006; Lipieta and Malawski 2021). In some cases, the environment can be identified with the economic structure, while the properties of the outcomes and the system of exchanging messages determine the properties of the mechanism. If the outcomes of the mechanism are observed in the economic structure determined by the set of mechanism’s environments, then the mechanism is said to be static; if they are noted in the transformation of the economic system, the mechanism is said to be dynamic. Some properties of mechanisms in the private ownership economy can be found in Lipieta and Malawski (2021).

We will analyze dynamic mechanisms in which the environment with the price vector p can be identified with the private ownership economy at time t, while the outcomes are obtained at time $t^{\prime }$, in such a transformation of this economy in which the consumption system is the same as at the time t. Let us notice that in this approach the agents have full access to information.

Consider an economy $\mathcal {E}$ in which producers and consumers operate on the market in a period t (t > 0). The last means that agents’ characteristics listed in Definition 1 do not change during this period. Thus, the economic environment e^k(t) of every agent k ∈ K = B ∪ H is of the form:

$$e^{k}(t)=\left( Y^{k} (t),X^{k} (t),\varepsilon_{t} (k),\epsilon_{t} (k),\theta_{t} (k,\cdot)\right),$$

(4)

where

$$Y^{k}(t)=\left\{\begin{array}{cc} Y^{k}, & k \in B \\ \{0 \}, & k \notin B \end{array},\right.\;\;\;\;\;\; X^{k}(t)=\left\{\begin{array}{cc} X^{k}, & k \in H\\ \{0 \}, & k \notin H \end{array},\right.$$

$$\varepsilon_{t} (k)=\left\{\begin{array}{cc}\preceq_{k}, & k \in H \\ \emptyset,& k \notin H \end{array},\right.\;\;\;\;\;\;\; \epsilon_{t} (k)= \left\{\begin{array}{cc}\omega^{k}, & k \in H\\ 0 \in \mathbb{R}^{l}, & k \notin H \end{array}\right.$$

and the mapping $\theta _{t}: K\times K \rightarrow [0,1]$ is such that

$$\left\{\begin{array}{cc} \theta_{t} (k,\cdot)\equiv 0, & k \notin H \\ \theta_{t} (\cdot, k)\equiv 0, & k \notin B\\ \theta_{t}(a,b)= \theta(a,b), & a \in H, b \in B \end{array}.\right.$$

According to the notion above, the set of agent’s k ∈ K environments in the period t has the following form:

$$E^{k}(t)=\{e^{k}(t): e^{k}(t) \in 2^{\mathbf{R}^{l}}\times \mathbf{R}^{l} \times 2^{\mathbf{R}^{l}} \times \mathbf{R}^{l} \times \mathcal F \}$$

where $\mathcal F$ is the set of all functions defined in the set K × K with values in the interval [0,1].

Denote the number of economic agents in the economy $\mathcal {E}$ by κ (i.e., κ = #K). Then

$$E(t)=E^{k_{1}}(t)\times {\ldots} \times E^{k_{\kappa}}(t)$$

(5)

is the set of environments in the period t.

The plans of actions realized at time t can be interpreted as a feasible response to the prices given by a vector p(t). Therefore, for each k ∈ K, the environment e^k(t) determines the set of agent’s k messages at t, also dependent on the prices of commodities at t. Thus, if the agent k as a consumer realizes the plan x^k(t) ∈ X^k(t) and as a producer he/she realizes the input-output vector y^k(t) ∈ Y^k(t), then his/her message at time t at prices p(t) has the form:

$$m^{k}\left( e(t) \right)=\left( p(t),y^{k}(t),x^{k}(t) \right) .$$

(6)

Potentially, for a given price vector p(t), the agent k can choose from more than one message of the form (6). The sequence $m^{k}\left (e(t)\right )$ is said to be a feasible message at the time t. It consists of the price vector, the agent’s k plan of action as a producer and his/her plan of action as a consumer. In the message $m^{k}\left (e(t)\right )$, we can see the plans of action that agent k realizes at time t under the prices p(t) in the environment (4). The set of feasible messages at the time t is assumed to be non-empty and denoted by $M^{k}\left (e(t)\right )$.

The environment e(t) determines the set of the messages:

$$M\left( e(t)\right)= M^{k_{1}}\left( e(t)\right)\times {\ldots} \times M^{k_{\kappa}}\left( e(t)\right),$$

(7)

while every message $m\left (e(t)\right ) \in M\left (e(t)\right )$ is of the form:

$$m\left( e(t)\right)=\left( \left( (p(t),y^{k_{1}}(t),x^{k_{1}}(t)\right), \ldots, \left( p(t),y^{k_{\kappa}}(t),x^{k_{\kappa}}(t)\right)\right).$$

(8)

Let

$$M(t)=\bigcup_{e(t) \in E(t)} M\left( e(t)\right).$$

(9)

A correspondence $\mu : E(t) \rightarrow M(t)$ to every environment e(t) ∈ E(t) assigns a set $M\left (e(t)\right )$ of feasible messages send at time t in the environment e(t).

Let E(t) be the set of environments of the form (5). Suppose that the environment e(t) ∈ E(t) of the form (4) with the price vector p(t) is identified with the economy $\mathcal {E}$. Consider a mapping $Q: \mathbf{R}^{l} \rightarrow \mathbf{R}^{l}.$

Theorem 1

If, for every k ∈ K and y^k ∈ Y^k, plan Q(y^k) is feasible at time $t^{\prime }$, then the mapping Q determines the Hurwicz mechanism, which in the period $t^{\prime }$, $t^{\prime }>t$ results in such a transformation $\mathcal {E}^{\prime }$ of the economy $\mathcal {E}$ in which ${C}^{\prime }={C}$ and one of the following is satisfied $P \subset _{in} P^{\prime }$ or $P \subset _{im} P^{\prime }$.

Proof

To prove the theorem, it is necessary to determine components of the mechanism. We put

• $\mu \left (e(t)\right )=M\left (e(t)\right )$ for every e(t) ∈ E(t),

• $Z=\{(x^{k_{1}}(t^{\prime }), \ldots , x^{k_{\kappa }}(t^{\prime })), (y^{k_{1}}(t^{\prime }), \ldots , y^{k_{\kappa }}(t^{\prime })):\forall k \in K:x^{k}(t^{\prime }) \in X^{k}(t^{\prime }) \wedge y^{k}(t^{\prime }) \in Y^{k}(t^{\prime }) \},$

• $h:M(t) \rightarrow Z$

  $$h\left( m\left( e(t)\right)\right)=h\left( \left( (p(t),y^{k_{1}}(t),x^{k_{1}}(t)\right), {\ldots} \left( p(t),y^{k_{\kappa}}(t),x^{k_{\kappa}}(t)\right)\right)=$$
  $$=\left( \left( x^{k_{1}}(t^{\prime}),\ldots, x^{k_{\kappa}}(t^{\prime})\right), \left( y^{k_{1}}(t^{\prime}), \ldots, y^{k_{\kappa}}(t^{\prime})\right)\right),$$

  where $x^{k}(t^{\prime })=x^{k}(t)$ and $y^{k}(t^{\prime })=Q(y^{k}(t))$ for every k ∈ K.

To end the proof it is necessary to define the components of economy $\mathcal {E}^{\prime }$. Put $H^{\prime }=H$, $B^{\prime }=B$ as well as

• $Y^{{\prime }b}=Q(Y^{b}(t)),$ for every b ∈ B,

• $X^{{\prime }a}=X^{a}(t)$, for every a ∈ H,

• $\varepsilon ^{\prime } =\varepsilon ,$

• $\epsilon ^{\prime }=\epsilon ,$

• $\theta ^{\prime }=\theta .$

The mechanism Γ = (M,μ,h) is the dynamic mechanism. □

It is easy to see that (see also Lipieta and Malawski 2021), that:

• if Q(Y (t)) ⊂ Y (t), then $P\subset _{im} P^{\prime }$;

• if $P\subset _{im} P^{\prime }$ and for every k ∈ K, Y^k(t) ⊂ Q(Y^k(t)), then $P\subset _{c} P^{\prime }$;

• if there exists k ∈ K and y^k(t) ∈ Y^k(t) such that Q(y^k(t))∉Y (t), then $P\subset _{in} P^{\prime }$;

• if there exists k ∈ K and y^k(t) ∈ Y^k(t) such that y^k(t)∉Q(Y (t)), then $P\subset _{d} P^{\prime }.$

Let us recall that the type of mechanism depends on the type of transformation of the economy (i.e. innovative, imitative, etc.; see Lipieta and Malawski 2021). However, if ${C}^{\prime }={C},$ the type of mechanism depends on the type of transformation of the production system. Thus, for mechanisms constructed in the proof of Theorem 1 we get the following :

• $P\subset _{im} P^{\prime } \Leftrightarrow$ mechanism Γ is imitative,

• $P\subset _{in} P^{\prime } \Leftrightarrow$ mechanism Γ is innovative,

• $P\subset _{c} P^{\prime }\Leftrightarrow$ mechanism Γ is cumulative,

• $P\subset _{in} P^{\prime }$ and $P\subset _{d} P^{\prime }\Leftrightarrow$ mechanism Γ is the creative destruction.

Corollary 1

Let Γ = (M, μ, h) be the dynamic mechanism constructed in the proof of Theorem 1. Then in the case of

• an imitative Γ a diversity value of the production system does not rise;

• an innovative Γ a diversity value of the production system does not fall;

• a cumulative Γ a diversity value of the production system does not change;

• Γ being creative destruction any change in a diversity value is possible.

Let us notice that due to the fact that there are many mappings Q that could determine a mechanism considered in Theorem 1, we face with the variety of the mechanisms which would result in a transformation of the economy $\mathcal {E}$.

4.1 Eco-innovation

Suppose in addition that there is a harmful commodity in the economy $\mathcal {E}$. Without loss of generality, we can assume that it is the first commodity. If consumer k is an eco-consumer, then X^k ⊂ V where

$$V = \{x=(x_{1}, x_{2}, \ldots, x_{l},0, \ldots) \in \mathbf{R}^{l}: x_{1}=0\}.$$

(10)

Eco-consumers do not want to consume harmful or obsolete commodities, and they also require producers to eliminate such commodities from their manufacturing processes. If each consumer is an eco-consumer, i.e.

$$\forall a \in H: X^{a} \subset V,$$

(11)

then V is a subspace of R^l without the first commodity, and therefore it is the space of eco-bundles.

If the assumption (11) is satisfied, then it is reasonable to model the economic mechanism in which in the period $t^{\prime }$ the first commodity will be eliminated from production processes too, i.e,

$$\forall b \in B: Y^{{\prime}b} \subset V,$$

(12)

and also the condition adequate to (11) is satisfied in the economy $\mathcal {E}^{\prime }.$ In this context, under the previous notation and assumptions, the following is presented:

Theorem 2

Let $\mathcal {E}$ be a private ownership economy with eco-consumers satisfying condition (11). There exists a Hurwicz mechanism which in a period $t^{\prime }$ results in such a transformation $\mathcal {E}^{\prime }$ of the economy $\mathcal {E}$ in which ${C}^{\prime }={C}$ and production sets from the system ${P}^{\prime }$ satisfy condition (12).

Proof

The proof goes in the same way as the proof of Theorem 1. However, to have the condition (12) satisfied we should precise a formula of mapping Q. Let $g:\mathbf{R}^{l} \rightarrow \mathbf{R},$ g(x₁,…,x_l) = x₁. There exist a vector q ∈R^l satisfying g(q) = 1. Putting $Q:\mathbf{R}^{l} \rightarrow V \subset \mathbf{R}^{l}$, Q(x) = x − g(x)q we get the result, since Q is a projection into V (see Cheney 1966). □

If there exists k ∈ K and y^k(t) ∈ Y^k(t) such that Q(y^k(t))∉Y (t), then the mechanism considered in Theorem 2 results in a technological eco-innovation, namely the elimination of a harmful commodity from the producers’ processes. Then that mechanism is called eco-innovative (compare to Lipieta and Malawski 2021).

Let a diversity function $v:2^{\mathbf{R}^{l}}\rightarrow \mathbb {R}$ with a finite family Λ of relevant attributes be given. Assume that we are dealing with a process of a v-creative destruction. One can see that “not being a harmful commodity” is in fact an attribute connected with the set V ⊂ R^l defined by (10). We refer to an innovative production plan y ∈ V as an eco-innovation. Assume that V ∈ Λ, i.e. being an eco-innovation is a relevant attribute with weight λ_V > 0. Then, due to Remark 6, we have the following observation.

Remark 7

In the case of the $\mathcal v$-creative destruction, eco-innovation increases the diversity of the production system.

5 Discussion

In common language, diversity is “the condition of having or being composed of differing elements” (https://www.merriamwebster.com/dictionary/diversity), whereas variety is understood as “the quality or state of having different forms or types” (https://www.merriamwebster.com/dictionary/variety). L. Hurwicz in his early papers (1972, 1973) pointed out that the variety of economic processes, outcomes and institutions is so extremely high that there is a need to formalize many objects in the same framework, to make the economic analysis more feasible. Although the study of variety in economics was not at the core of his interest, Hurwicz provided examples of the importance of variety, and thus also diversity, in economic analysis. Some of Hurwicz’s results on designing institutional mechanisms also can be viewed as a kind of macroeconomic analysis based on microfoundations (see for example Hurwicz et al. 1975).

The potential emergence, disappearance, and dynamics of diversity in an economic system are of keen interest to the evolutionary approach in economics. Fatás-Villafranca et al. (2009), in their model of consumption patterns, observed the “Dynamic Diversity” regime, that is the persistence of consumption patterns over time in the heterogeneous society. In such a case, for some values of the parameters, no social group is disappearing and there is a continuous flow of consumers who modify their lifestyles by passing from one social group to another. In their two-sector model, Almudi et al. (2020) characterized alternative institutional systems by the properties of the generative stochastic structure Beta distribution. As every new firm randomly derives its understanding-cognitive radius from a Beta distribution with some positive parameters, it was possible to analyze the influence of skewness of Beta on the probability of technological overshooting (represented by the probability of the system’s collapse). A higher skew (a right-tailed Beta-distribution) tends to generate firms with a low understanding radius (low absorptive capabilities), and consequently, it produces a higher probability of collapse.

Our understanding of diversity, based on the definition of Nehring and Puppe (2002) is slightly different that those used above. According to the definition of diversity function (Definition 7) and the whole Section 3.3 what decides about the value of diversity of a production system is the choice of the family of relevant attributes together with their weights. The relevant attribute may be of many forms, but if it is connected to innovation, the diversity of the modified production system increases (Theorem 1, Corollary 1). This can be caused, for example, by the pro-ecological attitude of consumers (Theorem 2, Remark 7).

The approach to diversity presented by Nehring and Puppe (2002) (and applied by us to the production system of a given economy) is very general. And while it differs from those used by Fatás-Villafranca et al. (2009), Almudi et al. (2020) or Almudi and Fatás-Villafranca (2021), it seems to complement each of them. The “Dynamic Diversity” regime observed by Fatás-Villafranca et al. (2009), can be seen as the persistence of attributes of the type “being a member of a given social group”. It is also possible to characterize alternative institutional systems in two-sector production model of Almudi et al. (2020) by the family of relevant attributes, but it would be much more difficult (or even impossible) to obtain their calculation results.

We showed that it is possible to implement such mechanisms which result in an increase of the production system’s diversity. But that diversity’s increase is an effect of the behavior of producers (among which there is at least one innovator) and consumers (who have a pro-ecological attitude (see assumption (11))). Combing the results obtained in the paper with the results of Pliś (2020) we showed that the increase in diversity is caused by the introduction of relevant innovations, including eco-innovations desired by consumers. Therefore we can conclude that in our model and consequently in the models presented by Lipieta and Lipieta (2017), economic development as well as the sustainable development do not appear, if the diversity of the competitive economy does not increase. Thus, the dynamics of diversity is a determinant of both: economic development and sustainable development.

6 Conclusions

Summarizing: the concepts of diversity, economic transformation and economic mechanism are closely connected. In the model presented, an economic mechanism determines a transformation of an initial economy. If the mechanism is innovative it results in an increase of the value of the diversity function. Hence in our approach, there is no economic development without an increase of diversity.

The above, combined with studies analyzing innovative mechanisms resulting in equilibrium (see for example Lipieta and Ćwięczek 2020, Lipieta and Malawski 2021, Lipieta 2018 and Lipieta and Lipieta 2021)) means that in some cases, diversity may play a key role in sustainable development. That, next, evokes that diversity can lead to economic growth. The latter hypothesis, however, needs to be widely explained in the approach presented and therefore it is not verified in the current paper.

The diversity function defined in the paper gives us tools to analyze the qualitative properties of the analyzed mechanisms and transformations of the economy in such a way that the increase of the value of the diversity function means in fact an improvement of the economic positions of some consumers or an increase in the innovativeness of the economic system. Details can be found in Lipieta and Malawski (2018).

On the basis of the analysis presented in Lipieta and Lipieta (2017), it can be seen from a broader perspective of the evolution of the economy modeled in the Hurwiczian approach, that in a longer time interval, changes in an economy are caused by innovative mechanisms, while in a shorter time interval by either innovative or cumulative mechanism, or a mechanism that is neither innovative nor cumulative. Therefore it can be concluded that in a longer time interval an increase in the value of the diversity function is observed, as opposed to a shorter time, when its value may increase, decrease or remain unchanged. Thus analyzed mechanisms of economic evolution have qualitative properties as they enable the observation and analysis of the economic situation of some group of economic entities.

A more detailed analysis of the relationship between diversity and economic growth, and between diversity and mechanisms that would realize the aim of economic agents in Pareto sense, remains in our research perspectives.

The application of the theory of mechanism design apparatus to model the introduction of innovative changes inspired us to a deep understanding of their structures. The application of the Hurwicz approach revealed the significant role of signals sent and analyzed by the economic agents in the processes of obtaining the desired goals as well as allowed to distinguish the relationship between diversity and mechanisms. Indirectly, it also pointed to the relationship between diversity of the economy and the importance of the R&D sector in the economy, and thus higher education in the society. The presented results do not aspire to be the best or most effective. They should be rather regarded as an attempt to adapt new concepts and methods for exploring the existing problems in order to more fully understand the role of diversity in the Schumpeterian economic development.