The age distribution of business firms

Abstract

We investigate upon the shape and the determinants of the age distribution of business firms. By employing a novel dataset covering the population of French businesses, we highlight that a geometric law provides a reasonable approximation for the age distribution. However, relevant systematic deviations and sectoral heterogeneity appear. We develop a stochastic model of firm dynamics to explain the mechanisms behind this evidence and relate them to business dynamism. Results reveal a long-term decline in entry rates and lower survival probabilities of young firms. Our findings bear important implications for aggregate outcomes, notably employment growth.

1 Introduction

The size and growth distributions of businesses, and the mechanisms behind their shape, have been extensively studied in the literature (see notably Simon and Bonini, 1958; Axtell, 2001; De Wit, 2005; Bottazzi and Secchi, 2006; Arata, 2019, among the others). Considerably less attention has been devoted to the firm age distribution, although the age composition of economies, and of sectors of activity, has important implications for industrial dynamics, job creation, and innovation (see Coad 2018 for a recent survey). In fact, young firms are the engine of creative destruction (Schumpeter 1934), often driving the introduction of radical innovations (Baumol 2002), and significantly contributing to job creation (Haltiwanger et al. 2013; Criscuolo et al. 2014), with a key role played by few rapidly growing gazelles (Nightingale and Coad 2014).

In this paper we fill this gap and we study in detail the shape and determinants of the age distribution of business firms by combining new empirical evidence with a calibrated stochastic model of firm dynamics.

The empirical analysis employs a new database that covers the population of businesses in France in 2018 and uncovers three stylised facts. First, a geometric law appears to be a reasonable first-order approximation for the aggregate age distribution; second, there are however significant deviations from the geometric benchmark at aggregate level; third, significant cross-sectoral heterogeneity in the slope of the age log-distribution is evident, with more significant deviations from the geometric benchmark at finer-grained levels of sectoral classification.

We develop a relatively simple stochastic model of firm dynamics to disclose the mechanisms behind these stylised facts and to guide the interpretation of empirical findings. In particular, we consider an economy in discrete time. At each period a number of new firms, proportional to the amount of incumbents, enters the economy. All firms have a given survival probability and can exit the market. Our modelling strategy provides a novel non-trivial mechanism to generate a geometric age distribution and allows us to explain deviations from such a benchmark. We also introduce sectoral heterogeneity and we show that the aggregation of a finite number of geometric distributions with heterogeneous coefficients, each representing one sector, can lead to the emergence of an approximated geometric distribution at the aggregate level.

The combination of empirical and model implications reveals (i) the existence of a long-term decline in entry rates, highlighted by a lower slope of the age log-distribution for firms with less than 30 years; and (ii) the presence of a lower survival probability for young firms, which results in a relatively steeper log-distribution for businesses with age lower than 10 years. Our findings also point to a short-term effect of the Great Recession, which generates a blip in the age distribution for firms born around 2008. Effects of the Great Depression, the Second World War, and the subsequent post-war recovery (Trente Glorieuses) are also visible, although the data have been collected less systematically before 1980. Further examination of the age distribution at finer grained level of aggregation reveals that the geometric benchmark appears to broadly hold also within 2-digit sectors, but with the slopes of the sectoral log-distributions being significantly heterogeneous. This suggests that different sectors are at different stages of their life-cycle, with our analysis providing an indirect measure and showing that the aggregate behaviour reflects important sectoral composition effects. More significant deviations from the geometric benchmark at very disaggregated levels (3-digit sectors) may suggest that evolutionary life-cycle dynamics become better observable in more detailed sectors.

The overall evidence on the shape of the age distribution, its structural and cyclical determinants, contribute to the debate on the role of young firms in the economy, on declining business dynamism, and on sectoral differences in industrial dynamics.

The analysis is particularly novel along a number of dimensions. First, it uses for the first time new comprehensive cross-sectional French data to study in detail the age distribution of all businesses, disclosing the three above mentioned stylised facts. Second, it develops a novel stochastic model of firm dynamics characterising the age distribution and explaining the mechanisms behind its shape. As a matter of fact, under the baseline setting the intuition proposed by our model is that, in order to achieve age a, a firm has to be in the group of entrants in one period and has to remain among the group of incumbents for a − 1 periods. Since the ratio between the two groups remains constant over time, multiplying accordingly a geometric distribution is obtained. Moving to more complete scenarios, more apt at coping with violations of the geometric law, our model suggests that different slopes of the age log-distribution are related to variations in entry rates, to heterogeneity in the survival probabilities, or to sectoral differences. Third, our analysis highlights how the slope of the cross-sectional age log-distribution – pictured at a single given point in time – is an important structural parameter that has significant links with the long-term evolution of business dynamism and the life-cycles of industries, with relevant implications for economic outcomes, notably employment growth. Our analysis is particularly relevant because accessing panel-data covering the whole population of firms, from which one can extract business dynamism trends, is particularly challenging – especially over long time-horizons.

The remainder of the paper is organised as follows. Section 2 provides a brief overview of the literature related to this study. Section 3 describes the data used for the empirical analysis and presents three key stylised facts related to the age distribution of business firms. Section 4 formalizes a stochastic model of firm dynamics, solved under different assumptions on survival probabilities and entry rates, and presents several comparative statics exercises that guide the interpretation of stylised facts. Section 5 presents a calibration exercise of the stochastic model and confirms its validity. Section 6 discusses the stylised facts, in the light of both model prescriptions and its calibration and suggests that sectoral differences in age distributions have important implications for employment growth. Section 7 concludes and discusses avenues for further research.

2 A brief overview of the literature

Only few empirical analyses provide comprehensive insights on the firm age distribution. These existing studies include the work by Coad (2010b), Barba Navaretti et al. (2014), Kinsella (2009), and Grazzi and Moschella (2018). In particular, Coad (2010b) investigates and compares the age distributions of small scale Indian businesses, of young establishments in the United States, of samples of Italian and Spanish firms, and of firms in the international airline industry, providing a first broad investigation of cross-sectional age distributions using different data sources. Furthermore, Barba Navaretti et al. (2014) estimates the age distribution for a sample of firms in Italy, France and Spain, Kinsella (2009) instead focuses on a sample of Irish firms, while Grazzi and Moschella (2018) as a side exercise to their core analysis, provide some insights on the age distribution of Italian exporters vs. non-exporters.

These studies suggest that the firm age distributions of the samples or groups of firms analysed approximate an exponential law, the continuous counterpart of the geometric distribution.¹ Despite being highly informative, these existing studies do not provide a complete characterisation of the aggregate age distribution of business firms. As a matter of fact, they are mainly based on samples rather than whole populations of businesses. Furthermore, at the best of our knowledge, discussions about the mechanisms behind the shape of the age distribution, systematically linking it to entry rates and survival, to the debate on the evolution of business dynamism and industry life-cycles, or more generally to industrial dynamics, have been very limited.

A relevant exception is the work by Steindl (1965) that employs the firm age distribution to provide an explanation of the emergence of a Pareto firm size distribution in a stochastic model of firm dynamics. A similar approach is taken by Coad (2010a), who takes instead an exponential age distribution as an assumption, to derive the Pareto firm size distribution. In particular, Coad (2010a) suggests that there are two possible frameworks under which a perfect exponential age distribution would emerge. The first case is a model in which a constant number of firms enter the market, but a constant proportion of these entrants exit the market in each year. The second case, instead, is a model in which firms do not exit and an exponentially increasing number of firms enter the market in each period (see ; Simon 1955). Our approach generalizes the previous ones considering entry rates and introducing stochastic exit. Moreover, allowing for dynamics in entry rates, heterogeneity in survival probabilities, and sectoral differences, we are able to account for deviations from the exponential (or geometric) benchmark.

Indeed, this paper directly links the age distribution of businesses to the dynamics of entry and survival. In that, it is closely related to the recent literature focusing on the evolution of business dynamism. In particular, there is a lively debate on the extent to which business dynamism, and notably entry rates, have been declining in the last decades. Significant declines have been observed in the United States (see Decker et al., 2014; Goldschlag and Tabarrok, 2018), Belgium (Bijnens and Konings 2020), and across countries (Criscuolo et al. 2014; Calvino and Criscuolo 2019). However, the lack of availability of very long and consistent time series of entry and exit rates, especially at detailed sectoral levels of aggregations, has been a significant limit for this stream of research. Focusing on the cross-sectional age distribution represents an indirect way to analyse the longer-term evolutions of business dynamism, also detailing sectoral patterns, as will be further discussed along this paper.

Our analysis also links sectoral differences in age distributions with industry evolution, revealing that sectors may be at different phases of their life-cycles. We therefore relate to the literature on the evolution of industries, and importantly to the legacy of Klepper (1996). In particular, the seminal contribution by Klepper (1996) suggests that at the beginning of the life-cycle of many industries entry is high, there is a growing number of producers, with market shares changing rapidly and significant product innovations. As industries evolve, entry starts declining, there is a shake-out reducing the number of producers, and the industry leadership stabilises. In this stage product innovation and the diversity of product varieties decline, with firms’ innovative activity shifting to process innovation. In this framework, analysing differences in sectoral age distributions is particularly promising to identify the stages at which different sectors stand, as will be further discussed in the following.

Finally, the analysis is also more broadly related to different streams of research in industrial economics that examine patterns in business demography and the life duration of new firms (Agarwal, 1998; Bartelsman et al., 2005; Strotmann, 2007), the role of firm age for performance and survival (Evans, 1987; Dunne and Hughes, 1994; Huergo and Jaumandreu, 2004; Mata and Portugal, 2004; Balasubramanian and Lee, 2008; Huynh and Petrunia, 2010; Coad et al., 2013; Coad et al., 2016; Calvino et al., 2018); or model the dynamics and evolution of industries (Dosi et al., 1995; Klepper, 1997; Malerba and Orsenigo, 1996; Marsili, 2001; Dosi et al., 2017).

3 Data and stylised facts

The analysis is based on a novel data source produced and published by the French National Institute of Statistics (INSEE), the Sirene database. The data covers the population of all enterprises and of all their establishments in France and encompasses about 10 million establishments in all sectors of the economy.² This is the most appropriate database to study firm age distributions, given the comprehensiveness of its coverage and the ability to provide information on establishment and enterprise age also for very old businesses. Using this data source represents a significant novelty with respect to previous empirical investigations on the topic.

The dataset includes information on enterprise and establishment identifiers, detailed sectoral and geographical codes, and – most importantly for the aim of this study – information on the date of creation of each enterprise and establishment.³

Our analysis, thus, focuses on all businesses in France métropolitaine and we exclude regions oversea, called in French the départements d’outre-mer, i.e., Guadeloupe, Guyane, Martinique, Mayotte et Réunion and Saint-Pierre et Miquelon. Also, given the focus on business firms, the main body of the paper excludes the non-business sectors and focuses mainly on manufacturing and non-financial market services.⁴

We focus on the cross-sectional stock of enterprises and establishments at the 1^st of January 2018. Additionally, the data have been cleaned to take into account common issues, such as avoiding situations in which a multi-establishment business owned an establishment which was registered before the enterprise itself. The filtering procedure of sectors, in addition, has been performed at the establishment level. This allows us to keep in our clean dataset also the single establishments operating in business sectors, of the multi-establishment enterprises whose core activity does not fall into business industries. The final population used for the analysis, includes 6519413 enterprises and 7155860 establishments belonging to 608 different 4-digit sectors. Age is defined as the number of years between the creation date and 2018. Thus, in what follows age shall be intended as a discrete variable.⁵ This choice is fairly natural and allows us to avoid possible seasonality issues. A first set of descriptive statistics concerning the age of these firms is provided in Table 1.

Table 1 Descriptive statistics of the age of establishments (AGE_et) and enterprises (AGE_en) age

Table 1 highlights that aggregate age distributions are right-skewed, as the average establishment and enterprise ages lie at the right than the two medians. Reasonably, enterprises are in general older than establishments due to the possibility that multi-establishment businesses might have built new plants after the creation of the enterprise itself. Based on these data, the remainder of this section presents more in detail three key stylised facts on the age distribution of businesses in France from a purely empirical viewpoint. The discussion of their implications through the lenses of an economic model is left to Section 6.

3.1 Fact 1: geometric law as a first-order approximation for the age distribution

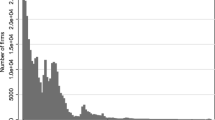
The first part of the empirical analysis focuses on the aggregate cross-sectional age distribution of businesses in France in 2018. As a first exercise, we show the plots of the age log-distributions at the establishments and enterprises levels in Fig. 1, where the ordinary least squares (OLS) line of best fit is also depicted.⁶

Fig. 1

Pooled age distribution at the establishment (left panel) and enterprise (right panel) levels. In black we depict the empirical distribution and in blue the OLS fit

From Fig. 1 – where we depict log-frequencies on the y-axis – one can observe that a geometric law can provide a reasonable first-order approximation of the two empirical age distributions. As a matter of fact, in a perfect geometric case, the log-distribution would be represented by a perfectly straight line. Plots similar to the ones observed in Fig. 1 are also visible when taking a slightly lower aggregation level. Indeed, even by separating firms and establishments between manufacturing or services, the aggregate results remain unchanged both qualitatively and quantitatively. We show this in a simple regression framework in which we estimate by means of ordinary least squares the linear model:

$$ \log(count_{i}) = \beta_{0} + \beta_{1} age_{i} + \varepsilon_{i} $$

(1)

where the subscript $i \in \left \{\text {Aggregate,~Manufacturing,~Services}\right \}$ denotes the level of aggregation. We collect the results in Table 2 for establishments and enterprises. It is possible to observe that not only at aggregate level, but also when focusing separately on manufacturing and services, the estimated coefficients for the slope of the log-distribution is between − 0.10 and − 0.12. This suggests that for each additional year of life, on average, there are 10.4% fewer firms.

Table 2 Estimation of the geometric distributions via OLS for the age of establishments (left) and enterprises (right) at the aggregate level and in the manufacturing and services broad sectoral aggregates

The OLS estimation shall only be considered as an approximation. As a matter of fact, recent contributions to the literature highlight that there may be some challenges when carrying out this type of OLS estimation (see Bottazzi et al., 2015 for a critical discussion).⁷ An alternative way to estimate the slope parameter is to assume ex-ante that the overall age distribution follows a geometric law. Under this strong assumption, one can consistently and efficiently estimate the parameter λ characterizing the geometric distribution λ(1 − λ)^x− 1 by means of maximum likelihood (ML). A relevant difference between the OLS and the geometric ML fit lies in the way observations are weighted. The former assigns the same weight to every age profile disregarding their size in terms of observations. The latter, instead, takes into account the fact that many more observations are available for low age profiles. Thus, the ML fit of a geometric law is designed to better capture the slope of the age distribution for younger firms, at the cost of a poor fit in the right tail of the distribution, for the few very old firms. Results from this exercise support the intuition provided by the simpler but biased OLS (see Fig. 9).

In general, also considering the very high levels of adjusted R² from the regression exercises equally weighting all age bins, we conclude that at broad levels of aggregations – similarly to what pointed out by Coad (2018) among the others – the geometric distribution provides a reasonable first-order approximation of the age distribution of businesses. However, as already evident in Fig. 1, the geometric fit is not perfect. A formal quantitative statistical evaluation carried out exploiting the ML framework (e.g. by a χ² test, which is presented in Appendix Appendix) leads to a strong rejection of the null hypothesis of a perfect geometric shape.⁸ This is further explored in the next stylised fact.

3.2 Fact 2: significant deviations from the geometric benchmark in the aggregate

Examining more closely Fig. 1, one can however notice that the geometric fit, despite being reasonable at first glance, has limitations. The deviations from the geometric benchmark display, as a matter of fact, a clustered pattern over the age support (or over time reading Fig. 1 from the right to the left). As we move from the youngest firms to the oldest ones in Fig. 1 we can observe i) a flatter distribution for firms with age between 1 and about 30 years old and ii) a steeper distribution for firms in the 30–50 years old region.

After that age, we observe more significant variations from the geometric benchmark. The distribution appears to some extent even steeper – but more volatile – for firms older than 50 but younger than 75 years old, and much flatter after that. These patterns need to be taken with more caution due to the absence of a sufficiently high number of observations and the fact that the dates of creation of firms have been more systematically collected only since 1980.

In order to explore more in detail the deviations from the geometric benchmark we perform further analysis of the residuals and their correlation. This is reported in Fig. 2, which shows that, the deviations from the perfect geometric benchmark are non-random over time and they rather display very high levels of auto-correlation at several lags (i.e., age differences). This indicates that the patterns of the age distribution identified (e.g., the increasing residuals between 1 and about 30 and the decreasing ones between 30 and 50) are likely due to some long-run trends in the economic system that characterize the degree of market turbulence. This will be further discussed in the following sections.

Fig. 2

Time series (top panels) and autocorrelation function (bottom panels) of the geometric fit residuals for aggregate data at the establishment (left panels) and enterprise (right panels) levels

We then enrich the analysis based on simple OLS estimates complementing the residuals analysis with the maximum likelihood estimation of a piecewise geometric distribution. We define it as the distribution that assigns to every $x\in \mathbb {N}$ a probability

$$ \begin{aligned} \mathcal{G}(x;\boldsymbol{\lambda},\textbf{k})=&g_{0}(\boldsymbol{\lambda},\textbf{k})\left( \vphantom{\sum\limits_{i=2}^{K}}H(k_{1}-x)\lambda_{1}(1-\lambda_{1})^{x-1}\right. \\ &+\sum\limits_{i=2}^{K} H(x-k_{i-1}+1)H(k_{i}-x)\lambda_{i}(1-\lambda_{i})^{x-1}\\ &+\left.H(x-k_{K}+1)\lambda_{K+1}(1-\lambda_{K+1})^{x-1}\vphantom{\sum\limits_{i=2}^{K}}\right) , \end{aligned} $$

(2)

where k = (k₁,k₂,…,k_K) is a vector of K breaks (that is, points in which the distribution changes its shape), λ = (λ₁,λ₂,…,λ_K+ 1) is a vector containing the parameters which determine the shape of the different pieces, H(x) represents the Heaviside function (such that H(x) = 1 if x > 0 and H(x) = 0 otherwise), and g₀(λ,k) is a normalization term reading

$$ g_{0}(\boldsymbol{\lambda},\textbf{k})=\Bigg{(} 1-\sum\limits_{i=1}^{k_{K}-1}\lambda_{K+1}(1-\lambda_{K+1})^{i-1}+\sum\limits_{i=1}^{k_{1}-1}\lambda_{1}(1-\lambda_{1})^{i-1}+\sum\limits_{j=2}^{K} \sum\limits_{i=k_{j-1}}^{k_{j}-1}\lambda_{j}(1-\lambda_{j})^{i-1}\Bigg{)}^{-1} . $$

The results are reported in Fig. 3, where we set k = (10,20,30,40) and zoom on firms younger than 50 years old.⁹ The slope of the geometric fit is steeper in the interval (0,10) than in [10,30), i.e., when contrasting younger with older businesses. Similarly, the distribution is steeper for firms with age a ≥ 30 with respect to firms with age a ∈ [10,30), i.e. when contrasting firms born during the 1970s and 1980s with firms born during the great moderation.¹⁰

Fig. 3

Empirical distribution (for firms with a ≤ 50) and piecewise geometric fit obtained multiplying estimated probabilities by the total number of firms

So far the analysis has focused on aggregate or very broad macro-sectoral features of the age distribution of businesses. But these aggregate behaviours can hide important compositional effects. For this reason, we focus on more disaggregated sectoral groups and analyse their age distributions in the next sub-section.

3.3 Fact 3: significant sectoral heterogeneity, with stronger deviations at finer grained levels

In this section we further explore the properties of the age distribution of French businesses in 2018 focusing on lower levels of aggregation. As previously mentioned, this is relevant to better understand the extent to which sectoral heterogeneity affects the aggregate distribution.

In particular, we plot the empirical age distributions and perform OLS geometric fits separately for different 2- and 3-digit sectors.¹¹ Although we have plotted age distributions of every single 2- and 3-digit sectors, we report the plots of the empirical distributions with geometric fits for nine selected 2-digit sectors, in Fig. 4 below, and nine selected 3-digit sectors in Fig. 10 in Appendix Appendix.

Fig. 4

Age distribution of establishments at the 2-digit level for nine selected industries

Focusing on those figures, it is already possible to observe that the geometric fit still appears as a reasonable first-order approximation of the empirical distribution in many sectors, but that the coefficient estimates are heterogeneous across sectors. For example, Fig. 4 suggests that the slope of the log-distribution of the food manufacturing industry (10) is significantly flatter than the slope of the computer programming, consultancy and related activities industry (62). Furthermore, Fig. 10 highlights that this result holds true at more disaggregated levels, when comparing the manufacturing of dairy products (105) with computer programming, consultancy and related activities (620).

Significant heterogeneity of the slopes of the log-distributions with relatively good geometric fit are also observed at the 2-digit level. Results of the linear regression estimates are reported by Table 6. In order to summarise the sectoral heterogeneity in the slopes of the log-distributions and the goodness of their geometric fit, we present in Fig. 5 the distributions of the slope coefficients and the adjusted R² (retrieved from the estimation of Eq. 1 at the 2- and 3-digit levels). The results suggest that the more one looks at the microeconomic level, by focusing on narrower sectors, the higher the heterogeneity in the estimated slope and the lower the quality of the geometric fit. The goodness of fit seems to confirm that the geometric distribution appears as a reasonable first-order approximation also when focusing on 2-digit sectors, but at the 3-digit sectoral disaggregation, more important deviations are revealed, as highlighted by the fatter left tail of the adjusted R² distribution (bottom right panel).

Fig. 5

Heterogeneity of the age distribution geometric fit at the 2- and 3-digit levels for establishments

Sectoral heterogeneity and deviations from the geometric fit are likely related to sectoral characteristics and industrial dynamics. An important dimension to consider appears to be related to the phase of their life-cycle, as will be further discussed in the following. Furthermore, the significant sectoral heterogeneity suggests that the generalized geometric pattern observed at the aggregate level (see Table 2) is therefore conceivable as an emergent property and that compositional effects play an important role.

4 Model

In order to better understand the mechanisms behind the shape of the age distribution, its deviations from the geometric benchmark, and the sectoral heterogeneity discussed in the previous section, we propose a stylised stochastic model of firm dynamics. The model suggests that the age distribution is nothing but an emergent property – an unconditional object using the language of Brock (1999) – whose cross-sectional distributional shape is determined by the evolution of the rates of entry and survival of businesses as well as by their difference.

This model abstracts from several aspects of the reality – e.g. it does not account for growth dynamics nor considers firm size – but has the ability of supporting us in a better understanding of the stylised facts discussed in the previous section. This approach is consistent with some of the intuitions put forward by Coad (2010a).

We consider an economy in discrete time indexed by $t\in \mathbb {N}$. Define $N_{t}\in \mathbb {N}$ as the number of firms present in the economy at the end of t. We assume that at the beginning of time t = 1 a number $N_{0}\in \mathbb {N}$ of firms are created, while, in every period t > 1, ϕ_tN_t− 1 new firms enter the economy.¹² Thus, ϕ_t is the entry rate. Each firm is uniquely identified by a number $i\in \mathbb {N}$ which is progressively assigned. Define F_t as the set of firms present in the economy at the end of time t (such that N_t = |F_t|) and f_t as the set of new entrants at time t. Each firm i ∈{F_t− 1 ∪ f_t} has a probability ρ_i,t of surviving time t and, thus, of belonging to F_t. It follows that the probability of firm i to exit the economy at time t is 1 − ρ_i,t. Defining F₀ = {∅}, in mathematical terms we have that for any i ∈{F_t− 1 ∪ f_t} and $t\in \mathbb {N}$ it is Prob{i ∈ F_t} = ρ_i,t. Finally, the age of firm i ∈ F_t, which entered the economy at time t_i, is defined as a_i,t = t − t_i + 1 and the number of firms of age a at time t is $\mathcal {N}_{t}(a)=|\{i\in F_{t} | a_{i,t}=a\}|$.

4.1 Solving the model

We solve the model for the expected number of firms of a given age at a generic time period t under different assumptions on survival probabilities and entry rates – i.e. different scenarios. Looking at the expected number for different age levels, one recovers a sort of theoretical histogram that can be easily interpreted as a theoretical age distribution. In the simplest scenario we are able to go further and derive asymptotic relative frequencies. This exercise helps in understanding how the geometric behaviour originates. The fundamental idea underlying our analysis is that the event “firm i survives time t” can be expressed in terms of a Bernoulli random variable s_i,t ∈{0,1} with Prob{s_i,t = 1} = ρ_i,t. As we shall explain, even if such process let the age of a firm at the moment of failure be geometrically distributed, obtaining that the distribution of firms’ age at a given time is geometric is not trivial.

Baseline scenario: constant entry rate and survival probability.

Let us begin from the simplest case by assuming that the survival probability is constant for all firms and all periods, ρ_i,t = ρ ∀t,i, and the entry rate is constant over time, ϕ_t = ϕ ∀t > 1. The number of firms in the economy at the end of time t can be expressed using the Bernoulli random variables just introduced. More specifically one has

$$ N_{t}=\underset{i\in \{F_{t-1}\cup f_{t}\}}{\sum} s_{i,t} . $$

(3)

Since |{F_t− 1 ∪ f_t}| = N_t− 1(1 + ϕ) for t > 1, |{F₀ ∪ f₁}| = N₀, and the Bernoulli random variables are i.i.d., we can write

$$\mathbb{E}[N_{t}]=\mathbb{E}\left[\mathbb{E}\left[\left.\underset{i\in \{F_{t-1}\cup f_{t}\}}{\sum} s_{i,t}\right|N_{t-1}\right]\right]=\mathbb{E}[N_{t-1}](1+\phi)\rho .$$

Iterating the map one gets

$$ \mathbb{E}[N_{t}]=N_{0}(1+\phi)^{t-1}\rho^{t} . $$

(4)

Then, exploiting the definition of the Bernoulli random variables, the number of firms with age a at time t can be written as

$$ \mathcal{N}_{t}(a)= \underset{i\in f_{t-a+1}}{\sum} \prod\limits_{\tau=t-a+1}^{t} s_{i,\tau} . $$

(5)

Recalling that |f_t| = N_t− 1ϕ for t > 1 and N₀ for t = 1, its expectation for the case a < t is

$$ \mathbb{E}[\mathcal{N}_{t}(a)]=\mathbb{E}[N_{t-a}]\phi\rho^{a} $$

(6)

and, substituting with Eq. 4 computed at time t − a, the expected number of firms with age a reads

$$ \mathbb{E}[\mathcal{N}_{t}(a)]= \begin{cases} N_{0}\rho^{t} & \text{if} a=t ,\\ N_{0} \phi (1+\phi)^{t-a-1} \rho^{t} & \text{if} a<t . \end{cases} $$

(7)

The case a = t is derived from Eq. 6 noticing that the expected number of firms created at time t = 1 is indeed known and equal to N₀. Notice that $\log \mathbb {E}[\mathcal {N}_{t}(a)]$ is linear in a and the coefficient of a is − (1 + ϕ). This means that the slope of the age log-distribution depends only on the entry rate, while the survival probability influences only the log-distribution intercept.

To better understand how the results originate, we compute the asymptotic relative frequencies of the age variable, under the assumption that the number of firms in the economy is sufficiently large in every period. In particular, it is enough to assume $N_{0}\to +\infty$ and ϕ ≥ (1 − ρ)/ρ, such that the expected number of firms cannot converge to zero for large t.¹³ Under those assumptions, the Strong Law of Large Numbers implies that, almost surely with respect to the probability measure of the Bernoulli trials $(s_{i,t})_{i\in \mathbb {N},t\in \mathbb {N}}$, it is $\lim _{N_{0}\to \infty }N_{1}/N_{0}=\rho$ in the first period and $\lim _{N_{0}\to \infty }N_{t}/N_{0}=(1+\phi )^{t-1}\rho ^{t}$ for any t > 1.¹⁴ The relative frequency of firms with age a at time t can be computed as the ratio of the number of firms born at t − a + 1 and survived until t over the sum of all the firms survived until t. Calling $\mathcal {F}_{t}(a)$ such quantity, we have

$$ \mathcal{F}_{t}(a)=\frac{\underset{i\in f_{t-a+1}}{\sum} \prod\limits_{\tau=t-a+1}^{t}s_{i,\tau}}{\sum\limits_{\tau^{\prime}=1}^{t}\underset{j_{\tau^{\prime}}\in f_{\tau^{\prime}}}{\sum} \prod\limits_{\tau^{\prime\prime}=\tau^{\prime}}^{t} s_{j_{\tau^{\prime}},\tau^{\prime\prime}}}=\frac{\left( \underset{i\in f_{t-a+1}}{\sum} \prod\limits_{\tau=t-a+1}^{t}\frac{s_{i,\tau}}{N_{t-a}}\right)\frac{N_{t-a}}{N_{0}}}{\sum\limits_{\tau^{\prime}=1}^{t}\left( \underset{j_{\tau^{\prime}}\in f_{\tau^{\prime}}}{\sum}\prod\limits_{\tau^{\prime\prime}=\tau^{\prime}}^{t} \frac{s_{j_{\tau^{\prime}},\tau^{\prime\prime}}}{N_{\tau^{\prime}-1}}\right)\frac{N_{\tau^{\prime}-1}}{N_{0}}} $$

and, by the Strong Law of Large Numbers, we almost surely obtain

$$ \underset{N_{0}\to\infty}{\lim} \mathcal{F}_{t}(a)=\frac{\phi(1+\phi)^{t-a-1}\rho^{t}}{\rho^{t}+\sum\limits_{n=1}^{t-1}\phi(1+\phi)^{t-n-1}\rho^{t}} . $$

Factorizing and taking the limit for $t\to \infty$, we get the asymptotic relative frequency of firms with age a, $\mathcal {F}(a)$, which almost surely reads

$$ \mathcal{F}(a)=\underset{t\to\infty}{\lim} \left( \underset{N_{0}\to\infty}{\lim} \mathcal{F}_{t}(a)\right)=\frac{(1+\phi)^{-a}}{\sum\limits_{i=1}^{\infty} (1+\phi)^{-i}} . $$

Solving for the geometric series at the denominator and defining λ = ϕ/(1 + ϕ), we almost surely have

$$ \mathcal{F}(a)=\lambda(1-\lambda)^{a-1}, $$

which clearly shows the geometric behaviour of the firm age distribution. Given the way in which the random variable s_i,t is defined, obtaining that age is geometrically distributed may appear trivial. But this is not the case. First, because the age of a firm at a given time t cannot be interpreted as the number of Bernoulli trials (i.e. periods) needed to have a firm to fail. In other words, age is not computed as how old a firm is at the time of exiting the economy; a firm can in fact continue to survive even in the following periods. Second, because the number of new firms entering the economy changes over time and it is strictly connected to the amount of incumbent firms. Thus, we cannot see cohorts of firms with different ages as random samples from the same underlying process observed at different stages. This is evident by noticing that $\mathcal {F}(a)$ only depends upon the entry rate ϕ, and not on the survival rate ρ.

The emergence of the geometric behaviour in our framework can be understood considering the following intuition. Notice that λ is the fraction of new firms in the economy at the beginning of a given period – i.e. λ = |f_t|/|{F_t− 1 ∪ f_t}| $\forall t\in \mathbb {N}$ – while 1 − λ is the fraction of incumbents. Hence, in order to show an age equal to a, a firm has to belong to the new entrants group for 1 period, and to the incumbents group for a − 1 periods. Multiplying such fractions accordingly, the asymptotic relative frequency $\mathcal {F}(a)$ is obtained and the geometric behaviour emerges. This also explains why the slope of the log-distribution is only influenced by the entry rate. Ultimately, ϕ is the unique determinant of relative sizes of different age profiles.

Unconditional scenario: time-dependent entry rate and homogeneous survival probabilities.

We consider now the case in which survival probabilities and entry rates change over time. We keep, however, the assumption that survival probabilities are homogeneous and do not depend on firms’ characteristics. That is, ρ_i,t = ρ_t ∀i,t. Concerning the entry rate, we distinguish two cases. In the first one, ϕ_t is an independent random variable such that $\mathbb {E}[\phi _{t}]=\phi$ ∀t. In the second one, ϕ_t varies over time according to a certain deterministic process, such that (ϕ₂,ϕ₃,…,ϕ_t,…) is a known sequence of parameters. For what concerns the expected number of firms with a given age at a generic time t, the second case is equivalent to assume that every entry rate is an independent random variable with time-dependent expectation. Under this interpretation, we abuse notation letting ϕ_t be interpreted as the expected entry rate at time t. In the first case, taking the expectation of Eq. 3 we obtain

$$\mathbb{E}[N_{t}]=\mathbb{E}[N_{t-1}](1+\phi)\rho_{t}$$

and by iterating the map backward, the expected number of firms at time t becomes

$$ \mathbb{E}[N_{t}]=N_{0}(1+\phi)^{t-1}{\prod}_{\tau=1}^{t}\rho_{\tau} . $$

(8)

Then, since the number of firms with age a at time t can be written as in Eq. 5, we obtain

$$\mathbb{E}[\mathcal{N}_{t}(a)]=\mathbb{E}[N_{t-a}]\phi\prod\limits_{\tau=t-a+1}^{t}\rho_{\tau} $$

and, substituting with Eq. 8 computed at time t − a while recalling the different specification for firms of age t, one has

$$ \begin{aligned} \mathbb{E}[\mathcal{N}_{t}(a)]= \begin{cases} N_{0} {\prod}_{\tau=1}^{t} \rho_{\tau} & \text{if} a=t ,\\ N_{0} \phi (1+\phi)^{t-a-1} {\prod}_{\tau=1}^{t} \rho_{\tau} & \text{if} a<t . \end{cases} \end{aligned} $$

(9)

Taking the log of $\mathbb {E}[\mathcal {N}_{t}(a)]$ one immediately notices that, as in the previous case, the expected numerosity of firms with age a is a linear map of a with coefficient $-\log (1+\phi )$. Thus, once again, we infer that the survival probability ρ_t does not impact on the slope of $\log \mathbb {E}[\mathcal {N}_{t}(a)]$ but it influences the intercept.

For the second case, we solve using the same steps, but taking into account that ϕ_t varies deterministically over time. Thus, the expected number of firms is $\mathbb {E}[N_{t}]=\mathbb {E}[N_{t-1}](1+\phi _{t})\rho _{t}$ and, by iteration, one obtains

$$ \mathbb{E}[N_{t}]=N_{0}\prod\limits_{\tau^{\prime}=2}^{t}(1+\phi_{\tau^{\prime}}){\prod}_{\tau=1}^{t}\rho_{\tau} . $$

The expected number of firms with age a at time t now reads $\mathbb {E}[\mathcal {N}_{t}(a)]=\mathbb {E}[N_{t-a}]\phi _{t-a+1}\prod \limits _{\tau =t-a+1}^{t}\rho _{\tau }$ and substitution leads to

$$ \begin{aligned} \mathbb{E}[\mathcal{N}_{t}(a)]= \begin{cases} N_{0} {\prod}_{\tau=1}^{t} \rho_{\tau} & \text{if} a=t ,\\ N_{0} \phi_{t-a+1} {\prod}_{\tau^{\prime}=2}^{t-a}(1+\phi_{\tau^{\prime}}) {\prod}_{\tau=1}^{t} \rho_{\tau} & \text{if} a<t . \end{cases} \end{aligned} $$

(10)

Taking the log of $\mathbb {E}[\mathcal {N}_{t}(a)]$ for a ∈{1,2,…,t − 1}, one obtains

$$ \log\mathbb{E}[\mathcal{N}_{t}(a)]=\log\left( N_{0} \phi_{t-a+1} {\prod}_{\tau=1}^{t} \rho_{\tau}\right) +(t-1)\sum\limits_{\tau^{\prime}=2}^{t-a}\frac{\log(1+\phi_{\tau^{\prime}})}{t-a-1}-a\sum\limits_{\tau^{\prime}=2}^{t-a}\frac{\log(1+\phi_{\tau^{\prime}})}{t-a-1} . $$

Thus, if entry rates change deterministically over time – or, equivalently, they are independent random variables with time-changing expectations – for any age profile we have that the coefficient of a is an arithmetic average of $-\log (1+\phi _{\tau ^{\prime }})$ for the periods ranging from 2 to the one before entry. Also this case implies that the variations in the survival probability ρ_t have no age specific effects on the log-distribution.

Conditional scenario: time-dependent entry rate and heterogeneous survival probabilities.

Here we analyse the case in which survival probabilities depend on firms’ characteristics, focusing on age. Indeed, empirical evidence suggests that young firms have, on average, lower survival rates (see for instance ; Calvino et al. 2018). We account for the presence of such a stylised fact assuming that

$$ \rho_{i,t} = \begin{cases} \rho_{Y} & \text{if } i\in f_{t} \text{or} a_{i,t-1} < \bar{a} \\ \rho_{O} & \text{otherwise} \end{cases} $$

where $\bar {a}\in \mathbb {N}$ represents the age after which a firm is considered as old. Setting the condition ρ_Y < ρ_O provides coherence between our modelling framework and the above mentioned empirical evidence. We assume that every ϕ_t is an independent random variable with $\mathbb {E}[\phi _{t}]=\phi \forall t>1$.¹⁵ When survival probability is age-dependent, deriving the expected number of firms with a given age becomes more complicated. Indeed, one has that the expected number of firms at time t is

$$ \mathbb{E}[N_{t}]=\phi\sum\limits_{k=1}^{\bar{a}-1}\mathbb{E}[N_{t-1-k}]{\rho_{Y}^{k}}+\phi\rho_{Y}^{\bar{a}}\sum\limits_{\tau=0}^{t-\bar{a}}\mathbb{E}[N_{t-\tau-\bar{a}}]\rho_{o}^{\tau} . $$

(11)

where the first component represents the expected number of young firms at time t and the second accounts for the old ones.

Considering the map for $\mathbb {E}[N_{t-1}]$ and rearranging terms, one gets

$$\phi\rho_{Y}^{\bar{a}}\sum\limits_{\tau=0}^{t-\bar{a}-1}\mathbb{E}[N_{t-1-\tau-\bar{a}}]\rho_{o}^{\tau}=\mathbb{E}[N_{t-1}]-\phi\sum\limits_{k=1}^{\bar{a}-1}\mathbb{E}[N_{t-1-k}]{\rho_{Y}^{k}}$$

and, substituting in Eq. 11, the expected number of firms at time $t\geq \bar {a}$ can be obtained iterating the recursive map

$$ \begin{aligned} \mathbb{E}[N_{t}]=(\phi\rho_{Y}+\rho_{O})\mathbb{E}[N_{t-1}]+\phi(\rho_{Y}-\rho_{O})\sum\limits_{\tau=1}^{\bar{a}-1}\mathbb{E}[N_{t-\tau-1}]\rho_{Y}^{\tau} \end{aligned} $$

(12)

with initial conditions $\mathbb {E}[N_{k}]=N_{0}(1+\phi )^{k-1}{\rho _{Y}^{k}}$ for $k\in \{1,2,\ldots ,\bar {a}-1\}$ and, with a slight abuse of notation, $\mathbb {E}[N_{0}]=N_{0}/\phi$.¹⁶ Once the sequence of expected number of firms in each period is available, the expected number of firms for a given age can be derived as

$$ \mathbb{E}[\mathcal{N}_{t}(a)]= \begin{cases} N_{0}\rho_{Y}^{\bar{a}} \rho_{O}^{t-\bar{a}} & \text{if} a=t \\[0.2cm] \mathbb{E}[N_{t-a}]\phi\rho_{Y}^{\bar{a}}\rho_{O}^{a-\bar{a}} & \text{if} \bar{a}\leq a <t ,\\[0.2cm] \mathbb{E}[N_{t-a}]{\phi\rho_{Y}^{a}} & \text{if} a<\bar{a} . \end{cases} $$

(13)

In this case interpreting the analytical distribution is more complicated; it is also more difficult to understand how variations in entry or survival rates affect the emerging distribution. Thus, we rely on comparative statics exercises presented in Section 4.2. As we shall see, age-dependent heterogeneity in survival probabilities significantly affects the shape of the log-distribution, with a steeper slope of the log-distribution on the left of its support, corresponding to the effect of lower survival probabilities of young firms. That is, contrary to the previous scenarios, a different survival probability for young firms with respect to old ones has age-specific consequences on the age distribution.

Sectoral scenario: sector-specific time dependent entry rates and sector-specific survival probabilities.

To cope with the significant sectoral heterogeneity highlighted in the previous section, we consider a case in which each firm belongs to one (and only one) among K sectors. One can thus consider a firm as a single establishment, rather than a multi-establishment enterprise. In this case, each sector k ∈{1,2,…,K} is characterized by a specific entry rate ϕ_k and all the firms of such sector have survival probability ρ_k. Also in this case, we can alternatively (and equivalently) assume that entry rates are sector specific independent random variables with $\mathbb {E}[\phi _{k,t}]=\phi _{k}$ ∀k and ∀t > 1. We further assume that once a firm is born in a sector it remains in that sector for all of its life and that the number of entrants is influenced only by the number of existing firms in the sector. In this way, the expected number of firms with age a in sector k, $\mathbb {E}[\mathcal {N}_{k,t}(a)]$, can be derived following the same mathematical steps of the baseline scenario (if a constant entry rate is assumed) or adapting those of the unconditional scenario (first case, if a random entry rate is assumed). Indeed, denoting by N_k,0 the initial number of firms in sector k, one obtains

$$ \mathbb{E}[\mathcal{N}_{k,t}(a)]= \begin{cases} N_{k,0}{\rho_{k}^{t}} & \text{if} a=t ,\\ N_{k,0} \phi_{k} (1+\phi_{k})^{t-a-1} {\rho_{k}^{t}} & \text{if} a<t . \end{cases} $$

(14)

The expected number of firms with age a at time t in the whole economy is obtained by simple aggregation over the K sectors

$$ \mathbb{E}[\mathcal{N}_{t}(a)]= \sum\limits_{k=1}^{K}\mathbb{E}[\mathcal{N}_{k,t}(a)] . $$

(15)

This setting allows for composition effects. To shed light on the effects of aggregation of heterogeneous sectors, we consider the function $g:\mathbb {R}\to \mathbb {R}$, x↦g(x), defined as

$$ g(x)=\log\left( \sum\limits_{k=1}^{K}N_{k,0} \phi_{k} (1+\phi_{k})^{t-x-1} {\rho_{k}^{t}}\right) . $$

Applying the Mean Value Theorem, for any x > 0 we obtain

$$ g(x)=\log\left( \sum\limits_{k=1}^{K} N_{k,0} \phi_{k} (1+\phi_{k})^{t-1} {\rho_{k}^{t}}\right)-x\sum\limits_{k=1}^{K}\frac{N_{k,0} \phi_{k} (1+\phi_{k})^{t-\xi-1} {\rho_{k}^{t}}}{{\sum}_{j=1}^{K} N_{j,0} \phi_{j} (1+\phi_{j})^{t-\xi-1} {\rho_{j}^{t}}}\log(1+\phi_{k}) $$

with ξ ∈ (0,x). The function g(x) can be used to compute the logarithm of $\mathbb {E}[\mathcal {N}_{t}(a)]$ for any age level a. That is, for any a ∈{1,2,…,t − 1}, there exists a ξ_a ∈ (0,a) such that¹⁷

$$ \begin{array}{@{}rcl@{}} \log \mathbb{E}[\mathcal{N}_{t}(a)]&=& g(a)=\log\left( \sum\limits_{k=1}^{K} N_{k,0} \phi_{k} (1+\phi_{k})^{t-1} {\rho_{k}^{t}}\right)\\ &&-a\sum\limits_{k=1}^{K}\frac{N_{k,0} \phi_{k} (1+\phi_{k})^{t-\xi_{a}-1} {\rho_{k}^{t}}}{{\sum}_{j=1}^{K} N_{j,0} \phi_{j} (1+\phi_{j})^{t-\xi_{a}-1} {\rho_{j}^{t}}}\log(1+\phi_{k}) . \end{array} $$

According to our model at the sector level, the logarithm of $\mathbb {E}[\mathcal {N}_{k,t}(a)]$ is linear in a and can be written as $\log \mathbb {E}[\mathcal {N}_{k,t}(a)]=\beta _{0,k}+\beta _{k,1}a$, with $\beta _{k,0}=\log (N_{k,0} \phi _{k} (1+\phi _{k})^{t-1} {\rho _{k}^{t}})$ and $\beta _{k,1}=-\log (1+\phi _{k})$. Then, at the economy level we obtain

$$ \log\mathbb{E}[\mathcal{N}_{t}(a)]=\log\sum\limits_{k=1}^{K} e^{\beta_{k,0}}+a\sum\limits_{k=1}^{K}\frac{e^{\beta_{k,0}+\xi_{a}\beta_{k,1}}}{{\sum}_{j=1}^{K} e^{\beta_{j,0}+\xi_{a}\beta_{j,1}}}\beta_{k,1} . $$

Notice that the coefficient of a is an age dependent convex combination of the sectoral coefficients. This implies that at the aggregate level the slope of the log-distribution is bounded from above by the maximum sectoral slope while it is bounded from below by the minimum one. Thus, an approximated geometric behaviour can emerge at the economy level from perfect sector-wise geometric distributions. At the same time, aggregate deviations can also be generated by the sectoral heterogeneity.

4.2 Comparative statics

In this section we firstly analyse the comparative statics of the age distribution for different values of entry rate and survival probabilities. We then study how structural shocks might affect the shape of the theoretical age distribution. We present results for both unconditional and conditional shocks to survival rates. Coherently with the previous section, we consider the former as shocks that affect all the firms alike (independently of their age); the latter as shocks that affect different groups of firms (e.g. young and old firms) in an heterogeneous manner.¹⁸ In all the following exercises we compute the age distribution at time t = T = 100 and we set N₀ = 10⁶.

Comparative statics with no shocks

We start considering the baseline scenario and compare the distributions that emerge under different assumptions on the parameter values. In Fig. 6 we plot the expected number of firms with age {1,2,…,100} both for the particular case ϕ = 1 − ρ (which we denote as baseline) and for cases in which either the entry rate or the survival probability is higher.

Fig. 6

Comparative statics analysis of the age distribution for three different parametrizations. Baseline: ρ = 0.9, ϕ = 0.1. Higher survival: ρ = 0.95, ϕ = 0.1. Higher entry: ρ = 0.9, ϕ = 0.15

The exercise confirms our analytical findings. In particular, keeping ϕ constant, if the survival probability is higher, the unique observable variation is that the equilibrium distribution becomes more populated and moves outward, with the slope of the distribution remaining unchanged (see the short-dashed line of Fig. 6). Alternatively, if the entry probability is higher, one can observe a variation in the slope of the distribution which becomes steeper (long-dashed line in Fig. 6). Conversely, if the entry probability were lower, the distribution would be flatter.

Unconditional shocks.

A more interesting situation is a dynamic one, in which either the entry rate or the survival probability are hit by a shock at a specific point in time. How does the shock affect the age distribution in the medium run? To answer this question we use the unconditional scenario (second case) presented in advance assuming that ϕ_t and ρ_t maintain the baseline values (solid line) until time t_c and shift to different values for t ≥ t_c.¹⁹ In this way we capture the effects of a persistent shock – e.g. a structural change, possibly generated by a new policy regime, that hits either the survival probability (short-dashed line) or the entry rate (long-dashed line). We fix the critical period at which the shock hits our economy at t_c = 80.

When the shock is unconditional there are two main conclusions that we can grasp (see Fig. 7). First, a fall (an increase) in the survival rate shifts downward (upward) the distribution without however changing the slope of the distribution (cfr. the short dashed line translated below with respect to the solid line representing the baseline without shocks). This is due to the fact that all the firms are hit homogeneously. Both the firms that were already in the market before the shock has been hitting (i.e. at the right of the dotted blue vertical line) and the ones that have entered the market after the shock has hit (i.e. at the left of the shock line) are equally affected. This is also consistent with the intuition provided in Section 4 and with the comparative statics observed in Fig. 6: survival rates only impact upon the intercept of the distribution. Second, a fall (an increase) in the entry rate shifts downward (upward) the distribution only after the shock hits (i.e. at the left of the shock vertical line) and also affects the slope of the distribution which becomes relatively flatter (steeper).

Fig. 7

Age distribution with unconditional shocks. Baseline: ρ_t = 0.9, ϕ_t = 0.1 ∀t. Decrease survival: ρ_t = 0.85 and ϕ_t = 0.1 for t ≥ 80, baseline for t < 80. Decrease entry: ρ_t = 0.9 and ϕ_t = 0.08 for t ≥ 80, baseline for t < 80

Conditional shocks.

Relaxing the assumption that the survival rate is independent from age provides additional relevant insights. Hence, we consider the case in which at a given time t_c the economy moves from the baseline to the conditional scenario.²⁰ Thus, in Fig. 8 we investigate the case in which young firms (without loss of generality, less than or equal to 10 years old) have the same survival probability of older ones. But when a shock hits, only the survival rate of these young firms declines.

Fig. 8

Age distribution with shock only to young firms. Baseline: ρ_Y = ρ_O = 0.9, and ϕ = 0.1. Conditional shock: ρ_Y = 0.9 before the shock and ρ_Y = 0.85 after the shock; ρ_O = 0.9, ϕ = 0.1

Here the shock hits at t_c = 60. Firms that have a_i,T > 50 in Fig. 8 were already old when the shock hits; hence for age level larger than 50, the distribution resembles the perfect geometric shape of the baseline case without shock. Since when the shock hits it decreases the survival rate of the young firms, the cohorts of firms that were still young at t_c are partially hit. For example, the set of firms with $a_{i,t_{c}-1} = 9$ is affected for only one period while the set of firms with $a_{i,t_{c}-1} = 3$ is affected for 7 periods. This leads to the declining slope observed in the interval (40,50] of Fig. 8. Further on the left in the same panel – i.e. for all firms born after the shock – we can clearly observe a piecewise geometric behaviour: one for old firms with a_i,T ∈ (10,40] – whose rate of exit is lower – and one for young firms with a_i,T ≤ 10 – whose rate of exit is higher. Consistently with the analytical results outlined before, in the presence of conditional effects, also the survival rate affects the slope of the age distribution.

5 Model calibration

An important exercise to validate our modelling framework and to relate it with the empirical evidence on business dynamism is to analyse the entry and exit rates implied by our model. We calibrate the unconditional scenario (first case) specification of Section 4 assuming that the survival probability is constant over time: ρ_t = ρ∀t. For this exercise we also employ the empirical estimates presented in Section 3. We have observed that the linear fit in Section 3 provides correlated residuals (cfr. Fig. 2).

This exercise has to be thought as a rough indication of what values are reasonable for the average entry rate and survival probability in order to obtain a log-distribution comparable to the real one, but one shall keep into account that requires the additional assumption of time-independence of entry rates. Still, this is very informative as it allows to infer rough averages of entry and exit rates over a very long time period. With this caveat in mind, our fitted model reads

$$ \hat{\beta}_{0}+\hat{\beta}_{1} a = \log(N_{0}^{*}\phi^{*}(1+\phi^{*})^{t-1}\rho^{*t})-\log(1+\phi^{*}) a $$

from which, knowing that the slope is determined only by the entry rate, we can directly derive the calibrated value of the average entry rate. This writes $\phi ^{*}=e^{-\hat {\beta }_{1}}-1$. Concerning the other two parameters to calibrate, we have to rely on a more sophisticated methodology because of an under-identification problem. We thus employ the indirect inference technique. The literature on calibration and estimation of heterogeneous agents models has prospered during the last decades with the development of new techniques for accomplishing these computationally heavy tasks (see ; Fagiolo et al. 2019). Many contributions, in particular aimed at enriching the indirect inference technique originally developed by Gourieroux et al. (1993), have allowed the estimation of models for financial markets (Franke and Westerhoff 2012), for industry dynamics (Alfarano et al. 2012) and for aggregate macroeconomics dynamics (Grazzini et al. 2017). In this case, given the stylised nature of our model and its small dimensionality in both the parameter space and the output, we use a simple calibration framework. We employ the indirect inference method exploiting the analytical closed form equation for the target variable to be matched by the model. Hence, we numerically calibrate the model by plugging a finite combinations of parameters, selected from a regular two-dimensional lattice, into this equation.

We design a strategy aiming at minimizing the absolute deviations between the model prediction and the empirical estimates. Thus, we define as target variable $\hat {y}$ the empirically estimated intercept $\hat {\beta _{0}}$. We instead define as elements of the vector of key structural parameters to be calibrated 𝜃^∗ the survival rate ρ and the initial number of firms N₀.²¹ We then explore the parameter space by selecting a discrete set Θ of values and we compute the model generated target variable $\bar {y}(\mathbf {\theta })$ for each parameter combination 𝜃 ∈Θ. We select the optimal parameter vector such that

$$ \mathbf{\theta}^{*} = \underset{\mathbf{\theta} \in {\Theta}}{\arg \inf} ~ |\bar{y}(\mathbf{\theta}) - \hat{y}| $$

(16)

where $\bar {y}(\mathbf {\theta })$ represents the intercept predicted by the model under the specific parameter choice – i.e. $\bar {\beta _{0}}(\mathbf {\theta }^{*}) = \bar {\beta _{0}}(N_{0}^{*},\rho ^{*})$). The model prediction for this intercept is formally described by the following equation:

$$ \bar{\beta_{0}}(N_{0},\rho) = \log(N_{0}) \phi^{*} \rho^{t} + (t-1) \log(1+\phi^{*}). $$

(17)

Our design selects the optimal parameters by minimizing the euclidean distance of the model predicted intercept $\bar {\beta _{0}}$ and the empirically estimated one $\hat {\beta _{0}}$. Before discussing the calibration results, it is important to remark that the number of statistics to be matched is lower than the number of parameters to be calibrated. This gives rise to an under-identification problem and to the possibility of a multiplicity of optimal points.

The result of our calibration exercise for the establishments of all aggregated sectors is presented in Fig. 11 in Appendix Appendix. A single optimal value $(N_{0}^{*},\rho ^{*})$ can be found, and is represented as a red dot over the N₀,ρ plane. However, its relative performance with respect to a countable number of other parameter configurations, represented along the blue corridor, is relatively small. This is the result of the under-identification issue. However, the set of points close to the local optimum are all located along an almost horizontal line, except for very small values of N₀. They are therefore characterized by a survival rate ρ between 90% and 95% and by a large variability in terms of N₀. But the value of N₀ does not have a direct economic interpretation, while ρ does. We conclude therefore that it can be almost arbitrary fixed in order to accommodate a a reasonable value of the survival rate. This is a good property for the possible empirical application of our model to datasets from other national economies, with the aim of performing a comparative exercise.

All the results of the entry and exit rates stemming from our calibration exercise at broad aggregation levels (i.e. for the aggregate, manufacturing, services) and at the enterprise and establishment levels, are presented in Table 3. These calibrated values provide a rough indication of the level of entry and exit rates over the period of time spanning from the date of birth of the oldest firm in the sample (i.e. around 1918) to the year of the observation (i.e. 2018).

Table 3 Calibrated entry (ϕ^∗) and exit (1 − ρ^∗) rates at the largest levels of aggregation

Over this long time-horizon our results point to higher entry rates and lower exit rates for services rather than manufacturing. This is consistent with the fact that over the last century a structural transformation affected the French economy, as the economies of many advanced countries. In particular, a process of de-industrialization took place with the heavy industrial activity slowing down and leaving the space to the creation of new business in the service sectors, as the entry costs for the generation of new businesses declined. Overall, we conclude that our model is sufficiently good for the combination of an empirically estimated value of the entry rate and a reasonable value of exit rates. Comparing our results with the values of entry and exit rates for establishments in France over the period 1993-2014 reported by Aghion et al. (2018) (cfr. Figure 9a in particular), we notice that our calibrated entry rate is in line with their estimates, while our exit rate results are slightly below the estimates therein provided. Even if there are differences in the datasets employed and in the considered periods, this result confirms the good performance of our model for identifying entry rates.

In Appendix Appendix (cfr. Table 7) we also present the detailed results for the 2-digit level of aggregation. But in this case a note of caution shall be spelled out. We shall indeed take into account the evidence presented in Fig. 5 as the presence of deviations from a well behaved geometric distribution might limit the validity of the calibration exercise. Especially for young sectors, in which only few observations are available and the uncertainty in the calibration exercise can be relevant. Our results, however, point to some interesting features of business dynamism. We find that sectors with higher business dynamism (the sum of entry and exit rates) are the ones concerning programming and broadcasting activities, telecommunications, computer programming, consultancy and the postal and courier activities, consistently with international evidence (Calvino and Criscuolo 2019). Also in this case, we conclude that our simple model is able to capture some important features of the French business dynamism. In particular, we argue that the relationship between the age distribution and business dynamism is a solid one and is further discussed in the next section.

6 Discussion

The model with different scenarios, together with the comparative statics and calibration exercises carried out thereafter, are particularly helpful in guiding the interpretation of the stylised facts discussed in Section 3. In particular, building upon archetypal situations generated by our theoretical framework, we can provide some suggestive evidence that helps uncover the underlying mechanisms behind the shape of the age distribution.

The first stylised fact presented, i.e., that the geometric law is a first approximation for the aggregate and macro-sectoral age distributions can be interpreted in the light of the fact that, on average over a long time period, a roughly stable entry rate – around 12% – may not be too far from reality, at least as a rough first-order approximation. However, the significant aggregate deviations from the geometric distribution discussed in the second stylised fact may be interpreted as indicative of differences and variations in business dynamism, across firms with different characteristics and over time.

In particular, a first relevant structural break highlighted in Section 3 indicates that the slope of the age distribution is steeper for a < 10 than for a ∈ [10,30), as discussed in the second stylised fact and evident in Fig. 12. This can be explained by the presence of heterogeneous survival rates. In particular, according to our results and consistently with empirical evidence, a lower survival probability for young businesses seems to be the most plausible explanation.²² Such effect could actually be even stronger, considering that a decline in entry rates after the crisis (or a more secular one, as discussed next) would have acted in the opposite direction.

A second structural break highlighted in Section 3 divides the age distribution between firms with a < 30 (born during the great moderation) and firms with a ∈ [30,50). The change of steepness, following the interpretations stemming from our model, would be consistent with a decline in entry rates. This is also evident when focusing on the estimated parameters of the piecewise geometric distribution (based on Eq. 2), which depict a lower λ_i towards the left of the support (see Fig. 12).²³ Furthermore, the downward jump at age equal to 10 would be consistent with a one period drop in entry rates which follows the beginning of the global financial crisis.

The last three decades appear therefore characterized by a lower rate of entry with respect to the number of incumbents. This interpretation suggests that business dynamism in France has declined during the great moderation period and that it was instead larger between the beginning of the 1970s and the beginning of the 1990s. This result is also consistent with the evidence that Decker et al. (2016, May), Goldschlag and Tabarrok (2018), and Calvino and Criscuolo (2019) have put forward and might indicate a global pattern of declining entry rates in several advanced economies.

For a ≥ 50, deviations from the geometric benchmark are more relevant and may be more difficult to interpret, also due to the less systematic data collection procedures. However, the steeper and more volatile age log-distribution for firms older than 50 but younger than 75 years old may correspond to higher rates of entry over the post-war recovery period (Trente Glorieuses). Around the Second World War instead a significant downward jump in the log-distribution is evident, just before firms aged 75. This would be consistent with a notable drop in entry rates. A flatter log-distribution in correspondence to firms older than 75 may instead reflect the effects of the Great Depression.

Sectoral heterogeneity appears as a characteristic feature of age distributions, as highlighted discussing the third stylised fact in Section 3. Cross-sectoral variation in age distributions appears importantly related to differences in the stage of the life-cycle in which different industries stand (see ; Klepper 1996). Importantly, and as highlighted in the previous section, younger sectors – such as the Computer programming, consultancy and related activities industry (62) – tend to have a steeper age log-distribution, consistently with higher average entry rates over a given period of time. Differently, more traditional sectors, such as the food manufacturing industry (10), tend to have flatter age log-distributions, consistently with lower average entry rates that characterise more mature sectors.

Furthermore, focusing again on Figs. 4 and 10 and on Table 6, one can observe that more mature industries tend to have larger average, median and maximal ages. They thus have a longer right-tail and tend to be more populated (see e.g. sector 105 representing the manufacture of dairy products). Young industries, have been born less than 100 years ago and display a short cut to the tail and a possible fast increase in the log-count of firms, when reading the graph from the right to the left (see e.g. sector 620 representing computer programming, consultancy and related activities).²⁴

Aggregation of relatively broad sectors that are approximately geometrically distributed yields – as a reasonable approximation – an aggregate geometric distribution whose decay depends upon sector-specific weight and decays. This suggests that the stage of life-cycle of different sectors also affects the overall maturity of the economy and that cross-country comparisons of the slope of aggregate age log-distributions may be interesting.

More significant deviations from the geometric benchmark arise when analysing 3-digit sectors’ dynamics. This may be indicative of the fact that – in more detailed sectors – entry rates are less constant in given time periods, and that evolutionary dynamics of entry and exit over the industry life-cycle become better observable at finer-grained levels of aggregation. In this context, a reasonable conjecture seems to be that what is observed at more aggregate levels can be reasonably approximated by a more constant quantity resulting from the composition of life-cycle evolutionary dynamics occurring at the more micro level. This may occur as the process of technological change and industry evolution is continuous, with new sectors being born as old ones get closer to maturity.

Differences in the age distribution of businesses have significant implications for economic outcomes. Indeed, the age composition of countries and sectors of activity is an important feature of industrial dynamics, with relevant implications in terms of job creation, innovation, and ultimately economic growth. Building upon the literature on the role of young firms and their importance for job creation (Haltiwanger et al. 2013; Criscuolo et al. 2014), and the literature on the evolution of industries, which highlights that younger sectors are more prone to labour-friendly product innovations (Klepper 1996), we explore the relationship between employment growth in France and the calibrated sectoral entry and net entry rates derived in Section 5.

We source employment growth rate at sectoral level from the OECD STAN database, focusing on France for the period 2006-2016 (the last available years).²⁵ We then carry out an association exercise by estimating the simple linear model by means of ordinary least squares with robust standard errors:

$$ {\Delta} \log(emp)_{s,t} = \alpha ~ entry_{s} + \theta ~ X_{s,t} + \gamma_{t} + \epsilon_{s,t} , $$

(18)

where ${\Delta } \log (emp)_{s,t}$ measures employment growth, entry_s stands for the calibrated entry rate $\phi ^{*}_{s}$ or, alternatively, for the net entry rate defined as $\phi ^{*}_{s} - (1-\rho ^{*}_{s})$, which are both reported in Table 7; X_s,t represents a set of control including sector size, measured in terms of employment (i.e. emp_s,t); γ_t refers to year fixed effects and 𝜖_s,t is the usual error term. Subscripts s and t indicate sectors and time, respectively.

Results, reported in Table 4, highlight a positive association between sectoral employment growth rates and entry, suggesting that industries in the earlier phases of their life-cycle present more labour-friendly dynamics. This confirms the importance of young firms for employment growth, and is possibly related to a more significant share of product innovations in younger industries. Results also hold when controlling for the size of the sector, as measured by total sectoral employment.

Table 4 Robust standard errors in parentheses. *** p < 0.01, ** p < 0.05, * p < 0.1

Of course this last exercise is only a first and suggestive application in order to highlight the potential and relevance of studying features of age distributions, and in particular its coefficients. As a matter of fact, in the framework of the model we have proposed, they have a relevant link with entry rates and the life-cycle of industries. Future analysis may further explore and relate the parameters of age distributions, and the calibrated entry and exit rates, to different economic outcomes.

7 Conclusions

In this paper we have studied in detail the shape and determinants of the age distribution of business firms. This has been a subject overlooked by most of the literature, although important given the key role of young firms in market economies.

Using a new comprehensive cross-sectional database of French firms we presented three stylised facts. First, a geometric shape appears to be a reasonable first-order approximation for the aggregate age distribution; second, there are however significant deviations from the geometric benchmark at aggregate level; third, significant cross-sectoral heterogeneity in the slope of the age log-distribution emerges, with larger deviations from the geometric benchmark at very fine levels of aggregation.

We have then developed and calibrated a stochastic model of firm dynamics to better understand the mechanisms behind the stylised facts and guide the interpretation of the empirical findings through comparative statics exercises. Our modelling strategy provides a novel non-trivial mechanism to generate a geometric age distribution and to explain deviations from such a benchmark. We also introduce sectoral heterogeneity and we show that the aggregation of a finite number of geometric distributions with heterogeneous coefficients, each representing one sector, can lead to the emergence of an approximated geometric distribution at the aggregate level.

Combining the empirical evidence with the model prescriptions, we suggested the existence of a long-term decline in entry rates, which flattens the age log-distribution for firms with less than 30 years, and of a lower survival probability for young firms, which induces a relatively steeper distribution for businesses with less than 10 years of age. The findings also pointed to a short-term effect of the Great Recession, which generates a blip in the age distribution for firms born around 2008. Effects of the Great Depression, the Second World War, and the subsequent post-war recovery were also visible, although should be taken more cautiously as older data may have been collected less systematically.

Further examination of the age distribution at lower level of aggregations revealed that the geometric benchmark broadly holds also within 2-digit sectors. But with sectors-specific slopes that are significantly different from each other. This suggested that different sectors are at different stages of their life-cycle, providing an indirect way to measure them, and that the aggregate behaviour reflects important compositional effects. More significant deviations from the geometric benchmark at very fine grained (3-digit) levels of aggregation may suggested that evolutionary life-cycle dynamics become even more observable in more detailed sectors. We have ultimately extensively discussed the main findings and provided a first application, in order to highlight the relevance of the age distribution – and its parameters – for economic outcomes, notably for employment growth.

This work can be extended along different dimensions. From an empirical perspective, slopes of the age log-distributions can be studied beyond France, across sectors of different countries (or across countries), in order to assess differences in the maturity of sectors to their life-cycle. Furthermore, additional applications can relate the parameters of the age distributions to different economic outcomes, beyond employment growth. From a theoretical perspective, instead, a more ambitious extension would study the age distribution jointly with the size and growth distributions of firms. Building a stochastic model that has the ability of replicating and explaining all the three empirical patterns can disclose new information on the mechanism behind firms and industry dynamics which might be relevant also for policy makers.

Appendices

Appendix A: Additional tables and figures

Table 5 Results of the χ² test

Table 6 Estimated values of β₀ and β₁ representing the geometric shape in Eq. 1 for aggregate data and for sectors at the 2 digit levels

Table 7 Optimal calibrated values for survival rate ρ^∗ and entry rate ϕ^∗ for 2-digits sectors, establishment data

Fig. 9

Pooled age distribution at the establishment (left panel) and enterprise (right panel) levels. The continuous black line represents the empirical distribution; the red dashed-dotted line the geometric fit estimated with MLE

Fig. 10

Age distribution of establishments at the 3-digit level for nine selected industries. The selected 3-digit industries here depicted are sub-sectors of the nine 2-digit sectors displayed in Fig. 4

Fig. 11

Calibration exercise. The figure represents the log of the loss function (Euclidean distance) described by the minimization problem in Eq. 16. The red dot represents the optimal combination of parameters

Fig. 12

ML estimates of λ = (λ₁,λ₂,…,λ₅) from the piecewise geometric distribution in Eq. 2 with k = (10,20,30,40)

Appendix B: Technical Annex

Conditional scenario - dynamical system setting

Using matrix notation, Eq. 12 becomes

$$ \begin{aligned} \left[ \begin{array}{ll} \mathbb{E}[N_{t}]\\ \mathbb{E}[N_{t-1}]\\ \mathbb{E}[N_{t-2}]\\ \vdots\\ \mathbb{E}[N_{t-\bar{a}+1}] \end{array} \right] =\left[ \begin{array}{lllll} \phi\rho_{Y} +\rho_{o} & x_{1} &\cdots& x_{\bar{a}-2} & x_{\bar{a}-1}\\ 1 & 0 & {\cdots} & 0 & 0\\ 0 & 1 & {\cdots} & 0 & 0\\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & \vdots\\ 0 & 0 & {\cdots} & 1 & 0 \end{array} \right] \left[ \begin{array}{ll} \mathbb{E}[N_{t-1}]\\ \mathbb{E}[N_{t-2}]\\ \mathbb{E}[N_{t-3}]\\ \vdots\\ \mathbb{E}[N_{t-\bar{a}}] \end{array} \right] \end{aligned} $$

with $x_{k}={\phi \rho _{Y}^{k}}(\rho _{Y}-\rho _{O})$ for $k\in \{1,2,\ldots ,\bar {a}-1\}$. Iterating the map one has

$$ \begin{aligned} \left[ \begin{array}{ll} \mathbb{E}[N_{t}]\\ \mathbb{E}[N_{t-1}]\\ \mathbb{E}[N_{t-2}]\\ \vdots\\ \mathbb{E}[N_{t-\bar{a}+1}] \end{array} \right]=\left[ \begin{array}{lllll} \phi\rho_{Y} +\rho_{o} & x_{1} &\cdots& x_{\bar{a}-2} & x_{\bar{a}-1}\\ 1 & 0 & {\cdots} & 0 & 0\\ 0 & 1 & {\cdots} & 0 & 0\\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & \vdots\\ 0 & 0 & {\cdots} & 1 & 0 \end{array} \right]^{t-\bar{a}+1} \left[ \begin{array}{ll} \mathbb{E}[N_{\bar{a}-1}]\\ \mathbb{E}[N_{\bar{a}-2}]\\ \mathbb{E}[N_{\bar{a}-3}]\\ \vdots\\ \mathbb{E}[N_{0}] \end{array} \right] . \end{aligned} $$

Initial conditions can be computed using Eq. 4 with $t\in \{1,2,\ldots ,\bar {a}-1\}$ and ρ_Y in the place of ρ. $\mathbb {E}[N_{0}]$ is not defined, with an abuse of notation we impose it equal to N₀/ϕ, such that the map in Eq. 12 is well-defined for each $t\geq \bar {a}$. The dynamical system can be solved using the standard spectral decomposition technique and one obtains the expected number of firms in each period t. The formula for the expected number of firms with age a at time t in Eq. 13 is derived adapting Eq. 6 to the age-dependent survival probability.

From baseline to conditional

In what follows we assume that at time t_c the economy shifts from the baseline scenario to the conditional scenario. Let us start from the expected number of firms in the economy and notice that for t < t_c $\mathbb {E}[N_{t}]$ can be easily recovered from Eq. 4. If t = t_c one should carefully consider the fact that firms with $a_{i,t_{c}-1}<\bar {a}$ and newly created ones now have a different survival probability, hence it is

$$ \begin{aligned} \mathbb{E}[N_{t_{c}}]=\mathbb{E}[N_{t_{c}-1}]\phi\rho_{Y}+\mathbb{E}[N_{t_{c}-2}]\phi\rho_{Y}\rho_{O}+\ldots+\mathbb{E}[N_{t_{c}-\bar{a}}]\phi\rho_{Y}\rho_{O}^{\bar{a}-1}+\mathbb{E}[N_{t_{c}-\bar{a}}]\rho_{O}^{\bar{a}} . \end{aligned} $$

Following the same reasoning line, for $t\in (t_{c},t_{c}+\bar {a})$ it is possible to derive the expected number of firms iteratively according to the map

$$ \begin{aligned} \mathbb{E}[N_{t_{c}+k}]=&\phi\sum\limits_{j=0}^{k-1}\mathbb{E}[N_{t_{c}-j}]\rho_{Y}^{k-j}+\phi\rho_{Y}^{k+1}\sum\limits_{m=1}^{\bar{a}-k}\mathbb{E}[N_{t_{c}-m}]\rho_{O}^{m-1}\\&+\phi\sum\limits_{n=0}^{k-1}\mathbb{E}[N_{t_{c}-\bar{a}+n}]\rho_{Y}^{n+1}\rho_{O}^{\bar{a}+k-2n-1}+\mathbb{E}[N_{t_{c}-\bar{a}}]\rho_{O}^{\bar{a}+k} \end{aligned} $$

with $k\in \{1,2,\ldots ,\bar {a}-1\}$. Then, for $t\geq t_{c}+\bar {a}$ one can use the dynamical system approach presented in advance, obtaining

$$ \begin{aligned} \left[ \begin{array}{ll} \mathbb{E}[N_{t}]\\ \mathbb{E}[N_{t-1}]\\ \mathbb{E}[N_{t-2}]\\ \vdots\\ \mathbb{E}[N_{t-\bar{a}+1}] \end{array} \right]=\left[ \begin{array}{lllll} \phi\rho_{Y} +\rho_{o} & x_{1} &\cdots& x_{\bar{a}-2} & x_{\bar{a}-1}\\ 1 & 0 & {\cdots} & 0 & 0\\ 0 & 1 & {\cdots} & 0 & 0\\ {\vdots} & {\vdots} & {\ddots} & {\vdots} & \vdots\\ 0 & 0 & {\cdots} & 1 & 0 \end{array} \right]^{t-t_{c}-\bar{a}+1} \left[ \begin{array}{ll} \mathbb{E}[N_{t_{c}+\bar{a}-1}]\\ \mathbb{E}[N_{t_{c}+\bar{a}-2}]\\ \mathbb{E}[N_{t_{c}+\bar{a}-3}]\\ \vdots\\ \mathbb{E}[N_{t_{c}}] \end{array} \right] \end{aligned} $$

with $x_{1},x_{2},\ldots ,x_{\bar {a}-1}$ defined as before. Finally, Eq. 6 can be adapted such that one gets

$$\mathbb{E}[\mathcal{N}_{t}(a)]= \begin{cases} N_{0}{\rho_{O}^{t}} & \text{if} a=t ,\\ N_{0}\phi(1+\phi)^{t-a-1}{\rho_{O}^{t}} & \text{if} t-t_{c}+\bar{a}<a<t ,\\ \phi\mathbb{E}[N_{t-a}]\rho_{Y}\rho_{O}^{a-1} & \text{if} a=t-t_{c}+\bar{a} ,\\ \phi\mathbb{E}[N_{t-a}]{\rho_{Y}^{2}}\rho_{O}^{a-2} & \text{if} a=t-t_{c}+\bar{a}-1 ,\\ \phi\mathbb{E}[N_{t-a}]{\rho_{Y}^{3}}\rho_{O}^{a-3} & \text{if} a=t-t_{c}+\bar{a}-2 ,\\ \quad{\vdots} & \quad\vdots\\ \phi\mathbb{E}[N_{t-a}]\rho_{Y}^{\bar{a}-1}\rho_{O}^{a-\bar{a}+1} & \text{if} a=t-t_{c}+1 ,\\ \phi\mathbb{E}[N_{t-a}]\rho_{Y}^{\bar{a}}\rho_{O}^{a-\bar{a}} & \text{if} \bar{a}<a\leq t-t_{c} ,\\ \phi\mathbb{E}[N_{t-a}]{\rho_{Y}^{a}} & \text{if} a<\bar{a} . \end{cases} $$