1 Introduction

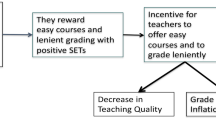
Although employee evaluation is a common practice in work environments (Rynes et al. 2005; Cahuc et al. 2014), in the case of higher education teachers the anomalous aspect is that the evaluation is generally carried out by their students – a peculiarity that raises concerns of validity and reliability (Zhao and Gallant 2012). In traditional workplace settings, the responsibility of the evaluation is with the worker’s supervisor, namely a subject in a higher hierarchical position who is strategically interacting with the worker in a classical principal-agent context (Chauvet et al. 2015). In such context, the evaluation of the worker’s performance is an integral part of the principal-agent scheme itself (Mitusch 2006). In the case of the student evaluation, however, the evaluator is in a strategically subordinate position, although protected by anonymity. Student evaluations of teachers are largely adopted in higher education institutions, and their outcome may have a significant impact on the latter’s professional opportunities and even career prospects (Krautmann and Sander 1999). Student Evaluation of Teaching (SET) is therefore considered an integral part of the educational and training process, and such evaluations are today the most important, and sometimes the sole, measure of a teacher’s ability other than traditional forms of peer evaluation or self-assessment (Greenwood and Ramagli 1980). This creates a natural incentive for teachers to manipulate the scheme to their own advantage (Roberts 2016), e.g. by inflating grades to positively influence students’ evaluations (Ewing 2012), with an obvious information bias on both actual quality of teaching and students’ performance (Langbein 2008).

In terms of how SET is carried out and used by school and university deans, however, there is a far from uniform situation, both across different national institutions and a fortiori at an international level. SET is usually administered through anonymous questionnaires filled by students, but its structure, the way in which it is administered and collected, data processing, techniques of analysis and performance indicators, and the nature of the feedback to the evaluated teachers may all largely differ from case to case. In most cases, deans are the only ones to whom full information about the performance of teachers and the respective performance indicators is disclosed (apart from the confidential performance report received by each teacher on his/her own courses), with an implied large amount of discretional power as to how they are interpreted, circulated (or purposefully leaked), and used in decision-making. As a rule, all questionnaires focus upon basic features of teaching such as clarity, perceived competence, relevance, internal consistency, syllabus appropriateness, quality of teaching materials and reading lists, fair balance between course requirements and credits, and contextual features such as availability to students and punctuality both in class and at office hours, performance of teaching assistants, classroom logistics, etcetera (Braga et al. 2014).

The debate on whether SET is a useful tool for teachers’ evaluation or not, and consequently on whether they are a source of biases in teachers’ grading choices, is still open and heated. The literature is not entirely conclusive about the usefulness of SET in the light of the possible incentive compatibility problems that it raises (Darwin 2017), of the necessity of further methodological development (Setari et al. 2016), and of the ambiguity of the very notion of ‘good’ teaching from the viewpoint of students (Nasser-Abu Alhija 2017), which in turn also partially depends on cultural differences (Georgakopoulos and Guerrero 2010). On the other hand, constructive feedback from student evaluations seems to be helpful in improving teachers’ performance (Knol M.H. et al. 2013), and teachers’ perceived care for students may have a larger positive effect on student evaluation than expected grades (Gotlieb 2013). The main issue is of course the tradeoff between securing a high quality of teaching vs. manipulating the scheme at the advantage of both parties. In principle, both teachers and students profit from a high-quality teaching environment. Students benefit from the high level of professional qualification they acquire through attendance and study, and from a higher level of intrinsic motivation and engagement (Griffin 2016). Teachers get the reputational benefits from teaching in an institution that provides excellent education, which may result in further professional opportunities and career advances, and moreover they enjoy a fulfilling professional experience. On the other hand, there is a clear public good dilemma in that, once the high reputation of the institution has been established, there is an incentive to free-ride for both teachers and students (Matos-Diaz 2012), or to set up positive reciprocation schemes (Cho et al. 2015). Students may be tempted to find ways to get high grades while economizing on studying effort (Mangan and Fleck 2011), whereas teachers may be in turn tempted to receive good evaluations by accommodating the students’ shirking attitude through grade inflation, getting higher chances of out-competing colleagues for tenured positions (Johnson 2003). If this is the case, the overall performance of the educational institution is compromised, and this will eventually cause a loss in reputation. The SET mechanism, unfortunately, may implicitly set up incentives for both parties to mutually adjust in terms of individually rational free-riding, and may even penalize pedagogical innovation (Walder 2017). In terms of social optimum, as it is typical of public good problems, the high-quality equilibrium may be Pareto superior to the low-quality one. However, the outcome of a SET-driven quality monitoring strategy may be Pareto-suboptimal due to the dysfunctional incentive structure, moreover causing a reduction of the signaling value of education for the screening of workers in the labor market. Recent evidence suggests, though, that only less than half of the increase in average grades over two decades at a large US public university (Clemson) may be attributable to grade inflation factors (Hernández-Julián and Looney 2016).

The modelling of the interaction between teachers and students in a SET environment naturally lends itself to be deployed in game-theoretic terms, and there is a substantial amount of literature that follows this route. However, relatively little attention has been devoted so far to the social influence dynamics that govern strategic behavior in this context. The extent to which teachers may be prone to inflate their grades, or students to shirk on their performance, may also depend upon social incentives, such as conforming to established collective behaviors. However, the literature so far tends to regard choices on both sides as individual ones, with little attention to the social environment. This paper offers a new contribution to the literature on SET-related strategic interaction that places it in a social context, and where consequently social selection of behaviors takes place. Moreover, our model considers a sequential strategic interaction where teachers’ quality choices in a course affect students’ performance in a subsequent, related course, as students’ performance in the second course is also dependent on the knowledge acquired in the first. Therefore, if most students fail in the second course, this may be seen as an indirect signal of negative quality of the teaching in the first course (although, as shown by Carrell and West, 2010, teaching methods that positively affect students’ evaluations of a course might also harm their follow-up achievement in subsequent, more advanced courses). In our model, then, reputation effects for teachers play an important role in their strategic decisions.

We characterize the conditions under which a Pareto efficient outcome where teachers provide quality classes and students work hard and reward teachers with good evaluations emerges as the result of social selection. Depending on cases, the efficient outcome may prevail for all initial distributions of behavioral types across the population of teachers, or it may require that an initial high enough critical threshold of high-performing teachers is found. Intuitively, a critical role in determining these conditions is played by the discount factor: the more teachers keep into account the effect of their teaching performance on the students’ preparedness in the subsequent course (and therefore their own future evaluation on the basis of the students’ performance in the subsequent course), the more likely they will choose to teach a good course. The more such a forward-looking attitude pays off for teachers, the more it tends to spread socially across the population of teachers, and to become an ingrained feature of the educational environment, and vice versa. However, the welfare evaluation of the possible states that are socially selected is complex, and depends among other factors on teachers’ motivation and on the relative benefits of high-quality vs. low-quality teaching. As a consequence, the prevalence of high-quality teaching is not necessarily the socially optimal outcome in all circumstances.

The remainder of the paper is organized as follows. Section 2 presents the literature review. Section 3 introduces the model. Section 4 studies the social dynamics and illustrates the basic results. Section 5 develops the welfare analysis. Section 6 provides a final discussion and concludes.

2 The under-recognized social dimension of SET

The literature on SET has a long history, dating back to more than 80 years (Linse 2017), and an interesting persistence. The contemporary debate is still influenced to some extent by comprehensive assessments from the mid-70s (Page 1974), and by statistical approaches to the measurement of their effectiveness developed in the early 80s (McCready 1981). Also the literature on the behavioral implications of SET mechanisms spans several decades. Rotem and Glasman (1979) provide an early warning on the source and nature of the bias that characterizes SET, and Kroman (1978) underlines how the teacher’s and student’s perspectives in SET may be both limited in their focus and incapable to take the other side’s position properly into account. Brown and Saks (1987) analyze teachers’ time allocation choices and consider how strategic behavior can affect them. Wilson (1998) presents a review of the fundamental critical issues to be tackled by SET designers. By the late 90s, however, SET had become a fully established practice, with a key role in faculty hiring and promotion decisions (Becker and Watts 1999).

In the subsequent years, the literature on SET has proliferated to an extent that makes it almost impossible to make a fair appraisal of the pros and cons of its use, while taking into account all of the available evidence (Pounder 2007). Despite the huge research and measurement effort, the literature is still inconclusive, and evaluation studies have not managed so far to bring about consensus about the effectiveness of SET. The available evidence leaves ample room for concern. Stark and Freishtat (2014), for example, suggest that SET does not measure teaching effectiveness because a teacher’s performance should be basically assessed in terms of the ability to facilitate learning, but measuring learning facilitation is hard, and the evaluations given by students after the course are only poor proxies. In addition, Emery et al. (2003) show that SET can fail to capture the teacher’s ability to foster effective learning and is not conducive to the improvement of the educational outcome. Crumbley et al. (2001), in their examination of students’ perception of the SET, show that poor SET scores may be a signal of inadequacy of student effort, of poor quality of the teacher’s instructional input, or of both, and observe that SET scores may also be used by students as a retaliation against teachers for bad grades, heavy workloads, and so on. Meta-analyses of the literature even suggest that there might be no significant relationship between students’ evaluations of a teacher’s performance and the extent to which students actually learn from that teacher (Clayson 2009; Uttl et al. 2017). The main conclusion that can be drawn from this body of work seems to be that we are still lacking a clear conceptual framework and evaluation methodology to be able to assess to what extent SET is useful, for what specific purposes, and what are the essential limitations of its use.

In this paper, we move from the acknowledgement of the intrinsic limitations of SET as pointed out by the literature, but we also observe that, as SET is so widely used in the current educational practice, it is important to understand at least how to design incentive schemes for SET administration that bring about socially beneficial outcomes to some extent. This does not amount to legitimizing SET as the appropriate tool for the monitoring of instructional quality. Our goal is to contribute to the optimization of its use while waiting for a more solid scientific consensus for or against its adoption. In particular, we study the role of social incentives in determining both teachers’ and students’ behavior, in their strategic interplay with the incentives set up by the functioning of the SET mechanism itself. The social dimension plays a truly important part in SET, as the teacher-students relationship takes place in the micro-social environment of the classroom. Moreover, teachers and students constantly interact with their peers, both within the context of their own educational institution and of other, often spatially close, ones. These interactions inevitably influence many different aspects of teachers’ and students’ behaviors, from role models and perceived social norms, to expectations about incentives and rewards, to the framing of future career prospects, and so on. Therefore, evaluating the effects of SET as abstract mechanisms without keeping into account the specific social conditions in which a given mechanism operates may be misleading. Depending on the social environment, the same mechanism could yield either socially optimal or disappointing results, according to circumstances.

Recent research is starting to reflect these subtleties, although generally without an explicit focus on the role of the social environment. As a rule, relatively more motivated, committed, well-performing students tend to participate in the evaluation process more than other types of students. Therefore, where educational systems work well, we expect higher levels of participation in, and possibly a more effective functioning of, SET (Kherfi 2011). Gaertner (2014) reports for instance the results of a German case study where students provide reliable assessments of teachers’ performance, and teachers constructively discuss students’ feedback with them and adapt their teaching methods accordingly. However, the extent to which these results may depend on the deeply ingrained cooperative social governance model of German society cannot be ignored (Orrù et al. 1998). Likewise, students at the Belgian University of Antwerp tend to provide better SET evaluations the more they perceive SET to have a value as a tool for improving quality of teaching (Spooren and Christiaens, 2017), implicitly manifesting their reliance on evaluation mechanisms in a social context which has historically been characterized by high levels of formalized social monitoring (Hofman 2014). On the other hand, in contexts with low social capital and strong reliance on informal ties and familism, such as in Southern Italy, the evaluation of teachers may be less compelling, and systematic patterns of grade inflation may be observed (Argentin and Triventi 2015).

In the existing literature on SET, the role of social incentives pops up often although unsystematically, but generally lacks a clear conceptual framework that highlights the potential connections between different results. One key aspect of traditional, university-administered SET is its confidential character, and the fact that its result is not disclosed to students or peers unless the teacher intentionally does it. Therefore, from the point of view of social influence mechanisms, analysis of publicly available sources of information on teacher evaluation, such as online platforms for the evaluation of teachers like ratemyprofessors.com, may be of special interest, as these platforms provide the basis for ‘electronic word-of-mouth communication’ (Hartman and Hunt 2013). In such platforms, students voluntarily post their assessment of a teacher’s educational performance, and it turns out that such pooling of information not only impacts other students’ expectations about classroom experience and attitude toward the class, but also improves their perceived control, both at the undergraduate (Kowai-Bell et al. 2011) and at master level (Kowai-Bell et al. 2012). This establishes in turn a powerful channel of social influence where single reviews may acquire a disproportionate weight. Not surprisingly, it is found that the availability of such kind of information tends to influence students’ course choices independently of its reliability, and leads to strong biases in choice (Li and Wang 2013). On the other hand, such online evaluations, despite their well-known limitations in reliability and representativeness (that can in principle be overcome by using random sampling schemes for students, see Goos and Salomons, 2017), also impact upon teachers’ affect and self-efficacy (Boswell 2016), though not upon their self-concept of competence (Kowai-Bell et al. 2012).

Perhaps more surprisingly, another result that emerges from the literature and points to social influence effects is that SET tends to be sensitive to race and gender (Basow and Silberg 1987; Bavishi et al. 2010; Basow et al. 2013), and is even systematically influenced by the perceived sexual attractiveness of the teacher (both male and female) – an aspect which is clearly uncorrelated with teaching performance (Riniolo et al. 2006; Fenton et al. 2008). Wagner et al. (2016) find evidence of a particularly strong negative gender bias against women teachers even in a diverse, multi-ethnic, multicultural sample of students and teachers from a Dutch university, and Boring (2017) finds similar evidence of negative gender bias against women in a French university. Fah and Osman (2011), analyzing the relationship between tutorial ratings, course and teacher characteristics in Canadian SET show that, whereas gender seems to have no effect on students’ rating, ethnicity does. Students of Indian origin tend to assign higher course scores compared to other ethnicities, and this might depend on the fact that, as courses are taught in English, they encounter less problems than non-native English speakers from other overseas countries. Goos and Salomons (2017), moreover, point out that SET, and the related response rate, is affected by the disciplinary field and type of course attended by students, and that the response rate may be strongly improved when even a very small grade incentive is offered in exchange (see also, Dommeyer et al., 2004). A more ambiguous variable is the amount of social interaction between teacher and student, that consistently predicts positive student evaluation and may be partially related to teaching quality, but certainly also accounts for social communication and influence factors (Sheer and Fung 2007). There is moreover a significant amount of subjective variation in students’ relational responsiveness to different teachers, with potential gains from appropriate matches (Gross et al. 2015). Finally, although the perceptions of students and teachers with regard to effective teaching are positively correlated, differences exist as well (Bosshardt and Watts 2001). For example, students care more about the teacher’s preparation for class than instructors do. Pan et al. (2009) find that, contrary to widespread opinion, students tend to value the quality of teaching (e.g., ability to explain, facilitation of understanding) more than teachers’ personality traits (e.g., sense of humor, charisma, extraversion, and so on).

The previous discussion shows that there is a variety of social incentives at work that may influence the functioning of SET in various ways and directions. Therefore, failing to take into account social influence effects may be a major modeling shortcoming in the attempt to understand under what conditions SET may be conducive to socially optimal results. We will now present a simple evolutionary game-theoretic model that provides a conceptual context for the study of the social selection of SET-driven optimal outcomes.

3 The model

Several game-theoretic models of teacher/student and teacher/teacher strategic interactions are currently available. Building on the seminal works of Marchi and Miguel (1974) and Hamburger (1979), Correa and Gruver (1987) model the teacher/student strategic interaction with a continuous strategy set, and find that non-optimal allocations can emerge due to a suboptimal level of effort provided by both teachers and students. However, the introduction of a teacher evaluation system may lead to a higher level of effort than required by the social optimum, possibly leading to dysfunctional over-commitment effects (Reimann 2016). An early, similar modeling of the teacher/teacher interaction is proposed by McKenzie (1979), who considers the joint offering of a course by two teachers in two distinct modules, with the common aim of attracting the largest possible number of students and of getting high rating. The model suggests that, since students are able to understand the quality of teachers, when professors are equal in every other respect, the teacher who offers more generous grading will tend to receive the highest student ratings. Alternatively, if the teachers are viewed as distinctively different by students, the one with the lower rating can offset the differential by easing up grading criteria, thus leading to grading inflation. Correa (2001) shows that this setting naturally leads to a social dilemma situation with the well-known sub-optimality issues. Correa (2003) considers the strategic interaction among one teacher and n students with different abilities and attitudes toward effort, analyzing the incentives for the teacher to provide a more vs. less committed approach to teaching, and introducing the issue of diversity in players’ capabilities and ethical standards. Strategic behavior of teachers is of relevance in view of the consolidated evidence that teachers are sensitive to economic incentives (Figlio and Kenny 2007), and that monetary incentives may crowd out teachers’ intrinsic motivation and attitude toward unpaid work (Jones 2013). In this paper, we combine some of the previous elements by considering a situation where two teachers are called to cooperate in the achievement of high teaching standards having both to choose between two different levels of teaching output. However, we also add a sequential element to our model, namely, that the teacher’s output influences the performance of students in a subsequent course, thus introducing a reputational effect that plays against the incentive to free ride on effort.

Teachers are evaluated in two stages: immediately after the end of their course, and once more at the end of a second, related course that their students attend subsequently. Students’ evaluation of the second course also provides an additional source of evaluation of the teachers of the first course, whose overall evaluation is a weighted sum of the two. By providing low effort teaching output, teachers of the first course therefore make it less likely that the students are well prepared for the second course. Consequently, students obtain relatively worse evaluations for the second course, that also negatively affect the teachers of the first course, who may consequently have an extra incentive to provide high effort output ceteris paribus. Will this be enough to ensure that the social optimum is reached?

More formally, teachers face a strategic choice between offering a demanding (Difficult, D) or a less demanding (Easy, E) course. We consider a large population of teachers where, at any time t (time is continuous), a number of couples of teachers are matched to play an evaluation game, one for each matched couple. The payoffs to the strategies D and E are determined through a two-stage evaluation process. The two stages are indicated as I and II, respectively. At stage I, teachers are evaluated by their students. At stage II, they receive a second evaluation as their students, on the basis of their performance in a subsequent, related course, retrospectively rate the first course professor’s actual contribution to their preparedness for the second course. As far as stage I evaluation is concerned, we assume that students prefer professors who give them a relatively light study load and relatively good grades, that is, they prefer to attend an E rather than a D course. Consequently, we assume for simplicity that at stage I, E ensures better student evaluations than D, and that such difference in evaluations reflects into teachers’ payoffs. On the other hand, we assume that teachers’ payoffs are not influenced by socially relevant factors of teacher evaluation such as gender, ethnicity, or sexual attractiveness. The only social incentives that matter in our model are therefore linked to the frequency of adoption of certain behaviors, but not to players’ (teachers’) personal traits. Finally, we assume that the game is symmetric; that is, teachers do not differ in terms of skills, or other features that may generate asymmetries in payoffs. In terms of the evaluation game for the two teachers, the (symmetric) payoff matrix for stage I is:

$$ \text{Stage }I: \ \ \ \begin{array}{ccc} & D & E \\ D & \alpha & 0 \\ E & 1 & \beta \end{array} $$
(1)

where 1 > α,β > 0. For a (row) teacher, the outcome (E,D) is the optimal one in that the teacher provides low effort and receives a good evaluation, and specifically a better one than the column teacher providing high effort (Krautmann and Sander 1999; Oleinik 2009). Accordingly, the worst outcome is the (D,E) one, where the teacher provides high effort and receives a worse evaluation than the other teacher providing low effort. Notice that strategy E dominates D in the single-stage game. Moreover, if α > β, the game turns into a Prisoner’s Dilemma, with (E,E) as the unique Nash equilibrium and (D,D) as the social optimum. This payoff structure might hold if teachers, even when sensitive to the strategic temptation to shirk, still maintain some level of intrinsic motivation for teaching quality that makes socially uniform levels of high effort teaching preferable to uniform levels of low effort teaching when no personal strategic advantage may be reaped from the interaction. If we admit moreover the possibility that α > 1, so that teachers strongly prefer the uniformly high effort social situation to free riding, then the game admits two Pareto-ranked Nash equilibria. From the students’ perspective, (D,D) could be rationally preferred to (E,E) in that, in a long-term perspective, they have an interest in maximizing the knowledge return to their educational investment – a judgment which conflicts with their short-term interest to reward teachers who offer low effort courses, minimizing their study burden. In what follows, however, we restrict for simplicity the analysis to the case α < 1.

At stage II, we assume that D ensures teachers a better evaluation than E, and that such difference in evaluation reflects into teachers’ payoffs, whereas again other socially relevant individual characteristics such as gender, ethnicity or sexual attractiveness do not matter. The payoff matrix for teachers is then the following:

$$ \text{Stage }II: \ \ \ \begin{array}{ccc} & D & E \\ D & a & 1 \\ E & 0 & b \end{array} $$
(2)

where a > 0 and 1 > b > 0. Now, from the second course’s perspective, it is optimal for the teacher to have provided a high effort teaching output at stage I, since this now ensures a positive retrospective evaluation by students after they have taken the second course. The relative size of parameters a and b depends on teachers’ attitudes toward their teaching duties, and ultimately on their motivations. More specifically, if a < 1, then the teacher choosing D gets a higher payoff if the other teacher provided a low effort teaching output E, with a consequent lower overall preparation for the students. Vice-versa if a > 1. Analogously, if a > b (this is always true in the context where a > 1), then both teachers obtain in (D,D) a higher payoff than in (E,E); vice-versa if a < b. Therefore, the nature of the strategic interaction is heavily affected by the teachers’ normative orientation and thus, ultimately, by the ‘cultural’ factors that shape the prevailing set of effort-related social norms. As already anticipated in our discussion of the literature, this modeling feature points out how the analysis of the effectiveness of a SET scheme should always be related to the specific social environment in which it takes place. In different environments, teachers and students might be literally playing different kinds of games.

With respect to stage I, the payoff structure is now overturned, and in the single stage II game strategy D dominates E so that, if the strategic interaction were limited to stage II, all teachers would choose to provide a high effort teaching output in the first course. To compute the teachers’ payoffs over the two stages, we assume that payoffs earned at stage II are weighted (discounted) by a factor 𝜃 ∈ (0,1). Therefore, the overall payoffs are given by the matrix:

$$ \text{Stage }I\text{ \& Stage }II{: \ \ \ } \begin{array}{ccc} & D & E \\ D & \alpha+\theta a & \theta \\ E & 1 & \beta+\theta b \end{array} $$
(3)

Under the postulated payoff structure of the two stages combined, teachers now face a trade-off: getting a better payoff in the short run by playing E, or being focused on the long run by playing D. In the following section we will assume that the adoption process of strategies D and E is driven by a payoff-monotonic evolutionary dynamics, and we will highlight the dynamic regimes that may be observed under the payoff matrix (3).

4 Social selection dynamics

4.1 Evolutionary dynamics

Assume that the population of teachers is very large, and that at each time t (a number of couples, each one consisting of) two teachers are randomly selected from the population to play the two-stage evaluation game (1)-(2) introduced in the previous section. In this context, time t may be interpreted as a parameter that orders the evaluation events. Teachers choose their strategies ex-ante, without knowing the strategy chosen by the other teacher (courses need time to be prepared and syllabuses are published in advance). Denote by x(t) the share of teachers choosing strategy D at time t. Strategy E will be consequently chosen by 1 − x(t) teachers at t, with 1 ≥ x(t) ≥ 0. The population shares of the two strategies also represent, in a random matching environment from a large population, the probabilities to be matched to a teacher choosing the respective strategy. Hence, according to the payoff matrix (3), the expected payoffs accruing to strategies D and E are given, respectively, by:

$$ \pi_{D}(x)=\left[ \alpha+\theta(a-1)\right] x+\theta $$
(4)
$$ \pi_{E}(x)=\left( 1-\beta-\theta b\right) x+\beta+\theta b $$
(5)

We model the social selection dynamics for the two strategies in terms of a payoff-monotonic evolutionary dynamics which, in the case of two strategies, may be specified without loss of generality in terms of the replicator dynamics (Weibull 1995):

$$ \overset{\cdot}{x}=x(1-x)\left[ \pi_{D}(x)-\pi_{E}(x)\right] $$
(6)

where \(\overset {\cdot }{x}\) is the time derivative of x(t), whereas the payoff differential is given by:

$$ \pi_{D}(x)-\pi_{E}(x)=\theta(1-b)-\beta+\left[ \alpha+\beta-1+\theta\left( a+b-1\right) \right] x $$
(7)

The dynamic behavior of the replicator dynamics (6) is qualitatively equivalent here to that of any sign preserving dynamics of the type:

$$ \overset{\cdot }{x}=F\left( \pi_{D}(x)-\pi_{E}(x)\right) $$

where F is a differentiable function for every x in the interval (0,1) such that \(\overset {\cdot }{x}>0\) (respectively, < 0 and = 0) if πD(x) − πE(x) > 0 (respectively, < 0 and = 0). Moreover, under every sign preserving dynamics, the following statements are all true: i) a stationary state \(\overline {x}\in (0,1)\) of equation 6, where \(\pi _{D}(\overline {x})=\pi _{E}(\overline {x})\), corresponds to a mixed strategy Nash equilibrium of the static game (3), where both teachers play strategy D with probability \(\overline {x}\), and strategy E with probability \(1- \overline {x}\); ii) the states x = 0 and x = 1 are locally attractive stationary states if, respectively, (D,D) and (E,E) are (strict) Nash equilibria of the two-stage game defined by the payoff matrix (3).

The social selection dynamics (6) describe a process where teachers are boundedly rational in that at each instant of time only a small fraction of them considers the possibility of revising their strategy, and the higher the payoff differential between the two strategies at that time, the stronger the (smooth) aggregate shift of strategy-revising teachers from the worse performing strategy to the better performing one.

4.2 Dynamic regimes

The dynamic regimes of the social selection dynamics (6) can be classified as follows:

  1. 1.

    If πD(x) − πE(x) ≥ 0 (respectively, πD(x) − πE(x) ≤ 0) for every x ∈ [0,1], then we shall say that strategy D dominates strategy E (respectively, E dominates D). If D dominates E, then whatever the initial distribution of strategies x(0) ∈ (0,1), the trajectory starting from it approaches the attractive stationary state x = 1 (where all teachers play D). Vice-versa, if E dominates D, for any interior initial condition x(0) ∈ (0,1), the trajectory starting from it approaches the attractive stationary state x = 0 (where all teachers play E).

  2. 2.

    If there exists a repulsive interior stationary state \(\overline {x} \in (0,1)\) (where both strategies coexist), separating the basins of attraction of the attractive stationary states x = 0 and x = 1, then we shall say that a bistable dynamic regime occurs.

  3. 3.

    If there exists an interior stationary state \(\overline {x}\in (0,1)\) and, for any initial distribution of strategies x(0) ∈ (0,1), the trajectory starting from it approaches \(\overline {x}\), then we shall say that a coexistence dynamic regime occurs.

Note that the payoff differential (7) is a strictly increasing function of x if:

$$ \alpha+\beta-1+\theta\left( a+b-1\right) >0 $$
(8)

If condition (8) holds, then the relative performance of strategy D, with respect to strategy E, improves as the share x of teachers adopting D increases, and vice-versa if (8) is strictly violated. The context in which (8) is not met favours the coexistence between teachers playing different strategies, whereas when it is met the extinction of one strategy is generically observed. Essentially, the left-hand side of (8) measures how the social incentives at work tend to depend on the aggregate distribution of behaviors across teachers. In a situation where the payoff differential between D and E increases with the share x of teachers adopting D (and, accordingly, decreases with the share 1 − x of teachers adopting E), we have a ‘snowball’ social selection dynamics where the behavior that becomes socially prevailing eventually takes over at the expense of the other one. When on the contrary the payoff differential between D and E decreases with the share x of teachers adopting D, we have a ‘homeostatic’ social selection dynamics that tends to preserve diversity of behaviors across the population of teachers, and to reduce the relative share of a certain behavioral type if it becomes too prevalent. As already remarked, the social selection is entirely governed here by the frequency of adoption of the available behaviors, and not by the individual characteristics of the players (teachers). In particular, this also means that the individual characteristics of the teachers make no difference in terms of the social salience of their choice from the point of view of the adoption or diffusion dynamics. It is possible to imagine alternative social selection dynamics where this symmetry is violated, and the adoption dynamics is biased by factors such as gender, ethnicity, sexual attractiveness, etcetera.

In order to gain more insight into the structure of the dynamic regimes of the model that will be presented below, it is convenient to have first a closer look into how the model’s parameters contribute to condition (8) being met or not. The validity of condition (8) (‘snowball’ social selection dynamics) is favored by relatively larger values of α and a. These are the parameters that control how rewarding it is for teachers to coordinate upon a difficult (D) course at stages I and II of the game, respectively. Likewise, the onset of the ‘snowball’ regime is also favored by relatively higher values of β and b, namely the rewards associated to coordinating upon an easy (E) course at stages I and II, respectively. The intuition behind this is clear: the more rewarding a given strategic option becomes, the more likely that the social dynamics will imply its widespread adoption once a critical mass of teachers has already adopted it. The structure of condition (8) also highlights the importance of the relative size of the rewards that characterize each stage of the game. The sign of the left-hand side of (8) depends in particular on whether the sum of the rewards from the coordinated outcomes at each stage, where both teachers play the same strategy (i.e. they both choose D or E) exceeds or not 1, namely, the sum of the payoffs from the non-coordinated outcomes where teachers choose different strategies at the same stage. Remember that in our payoff normalization, the latter quantity has been set constant to 1. In particular, the relative payoff from coordination vs. mis-coordination at stage II (a + b − 1) determines whether the discount factor 𝜃 has a positive or negative impact on the condition (8). When a + b > 1, that is, when the value of coordination at stage II exceeds the value of mis-coordination, a higher discount factor favors the onset of the ‘snowball’ scenario where all teachers coordinate upon the same effort level, and where therefore the suboptimal equilibrium with low educational quality may eventually emerge. When a + b > 1 and most teachers choose low teaching effort, there is little incentive for the other teachers to go for high teaching effort, as unilateral deviations are relatively non-rewarding: hence the low effort equilibrium eventually prevails, and all the more so the higher the weight teachers place upon the payoffs from stage II (i.e., the higher 𝜃). A similar reasoning makes the emergence of the high effort equilibrium likely when most teachers choose high effort under the same condition. On the contrary, if a + b < 1, the value of mis-coordination at stage II is relatively high, and this gives teachers an incentive to go for high effort when most teachers choose low effort or vice versa. Under this condition, the higher the weight teachers tend to assign to the payoffs at stage II (i.e., the higher 𝜃), the more likely that they will go against the trend and choose a level of effort that is different from the one chosen by most teachers. As a consequence, a higher 𝜃 plays now against the onset of the ‘snowball’ dynamic regime and in favor of the ‘homeostatic’ one. In a nutshell, therefore, what condition says is that the ‘snowball’ regime will prevail whenever the total net value of coordination (that is, the value of coordination at stage I minus the value of mis-coordination at stage I, plus the weighted value of coordination at stage II minus the weighted value of mis-coordination at stage II) is positive. Vice versa, the ‘homeostatic’ regime will prevail when the total net value of coordination as defined above is negative (and therefore there is a stable incentive to mis-coordinate).

In the light of the above remarks, the formal characterization of the dynamic regimes as offered by Propositions 1 and 2 below is easily read and interpreted. In particular, Proposition 1 characterizes the ‘snowball’ regime and Proposition 2 the ‘homeostatic’ regime.

Proposition 1

If condition (8) holds, then:

  1. (i)

    Strategy D dominates strategy E if:

    $$ \theta\geq\frac{\beta}{1-b} $$
    (9)
  2. (ii)

    Strategy E dominates strategy D if:

    $$ \theta\leq\frac{1-\alpha}{a} $$
    (10)
  3. (iii)

    The bistable dynamic regime is observed if:

    $$ \frac{\beta}{1-b}>\theta>\frac{1-\alpha}{a} $$
    (11)

The interpretation of the role of the parameters in the conditions of Proposition 1 is relatively straightforward. Consider for instance condition (9) for the dominance of D. The larger β and the closer b to 1 (i.e., the more rewarding ceteris paribus the coordination on the low effort strategy E at stages I and II, respectively), the less likely that dominance of D may occur, as the viable values of the weight 𝜃 are more tightly constrained. Likewise, the larger α and a (i.e., the more rewarding ceteris paribus the coordination on the high effort strategy D at stages I and II, respectively), the less likely that dominance of E may occur, again due to tighter constraints on 𝜃. The bistable pattern emerges when the two previous conditions for dominance are both simultaneously violated, and 𝜃 sits in an intermediate range of (feasible) values.

Proposition 2

If condition (8) is strictly violated, then:

  1. (i)

    Strategy D dominates strategy E if:

    $$ \theta\geq\frac{1-\alpha}{a} $$
    (12)
  2. (ii)

    Strategy E dominates strategy D if:

    $$ \theta\leq\frac{\beta}{1-b} $$
    (13)
  3. (iii)

    The coexistence dynamic regime is observed if:

    $$ \frac{1-\alpha}{a}>\theta>\frac{\beta}{1-b} $$
    (14)

The intuition for the interpretation of the conditions in Proposition 2 is an easy adaptation of that for the conditions in Proposition 1. Again, we have a condition for the dominance of D that is less likely met the smaller (ceteris paribus) the payoff from high effort at both stages I and II, as this makes the constraint on the value of 𝜃 tighter; and a condition for the dominance of E that is less likely met the smaller (ceteris paribus) the payoff from low effort at stages I and II, for a similarly tightening constraint on 𝜃. Coexistence occurs when both dominance conditions are simultaneously violated, and 𝜃 sits in an intermediate range of (feasible) values.

Proofs of Propositions 1 and 2 are straightforward. The various dynamic regimes are illustrated by Figs. 1, 2, 3, where full dots and empty dots represent, respectively, attractive and repulsive stationary states. For cases (iii) of Propositions 1 and 2, the interior stationary state is given by:

$$ \overline{x}=\frac{\beta-\theta(1-b)}{\alpha+\beta-1+\theta\left( a+b-1\right) } $$
(15)
Fig. 1
figure 1

Panel a: Takeover of high effort strategy D . Panel b: Takeover of low effort strategy

Full size image
Fig. 2
figure 2

Bistable regime. Arrows in figure are related to the red solid curve. The dashed blue curve shows the shift of the basin of attraction of the stationary state x = 1 induced by an increase in 𝜃 (notice the new \(\overline {x}\) depicted in blue)

Full size image
Fig. 3
figure 3

Coexistence regime. Arrows in figure are related to the red solid curve. The dashed blue curve shows the increase in the share of teachers playing D induced by an increase in 𝜃 (notice the new \(\overline {x}\) depicted in blue)

Full size image

Note that, in the bistable dynamic regime, the point \(\overline {x}\) separates the basins of attraction of the stationary state x = 0 (the interval \([0,\overline {x})\)) and of the stationary state x = 1 (the interval \((\overline {x},1]\)). If the value of \(\overline {x}\) increases, then \([0, \overline {x})\) expands whereas \((\overline {x},1]\) shrinks. The following proposition shows how the value of \(\overline {x}\) varies in response to a variation in the discount parameter 𝜃, which is of special interest in the interpretation of our results.

Proposition 3

It holds:

$$ \text{sign }\frac{\partial\text{ }\overline{x}}{\partial\text{ }\theta }= \text{sign }\left( 1+\alpha b-b-\alpha-\beta a\right) $$
(16)

where 1 + αb − b − α − βa < 0 (respectively, > 0) in the bistable dynamic regime (respectively, in the coexistence dynamic regime).

Proof of Proposition 3 is straightforward. As a consequence of equation 16, we have that:

  1. 1.

    In the bistable dynamic regime, an increase in 𝜃 expands the basin of attraction \((\overline {x},1]\) of the stationary state x = 1 (where all teachers play D) at the expenses of the basin \([0,\overline {x})\) of the stationary state x = 0; this implies that, assuming that the initial distribution x(0) of strategies is randomly determined, an increase in 𝜃 has the effect to increase the probability that the state x = 1 is eventually reached (i.e. that strategy D takes over).

  2. 2.

    In the coexistence dynamic regime, an increase in 𝜃 has the effect to increase the share of teachers playing D at the globally attractive stationary state \(\overline {x}\) (i.e. in the equilibrium mix of behaviors, high effort teachers are more represented).

The weight of stage II payoffs 𝜃 plays here an intuitively plausible role. The larger the weight that teachers place on the evaluation of their teaching performance at stage II (i.e., the less they discount future evaluation at the moment of choosing their strategy at stage I), the more strategy D will be represented at equilibrium. In particular, it will eventually take over if the social selection dynamics is of the ‘snowball’ type, or it will be increasingly represented at the equilibrium if the social selection dynamics is ‘homeostatic’. All policy measures that will make the follow-up evaluation more salient for teachers, by consequently influencing the size of 𝜃, will therefore prompt a higher incidence of high effort performances across the population of teachers.

5 Welfare analysis

In evaluating the welfare implications of our results, we assume that, for students, a high effort performance of teachers is always preferable to a low effort one, in that students are interested in maximizing the return of their educational investment (Catsiapis 1987; Levin 1989; Sun 1998) – that is, we prioritize their ‘rational’ long-term preferences over their possibly conflicting impulsive, short-term ones. Therefore, from the viewpoint of students, the higher the share of strategy D at equilibrium, the better off the students. From the point of view of teachers, however, the welfare implications are less straightforward. In view of the payoff structure (1)-(2), teachers’ payoffs evaluated at the stationary states x = 0 and x = 1 are respectively given by:

$$ \pi_{E}(0)=\beta+\theta b $$
$$ \pi_{D}(1)=\alpha+\theta a $$
$$ \pi_{D}(\overline{x})=\pi_{E}(\overline{x})=\left[ \alpha+\theta(a-1)\right] \overline{x}+\theta $$

It is easy to prove the following:

Proposition 4

In the bistable dynamic regime, where x = 0 and x = 1 are both attractive, condition πD(1) > πE(0) holds if:

$$ \alpha-\beta>-\theta(a-b) $$
(17)

In the coexistence dynamic regime, where \(\overline {x}\) is globally attractive, condition \(\pi _{D}(1)>\pi _{D}(\overline {x})=\pi _{E}(\overline {x} ) \) holds if:

$$ \alpha+\theta(a-1)>0 $$
(18)

Notice that if a ≥ 1, then (18) is always satisfied; if a < 1, then (18) holds if:

$$ \mathbf{\ }\theta<\frac{\alpha}{1-a} $$
(19)

To understand the meaning of Proposition 4, let us consider the bistable dynamic regime, and remember that the difference α − β represents the payoff gain (or loss, if negative) that each teacher gets passing from the uniform high effort state (D,D) to the low effort state (E,E), in stage I of the game. Analogously, the difference a − b represents the payoff gain (or loss, if negative) that each teacher gets passing from the uniform high effort state (D,D) to the low effort state (E,E), in stage II of the game. Let’s assume, to fix ideas, that α > β, i.e. that the stage I game is a prisoner’s dilemma where teachers would prefer a uniformly high level of effort (D,D), but due to the benefits of free riding the uniform low effort state (E,E) is the only Nash equilibrium of the stage I game. In this case, α − β is the welfare gain for each teacher from achieving the social optimum (D,D) instead of the Nash equilibrium (E,E), that is, the negative of the welfare loss at the Nash equilibrium. If teachers also maintain the same preferences at stage II, that is, if a > b and therefore they still prefer a uniform high effort state (D,D) to a low effort one (E,E) from the point of view of the students’ performance in the follow-up exam,Footnote 1 then condition (17) is trivially satisfied, and this means that the high effort equilibrium (D,D) is welfare improving upon the low effort one (E,E) in the bistable regime. In this case (which we could call the ‘goodwill scenario’), therefore, if the initial share of teachers choosing D is too small, the social dynamics eventually select the Pareto inferior equilibrium. If, on the contrary, a < b holds, and therefore the teachers’ rewards are not strongly dependent on their students’ performance at the follow-up exam (despite still preferring to uniformly exert high effort when teaching at their own course, rather than the uniformly low effort, a case that we could term the ‘direct responsibility scenario’), then the high effort equilibrium (D,D) will be Pareto optimal only if the stage II welfare gain b − a from low effort is discounted enough by teachers, or if alternatively such gain is smaller than the stage I gain α − β from providing uniformly high effort even when the stage II gain is not discounted at all.

Alternatively, if teachers always prefer the uniformly low effort equilibrium (E,E) from the perspective of both stages I and II (and thus, in particular, α < β and a < b hold), for instance because the blame for the students’ performance in the follow-up exam is not put on the teachers according to the prevailing social norms (a case that we could term the ‘shirking scenario’), then condition (17) is trivially violated and in the bistable regime the low equilibrium effort is always Pareto optimal, thus creating a trade-off between the welfare benefit for teachers and that for students. In this case, therefore, an excessive initial share of teachers choosing the high effort strategy leads to a Pareto inferior outcome for teachers (but at the same time to an optimal outcome for students) – and this explains why in regimes where shirking-on-the-job social norms prevail, people providing high effort tend to be sanctioned or ostracized by low effort peers (Kitts 2006). Finally, in the case where teachers prefer a uniform low effort state (E,E) from the point of view of stage I (i.e., α < β) but prefer a uniform high effort state (D,D) from the point of view of stage II (i.e. a > b, e.g. because despite their weak commitment to effortful teaching they either get monetary or career benefits if their students do well in the follow-up course, a case that we could term the ‘instrumentalist scenario’), the welfare comparison between the two equilibria will depend again upon the comparison between the sizes of the welfare loss α − β from a uniform high effort state at stage I and the (discounted) welfare gain 𝜃(b − a) from a uniform high effort state at stage II. In this case, the high effort equilibrium will be Pareto optimal only if the discounted welfare gain from the high effort uniform state at stage II will be large enough compared to the welfare loss from the same state at stage I.

In the coexistence dynamic regime, instead, all that matters for the welfare evaluation are the relative sizes of the payoffs at the uniform high effort state in the two stages, and the size of the discount factor. Here, we will always observe a coexistence of the two strategies at the equilibrium, and therefore the initial distribution of types does not have implications for the optimality of the equilibrium state, provided that it lies in the interior of the state space. In this case, then, the high effort equilibrium may only be selected if all players choose the high effort strategy D from the beginning (that is, if the initial distribution of strategies is x(0) = 1 ).

According to condition (18), the higher the payoffs from the uniform high effort state (D,D) at stages I and II, respectively α and a, the more likely that (18) is met. Notice that condition (18 ) is always satisfied if a ≥ 1, that is, if in the stage II game we have that playing D against D gives a higher payoff than playing D against E. If a < 1, then the smaller 𝜃 (i.e. the more the payoff at stage II is discounted) the more likely that the condition (18) is met. If teachers’ payoffs associated to (D,D) are high enough, in both stages of the game, then they prefer the high effort stationary state x = 1 to the interior stationary state \(\overline {x}\), where both strategies coexist, and therefore it is enough that any small fraction of teachers initially fails to be motivated by providing low effort to cause a general welfare loss. The opposite holds if α and a are low enough, that is, if teachers are not motivated about the overall performance of their students at both stages I and II.

Notice moreover how conditions (17)-(18) are compatible with conditions (11)-(14), which identify the bistable and coexistence dynamic regimes, respectively, but are not implied by them. This amounts to say that, as we have seen, from the viewpoint of teachers the convergence to either the high effort or the low effort equilibrium may be Pareto optimal in the bistable regime, according to cases, and that, analogously, either convergence to the mixed equilibrium or permanence in the high effort equilibrium may be Pareto optimal in the coexistence regime, according to cases.

6 Conclusions

This paper provides a first analysis of the role of social incentives in determining the effectiveness of SET in the implementation of high effort social standards of teaching. When SET is compelling enough to make teachers accountable for their students’ performance in the follow-up exam, the temptation to free ride by getting high scores while offering a low effort course may be overcome in principle but, depending on the details of the incentive structure, this might only happen when an initial critical mass of teachers are willing to provide high effort from the beginning, so that the possibility of being matched to a free riding, low effort teacher is relatively small. If teachers’ SET-driven accountability in the follow-up exam is strong enough, however, the high effort equilibrium might prevail eventually even if the initial share of free riders is disproportionately high. Clearly, however, the viability of a strict SET enforcement in the presence of a very high share of low effort teachers may be critical in social and political terms.

Our analysis shows how the effectiveness of SET in fostering the emergence of high effort equilibria (that best serve the long-term interest of students) is significantly improved when teachers have an intrinsic motivation to provide high effort. Attaching an intrinsic value to the offering of quality education reduces teachers’ benefit to free ride by providing a low effort course, and reinforces the incentive related to teachers’ accountability for the students’ performance in the follow-up exam. Social incentives may therefore play a major role in the broader context of SET-driven incentive structures for teachers. On the other hand, the analysis also shows that there may be a conflict between the interest of teachers and that of students as far as welfare considerations are concerned, and the socially optimal outcome for teachers may be one where students do not maximize their educational investment. One might argue that, if students have an objective interest in teachers to provide high effort courses, they should not reward teachers who give a low effort course with better evaluations. However, this remark does not consider the fact that student preferences may be time inconsistent: in the immediate, they tend to prefer an easy pass to a difficult one in a given exam because of limited time resources and pressing deadlines (Zelby 1974; Brodie 1998), even if they may be seriously concerned about their educational investment (Entwistle et al. 1974), and the complexity and extent of such inconsistencies substantially depend on different possible learning styles (Entwistle et al. 1979).

In our model, different levels of teacher effort may coexist, or alternatively one specific effort level may take over, depending on parameter values, and in particular on the motivation and discount rates of teachers (that is, on individual characteristics) and on the ‘extrinsic’ reward to high-effort teaching on the basis of students’ performance in the follow-up task (that is, on systemic characteristics). However, as we have seen, such individual characteristics may lead to different social outcomes, either optimal or not, depending on the social dynamics, and specifically on the initial distribution of behavioral types in the bistable dynamic regime. This result underlines the role of cultural ‘contextual’ factors, i.e. of the cultural salience of certain behaviors. It may therefore happen that, in regions or countries where established social conventions lead teachers to focus on high effort behaviors, the eventual outcome of the social selection may be opposite to that of other regions where the ruling conventions make low effort teaching salient, despite that both the underlying individual characteristics and the systemic characteristics may in fact be identical. The role of ‘critical mass effects’ in social selection processes must therefore be carefully evaluated from the viewpoint of policy design. Sometimes, acting on established cultural conventions and social norms may be more effective in terms of the aggregate outcome than manipulating policy parameters or regulating teachers’ behaviors through specific evaluation mechanisms such as SET.

It should also be remarked that SET need not be the only possible way to incentivize teachers to provide high effort courses. The experiment undertaken in countries such as Finland in terms of de-structuring educational programs to allow teachers and students to build their own approach in an open-ended, self-responsible way, is particularly interesting in this regard (Sahlberg 2015), also in view of its considerable success in helping Finnish students to achieve very high PISA scores. It must be noted, however, that such an achievement is also made possible by the high social prestige of the teacher role (Hargreaves 2009) and by the egalitarian orientation of Finnish society in terms of equality of opportunity (Sahlberg 2012) – the combined effect of which certainly motivates Finnish teachers to offer quality courses and to expect commitment to learning by students without the need to rely upon formal accountability systems like SET (Toom and Husu 2012). This is an example of how, in certain socio-cognitive contexts, excellence in education may be successfully pursued through mainly intrinsic rather than extrinsic incentives. The relative effectiveness of formal accountability schemes like SET vs. alternative forms of social control in educational systems within different cultural contexts is a still under-researched topic that would deserve more attention.

Placing our results in the context of the existing literature yields some interesting implications. First of all, the analysis of social incentives shows clearly how the evaluation of the effectiveness of a given SET scheme must necessarily be content specific, and that the same scheme may lead to different levels of effectiveness in promoting educational quality depending on the environmental conditions. Secondly, in certain circumstances even small changes in the structure of incentives may bring about substantial changes in the dynamic regime (and in the long-term outcomes), whereas in other cases even relatively large changes do not essentially alter the social dynamics — it all depends on how close the system parameters are to the frontier that separates different regimes (or their sub-regimes as described by Propositions 1 and 2). Finally, the welfare implications of changes in the structure of incentives may be very complex, and without a proper understanding of the underlying structure of the strategic interaction policy interventions may not provide the desired results. The basic message behind our model is therefore that keeping social incentives explicitly into account may substantially alter our analysis and assessment of SET schemes in specific socio-cultural contexts and under specific circumstances.

Our model presents the simplest possible version of a social selection dynamics of teachers’ choices, but clearly one can also consider more complex models in which socially relevant factors such as gender or ethnicity or personal attractiveness matter, both in terms of students’ evaluation and of the demonstrative value of teachers’ choice at the social level. It would be particularly interesting to study how the selection dynamics operate on social networks with specific relational structures and significant anisotropy in the social interaction patterns. Also, it would be interesting to study models where students with different learning styles, educational investment modes and intertemporal preferences evaluate teachers with different propensities to effort, so that the distribution of teachers’ and students’ attitudes in the respective populations co-evolve. Evaluating the impact and welfare properties of SET is a rich theme, that lends itself to multiple generalizations with substantial interest both at the theoretical and at the policy level. Our goal in the present paper was to illustrate how such developments appear particularly promising in the so far unexplored dimension of the social selection of teachers’ attitudes. Now that the point has been made, we look forward to more research that explores this promising path in its full potential.