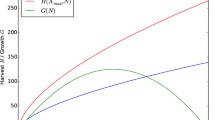
Abstract
In this paper, we investigate the relationship between market dynamics, dynamic resource management and environmental policy. In contrast to static market entry games, this paper draws attention to the effects of market dynamics on resource dynamics et vice versa, because (1) we show that feedback processes are necessary for obtaining a better understanding of what drives the dynamics between the evolution of common-pool resources and the number of harvesters and more importantly, (2) this analysis provides an environment discussing sustainability in an appropriate inasmuch dynamic way. The paper makes the following points: based on a co-evolutionary model, which incorporates resource and market dynamics simultaneously, it is shown that an increasing number of harvesters does not necessarily imply a lower stock of the common-pool resource in the long run. Further it is shown that a tax-scheme establish an output-sharing solution for coping with the overuse of common-pool resources. This results is in contrast to the prevailing literature, which mainly discusses tax-schemes and out-sharing as substitutes rather than as complements for solving the commons-problem. This conclusion holds even if we additionally assume harvesting-cost-reducing technological progress. On the other side if policy interventions ceased, strong resource sustainability in the sense of resource conservation is not possible, given technological progress is a relevant issue.





Similar content being viewed by others
Notes
Albeit the watch-wording sustainable development has been the focal point of many recent works, both in economics and ecology, surprisingly or not, there is a considerable hot debate on the conceptual as well as on the operational level of what sustainability actually contains and implies (Baumgärtner and Quaas 2010). At the end of the day, sustainability remains a more or less obscure item.
We skip the variable-specific time-indices in the following paragraphs.
See, for instance, Dasgupta and Heal (1979).
We define the profits per unit analogously to the per unit cost function as suggested by Bradley (2001).
Because of the fact that firms are assumed to be symmetric with the exception of their cost and harvesting effort, the same arguments as stated in the text above can be used to model the market share evolution of firm j.
The assumption of a constant price level seems to be problematic when analyzing the demand side of the model.
We desist from assuming that firms are engaged in cost reducing R&D. We believe that ignoring this issue will not change the results qualitatively at all. In the absence of C fix,h , the growth rate of cost reducing technology progress is given by \(\frac{\dot{C}_{h}}{C_{h}}=\theta.\)
Of course, the production function is linear as well as the cost function. Associated with fixed output price this leads to conceptual problems in profit maximization, given we would do so. Instead, we have assumed a selection-mechanism based on profit-differentials which is not based on profit maximization.
This argument is in line with Verspagen (2001), who states that radical innovation shocks the preceding economic structures and, more important, the dependencies characterize the economic structure. Non-drastic innovations, however, are directly associated with the diffusion of drastic innovation. For the fishery-example this implies that discovering a new cost-reducing fishery-technique explains a technology gap between the inventor and the other competitors in the market. Over time, the new technique spills-over to the competitors as the radical innovation now becomes the superior technology in the fishery industry by replacing the older one. Consequently, cost heterogeneity decreases and finally disappears. At this point, the cost-reducing potential employing the new technology is entirely exhausted. A new radical innovation is needed to restart the explained chain again.
Of course, this assumption does not limit the explanatory power of the model, because focusing only on the life-cycle perspective but leaving-out the discussion of the closely related market-entry and exits pattern of firms does not gain extra power regarding the robustness of the model and the major points made by the paper. Integrating the latter mentioned point is, of course, an interesting issue but clearly beyond the scope of this paper and it is therefore left open as an avenue for further research.
Of course, we can reduce the dimension from five to two equations if we solve the differential Eq. 5 for firm i. We are going to exploit this fact later on when discussing the global stability of the obtained steady states of the co-evolutionary system.
Analogously, we can use the same harvesting strategy to discuss the dynamic of firm j.
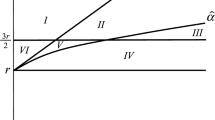
Please note that on the steady-state, the evolution of s i is entirely governed by the endogenous variable N and some constants or parameter. To make clear that s i is c.p. decreasing by increasing N, we write s i ≡ g(N). This is particular from importance for the phase-diagram analysis which will be accomplished in Section 3.4 of this paper.
Of course, if θ = 0, we meet the condition \(\dot{C}_{i}=0\).
As N = 0, from Eq. 9 we conjecture that the market share remains constant for all t.
Please note that \(\underline{N}\) corresponds to \(\underline{C}_{i}\), whereas \(\overline{N}\) corresponds to \(\overline{C}_{i}\). On the steady-state, from Eq. 10 we have \(\underline{N}\equiv h(\underline{C}_{i})\) and \(\overline{N}\equiv h(\overline{C}_{i})\).
The right hand’s side of expression (15) is strictly positive, given (e i C fix,i > e j C fix,j ) which is ensured by the assumption stated in Eq. 7 and e i > e j . The left hand side of Eq. 15 is strictly non- negative, given \((N+1)\geq\left(\frac{e_{i}\Omega_{i}-e_{j}\Omega_{j}}{p(e_{i}-e_{j})}\right)\).
In fact, the irrelevance of fix costs qualitatively does not change the results, unless the initial cost structure is zero which is not imposed for the steady state D 2.
This result is conform to Proposition 4.
This replicates the implications derived from Propositions 5 and 6.
Realizing A 2, the profits per unit N reads as: \(\overline{\pi}=\pi_{i}=0.56\) and π j = 0.44.
The profits per unit N reads as: \(\overline{\pi}=\pi_{i}=1.12\) and π j = 0.89.
The implication is, if neither of these two mentioned criteria are satisfied, there may be periodic solutions or not.
For this choice, the Dulac’s and Benedixon’s criterion coincide.
This implies that Θ > 0 and θ ∈ (0,1) or θ = 0.
This requires that Θ < 0 and θ ∈ (0,1) or θ = 0.
Suppose for a moment that Θ > 0. Then A 1 and A 2 can be described as stable nodes, but B 1 and B 2 are saddle path equilibria, et vice versa for Θ < 0.
The non-degenerate conditions are tr(Jac) = 0 or χ 2 ≠ 0.
References
Atzenhoffer J-P (2010) A note on imitation-based competition in common-pool resources. Environ Resour Econ 47:299–304
Baumgärtner SM, Quaas MF (2010) What is sustainability economics? Ecol Econ 69:445–450
Berkes F, Mahon R, McConney P, Pollnac R, Pomeroy R (2000) Managing small-scale fisheries: alternative directions and methods. IDRC Books, Ottawa
Boulding KE (1978) Ecodynamics: a new theory of societal evolution. Sage, Beverly Hills
Boulding KE (1981) Evolutionary economics. Sage, Beverly Hills
Bradley PG (1970) Some seasonal models of the fishing industry. In: Inst. animal resource ecology (ed) Economics of fisheries management: a symposium. University of British Columbia, Vancouver
Brekke KA (1997) Economic growth and the environment: on the measurement of income and welfare. Edward Elgar, Cheltenham
Bretschger L, Smulders S (2007) Sustainable resource use and economic dynamics. Environ Resour Econ 36:1–13
Bulte EH, Damania R (2005) A note on trade liberalization and common pool resources. Can J Econ 38:883–899
Copeland BR (1994) International trade and the environment: policy reform in a small open economy. J Environ Econ Manage 26:44–65
Costanza R, Norton BG, Haskell BD (1991) Goals, agenda and policy recommendations for ecological economics. In: Costanza R (ed) Ecological economics: the science and management of sustainability. Columbia University Press, New York
Dasgupta P, Heal G (1979) Economic theory and exhaustible resources. Cambridge University Press, Cambridge
De Groot R, der Perk JV, Vliet AV (2003) Importance and threat as determining factors for criticality of natural capital. Ecol Econ 44:187–204
Gordon HS (1954) The economic theory of a common-property. J Polit Econ 62:124–142
Hardin G (1968) The tragedy of the commons. Science 162:1243–1248
Harms J, Sylvia G (2001) A comparison of conservation perspectives between scientists, managers, and industry in the West Coast groundfish fishery. Fisheries 26:6–15
Heintzelman MD, Salant SW, Schott S (2008) Putting free-riding to work: a partnership solution to the common-property problem. J Environ Econ Manage 57:309–320
Hilborn R, Walters CJ, Ludwig D (1995) Sustainable exploitation of renewable resources. Ann Rev Ecolog Syst 26:45–68
Howarth RB (2007) Towards an operational sustainability criterion. Ecol Econ 63:656–663
Illge L, Schwarze R (2009) A matter of opinion—how ecological and neoclassical environmental economists and think about sustainability and economics. Ecol Econ 68:594–604
Jensen CL (2002) Reduction of the fishing capacity in “common pool” fisheries. Mar Policy 26:155–158
Lopez R (1998) The tragedy of the commons in Côte d’Ivoire agriculture: empirical evidence and implications. J Am Stat Assoc 58:993–1010
Mazzucato M (1998) A computational model of economies of scale and market share instability. Struct Chang Econ Dyn 9:55–83
Nelson RP, Wolf EN (1997) Factors behind cross-industry differences in technical progress. Struct Chang Econ Dyn 8:205–220
Noailly J, van den Bergh JCJM, Withagen CA (2003) Evolution of harvesting strategies: replicator and resource dynamics. J Evol Econ 13:183–200
Ostrom E (1990) Governing the commons: the evolution of institutions for collective action. Cambridge University Press, Cambridge
Ostrom E, Gardner R, Walker J (1994) Rules, games, and common-pool resources. The University of Michigan Press, Ann Arbor
Pavitt K (1984) Sectoral patterns of technical change: towards a taxonomy and a theory. Res Policy 1:343–373
Pearce DW, Atkinson G (1995) Measuring sustainable development. In: Bromley DW (ed) The handbook of environmental economics. Blackwell, Oxford
Regev U, Gutierez AP, Schreiber SJ, Zilberman D (1998) Biological and economic foundations of renewable resource exploitation. Ecol Econ 26:227–242
Ruseski G (1998) International fish wars: the strategic roles for fleet licensing and effort subsidies. J Environ Econ Manage 36:70–88
Sandal LK, Steinshamn SI (2004) Dynamic cournot-competitive harvesting of a common pool resource. J Econ Dyn Control 28:1781–1799
Schott S, Buckley N, Mestelman S, Muller RA (2007) Output sharing in partnerships as a common pool resource management instrument. Environ Resour Econ 37:697–711
Stewart KM (2003) The African cherry (Prunus africana): can lessons be learned from an over-exploited medicinal tree? J Ethnopharmacol 89:3–13
Van den Bergh JCJM (2007) Evolutionary thinking in environmental economics. J Evol Econ 17:521–549
Verspagen B (2001) Economic growth and technological change: an evolutionary interpretation. In: OECD Science, technology and industry working papers, 2001/01. OECD Publishing
Walker JM, Gardner R (1992) Probabilistic destruction of common-pool resources: experimental evidence. Econ J 102:1149–1161
Walker JM, Gardner R, Ostrom E (1990) Rent dissipation in a limited-access common-pool resource: experimental evidence. J Environ Econ Manage 19:203–211
Yamamoto T (1995) Development of community-base fishery management system in Japan. Marin Resour Econ 10:21–34
Acknowledgement
The author would like to thank one anonymous referee for comments and suggestions that helped to improve the paper considerably. All remaining errors are, of course, my own.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 Steady states
Proof of the global stability of the obtained steady states of system (8)
Remarks
In this section, we prove the local as well as the global stability of the identified fixed-points of system (8). First, we prove the local stability of the obtained steady states of the non-linear system (8). It is known that for a hyperbolic fixed-point (the real part of the Eigenvalues are nonzero), the flow of the linearized fixed-point is homeomorphic to the non-linear flow (sufficiently close to the fixed-point). Before we proceed, we transform system (8) which consists of three differential equations to a system of two differential equations. We can follow this way because we know that Eq. 5 is a first order autonomous differential equation with the solution given by Eq. 6. Inserting expression (6) into Eq. 8 leads to
We obtain this system assuming C h = C fix,h that is t→ ∞. The Jacobian matrix of system (17) reads as:
with \(\Theta\equiv\frac{N}{N+1}\left[p(e_{i}-e_{j})-e_{i}c_{i}+e_{j}c_{j}\right]=\pi_{i}-\pi_{j}.\) Hence, Θ is the payoff difference between the profit streams of firm i and j.
Proof of Proposition 1
We start with the proof of the local stability of equilibrium A 1,A 2,A 3 and A 4 by evaluating the Jacobian matrix at A 1,A 2,A 3 and A 4 each. Table 2 shows the Eigenvalues and their respective signs for each fixed-point.
The sign of the second Eigenvalue χ 2 for the steady states A 1,A 2,A 3 and A 4 is clearly determined to be negative due to the fact that N > 0. However, the sign of the first Eigenvalue for A 1 and A 2 is not determined ex ante: It could be positive, zero or negative.
If the sign is positive, we obtain a saddle path for A 1 and A 2. If χ 1 and χ 2 are negative, A 1 and A 2 define a stable node. Given the Eigenvalues are zero, we obtain a later line equilibrium because the Jacobian matrix turns out to be singular.
From Proposition 1, it follows that s i = 1 which leads to the conclusion that A 1 and A 2 are strictly negative because Θ > 0 which stems directly from π i > π j . The first Eigenvalue for the fixed-points A 3 and A 4 is clearly negative due to the fact that e i > e j . Therefore, the fixed-points A 1,A 2,A 3 and A 4 are locally stable.
The next point is to show that the equilibrium points A 1,A 2,A 3 and A 4 are asymptotically globally stable. This can be done by ruling out closed orbits. Referring to the literature, two important results provide sufficient conditions that rule out the possibility of periodic solutions: the Benedixon’s and Dulac’s criterion, whereas it turns out that the Benedixon’s criterion can be traced back to the Dulac’s criterion as a special case.Footnote 26
Theorem 1
(Dulac’s criterion) Assume that \(\dot{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{x})\) is a continuously differentiable vector field, on a simply connected open subset of \(\mathcal{R}\times\mathcal{R}\) . If there exists a continuously differentiable, real-valued function \(k(\boldsymbol{x})\) with \(\{N,s_{i}\}\in\boldsymbol{x}\) such that \(\nabla\cdot(k\dot{\boldsymbol{x}})\) has one sign throughout \(\mathcal{R}\) , there are no periodic orbits of the autonomous system in \(\mathcal{R}\) .
Proof
Assume that there is a closed orbit \(\mathcal{C}\) in the simple connected region \(\mathcal{R}\). Let \(\mathcal{D}\) denote the interior of \(\mathcal{C}\). When \(\mathcal{C}\) is transversed counterclockwise, Green’s Theorem in the plane gives the following identity:
where \(\boldsymbol{n}\) is the outward normal and dl is the element of arc length along \(\mathcal{C}\). The integral on the left hand’s side of Eq. 20 must be nonzero, because \(\nabla\:(k\dot{x})\) has one sign in \(\mathcal{R}\). The line integral on the right hand side of Eq. 20 equals to zero because \(\mathcal{C}\) is a trajectory. Thus, the tangent vector of \(\mathcal{C}\), \(\dot{\boldsymbol{x}}\), is orthogonal to \(\boldsymbol{n}\) which leads to \(\dot{\boldsymbol{x}}\boldsymbol{n}=0\). This contradiction implies that no such \(\mathcal{C}\) can exist.□
The problem which comes along with applying the Dulac’s and Benedixon’s criterion is that it is sometimes pretty hard determining an appropriate weighting function \(k(\boldsymbol{x})\), because there is no algorithm providing such a function. With respect to system (17), we choose \(k(\boldsymbol{x})=1\) Footnote 27 which, as we will see, is a good choice helping us to provide a sufficient condition for the exclusion of periodic orbits.
Applying Dulac’s criterion, we can write:
Using the steady state condition s i = 1 associated with the steady states A 1,A 2,A 3 and A 4, we can evaluate expression (21) further as:
Expression (22) turns out to be strictly negative, given N > 0 by assumption and Θ > 0 because of the fact that π i > π j . Hence, \(\nabla(k\dot{\boldsymbol{x}})\) does not change sign in \(\mathcal{D}\). Since the region s i = 1 and N > 0 is simply connected and k(·) and \(\boldsymbol{f}(\cdot)\) are smooth, Dulac’s criterion implies that there are no closed orbits in the positive quadrant. Therefore, A 1,A 2,A 3 and A 4 are asymptotically globally stable.
Proof of Proposition 2
The steady states B 1 and B 2 are locally stable which can be seen from Table 3. Please note that Θ turns out to be negative because of π j > π i .
Applying Dulac’s criterion once again, we find with the steady state condition s i = 0:
which is clearly negative, since Θ < 0. Hence, the fixed-points B 1 and B 2 are asymptotically globally stable since the region N > 0 and s j = 1 is simply connected and k(·) and \(\boldsymbol{f(\cdot)}\) fulfill the smoothness conditions implied by Dulac’s criterion.□
Proof of Proposition 3
Proposition 3 tells that \(C_{i}\in(\underline{C}_{i};\overline{C}_{i})\), which implies π i = π j . Further, the condition \(C_{i}>\frac{1}{e_{i}}\left[p(e_{i}-e_{j})+e_{j}C_{j}\right]\) must hold. If π i = π j , it follows immediately that Θ = 0. For Θ = 0, the Jacobian becomes singular. Thus, at least one Eigenvalue must be zero which can be seen from Table 4.
For this constellation, system (17) exhibits an entire line of fixed-points on g(N), whereas the Eigenvector associated with the Eigenvalue zero is the direction vector of the system. We know that one existence condition for D 1 and D 2 postulates that Θ = 0. Obviously, any marginally, infinitesimally change of Θ in the positive or negative direction drives the flow of system (17) completely out of these equilibria towards A 1 or A 2 Footnote 28 or to B 1 or B 2.Footnote 29 In the case of Θ = 0, linearization of system (17) is not sufficient to deduce any information about the dynamic behaviour of the non-linear system (17), because Θ = 0 serves as a cut-off variable which separates saddle path equilibria and nodes.Footnote 30 Hence, Θ is defined as the so-called fold bifurcation point, because one stable node and one saddle collide and both disappear right at Θ = 0. A necessary condition for fold bifurcation is that det(Jac) = 0 or χ 1 = 0, which obviously holds for system (17). Because of the fact that tr(Jac) ≠ 0, we call the fold bifurcation equilibrium a degenerate equilibrium.Footnote 31
The center subspace E C is the space spanned by the Eigenvector of the linearization with Eigenvalue χ 1 = 0. Based on the center manifold theorem we know, that this guarantees the existence of a manifold W C tangent to E C at the origin. In this case, χ 1 passes through zero at Θ = 0, and given χ 2 < 0, then W C is of dimension one and the evolution on W C is \(\dot{x}=f(x,\Theta)\). We can conclude, that the fixed points D 1 and D 2 are locally saddle-node stable, because χ 1 = 0, which guarantees a steady-state bifurcation.
If we could further exclude the possibility of closed orbits, obviously no limit circle bifurcation can occur globally. To show this, we use the Poincaré map, together with Dulac’s criterion. As shown before, the steady states A 1 to A 4 and B 1 and B 2 are globally asymptotically stable. With respect to a Poincaré mapping, this implies that every trajectory from a given starting point converges to the steady state und thus no closed orbits may occur. Referring to Eq. 21 and considering the fact that Θ = 0, we obtain:
which is clearly negative due to the fact that N > 0. Since the region N > 0 and s i ∈ (0,1) is simply connected and k(·) and \(\boldsymbol{f(\cdot)}\) again fulfill the smoothness conditions implied by Dulac’s criterion, the existence of limit circles can be ruled out. Hence, no limit circle bifurcation can occur globally and thus the steady states D 1 and D 2 are saddle-node-stable.□
Time series for s h , π h , \(\bar{\pi}\) and N
Rights and permissions
About this article
Cite this article
Klarl, T. Market dynamics, dynamic resource management and environmental policy in the context of (strong) sustainability. J Evol Econ 23, 861–888 (2013). https://doi.org/10.1007/s00191-012-0278-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00191-012-0278-0