Learning to trust strangers: an evolutionary perspective

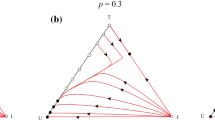
Abstract

What if living in a relatively trustworthy society was sufficient to blindly trust strangers? In this paper we interpret generalized trust as a learning process and analyse the trust game paradox in light of the replicator dynamics. Given that trust inevitably implies doubts about others, we assume incomplete information and study the dynamics of trust in buyer-supplier purchase transactions. Considering a world made of “good” and “bad” suppliers, we show that the trust game admits a unique evolutionarily stable strategy: buyers may trust strangers if it is not too risky to do so. Examining the situation where some players may play either as trustor or as trustee we show that this result is robust.

Appendix

Proof of Proposition 1

The Jacobian of the replicator dynamics at any point r = (p₁, p_2G, p_2B) can be expressed as follows:

$$ \mbox{J}\left( \mbox{r} \right)=\left( {{\begin{array}{*{20}c} {\partial \dot{\rm p}_1 /\partial {\rm p}_1 } \quad\quad& {\partial \dot{\rm p}_1 /\partial {\rm p}_{2{\rm G}} } \quad\quad& {\partial \dot{\rm p}_1 /\partial {\rm p}_{2{\rm B}} } \\ {\partial \dot{\rm p}_{2{\rm G}} /\partial {\rm p}_1 } \quad\quad& {\partial \dot{\rm p}_{2{\rm G}} /\partial {\rm p}_{2{\rm G}} } \quad\quad& {\partial \dot{\rm p}_{2{\rm G}} /\partial {\rm p}_{2{\rm B}} } \\ {\partial \dot{\rm p}_{2{\rm B}} /\partial {\rm p}_1 } \quad\quad& {\partial \dot{\rm p}_{2{\rm B}} /\partial {\rm p}_{2{\rm G}} } \quad\quad& {\partial \dot{\rm p}_{2{\rm B}} /\partial {\rm p}_{2{\rm B}} } \\ \end{array} }} \right), $$

and therefore:

$$ {\rm J}({\rm r}) \!=\!\!\left(\!{{\begin{array}{*{20}c} {\left( {1\!\!-\!\!2{\rm p}_1 } \right)\left[ {\mbox{pp}_{2{\rm G}} {\rm c}_1 \!\!+\!\!{\rm p}\left( {1\!\!-\!\!{\rm p}_{2{\rm G}} } \right){\rm b}_1 \!\!+\!\!\left( {1\!\!-\!\!{\rm p}} \right){\rm p}_{2{\rm B}} {\rm c}_1 \!\!+\!\!\left( {1\!\!-\!\!{\rm p}} \right)\left( {1\!\!-\!\!{\rm p}_{2{\rm B}} } \right){\rm b}_1 } \right]} \hfill & {{\rm p}_1 \left( {1\!\!-\!\!{\rm p}_1 } \right){\rm p}\left( {{\rm c}_1 \!\!-\!\!{\rm b}_1 } \right)} \hfill & {\!\!-\!{\rm p}_1 \left( {1\!\!-\!\!{\rm p}_1 } \right)\left( {1\!\!-\!\!{\rm p}} \right)\left( {{\rm c}_1 \!\!-\!\!{\rm b}_1 } \right)} \hfill \\[3pt] {{\rm p}_{2{\rm G}} \left( {1\!\!-\!\!{\rm p}_{2{\rm G}} } \right)\left( {{\rm c}_2 \!\!+\!\!\varepsilon \!-\!{\rm b}_2 } \right)} \hfill & {\left( {1\!-\!2{\rm p}_{2{\rm G}} } \right){\rm p}_1 \left( {{\rm c}_2 \!+\!\varepsilon \!\!-\!\!{\rm b}_2 } \right)} \hfill & 0 \hfill \\[3pt] {{\rm p}_{2{\rm B}} \left( {1\!\!-\!\!{\rm p}_{2{\rm B}} } \right)\left( {{\rm c}_2 \!\!+\!\!\beta \!-\!{\rm b}_2 } \right)} \hfill & 0 \hfill & {\left( {1\!\!-\!\!2{\rm p}_{2{\rm B}} } \right){\rm p}_1 \left( {{\rm c}_2 \!\!+\!\!\beta \!\!-\!\!{\rm b}_2 } \right)} \hfill \\ \end{array} }} \!\right) $$

According to definition (1), in order to characterize the ESS we should study the eigenvalues of the matrix J in each of the 8 points that are candidates.

Let r* = (1,1,1). The Jacobian is:

$$ \mbox{J}\left( 1,\!1,\!1 \right)=\left( {{\begin{array}{*{20}c} {-\mbox{c}_1 } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {-\left( {\mbox{c}_2 +\varepsilon -{\rm b}_2 } \right)} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {-\left( {\mbox{c}_2 +\beta -{\rm b}_2 } \right)} \hfill \\ \end{array} }} \right). $$

The eigenvalues are: –c₁, –(c₂ + ε – b₂), –(c₂ + β – b₂). They are all negative (which shows that (1,1,1) is hyperbolically stable) if:

$$ \mbox{c}_1 >0,\;({\rm c}_2 +\varepsilon -{\rm b}_2 )>0\;{\rm and}\;({\rm c}_2 +\beta -{\rm b}_2 )>0. $$

The condition on the gains of 2^B (i.e. (c₂ + β – b₂) > 0) contradicts one of the assumption of the trust game and we deduce that (1,1,1) is not an ESS. In the same manner, we show that (1,0,1) and (1,0,0) are also not ESS.

We focus now on (1,1,0), (0,1,1), (0,1,0), (0,0,1) and (0,0,0). For (1,1,0), we have:

$$ \mbox{J}(1,\!1,\!0)=\left( {{\begin{array}{*{20}c} {-\!\left[\mbox{pc}_1 +(1-{\rm p}){\rm b}_1\right]} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {-({\rm c}_2 +\varepsilon -{\rm b}_2 )} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {(\mbox{c}_2 +\beta -{\rm b}_2 )} \hfill \\ \end{array} }} \right). $$

and this point is an ESS because conditions on the gains of the two types of player 2 do not contradict the assumptions of the model. We have: c₂ + ε − b₂ > 0 and c₂ + β − b₂ < 0 and these conditions are verified for:

$$ {\rm p}>\frac{-{\rm b}_1}{{\rm c}_1 -{\rm b}_1 }>0. $$

Regarding (0,1,1), (0,1,0), (0,0,1) and (0,0,0), we obtain respectively:

$$ {\begin{array}{*{20}c} {\mbox{J}(0,\!1,\!1)=\left( {{\begin{array}{*{20}c} {\mbox{c}_1 } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\;\mbox{J}(0,\!1,\!0)=\left( {{\begin{array}{*{20}c} {\mbox{pc}_1 +(1-{\rm p}){\rm b}_1 } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),} \\[30pt] {\mbox{J}(0,\!0,\!1)=\left( {{\begin{array}{*{20}c} {\mbox{pb}_1 +(1-{\rm p}){\rm c}_1 } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\;\mbox{J}(0,\!0,\!0)=\left( {{\begin{array}{*{20}c} {\mbox{b}_1 } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right).} \\ \end{array} } $$

For each of those cases, 0 is an eigenvalue and they are not ESS which concludes the proof.□

Proof of Proposition 2

We proceed as in proposition 1, the difference being that now there is a third type of player that may both play as buyer or seller. We denote by p_3G (respectively p_3B) the proportion of players 3^G (respectively 3^B) choosing T when buying and choosing H when selling. The complement 1 − p_3G (respectively 1 − p_3B) is the proportion of players 3^G (respectively 3^B) choosing M when buying and E when selling.

We start determine the replication equation associated to the behaviour of player 1. If she matches a player 2, her expected payoff is pp_2Gc₁ + p(1 − p_2G)b₁ + (1 − p)p_2Bc₁ + (1 − p)(1 − p_2B)b₁ and if she matches a player 3, her expected payoff is pp_3Gc₁ + p(1 − p_3G)b₁ + (1 − p)p_3Bc₁ + (1 − p)(1 − p_3B)b₁. Since player 1 matches a player 2 with probability 1/2 and a player 3 with a probability 1/2, her expected payoff is:

$$\begin{array}{rll} \pi_1 &=& \frac{1}{2}\left[{\rm p}({\rm p}_{2{\rm G}} +{\rm p}_{3{\rm G}} ){\rm c}_1 +{\rm p}(2-{\rm p}_{2{\rm G}} -{\rm p}_{3{\rm G}} ){\rm b}_1 \right. \\ && \left.+\,(1-{\rm p})({\rm p}_{2{\rm B}}+{\rm p}_{3{\rm B}} ){\rm c}_1 +(1-{\rm p})(2-{\rm p}_{2{\rm B}} +{\rm p}_{3{\rm B}} ){\rm b}_1 \right]. \end{array} $$

The average gain of all 1-players is $\pi_1^{\rm m} ={\rm p}_1\pi_1 +(1-{\rm p}_1 )0$ and the growth rate of p₁ is $\dot{\rm p}_1 ={\rm p}_1 (1-{\rm p}_1 )\pi_1 ={\rm p}_1 (1-{\rm p}_1 )\frac{1}{2}[{\rm p}({\rm p}_{2{\rm G}} +{\rm p}_{3{\rm G}} ){\rm c}_1 +{\rm p}(2-{\rm p}_{2{\rm G}} -{\rm p}_{3{\rm G}} )\mbox{b}_1 +(1-{\rm p})({\rm p}_{2{\rm B}} +{\rm p}_{3{\rm B}}){\rm c}_1 +(1-{\rm p})(2-{\rm p}_{2{\rm B}} +{\rm p}_{3{\rm B}} ){\rm b}_1 ]$.

Consider now player 2^G. If he matches with a player 1, his expected payoff is p₁ (c₁ + ε). If he matches with a player 3, his expected payoff is pp_3G (c₂ + ε) + (1 − p)p_3B(c₂ + ε). Again, given player 2^G matches with a player 1 with a probability 1/2 and with a player 3 with a probability 1/2, his expected gain is:

$$ \pi_{2{\rm G}} =\frac{1}{2}(\mbox{c}_2 +\varepsilon )\left[{\rm p}_1+{\rm pp}_{3{\rm G}} +(1-{\rm p}){\rm p}_{3{\rm B}} \right]. $$

The average gain of all 2^G-players is:

$$ \pi_{2{\rm G}}^{\rm m} =\frac{1}{2}\left[{\rm p}_{2{\rm G}} ({\rm c}_2 +\varepsilon )+(1-{\rm p}_{2{\rm G}} )\mbox{b}_2 \right]\left[{\rm p}_1 +{\rm pp}_{3{\rm G}} +(1-{\rm p}){\rm p}_{3{\rm B}}\right] $$

and the growth rate of p_2G is:

$$ \dot{\rm p}_{2{\rm G}} ={\rm p}_{2{\rm G}} (1-{\rm p}_{2{\rm G}} )\frac{1}{2}({\rm c}_2 +\varepsilon -{\rm b}_2 )\left[{\rm p}_1 +{\rm pp}_{3{\rm G}} +(1-{\rm p}){\rm p}_{3{\rm B}} \right]. $$

Similarly, we deduce that:

$$ \dot{\rm p}_{2{\rm B}}={\rm p}_{2{\rm B}} (1-{\rm p}_{2{\rm B}} )\frac{1}{2}({\rm c}_2 +\beta -{\rm b}_2 )\left[{\rm p}_1 +{\rm pp}_{3{\rm G}} +(1-{\rm p}){\rm p}_{3{\rm B}} \right]. $$

Finally, consider a hybrid player 3^G. If acting as a buyer, his expected payoff is pp_2Gc₁ + p(1 − p_2G)b₁ + (1 − p)p_2Bc₁ + (1 − p)(1 − p_2B)b₁ and if acting as a supplier, his expected payoff is p₁ (c₂ + ε). Total expected gain is then:

$$\begin{array}{rll} \pi_{3{\rm{G}}} &=&\frac{1}{2}\left[{\rm p}_1 ({\rm c}_2 +\varepsilon )+\mbox{pp}_{2{\rm G}} {\rm c}_1 +{\rm p}(1-{\rm p}_{2{\rm G}} )\mbox{b}_1\right. \\&&\left.+\;(1-{\rm p}){\rm p}_{2{\rm B}} {\rm c}_1 +(1-{\rm p})(1-{\rm p}_{2{\rm B}})\mbox{b}_1 \right] \end{array} $$

and we deduce:

$$ \pi_{3{\rm G}}^{\rm m} ={\rm p}_{3{\rm G}} \pi_{3{\rm G}} +\frac{1}{2}(1-{\rm p}_{3{\rm G}} ){\rm p}_1 {\rm b}_2 . $$

The growth rate of p_3G is:

$$\begin{array}{rll} \dot{\rm p}_{3{\rm G}} &=& \frac{1}{2}{\rm p}_{3{\rm G}} (1-{\rm p}_{3{\rm G}})\left[{\rm p}_1 ({\rm c}_2 +\varepsilon -{\rm b}_2 )+{\rm pp}_{2{\rm G}} {\rm c}_1 \right. \\ && \left.+\;{\rm p}(1-{\rm p}_{2{\rm G}} ){\rm b}_1 +(1-{\rm p}){\rm p}_{2{\rm B}} {\rm c}_1 +(1-{\rm p})(1-{\rm p}_{2{\rm B}} )\mbox{b}_1 \right]. \end{array} $$

Similarly, we obtain:

$$\begin{array}{rll} \dot{\rm p}_{3{\rm B}} &=& \frac{1}{2}{\rm p}_{3{\rm B}} (1-{\rm p}_{3{\rm B}} )\left[{\rm p}_1 ({\rm c}_2 +\beta -{\rm b}_2 )+{\rm pp}_{2{\rm G}} {\rm c}_1\right. \\&&\left.+\;{\rm p}(1-{\rm p}_{2{\rm G}} )\mbox{b}_1 +(1-{\rm p}){\rm p}_{2{\rm B}} {\rm c}_1 +(1-{\rm p})(1-{\rm p}_{2{\rm B}} ){\rm b}_1 \right]. \end{array} $$

The Jacobian of the coefficient matrix of the above dynamics is the following:

$$ {\rm J(r)}=\left( {{\begin{array}{*{20}c} {\displaystyle\frac{\partial \dot{\rm p}_1 }{\partial {\rm p}_1 }} \hfill &{\displaystyle\frac{\partial \dot{\rm p}_1 }{\partial {\rm p}_{2{\rm G}} }} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_1 }{\partial {\rm p}_{{\rm 2B}} }} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_1 }{\partial {\rm p}_{{\rm 3G}} }} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_1 }{\partial {\rm p}_{{\rm 3B}} }} \hfill \\[15pt] {\displaystyle\frac{\partial \dot{\rm p}_{2{\rm G}} }{\partial {\rm p}_1 }} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{2{\rm G}} }{\partial {\rm p}_{2{\rm G}} }} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 2G}} }{\partial {\rm p}_{{\rm 2B}} }} \hfill &{\displaystyle\frac{\partial \dot{\rm p}_{{\rm 2G}} }{\partial {\rm p}_{{\rm 3G}} }} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 2G}} }{\partial {\rm p}_{{\rm 3B}} }} \hfill \\[15pt] {\displaystyle\frac{\partial \dot{\rm p}_{2{\rm B}} }{\partial {\rm p}_1 }} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{2{\rm B}}}{\partial {\rm p}_{2{\rm G}}}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 2B}}}{\partial {\rm p}_{{\rm 2B}}}} \hfill &{\displaystyle\frac{\partial \dot{\rm p}_{{\rm 2B}} }{{\rm p}_{3{\rm G}}}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 2B}} }{{\rm p}_{{\rm 3B}} }} \hfill \\[15pt] {\displaystyle\frac{\partial \dot{\rm p}_{3{\rm G}}}{\partial {\rm p}_1}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{3{\rm G}}}{\partial {\rm p}_{{\rm 2G}}}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 3G}}}{\partial {\rm p}_{{\rm 2B}}}} \hfill &{\displaystyle\frac{\partial \dot{\rm p}_{{\rm 3G}}}{\partial {\rm p}_{{\rm 3G}}}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 3G}}}{\partial {\rm p}_{{\rm 3B}}}} \hfill \\[15pt] {\displaystyle\frac{\partial \dot{\rm p}_{3{\rm B}}}{\partial {\rm p}_1}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 3B}}}{\partial {\rm p}_{{\rm 2G}}}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 3B}}}{\partial {\rm p}_{{\rm 2B}}}} \hfill &{\displaystyle\frac{\partial \dot{\rm p}_{{\rm 3B}}}{\partial {\rm p}_{{\rm 3G}}}} \hfill & {\displaystyle\frac{\partial \dot{\rm p}_{{\rm 3B}}}{\partial {\rm p}_{{\rm 3B}}}} \hfill \\ \end{array} }} \right) $$

For point r^∗ = (1,1,0,1,1), we obtain:

$$ \begin{array}{rll} && {\rm J}(1,\!1,\!0,\!1,\!1) \\ &&=\left( {{ \begin{array}{*{20}c} -\frac{ {\left[(1+\rm p){c}_1 +(1-\rm p){b}_1\right.}{2}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\[3pt] 0 \hfill & {-(\mbox{c}_2 +\varepsilon -{\rm b}_2 )} \hfill & 0 \hfill &0 \hfill & 0 \hfill \\[3pt] 0 \hfill & 0 \hfill & {(\mbox{c}_2 +\beta -{\rm b}_2 )} \hfill & 0 \hfill & 0 \hfill \\[3pt] 0 \hfill & 0 \hfill & 0 \hfill & {-\frac{[\mbox{c}_2 +\varepsilon -{\rm b}_2 +{\rm pc}_1 +(1-{\rm p}){\rm b}_1 ]}{2}} \hfill & 0 \hfill \\[3pt] 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {-\frac{[\mbox{c}_2 +\beta -{\rm b}_2 +{\rm pc}_1 +(1-{\rm p}){\rm b}_1 ]}{2}} \hfill \\ \end{array} }} \right) \end{array} $$

And we deduce that the eigenvalues are negatives if:

$$ (1+\mbox{p)c}_1 +(1-{\rm p)b}_1 >0 $$

(2)

$$ \mbox{c}_2 +\varepsilon -{\rm b}_2 >0 $$

(3)

$$ \mbox{c}_2 +\beta -{\rm b}_2 <0 $$

(4)

$$ \mbox{c}_{\rm 2} +\varepsilon -{\rm b}_2 +{\rm pc}_1 +(1-{\rm p}){\rm b}_1 >0 $$

(5)

$$ \mbox{c}_{\rm 2} +\beta -\mbox{b}_2 +{\rm pc}_{\rm 1} +(1-{\rm p}){\rm b}_1 >0. $$

(6)

By assumption, Eqs. 3 and 4 are always true and Eqs. 2, 5 and 6 lead to the following inequality:

$$ {\rm p}>\mbox{Max}\left( {\frac{-\mbox{b}_1 -{\rm c}_1 }{{\rm c}_1 -{\rm b}_1 },\frac{\mbox{b}_2 -{\rm c}_2 +\beta -{\rm b}_1 }{{\rm c}_1 -{\rm b}_1 },\frac{\mbox{b}_2 -{\rm c}_2 -\varepsilon -{\rm b}_1 }{\mbox{c}_1 -{\rm b}_1 }} \right). $$

Given the assumption of the model, we deduce that (1,1,0,1,1) is an ESS when:

$$ {\rm p}>\frac{\mbox{b}_2 -{\rm c}_2 +\beta -{\rm b}_1 }{{\rm c}_1 -{\rm b}_1 }. $$

For point r* = (1,1,0,1,0), the Jacobian is:

$$ \begin{array}{rll} &&\mbox{J}(1,\!1,\!0,\!1,\!0)\\&&=\left( {{\begin{array}{*{20}c} {-[\mbox{pc}_1 +(1-\mbox{p)b}_1 ]} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {\frac{(1+\mbox{p)(c}_2 +\varepsilon -\mbox{b}_2 )}{2}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\frac{(1+\mbox{p)(c}_2 +\beta -{\rm b}_2 )}{2}} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {-\frac{[\mbox{c}_2 +\varepsilon -{\rm b}_2 +{\rm pc}_1 +(1-{\rm p}){\rm b}_1 ]}{2}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\frac{[\mbox{c}_2 +\beta -{\rm b}_2 +{\rm pc}_1 +(1-{\rm p}){\rm b}_1 ]}{2}} \hfill \\ \end{array} }} \right) \end{array} $$

and we deduce that the eigenvalues are negatives if:

$$ \mbox{pc}_1 +(1-{\rm p})\mbox{b}_1 >0 $$

(7)

$$ \mbox{c}_2 +\varepsilon -{\rm b}_2 >0 $$

(8)

$$ \mbox{c}_2 +\beta -{\rm b}_2 <0 $$

(9)

$$ \mbox{c}_2 +\varepsilon -{\rm b}_2 +{\rm pc}_1 +(1-{\rm p})\mbox{b}_1 >0 $$

(10)

$$ \mbox{c}_2 +\beta -{\rm b}_2 +\mbox{pc}_1 +(1-{\rm p})\mbox{b}_1 <0. $$

(11)

Inequalities (8) and (9) are always true and we deduce from Eqs. 7, 10 and 11 that:

$$ \frac{\mbox{b}_2 -{\rm c}_2 -\beta -{\rm b}_1 }{{\rm c}_1 -{\rm b}_1 }>{\rm p}>{\rm Max}\left( {\frac{-\mbox{b}_1 }{{\rm c}_1 -{\rm b}_1 },\frac{\mbox{b}_2 -{\rm c}_2 -\varepsilon -{\rm b}_1 }{{\rm c}_1 -{\rm b}_1 }} \right). $$

Given − b₁ > b₂ − c₂ − ε − b₁, we deduce:

$$ \frac{\mbox{b}_2 -{\rm c}_2 -\beta -{\rm b}_1 }{{\rm c}_1 -{\rm b}_1 }>{\rm p}>\frac{-\mbox{b}_1 }{{\rm c}_1 -{\rm b}_1 } $$

which is the condition for (1,1,0,1,0) to be an ESS. End of the proof. □