Abstract
Cooperation in joint enterprises poses a social dilemma. How can altruistic behavior be sustained if selfish alternatives provide a higher payoff? This social dilemma can be overcome by the threat of sanctions. But a sanctioning system is itself a public good and poses a second-order social dilemma. In this paper, we show by means of deterministic and stochastic evolutionary game theory that imitation-driven evolution can lead to the emergence of cooperation based on punishment, provided the participation in the joint enterprise is not compulsory. This surprising result—cooperation can be enforced if participation is voluntary—holds even in the case of ‘strong altruism’, when the benefits of a player’s contribution are reaped by the other participants only.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Team efforts and other instances of ‘public good games’ display a social dilemma, since each participant is better off by not contributing to the public good. If players maximize their utility in a rational way, or if they simply imitate their successful co-players, they will all end up by not contributing, and hence fail to obtain a collective benefit (Samuelson 1954; Hardin 1968). It is only through positive or negative incentives directed selectively toward specific individuals in the team (e.g. by imposing sanctions on cheaters or dispensing rewards to contributors) that the joint effort can be maintained in the long run (Olson 1965; Ostrom 1990).
But how can the sanctioning system be sustained? It is itself a public good (Yamagishi 1986). This creates a ‘second order social dilemma’. By appealing to localised interactions (Brandt et al. 2003; Nakamaru and Iwasa 2005), group selection (Boyd et al. 2003), or the effects of reputation (Sigmund et al. 2001; Hauert et al. 2004) and conformism (Henrich and Boyd 2001), the stability of a well-established system of incentives can be explained under appropriate conditions. However, the emergence of such a system has long been considered an open problem (Hammerstein 2003; Gardner and West 2004; Colman 2006; see also Fowler 2005a).
A series of papers (Fowler 2005b; Brandt et al. 2006; Hauert et al. 2007; Boyd and Mathew 2007; Hauert et al. 2009) has recently attempted to provide a solution by considering team efforts which are non-compulsory. If players can decide whether to participate in a joint enterprise or abstain from it, then costly punishment can emerge and prevail for most of the time, even if the population is well-mixed. If the same joint effort game is compulsory, punishers fail to invade and defection dominates.
Roughly speaking, the joint enterprise is a venture. It succeeds if most players contribute, but not if most players cheat. The availability of punishment turns this venture into a game of cops and robbers. If the game is compulsory, robbers win. But if the game is voluntary, cops win.
This effect is due to a rock-paper-scissors type of cycle between contributing, defecting and abstaining. Players who do not participate in the joint enterprise can rely on some autarkic income instead. We shall assume that their income is lower than the payoff obtained from a joint effort if all contribute, but higher than if no one contributes. (Only with this assumption does the joint effort turn into a venture.) In a finite population, cooperation evolves time and again, although it will then be quickly subverted by defection, which in turn gives way to non-participation (Hauert et al. 2002a, b; Semmann et al. 2003). If costly punishment of defectors is included in the game, then eventually one of the upsurges of cooperation will lead to a population dominated by punishers, and such a regime will last considerably longer before defectors invade again. Cooperation safeguarded by the costly punishment of defectors dominates most of the time.
This model has been based on the classical ‘public good game’ used in many theoretical and experimental investigations (Boyd and Richerson 1992; Camerer 2003; Fehr and Gächter 2000, 2002; Hauert et al. 2007; Brandt et al. 2003; Nakamaru and Iwasa 2006). It suffers from a weakness which makes it less convincing than it could be. Indeed, whenever the interacting groups are very small (as happens if most players tend not to participate in the joint effort), the social dilemma disappears; it only re-appears when the game attracts sufficiently many participants. In a frequently used terminology, cooperation in such a public good game is ‘weakly altruistic’, because cooperators receive a return from their own contribution (Kerr and Godfrey-Smith 2002; Fletcher and Zwick 2004, 2007, see also Wilson 1990 for a related notion).
In this note, we show that the same result—in compulsory games, robbers win; in optional games, cops do—holds also for ‘strong altruism’, or more precisely in the ‘others-only’ case, i.e. when no part of the benefit returns to the contributor. It is always better, in that case, not to contribute. Nevertheless, cooperation based on costly punishment emerges, if players can choose not to participate. If the game is compulsory, defectors will win.
According to the ‘weak altruism’ model, players have to decide whether or not to contribute an amount c, knowing that the joint contributions will be multiplied by a factor r > 1 and then divided equally among all S participants. Rational players understand that if they invest an amount c, their personal return is rc/S. If the group size S is larger than r, their return is smaller than their investment, and hence they are better off by not contributing. In that case, we encounter the usual social dilemma: a group of selfish income maximizers will forgo a benefit, by failing to earn (r − 1)c each. The proverbial ‘invisible hand’ fails to work. However, if the group size S is smaller than r, selfish players will contribute, since the return from their personal investment c is larger than their investment. In that case, the social dilemma has disappeared.
In all the models of voluntary public good games mentioned so far, it has been assumed that a random sample of the population of size N is faced with the decision whether or not to participate in a game of the ‘weakly altruistic’ type described above. If most players tend not to participate, the resulting teams will mostly have a small size S, and therefore the social dilemma will not hold. (This effect of population size is well-known, see eg. Pepper 2000). Small wonder, then, that cooperation emerges in such a situation. A well-meaning colleague even called it a ‘sleight of hand’.
In the ‘strong altruism’ variant considered here, players have to decide whether or not to contribute an amount c, knowing that it will be multiplied by a factor r > 1 and then divided equally among all the other members of the group. A player’s contribution benefits the others only. The social dilemma always holds, in this case, no matter whether the group is large or small. We shall show that nevertheless, a rock-paper-scissor cycle leading to cooperation still emerges, and that the population will be dominated by players who punish defectors. This is a striking instance of the general phenomenon that complex dynamics can play an important role even in very simple types of economic models (see eg Kirman et al. 2004).
Before proceeding, a terminological remark is in order. The traditional term for the interactions we are considering is ‘public goods games’. For the variants discussed here, the term is misleading. Indeed, public goods are by definition non-excludable. Why should a player, in the ‘others only’ version, be prevented from using the result of the own contribution? Moreover, it goes against the definition of non-excludability to assume that players can abstain, or for that matter that they can be forbidden to use the good via ostracism, for instance. Instead of public goods game, we therefore use the term joint effort game, but want to emphasize that it is just a re-christening of a traditional model.
The idea of considering a joint effort game of ‘others only’ type is not new. It was used in Yamagishi (1986), a brilliant forerunner to Fehr and Gächter (2000). Yamagishi’s motivation was interesting: he made ‘public good game’ experiments using small groups (the small size is almost a necessity, due to practical reasons), but he wanted to address the issue of public goods in very large groups. Since in large groups, the effect of an individual decision is almost negligible, Yamagishi opted for a treatment which excludes any return from the own contribution.
In this paper, we investigate the evolutionary dynamics of voluntary joint effort games with punishment, using for the joint effort interaction the ‘others-only’ variant OO rather than the ‘self-returning’ (or ‘self-beneficial’) variant SR. We consider the evolutionary dynamics in well mixed populations which can either be infinite (in which case we analyze the replicator dynamics, see Hofbauer and Sigmund 1998), or of a finite size M (in which we case we use a Moran-like process, see Nowak 2006). We will show that for finite populations, voluntary participation is just as efficient for ‘strong altruism’ as for ‘weak altruism’. Thus even if the social dilemma holds consistently, cooperation based on costly punishment emerges.
In the usual scenarios, it is well-known that while weakly altruistic traits can increase, strongly altruistic traits cannot (see e.g. Kerr and Godfrey-Smith 2002). Our paper shows, in contrast, that strongly altruistic behavior can spread if players can inflict costly punishment on defectors and if they can choose not to participate in the team effort. In a sense to be explained later, the mechanism works even better than for weak altruism.
2 The model
We consider a well-mixed population, which is either infinite or of finite size M. From time to time, a random sample of size N is presented with the opportunity to participate in a ‘joint effort game’. Those who decline (the non-participants) receive a fixed payoff σ which corresponds to an autarkic income. Those who participate have to decide whether or not to contribute a fixed amount c. In the ‘self-returning’ case SR, the contribution will be multiplied by a factor r and the resulting ‘public good’ will be shared equally among all participants of the game; in the ‘others-only’ case OO, it will be shared among all the other participants of the game. (We note that in this case, if there are only two participants, we obtain a classical Prisonners’ Dilemma scenario, which can be interpreted as a donation game: namely whether or not to provide a benefit b = rc to the co-player at a cost c to oneself, with r > 1).
In both types of joint effort games, the participants obtain their share irrespective of whether they contributed or not (it is in this sense that the participants create a public good that is non-excludable within the group of participants). If only one player in the sample decides to participate, we shall assume that the joint effort game cannot take place. Such a player obtains the same payoff σ as a non-participant. This concludes the first stage of the interaction. In the second stage, participants in the game can decide to punish the cheaters in their group. Thus we consider four strategies: (1) non-participants; (2) cooperators, who participate and contribute, but do not punish; (3) defectors, who participate, but neither contribute nor punish; and (4) punishers, who participate, contribute, and punish the defectors in their group. Needless to say, other strategies could also be investigated. We return to this issue in the discussion. The relative frequencies of cooperators, defectors, non-participants and punishers in the infinite population will be denoted by x,y,z and w, and their numbers in the finite population by X,Y,Z and W, respectively (with X + Y + Z + W = M, and x + y + z + w = 1). Their frequencies in a given random sample of size N are denoted by N x ,N y ,N z and N w respectively (with N x + N y + N z + N w = N, and N x + N y + N w = S the number of participants in the public good game).
Following the usual models, we shall assume that in the second stage of the game, each punisher imposes a fine β on each defector, at some cost γ, so that punishers have to pay γN y and defectors βN w . The total payoff is the sum of a ‘public good term’ (which covers the first stage of the interaction) and a punishment term (which covers the second stage).
3 The infinite population case
Let us assume first that the population size is infinite. Each players’ payoff is the sum of a public good term (which is σ if the player does not participate in the joint effort) and a punishment term (which is 0 for non-participants and cooperators). The expected punishment terms are easily seen to be − βw(N − 1) for the defectors and − γy (N − 1) for the punishers.
As shown in Brandt et al. (2006), the public good term of the payoff is given in the SR case by
for the defectors, and
for the cooperators and the punishers, with
The payoff for non-participants is σ. As shown in the Appendix, the return from the joint effort in the OO case is
which is the public good term for defectors. The public good term for cooperators and punishers is the same term, reduced by \(c\big(1-z^{N-1}\big)\) (this is the cost of contributing, given that there is at least one co-player).
Let us now consider the replicator dynamics for the OO-case. After removing the common term σz N − 1 from all payoffs, we obtain for the expected payoff values of non-participants, defectors, cooperators and punishers
In the interior of the simplex S 4 there is no fixed point since P w < P x . Hence all orbits converge to the boundary (see Hofbauer and Sigmund 1998). On the face w = 0, we find a rock-paper-scissors game, as in the SR case: non-participants are dominated by cooperators who are dominated by defectors who are dominated by non-participants again. In the interior of this face there is no fixed point, since P x < P y ; all orbits are homoclinic orbits, converging to the non-participant state z = 1 if time converges to ± ∞ (see Fig. 1). This contrasts with the SR case, where the face w = 0 is filled with periodic orbits for r > 2 (see also the corresponding phase portraits in Brandt et al. 2006).
The replicator equation for the OO-case. Part a shows the phase portrait on the boundary faces of the state space simplex S 4. Part b shows what happens in the interior of the simplex. Bright orbits converge to the state z of only non-participants, despite the local instability of this fixed point. Dark orbits converge to a cooperative mixture of punishers w and cooperators x. The starting points of the orbits are depicted in gray. Parameter values are N = 5, r = 3, c = 1, β = 1.2, γ = 1 and σ = 1
It is easy to see that punishers dominate non-participants, and that punishers and defectors form a bistable system if c + γ < β(N − 1). The edge of cooperators and punishers (y = z = 0) consists of fixed points, those with
are saturated and hence Nash-equilibria.
Altogether, this system has a remarkable similarity with the replicator system for SR originally proposed by Fowler (2005b) (and criticized by Brandt et al. 2006), provided Fowler’s second-order punishment term is neglected.
4 Finite populations
We now turn to finite populations of size M. As learning rule, we shall use the familiar Moran-like process: we assume that occasionally, players can update their strategy by copying the strategy of a ‘model’, namely a player chosen at random with a probability which is proportional to that player’s fitness. This fitness in turn is assumed to be a convex combination (1 − s)B + sP, where B is a ‘baseline fitness’ (the same for all players), P is the payoff (which depends on the strategy, and the state of the population), and 0 ≤ s ≤ 1 measures the ‘strength of selection’, i.e. the importance of the game for overall fitness. We shall always assume s small enough to avoid negative fitness values. This learning rule corresponds to a Markov process. We note that in the limiting case of an infinite population, the rate for switching from strategy j to strategy i is (1 − s)B + sP i (with i,j ∈ {x,y,z,w}), independently of j, see Traulsen et al. (2005). According to Hofbauer and Sigmund (1998), this leads to the replicator equation. For finite populations, the Markov process has four absorbing states, namely the homogeneous states: if all players use the same strategy, imitation leads to nothing new. Hence we assume that with a small ‘mutation probability’ μ, players chose a strategy at random, rather than imitate another player. This yields an irreducible Markov chain with a unique stationary distribution. (We emphasize that the terms ‘selection’ and ‘mutation’ are used for convenience only, and do not imply a genetic transmission of strategies.)
In the limiting case of small mutation rates μ < < M − 2, we can assume that the population consists, most of the time, of one type only. Mutants occur rarely, and will be eliminated, or have reached fixation, before the next mutation occurs. Hence we can study this limiting case by an embedded Markov chain with four states only. These are the four homogeneous states, with the population consisting of only cooperators, only defectors, only non-participants or only punishers, respectively. It is now easy to compute the transition probabilities. For instance, ρ xy denotes the probability that a mutant defector can invade a population of cooperators and reach fixation. The corresponding stationary distribution (π x , π y , π z , π w ) describes how often (on average) the population is dominated by cooperators, defectors etc.
The transition probabilities are given by formulas of the type
where P XY denotes the payoff obtained by a cooperator in a population consisting of X cooperators and Y = M − X defectors (see Nowak 2006). Hence all that remains is to compute these expressions. Again, these payoffs consist of two terms: the contribution from the public good round, and those from the punishment round.
Clearly, if there are W punishers and Y defectors (with W + Y = M), the former must pay γY(N − 1)/(M − 1) and the latter βW(N − 1)/(M − 1) on average.
The payoff obtained from the public good term has been computed in Hauert et al. (2007) for the SR-case. We now compute it for the OO-case. In a population consisting of X cooperators and Y = M − X defectors, a co-operator obtains
Defectors in a population of Y defectors and X = M − Y cooperators (or punishers) obtain from the public good
The probability to be the only participant in the sample is
where Z k : = Z(Z − 1)...(Z − k + 1). Hence in a population with Z non-participants, if the rest is composed only of punishers (or of cooperators), the participants obtain from the public good
In a population consisting only of punishers and cooperators, the public good term of the payoff is
We can now compute the stationary distributions. As shown in Figs. 2 and 3, the outcome is clear: in the compulsory case, defectors take over; in the optional case, punishers dominate. The results are derived for the limiting case of very small mutation rates (μ < < M − 2), but computer simulations show that they are valid for larger mutation rates too. In interactive computer simulations (see for instance http://www.wu-wien.ac.at/usr/ma/hbrandt/simulations.html and http://www.univie.ac.at/virtuallabs/), it is possible to experiment with different parameter values (for M, N, σ, r, c, β and γ) and with other learning processes, which provide convincing evidence that the outcome is robust. We note in particular that punishers are even more frequent for the strongly altruistic ‘others-only’ scenario than for the weakly altruistic ‘self-returning’ variant. The reason behind this seems to be that the cooperators are less frequent in the OO-case (and each percent they lose is gained by the punishers). Why are they less frequent? In the SR case, cooperators can invade non-participants more easily, since they do get a return for their contribution. However, such an invasion has no lasting effect, because the cheaters can quickly replace the cooperators. All that these short episodes of cooperation without punishment achieve is that they stand in the way of cooperation with punishment.
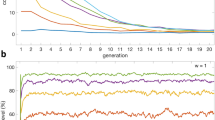
Time evolution of the frequencies in a finite population a if all four strategies are allowed and b if the game is compulsory, i.e. if there are no non-participants. We see that in the latter case, defectors quickly come to near-fixation; in the former case, a rock-paper-scissors type of cycle leads eventually to a cooperative regime dominated by punishers, which lasts for a long time. (It will eventually by subverted through random drift, in which case the oscillations start again). (Parameter values as in Fig. 1 with M = 100, μ = 0.001, B = 1, s = 0.1)
The frequencies of strategies in the stationary distribution, as a function of the selection strength s. a In the case of weak altruism, the punisher’s strategy is the most frequent; b this also holds for strong altruism, with the additional feature that non-punishing cooperators are even less frequent; c if the game is compulsory (i.e. non-participants are excluded from the simulations), the defectors emerge as clear winners. This is shown here for the case of strong altruism, the weak-altruism case is similar. The lines describe the frequencies as computed in the limiting case μ→0. The dots describe the results of numerical simulations averaged over 107 periods for μ = 0.001. Parameter values are M = 100, N = 5, r = 3, c = 1, β = 1, γ = 0.3 , σ = 1 and B = 1
5 Discussion
As we have shown, individual-based selection can lead to the emergence of cooperation based on punishment, even in situations of so-called ‘strong altruism’ (in particular, when the own contribution yields zero benefit to contributors, and only entails costs). This requires that the participation to the joint effort is voluntary, rather than compulsory.
We have dealt with a model which has been frequently used and by now can almost be viewed as traditional. It may be appropriate here to stress its limitations. First of all, peer-punishment of cheaters is certainly not the only way to promote cooperation in a joint effort. Other forms of sanctions are possible, and so are positive incentives (for instance, through additional rounds of indirect reciprocity, see Milinski et al. 2002 and Panchanathan and Boyd 2006). The threat of ostracizing defectors from future joint effort games is also very effective, see Güth et al. (2007)). As mentioned already in Hauert et al. (2007), the connection between ostracism cheaters and voluntary abstention from a joint effort demands to be studied.
Second, the restricted number of strategies is a feature justified only by the need to simplify the analysis. Many more strategies are conceivable. For instance, the decision to participate or not, or to punish or not, could depend on the number of like-minded players in the sample. Defectors could punish other players, or retaliate against punishment. Punishers could also punish non-participants, or cooperators who do not punish (second-order punishment). However, numerical simulations for the self-returning case have shown that these effects are usually small. In particular, second-order punishers can single out cooperators unwilling to punish only if there are defectors around: this requires the simultaneous presence of three types, which is unlikely in a finite population if μ is sufficiently small. Moreover, experimental evidence for second-order punishment is rather scarce. Nevertheless, it would be interesting to include other strategies into the analysis of joint effort games.
Punishment of free riders is widespread in human societies (Ostrom 1990; Ostrom and Walker 2003; Henrich et al. 2006; Sigmund 2007). The main result of our paper is that a joint effort game with punishment is much more likely to lead to a cooperative outcome if participation is voluntary, rather than compulsory. For the ‘weakly altruistic’ SR case, this is well established, see Hauert et al. (2007, 2009). But here, we show that it also holds in the ‘strongly altruistic’ OO-case, i.e. if the benefit of a contribution is exclusively directed at others.
The mechanism thus operates without a ‘sleight of hand’. The fact that in sufficiently small groups playing the SR public goods game, it is in the selfish interest of a player to contribute, is not essential. Even if the social dilemma is unmitigated, as in the OO case, voluntary participation allows cooperators to emerge again and again from a population of non-participants. Indeed, if non-participants are frequent, the random samples of N players will usually provide only small groups willing to participate in the public goods game. In such small groups, it can happen by chance that most members contribute. These groups will have a high payoff and their members will be quickly imitated.
This is an instance of the well-known Simpson’s paradox (see Sober and Wilson 1998): although within each group, free-riders do better than contributors, in can happen that on average, across the whole population, contributors do better than free-riders. A similar effect also holds in a model of Killingback et al. (2006): in that scenario, the population is structured in groups of variable size, with dispersal between groups, whereas our model considers individual selection in a well-mixed population. For other investigations of the effect of finite population size and stochastic shocks, see e.g. (Peyton Young and Foster 1995).
Non-punishing cooperators can invade a population of non-participants. However, this state will quickly be invaded by defectors, who in turn foster non-participation. But the resulting rock-paper-scissors cycle, which can be viewed as an extremely simple model of an endogenous business cycle (cf Dosi et al. 2006), will eventually lead from non-participants to punishers (rather than to non-punishing cooperators). In that case defectors will have a much harder time to come back.
In their lucid discussion of strong vs. weak altruism, Fletcher and Zwick (2007) argue that what counts for selection are fitness differences, i.e. relative fitnesses rather than absolute fitnesses (cf Hamilton 1975 and Wilson 1975). Although with weak altruism (which has been called ‘benevolence’ by Nunney 2000), a contribution directly benefits the contributor, it benefits the co-players just as well. Even if the return to the contributor exceeds the cost of the contribution, defectors in the public goods group are still better off. In this sense, the difference between weak and strong altruism is less than may appear, despite the ‘conventional wisdom’ (Fletcher and Zwick 2007) stating that under the usual assumptions, weak altruism evolves and strong altruism does not.
In particular, while most models leading to cooperation assume weak altruism, Fletcher and Zwick (2004) have shown that strong altruism can prevail in public goods games of ‘others-only’ type if groups are randomly reassembled, not every generation, but every few generations. Our scenario emphasizes a different, but related point. In voluntary public goods games with punishment, for strong and weak altruism alike, cooperation can emerge through individual selection.
References
Boyd R, Mathew S (2007) A narrow road to cooperation. Science 316:1858–1859
Boyd R, Richerson RJ (1992) Punishment allows the evolution of cooperation (and anything else), in sizable groups. Ethol Sociobiol 13:171–195
Boyd R, Gintis H, Bowles S, Richerson P (2003) The evolution of altruistic punishment. Proc Natl Acad Sci USA 100:3531–3535
Brandt H, Hauert C, Sigmund K (2003) Punishment and reputation in spatial public goods games. Proc R Soc B 270:1099–1104
Brandt H, Hauert C, Sigmund K (2006) Punishing and abstaining for public goods. Proc Natl Acad Sci USA 103(2):495–497
Camerer C (2003) Behavioural game theory: experiments in strategic interactions. Princeton University Press, Princeton
Colman A (2006) The puzzle of cooperation. Nature 440:744–745
Dosi G, Fagiolo G, Roventini A (2006) An evolutionary model of endogenous business cycles. Comput Econ 27:3–34
Fehr E, Gächter S (2000) Cooperation and punishment in public goods experiments. Am Econ Rev 90:980–994
Fehr E, Gächter S (2002) Altruistic punishment in humans. Nature 415:137–140
Fletcher JA, Zwick M (2004) Strong altruism can evolve in randomly formed groups. J Theor Biol 228:303–313
Fletcher JA, Zwick M (2007) The evolution of altruism: game theory in multilevel selection and inclusive fitness. J Theor Biol 245:26–36
Fowler JH (2005a) The second-order free-rider problem solved? Nature 437:E8
Fowler JH (2005b) Altruistic punishment and the origin of cooperation. Proc Natl Acad Sci USA 102(19):7047–7049
Gardner A, West SA (2004) Cooperation and punishment, especially in humans. Am Nat 164:753–764
Güth W, Levati MV, Sutter M, van der Heijden E (2007) Leading by example with and without exclusion power in voluntary contribution experiments. J Public Econ 91:1023–1042
Hamilton WD (1975) Innate social aptitudes of man: an approach from evolutionary genetics. In: Fox R (ed) Biosocial anthropology. Wiley, New York, pp 133–155
Hammerstein P (ed) (2003) Genetic and cultural evolution of cooperation. MIT, Cambridge
Hardin G (1968) The tragedy of the commons. Science 162:1243–1248
Hauert C, De Monte S, Hofbauer J, Sigmund K (2002a) Volunteering as a red queen mechanism for cooperation. Science 296:1129–1132
Hauert C, De Monte S, Hofbauer J, Sigmund K (2002b) Replicator dynamics for optional public goods games. J Theor Biol 218:187–194
Hauert C, Haiden N, Sigmund K (2004) The dynamics of public goods. Discrete Continuous Dyn Syst Ser B 4:575–585
Hauert C, Traulsen A, Brandt H, Sigmund K, Nowak MA (2007) Via freedom to coercion: the emergence of costly punishment. Science 316:1905–1907
Hauert C, Traulsen A, De Silva H, Nowak MA, Sigmund K (2009) Public goods with punishment and abstaining in finite and infinite populations. Biol Theor 3(2):114–122
Henrich J, Boyd R (2001) Why people punish defectors? J Theor Biol 208:79–89
Henrich J et al (2006) Costly punishment across human societies. Science 312:1767–1770
Hofbauer J, Sigmund K (1998) Evolutionary games and population dynamics. Cambridge University Press, Cambridge
Kerr B, Godfrey-Smith P (2002) Individualist and multi-level perspectives on selection in structured populations. Biol Philos 17:477–517
Killingback T, Bieri J, Flatt T (2006) Evolution in group-structured populations can solve the tragedy of the commons. Proc R Soc B 273:1477–1481
Kirman A, Gallegatti M, Marsili P (eds) (2004) The complex dynamics of economic interaction. Springer, Heidelberg
Milinski M, Semmann D, Krambeck HJ (2002) Reputation helps solve the tragedy of the commons. Nature 415:424–426
Nakamaru M, Iwasa Y (2005) The evolution of altruism by costly punishment in lattice-structured populations: score-dependent viability vs score-dependent fertility. Evol Ecol Res 7:853–870
Nakamaru M, Iwasa Y (2006) The coevolution of altruism and punishment: role of the selfish punisher. J Theor Biol 240:475–488
Nowak M (2006) Evolutionary dynamics. Harvard University Press, Harvard Mass
Nunney L (2000) Altruism, benevolence and culture: commentary discussion of Sober and Wilson’s ‘Unto Others’. J Conscious Stud 7:231–236
Olson M (1965) The logic of collective action. Harvard University Press, Cambridge
Ostrom E (1990) Governing the commons. Cambridge University Press, New York
Ostrom E, Walker J (2003) Trust and reciprocity: interdisciplinary lessons from experimental research. Russell Sage Foundation, New York
Panchanathan K, Boyd R (2006) Indirect reciprocity can stabilize cooperation without the second-order free rider problem. Nature 432:499–502
Pepper JW (2000) Relatedness in trait group models of social evolution. J Theor Biol 206:355–368
Peyton Young H, Foster D (1995) Learning dynamics in games with stochastic perturbations. Games Econom Behav 11:330–363
Samuelson PA (1954) The pure theory of public expenditure. Rev Econ Stat 36:387–389
Semmann D, Krambeck H-J, Milinski M (2003) Volunteering leads to rock-paper-scissors dynamics in a public goods game. Nature 425:390–393
Sigmund K (2007) Punish or perish? Retaliation and collaboration among humans. Trends Ecol Evol 22:593–600
Sigmund K, Hauert C, Nowak M (2001) Reward and punishment. Proc Natl Acad Sci USA 98:10757–10762
Sober E, Wilson DS (1998) Unto others. The evolution and psychology of unselfish behaviour. Harvard University Press, Cambridge
Traulsen A, Claussen JC, Hauert C (2005) Evolutionary dynamics: from finite to infinite populations. Phys Rev Lett 95:238701
Wilson DS (1975) A theory of group selection. Proc Natl Acad Sci 72:143–146
Wilson DS (1990) Weak altruism, strong group selection. Oikos 59:135–140
Yamagishi T (1986) The provision of a sanctioning system as a public good. J Pers Soc Psychol 51:110–116
Acknowledgements
We thank Martin Nowak for helpful discussions. Part of this work is funded by EUROCORES TECT I-104 G15. C.H. is supported by the John Templeton Foundation, NSERC, and the NSF/NIH joint program in mathematical biology (NIH grant R01GM078986). A.T. is supported by the Emmy-Noether program of the DFG.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
In the OO case, the public goods term of the payoff can be computed as follows: The probability that a focal player has h co-players who participate is
for h = 0,...,N − 1. The probability that m of these are contributing is
for m = 0,...,h (if h > 0).
The focal player’s expected gain stemming from the h co-participants is
which is independent of h (for h = 1,...,N − 1).
Hence the payoff obtained from the joint effort is given by
for a defector. Cooperators and punishers obtain as public goods term the same, reduced by \(c\big(1-z^{N-1}\big)\).
We now compute the public goods terms for the finite OO-case. In a population of size M with m i individuals of type i and m j = M − m i of type j, the probability to select k individuals of type i and N − k individuals of type j in N trials is
Therefore, in a population consisting of X cooperators and Y = M − X defectors, a co-operator obtains (if k is the number of other cooperators)
Since the first sum is \((X-1)\frac {N-1}{M-1}\) and the second is 1, this yields
Defectors in a population of Y defectors and X = M − Y cooperators or punishers obtain from the public good
The probability to be the only participant in the sample is
Hence in a population with Z non-participants, if the rest is composed only of punishers (or of cooperators), the participants obtain from the public good
In a population consisting only of punishers and cooperators, the public good term of the payoff is
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
De Silva, H., Hauert, C., Traulsen, A. et al. Freedom, enforcement, and the social dilemma of strong altruism. J Evol Econ 20, 203–217 (2010). https://doi.org/10.1007/s00191-009-0162-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00191-009-0162-8
Keywords
- Evolutionary game theory
- Public goods games
- Cooperation
- Costly punishment
- Social dilemma
- Strong altruism
- Voluntary interactions